Ultra-small PbS nanocrystals as sensitizers for red-to-blue triplet-fusion upconversion

Abstract

Photon upconversion is a strategy to generate high-energy excitations from low-energy photon input, enabling advanced architectures for imaging and photochemistry. Here, we show that ultra-small PbS nanocrystals can sensitize red-to-blue triplet-fusion upconversion with a large anti-Stokes shift (ΔE = 1.04 eV), and achieve max-efficiency upconversion at near-solar fluences (I_th = 220 mW cm⁻²) despite endothermic triplet sensitization. This system facilitates the photo-initiated polymerization of methyl methacrylate using only long-wavelength light (λ_exc: 637 nm); a demonstration of nanocrystal-sensitized upconversion photochemistry. Time-resolved spectroscopy and kinetic modelling clarify key loss channels, highlighting the benefit of long-lifetime nanocrystal sensitizers, but revealing that many (48%) excitons that reach triplet-extracting carboxyphenylanthracene ligands decay before they can transfer to free-floating acceptors—emphasizing the need to address the reduced lifetimes that we determine for molecular triplets near the nanocrystal surface. Finally, we find that the inferred thermodynamics of triplet sensitization from these ultra-small PbS quantum dots are surprisingly favourable—completing an advantageous suite of properties for upconversion photochemistry—and do not vary significantly across the ensemble, which indicates minimal effects from nanocrystal heterogeneity. Together, our demonstration and study of red-to-blue upconversion using ultra-small PbS nanocrystals in a quasi-equilibrium, mildly endothermic sensitization scheme offer design rules to advance implementations of triplet fusion, especially where large anti-Stokes wavelength shifts are sought.

---

Introduction

Triplet-fusion upconversion (TUC) is an emerging strategy for generating high-energy photons from incoherent long-wavelength light at low fluences.^1,2 TUC takes advantage of the long lifetimes of molecular spin-triplet excitons to build sufficient excited-state population to favour the bimolecular fusion of spin-triplet excitons over parasitic monomolecular decay channels.^2,3 However, because of their oft-negligible electric dipole,^4,5 molecular triplets are commonly generated using a sensitizer⁶via sequential photon absorption, spin-dephasing, and triplet energy transfer (TET) to a molecular acceptor.⁷ Examples of sensitizers include coordination complexes, due to their strong absorption bands and high triplet yield via intersystem crossing,^6,8–15 as well as colloidal quantum dots (QDs),^16–23 metal-halide perovskite films and nanocrystals,^24–26 and materials containing lanthanide atoms.^5,27 Triplet fusion (TF) occurs when the energy from two or more triplet-excited acceptors are combined to yield a higher-energy excited state, which may generate a spin-singlet excitation capable of emitting a photon.^1,6,9,28,29

Importantly, it was recently demonstrated that triplet-fusion upconversion can enable photochemical transformations using incident long-wavelength light at low fluences appropriate for tissue penetration.^{13,14,30–32} This is motivating an exploration of photochemical and biomedical applications, where large anti-Stokes shift upconversion could permit targeted drug-delivery without the non-specific photochemistry that accompanies the use of direct ultraviolet excitation.³¹ Thus, red-to-blue upconversion—achieving large anti-Stokes shift while creating excited states with enough energy (≈3.0 eV) to make and break chemical bonds—has emerged as an important step towards applications.^{6,12,23,33–35}

Triplet sensitization using QDs is an increasingly common strategy to achieve triplet-fusion upconversion (TUC) due to latent advantages such as their size-tunable optical gap, large molar absorption cross-section, rapid/near-isoergic spin-dephasing, and modifiable surface chemistry.^{16–23,34,36–40} By combining these properties with the long intrinsic lifetimes of triplet excitons on many molecular chromophores, TUC performance has been able to access new performance regimes of incident wavelength, anti-Stokes shift, quantum yield, and low-threshold operation.^{18,20,23,40,41} Specifically, lead sulfide (PbS) QDs possess advantageously long excited-state lifetimes compared to other commonly employed semiconductor nanocrystals.^38,42 However, PbS QDs are typically used as near- and short-wave infrared (NIR, SWIR) absorbers/emitters,^19,43,44 in part because of challenges in the synthesis of ultra-small particles with optical gaps in the visible regions of the electromagnetic spectrum. Recently, we showed that PbS QDs can be made sufficiently small to display optical gaps greater than ∼1.70 eV (λ: 560–730 nm, measured at the peak of the lowest-energy excitonic feature in the absorption spectrum), while conserving the narrow ensemble linewidths required for optoelectronic applications.^45,46 This synthetic advance allows PbS QDs to align energetically with the triplet exciton energies of commonly used deep-blue-emitting (λ_em < 450 nm) fluorophores for triplet-fusion upconversion, including the ubiquitous diphenylanthracene (DPA).

Harnessing these recent advances, we now demonstrate successful red-to-blue TUC using ultra-small PbS QDs as red-light (λ = 637 nm) absorbers and achieve a maximum anti-Stokes shift of ΔE = 1.04 eV. We present proof-of-concept results showing the applicability of this composite upconversion system to photochemistry by initiating the polymerization of methyl methacrylate (MMA) via excitation at λ_exc = 637 nm. We observe promising, near-solar intensity, max-efficiency thresholds as a direct benefit of the long excited-state lifetimes of PbS QDs. Time-resolved photoluminescence spectroscopy (TRPL) and kinetic modelling accurately capture the quasi-equilibrium dynamics of the mildly endothermic triplet energy transfer process to exciton-extracting ligands, and highlight unexpected research avenues for future performance improvements. Finally, we show that the excited-state equilibrium between sensitizing QDs and surface-bound acene acceptors is remarkably consistent across the ensemble emission spectrum of these ultra-small QDs, indicating that heterogeneous contributions to the fluorescence linewidth are minimal, even in these exceptionally small nanocrystals. Taken together, our results show that ultra-small PbS QDs are useful sensitizers of molecular triplets—even with energies up to 1.8 eV, thereby capable of generating blue light (λ_em < 450 nm) after fusion—highlighting the general importance of the sensitizer excited-state lifetime when striving for TUC with a maximal anti-Stokes shift.

Results & discussion

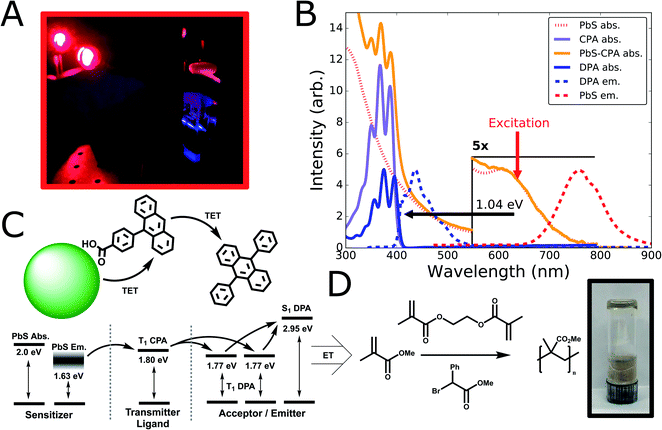
To test the suitability of ultra-small PbS QDs for photon upconversion, we studied a standard TUC system comprised of QD sensitizers functionalized with exciton-extracting ligands, and a free-floating emitter.^16,17 Materials and methods for synthesis and fabrication are described in detail in the ESI.† In brief, we synthesized ultra-small PbS QDs (d ∼ 1.9 nm) with the aide of an oleylamine additive as we have reported previously.⁴⁶ Post-synthesis, the native oleic acid ligands were partially exchanged with carboxyphenyl-anthracene (CPA) ligands (synthesized as previously described;⁴⁷ see ESI Section 1 for details†), chosen for their expected triplet energy level and previous demonstrations as exciton extractors.⁴⁷ Subsequently, we prepared upconversion solutions by combining the hybrid PbS-CPA sensitizer with the canonical diphenylanthracene (DPA) annihilator/emitter.⁶

From these solutions, we observe blue upconverted emission upon excitation at λ_exc = 637 nm (Fig. 1A), consistent with the expected absorption and emission energies from steady-state optical spectra (Fig. 1B). The ultra-small PbS QDs used in this study exhibit a first excitonic absorption peak centered at λ = 620 nm (hν = 2.0 eV; Fig. 1B) and broad photoluminescence centered at λ = 760 nm (Fig. 1B). These linewidths are comparable to the narrowest reported for ultra-small PbS QDs,⁴⁶ for which an estimated upper-bound on the size-dispersity is 7%.^46,48Fig. 1B displays the absorption spectrum of CPA in solution as well as the composite PbS-CPA QDs, where characteristic features of the CPA absorption are clearly visible after ligand exchange and purification (Fig. 1B, and S1†). By selectively exciting the PbS QDs at λ_exc = 637 nm, blue UC emission from DPA is readily observed spectroscopically (λ = 415–500 nm, Fig. 1B; and S2†) and photographically (Fig. 1A), achieving a maximum anti-Stokes shift of 1.04 eV from the excitation wavelength to the 0–0 shoulder of the DPA fluorescence. Control experiments show that parasitic FRET from DPA to the PbS QDs is not a significant decay channel, but that the intensity of the 0–0 feature in the DPA emission is attenuated in UC solutions due to far-field photon reabsorption by QDs (Fig. S2 and S3†). Together, these data are the first report of red-to-blue TUC (i.e. upconverted emission λ < 500 nm) sensitized by PbS QDs.

Fig. 1 (A) Photo of blue (λ_peak = 430 nm) upconverted emission upon excitation at λ_exc= 637 nm, taken through a λ: 500 nm shortpass optical filter (B) steady-state absorption and emission spectroscopy of relevant materials in this study. The absorption spectra of native PbS and PbS-CPA QDs are normalized at λ: 620 nm (and the QD fluorescence scaled to the same value), and the region near the QD excitonic peak is magnified 5-fold relative to the remainder of the spectra for closer inspection. (C) Schematic of the triplet-fusion upconversion system employed in this study. Sensitizing QDs absorb incident light (λ_exc = 637 nm) and transfer excitations to the lowest-energy triplet state of CPA ligands, which in turn sensitizes free-floating DPA. (D) Reaction scheme of photoinitiated MMA polymerization after electron/energy transfer (ET) from singlet-excited DPA generated via triplet fusion.

The energetic scheme (Fig. 1C) displays the expected energetic pathways and highlights the ambiguous thermodynamics of the exciton transfer from the QD to the ligand. By a conventional measure,^16,18 taken from the peak of the QD emission spectrum (hν ∼ 1.63 eV) to the expected energy of the triplet state of the CPA extractor ligands (hν ∼ 1.80 eV),^16,47 this transfer is significantly endothermic (∼6kT). However, it has been proposed that the anomalously large Stokes shifts in ultra-small metal-chalcogenide nanocrystals arise from considerable ground-state exciton–phonon coupling in fluorescence,^49–55 and it is unclear that exchange-mediated transfer to a molecular chromophore would experience the same selection rules. To aid subsequent discussion, Fig. 1C also displays the lowest-lying excitonic absorption peak of the ground-state QD (hν ∼ 2.0 eV) as an upper bound on the energy of a thermalized exciton. Though we cannot rule out a small amount of transfer from the ‘hot’ excited state formed immediately after photon absorption, we observe that the photoluminescence quantum yield (PLQY) of CPA-functionalized QDs is wavelength-independent in this region (Table S1 and Fig. S4†), which is consistent with previous demonstrations that thermalization is rapid (∼ps) in larger PbS nanocrystals.⁵⁶

To explore the photochemical potential of this novel red-to-blue TUC system, we combined it with the requisite reagents for the atom transfer radical polymerization (ATRP) of methyl methacrylate (MMA) using a photoinitiator and a cross-linking additive (Fig. 1D; see ESI for Methods†). We observe the formation of poly (methyl methacrylate) (PMMA) gel after excitation at λ = 637 nm for 30 minutes (Fig. 1D, photo inset), validating the concept of QD-sensitized TUC-mediated photocatalysis. Control experiments where either the sensitizing PbS-CPA nanocrystals or DPA are removed show no gel formation (Fig. S5†), consistent with previous reports that achieve photoinitiation via upconversion,^13,30,32 or via direct excitation with higher-energy photons.^57,58 Thus, we observe that the higher-energy DPA spin-singlet excited state generated via triplet fusion is able to activate the homolytic cleavage of the initiator, in line with other recent demonstrations of TUC-mediated photochemistry with other material systems.^13,14,30 Notably, the low concentrations (4 μM) of PbS used in this polymerization reaction were consistent with other TUC-mediated photochemistry systems,^13,14 as well as direct QD-catalyzed polymerizations.⁵⁷ Given the susceptibility of these ultra-small QDs to degrade in the presence of an active radical catalyst, future work should be focused towards other photochemical transformations,^13,31,59 stabilizing QD sensitizers to these reaction conditions,⁵⁷ and improvements to the overall efficiency of this photochemical reaction via optimization of sensitizer and annihilator concentrations , which may improve the maximum upconversion quantum efficiency (UCQE) for this system.

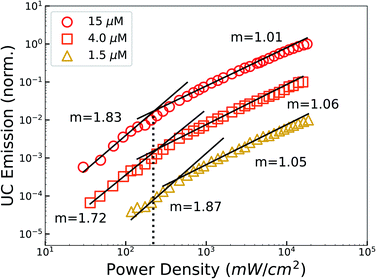
The bimolecular nature of TUC causes the emission intensity to vary with the incident photon flux, exhibiting a quadratic-to-linear power dependence as excitation power is increased and bimolecular recombination becomes dominant.² The requisite incident intensity threshold (I_th) to reach this linear regime—where UC efficiency is maximized—is an important performance metric.^2,3 Thus, we measured the power dependence of UC emission at different sensitizer concentrations to evaluate the performance of PbS QDs (Fig. 2). Most notably, we observed a max-efficiency threshold as low as I_th = 220 mW cm⁻² (∼2× the integrated AM1.5 irradiance), achieved at the highest sensitizer concentration studied (15 μM). From these levels, a 4-fold decrease in sensitizer concentration (4 μM) only marginally elevates the threshold (245 mW cm⁻²), indicating that these sensitizer concentrations approach the useful limit due to the saturation of photon absorption and rise of parasitic decay channels.⁶⁰ However, the intensity threshold quickly elevates with further reductions in the sensitizer concentration, due to the reduced number of triplet excitations introduced into the free-floating DPA population.⁹ These threshold values compare favourably to contemporary nanocrystal-sensitized TUC systems,^16,39,40,61 are 5 times lower than a recent report of red-to-blue TUC using core–shell CdSe|ZnS QDs,³⁴ and are comparable to a very recent report using extended 1D CdTe nanorod sensitizers and λ: 520 nm excitation.²³

Fig. 2 Intensity dependence of spectrally-integrated upconverted emission at various sensitizer (PbS-CPA) concentrations, showing the characteristic quadratic-to-linear transition as bimolecular triplet fusion becomes the dominant decay channel. The lowest threshold observed for max-efficiency upconversion from this system was I_th = 220 mW cm⁻² (dotted line).

Important to our demonstration of low-threshold red-to-blue TUC is our use of PbS QDs, which have longer excited-state lifetimes compared to the CdSe or CdTe QD sensitizers previously employed in this spectral range.^{23,34,37,61,62} Indeed, we measured the photoluminescence kinetics of the ultra-small PbS QDs used in this study (Fig. 3; S6, Tables S2 and S3†), and found that the microsecond-scale excited-state lifetime is consistent with the larger PbS QDs previously employed for TUC.^18,63,64 While the performance benefits of a longer intrinsic sensitizer lifetime are qualitatively evident—reduced kinetic competition from sensitizer deactivation will generate greater triplet flux to the acceptor ligands, all else equal (Fig. S8†)—we sought to quantitatively assess the importance of this effect in a functionalized nanocrystal. In general, to maximize the achievable anti-Stokes shift it is advantageous to reduce the exothermicity of each transfer event. Accordingly, a quasi-equilibrium with an appreciable time-weighted population of excitations on the sensitizer in such systems is expected.^65–68 Thus, the slow QD decay rate has heightened importance in our system, because it is expected that TET (PbS QD → ligand) is endothermic—hence reverse TET (rTET) will be appreciable.

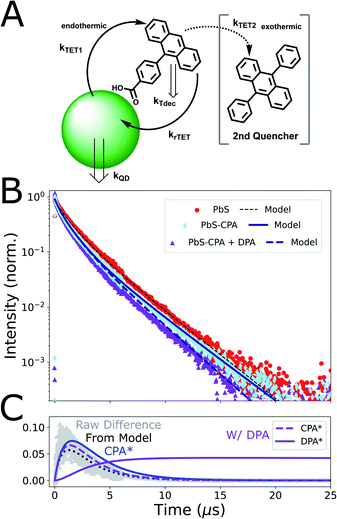Fig. 3 Time-resolved photoluminescence results and model. (A) Scheme of kinetic model: Triplet energy transfer (TET) occurs from PbS QDs to CPA ligands, but backtransfer (rTET) to QDs is appreciable. Adding a secondary acceptor (DPA) to the system provides a new energy outlet for triplet-excited CPA (³CPA*). (B) TRPL of solutions containing PbS only (red circles), CPA-functionalized PbS (light blue diamonds) and PbS-CPA with free-floating DPA (violet triangles). The early-time PL decay of CPA-functionalized QDs is accelerated due to TET. Conversely, late-time kinetics are slowed relative to PbS-only controls because of reverse TET of molecular triplets. Backtransfer is reduced in the presence of DPA. Kinetic traces from our model are added (solid/dashed lines; Table S5†). The inclusion of these quasi-equilibrium dynamics gives good agreement to experiments. Raw data is re-binned to 4 ns (0–6 μs) and 128 ns (>6 μs) time-steps to balance shot noise while highlighting differences in late-time kinetics. Data from solutions without free-floating DPA are normalized to the peak, while the trace with DPA is scaled to the PbS-CPA data at 150 ns due to parasitic DPA emission <100 ns (Fig S9†). (C) Kinetic modelling of ³CPA* and ³DPA* populations. Grey triangles are the simple difference between the experimental PbS and PbS-CPA traces in B, which is well-reproduced by our model (dotted black line). This experimental quantity is a convenient proxy for the population of ³CPA* (blue line), which is non-emissive. Additional modelled curves (purple) represent the microsecond-scale population dynamics of both ³CPA* and ³DPA* in the full system.

To clarify the impact of this equilibrium excited-state partitioning, we extended our previous kinetic simulation,⁹ which was itself inspired by foundational work on solution-phase TUC.^2,3,39 In brief, we consider the relevant excitation, transfer, and decay channels in our system (Fig. 3A), and model the time-resolved excited-state PbS population (see ESI for kinetic equations and additional discussion†). To capture the expected equilibrium dynamics, we relax the assumption of irreversible transfer, and explicitly model back-transfer from a population of excitations on the ligands.^39,66 Though some cases are analytically tractable, we treated the resulting system of ODEs numerically to avoid simplifying assumptions, and to facilitate the ultimate incorporation of non-linear (e.g. bimolecular) decay channels.

Our results from time-resolved photoluminescence spectroscopy (TRPL; Fig. 3) allow this model to be constrained and tested. We first considered the PL decay of the QDs without exciton extracting ligands (Fig. 3B; λ_exc = 470 nm). Consistent with many experiments on comparable nanocrystal ensembles (i.e. with low size-dispersity, but without a passivating shell), the fluorescence decay dynamics of the QDs alone were clearly non-monoexponential.^16,69,70 Though the involvement of a surface-oriented ‘trap’ state has been proposed to explain the triplet-transfer dynamics of larger functionalized PbS QDs,^64,71 we found that a kinetic model considering a uniform, emissive band-edge population in equilibrium with a single, non-emissive ‘trap’ state (with a characteristic energy/rate constant) was not well-matched to our observations, and left parameters poorly constrained (Fig. S10†). Lacking a clear physical justification for any particular model for QD dynamics, we adopted a parametrized three-population description of the intrinsic QD decay kinetics (Fig. S6 and Table S2†), motivated by previous work on carboxylic acid ligand binding to CdS nanocrystals,⁷² and exciton extraction in the widely studied CdSe/9-ACA hybrid sensitizer.⁷⁰ This parametrization accurately reproduces the measured QD decay kinetics (Fig. 3B and Table S5†), thus providing the starting point for the full equilibrium model.

We combined the three-population model for QD photophysics with the rate equations incorporating equilibrium dynamics and generated kinetic simulations that could be compared to our TRPL measurements of functionalized QDs (Fig. 3B). Qualitatively, the early-time decay dynamics of CPA-functionalized PbS QDs are accelerated by the presence of a small number (〈n〉 = 1.5; Fig. S1†) of CPA ligands on the QD surface. Corroborated by our observation of upconverted fluorescence from the complete system (Fig. 1A), this is clear evidence of TET from the QD to the ligand. The extended model captures these kinetics (Fig. 3B) and we find that a characteristic transfer time of 1/k_TET = 5.4 μs gives best agreement to our data. Our data provides an intuitive check of this estimate, with the simple difference between PbS and PbS-CPA traces displaying a similar rise time, representing the disappearance of excitations from PbS nanocrystals (Fig. 3C). This difference would correspond exactly to the population of ³CPA* ligands in the absence of other decay channels (ESI section 2†).

This triplet transfer time is slower than previous reports of NC-sensitized TET to acene acceptors,^{18,23,47,63,64,71} and we consider that three factors are primarily responsible. Firstly, compared to acenes where the conjugated core is directly carboxylated,^16,63 the phenyl spacer in CPA is known to slow TET from QDs^41,47 due to the exponential distance-dependence of through-space dexter-like energy transfer.^7,73,74 Secondly, PbS sensitizers commonly display longer transfer times than Cd chalcogenide sensitizers, as the dielectric constant and electronic structure of the nanocrystal may play a role.^37,38 Lastly, though this first demonstration of PbS to anthracene TET was enabled by the ability to synthesize low-dispersity ultra-small PbS QDs,⁴⁶ TET in this system is expected to be endothermic. Specifically, the expected CPA triplet energy^47,75 is ∼170 meV higher in energy than the emission peak of these PbS QDs (Fig. 1C). The microsecond-scale forward transfer and quasi-equilibrium dynamics are similar to a very recent report of Si QDs functionalized with a perylene derivative.⁶⁷ Additionally, while we discuss our results in the context of (correlated) excitonic energy transfer, we cannot rule out that transfer also occurs via a sequential mechanism following single-carrier trapping—a model that is consistent with experiments on larger QDs paired with triplet acceptors.^64,71,76,77 Exothermic carrier trapping on the QD would slow TET (relative to transfer from band-edge states) by increasing the effective endothermicity of the key QD → molecule transfer, but our experiments do not discern between these hypotheses.^42,78 However such trapping is not unique to PbS,^76,79 nor it is exclusively observed in ultra-small particles,⁶⁴ so we do not consider that its presence is the primary origin of the slow (∼5.4 μs) TET dynamics that we observe. Still, ongoing^77,80 and future work to reveal the chemical nature of electronic trap states in these materials may establish whether a sequential mechanism would have stronger coupling or an overall efficiency benefit.

Closer inspection of the TRPL trace with our model provides additional support that TET from PbS to CPA is endothermic in this system. Notably, after the accelerated initial decay, the long-time dynamics (t > 6 μs) of CPA-functionalized PbS QDs display a slight deceleration compared to nanocrystals alone (Fig. 3, light blue diamonds; Fig. S6 and Table S3†), giving rise to kinetics consistent with thermally-activated delayed fluorescence.^81–83 Our model only predicts such an effect when considering equilibrium TET dynamics (Fig. S11†). We extract an equilibrium constant of K = 0.66 ± 0.06 (k_TET/k_rTET), which implies that TET is slightly endothermic in this system. We discuss this further below. Modelling of our experiments also indicates that the excited-state lifetime of triplets on CPA ligands is 3.3 μs (Fig. S12†), which is considerably shorter than other phenylated anthracenes in solution.⁸⁴ This observation is consistent with extrinsic acceleration of the excited-state decay rate for ligands bound to the QD surface.^5,41,63 Branching fractions extracted from our model predict that approximately 16% of all photoexcitations in this system decay via monomolecular ³CPA* decay in the absence of other quenching outlets (Fig. S13–S16, Tables S6 and S7†). This is in good agreement with our experimental observation of a 19% reduction in PbS QD PLQY after functionalization with CPA ligands (Table S8†).

We sought to clarify this quasi-equilibrium effect by introducing a secondary, exothermic triplet quencher to the system. The presence of free-floating DPA (E_T1 = 1.77 eV)^16,84 at 15 mM causes notable differences in the TRPL data (Fig. 3B; and S6†). Most importantly, the long-time PbS photoluminescence dynamics that were previously decelerated by CPA are now accelerated by excess DPA (Fig. S6 and Table S3†). This is consistent with ³CPA* population being drained via exothermic TET to free-floating DPA, which reduces the population of ³CPA* that could re-populate the QDs via rTET (Fig. S13†). Our kinetic model captures the consequences of this new population sink: the quasi-equilibrium between PbS* and ³CPA* is shifted forward (Fig. 3B) and the ³CPA* population decay is accelerated by the addition of the DPA outlet (Fig. 3C). We observe that our model does not fully capture the accelerated early-time (t < 2 μs) decay of PbS under these conditions, which could arise from some direct QD quenching by the enormous excess of DPA (1000 DPA: 1 PbS). Control experiments studying CPA-functionalized PbS QDs with 150-fold lower DPA concentrations displayed the same PL kinetics as the functionalized QDs alone (Fig. S6†), supporting the view of diffusion-mediated transfer rather than the preferential aggregation of DPA with molecules in the ligand shell.^85,86

Finally, time-integrations of our simulation predicts that approximately 6% of total photoexcitations ultimately reach the DPA acceptor, even at the highest DPA concentrations (Fig. 3C; S14, Tables S5 and S6†). Though the model does not include a direct transfer channel, this lower-bound estimate permits a useful conceptual test. Upconversion quantum efficiencies (UCQE, scaled to 100% utilization of input photoexcitations) up to 18.6% have been reported for DPA-based upconversion, using sensitization schemes optimized for quantum yield rather than anti-Stokes shift.²⁰ Using this experimental value as a proxy for the ideal performance of the DPA annihilator/emitter, and accounting for the 6% sensitizing efficiency extracted from our model, we would predict a UCQE of 1.0% for our system when driven into the linear regime. This agrees well with the 0.6% UCQE that we measure (Table S8†), validating our approach. Accordingly, we use the results of the model to identify the following performance factors as leading targets for improvement. First, our results provide important evidence that the monomolecular ³CPA* lifetime is much shorter for molecules coordinated to PbS QDs than in free solution, which contributes directly to the relatively inefficient transfer to DPA even at high concentrations. The best-fit parameters for our modelled population dynamics show that 48% of ³CPA* ultimately undergo monomolecular decay, rather than transferring to DPA (22%) or decaying on the QD following back-transfer (30%) (Table S7†). As a result, mitigation of this shortened triplet-excited ligand lifetime, presumably due to through-space external heavy atom⁴¹ or spin–spin effects,⁵ should be a key goal moving forward. This highlights a significant design trade-off, because it has been shown that extractor ligands with conjugated cores closer to the QD boost the rate of dexter-type TET.^41,47,73 Here, recent bridged transfer schemes are an attractive research direction.⁸⁷

Then, further advances in the synthesis and passivation of these QDs are an immediate target. From our three-population parametrization of the photoluminescence dynamics, we infer that 16% of photoexcitations on our ultra-small, core-only PbS QDs decay with a characteristic lifetime of τ = 370 ns, and a further 40% with τ = 1.3 μs. With other QD systems, shelling and surface passivation schemes have resulted in monoexponential decay dynamics that approach the longest lifetime initially observed.^34,88 If all ultra-small PbS QDs had the lifetime of our longest-lived sub-population (τ = 2.7 μs), our model predicts that the fraction of excitations reaching the DPA would nearly double (to ∼11%, Fig. S15†), despite the endothermicity of the present system. Improved QD passivation may also permit a greater density of triplet-extracting ligands to be achieved, accelerating forward TET, as well as providing additional acceptor microstates to push the population equilibrium forward.^83,89 Lastly, because the timescale of TET is slow in this system (as discussed above), it is only the comparatively long lifetime of PbS that permits meaningful transfer. All else equal, our model predicts that only ∼0.1% of excitations on hypothetical absorbers with a lifetime matching CdSe QDs (i.e. 30 ns; Fig. S16†) would contribute to upconversion, leading to lower efficiencies and high linear-regime thresholds (Fig. S8†). Indeed, the deleterious effects that we discuss here did not prevent the achievement of a near-solar max-efficiency threshold in our implementation of red-to-blue TUC with ultra-small PbS.

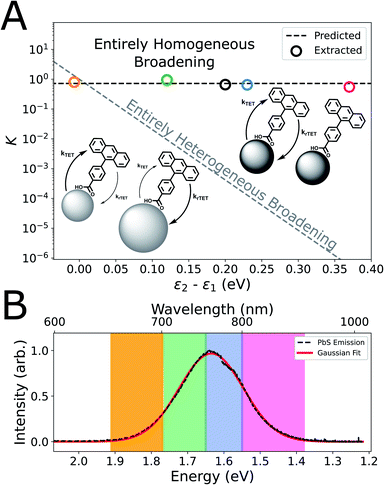
Finally, we sought to clarify the possible role of ensemble size-dispersity on the equilibrium transfer dynamics in our CPA-functionalized PbS QDs, because the physical origin of the broad and strongly Stokes-shifted emission of the ultra-small PbS QDs employed in this study is uncertain.^46,49,79,90 Particularly, we would expect highly endothermic TET (ΔE ≈ 6kT at room temperature) considering the peak wavelength of QD emission (λ: 760 nm, hν: 1.63 eV) and the expected energy of the CPA triplet (λ: 689 nm, hν: 1.80 eV), but we instead observe dynamics that indicate only a mildly endothermic equilibrium (K = 0.66; ΔE ≈ 0.5kT at room temperature). Conceptually, if the broad QD PL linewidth predominantly resulted from heterogeneous optical gaps (e.g. size-dispersity via quantum confinement), we would expect very different equilibria based on the relative driving force for TET between each sub-ensemble of QDs.^91,92 For instance, the highest-energy spectral window would selectively interrogate the dynamics of small-diameter (i.e. large-bandgap) QDs, where TET would be isoergic. Conversely, the long-wavelength emission would preferentially monitor the largest QDs in the ensemble, thus interrogating a sub-ensemble where TET would be strongly endothermic.

Therefore, we measured wavelength-resolved TRPL from our ensembles of as-synthesized and CPA-functionalized PbS QDs and used our kinetic model to extract equilibrium constants considering each spectral regime as a sub-ensemble (Fig. S17–S22†). We observe similar values of K across the emission spectrum (0.6 < K < 0.9, mean of 0.72; Fig. 4A), which is inconsistent with a QD PL linewidth that predominantly arises from ensemble heterogeneity. The contrast is most apparent in comparison to the large thermodynamic variation of K that would be expected if the broadening was purely heterogeneous (Fig. 4A, grey dashed line).⁹³ Indeed, a significant heterogeneous contribution to the linewidth could give rise to asymmetric quenching of the steady-state ensemble QD PL,^67,94 which we do not observe (Fig. S4†). Thus, we consider that the effect of ensemble heterogeneity is minor compared to the effective single-particle PL linewidth of these ultra-small PbS QDs. This hypothesis is in-line with our previous demonstration that batches of comparable QDs have low size-dispersities (<7%),⁴⁶ and these results are indirect evidence that the homogeneous emission linewidth of ultra-small PbS QDs is broad.

Fig. 4 Consideration of the role of QD size-dispersity in ensemble dynamics. (A) Using our kinetic model, equilibrium constants (K) are extracted from TRPL of CPA-functionalized PbS considering either the ensemble as a whole (hollow black circle), or by treating the dynamics from distinct spectral regions as sub-ensembles (hollow circles; colours correspond to shaded spectral regions in (B)). Dashed lines represent the predicted variation of K under the assumptions that the QD PL linewidth arose from purely homogeneous broadening (black) or purely heterogeneous broadening due to size-dispersity and quantum confinement (grey). Though the emission from these ultra-small nanocrystals is broad, the unvarying K is consistent with a QD ensemble with low size-dispersity. Inset graphic: illustrative depiction of triplet energy transfer in QD ensembles. (B) Ensemble photoluminescence spectra from the QDs interrogated in (A), with spectral regions highlighted, and a representative Gaussian fit.

It has been proposed that the analogous, broad, highly Stokes-shifted emission from ultra-small cadmium chalcogenide nanocrystals is caused by strong exciton–phonon coupling of surface-oriented states, rather than evidence of deep trap states within the optical gap.^51,52 Similarly, exciton–phonon coupling has been proposed as the dominant origin of the room-temperature PL linewidth and dynamics of larger PbS QDs,^49,53,90,95 is expected to strengthen as the QD radius decreases,^54,96,97 and has been invoked to explain charge-transfer intermediates in the sensitization of triplet excited-states of larger acenes.^64,71 Naturally, any homogenous origin for the broad emission of these ultra-small PbS QDs would explain the spectral invariance that we observe for the K describing the TET quasi-equilibrium. However, the hypothesis that the room-temperature photoluminescence peak may under-estimate the chemical potential of photoexcited ultra-small QDs⁵¹ is intriguing, because it would also rationalize the surprisingly small endothermicity of the equilibrium that we observe relative to our expectations from steady-state spectroscopy (Fig. 1B).

The size-tunable optical gap of PbS QDs offers some ability to test this hypothesis. Unfortunately, QDs smaller than those that give the best photochemical performance exhibited poor colloidal stability and ripened during ligand exchange (see discussion in ESI section 3.1†). However, as expected, TRPL measurements with slightly larger PbS QDs functionalized with the same CPA ligands (Fig. S23†) exhibited rapidly diminished quenching (Fig. S24 and S25†). These dynamics can again be captured by the kinetic model, where the fitted equilibrium constant provides an independent measure of the effective endothermicity of TET relative to the energetically-defined molecular triplet (E_T = 1.8 eV). We observe appreciable quenching (K = 0.3 ± 0.05) for QDs with an absorption peak energy of 1.88 eV, but marginal quenching (K = 0.1 ± 0.1) for QDs with a peak at 1.65 eV (Fig. S23 and Table S11†). In contrast, a direct estimate of the thermodynamics of TET from the QD photoluminescence peak would predict strongly endothermic transfer from all three sizes of QDs (ΔE_TET: 170, 200, 340 meV, respectively) so that the associated quenching at equilibrium would be undetectable in our measurements. Still, we consider that the energy of the absorption peak remains an over-estimate. This is both on fundamental grounds, because exciton–phonon coupling in these nanocrystals is non-zero,^49,53 and because we do not observe an exothermic transfer equilibrium (i.e. K > 1) in the primary experiment (Fig. 3 and Table S11†).

Thus, the free energy for triplet sensitization in ultra-small PbS QDs follows a trend intermediate between the energies of the absorption and emission peaks (Fig. S26†). Extrapolating from our calculated equilibrium constants, we find that triplet transfer is at least 150 meV less endothermic than predicted from the steady-state emission spectra of each QD ensemble (Table S11†). This indicates that peak of the emission spectrum significantly under-estimates the free energy of the electronic excited state in ultra-small QDs, which supports the interpretation that their photon emission involves significant ground-state phonon coupling.⁵¹ However, a complicating factor is the uncertain role of entropy in this system, given that the appropriate degeneracies of the donating and accepting states are unclear. Here, recent work has begun to address the role of entropy from the multiplicity of ligand loading.^83,89 Then, while the band-edge degeneracy of PbS NCs has been established,⁶² there is a wide variation in the expected number of surface-oriented states.⁶⁴ Further experiments are warranted to explore the origin of the anomalously broad, strongly Stokes-shifted photoluminescence from ultra-small colloidal quantum dots. Indeed, a very recent paper has proposed a method to analyze ultrafast, 2D spectroscopy measurements and estimate the chemical potential of photoexcited states, and applied it to larger PbS nanocrystals.⁹⁵ Similar approaches have historically encountered challenges in capturing the behaviour of molecular systems,^95,98 where structural fluctuations/reorganization are significant. We note that analogous concerns are expected for ultra-small 0D semiconductor materials where few atoms experience a bulk-like environment, particular given the possibility that defect states⁴⁹ involving surface reconstruction are involved in the photophysics.⁹⁹ Thus, there is an opportunity to extend this theoretical framework to capture such complex chromophores, especially where their unique properties may aid applications. In this effort, the thermodynamic quantities that we estimate for the product state resulting from photoexcitation of ultra-small PbS QDs (by characterizing its equilibrium with a molecular spin-triplet exciton with well-defined energy) may offer an intriguing opportunity for testing and calibration. Such fundamental insight would not only help to extend the maximum achievable anti-Stokes shift via nanocrystal-sensitized triplet-fusion, but also inform advances in the synthesis and implementation of semiconducting particles with extreme wavefunction confinement.

Conclusions

In this work, we have introduced ultra-small PbS QDs as triplet sensitizers for red-to-blue triplet-fusion upconversion, achieving a proof-of-concept QD-sensitized photochemical polymerization under irradiation at λ = 637 nm. This triplet-fusion upconversion exhibited a large anti-Stokes shift (ΔE = 1.04 eV) and reached maximum efficiency at a threshold excitation intensity of 220 mW cm⁻², which is comparable to contemporary red-to-blue TUC systems. We then used transient photoluminescence spectroscopy to clarify the flow of photoexcitations in the quasi-equilibrium between PbS sensitizers, triplet-excited extractor ligands, and free-floating molecular acceptors. We developed a kinetic model that provides quantitative insight, as global best-fit parameters reproduce the photophysical dynamics observed across control experiments and time-integrated predictions match steady-state observables. Our analysis showed that the characteristic timescale of triplet exciton transfer in this system is long (1/k_TET = 5.4 μs), consistent with expectations, so the long excited-state lifetime of PbS QDs is essential in enabling the near-solar intensity threshold in this red-to-blue system. However, our work highlighted that the decay of molecular triplet excitations is accelerated in proximity to the QD surface, which causes significant population loss in our system and is a leading cause of the modest UCQE (0.6%, of a maximum 100%) that we observe. Noting the strong distance dependence of the rate of through-space energy transfer, molecular architectures that address this design trade-off will be vital for improved performance. Lastly, we also found evidence of a lower endothermicity to triplet energy transfer (ΔE ≈ 0.5kT) than the known triplet energy and the measured QD photoluminescence peak would suggest (ΔE ≈ 6kT). This improves the general outlook for ultra-small nanocrystals as triplet sensitizers in upconversion applications seeking maximal overall anti-Stokes shifts. Further, combined with wavelength-resolved QD photoluminescence dynamics that do not indicate significant ensemble size-dispersity, these experiments raise questions regarding the nature of the emissive states in ultra-small QDs that approach the molecular limit. Together, our results highlight the utility of ultra-small PbS QDs as sensitizers for red-to-blue triplet fusion upconversion, provide a clearer picture of the transfer and decay channels at quasi-equilibrium in functionalized nanocrystals, and offer design rules to guide the implementation of QD-sensitized triplet-fusion upconversion.

Data availability

All relevant data have been included in the ESI.†

Author contributions

CJI conceived the project and performed experiments with the assistance of PBG and MH, under the direction of MWBW. The manuscript was written by CJI and MWBW, and all authors have given approval to the final version.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

CJI acknowledges support from an NSERC PGS-D scholarship. PBG acknowledges support from an Ontario Graduate Scholarship. Authors thank Kazuhiro Hotta and Alán Aspuru-Guzik for access to the λ: 375 nm excitation source. MWBW acknowledges the support of the University of Toronto, including a Connaught New Researcher Award; the Natural Sciences and Engineering Research Council of Canada (NSERC) via RGPIN-2017-06666; and support for research infrastructure from the Canada Foundation for Innovation [JELF-35991], and the Ontario Research Fund [SIA-35991].

References

1. J. Zhou, Q. Liu, W. Feng, Y. Sun and F. Li, Chem. Rev., 2015, 115, 395–465.
2. A. Haefele, J. Blumhoff, R. S. Khnayzer and F. N. Castellano, J. Phys. Chem. Lett., 2012, 3, 299–303.
3. Y. Y. Cheng, B. Fuckel, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. Lett., 2010, 1, 1795–1799.
4. M. A. El-Sayed, Acc. Chem. Res., 1968, 1, 8–16.
5. S. Han, R. Deng, Q. Gu, L. Ni, U. Huynh, J. Zhang, Z. Yi, B. Zhao, H. Tamura, A. Pershin, H. Xu, Z. Huang, S. Ahmad, M. Abdi-Jalebi, A. Sadhanala, M. L. Tang, A. A. Bakulin, D. Beljonne, X. Liu and A. Rao, Nature, 2020, 587, 594–599.
6. T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573.
7. D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850.
8. C. Ye, L. Zhou, X. Wang and Z. Liang, Phys. Chem. Chem. Phys., 2016, 18, 10818–10835.
9. C. J. Imperiale, P. B. Green, E. G. Miller, N. H. Damrauer and M. W. B. Wilson, J. Phys. Chem. Lett., 2019, 10, 7463–7469.
10. A. B. Pun, S. N. Sanders, M. Y. Sfeir, L. M. Campos and D. N. Congreve, Chem. Sci., 2019, 10, 3969–3975.
11. A. B. Pun, L. M. Campos and D. N. Congreve, J. Am. Chem. Soc., 2019, 141, 3777–3781.
12. S. Baluschev, V. Yakutkin, T. Miteva, Y. S. Avlasevich, S. Chernov, S. Aleshchenkov, G. Nelles, A. Cheprakov, A. Yasuda, K. Müllen and G. Wegner, Angew. Chem. Int. Ed., 2007, 46, 7693–7696.
13. B. D. Ravetz, A. B. Pun, E. M. Churchill, D. N. Congreve, T. Rovis and L. M. Campos, Nature, 2019, 565, 343–346.
14. L. Huang, W. Wu, Y. Li, K. Huang, L. Zeng, W. Lin and G. Han, J. Am. Chem. Soc., 2020, 142, 18460–18470.
15. B. Joarder, A. Mallick, Y. Sasaki, M. Kinoshita, R. Haruki, Y. Kawashima, N. Yanai and N. Kimizuka, ChemNanoMat, 2020, 1, 2–6.
16. Z. Huang, X. Li, M. Mahboub, K. M. Hanson, V. M. Nichols, H. Le, M. L. Tang and C. J. Bardeen, Nano Lett., 2015, 5552–5557.
17. C. Mongin, S. Garakyaraghi, N. Razgoniaeva, M. Zamkov and F. N. Castellano, Science, 2016, 351, 369–373.
18. M. Wu, D. N. Congreve, M. W. B. Wilson, J. Jean, N. Geva, M. Welborn, T. Van Voorhis, V. Bulović, M. G. Bawendi and M. A. Baldo, Nat. Photonics, 2016, 10, 31–34.
19. E. M. Gholizadeh, S. K. K. Prasad, Z. L. Teh, T. Ishwara, S. Norman, A. J. Petty, J. H. Cole, S. Cheong, R. D. Tilley, J. E. Anthony, S. Huang and T. W. Schmidt, Nat. Photonics, 2020, 14, 585–590.
20. Y. Han, S. He, X. Luo, Y. Li, Z. Chen, W. Kang, X. Wang and K. Wu, J. Am. Chem. Soc., 2019, 141, 13033–13037.
21. K. Okumura, K. Mase, N. Yanai and N. Kimizuka, Chem. - Eur. J., 2016, 22, 7721–7726.
22. Z. Xu, Z. Huang, T. Jin, T. Lian and M. L. Tang, Acc. Chem. Res., 2020, 51, 70–80.
23. Z. A. VanOrman, C. R. Conti, G. F. Strouse and L. Nienhaus, Chem. Mater., 2021, 33, 452–458.
24. L. Nienhaus, J. P. Correa-Baena, S. Wieghold, M. Einzinger, T. A. Lin, K. E. Shulenberger, N. D. Klein, M. Wu, V. Bulović, T. Buonassisi, M. A. Baldo and M. G. Bawendi, ACS Energy Lett., 2019, 4, 888–895.
25. S. Wieghold, A. S. Bieber, Z. A. VanOrman, L. Daley, M. Leger, J. P. Correa-Baena and L. Nienhaus, Matter, 2019, 1–15.
26. X. Luo, R. Lai, Y. Li, Y. Han, G. Liang, X. Liu, T. Ding, J. Wang and K. Wu, J. Am. Chem. Soc., 2019, 141, 4186–4190.
27. N. Kiseleva, P. Nazari, C. Dee, D. Busko, B. S. Richards, M. Seitz, I. A. Howard and A. Turshatov, J. Phys. Chem. Lett., 2020, 11, 2477–2481.
28. D. G. Bossanyi, M. Matthiesen, S. Wang, J. A. Smith, R. C. Kilbride, J. D. Shipp, D. Chekulaev, E. Holland, J. E. Anthony, J. Zaumseil, A. J. Musser and J. Clark, Nat. Chem., 2020, 13, 163–171.
29. A. J. Musser and J. Clark, Annu. Rev. Phys. Chem., 2019, 70, 323–351.
30. N. Awwad, A. T. Bui, E. O. Danilov and F. N. Castellano, Chem, 2020, 6, 1–15.
31. G. Jalani, R. Naccache, D. H. Rosenzweig, L. Haglund, F. Vetrone and M. Cerruti, J. Am. Chem. Soc., 2016, 138, 1078–1083.
32. Z. Wang, Y. Hou, Z. Huo, Q. Liu, W. Xu and J. Zhao, Chem. Commun., 2021, 57, 9044.
33. N. Nishimura, V. Gray, J. R. Allardice, Z. Zhang, A. Pershin, D. Beljonne and A. Rao, ACS Mater. Lett., 2019, 660–664.
34. R. Lai and K. Wu, J. Chem. Phys., 2020, 153, 114701.
35. T. N. Singh-Rachford and F. N. Castellano, J. Phys. Chem. Lett., 2010, 1, 195–200.
36. Y. Tian, Y. Li, B. Chen, R. Lai, S. He, X. Luo, Y. Han, Y. Wei and K. Wu, J. Phys. Chem. Lett., 2020, 11, 2247–2255.
37. Z. Huang and M. L. Tang, J. Phys. Chem. Lett., 2018, 9(21), 6198–6206.
38. L. Nienhaus, M. Wu, V. Bulović, M. A. Baldo and M. G. Bawendi, Dalton Trans., 2018, 47, 8509–8516.
39. A. Ronchi, P. Brazzo, M. Sassi, L. Beverina, J. Pedrini, F. Meinardi and A. Monguzzi, Phys. Chem. Chem. Phys., 2019, 21, 12353–12359.
40. J. De Roo, Z. Huang, N. J. Schuster, L. S. Hamachi, D. N. Congreve, Z. Xu, P. Xia, D. A. Fishman, T. Lian, J. S. Owen and M. L. Tang, Chem. Mater., 2020, 32, 1461–1466.
41. Z. Xu, Z. Huang, C. Li, T. Huang, F. A. Evangelista, M. L. Tang and T. Lian, ACS Appl. Mater. Interfaces, 2020, 12, 36558–36567.
42. I. Moreels, K. Lambert, D. De Muynck, F. Vanhaecke, D. Poelman, J. C. Martins, G. Allan and Z. Hens, ACS Nano, 2009, 3, 3023–3030.
43. O. T. Bruns, T. S. Bischof, D. K. Harris, D. Franke, Y. Shi, L. Riedemann, A. Bartelt, F. B. Jaworski, J. A. Carr, C. J. Rowlands, M. W. B. Wilson, O. Chen, H. Wei, G. W. Hwang, D. M. Montana, I. Coropceanu, O. B. Achorn, J. Kloepper, J. Heeren, P. T. C. So, D. Fukumura, K. F. Jensen, R. K. Jain and M. G. Bawendi, Nat. Biomed. Eng., 2017, 1, 1–11.
44. S. A. Mcdonald, G. Konstantatos, S. Zhang, P. W. Cyr, E. J. D. Klem, L. Levina and E. H. Sargent, Nat. Mater., 2005, 4, 138–142.
45. P. B. Green, Z. Wang, P. Sohn, C. J. Imperiale, O. Voznyy and M. W. B. Wilson, J. Mater. Chem. C, 2020, 8, 12068–12074.
46. P. B. Green, P. Narayanan, Z. Li, P. Sohn, C. J. Imperiale and M. W. B. Wilson, Chem. Mater., 2020, 32, 4083–4094.
47. X. Li, Z. Huang, R. Zavala and M. L. Tang, J. Phys. Chem. Lett., 2016, 7, 1955–1959.
48. M. C. Weidman, M. E. Beck, R. S. Hoffman, F. Prins and W. A. Tisdale, ACS Nano, 2014, 8, 6363–6371.
49. J. R. Caram, S. N. Bertram, H. Utzat, W. R. Hess, J. A. Carr, T. S. Bischof, A. P. Beyler, M. W. B. Wilson and M. G. Bawendi, Nano Lett., 2016, 16, 6070–6077.
50. H. Fröhlich, Adv. Phys., 1954, 3, 325–361.
51. T. G. Mack, L. Jethi and P. Kambhampati, J. Phys. Chem. C, 2017, 121, 28537–28545.
52. L. Jethi, T. G. Mack and P. Kambhampati, J. Phys. Chem. C, 2017, 121, 26102–26107.
53. D. Bozyigit, N. Yazdani, M. Yarema, O. Yarema, W. M. M. Lin, S. Volk, K. Vuttivorakulchai, M. Luisier, F. Juranyi and V. Wood, Nature, 2016, 531, 618–622.
54. E. R. Kennehan, G. S. Doucette, A. R. Marshall, C. Grieco, K. T. Munson, M. C. Beard and J. B. Asbury, ACS Nano, 2018, 12, 6263–6272.
55. J. H. Warner, E. Thomsen, A. R. Watt, N. R. Heckenberg and H. Rubinsztein-Dunlop, Nanotechnology, 2005, 16, 175–179.
56. E. Istrate, S. Hoogland, V. Sukhovatkin, L. Levina, S. Myrskog, P. W. E. Smith and E. H. Sargent, J. Phys. Chem. B, 2008, 112, 2757–2760.
57. K. P. McClelland, T. D. Clemons, S. I. Stupp and E. A. Weiss, ACS Macro Lett., 2020, 9, 7–13.
58. J. A. Caputo, L. C. Frenette, N. Zhao, K. L. Sowers, T. D. Krauss and D. J. Weix, J. Am. Chem. Soc., 2017, 139, 4250–4253.
59. Y. Jiang, C. Wang, C. R. Rogers, M. S. Kodaimati and E. A. Weiss, Nat. Chem., 2019, 11, 1034–1040.
60. E. M. Gholizadeh, L. Frazer, R. W. MacQueen, J. K. Gallaher and T. W. Schmidt, Phys. Chem. Chem. Phys., 2018, 20, 19500–19506.
61. E. M. Rigsby, T. Miyashita, P. Jaimes, D. A. Fishman and M. L. Tang, J. Chem. Phys., 2020, 153, 114702.
62. J. C. Johnson, K. A. Gerth, Q. Song, J. E. Murphy, A. J. Nozik and G. D. Scholes, Nano Lett., 2008, 8, 1374–1381.
63. Z. Huang, Z. Xu, M. Mahboub, Z. Liang, P. Jaimes, P. Xia, K. R. Graham, M. L. Tang and T. Lian, J. Am. Chem. Soc., 2019, 141, 9769–9772.
64. J. A. Bender, E. K. Raulerson, X. Li, T. Goldzak, P. Xia, T. Van Voorhis, M. L. Tang and S. T. Roberts, J. Am. Chem. Soc., 2018, 140, 7543–7553.
65. J. Isokuortti, S. R. Allu, A. Efimov, E. Vuorimaa-Laukkanen, N. V. Tkachenko, S. A. Vinogradov, T. Laaksonen and N. A. Durandin, J. Phys. Chem. Lett., 2020, 11, 318–324.
66. D. Meroni, A. Monguzzi and F. Meinardi, J. Chem. Phys., 2020, 153, 114302.
67. T. Huang, T. T. Koh, J. Schwan, T. T.-T. Tran, P. Xia, K. Wang, L. Mangolini, M. L. Tang and S. T. Roberts, Chem. Sci., 2021, 12, 6737.
68. Y. Y. Cheng, B. Fückel, T. Khoury, R. G. C. R. Clady, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. A, 2011, 115, 1047–1053.
69. J. Cui, A. P. Beyler, T. S. Bischof, M. W. B. Wilson and M. G. Bawendi, Chem. Soc. Rev., 2014, 43, 1287–1310.
70. G. B. Piland, Z. Huang, M. Lee Tang and C. J. Bardeen, J. Phys. Chem. C, 2016, 120, 5883–5889.
71. C. M. Papa, S. Garakyaraghi, D. B. Granger, J. E. Anthony and F. N. Castellano, Chem. Sci., 2020, 11, 5690–5696.
72. X. Li, V. M. Nichols, D. Zhou, C. Lim, G. S. H. Pau, C. J. Bardeen and M. L. Tang, Nano Lett., 2014, 14, 3382–3387.
73. L. Nienhaus, M. Wu, N. Geva, J. J. Shepherd, M. W. B. Wilson, V. Bulović, T. Van Voorhis, M. A. Baldo and M. G. Bawendi, ACS Nano, 2017, 11, 7848–7857.
74. N. J. Thompson, M. W. B. Wilson, D. N. Congreve, P. R. Brown, J. M. Scherer, T. S. Bischof, M. Wu, N. Geva, M. Welborn, T. Van Voorhis, V. Bulović, M. G. Bawendi and M. A. Baldo, Nat. Mater., 2014, 13, 1039–1043.
75. P. Xia, Z. Huang, X. Li, J. J. Romero, V. I. Vullev, G. S. H. Pau and M. L. Tang, Chem. Commun., 2017, 53, 1241–1244.
76. R. Lai, Y. Liu, X. Luo, L. Chen, Y. Han, M. Lv, G. Liang, J. Chen, C. Zhang, D. Di, G. D. Scholes, F. N. Castellano and K. Wu, Nat. Commun., 2021, 12, 1532.
77. T. Jin and T. Lian, J. Chem. Phys., 2020, 153, 074703.
78. J. Hwang, A. Wan and A. Kahn, Mater. Sci. Eng., R, 2009, 64, 1–31.
79. S. Palato, L. Mcgovern, T. G. Mack, L. Jethi and P. Kambhampati, J. Phys. Chem. C, 2017, 121, 26519–26527.
80. A. Ronchi, C. Capitani, V. Pinchetti, G. Gariano, M. L. Zaffalon, F. Meinardi, S. Brovelli and A. Monguzzi, Adv. Mater., 2020, 32(37), 2002953.
81. C. Mongin, P. Moroz, M. Zamkov and F. N. Castellano, Nat. Chem., 2018, 10, 225–230.
82. H. Noda, H. Nakanotani and C. Adachi, Sci. Adv., 2018, 4, 1–8.
83. D. T. Yonemoto, C. M. Papa, S. Sheykhi and F. N. Castellano, J. Phys. Chem. Lett., 2021, 12, 3718–3723.
84. A. Maciejewski and R. P. Steer, J. Photochem., 1986, 35, 59–69.
85. O. Voznyy, L. Levina, F. Fan, G. W. Walters, J. Z. Fan, A. Kiani, A. H. Ip, S. M. Thon, A. H. Proppe, M. Liu and E. H. Sargent, Nano Lett., 2017, 17, 7191–7195.
86. C. Ye, V. Gray, J. Mårtensson and K. Börjesson, J. Am. Chem. Soc., 2019, 141, 9578–9584.
87. Z. Huang, Z. Xu, T. Huang, V. Gray, K. Moth-Poulsen, T. Lian and M. L. Tang, J. Am. Chem. Soc., 2020, 142, 17581–17588.
88. X. Peng, M. C. Schlamp, A. V. Kadavanich and A. P. Alivisatos, J. Am. Chem. Soc., 1997, 119, 7019–7029.
89. J. Zhang, H. Kouno, N. Yanai, D. Eguchi, T. Nakagawa, N. Kimizuka, T. Teranishi and M. Sakamoto, ACS Photonics, 2020, 7, 1876–1884.
90. J. Cui, A. P. Beyler, I. Coropceanu, L. Cleary, T. R. Avila, Y. Chen, J. M. Cordero, S. L. Heathcote, D. K. Harris, O. Chen, J. Cao and M. G. Bawendi, Nano Lett., 2016, 16, 289–296.
91. S. A. Crooker, J. A. Hollingsworth, S. Tretiak and V. I. Klimov, Phys. Rev. Lett., 2002, 89, 18–21.
92. D. Zhitomirsky, O. Voznyy, S. Hoogland and E. H. Sargent, ACS Nano, 2013, 7, 5282–5290.
93. M. Mahboub, H. Maghsoudiganjeh, A. M. Pham, Z. Huang and M. L. Tang, Adv. Funct. Mater., 2016, 26, 6091–6097.
94. P. Xia, E. K. Raulerson, D. Coleman, C. S. Gerke, L. Mangolini, M. L. Tang and S. T. Roberts, Nat. Chem., 2020, 12, 137–144.
95. J. Ryu, S. D. Park, D. Baranov, I. Rreza, J. S. Owen and D. M. Jonas, Sci. Adv., 2021, 7, eabf4741.
96. T. Takagahara, Phys. Rev. Lett., 1993, 71, 3577–3580.
97. M. J. Fernée, P. Jensen and H. Rubinsztein-Dunlop, J. Phys. Chem. C, 2007, 111, 4984–4989.
98. R. L. van Metter and R. S. Knox, Chem. Phys., 1976, 12, 333–340.
99. B. Guzelturk, B. L. Cotts, D. Jasrasaria, J. P. Philbin, D. A. Hanifi, B. A. Koscher, A. D. Balan, E. Curling, M. Zajac, S. Park, N. Yazdani, C. Nyby, V. Kamysbayev, S. Fischer, Z. Nett, X. Shen, M. E. Kozina, M. F. Lin, A. H. Reid, S. P. Weathersby, R. D. Schaller, V. Wood, X. Wang, J. A. Dionne, D. V. Talapin, A. P. Alivisatos, A. Salleo, E. Rabani and A. M. Lindenberg, Nat. Commun., 2021, 12, 1–9.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc04330g

---