Open Access Article
Open Access ArticleStrain- and field-induced anisotropy in hybrid elastomers with elongated filler nanoparticles†
Julian
Seifert
a,
Damian
Günzing
 b,
Samira
Webers
b,
Samira
Webers
 b,
Martin
Dulle
c,
Margarita
Kruteva
b,
Martin
Dulle
c,
Margarita
Kruteva
 c,
Joachim
Landers
b,
Heiko
Wende
c,
Joachim
Landers
b,
Heiko
Wende
 b and
Annette M.
Schmidt
b and
Annette M.
Schmidt
 *a
*a
aChemistry Department, Universität zu Köln, 50939 Köln, Germany. E-mail: annette.schmidt@uni-koeln.de
bFaculty of Physics and Center for Nanointegration Duisburg-Essen (CENIDE), University of Duisburg-Essen, Lotharstraße 1, 47057 Duisburg, Germany
cForschungszentrum Jülich GmbH, Jülich Centre for Neutron Science (JCNS-1: Neutron Scattering and Biological Matter), 52425 Jülich, Germany
First published on 29th July 2021
Abstract
The implementation of anisotropy to functional materials is a key step towards future smart materials. In this work, we evaluate the influence of preorientation and sample architecture on the strain-induced anisotropy in hybrid elastomers containing covalently attached elongated magnetic filler particles. Accordingly, silica coated spindle-type hematite nanoparticles are incorporated into poly(dimethylsiloxane)-based elastomers, and two types of composite architectures are compared: on the one hand a conventional architecture of filled, covalently crosslinked elastomers, and on the other hybrid elastomers that are crosslinked exclusively by covalent attachment of the polymer chains to the particle surface. By the application of external strain and with magnetic fields, the orientational order of the elongated nanoparticles can be manipulated, and we investigate the interplay between strain, magnetic order, and orientational order of the particles by combining 2D small angle X-ray scattering experiments under strain and fields with Mössbauer spectroscopy under similar conditions, and supplementary angular-dependent magnetization experiments. The converging information is used to quantify the order in these interesting materials, while establishing a direct link between the magnetic properties and the spatial orientation of the embedded magnetic nanoparticles.
Introduction
Living matter is an important source of inspiration for scientific research, as biological tissue shows an enormous amount of functionality that is unreached by man-made objects in many fields.1,2 While the elastic modulus of common biological tissue is very similar to typical polymer matrices, the latter are far from reaching the complexity and functionality biological tissues possess.3 One major difference between biological and common synthetic systems is the degree of anisotropy. While biological structures, like muscles as a prominent example, are built up from hierarchically organized anisotropic structures, which enable their functionality,4 common polymer matrices such as gels and elastomers are synthesized by homogeneous polymerization techniques, yielding macroscopically isotropic materials.5The incorporation of functionality into polymer matrices is a major field of scientific research in the context of stimuli-responsive or smart materials.6,7 Yet, these materials significantly lack to show similar properties to biological tissues, when the responsiveness is not directed by the anisotropy of the matrix. Comparing actuation behavior, the biological system, which is a muscle, allows a reversible uniaxial contraction. The analogous isotropic polymer matrix, e.g. a poly(N-isopropylacrylamide) hydrogel, only allows a complete collapse of the structure, and thus a significantly smaller contraction effect per spatial direction.8 In the case that the implementation of anisotropic structural and mechanical properties to a functional material becomes accessible, manifold options arise towards the development of bioinspired, more complex functional or even stimuli-responsive materials. It becomes possible to tailor the direction-dependent behavior of such systems towards strain, temperature, or external fields. A prominent example that has attracted considerable attention and is still an active area of research is liquid crystalline elastomers, that, if processed with manifested anisotropy in the monodomain, can show an uniaxial contraction similar to a natural muscle fiber when exposed to elevated temperatures.9,10 The incorporation of anisotropy in polymer matrices thus opens the opportunity for directing the response.11
In this work, we focus on the introduction of anisotropic material response by using elongated magnetic nanoparticles in elastomeric matrices. The peculiar properties of the filler particles allow the manifestation of two types of anisotropy into the nanocomposites. On the one hand, in the case of anisotropic filler particles, if the particles show a preferred orientation in the polymer matrix, the resulting mechanical properties of the network become direction-dependent, as shown for fiber reinforced elastomers.12 On the other hand, the magnetic moment of the particles can be aligned with an external magnetic field. If the particles are subsequently immobilized by the crosslinking process, the magnetic order is retained for thermally blocked particles, leading to direction-dependent magnetic properties.13,14
The aim of this study is to in-depth analyze and compare the interplay between mechanical strain, magnetic field, and the internal geometric and magnetic order of the nanoparticles by using a combination of complemental methods. We investigate the strain- and field-induced geometric and magnetic orientation of the elongated magnetic filler particles in an elastomeric matrix, and how this interplay is influenced by the network architecture and by an intrinsic preorientation of the filler particles.15 Therefore, we compare conventionally crosslinked poly(dimethylsiloxane) elastomers filled with spindle-like hematite nanoparticles with materials of similar composition, but with an architecture based on covalent particle crosslinking. The latter materials are recently introduced by us as a novel architecture of elastomers, that are crosslinked exclusively via surface-attachment of the polymer chains to magnetic nanoparticles.16–20 These novel hybrid materials show strongly particle content dependent properties. In the case of poly(dimethylsiloxane)-based elastomers crosslinked via elongated hematite fillers, the mechanical properties are characterized by an enormous strain at break of up to 1700% and a pronounced strain-hardening regime.16 Due to their unique properties, they are excellent candidates for an in-depth analysis of the influence of network architecture on the strain-induced order in particle filled elastomers, and their properties will be compared to conventionally crosslinked elastomers throughout this paper. In addition, we investigate the influence of intrinsic particle preorientation in conventionally crosslinked elastomers by immobilization of a preoriented particle structure during the crosslinking process.13,21 The strain-and field-induced geometric and magnetic order in the elastomers of different architecture and preorientation is investigated in detail using 2D small angle X-ray scattering experiments and Mössbauer spectroscopy, accomplished by angular-dependent magnetization experiments.
Experimental section
Chemicals
Ammonium hydroxide (25 m% in water), bis(2-ethylhexanoate)tin, hydroxyl terminated poly-dimethylsiloxane (PDMS-OH-L, 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–150
000–150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cSt, Mn = 34
000 cSt, Mn = 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 g mol−1, PDI = 3.2; molar mass determined by GPC), tetraethoxysilane (TEOS, ≥99.9%), and trimethylsiloxy terminated polydimethylsiloxane (PDMS–TMS, 5.0 cSt, M = 770 g mol−1; according to supplier) are purchased from ABCR. Sodium dihydrogen phosphate monohydrate is obtained from Alfa Aesar in ACS reagent grade. Iron(III) chloride hexahydrate is purchased in pure quality from Applichem. Diethyl ether and acetone in technical grade is purchased from BCD Chemie. Absolute ethanol (≥99.8%, HPLC grade), toluene (≥99.8%, HPLC grade), iron(III) nitrate nonahydrate (laboratory reagent grade), and technical grade nitric acid (65 m% in water) are obtained from Fisher Chemicals. Citric acid monohydrate (≥99.5%) is obtained from Jungbunzlauer GmbH. Hydroxyl terminated poly-dimethylsiloxane (PDMS-OH-S, 750 cSt, Mn = 17
400 g mol−1, PDI = 3.2; molar mass determined by GPC), tetraethoxysilane (TEOS, ≥99.9%), and trimethylsiloxy terminated polydimethylsiloxane (PDMS–TMS, 5.0 cSt, M = 770 g mol−1; according to supplier) are purchased from ABCR. Sodium dihydrogen phosphate monohydrate is obtained from Alfa Aesar in ACS reagent grade. Iron(III) chloride hexahydrate is purchased in pure quality from Applichem. Diethyl ether and acetone in technical grade is purchased from BCD Chemie. Absolute ethanol (≥99.8%, HPLC grade), toluene (≥99.8%, HPLC grade), iron(III) nitrate nonahydrate (laboratory reagent grade), and technical grade nitric acid (65 m% in water) are obtained from Fisher Chemicals. Citric acid monohydrate (≥99.5%) is obtained from Jungbunzlauer GmbH. Hydroxyl terminated poly-dimethylsiloxane (PDMS-OH-S, 750 cSt, Mn = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 g mol−1, PDI = 1.6; molar mass determined by GPC) and tetramethylammonium hydroxide solution (TMAOH, 25 m% in water) are obtained from Sigma Aldrich. Deionized water is used in all the following experiments generated by a reverse osmosis system (RO2000Dss + ME + KS_SPS_BA, Stakpure GmbH, Niederahr, Germany) with a residual conductance of <10 μS.
450 g mol−1, PDI = 1.6; molar mass determined by GPC) and tetramethylammonium hydroxide solution (TMAOH, 25 m% in water) are obtained from Sigma Aldrich. Deionized water is used in all the following experiments generated by a reverse osmosis system (RO2000Dss + ME + KS_SPS_BA, Stakpure GmbH, Niederahr, Germany) with a residual conductance of <10 μS.
The following material constants and literature values are used: bulk density of hematite: ρFe2O3 = 5256 kg m−3,22 density of amorphous silica: ρSiO2 = 2200 kg m−3,23 density of poly(dimethylsiloxane): ρPDMS = 980 kg m−3 according to supplier, density of PDMS–TMS: ρPDMS–TMS = 913 kg m−3 according to supplier.
Synthesis
In a next step, the particles are electrostatically stabilized following the procedure proposed by Ewijk et al.25,26 The particles dispersed in water (V = 45 mL, c ≈ 45 mg mL−1) are added to 25 mL of nitric acid (c = 2.0 mol L−1). After 5 min, 25.0 mL of an aqueous iron(III) nitrate solution (c = 0.35 mol L−1) are added, and the dispersion is heated to 100 °C for 1 h. After cooling the dispersion to ambient temperature, the particles are washed once with 25.0 mL nitric acid and afterwards three times with water by collection in a centrifuge. Subsequently, a solution of citric acid in water (c = 0.01 mol L−1) is added until the particles flocculate (V ∼ 100 mL). The particles are redispersed by raising the pH to 8 by addition of TMAOH. Excess ions are removed by washing with water three times.
In order to coat the nanoparticles with silica, a modified Stöber synthesis is employed.26,27 The particles are therefore dispersed in a mixture of ethanol, water and ammonium hydroxide solution with a volume-based composition of 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at a particle-concentration of 1.17 mg mL−1. The reaction is carried out at room temperature in an ultrasound bath at a frequency of 45 kHz.
1 at a particle-concentration of 1.17 mg mL−1. The reaction is carried out at room temperature in an ultrasound bath at a frequency of 45 kHz.
Two different batches of silica coated hematite nanoparticles are prepared under analogous synthetic conditions (Fe2O3@SiO2-1 and Fe2O3@SiO2-2). For the both batches, in each case 8.3 μmol TEOS per mg hematite particles are used. The respective amount of TEOS is divided into three portions, with one portion added every 60 min. After the last addition, the reaction is allowed to proceed for 0.5 h under ultrasound and is then kept overnight at room temperature under magnetic stirring. The obtained particle dispersion is purified by repeated centrifugation with ethanol and then transferred to toluene by centrifugation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 g mol−1) and the catalyst bis(2-ethylhexanoate)tin. By variation of the ratio of PDMS-OH-L to the particle dispersion the particle volume fraction, Φv, of the final elastomers is varied. For all reactions, a catalyst concentration of 3 m% is chosen. After thorough mixing, the reaction mixture is transferred to a poly(tetrafluoroethylene) mold (20 mm × 15 mm × 2.5 mm) and the dispersant toluene is removed at room temperature by application of a vacuum. Subsequently, the polymerization mixture is placed in a vacuum drying oven at 363 K for 33 d.
400 g mol−1) and the catalyst bis(2-ethylhexanoate)tin. By variation of the ratio of PDMS-OH-L to the particle dispersion the particle volume fraction, Φv, of the final elastomers is varied. For all reactions, a catalyst concentration of 3 m% is chosen. After thorough mixing, the reaction mixture is transferred to a poly(tetrafluoroethylene) mold (20 mm × 15 mm × 2.5 mm) and the dispersant toluene is removed at room temperature by application of a vacuum. Subsequently, the polymerization mixture is placed in a vacuum drying oven at 363 K for 33 d.
After the reaction time, the sample is removed from the polytetrafluoroethylene mold and swollen in a large excess of diethyl ether for at least 48 h, in order to remove the catalyst and any unreacted PDMS-OH-L. During this time the solvent is exchanged at least once. The sample is then deswollen in acetone, a non-solvent to polydimethylsiloxane, and dried overnight at 348 K.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 g mol−1) in order to achieve a homogeneous distribution. Subsequently, the toluene is removed from the mixture at ambient temperature in vacuum. By variation of the ratio of PDMS-OH-S to the particle dispersion the particle mass fraction of the final elastomers is varied. To a poly(tetrafluoroethylene) mold (20 mm × 15 mm × 2.5 mm), an amount of TEOS is added directly, corresponding to a molar ratio of TEOS to PDMS-OH-S of 0.125 (nTEOS = 0.125nPDMS-OH-S). For all reactions a catalyst concentration of 3 m% is chosen. After addition of the catalyst, the reaction mixture is thoroughly mixed, bubbles are removed by application of reduced pressure, and the reaction is allowed to proceed for 1 hour at ambient conditions. Subsequently, the polymerization mixture is placed in a vacuum drying oven at 363 K for 7 d.
450 g mol−1) in order to achieve a homogeneous distribution. Subsequently, the toluene is removed from the mixture at ambient temperature in vacuum. By variation of the ratio of PDMS-OH-S to the particle dispersion the particle mass fraction of the final elastomers is varied. To a poly(tetrafluoroethylene) mold (20 mm × 15 mm × 2.5 mm), an amount of TEOS is added directly, corresponding to a molar ratio of TEOS to PDMS-OH-S of 0.125 (nTEOS = 0.125nPDMS-OH-S). For all reactions a catalyst concentration of 3 m% is chosen. After addition of the catalyst, the reaction mixture is thoroughly mixed, bubbles are removed by application of reduced pressure, and the reaction is allowed to proceed for 1 hour at ambient conditions. Subsequently, the polymerization mixture is placed in a vacuum drying oven at 363 K for 7 d.
The samples with an anisotropic orientational distribution of the embedded filler particles (ACE-1 and ACE-2) are obtained by placing the reaction mixture in a homogeneous magnetic field with a flux density of 200 kA m−1 generated by two rectangular permanent magnets. The reaction time is 7 d for sample ACE-1 and 8 d for sample ACE-2. After the reaction time, the sample is removed from the polytetrafluoroethylene mold and directly analyzed without further swelling or purification.
Instrumentation
Throughout this work the particle content is given as a mass fraction. By VSM, the experimental mass fraction Φm is directly accessible as the fraction of the spontaneous magnetization of the respective elastomer Ms,elast. over the spontaneous magnetization of the pure core–shell particles in powder state Ms,part.
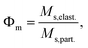 | (1) |
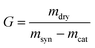 | (2) |
Here, msyn denotes the mass of the elastomer after synthesis (before swelling). The volume based equilibrium swelling degree ΓV is given by the ratio of the volume of the swelling medium taken up by the elastomer sample relative to its own volume without the magnetic nanoparticles, as those due not contribute to the swelling.18,20
 | (3) |
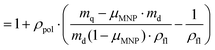 | (4) |
Here, Vpol and Vfl, and ρpol and ρfl denote the volume and the bulk density of the polymer and the swelling medium, respectively. mq is the mass of the swollen network, md the mass of the dry elastomer and mMNP the mass of the embedded nanoparticles, as obtained from static magnetometry. For all swelling experiments PDMS–TMS is employed as swelling medium and the equilibrium swelling is determined after swelling in a great excess of PDMS–TMS for at least 7 days.
Results and discussion
The idea of this work is to investigate the interplay between the magnetic, and geometric degrees of order found in hybrid elastomers filled with elongated magnetic nanoparticles. For this purpose, we analyze the internal structure in well-defined hybrid elastomers of different architecture by means of a combination of methods under the influence of strain or magnetic fields. We compare the behavior of elastomers exclusively crosslinked via covalent polymer-particle linkage,16 to that of conventionally crosslinked networks of similar composition with initially either isotropic or anisotropic distribution of the nanoparticles within the matrix. Comparing the materials with different architecture, we correlate the differences in material behavior and architecture to the strain-induced orientation behavior of the embedded filler particles.As particulate fillers, spindle type hematite nanoparticles are employed, which show a magnetic as well as a tunable geometric anisotropy. In order to induce a functional particle surface and to compatibilize the particles with the PDMS matrix, in a first step the analyzed particles are coated with a silica shell. After incorporation in the elastomer matrix, the strain- and magnetic field-induced orientation behavior of these nanoparticles with anisotropic shape is analyzed.
Particle characteristics
Spindle-type hematite nanoparticles bring along a number of peculiar properties that make them attractive as a model system. The synthesis and surface modification chemistry of these nanoparticles is well-studied and scalable, so that in one lab-scale step, highly stable particles in dispersion are accessible in a gram scale yield.17,24,29 The shape of the nanoparticles can be varied between spherical and spindle-like in different aspect ratios by variation of the synthesis conditions.30 Under proper conditions, the nanoparticles are reproducibly obtained with low polydispersity. The latter property greatly facilitates the analysis of the internal structure and order in their composites by scattering techniques.31,32Further, spindle-type hematite nanoparticles have particulate magnetic properties that arise from their internal atomic structure. Hematite crystalizes in the trigonal–hexagonal scalenohedral class structure with the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c.33 Hematite is an antiferromagnet with a Morin transition temperature at 263 K in bulk that decreases rapidly with the grain size for nanoparticles below 100 nm.34 Below the Morin transition the spin moments are arranged parallel to the trigonal c axis. Above the Morin transition, the spins are located within the basal plane and are slightly canted, leading to a minor net magnetic moment perpendicular to as well the c axis and the spin preferred alignment, respectively.35 For the silica coated, spindle-shaped hematite nanoparticles employed in this study, over the whole temperature range spanning from 4 K to ambient, a nuclear quadrupole level shift of approximately −0.2 mm s−1 is experimentally observed,34 proving a perpendicular orientation between the individual spins and the hematite polarization axis. This result confirms that the magnetic cores are really in the weakly ferromagnetic state that is usually found above the Morin transition. Consequently, as in the spindle-type nanoparticles the c axis is parallel to the long particle axis, the small net magnetic moment m of an individual particle is, contrary to most anisotropic magnetic nanoparticles, oriented perpendicular to the long particle axis l.36
c.33 Hematite is an antiferromagnet with a Morin transition temperature at 263 K in bulk that decreases rapidly with the grain size for nanoparticles below 100 nm.34 Below the Morin transition the spin moments are arranged parallel to the trigonal c axis. Above the Morin transition, the spins are located within the basal plane and are slightly canted, leading to a minor net magnetic moment perpendicular to as well the c axis and the spin preferred alignment, respectively.35 For the silica coated, spindle-shaped hematite nanoparticles employed in this study, over the whole temperature range spanning from 4 K to ambient, a nuclear quadrupole level shift of approximately −0.2 mm s−1 is experimentally observed,34 proving a perpendicular orientation between the individual spins and the hematite polarization axis. This result confirms that the magnetic cores are really in the weakly ferromagnetic state that is usually found above the Morin transition. Consequently, as in the spindle-type nanoparticles the c axis is parallel to the long particle axis, the small net magnetic moment m of an individual particle is, contrary to most anisotropic magnetic nanoparticles, oriented perpendicular to the long particle axis l.36
This preferred orientation of the magnetic moment opens the possibility to orient the particles giving access to anisotropic materials and can additionally be used as a probe to detect order of the magnetic nanoparticles due to the coupling of the magnetic moment to the geometric anisotropy. The nanoparticles are reported to show three magnetic easy axes located within the basal plane and one magnetic hard axis given by the long particle axis parallel to the c axis.13 The energy barrier for transition of the magnetic moment to another easy axis within the basal plane is low, thus almost superparamagnetic behavior is observed within the basal plane.13
The shape and geometric parameters of the nanoparticles with and without silica shell are determined using TEM as exemplarily shown in Fig. 1, and the results for the geometric scales of the parameters according to TEM are summarized in Table 2 in comparison to the results of other methods. Two batches have been prepared with analogous synthesis conditions, resulting in two particle batches with similar size and aspect ratio within the reproducibility expectations. For both batches, a particle ensemble of uniform size is observed with a clear spindle-like shape of the core particle. The particles have a mean core length of 370 nm, a core width of 71 nm, and a silica shell thickness of 12 nm (see Table 2). The silica shell around the particle is homogeneous, and pores are not observed. Furthermore, the silica shell is of homogeneous thickness on the surface. The spindle-type shape of the core particle transforms consequently to a more ellipsoid-like shape.
 | ||
| Fig. 1 Representative TEM image of spindle-type hematite nanoparticles from batch Fe2O3@SiO2-1 (a) without silica shell and (b) with silica shell. | ||
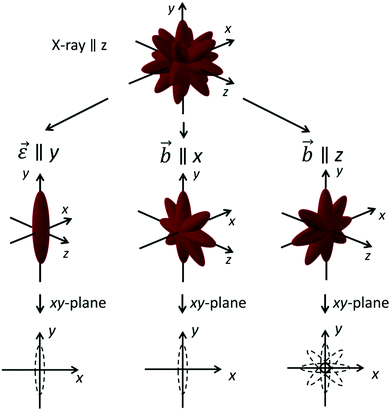
The composite materials synthesized in this work either show a permanent or temporarily induced anisotropic orientation of the embedded spindle-type hematite nanoparticles, which is schematically illustrated in Fig. 2. Under isotropic conditions, thus without action of an external orienting field or strain, the dipolar particle interactions due to the low magnetic moment of the particles are neglectable, and accordingly on a global scale, the orientation of the particles with respect to the axis of investigation is isotropic in all directions. Upon application of a homogeneous magnetic field along the x direction, the magnetic moment within the basal plane of the particles preferably orients along the field, with arbitrary angles of the long particle axis perpendicular to the field direction, thus in the yz plane. This leads to a preferred uniplanar orientation of the particle geometry. On the other hand, straining of the matrix surrounding elongated particles is expected to induce a preferential uniaxial orientation of the particle long axis parallel to the applied strain,15 as response to a torque produced by the surrounding matrix. For conventionally crosslinked elastomer networks with a mesh size smaller than the particle size, the torque is obvious, as the mesh will be deformed in direction of the applied strain. For the novel particle-crosslinked elastomers, this will only lead to very small torques on the particle, as the mesh size is essentially the particle distance and the particles are connected by very long polymer chains.16 Thus, we interpret the torque on the particles as additionally originating from a friction component of the disentangling polymer chains on the particle surface, in analogy to the orientation of elongated particles dispersed in a viscous matrix in shearing experiments.
Synthesis and properties of particle-filled elastomers with different architectures
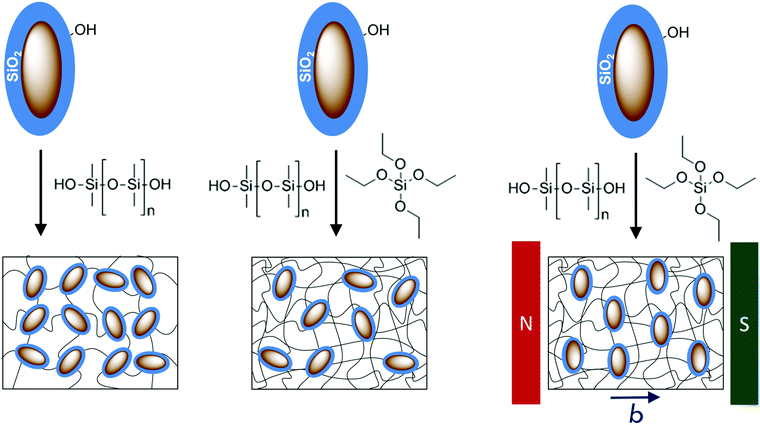
Samples with three different architectures are prepared, and the influence of sample architecture on the strain-induced ordering of dispersed spindle-type hematite nanoparticles is analyzed by a combination of methods.Particle-crosslinked elastomers,16 contrary to other elastomer networks, contain no specific crosslinker except for the multifunctional, inorganic nanoparticles, which leads to networks having highly functional nodes based on inorganic nanoparticles connected by long polymer chains. The resulting material properties of these particle-crosslinked elastomers are strongly dependent on the particle content. The samples are denoted as FE (“ferroelastomer”) throughout this work.
The particle-crosslinked elastomers are obtained by reacting hydroxy-terminated poly(siloxanes) in bulk in the presence of catalyst and silica-coated hematite particles. As shown in our previous work,16 using a reaction temperature of 90 °C and an efficient removal of the forming water in vacuum, stable elastomers are obtained, without additional crosslinker, except for the nanoparticles. By condensation of hydroxy end groups of the polymer chains with the particle surface, the nanoparticles serve as multifunctional inorganic crosslinkers for the network, and a unique architecture results.
These structures are compared to conventional networks based on crosslinked polymer chains. Here, the tetrafunctional crosslinker TEOS is employed at low molar fraction and in the presence of bifunctional PDMS-OH-S, the filler particles and catalyst. TEOS and PDMS-OH-S readily react at ambient temperatures to form a prepolymer, which is then completely cured at 90 °C in vacuum.37,38 Due to the employed stoichiometry (nTEOS = 0.125nPDMS-OH) and the functionality of PDMS-OH-S (f = 2) and TEOS (f = 4), we expect the formation of a prepolymer. After formation of the prepolymer, 75% of the employed PDMS-OH hydroxyl functionalities have not reacted and in the following reaction steps at 90 °C the network is cured completely under reaction of hydroxyl functionalities of the PDMS-OH-S reactant with itself and additionally covalent attachment to the surface of the embedded filler particles. The obtained conventionally crosslinked elastomers are denoted CE (“conventionally crosslinked elastomer”).
In addition, a particle-related anisotropy structure can be manifested in the materials already during the synthesis by the application of an external homogeneous magnetic field during the crosslinking process. The magnetic moment of spindle-type hematite nanoparticles allows their magnetic orientation, and opens a pathway to inscribe a preordered structure to the sample, if the magnetically induced order is conserved by dense crosslinking around the oriented particles. The magnetic moment is coupled to the basal plane leading to an orientation with the basal plane oriented parallel to the applied field, while the long particle axis is statistically distributed in the plane perpendicular to the applied field direction (see Fig. 2). Samples with this architecture, based on conventionally crosslinked elastomers with an anisotropic orientational distribution of the embedded filler particles are denoted ACE (anisotropic conventionally crosslinked elastomer) in the following, and the direction of the magnetic field during synthesis is referred to as axis b.
A reaction scheme for all architectures is found in Fig. 3 and relevant parameters of the prepared elastomers are compiled in Table 1. For all samples, high gel contents above 75 m% are found. The gel content is the mass fraction of initial monomers and particles that is irreversibly immobilized in the final network after synthesis. A high gel content is important to ensure a good homogeneity of the sample. For the particle-crosslinked elastomers, the part of the sample that has not been attached to the network yet is removed. This is achieved by swelling the sample in a large amount of diethyl ether and careful deswelling in acetone. For analysis of the final compositions, see Table 1.
| Sample | FE-1 | FE-2 | FE-3 | CE | ACE-1 | ACE-2 |
|---|---|---|---|---|---|---|
| Particle mass fraction Φm [m%] | 16.7 | 27.5 | 32.3 | 9.6 | 10.9 | 11.8 |
| Gel content G [m%] | 78.5 ± 1.0 | 75.9 ± 1.0 | 80.0 ± 1.0 | 98.2 ± 2.3 | 94.0 ± 3.2 | 86.3 ± 3.2 |
| Equilibrium swelling degree Γv | 23.7 ± 1.4 | 14.0 ± 1.9 | 11.0 ± 1.1 | 3.8 ± 0.4 | 5.2 ± 0.8 | 6.1 ± 0.7 |
For the chemically crosslinked elastomer samples, the gel content is so high that this procedure is not necessary. Additionally, for the sample ACE upon swelling a reorientation of the embedded filler particles is conceivable, which should be prevented for proper analysis.
For the particle-crosslinked elastomers, the volume-based equilibrium swelling degree decreases with increasing particle content attributed to denser crosslinked network structure upon increasing the content of crosslinking particles.18,20 For the conventionally crosslinked samples, lower values for the swelling degree are observed, due to the higher crosslinking density resulting from addition of the crosslinker TEOS. The equilibrium swelling degree of the sample ACE-1 and ACE-2 is equal within error margin. For sample CE a lower value is observed, which is still in a similar size range considering the error margins. The higher swelling degrees for the samples ACE-1 and ACE-2 furthermore correlate to their lower gel contents. The deviations may be attributed to a fluctuation of the crosslinking density due to either a locally or globally different crosslinker concentration or network defects, such as dangling ends. As the crosslinker concentration is low, even small deviations may have a large impact on the crosslinking density.
For this study, we in-depth analyze the internal structure for the different architectures based on 2D small angle X-ray scattering, Mössbauer spectroscopy, magnetization measurements, and Monte Carlo simulations.
Small angle X-ray scattering analysis of strain- and field-induced order phenomena
Small angle X-ray scattering (SAXS) is a powerful tool to investigate the internal structure of complex matter on the nanoscale, including the size, shape, and structure of nanoparticles in various media.39 In the case of anisotropic nanoparticles, a suitable experimental setup with two-dimensional detection gives access to the angular distribution of particle orientation. In case of elongated (prolate) particles with a preferential orientational axis within a polymer composite, an azimuthally anisotropic distribution of the scattered intensity is expected and can be analyzed for its information on the order parameter using well-stablished approaches.31,32In this work, the X-ray scattering contrast between elongated core–shell nanoparticles and their PDMS matrix is exploited to extract information on the strain- and field-induced particle orientation in filled elastomers of different architecture (FE, CE, and ACE, see above). After discussing the small angle X-ray diffractograms of the samples without external field or deformation, we demonstrate how the application of external strain or magnetic fields influences the internal orientational order of the nanoparticles in the elastomeric matrix.
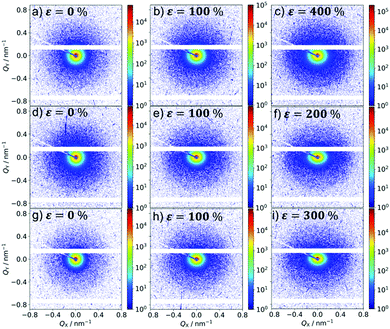
The analyzed Q regime is 0.07 nm−1 to 3.0 nm−1, and thus the accessible real space according to Braggs law is approximately between 90 nm and 2 nm.40 Hence, structural and orientational information from scattering experiments in the accessible Q regime is mainly expected from the particle shell (thickness ∼ 12 nm according to TEM, see Table 2) and from the short particle axis (∼71 nm), while the long axis (∼370 nm) is too long for a significant contribution. An exemplary set of 2D scattering patterns as obtained in this work are shown in Fig. 4.
| Batch/parameter | Fe2O3@SiO2-1 | Fe2O3@SiO2-2 | |||
|---|---|---|---|---|---|
| TEM | SAXS FE | TEM | SAXS CE | SAXS ACE | |
| Particle core length [nm] | 377 ± 42 | — | 363 ± 39 | — | — |
| Particle core width [nm] | 70.6 ± 8.7 | 54 ± 22 | 72.0 ± 8.4 | 55 ± 22 | 54 ± 22 |
| Shell thickness [nm] | 12.3 ± 1.3 | 11.7 ± 0.3 | 11.7 ± 1.4 | 12.2 ± 0.3 | 12.6 ± 0.3 |
For the reference samples that are prepared without external field, (FE-1 and CE), the scattering patterns are isotropic for the unstrained case (see Fig. 4a and d), as we would expect for essentially isotropic samples. The scattering response of sample ACE-1, prepared under field influence, is discussed further below.
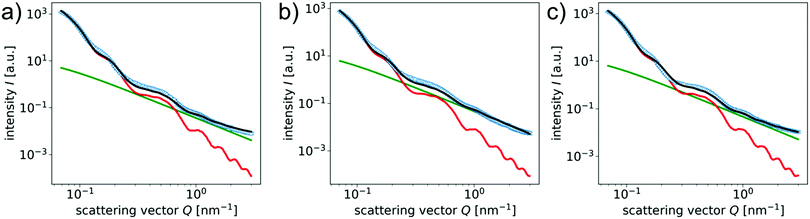
A detailed analysis of the scattering intensity over the observable Q regime is performed based on a proper model that takes into account the contributions of the different characteristic length scales present in the filler particles, and the polymer matrix. A proper description of the experimental data is obtained using a linear combination of the form factor of a polydisperse ellipsoid with a constant shell thickness with a structure factor based on the Ornstein–Zernicke correlation function, accounting for the polymer scattering. The Ornstein–Zernicke scattering function is defined as:41
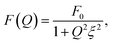 | (5) |
The form factor of the ellipsoid PMSE with a shell of constant thickness is described as follows, where Fa denotes the form factor amplitude.28,43,44
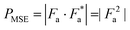 | (6) |
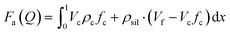 | (7) |
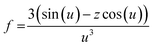 | (8) |
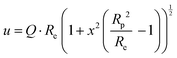 | (9) |
 | (10) |
In these equations the index c characterizes the hematite core, sil denotes the silica shell, and no index is used for the whole particle, as obtained as the sum of both respective radii. The volume of the particles is calculated according to eqn (10), where Re denotes the equatorial radius and Rp is the radius at the poles. The X-ray scattering length densities are denoted as ρ and are calculated using the calculator supplied by NIST from the elemental composition, the bulk density, and the energy of the employed radiation (Ga-Kα). The employed scattering length densities are corrected for the scattering of the polymer by subtraction of the scattering length density of PDMS. Polydispersity is introduced to the system by considering a distribution of the equatorial and polar radius, as well as the silica shell. As the polar radius is not visible in the analyzed Q regime, it is set to an arbitrary value of 220 nm and a polydispersity of 40 nm is employed to prevent contributions from this semiaxis in the fit. The distribution of the particle core is modeled by a lognormal function, in agreement with the growth mechanism, and the distribution of the silica shell is considered as a Gaussian distribution.
The final model for description of the scattering of our samples is obtained by linear coupling of the discussed equations and considering a constant background as a free parameter. All form factors and functions employed for the fit are taken from the program jscatter.28 The individual contributions of the respective form and structure factors to the overall fit can be seen as the solid red and green line in Fig. 5. As the system consists of spindle-type hematite particles with a rather ellipsoidal silica shell in a continuous polydimethylsiloxane matrix, this combination describes our system very well. Deviations of the fit from the experimental data at high Q values might originate from a small background resulting from diffuse background scattering, as no proper background subtraction is possible due to the unique network architecture of the particle-crosslinked elastomers and thus no background subtraction is performed. The satisfying agreement of the fits of the sample system with the experimental data is a good indication that the observed anisotropy really originates from a preferred orientation of the embedded silica coated hematite particles.
In Table 2 the important fit parameters for the size of the particles and their polydispersity are summarized. The silica shell thickness is in excellent agreement with the experimental value determined by TEM analysis and can be described with low values for the polydispersity. For the particle core, deviations are expected as the radius of curvature for an ellipsoid differs significantly from the respective one of a spindle.30 In our model this is found as a high value for the polydispersity of the particle core, which is necessary to describe the first feature of the curve of the experimental data at low values for Q. Another reason for the high polydispersity is the surface roughness of the particles as observed in the TEM images in Fig. 1.31 The value for the particle core width itself is considering the error margins in good agreement with the value determined by TEM, although it is lower, which might be due to the larger ensemble of particles probed.
In case of the anisotropic reference sample ACE-1 that is prepared in the presence of a homogeneous magnetic field, we expect a preferred orientation of one of the nanoparticles magnetic easy axes in the basal plane parallel to the field direction, and a resulting preferred orientation of the long particle axis in the plane perpendicular to the original field axis b during synthesis,30 as schematically shown in Fig. 2. For the SAXS investigation we therefore have to distinguish two geometric configurations.
If the sample is probed by SAXS in a configuration, where the beam is parallel to the original field direction b, this results in an isotropic scattering pattern in SAXS measurements according to the isotropic, disk-like shape of the electron density, as schematically indicated in Fig. 2. The obtained isotropic scattering pattern is shown in Fig. 4g. It is readily analyzed following the model described above, and the corresponding parameters for the particle geometries are shown in Table 2 with good correspondence to the TEM results. For the investigation of the strain-induced order in ACE-1, this axis of investigation (beam direction z parallel to b) is chosen in order to guarantee best comparability to the corresponding experiments involving the non-preoriented samples FE-1 and CE.
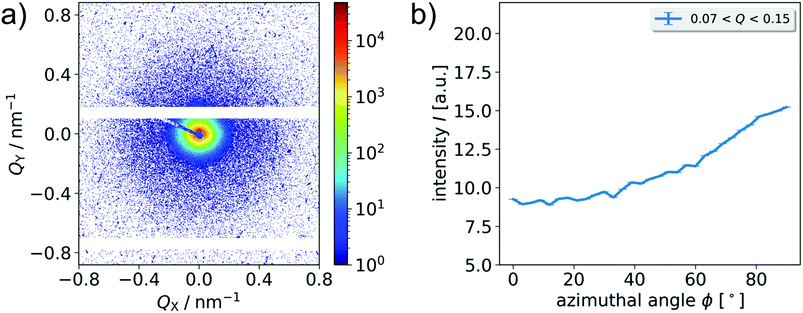
More interesting however, concerning the intrinsic anisotropy in the sample ACE-1 that is conserved during the synthesis is the analysis of the sample structure of ACE-1 perpendicular to the original field axis b. This is achieved, by probing the sample with the beam axis z perpendicular to b, with b placed along the x axis of the experimental setup. The resulting 2D scattering pattern is shown in Fig. 6a. The pattern, in contrast to the respective analysis along the b axis, shows an anisotropic scattering intensity, with enhanced scattering intensity parallel to Qx on cost of intensity parallel to Qy. This can be displayed in more detail by plotting the scattering intensity in a certain Q range in dependence on the azimuthal angle (Fig. 6b).
It can readily be anticipated that the observed anisotropy is a result of the preordering of the nanoparticles during the synthesis caused by the magnetic field, and its manifestation in the crosslinking process. In the configuration discussed here, the scattering pattern indicates that the particle short axis show a preferred orientation in x direction. This is in full correspondence with the expectation, as the particles are preferably magnetized in the basal plane, see also Fig. 2 for an overview about the relevant orientations of X-ray beam, magnetic field, and particle orientation probed in this work.
From the azimuthal intensity distribution, we calculate the order parameter of the particle short axes with respect to the x axis of the setup following the procedure described further below in the context of SAXS analysis of strained samples (eqn (11)). The 2D scattering analysis of the intrinsic anisotropy of the ACE-1 sample in this specific geometry reflects the degree of order corresponding to a 2D projection of the ensemble and is actually of planar nature. For practical reasons, we prefer to define the order parameters in this study with respect to the long particle axis, and due to the perpendicularity, the result is equal to the order parameter of the long particle axis l with respect to the y axis and thus is assigned as Sy. The order parameter of this projection is obtained as Sy = 0.26 ± 0.01 in the low Q regime (0.07 nm−1 < Q < 0.15 nm−1) and Sy = 0.29 ± 0.02 obtained in the high Q regime (0.4 nm−1 < Q < 1.5 nm−1). For a completely ordered sample (here: perfect alignment of the long axis perpendicular to the axis b), Sy is expected to be 1, while a value of 0 indicates no preferential orientation. The experimental result thus represents significant, but incomplete ordering of the particle axis in the expected plane.
The data can be used to estimate also the order parameter of the long axis l with respect to the original field axis b (assigned as Sb), in order to better describe the actual, equatorial preference of the configuration, and to compare it to the results of Mössbauer spectroscopy (see below). Under this definition, a result of −0.5 indicates full orientation of the long particle axes l in a plane perpendicular to b. This order can be quantified by a phase shift of the azimuthal scattering intensity by 90°, thereby the order parameter of the long particle axis l is determined with respect to b. Experimentally, we obtain Sb = −0.25 ± 0.01 in the low Q regime and Sb = −0.28 ± 0.03 in the high Q regime, respectively, confirming that the permanent geometric anisotropy as analyzed by SAXS in sample ACE-1 is significant, but not complete.
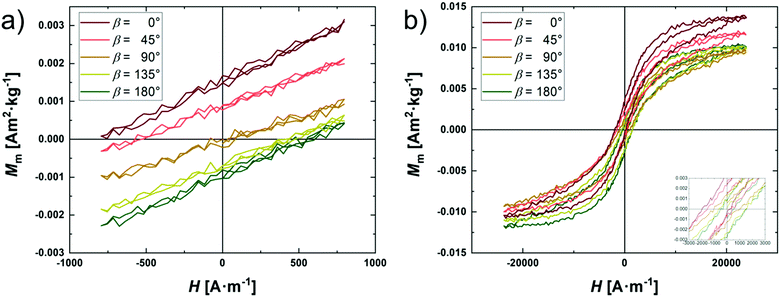
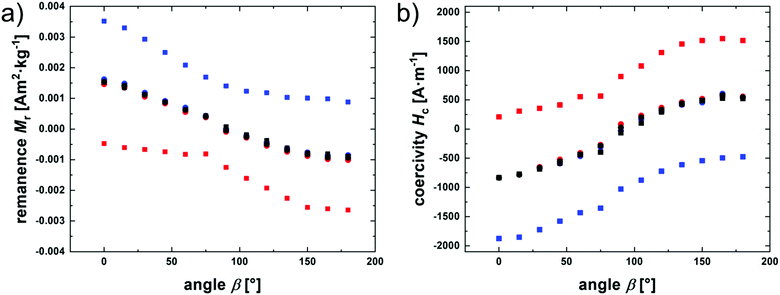
Additional information on the degree of magnetic order conserved by the crosslinking process in the magnetic field for ACE samples is accessible by magnetization experiments. The magnetic properties of isotropic conventionally and particle-crosslinked elastomers have been reported in our previous work,16 and are thus not presented here again. Generally for the particle-filled elastomers, an open hysteresis loop and magnetic characteristics comparable to the nanoparticles in powder state are observed. As sample ACE-1 has an anisotropic distribution of the embedded magnetic nanoparticles, an angular-dependence of the magnetic properties are expected. In order to analyze this, angular-dependent magnetization curves are collected for sample ACE-1 at ambient temperature in 15° steps (Fig. 7 and 8). The reference axis (β = 0) thereby is the anisotropy axis of the sample, b. Two series of experiments are performed with different field amplitude of 0.8 kA m−1 and 24 kA m−1, respectively. The magnetization curves measured with the lower field amplitude do not show a hysteresis (Fig. 7a), yet a systematic shift of the curve along the M axis depending on the angle is observed. With increasing angle β, the curve intersects the M axis at a higher magnetization value. While the intersection for the curve obtained at 90° crossed nearly the origin, the curves at 0° and 180° intersect the axis at values of ±0.0015 A m2 kg−1. In contrast, for the higher maximum field amplitude of 24 kA m−1, an open hysteresis loop is observed. Again, the curves are systematically shifted along the M axis depending on the field angle. In Fig. 8, the remanence and coercivity of both measurements are shown in dependence on the field angle. The measurements at lower maximum field strength show a decrease of the remanence from positive values at β = 0° over zero at 90° to a negative maximum at 180°. The coercivity in Fig. 8a shows the opposite trend, starting from a minimum at 0° going to the maximal, negative value at β = 180°, while also crossing zero at 90°.
The courses are qualitatively understood on the base of the Stoner–Wohlfarth model by considering a respective particle ensemble that is probed with a maximum field amplitude either below or above the coercivity caused by the particles.45,46 In the case that the maximum field strength is well below the critical strength for an internal (NéeI type) remagnetization of the particles, the magnetic moment of the particles will return to its initial easy axis, and thus, full reversibility is achieved, and no hysteresis is observed. In the direction of the original magnetization, even in the field-free case, a net magnetization of about 0.0015 A m2 kg−1 is detected, representing the preferential orientation of the local magnetic moments with the field axis. The intersection of the magnetization curves with the M axis then decreases with increasing field angle, until at 90° an intersection at about M = 0 is observed, in correspondence with the model. By further increasing the angle, the magnitude of the remanence increases again with opposite sign. An analogous argumentation is valid for the angular coercivity trend.
For the measurements at higher field amplitude, an internal magnetization reversal of the particles becomes possible, and accordingly, the results for Mr and Hc depend on the history of the material. Consequently, the corresponding magnetization curves are hysteretic, and different values for the increasing and decreasing field branches are found. Information on the respective, angular-dependent curve shift can be obtained by calculating the average between the two values, and the corresponding values match those for the small field amplitude series, as seen in Fig. 8a, showing that the conserved magnetic anisotropy leads to magnetic switching at higher fields, but under conservation of the preferred axis.
The model this qualitatively explains the dependence of the outcomes on the maximum applied field strength, attributed to the critical field strength for an internal reorientation of the magnetic moment inside the particles at high fields. A more quantitative interpretation of the magnetization curve with this model, however, is beyond the scope of this work, realizing that in contrast to a simple Stoner–Wohlfarth particle that typically is assigned to have one, strongly preferred, easy magnetization axis, the hematite nanoparticles are shown to have a more complex magnetic signature. In place of one easy axis, the nanoparticles are discussed to show three easy magnetization axes organized in the basal plane of the spindle.13 By magnetic saturation at high fields, a reorientation of the magnetic moment toward the opposite or into one other axis is thus still possible.
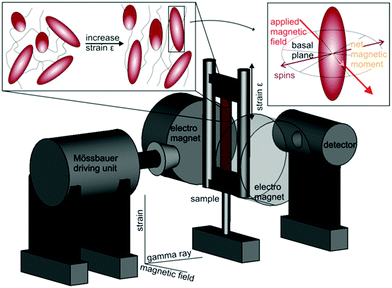
Therefore, stripes of the samples FE-1, CE, and ACE-1 are placed in a house-built straining apparatus, and 2D SAXS scattering pattern are recorded for various degrees of strain for the different samples. The strain is varied between 0% and 400%. In all experiments, the X-ray beam is along the z axis, and the strain is applied perpendicular to the beam along the Qy axis, as visualized in Fig. 2.
For all samples, upon increasing the strain, an anisotropic, non-spherical 2D scattering pattern is obtained. The shape of the scattering pattern is elongated along the x axis, if a strain is applied. The patterns become increasingly anisotropic with increasing applied strain ε.
As only the orientation of the short axis and the preferred silica shell orientation is relevant in the accessible Q range, the shape of the scattering pattern indicates a preferential orientation of the two vectors parallel to the Qx axis, resulting in an enhancement of the scattered intensity parallel to Qx on cost of intensity parallel to Qy. Due to the perpendicularity, a preferred orientation of the short axis and silica shell vectors in Qx indicate a preferred orientation of the long axis in Qy (along the strain ε).
The behavior is qualitative similar for all three investigated samples. This effect is explained by an increasingly preferred orientation of the elongated nanoparticles in the strain direction due to a matrix-induced reorganization of the fillers. Once strain is applied, the polymer coils inside the elastomer matrix elongate in direction of the applied strain. The nanoparticles are on the one hand covalently attached to the polymers and on the other hand are influenced by the elongating polymer coils due to viscous friction on the particle surface, and both effects lead to an orientation of the particles with their long axis parallel to the applied strain (Fig. 2, left).
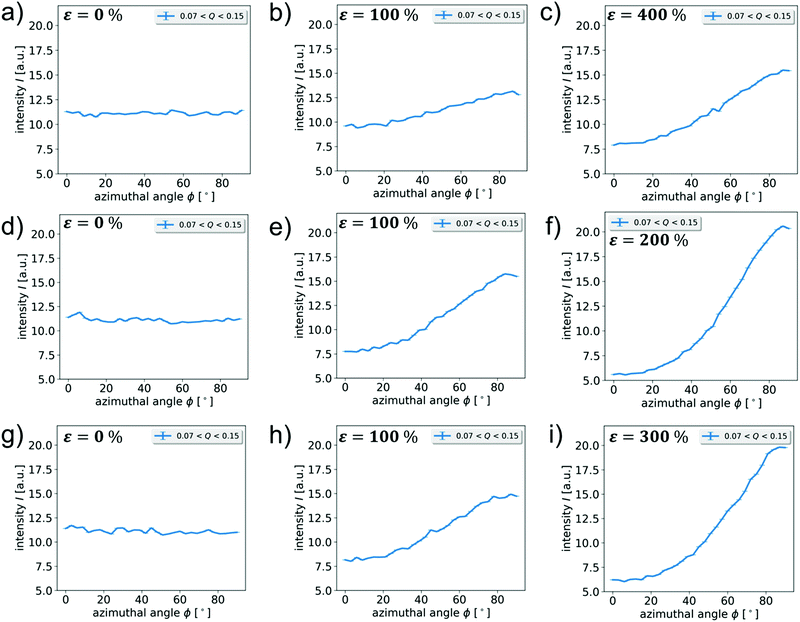
For a more quantitative analysis of the strain-induced order, we plot the azimuthal distribution of the intensity by averaging it in sectors with a width of 3° in two different Q regimes. In the regime 0.07 nm−1 < Q < 0.15 nm−1, which corresponds to dimensions in real space of 42 nm to 90 nm, and thus mainly contributions from the short axis of the particle core are expected. Additionally, the regime 0.4 nm−1 < Q < 1.5 nm−1 is analyzed, where the scattered intensity predominantly arises from contributions of the silica shell.
In Fig. 9, the azimuthal dependence of the averaged intensity is shown exemplarily for FE at a strain of ε = 400% for the complete scattering image (angles from 0° to 360°) for the lower Q regime (0.07 nm−1 < Q < 0.15 nm−1). Additional plots of the azimuthally averaged intensity can be found in the ESI† (Fig. S2). Although between ϕ = 100° and 120°, no experimental data is accessible due to the beam stop position, we can report the confirmation of the expected high symmetry of I(ϕ) with two mirror planes at 90° and 180° within the limits of experimental accuracy for all samples investigated under the respective geometric circumstances (Fig. 4). For further analysis of the data, it is therefore sufficient to analyze the interval between ϕ = 0° and 90°.
 | ||
| Fig. 9 Azimuthal scattering intensity depending on the azimuthal angle for sample FE at ε = 400%. The intensity is averaged in the Q regime 0.07 nm−1 < Q < 0.15 nm−1 representative for the small nanoparticle axes. The lack of experimental data and the significant drop of the intensity at angles between ϕ = 100°–120° originate from the beam stop (compare also to the 2D scattering patterns in Fig. 4). | ||
In Fig. 10, the azimuthal intensity distributions for the 2D scattering patterns in Fig. 4 are shown. If no strain is applied (ε = 0%), the intensity depending on the azimuthal angle is a flat line for all samples, indicating an isotropic orientational distribution of the dispersed nanoparticles. Upon increasing the strain a systematic, significant change in the structure of the I(ϕ) curve is observed, with the maximum at 90° and 270° (x axis) getting more and more pronounced with increasing ε on cost of intensity along the y axis (ϕ = 0).
For quantitative analysis of the strain-induced order in particle-filled elastomers, the order parameter is evaluated. The calculation is performed according to an approach presented by Lovell and Mitchel as an averaged over the second Legendre polynomial, which is given by the following equation.47
 | (11) |
Here, S is the order parameter, ϕ is the azimuthal angle (y axis corresponds to ϕ = 0), and I(ϕ) is the intensity value at a given azimuthal angle. The order parameter S is expected to be 0 for statistically distributed, non-oriented particles, 1 for particles whose director is parallel to the test axis, and −0.5 for perfectly orthogonal alignment perpendicular to the test axis. In this case, the short particle axis is defined as the director and the direction Qx is the test axis. As explained earlier, the perpendicularity allows to equally ascribe this value to the order of the long particle axis l with respect to the y axis, which is strain direction. Thus, the determined order parameter is assigned as Sε here. Hence, we expect Sε = 1 for perfect alignment of the short axis to Qx and, thus, alignment of the long axis parallel to the applied strain, as is exemplarily shown in the scheme in Fig. 2.
For a quantitative analysis, a background intensity originating from diffuse air scattering as well as unspecific scattering contributions from the sample has to be subtracted before eqn (8) can be used correctly.48 The procedure on how to determine the background intensity is described in detail in the ESI† (see Section S3).
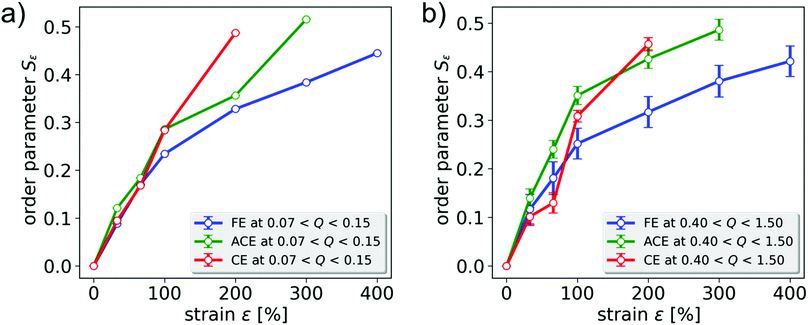
The obtained order parameters for all samples depending on strain are shown individually in the ESI† (Fig. S4) and sorted by the respective Q regime of averaging in Fig. 11. The courses of the data points obtained for the low Q regime, at 0.07 nm−1 < Q < 0.15 nm−1, corresponding to the short axis of the particle core and for the higher Q regime, at 0.4 nm−1 < Q < 1.5 nm−1, corresponding to the silica shell show the same trend and the individual data points for one sample are almost always identical within error margin. By assuming the azimuthal trend in the two different Q regimes to originate from predominantly the short particle axis orientation and the silica shell normal vector, this coincidence can easily be explained by the predominately parallel orientation of the shell layer with the long particle axis (Fig. 2 and Fig. S4, ESI†) and thus confirms the expectations.
In Fig. 11, the strain-induced order parameters Sε of all samples are shown sorted by their respective Q regime. For all samples, the degree of order as calculated from the scattering patters, thus assigned to the preferred orientation of short particle axis in the x direction, increases steadily with increasing strain, indicating a preferred orientation of the long axis in the direction of strain. This is thus in accordance with the expectations discussed above.
In comparison of the three investigated samples, we observe that the obtained value and trend of the order parameter Sε with strain is found to be coinciding for the two chemically crosslinked samples, CE and ACE, within the experimental accuracy, in both Q regimes. In order to understand this, we should point out that in the given geometry, the scattering patterns of the unstained samples CE and ACE-1 are found to be isotropic, and that the intrinsic order in sample ACE-1 is limited to the axis that is now oriented parallel to the beam. In addition, both samples are synthesized under identical synthetic conditions, including composition and reaction time, and can thus be expected to be of similar chemical crosslinking density. As discussed above, the scattering pattern of magnetically oriented particles is either isotropic or anisotropic depending on the test axis, parallel or perpendicular to the applied field respectively. For maximal comparability of the experimental data, the isotropic direction is chosen as the test axis in our strain-dependent experiments. With respect to the axis of observation, the architecture and distribution of nanoparticles inside the chemically crosslinked elastomers is thus comparable, and no direct influence on the strain-induced orientation behavior is found. We thus conclude that for the analyzed test axis the strain-induced order of the embedded magnetic nanoparticles is independent of the preorientation of the analyzed filler particles in the xy plane.
In contrast, for the particle-crosslinked sample FE-1, two regimes can be identified. For small strains up to ε = 66%, no significant difference in the strain-induced order parameter Sε between chemically and particle-crosslinked elastomers is found, and a nearly linear increase of the order parameter with strain is observed. For larger strain values, the stain dependence for the particle-crosslinked elastomers is weaker than for the conventionally crosslinked elastomers. This behavior coincides with the differences found for the mechanical properties of corresponding elastomers with different sample architectures as reported in our previous report: for particle crosslinked-elastomers, the stress–strain curves show a saddle point and a following regime with a low slope of the stress–strain curve, sometimes referred to as rubber elastic plateau, beginning above strains of ε = 50%. This plateau is characterized on the mesoscopic length scale by a disentanglement of the long polymer chains linking the particles. The chemically crosslinked elastomers on the other hand do not show a significant rubber elastic plateau and only a small decrease of the slope of the stress–strain curve, similarly observed for the order parameter of these samples in Fig. 11.16 Additionally, they show significantly lower strain at break, leading to material failure of the analyzed samples CE, and ACE-1 at 200% and 300%, respectively.
We therefore address the nearly linear increase of the order parameter at small strains to the Hookean-type elongation of the sample, that follows similar principles in particle-crosslinked as well as chemically crosslinked elastomers. Upon reaching the rubber elastic plateau, the additional elongation accessible in both architectures is gained by different mechanisms. For the particle-crosslinked sample FE-1, the particle orientation towards the strain direction results from a minimization of the friction on the particle surface that is induced by the polymer chains orienting parallel to the applied strain vector. In case of the chemically crosslinked sample CE-1 and ACE-1, the meshes of the polymer network are elongated in the strain direction in the tensile deformation. The elongation of the network meshes generates a torque on the particle directing the long axis parallel to the applied strain. This torque is additional for chemically crosslinked polymer networks, and thus a systematically higher order parameter is observed at strains above 66%. It can be anticipated that this reduced strain-induced ordering of particle-crosslinked elastomers is correlated to the high extensibility of these elastomers with strains at break of up to 1700%.
Mössbauer spectroscopy of strain-and field-induced order in magnetic elastomers
In contrast to the SAXS measurements, 57Fe Mössbauer spectroscopy is sensitive to the iron-bearing particle cores and provides a powerful technique to unravel their spin and spatial dynamics simultaneously. This has already been shown for spherical nanoparticles in liquid solutions by employing an uniaxial magnetic anisotropy approximation.49 Here, we exploit this technique to investigate the spatial alignment of spindle-shaped hematite nanoparticles, which exhibit a more complex, sixfold anisotropy within the crystals’ basal plane.22,50In this work, Mössbauer spectra of the samples FE-2, FE-3 and ACE-2 are recorded with and without the application of an external magnetic field, and with or without uniaxial deformation of the sample at different strain values at ambient conditions as well as at 4 K.
In order to get information on the orientation of the magnetic filler particles in the non-isotropic samples, and under the influence of strain and/or external fields, we make use of the condition that the intensity ratios in the typical sextet as obtained in Mössbauer spectroscopy depends on the magnetic alignment of the spins, and can be related to the spatial orientation of the nanoparticles using a Monte Carlo simulation, as described below. The angle θ between the spin orientation, determined as the average over all individual spin orientations in the particle, and incident gamma ray, as obtained by Mössbauer spectroscopy, follows from the Wigner–Eckart theorem, from which an exact angular relationship can be described, resulting in an angle-dependent relative line intensity ratio A23 of Mössbauer line 2 and 3 (or 4 and 5 due to the inherent symmetry), respectively:51
 | (12) |
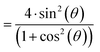 | (13) |
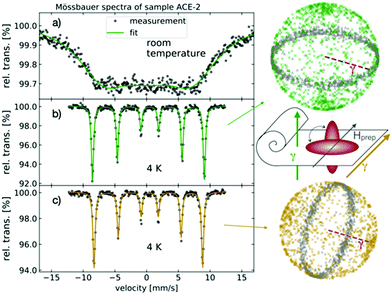
In order to obtain this value, the experimentally obtained Mössbauer spectra are reproduced by superpositioning two sextet subspectra, as shown as inlay in the upper right spectrum of Fig. 14a. The two sextets indicate two different types of particle dynamics within the sample. The line intensity ratio A23 is calculated based on the area of the respective absorption lines of the fitted spectrum. Based on A23 and Monte Carlo simulations (see below), information on the mutual orientation of the magnetically and strain-induced order becomes accessible. In the following, the procedure is confirmed for the reference samples and the theoretical limiting cases for the line absorption ratio for statistically oriented as well as completely aligned particles are elaborated.
For zero field and no strain, the particles are randomly oriented within the sample for the isotropic sample FE-2 and FE-3. The experimentally observed line intensity ratio A23 is about 2 for the reference case of no strain and no applied field for the samples FE-2 (1.96 ± 0.06) and FE-3 (1.93 ± 0.05), thus confirming the expectations for isotropic samples.
There are a few other configurations relevant in this study, each of which corresponds to a characteristic line intensity ratio A23. First, for a particle ensemble that is perfectly uniaxially oriented with the long particle axis perpendicular to the beam, in the absence of magnetic fields the spins are randomly distributed in the particles’ basal plane, and the corresponding line intensity ratio expected for this particle ensemble is 4/3. Second, in case that a sufficiently strong magnetic field is applied to a randomly oriented particle ensemble, the particles’ magnetic moment aligns with the applied field. In consequence, the direction of the spin alignment, being perpendicular to particles’ magnetic moment, is in a two dimensional random distribution, with the corresponding expected A23 value of 4/3. Third, for a fully uniaxially oriented particle ensemble perpendicular to the gamma ray subjected to a strong magnetic field that is both, perpendicular to strain as well as the incident gamma ray, the spins orient parallel to the gamma ray, and a line intensity ratio of 0 is observed. Finally, a numerically calculated reference value of A23 = 2.35 is obtained for a completely aligned particle ensemble in the sample ACE-2, when the preparation field is parallel to the Mössbauer gamma ray. A scheme of the respective particle orientations for this last case can be found in Fig. 13.
We introduce the order parameter Si(α) for the quantification of the spatial distribution. It is based on the average of the second Legendre polynomial, where α is the angle between the particles’ c axis and the reference axis i. In this study, dependent on the experiment at hand, i can be either the anisotropy axis of the sample b, or an experimental axis (e.g., y or strain direction ε):
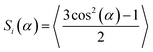 | (14) |
Accordingly, the order parameters assigned with Sε are extracted from the straining experiments, where α is the angle between particle long axis and straining direction. Order parameters denoted as Sb correspond to the configuration of the particle axes l with respect to the sample anisotropy axis b in ACE samples.
The correlation between the experimentally observed A23 values and the simulated particle configuration is obtained by starting from an ensemble of isotropically oriented particles with a spherical vector distribution that represents the particles c axes in the absence of an external stimulus like strain or magnetic field. In this configuration, the magnetically easy directions are located randomly in the basal plane. We simulate a preferential orientation of the particles by uniaxial elongating the vector distribution, while in-field a statistic magnetic alignment is considered by assuming a statistically uniform spin distribution up to a value of 25° around the magnetic field direction within the basal plane. This small deviation is suggested by calculations in a Stoner–Wohlfarth model for the magnetic landscape in a sixfold symmetry with the corresponding fields and anisotropy constants. The calculated order parameters from Mössbauer spectroscopy as well the order parameters obtained from SAXS measurements are compared in Fig. 14c. Here, the simulation is employed to link the orientational distribution of the simulated particle ensemble to the experimentally accessible line absorption ratio of the analyzed samples.
Although the sample is cooled down below the Morin transition temperature of ca. 260 K observed in macroscopic samples, no indication for a Morin transition is observed, which would be indicated as a distinct change in the nuclear quadrupole level shift.52 From the line intensity ratio A23, it is possible to extract information on the particle spatial distribution, as indicated above in eqn (12) and (13) and the Monte Carlo simulation results. As for this sample ACE-2, we expect different degrees of anisotropy in parallel and in perpendicular direction with respect to the sample anisotropy axis b, the sample is analyzed in both configurations to obtain the full picture.
In one configuration (depicted in yellow in Fig. 13), the incident gamma ray is out of plane defined by particles’ c-axes and parallel to b, the magnetic field axis employed during synthesis, while in the second case, a perpendicular arrangement between the beam and anisotropy axis b is chosen.
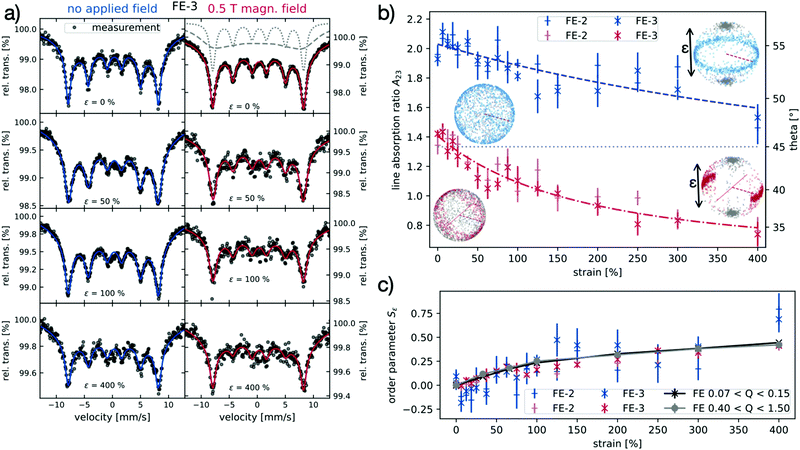
In the first case, a narrow, regular sextet is obtained, that allows the calculation of line intensity ratios, as shown in Fig. 13c. The result for the line absorption ratio is 1.81. As discussed above, for completely aligned nanoparticles a reference value of 4/3 would be expected in this case. The corresponding geometric order parameter S(α) that is obtained by the simulation approach amounts to Sb = −0.15 ± 0.03. For the second configuration, in the case of a perpendicular arrangement (Fig. 13b), a line intensity ratio of 2.18 is obtained. The completely ordered sample would show an A23 value of 2.35. The experimental value accordingly corresponds to a geometric order parameter of about Sb = −0.25 ± 0.06. The negative value of the order parameter, in accordance with the finding from SAXS (see above), describes that the c axes of the nanoparticles are oriented within a plane perpendicular to the applied field during preparation (see schematic drawing of sample in Fig. 13). Results from Mössbauer spectroscopy and SAXS are nearly equivalent, and their variation is due to experimental limits.
To get information on the intercorrelation of particle order parameter Sε, strain and magnetization, the isotropically prepared samples FE-2 and FE-3 are analyzed by Mössbauer spectroscopy under the influence of strain and magnetic field perpendicular to the beam direction, respectively. Therefore, the samples are stretched to various extension values of up to 400%. In contrast to the ACE-2 sample, the samples FE-2 and FE-3 show a sufficiently high line resolution even at ambient conditions. This indicates a different mobility of the embedded nanoparticles in the hybrid elastomer networks of different architecture at the time scale of the Mössbauer experiment,19 which is an interesting effect that may be subject of future investigations, but is beyond the scope of this paper. When the particle-crosslinked elastomers are uniaxially strained, a continuous change in the Mössbauer spectra (see Fig. 14a (left)) is obvious. The second and fifth line of the spectrum decrease in intensity with increasing strain, both in the field-off (B0 = 0 T) and the field-on case (B0 = 0.5 T, see Fig. 12). The corresponding line intensity ratio A23 is depicted in Fig. 14b for all experiments. For the field-free case, this change in the line intensity ratio, although originally caused by preferential alignment of spins, can be straightly quantified by help of eqn (12) and (13), indicating a narrowing angle between gamma ray and spin with decreasing intensity ratio. This can be explained by the nanoparticles’ long axes aligning along the strain direction, leading to a preferred orientation of the easy axes of the particles and thus their basal planes in the beam direction. A lucid visualization of the strain process can be also obtained from Monte Carlo simulations, exemplarily shown in Fig. 14b. For a fully oriented sample, the expected intensity ratio reaches its theoretical limit of a 2-dimensional random orientation at (A23 = 4/3). This can be confirmed by the experimental findings as seen in Fig. 14: at high strain values, an intensity ratio A23 of about 1.6 is observed. This course is identical within error margin for both samples, FE-2 and FE-3, indicating that the particle fraction does not have an effect on the strain-induced particle orientation, as determined within the accuracy of the Mössbauer experiment.
In the next experiment, we analyze the situation where instead of strain, a magnetic field of 0.5 T is applied perpendicular to the beam during the Mössbauer experiment. Under the influence of the magnetic field, in the absence of mechanical strain, the intensity ratio A23 is about 1.4, thus being close to the expected ideal value of 4/3 for the case of a full orientation of the magnetic spins in the plane perpendicular to the beam, which arises due to the unique magnetic characteristics of the nanoparticles. The deviation between theoretical and experimental result is attributed to remaining thermal fluctuation at this field strength and the simplicity of the underlying model.
When the sample is additionally subjected to external strain in the third available dimension, the line intensity ratio decreases further, as seen in Fig. 14b. For this configuration, we can expect the two external stimuli (magnetic field and strain) both to support the orientation of the filler particles. In a case that a full geometric and magnetic orientation would be achieved, the intensity ratio A23 of 0 is expected, corresponding to a spin orientation being completely coaxial to the gamma ray propagation direction. The spins behave differently in the field-free and field-on case and thus the corresponding expected reference values for the line absorption ratio differ, as the particles’ canted magnetic moment interacts with the applied magnetic field. Again, for the field-assisted experiments under strain, no significant influence of the particle content on intensity ratio A23 parameter nor the order parameter is found.
Employing the results of Monte Carlo simulations the obtained A23 values are converted to the order parameter Sε, which is found to systematically increase with the applied strain in Fig. 14c.
Thereby, the order parameter Sb is calculated for anisotropically synthesized elastomers, that possess an intrinsic anisotropy axis b arising from the field vector during synthesis. From SAXS, the result for ACE-1 is Sb = −0.25 ± 0.01 for the low Q regime, while from Mössbauer spectroscopy, the two different configurations give two individual results of −0.25 ± 0.06 and −0.15 ± 0.03, respectively. All results are negative in a similar range, and confirm the preferred orientation of the long particle axis preferentially in a plane perpendicular to b. While SAXS results show a higher accuracy, the information from Mössbauer spectroscopy additionally comprises the magnetic orientation, which is not accessible by SAXS alone. This is possible, as contrary to SAXS, Mössbauer spectroscopy does not probe a two dimensional projection of the real system, but is sensitive to contributions of all nanoparticles, irrespective of their orientation.
Comparing the results based on Mössbauer spectroscopy experiments and Monte Carlo simulations with the results obtained from SAXS measurements for strain-induced ordering experiments (see Fig. 14c), a good consistency regarding the strain-dependent degree of spatial particle ordering is found. The observed trend is analogous from the both methods. Here, the better accuracy of SAXS is obvious, while Mössbauer results confirm the magneto-geometric expectations from the particle intrinsic properties. In addition, the application of an external field is shown to increase the reliability of the analysis, yet a stronger particle orientation is not observed under the conditions analyzed. In an upcoming study, this aspect will be addressed in further detail by performing corresponding field-assisted experiments in the SAXS setup. In addition, we look for more sensitive information on the influence of the particle volume fraction for this relatively complex magnetic system.
In this work, a direct link between the magnetic properties and the spatial orientation is achieved. We prove that Mössbauer spectroscopy is a powerful tool to analyze the spatial orientation as well as anisotropic distributions of the spin moments of iron-bearing nanoparticles in complex matrices. It becomes obvious that just the combination of both methods, as performed in this work, delivers the full set of data that is necessary to understand the mutual interdependence of particle orientation, strain, and magnetic field, and is thus particularly valuable for the precise determination of the magnetic as well as orientational anisotropy of magnetic particles in elastic matrices. While SAXS results are more accurate, the results from Mössbauer spectroscopy in combination with Monte Carlo simulations are shown to be advantageous in terms of the information content, as, contrary to SAXS, the analysis allows access to the full orientational information. SAXS data allows analysis of the two-dimensional projection of the true 3D orientation, only. In a follow up paper, we aim to further investigate the influence of applied magnetic fields as well as the particle volume fraction on the orientational anisotropy in particle-crosslinked elastomers.
Conclusions
In this work, a series of exclusively particle-crosslinked elastomers with systematically varied particle volume fraction and crosslinking degree is prepared, and their strain- and magnetic field-induced increase in geometric and magnetic order is compared to additionally conventionally crosslinked hybrid elastomers.For this, we employ a combination of Small Angle X-ray Scattering (SAXS) and Mössbauer spectroscopy. Detailed analysis of the 2D SAXS scattering patterns of respective samples in various geometries allow insight into the interplay between orientational and magnetic order in such materials, in dependence of their internal architecture. In addition, in a fully new approach, Mössbauer spectroscopy is employed to in-depth analyze in analogous experiments the orientational order of the magnetic spins by line intensity analysis and Monte Carlo simulations.
By synthesizing the conventionally crosslinked elastomer network in the presence of an external homogeneous magnetic field, the magnetically induced order of the embedded filler particles can be conserved in the subsequent crosslinking process. The resulting intrinsic anisotropy of this architecture conserved in the crosslinking process is analyzed by SAXS and Mössbauer spectroscopy, in order to determine the resulting orientational and magnetic degree of order within the elastomeric matrices. For such samples, an order parameter of Sb = −0.25 ± 0.01 in the low Q regime and Sb = −0.28 ± 0.03 in the high Q regime is obtained for from SAXS analysis, while from line intensity analysis in Mössbauer spectroscopy values of Sb = −0.15 ± 0.03 and −0.25 ± 0.06 are determined, depending on the probed direction. Both results are good correspondence, considering the experimental limits and the fact that two fully independent methods are employed, and indicate not fully aligned nanoparticles, but still a significant degree of order. The correlation between experimentally measured magnetic and the structural orientation is determined via Monte Carlo simulation. This orientational order is also found to translate to a magnetic anisotropy. Systematically angular-dependent magnetic properties are observed for sample ACE-1 that can be qualitatively explained on the base of a modified Stoner–Wohlfarth model.
Upon straining the elastomer samples, for all samples the order parameter of the embedded nanoparticles increases systematically with the applied strain. The strain-induced order is probed by SAXS as well as Mössbauer spectroscopy, and the results of both techniques are found to coincide. For the conventionally crosslinked elastomers, the strain-induced anisotropy seems to be independent on the preorientation, and a strong increase of order parameter depending on strain is found with maximum order parameters of Sε = 0.50. For the particle-crosslinked elastomers, lower values are obtained, but as the structures can be extended to significantly higher extends, here also maximum order parameters of Sε = 0.45 are achieved. The dependence of the order parameter on the strain of the respective samples is related to the mechanical properties, and thereby also to the molecular architecture of the prepared hybrid elastomers.
Using this unique method, additional information becomes available by analysis of the strain-induced order in dependence of an externally applied magnetic field. Although in the configurations employed here, an external field has no significant impact on the strain-induced order within the experimental error, this option will be investigated in more detail in future experiments under optimized conditions.
Our results use new and original approaches based on SAXS and Mössbauer spectroscopy to obtain a detailed picture on the interplay between orientational and magnetic strain induced order and find a direct link between the magnetic structure and the spatial orientation of anisotropic magnetic nanoparticles in elastomeric matrices with different architecture.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support is acknowledged from DFG-SPP 1681 “Feldgesteuerte Partikel-Matrix-Wechselwirkungen” (SCHM1747/10, WE2623/7), as well as the Collaborative Research Centre/Transregio (CRC/TRR) 270 (Project-ID 405553726, sub-project A03) and the CRC/TRR 247 (Project-ID 388390466, sub-project B02).Notes and references
- J. Tao and X. (Bill) Yu, Smart Mater. Struct., 2012, 21, 113001 CrossRef.
- S. Coyle, C. Majidi, P. LeDuc and K. J. Hsia, Ext. Mech. Lett., 2018, 22, 51–59 CrossRef.
- W. L. K. Chen and C. A. Simmons, Adv. Drug Delivery Rev., 2011, 63, 269–276 CrossRef CAS PubMed.
- A. Weber and J. M. Murray, Physiol. Rev., 1973, 53, 612–673 CrossRef CAS PubMed.
- K. Sano, Y. Ishida and T. Aida, Angew. Chem., Int. Ed., 2018, 57, 2532–2543 CrossRef CAS PubMed.
- A. M. Menzel, Phys. Rep., 2015, 554, 1–45 CrossRef CAS.
- H. Ko and A. Javey, Acc. Chem. Res., 2017, 50, 691–702 CrossRef CAS PubMed.
- C. Scherzinger, A. Schwarz, A. Bardow, K. Leonhard and W. Richtering, Curr. Opin. Colloid Interface Sci., 2014, 19, 84–94 CrossRef CAS.
- H. Wermter and H. Finkelmann, e-Polymers, 2001, 1, 1–13 Search PubMed.
- M. Winkler, A. Kaiser, S. Krause, H. Finkelmann and A. M. Schmidt, Macromol. Symp., 2010, 291–292, 186–192 CrossRef CAS.
- S. Backes, M. U. Witt, E. Roeben, L. Kuhrts, S. Aleed, A. M. Schmidt and R. von Klitzing, J. Phys. Chem. B, 2015, 119, 12129–12137 CrossRef CAS PubMed.
- S. Mortazavian and A. Fatemi, Composites, Part B, 2015, 72, 116–129 CrossRef CAS.
- L. Roeder, P. Bender, M. Kundt, A. Tschöpe and A. M. Schmidt, Phys. Chem. Chem. Phys., 2015, 17, 1290–1298 RSC.
- P. Bender, A. Günther, A. Tschöpe and R. Birringer, J. Magn. Magn. Mater., 2011, 323, 2055–2063 CrossRef CAS.
- A. Sánchez-Ferrer, R. Mezzenga and H. Dietsch, Macromol. Chem. Phys., 2011, 212, 627–634 CrossRef.
- J. Seifert, S. Roitsch and A. M. Schmidt, ACS Appl. Polym. Mater., 2021, 3(3), 1324–1337 CrossRef CAS.
- N. Frickel, R. Messing, T. Gelbrich and A. M. Schmidt, Langmuir, 2010, 26, 2839–2846 CrossRef CAS PubMed.
- R. Messing, N. Frickel, L. Belkoura, R. Strey, H. Rahn, S. Odenbach and A. M. Schmidt, Macromolecules, 2011, 44, 2990–2999 CrossRef CAS.
- J. Landers, L. Roeder, S. Salamon, A. M. Schmidt and H. Wende, J. Phys. Chem. C, 2015, 119, 20642–20648 CrossRef CAS.
- L. Roeder, M. Reckenthäler, L. Belkoura, S. Roitsch, R. Strey and A. M. Schmidt, Macromolecules, 2014, 47, 7200–7207 CrossRef CAS.
- P. Bender, A. Günther, A. Tschöpe and R. Birringer, J. Magn. Magn. Mater., 2011, 323, 2055–2063 CrossRef CAS.
- F. Bødker, M. F. Hansen, C. B. Koch, K. Lefmann and S. Mørup, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 6826–6838 CrossRef.
- M. Kobayashi, F. Juillerat, P. Galletto, P. Bowen and M. Borkovec, Langmuir, 2005, 21, 5761–5769 CrossRef CAS PubMed.
- M. Ozaki, S. Kratohvil and E. Matijević, J. Colloid Interface Sci., 1984, 106, 146–151 CrossRef.
- G. A. Van Ewijk, G. J. Vroege and A. P. Philipse, J. Magn. Magn. Mater., 1999, 201, 31–33 CrossRef CAS.
- J. Wagner, T. Autenrieth and R. Hempelmann, J. Magn. Magn. Mater., 2002, 252, 4–6 CrossRef CAS.
- W. Stöber, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62–69 CrossRef.
- R. Biehl, PLoS One, 2019, 14, 1–18 Search PubMed.
- L. Roeder, M. Reckenthäler, L. Belkoura, S. Roitsch, R. Strey and A. M. Schmidt, Macromolecules, 2014, 47, 7200–7207 CrossRef CAS.
- C. Märkert, B. Fischer and J. Wagner, J. Appl. Crystallogr., 2011, 44, 441–447 CrossRef.
- M. Reufer, H. Dietsch, U. Gasser, A. Hirt, A. Menzel and P. Schurtenberger, J. Phys. Chem. B, 2010, 114, 4763–4769 CrossRef CAS PubMed.
- A. Nack, J. Seifert, C. Passow and J. Wagner, J. Appl. Crystallogr., 2018, 51, 87–96 CrossRef CAS.
- N. Dzade, A. Roldan and N. de Leeuw, Minerals, 2014, 4, 89–115 CrossRef.
- Ö. Özdemir, D. J. Dunlop and T. S. Berquó, Geochem., Geophys., Geosyst., 2008, 9, Q10Z01 CrossRef.
- R. N. Bhowmik and A. Saravanan, J. Appl. Phys., 2010, 107, 053916 CrossRef.
- T. Sugimoto, Y. Wang, H. Itoh and A. Muramatsu, Colloids Surf., A, 1998, 134, 265–279 CrossRef CAS.
- W. F. Willem, Makromol. Chem., 1979, 2548, 2541–2548 Search PubMed.
- J. Cervantes, R. Zárraga and C. Salazar-Hernández, Appl. Organomet. Chem., 2012, 26, 157–163 CrossRef CAS.
- T. Li, A. J. Senesi and B. Lee, Chem. Rev., 2016, 116, 11128–11180 CrossRef CAS PubMed.
- T. Narayanan, in Soft Matter Characterization, ed. R. Borsali and R. Pecora, Springer, 2008, pp. 900–952 Search PubMed.
- I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley & Sons, Inc., 2002 Search PubMed.
- J. E. Mark, Polymer Data Handbook, Oxford University Press, USA, 1st edn, 1999 Search PubMed.
- L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Springer US, Boston, MA, 1987 Search PubMed.
- M. Kotlarchyk and S. Chen, J. Chem. Phys., 1983, 79, 2461–2469 CrossRef CAS.
- K. M. Krishnan, Fundamentals and Applications of Magnetic Materials, Oxford University Press, 2016 Search PubMed.
- E. C. Stoner and E. P. Wohlfarth, Philos. Trans. R. Soc., A, 1948, 240, 599–642 CrossRef.
- R. Lovell and G. R. Mitchell, Acta Crystallogr., Sect. A: Found. Crystallogr., 1981, 37, 135–137 CrossRef.
- G. R. Mitchell and A. H. Windle, Polymer, 1983, 24, 1513–1520 CrossRef CAS.
- J. Landers, S. Salamon, H. Remmer, F. Ludwig and H. Wende, ACS Appl. Mater. Interfaces, 2019, 11, 3160–3168 CrossRef CAS PubMed.
- P. J. Flanders and W. J. Schuele, Philos. Mag., 1964, 9, 485–490 CrossRef CAS.
- B. V. Thosar and P. K. Iyengar, Advances in Mössbauer spectroscopy: applications to physics, chemistry, and biology (Studies in physical and theoretical chemistry), Elsevier Scientific Pub. Co., 1983 Search PubMed.
- T. Ruskov, T. Tomov and S. Georgiev, Phys. Status Solidi, 1976, 37, 295–302 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm02104k |
| This journal is © The Royal Society of Chemistry 2021 |