Introduction to remodeling of biomembranes

---

Abstract

In general, biomembranes and giant vesicles can respond to cues in their aqueous environment by remodeling their molecular composition, shape, or topology. This themed collection focuses on remodeling of membrane shape which is intimately related to membrane curvature. In this introductory contribution, we clarify the different notions of curvature and describe the general nanoscopic mechanisms for curvature generation and membrane scaffolding. At the end, we give a brief outlook on membrane tension.

---

Reinhard Lipowsky

Reinhard Lipowsky obtained his PhD in 1982 at the University of Munich and then worked as a research associate at Cornell University, New York. In 1990, he was appointed full professor at the University of Cologne and director at the Forschungszentrum Jülich. Three years later, he became one of the founding directors of the Max Planck Institute of Colloids and Interfaces, Potsdam. He is a member of the Berlin-Brandenburg Academy of Sciences and has honorary professorships at the University of Potsdam and at the Humboldt-Universität zu Berlin. He is the speaker of the International Max Planck Research School (IMPRS) on “Multiscale Biosystems”, a main focus of his research.

Rumiana Dimova

Rumiana Dimova obtained her PhD at Bordeaux University (France) in 1999. Afterwards she joined the Max Planck Institute of Colloids and Interfaces (Germany) as a postdoctoral fellow, where she became a group leader in 2000 leading the Biophysics Lab. Her main research interests are in the field of membrane biophysics. She has been tackling a variety of open questions in cell membrane biophysics and synthetic biology, while employing giant vesicles as a platform to develop new methods for the biophysical characterization of membranes and the processes involving them. In 2014, she was awarded with the Emmy Noether Distinction for Women in Physics of the European Physical Society.

---

Introduction

In this themed collection, several soft matter systems will be discussed that are built up from biomembranes interacting with additional molecular or colloidal components. Biomembranes consist of molecular bilayers which are assembled from lipids and other amphiphiles in water. The lipids and amphiphiles have hydrophobic tails and hydrophilic head groups. In order to prevent any contact between tails and water, the membranes avoid bilayer edges and form closed vesicles.

All biomembranes considered here are fluid in the sense that the molecular components of the bilayers undergo fast lateral diffusion. Because of their fluidity, the membranes exhibit a fascinating diversity of different morphologies and undergo remodeling processes from one morphology to another. In general, these processes can change the molecular composition, the shape, or the topology of these membranes.

The various membrane systems addressed in the following differ in the complexity of their molecular building blocks. Very versatile systems are provided by giant unilamellar vesicles (GUVs) which are typically formed by single bilayers of lipid molecules.^1–7 The remodeling of GUVs can be directly observed in the light microscope and can be controlled by exposing the GUV membranes to different types of molecules.^8,9 The associated molecular interactions change the membrane elasticity at the nanoscale which leads to the remodeling of the GUVs at the micrometer scale.

GUVs can also be formed by other amphiphiles. One example are GUVs formed by block-copolymers, so-called polymersomes.^10–12 Another example is provided by dendrimersomes assembled from amphiphilic dendrimers,^13,14 as described in the contribution by Kostina et al.¹⁵ GUVs can also be obtained from large segments of cellular plasma membranes, as produced by chemical blebbing of eukaryotic cells,^16–20 see contribution by Florentsen et al.²¹

This themed collection focuses on the remodeling of membrane shape, a process that is intimately related to membrane curvature. As a consequence, this curvature plays a prominent role in most contributions of the collection. However, different contributions emphasize different notions of membrane curvature which may lead to some confusion and will be clarified in the following section.

Different notions of membrane curvature

We pursue a bottom-up approach and start from the simple view that individual lipid molecules have a certain shape²² which leads to the notion of intrinsic lipid curvature as emphasized in the contribution of Semeraro et al.²³ We then discuss the idea that the lipid molecules become ‘frustrated’ when they are packed into a bilayer.²⁴ In fact, from our point of view, this putative frustration together with the fluidity of the lipid bilayers implies that the shape of a lipid molecule is variable and depends on its local environment. Therefore, as emphasized in several of the subsequent contributions,^8,15,25–27 the crucial curvature parameter for molecular bilayers is provided by the spontaneous curvature which describes the asymmetry between the two leaflets of these bilayers.

Intrinsic lipid curvature from inverted hexagonal phases

A phospholipid consists of a head with a phosphate group, a glycerol backbone, and two hydrocarbon chains. It is tempting to assume that such a molecule has a certain, well-defined shape. Such a shape concept for individual lipid molecules has been used to explain the complex phase behavior of aqueous lipid dispersions, which involve a variety of non-bilayer phases. In particular, many phospholipids form an inverted hexaganol phase, in which the lipids are assembled around cylindrical water channels. These channels form a 2-dimensional hexagonal lattice which can be studied by X-ray and neutron scattering.

Using the latter techniques, one can measure the radius R₀ of the cylindrical interface between a single water channel and the glycerol backbone of the phospholipids as defined in Fig. 4A of Semeraro et al.²³ This interfacial radius has been used to define the magnitude of the intrinsic lipid curvature C₀via |C₀| = 1/R₀, see Table 3 of Semeraro et al.²³ For those lipids that actually form an inverted hexagonal phase, the values of R₀ vary between 2.5 nm and 3 nm, which is smaller than the typical thickness of a lipid bilayer. However, the assumption that a lipid molecule has a certain, fixed shape is problematic for several reasons.

Limitations of the intrinsic curvature concept

First, most lipids that form an inverted hexagonal phase form other non-bilayer and bilayer phases as well.²⁸ In these different phases, the lipids are packed locally in a different manner. Therefore, the observed polymorphism of aqueous lipid dispersions does not support the idea that a certain type of lipid always has the same shape. Indeed, the shape of an individual lipid molecule must depend on the interactions of this molecule with the other molecules in its neighborhood, and this molecular neighborhood is clearly different when the lipid resides in different lipid–water phases.

Second, thermal noise will affect both the lipid molecule under consideration and its molecular neighborhood. One direct consequence of thermal noise is the lateral diffusion of an individual lipid within the lipid assembly. As a result, the diffusing lipid will encounter different local neighborhoods, in particular when this assembly contains several lipid components.

Third, the biomembranes discussed in this themed collection are based on lipid bilayers which involve two lipid monolayers or leaflets in close proximity. When we consider rigid lipid molecules with a non-cylindrical shape and try to pack them into such a bilayer, the lipids would become ‘frustrated’, see Fig. 1. It was originally proposed²⁴ that such a frustration leads to packing defects or voids. However, this proposal ignores the flexibility of the lipids and the fluidity of the bilayers. Indeed, if the lipids form a fluid bilayer, packing defects or voids will be mobile and will be averaged out by local density fluctuations and lateral lipid diffusion.

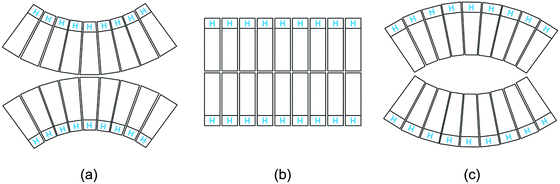Fig. 1 Intrinsic lipid curvature and bilayers: (a) if the lipids resemble inverted cones, with the head groups (blue H) having a smaller cross-sectional area than the hydrocarbon chains, the two leaflets prefer to curve towards each other; (b) lipids with a cylindrical shape form a bilayer without any ‘frustration’; and (c) if the lipids have a cone shape, the two leaflets prefer to curve away from each other.²⁴

Spontaneous curvature of bilayer membranes

For a symmetric bilayer of lipids, the intrinsic curvatures of the lipids in the two leaflets must, on average, cancel out, irrespective of the assumed shape of the lipids. However, bilayer membranes are typically not symmetric because the two leaflets can differ in their molecular composition and can be exposed to different aqueous solutions. Some examples for such asymmetric bilayers are displayed in Fig. 2.^9,29–31 Other examples are provided by bilayers exposed to asymmetric solutions of simple sugars⁸ or of salt and sugar.³²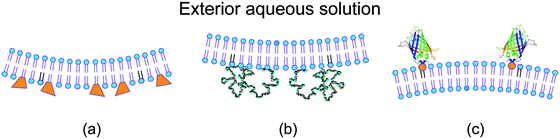

Fig. 2 Different molecular mechanism for the generation of transbilayer asymmetry and spontaneous curvature: (a) compositional asymmetry arising from glycolipids (GM1, orange) in the inner leaflet;^29,30 (b) adsorption of PEG chains onto the inner leaflet from the adjacent semidilute solution;³¹ and (c) binding of His-tagged GFP to anchor-lipids (orange) in the outer leaflet from a very dilute nanomolar solution.⁹ The adsorbed PEG layer is crowded, whereas the membrane-bound GFP layer is dilute.

This local asymmetry between the two leaflets defines the spontaneous curvature of the bilayers as originally introduced by Helfrich,³³ in close analogy to the curvature elasticity of liquid crystals.³⁴ The corresponding elastic energy of biomembranes defines the spontaneous curvature model.^35,36

Transbilayer flip-flops of lipids

If the lipids do not undergo flip-flops between the two leaflets on the experimentally relevant time scales, the numbers of lipids are conserved in each leaflet separately. For a bilayer that forms a closed vesicle, these conserved lipid numbers lead to a constraint on the area difference between the two leaflets. When such a global constraint is added to the spontaneous curvature model, one arrives at the area-difference-elasticity (ADE) model.^37,38 Alternatively, one may start from the bilayer coupling model,³⁹ which imposes a fixed area difference between the two leaflets, and then soften this constraint on the area difference to arrive at the ADE model.⁴⁰

On the other hand, lipid bilayers often contain (at least) one lipid species that undergoes frequent flip-flops. Examples for such fast flip-flopping lipid species are provided by cholesterol and other sterols which have flip-flop times of seconds^41,42 or even milliseconds.⁴³ Therefore, if the bilayer contains cholesterol, the spontaneous curvature model is expected to provide a reliable description for the curvature elasticity of membranes as recently confirmed by several experimental studies of GUVs with cholesterol-containing membranes.^8,9,29,31

Transbilayer asymmetry of polyunsaturated lipids

Polyunsaturated lipids are known to be highly enriched in the plasma membranes and synaptic vesicles of neurons.⁴⁴ In synaptic vesicles, for example, up to 80% of the phospholipids contain one polyunsaturated acyl chain.⁴⁵ Even though these lipids play an important role in the nervous system, their precursors, polyunsaturated fats, cannot be synthesized by the human body but must be ingested as part of the diet.⁴⁶ A diet with polyunsaturated fats is also believed to be beneficial by lowering levels of low-density lipoprotein (LDL) in the human blood.⁴⁷

In general, the acyl chain profiles of phospholipids show striking differences between cell types and between organelles.^48,49 In particular, these profiles are modified by supplementing polyunsaturated fats to human mesenchymal stem cells which affects the differentiation of these cells.⁵⁰ The acyl chain profiles can be determined by mass spectroscopy as described in the contribution of Symons et al.⁵¹ This method shows that polyunsaturated lipids are more abundant in primary cells from living tissues than in cultured cells.

A polysaturated lipid has one polyunsaturated chain with several double bonds that generate kinks along the chain. Therefore, polyunsaturated chains have the ability to adopt many bent conformations. The resulting conformational plasticity of the polyunsaturated lipids is thought to facilitate membrane deformation and fission by endocytic proteins.^52,53 In the contribution by Tiberti et al.,⁵⁴ the increased membrane deformability is studied by coarse-grained molecular dynamics simulations. A bilayer patch is assembled with two leaflets that differ in their mole fractions of polyunsaturated lipids. When this membrane is deformed by a locally applied pulling force, a larger deformation is obtained when the pulling force is applied to the leaflet that is enriched in the polyunsaturated lipids. Tiberti et al.⁵⁴ interpret this result in terms of a decreased bending rigidity of the membrane⁵³ and conclude that this lower bending rigidity facilitates membrane budding and vesiculation. It is important to note, however, that both the spontaneous curvature model and the ADE model predict that budding and vesiculation can only occur when the spontaneous curvature exceeds a certain threshold value.³⁶ This prediction has been recently confirmed by several experimental studies on GUV morphologies.^8,9,27

Remodeling of GUV morphologies

Next, consider GUVs that are formed by the lipid bilayers depicted in Fig. 2. When we start with initially spherical shapes and reduce the vesicle volume by osmotic deflation, we observe shape transformations towards the morphologies in Fig. 3. A systematic analysis of these morphologies based on the theory of curvature elasticity provides reliable estimates of the corresponding spontaneous curvature. This curvature is found to be −1/(95 nm), −1/(100 nm), and +1/(140 nm) for the three morphologies displayed in Fig. 3(a), (b), and (c), respectively. In this way, curvature elasticity provides a direct connection between the GUV morphologies as observed at the micrometer scale (Fig. 3) and the transbilayer asymmetry of the lipid bilayers at the nanometer scale (Fig. 2).

Fig. 3 Remodeling of GUVs induced by the transbilayer asymmetries in Fig. 2: formation of nanotubes arising (a) from the compositional asymmetry of glycolipids (GM1)²⁹ and (b) from PEG adsorption to the interior leaflet;³¹ and (c) binding of His-tagged GFP to anchor-lipids in the outer bilayer leaflet.⁹ In (c), a small increase of the nanomolar GFP concentration leads to the fission of the membrane neck and to the division of the GUV. All scale bars: 5 μm.

The two GUV morphologies in Fig. 3(a and b) provide examples for the spontaneous tubulation of GUVs. In both cases, the width of the tubes is below optical resolution and comparable to the inverse spontaneous curvature which is about 100 nm. Vice versa, if a GUV forms membrane nanotubes in the absence of locally applied forces, we can conclude that its membrane has a significant spontaneous curvature that is large compared to the inverse vesicle size.^55,56

Force-induced tubulation of GUVs

Membrane nanotubes can also be generated by force-induced tubulation, i.e., by pulling nanotubes from the GUVs via locally applied forces. A variety of experimental protocols for this force-induced tubulation have been developed as summarized in ref. 57. A particularly useful set-up is provided by micropipette aspiration of the GUVs combined with membrane-bound nanobeads that are pulled by magnetic tweezers⁵⁸ or optical traps.^59–61 The theoretical analysis of this set-up reveals that the mechanical balance between the aspiration pressure and the locally applied force depends both on the spontaneous curvature and on the total membrane tension.^55,57 This tension represents the sum of the mechanical and the spontaneous membrane tension, with the spontaneous tension being proportional to the square of the spontaneous curvature. Furthermore, the dependence on the total membrane tension can be eliminated by pulling in- and out-tubes from the same vesicle.^30,57 The approach of force-induced tubulation has been recently used to determine the spontaneous curvature of GUV membranes which possess a transbilayer asymmetry of GM1,³⁰ or are exposed to asymmetric salt and sugar solutions.³² In addition, force-induced tubulation can be used to study the enrichment of certain membrane-bound molecules in the highly curved membrane segments of the nanotubes. One example is provided by the ENTH binding domain of epsin proteins as explained in the review of Steinem et al.⁶²

Subcompartments connected by membrane necks

One particularly intriguing remodeling process of GUVs is the formation of membrane subcompartments that are connected by narrow or closed membrane necks. One example is shown in Fig. 3(c) where the GUV membrane encloses two subcompartments connected by one membrane neck. Several contributions of this themed collection provide additional examples for membrane necks. Bhatia et al.⁸ describe a striking variety of multispherical GUV morphologies with many necks, induced by two simple sugars—sucrose in the interior and glucose in the exterior solution. Rather similar morphologies are observed by Kostina et al.¹⁵ for dendrimersomes which are formed by bilayers of amphiphilic, photoresponsive dendrimers. As a consequence, morphological transformations of the dendrimersomes can be induced by light, see Fig. 5 of Kostina et al.¹⁵ Furthermore, Christ et al.²⁷ study the shape oscillations between symmetric and asymmetric dumbbells as observed for GUVs filled with two Min proteins.⁶³ These proteins hydrolyze ATP to undergo cycles of membrane-bound and membrane-unbound states. As a result, the GUVs undergo active shape oscillations with alternating closure and opening of membrane necks, a cyclic process that can be understood in terms of a time-dependent spontaneous curvature.²⁷

Division of GUVs into two daughter vesicles

In Fig. 3(c), the two spherical subcompartments of the GUV are still connected by a narrow membrane neck. A further increase of the nanomolar GFP concentration in the exterior solution leads to the fission of the neck and the complete division of the GUV.⁹ These observations demonstrate that the spontaneous curvature generates constriction forces around the membrane neck³⁶ and that these forces can easily cover the force range found in vivo. Furthermore, the fission and division process is obtained for rather low densities of the membrane-bound GFPs. Indeed, the average separation of the lipid-anchored GFPs exceeded 24 nm, which is much larger than GFP's lateral size of about 3 nm.⁶⁴ This low density of the membrane-bound GFP molecules leaves ample space for other proteins to be accommodated at or in the GUV membranes. Therefore, the controlled division of the GUVs via membrane-bound GFPs⁹ provides a promising and extendible module for the bottom-up assembly of synthetic cells.

Alternative approaches that have been pursued to divide GUVs, include the reconstitution of the bacterial division machinery provided by FtsZ proteins. The formation of relatively large rings of these proteins within GUVs has been observed, albeit with rather low frequency.⁶⁵ For about 1.2 percent of the GUVs, Z rings were observed to induce progressive constrictions of the GUVs, in some cases leading to two subcompartments connected by closed membrane necks. However, the subsequent division into two separate membrane compartments has not been reported.

His-tagged GFP was also used to divide extruded vesicles with a diameter of 200 nm.⁶⁶ In these latter experiments, the anchor-lipid mole fraction was at least 20 times higher and the GFP solution concentration was at least 128 times larger than in our systems. In fact, it was concluded in ref. 56 that crowding of membrane-bound GFP is a prerequisite for successful vesicle division,⁶⁶ in contrast to the low densities of membrane-bound GFPs used by us in Fig. 3(c).

In ref. 67, GUVs in microfluidic channels were mechanically split into two daughter vesicles. The GUVs were formed from double-emulsion droplets and subsequently pushed by microfluidic flow against the sharp edge of a wedge-shaped junction. The probability for division was observed to depend strongly on the size of the GUV and to follow a bell-shaped curve with a maximum at a GUV diameter of about 6 μm. Both for smaller and for larger sizes, the division probability rapidly decreased to zero. In contrast, the constriction force that leads to the division of the vesicle in Fig. 3(c) does not depend on the vesicle size.

Scaffolding by membrane-bound colloids

The examples for curvature generation in Fig. 2 and 3 can be understood intuitively in terms of local membrane bending by those molecules (GM1, PEG, GFP) that are distributed in an asymmetric manner across the bilayer. Alternatively, we may think of effectively repulsive interactions between these membrane-bound molecules. A somewhat different mechanism for generation of membrane curvature is obtained for larger membrane-bound colloids that act as scaffolds for the membrane. Examples for such colloids include rigid nanoparticles, liquid droplets, long chain molecules, protein assemblies, and semi-flexible filaments. In order to act as scaffolds, these colloids must have two properties. First, they must have at least one linear dimension that is large compared to the bilayer thickness of 4 to 5 nm. Second, they must adhere to the membrane or must be anchored to it.

Scaffolding by adhesion to rigid nanoparticles and filaments

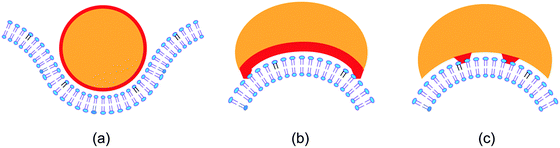
The simplest example for membrane scaffolding is presumably provided by a rigid nanoparticle with a spherical shape as depicted in Fig. 4(a). In this example, the radius of the nanoparticle is about 2.5 times the thickness of the bilayer and the particle is partially engulfed by the membrane. Partial engulfment is stable if the spontaneous curvature of the membrane is opposite to the curvature of the particle-bound membrane segment.^26,68 In general, a nanoparticle can have many different shapes with different patterns of adhesive surface domains. Two such patterns are displayed in Fig. 4(b and c). In Fig. 4(b), the whole concave surface domain is adhesive (red), which implies curvature generation after adhesion (induced fit). In Fig. 4(c), the adhesive surface domains (red) are buried inside the concave part of the particle surface, and the membrane must first bend before it can bind to the particle (conformational selection). In the contribution of Bonazzi et al.,⁶⁹ the diverse membrane morphologies arising from arc-shaped nanoparticles are studied by coarse-grained simulations. Similar simulation methods are used in the contribution of Xu et al.⁷⁰ to study the diffusive transport of nanoparticles bound to lipid bilayers.

Fig. 4 Adhesion-induced scaffolding of membranes by rigid nanoparticles (orange): (a) a spherical nanoparticle with a diameter of about 10 nm and a uniform adhesive surface (red). Sufficiently strong adhesion leads to the engulfment of the particle by the membrane; and (b and c) two types of convex–concave nanoparticles with different patterns of adhesive surface domains.

Two contributions to this themed collection consider the remodelling of membranes arising from interactions with rigid filaments. Franquelim et al.⁷¹ study the membrane deformations arising from synthetic filaments as provided by straight DNA origami. In this case, the membranes are deformed into nanotubes that are stabilized by bundles of filaments, see Fig. 5A of Franquelim et al.⁷¹ Furthermore, Kusters et al.⁷² study the coupling between GUV membranes and actin shells obtained via the polymerization of actin filaments. When the GUVs are osmotically deflated, the actin shells undergo buckling and wrinkling transformations, see Fig. 1 of Kusters et al.⁷²

The tissues of multicellular organisms contain extracellular matrices provided by large networks of extracellular filaments. As explained in the contribution by Alisafaei et al.,⁷³ these filament networks lead to long-range mechanical signaling between cells that are very far apart within the tissue. The mechanical signals include direct transmission of force from one cell to another, as well as changes in the alignment, density and stiffness of the extracellular matrix, and allow the cells to sense other cells over distances that are 20 to 40 times larger than the cell diameters.

Entropic scaffolding by flexible chain molecules

The scaffolding by rigid nanoparticles and filaments arises from the adhesion between the nanoparticles and the membrane. In contrast, the scaffolding by long chain molecules is caused by the loss of configurational entropy of the chains resulting from the steric hindrance of the chains by the membrane.^74–76 In order to stay close to the membrane, the chain molecule must, however, be anchored to the membrane. Several cases for this anchorage of a linear chain molecule need to be distinguished, see Fig. 5.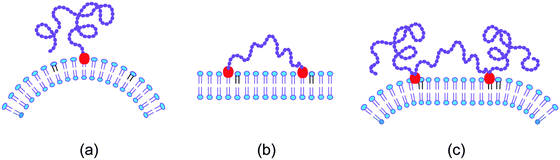

Fig. 5 Entropic scaffolding of membranes by flexible chain molecules (purple) with one or two anchor segments (red): (a) if the chain is anchored to the membrane at only one end, the membrane is bent away from the chain by the configurational entropy of the chain; (b) in contrast, the membrane remains essentially flat if the chain is anchored at both ends; and (c) for a chain with two intermediate anchor segments, the membrane is bent away from the loose chain ends as follows by combining the two cases in (a) and (b).^74,75

The simplest case is provided by a linear chain with a single anchor at one end as depicted in Fig. 5(a). In this case, the membrane bends away from the anchored chain in order to increase the spatial region that is accessible to the other end of the chain.^74,76 On the other hand, if we anchor this other chain end to the membrane as well, see Fig. 5(b), the membrane remains essentially flat because the entropic scaffolding is now limited to chain configurations, for which both anchors are close together, whereas large anchor–anchor separations stretch the chain molecule and curve the membrane in the opposite direction.⁷⁵

Scaffolding by membrane-bound proteins

Proteins are linear chain molecules which can form both folded and intrinsically disordered domains. The folded domains are expected to be rather rigid whereas the intrinsically disordered domains should behave as flexible chains. Therefore, a membrane-bound protein that contains both intrinsically disordered and rigidly folded domains will deform the membrane by both entropic and adhesion-induced scaffolding. This combined mechanism is explored in the contribution by Zeno et al.,²⁵ who discuss the remodeling of GUV membranes by membrane-bound amphiphysin, which involves both types of protein domain.

A different view about the membrane–protein interactions is described in the contribution by Breuer et al.,⁷⁷ who study the preferential binding of I-BAR proteins to the inner leaflets of filopodia in living cells. To explain this preference for negative membrane curvature, it is assumed that the rod-like I-BAR protein has itself a certain preferred curvature and that the coupling between this protein and the membrane is governed by a “mismatch” energy^78–80 that depends on the deviation of this preferred protein curvature from the mean curvature of the membrane. These two assumptions are plausible, but Breuer et al.⁷⁷ also assume that the mean curvature of the membrane is fixed and that the membrane does not respond to local interactions with the proteins. It seems difficult to justify the latter assumption, both intuitively and in view of the other contributions of this collection.

Outlook on membrane tension

A particularly intriguing and confusing aspect of membrane remodeling is the role of membrane tension. In general, this tension can be decomposed into two contributions, a mechanical tension, that acts to stretch the membrane, and a spontaneous tension proportional to the square of the spontaneous curvature.^55,81 The mechanical tension depends on the size and shape of the membrane whereas the spontaneous tension is a material parameter, in close analogy to the interfacial tension of liquid droplets as confirmed by micropipette experiments on tubulated GUVs.²⁹ The spontaneous tubulation of GUVs implies that the mechanical tension is much smaller than the spontaneous tension.⁵⁵ On the other hand, if the membrane has a negligible spontaneous curvature, the mechanical tension can be measured by superresolution (STED) microscopy as recently demonstrated by pulling tubes from GUVs.⁸² It would be rather interesting to extend this experimental method to lipid bilayers with a significant spontaneous curvature as well as to the nanotubes formed by cellular membranes.

The mechanical tension within a bilayer membrane can be divided up into two leaflet tensions that act within the individual leaflets of the bilayer.^81,83,84 In mechanical equilibrium, each of these leaflet tensions must be laterally uniform because each leaflet represents a two-dimensional liquid. In the absence of flip-flops between the two leaflets, each leaflet tension depends on the vesicle volume and on the number of lipids assembled in this leaflet. In molecular dynamics simulations of nanovesicles, one can vary the two leaflet tensions by changing the initially assembled lipid numbers and, in this way, control the polymorphism and shape transformations of the nanovesicles during deflation.⁸⁵ On the other hand, when the bilayer contains (at least) one lipid component that undergoes frequent flip-flops, the two leaflet tensions relax towards the same value, corresponding to half the bilayer tension.⁸⁶

Acknowledgements

We thank all our collaborators for fruitful and enjoyable interactions as well as the MaxSynBio consortium, jointly funded by the Max Planck Society and the Federal Ministry of Research, Germany, for providing a stimulating scientific environment.

References

1. Structure and Dynamics of Membranes, ed. R. Lipowsky and E. Sackmann, Elsevier, Amsterdam, 1995, vol. 1.
2. R. Dimova, S. Aranda, N. Bezlyepkina, V. Nikolov, K. Riske and R. Lipowsky, J. Phys.: Condens. Matter, 2006, 18, S1151–S1176.
3. P. Walde, K. Cosentino, H. Engel and P. Stano, ChemBioChem, 2010, 11, 848–865.
4. S. F. Fenz and K. Sengupta, Integr. Biol., 2012, 4, 982–995.
5. Physics of Biological Membranes, ed. P. Bassereau and P. Sens, Springer Nature, 2018.
6. R. Dimova, Annu. Rev. Biophys., 2019, 48, 93–119.
7. The Giant Vesicle Book, ed. R. Dimova and C. Marques, Taylor & Francis, 2020.
8. T. Bhatia, S. Christ, J. Steinkühler, R. Dimova and R. Lipowsky, Soft Matter, 2020, 16, 1246–1258, themed collection.
9. J. Steinkühler, R. L. Knorr, T. Bhatia, S. Bartelt, S. Wegner, R. Dimova and R. Lipowsky, Nat. Commun., 2020, 11, 905.
10. B. M. Discher, Y.-Y. Won, D. S. Ege, J. C.-M. Lee, F. S. Bates, D. E. Discher and D. A. Hammer, Science, 1999, 284, 1143–1146.
11. J. Thiele, V. Chokkalingam, S. Ma, D. A. Wilson and W. T. S. Huck, Mater. Horiz., 2014, 1, 96–101.
12. E. Rideau, R. Dimova, P. Schwille, F. R. Wurm and K. Landfester, Chem. Soc. Rev., 2018, 47, 8572–8610.
13. V. Percec, D. A. Wilson, P. Leowanawat, C. J. Wilson, A. D. Hughes, M. S. Kaucher, D. A. Hammer, D. H. Levine, A. J. Kim, F. S. Bates, K. P. Davis, T. P. Lodge, M. L. Klein, R. H. De-Vane, E. Aqad, B. M. Rosen, A. O. Argintaru, M. J. Sienkowska, K. Rissanen, S. Nummelin and J. Ropponen, Science, 2010, 328, 1009–1014.
14. N. Y. Kostina, K. Rahimi, Q. Xiao, T. Haraszti, S. Dedisch, J. P. Spatz, U. Schwaneberg, M. L. Klein, V. Percec, M. Möller and C. Rodriguez-Emmenegger, Nano Lett., 2019, 19, 5732–5738.
15. N. Y. Kostina, A. M. Wagner, T. Haraszti, K. Rahimi, Q. Xiao, M. L. Klein, V. Percec and C. Rodriguez-Emmenegger, Soft Matter, 2020,  10.1039/d0sm01097a, themed collection.
16. R. E. Scott, Science, 1976, 194, 743–745.
17. T. Baumgart, A. T. Hammond, P. Sengupta, S. T. Hess, D. A. Holowka, B. A. Baird and W. W. Webb, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3165–3170.
18. H. Keller, M. Lorizate and P. Schwille, ChemPhysChem, 2009, 10, 2805–2812.
19. J. Steinkühler, B. Rózycki, C. Alvey, R. Lipowsky, T. R. Weikl, R. Dimova and D. E. Discher, J. Cell Sci., 2019, 132, jcs216770.
20. J. Steinkühler, E. Sezgin, I. Urbančič, C. Eggeling and R. Dimova, Commun. Biol., 2019, 2, 337.
21. C. D. Florentsen, A. Kamp-Sonne, G. Moreno-Pescador, W. Pezeshkian, A. A. H. Zanjani, H. Khandelia, J. Nylandsted and P. M. Bendix, Soft Matter, 2020,  10.1039/d0sm00241k, themed collection.
22. J. Israelachvili, S. Marcelja and R. Horn, Q. Rev. Biophys., 1980, 13, 121–200.
23. E. F. Semeraro, L. Marx, M. P. K. Frewein and G. Pabst, Soft Matter, 2020,  10.1039/c9sm02352f, themed collection.
24. J. F. Sadoc and J. Charvolin, J. Phys., 1986, 47, 683–691.
25. W. F. Zeno, W. T. Snead, A. S. Thatte and J. C. Stachowiak, Soft Matter, 2019, 15, 8706–8717, themed collection.
26. J. Agudo-Canalejo, Soft Matter, 2020,  10.1039/c9sm02367d, themed collection.
27. S. Christ, T. Litschel, P. Schwille andR. Lipowsky, Soft Matter, 2020,  10.1039/d0sm00790k, themed collection.
28. J. M. Seddon and R. H. Templer, Structure and Dynamics of Membranes, Elsevier Science, 1995, ch. 3, vol. 1, pp. 97–160.
29. T. Bhatia, J. Agudo-Canalejo, R. Dimova and R. Lipowsky, ACS Nano, 2018, 12, 4478–4485.
30. R. Dasgupta, M. S. Miettinen, N. Fricke, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5756–5761.
31. Y. Liu, J. Agudo-Canalejo, A. Grafmüller, R. Dimova and R. Lipowsky, ACS Nano, 2016, 10, 463–474.
32. M. Karimi, J. Steinkühler, D. Roy, R. Dasgupta, R. Lipowsky and R. Dimova, Nano Lett., 2018, 18, 7816–7821.
33. W. Helfrich, Z. Naturforsch., 1973, 28c, 693–703.
34. F. C. Frank, Discuss. Faraday Soc., 1958, 25, 19–28.
35. U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202.
36. R. Lipowsky, The Giant Vesicle Book, Taylor & Francis, 2020, ch. 5, pp. 73–168.
37. U. Seifert, L. Miao, H.-G. Döbereiner and M. Wortis, The Structure and Conformation of Amphiphilic Membranes, Springer-Verlag, 1992, pp. 93–96.
38. H.-G. Döbereiner, E. Evans, M. Kraus, U. Seifert and M. Wortis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4458–4474.
39. S. Svetina and B. Zeks, Eur. Biophys. J., 1989, 17, 101–111.
40. S. Svetina and B. Žekš, The Anatomical Record, 2002, 268, 215–225.
41. T. L. Steck, J. Ye and Y. Lange, Biophys. J., 2002, 83, 2118–2125.
42. J. A. Hamilton, Curr. Opin. Lipidol., 2003, 14, 263–271.
43. R. J. Bruckner, S. S. Mansy, A. Ricardo, L. Mahadevan and J. W. Szostak, Biophys. J., 2009, 97, 3113–3122.
44. W. C. Breckenridge, G. Gombos and I. G. Morgan, Biochim. Biophys. Acta, 1972, 266, 695–707.
45. J. R. Marszalek and H. F. Lodish, Annu. Rev. Cell Dev. Biol., 2005, 21, 633–657.
46. L. Weiss, G. Hoffmann, R. Schreiber, H. Andres, E. Fuchs, E. Korber and H. J. Kolb, Biol. Chem., 1986, 367, 905–912.
47. Y. S. A. Diniz, A. C. Cicogna, C. R. Padovani, L. S. Santana, L. A. Faine and E. L. B. Novelli, Nutrition, 2004, 20, 230–234.
48. B. Antonny, S. Vanni, H. Shindou and T. Ferreira, Trends Cell Biol., 2015, 25, 427–436.
49. T. Harayama and H. Riezman, Mol. Cell. Biol., 2018, 19, 281–296.
50. K. R. Levental, M. A. Surma, A. D. Skinkle, J. H. Lorent, Y. Zhou, C. Klose, J. T. Chang, J. F. Hancock and I. Levental, Sci. Adv., 2017, 3, eaao1193.
51. J. L. Symons, K.-J. Cho, J. T. Chang, G. Du, M. N. Waxham, J. F. Hancock, I. Levental and K. R. Levental, Soft Matter, 2020,  10.1039/d0sm00404a, themed collection.
52. M. Pinot, S. Vanni, S. Pagnotta, S. Lacas-Gervais, L.-A. Payet, T. Ferreira, R. Gautier, B. Goud, B. Antonny and H. Barelli, Science, 2014, 345, 693–697.
53. M. M. Manni, M. L. Tiberti, S. Pagnotta, H. Barelli, R. Gautier and B. Antonny, eLife, 2018, 7, e34394.
54. M. L. Tiberti, B. Antonny and R. Gautier, Soft Matter, 2020, 16, 1722–1730, themed collection.
55. R. Lipowsky, Faraday Discuss., 2013, 161, 305–331.
56. Y. Li, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4731–4736.
57. R. Lipowsky, Physics of Biological Membranes, Springer, 2018, pp. 1–44.
58. V. Heinrich and R. E. Waugh, Ann. Biomed. Eng., 1996, 24, 595–605.
59. D. Cuvelier, I. Derenyi, P. Bassereau and P. Nassoy, Biophys. J., 2005, 88, 2714–2726.
60. B. Sorre, A. Callan-Jones, J. Manzi, B. Goud, J. Prost, P. Bassereau and A. Roux, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 173–178.
61. M. Simunovic, K. Y. C. Lee and P. Bassereau, Soft Matter, 2015, 11, 5030–5036.
62. C. Steinem and M. Meinecke, Soft Matter, 2020,  10.1039/c9sm02437a, themed collection.
63. T. Litschel, B. Ramm, R. Maas, M. Heymann and P. Schwille, Angew. Chem., Int. Ed., 2018, 57, 16286–16290.
64. J. A. J. Arpino, P. J. Rizkallah and D. D. Jones, PLoS One, 2012, 7, e47132.
65. M. Osawa and H. P. Erickson, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11000–11004.
66. W. T. Snead, C. C. Hayden, A. K. Gadok, C. Zhao, E. M. Lafer, P. Rangamani and J. C. Stachowiak, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3258–E3267.
67. S. Deshpande, W. K. Spoelstra, M. van Doorn, J. Kerssemakers and C. Dekker, ACS Nano, 2018, 12, 2560–2568.
68. J. Agudo-Canalejo and R. Lipowsky, ACS Nano, 2015, 9, 3704–3720.
69. F. Bonazzi, C. K. Hall and T. R. Weikl, Soft Matter, 2020,  10.1039/c9sm02476j, themed collection.
70. Z. Xu, L. Gao, P. Chen and L.-T. Yan, Soft Matter, 2020, 16, 3869–3881, themed collection.
71. H. G. Franquelim, H. Dietz and P. Schwille, Soft Matter, 2020,  10.1039/d0sm00150c, themed collection.
72. R. Kusters, C. Simon, R. L. D. Santos, V. Caorsi, S. Wu, J.-F. Joanny, P. Sens and C. Sykes, Soft Matter, 2019, 15, 9647–9653, themed collection.
73. F. Aisafaei, X. Chen, T. Leahy, P. A. Janmey and V. B. Shenoy, Soft Matter, 2020,  10.1039/d0sm01442g, themed collection.
74. R. Lipowsky, Europhys. Lett., 1995, 30, 197–202.
75. R. Lipowsky, H. G. Döbereiner, C. Hiergeist and V. Indrani, Phys. A, 1998, 249, 536–543.
76. V. Nikolov, R. Lipowsky and R. Dimova, Biophys. J., 2007, 92, 4356–4368.
77. A. Breuer, L. Lauritsen, E. Bertseva, I. Vonkova and D. Stamou, Soft Matter, 2019, 15, 9829–9839, themed collection.
78. B. Bozic, V. Kralj-Iglic and S. Svetina, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041915.
79. C. Prevost, H. Zhao, J. Manzi, E. Lemichez, P. Lappalainen, A. Callan-Jones and P. Bassereau, Nat. Commun., 2015, 6, 8529.
80. K. R. Rosholm, N. Leijnse, A. Mantsiou, V. Tkach, S. L. Pedersen, V. F. Wirth, L. B. Oddershede, K. J. Jensen, K. L. Martinez, N. S. Hatzakis, P. M. Bendix, A. Callan-Jones and D. Stamou, Nat. Chem. Biol., 2017, 13, 724–733.
81. R. Lipowsky, Multiresponsive Behavior of Biomembranes and Giant Vesicles, Academic press, 2019, ch. 3, vol. 30, pp. 105–155.
82. D. Roy, J. Steinkühler, Z. Zhao, R. Lipowsky and R. Dimova, Nano Lett., 2020, 20, 3185–3191.
83. B. Różycki and R. Lipowsky, J. Chem. Phys., 2015, 142, 054101.
84. A. Sreekumari and R. Lipowsky, J. Chem. Phys., 2018, 149, 084901.
85. R. Ghosh, V. Satarifard, A. Grafmüller and R. Lipowsky, Nano Lett., 2019, 19, 7703–7711.
86. M. Miettinen and R. Lipowsky, Nano Lett., 2019, 19, 5011–5016.

---