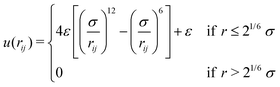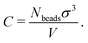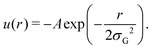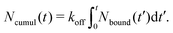Open Access Article
Open Access ArticleStress relaxation in tunable gels
Chiara
Raffaelli
a and
Wouter G.
Ellenbroek
 *ab
*ab
aDepartment of Applied Physics, Eindhoven University of Technology, P. O. Box 513, NL-5600 MB Eindhoven, The Netherlands. E-mail: w.g.ellenbroek@tue.nl
bInstitute for Complex Molecular Systems, Eindhoven University of Technology, P. O. Box 513, NL-5600 MB Eindhoven, The Netherlands
First published on 26th March 2021
Abstract
Hydrogels are a staple of biomaterials development. Optimizing their use in e.g. drug delivery or tissue engineering requires a solid understanding of how to adjust their mechanical properties. Here, we present a numerical study of a class of hydrogels made of 4-arm star polymers with a combination of covalent and reversible crosslinks. This design principle combines the flexibility and responsivity associated with reversible linkers with stability provided by chemical crosslinks. In molecular dynamics simulations of such hybrid gel networks, we observe that the strength of the reversible bonds can tune the material from solid to fluid. We identify at what fraction of reversible bonds this tunability is most pronounced, and find that the stress relaxation time of the gels in this tunable regime is set directly by the average lifetime of the reversible bonds. As our design is easy to realize in the already widely-used tetraPEG gel setting, our work will provide guidelines to improve the mechanical performance of biomedical gels.
Hydrogels are swollen polymeric networks that contain a large amount of water, some over 99%, while maintaining a three-dimensional network structure. Because they are so sparse, cells or drugs can be embedded into them, which makes them ideal for biomedical applications as scaffold materials for tissue engineering or drug carriers, respectively.1–4 For optimal functioning in these types of applications, control over the mechanical properties such as elastic moduli and toughness is essential, mainly because the behavior and viability of cells in the gels depends on it. In particular, cells thrive best if the artificial matrix that the hydrogel provides is mechanically similar to the actual extracellular matrix of the tissue being engineered.5,6
Many applications require gels at very low concentrations of polymer in order to allow cells to enter into the gel. A common way to make such gels is by swelling a network that was initially created at a higher concentration of polymer. However, the need for post-synthesis swelling has downsides. Swelling puts strain on the polymer chains, and this can negatively affect the mechanical properties of the gels, e.g. by making them brittle.7 It is therefore advantageous to directly form the hydrogels at a lower concentration of polymer. Gelation at lower concentrations, however, can introduce defects in the gel structure, such as more dangling ends, a less homogeneous structure, or even a lack of percolation resulting in a solution of clustered monomers rather than a solid macroscopic gel. A commonly used hydrogel that can be formed at low concentrations was developed by Sakai et al. in 2008,8 starting from tetraPEG polymers with different types of functionalized ends. This approach to making gels has become popular because of their superior mechanical properties, which are attributed to an elevated level of structural homogeneity.9–11 Furthermore, tetraPEG hydrogels are attractive for biomedical applications because they are biocompatible and non-immunogenic.5 An essential design feature of tetraPEGs that are to be gelled at low volume fraction is the use of an A–B type reaction and a precursor of only A4 and B4 molecules. This avoids the intramolecular bond formation that would be prevalent in homofunctional A4 units when a A–A type chemistry is used.
While traditional tetraPEG gels are covalently crosslinked, the biological environment in which they are applied is fundamentally dynamic in nature.12,13 Endowing biomedical hydrogels with reversibly binding moieties therefore enhances their versatility and performance in many applications. The bond dynamics directly couples to the mechanics, so that the gels can behave like solids on short time scales, but ultimately are able to flow. Ideally, these moieties are chosen such that they are sensitive to external stimuli such as temperature, pH, or concentration of certain biologically relevant substances.14–16 This will result in gels that, for example, can be tuned from fluid to solid through a small external stimulus, which means they can be used as injectable hydrogels that behave like liquids in the syringe but become solid gels of the appropriate stiffness once inside the body.17–19 In addition, reversible crosslinking can be used to enhance the toughness of polymeric materials if the time scales of the bond dynamics and the deformations are comparable.20,21
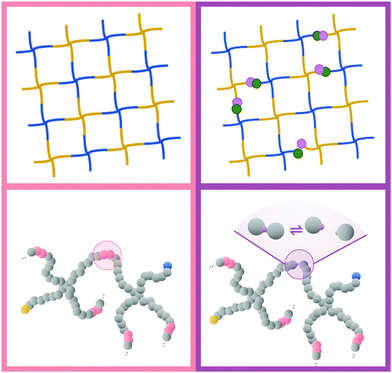
The next level of tunability in these gels is achieved by combining two or more modes of crosslinking to achieve what we will call hybrid gels, also known as dual-crosslink gels. A recent example is the use of two reversibly linking chemistries in order to achieve stress relaxation behavior that interpolates between the two individual extremes.22 A few years earlier, Narita and coworkers showed that adding a fraction of permanent crosslinks to an otherwise physically crosslinked gel will allow it to retain the intermediate-timescale relaxation mode associated with the unbinding of the reversible crosslinks, while the slowest mode associated with diffusion of non-percolating clusters is eliminated.23 In other words: These hybrid gels will retain their integrity more easily than purely physical gels, and at the same time they should have a stress relaxation behavior that one can tune via the properties of the reversible links.
In this paper, we focus on the latter class of hybrid gels, combining permanent and reversible crosslinks. In the context of tetraPEG hydrogels, where the total number of functional groups on each molecule is fixed at four, we vary both the ratio between the numbers of each type of crosslink as well as the strength of the reversible ones, in order to answer the following main questions in a numerical simulation model: (1) what ratios of permanent to reversible crosslinker numbers yield polymer structures that are fluid-like when the reversible linkers are weak or off, and solid-like when they are strong? (2) What sets the final stress relaxation in the resulting gels?
We will make use of the fact that reversible crosslinks whose strength depends on externals stimuli are known to exist and simply study them by varying a binding strength parameter in our simulations, leaving the precise determination of how binding strength depends on pH, temperature, salt concentration and other possible stimuli to other studies.14,15 Similarly, we do not rely upon a single chemistry for the permanent crosslinks, allowing us to focus on the network-level physical effects of having a mixture of permanent and reversible crosslinks. As such, our results on dynamics do not pertain to absolute time scales that describe particular materials, but rather identify relations between microscropic and macroscopic times, and how those depend on structural quantities.
We employ a numerical model based on molecular dynamics simulations to study the formation, percolation properties, and stress relaxation modulus of hybrid tetraPEG gels. Starting from a network that represents a fully connected tetraPEG gel, we replace a fraction of the crosslinks by reversible ones of a controllable strength. The resulting polymer networks are fully tunable between elastic solid in which applied stresses never fully relax, and polymer solutions in which they do.
Our main results are (1) when replacing 50% of the crosslinks by reversible ones, we obtain a material that never percolates by virtue of its covalent bonds alone, so that the strength of the reversible bonds determines the mechanical behavior: Including them in the percolation analysis, we find a bond-strength-dependent percolation transition. (2) In this tunable regime, the long-time decay of the stress relaxation modulus is governed by the lifetime of the reversible crosslinkers, which follows an Arrhenius law. Thus, our results provide a guideline for the design of mechanically tunable gels based on stimuli-responsive crosslinkers.
Our paper is organized as follows: we first introduce our coarse-grained model of hybrid tetraPEG gels, including our procedure to generate a realistic starting configuration for the networks. We then discuss the percolation properties of the resulting networks. For the case of intermediate-strength reversible links, which turns out to be the most interesting scenario, we then show how the reversible crosslinks affect the stress relaxation in these materials, and relate these results to the strength of the reversible crosslinks.
1 Numerical methods
In order to isolate the effect of reversible crosslinking on the mechanical properties of the gels from any effects due to network topology, we use a numerical model of fully covalent tetraPEG networks as the basis for our study. Reversible crosslinks are then incorporated by replacing a fraction (1 − η) of the covalent bonds by reversibly binding units.In this section we will first define our tetraPEG model and describe the simulations of the gelation process that produce the fully covalent “starting” networks. Then, we will present our implementation of reversible crosslinking and discuss how we determine the percolation properties and mechanical properties of the resulting polymer networks.
1.1 Coarse-grained model for tetraPEG
The gel model is based on end-functionalized 4-arm star polymers, using two types of functionalization that we will call A and B, such that A can react to B to form a covalent bond. Chemically, A and B could for example represent azide and alkyne groups to make click gels,24,25 or amine and succinimidyl esters such as employed in the pioneering work by Sakai et al.8To create a fully covalent gel, we mix equal amounts of functionalized four-arm star polymers, denoted as A4 and B4. The polymers are coarse-grained to strings of N = 10 beads connected by springs of unit length. The last bead on each arm will be used to implement the reaction and is denoted with bead type “A” or “B”. The other beads are of type “C” and are inert. The interactions between all beads are defined by the purely repulsive cut and shifted Lennard Jones potential (WCA).26
Because the coarse-grained beads in the model are spherical and occupy some space that in the physical system is taken up by solvent, the values of C that we encounter will typically be a bit larger than the true concentration in vol% or wt% of the real material.
We perform Molecular Dynamics simulations using LAMMPS27 for initial gelation via click reactions as well as for measuring the dynamic percolation properties and stress relaxation modulus of the hybrid gels. The solvent is implicit: we only simulate the coarse grained polymer beads. In all types of simulation, we employ a Verlet integrator coupled to a Langevin thermostat. Except where noted otherwise, we use the WCA energy scale ε = 1 and the bond length b = 1 to define our units of energy and length, and set the temperature to T = 0.6. Setting the mass of the polymer beads to m = 1, these choices also fix our unit of time via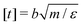 . The WCA length scale is set to σ = 1.3. Gelation simulations are performed with an integration timestep of 0.005, while the simulations that include reversible bonds use a timestep of 0.001. The harmonic springs that make up the polymer backbones have a stiffness of 50ε/b2, which is enough to prevent chains from crossing through each other.
. The WCA length scale is set to σ = 1.3. Gelation simulations are performed with an integration timestep of 0.005, while the simulations that include reversible bonds use a timestep of 0.001. The harmonic springs that make up the polymer backbones have a stiffness of 50ε/b2, which is enough to prevent chains from crossing through each other.
1.2 Gelation simulations
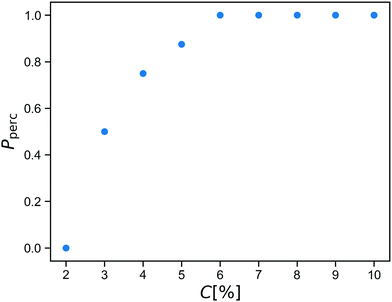
Before starting the gelation process, we equilibrate the solution of star polymers in order to relax their conformations and equilibrate their distribution in the simulation box. The gelation is a mimic of a click process28,29 in which a spring is added between an A-bead and a B-bead when they are within a cutoff distance during the simulation. After reacting this way, the A-bead and B-bead are changed to inert bead types A0 and B0, so that each reactive group forms at most one bond.We run the gelation simulation until at least 98% of bonds have reacted, which takes up to 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time units for the lowest concentrations studied. After this, we test for percolation across all three periodic boundaries using an improved burning-type algorithm that checks explicitly for independent percolation in each direction.30 This is important because numerical simulations always concern finite systems, in which statistical fluctuations may yield networks that percolate in some directions but not in all three directions independently. These would behave as a fluid if sheared along a non-percolating direction. The fraction Pperc of resulting networks that do percolate across all boundaries is shown as a function of concentration C in Fig. 2.
000 time units for the lowest concentrations studied. After this, we test for percolation across all three periodic boundaries using an improved burning-type algorithm that checks explicitly for independent percolation in each direction.30 This is important because numerical simulations always concern finite systems, in which statistical fluctuations may yield networks that percolate in some directions but not in all three directions independently. These would behave as a fluid if sheared along a non-percolating direction. The fraction Pperc of resulting networks that do percolate across all boundaries is shown as a function of concentration C in Fig. 2.
We see that within our click gel model, percolation happens between C = 2% and C = 6%. At lower concentration, the click procedure yields only isolated finite clusters of stars. We estimate that C = 6% corresponds to a weight percentage of between 2 and 3, which is a reasonable range given that our polymer arms are not particularly long.8
While the percolation curve is specific to our model and our definition of concentration, it is useful when comparing to experiments. After all, when studying phenomena related to percolation and rigidity transitions, a good indicator how far from the percolation point a network is in terms of structure is more informative than exact numbers which often depend on choices made during the definition of the coarse-grained model.
For the rest of this paper, we therefore choose to work with a concentration of C = 8%, so that the fully covalent networks will always percolate, but we are close enough to the percolation threshold that replacing a reasonable fraction of the bonds with reversible crosslinks will drive the material to the other side of it.
Fig. 3 shows a typical snapshot from the simulation. We can see that this network, while nearly devoid of dangling ends, still presents a very irregular structure (as opposed to the traditional square lattice cartoon shown in Fig. 1). We note that, although our criterion that all samples percolate in three independent directions guarantees that there is no macroscopic phase separation, density fluctuations on smaller length scales are still possible within this model.
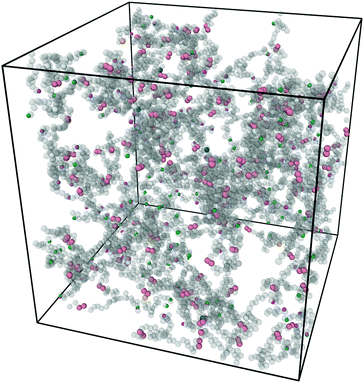 | ||
| Fig. 3 Snapshot of the simulation box after equilibration and click gelation at concentration C = 8% with half of the covalent bonds replaced by reversible linker pairs η = 0.5. Figure produced with Ovito.31 | ||
1.3 Adding reversible crosslinks
To make a hybrid gel out of our covalent gel network, we randomly convert a fraction (1 − η) of AB and A0B0 bead pairs to A′ and B′ sticker beads. The majority will be A0B0 pairs that have been bonded through the gelation process and are converted as a pair, resulting in a reversible A′B′ crosslink that is in a bound state at the beginning of the next simulation. A small fraction of the converted beads will be unreacted A and B beads, which are also selected in pairs to keep the total number of A′ and B′ beads equal, but these start unbound because they will generally be far away from each other. The parameters of the stickers are such that they only bind 1-to-1.This 1-to-1 binding is achieved by using a small attractive patch in the surface of an otherwise repulsive bead.21,32 The attraction works only between the patches, and once two patches form a bond, the repulsive surroundings prevent any third patch from getting close enough to bind. We denote the patchy beads with bead types A′ and B′, respectively.
In practice, to replace the bond, we remove the bonded interaction between the A0 and B0 beads that was created during the gelation process, and attach a small bead to each of them using a stiff spring of length 0.45. These “patch” beads interact with each other via an attractive Gaussian well potential of strength A and width σG,
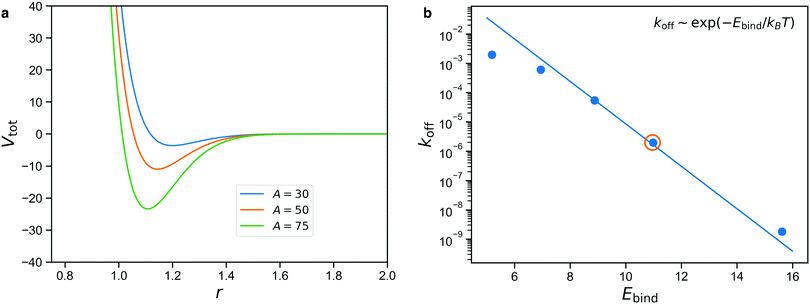
The net binding strength of the patchy beads is thus determined by the combination of their Gaussian potential and the WCA repulsion of the beads in which they are embedded.33 Throughout this paper, we use σG = 0.19, which gives rise to the net potentials shown in Fig. 4a. Note that the strength parameter A shifts the location of the minimum, but that this shift is small compared to the size of the beads which is σ = 1.3. We denote the depth of these net potential wells as the binding energy Ebind.
We use calibration simulations to verify that the unbinding rate of the patchy reversible bonds satisfies the Arrhenius equation
| koff ∼ exp(−Ebind/kBT), | (1) |
The result is shown in Fig. 4b for simulations performed with A = 35, 40, 45, 50, 60, with the solid line denoting the Arrhenius expectation given by eqn (1). We note that only the prefactor of this line is a free parameter and the slope is predetermined.
We see from Fig. 4b that there is a rather limited range of values of Ebind for which the reversible bonds live long enough to have an appreciable effect on the mechanical properties of the gel, while still displaying some exchange dynamics over the course of the simulation. The circled data point denotes A = 50, which we will consider in the rest of this study. Higher values of A give rise to long lifetimes that make the reversible bonds nearly indistinguishable from permanent ones on the time scale of the simulation, while lower values give bonds that are so short-lived that they barely affect the stresses in the network. In the results section, we will show how varying A can be used to describe stimuli-responsive networks, and for the intermediate case of A = 50, demonstrate how reversible crosslinks affect the stress relaxation.
In most of our simulations, we have the patchy interaction only defined between A′B′-pairs, and there is no interaction between patches of the same type. We will, for comparison, also include one set of simulations in which all reversibly binding beads are of the same A′ type, and the attraction is defined between A′A′-pairs in order to model self-complementary binding moieties.
1.4 Stress relaxation analysis
The stress relaxation modulus is the function G(t) that describes the time evolution of the stress σ(t) after the application of a step strain γ0. Defined as G(t) = σ(t)/γ0, it is independent of γ0 as long as it is small enough to be in the regime of linear viscoelasticity. As the compressive properties of gels are dominated by the solvent, which we do not include in our simulations, it will suffice to study the response to shear deformations.In order to get good statistics over many decades of stress, we restrict ourselves to this linear regime, and obtain the stress relaxation G(t) from the autocorrelation function of the stress, using
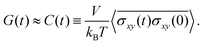 | (2) |
While this approach requires corrections when using it to determine the equilibrium shear modulus G(∞) of solids,34–36 we merely use it to assess time scales and distinguish liquids from solids, making those corrections unnecessary. In addition, we note that the raw G(t) obtained from this method is always very noisy, so in practice we plot
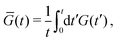 | (3) |
2 Results
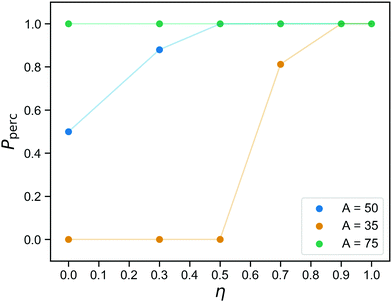
The networks we obtain at the end of the gelation stage contain only covalent bonds and therefore have a fixed topology. The question if they are percolating in three directions has a set answer for each network, and the probability that is indeed the case for a randomly chosen sample prepared at concentration C was already shown in Fig. 2. After replacing part of the bonds with reversible ones, percolation becomes a two-part question, even for a single sample: (1) Is this network percolating if we merely consider the covalent bonds? (2) If it is not, what is the probability that it is percolating at a given time, taking into account both covalent and reversible bonds?Fig. 6 shows the probability to observe a percolating network as a function of the fraction of covalent bonds η, for three values of the reversible binding strength parameter A. Each data point is an average over 16 networks and over time. As expected (see Fig. 4b, and bond lifetime as a function of wall depth), for A = 75, the patchy interactions are so strong that the physical bonds are effectively permanent and the network always percolates. The curve for A = 35 is indistinguishable from the curve one would obtain by only considering the covalent bonds: the number of bound reversible crosslinkers remains too small to affect the percolation properties. As argued in the previous section, the case A = 50 represents an intermediate regime where the reversible linkers are dynamic, flipping back and forth between percolating and non-percolating due to the linker fluctuations. This, then, identifies the regime where we predict good tunability: 50% of the bonds is always present, so the network is always close to percolation. It never actually percolates by virtue of the covalent bonds alone, but it only needs a small number of reversible bonds to form in order to become a gel.
The effect of stimuli-reponsive crosslinks can be captured phenomenologically by changing the value of A during the course of a simulation. In Fig. 5, we demonstrate the evolution of the connectivity in such a network with with 150 covalent and 150 reversible linkers (so η = 0.5), that occurs upon sudden activation of the reversible linkers. The figure shows the number of bound reversible linker pairs as a function of time, that occurs when the reversible linker strength is jumped a finite value (ranging from A = 35 to A = 60) after equilibrating the network at A = 0. As expected from the inverse bond lifetimes shown in Fig. 4b, appreciable numbers of bound reversible linkers are only achieved for A = 50 and above. This demonstrates the potential of these hybrid tetraPEG networks to form switchable gels. As we will demonstrate towards the end of the paper, the network with unbound reversible linkers behaves like a liquid, while the network with bound reversible linkers has a solid-like response up to a timescale that is set by the bond lifetimes.
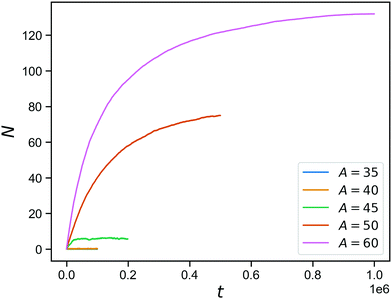 | ||
| Fig. 5 Reversible bond formation as a function of time, for a network with a concentration of 50% bonds for a range of A values. | ||
Let us zoom in on the equilibrium properties of the dynamic hybrid gel regime, using A = 50 so we can see the effects of the reversible bond dynamics. Following the discussion around Fig. 6, we expect the most visible effect of the reversible bonds on the stress relaxation for intermediate values of η ≈ 0.5. For lower values of η, the covalent network is so far from the percolation point that the reversible bonds are unable to close the gap, and the stress relaxation will be fluid-like, while for larger values of η, the covalent network will percolate on its own and the mechanical properties will be dominated by the covalent bonds.
Indeed, from the stress relaxation modulus plotted in Fig. 7, we see that we can interpolate between the fully covalent solid-like gel and the viscoelastic fluid obtained when replacing all bonds with reversible ones. Consistent with Fig. 6, we see G(t) go to a solid-like plateau for networks that still have 70% or more covalent bonds (η ≥ 0.7). Fully reversible gels (η = 0) behave like liquids. We note that Ḡ(t) ∼ 1/t is the decay one expects for this integrated quantity when the bare G(t) decays rapidly, e.g. exponentially. The plot includes a dashed line that marks this 1/t-behavior, to facilitate identifying any deviations from it. Where such deviations are identical between panels a and b, they must be attributed to the covalent network, which is indeed dominant for η ≥ 0.7, and where the are transient, they are due to the reversible crosslinks.
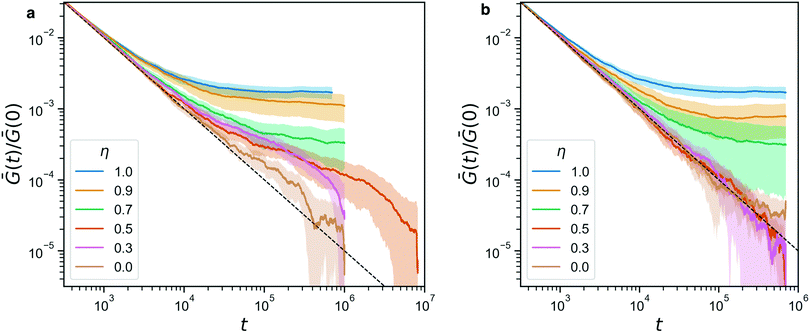 | ||
| Fig. 7 (a) The stress relaxation modulus of hybrid gels (with A′B′ reversible beads) for a range of η. For η = 0.5 we performed a longer simulation to verify that it indeed relaxes to 0 ultimately. The dashed line indicates the 1/t-artifact resulting from the averaging procedure described in eqn (3). (b) The stress relaxation modulus for the same range of η, in a control experiment where the sticker interaction has been turned off. In both panels, the shaded area indicates the standard deviation of the full data. | ||
For the dynamic hybrid gels, we see a clear signature of the reversible crosslinks in the stress relaxation. The time scale over which the reversible bonds affects the stress relaxation matches the typical bond lifetime of 5.1 × 105 that we reported in Fig. 4b. In fact, the bond lifetime clearly marks the point in the curve where both for η = 0.3 and for η = 0.5, the final decay of Ḡ(t) begins. We note that the curves are normalized by their starting value Ḡ(0), in order to make the plots more readable, but the differences in Ḡ(0) between our samples are small (within a factor of 3 when comparing η = 1 to η = 0), so this normalization does not affect the analysis of the stress relaxation in a significant way.
Fig. 7b shows a control experiment in which the reversible links have been made inactive. The curves obtained for η ≥ 0.7 are indistinguishable from their counterparts in panel a, confirming that these are networks whose mechanics is dominated by the covalent bonds. Furthermore, the curves for η ≤ 0.5 are now on top of each other, re-affirming that indeed the reversible crosslinkers were responsible for the delayed stress relaxation for η = 0.3, 0.5 in the full experiment.
Finally, we go back to the question of having mutually complementary A′B′-binding versus self-complementary A′A′-binding. In the click gelation that serves as the starting point of this work, the A′B′-binding helps to get percolation at low concentrations, but how much difference does this still make when the network architecture has already formed? In Fig. 8, we compare the stress relaxation modulus of the hybrid gels in which the reversible linkers are of the A′B′-type, which we also used in Fig. 7, to that of hybrid gels in which the reversible linkers are A′A′. As expected, the difference is negligible for η ≥ 0.7, because the reversible linkers are unimportant for the stress relaxation in those networks, and even at η = 0.5 we do not observe any difference. However, when the majority of the bonds has been made reversible (η ≤ 0.3), the A′A′-type bonds seem to provide a faster stress relaxation. We speculate that this is due to the fact that, because all arms ends of the tetraPEGs are now equivalent, the reversible bonds can form between two arms on the same star, creating a loop that no longer contributes to the rigidity of the network in any way. This effect, although it shows itself much more weakly here, is reminiscent of what happens with stress relaxation in star polymer vitrimers.37 We note that the difference between A′A′ and A′B′ is most pronounced at η = 0.3, while at η = 0 the difference is smaller again, most likely due to the fact that these networks are further from the gel point to begin with, so that even if all reversible binding events form bridges (not loops) and thus contribute to the rigidity, there are simply not enough of them to give a noticeable effect on the stress relaxation modulus.
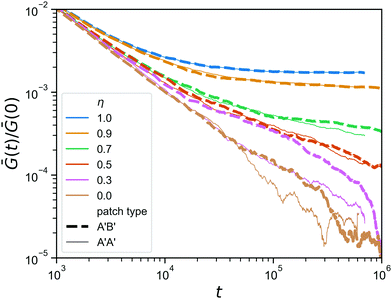 | ||
| Fig. 8 Comparison between the stress relaxation modulus (zoom in) of hybrid gels for two types of reversible patches, for a range of η; A′B′ in a thick dashed line, A′A′ in a thin solid line. | ||
3 Discussion
Hybrid gels, defined here as gels that are held together by a combination of chemical and physical bonds, provide two extra knobs to tune the structural and mechanical properties of gels for biomedical applications. The first is the fraction of bonds η in the gel that is still covalent, and is determined at time of synthesis. The other is the strength of the reversible bonds, which can be affected not only by choice of chemical moiety but also by a range of environmental parameters. In this work, we have focused on networks built from 4-arm star polymers and shown that, for intermediate values of η, one obtains tunable gels that, depending on the reversible bond strength, show liquid-like or solid-like behavior. First, we demonstrated that the resulting gels are switchable, in the sense that they behave like liquids when the reversible bonds are relatively weak and few in number, but they become solid when the bond strength is increased and more bonds form, creating a stronger network. Secondly, we have shown that the reversible bonds in these switchable networks dominate the stress relaxation modulus, in particular the longest relaxation time in the network that marks the time scale beyond which the material should be considered a liquid. For the latter effect to be visible, the network needs to be in the regime where the covalent backbone alone is not sufficient to provide rigidity, and the result is an increase of the stress relaxation time to something of the order of the bond lifetime.The fact that our gels have a partly covalent nature is important for reaching the observed situation that the stress relaxation time is set primarily by the bond lifetime. While the bond lifetimes for binding strength A = 50 are of order 106, we only see significant solid-like behavior up to that timescale in our samples where 30% to 50% of the bonds are covalent: The all-reversible network at the same binding strength only percolates about 50% of the time (see Fig. 6) and barely shows any deviations from the liquid-like response (Fig. 7). We interpret this behavior by noting that, while the samples for η ≈ 0.5 are always non-percolating by virtue of their permanent bonds only, the permanent bonds keep the system much closer to the percolation threshold, so that only relatively few reversible bonds need to form in order to obtain a gel. This means the presence of the permanent bonds improve the tunability provided by the reversible ones. This obeservation is of course closely related to the findings by Narita and coworkers that combinining permanent and dynamic crosslinks is a means to get rid of the slow relaxation mode characterizing diffusion of non-percolation clusters.23
Focusing on 4-arm star polymers has kept us close the commonly used tetraPEG gels, the synthesis of which is routine. Still, we speculate that going to more complex building blocks might allow for even more control over the mechanics. For example, using building blocks with more reversible binding units may allow for cooperative effects between the reversible links,38 that could increase the stress relaxation time beyond the typical lifetimes of individual bonds – an effect that we have not observed in our model. Another opportunity for further optimization of these gels is to consider the role of the binding process, and therefore the on-rate, of the reversible links. This has been difficult to control in our approach, as it is set by a combination of the extent of environment exploration of the dangling ends and the likelihood that two patches that get near each other will manage to settle in the deep minumum of their binding potential.
Our reversible binding model, based on the interaction potential of pairs of patchy particles, has the nice feature that the force-dependence of the unbinding process is captured naturally, unlike MCMD-hybrid approaches where the topology of the polymer network is adapted via Monte Carlo steps that are performed in between stretches of MD simulation.33 On the other hand, the use of potentials to model strong bonds has limited our choice of simulation timestep, and in order to reach longer time scales this choice should be reconsidered. Several open questions remain on the simulation side that we feel need to be explored, including a more detailed comparison of the network structures obtained at the end of the click gelation to the network structures that result in equilibrated samples, particularly in the intermediate η regime where the reversible crosslinks dominate the mechanical properties. Furthermore, a more detailed study of how blends of reversible crosslinks with different lifetimes work together to determine the network mechanics would be worthwhile: While Yesilurt and coworkers found a rather smooth interpolation of relaxation times,22 in our system where one of the crosslinkers did not relax at all, we did not see any clear indications of such interpolation.
TetraPEG gels, including those with reversible linkers, are already a common platform for biomaterials design. With our results, we hope to give this application a new dimension, allowing for more precise control over their basic mechanical properties as well as their responsivity to external stimuli.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank S. Paquay, S. Ciarella, A. Bose, N. B. Tito, and C. Storm for stimulating discussions and helpful suggestions. This work is part of the research programme of the Netherlands Organization for Scientific Research (NWO), via grant 15PR3223.References
- K. Y. Lee and D. J. Mooney, Chem. Rev., 2001, 101, 1869–1880 Search PubMed.
- A. S. Hoffman, Adv. Drug Delivery Rev., 2002, 54, 3–12 Search PubMed.
- D. W. Hutmacher, Biomaterials, 2000, 21, 2529–2543 Search PubMed.
- T. Kissel, Y. Li and F. Unger, Adv. Drug Delivery Rev., 2002, 54, 99–134 Search PubMed.
- J. Zhu, Biomaterials, 2010, 31, 4639–4656 Search PubMed.
- S. V. Graeter, J. Huang, N. Perschmann, M. López-García, H. Kassler, J. Ding and J. P. Spatz, Nano Lett., 2007, 7, 1413–1418 Search PubMed.
- H. Kamata, X. Li, U.-I. Chung and T. Sakai, Adv. Healthcare Mater., 2015, 4, 2360–2374 Search PubMed.
- T. Sakai, T. Matsunaga, Y. Yamamoto, C. Ito, R. Yoshida, S. Suzuki, N. Sasaki, M. Shibayama and U.-I. Chung, Macromolecules, 2008, 41, 5379–5384 Search PubMed.
- T. Matsunaga, T. Sakai, Y. Akagi, U.-I. Chung and M. Shibayama, Macromolecules, 2009, 42, 1344–1351 Search PubMed.
- T. Matsunaga, T. Sakai, Y. Akagi, U.-I. Chung and M. Shibayama, Macromolecules, 2009, 42, 6245–6252 Search PubMed.
- Y. Akagi, T. Katashima, Y. Katsumoto, K. Fujii, T. Matsunaga, U.-I. Chung, M. Shibayama and T. Sakai, Macromolecules, 2011, 44, 5817–5821 Search PubMed.
- C. Frantz, K. M. Stewart and V. M. Weaver, J. Cell Sci., 2010, 123, 4195–4200 Search PubMed.
- J. S. Mohammed and W. L. Murphy, Adv. Mater., 2009, 21, 2361–2374 Search PubMed.
- C. D. L. H. Alarcón, S. Pennadam and C. Alexander, Chem. Soc. Rev., 2005, 34, 276–285 Search PubMed.
- D. E. Apostolides, T. Sakai and C. S. Patrickios, Macromolecules, 2017, 50, 2155–2164 Search PubMed.
- V. Yesilyurt, M. J. Webber, E. A. Appel, C. Godwin, R. Langer and D. G. Anderson, Adv. Mater., 2016, 28, 86–91 Search PubMed.
- L. Yu and J. Ding, Chem. Soc. Rev., 2008, 37, 1473–1481 Search PubMed.
- M. Liu, X. Zeng, C. Ma, H. Yi, Z. Ali, X. Mou, S. Li, Y. Deng and N. He, Bone Res., 2017, 5, 17014 Search PubMed.
- Y. Li, J. Rodrigues and H. Tomás, Chem. Soc. Rev., 2012, 41, 2193–2221 Search PubMed.
- Z. S. Kean, J. L. Hawk, S. Lin, X. Zhao, R. P. Sijbesma and S. L. Craig, Adv. Mater., 2014, 26, 6013–6018 Search PubMed.
- N. B. Tito, C. Creton, C. Storm and W. G. Ellenbroek, Soft Matter, 2019, 15, 2190–2203 Search PubMed.
- V. Yesilyurt, A. M. Ayoob, E. A. Appel, J. T. Borenstein, R. Langer and D. G. Anderson, Adv. Mater., 2017, 29, 1605947 Search PubMed.
- T. Narita, K. Mayumi, G. Ducouret and P. Hébraud, Macromolecules, 2013, 46, 4174–4183 Search PubMed.
- C. A. DeForest, B. D. Polizzotti and K. S. Anseth, Nat. Mater., 2009, 8, 659–664 Search PubMed.
- J. Zheng, L. A. Smith Callahan, J. Hao, K. Guo, C. Wesdemiotis, R. A. Weiss and M. L. Becker, ACS Macro Lett., 2012, 1, 1071–1073 Search PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 Search PubMed.
- W. Xi, T. F. Scott, C. J. Kloxin and C. N. Bowman, Adv. Funct. Mater., 2014, 24, 2572–2590 Search PubMed.
- K. Oshima, T. Fujimoto, E. Minami and Y. Mitsukami, Macromolecules, 2014, 47, 7573–7580 Search PubMed.
- C. Raffaelli and W. G. Ellenbroek, 2021, in preparation.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 Search PubMed.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301 Search PubMed.
- R. S. Hoy and G. H. Fredrickson, J. Chem. Phys., 2009, 131, 224902 Search PubMed.
- J. P. Wittmer, H. Xu and J. Baschnagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 22107 Search PubMed.
- I. Kriuchevskyi, J. P. Wittmer, O. Benzerara, H. Meyer and J. Baschnagel, Eur. Phys. J. E, 2017, 40, 43 Search PubMed.
- J. P. Wittmer, I. Kriuchevskyi, A. Cavallo, H. Xu and J. Baschnagel, Phys. Rev. E, 2016, 93, 62611 Search PubMed.
- S. Ciarella, F. Sciortino and W. G. Ellenbroek, Phys. Rev. Lett., 2018, 121, 058003 Search PubMed.
- M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 2754–2794 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |