Open Access Article
Open Access ArticleRelaxation in aging thermoreversible gels: the role of thermal history†
Stefano
Buzzaccaro
 *,
Andrea Francesco
Mollame
and
Roberto
Piazza
*,
Andrea Francesco
Mollame
and
Roberto
Piazza

Department of Chemistry, Materials Science, and Chemical Engineering (CMIC), Politecnico di Milano, Edificio 6, Piazza Leonardo da Vinci 32, 20133 Milano, Italy. E-mail: stefano.buzzaccaro@polimi.it
First published on 12th August 2021
Abstract
The fast setting of gels originating from an arrested phase separation leads to solid structures that incorporate a substantial amount of frozen-in stresses. Using a colloidal system made of particles whose interactions can accurately be tuned with temperature and exploiting Photon Correlation Imaging (PCI), an optical correlation technique blending the powers of scattering and imaging, we show that the relaxation of these internal stresses, which occurs through a cascade of microscopic restructuring events, is strongly influenced by the thermal history of the sample. By changing with a temperature jump the interparticle interactions in an already set gel, we specifically show that gels formed by a deep quench within the coexistence region store a lot of residual stress. This stress quickly relaxes when the interparticle attractions are weakened by decreasing temperature. Conversely, the relaxation of stresses accumulated in gels obtained by a shallower quench comes to a halt by a temperature jump that hardens the gel structure. The evidence we collected may provide useful hints about tempering and annealing processes in disordered solids.
Rapid freezing often generates disordered solids that contain ‘frozen-in’ stresses.1–3 A well-known evidence of the presence of these stresses and of their dramatic effect on the mechanical properties of the material is the breaking of Prince Rupert's drops. These tadpole-shaped glass beads, created by dripping molten glass into cold water, can withstand a hammer's blow on their body, but immediately burst when the slightest damage is inflicted upon their tail.4 In fact, controlling the spatial distribution and magnitude of residual stresses may give a material better mechanical properties.5,6 The way to obtain this result is not trivial, and depends on the specific application, For instance, while the strength and durability of glass objects is often improved by annealing processes in temperature-controlled kilns that reduce their residual stresses, smartphone displays are often strengthened by deliberately pre-stressing them during manufacturing.
Glasses are not the only materials that are produced by nonequilibrium routes.7,8 A standard method to obtain physical gels involves indeed the quenching of a homogeneous colloidal fluid into a phase separation region. The phase separation process generates bicontinuous structures that rapidly coarsen in time until the denser phase forms an arrested solid structure and the phase separation is kinetically arrested.9–11 The microscopic structural and dynamic properties of these gels, however, further evolve over timescales that can be very long. Several experimental evidences suggest that gel aging is more complex than the aging processes observed in conventional glassy materials.3,7,12,13 During the gel aging the temporal dynamics is indeed characterized by an intermittent sequence of spatially-localized ‘quakes’ that eventually lead to global rearrangements of the whole structure, in striking contrast with the much smaller-ranged dynamic heterogeneity observed in glassy materials. Such peculiar behaviour is attributed the intermittent release of residual stresses that relax the fractal backbone of the gel.14
Colloidal gels may then be regarded as useful model systems to investigate the dependence of the amount and distribution or residual stresses on the thermal history of the sample. Unfortunately, when phase separation and gelation is induced by increasing the interparticle attractions with the addition of a depletant agent,9,10,15 the speed and spatial homogeneity of the quench within the coexistence region cannot easily be controlled. Besides, it is hardly feasible to modify the structure of an already formed gel by tuning the amount of depletant, since this requires a vigorous mixing that erases the stress pattern originally imprinted in the gel structure. To this specific aim, inducing gelation by varying the ionic strength or pH via internal enzymatic reactions,16 which usually leads to much more homogenous gels, is not a better strategy.
In this work we show that colloidal gels made of particles whose interactions can be tuned with temperature allow an extensive and accurate investigation of the effects on the gel structure of thermal cycles that closely mimic those commonly used in the production and treatment of molecular amorphous solids. The particles we use, which have a radius R = 50 ± 2 nm (polydispersity = 4%), are made of a fluorinated polymer with low refractive index ρp = 1.49 g cm−3 and are synthesized using a sophisticated form of emulsion polymerization (RAFT, Reversible Addition Chain Transfer) that provides an extremely good particle stabilization by means of a covalently linked poly-ethyleneglycol (PEG) surface layer.17 The low refractive index of the particles can be easily matched using as solvent mixtures of water with 2,2′-thiodiethanol (TDE), a nonionic liquid with refractive index nTDE = 1.5215, miscible with water in any ratio,18 which allows the structure of highly concentrated suspensions to be investigated using scattering techniques.
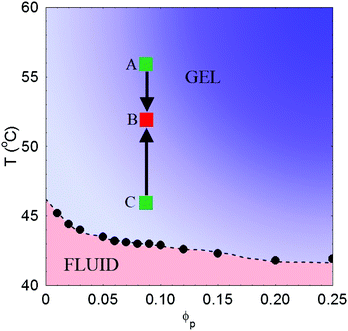
Besides, interparticle interactions between these PEG-grafted particles can be tuned by exploiting the temperature dependence of the solubility of short PEG chains in water. The solubility of PEG is strongly affected by the amount and kind of added electrolytes.17,19 A kosmotropic salt like ammonium sulfate weakens for instance the hydrogen bonds between PEG and water, which becomes a marginal solvent for the stabilizing polymer layer turning the effective interparticle forces from repulsive to attractive. When about 0.6 M of Na2SO4 is added to water, the colloidal suspensions we investigated display indeed a liquid–liquid phase separation above a temperature Tps(ϕ) that depends on particle volume fraction ϕ (see Fig. 1). Because the range of these effective attractions is much smaller than the particle size, when quenched inside the coexistence gap the colloid does not undergo a full phase segregation into equilibrium phases, but rather gets arrested into an amorphous gel phase that is fully thermo-reversible. The mechanical strength of these gels depends on the quench depth, namely the deeper the quench the harder the gels. Consequently, gels formed at higher temperature compress less under their own weight than those solidified at lower T. The restructuring process in gels obtained for different temperatures may actually be qualitatively different because the extent and spatial inhomogeneity of the frozen-in stresses depend on the quench depth.
We have investigated the restructuring dynamics of these gels and the changes an already-formed gel undergoes as a result of a temperature jump using Photon Correlation Imaging (PCI). PCI is an optical technique that provides the time-correlation function of the scattered light like in standard Dynamic Light Scattering (DLS), but with the major advantage of allowing for spatial resolution by probing the local dynamics at distinct points within the scattering volume.20 Basically, the experiment consists in forming on a multi-pixel camera an image of the scattering volume, observed at a scattering angle ϑ = 90° through a suitably stopped-down optics that, besides selecting the scattering wave-vector q ≃ 23 μm−1, causes the image to become ‘speckled’ because the intensity at each given point on the image plane originates from the interference of the field scattered by a finite-size region in the sample plane. For the purposes of this investigation, however, we shall only consider averages of the time dynamics over all the pixels of the detector, thus renouncing to spatial resolution, to be able to obtain a fast ensemble averaging of the intensity correlation function, crucial when investigating samples with a very slow dynamic. The time dynamics is quantified by means of the so-called ‘correlation index’ cI(τ;t) between two images taken at times t and t + τ, defined as
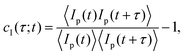 | (1) |
Settling of gels upon fast quenching
Since the strength of attractive interactions depend on temperature, the restructuring processes in gels obtained for different quench depth inside the coexistence gap may be expected to differ because of a different amount and spatial distribution of the frozen-in elastic stresses. Let us then compare how the restructuring dynamics of three samples A, B, C, prepared at a same initial particle volume fraction ϕ0 = 0.09 and quickly brought within the miscibility gap, depends on the quench depth. The gelation temperatures we choose are respectively TA = 56 °C, TB = 52 °C, and TC = 46 °C (see Fig. 1). Defining for each sample i a relative quench depth Δi = (Ti − Tc)/Tc, where Tc is the temperature (in Kelvin) where the sample cross the phase-separation line in Fig. 1 (Tc ≃ 316 K at ϕ = 0.09), we have then ΔA ≃ 0.04, ΔB ≃ 0.03, ΔC ≃ 0.01.Temperature quenches were performed by initially pouring the samples at a temperature well below Tc in a scattering cuvette, which was then quickly transferred into the cell holder already thermalized within ±0.5 °C about the final temperature. Full sample thermalization required about two minutes, after which a substantial slowing down of the speckle pattern dynamics marks the onset of gelation. After an initial and rather unpredictable time lag the gels underwent two clearly separated restructuring phases, consisting in a relatively fast gravity compression stage (but with no sign of gel rupture) lasting for about 30′ followed by a much slower compaction stage. Here we shall solely focus only on the latter, taking as t = 0 the time at which when the gels have began the compaction stage.
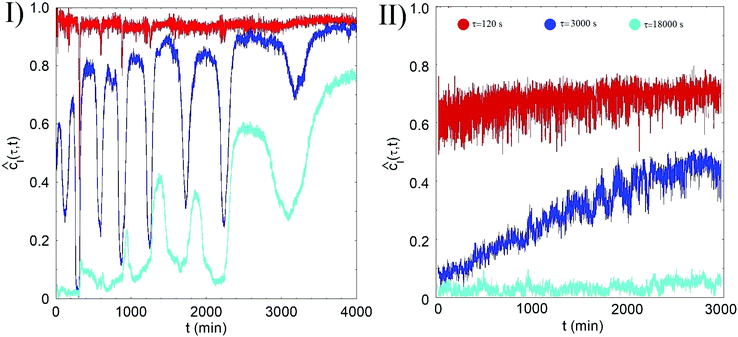
The dependence on the aging time t of ĉI(τ;t) for sample B, is shown in the panel I of Fig. 2 for some values of the delay time τ. Focusing on the behavior of ĉI(τ;t) for the shortest delay time, τ = 120 s, we first observe that ĉI(120 s;t) is finite and consistently larger than zero for all values of the aging time t. To compare, in the colloidal fluid region (T < Tps) the DLS correlation functions at the same q-vector fully decay in a few tens of a millisecond, which confirms that at t = 0 the system is already a quasi-arrested gel. Notice however that ĉI(120 s;t) < 1 for all values of t, arguably because the relaxation of fast internal relaxation modes causes a decay of the correlation functions of about 5% over very short time.
On a longer delay τ = 3000 s, however, the normalized correlation index displays a peculiar ‘spiky’ behavior characterized by sudden drops that reflect an abrupt change of the speckle pattern. More specifically, an irregular sequence of minor drops that lower ĉI by less than 5–10% is punctuated by a few big decorrelation events, during which the correlation index drops to much lower values. We refer to these huge restructuring events as to ‘macro-quakes’ (MQ), whereas smaller events will be called ‘micro-quakes’ (μQ). The qualitative feature of this aging dynamics are akin to what has been recently observed in a similar thermoreversible gel, where the microscopic dynamics is characterized by an intermittent sequence of spatially-localized ‘micro-quakes’ eventually leading to global re-arrangements.12 The evolution of the gel towards a more homogeneous state is witnessed by a fading of the fluctuations in cI and by a progressive decrease of the frequency of the MQs.
The behavior of ĉI(18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s;t) shows that the sample, after more than two days, is still aging: while at the beginning a MQ is sufficient to complete rearrange the sample, starting from t = 2000 min the sample remains correlated also after a MQ.
000 s;t) shows that the sample, after more than two days, is still aging: while at the beginning a MQ is sufficient to complete rearrange the sample, starting from t = 2000 min the sample remains correlated also after a MQ.
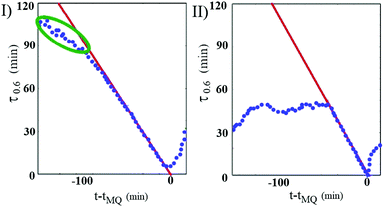
Sample A shows a rather similar aging behaviour, although an interesting difference in the sample dynamics just before a MQ event takes place can actually be spotted. The different behaviours of the sample A and B can be appreciated in Fig. 3, where we plotted, for each sample, the curves τ0.6(t) that give, as a function of t, the values of ĉI(τ;t) at which the correlation index takes on a fixed value equal to 0.6. Notice that, because of the way it is constructed, ĉI(τ;t) at a given time implicitly bears information about the subsequent behavior of the correlation index up to t + τ. Hence, if a strong decorrelation event takes place in the time interval between t and t + τ, ĉI(τ;t) will drop to zero. Therefore, we can define for each MQ a sort of ‘event horizon’ as the straight line τ = tMQ − t. In fact, for fixed τ the evolution of the correlation index with the gel age is meaningful only to the left of this line, since crossing the event horizon erases any memories of the previous behavior. While for sample B a MQ event is heralded by a spontaneous speeding up of the microscopic dynamics, as highlighted by the green ellipse in the first panel of Fig. 3, we did not detect anything similar for the deeper-quenched sample A, whose microscopic dynamics is more similar what has been found in alginate polymer gels.7 Such a different approach may somehow remind of a ductile to brittle transition of the gel. Indeed, while the failure of a ductile material is anticipated by a weakening of the material that slowly propagates through the structure, similarly to what is found for sample B, the rupture of a brittle material is abrupt and takes place at high speed, like in sample A.
The aging processes of sample C looks instead markedly different. As shown in the panel I of the Fig. 2, no sign of system-spanning decorrelation events is indeed observed, and the gel ages in a much smoother way. At the same aging time cI(120 s;t,r) shows a lower value and a larger variance than in sample B (see Fig. 2), which implies a faster microscopic dynamics evolving only by localized rearrangements. This evidence strongly suggests that the frozen-in stresses relax faster and more extensively than in samples A and B.
Temperature adjustment effects on settled gels (TA → TB, TC → TB)
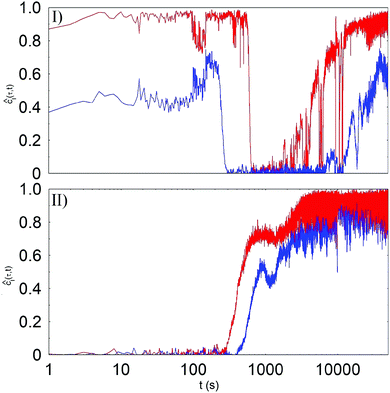
The evolution of the microscopic dynamics of samples A and C when they are brought at TB = 52 °C after having been kept at TA and TC for a week (see the arrows in Fig. 1) is strikingly different. Panel I of Fig. 4 shows indeed that when the temperature is lowered from TA → TB the dynamics of sample A speeds up, with cI(50 s;t) decreasing from about 0.96 to a value close to 0 and taking more than 10 h to recover a value close to the initial one. As time goes on, the sample dynamics slows down, displaying the usual complex ageing process characterized by a spatially and temporally heterogeneous dynamics, accompanied by sudden global restructuring events whose frequency decreases with time. In sample A, lowering T lowers the attractive force between the particles, weakening the gel bonds and facilitating stress release. Conversely, panel II shows that right after T is increased from TC to TB the dynamics of sample C looks fully arrested, with the correlation index at τ = 400 s that is significantly larger than zero, reaching a stationary value of 0.85 after about 3 h. We have followed the aging of sample C for several days finding no evidence of further significative restructuring events.‡This evidence indicates that the aging dynamics of thermoreversible gels is strongly influenced by its thermal history. The magnitude and spatial distribution of the elastic stress stored in the material during gelation control the material aging and failure. The occurrence of residual stresses implies that the gels we have studied are not simply characterized by the thermodynamic control variables ϕ and T. Different preparation histories may then result in materials that differ in structure and possibly in mechanical properties too. A detailed study of the mechanical properties and aging dynamics of thermoreversible gels subjected to thermal cycles may then help to elucidate the mechanisms governing the annealing of other materials dynamically frozen in a nonequilibrium structure.
From a practical point of view, the design and control of the thermal profiles inside the sample, using controlled spatial temperature gradients, may allow to control stress relaxation in colloidal solids. To this aim, a series of experiments devoted to the study of stress relaxation in gels subjected to temperature gradients has recently been performed on board of the International Space Station in the framework of the project ‘ACE-T10’, funded by NASA, while T-cycling experiments in microgravity condition will be made in the next future in the framework of the ‘Colloid Solidification in Space’ project of the European Space Agency.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge funding from the Italian Ministry for Education, University and Research (PRIN Project ID 2017Z55KCW – ‘Soft Adaptive Networks’) and thank U. C. Palmiero for particle synthesis.Notes and references
- P. Withers, Rep. Prog. Phys., 2007, 70, 2211 CrossRef.
- M. Ballauff, J. M. Brader, S. U. Egelhaaf, M. Fuchs, J. Horbach, N. Koumakis, M. Krüger, M. Laurati, K. J. Mutch and G. Petekidis, et al. , Phys. Rev. Lett., 2013, 110, 215701 CrossRef CAS PubMed.
- S. Buzzaccaro, M. D. Alaimo, E. Secchi and R. Piazza, J. Phys.: Condens. Matter, 2015, 27, 194120 CrossRef PubMed.
- S. Chandrasekar and M. Chaudhri, Philos. Mag. B, 1994, 70, 1195–1218 CAS.
- Y. Zhang, W. Wang and A. Greer, Nat. Mater., 2006, 5, 857–860 CrossRef CAS PubMed.
- L. Wang, H. Bei, Y. Gao, Z. P. Lu and T. Nieh, Acta Mater., 2011, 59, 2858–2864 CrossRef CAS.
- E. Secchi, T. Roversi, S. Buzzaccaro, L. Piazza and R. Piazza, Soft Matter, 2013, 9, 3931 RSC.
- E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101 CrossRef.
- S. Buzzaccaro, R. Rusconi and R. Piazza, Phys. Rev. Lett., 2007, 99, 098301 CrossRef PubMed.
- P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499 CrossRef CAS PubMed.
- F. Cardinaux, T. Gibaud, A. Stradner and P. Schurtenberger, Phys. Rev. Lett., 2007, 99, 118301 CrossRef PubMed.
- Z. Filiberti, R. Piazza and S. Buzzaccaro, Phys. Rev. E, 2019, 100, 042607 CrossRef CAS PubMed.
- B. W. Mansel and M. A. Williams, Soft Matter, 2015, 11, 7016 RSC.
- M. Bouzid, J. Colombo, L. V. Barbosa and E. Del Gado, Nat. Commun., 2017, 8, 15846 CrossRef CAS PubMed.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256 CrossRef CAS.
- S. Aime, L. Ramos and L. Cipelletti, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 3587–3592 CrossRef CAS PubMed.
- U. C. Palmiero, A. Agostini, E. Lattuada, S. Gatti, J. Singh, C. T. Canova, S. Buzzaccaro and D. Moscatelli, Soft Matter, 2017, 13, 6439–6449 RSC.
- T. Staudt, M. C. Lang, R. Medda, J. Engelhardt and S. W. Hell, Microsc. Res. Tech., 2007, 70, 1–9 CrossRef CAS PubMed.
- J. Ulama, M. Z. Oskolkova and J. Bergenholtz, J. Phys. Chem. B, 2014, 118, 2582–2588 CrossRef CAS PubMed.
- A. Duri, D. Sessoms, V. Trappe and L. Cipelletti, Phys. Rev. Lett., 2009, 102, 085702 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00711d |
| ‡ The difference between the two samples can be further appreciated by considering two correlation functions obtained about 20 h after the temperature is set at 52 °C. As shown in Fig. S1 of the ESI,† the microscopic dynamics in sample A is indeed almost 5 times faster than in sample C. |
| This journal is © The Royal Society of Chemistry 2021 |