Whole tissue and single cell mechanics are correlated in human brain tumors

Abstract

Biomechanical changes are critical for cancer progression. However, the relationship between the rheology of single cells measured ex-vivo and the living tumor is not yet understood. Here, we combined single-cell rheology of cells isolated from primary tumors with in vivo bulk tumor rheology in patients with brain tumors. Eight brain tumors (3 glioblastoma, 3 meningioma, 1 astrocytoma, 1 metastasis) were investigated in vivo by magnetic resonance elastography (MRE), and after surgery by the optical stretcher (OS). MRE was performed in a 3-Tesla clinical MRI scanner and magnitude modulus |G*|, loss angle φ, storage modulus G′, and loss modulus G′′ were derived. OS experiments measured cellular creep deformation in response to laser-induced step stresses. We used a Kelvin-Voigt model to deduce two parameters related to cellular stiffness (μ_KV) and cellular viscosity (η_KV) from OS measurements in a time regimen that overlaps with that of MRE. We found that single-cell μ_KV was correlated with |G*| (R = 0.962, p < 0.001) and G'' (R = 0.883, p = 0.004) but not G' of the bulk tissue. These results suggest that single-cell stiffness affects tissue viscosity in brain tumors. The observation that viscosity parameters of individual cells and bulk tissue were not correlated suggests that collective mechanical interactions (i.e. emergent effects or cellular unjamming) of many cancer cells, which depend on cellular stiffness, influence the mechanical dissipation behavior of the bulk tissue. Our results are important to understand the emergent rheology of active multiscale compound materials such as brain tumors and its role in disease progression.

---

Introduction

Cancer progression relies on contradictory mechanical properties. For metastasis, individual cancer cells or small clusters have to move in a fluid-like fashion, i.e., flow through their microenvironment by overcoming the yield stress, which holds a cancer cell back.¹ On the other hand, a tumor has to resist its microenvironment to permit cell proliferation and the subsequent spreading of the tumor mass.² These seemingly opposing requirements can be met simultaneously when cells with a broad range of mechanical properties coexist in heterogeneous tumors. Soft, unjammed cancer cells foster cell motility and proliferation, while rigid, jammed cancer cells and fibrotic stroma provide a backbone that mechanically stabilizes the tumor against the surrounding tissue.³ In agreement with this hypothesis, rigid and soft areas with jammed and unjammed cancer cells, respectively, have been recently found in cervix and breast carcinoma.⁴ The existence of cancer cell unjamming transitions that control the emergent tissue state of matter already illustrates that the viscoelastic behavior of single cells is not one-to-one mirrored in bulk tissue properties. The way in which cancer cells, cancer-associated cells and fibrotic stroma collectively shape the viscoelastic properties of a tumor mass and their surrounding host tissue in vivo remains elusive due to the lack of measurement methods, which are sensitive to single cell properties as well as tissue viscoelastic parameters, preferably in vivo.

Individual cell properties must be examined with reasonably high throughput on a larger number of cells to obtain statistically relevant data on the broad distributions of cells’ biomechanical behavior. A device to accomplish this task is the optical stretcher (OS).⁵ However, an inherent limitation of measuring the mechanical properties of individual cells in sufficiently large samples is that they have to be conducted in vitro, i.e., under non-physiological conditions. The OS probes the mechanics of single cells in suspension, which means that no interactions with the microenvironment stimulate mechanosensitive cellular responses. Consequently, the cells probed are in their mechanical “ground state”, in which they do not reveal their complex, emergent multiscale behavior.

Magnetic resonance elastography (MRE) allows quantification of mechanical bulk properties of soft tissues in vivo.⁶ Using shear waves excited in an audible frequency range and phase-contrast magnetic resonance imaging (MRI), MRE generates maps of viscoelastic parameters for clinical diagnosis.⁷ The resolution that can be probed by in vivo MRE is on the order of millimeters. MRE is sensitive to the type and stage of cancer in a variety of organs including the liver,^8–10 pancreas,^11,12 prostate^13–15 and brain.^16–19 However, while most solid tumors appear stiffer than their healthy surrounding tissue, the in vivo mechanical profiles of brain tumors suggest that viscosity and the degree of fluid behavior critically influence their invasiveness, rather than changes in stiffness.²⁰ To translate these findings into a causal understanding of how single cell properties are related to tissue architecture and mechanics, it is necessary to mechanistically interpret MRE data using microstructural data. Unfortunately, there is a general lack of data showing how microarchitecture and cellular properties scale into the resolution of MRE parameters.^21,22

Therefore, we pair ex-vivo OS and in vivo MRE examinations of brain tumors to correlate, for the first time, cell mechanical properties with tissue viscoelasticity measured in patients. Our study population includes the most prominent brain tumor types. The most common benign brain tumors, meningiomas (MEN), originate from meningothelial cells and are characterized by slow growth and sharp tumor boundaries, and are in general well treatable by surgery.^23–25 In contrast, glioblastomas (GBM), the most common malignant brain tumors, originate from glial cells in the brain or spine. These grade-IV gliomas, according to the classification of the World Health Organization (WHO) are characterized by rapid and diffusive growth without clearly detectable boundaries.²⁶ The recurrence risk after surgery is high, resulting in poor clinical prognosis.²⁷ Finally, we included an astrocytoma (AST), a lower-grade glioma (WHO grade II) with a good prognosis, and a lung metastasis (MET) of cancer cells from outside the central nervous system. Our hypothesis is that the mechanics of individual cancer cells influences the collective, emergent properties of cancer tissue measured by MRE. Since tissue viscosity is particularly sensitive to motility and friction within relevant architectural elements such as cells,²⁸ we expect deeper insights into the mechanical properties of malignant tumors from the combined use of OS and MRE.

Methods

Study population and tissue samples

The study was approved by the ethics committee of the University of Leipzig. All participants gave written informed consent according to the declaration of Helsinki (nr. 278-13-07102013). In total, eight brain tumors were investigated: three glioblastomas (GBM), one metastasis (MET), one low-grade astrocytoma (AST), and three meningiomas (MEN). Descriptive data of all patients are summarized in Table 1. All patients underwent clinical MRI and MRE for diagnostic workup and were managed by surgery. Tissue samples were obtained after surgery. Apparent tissue heterogeneities such as vessels and necroses were excluded. Therefore, a smaller portion of macroscopically homogeneous tissue from a central tumor region was selected for the OS study. These regions was later included in the image-based MRE analysis. For transport, the tissue samples were stored in Ham's F-10 supplemented with 2% penicillin/streptomycin/amphotericin B at 4 °C. Before further processing the tissues were washed several times thoroughly with buffer solution to get rid of any blood residues. For enzymatic dissociation of the tissue samples, a brain tumor dissociation kit was used (Miltenyi Biotech, cat. no. 130-095-942). Additionally, dissociation was supported by a mechanical stimulus induced by rotation (gentleMACS dissociator and MACSmix tube rotator, Miltenyi Biotec Co. KG, Teterow, Germany). As cells and their mechanical properties adapt rapidly to culture conditions (e.g., cell culture flasks),²⁹ OS measurement was performed immediately after dissociation to ensure that they are as close as possible to their original physiological conditions. No additional cell sorting was performed before the OS in order to ensure that the investigated cells reflect the average population of cells within the tumor. A diagram of the procedure is presented in Fig. 1.

Table 1 Patient demographics and characteristics of brain tumors (MET: metastasis, GBM: glioblastoma, AST: astrocytoma, MEN: meningioma)

	Sex	Age	Tumor	WHO	Comment
a IDH-mutation and MGMT promotor methylation status.
1	m	52	MET	Metastasis	Lung
2	m	61	GBM	IV	R132H neg./partially methylated
3	m	75	GBM	IV	R132H neg./not methylated
4	f	60	GBM	IV	R132H neg./partially methylated
5	f	67	AST	II	Wild type
6	f	75	MEN	I	Transitional
7	f	50	MEN	I	Fibrous
8	f	51	MEN	I	Transitional

---

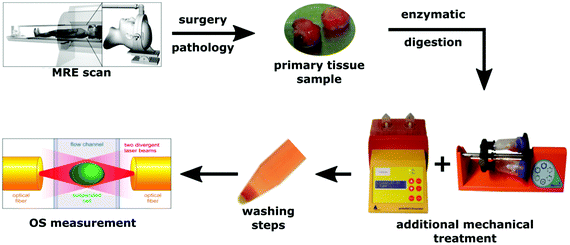Fig. 1 Schematic representation of the experiments including in vivo MRE and OS measurements of isolated single cells.

in vivo MRE

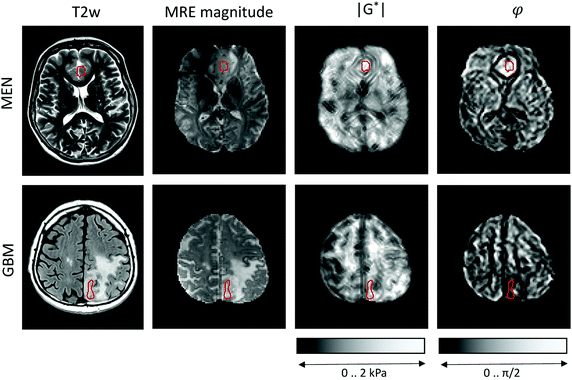
MRE was performed in a clinical 3-Tesla MRI scanner (Siemens Trio, Erlangen, Germany) using a driver built from an acoustic subwoofer connected via a telescopic carbon fiber rod to a custom-designed cradle and located inside the head coil¹⁷ (Fig. 1). Seven harmonic frequencies from 30 to 60 Hz (5 Hz increments) were consecutively applied and their vibration responses captured by a multislice single-shot, echo-planar imaging sequence with flow-compensated motion-encoding gradients.³⁰ Thus, our MRE measurement probes tissues with deformations on a timescale of a few tens of milliseconds. Further MRE image acquisition parameters were: 3 s repetition time (TR), 71 ms echo time (TE), 128 × 96 matrix, 2 × 2 × 2 mm³ voxel size, 15 contiguous slices, 8 instances per vibration cycle dynamic resolution, parallel acquisition factor 2, and 9 min total scan time. MRE parameter maps were reconstructed for |G*| and φ, the magnitude and the phase angle of the complex shear modulus, by multifrequency dual elasto-visco (MDEV) inversion.³⁰ MDEV inversion relies on averaged multifrequency, multicomponent wave analysis based on two separate solutions of the Helmholtz equation for |G*| and φ.³¹ The analysis pipeline is in the public domain and available at http://https:\\bioqic-apps.charite.de. Storage and loss modulus (|G*| = G′ + i·G′′) were derived from |G*| and φ according to G* = |G*| exp(i·φ). Regions of interest (ROIs) were defined using the magnitude image contrast of MRE and then confirmed based on T₁- and T₂-weigthed anatomical MRI scans by the associated neuroradiologist and neuropathologist who provided tumor tissue samples for use in the OS. ROIs were carefully delineated to ensure that as much tumor tissue as possible was captured from the region selected for OS studies, while larger vessels and necrotic areas were excluded. Example regions are shown in Fig. 2.

Fig. 2 Clinical MRI and MRE maps of two representative cases with meningioma (MEN) and glioblastoma (GBM). Regions of interest are demarcated by red lines. T₂w: T₂-weighted image (with fluid suppression for GBM) for anatomical orientation, |G*|: magnitude shear modulus, φ: loss angle of the complex shear modulus.

Optical cell stretching

A microfluidic OS (RS Zelltechnik GmbH, Schöllnach, Germany) was used to quantify the mechanical deformability of single, suspended cells. The system contained a microfluidic chip with two counter-propagating divergent laser beams emitted from opposing fibers, perpendicular to the channel. The lasers generated a step stress with a power of 0.8 W, to which each suspended cancer cell was exposed for 2 s.⁵ Cells are kept at an ambient temperature of 23 °C, and are heated to about 37 °C by absorption of laser light by the surrounding water content of the medium. The time scale of the induced transient stresses overlaps with that of MRE. The OS typically measures a few hundred up to thousands of cells to capture the full range of cellular properties. Similar to MRE, OS relies on small deformations that probe the linear elastic regime. Deformation was detected by video microscopy converted to time-dependent creep deformation J(t) from the surface forces according to.³² Furthermore, J_max was detected as a measure of maximal deformation by taking the mean of the last five data points before the end of the step stress. A Kelvin-Voigt model³³ was then used to convert J(t) into an elastic stiffness parameter (μ_KV) and viscous parameter (η_KV). Note that even an isolated, suspended cell is a highly complex compound material, and OS predominantly captures the properties of the actin cortex. Consequently, OS-measured viscoelastic constants are mostly determined by geometrical factors such as the thickness of the cortical actin rim.³⁴ Thus, the Kelvin-Voigt model merely provides a relative measure of the cells’ mechanical properties, precluding a direct quantitative comparison with the mechanical constants measured by MRE. Cancer cells adapt to changes in their mechanical environment.³⁵ Consequently, they also adapt to rigid cell culture dishes when grown ex-vivo and therefore do no longer reflect their physiological mechanical state.^36,37 Conversely, when measured directly after isolation (as done in this study), the suspended cells are in a ground state without stimuli from the surrounding microenvironment.

Correlation analysis

As a direct quantitative comparison of material constants between MRE (unmodelled |G*| and φ) and OS (μ_KV and η_KV) is not possible, we performed correlation analysis to elucidate the impact of single-cell properties on whole-tissue properties. Therefore, the statistical significance of linear correlation between viscoelastic constants measured by MRE and OS was tested using Pearson's linear correlation coefficient. Wilcoxon's rank sum test for equal medians was used for group comparisons. p < 0.05 was considered statistically significant.

Results

in vivo MRE results

Representative maps of MRE are shown in Fig. 2. They clearly display the pathological changes in tissue mechanics throughout the solid brain tumors. We measured the average magnitude and real part of the complex shear modulus as measures of resistance. The bulk tumor values of less invasive tumors with good prognosis (MEN + AST, |G*| = 1517 ± 200 Pa, G′ = 930 ± 170 Pa) were not markedly different (p = 0.2) from those of invasive tumors with a poorer prognosis (GBM + MET, |G*| = 1278 ± 142 Pa, G′ = 1080 ± 110 Pa). In contrast, the loss angle φ, a measure of the ratio of energy lost to energy stored, was larger in MEN + AST than in GBM + MET (φ = 0.88 ± 0.10 rad vs. 0.51 ± 0.06 rad, p = 0.028), which is in agreement to the literature.²⁰ MEN + AST behave more like at the transition between a fluid and a solid and the closeness to a fluid permits them to dissipate more mechanical energy. While GBM + MET behave more elastically and dissipate less mechanical energy. Correspondingly, the loss modulus G′′ showed a trend towards higher values in MEN + AST than in GBM + MET (G′′ = 1084 ± 222 Pa vs. 623 ± 92 Pa, p = 0.057). In Fig. 3, where |G*| is plotted versus φ, illustrates that the viscous resistance significantly contributes to the total mechanical resistance. Thus, we found a less dissipative, more elastic restoring behavior of brain tumors with a poorer prognosis. Comparing MEN with neural tumors revealed trends in GBM and AST towards lower values of |G*| (1630 ± 56 Pa vs. 1262 ± 149 Pa), φ (0.91 ± 0.10 rad vs. 0.58 ± 0.13 rad) and G′′ (1190 ± 144 Pa vs 662 ± 110 Pa, all p = 0.57) but not G′.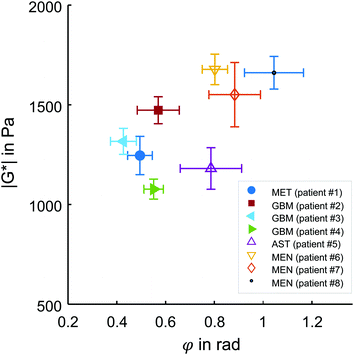

Fig. 3 in vivo MRE results in brain tumors. Subgroups of tumors with poor (MET + GBM) and good prognosis (AST + MEN) are represented by solid and open symbols, respectively. While no separation of these groups is possible based on the magnitude shear modulus |G*|, the loss angle φ, indicating tissue fluidity, allows good separation of the two subgroups, similar to the results reported in ref. 20. Patient numbers refer to Table 1.

Cell properties

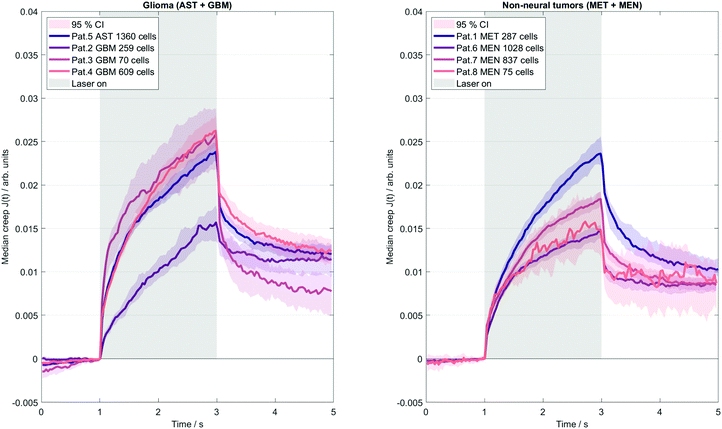
Fig. 4 illustrates the deformation response of cells in a creep experiment to step stress induced by the OS system. The results indicate much lower single cell elastic stiffness than the elastic modulus measured with in vivo MRE (mean μ_KV = 34 ± 7 Pa obtained by the OS, versus the corresponding mean MRE G′ = 1004 ± 161 Pa). The disparity of stiffness values of individual cells and bulk tissue properties reflects well-known differences in rheological constants obtained by different measurement methods and the applied underlying viscoelastic models that cannot describe the complex multiscale emergent rheological behavior.³⁸ Moreover, as already mentioned, collective cell and stroma effects can strongly modulate the viscoelastic properties of tissues. This is further reflected by single cell viscosity (mean η_KV = 18 ± 8 Pa s), which, converted to G′′ at 45 Hz mean excitation frequency (G′′ = 2π·45 Hz·η_KV), exceeds 5000 Pa (versus G′′ = 853 ± 286 Pa measured by in vivo MRE). Comparison of tumors with a good prognosis (AST + MEN) versus poor prognosis (MET + GBM) revealed no difference in cell properties (μ_KV = 38 ± 7 Pa vs. 30 ± 3 Pa, p = 0.2, η_KV = 16 ± 3 Pa s vs. 19 ± 10 Pa s, p = 0.88; J_max: 0.018 ± 0.003 vs. 0.022 ± 0.004, p = 0.22). However, considering meningioma versus glioma, a trend towards stiffer properties in MEN compared with GBM + AST was found (μ_KV = 42 ± 4 Pa vs. 30 ± 3 Pa, p = 0.057). MRE and OS results per patient are summarized in Table 2. Our data raise the question to what extent the considerable intracellular viscoelasticity plays a role in the all-over dissipative behavior of the in vivo tissue.

Fig. 4 Laser pattern used for all OS measurements presented in this study. Data are arranged into two subgroups of glioma (GBM and AST) and non-neural tumors (MEN and MET). Gray bars indicate the timing of step stress functions induced by the lasers.

Table 2 MRE and OS results per patient (SD, *confidence intervals in brackets)

Pat #	Tumor	MRE				OS
		|G*| Pa	φ rad	G′ Pa	G′′ Pa	J max ^a a.u.	μ KV ^a Pa	η KV ^a Pa s
1	MET	1246 (318)	0.49 (0.17)	1064 (207)	612 (322)	0.023 (0.001)	29.9 (2.3)	19.2 (1.2)
2	GBM	1473 (241)	0.57 (0.31)	1176 (308)	776 (388)	0.015 (0.002)	33.2 (3.9)	35.5 (6.4)
3	GBM	1317 (213)	0.43 (0.17)	1174 (175)	553 (255)	0.025 (0.004)	32.2 (2.5)	7.4 (0.8)
4	GBM	1077 (229)	0.55 (0.18)	906 (230)	551 (190)	0.026 (0.002)	25.8 (2.2)	15.4 (1.9)
5	AST	1181 (373)	0.79 (0.45)	764 (460)	767 (393)	0.023 (0.001)	28.0 (2.6)	11.8 (1.6)
6	MEN	1677 (347)	0.80 (0.24)	1143 (405)	1164 (333)	0.014 (0.001)	45.7 (4.1)	18.4 (2.6)
7	MEN	1551 (593)	0.88 (0.39)	1050 (676)	1029 (379)	0.018 (0.001)	37.0 (3.0)	19.4 (2.3)
8	MEN	1661 (228)	1.04 (0.34)	763 (424)	1378 (398)	0.015 (0.003)	42.5 (5.3)	15.0 (1.9)

---

Correlation analysis

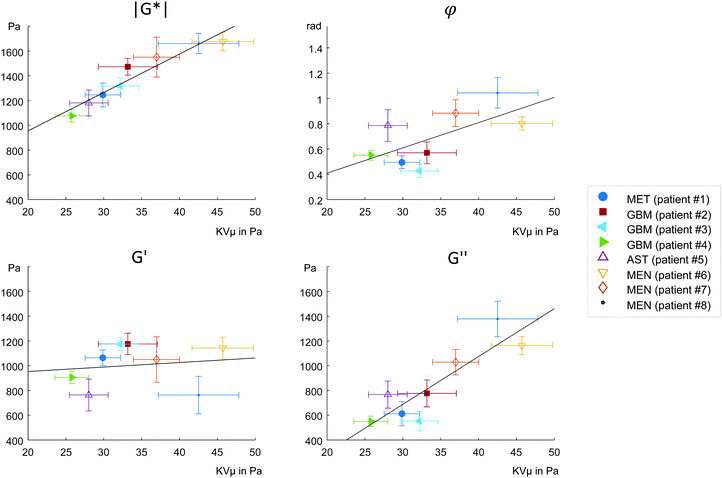
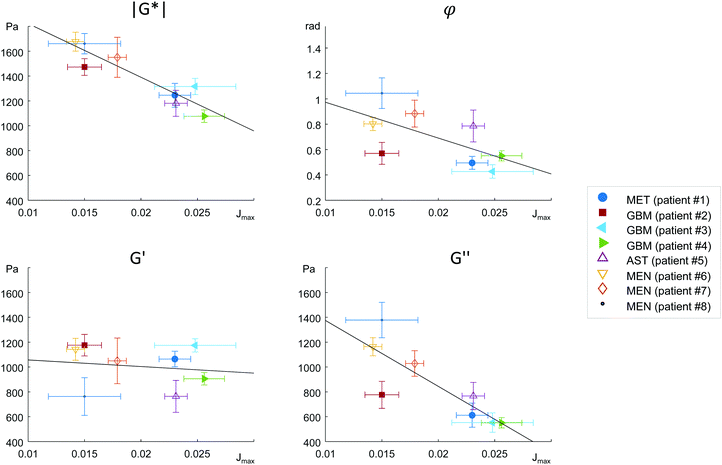
MRE parameters that characterize the tumor tissue are plotted versus the single cell data derived from OS measurement. Best linear correlation was found for the total (viscous and elastic) bulk resistance |G*| (R = 0.962, p < 0.001), followed by the bulk loss modulus G′′ (R = 0.883, p = 0.004) with the single cell stiffness μ_KV, while the elastic bulk storage modulus G′ and the bulk loss angle φ did not correlate with μ_KV (Fig. 5) (R = 0.15, p = 0.72 and R = 0.64, p = 0.08 respectively). These results suggest that tissue resistance and bulk viscosity is determined by single cell stiffness and not single cell viscosity. This dependence of bulk tissue dissipation on single cell stiffness agrees with the correlation of the total bulk resistance |G*| and the bulk loss modulus G′′ with the OS parameter, single cell compliance J_max, determined independently of the Kelvin-Voigt model (R = −0.918, p = 0.001 and R = −0.831, p = 0.011, respectively) (Fig. 6).

Fig. 5 Correlation analysis of viscoelastic parameters obtained by MRE in in vivo brain tumors and by OS in single cancer cells. MRE measured magnitude (|G*|), loss angle (φ), real part (G′) and imaginary part (G′′) of the complex shear modulus G*. OS deformations were converted to stiffness according to the Kelvin-Voigt model (KVμ).

Fig. 6 Correlation analysis of viscoelastic parameters obtained by MRE in in vivo brain tumors and by OS in single cancer cells. MRE measured magnitude (|G*|), loss angle (φ), real part (G′) and imaginary part (G′′) of the complex shear modulus G*. Maximum OS deformations (J_max) were measured and used without further modelling.

We pooled all cases into two groups of equal sizes (4), which are associated with either poor prognosis (GBM + MET) or good prognosis (MEN + AST). In the poor prognosis subgroup, there was a linear correlation between G′ and μ_KV (R = 0.993, p = 0.007), and between G′′ and η_KV (R = 0.957, p = 0.043), as well as between |G*| and μ_KV (R = 0.961, p = 0.039). For the subgroup of tumors with better prognosis (MEN + AST), only |G*| and μ_KV showed a significant linear correlation (R = 0.968, p = 0.032), suggesting a more indirect correlation between single cells and bulk properties through emergent collective effects. This raises the question whether different emergent effects (e.g. cell-ECM interactions)p = in the two groups play a role for the relation of single-cell to bulk tumor rheology. The group of glioma (AST + GBM) showed a correlation in |G*| versus μ_KV (R = 0.966, p = 0.034) while no correlation between MRE and cell properties was observed in MEN.

Discussion

Cancer cells are highly mechanosensitive and adapt their proteomic expression profile by cellular mechanotransduction and consequently their mechanics to the surrounding microenvironment.^29,39,40 When measured directly after extraction of the tumor explant (as done in this study) the suspended cells in the OS are in an unstimulated ground state representing the cancer cells’ inherent mechanical phenotype as determined by their physiologic microenvironment through cellular mechanotransduction.

Our correlation analysis revealed relationships between the properties of single suspended cells with the complex collective tissue properties of a brain tumor. However, our results demonstrate that the mechanical behavior of the individual cancer cells cannot be directly transferred to the tissue scale since the bulk tissue is influenced by emergent collective effects that generate mechanical properties beyond the properties of individual cells.

We find correlations between parameters which are related to the viscous bulk properties of tumor tissue, such as |G*| and G′′, with individual cancer cell stiffness μ_KV, but not with single cell viscosity η_KV. Neither the bulk elastic modulus G′ nor the loss angle φ were correlated to single cell parameters. These results raise the question, which effects mediate between single-cell and bulk mechanics.

To start with, the fact that single-cell viscosity η_KV did not correlate with bulk dissipation means that cancer cells do not act as simple additive dampers. The apparent contradiction between the tissue and single-cell results can be caused by emergent, large-scale effects,^1,4 that provide additional dissipative collective channels or by non-cellular, dissipative tissue components, such as the stroma. Tumor tissue is highly heterogeneous (extracellular matrix, cancer cell clusters, blood vessels, tumor associated cells, etc.), which permits bulk tissue properties not found in a homogeneous material. In a heterogeneous tissue, fluid areas can be highly dissipative while a percolating backbone can still cause an allover solid behavior. Shape-induced cancer cell unjamming, which is an emergent effect, requires cells to squeeze by each other in order to become motile.⁴ Thus, within this framework, single cell rigidity is directly connected to tissue fluidity. In fact, the only global correlations we observed were between single cell μ_KV and bulk tissue G′′ and between μ_KV and |G*|, which is associated with G′′ as the absolute sum of G′ and G′′. Accordingly, we found softer cells in the tissues with lower viscosity G′′ and lower overall modulus |G*|, while stiffer cells were connected to tissue with both higher G′′ and |G*|.

Our correlations analysis surprisingly revealed relationships between single cells that do not feel their tissue environment with complex tissue properties of solid brain tumors. These correlations must be due to phenotypical expression changes in the cytoskeleton of cancer cells leading to inherent differences in cell stiffness in progressing tumors. In a recent more advanced cell jamming model,⁴¹ a heterogeneous mixture of stiff and soft cancer cells can assume three states: a fully fluid phase with a vanishing tissue elastic modulus dominated by soft cells, a heterogeneous fluid phase of soft cells with island of stiff cells with a finite elastic modulus caused by tension percolation and a solid phase caused by a percolated backbone of stiff or jammed cells. Thus, a mostly unjammed fluid tissue can simultaneously have a finite shear modulus and an increase in cell heterogeneity can even lead to a solidification of an otherwise fluid, i.e. unjammed tissue. This might explain why we do not find a collapsing elastic modulus for fluid tissues. The bulk viscosity is then predominately determined by the dissipation mechanisms between the motile cells. As a consequence, the loss angle, which is also understood as bulk tissue fluidity, increases as the tissue becomes more jammed induced by an increase in stiff cells (Fig. 5b). The bulk elastic stiffness G′ only weakly depends on the individual elastic cell stiffness because cell stiffness only indirectly regulates the tissue's G′ through the amount of jammed cells (Fig. 5c). Bulk tissue viscosity G′′ depends more directly and strongly on the individual cell stiffness (Fig. 5d) since cell stiffness is an important determinant of cell–cell interactions including intercellular dissipation. The total mechanical bulk resistance |G*| takes over the dependence on the individual cell stiffness as the sum of G′ and G′′ (Fig. 5a). The more jammed-like tissues with higher μ_KV have both higher |G*| and G′′ than the unjammed tissues and thus feel more rigid.

Although having a too small number of samples at hand for a reliable proof, we see a trend that makes us hypothesize that this behavior might be connected to the different type of ECM within these tumor entities. When only analyzing the GBM subgroup we find the trend between single cell μ_KV and bulk G′ (R = 0.99, p = 0.08) as expected for a viscoelastic material. Contrary to that, in the MEN subgroup no such trend is visible (R = 0.085, p = 0.95). The higher amount of fibrous ECM, such as collagen in MEN²⁰ might partially mask cellular properties and thus account for the weaker correlation between OS and MRE parameters in the less aggressive tumors. Even a low volume density of collagen (<1%) is sufficient to create networks which significantly determine bulk properties²² and provide a scaffolding for cells to attach and mechanically adapt to. Studies in decellularized tissues using MRE showed the dominating mechanical properties of sparse collagen ECM networks over large amounts of pore fluid.⁴² This might also explain why cellular properties better correlate with bulk properties in our glioma subgroup (AST + GBM) than in MEN. Here it is worthwhile to mention, that throughout the rest of the body, most solid tumors are associated with fibrosis and are characterized by stiff-fluid properties (high |G*| and φ) while, conversely, GBM are mostly soft and solid (low |G*| and φ).^19,20

Our study can only be a first step in unraveling the complexity of cell and tissue mechanics. Brain tissue is a multiscale compound material with superviscous anomalous viscous properties at the length scales that are typically investigated by MRE.⁴³ Therefore, a large dispersion of viscoelastic constants is expected within a relatively small dynamic range from 1 to 20 Hz, in which shear modulus values increase by more than an order of magnitude.⁴³ A similarly strong viscoelastic dispersion is expected for brain tumors.^17,30 Therefore, it is not surprising that we observed quantitative differences in the material constants measured by MRE and OS. Of note, already at the cell level, we have no complete understanding of the complex mechanical interplay of cellular constituents. With increasing scale, it becomes more and more clear that tissues are not the simple sum of the mechanical properties of their building blocks. Emergent effects such as cell jamming transitions lead to new mechanical properties on larger scales. Tumor invasion requires optimal mechanical properties on all scales, which permits cancer to become a systemic disease.

In conclusion, cell and tissue mechanics cannot comprehensively be investigated by one technique alone that is sensitive to only one length scale. Therefore, we paired, for the first time, micromechanical tests of cells with in vivo MRE in brain tumors. We observed a strong correlation between viscous dissipation of the whole tissue with individual cell stiffness, while single cell viscosity was not correlated with bulk tissue properties. Emergent effects such as partial tissue fluidization through cell unjamming in local cancer cell clusters might explain how stiffness of individual cancer cells influences dissipation properties of the bulk tumor tissue in vivo. Taken together, our data suggest that the mechanical properties of individual cells are crucial for the macroscopic viscoelastic properties of an active multiscale compound material such as in vivo brain tumors and also highlight the importance of considering the bulk loss modulus in cell jamming models.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by the German Research Foundation (DFG, GRK2260 BIOQIC, CRC1340, Sa901/17-2), the European Research Council (ERC-741350) and the European Commission (Horizon 2020 ID 668039, FORCE –Imaging the Force of Cancer).

References

1. L. Oswald, S. Grosser, D. M. Smith and J. A. Käs, J. Phys. D. Appl. Phys., 2017, 50, 483001.
2. E. Jonietz, Nature, 2012, 491, S56–S57.
3. O. Ilina, P. G. Gritsenko, S. Syga, J. Lippoldt, C. A. M. La Porta, O. Chepizhko, S. Grosser, M. Vullings, G. J. Bakker, J. Starruß, P. Bult, S. Zapperi, J. A. Käs, A. Deutsch and P. Friedl, Nat. Cell Biol., 2020, 22, 1103–1115.
4. S. Grosser, J. Lippoldt, L. Oswald, M. Merkel, D. M. Sussman, F. Renner, P. Gottheil, E. W. Morawetz, T. Fuhs, X. Xie, S. Pawlizak, A. W. Fritsch, B. Wolf, L.-C. Horn, S. Briest, B. Aktas, M. L. Manning and J. A. Käs, Phys. Rev. X, 2021, 11, 011033.
5. J. Guck, R. Ananthakrishnan, H. Mahmood, T. J. Moon, C. C. Cunningham and J. Käs, Biophys. J., 2001, 81, 767–784.
6. R. Muthupillai, D. J. Lomas, P. J. Rossman, J. F. Greenleaf, A. Manduca and R. L. Ehman, Science, 1995, 269, 1854–1857.
7. S. Hirsch, J. Braun and I. Sack, Magnetic Resonance Elastography - Physical Background and Medical Applications DOI:10.1002/9783527696017, accessed 7 January 2021.
8. P. Garteiser, S. Doblas, J. L. Daire, M. Wagner, H. Leitao, V. Vilgrain, R. Sinkus and B. E. Van Beers, Eur. Radiol., 2012, 22, 2169–2177.
9. S. K. Venkatesh, M. Yin, J. F. Glockner, N. Takahashi, P. A. Araoz, J. A. Talwalkar and R. L. Ehman, Am. J. Roentgenol., 2008, 190, 1534–1540.
10. M. Shahryari, H. Tzschatzsch, J. Guo, S. R. Marticorena Garcia, G. Boning, U. Fehrenbach, L. Stencel, P. Asbach, B. Hamm, J. A. Kas, J. Braun, T. Denecke and I. Sack, Cancer Res., 2019, 79, 5704–5710.
11. L. Zhu, J. Guo, Z. Jin, H. Xue, M. Dai, W. Zhang, Z. Sun, J. Xu, S. R. Marticorena Garcia, P. Asbach, B. Hamm and I. Sack, Eur. Radiol., 2020, 1–9.
12. S. R. Marticorena Garcia, L. Zhu, E. Gültekin, R. Schmuck, C. Burkhardt, M. Bahra, D. Geisel, M. Shahryari, J. Braun, B. Hamm, Z. Jin, I. Sack and J. Guo, Invest. Radiol., 2020, 55, 769–774.
13. P. Asbach, S. R. Ro, N. Aldoj, J. Snellings, R. Reiter, J. Lenk, T. Köhlitz, M. Haas, J. Guo, B. Hamm, J. Braun and I. Sack, Invest. Radiol., 2020, 55, 524–530.
14. B. Hu, Y. Deng, J. Chen, S. Kuang, W. Tang, B. He, L. Zhang, Y. Xiao, J. Chen, P. Rossman, A. Arani, Z. Yin, K. J. Glaser, M. Yin, S. K. Venkatesh, R. L. Ehman and J. Wang, Abdom. Radiol., 2021, 46, 3387–3400.
15. M. Li, J. Guo, P. Hu, H. Jiang, J. Chen, J. Hu, P. Asbach, I. Sack and W. Li, Radiology, 2021, 201852.
16. M. C. Murphy, J. Huston, K. J. Glaser, A. Manduca, F. B. Meyer, G. Lanzino, J. M. Morris, J. P. Felmlee and R. L. Ehman, J. Neurosurg., 2013, 118, 643–648.
17. M. Reiss-Zimmermann, K. J. Streitberger, I. Sack, J. Braun, F. Arlt, D. Fritzsch and K. T. Hoffmann, Clin. Neuroradiol., 2015, 25, 371–378.
18. M. Simon, J. Guo, S. Papazoglou, H. Scholand-Engler, C. Erdmann, U. Melchert, M. Bonsanto, J. Braun, D. Petersen, I. Sack and J. Wuerfel, New J. Phys., 2013, 15, 085024.
19. A. Bunevicius, K. Schregel, R. Sinkus, A. Golby and S. Patz, Neuroimage, 2020, 25, 102109.
20. K.-J. Streitberger, L. Lilaj, F. Schrank, J. Braun, K.-T. Hoffmann, M. Reiss-Zimmermann, J. A. Käs and I. Sack, Proc. Natl. Acad. Sci. U. S. A., 2019, 201913511.
21. I. Sack, K. Jöhrens, J. Würfel and J. Braun, Soft Matter, 2013, 9, 5672.
22. F. Sauer, L. Oswald, A. Ariza de Schellenberger, H. Tzschätzsch, F. Schrank, T. Fischer, J. Braun, C. T. Mierke, R. Valiullin, I. Sack and J. A. Käs, Soft Matter, 2019, 15, 3055–3064.
23. S. Oya, S. H. Kim, B. Sade and J. H. Lee, J. Neurosurg., 2011, 114, 1250–1256.
24. M. Lim, Y. Xia, C. Bettegowda and M. Weller, Nat. Rev. Clin. Oncol. 2018 157, 2018, 15, 422–442.
25. M. Preusser, P. K. Brastianos and C. Mawrin, Nat. Rev. Neurol. 2018 142, 2018, 14, 106–115.
26. M. Weller, W. Wick, K. Aldape, M. Brada, M. Berger, S. M. Pfister, R. Nishikawa, M. Rosenthal, P. Y. Wen, R. Stupp and G. Reifenberger, Nat. Rev. Dis. Prim. 2015 11, 2015, 1, 1–18.
27. R. Stupp, W. P. Mason, M. J. van den Bent, M. Weller, B. Fisher, M. J. B. Taphoorn, K. Belanger, A. A. Brandes, C. Marosi, U. Bogdahn, J. Curschmann, R. C. Janzer, S. K. Ludwin, T. Gorlia, A. Allgeier, D. Lacombe, J. G. Cairncross, E. Eisenhauer and R. O. Mirimanoff, N. Engl. J. Med., 2005, 352, 987–996.
28. M. Plodinec, M. Loparic, C. A. Monnier, E. C. Obermann, R. Zanetti-Dallenbach, P. Oertle, J. T. Hyotyla, U. Aebi, M. Bentires-Alj, R. Y. H. Lim and C. A. Schoenenberger, Nat. Nanotechnol., 2012, 7, 757–765.
29. M. J. Paszek, N. Zahir, K. R. Johnson, J. N. Lakins, G. I. Rozenberg, A. Gefen, C. A. Reinhart-King, S. S. Margulies, M. Dembo, D. Boettiger, D. A. Hammer and V. M. Weaver, Cancer Cell, 2005, 8, 241–254.
30. K. J. Streitberger, M. Reiss-Zimmermann, F. B. Freimann, S. Bayerl, J. Guo, F. Arlt, J. Wuerfel, J. Braun, K. T. Hoffmann and I. Sack, PLoS One, 2014, 9(10), e110588.
31. S. Papazoglou, S. Hirsch, J. Braun and I. Sack, Phys. Med. Biol., 2012, 57, 2329–2346.
32. T. R. Kießling, R. Stange, J. A. Käs and A. W. Fritsch, New J. Phys., 2013, 15, 045026.
33. M. A. Meyers and K. K. Chawla, Mechanical Behavior of Materials, Cambridge University Press, Cambridge, 2008.
34. R. Ananthakrishnan, J. Guck, F. Wottawah, S. Schinkinger, B. Lincoln, M. Romeyke and J. Käs, Curr. Sci., 2005, 88, 1434–1440.
35. M. W. Pickup, J. K. Mouw and V. M. Weaver, EMBO Rep., 2014, 15, 1243–1253.
36. E. E. Charrier, K. Pogoda, R. G. Wells and P. A. Janmey, Nat. Commun. 2018 91, 2018, 9, 1–13.
37. D. E. Discher, P. Janmey and Y.-L. Wang, Science, 2005, 310, 1139–1143.
38. P. H. Wu, D. R. Aroush, A. Asnacios, W. C. Chen, M. E. Dokukin, B. L. Doss, P. Durand-Smet, A. Ekpenyong, J. Guck, N. V. Guz, P. A. Janmey, J. S. H. Lee, N. M. Moore, A. Ott, Y. C. Poh, R. Ros, M. Sander, I. Sokolov, J. R. Staunton, N. Wang, G. Whyte and D. Wirtz, Nat. Methods, 2018, 15(7), 491–498.
39. J. Solon, I. Levental, K. Sengupta, P. C. Georges and P. A. Janmey, Biophys. J., 2007, 93, 4453–4461.
40. S. Y. Tee, J. Fu, C. S. Chen and P. A. Janmey, Biophys. J., 2011, 100, L25–L27.
41. X. Li, A. Das and D. Bi, Phys. Rev. Lett., 2019, 123, 058101.
42. H. Everwien, A. Ariza de Schellenberger, N. Haep, H. Tzschätzsch, J. Pratschke, I. M. Sauer, J. Braun, K. H. Hillebrandt and I. Sack, J. Mech. Behav. Biomed. Mater., 2020, 104, 103640.
43. H. Herthum, S. C. H. Dempsey, A. Samani, F. Schrank, M. Shahryari, C. Warmuth, H. Tzschätzsch, J. Braun and I. Sack, Acta Biomater., 2021, 121, 393–404.

---