Introduction to force transmission by nonlinear biomaterials

Xiaoming Mao

Xiaoming Mao completed her PhD at the University of Illinois at Urbana Champaign in 2008, and was a postdoctoral fellow at the University of Pennsylvania during 2008–2012. She joined the faculty of the University of Michigan in 2012. Xiaoming's research group studies a range of questions in fields ranging from soft matter to materials and biophysics, including rigidity and flow in disordered systems, topological mechanical metamaterials, self-assembly of complex and open structures at the nano and colloidal scales, and motility of cells in the extracellular matrix.

Yair Shokef

Yair Shokef completed his PhD at the Technion – Israel Institute of Technology, and was a postdoctoral fellow at the University of Pennsylvania, and subsequently at the Weizmann Institute of Science, before joining the faculty of Tel Aviv University in 2011. The research group that he leads theoretically studies statistical mechanics phenomena in soft condensed matter systems, ranging from geometric frustration in colloidal and mechanical metamaterials to irreversibility and non-reciprocity in biological as well as synthetic active matter systems.

Introduction

Biomaterials are fascinating and complex mechanical objects. They are usually comprised of disordered networks—the cytoskeleton inside the cell, the extra-cellular matrix (ECM) to which cells adhere, or confluent sheets of cells that form epithelia. Building blocks of these materials include various biopolymers and motor proteins, which taken together introduce both passive and active mechanical ingredients. Given their complex disordered structures and the active driving from biological processes, biomaterials demonstrate a number of unusual mechanical properties, from nonlinear elasticity to out-of-equilibrium fluctuations. This collection provides a timely combination of new advances in theoretical, computational and experimental studies of various mechanical phenomena in nonlinear biomaterials.

Prominent directions in current research of force transmission in biomaterials include (see Fig. 1): (i) elasticity, including heterogeneity at the microscale and nonlinearity at the macroscale, (ii) out-of-equilibrium dynamics and cell–ECM interactions, (iii) novel microscopy methods, and (iv) applications of these materials in biomedical and in engineering fields. The papers in this collection cover all these exciting directions. In this editorial, we review the state-of-the-art in each of these directions, and discuss interesting results from papers in this collection in these four directions.

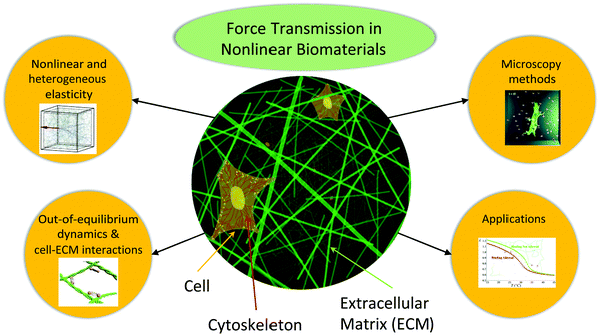Fig. 1 Schematic figure showing the fibrous nature of the intra-cellular cytoskeleton as well as that of the extra-cellular matrix. The papers in this collection address the topics related to the nonlinear mechanics of these systems, as depicted by the objects surrounding the schematic. Inset figures reproduced with permission from the Royal Society of Chemistry, DOI: 10.1039/D0SM01177K, DOI: 10.1039/D0SM01558J; DOI: 10.1039/D0SM00789G and DOI: 10.1039/D0SM00145G.

Nonlinear and heterogeneous elasticity

Most biomaterials are mechanically “under-constrained” and this leads to interesting nonlinearities and heterogeneities. To see this, let us consider some extremely simple models of biomaterials, e.g., mass- and-spring models for biopolymer networks where crosslinking points are denoted as mass points and polymer sections as springs (in the form of freely bending Mikado models or diluted lattice models^1–4) or alternatively, stress-free foam models for epithelial tissues.⁵ Following Maxwell's counting criterion for mechanical stability,⁶ these models have fewer constraints than degrees of freedom, and thus exhibit no rigidity at all in the linear regime. The counting is particularly simple for the case of fiber networks: mass-and-spring networks need mean coordination number (z) ≥ 2d (where d is the spatial dimension) to be rigid. However, for typical fiber networks, (z) < 4 – both in two and in three dimensions – since two fibers cross at each crosslink, and there could be nodes with fewer bonds at ends of fibers. Similar counting arguments have been discussed for epithelial tissues.⁷ As a result, these models are characterized by “floppy modes,” for which in the linear regime deformations cost no elastic energy.

Powerful predictions stem from this simple observation. First, in the linear regime, elastic moduli are proportional to additional weak interactions in the material, such as bending stiffness for biopolymer networks,^3,8,9 because the simple models do not exhibit elastic moduli. Second, prestress or nonlinear strain can stretch these networks into a nonlinear regime, in which the network exhibits elastic moduli even without weak interactions.^5,10–13 This phenomenon has been generally called the “bending-to-stretching” crossover in the case of fiber networks, and it has been shown that it becomes a well-defined continuous transition in the limit of no weak interactions.¹² Interesting fracturing behaviors also arise due to this nonlinearity.^14,15 Third, strong heterogeneities show up in the mechanical response of these network to local probes, such as pulling from cells in the ECM,¹⁶ and this is intimately related to the floppy modes of the network.

Papers in this collection cover a number of interesting new contributions to the general problem of nonlinear and heterogeneous elasticity of biomaterials; Baumgarten and Tighe (DOI: 10.1039/D1SM00551K) discuss how shear moduli of Mikado models are determined by low-frequency, or soft vibrational modes, revealing a new connection between modes and moduli as well as scaling exponents. Proestaki et al. (DOI: 10.1039/D1SM00312G) discuss the heterogeneity in the context of cells sensing their mechanical environment and show via experiments and simulations that a single cell cannot “feel” a rigid inclusion since fluctuations overwhelm the signal, but a group of cells can. Grill et al. (DOI: 10.1039/D0SM01177K) study the heterogeneity of force transmission in semiflexible networks. Using elegant finite-element simulations, they demonstrate an intriguing relation between heterogeneous force distributions and tensile force chains, in an analogy to force chains in granular matter.¹⁷

Negi and Picu (DOI: 10.1039/D0SM01297A) discuss the geometric notion of entanglements in athermal random networks by considering minimal loops between contacts in the network. They show how these entanglements stabilize the network and thus increase its stiffness. Biswas et al. (DOI: 10.1039/D0SM00145G) develop a computational model to design polymer gels encompassing cryptic sites in lower critical solution temperature gels that swell with a decrease in temperature. Thus, when external forces are applied, these cryptic sites are exposed, which leads to the formation of new bonds that reinforce the biomaterial.

Out-of-equilibrium dynamics and cell–ECM interactions

Activity in biomaterials generates nonlinear active stress^18,19 and gives rise to microstructure rearrangements,²⁰ which in turn lead to viscoelasticity in the form of frequency dependent response.²¹ This mechanical activity drives fiber networks away from thermodynamic equilibrium. The time asymmetry, or broken detailed balance of local dynamics has been shown to lead to non-equilibrium circulation currents in the fluctuations spectrum of such systems.^22,23 Activity in biomaterials occurs also on larger length scales, due to the contraction of entire cells that are adhered to the ECM.^24–26 The nonlinear elastic response of the ECM to such cell contraction has been described by discrete fiber network models,^11,27–30 as well as by nonlinear continuum elasticity models.^31–34 These combined efforts have shown how the nonlinear and heterogeneous nature of the ECM can strengthen matrix-mediated elastic interactions between distant cells.³⁵

This collection includes research of non-equilibrium dynamics due to binding and unbinding within biopolymer networks; Raffaelli and Ellenbroek (DOI: 10.1039/D1SM00091H) employ simulations of hydrogels with a combination of permanent and reversible bonds to show that the strength and concentration of the reversible bonds tune the stress relaxation dynamics. Slater et al. (DOI: 10.1039/D0SM01911A) quantify the spatiotemporal evolution of generation, propagation, and relaxation of stresses induced by a contracting cell in the ECM. Wei et al. (DOI: 10.1039/D0SM01558J) find that continuous breakage and rebinding of cross-linkers results in a loss modulus that reflects the fact that maximum energy dissipation is achieved when the driving frequency of the applied oscillating shear is comparable to the dissociation–association rate of the crosslinking molecules. Consequently, either strain hardening or strain softening occurs, depending on the ratio between the loading rate and the unbinding speed of cross-linkers, and mechanical memory can emerge following the application of large stress. Finally, Tah et al. (DOI: 10.1039/D0SM01575J) employ machine-learning methods to investigate rearrangement events in epithelial tissues, and extract a new “softness” parameter, which accurately predicts the temperature dependence of the relaxation time.

Microscopy methods

Most experimental studies of the mechanics of nonlinear biomaterials rely on optical microscopy. This is the case with the contributions in this collection that include experimental measurements (DOI: 10.1039/D1SM00312G, DOI: 10.1039/D0SM01911A, DOI: 10.1039/D0SM01182G and DOI: 10.1039/D0SM00753F). Many current experiments do not rely solely on bright-field two-dimensional (2D) imaging, but also use fluorescence to see fibers and other molecules, and employ confocal microscopy to image three-dimensional (3D) situations. Microscopy is also currently being used in conjunction with other methods in order to obtain a more complete picture of the biophysical processes at the cellular level. For instance, there is current interest in the effect that mechanics induced fiber alignment has on molecular transport within the cell.^36–39 Another promising direction is the combination of optical microscopy with atomic force microscopy nanoindentation to directly probe the local stiffness within cells.⁴⁰ There have been many experimental studies on the effects of nonlinear mechanics on the mechanobiology of cells,^41–44 and it would be exciting to see future experimental work that will also relate more closely to the nonlinear mechanics at more microscopic scales.

One of the main thrusts of experimental efforts in the context of mechanics in nonlinear biomaterials is obtaining forces from microscopy. Traction force microscopy was originally developed for inferring the traction forces that cells exert on a linearly elastic material in a 2D geometry, based on measurements of displacements in the medium.⁴⁵ Solving this inverse problem in nonlinear elastic media and in 3D geometries pose many challenges.^46–48 In a paper in this collection, Sanz-Herrera et al. (DOI: 10.1039/D0SM00789G) present a new inverse and physically-consistent traction force microscopy method developed and implemented in the context of 3D nonlinear elasticity, and prove its enhanced accuracy by applying it to real cases of cells cultured in a 3D hydrogel. A closely related approach has subsequently been implemented.⁴⁹

Applications

Understanding and manipulating the mechanics of biomaterials are important for many applications in various biomedical and materials engineering fields. A prominent direction of these applications in biomedical fields is “tissue engineering”, where natural and synthetic materials are used to restore, maintain, improve, or replace different types of biological tissues.⁵⁰ Among the many properties of these engineered tissues, mechanics plays a central role. For example, various materials, from carbon nanotubes to silicone and polymers, have been tested as “tissue scaffolds” to support the growth of cells in engineered tissues.⁵¹ Endowing the scaffolds with mechanical properties close to those of natural biomaterials is essential, which requires a deep understanding of the relationship between the structure and nonlinear mechanics of biomaterials. Applications of biomaterials in materials engineering has also led to many designs where the unique mechanical properties of these biomaterials are utilized for novel metamaterials with features such as nonlinearity, stimuli response, and self-healing.^52–54

A number of interesting applications of biomaterials are discussed in this collection. Aliabouzar et al. (DOI: 10.1039/D0SM00753F) study how ultrasound can be used in an on-demand, spatiotemporally controlled manner, via the mechanism of acoustic droplet vaporization, to tune the microstructures of acoustically-responsive fibrin hydrogels. The noninvasive feature of the ultrasound makes this a potential candidate for biomedical applications such as drug delivery and tissue regeneration. Papers in this collection also contribute insightful new ideas to applications of biopolymer networks as novel materials. Raffaelli and Ellenbroek (DOI: 10.1039.D1SM00091H) numerically study star polymers with a combination of covalent and reversible crosslinks. They show that the strength of the reversible bonds can tune the material from solid to fluid. Biswas et al. (DOI: 10.1039/D0SM00145G) study how “cryptic sites”, binding sites which lie hidden in folded biomolecules that are only exposed under deformation, can be used to design gels with self-stiffening behavior in response to a temperature-induced internal stress or external force. The collection also includes important studies contributing to understanding biological situations or aimed at biomedical applications; The work of Slater et al. (DOI: 10.1039/D0SM01911A) relates to wound healing. Kim et al. (DOI: 10.1039.D0SM01182G) study the response to incision by stretching a synthetic tissue, performing a cut in it, and recording the evolution with time of the edge of the synthetic tissue. Their simulation results quantitatively capture the experimentally observed complex shape changes during tissue formation and as a response to surgical disruption of tissue boundaries, allowing precise calibration of the parameters of their 3D model.

As detailed above, current research on the nonlinear mechanics of biomaterials employs multiple complementary approaches. It is important for understanding biological processes, and contributes to non-equilibrium statistical mechanics and to nonlinear mechanics and soft condensed matter physics. This basic research promotes applied research aimed at biomedical as well as materials engineering. The papers in this collection represent some of the ongoing efforts at the state-of-the-art of this exciting field.

References

1. D. Head, A. Levine and F. MacKintosh, Phys. Rev. E, 2003, 68, 061907.
2. M. Das, F. MacKintosh and A. J. Levine, Phys. Rev. Lett., 2007, 99, 038101.
3. C. P. Broedersz, X. Mao, T. C. Lubensky and F. C. MacKintosh, Nat. Phys., 2011, 7, 983–988.
4. X. Mao, Gels and Other Soft Amorphous Solids, ACS Publications, 2018, pp. 199–210.
5. D. Bi, J. Lopez, J. M. Schwarz and M. L. Manning, Nat. Phys., 2015, 11, 1074–1079.
6. J. C. Maxwell, Philos. Mag., 1864, 27, 294–299.
7. L. Yan and D. Bi, Phys. Rev. X, 2019, 9, 011029.
8. X. Mao, O. Stenull and T. C. Lubensky, Phys. Rev. E, 2013, 87, 042601.
9. X. Mao, O. Stenull and T. C. Lubensky, Phys. Rev. E, 2013, 87, 042602.
10. P. Onck, T. Koeman, T. Van Dillen and E. van der Giessen, Phys. Rev. Lett., 2005, 95, 178102.
11. J. Feng, H. Levine, X. Mao and L. M. Sander, Phys. Rev. E, 2015, 91, 042710.
12. A. Sharma, A. Licup, K. Jansen, R. Rens, M. Sheinman, G. Koenderink and F. MacKintosh, Nat. Phys., 2016, 12, 584–587.
13. J. Feng, H. Levine, X. Mao and L. M. Sander, Soft Matter, 2016, 12, 1419–1424.
14. L. Zhang, D. Z. Rocklin, L. M. Sander and X. Mao, Phys. Rev. Mater., 2017, 1, 052602.
15. S. Dussi, J. Tauber and J. Van Der Gucht, Phys. Rev. Lett., 2020, 124, 018002.
16. F. Beroz, L. M. Jawerth, S. Münster, D. A. Weitz, C. P. Broedersz and N. S. Wingreen, Nat. Commun., 2017, 8, 1–11.
17. A. Mann, R. S. Sopher, S. Goren, O. Shelah, O. Tchaicheeyan and A. Lesman, J. R. Soc., Interface, 2019, 16, 20190348.
18. P. Ronceray, C. P. Broedersz and M. Lenz, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 2827–2832.
19. P. Ronceray, C. P. Broedersz and M. Lenz, Soft Matter, 2019, 15, 331–338.
20. Y. Ideses, A. Sonn-Segev, Y. Roichman and A. Bernheim-Groswasser, Soft Matter, 2013, 9, 7127–7137.
21. M. S. e Silva, B. Stuhrmann, T. Betz and G. H. Koenderink, New J. Phys., 2014, 16, 075010.
22. J. Gladrow, N. Fakhri, F. MacKintosh, C. Schmidt and C. Broedersz, Phys. Rev. Lett., 2016, 116, 248301.
23. F. S. Gnesotto, F. Mura, J. Gladrow and C. P. Broedersz, Rep. Prog. Phys., 2018, 81, 066601.
24. U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327–1381.
25. D. Vader, A. Kabla, D. Weitz and L. Mahadevan, PLoS One, 2009, 4, e5902.
26. L. M. Sander, J. Biomech. Eng., 2013, 135, 071006.
27. J. Kim, J. Feng, C. A. R. Jones, X. Mao, L. M. Sander, H. Levine and B. Sun, Nat. Commun., 2017, 8, 842.
28. R. S. Sopher, H. Tokash, S. Natan, M. Sharabi, O. Shelah, O. Tchaicheeyan and A. Lesman, Biophys. J., 2018, 115, 1357–1370.
29. S. Goren, Y. Koren, X. Xu and A. Lesman, Biophys. J., 2020, 118, 1152–1164.
30. H. Wang, A. S. Abhilash, C. S. Chen, R. G. Wells and V. B. Shenoy, Biophys. J., 2014, 107, 2592–2603.
31. Y. Shokef and S. A. Safran, Phys. Rev. Lett., 2012, 108, 178103.
32. D. Ben-Yaakov, R. Golkov, Y. Shokef and S. A. Safran, Soft Matter, 2015, 11, 1412–1424.
33. H. Wang and X. Xu, Soft Matter, 2020, 16, 10781–10808.
34. C. Sirote and Y. Shokef, Phys. Rev. E, 2021, 104, 024411.
35. F. Alisafaei, X. Chen, T. Leahy, P. A. Janmey and V. B. Shenoy, Soft Matter, 2021, 17, 241–253.
36. D. Gomez, S. Natan, Y. Shokef and A. Lesman, Adv. Biosyst., 2019, 3, 1900192.
37. D. Gomez, E. Teomy, A. Lesman and Y. Shokef, New J. Phys., 2020, 22, 103008.
38. S. Natan, Y. Koren, O. Shelah, S. Goren and A. Lesman, Mol. Biol. Cell, 2020, 31, 1474–1485.
39. W.-H. Jung, N. Yam, C.-C. Chen, K. Elawad, B. Hu and Y. Chen, Biomaterials, 2020, 234, 119756.
40. B. L. Doss, M. Pan, M. Gupta, G. Grenci, R.-M. Mège, C. T. Lim, M. P. Sheetz, R. Voituriez and B. Ladoux, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12817–12825.
41. J. P. Winer, S. Oake and P. A. Janmey, PLoS One, 2009, 4, e6382.
42. T. Pompe, S. Glorius, T. Bischoff, I. Uhlmann, M. Kaufmann, S. Brenner and C. Werner, Biophys. J., 2009, 97, 2154–2163.
43. A. Lesman, J. Notbohm, D. A. Tirrell and G. Ravichandran, J. Cell Biol., 2014, 205, 155–162.
44. S. Abuhattum, A. Gefen and D. Weihs, Integr. Biol., 2015, 7, 1212–1217.
45. J. P. Butler, I. M. Tolić-Nørrelykke, B. Fabry and J. J. Fredberg, Am. J. Physiol.: Cell Physiol., 2002, 282, C595–C605.
46. J. Palacio, A. Jorge-Peñas, A. Muñoz-Barrutia, C. Ortiz-de Solorzano, E. de Juan-Pardo and J. M. García-Aznar, J. Biomech., 2013, 46, 50–55.
47. L. Dong and A. A. Oberai, Comput. Methods Appl. Mech. Eng., 2017, 314, 296–313.
48. C. Mark, T. J. Grundy, P. L. Strissel, D. Böhringer, N. Grummel, R. Gerum, J. Steinwachs, C. C. Hack, M. W. Beckmann, M. Eckstein, R. Strick, G. M. O’Neill and B. Fabry, eLife, 2020, 9, e51912.
49. S. Hervas-Raluy, M. J. Gomez-Benito, C. Borau-Zamora, M. Cóndor and J. M. Garcia-Aznar, PLoS One, 2021, 16, 1–19.
50. R. Lanza, R. Langer, J. P. Vacanti and A. Atala, Principles of tissue engineering, Academic Press, 2020.
51. P. F. Egan, Materials, 2019, 12, 2355.
52. J. D. Schiffman and C. L. Schauer, Polym. Rev., 2008, 48, 317–352.
53. S. S. D. Kumar, N. K. Rajendran, N. N. Houreld and H. Abrahamse, Int. J. Biol. Macromol., 2018, 115, 165–175.
54. A. Chilkoti, T. Christensen and J. A. MacKay, Curr. Opin. Chem. Biol., 2006, 10, 652–657.

---