Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Small-angle scattering to reveal the colloidal nature of halide perovskite precursor solutions†
Marion A.
Flatken
 a,
Armin
Hoell
a,
Armin
Hoell
 *a,
Robert
Wendt
*a,
Robert
Wendt
 a,
Eneli
Härk
a,
Eneli
Härk
 a,
André
Dallmann
a,
André
Dallmann
 b,
Albert
Prause
b,
Albert
Prause
 c,
Jorge
Pascual
c,
Jorge
Pascual
 a,
Eva
Unger
a,
Eva
Unger
 a and
Antonio
Abate
a and
Antonio
Abate
 *a
*a
aHelmholtz-Zentrum Berlin für Materialien und Energie GmbH, Hahn-Meitner-Platz 1, 14109 Berlin, Germany. E-mail: antonio.abate@helmholtz-berlin.de; hoell@helmholtz-berlin.de
bHumboldt Universität zu Berlin, Brook-Taylor-Str. 2, Rudower Chaussee 25, 12489 Berlin, Germany
cTechnische Universität Berlin, Straße des 17. Juni 135, 10623 Berlin, Germany
First published on 19th May 2021
Abstract
Halide perovskites are crystalline semiconductors gaining increasing attention as low-cost, high-performance materials for optoelectronics. Their processing from solution at low temperatures is compatible with rapid manufacturing of thin-film devices, including solar cells and light-emitting diodes. Therefore, understanding the coordination chemistry in metal halide perovskite precursor solutions would allow controlling the crystallization of thin films, their material properties and device performance. Here, we present a direct nanostructural technique to characterize the colloidal structure of perovskites in precursor solutions. Small-angle scattering is particularly adept for measuring nanoparticles in solution. Applying this technique to perovskite precursor solutions, we can study their colloidal properties. We show that not only do the colloids themselves matter, but also we can reveal their strong interactions in the early stages of crystallization. In particular, we focus on the prearrangement of particles into cluster-like formations. As an example, we present the concentration dependence, which is additionally supported using 207Pb NMR.
In recent years, the efficiency of perovskite solar cells (PSCs) has increased in record speed. Due to their outstanding properties, lead halide perovskites are not only considered to be the future in the photovoltaic industry, but also find application as light-emitting diodes, nanowire lasers or photo-detectors.1–3 Besides their excellent photovoltaic properties, the low temperature, solution-based perovskite fabrication procedure is another criterion for why they are particularly well suited for rapid and cost-efficient manufacturing.1,4 The absorber material, perovskite, is however not sufficiently understood to control the device efficiency systematically or to explain and selectively influence observed photovoltaic properties. One approach to gain further knowledge that has received considerable attention is to study the chemical organization in the precursor solution used to synthesize the perovskite thin film.5,6 As the crystalline thin film grows directly from solution, a detailed understanding of the crystallization mechanism is critical to enable control of perovskite formation. In this regard, the colloidal chemistry of perovskite precursor solutions contributes significantly to the crystallization process and thus to the perovskite morphology, which is known to have a direct impact on the performance of PSCs.5,7,8 In a theoretical study, Radicchi et al.9 present the iodoplumbate complexes [PbImXn]2−m that can be expected in a certain solvent, with X being solvent molecules, such as N,N-dimethylformamide (DMF) and dimethyl sulfoxide (DMSO), with lead as the central atom. The role of solvents and coordination chemistry of the central atom Pb is one of the key topics in the field of solution chemistry for perovskite precursors.6,9,10 Weakly coordinating solvents tend to favour faster crystallization, whereas stronger coordinating solvents like DMSO form an intermediate state, which leads to a slower crystallization process and thus better film morphology.11,12 However, though trends are observable and the resulting film properties are characterised in detail, the actual solution chemistry, including the specific structure of colloidal particles and a mechanism to explain the rapid, low-temperature crystallization, remains unclear.13
Methods preferably used for solution characterization, like dynamic light scattering (DLS), UV-vis spectroscopy or cryogenic transmission electron microscopy (cryo-TEM) should be used with caution, as often the nature of the regarded system slightly differs, or crucial properties are only indirectly determined.5,7,14–16 Considering the origin of biochemical solutions (e.g. micelle formation), DLS is particularly suitable to detect larger nanostructures in the range of 5 to 1000 nm. It measures fluctuations, which can be related to the Brownian diffusivity of particles and not particle size directly. Though one can then calculate the particle size, this implies making assumptions that are not suitable for every colloidal system.17 Thus, it occurs that derived particle sizes from a microscopy technique (e.g. TEM) differ from the calculated distributions derived by DLS. Kim et al. report colloidal sizes in the range of 100 nm based on DLS studies.5,18 In contrast, a study using cryo-TEM reveals first insights into the size of colloidal structures found in perovskite precursor solutions, which is in the range of 1 nm.14 Still, it remains unclear what effect cryo shock freezing has on the nature of colloid chemistry in solution.19 Unfortunately, colloidal interactions in liquid are also not considered. UV-vis spectroscopy is frequently used to identify characteristic absorption spectra, which can be used to determine possible species in solution.6,7 However, it is challenging to apply this method to solution concentrations above 1 mol L−1 typically used for thin-film deposition in solar cell fabrication.5 Considering that the majority of PSCs are fabricated by a solution-based deposition process, it is of utmost importance to characterize the solution properties and their nature close to application.
Herein, we apply small-angle scattering using synchrotron radiation (SAXS) as well as neutrons (SANS) to characterize a perovskite precursor solution on the nanostructural level. We observe well-structured colloidal nanoparticles in solution, interacting and forming a dynamic arrangement. We demonstrate that this method can be applied directly to the precursor solution used for processing PSCs without the need for further adjustments.
Earlier recorded DLS data (Fig. S6, ESI†) indicate that large higher-level structures in the micrometer range are present in perovskite precursor solutions (1 mol L−1). In addition, particles having small sizes in the order of nanometers have also been detected. By combining DLS with diffusion ordered spectroscopy (DOSY), we can prove that these can be assigned to the solute and cannot be traced back to the solvent itself (Fig. S8, ESI†). In order to better understand these sub-nanometer scale particles and simultaneously explain the occurrence of large sized particles, we decided to use SAXS and SANS for further characterization.
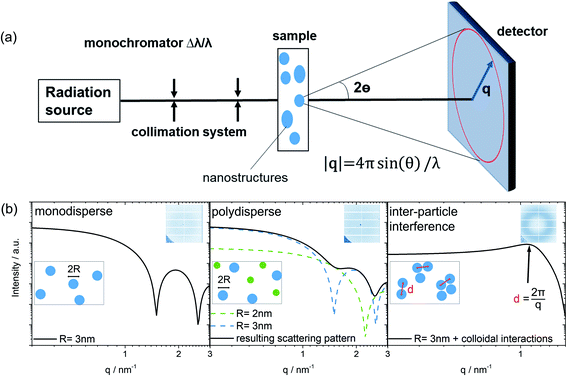
Small-angle scattering (SAS) is a characterization technique used to determine the structure of nanometer sized particles, distances, and arrangements in a material system.20–22 A scheme of the general SAS technique is provided in Fig. 1. Azimuthal integration of the 2D detector image produces the final 1D scattering pattern. The variations of the resulting scattering pattern offer the first indication about changes of size, size distributions, shape and the possible arrangement of colloidal particles observed in the sample. Simulated scattering patterns of a typical spherical-shaped form factor for a monodisperse sample as well as for a polydisperse sample are modeled in Fig. 1b. The form factor contains the primary information about the nanosized shape, whereas the structure factor describes the inter-particle interaction between the colloidal particles (for more information see the ESI†).21,23 Thus, most simply, for a monodisperse colloidal solution without any particle interaction, the experimentally derived scattering pattern can be expressed as the form factor multiplied by the number of colloids that are in the beam.
The peak maximum in a 1D scattering pattern evolves due to the interaction of particles (e.g. in solution). This leads to a dominant influence of the structure factor in the scattering pattern, which becomes evident by the formation of a broad peak. In this case, the scattering intensity of single spheres is reduced to the benefit of an arising peak at q = 2π/d as indicated by the black arrow in Fig. 1b. The mean spacing d between the mass centers of interacting colloidal particles can be calculated (Fig. 1b, on the right) using the magnitude of q at the peak maximum as discussed by Raghuwanshi et al.24
In the current case, we focus on the characterization of perovskite precursor solutions, in particular methylammonium lead iodide (MAPbI3) precursor solutions using a solvent mixture of DMF and DMSO. As it is known from the literature, the instability of perovskite devices, as well as perovskite solutions is a crucial topic in the research field and leads to suspicion of radiation damage.25,26 At Helmholtz-Zentrum Berlin für Materialien und Energie (HZB), we were able to use synchrotron radiation at BESSY II as well as neutrons at BER II to perform SAXS and SANS on perovskite precursor solutions. Using SAXS with X-ray energies of 8 keV and 10 keV (±2 eV), respectively, we cover a broad q-range from 0.05 to 8.5 nm−1 (size range: 209.4–0.74 nm) to obtain a good overview of particles and size distribution in the perovskite precursor. With SANS we cover a q-range from 0.5 to 8.5 nm−1 (size range: 12.6–0.78 nm), measured on the V4 instrument at the BER II reactor with a wavelength of 0.45 nm. Two critical advantages of uncharged neutrons is their weak interaction and high penetration depth that enable them to probe the bulk of the sample non-destructively. Without further modifying the precursor solution, SAS provides direct information about the colloidal structure.
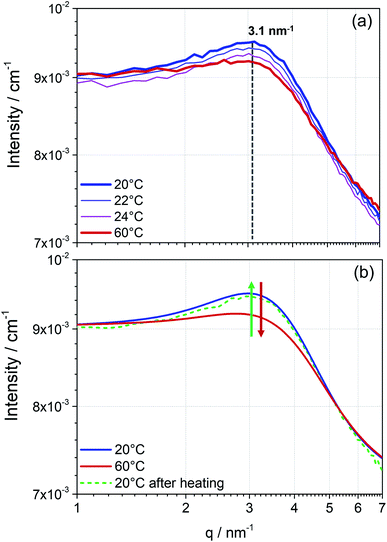
The measured scattering intensity obtained from the SANS pattern (Fig. 2) first proves the presence of particles in the perovskite solution. As already indicated by the DLS data, the curve of scattering intensity gives rise to the assumption of the existence of two phases in solution, particles and solvent. Additionally, the integrated detector signal in the 1D pattern of the perovskite precursor solution exhibits features of inter-particle interference (Fig. 1b). An arising broad peak in the SANS pattern reveals that these particles interact, which allows us to suspect that these particles form a dynamic colloidal network explaining the formation of higher-level structures observed in DLS. In the case of the 1.3 mol L−1 MAPbI3 precursor solution shown in Fig. 2, the colloidal arrangement is characterised by a mean spacing d between the mass center of individual particles of approximately 2 nm (maximum of the peak position at q = 3.1 nm−1). This inter particle short-range order might indicate the starting points for growth into long-range ordered crystals. Hence, the strong interaction seems to indicate the “quasi-crystalline” prearrangement of colloidal particles in the early stages of crystallization.27,28
To obtain further information about the colloidal network, the precursor solution was stepwise heated up to 60 °C (Fig. 2a). With increasing temperature, an apparent reduction of the maximum intensity is observed. Due to higher mobility caused by rising temperature, the observed network exhibits less inter-colloidal forces, and consequently, the peak maximum in the measured scattering pattern decreases. Accordingly, the observed effect of the structure factor in the scattering pattern significantly decreases. On cooling the solution to room temperature the peak maximum is again more pronounced and in the same position as before, concluding that the assembly process as well as breaking of the assembly due to external temperature effects is reversible (Fig. 2b).
In conclusion, SANS can provide fast and direct information about the colloidal interactions observed in perovskite precursor solutions. Furthermore, the reproducibility of each measurement run proves the non-destructive character of the neutron source. For each temperature and sample, four SANS curves were measured, which were merged to achieve better statistical results (Fig. S1, ESI†).
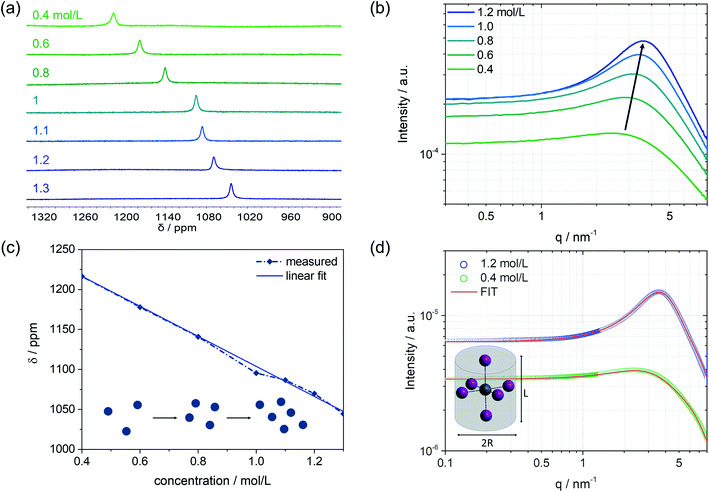
Besides the colloidal interaction in solution, further information about the nanoparticle structure itself, which represents the subunits of the colloidal network, can be obtained. In particular, a concentration series of the MAPbI3 precursor solutions is analyzed using the SAXS technique in combination with 207Pb NMR, Fig. 3. On increasing the concentration from 0.4 mol L−1 to higher concentrations, an upfield chemical shift can be seen in the 207Pb NMR spectrum (Fig. 3a). The chemical environment of the probed atom (here: Pb) can influence its electron density through the polar effect. According to Lenz's law, atoms with higher electron density have higher induced fields, and therefore the nucleus is more shielded. To exclude any electronic effects of the environment, we kept the solvent mixture unchanged (i.e. DMF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO, v/v 6
DMSO, v/v 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The electron-donating effect of iodides, as direct neighbors to Pb, can explain the increase in electron density leading to an upfield shift. We can assume that the more concentrated the precursor solution is, the more iodides will be near the central atom Pb. This can be interpreted to mean that a colloidal network of iodoplumbates becomes larger with increasing concentration, which results in higher shielding of the regarded lead core and thus causes a shift to lower ppm values (Fig. 3a). The SAXS scattering cross-sections of the precursor solutions show a substantial increase in intensity from 0.4 mol L−1 to 1.2 mol L−1 (Fig. 3b). The higher the concentration, the more colloidal particles contribute to the scattering pattern, which leads to an increase in intensity.
1). The electron-donating effect of iodides, as direct neighbors to Pb, can explain the increase in electron density leading to an upfield shift. We can assume that the more concentrated the precursor solution is, the more iodides will be near the central atom Pb. This can be interpreted to mean that a colloidal network of iodoplumbates becomes larger with increasing concentration, which results in higher shielding of the regarded lead core and thus causes a shift to lower ppm values (Fig. 3a). The SAXS scattering cross-sections of the precursor solutions show a substantial increase in intensity from 0.4 mol L−1 to 1.2 mol L−1 (Fig. 3b). The higher the concentration, the more colloidal particles contribute to the scattering pattern, which leads to an increase in intensity.
Considering the previously explained effects of form and structure factors, the precursor solution with a concentration of 0.4 mol L−1 is mainly determined by the form factor that holds information about the shape and size of the colloidal subunits (Fig. S3, ESI†). Moving towards higher concentrations, the influence of the structure factor on the scattering pattern increases, meaning that the colloidal interaction increases. The evolving broad peak maximum, which is similar to the one measured by SANS, slightly shifts with higher concentrations to higher q values and lower mean d spacing between the colloidal particles. The trend of the reduced inter-particle distance is depicted in Fig. S10.† The lower mean d spacing can be directly related to higher shielding with increasing concentration, as observed by 207Pb NMR. Fig. 3c illustrates the linear dependence of the chemical shift on solution concentration. The blue spheres represent the colloids in solution and schematically describe their increasing interaction with higher concentration, as observed in the respective SAXS pattern. With a more pronounced interaction, higher electron density at the Pb nucleus is observed (upfield shift in NMR). Simultaneously, as the interaction of the colloidal particles becomes more robust and the distance d between the particles shortens, the density of the electron-donating iodides around lead increases and becomes apparent by a lower chemical shift (Fig. 3a and c). Combining the information derived from SAXS with 207Pb NMR, that complement each other, we can postulate that the observed interacting nanoparticles are indeed subunits of coordinated lead that agglomerate to an extent that depends on the concentration of the solution.
To extract the structural information from the scattering curves, the SASfit© software was used to fit a specific form factor to the measured scattering pattern. The software SASfit©29 offers several different models of form factors describing different shapes of colloidal particles. As an example, the solution with a concentration of 0.4 mol L−1 with almost no contribution from the structure factor as well as the 1.2 mol L−1 solution with the most pronounced maximum is discussed further. Under inclusion of highly valent iodoplumbates, we hypothesize that the octahedral colloidal species present in the solution are stretched due to Jahn–Teller distortion.30–32 To describe this using a model, a cylindrical shape can be taken as an approximation. Therefore, the form factor for a long cylinder was used, including the input parameters: radius of the cylinder R and length of the cylinder L as given in Fig. 3d. The best fit, shown in red, was achieved with the form factor having input parameters of R = 2.5 Å and L = 6.5 Å for 0.4 mol L−1, and for 1.2 mol L−1, the parameters were slightly modified to R = 2.5 Å and L = 7.5 Å.
Furthermore, the structure factor in the form of a hard-sphere model was included in the fit (for further details see the ESI†). Here, a volume fraction of 0.035 was used to model the 0.4 mol L−1 solution, whereas the 1.2 mol L−1 solution shows a significantly higher volume fraction of 0.14. Thereby, the volume fraction is the measure of interacting nanoparticles in the colloidal network.23 Taking into account an average atomic distance of 3 Å between the center atom lead and iodide,33 the values given by the applied model could fit the proposed highly valent iodoplumbate formation in solution. From previous work, it is known that we can expect iodoplumbates in solution and that the number of iodides surrounding lead increases with concentration.6,33,34 So far, experiments, e.g. UV-vis, were mostly carried out for extremely diluted solutions, based on experimental limitations,6,7 and thus generally only lower valent iodoplumbates were observed. SAS is now providing new opportunities to probe even moderately and more concentrated solutions to expand the knowledge derived so far. Furthermore, including the information of the structure factor, we know of the emergence of strong interactions in the probed solution with which we can postulate the presence of large aggregates, which are formed by a fine arrangement of small subunits of iodoplumbates.
The relevance of the different characteristics of a colloidal network in solution, as discussed based on the concentration dependence, becomes apparent when considering the resulting thin-film crystallinity using different solutions with different concentrations (Fig. S9, ESI†). Further elaboration of this influence will be part of a follow-up project.
Note that this methodology can equally be applied to further compositions (and of course different solvents, e.g. for solvent engineering approaches).
Conclusions
To conclude, we demonstrated that SAS is an analytical technique that can provide direct insights into the shape and size of colloidal subunits within halide perovskite precursor solutions. SAS overcomes the limitations of more often employed traditional techniques, such as UV-vis or DLS, which are more challenging to implement at typical precursor concentrations used for halide perovskite solar cell fabrication. We are able to probe the arrangement of colloidal subunits, which is expected to have a significant impact on the early stages of the crystallization process and thus on the final absorber layer of the perovskite materials. The consistency of the SAS analysis using X-ray photons as well as neutrons on samples under different testing conditions was verified. Moreover, we supported our data interpretation with 207Pb NMR analysis. The current findings give reason to assume the existence of interacting, highly valent iodoplumbates of sub-nm size in concentrations of the precursor solution that are close to application.We proved that SAS is a non-destructive technique for studying the colloidal chemistry of the size, shape and arrangement of perovskite precursor solutions. Understanding mechanisms, for example those linked to the use of additives that are not being included in the resulting crystal structure and still show a significant influence on the device performance can be approached from an entirely new perspective.35,36 Hence, SAS is convincing as a characterization technique that can help to unravel novel crystallization mechanisms in future research.
Author contributions
M. A. Flatken: conceptualization, investigation, data curation, project administration, writing – original draft. R. Wendt and J. Pascual: data curation, writing – original draft. E. Härk and A. Dallmann: investigation. A. Prause: Investigation, Data curation. E. Unger: writing – reviewing and editing. A. Hoell: investigation, supervision, writing – reviewing and editing. A. Abate: supervision, resources, funding acquisition, writing – reviewing and editing.Conflicts of interest
There are no conflicts to declare.Notes and references
- Y. Zhou, J. Chen, O. M. Bakr and H. T. Sun, Chem. Mater., 2018, 30, 6589–6613 CrossRef CAS.
- Q. Van Le, J. B. Kim, S. Y. Kim, B. Lee and D. R. Lee, J. Phys. Chem. Lett., 2017, 8, 4140–4147 CrossRef PubMed.
- S. Zhang, C. Yi, N. Wang, Y. Sun, W. Zou, Y. Wei, Y. Cao, Y. Miao, R. Li, Y. Yin, N. Zhao, J. Wang and W. Huang, Adv. Mater., 2017, 29, 1–6 Search PubMed.
- I. Mathews, S. Sofia, E. Ma, J. Jean, H. S. Laine, S. C. Siah, T. Buonassisi and I. M. Peters, Joule, 2020, 4, 822–839 CrossRef.
- J. Kim, B. W. Park, J. Baek, J. S. Yun, H. W. Kwon, J. Seidel, H. Min, S. Coelho, S. Lim, S. Huang, K. Gaus, M. A. Green, T. J. Shin, A. W. Y. Ho-Baillie, M. G. Kim and S. Il Seok, J. Am. Chem. Soc., 2020, 142, 6251–6260 CrossRef CAS PubMed.
- O. Shargaieva, L. Kuske, J. Rappich, E. L. Unger and N. H. Nickel, Phys. Chem. Chem. Phys., 2020, 21, 1–8 CrossRef.
- G. S. Shin, S. Kim, Y. Zhang and N. Park, Small, 2019, 1–10 Search PubMed.
- N. K. Noel, M. Congiu, A. J. Ramadan, S. Fearn, D. P. McMeekin, J. B. Patel, M. B. Johnston, B. Wenger and H. J. Snaith, Joule, 2017, 1, 328–343 CrossRef CAS.
- E. Radicchi, E. Mosconi, F. Elisei, F. Nunzi and F. De Angelis, ACS Appl. Energy Mater., 2019, 2, 3400–3409 CrossRef CAS.
- K. H. Stone, A. Gold-Parker, V. L. Pool, E. L. Unger, A. R. Bowring, M. D. McGehee, M. F. Toney and C. J. Tassone, Nat. Commun., 2018, 9, 1–7 CrossRef CAS PubMed.
- L. Li, Y. Chen, Z. Liu, Q. Chen, X. Wang and H. Zhou, Adv. Mater., 2016, 28, 9862–9868 CrossRef CAS PubMed.
- C. J. Dahlman, N. R. Venkatesan, P. T. Corona, R. M. Kennard, L. Mao, N. C. Smith, J. Zhang, R. Seshadri, M. E. Helgeson and M. L. Chabinyc, ACS Nano, 2020, 14, 11294–11308 CrossRef CAS PubMed.
- B. Li, D. Binks, G. Cao and J. Tian, Small, 2019, 15, 1–24 Search PubMed.
- N. Dutta, N. Noel and C. Arnold, J. Phys. Chem. Lett., 2020, 11, 5980–5986 CrossRef CAS PubMed.
- F. Qin, Z. Wang and Z. L. Wang, ACS Nano, 2016, 10, 9787–9793 CrossRef CAS PubMed.
- P. A. Hassan, S. Rana and G. Verma, Langmuir, 2015, 31, 3–12 CrossRef CAS PubMed.
- J. Stetefeld, S. A. McKenna and T. R. Patel, Biophys. Rev., 2016, 8, 409–427 CrossRef CAS PubMed.
- B. Li, M. Li, C. Fei, G. Cao and J. Tian, J. Mater. Chem. A, 2017, 5, 24168–24177 RSC.
- I. Drulyte, R. M. Johnson, E. L. Hesketh, D. L. Hurdiss, C. A. Scarff, S. A. Porav, N. A. Ranson, S. P. Muench and R. F. Thompson, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 560–571 CrossRef CAS PubMed.
- H. Schnablegger and Y. Singh, The SAXS Guide, Anton Paar GmbH, 2013 Search PubMed.
- O. Glatter and O. Kratky, Small Angle X-Ray Scattering, Academic Press, 1982 Search PubMed.
- L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Springer, 1987, vol. 1 Search PubMed.
- R. Botet, S. Kwok and B. Cabane, J. Appl. Crystallogr., 2020, 53, 1570–1582 CrossRef CAS.
- V. S. Raghuwanshi, M. Ochmann, A. Hoell, F. Polzer and K. Rademann, Langmuir, 2014, 30, 6038 CrossRef CAS PubMed.
- B. Park and S. Il Seok, Adv. Mater., 2019, 31, 1805337 CrossRef PubMed.
- N. Klein-Kedem, D. Cahen and G. Hodes, Acc. Chem. Res., 2016, 49, 347–354 CrossRef CAS PubMed.
- X. Hao, M. Chen, L. Wang, Z. Cao, Y. Li, S. Han, M. Zhang, K. Yu and J. Zeng, Chem. Commun., 2020, 56, 2031–2034 RSC.
- J. J. De Yoreo, P. U. P. A. Gilbert, N. A. J. M. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Cölfen and P. M. Dove, Science, 2015, 349, aaa6760 CrossRef PubMed.
- I. Breßler, J. Kohlbrecher and A. F. Thünemann, J. Appl. Crystallogr., 2015, 48, 1587–1598 CrossRef PubMed.
- A. J. Neukirch, I. I. Abate, L. Zhou, W. Nie, H. Tsai, L. Pedesseau, J. Even, J. J. Crochet, A. D. Mohite, C. Katan and S. Tretiak, J. Phys. Chem. Lett., 2018, 9, 7130–7136 CrossRef CAS PubMed.
- L. Zhou, C. Katan, W. Nie, H. Tsai, L. Pedesseau, J. J. Crochet, J. Even, A. D. Mohite, S. Tretiak and A. J. Neukirch, J. Phys. Chem. Lett., 2019, 10, 3516–3524 CrossRef CAS PubMed.
- R. F. Moral, L. G. Bonato, J. C. Germino, W. X. Coelho Oliveira, R. Kamat, J. Xu, C. J. Tassone, S. D. Stranks, M. F. Toney and A. F. Nogueira, Chem. Mater., 2019, 31, 9472–9479 CrossRef CAS.
- A. Sharenko, C. Mackeen, L. Jewell, F. Bridges and M. F. Toney, Chem. Mater., 2017, 29, 1315–1320 CrossRef CAS.
- E. Radicchi, A. Kachmar, E. Mosconi, B. Bizzarri, F. Nunzi and F. De Angelis, J. Phys. Chem. Lett., 2020, 11, 6139–6145 CrossRef CAS PubMed.
- D. J. Kubicki, D. Prochowicz, A. Hofstetter, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 14173–14180 CrossRef CAS PubMed.
- M. Abdi-jalebi, Z. Andaji-garmaroudi, A. J. Pearson, G. Divitini, S. Cacovich, B. Philippe, H. Rensmo, C. Ducati, R. H. Friend and S. D. Stranks, ACS Energy Lett., 2018, 3, 2671–2678 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta01468d |
| This journal is © The Royal Society of Chemistry 2021 |