 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Anti-perovskites for solid-state batteries: recent developments, current challenges and future prospects
James A.
Dawson
 *ab,
Theodosios
Famprikis
*ab,
Theodosios
Famprikis
 c and
Karen E.
Johnston
c and
Karen E.
Johnston
 d
d
aChemistry – School of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK. E-mail: james.dawson@newcastle.ac.uk
bCentre for Energy, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK
cStorage of Electrochemical Energy, Department of Radiation Science and Technology, Delft University of Technology, Delft, The Netherlands
dDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK
First published on 6th July 2021
Abstract
Current commercial batteries cannot meet the requirements of next-generation technologies, meaning that the creation of new high-performance batteries at low cost is essential for the electrification of transport and large-scale energy storage. Solid-state batteries are being widely anticipated to lead to a step improvement in the performance and safety of batteries and their success is heavily dependent on the discovery, design and optimisation of the solid electrolytes that they are based on. In recent years, Li- and Na-rich anti-perovskite solid electrolytes have risen to become highly promising candidate materials for solid-state batteries on the basis of their high ionic conductivity, wide electrochemical window, stability, low cost and structural diversity. This perspective highlights experimental and atomistic modelling progress currently being made for Li- and Na-rich anti-perovskite solid electrolytes. We focus on several critical areas of interest in these materials, including synthesisability, structure, ion transport mechanisms, anion rotation, interfaces and their compatibility with anti-perovskite cathodes for the possible formation of anti-perovskite electrolyte- and cathode-based solid-state batteries. The opportunities and challenges for the design and utilisation of these materials in state-of-the-art solid-state batteries are also discussed. As featured throughout this perspective, the versatility, diversity and performance of anti-perovskite solid electrolytes make them one of the most important materials families currently under consideration for solid-state batteries.
1. Introduction
The pursuit of improved energy storage is currently one of the most important scientific challenges. As research priorities continue to align with global ambitions of achieving net zero emissions, it has become clear that energy storage will play a critical role in this challenge by driving both the electrification of transport and the large-scale storage of renewable energy, often from intermittent sources.1–3 Despite revolutionising the portable electronics industry, current Li-ion batteries cannot meet the requirements of next-generation technologies and incremental improvements in their performance will not be sufficient in bridging the gap between current and future energy storage demands.4–7To achieve the transformational improvements in energy and power densities, cost, safety and lifetime required for future power-hungry applications, it is necessary to look beyond traditional Li-ion battery technologies to promising alternative battery architectures with the potential for radical enhancements in performance.8–11 One such example architecture is the solid-state battery,8,12–15 which relies on solid electrolytes and the fast ion conduction they deliver. Solid-state batteries are often touted as having two main advantages over conventional Li-ion batteries. The first is the increased safety that results from separating the electrodes with the solid electrolyte to avoid Li build-up that can trigger short-circuiting.16–19 The second is the energy density gains resulting from the use of an energy dense Li-metal anode.20–23 However, these advantages have yet to be fully realised and there are many fundamental challenges to overcome, including electrochemical stability, interfacial resistance, the utilisation of a metal anode and the maintenance of physical contact between solid particles.8,24–26 Solid-state batteries have been described as the battery technology of the 2030s but the research challenge of the 2020s.27
Ionic conduction in the solid state is the key enabler of solid-state batteries and is delivered through the use of solid electrolytes that can exhibit ion conductivity at levels competitive with that of liquid electrolytes. With the development of solid-state batteries in recent years, extensive research has been undertaken to identify and design suitable solid electrolytes from a plethora of materials families with suitable conductivity, electrochemical stability and mechanical properties.8,12–14,17,28 These solid electrolytes can be inorganic, polymer based or hybrids of the two. For inorganic Li-based solid electrolytes, the most competitive materials in terms of conductivity are generally sulphides, typified by Li10GeP2S12, which offers a very high conductivity of 10−2 S cm−1 but suffers from instability when in contact with a Li metal anode.29–34 Another Li-based solid electrolyte that has seen significant recent development is the garnet-structured Li7La3Zr2O12, which presents both good conductivity (10−3 S cm−1) and stability against Li metal.34–38 Oxides (e.g., β′′-alumina and NASICONs) and sulphides (e.g., Na3PS4 and Na10SnP2S12) also dominate the most promising Na-based candidates for solid-state batteries,13,39–43 with recent compositions offering ion conductivities higher than even that of Li10GeP2S12, such as Na2.88Sb0.88W0.12S4.44
Among the wealth of solid electrolytes currently under consideration for solid-state batteries, Li- and Na-based anti-perovskites, exemplified by X3OA (X = Li or Na; A = Cl, Br, I or a mixture of halides), have received a surge in attention in the last decade.45–50 This interest has arisen from their important advantages, which include high ionic conductivity (10−3 S cm−1), a wide electrochemical stability window, soft mechanical properties and even stability against Li metal.45,51–54 In addition, benefitting from their flexible crystal structure, the performance, properties and ion transport mechanisms of anti-perovskite solid electrolytes can be uniquely tailored through, for example, chemical substitution, defect tuning and microstructural manipulation, thereby providing considerable chemical diversity.45–47,49,55–57
Nevertheless, as with all promising solid electrolyte candidates, these materials still face several critical challenges before their full utilisation can be considered, including their strong hygroscopic nature, misconceptions and confusion regarding their synthesisability and composition, stability and interfacial resistance.46,54,58–61 Despite their importance in this burgeoning field and the wealth of experimental and computational studies dedicated to their design and performance, to the best of our knowledge, anti-perovskite solid electrolytes for batteries have yet to be thoroughly reviewed in the literature.
In this perspective, we highlight the fundamental progress that has been made for anti-perovskite solid electrolytes in a number of exiting areas via the combined efforts of experimentalists and modellers. We also draw attention to potential future trends and opportunities for these versatile materials and the challenges they face for their application in solid-state batteries. The anti-perovskite structure and its compositional diversity, as well as a brief history of fast ion transport in anti-perovskites, are first presented. Synthesisability is a complex issue for anti-perovskite solid electrolytes and has resulted in significant confusion within the battery community. We assess the synthesisability of these materials with a particular focus on the fundamental differences between dry and hydrated Li- and Na-rich anti-perovskites. The structures of these hydrated materials are also heavily debated and we seek to clarify some of the misconceptions in this area. We next consider the atomic-scale mechanisms that govern ion transport in these materials and the factors that drive them. One such factor is anion rotation and its considerable influence on ion diffusion in anti-perovskites is addressed here. Finally, we review the microstructural properties of anti-perovskites and their compatibility with electrodes, including anti-perovskite cathodes for the potential design of a solid-state battery with both an anti-perovskite electrolyte and cathode.
2. Fundamentals and history of anti-perovskite solid electrolytes
Anti-perovskites (also referred to as inverse perovskites) have a rich history and have been applied in many technological applications based on their diverse and unique properties that result from their versatile and tailorable structure.62–66 In the conventional ABX3 perovskite structure, the A and B sites are occupied by cations while the X site is an anion, with the archetypal example being CaTiO3, which was first discovered in the Ural Mountains of Russia in 1839.67 In anti-perovskites, the cation and anion sublattices are inverted so that the A and B sites are now occupied by anions and the X site is a cation, as shown in Fig. 1. The B-site anion is octahedrally coordinated to six cations and the A-site anions are cuboctahedrally coordinated to 12 nearest-neighbour cations. The ideal (anti-)perovskite structure is cubic (Pm3m, no. 221) but can also readily exhibit tetragonal, orthorhombic, rhombohedral and hexagonal phases, depending on temperature, pressure and the composition of the material.68,69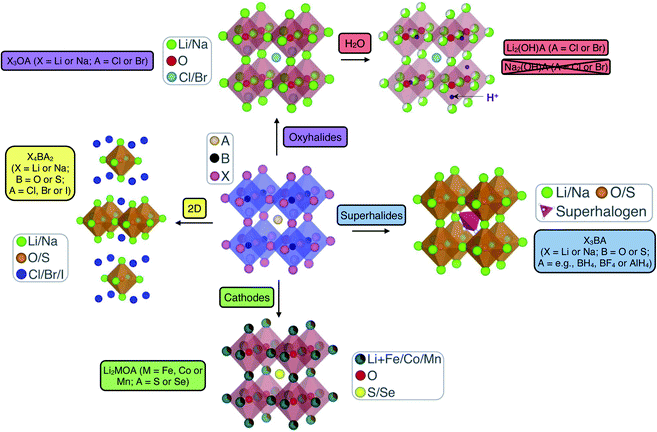 | ||
| Fig. 1 Schematic highlighting the structural and compositional versatility of anti-perovskite battery materials. | ||
Anti-perovskites can behave as metals, semiconductors, insulators and even superconductors, meaning they can exhibit a range of interesting (and sometimes unusual) physical properties, including giant magnetoresistance (e.g., Mn3GaC),70 superconductivity (e.g., Ni3MgC),65 zero thermal expansion (e.g., Mn3CuN),71 piezomagnetism (e.g., Mn3GaN)72 and electrocatalytic activity (e.g., Ni3CuN).63 Hence, they have the potential to be used in an array of applications. Whilst the research focus for anti-perovskites has mostly been on the vast array of synthesised compositions, naturally occurring variants are also common and represent important structural units in various minerals.66
In this perspective, we focus on Li- and Na-rich anti-perovskites for solid-state battery applications, which have experienced a remarkable rise in interest in recent years. Before discussing recent developments in this area, here we provide a short historical overview of their discovery and development. The first structural and conductivity analyses of Li-rich anti-perovskites (Li2(OH)Br and Li2(OH)Cl) were reported by Hartwig et al.73,74 in 1981 during their investigations of the phase equilibria of the quasi-binary systems of LiBr–LiOH and LiCl–LiOH. This work extended the much earlier phase-diagram investigations of lithium-hydroxide-lithium-halide systems.75,76 In the anti-perovskite structure of these two materials, two thirds of the X sites are occupied by Li ions while the rest are vacant. The A and B sites are fully occupied by hydroxyl and halide groups, respectively. Despite the high lithium vacancy concentration in Li2(OH)Br and Li2(OH)Cl, both materials showed unexpectedly low ionic conductivities of 5 × 10−5 and 3 × 10−5 S cm−1 at 473 K, respectively. A high activation energy of 0.97 eV was also reported for Li2(OH)Cl. In addition to this, both materials readily reacted with lithium metal.73,74
The dehydrated form of Li2(OH)Br (Li3OBr) was reportedly first prepared and characterised by Wortmann et al. in 1989.77 This material shares the same cubic structure as Li2(OH)Br but with all lithium sites now fully occupied. No information regarding its ionic conductivity was reported. A later study by Eilbracht et al.78 examined the deuterated forms of these materials, as well as the related LiBr·D2O anti-perovskite using X-ray and neutron diffraction and NMR spectroscopy. They discovered that both Li2(OD)Cl and LiBr·D2O exhibited a first-order transition from orthorhombic to cubic symmetry at 330 and 305 K, respectively. Solid-state 2H NMR spectroscopy also indicated a dynamical orientational disordering of the OD− and D2O molecules in high-temperature cubic modifications, indicative of free deuteron rotation.
Schwering et al.79 extended this work by systematically investigating the phase transitions and Li-ion conductivity of Li3−n(OHn)A (0.83 ≤ n ≤ 2; A = Cl or Br) using a range of experimental techniques. The authors confirmed the previous phase transitions observed by Eilbracht et al.78 and showed that the OH− and H2O species in the non-cubic phases are static and block lithium ions, thereby suppressing the Li-ion conductivity (<10−8 S cm−1) in these materials. In contrast, in the cubic phases, where the OH− and H2O species rotate freely, the number of accessible positions for the Li ions increases and the ionic conductivity (∼10−4 S cm−1 at 323 K for Li2(OH)Cl) is therefore enhanced. A wide range of activation energies for Li-ion conduction in the cubic materials were also reported, with values of ∼0.56–0.88 and ∼0.26–0.46 eV from impedance and 7Li NMR measurements, respectively. Generally, the Cl-based materials had the highest conductivities and lowest activation energies, while the opposite was true for Br-based systems. It is noteworthy that even a decade before the current interest in anti-perovskite solid electrolytes began, Schwering et al.79 had noted the potential of these materials as ion conductors with tuneable properties.
The first report of a Na-rich anti-perovskite was Na3NO3 by Zintl and Morawietz80 in 1938. In this material, the X sites are occupied by Na ions and the A and B sites are occupied by NO2− and oxide anions, respectively. This initial investigation of Na3NO3 was then extended by Klemenc and Gutmann81 and Jansen82 in 1950 and 1977, respectively, with the latter utilising X-ray experiments on single crystals to determine that the NO2− anion is disordered, a feature we return to below. It was not until 50 years after the discovery of Na3NO3 that the synthesis of the first alkali metal chalcogenide halides, Na3OCl and Na3OBr, was reported by Sabrowsky et al.83 This work help to lay the foundation for the current renaissance in Na-rich anti-perovskite solid electrolyte research.
The first Na-ion conductivity studies of Na3OBr and Na3NO3, as well as another anti-perovskite Na3OCN, were led by Jansen et al.84,85 in the early 1990s. The authors reported substantial increases in conductivity at specific temperatures for each of these three materials. In the case of Na3NO3 and Na3OCN,85 these increases were ascribed to either melting of the sodium sublattice or the rotational disorder of the NO2− and CN− anions at higher temperatures. The coupling between cation transport and the rotational motion of anions is known as the “paddlewheel” mechanism and is an important factor in enhancing the conductivity of many solid electrolytes,86–89 including anti-perovskites, as discussed below. For example, in the case of Na3OCN, Jansen et al.85 observed an increase in Na-ion conductivity of around three orders of magnitude from ∼10−5 S cm−1 at 480 K to ∼10−2 S cm−1 at 500 K.
Interest in anti-perovskite materials has risen dramatically recently due to the discovery of their potential as Li- and Na-based solid electrolytes for solid-state batteries. This surge in attention primarily arose from the work of Zhao and Daemen45 in 2012, who reported superionic conductivity in the Li-rich anti-perovskites Li3OCl (first reported a year before by Reckeweg et al.90), Li3OBr and Li3OCl0.5Br0.5 for the first time. The authors reported Li-ion conductivities of >10−3 S cm−1 at room temperature with low activation energies (0.2–0.3 eV), low electronic conductivity and favourable voltage and current operation windows for these materials. They also emphasised the benefits of the anti-perovskite structure in terms of structural manipulation and electronic tailoring. However, as we discuss in subsequent sections, the structural determination in these studies is limited by the fact that they only use X-ray diffraction, which is not sensitive to lighter elements, such as lithium or hydrogen content, meaning that differentiation between dry and hydrated phases (e.g., Li3OCl vs. Li2OHCl) is not possible.
This discovery has led to a wealth of studies on the ion transport, stability and interfacial properties of Li- and Na-rich anti-perovskite solid electrolytes. While the main focus on these materials has been centred on the tuning and performance of cubic Li- and Na-based oxyhalides, recent developments, as detailed below, have seen the synthesis, modelling and characterisation of more diverse and exotic compositions, including mixed-halide, superhalide and mixed-chalcogenide and double and Ruddlesden–Popper anti-perovskite structures. The application of Li-rich and Na-based Ruddlesden–Popper anti-perovskites as battery cathode materials has even been proposed in recent years, which raises the question of whether solid-state batteries with both anti-perovskite electrolytes and cathodes could be designed in the near future.
3. Synthesisability challenges for anti-perovskite solid electrolytes
A crucial first step when designing new (anti-)perovskite materials is an assessment of their stability. The stability of a given (anti-)perovskite can be estimated using the Goldschmidt tolerance factor, t,68,91 which is a dimensionless parameter calculated from the ratio of the ionic radii of the constituent ions in the material: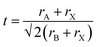 | (1) |
Fig. 2 presents a schematic summary of Li- and Na-anti-perovskite compositions that have been successfully synthesised, attempted and predicted so far (see also Table 1). This representation makes it apparent that the tolerance factor is not an adequate descriptor of stability for anti-perovskite battery materials. The most successfully synthesised compositions lie in the range 0.75 < t < 0.9 and they contain a small selection of B-site anions (O2−, OH− or H−; see diagonal ribbons in Fig. 2). Despite many predictions (see Table 1) and some attempts,93–95 no successful synthesis of Li- or Na-anti-perovskites with S2− on the B site has been reported; even when combined with a large B-site cation so that the tolerance factor falls in the above identified range, e.g., Na3SPF6. In this sense, the identity of the B-site anion is a better indicator of stability than the tolerance factor.95 Larger A-site cations and smaller B-site anions that push the tolerance factor closer to unity do not lead to synthesisable compositions, as highlighted by the examples of Na3OI and Na3FS, respectively.
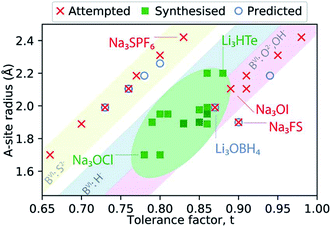 | ||
| Fig. 2 Synthesisability of anti-perovskite battery materials as a function of the A-site anion radius and the Goldschmidt tolerance factor. The thermochemical radii used for anions are taken from ref. 96 and 97 (as listed in Table 1). The radii for Li+ and Na+ are taken from ref. 98. | ||
| Anion | Shape (point group) | Shannon radiusa,98 (Å) | Thermochemical radiusb (Å)96,97 | Notable compositions |
|---|---|---|---|---|
| a For Shannon radii, the ionic radius is taken for VI coordination for the A site and XII coordination for the B site where available, otherwise the value of the closest coordination available is listed in parentheses. b For thermochemical radii, two values are listed when there are two available from the two different sources. c Distorted perovskite. | ||||
| B site (VI) | ||||
| F− | Spherical (K) | 1.33 | 1.26 | Na3FS predicted55 |
| Na3FSO4 synthesisedc,104,105 | ||||
| O2− | Spherical (K) | 1.40 | 1.41/1.49 | Li3OCl and Li3OBr reportedly synthesised45 |
| Na3OA (A = Cl, Br, I, CN, NO2 or BH4) synthesised83,94,95,106–109 | ||||
| H− | Spherical (K) | N/A | 1.48/1.73 | M3HCh (M = Li or Na; Ch = S, Se or Te) synthesised110 |
| S2− | Spherical (K) | 1.84 | 1.89/1.91 | Li3SBH4, Li3SBF4 and Na3SBCl4 predicted53,111 |
| Li6OSI2 and Na6OSI2 predicted112,113 | ||||
| Na3SI predicted55 | ||||
| OH− | Linear, dipolar (C∞v) | 1.37 | 1.33/1.52 | Li2OHCl and Li2OHBr synthesised58,78,114–118 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| A site (XII) | ||||
| Cl− | Spherical (K) | (1.81)a | 1.68/1.72 | Li3OCl reportedly synthesised45 |
| Na3OCl synthesised83,95,108,109 | ||||
| Br− | Spherical (K) | (1.96)a | 1.88/1.90 | Li3OBr reportedly synthesised45 |
| Na3OBr synthesised83,95,106–108 | ||||
| I− | Spherical (K) | (2.20)a | 2.10/2.11 | Na3OBr0.6I0.4 synthesised108 |
| S2− | Spherical (K) | (1.84)a | 1.89/1.91 | Li3HS synthesised110 |
| Li2FeOS, Li2MnOS and Li2CoOS synthesised100,119 | ||||
| Se2− | Spherical (K) | (1.98)a | 1.81/2.09 | Li3HSe and Na3HSe synthesised110 |
| Li2FeOSe, Li2MnOSe and Li2CoOSe synthesised100,119 | ||||
| Te2− | Spherical (K) | (2.21)a | 2.20 | Li3HTe and Na3HTe synthesised110 |
| Li2FeOTe synthesisedc,100 | ||||
| CN− | Linear, dipolar (C∞v) | N/A | 1.87/1.91 | Na3OCN synthesised84,86 |
| NO2− | Trigonal planar, V-shaped (C2v) | N/A | 1.87/1.92 | Na3ONO2 (Na3NO3) synthesised80–82,86,120,121 |
| BH4− | Tetrahedral (Td) | N/A | 1.93/2.05 | Na3OBH4 synthesised94,95 |
| Li3OBH4 and Li3SBH4 predicted53,122 | ||||
| BF4− | Tetrahedral (Td) | N/A | 2.05/2.32 | Li3OBF4 and Li3SBF4 predicted53 |
| Na3OBF4 predicted111 | ||||
| AlH4− | Tetrahedral (Td) | N/A | 2.26 | Li3SAlH4 predicted53 |
| Na3OAlH4 predicted111 | ||||
| BCl4− | Tetrahedral (Td) | N/A | 3.10 | Na3SBCl4 predicted111 |
| SO42− | Tetrahedral (Td) | N/A | 2.18/2.58 | Na3FSO4 synthesisedc,104,105 |
In addition to our own analysis presented above, a recent study has highlighted the limited performance of this factor in predicting the structures for regular perovskites with heavier halides, such as Cl, Br and I.99 This is clearly a severe limiting factor for anti-perovskite solid electrolytes given that they generally contain halide ions.
It is feasible that some of the limitations associated with the tolerance factor could be linked directly to the specific values of the input parameters, i.e., the Shannon radii values typically used.98 For example, in the case of halide containing anti-perovskites, the values used may not be an accurate or true representation of the cation/anion environment within the structure, e.g., the Shannon radii values reported for the halides are not representative of the 12-coordinate sites they occupy.98 Similarly, the values reported for Li and Na do not necessarily account for any mobility/motion exhibited by the ions in this specific structure, i.e., in reality, the effective radii are likely to be larger than those tabulated, in agreement with the large cation voids and thermal atomic displacements reported for anti-perovskite cathode materials.100 In addition, this issue is further exacerbated by the fact that the coordination of Li and Na is not binary but ternary (i.e., combined coordination with two anions) in these materials, leading to discrepancies in Li–O and Li-halide bonds, as discussed in Ahiavi et al.95 Hence, for anti-perovskite battery materials, it is possible that using Shannon radii values not fully representative of the environment of the ion could be contributing to the inaccuracies exhibited by the Goldschmidt tolerance factor. As such, a number of recent studies have attempted to refine the input radii for such calculations.99,101–103
Similarly, it is difficult to utilise Shannon-type radii for calculations of the Goldschmidt tolerance factor for anti-perovskites containing cluster ions (e.g., BH4−, BF4−, NO2− and so on). This is because there are no straightforward methods to approximate an equivalent spherical radius for a non-spherical molecular anion. In addition, such an equivalent spherical radius of a molecular anion would be effectively dependent on its orientation in a given structure, i.e., smaller for an ordered (immobile) instance of the polyanion and larger for a disordered (possibly mobile) instance of the same. A practical solution might be to switch to a method that can derive radii for atomic and cluster species self-consistently. One such approach is to utilise thermochemical radii, derived from thermodynamic calculations of the lattice energy of crystals.96,97 This approach is agnostic of the crystal structure, shape and orientation of cluster ions and treats all ions (atomic or molecular) as spherical, deriving an equivalent spherical radius. Table 1 shows a comparison of Shannon-type and thermochemical radii for atomic anions, as well as the thermochemical radii for common complex anions considered in anti-perovskite research.
Whilst there are challenges associated with predicting the stability of anti-perovskites, experimentally, their hygroscopic nature makes them challenging to synthesise and, as such, their preparation has been the subject of considerable debate in recent years.47,51,73,79 Numerous synthetic strategies have been attempted for some of the most commonly reported anti-perovskites, including X3OA (X = Li or Na; A = Cl or Br) and Li2OHCl, a summary of which is given in Table 2.
| Composition | Reagents and method | Remarks | Reference |
|---|---|---|---|
| a Method also used for synthesis of Li3OBr using LiBr. | |||
| Li3OCl (bulk powder) | LiCl and LiOH annealed (330–360 °C) under vacuum for several daysa | Limited/vague synthetic conditions provided, e.g., use of a ‘high vacuum pump’ and ‘long time heating under vacuum’ | Zhao and Daemen45 |
| Dehydration of Li3(OH)2Cl via high-pressure/temperature (0.64 GPa, 423 K) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of Li2O 1 molar ratio of Li2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiCl used to prepare Li3(OH)2Cl LiCl used to prepare Li3(OH)2Cl |
Zhang et al.123 | |
Li metal, LiOH and LiCl mixed in 1.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio and annealed at 600 °C for 10 h under vacuuma 1 molar ratio and annealed at 600 °C for 10 h under vacuuma |
Li metal used as a reducing agent. Additional grinding and heating steps needed to improve sample purity | Li et al.126 | |
LiH, LiOH and LiCl mixed in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio and annealed at 480 °C for 1 ha 1 molar ratio and annealed at 480 °C for 1 ha |
LiH used as a reducing agent. Additional grinding and heating steps needed to improve sample purity | Li et al.126 | |
| Li3OCl (‘glassy’) | Hydrothermal synthesis (via a Teflon reactor) using LiCl, LiOH and deionised H2O, annealed at 220–240 °C for at least 4 d | Surprising use of water during synthesis | Braga et al.48,124 |
| Hydrothermal synthesis (via a Teflon reactor) using LiCl, LiOH and deionised H2O, annealed at 493 K (220 °C) for 3 d. Sample dried in vacuum chamber at 373 K (100 °C) for 24 h | Repeat of method initially reported by Braga et al.,124 with formation of LiCl·xH2O and Li2CO3 reported on exposure to air | Hanghofer et al.116 | |
| Li3OCl (thin film) | Li3OCl target for pulsed laser deposition (PLD) prepared via annealing LiOH and LiCl under vacuum at 300 °C for 48 h | Li3OCl powders obtained described as containing ‘some hydroxyl radicals’ | Lü et al.125 |
| Li3OCl films deposited on substrate (LaAlO3, Ag or Li coated stainless steel) by PLD using KrF laser, 248 nm, 20 Hz, 4.0 J cm−2, 175 °C, 60 min under vacuum using the as-prepared Li3OCl target | Protective layer of TiO2 deposited on top of Li3OCl films deposited on LaAlO3 | Lü et al.125 | |
Composite target for PLD prepared from Li2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiCl (1 LiCl (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio), pressed into pellet (3000 psi) and annealed at 350 °C in a controlled environment for 4 h 1 molar ratio), pressed into pellet (3000 psi) and annealed at 350 °C in a controlled environment for 4 h |
Lü et al.52 | ||
| Li3OCl films deposited on Li-coated silicon and polished stainless-steel substrates by PLD using KrF laser, 248 nm, 20 Hz, 4.0 J cm−2, 175 °C, 60 min under vacuum using the as-prepared composite target | Protective layer of ZnO deposited on top of Li3OCl films | Lü et al.52 | |
| Li3OBr (bulk powder) | Direct reaction of Li2(OH)Br and Li metal | Method disputed by Friese et al.129 who claim the related Li5(OH)2Br3 phase is instead formed, which is accompanied by Li2(OH)Br, LiBr and Li2O | Wortmann et al.,77 Friese et al.129 |
| Dehydration of Li5(OH)4Br via high-pressure/temperature (423–459 K and 2.95–3.5 GPa) | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio Li2O 1 molar ratio Li2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiBr used to prepare Li5(OH)4Br LiBr used to prepare Li5(OH)4Br |
Zhang et al.123 | |
| LiOH and LiBr annealed to 400 °C over a 2 h period, held for 15 min and quenched onto copper block | Reagents initially dried under Ar atmosphere at 150 °C for 48 h | Schroeder et al.130 | |
| Li2O and LiBr mixed, annealed at 480 °C for 16 h and ball milled for 1 h. Annealing and milling cycles repeated three times to improve purity | Zhu et al.128 | ||
| Li2OHCl (bulk powder) | LiOH and LiCl (in 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.9 molar ratio) rapidly heated to 350 °C, held for 24 h then cooled to 250 °C at 2 °C h−1, held for 48 h then cooled to room temperature at 5 °C h−1 in a Ag crucible 1.9 molar ratio) rapidly heated to 350 °C, held for 24 h then cooled to 250 °C at 2 °C h−1, held for 48 h then cooled to room temperature at 5 °C h−1 in a Ag crucible |
Schwering et al.79 | |
| LiOH and LiCl annealed followed by controlled cooling of samples from 350 to 250 °C at 8 °C h−1 termed ‘slow cooled’. Rapid cooling of samples for ≥350 °C to room temperature in ∼20 min termed ‘fast cooled’ | Precise annealing temperatures and times not specified | Hood et al.51 | |
| LiCl and LiOH rapidly heated to 650 °C using an induction heater before being cooled to 450 °C, with the molten sample poured onto graphite plate | Graphite mould used to minimise the presence of impurities. Method also used for preparation of Li2+xOH1−xCl and Li2OHBr | Song et al.58 | |
| LiCl and LiOH annealed at 350 °C for 30 min inside a muffle furnace in a Ar-filled glovebox | Dawson et al.115 | ||
| LiCl and LiOH pressed into pellets and annealed at 673 K, with or without a dwelling period of 30 min, after which they were naturally cooled to room temperature | Hanghofer et al.116 | ||
LiCl and LiOH mixed in molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.05 and heated at 573 K (320 °C) for 2 h before being poured into a Teflon die and allowed to cool. Sample was then ball milled for 10 min 1.05 and heated at 573 K (320 °C) for 2 h before being poured into a Teflon die and allowed to cool. Sample was then ball milled for 10 min |
Wang et al.117 | ||
| Na3OCl (bulk powder) | Na2O and NaCl sintered in closed silver crucibles between 573 and 873 K in an Ar atmosphere (3 bar) | Hippler et al.109 | |
| Na3OCl and Na3OBr (bulk powder) | NaOH and NaCl/Br are mixed before being paved onto Na metal. The resulting mixture is placed in a capped alumina crucible, sealed in a quartz tube and heated to 150 °C (1.5 °C min−1) then 350 °C (10 °C min−1) under vacuum. After annealing for 3 h samples are cooled naturally to room temperature. To improve sample purity, grinding and heating cycles are repeated three times | Wang et al.108 | |
| Na metal, NaOH and NaCl/Br mixed and annealed at 300–400 °C. A 5–10% excess of Na metal is needed to eliminate the presence of OH− | Specific annealing temperatures and times not provided. Synthesis challenges related to the purity of commercially available Na2O. Hence, advisable to prepare Na2O ‘in house’ | Wang et al.108 | |
| Equimolar mixtures of pure Na2O and NaCl/Br mixed in an Ar-filled glovebox and loaded into ZrO2 milling jars for mechanochemical synthesis at 600 rpm for a total effective milling time of 24 h with a 5 min pause every 20 min of milling | Similar comments raised regarding purity of Na2O and again advised to prepare ‘in house’ to ensure sample purity | Ahiavi et al.95 | |
In the case of Li3OCl, conventional solid-state methods have been proposed, with the starting reagents (typically Li2O or LiOH and LiCl) mixed in specific molar ratios and annealed at various temperatures for a variety of different times. The pressing of powders into pellets, mechanochemistry (i.e., ball milling) and the effects of different cooling strategies have all been explored to determine their influence on both the structure and resulting physical properties. Similarly, hydrothermal-based methods and the preparation of thin films via pulsed laser deposition (PLD) methods have all been investigated to establish their feasibility.
The favourable hydration of Li3OCl makes it particularly difficult to prepare truly H-free samples of Li3OCl. Zhao and Daemen45 reported the apparent synthesis of Li3OCl via solid-state methods (albeit with very limited synthetic details). Since then, it has been suggested that the as-prepared samples presented were in fact the hydrated composition, Li2OHCl, owing to their propensity to take up moisture.47,115,116 A recurring issue in many studies of anti-perovskite materials, and particularly in the case of Li3OCl, is a lack of comprehensive structural characterisation and analysis. Typically, only the raw diffraction patterns are presented, with no corresponding Rietveld analysis performed, making it difficult to confirm the composition of the sample. As previously mentioned, determining whether samples are truly moisture free is challenging using solely X-ray diffraction and, as a result, it is also difficult to know whether the conductivities reported are accurate or enhanced due to the presence of protons/hydroxide anions.45
Zhang et al.123 reportedly prepared samples of Li3OCl via the dehydration of Li3(OH)2Cl using high-pressure/temperature methods, whilst Braga et al.,48,124 reported the preparation of ‘glassy’ samples of Li3OCl using hydrothermal-based methods (Table 2). One notable feature of their synthesis was their intentional addition of deionised water to the precursor powder mixture, which is somewhat surprising given the widely reported hygroscopic nature of the target composition. Hanghofer et al.116 also investigated the hydrothermal method reported by Braga and co-workers and found that samples contained Li2OHCl (not Li3OCl), in addition to Li4(OH)3Cl and LiCl. Upon exposure to air, degradation started immediately, forming Li2CO3 and glassy LiCl·xH2O. These authors also suggested that the formation of LiCl·xH2O could be responsible for the extraordinary transport properties reported by Braga et al. (∼1.2 × 10−4 S cm−1 at room temperature).
Thin films of Li3OCl were also reportedly fabricated via PLD methods using ‘Li3OCl’ targets.125 Room-temperature ionic conductivities were reported for both the film (8.9 × 10−6 S cm−1) and source material for the target (5.8 × 10−7 S cm−1). A subsequent study by the same research team explored PLD of Li3OCl films on a composite target (Li2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiCl, 1
LiCl, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio) with the use of a protective layer of ZnO on top of the Li3OCl films to prevent any exposure to air or moisture during characterisation.52 It is suggested that using a composite target, without pre-formation of the desired Li3OCl, is efficient and the prepared target has a greater stability. An ionic conductivity of 2.0 × 10−4 S cm−1 was reported at room temperature, which is higher than in their initial study.52,125 The cyclability and compatibility of the Li3OCl films prepared were also evaluated using symmetric Li/Li3OCl/Li cells. However, given the uncertainties surrounding the precise composition of the films, these findings should be treated with a degree of caution.52,125
1 molar ratio) with the use of a protective layer of ZnO on top of the Li3OCl films to prevent any exposure to air or moisture during characterisation.52 It is suggested that using a composite target, without pre-formation of the desired Li3OCl, is efficient and the prepared target has a greater stability. An ionic conductivity of 2.0 × 10−4 S cm−1 was reported at room temperature, which is higher than in their initial study.52,125 The cyclability and compatibility of the Li3OCl films prepared were also evaluated using symmetric Li/Li3OCl/Li cells. However, given the uncertainties surrounding the precise composition of the films, these findings should be treated with a degree of caution.52,125
In 2016, Li et al.126 explored alternative solid-state routes for the synthesis of proton-free samples of Li3OCl, specifically the use of Li metal and LiH as reducing reagents in the starting mixture to assist with the removal of any residual OH in the products formed. LiH was identified as an effective reducing agent, with the apparent formation of Li3OCl. However, the presence of residual starting reagents and/or the formation of hydrated phases could not be ruled out using these methods. Nevertheless, the authors showed that the presence of OH− in their samples could be tracked using FTIR when targeting a purely H-free product.
Based on our own findings, as well as those of the community, we believe that the formation of Li3OCl is experimentally challenging, if not unfeasible, and, to date, has not been achieved or sufficiently proven via experiment. As such, we strongly believe that most, if not all, of the samples presented as ‘Li3OCl’ are in fact hydrated phases, most likely Li2OHCl or a similar composition along the LiOH–LiCl pseudo-binary phase diagram. This is in line with various computational studies in which Li3OCl is predicted to have a strongly exothermic hydration enthalpy115 and a positive formation energy relative to a two-phase mixture of LiCl and Li2O.60,127 Even when using ‘dry’ reagents, it is notoriously difficult to fully remove the presence of water, likely owing to the large O–H bond enthalpy. Based on the studies and finding presented, we recommend that all studies detailing the apparent synthesis of Li3OCl be treated with a degree of caution. Hence, the pursuit of obtaining H- and moisture-free samples of Li3OCl continues.
Interestingly, the significant experimental challenges detailed above are not limited to solely Li3OCl, with reports that the synthesis of Li3OBr is equally as challenging. Again, computational studies have suggested the starting reagents, LiBr and Li2O, are more stable than the desired product.128 Numerous synthetic strategies have been utilised to try and prepare samples of Li3OBr, as summarised in Table 2. Of these, the most notable are the studies of Li et al.126 and Zhu et al.,128 where a combination of solid-state and ball milling methods was used to prepare samples of Li3OBr from Li2O and LiBr. Despite their ‘phase pure’ samples of Li3OBr containing small quantities of the starting reagents, this perhaps represents the most likely preparation of Li3OBr to date, as any potential source of water/hydroxide anions has been eliminated from the outset.
Our own studies of Li3OBr (unpublished) have suggested the presence of the related composition, Li7O2Br3, in addition to the staring reagents, again questioning the feasibility of preparing Li3OBr. Theoretical studies have suggested that both Li3OBr and Li7O2Br3 are meta-stable relative to the starting reagents Li2O and LiBr.128 Hence, additional studies are needed to determine whether these anti-perovskite phases can actually be prepared.
As detailed above, hydrated Li-rich anti-perovskites can be (albeit often inadvertently) prepared with considerable ease. In Li2OHA (A = Cl or Br), two thirds of the available Li sites per unit cell are occupied.78 It is the presence of these vacancies that is believed to result in Li-ion diffusion and enhanced conductivities. Hence, similar to their non-hydrated counterparts, there is considerable interest in them as potential solid electrolytes and ion conductors. The potential influence of the proton position and dynamics on the diffusion of the Li+ ions is discussed in the following section.
The presence of OH− and halogens makes Li2OHA reactive and, as such, considerable care needs to be taken during synthesis to avoid any uncontrollable doping from occurring via unwanted reaction with the crucibles used, e.g., aluminium, nickel and silver.45,51,79 This is particularly important, as metal dopants can significantly alter the physical properties, namely the ionic conductivity of the system. Similarly, it is vital that moisture is avoided, both during synthesis and subsequent characterisation by using a well-controlled, air-tight environment for both. Only then can it be said with both certainty and accuracy as to what the true composition of the sample is and how it relates to the physical properties observed.
In contrast to Li3OA (A = Cl or Br), where a synthetic strategy could not be agreed upon, there is general agreement that solid-state methods can be used to prepare samples of Li2OHA (A = Cl or Br). Whilst the precise method can vary, i.e., different annealing times, with or without ball milling, fast versus slow cooling and so on, the same general strategy is adopted with LiCl and LiOH as the starting reagents. To date, numerous studies of Li2OHCl have been presented by a variety of different authors, including Schwering et al.,79 Hood et al.,51 Song et al.,58 Dawson et al.,115 Hanghofer et al.116 and Wang et al.,117 as detailed in Table 2.
Hood et al.51 explored the effects of different cooling rates on Li2OHCl where it was determined that, at elevated temperatures, ‘fast cooled’ samples of Li2OHCl exhibited the highest ionic conductivity. However, it is noted that no detailed explanation is given for the enhancement in conductivity and it is merely suggested that the increase is a result of defects in the crystal lattice.
Song et al.58 recently prepared samples of Li2OHCl, Li2+xOH1−xCl and Li2OHBr via a melt-casting method using an induction heater, graphite crucible and graphite mould. It has been suggested that rapid heating via induction heaters could enable materials to be synthesised quickly and in a scalable manner. Furthermore, the use of a graphite crucible and mould is an effective way of reducing unwanted side reactions and/or impurities. The authors noted the challenges associated with accurately identifying the presence of Li2OHCl by highlighting the numerous characterisation methods used when determining the composition of the sample.
Solid-state methods can also be used to prepare Li2OHBr (using LiBr and LiOH as the starting reagents).47,58 In contrast to Li2OHCl, the room-temperature structure of Li2OHBr is reported to be cubic and remains so as a function of temperature. However, it has been noted by Song et al.58 that, as samples are heated, the irreversible formation of LiBr is observed. However, relatively speaking, Li2OHBr is a somewhat ‘easier’ system to study, both synthetically and structurally.
Numerous doping strategies have been suggested for improving the ionic conductivities of anti-perovskites, including halogen mixing (Li3OCl0.5Br0.5), cationic doping (Li3−xCax/2OCl) or a combination of the two (Li3−xCax/2OCl0.5Br0.5).45,123,124 However, to date, few have been achieved experimentally, likely owing to the synthetic challenges associated with preparing Li3OA (A = Cl or Br)-based compositions, as detailed above. Zhao and Daemen initially suggested the mixed halogen composition Li3OCl0.5Br0.5 could be a promising ion conductor after reportedly obtaining ionic conductivities of 1.94 × 10−3 and 6.05 × 10−3 S cm−1 at room temperature and 250 °C, respectively.45 However, these findings have yet to be experimentally reproduced and validated. Other doping strategies have been reported, including those by Zhang et al. (Li3−xCax/2OCl),123 Braga et al. ((Li3−2xMxOA), where M = Mg, Ca or Ba, x = 0.005 and A = Cl− or I−),124 Li et al. (Li2(OH)1−xFxCl)47 and Dawson et al. (Li3−xOHxCl (x = 0.25, 0.5 or 0.75)),115 with varying degrees of success reported for each.
Like their Li counterparts, Na-based anti-perovskites have garnered considerable interest in recent years. Reports of superb ionic conductivities at room temperature for compositions such as Na3OBH4 have added to the excitement surrounding these systems.94 Similar to Li3OA (A = Cl or Br), the synthesis of the equivalent Na-based compositions via the direct reaction from sodium hydroxide and the respective halide by melting them together and removing the redundant water has not been reported, again likely owing to the difficulty of dehydrating NaOH. However, the successful synthesis of Na3OCl has been reported via the reaction of Na2O and NaCl (Table 2).108,109 Similar to the synthesis of Li-based compositions, trace amounts of the sodium halides are often observed as impurity phases. It has been suggested that a significant challenge associated with the synthesis of all Na-based anti-perovskites is the purity of the Na2O used during synthesis, with a particular emphasis on the importance of using high purity Na2O, which is rarely available commercially. Hence, to circumvent this, it is recommended that Na2O is made ‘in house’. This presents an additional advantage when it is prepared from Na metal because Na metal is also an efficient scavenger for any residual hydroxyls in the system.108
Ahiavi et al.95 recently demonstrated the use of mechanochemical methods (ball milling) for the efficient synthesis of numerous Na-rich anti-perovskites, Na3OA (A = Cl, Br, I and/or BH4). Using solely a planetary ball mill (i.e., no annealing) they were able to produce high-purity samples. Similar mechanochemical methods have also been used by Fan and co-workers to prepare other compositions, including Na3SO4F.57 Similar to Li-based anti-perovskites, various doping strategies can be used to improve the ionic conductivities. Again, as for Li-rich anti-perovskites, divalent doping in the Na+ sites will introduce more vacancies which are essential for high ionic conductivity and, at present, there are many possible doping strategies that still need to be evaluated to determine, not only their feasibility, but also their significance and influence.
It is noteworthy that, unlike their Li equivalents, there are currently no reports of any Na2OHA (A = Cl or Br)-based compositions. As highlighted above, it is of particular note that Li3OA cannot be readily synthesised, whereas Na3OA can. Inversely, Li2OHA can be synthesised whereas Na2OHA cannot. Given that the effective radii of O2− and OH− are practically identical, and the trends are reversed between Li and Na, these observations cannot be easily explained through ionic radii arguments and there must be other, more fundamental considerations that need to be taken into account. As this continues to be a topical area of interest, with various synthetic strategies and optimisations being proposed and explored for a variety of Li- and/or Na-based compositions, it is hoped that some of the outstanding challenges can be resolved and explained, as this will undoubtedly assist in driving the area forward and developing better ion conductors.
4. Structural elucidation complexities in anti-perovskite solid electrolytes
A crucial first step in determining structure–property relationships is structural determination, i.e., the structure must be known if structure–property relationships are to be accurately identified and characterised. In the case of Li2OHCl, this is still the subject of considerable debate. It is widely accepted that Li2OHCl undergoes a phase transition to cubic symmetry (Pm3m) above ∼40 °C and it is the existence of this phase that is reported to coincide with a substantial increase in ionic conductivity.79,117 It has been suggested by both theorists and experimentalists that a complex interplay exists between Li-ion migration and rotation of the OH− anions. Howard et al.114 demonstrated that OH− bond orientations influenced the Li+ motion, whilst Song et al.58 argued that there was correlated motion between OH− and Li+. Schwering et al.79 also suggested that defect sites were formed within the structure by replacement of the Li ions with H, forming OH− or OH2 units which ‘freely’ rotate in the high-temperature cubic phase of Li2OHCl. They also suggested there was a strong correlation between Li motion and OH−/OH2 group rotation.Experimentally, the existence of a complex relationship between the OH− groups and Li ions was verified by Dawson et al.,115 using a combination of 2H magic-angle spinning (MAS) and 1H and 7Li pulsed-field gradient (PFG) NMR spectroscopy. Here, the presence of long-range Li-ion mobility and limited H mobility in the high-temperature phase of Li2OHCl was confirmed, with the H identified as pointing towards Li vacancy sites and rotating around the O atoms. The presence of localised OH− groups was also later confirmed by Wang et al.117 Using 2H MAS NMR spectroscopy, Dawson et al.115 confirmed the presence of two different OH− environments in the cubic phase of Li2OHCl, both static and locally rotating OH− groups. Early 2H NMR studies by Eilbracht et al.78 indicated dynamical orientational disordering of the hydroxide ions. Dynamic disorder of the OH− anion was also identified by Wang et al.117via maximum entropy method analysis of the neutron powder diffraction data obtained. As a result, the relative positions of the O and H could not be resolved.
In contrast, the room-temperature structure of Li2OHCl remains somewhat elusive. In recent years, numerous structures and space groups have been suggested, based on both experimental and/or computational studies, all of which are summarised in Table 3. However, to date, very few complete and accurate structural models have been presented. In addition, of those presented, none have, as yet, been reproduced or verified by the community, further highlighting the complexities associated with determining the room-temperature structure of this material. Early diffraction studies by both Barlage and Jacobs131 and Eilbracht et al.78 hinted at the significant challenges associated with determining the structure of Li2OHCl. Barlage and Jacobs131 initially suggested Li2OHCl was orthorhombic in space group Pmma. Eilbracht and co-workers78 were able to identify weak superstructure reflections and subtle orthorhombic splittings, but were unable to determine the structure, or even propose a space group from their neutron diffraction data. Since then, Schwering et al.,79 Hood et al.,51 Song et al.,58 Howard et al.,114,132 Hanghofer et al.116 and Wang et al.117 have all proposed different possible structures and/or space groups for the room-temperature phase of Li2OHCl, as summarised in Table 3. Whilst a comprehensive review of each structure/model is beyond the scope of this work, it is important to highlight the notable features of each study, as well as any discrepancies between studies, as outlined below.
| Study | Space group | Symmetry | Lattice parameters | Model available | Comments |
|---|---|---|---|---|---|
| Barlage and Jacobs131 | Pmma | Orthorhombic | a = 7.680 Å, b = 4.001 Å, c = 3.899 Å | No | X-ray diffraction study |
| Eilbracht et al.78 | — | Orthorhombic | — | No | Neutron diffraction study. Weak superstructure reflections and small orthorhombic splittings identified |
| Schwering et al.79 | Amm2 | Orthorhombic | a = 3.8220 Å, b = 7.9968 Å, c = 7.7394 Å | No | X-ray diffraction study |
| Song et al.58 | Pmmm | Orthorhombic | a = 3.8945 Å, b = 3.9937 Å, c = 7.6634 Å | No | In situ X-ray diffraction study. Structure observed at 26 °C |
| Song et al.58 | P4mm | Tetragonal | a = b = 3.9129 Å, c = 3.9188 Å | No | In situ X-ray diffraction study. Structure observed at 40 °C |
| Howard et al.114 | P4mm | Tetragonal | a = b = 3.794 Å, c = 3.578 Å | Yes | DFT predicted ground-state structure using non-standard coordinates |
| Howard et al.114 | Pmc21 | Orthorhombic | a = 3.831 Å, b = 3.617 Å, c = 7.985 Å | Yes | DFT predicted metastable structure state |
| Howard and Holzwarth132 | Cmcm | Orthorhombic | a = 7.91 Å, b = 7.74 Å, c = 7.42 Å | Yes | DFT predicted structure |
| Hanghofer et al.116 | Pban | Orthorhombic | a = 7.74574 Å, b = 7.99730 Å, c = 3.8229 Å | Yes | Neutron diffraction study. Sample not deuterated. Structure refined at both 300 and 4 K. Parameters shown for data obtained at 300 K |
| Hanghofer et al.116 | Pmmm | Orthorhombic | a = 7.74898 Å, b = 8.00215 Å, c = 3.8251 Å | Yes | Neutron diffraction study. Sample not deuterated. Structure refined at both 300 and 4 K. Parameters shown for data obtained at 300 K |
| Wang et al.117 | Pban | Orthorhombic | a = 7.7578 Å, b = 7.9963 Å, c = 3.8254 Å | No | Combined synchrotron X-ray and neutron diffraction study. Three similar orthorhombic phases needed to fit synchrotron X-ray diffraction data and only one needed to fit neutron diffraction data (parameters shown). Sample deuterated |
Schwering et al.79 suggested an orthorhombic structure, in space group Amm2. However, no corresponding structural model was presented, making it difficult for it to be evaluated. Hood et al.51 explored the effects of post synthetic cooling strategies and their influence on the phases of Li2OHCl formed. It was concluded that their ‘fast cooled’ samples exhibited a more complex crystal structure, with increased defects owing to the overcooling effect. Whilst the performance of their samples was discussed in detail, no Rietveld analysis was completed and only a comment regarding the presence of an orthorhombic phase at room temperature was made, without the suggestion of a space group.
Using a Pawley refinement, Song and co-workers58 suggested the room-temperature phase of Li2OHCl to be orthorhombic and, upon heating to 40 °C, an orthorhombic (Pmmm) to tetragonal (P4mm) phase transition was reportedly observed. They highlight this phase transition as routinely being mistakenly treated as the widely reported orthorhombic to cubic phase transition. An additional phase transition was observed at 60 °C, corresponding to the known cubic phase. Whilst schematic structural representations are given depicting the possible phase transitions, no structural models are provided.58
Combining the results of theoretical methods with experimental findings for a series of ‘slow cooled’ samples, Howard and co-workers114 proposed two potential structures of Li2OHCl: a tetragonal ground-state structure (P4mm) and a metastable state structure (Pmc21). The major difference between the two is the position of the OH− groups. In the ground-state structure, all of the OH− groups are oriented along the b axis, whereas in the metastable phase, the OH− groups are in opposite directions along the b axis. In a later study, also by Howard and Holzwarth,132 an additional ground-state structure (Cmcm) was proposed for Li2OHCl.
Using neutron diffraction, Hanghofer et al.116 explored a variety of different structural models for Li2OHCl and finally proposed an orthorhombic Pban structure. Most notably, similar to the structure proposed by Schwering et al.,79 a doubling of the unit cell was required to obtain the best fit for the experimental data. The authors comment on the similarity of their refinements using the Pban and Pmmm models. However, the Pban structure provided the best refinement for the room-temperature neutron diffraction data. Full structural models, inclusive of H positions, are provided for both the Pban and Pmmm structures. The authors also highlight the possible presence of Li disordering.116 It is noted that the authors did not deuterate their samples for analysis via neutron diffraction, which is in contrast to many other neutron diffraction studies involving proton-containing samples.117
Wang and co-workers117 also recently investigated the room-temperature structure of Li2OHCl using a combination of high-resolution X-ray and neutron diffraction, quasi-elastic neutron scattering and conductivity measurements with ab initio molecular dynamics (AIMD) simulations. Combining the high-resolution neutron diffraction data with AIMD calculations, an orthorhombic defective anti-perovskite model was identified in space group Pban, containing six separate Li positions and H-occupied sites split into four possible positions. In addition, positional disordering was identified across the O, H and Li sites, which is in contrast to the earlier work of Hanghofer et al.116 Interestingly, to accurately fit the room-temperature X-ray diffraction data obtained, three distinct, yet very similar, orthorhombic phases were needed, whereas a single phase was sufficient to fit the neutron diffraction data. Again, this highlights the challenges associated with elucidating the room-temperature phase of Li2OHCl. It has been proposed that different cooling strategies from the high-temperature cubic phase could be responsible for the structural discrepancies observed between the Hanghofer et al.116 and Wang et al.117 models.
The structural studies presented highlight the complexities associated with accurately determining the room-temperature structure of Li2OHCl, with the structure being considerably more complex than initially thought. For example, even the symmetry of the unit cell is still widely disputed, with both tetragonal and orthorhombic structures having been proposed. Several studies have also hinted at the presence of positional disordering, as well as possible microstructure effects based on sample preparation methods, all of which make structural elucidation considerably more challenging. Hence, at present, the room-temperature structure of Li2OHCl remains under investigation.
5. Li- and Na-ion transport mechanisms in anti-perovskite solid electrolytes
Given the central role ion transport plays in the performance, design and utilisation of solid electrolytes for solid-state batteries, it is not surprising that there is a vast collection of studies in the literature dedicated to increasing the ionic conductivity, lowering the activation energy and understanding the underlying mechanistic features of ion transport in fast ion conductors.8,12,13,17,28,133 The anti-perovskite family of solid electrolytes is no exception, as clearly illustrated in Table 4, which summarises the reported ionic conductivities and activation energies (both from experiment and modelling) for a vast array of anti-perovskites.| Composition | Conductivity (S cm−1) | Activation energy (eV) | Study |
|---|---|---|---|
| Li3OCl | 0.85 × 10−3 (RT) | 0.26 | Zhao and Daemen45 |
| 4.82 × 10−3 (523 K) | |||
| 0.12 × 10−3 (300 K) | — | Zhang et al.134 | |
| 4.58 × 10−2 (480 K) | |||
| Li3OCl (thin film) | 8.9 × 10−6 (RT) | — | Lü et al.125 |
| 2.0 × 10−4 (RT) | Lü et al.52 | ||
| Li3OCl (PLD target) | 5.8 × 10−7 (RT) | — | Lü et al.125 |
| Li3OCl (glassy) | 2.5 × 10−4 (RT) | — | Heenen et al.135 |
| Li3OBr | 5.36 × 10−2 (450 K) | — | Zhang et al.134 |
| Li3OA (A = Cl or Br) | ∼5 × 10−3 (500 K) | 0.27–0.31 | Dawson et al.136 |
| Li3OCl0.5Br0.5 | 1.94 × 10−3 (RT) | 0.18 | Zhao and Daemen45 |
| 6.05 × 10−3 (523 K) | |||
| 0.21 × 10−3 (300 K) | — | Zhang et al.134 | |
| 3.56 × 10−3 (500 K) | ∼0.30 | Dawson et al.136 | |
| Li3OCl1−xBrx (0 < x < 1) | 0.7–2.5 × 10−5 | 0.37–0.39 | Deng et al.56 |
| Li2OHCl | 3 × 10−5 (473 K) | 0.97 | Hartwig et al.73,74 |
| ∼10−4 (323 K) | ∼0.56–0.88 (impedance) | Schwering et al.79 | |
| ∼0.26–0.46 (7Li NMR) | |||
| ∼1.7 × 10−4 | 0.41 | Dawson et al.115 | |
| — | 0.57 (cubic) | Song et al.137 | |
| 1.80 (orthorhombic) | |||
| 0.16 × 10−3 (373 K) | 0.48 | Effat et al.61 | |
| 1.2 × 10−8 (310 K) | 0.64 | Wang et al.117 | |
| 1.4 × 10−6 (312 K) | 0.55 | ||
| Li3−xOHxCl (x = 0.2–1) | — | 0.24–0.26 | Song et al.58 |
| — | 0.30–0.42 | Dawson et al.115 | |
| Li2(OH)0.9F0.1Cl | 3.5 × 10−5 (298 K) | — | Li et al.47 |
| 1.9 × 10−3 (373 K) | |||
| 0.05 × 10−3 (298 K) | 0.40 | Effat et al.61 | |
| 0.94 × 10−3 (373 K) | |||
| Li2OHF0.1Cl0.9 | 0.38 × 10−3 (298 K) | 0.35 | Effat et al.61 |
| 4.78 × 10−3 (373 K) | |||
| Li2OHBr | 5 × 10−5 (473 K) | — | Hartwig et al.73,74 |
| Li3SI | — | 0.27 (vacancy) | Wang et al.112 |
| 0.16 (interstitial) | |||
| Li6OSI2 | 1.03 × 10−3 (300 K) | 0.26 (vacancy) | Wang et al.112 |
| 5 × 10−3 (300 K) | 0.22 (interstitial) | ||
| Li3SBF4 | 0.14 × 10−2 (RT) | 0.21 | Fang et al.53,122 |
| Li3SCl0.5(BF4)0.5 | >10−1 | ∼0.18–0.30 | Fang et al.53,122 |
| Li3OCl0.5(BH4)0.5 | ∼10−4 to 10−1 (RT) | — | Fang et al.53,122 |
| Na3OA (A = Cl or Br) | ∼2 × 10−4 (500 K) | 0.26–0.29 | Dawson et al.136 |
| Na3OCl0.5Br0.5 | — | 0.680 | Zhu et al.107 |
| Na3OCl0.5Br0.5 | 1.2 × 10−5 (RT) | 0.35 | Fang and Jena111 |
| Na3OCl0.5Br0.5 | 1.26 × 10−4 (500 K) | ∼0.2 | Dawson et al.136 |
| Na3OCN | ∼10−5 (480 K) | — | Jansen et al.84,85 |
| ∼10−2 (500 K) | |||
| Na2.875OCl | 3.92–8.19 × 10−6 | 0.42 | Wan et al.138 |
| Na2.75Ca0.125OCl | 0.53–4.41 × 10−6 | 0.47 | Wan et al.138 |
| Na4OI2 | |||
| Na4OICl | — | 0.65 | Zhu et al.107 |
| Na4OICl | 4.17 × 10−7 (223 K) | 0.37 | Yu et al.139 |
| 5.89 × 10−5 (300 K) | |||
| Na4OICl | 2.54 × 10−9 (223 K) | 0.44 | Yu et al.139 |
| 8.79 × 10−7 (300 K) | |||
| Na4S0.5O0.5I2 | 1.6 × 10−5 (223 K) | 0.23 | Yu et al.139 |
| 3.47 × 10−4 (300 K) | |||
| Na3LiS0.5O0.5I2 | 1.31 × 10−3 (223 K) | 0.12 | Yu et al.139 |
| 6.3 × 10−3 (300 K) | |||
| Na6OSI2 | ∼10−2 (RT) | ∼0.16 | Wang et al.112 |
| Na3S(BCl4) | 2.8 × 10−3 (RT) | 0.17 | Fang and Jena111 |
| Na3S(BCl4)0.5I0.5 | 3.8 × 10−3 (RT) | 0.15 | Fang and Jena111 |
| Na3OBH4 | 4.4 × 10−3 (RT) | 0.25 | Sun et al.94 |
| 1.1 × 10−2 (328 K) | |||
| ∼1 × 10−7 (373 K) | 0.81 | Ahiavi et al.95 | |
| M3HCh (M = Li or Na; Ch = S, Se or Te) | — | 0.44–0.53 | Gao et al.49 |
| Na3HS (ortho) | — | 0.30 | Gao et al.49 |
| Na2.9H(Se0.9I0.1) | 1 × 10−4 (373 K) | 0.18 | Gao et al.49 |
With regards to modelling, significant efforts have been committed to comprehending the atomistic features that control the motion of Li and Na ions in these materials. The first computational study to investigate the ion transport mechanisms in Li3OCl, Li3OBr and Li3OCl0.5Br0.5 was by Zhang et al.134 in 2013. Using density functional theory (DFT) and AIMD simulations, the authors reported that Li vacancies and structural disorder are key to reducing the enthalpy barriers for Li-ion transport. The calculated Li-ion conductivities and activation energies from AIMD were in good agreement with the experimental work of Zhao and Daemen for Li3OCl and Li3OBr,45 but the authors could not reproduce the enhanced Li-ion conductivity in the mixed Li3OCl0.5Br0.5 phase. Alternatively, Emly et al.60 carried out DFT calculations on the same materials and found a very low Li-ion migration barrier of ∼0.17 eV for all three systems via a three-ion hop mechanism involving Li interstitial dumbbells, as illustrated in Fig. 3(a). This mechanism is indicative of concerted Li-ion motion, a widely-reported phenomenon in a variety of solid electrolytes.88,140–142 Nevertheless, despite this low energy pathway, the formation energies of Li interstitials in these materials were found to be high, meaning that it is unlikely that this is the mechanism responsible for the observed high conductivity.
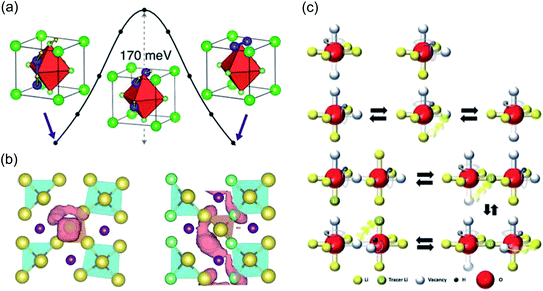 | ||
| Fig. 3 Ion transport mechanisms determined from DFT. (a) Low energy migration pathway for a Li interstitial dumbbell in Li3OCl. Reproduced with permission from ref. 60 Copyright (2013) American Chemical Society. (b) Projections of Na-ion diffusion trajectories for Na4S0.5O0.5I2 (left) and Na3LiS0.5O0.5I2 (right) over a AIMD simulation time of 90 ps at 800 K. Reproduced with permission from ref. 139 Copyright (2019) Royal Society of Chemistry. (c) Mechanisms of and correlations between Li and H dynamics in Li2OHCl. Reproduced with permission from ref. 137 Copyright (2020) Wiley. | ||
Through the use of classical atomistic simulations, Mouta et al.143 also investigated defect formation and Li-ion migration in Li3OCl. In agreement with earlier computational works, they reported low Li vacancy and high Li interstitial formation energies, with LiCl Schottky defects dominating the defect chemistry. Similar to Emly et al.,60 the authors found a larger vacancy migration enthalpy of 0.30 eV compared to a value of 0.13 eV for interstitial migration. However, given the predicted six orders of magnitude greater concentration of Li vacancies compared to Li interstitials, Li vacancies were deemed to be the major charge carriers and therefore vacancy migration the dominant transport mechanism. The same conclusion was also reached from combined DFT and larger scale classical molecular dynamics simulations of Li3OCl.144 In contrast, in a later study, Mouta et al.145 reported that Li interstitials can become the dominant charge carriers in Li-rich anti-perovskites when they are sufficiently Li–halide deficient with oxide ions occupying the vacant chloride sites. The conflicting results from early theoretical studies have undoubtedly contributed to the confusion regarding the defect chemistry of these complicated materials.
Deng et al.56 utilised DFT, AIMD and nudged elastic band (NEB) calculations in combination with a bond percolation model to optimise the conductivity in the Li3OCl1−xBrx series. They predicted that Li3OCl0.75Br0.25 has a higher Li-ion conductivity than even Li3OCl0.5Br0.5 based on low migration barriers for Li-rich channels with Br-rich end points. We also investigated both Li- and Na-based mixed halide anti-perovskites (Li3−xNaxOCl1−yBry) using large-scale molecular dynamics.136 Our calculations revealed low formation energies for alkali-halide Schottky defects and that the Li-ion conductivity was significantly higher than the Na-ion conductivity in these materials. In contrast to some earlier studies, our simulations suggested that the effect of Cl/Br mixing on ionic conductivity was small. We also considered ion transport in theoretical Li/Na mixed materials, e.g., Li2NaOCl and LiNa2OCl, but found their conductivities to be low and their activation energies high compared to Li3OCl and Na3OCl. Li- and Na-ion transport was shown to be proportional to the Li and Na vacancy concentration, respectively, while their activation energies were relatively insensitive to the vacancy concentration. These results were also found in a subsequent study that utilised deep potential molecular dynamics.146
As with other solid electrolytes, doping is critical to realising the full potential of anti-perovskite solid electrolytes and particularly for enhancing ion conduction. On this basis, we recently carried out defect and MD simulations to investigate the influence of divalent cations (Mg2+, Ca2+, Sr2+ and Ba2+) and F− doping on ion conduction in Li3OCl.147 Whilst F-doped Li3OCl was revealed to be a poor conductor due to the high binding energies between dopant-Li vacancy pairs, Mg-doped Li3OCl was predicted to have high Li-ion conductivity and low migration barriers based on weaker dopant-vacancy binding energies. Our work therefore presented a viable doping strategy to improve the electrochemical performance of Li3OCl and potentially other anti-perovskites.
Kim and Siegel55 systematically studied a series of 24 model Li- and Na-based anti-perovskite ion conductors using DFT calculations. By controlling the lattice distortion based on the Goldschmidt tolerance factor using isovalent composition variation of anti-perovskites, the authors were able to elucidate the relationships between the distortion and ion mobility and thermodynamic stability. They reported that highly distorted anti-perovskites tend to exhibit the lowest ion migration barriers through the widening of migration channels and the destabilisation of equilibrium configurations. Given that larger distortions inevitably correlate with reduced stability, a delicate balance must be struck between mobility and stability in these materials to realise their optimum performance. Na3SI was identified as an anti-perovskite that can potentially achieve such a balance. Although not considered explicitly, Wang et al.148 hypothesised that the bcc packing of anions in the anti-perovskite structure will be particularly favourable for ion conduction based on design principles for solid-state Li superionic conductors.
Zhu et al.107 carried out the first combined experimental-computational study of Na3OBr and the modified layered anti-perovskite Na4OI2 (first reported by Sabrowsky et al.83 in 1989). The authors reported a low Na migration energy of 0.34 eV for an occupied Na site to a neighbouring vacant site in Na3OBr based on DFT calculations. Three Na migration energies of 0.30, 0.45 and 1.10 eV were obtained for the anti-Ruddlesden–Popper phase Na4OI2 based on the different Na sites present in the material. A DFT investigation by Yu et al.139 extended this work to consider a series of stable anti-Ruddlesden–Popper phases with the general formula Na4−xLixBA4 (B = O and/or S; A = I and/or Cl). These materials were proposed to be excellent solid electrolytes for Na-based solid-state batteries. In particular, Na3LiS0.5O0.5I2 was reported to have an extremely low activation energy for Na-ion transport (0.12 eV) and a high conductivity of 6.3 × 10−3 S cm−1 at room temperature. The Na-ion diffusion profiles of Na4S0.5O0.5I2 and Na3LiS0.5O0.5I2 from this study are presented in Fig. 3(b).
Wan et al.138 focused on Na3OCl and its alkaline earth doping using a combination of NEB and AIMD simulations. In analogy with Li3OCl, it was found that NaCl Schottky pairs are the dominant defects in Na3OCl and this results in Na-ion transport occurring through a vacancy hopping mechanism. Ca was identified as a promising dopant for this material on the basis that its incorporation results in charge compensating Na vacancies and because it exhibits the lowest binding energy with Na vacancies of the dopants (Mg, Ca, Sr and Ba) tested.
In addition to the substitution of halide ions, researchers have also considered the role of superhalogens/cluster ions in improving the performance of anti-perovskite solid electrolytes. Modelling work in this area has been particularly driven by Fang and Jena, who have proposed and predicted the performance of numerous anti-perovskite superionic conductors based on superhalogens.53,111,122 Fang et al.53,122 used DFT and AIMD calculations to probe the stability, defects and migration barriers in Li3OBH4 and Li3SBF4, as well as mixed phases of Li3OCl0.5(BH4)0.5 and Li3SCl0.5(BF4)0.5. They found that these materials exhibit high Li-ion conductivities of between 10−4 and 10−1 S cm−1 at room temperature, resulting from Li vacancy migration, with activation energies of ∼0.18–0.30 eV. The influence of the superhalogens was also investigated and it was revealed that their translation and rotation are critical in enhancing the Li-ion migration in these systems (via a ‘paddlewheel’ effect). This behaviour is fundamental to ion conduction in many anti-perovskites and indeed other solid electrolytes and is discussed in more detail in the next section.
The same authors also extended their analysis in this area by providing guidelines for the rational design of Na-rich anti-perovskite superionic conductors, again based on the use of superhalogens.111 Based on their guidelines, they proposed Na3S(BCl4) and Na3S(BCl4)0.5I0.5, which possessed Na-ion conductivities of >10−3 S cm−1 with remarkably low activation energies of <0.20 eV. Na ion motion was found to be highly correlated in these materials and once again, the motion of the cluster ions was key to lowering the migration barriers, as hypothesised decades earlier by Jansen et al.85 for Na3NO3 (and also recently confirmed using DFT121) and Na3OCN.
Inspired by these studies, the first synthesis of Na3OBH4 was reported in 2019 by Sun et al.94 In addition to their experimental characterisation, the authors performed NEB and AIMD simulations to clarify the mechanism responsible for the excellent Na-ion transport in this material. They found that the Na migration barrier is 0.1 eV lower in Na3OBH4 than Na3OBr and confirmed that the nearly free rotation of the BH4 molecules is central to this reduction. However, in our own recent experimental-computational study of Na3OA (A = Cl, Br, I and/or BH4),95 we could not reproduce the high Na-ion conductivity reported by Sun et al.94 despite also observing the same anion rotation.
As a result of its strongly hygroscopic nature,115 there has been significant confusion over the synthesis and characterisation of Li3OCl, with suggestions that previous as-prepared samples of Li3OCl were actually hydrated.47,58,115 Numerous studies have attempted to clarify some of the misconceptions regarding the synthesis of these materials and understand the influence of protons on their overall ionic conductivity. The first major study of this kind was conducted by Song et al.,58 who used a large combination of materials characterisation techniques and AIMD simulations to carefully identify the compositions of Li2+x(OH1−x)Cl (0 ≤ x < 0.7) and Li2(OH)Br and revealed an interesting Li-ion transport mechanism involving the creation of Li Frenkel defects resulting from OH− group rotation. This mechanism resulted in a significant enhancement in the Li-ion conductivity of Li2(OH)Cl. In an integrated AIMD and 1H, 2H and 7Li solid-state NMR study,115 we also investigated the Li3−x(OHx)Cl system and discovered a strong relationship between Li-ion and proton dynamics based on Li-ion hopping and OH− rotation (see Fig. 4). We also ruled out the possibility of long-range proton transport in these materials based on the large separation between oxide ions of ∼4 Å. Similar conclusions were also found by Song et al.137 (see Fig. 3(c)) and Effat et al.61 in later studies.
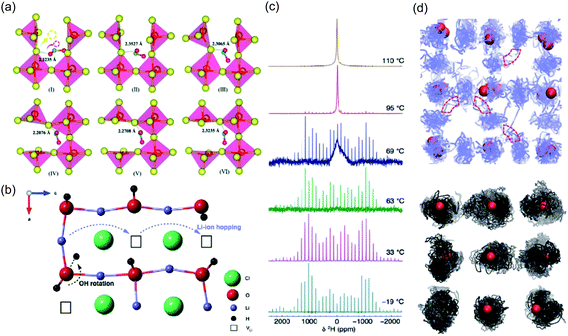 | ||
| Fig. 4 Influence of cluster ion rotation on ion transport. (a) Na-ion conduction mechanism in Na3NO3 demonstrated through successive frames of an atomic simulation at 485 K. The yellow and red arrows in the first frame indicate the correlated motion of the migrating Na+ cation and rotation of the terminal oxygen anion of the NO2− group, respectively. Reproduced with permission from ref. 121 Copyright (2020) Royal Society of Chemistry. (b) Li-ion migration mechanism in Li2OHCl. (c) Variable-temperature 2H MAS NMR spectra acquired for Li2ODCl at 19, 33, 63, 69, 95 and 110 °C. (d) Density plots of trajectories for Li and H in blue and black respectively, from AIMD of Li2OHCl at 800 K. Oxygen atoms are shown in red and chlorine atoms omitted for clarity. Reproduced with permission from ref. 115 Copyright (2018) Royal Society of Chemistry. | ||
Howard et al.114 used DFT to complete an in-depth study of the structural and ion transport properties of the different phases of Li2(OH)Cl. In addition to the known ordered orthorhombic and disordered cubic phases, the authors also considered a tetragonal ground state that is not observed experimentally. A large Haven ratio for the highly Li-ion conducting cubic phase was found, suggesting the existence of highly correlated Li-ion transport in this phase, in contrast to the low-temperature orthorhombic and tetragonal phases. The OH− groups were again found to strongly affect the Li-ion motion. Despite the many studies on the relationship between Li-ion and proton dynamics in anti-perovskites, interest in this area continues, with a recent experimental-computational study from Wang et al.117 reaffirming earlier results regarding the increased OH− rotation in the cubic phase of Li2(OH)Cl and its enhancement of the Li-ion conductivity (paddlewheel effect).
As well as the intense research into Li- and Na-ion transport in anti-perovskites, there is also debate over the nature of oxide- and halide-ion diffusion in the materials, particularly Li3OCl. The possibility of O and Cl diffusion in crystalline Li3OCl, Li3OBr and Li3OCl0.5Br0.5 was actually considered by Zhang et al.134 in the first computational study of Li-ion transport in this material, but it was not observed with AIMD, even at 2000 K. Furthermore, they reported that the exchange of a Cl ion and an O ion was thermodynamically unfeasible and even when such an exchange was forced, the ions showed no tendency to return to their starting positions. However, when glassy Li3OCl was considered using classical molecular dynamics by Heenen et al.,135 significant Cl-ion conductivity was observed, even at room temperature (2.5 × 10−4 S cm−1). Oxide ions were found to still be immobile in this glass material. In a very recent study, Serejo et al.54 also predicted the existence of Cl and even O diffusion in Li3OCl using classical molecular dynamics simulations, albeit “sluggish” compared to Li-ion diffusion.
Using a materials genome approach based on DFT, Wang et al.112 reported two new potential Li-ion conducting anti-perovskites with compositions of Li3SI and Li6OSI2 (a double anti-perovskite), as well as determining the stability and ion transport characteristics of a variety of other Li-based anti-perovskites. The Li6OSI2 double perovskite exhibited both energetic and dynamic stability, with a lower activation energy for Li interstitial transport (0.18 eV) compared to Li vacancy transport (0.26 eV). The same authors then extended their work to consider the Na analogue of this new material, i.e., Na6OSI2. Using AIMD simulations, they showed that moderate off-stoichiometry in the material resulted in a low activation barrier for Na-ion transport of ∼0.16 eV and a very high conductivity of ∼10−2 S cm−1 at room temperature.
In addition to the earlier work on the anti-Ruddlesden–Popper Na4OI2 material,107 recent computational studies have also considered fast Li-ion conduction and its mechanisms in low-dimensional (2D, 1D and 0D) Li-based anti-perovskites. Based on the archetypal Li3OCl, Lu et al.149 used DFT and AIMD simulations to illustrate the potential for Li-ion conductivity of >10−2 S cm−1 in 2D Li4OCl2 (anti-Ruddlesden–Popper), 1D Li5OCl3 and 0D Li6OCl4. The authors reported increased conductivity with decreasing dimensionality as a result of decreased Li-ion migration bottlenecks and the softening of rotation modes of the octahedra in the structures. They also proposed that lowering the dimensionality of the primitive structural units in superionic conductors could be a new design principle for solid electrolytes. In a similar study, the migration mechanisms of alkali ions in Ruddlesden–Popper anti-perovskites with the general formula X4OA2 (X = Li or Na; A = Cl, Br or I) were investigated.150 Both vacancy and interstitial migration were simulated, with interstitials predicted to have lower migration barriers than vacancies and therefore play a significant role in the ionic conduction of these materials.
The design of new ion conducting anti-perovskites has recently even led to the synthesis, characterisation and modelling of hydride-based systems with soft anionic sublattices. Gao et al.49 successfully synthesised M3HCh (M = Li or Na; Ch = S, Se or Te) anti-perovskites and despite the large variation in the ionic radii of these ions, all the materials were found to exhibit the ideal cubic structure, with the exception of Na3HS, which was orthorhombic. NEB calculations were used to estimate the cation migration barriers for vacancy and interstitial dumbbell hopping in these materials. As noted previously for Li3OCl and related anti-perovskites, the dumbbell migration mechanism was shown to be particularly favourable with low values of 0.05–0.14 eV (compared to 0.15–0.32 eV for vacancy migration). These low migration barriers and the high ionic conductivity observed experimentally were proposed to be the result of a soft phonon mode associated with the rotational motion of HM6 octahedra.
One of the greatest challenges in materials science is the ability to accurately determine the relationship between structure and dynamic properties. It is now widely accepted that, in order to gain a comprehensive structural understanding of a system, including the identification and characterisation of complex structure–property relationships, a combined experimental and computational approach is required. This is particularly true for anti-perovskites, where structural and/or compositional subtleties can lead to enhancements in both the functionality and performance. As detailed above, numerous computational studies currently exist for anti-perovskite solid electrolytes. In contrast, there are relatively few experimentally verified studies in which ion transport mechanisms have been identified and/or confirmed. This is not unique to anti-perovskites, or indeed battery-related materials, this is a significant challenge faced by all classes of functional materials, i.e., verifying the means by which a material is classed as ‘functional’. There are many reasons why probing conduction mechanisms via experimental methods is challenging. Ideally, to verify how an ion moves within a particular system, real time measurements are needed in which the movement of the mobile species is monitored in situ. At present, many of the characterisation methods typically used are limited in their ability to perform such in situ measurements, owing to factors such as hardware limitations or an inability to host systems requiring specialist environments, e.g., air sensitive systems. For example, in NMR spectroscopy it is possible to probe ion mobility; however, the temperature range over which this can be done is severely limited using conventional hardware. Furthermore, to carry out in situ experiments specialist, non-standard experimental setups and hardware are required that are often costly. Experimental time can be applied for at national facilities, for example, using techniques such as muon spin relaxation spectroscopy to probe ion mobility. However, as time at such facilities becomes increasingly competitive, it can be difficult to secure experimental time. It is for these types of reasons that relatively few experimental studies currently exist for anti-perovskites in which the ion mobility mechanisms and conduction pathways have been experimentally verified.
Instead, various combined experimental and computational studies exist where, using experimental findings, conduction pathways and mechanisms are proposed or hypothesised using theory. Ionic conductivities are routinely reported. However, often these values are simply stated and not fully evidenced, i.e., the conduction pathway leading to such ionic conductivities is not detailed. Granted, this can be very challenging to do, particularly in the case of anti-perovskites given their hygroscopic nature. However, without an appreciation or understanding of how or why that conductivity is generated, it is difficult for it to be optimised further. Experimentally, techniques including impedance spectroscopy and variable-temperature solid-state NMR spectroscopy have been used to try and probe ion dynamics within anti-perovskites, alongside methods such as powder diffraction and microscopy. Typically, experimental data is collected for an array of samples and, from each dataset, an activation energy and conductivity are obtained. The challenge is then deciphering how and why there are variations across the datasets, and then being able to determine the correlation (if any) between each dataset. These are just some of the complexities and challenges associated with characterising functional materials and, in particular, ion conductors.
The Li- and Na-ion conduction mechanisms in anti-perovskites remain a particularly topical area of interest. As established above, many conflicting ideas have been proposed in recent years regarding the precise conduction pathways and mechanisms, the majority of which have been made via theoretical methods. Experimentally, pathways and mechanisms are often merely inferred from the impedance data obtained, alongside a consideration of the crystal structure. Whilst the inferred mechanisms may be correct, it is important that they are experimentally verified. At present, the work of Dawson et al.115 stands out as one of the very few experimental studies in which Li-ion diffusion and OH− rotation was confirmed via PFG NMR experiments and variable 2H MAS NMR for the cubic phase of Li2OHCl (Fig. 4(c)). As previously discussed, determining whether alkali vacancies or interstitials are the dominant charge carriers has been the subject of much debate in recent years, with arguments for both being presented for a variety of different compositions. Experimentally, there are many factors that can influence the ion conduction capabilities of a system, including composition, (dis)ordering, the thermal/physical/electrochemical history of the sample, pressure, pellet texture and so on. These can all play a significant role and, unfortunately, such factors are often ignored during characterisation. This further highlights the complexities associated with experimentally validating the conduction pathways and ion transport mechanisms within a system.
6. Role of cluster ion rotation in anti-perovskite solid electrolytes
The components of the archetypical oxyhalide composition (e.g., Li3OCl) can be replaced with atomic clusters (i.e., polyanions) with similar chemical function. The majority of such substitutions target the halide site (i.e., the larger anion site) in anti-perovskites. Polyanions with a net charge of −1, such as CN−, NO3− and BH4−, which can be referred to as superhalogens, have already been successfully substituted at the halide site of sodium anti-perovskites.The effects that the inclusion of such cluster ions can have on solid electrolytes are multifold. For example, they can lead to an overall expansion of the lattice and, as such, an enlargement of the conduction bottlenecks, with positive effects on ionic conductivity. Although the largest usable halide is iodine, one can envisage using superhalogens larger than iodine to create anti-perovskites with even larger lattice volumes. They can also affect the electrochemical stability of anti-perovskites, in particular oxidative stability, i.e., high-voltage stability in electrochemical applications, including batteries. The oxidative stability, to a first approximation depends on the propensity of the anions (and particularly the halide in anti-perovskites) to release electrons. Certain cluster ions could actually have higher electron affinities than the atomic anions they replace and therefore be harder to oxidise, opening up routes to the design of solid electrolytes with greater stability at high voltages. Furthermore, as a result of covalent, intramolecular bonding, the electronic density of polyanions will be anisotropic, compared to an atomic anion, thereby effectively altering the potential energy landscape for mobile cations, such as Li+ and Na+. This can have distinct implications on ion transport, especially considering that the inclusion of cluster ions can also result in unique coupling between anion and cation dynamics. Such effects have been considered for decades in the solid electrolyte literature86 and such discussions have been reignited recently, in large part in connection to anti-perovskite ion conductors, as elaborated below.
Fang and Jena extended the concept of superhalogens to “superalkalis” in anti-perovskite solid electrolyte research,53,111,122i.e., cluster cations that behave chemically as alkali metal ions, such as Li3O+/Li3S+. Anti-perovskite compositions can then be thought of as equimolar pseudo-binary “supersalt” mixtures of superalkalis and superhalides, e.g., Na3O+ and BH4− (in direct comparison with an equimolar mixture of alkali and halide, e.g., rocksalt NaCl). The smaller ionisation potentials of superalkalis compared to alkali metals in principle make them more mobile in the anti-perovskite structure.
Na3O(NO2) (or Na3NO3) is likely the first sodium anti-perovskite discovered as early as 1938.80,81 Its Na-ion conduction characteristics were first investigated by Jansen and co-workers82,84,86,110 and they reported a link between the NO2− rotational disorder and ion conductivity. The room-temperature structure is already characterised by rotational disorder of the V-shaped NO2− exhibiting six different orientations.82,120,121 A clear transition is observed in the conductivity behaviour at ∼200 °C without any clear structural implications (i.e., a change in symmetry), with the ionic conductivity increased by approximately two orders of magnitude and the activation energy approximately halved from 0.8 to 0.4 eV.
This material has recently been reinvestigated by Zou and Zhao,121 who showed that the transition corresponds to the activation of dynamic disorder (i.e., continuous reorientational motions) of the V-shaped NO2− anion that facilitates ion transport. In particular, they propose that the terminal oxygen anions of the nitrite ion interact with the Na+ and effectively shuttle them between the available lattice sites. This mechanism is visualised in the consecutive simulation frames of Fig. 4(a). One of the terminal oxygen anions of the NO2− always points towards the migrating Na+. The correlated Na-ion hop/NO2− is initiated by the NO2− rotating so that the terminal O previously coordinating the mobile Na+ shifts in a way that prepares it to coordinate the Na+ in the initially vacant position. This rotation creates space, causing a momentary local expansion allowing for the Na+ hop. In essence, the process can be conceptualised as the NO2− rotation “dragging” the Na+ to its new position in the lattice. It is telling that when the authors of the study attempted the same model simulation but artificially restraining the NO2− rotation, the result was an impressive suppression of Na+ mobility. An analogous description might hold for Na3OCN featuring a linear CN− dipole and a similar thermally activated stepwise increase in ionic conductivity.84,86
A similar structure has been elucidated by X-ray94,95 and neutron diffraction94 for the recently discovered Na3OBH4, namely, featuring rotationally disordered BH4− tetrahedral anions in a cubic average structure. Although AIMD simulations demonstrate the dynamic nature of the BH4− rotation at high temperatures, the exact mechanistic influence of said rotations on Na+ diffusion remains to be investigated, although it is conceivable that a similar mechanism to Na3NO3 takes place, where the terminal hydrogen anions of the rotating BH4− cluster “drag” sodium ions to vacant sites.
We conclude the discussion of cluster anions in anti-perovskite ion conductors with the best-studied case of Li2OHCl, featuring a linear OH− dipole,58,78,114–118 this time on the B site in contrast to the previous examples. As discussed above, substitutions of molecular anions in the anti-perovskite structure can also be aliovalent with the protonation of Li3OCl to Li2OHCl, being a typical example. Protonation is concomitant with the removal of Li, i.e., the introduction of Li vacancies, since the added proton is much smaller than Li+ and is covalently bonded to oxygen instead of occupying Li+ sites. As such, hydration/protonation can be also considered as a strategy to increase ionic conductivity by generation of mobile defects.
Li2OHCl features a phase transition from an orthorhombic to a cubic phase close to room temperature (∼35 °C),58,78,79,115,117 widely associated with the onset of rotational mobility of the OH− dipole, as discussed in detail above. We highlight that this feature of a crystallographic phase transition is unique in Li2OHCl, in contrast to the other cluster-based anti-perovskites described in this section which remain in cubic average symmetry below the temperatures associated with the onset of mobility of their cluster anions (e.g., Na3NO3 and Na3OCN).
2H MAS NMR and 1H and 7Li PFG experiments and AIMD simulations converge to the combination of rotationally mobile (translationally fixed) OH− dipoles and increased Li+ mobility in the cubic phase,115 which is further confirmed by impedance spectroscopy experiments.79,116,117 As noted above, the substitution of O2− by OH− introduces vacant Li sites in Li2OHCl, as compared to the archetypal Li3OCl. It was shown through AIMD that the barycentre of the oxygen anion of OH− remains in the A site while the hydrogen cation (i.e., the positive end of the OH− dipole) is relatively mobile at a fixed radius around the central oxygen; again in contrast to NO2− or CN− that rotate as a whole about the A site, as seen by the molecular simulation of Fig. 4(d). Locally, the hydrogen cation (i.e., the positive end of the OH− dipole) is always pointing to the vacant Li sites contributing to the electrostatic stabilisation of the structure, as shown in Fig. 4(b). Li migration to vacant sites is accompanied with rotation of the OH− group about the central oxygen so that the hydrogen cation points to the newly vacant site, as confirmed by both 2H MAS NMR spectroscopy and 1H and 7Li PFG experiments and AIMD simulations.115
Finally, we also mention the recent report of hydride-based M3HCh (M = Li or Na; Ch = S, Se or Te) anti-perovskites.49 These do not formally contain covalently-bonded cluster polyanions and are “inverted” in the sense that the smaller B-site is occupied by the halogen-like hydride (H−, sp2), while the larger A-site is occupied by large chalcogenides (e.g., S2− or Se2−). Nevertheless, the authors propose the rotational motion of HM6 tetrahedra as a key mechanistic peculiarity in these materials, which might bear some relation to the discussions of concerted migration touched on above.
7. Interfacial stability and resistance of anti-perovskite solid electrolyte
Combined experimental and computational efforts have led to an unprecedented understanding of solid electrolytes at the bulk scale. However, the performance of a solid-state battery is not simply a combination of the properties of the individual materials that it consists of and is instead heavily dependent on the interfaces that they form. These interfaces can be heterogeneous (e.g., electrode–electrolyte) or microstructural (e.g., grain boundaries), with both types having the potential to act as bottlenecks in the performance of solid-state batteries.8,13 As famously stated by Prof. Herbert Kroemer during his lecture for receiving the Nobel Prize in Physics 2000, “the interface is the device”; however, despite this statement being particularly relevant to solid-state batteries, the current understanding of the interfaces in solid electrolytes is still in its infancy compared to the bulk materials.Nevertheless, there are a number of studies for anti-perovskite solid electrolytes focused on the interfacial stability and microstructural characteristics of Li3OCl and its hydrated form. We begin by considering electrode–electrolyte interfaces. One prominent example is the work of Hood et al.,51 where the interface between Li2OHCl and Li metal was explicitly investigated. Through the use of a fast-cooling process, the authors found that Li2OHCl could form an extremely stable interface with the metallic Li anode. Li/Li2OHCl/Li cells cycled at high temperatures (∼200 °C) still showed stability between the solid electrolyte and molten Li anode upon solid electrolyte interphase (SEI) formation (see Fig. 5(a)), with minimal interfacial resistance. The SEI was found to have a high concentration of oxygen, supporting the formation of a lithium oxide layer that stabilises the interface without significantly compromising the ionic conductivity. However, it should be noted that formation of such a lithium oxide layer implies the reduction of the hydroxide proton and the evolution of hydrogen gas, which might prove problematic in a practical setting.
 | ||
| Fig. 5 Experimental and computational studies of electrode-anti-perovskite solid electrolyte interfaces. (a) SEM image of Li/Li2OHCl/Li symmetric cell after 160 charge/discharge cycles showing the cross section of the SEI. Reproduced with permission from ref. 51 Copyright (2016) American Chemical Society. (b) EDS mapping of melt-infiltrated NCM (top left), graphite (top right) and Li4Ti5O12 electrodes (bottom left) and the cross-section of the all-solid-state battery cell, where purple represents combined Ni/Co/Mn, black represents C (graphite), red represents combined Ti/O (Li4Ti5O12) and the green colour represents Cl from Li1.9OHCl0.9 (SSE). Reproduced with permission from ref. 50 Copyright (2021) Springer Nature. (c) Relaxed structure of Cl- and O-terminated interfaces consisting of seven layers of Li3OCl (100) and bcc Li (100) planes. Reproduced with permission from ref. 154 Copyright (2019) American Chemical Society. | ||
Similar interfacial stability has also been proposed for Li3OCl on the basis of in-depth electrochemical testing and a variety of cell architectures.52,125,151 Beyond these more traditional approaches, significant interest has arisen in recent years from the use of cation-doped Li3OCl and Na3OCl glass solid electrolytes in “glass” batteries,48,152 as also discussed above. It was proposed that the anti-perovskite electrolytes in these glass batteries are not only wetted by the metallic anode but also have dielectric constants capable of creating large electric-double-layer capacitance at the electrode/electrolyte interfaces. While the ability to reversibly plate/strip an alkali-metal anode from a solid electrolyte clearly has transformative potential for solid-state batteries and energy storage, these results have been met with considerable scepticism and have so far not been reproduced.13,153
Most recently, Xiao et al.50 proposed a novel solid electrolyte melt infiltration technique based on Li1.9OHCl0.9 as a potential route to the scalable manufacturing of solid-state batteries. Benefitting from its low melting point of ∼300 °C, the solid electrolyte was infiltrated into dense and thermally stable electrodes (LiNi0.33Mn0.33Co0.33O2 as a cathode and Li4Ti5O12 and graphite as anodes) as a liquid that then solidifies during cooling. High-resolution SEM micrographs and EDS maps demonstrated a perfect wetting with sharp interfaces between the active materials and solid electrolyte, as illustrated in Fig. 5(b). This resulted in minimal interfacial resistance at the electrode–electrolyte interfaces, as confirmed by charge/discharge tests.
Regarding Na-based anti-perovskites, Fan et al.57 designed a solid-state battery based on a doped monoclinic Na3SO4F (Na2.98Mg0.01SO4F0.95Cl0.05) anti-perovskite solid electrolyte, Prussian blue as a cathode and a Na metal anode. The first discharge capacity for this solid-state cell was 83.3 mA h g−1; however, after only ten cycles, the capacity was attenuated to 34.5 mA h g−1 because of the poor interfacial stability or wettability of the Na metal used. As a result, a Na–Sn alloy was used to replace the Na anode and this enabled a higher discharge capacity of 91.0 mA h g−1 for the first cycle that was reasonably well maintained at 77.0 mA h g−1 after 20 cycles with a coulombic efficiency of close to 100%. A decomposition voltage of 4.75 V was obtained from linear scan voltammetry, suggesting a wide electrochemical window for Na2.98Mg0.01SO4F0.95Cl0.05.
Given the challenges of explicitly modelling electrode–electrolyte interfaces, computational studies of electrode-anti-perovskite electrolyte interfaces are also scarce. Nevertheless, Kim and Siegel154 were able to probe the Li3OCl–Li metal anode interface at the atomic scale using DFT (see Fig. 5(c)). The authors calculated a variety of properties, including the interfacial energy, work of adhesion, wettability, band edge shifts and electrochemical window, and found that the oxygen-terminated interface is the most thermodynamically stable, with the potential for low interfacial resistance. However, this strong interfacial interaction significantly reduced the electrochemical window of Li3OCl, implying a trade-off between strong interfacial bonding/wettability and electrochemical stability. Stegmaier et al.155 also used DFT to model Li3OCl surfaces, but in this case, in contact with a nearly ideal metallic intercalation cathode model using a polarisable continuum model with a large dielectric constant. They predicted that very large Li vacancy concentrations will build up in a single layer of Li3OCl at the cathode interface to form a compact double layer. They also calculated a potential drop across the interface of ∼3 V for a nearly full concentration of vacancies at the surface, suggesting that nearly all the cathode potential drop in Li3OCl occurs at the Helmholtz plane rather than in a diffuse space-charge region.
The interfacial stability of Li3OCl, Na3OBr and Na4OI2 has also been considered implicitly using a combination of DFT and thermodynamic calculations. In one of the earliest computational studies of Li3OCl, Emly et al.60 predicted the onset of oxidation of this material at 2.55 V (relative to metallic Li) with the formation of Li2O2 and LiCl. Furthermore, Li3OCl was also considered in the seminal work of Richards et al.,156 where the interfacial stability and anodic and cathodic reactions of a wide variety of solid electrolytes were considered. In this study, oxidation was predicted to occur from 3.00 V (relative to metallic Li), with LiCl, LiClO3 and ClO3 as the products. Given that these decomposition products are electronic insulators, a passivated interphase can be expected to form at high voltages, which may prevent further oxidation of Li3OCl.157
The same methodology was also used to study Na-based solid electrolytes.158 The authors predicted an oxidation limit of 1.79 V (relative to metallic Na) for Na3OBr, with anodic reaction products of Na2O2 and NaBr, similar to the Li and Cl equivalents suggested for Li3OCl by Emly et al.60 A similar value of 1.66 V (relative to metallic Na) was obtained for Na4OI2 and again with the formation of the corresponding metal halide (NaI) and metal halate (NaIO3). The oxidation limits of these two Na-based anti-perovskites were found to be close to that of Na2O (1.67 V, relative to metallic Na), consistent with the presence of fully reduced anions in all of these structures.
We now turn our attention to the internal interfaces that exist within polycrystalline anti-perovskite solid electrolytes. The compositional or structural inhomogeneities present at nanometre to micrometre scales often dominate the overall ionic conductivity of a material, either beneficially159,160 or detrimentally.46,161,162 Of these microstructural features, grain boundaries, which are surfaces of contact between crystallites of different orientation that often differ extensively from the bulk crystal in terms of structure and composition, are the prime example.
It is often challenging to separate the bulk and grain boundary contributions within an electrochemical impedance spectrum of a polycrystalline material. This is also the case for anti-perovskites, as typified by Schwering et al.,79 who attempted such a deconvolution for mixed-halide Li2OHA (A = Cl and/or Br) compositions and was able to obtain estimated activation energies of ∼0.62–0.73 and ∼0.31–0.38 eV for the grain boundary and bulk conductivities, respectively. This significant difference in activation energies suggests the presence of large grain boundary resistance in these materials, which is a typical feature for oxide-based solid electrolytes.46,163 In a later study, Lü et al.52,125 synthesised Li3OCl thin films with an activation energy of 0.35 eV, considerably lower than the value of 0.59 eV for the bulk material. This difference was explained by the larger grain size of the films compared to the bulk material and, as a result, the reduced grain boundary resistance. Furthermore, impedance measurements have also confirmed large grain boundary resistances and lower conductivities for Li3OBr.126,128 More recently, the conductivity hysteresis in Li2OHCl has also been attributed to grain boundary resistance.117 It is noteworthy that the cation-doped Li3OCl and Na3OCl glass (and therefore free of grain boundaries) solid electrolytes developed by Braga et al.48,152 were reported to have remarkably high conductivities of >10−2 S cm−1 at room temperature.
Despite the fundamental impact of grain boundaries in solid electrolytes, they are far from being fully understood and grain boundary resistance is rarely quantified or characterised in detail, especially on the atomic scale. In light of this, we used Li3OCl as a model polycrystalline electrolyte and applied large-scale molecular dynamics simulations to analyse ionic transport at the grain boundaries of this anti-perovskite.46 We predicted high concentrations of grain boundaries and showed that Li-ion conductivity is severely hindered through them, thereby confirming the high grain boundary resistance in this material. Based on our results, we also proposed a polycrystalline model to quantify the impact of grain boundaries on conductivity as a function of grain size. Furthermore, the findings from this study clearly illustrate the importance in directly considering grain boundary contributions to conductivity in solid electrolytes. This is particularly important in modelling, as the majority of first-principles and classical simulations on anti-perovskite solid electrolytes significantly underestimate the activation energy for ion conduction, since they only consider the bulk material.46 This study has led to similar works that also focus on characterising grain boundaries in Li3OCl.59,164
8. Anti-perovskite cathodes and their potential application in solid-state batteries
Benefitting from its ionic conduction properties, as well as a myriad of other functionalities,62 the anti-perovskite structure has also recently been demonstrated as being able to support reversible redox reactions with lithium (de-)insertion.100 This is achieved through partial substitution of transition metals M (e.g., Fe) on the lithium site, resulting in disordering of Li and M on the same crystallographic site, similar to disordered rocksalt cathodes,165 which are currently experiencing a surge in interest. In order to accommodate the increased formal charge on the cation site, large chalcogenides (e.g., S or Se) take the typical place of halides on the A site, resulting in bichalcogenide compositions, such as Li2FeOS.100Li2FeOS has been shown to accommodate reversible extraction and reinsertion of more than one Li ion per formula unit, corresponding to reversible Fe2+–Fe3+ redox, as well as anionic redox of the sulphur anion for increased capacity (see Fig. 6),166 similar to the so-called Li-rich compositions of layered cathodes.167,168 The lightweight framework of this material affords theoretical capacities directly competing with those of commercial LiCoO2 and NMC layered cathodes (∼280 mA h g−1 for 1.25 Li per formula unit for Li2FeSO). Most interestingly, high capacities have been demonstrated to be accessible at rather high rates, leading to very competitive power capability (e.g., >200 mA h g−1 at 1C for Li2FeSO, see Fig. 6(b)). The power capability is likely linked to the facile and isotropic Li-ion migration in the cubic anti-perovskite structure, as presented above, characterised by a low migration barrier of <0.35 eV.169 This combination of energy density, power capability and inexpensive reagents (e.g., Li2CO3, Fe and S in the case of Li2FeOS) could make such anti-perovskite cathodes very serious contenders in the various battery application markets that are currently in flux.
 | ||
| Fig. 6 Anti-perovskite cathode materials. (a) Schematic representation of a graphite|Li2FeSO battery cell. Reproduced with permission from ref. 100 Copyright (2017) American Chemical Society. (b) Specific capacity, coulombic efficiency and inset voltage profiles of a Li2FeSO|Li cell cycled at a 1C rate. Reproduced with permission from ref. 171 Copyright (2021) Frontiers. | ||
Beyond the preliminary studies of Li2FeSO, anti-perovskite cathodes would be expected to benefit from the chemical flexibility of the structure to tune their properties via substitutions.119,169–171 Any transition metal with an accessible M2+–M3+ redox pair is in principle usable, with Li2MnOS and Li2CoOS having already been synthesised119 and the properties of the Cr, Cu, Mo, Ni and V analogues having been probed through DFT calculations.169 Careful optimisation of the composition is expected to allow for the tailoring of properties, including the average operating voltage, electronic conductivity and phase stability,169 in close analogy with commercial NMC electrodes. For example, small amounts of Co incorporation were shown to dramatically increase the accessible capacity to >250 mA h g−1.171 No reports of sodium equivalent versions (e.g., Na2FeOS) currently exist yet, with the exception of the recently discovered anti-Ruddlesden–Popper phase Na2Fe2OS2.172
Moreover, anti-perovskite cathode materials possess certain intrinsic advantages with respect to their application in solid-state batteries. Firstly, similarities between the crystal structure and chemistry between electrode and electrolyte materials can be expected to lead to a compatible and unstrained interface. For example, the cubic lattice parameters of Li2FeSO and Li2OHCl are approximately equal (∼3.91 Å). Furthermore, anti-perovskite cathodes have shown minimal and isotropic electrochemical expansion upon cycling; as lithium is reversibly (de)inserted, the cubic lattice parameter varies by less than 1%.100,166,171 This is especially relevant for solid-state batteries where mechanical degradation mechanisms (e.g., interface delamination, loss of contact and cracking) are exacerbated and directly linked to localised stresses generated by the large electrochemical expansion of the layered cathode materials typically used. Finally, although the utilisation of M2+–M3+ redox pairs and the inclusion of sulphur tend to limit the operating voltage to ∼2.5 V vs. Li+/Li0, this can enable the use of solid electrolytes with limited electrochemical stability in oxidation.
9. Summary, remaining challenges and future directions
In this perspective, we have described and discussed the significant progress made and the challenges faced in the synthesis, design, development and understanding of anti-perovskite materials for solid-state batteries. In particular, we have highlighted how and why the Goldschmidt tolerance factor fails to accurately predict the synthesisability of anti-perovskites, the challenges facing the synthesis of H-free samples, the issues of structural determination associated with hydrated phases, the underlying atomic-scale mechanisms that make anti-perovskites excellent ion conductors, the role of cluster ion rotation, the microstructural properties of anti-perovskites and the interfaces they form with electrodes, and the recent development of anti-perovskite cathodes and their potential application in solid-state batteries. Despite recent progress and the fact that these materials have considerable potential as both battery materials and model systems for the understanding of solid electrolytes in general, a variety of challenges remain that continue to hinder their development. In this final section, we highlight some of these challenges, as well as their relationship to general challenges currently facing battery materials development. We then also explore the exciting potential opportunities for the application of solid electrolyte battery materials and the future directions their development may take.The Goldschmidt tolerance factor is an important tool for the design of perovskite materials, but in the case of Li- and Na-rich anti-perovskites, its predicative performance is severely limited. We have suggested a number of reasons for this, primarily based on the reliability of the input parameters (Shannon radii) used for anti-perovskites. Nevertheless, a number of new tolerance factors have been developed in recent years based on a variety of methods, including data-driven approaches,99 kernel support vector machines,173 gradient boosted decision trees174 and a random forest of decision trees.175 These new descriptors are generally far more accurate than the Goldschmidt tolerance factor in predicting the stability of perovskites; however, they have yet to be fully assessed specifically for Li- and Na-rich anti-perovskites.
The current literature for anti-perovskite solid electrolytes is dominated by Li3OA (A = Cl or Br); however, it remains unclear whether these H-free materials can even be synthesised. Given the dramatic impact that protons have in these systems with regards to conductivity and structure, it is essential that great care is taken in both the synthesis and characterisation of these anti-perovskites to avoid further confusion and scepticism within the battery community. In addition, in the case of Li2OHCl, even when the hydrated material is correctly determined, confusion remains over its room-temperature structure, with several different space groups having been proposed. These challenges clearly illustrate the need for state-of-the-art characterisation techniques when assessing the surprisingly complicated structures and properties of anti-perovskite solid electrolytes. Neutron-based techniques and NMR spectroscopy, uniquely sensitive to Li and H will be indispensable to gaining insight into the structural and dynamic subtleties of these materials. Another unexplained feature of these materials is the difference in the synthesisability of the Li- and Na-based compositions. For example, Li3OA cannot be readily synthesised, whereas Na3OA can. Inversely, Li2OHA can be synthesised whereas Na2OHA cannot. The underlying reasons for this discrepancy are not currently known and it is somewhat surprising that no computational study exists that assesses the hydration of Na3OA and the energetics of formation for Na2OHA.
This perspective has illustrated the power of computational modelling in regard to identifying the atomistic features and mechanisms that govern ion transport in solid electrolytes. However, the direct observation of such mechanisms with experiment remains highly challenging and this is certainly not only the case for anti-perovskites. Furthermore, another critical issue affecting the development of solid-state batteries in general is that our current understanding of interfaces in energy materials is far weaker than for the bulk materials, with anti-perovskites being no exception. This is true for both experimental and modelling studies of interfaces, with each facing their own unique obstacles. In order to address the grand challenge of net-zero emissions by 2050, it is vital that new techniques are developed for the characterisation and explicit modelling of realistic interfaces in energy materials. The complementarity of experiment and modelling is essential to revolutionise the fundamental understanding of ion transport and interfaces in energy materials over different length scales and has been regularly highlighted throughout this Perspective.
Since the study of Zhao and Daemen45 into superionic anti-perovskites almost a decade ago, there has been a surge in interest in these materials for battery applications. While the majority of the studies in this area have centred on the application of Li- and Na-rich solid electrolytes in solid-state batteries, other diverse uses of these versatile materials have begun to emerge in recent years. For example, the electrolyte melt infiltration reported by Xiao et al.50 based on Li1.9OHCl0.9 holds potential for the low-cost and scalable manufacturing of inorganic solid-state batteries with high volumetric energy density. Fine-tuning of the ionic conductivity of the anti-perovskite electrolyte (or indeed other electrolytes with low melting points) and its interfaces with the active materials will help to drive this new technology closer to large scales and improved cell performance. Guo et al.176 proposed another alternative application for Li2OHCl, namely, as a lithium reservoir for the prelithiation of anodes in high energy density batteries on the basis of its large lithium storage capacity.
Li3OCl has also been considered as a “quasi-solid-state electrolyte” to potentially overcome both the safety problems associated with liquid electrolytes and the high interfacial resistance typically associated with solid electrolytes.177 A 500 nm-thick Li3OCl layer was used to protect a Li anode and resulted in a remarkable drop in its polarisation, as well as inhibiting the decomposition of the routine solvents typically found in liquid electrolytes at <4.5 V. Li2OHCl has also been recently proposed as a coating material for other solid electrolytes. Lai et al.178 reported a simple aqueous method to prepare in situ Li2OHCl-coated garnet solid electrolytes and their method was shown to successfully reduce the sintering temperature of the garnet from 1200 to 350 °C, as well as enhancing its ability to suppress lithium dendrite growth.
The recent use of high-pressure synthesis to stabilise M3HCh (M = Li or Na; Ch = S, Se or Te)49 illustrates the potential of non-conventional syntheses in expanding the available phase space of anti-perovskite battery materials. Finally, in another recent study, Kim and Siegel179 moved beyond Li- and Na-based anti-perovskites to multivalent metal-ion-based anti-perovskites (Mg3NA, Ca3NA (where A = P, As, Sb or Bi), Ca3PSb and Ca3AsSb). Despite DFT calculations revealing their large formation energies for vacancies and interstitials, these materials do show some promise based on their predicted stability against Mg or Ca anodes and barriers for vacancy and interstitial migration of less than ∼500 and ∼200 meV, respectively. This is yet another illustration of the vast potential and versatility of these materials and a strong indication that research into anti-perovskite battery materials is only likely to increase in forthcoming years.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. A. D. gratefully acknowledges the EPSRC (EP/V013130/1) and Newcastle University (Newcastle Academic Track (NUAcT) Fellowship) for funding.References
- G. Crabtree, Science, 2019, 366, 422–424 CrossRef PubMed.
- M. Arbabzadeh, R. Sioshansi, J. X. Johnson and G. A. Keoleian, Nat. Commun., 2019, 10, 3413 CrossRef PubMed.
- L. Trahey, et al. , Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12550–12557 CrossRef CAS.
- E. C. Evarts, Nature, 2015, 526, S93–S95 CrossRef CAS PubMed.
- K. Turcheniuk, D. Bondarev, V. Singhal and G. Yushin, Nature, 2018, 559, 467–470 CrossRef CAS.
- A. Masias, J. Marcicki and W. A. Paxton, ACS Energy Lett., 2021, 6, 621–630 CrossRef CAS.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264 CrossRef.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291 CrossRef PubMed.
- Y. Liang, H. Dong, D. Aurbach and Y. Yao, Nat. Energy, 2020, 5, 646–656 CrossRef.
- W.-J. Kwak, et al. , Chem. Rev., 2020, 120, 6626–6683 CrossRef PubMed.
- C. P. Grey and D. S. Hall, Nat. Commun., 2020, 11, 6279 CrossRef.
- J. C. Bachman, et al. , Chem. Rev., 2016, 116, 140–162 CrossRef PubMed.
- Z. Zhang, et al. , Energy Environ. Sci., 2018, 11, 1945–1976 RSC.
- M. Pasta, et al. , JPhys Energy, 2020, 2, 032008 CrossRef.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141 CrossRef.
- T. Inoue and K. Mukai, ACS Appl. Mater. Interfaces, 2017, 9, 1507–1515 CrossRef CAS PubMed.
- Q. Zhao, S. Stalin, C.-Z. Zhao and L. A. Archer, Nat. Rev. Mater., 2020, 5, 229–252 CrossRef CAS.
- T. O. Ely, D. Kamzabek and D. Chakraborty, Front. Energy Res., 2019, 7, 71 CrossRef.
- J. A. Lewis, J. Tippens, F. J. Q. Cortes and M. T. McDowell, Trends Chem., 2019, 1, 845–857 CrossRef CAS.
- K. B. Hatzell, et al. , ACS Energy Lett., 2020, 5, 922–934 CrossRef CAS.
- T. Krauskopf, F. H. Richter, W. G. Zeier and J. Janek, Chem. Rev., 2020, 120, 7745–7794 CrossRef CAS.
- Y. Chen, et al. , Nature, 2020, 578, 251–255 CrossRef CAS PubMed.
- P. Albertus, et al. , ACS Energy Lett., 2021, 6, 1399–1404 CrossRef CAS.
- K. Kerman, A. Luntz, V. Viswanathan, Y.-M. Chiang and Z. Chen, J. Electrochem. Soc., 2017, 164, A1731–A1744 CrossRef.
- S. Xia, X. Wu, Z. Zhang, Y. Cui and W. Liu, Chem, 2019, 5, 753–785 Search PubMed.
- S. Lou, F. Zhang, C. Fu, M. Chen, Y. Ma, G. Yin and J. Wang, Adv. Mater., 2021, 33, 2000721 CrossRef.
- Solid-State Batteries: The Technology of the 2030s but the Research Challenge of the 2020s, Faraday Insights, Issue 5, February 2020 Search PubMed.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 16103 CrossRef.
- N. Kamaya, et al. , Nat. Mater., 2011, 10, 682–686 CrossRef.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef.
- S. Wenzel, S. Randau, T. Leichtweiß, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, Chem. Mater., 2016, 28, 2400–2407 CrossRef.
- Y. Su, L. Ye, W. Fitzhugh, Y. Wang, E. Gil-González, I. Kim and X. Li, Energy Environ. Sci., 2020, 13, 908–916 RSC.
- Y. Kato, S. Hori and R. Kanno, Adv. Energy Mater., 2020, 10, 2002153 CrossRef.
- F. Han, Y. Zhu, X. He, Y. Mo and C. Wang, Adv. Energy Mater., 2016, 6, 1501590 CrossRef.
- P. Canepa, J. A. Dawson, G. Sai Gautam, J. M. Statham, S. C. Parker and M. S. Islam, Chem. Mater., 2018, 30, 3019–3027 CrossRef.
- C. Wang, et al. , Chem. Rev., 2020, 120, 4257–4300 CrossRef PubMed.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC.
- C. Ma, Y. Cheng, K. Yin, J. Luo, A. Sharafi, J. Sakamoto, J. Li, K. L. More, N. J. Dudney and M. Chi, Nano Lett., 2016, 16, 7030–7036 CrossRef.
- J.-J. Kim, K. Yoon, I. Park and K. Kang, Small Methods, 2017, 1, 1700219 CrossRef.
- T. Famprikis, et al. , J. Am. Chem. Soc., 2020, 142, 18422–18436 CrossRef.
- W. D. Richards, T. Tsujimura, L. J. Miara, Y. Wang, J. C. Kim, S. P. Ong, I. Uechi, N. Suzuki and G. Ceder, Nat. Commun., 2016, 7, 11009 CrossRef.
- Z. Zhu, H. Tang, J. Qi, X.-G. Li and S. P. Ong, Adv. Energy Mater., 2021, 11, 2003196 CrossRef.
- A. Van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Chem. Rev., 2020, 120, 6977–7019 CrossRef.
- A. Hayashi, N. Masuzawa, S. Yubuchi, F. Tsuji, C. Hotehama, A. Sakuda and M. Tatsumisago, Nat. Commun., 2019, 10, 5266 CrossRef PubMed.
- Y. Zhao and L. L. Daemen, J. Am. Chem. Soc., 2012, 134, 15042–15047 CrossRef PubMed.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2018, 140, 362–368 CrossRef.
- Y. Li, et al. , Angew. Chem., Int. Ed., 2016, 55, 9965–9968 CrossRef.
- M. H. Braga, N. S. Grundish, A. J. Murchison and J. B. Goodenough, Energy Environ. Sci., 2017, 10, 331–336 RSC.
- S. Gao, et al. , Nat. Commun., 2021, 12, 201 CrossRef.
- Y. Xiao, K. Turcheniuk, A. Narla, A.-Y. Song, X. Ren, A. Magasinski, A. Jain, S. Huang, H. Lee and G. Yushin, Nat. Mater., 2021, 20, 984–990 CrossRef.
- Z. D. Hood, H. Wang, A. S. Pandian, J. K. Keum and C. Liang, J. Am. Chem. Soc., 2016, 138, 1768–1771 CrossRef.
- X. Lü, J. W. Howard, A. Chen, J. Zhu, S. Li, G. Wu, P. Dowden, H. Xu, Y. Zhao and Q. Jia, Adv. Sci., 2016, 3, 1500359 CrossRef.
- H. Fang and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11046–11051 CrossRef.
- J. A. S. Serejo, J. S. Pereira, R. Mouta and L. G. C. Rego, Phys. Chem. Chem. Phys., 2021, 23, 6964–6973 RSC.
- K. Kim and D. J. Siegel, J. Mater. Chem. A, 2019, 7, 3216–3227 RSC.
- Z. Deng, B. Radhakrishnan and S. P. Ong, Chem. Mater., 2015, 27, 3749–3755 CrossRef CAS.
- S. Fan, M. Lei, H. Wu, J. Hu, C. Yin, T. Liang and C. Li, Energy Storage Mater., 2020, 31, 87–94 CrossRef.
- A.-Y. Song, et al. , Adv. Energy Mater., 2018, 8, 1700971 CrossRef.
- K. Shen, Y. Wang, J. Zhang, Y. Zong, G. Li, C. Zhao and H. Chen, Phys. Chem. Chem. Phys., 2020, 22, 3030–3036 RSC.
- A. Emly, E. Kioupakis and A. Van der Ven, Chem. Mater., 2013, 25, 4663–4670 CrossRef CAS.
- M. B. Effat, J. Liu, Z. Lu, T. H. Wan, A. Curcio and F. Ciucci, ACS Appl. Mater. Interfaces, 2020, 12, 55011–55022 CrossRef CAS.
- Y. Wang, H. Zhang, J. Zhu, X. Lü, S. Li, R. Zou and Y. Zhao, Adv. Mater., 2020, 32, 1905007 CrossRef CAS PubMed.
- Y. Zhu, G. Chen, Y. Zhong, Y. Chen, N. Ma, W. Zhou and Z. Shao, Nat. Commun., 2018, 9, 2326 CrossRef.
- M. Oudah, A. Ikeda, J. N. Hausmann, S. Yonezawa, T. Fukumoto, S. Kobayashi, M. Sato and Y. Maeno, Nat. Commun., 2016, 7, 13617 CrossRef CAS.
- T. He, et al. , Nature, 2001, 411, 54–56 CrossRef CAS PubMed.
- S. V. Krivovichev, Z. Kristallogr. Cryst. Mater., 2008, 223, 109–113 CrossRef CAS.
- E. A. Katz, Helv. Chim. Acta, 2020, 103, e2000061 CrossRef CAS.
- H. D. Megaw, Proc. Phys. Soc., 1946, 58, 133–152 CrossRef CAS.
- A. S. Bhalla, R. Guo and R. Roy, Mater. Res. Innovations, 2000, 4, 3–26 CrossRef CAS.
- K. Kamishima, T. Goto, H. Nakagawa, N. Miura, M. Ohashi, N. Mori, T. Sasaki and T. Kanomata, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 24426 CrossRef.
- R. Huang, L. Li, F. Cai, X. Xu and L. Qian, Appl. Phys. Lett., 2008, 93, 81902 CrossRef.
- P. Lukashev, R. F. Sabirianov and K. Belashchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 184414 CrossRef.
- P. Hartwig, A. Rabenau and W. Weppner, J. Less-Common Met., 1981, 78, 227–233 CrossRef CAS.
- P. Hartwig and W. Weppner, Solid State Ionics, 1981, 3–4, 249–254 CrossRef.
- G. Scarpa, Atti Accad. Naz. Lincei Rend. Classe Sci. Fis. Mat. Nat. Set. V, 1915, 24, 476 Search PubMed.
- N. A. Reshetnikov and G. M. Unzhakov, J. Inorg. Chem., 1958, 3, 227 Search PubMed.
- R. Wortmann, S. Sitta and H. Sabrowsky, Z. Naturforsch., 1989, 44, 1348–1350 CrossRef.
- C. Eilbracht, W. Kockelmann, D. Hohlwein and H. Jacobs, Phys. B, 1997, 234, 48–50 CrossRef.
- G. Schwering, A. Hönnerscheid, L. van Wüllen and M. Jansen, ChemPhysChem, 2003, 4, 343–348 CrossRef PubMed.
- E. Zintl and W. Morawietz, Z. Anorg. Allg. Chem., 1938, 236, 372–410 CrossRef.
- A. Klemenc and V. Gutmann, Monatsh. Chem., 1950, 81, 361–371 CrossRef.
- M. Jansen, Z. Anorg. Allg. Chem., 1977, 435, 13–20 CrossRef.
- H. Sabrowsky, K. Paszkowski, D. Reddig and P. Vogt, Z. Naturforsch. B, 1988, 43, 238–239 CrossRef.
- W. Müller and M. Jansen, Z. Anorg. Allg. Chem., 1990, 591, 41–46 CrossRef.
- M. Jansen, C. Feldmann and W. Müller, Z. Anorg. Allg. Chem., 1992, 611, 7–10 CrossRef.
- M. Jansen, Angew. Chem., Int. Ed. Engl., 1991, 30, 1547–1558 CrossRef.
- Z. Zhang, H. Li, K. Kaup, L. Zhou, P.-N. Roy and L. F. Nazar, Matter, 2020, 2, 1667–1684 CrossRef.
- J. G. Smith and D. J. Siegel, Nat. Commun., 2020, 11, 1483 CrossRef PubMed.
- T. Famprikis, J. Dawson, F. Fauth, E. Suard, B. Fleutot, M. Courty, J.-N. Chotard, S. Islam and C. Masquelier, ACS Mater. Lett., 2019, 1, 641–646 CrossRef.
- O. Reckeweg, B. Blaschkowski and T. Schleid, Z. Anorg. Allg. Chem., 2012, 638, 2081–2086 CrossRef.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef.
- W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2016, 7, 4548–4556 RSC.
- L. Yin, M. Murphy, K. Kim, L. Hu, J. Cabana, D. J. Siegel and S. H. Lapidus, Inorg. Chem., 2020, 59, 11244–11247 CrossRef PubMed.
- Y. Sun, et al. , J. Am. Chem. Soc., 2019, 141, 5640–5644 CrossRef.
- E. Ahiavi, J. A. Dawson, U. Kudu, M. Courty, M. S. Islam, O. Clemens, C. Masquelier and T. Famprikis, J. Power Sources, 2020, 471, 228489 CrossRef.
- H. K. Roobottom, H. D. B. Jenkins, J. Passmore and L. Glasser, J. Chem. Educ., 1999, 76, 1570–1573 CrossRef.
- H. D. B. Jenkins and K. P. Thakur, J. Chem. Educ., 1979, 56, 576–577 CrossRef.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693 CrossRef.
- K. T. Lai, I. Antonyshyn, Y. Prots and M. Valldor, J. Am. Chem. Soc., 2017, 139, 9645–9649 CrossRef PubMed.
- M. W. Lufaso and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 725–738 CrossRef PubMed.
- H. Zhang, N. Li, K. Li and D. Xue, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 812–818 CrossRef.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715 RSC.
- M. S. Avdontceva, A. A. Zolotarev and S. V. Krivovichev, J. Solid State Chem., 2015, 231, 42–46 CrossRef.
- S. Fan, M. Lei, H. Wu, J. Hu, C. Yin, T. Liang and C. Li, Energy Storage Mater., 2020, 31, 87–94 CrossRef.
- H. Nguyen, S. Hy, E. Wu, Z. Deng, M. Samiee, T. Yersak, J. Luo, S. P. Ong and Y. S. Meng, J. Electrochem. Soc., 2016, 163, A2165–A2171 CrossRef CAS.
- J. Zhu, et al. , Inorg. Chem., 2016, 55, 5993–5998 CrossRef CAS.
- Y. Wang, Q. Wang, Z. Liu, Z. Zhou, S. Li, J. Zhu, R. Zou, Y. Wang, J. Lin and Y. Zhao, J. Power Sources, 2015, 293, 735–740 CrossRef CAS.
- K. Hippler, S. Sitta, P. Vogt and H. Sabrowsky, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1990, 46, 736–738 CrossRef.
- G. Klösters, L. Van Wüllen and M. Jansen, Phys. Chem. Chem. Phys., 2002, 4, 3461–3466 RSC.
- H. Fang and P. Jena, ACS Appl. Mater. Interfaces, 2019, 11, 963–972 CrossRef CAS PubMed.
- Z. Wang, H. Xu, M. Xuan and G. Shao, J. Mater. Chem. A, 2018, 6, 73–83 RSC.
- Y. Yu, Z. Wang and G. Shao, J. Mater. Chem. A, 2018, 6, 19843–19852 RSC.
- J. Howard, Z. D. Hood and N. A. W. Holzwarth, Phys. Rev. Mater., 2017, 1, 75406 CrossRef.
- J. A. Dawson, T. S. Attari, H. Chen, S. P. Emge, K. E. Johnston and M. S. Islam, Energy Environ. Sci., 2018, 11, 2993–3002 RSC.
- I. Hanghofer, G. J. Redhammer, S. Rohde, I. Hanzu, A. Senyshyn, H. M. R. Wilkening and D. Rettenwander, Chem. Mater., 2018, 30, 8134–8144 CrossRef CAS.
- F. Wang, H. A. Evans, K. Kim, L. Yin, Y. Li, P.-C. Tsai, J. Liu, S. H. Lapidus, C. M. Brown, D. J. Siegel and Y.-M. Chiang, Chem. Mater., 2020, 32, 8481–8491 CrossRef CAS.
- J. D. Howard and N. A. W. Holzwarth, Solid State Ionics, 2018, 325, 80–89 CrossRef CAS.
- K. T. Lai, I. Antonyshyn, Y. Prots and M. Valldor, Inorg. Chem., 2018, 57, 13296–13299 CrossRef CAS.
- G. Klösters, L. van Wüllen and M. Jansen, Phys. Chem. Chem. Phys., 2002, 4, 3461–3466 RSC.
- L. Gao, H. Zhang, Y. Wang, S. Li, R. Zhao, Y. Wang, S. Gao, L. He, H.-F. Song, R. Zou and Y. Zhao, J. Mater. Chem. A, 2020, 8, 21265–21272 RSC.
- H. Fang, S. Wang, J. Liu, Q. Sun and P. Jena, J. Mater. Chem. A, 2017, 5, 13373–13381 RSC.
- J. Zhang, J. Han, J. Zhu, Z. Lin, M. H. Braga, L. L. Daemen, L. Wang and Y. Zhao, Inorg. Chem. Commun., 2014, 48, 140–143 CrossRef CAS.
- M. H. Braga, J. A. Ferreira, V. Stockhausen, J. E. Oliveira and A. El-Azab, J. Mater. Chem. A, 2014, 2, 5470–5480 RSC.
- X. Lü, G. Wu, J. W. Howard, A. Chen, Y. Zhao, L. L. Daemen and Q. Jia, Chem. Commun., 2014, 50, 11520–11522 RSC.
- S. Li, J. Zhu, Y. Wang, J. W. Howard, X. Lü, Y. Li, R. S. Kumar, L. Wang, L. L. Daemen and Y. Zhao, Solid State Ionics, 2016, 284, 14–19 CrossRef CAS.
- M.-H. Chen, A. Emly and A. Van der Ven, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 214306 CrossRef.
- J. Zhu, et al. , Appl. Phys. Lett., 2016, 109, 101904 CrossRef.
- K. Friese, A. Hönnerscheid and M. Jansen, Z. Kristallogr. Cryst. Mater., 2003, 218, 536–541 CrossRef CAS.
- D. J. Schroeder, A. A. Hubaud and J. T. Vaughey, Mater. Res. Bull., 2014, 49, 614–617 CrossRef CAS.
- H. Barlage and H. Jacobs, Z. Anorg. Allg. Chem., 1994, 620, 471–474 CrossRef CAS.
- J. Howard and N. A. W. Holzwarth, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 14109 CrossRef CAS.
- S. Randau, et al. , Nat. Energy, 2020, 5, 259–270 CrossRef CAS.
- Y. Zhang, Y. Zhao and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134303 CrossRef.
- H. H. Heenen, J. Voss, C. Scheurer, K. Reuter and A. C. Luntz, J. Phys. Chem. Lett., 2019, 10, 2264–2269 CrossRef CAS.
- J. A. Dawson, H. Chen and M. S. Islam, J. Phys. Chem. C, 2018, 122, 23978–23984 CrossRef CAS.
- A.-Y. Song, K. Turcheniuk, J. Leisen, Y. Xiao, L. Meda, O. Borodin and G. Yushin, Adv. Energy Mater., 2020, 10, 1903480 CrossRef CAS.
- T. H. Wan, Z. Lu and F. Ciucci, J. Power Sources, 2018, 390, 61–70 CrossRef CAS.
- Y. Yu, Z. Wang and G. Shao, J. Mater. Chem. A, 2019, 7, 10483–10493 RSC.
- X. He, Y. Zhu and Y. Mo, Nat. Commum., 2017, 8, 15893 CrossRef CAS PubMed.
- R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Chem. Mater., 2013, 25, 425–430 CrossRef CAS.
- A. M. Nolan, Y. Zhu, X. He, Q. Bai and Y. Mo, Joule, 2018, 2, 2016–2046 CrossRef CAS.
- R. Mouta, M. Á. B. Melo, E. M. Diniz and C. W. A. Paschoal, Chem. Mater., 2014, 26, 7137–7144 CrossRef CAS.
- Z. Lu, C. Chen, M. Baiyee, X. Chen, C. Niu and F. Ciucci, Phys. Chem. Chem. Phys., 2015, 17, 32547–32555 RSC.
- R. Mouta, E. M. Diniz and C. W. A. Paschoal, J. Mater. Chem. A, 2016, 4, 1586–1590 RSC.
- H.-X. Li, X.-Y. Zhou, Y.-C. Wang and H. Jiang, Inorg. Chem. Front., 2021, 8, 425–432 RSC.
- M. J. Clarke, J. A. Dawson, T. J. Mays and M. S. Islam, ACS Appl. Energy Mater., 2021, 4, 5094–5100 CrossRef CAS.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS.
- Z. Lu, J. Liu and F. Ciucci, Energy Storage Mater., 2020, 28, 146–152 CrossRef.
- S. Zhao, C. Chen, H. Li and W. Zhang, New J. Chem., 2021, 45, 4219–4226 RSC.
- M. Dondelinger, J. Swanson, G. Nasymov, C. Jahnke, Q. Qiao, J. Wu, C. Widener, A. M. Numan-Al-Mobin and A. Smirnova, Electrochim. Acta, 2019, 306, 498–505 CrossRef CAS.
- M. H. Braga, A. J. Murchison, J. A. Ferreira, P. Singh and J. B. Goodenough, Energy Environ. Sci., 2016, 9, 948–954 RSC.
- D. A. Steingart and V. Viswanathan, Energy Environ. Sci., 2018, 11, 221–222 RSC.
- K. Kim and D. J. Siegel, ACS Appl. Mater. Interfaces, 2019, 11, 39940–39950 CrossRef CAS.
- S. Stegmaier, J. Voss, K. Reuter and A. C. Luntz, Chem. Mater., 2017, 29, 4330–4340 CrossRef CAS.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2016, 28, 266–273 CrossRef CAS.
- Y. Xiao, Y. Wang, S.-H. Bo, J. C. Kim, L. J. Miara and G. Ceder, Nat. Rev. Mater., 2020, 5, 105–126 CrossRef CAS.
- V. Lacivita, Y. Wang, S.-H. Bo and G. Ceder, J. Mater. Chem. A, 2019, 7, 8144–8155 RSC.
- Z. Liu, W. Fu, E. A. Payzant, X. Yu, Z. Wu, N. J. Dudney, J. Kiggans, K. Hong, A. J. Rondinone and C. Liang, J. Am. Chem. Soc., 2013, 135, 975–978 CrossRef CAS.
- H. Tsukasaki, S. Mori, H. Morimoto, A. Hayashi and M. Tatsumisago, Sci. Rep., 2017, 7, 4142 CrossRef.
- C. Ma, K. Chen, C. Liang, C.-W. Nan, R. Ishikawa, K. More and M. Chi, Energy Environ. Sci., 2014, 7, 1638–1642 RSC.
- A. R. Symington, M. Molinari, J. A. Dawson, J. M. Statham, J. Purton, P. Canepa and S. C. Parker, J. Mater. Chem. A, 2021, 9, 6487–6498 RSC.
- J. A. Dawson, P. Canepa, M. J. Clarke, T. Famprikis, D. Ghosh and M. S. Islam, Chem. Mater., 2019, 31, 5296–5304 CrossRef CAS.
- B. Chen, C. Xu and J. Zhou, J. Electrochem. Soc., 2018, 165, A3946–A3951 CrossRef CAS.
- R. J. Clément, Z. Lun and G. Ceder, Energy Environ. Sci., 2020, 13, 345–373 RSC.
- D. Mikhailova, L. Giebeler, S. Maletti, S. Oswald, A. Sarapulova, S. Indris, Z. Hu, J. Bednarcik and M. Valldor, ACS Appl. Energy Mater., 2018, 1, 6593–6599 CrossRef.
- G. Assat and J. M. Tarascon, Nat. Energy, 2018, 3, 373–386 CrossRef CAS.
- M. Ben Yahia, J. Vergnet, M. Saubanère and M. L. Doublet, Nat. Mater., 2019, 18, 496–502 CrossRef CAS.
- Z. Lu and F. Ciucci, J. Mater. Chem. A, 2018, 6, 5185–5192 RSC.
- M. V. Gorbunov, S. Carrocci, S. Maletti, M. Valldor, T. Doert, S. Hampel, I. G. Gonzalez Martinez, D. Mikhailova and N. Gräßler, Inorg. Chem., 2020, 59, 15626–15635 CrossRef CAS.
- M. V. Gorbunov, S. Carocci, I. G. Gonzalez Martinez, V. Baran and D. Mikhailova, Front. Energy Res., 2021, 9, 1–10 Search PubMed.
- J. Gamon, A. J. Perez, L. A. H. Jones, M. Zanella, L. M. Daniels, R. E. Morris, C. C. Tang, T. D. Veal, L. J. Hardwick, M. S. Dyer, J. B. Claridge and M. J. Rosseinsky, J. Mater. Chem. A, 2020, 8, 20553–20569 RSC.
- G. Pilania, P. V. Balachandran, C. Kim and T. Lookman, Front. Mater., 2016, 3, 19 Search PubMed.
- G. Pilania, P. V. Balachandran, J. E. Gubernatis and T. Lookman, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 507–513 CrossRef CAS PubMed.
- P. V. Balachandran, A. A. Emery, J. E. Gubernatis, T. Lookman, C. Wolverton and A. Zunger, Phys. Rev. Mater., 2018, 2, 43802 CrossRef CAS.
- L. Guo, et al. , Angew. Chem., Int. Ed., 2021, 60, 13013–13020 CrossRef CAS.
- C. Yan, R. Xu, J.-L. Qin, H. Yuan, Y. Xiao, L. Xu and J.-Q. Huang, Angew. Chem., Int. Ed., 2019, 58, 15235–15238 CrossRef CAS PubMed.
- Z. Lai, W. Feng, X. Dong, X. Zhou, Y. Wang and Y. Xia, J. Power Sources, 2021, 500, 229982 CrossRef CAS.
- K. Kim and D. J. Siegel, Chem. Mater., 2021, 33, 2187–2197 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |



