Anisotropic silica colloids for light scattering

Abstract

Scattering enhancers are a class of nanomaterials used in every colored or white material surrounding us: from paints and inks to food and cosmetics to packaging and paper. Such hiding pigments usually consist of non-absorbing, high refractive index nanoparticles, for example spherically shaped titanium dioxide nanopowders. However use of TiO₂ carries a high environmental burden. To offset the carbon footprint and health concerns inherent with the use of titanium dioxide, one could approach the challenge of scattering optimization by modifying the morphology of the scattering elements rather than their refractive index. Here, inspired by the bright anisotropic scattering system found in nature, we demonstrate that anisotropic sphero-cylindrical particles can outperform the scattering efficiency of their isotropic counterparts – obtaining an excellent scattering performances across the visible electromagnetic spectrum. We developed a class of micron-sized scattering enhancers composed only of silica. We show that these cylindrical colloids are easily assembled into scattering supracolloidal balls, a new class of pigment microspheres which can be used in formulations for ultrabright coatings.

---

The majority of colored objects surrounding us are obtained with pigment formulations containing scattering enhancers. Such materials are exploited to tune color tones (opacifying agents) and to produce a white base in paints and coatings. To improve the performance of scattering enhancers is therefore crucial to maximized multiple scattering of light.¹ A common strategy to achieve this is to employ scattering elements with a high refractive index such as titanium dioxide (n = 2.33–2.87 ^2,3). Although several alternatives such as clays, calcium carbonate, and zinc sulfide nanopowders have been proposed, titanium dioxide is by far the most widespread for its better performance. Beside the high environmental footprint in the production of titanium dioxide, recent studies have raised safety concerns on its extensive use in formulations,^4,5 highlighting the need for more bio-compatible alternatives.

In the natural world, similar scattering properties have been achieved using a low refractive index media, but by optimizing the shape of the scattering elements, such as in the case of Cyphochilus beetle scales.⁶ The exceptional optical performance of the beetle scales has been reported to be a product of efficient multiple scattering, allowing it to outperform almost all other known low-refractive-index materials.^7–9 The key parameters to its success are the anisotropic shape, dimensions and highly optimized filling fraction of the chitinous fibrils.^10,11

Recently, several groups attempted the fabrication of scattering networks with low refractive index polymers with performances comparable to the one of the Cyphochilus beetle. In particular, highly scattering material based on fibrillar-like networks were obtained by exploiting phase separation of polymers in a solvent mixture combined with kinetic arrest.^12–14 However, such self-assembly process are challenging to scale up maintaining the desired morphology of the scattering elements and the desired morphology as these parameters strongly rely on the exact dynamics of the evaporation of the solvents.

Here, we sought out a synthetic system whereby we can tune the anisotropy of the building blocks to achieve high scattering strength across the entire visible spectrum in very thin films – serving as ideal systems to experimentally investigate the importance of anisotropy in three-dimensional media. Moreover, we experimentally demonstrate that anisotropic silica colloids can outperform, in terms of scattering efficiency, their isotropic (spherical) counterpart.

Finally, we show that silica colloids can be self-assembled in a spherical supracolloidal geometry, and sintered to enhance mechanical robustness, preserving the optical properties of films. These self-assembled micron-sized spheres are thus ideal for use as micron-sized pigment particles. Additionally, the hierarchical porosity (nanoscale pores of silica and >100 nm air voids) may be advantageous in gas sensing applications. Further potential applications can be conceived through chemical modification of silica, for example: biodegradability,^15,16 triggered drug release^17,18 and sensing.¹⁹

Our chosen system employs silica (n = 1.46)²⁰ rod-shaped colloids as anisotropic scatterers, which have recently shown to improve light trapping in thin-film solar cells.^21,22 The length, L, and diameter, d, thus aspect ratio (L/d) of the rods can be readily tuned over the desired dimensions by changing the reaction conditions or via successive coating steps.^20,23 These colloids have already demonstrated their suitability as a model system for studying liquid crystalline phase behavior.^24,25 To synthesize anisotropic silica colloids, an inverse emulsion technique was used. This method allows for control of the morphology and size of silica particles by the initial emulsion conditions, i.e. the droplet size, the concentration of base etc.^20,26 Full experimental details and a schematic of the proposed growth mechanism are provided in the ESI,† (Fig. S2). Silica rods with the resultant range of radii (SEM) were used to assemble films: r_SEM = 135 ± 42, 171 ± 51, 225 ± 52 and 250 ± 58 nm.

The selection of high aspect ratio rods was motivated by biological,⁶ and numerical systems^10,11 which showcased the possibility of exploiting anisotropic building blocks for improved scattering efficiency in low refractive index media. It is important to note that the optical response of an ensemble of anisotropic colloids depends both on the single-particle properties (shape and dimensions) and by the structural ones (alignment and filling fraction).¹⁰ In this work, we mainly focus on the effect of the single-particle properties. We therefore consider random packing of anisotropic colloids – i.e., without control on their structural properties. As discussed in more details in the following, the scattering strength of these systems can be further optimised by controlling the degree of alignment, the filling fraction of the resulting materials, and by a broader exploration of the aspect ratio phase space.

To study the effect of anisotropy, isotropic spherical silica colloids with comparable dimensions (r_SEM = 113 ± 16, 172 ± 6, 224 ± 6 and 279 ± 7 nm) to the rods were synthesized by varying the ammonia concentration in a simple Stöber synthesis.²⁷ The measured dimensions and reaction conditions employed are reported in Table S1 (ESI†). Differences between rods and spheres in absolute density and hence nanoscale porosity were considered negligible, as found by Kuijk et al.²⁰

Attempts made to synthesize rod-shaped colloids with smaller radii using the current synthesis method resulted in more complex particle morphology such as bent, tapered or erratic, “worm-like” objects (in the SEM images in Fig. S1 (ESI†) and as reported previously by Murphy et al.²⁸) To avoid the additional complexity of varying building block morphology, these colloids were omitted from the study. Keeping to the conditions reported here (ESI,† Table S1), the synthesis of rod-shaped silica colloids was found to be highly reproducible.

Assembly of the colloidal building blocks into white films was achieved via drop-casting the colloidal dispersions with known volume fractions onto glass slides. For films of spherical colloids, salt (10⁻² M CaCl₂) was added to the suspension to promote the formation of a photonic glass.²⁹ It has been found that vertical gradients in volume fraction can occur when Péclet numbers (Pe = HĖ/D_p, H – film height, Ė – evaporation rate and D_p – particle diffusion rate) are high, i.e. Ė ≫ D_p resulting in an enrichment of particles in the upper layer of the film.³⁰ To maintain a uniform volume/packing fraction in the dried film, the evaporation rate was kept low by limiting the airflow. The processing time for these materials is thus primarily dictated by the drying time, which conforms with efficiencies expected in other waterborne coatings. The resultant films were randomly packed with high volume/packing fraction (0.45–0.67) throughout the film for both rods and spheres as seen in the SEM (Scanning Electron Microscopy) cross-sections (Fig. 1a). See ESI,† (Table S5) for estimation of the average packing fractions and discussion of sources of uncertainty. Films of either isotropic or anisotropic building blocks were prepared using similar conditions. To guarantee a fair comparison between scattering blocks, we compared films with similar filling fractions (and therefore a similar degree of short range correlation). It is important to note that whilst short range correlation is crucial to many optical properties of colloidal assemblies, e.g., structural colouration³¹ or transparency.³² However, ref. 10 shows that increasing the degree of short-range order in ensembles of low refractive index colloids—exploiting a numerical approach that allows to change the degree of correlation without changing the filling fraction of a material—does not have an impact on their scattering properties.

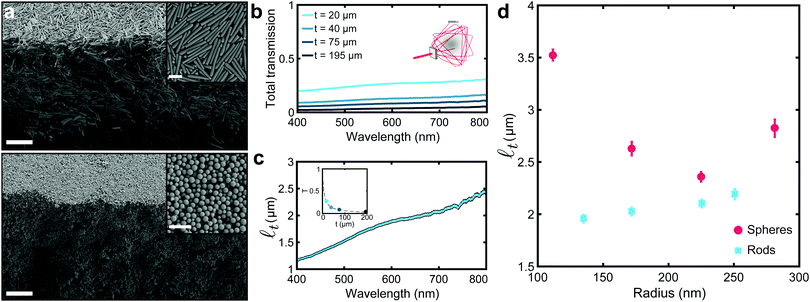Fig. 1 Optical characterization of white silica films. (a) SEM cross-sectional micrographs of films made of anisotropic and isotropic silica colloids, top and bottom panel, respectively. Insets show a zoomed-in top view of the films. Scale bar: 5 μm and 1 μm for cross-sectional and top view micrographs, respectively. (b) Total transmittance measurements for films with different thickness (t) and made of silica rod-shaped colloids with a radius r = (135 ± 42) nm and a length L = (4.92 ± 0.79) μm. Inset shows a schematic of the integrating sphere setup used. (c) Transport mean free path ([small script l]_t) in function of the wavelength. [small script l]_t is obtained by fitting the data in (b) with the theoretical expression for the total transmission in function of the thickness (as shown in the inset at a wavelength of 600 nm). (d) [small script l]_t values, obtained as described in (b and c), for films made of anisotropic and isotropic and anisotropic colloids of different sizes, red circles and cyan squares, respectively. Anisotropic colloids outperform their isotropic counterpart, showing shorter [small script l]_t. The values of the length of the anisotropic colloids can be found in Table S1, ESI.†

The scattering performance of films composed of different dimensions and shape colloids were quantified in terms of the transport mean free path ([small script l]_t). This quantity, which is inversely proportional to the scattering strength, represents the length light has to travel in a material before its propagation direction is randomized by scattering.^33–35 As [small script l]_t is independent of the thickness of a film, it is suitable to compare scattering performance of films with different morphologies. The transport mean free path was estimated, using a well established procedure,^12,13,36 by measuring the amount of light transmitted through a given system as a function of the thickness – as shown in Fig. 1b (experimental details in Methods). [small script l]_t was extrapolated using the analytical expression, which links the total transmission and the thickness of a film – as depicted in the inset of Fig. 1c (theoretical details in the ESI†).³⁷Fig. 1c shows the dependency of the transport mean free path on the wavelength, which is dictated by the spectral dispersion of the total transmission. A similar spectral behaviour, i.e. a monotonic rise of the transmission when the wavelength increases, was observed for both rods and spheres (see ESI,† Fig. S5) – therefore allowing us to compare the different systems by considering the value of [small script l]_t at the central wavelength of the visible range (600 nm).

Fig. 1d shows the role of the anisotropy of the colloids in the scattering strength. Previous theoretical works highlighted the potential for anisotropic building blocks to improve the scattering efficiency of low refractive index systems.^10,11 The experimental results here demonstrate that – in the range of dimensions we explored – ensembles of anisotropic colloids outperform their isotropic counterpart, showing shorter [small script l]_t and, therefore, higher scattering strength. Notably, while for spherical scatterers [small script l]_t is optimal (at r ≃ 225 nm, in agreement with the numerical predictions in Fig. S4, ESI†), the scattering strength of rod-shaped colloids could be further increased by fine-tuning of their dimensions and degree of alignment (as qualitatively shown in the two-dimensional study in ref. 10 and in three-dimensional networks in ref. 11).

The scattering strength of assemblies of rod-shaped colloids shows a less marked dependency on the wavelength than systems made of spherical building blocks, where the residual effect of Mie resonances typical of photonic glasses can be observed (Fig. S5 and S6, ESI†). The use of polydispersed colloids also contributes in averaging out single-particles’ resonances, leading to a scattering response less dependent on the wavelength—an effect which is beneficial for whiteness applications.¹⁰ Note that the Mie resonances represent small modulations of the spectra and they are not centered in λ = 600 nm, therefore justifying the comparison in Fig. 1d.

A clear application for such efficient broadband scatterers is their use as opacifying agents in paints and coatings, supracolloidal balls were fabricated via a facile emulsion-evaporation method to create micron-size object to disperse in pigment formulations. Briefly, an aqueous dispersion of rods (100 μl, 10 vol%) was added to a solution of oil-soluble surfactant (Span 80 – sorbitan oleate) in hexadecane (200 μl, 2 mol%) and vortexed. The formed emulsion was then poured into a plastic Petri dish containing Span 80 in hexadecane (2 ml, 0.5 mol%) and the aqueous phase allowed to slowly evaporate over ∼48 h, (see ESI†). As the emulsion-based method delivers polydisperse supraparticles, we explore the effects of confinement on assembly and subsequent whiteness for different supraparticle sizes.

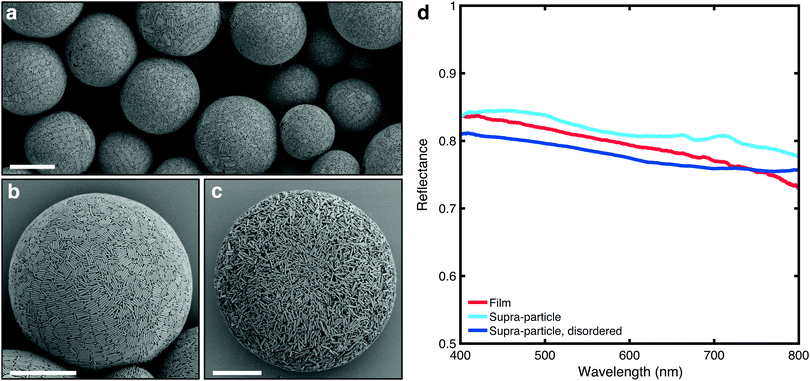
When confined to a spherical geometry in the form of an aqueous emulsion droplet, the rod-shaped silica particles arrange themselves at the interface, (Fig. 2a and b). One explanation is that the surfactant, Span 80, facilitates adhesion of the silica rods to the interface, generating a Pickering emulsion.³⁸ The adhered layer of silica rods can reorient itself and align. Alternatively, the presence of the oil–water interface simply acts as a boundary, to guide the alignment of the rods, in absence of adhesion.^39,40 The alignment at/near the interface provides nucleation sites at the droplet interface for liquid crystallization with further slow evaporation. Ordering into smectic domains that can be observed in Fig. 2b (rod orientations are colour-coded in Fig. S7, ESI†). Once a certain threshold in volume fraction is reached, the colloids jam preventing further ordering. This jamming event is likely preceded by limited aggregation of the colloids into flocs, as a result of increased concentrations of solutes due to water removal. The internal structure of the supracolloidal balls was examined by freeze fracturing a polymer film (nail varnish) with embedded particles (Fig. S8, ESI†). Ordering of rods can be seen most obviously in the lower left of the image in the outer layers of the ball only, and it does not propagate into the core. To examine whether this superficial ordering had an effect on the scattering properties, a completely isotropic, disordered structure was assembled (Fig. 2b) using an identical fabrication procedure except for addition of calcium chloride to the aqueous phase (10⁻² M) to facilitate early limited flocculation and jamming.

Fig. 2 SEM images and optical characterization of white silica supraparticles. (a) low magnification SEM image of supracolloidal balls, (b) higher magnification image of single supracolloidal balls, (c) supracolloidal ball assembled in the presence of 10⁻² M CaCl₂. Scale bars: (a) = 15 μm (b and c) = 10 μm. (d) Reflectance spectra comparing the scattering properties of supraparticles with films of similar size (thickness of 25 μm). Supraparticles show performance comparable to the corresponding films. Increasing the disorder reduces the scattering efficiency. The reflectance spectra for the supraparticles where measured using a microscope, while for the film they were retrieved from the total transmission data.

Fig. 2d compares the optical properties of silica supraparticles (measured using a similar, previously established method⁴¹) with films made of the same rod-shaped colloids. It is apparent that assembling anisotropic colloids in a spherical geometry preserves the optical properties of the films. Importantly, a decrease in reflectance is observed when the degree of orientational order of the supraparticle is reduced (Fig. 2b and c). This observation agrees with the predictions in ref. 10 and 11 and, as the ordering was only present at the surface of the supraparticle, it is expected that increasing the range of ordering by using more sophisticated fabrication methods could further improve the scattering strength. Sedimentation diffusion equilibrium experiments have demonstrated that smectic ordering of silica rods (with similar dimensions to those used here) only starts to occur after five days, noted by the onset of Bragg diffraction.²⁴ Spherical confinement may help reduce this time frame thus with a slightly slower evaporation rate and perhaps use of a refractive index matching solvent to screen inter-particle attraction, more ordered structures are likely possible. It is important to note that the comparison in Fig. 2d is qualitative, as the scattering properties of the supraparticles might be influenced by lateral losses – i.e., photons escaping in directions perpendicular to that of the exciting beam – which are absent in a film geometry sample. We expect these losses to be dependent on the ratio between the illumination/detection area and the size of the particles. In our comparison, with a fixed illumination/detection of ≃5 μm, we observed that this difference is marginal as the transmittance scales following the theory for non-absorbing, slab samples (Fig. 3c) – whereas the presence of lateral losses would affect the scaling law in the same way as the presence of absorption.⁴²

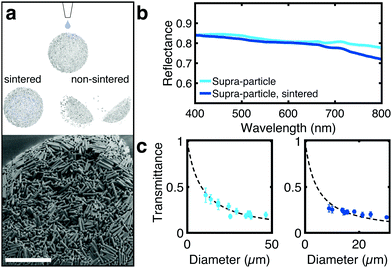Fig. 3 (a) Schematic showing the preservation of the supraparticle microstructure of sintered particles upon wetting (see Fig. S10, ESI†). SEM image of the sintered supracolloidal ball showing sintering throughout the structure as well as on the periphery. (b) Reflectance spectra comparing the scattering properties of supraparticles before and after sintering (size of 25 μm). Sintering does not significantly affect the optical properties. (c) Total transmission in function of the diameter of the particles before and after sintering, cyan and blue points, respectively.

To improve the mechanical stability of the supraparticles, rod-shaped particles were sintered together, maintaining the assembled structure of the supracolloidal balls (Fig. 3a and Fig. S9, S10, ESI†). Without sintering, the supraparticle disintegrated upon dispersion in water (Fig. S11, ESI†). Mild sintering conditions were used (650 °C) over an extended period (14 h) to promote fusion at rod edges only, preserving small internal air voids essential for scattering. As depicted in Fig. 3b, sintering does not strongly affect the optical properties of the supraparticle.

Interestingly, the sintering affects how the scattering strength scales with the size of the supraparticles (Fig. 3c). Conversely to non-sintered particles, for sintered particles a small deviation from the slab geometry predictions can observed. This deviation might indicate a change in light transport, with a higher likelihood for photons to escape the supraparticle from normal (equatorial) directions, or that sintering has a different effect on supraparticle with different dimensions. However, the absence of a theory that describes the propagation of light in spherical particles does not allow us to identify which phenomenon determines the deviation shown in Fig. 3c.

In conclusion, our work provides an experimental demonstration that ensembles of anisotropic colloids – with appropriate values of aspect ratio, dimensions and alignment – outperform their isotropic counterpart in terms of scattering efficiency. We report a method to fabricate photonic supracolloidal materials composed of silica rods with controlled size and aspect ratio. A clear advantage of using silica colloids is their ease of post-functionalization functionality, due to the reactivity of terminal Si–OH bonds, allowing their use for a multitude of applications. The wide range of available silanes provides compatibility with most any solvent system. Moreover, introducing a hydrophobic layer to the surface of the supracolloidal particles impedes the imbibition of water and polymer binder into the structure, allowing the maintenance of the same scattering strength in an aqueous dispersion. In an example formulation, the polymer binder of preference would be a slightly cross-linked soft polymer latex, like those produced by BASF,⁴³ with particle size greater than the supracolloidal pore size (>200 nm). Therefore, we believe that our system can additionally find application in a waterborne paint/coating formulation and has potential for use in gas sensing.

Author contributions

G. J., B. W. L., C. C. P., S. A. F. B and S. V. designed the experiments. B. W. L. synthesized and characterized colloids and materials. G. J. performed optical measurements. G. J. provided simulations. All authors gave critical feedback and helped shape the research, analysis and manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors thank Dr R. M. Parker for fruitful discussions. This work was supported in part by a BBSRC David Phillips Fellowship (BB/K014617/1), the European Research Council (ERC-2014-STG H2020639088).

Notes and references

1. D. S. Wiersma, Nat. Photonics, 2013, 7, 188–196.
2. H. K. Pulker, G. Paesold and E. Ritter, Appl. Opt., 1976, 15, 2986–2991.
3. G. E. Jellison, L. A. Boatner, J. D. Budai, B. S. Jeong and D. P. Norton, J. Appl. Phys., 2003, 93, 9537–9541.
4. A. Weir, P. Westerhoff, L. Fabricius, K. Hristovski and N. von Goetz, Environ. Sci. Technol., 2012, 46, 2242–2250.
5. S. Bettini, E. Boutet-Robinet, C. Cartier, C. Coméra, E. Gaultier, J. Dupuy, N. Naud, S. Taché, P. Grysan, S. Reguer, N. Thieriet, M. Réfrégiers, D. Thiaudière, J.-P. Cravedi, M. Carrière, J.-N. Audinot, F. H. Pierre, L. Guzylack-Piriou and E. Houdeau, Sci. Rep., 2017, 7, 40373.
6. H. L. Leertouwer, B. D. Wilts and D. G. Stavenga, Opt. Express, 2011, 19, 24061–24066.
7. M. Burresi, L. Cortese, L. Pattelli, M. Kolle, P. Vukusic, D. S. Wiersma, U. Steiner and S. Vignolini, Sci. Rep., 2014, 4, 6075.
8. L. Cortese, L. Pattelli, F. Utel, S. Vignolini, M. Burresi and D. S. Wiersma, Adv. Opt. Mater., 2015, 3, 1337–1341.
9. G. Jacucci, O. D. Onelli, A. De Luca, J. Bertolotti, R. Sapienza and S. Vignolini, Interface Focus, 2019, 9, 20180050.
10. G. Jacucci, J. Bertolotti and S. Vignolini, Adv. Opt. Mater., 2019, 7, 1900980.
11. F. Utel, L. Cortese, D. S. Wiersma and L. Pattelli, Adv. Opt. Mater., 2019, 7, 1900043.
12. J. Syurik, G. Jacucci, O. D. Onelli, H. Hölscher and S. Vignolini, Adv. Funct. Mater., 2018, 1706901.
13. W. Zou, L. Pattelli, J. Guo, S. Yang, M. Yang, N. Zhao, J. Xu and D. S. Wiersma, Adv. Funct. Mater., 2019, 29, 1808885.
14. S. L. Burg, A. Washington, D. M. Coles, A. Bianco, D. Mcloughlin, O. O. Mykhaylyk, J. Villanova, A. J. C. Dennison, C. J. Hill, P. Vukusic, S. Doak, S. J. Martin, M. Hutchings, S. R. Parnell, C. Vasilev, N. Clarke, A. J. Ryan, W. Furnass, M. Croucher, R. M. Dalgliesh, S. Prevost, R. Dattani, A. Parker, R. A. L. Jones, J. P. A. Fairclough and A. J. Parnell, Commun. Chem., 2019, 1–10.
15. L. Maggini, I. Cabrera, A. Ruiz-Carretero, E. A. Prasetyanto, E. Robinet and L. De Cola, Nanoscale, 2016, 8, 7240–7247.
16. L. Travaglini, P. Picchetti, R. Totovao, E. A. Prasetyanto and L. De Cola, Mater. Chem. Front., 2019, 3, 111–119.
17. S. Angelos, E. Choi, F. Vögtle, L. D. Cola and J. I. Zink, J. Phys. Chem. C, 2007, 111, 6589–6592.
18. E. A. Prasetyanto, A. Bertucci, D. Septiadi, R. Corradini, P. Castro-Hartmann and L. DeCola, Angew. Chem., Int. Ed., 2016, 55, 3323–3327.
19. A. Burns, P. Sengupta, T. Zedayko, B. Baird and U. Wiesner, Small, 2006, 2, 723–726.
20. A. Kuijk, A. Imhof, M. H. W. Verkuijlen, T. H. Besseling, E. R. H. van Eck and A. van Blaaderen, Part. Part. Syst. Charact., 2014, 31, 706–713.
21. M. M. Byranvand, N. Taghavinia, A. N. Kharat and A. Dabirian, RSC Adv., 2015, 5, 86050–86055.
22. M. M. Byranvand, A. N. Kharat, N. Taghavinia and A. Dabirian, ACS Appl. Mater. Interfaces, 2016, 8, 16359–16367.
23. A. Kuijk, A. van Blaaderen and A. Imhof, J. Am. Chem. Soc., 2011, 133, 2346–2349.
24. A. Kuijk, D. V. Byelov, A. V. Petukhov, A. V. Blaaderen and A. Imhof, Faraday Discuss., 2012, 159, 181–199.
25. B. Liu, T. H. Besseling, M. Hermes, A. F. Demirörs, A. Imhof and A. van Blaaderen, Nat. Commun., 2014, 5, 1–8.
26. B. W. Longbottom, L. A. Rochford, R. Beanland and S. A. F. Bon, Langmuir, 2015, 31, 9017–9025.
27. W. Stöber, J. Colloid Interface Sci., 1968, 69, 62–69.
28. R. P. Murphy, K. Hong and N. J. Wagner, J. Colloid Interface Sci., 2017, 501, 45–53.
29. P. D. García, R. Sapienza, Á. Blanco and C. López, Adv. Mater., 2007, 19, 2597–2602.
30. A. F. Routh and W. B. Zimmerman, Chem. Eng. Sci., 2004, 59, 2961–2968.
31. G. Jacucci, S. Vignolini and L. Schertel, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 23345–23349.
32. C. Salameh, F. Salviat, E. Bessot, M. Lama, J.-M. Chassot, E. Moulongui, Y. Wang, M. Robin, A. Bardouil, M. Selmane, F. Artzner, A. Marcellan, C. Sanchez, M.-M. Giraud-Guille, M. Faustini, R. Carminati and N. Nassif, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11947–11953.
33. P. Sheng, Introduction to Wave Scattering, Localization and Mesoscopic Phenomena, Springer; Berlin, 1995.
34. A. Ishimaru, Wave Propagation and Scattering in Random Media, Academic Press, San Diego, CA, 1989, vol. I and II.
35. E. Akkermans and G. Montambaux, Mesoscopic Physics of Electrons and Photons, Cambridge University Press, 2007.
36. N. Garcia, A. Z. Genack and A. A. Lisyansky, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 14475–14479.
37. N. Garcia, A. Z. Genack and A. A. Lisyansky, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 14475–14479.
38. P. Datskos, G. Polizos, M. Bhandari, D. A. Cullen and J. Sharma, RSC Adv., 2016, 6, 26734–26737.
39. B. De Nijs, S. Dussi, F. Smallenburg, J. D. Meeldijk, D. J. Groenendijk, L. Filion, A. Imhof, A. Van Blaaderen and M. Dijkstra, Nat. Mater., 2015, 14, 56–60.
40. J. Wang, U. Sultan, E. S. A. Goerlitzer, C. F. Mbah, M. Engel and N. Vogel, Adv. Funct. Mater., 2019, 30, 1907730.
41. D. P. Song, T. H. Zhao, G. Guidetti, S. Vignolini and R. M. Parker, ACS Nano, 2019, 13, 1764–1771.
42. P. Gaikwad, S. Ungureanu, R. Backov, K. Vynck and R. A. L. Vallée, Opt. Express, 2014, 22, 7503–7513.
43. P. C. Hayes and R. L. De Jong, WIPO PCT., WO2009123637A1, 2008.

---

Footnotes

† Electronic supplementary information (ESI) available: Materials methods, numerical simulations of the optical properties of silica spheres, wavelength dependency of lt, colourisation of rod orientations in supracolloidal assemblies, freezefractured cross-sectional SEM of supracolloidal ball, SEM of sintered supracolloidal ball surface, micrograph of immersed, sintered and non-sintered supraballs. See DOI: 10.1039/d1tc00072a

‡ These authors contributed equally to this work.

---