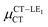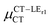Impact of chemical modifications on the luminescence properties of organic neutral radical emitters†‡
Eunkyung
Cho
 ,
Veaceslav
Coropceanu
,
Veaceslav
Coropceanu
 * and
Jean-Luc
Brédas
* and
Jean-Luc
Brédas
 *
*
Department of Chemistry and Biochemistry, The Univeszrsity of Arizona, Tucson, Arizona 85721-0088, USA. E-mail: coropceanu@arizona.edu; jlbredas@arizona.edu
First published on 17th May 2021
Abstract
Neutral organic radicals have recently attracted great attention as promising luminescent materials, which is a consequence of their strong doublet emission properties. Recent investigations have indicated that even minor chemical modifications can have a significant impact on the luminescence properties of these radical emitters. Here, we performed long range-corrected density functional theory calculations to evaluate how chemical modifications affect the electronic properties and radiative and nonradiative decay rates in a series of tris(2,4,6-trichlorophenyl)methyl-pyridoindole (TTM-xPyID) radicals vs. the TTM-carbazole radical. We find that the lowest excited state of these radical emitters has a charge-transfer (CT) character and its energy blue-shifts upon chemical modification from carbazole to xPyID, in agreement with experiment. An analysis of the transition dipole moments shows that hybridization between the CT and ground states of the TTM-xPyID radicals plays a dominant role in the radiative decay rates. On the other hand, hybridization between the CT state and the lowest local-excitation (LE) state on the TTM radical core has a significant contribution to the nonradiative rates in most of TTM-xPyID radicals, while it has only a minor influence on that rate in the TTM-carbazole radical. Our results underline that the hybridization of the CT state with both ground state and LE state can substantially influence the radiative and non-radiative rates in TTM-based radicals. Also, we show that the relative contributions of these two hybridization pathways depend in a subtle way on the properties of the donor fragment, such as its ionization potential and the intramolecular relaxion energy associated with its oxidation process. Finally, we propose a new design strategy to achieve high values of photoluminescence quantum yield in radicals with a donor–acceptor structural motif.
Introduction
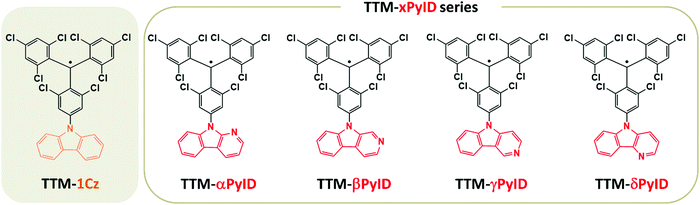
Stable neutral organic radicals have received a great deal of interest due to their possible applications in a variety of fields including optoelectronics, spintronics, magnets, and quantum information technologies.1–8 In particular, significant advances have been recently achieved in the field of organic light-emitting diodes (OLEDs).9–15 These radicals have an open-shell electronic configuration and in many instances both the ground state (D0) and the first-excited state (D1) have a spin-doublet character.16–19 This is in marked contrast with conventional closed-shell organic emitters where the emissive singlet state is located above the first excited triplet state; as a result, ∼75% of the electrically generated excitons are triplet excitons whose emission is spin-restricted. In their majority, the neutral radical emitters that are currently investigated have a donor–acceptor (D–A˙) chemical structure, in which an electron-poor acceptor radical (A˙) core, such as a stable tris(2,4,6-trichlorophenyl)methyl (TTM) or perchlorotriphenylmethyl (PTM) radical, is covalently linked to an electron-rich donor group (D), such as a carbazole (Cz) derivative. As a consequence, the D1 state has a charge-transfer nature9,14,15,17,20,21 and the radiative and nonradiative transitions back to D0 can be viewed as a back-electron transfer from the A− moiety to the D+ moiety.10,19In 2015, Peng et al.11 reported the first viable OLED based on the red TTM-1Cz radical emitter,9 which consists of a combination of the TTM radical with carbazole (see Fig. 1). TTM-1Cz displays a photoluminescence quantum yield (PLQY) of 53% in cyclohexane and high photostability, which motivated further investigations of organic radicals for OLED applications and led to the active development of a number of new radical emitters.14,15,22,23 The most efficient radical emitter OLEDs reported so far are those based on TTM-3NCz (9-(naphthalene-2-yl)-9H-carbazole), which have external quantum efficiencies (EQEs) of up to 27%.14
In D–A˙ radical emitters, the hybridization between the D1 charge-transfer (CT) state and the low-energy local-excitation (LE) states can play a significant role on the emissive properties. For instance, we have reported that in PTM-TAA radicals (where TAA denotes a substituted triarylamine), CT–LE hybridization significantly increases the non-radiative decay rates,19 while Abdurahman et al. suggested recently that in TTM-xPyID radicals (where PyID stands for pyridoindole, see Fig. 1), CT–LE hybridization contributes appreciably to the radiative decay of the CT states.17 To shed more light on the role of CT–LE hybridization on the radical emissive properties, we describe here the electronic structures and radiative and nonradiative decay rates of a series of TTM-xPyID radicals, as well as of TTM-1Cz for the sake of comparison.
Computational methods
In order to determine the ground-state electronic structures of the radical emitters, we performed density functional theory (DFT) calculations using the screened range-separated hybrid (SRSH) functional LC-ωhPBE with 20% Hartree Fock exchange and the 6-31G** basis set.24 In our recent work on PTM-TAA radicals, we found that this computational approach provides results that are in very good agreement with experiment.19 The range-separation parameters (ω) were optimized for each radical. We used a dielectric constant ε = 2 in the SRSH calculation to account for the screening of electrostatic electron–electron interactions due to the surroundings. The excited-state properties were obtained at the time-dependent DFT level within the Tamm–Dancoff approximation (TDA-TDDFT).25 Natural transition orbital (NTO) analyses were carried out to characterize the nature of the excited states. All DFT/TDDFT calculations were performed with the Gaussian 16 program.26Within the two-state model, the radiative decay rates from the CT states were obtained by means of eqn (1):27
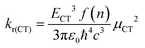 | (1) |
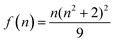 , accounts for the local electric field effect and is considered according to the Lorentz virtual cavity model;28 the value of n was set to 1.43 (corresponding to the refractive index of cyclohexane).
, accounts for the local electric field effect and is considered according to the Lorentz virtual cavity model;28 the value of n was set to 1.43 (corresponding to the refractive index of cyclohexane).
The nonradiative decay rates from the CT states were calculated in the framework of the Marcus–Levich–Jortner approach:29
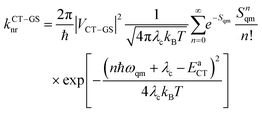 | (2) |
In order to account for the hybridization between the CT and LE states and consider its impact on the non-radiative rates in the TTM-1Cz and TTM-xPyID radicals, we followed the approach we described in our previous work:19,34
| knr = (1 − fCT–LE2)kCT–GSnr + fCT–LE2kLE–GSnr | (3) |
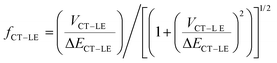 | (4) |
Results and discussion
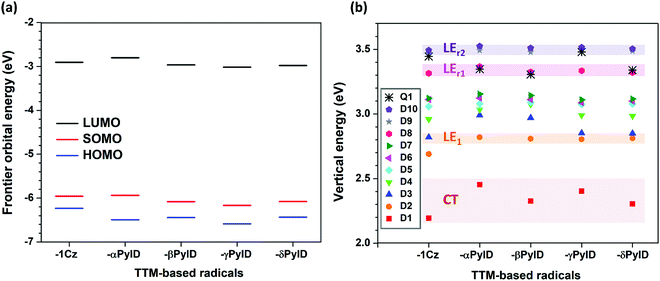
Fig. 2 displays the energies of the frontier molecular orbitals involved in the lowest ten excited doublet (D1–D10) states and the first excited quartet (Q1) state of the TTM-based radicals, as computed at the ground-state geometry. Although the singly occupied molecular orbital (SOMO) level of the TTM moiety is located below the highest doubly occupied molecular orbital (HOMO) levels of the Cz and xPyID fragments (see Fig. S1, ESI†), all D–A˙ radicals investigated here have an Aufbau electronic configuration, i.e., the SOMO level in the whole molecule is located above the doubly occupied HOMO level. In comparison to TTM-1Cz, the introduction of an additional nitrogen into carbazole to form pyridoindole does not result in any substantial change in the HOMO, SOMO, and lowest fully unoccupied molecular orbital (LUMO) energies (Fig. 2a). For all TTM-based radicals, the SOMO is delocalized over the entire molecule while the HOMO and LUMO are mainly localized on the donor moiety and the TTM moiety, respectively (see Fig. S2, ESI†).As seen from Fig. 2b, the D1 energy increases when replacing Cz with xPyID. This blue-shift in the D1 absorption band agrees well with the experimental data. The variation in D1 energy as a function of the nitrogen position within xPyID is small. Also, the D2 states in the TTM-xPyID radicals correspond to the first excited state localized on the TTM moiety (we label them as LE1 states) and their energies remain nearly constant along the series. We note that, in the case of TTM-1Cz, the first TTM local-excitation state corresponds to the D3 state. There are two high-energy LE states in the TTM-xPyID radicals, D8 and either D9 or D10 (which we label as LEr1 and LEr2 states), which are related to local excitations within the TTM core and have large oscillator strengths (see Tables S1 and S2, ESI†); their energies are also nearly constant in going from Cz to xPyID.
An analysis of the natural transition orbitals (NTOs, see Fig. 3) indicates that the D1 state in the TTM-1Cz and TTM-xPyID radicals has a CT nature, coming from an electron transfer from the Cz or xPyID donor to the TTM acceptor (which roughly corresponds to a HOMO-to-LUMO transition). The NTOs also confirm that the D2 (LE1), LEr1, and LEr2 states have a dominant LE character. These results are further supported by the evaluations of the CT components in each state, see Table 1.
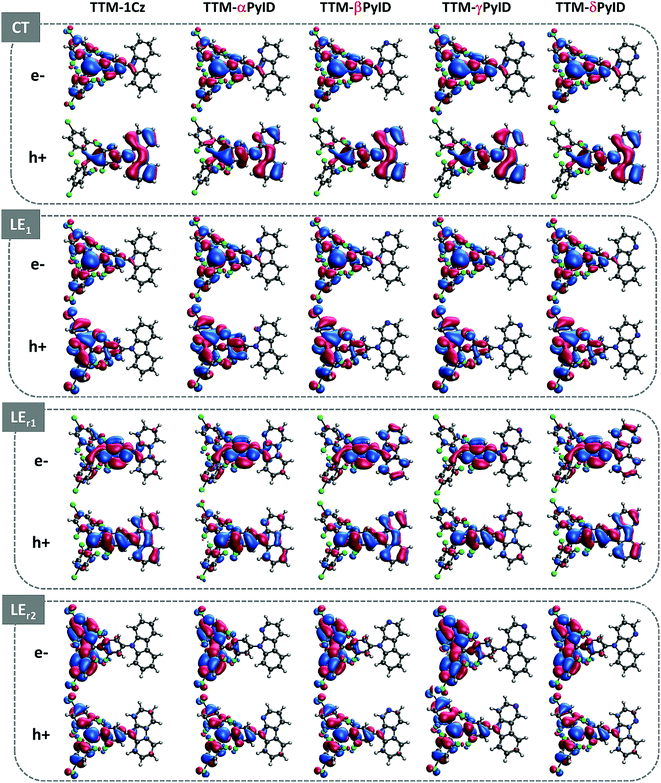 | ||
| Fig. 3 Electron and hole natural transition orbitals (NTOs) in the CT, LE1, LEr1, and LEr2 states of the TTM-1Cz and TTM-xPyID radicals. | ||
| State | TTM-1Cz | TTM-αPyID | TTM-βPyID | TTM-γPyID | TTM-δPyID |
|---|---|---|---|---|---|
| CT | 82 | 70 | 78 | 78 | 79 |
| LE1 | 9 | 5 | 5 | 3 | 18 |
| LEr1 | 23 | 24 | 2 | 26 | 19 |
| LEr2 | 36 | 14 | 28 | 28 | 31 |
The TD-DFT calculated radiative rates for the transition from the CT (D1) state back to the ground (D0) state are listed in Table 2, along the experimental rates. Overall, the DFT values compare very well with the experimental values, although in the case of TTM-βPyID and TTM-δPyID, the DFT estimates are somewhat smaller than the measured values.
In agreement with experiment, the computed radiative rates for the TTM-1Cz and TTM-xPyID radicals are about 3 to 6 times as large as the value of 3.5 × 106 s−1 measured for the TTM radical core.17 The increase in the radiative rate upon addition of a donor to the TTM moiety is thus related to the formation of a CT state as the first excited state of the D–A˙ systems.10,15,19 The question then becomes what does determine the value of the μCT transition dipole and make it larger than μD1 in TTM? We recall that in the diabatic approximation (where no coupling is considered between the CT state and any other state), μCT is zero. Therefore, the actual value of μCT comes from the hybridization of the CT state with the ground state (GS) and local excited states of the TTM and D moieties. Our TD-DFT calculations show that in all systems μCT is parallel to the vector connecting the centers of the D and A˙ units (see Fig. S3, ESI†); this is a strong indication that μCT is determined by the coupling of the CT state with the ground state.29 In contrast, Abdurahman et al.17 suggested recently that μCT in TTM-xPyID radicals is defined by the hybridization of the CT state with the TTM D2 state (which corresponds to an intensity borrowing effect). Our calculations show that in TTM the transitions from the lowest six excited states to the ground state have relatively small transition dipole moments. However, the transition dipole moments for the transitions from the D7 and D8 states to the ground state are significant (4.1 D), see Table S1 (ESI†). These two TTM states, as discussed above, correspond to D8 (LEr1) and either D9 or D10 (LEr2) in TTM-1Cz and TTM-xPyID (see Table S2, ESI†). As seen from Table 1, LEr1 and LEr2 have a significant CT component, which is consistent with the observed decrease in the intensity of the absorption band at about 3.2 eV, corresponding to these transitions, when going from TTM to TTM-1Cz. As such, these LE states of the TTM moiety could in principle contribute to μCT.
Next, in order to shed more light on this issue, we study in more detail the CT–GS and CT–LE contributions to μCT. The related electronic couplings are collected in Table 3. In the perturbation limit, the contributions to μCT due to CT–GS and CT–LE hybridizations are given by:35–37
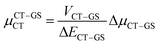 | (5) |
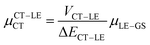 | (6) |
Expression (6) is the well-known Mulliken–Hush relation31,38–42 that connects the electronic coupling, VCT–GS, energy gap, ΔECT–GS, and transition dipole moment between the CT and GS states, μCT–GSCT, with the difference between the dipole moments of the diabatic CT and GS states, ΔμCT–GS. Since the latter is defined by the electron transfer distance from D to A, its value is usually much larger than those of the intra-molecular transition dipole moments, see Table 3. As a result, for similar V/ΔE ratios, the contribution due to CT–GS hybridization will be larger than that due to CT–LE coupling. Expression (6) defines the well-known intensity borrowing effect and is obtained by treating the coupling between CT and LE states as a perturbation.35 As an illustrative example, we can consider the absolute values of the transition dipole moments μCT–GSCT and μCT–LECT in TTM-αPyID, which is the emitter that overall displays the largest VCT–LE/ΔECT–LE hybridization coefficient between the GS state and LEr states. The μCT–GSCT value is estimated to be 3.32 D, which represents about 93% of the total μCT value (3.55 D). The μCT–LECT values due to the LEr1 and LEr2 states are equal to 0.9 D and 0.4 D, respectively. In order to appreciate the individual contributions to the total μCT value, since the transition dipole moments are vectors, their actual orientations must be taken into account. For instance, in all molecules, 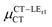 is antiparallel to the DFT-derived μCT vector (μCT–GSCT) while
is antiparallel to the DFT-derived μCT vector (μCT–GSCT) while 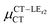 is nearly perpendicular to both
is nearly perpendicular to both 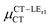 and μCT–GSCT (see Fig. S3, ESI†). Although an exact assessment of how much the LE states contribute to the radiative decay would require to compute the μCT–LECT contributions from all LE states, our study unambiguously demonstrates that the μCT values and consequently the radiative rates in the TTM-1Cz and TTM-xPyID radicals are dominated by the interactions between the CT and ground states.
and μCT–GSCT (see Fig. S3, ESI†). Although an exact assessment of how much the LE states contribute to the radiative decay would require to compute the μCT–LECT contributions from all LE states, our study unambiguously demonstrates that the μCT values and consequently the radiative rates in the TTM-1Cz and TTM-xPyID radicals are dominated by the interactions between the CT and ground states.
We now turn to a discussion of the nonradiative transitions from the CT state to the ground state. We start with the decay rate, kCT–GSnr, arising from the CT–GS electronic coupling. The DFT-calculated electronic couplings, VCT–GS, adiabatic CT energies, EaCT, and reorganization energies, λ, of all radicals are collected in Table S3 (ESI†). We note that, as shown in Table S4 (ESI†), the kCT–GSnr values strongly depend on the way λ is partitioned into classical (λc) and quantum (λqm) contributions. In order to gain a better understanding, we also computed the geometry relaxation energies of the TTM and donor (isolated) fragments occurring as a result of reduction and oxidation, respectively; the results are collected in Table S5 (ESI†). The sum of these two relaxation energies provides a good estimate of the intra-molecular contribution to the CT-state relaxation. The results show that, in the case of TTM-1Cz, about 65% of the λ value obtained from the CT-state geometry optimization can be attributed to λqm. In the case of the TTM-xPyID radicals, the contribution from λqm increases to ∼75%, except in the TTM-γPyID case where this value goes up to 85% (which is due to an increase of about 60 meV in the relaxation energy of the γPyID fragment in comparison to the other xPyID donors, a feature likely associated with the para-type interactions between the two nitrogens in this derivative).
The computed kCT–GSnr values based on the DFT-derived parameters are collected in Table 4. The results show that the kCT–GSnr values of the TTM-1Cz and TTM-γPyID molecules are much larger than in the other systems. In the case of TTM-1Cz, this is due to a relatively smaller CT-state energy; this can be related to the higher HOMO energy (lower ionization potential) of the carbazole donor in comparison to the other xPyID donors (see Fig. S1, ESI†). In the case of TTM-γPyID, the increase in kCT–GSnr is coming from the larger λqm value in the CT state, which is due to an increase in the relaxation energy of the γPyID donor upon oxidation in comparison to the other xPyID donors and carbazole. The contributions coming from the CT–LE hybridization, f2CT–LEkLE–GSnr, to the non-radiative rate are of the same order as kCT–GSnr in the case of TTM-αPyID, TTM-βPyID, and TTM-δPyID. As a result, the CT–LE hybridization plays a marginal role in the knr value of TTM-1Cz and TTM-γPyID while it is an important factor to consider in the other systems.
| State | k CT–GSnr × 107 s−1 | f 2CT–LE k LE–GSnr × 107 s−1 | k nr × 107 s−1 | k nr × 107 s−1 (exp)a | k nr × 107 s−1 (exp)b |
|---|---|---|---|---|---|
| a Measured in cyclohexane. b Measured in toluene.17 | |||||
| TTM-1Cz | 2.56 | 0.02 | 2.57 | 1.13 | 3.21 |
| TTM-αPyID | 0.07 | 0.09 | 0.16 | 0.90 | 0.33 |
| TTM-βPyID | 0.07 | 0.03 | 0.10 | 0.04 | 0.14 |
| TTM-γPyID | 1.80 | 0.04 | 1.84 | 1.71 | 1.81 |
| TTM-δPyID | 0.17 | 0.02 | 0.20 | 0.26 | 0.12 |
It is worth recalling that the experimental rates strongly depend on the measurement conditions. For instance, the rates for TTM-αPyID, TTM-βPyID, and TTM-δPyID substantially differ when measured in cyclohexane while they are very similar in toluene, see Table 4. Overall, the experimental data point to knr rates a few times faster in TTM-1Cz and TTM-γPyID compared to TTM-αPyID, TTM-βPyID, and TTM-δPyID, a trend that our calculations reproduce very well.
Conclusions
We have performed long–range corrected density functional theory calculations in order to evaluate the electronic structure and luminescence properties in donor–acceptor (D–A˙) radicals based on the combination of a pyridoindole (xPyID) or carbazole donor and a trichlorotriphenylmethyl (TTM˙) acceptor. We were especially interested in understanding the impact of hybridization between charge-transfer (CT) and local-excitation (LE) states on the radical emissive properties. Our calculations show that the electronic structures of the TTM-1Cz and TTM-xPyID radicals investigated here follow the Aufbau principle. The introduction of an additional nitrogen atom into carbazole to form pyridoindole leads to a slight increase in the energies of the lowest doublet excited states while the variation in the D1 energy as a function of the nitrogen position within the pyridoindole moiety is small, which is consistent with experiment.The D1 state for all TTM-based D–A˙ radicals has a CT nature, which arises from electron transfer from the Cz or xPyID donor to the TTM acceptor; adding the donor moiety leads to an increase in the radiative rates by 3 to 6 times vs. the (isolated) TTM radical. The computed radiative rates for the TTM-xPyID radicals are similar to that of TTM-1Cz. As analysis of the relative contributions of the CT–GS and CT–LE hybridizations to the transition dipole moments underscores that the radiative rates in these radicals are mainly dominated by the electronic couplings between the CT state and the ground state even though the high-energy LE states can have a significant CT component.
The chemical modification of the donor unit from carbazole to pyridoindole generally leads to a decrease in the nonradiative decay rates due to the increased energy of the CT state; an exception is the TTM-γPyID radical in which the increase in the relaxation energy of the γPyID donor upon oxidation results in a significant increase in the nonradiative rate. This result highlights the major impact that electron-vibrational interactions have on nonradiative transitions and the need to select donor moieties with very small relaxation energies; this is usually a characteristic of large-size, fully conjugated rigid molecules.
We find that the impact of the CT–LE hybridization on the nonradiative rates is moderate for TTM-1Cz and TTM-γPyID while it plays an important role in the case of the other TTM-xPyID radicals. The negative effect of the CT–LE hybridization on nonradiative transitions is expected to increase for TTM-D radicals with CT states approaching the D1 state of the TTM. Therefore, the non-emissive D1 state of TTM and PTM represents an intrinsic limitation to achieve efficient high-energy emitters based on a D–A˙ motif involving the TTM or PTM radical cores.
We also note that, while the VCT–GS and VCT–LE electronic couplings have a strong impact on both radiative and non-radiative rates, their impact on the emitter PLQY [PLQY = kr/(kr + knr)] is expected to be less significant. For instance, in the absence of CT–LE hybridization, according to eqn (1), (2), and (5) the PLQY is independent of the electronic coupling and instead is determined by ΔμCT–GS. An increase in ΔμCT–GS, which can be obtained by increasing the effective distance between the D and A fragments, is predicted to enhance the PLQY. In addition, the increase in D–A distance should also reduce VCT–LE and consequently minimize the negative impact of the CT–LE hybridization on nonradiative transitions. To the best of our knowledge, such a design strategy for D–A˙ radicals has not been tested yet.
Finally, a major point that follows from our study is that, in order to accurately describe the radiative and non-radiative transitions of the D–A˙ radicals, it is essential to take into account the hybridizations between both the charge-transfer and ground states (CT–GS hybridization) and the local-excitation and charge-transfer states (LE–CT hybridization).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the College of Science of the University of Arizona. The authors acknowledge the use of the computing facilities of the Partnership for an Advanced Computing Environment (PACE) at the Georgia Institute of Technology and the assistance of the PACE team.References
- M. Mas-Torrent, N. Crivillers, V. Mugnaini, I. Ratera, C. Rovira and J. Veciana, Organic Radicals on Surfaces: Towards Molecular Spintronics, J. Mater. Chem., 2009, 19, 1691–1695 Search PubMed
.
- S. Kumar, Y. Kumar, S. K. Keshri and P. Mukhopadhyay, Recent Advances in Organic Radicals and Their Magnetism, Magnetochemistry, 2016, 2, 42 Search PubMed
.
- R. Gaudenzi, J. de Bruijckere, D. Reta, I. D. P. R. Moreira, C. Rovira, J. Veciana, H. S. J. van der Zant and E. Burzurí, Redox-Induced Gating of the Exchange Interactions in a Single Organic Diradical, ACS Nano, 2017, 11, 5879–5883 Search PubMed
.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Molecular Spins for Quantum Computation, Nat. Chem., 2019, 11, 301–309 Search PubMed
.
- K. Kato and A. Osuka, Platforms for Stable Carbon-Centered Radicals, Angew. Chem., Int. Ed., 2019, 58, 8978–8986 Search PubMed
.
- A. Dragulescu-Andrasi, A. S. Filatov, R. T. Oakley, X. Li, K. Lekin, A. Huq, C. Pak, S. M. Greer, J. McKay, M. Jo, J. Lengyel, I. Hung, E. Maradzike, A. E. DePrince, S. A. Stoian, S. Hill, Y.-Y. Hu and M. Shatruk, Radical Dimerization in a Plastic Organic Crystal Leads to Structural and Magnetic Bistability with Wide Thermal Hysteresis, J. Am. Chem. Soc., 2019, 141, 17989–17994 Search PubMed
.
- V. Diez-Cabanes, D. C. Morales, M. Souto, M. Paradinas, F. Delchiaro, A. Painelli, C. Ocal, D. Cornil, J. Cornil, J. Veciana and I. Ratera, Effect of the Molecular Polarizability of SAMs on the Work Function Modification of Gold: Closed-versus Open-Shell Donor–Acceptor SAMs, Adv. Mater. Technol., 2019, 4, 1800152 Search PubMed
.
- L. Ji, J. Q. Shi, J. Wei, T. Yu and W. Huang, Air-Stable Organic Radicals: New-Generation Materials for Flexible Electronics?, Adv. Mater., 2020, 32, 1908015 Search PubMed
.
- V. Gamero, D. Velasco, S. Latorre, F. López-Calahorra, E. Brillas and L. Juliá, [4-(N-Carbazolyl)-2,6-dichlorophenyl]bis(2,4,6-trichlorophenyl)methyl Radical an Efficient Red Light-Emitting Paramagnetic Molecule, Tetrahedron Lett., 2006, 47, 2305–2309 Search PubMed
.
- A. Heckmann, S. Dümmler, J. Pauli, M. Margraf, J. Köhler, D. Stich, C. Lambert, I. Fischer and U. Resch-Genger, Highly Fluorescent Open-Shell NIR Dyes: The Time-Dependence of Back Electron Transfer in Triarylamine-Perchlorotriphenylmethyl Radicals, J. Phys. Chem. C, 2009, 113, 20958–20966 Search PubMed
.
- Q. Peng, A. Obolda, M. Zhang and F. Li, Organic Light-Emitting Diodes Using a Neutral π Radical as Emitter: The Emission from a Doublet, Angew. Chem., Int. Ed., 2015, 54, 7091–7095 Search PubMed
.
- A. Obolda, M. Zhang and F. Li, Evolution of Emission Manners of Organic Light-Emitting Diodes: From Emission of Singlet Exciton to Emission of Doublet Exciton, Chin. Chem. Lett., 2016, 27, 1345–1349 Search PubMed
.
- J. Guo, X.-L. Li, H. Nie, W. Luo, S. Gan, S. Hu, R. Hu, A. Qin, Z. Zhao, S.-J. Su and B. Z. Tang, Achieving High-Performance Nondoped OLEDs with Extremely Small Efficiency Roll-Off by Combining Aggregation-Induced Emission and Thermally Activated Delayed Fluorescence, Adv. Funct. Mater., 2017, 27, 1606458 Search PubMed
.
- X. Ai, E. W. Evans, S. Dong, A. J. Gillett, H. Guo, Y. Chen, T. J. H. Hele, R. H. Friend and F. Li, Efficient Radical-based Light-Emitting Diodes with Doublet Emission, Nature, 2018, 563, 536–540 Search PubMed
.
- H. Guo, Q. Peng, X.-K. Chen, Q. Gu, S. Dong, E. W. Evans, A. J. Gillett, X. Ai, M. Zhang, D. Credgington, V. Coropceanu, R. H. Friend, J.-L. Brédas and F. Li, High Stability and Luminescence Efficiency in Donor–Acceptor Neutral Radicals not Following the Aufbau Principle, Nat. Mater., 2019, 18, 977–984 Search PubMed
.
- H. Abroshan, V. Coropceanu and J.-L. Brédas, Radiative and Nonradiative Recombinations in Organic Radical Emitters: The Effect of Guest–Host Interactions, Adv. Funct. Mater., 2020, 30, 2002916 Search PubMed
.
- A. Abdurahman, T. J. H. Hele, Q. Gu, J. Zhang, Q. Peng, M. Zhang, R. H. Friend, F. Li and E. W. Evans, Understanding the Luminescent Nature of Organic Radicals for Efficient Doublet Emitters and Pure-Red Light-Emitting Diodes, Nat. Mater., 2020, 19, 1224–1229 Search PubMed
.
- Z. Cui, A. Abdurahman, X. Ai and F. Li, Stable Luminescent Radicals and Radical-Based LEDs with Doublet Emission, CCS Chem., 2020, 2, 1129–1145 Search PubMed
.
- E. Cho, V. Coropceanu and J.-L. Brédas, Organic Neutral Radical Emitters: Impact of Chemical Substitution and Electronic-State Hybridization on the Luminescence Properties, J. Am. Chem. Soc., 2020, 142, 17782–17786 Search PubMed
.
- D. Velasco, S. Castellanos, M. López, F. López-Calahorra, E. Brillas and L. Juliá, Red Organic Light-Emitting Radical Adducts of Carbazole and Tris(2,4,6-trichlorotriphenyl)methyl Radical That Exhibit High Thermal Stability and Electrochemical Amphotericity, J. Org. Chem., 2007, 72, 7523–7532 Search PubMed
.
- V. Diez-Cabanes, G. Seber, C. Franco, F. Bejarano, N. Crivillers, M. Mas-Torrent, J. Veciana, C. Rovira and J. Cornil, Design of Perchlorotriphenylmethyl (PTM) Radical-Based Compounds for Optoelectronic Applications: The Role of Orbital Delocalization, ChemPhysChem, 2018, 19, 2572–2578 Search PubMed
.
- Z. Cui, S. Ye, L. Wang, H. Guo, A. Obolda, S. Dong, Y. Chen, X. Ai, A. Abdurahman, M. Zhang, L. Wang and F. Li, Radical-Based Organic Light-Emitting Diodes with Maximum External Quantum Efficiency of 10.6%, J. Phys. Chem. Lett., 2018, 9, 6644–6648 Search PubMed
.
- A. Abdurahman, Y. Chen, X. Ai, O. Ablikim, Y. Gao, S. Dong, B. Li, B. Yang, M. Zhang and F. Li, A Pure Red Luminescent β-Carboline-Substituted Biphenylmethyl Radical: Photophysics, Stability and OLEDs, J. Mater. Chem. C, 2018, 6, 11248–11254 Search PubMed
.
- E. Cho, V. Coropceanu and J.-L. Brédas, Electronic Structure of Multicomponent Organic Molecular Materials: Evaluation of Range-Separated Hybrid Functionals, J. Chem. Theory Comput., 2020, 16, 3712–3719 Search PubMed
.
- S. Hirata and M. Head-Gordon, Time-Dependent Density Functional Theory within the Tamm–Dancoff Approximation, Chem. Phys. Lett., 1999, 314, 291–299 Search PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- R. C. Hilborn, Einstein Coefficients, Cross Sections, f Values, Dipole Moments, and All that, Am. J. Phys., 1982, 50, 982–986 Search PubMed
.
- D. Toptygin, Effects of the Solvent Refractive Index and Its Dispersion on the Radiative Decay Rate and Extinction Coefficient of a Fluorescent Solute, J. Fluoresc., 2003, 13, 201–219 Search PubMed
.
- V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Charge-Transfer Electronic States in Organic Solar Cells, Nat. Rev. Mater., 2019, 4, 689–707 Search PubMed
.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Charge Transport in Organic Semiconductors, Chem. Rev., 2007, 107, 926–952 Search PubMed
.
- R. J. Cave and M. D. Newton, Generalization of the Mulliken-Hush Treatment for the Calculation of Electron Transfer Matrix Elements, Chem. Phys. Lett., 1996, 249, 15–19 Search PubMed
.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Advances in Molecular Quantum Chemistry Contained in the Q-Chem 4 Program Package, Mol. Phys., 2015, 113, 184–215 Search PubMed
.
- N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, Cclib: A Library for Package-Independent Computational Chemistry Algorithms, J. Comput. Chem., 2008, 29, 839–845 Search PubMed
.
- I. R. Gould and S. Farid, Radiationless Decay in Exciplexes with Variable Charge Transfer, J. Phys. Chem. B, 2007, 111, 6782–6787 Search PubMed
.
- M. Bixon, J. Jortner and J. W. Verhoeven, Lifetimes for Radiative Charge Recombination in Donor-Acceptor Molecules, J. Am. Chem. Soc., 1994, 116, 7349–7355 Search PubMed
.
- R. J. Kokes and P. H. Emmett, The Role of Hydrogen in Raney Nickel Catalysts, J. Am. Chem. Soc., 1959, 81, 5032–5037 Search PubMed
.
- M. D. Newton, Quantum Chemical Probes of Electron-Transfer Kinetics: the Nature of Donor-Acceptor Interactions, Chem. Rev., 1991, 91, 767–792 Search PubMed
.
-
N. S. Hush, Progress in Inorganic Chemistry, John Wiley & Sons, 1967 Search PubMed
.
- R. A. Marcus, Relation between Charge Transfer Absorption and Fluorescence Spectra and the Inverted Region, J. Chem. Phys., 1989, 93, 3078–3086 Search PubMed
.
- N. S. Hush, Homogeneous and Heterogeneous Optical and Thermal Electron Transfer, Electrochim. Acta, 1968, 13, 1005–1023 Search PubMed
.
- R. S. Mulliken, Molecular Compounds and their Spectra. II, J. Am. Chem. Soc., 1952, 74, 811–824 Search PubMed
.
- C. Creutz, M. D. Newton and N. Sutin, Metal–Lingad and Metal–Metal Coupling Elements, J. Photochem. Photobiol., A, 1994, 82, 47–59 Search PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc01702k |
| ‡ Dedicated to Professor Concepció Rovira and Professor Jaume Veciana, in honor of their seminal contributions to the fields of molecular electronics and magnetism. |
| This journal is © The Royal Society of Chemistry 2021 |