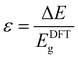Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational techniques for characterisation of electrically conductive MOFs: quantum calculations and machine learning approaches
Federica
Zanca†
a,
Lawson T.
Glasby†
a,
Sanggyu
Chong
 b,
Siyu
Chen
b,
Siyu
Chen
 c,
Jihan
Kim
b,
David
Fairen-Jimenez
c,
Jihan
Kim
b,
David
Fairen-Jimenez
 d,
Bartomeu
Monserrat
ce and
Peyman Z.
Moghadam
d,
Bartomeu
Monserrat
ce and
Peyman Z.
Moghadam
 *a
*a
aDepartment of Chemical and Biological Engineering, The University of Sheffield, Sheffield S13JD, UK. E-mail: p.moghadam@sheffield.ac.uk
bDepartment of Chemical and Biomolecular Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, South Korea
cCavendish Laboratory, University of Cambridge, J. J. Thomson Avenue, Cambridge CB3 0HE, UK
dThe Adsorption & Advanced Materials Laboratory (AAML), Department of Chemical Engineering & Biotechnology, University of Cambridge, Philippa Fawcett Drive, Cambridge CB3 0AS, UK
eDepartment of Materials Science and Metallurgy, University of Cambridge, 27 Charles Babbage Road, Cambridge CB3 0FS, UK
First published on 15th September 2021
Abstract
The customisability of metal–organic frameworks (MOFs) has attracted exponentially growing interest in the realm of materials science. Because of their porous nature, MOF research has been primarily focused on gas storage and separation. More recent investigations into MOFs have realised promising electronic characteristics suitable for applications in electrocatalysis, resistive sensing and energy storage. Despite high porosity and presence of organic linkers, — properties that contribute to the electrical insulating properties of most MOFs — several strategies have been developed to construct MOFs with high conductivity. These recent findings serve as strong encouragement that the incorporation of charge transport chemistries into MOFs leads to structures that exhibit conductive behaviour. However, our understanding behind the nature of conductivity in MOFs is not yet explicitly evident. The development of outstanding conductive MOFs would be greatly accelerated if we had an atomistic-level understanding of how low-energy charge transport pathways can be installed in MOFs. In this context, computational quantum mechanical methods can produce rich electronic structure details with sufficient accuracy to provide insights towards MOFs’ conductive behaviour. An emerging alternative design strategy is the use of machine learning to accelerate the way we screen and discover new conductive materials. In this review, we summarise the most widely used quantum mechanical techniques to characterise important band structure parameters and compare them with experimental measurements in the MOF literature. We also highlight the current state of the art in machine learning assisted screening of MOFs for their conductive properties and discuss the opportunities and challenges which lie ahead in this exciting field.
Introduction
Metal–organic frameworks (MOFs) are a diverse class of porous materials that consist of metal nodes connected by organic linkers.1,2 Despite the typically electrically insulating nature of these materials, recent research has been concerned with the development of electrically conductive and semiconductive MOFs for use in electronics applications such as sensors, transistors, resistors, quantum applications, and energy storage.3–7 From an application point of view, MOFs combining structural tunability, accessible porosity and high surface area as well as conductivity are highly desirable. However, such MOFs are not common due to the presence of redox-inactive organic linkers, hard metal ions, and high porosity: structural features that make it difficult to achieve efficient charge delocalisation. The generation of conductive MOFs is dependent on the existence of easy charge transport pathways that can be either achieved with extended π–π or π–d conjugation, following a “through-bond” approach, or with overlapping orbitals, following a “through-space” approach.8 Not only conductive, but semiconductive MOFs are also of interest, for example in the construction of transistors,9 as their conductivity and electronic properties can be regulated through interaction with guest molecules (e.g. chemical or redox doping) or variations in temperature. As a result, semiconductive materials with low band gap can still achieve high levels of conductivity after charge carrier alterations.10The experimental characterisation of conductivity in solid crystals including MOFs is carried out by measuring their conductivity, charge mobility and band gap. Such experimental efforts are often paired with computational analyses of materials to provide atomistic level insights into the conductivity mechanism. Computational characterisation is generally focused on electronic band structure calculations using density functional theory (DFT). One particularly important feature is the band gap prediction, which can be used to determine whether conductive behaviour can be expected from a given material. In general, materials with zero band gap are conductors, structures with band gap values between 0 and 3 eV are semiconductors, and those with larger band gaps above ∼4 eV are defined as insulators. In addition to band gap predictions, further information on the nature of materials conductivity can be obtained via analysis of the band structure and density of states (DoS). The band structure allows for the determination of electronic energy levels and the effective masses of the charge carriers, while the DoS represents the number of available states at each energy level that electrons are allowed to occupy.
In this review, we summarise the most common computational approaches to study MOFs’ electronic structure, as illustrated in Fig. 1. DFT calculations can be performed using periodic or non-periodic approaches i.e. the structure of the MOF can be considered either as a periodic crystal structure, or as a non-periodic molecule cut from the periodic geometry. We also describe details of the electronic structure calculations reporting the most widely used methodologies. Large structures with >500 atoms normally consume large amounts of computational resources and their optimisation is more difficult in reasonable timescales11 and, therefore, the choice of DFT approaches becomes essential to achieve optimum levels of accuracy while keeping computation time affordable.
 | ||
| Fig. 1 Flow chart of the computational approaches to analyse MOFs' band structure and electrical conductivity. | ||
Besides DFT approaches, an emerging research area is the use of machine learning (ML) algorithms for the characterisation and discovery of conductive MOFs. Several ML methods have been applied to MOFs with varying levels of success. Early ML algorithms were used in conjunction with MOFs to predict partial charges or metallicity, but more recently, novel techniques have emerged which search specifically for conductivity in MOFs via band gap prediction, attempting to bypass the need for computationally expensive DFT calculations. Towards the end of this review, we discuss some of the state-of-the-art ML approaches to discover new electrically conductive MOFs.
Quantum mechanical methods for characterisation of conductive MOFs
In this section, we give an overview of the most common computational techniques used to characterise the band structure of MOFs with insulating, semi-conducting and metallic behaviour. The study of electronic properties requires the use of quantum-mechanical-based approaches including wave function theory (WFT),12 density functional theory (DFT),13,14 or the many-body GW approximation,15 which will be briefly discussed in what follows. For a more detailed discussion on quantum calculations, we refer the reader to these publications.16–18 WFT is based on the solution of the electronic Schrödinger equation through electronic trial wave functions. This theory includes methods such as Hartree–Fock (HF),19,20 Moeller–Plesset (MP)21 perturbation theory, and coupled-cluster (CC).22 DFT is based on the principle that the ground state properties of the system can be described by the electron density.14 Practical calculations require the selection of an exchange–correlation (XC) functional, a basis set that can be localised or plane wave, and other numerical parameters which tune the accuracy and determine the computational resources required. Due to its balance between accuracy and computational cost, DFT is the most widely used method for periodic calculations and will be the focus of this review. The GW approximation is based on many-body perturbation theory and allows for estimation of the self-energy of a system in terms of the one-body Green's function (G) and the screened Coulomb interaction (W).23 This approximation is typically built on top of a single-particle theory, usually DFT. Therefore, it can be considered as an extension of DFT to obtain more accurate excited state properties. However, the associated computational cost makes it prohibitive for many studies, and it is mostly used on outstanding compounds that have already been characterised with DFT.With recent advancements in supercomputing power, a wide range of software packages for DFT calculations have been developed. For the structural and electronic characterisation of MOFs, the most popular software packages include, but are not limited to: VASP (Vienna Ab initio Simulation Package),24 CASTEP (CAmbridge Serial Total Energy Package)25 Quantum Espresso (Open-Source Package for Research in Electronic Structure, Simulation, and Optimization)26 and Cp2k.27 These software packages allow for periodic DFT calculations with plane wave (PW) basis sets. PW methods are generally the most common choice for periodic calculations because they converge smoothly to the target wavefunction. In contrast, localised basis sets can report convergence problems because of the similarity between different atoms’ functions: a problem caused by over-completeness.28 From a practical point of view, it is easier to set up PW calculations compared to localised basis sets as the accuracy is optimised by a single parameter controlling the size of the basis set, the cut-off energy. Many DFT studies based on localised basis sets can be found in the literature and are typically performed using software packages such as SIESTA (Spanish Initiative for Electronic Simulations with Thousands of Atoms),29 Crystal,30,31 Dmol3,32 Amsterdam Modelling Suite,33 DFTB+34 and Gaussian09.35
As mentioned earlier, DFT calculations require the selection of an XC functional which will influence the accuracy of the predicted properties. The simplest and least expensive functional is the local density approximation (LDA) which is based on the idealised model of the uniform electron gas.36 A more accurate class of functionals are those based on the generalised gradient approximation (GGA). GGA functionals, especially those based on the Perdew–Burke–Ernzerhof parametrisation (PBE37 or PBEsol38), as they usually provide the best compromise between accuracy and computational cost in large systems. Even though GGAs provide a more precise description of the system, they still present the same problems as LDA: both LDA and GGA approximations fail to accurately describe electron exchange and correlation.39 As a result, more precise functionals were devised to correct for this (we note that this error is usually relevant for electronic structure calculations, while it is negligible for geometry optimisations). Meta-GGA functionals are an extension of the GGA functionals. They have only been developed recently and are not always robust enough to be used without appropriate consideration for each calculation. For this reason, they are not often used for MOFs, especially in high-throughput calculations. Hybrid functionals are the most expensive and most accurate functionals that include a portion of HF exchange energy. This class of functionals is used for optimising MOFs only when highly accurate geometries are required, for example when small structural changes are significantly correlated to the band gap properties.40 For structures in which van der Waals interactions are significant, more accurate predictions can be obtained using correction schemes that take into account these interactions: for example the Grimme correction41 to highlight one amongst many.42 Another correction scheme is the Hubbard U method which can provide qualitative improvement for the electronic properties in systems with electronic correlation between partially filled d orbitals.43 In this case, the Coulomb interactions for localised electrons are not fully described by DFT, and instead the Hubbard U correction (DFT+U) accounts for it: this correction is expressed in terms of U and J, where U is the correction to the correlation energy, and J to the exchange energy. These are semi-empirical parameters that are usually estimated experimentally.
The trade-off between computational cost and accuracy can also be fine-tuned with different choices for the size of both the basis set and the k-point grid used to sample the Brillouin zone (BZ). The size of the basis set is defined by the cut-off energy, often set to 400–600 eV. Low cut-off energies require less computational effort but may prevent the electronic energy calculation from converging, or give incorrect results. The self-consistent field (SCF) convergence criterion itself is a parameter that is normally set to 10−7–10−5 eV per atom; higher values cause a drop in accuracy, while lower values force longer computations. The selection of these parameters is also affected by the choice of pseudopotential. Pseudopotentials are used to approximate the effect of the core electrons, meaning that the calculation focuses on the valence electrons, while the core electrons are considered “frozen” i.e. they are not involved in chemical bonding. Typical choices include ultrasoft pseudopotentials or the Projector Augmented Wave method (PAW).44 The k-point selection is another important aspect that directly relates to the resolution of the Kohn–Sham equation of the DFT calculation. The solution for periodic systems (e.g. ground state energy) requires integration over the BZ in reciprocal space. In practice, these integrals are approximated by sums that run over a finite number of k-points in the BZ, and there are several schemes for constructing a k-point set for the above approximation. A common choice is to adapt a regularly spaced k-point grid centred at the origin of the BZ (i.e. Gamma point). Most physical quantities are smoothly varying over the BZ, and therefore they converge quickly with respect to the size of the k-point grid. A computationally affordable k-point sampling density for geometry optimisation is about 0.05 2π Å−1, which means that given the large dimension of a typical MOF unit cell, it is acceptable to use only one k-point (Gamma only) for geometry optimisation. For accurate band gap calculations, a denser k-point grid with sampling density of 0.03–0.05 2π Å−1 can be used after the geometry relaxed structure is obtained.
Geometry optimisation
Electronic structure calculations normally begin with optimising the geometry of the material. Periodic optimisation of MOFs with large unit cells can be computationally expensive, in terms of both the simulation time and memory required. Moreover, when conducting large scale DFT investigations, the use of lower level DFT can be justified as a first-step screening approach, as high level DFT is typically reserved for small subsets of outstanding materials to maximise accuracy against available resources. Therefore, the choice of a DFT method should depend on the size of the materials observed, available computational resources as well as the number of structures to calculate. As previously described, the simplest XC functional is LDA, and even though it has been shown to provide sufficient optimisation of the structure, it is not a common choice because of the availability of more sophisticated approximations to the XC functional. Most of the time, PBE is considered reliable for geometry optimisation calculations without requiring too many computational resources. To improve its accuracy, it is often paired with modifications that include van der Waals interactions. For example, for the geometry optimisation of the Ni–HITP MOF synthesised by Sheberla and co-workers,45 the PBE-D2 functional was used to take into account strong van der Waals interactions between the MOF layers. This is a common approach, especially for bidimensional MOFs where π–π interactions are significant. The use of hybrid functionals for geometry optimisation is rare: the self-interaction error described in the previous section mostly affects the electronic structure calculations, therefore it would not be convenient to use an expensive hybrid functional for geometry optimisation, since the GGA functionals can already provide good results.When performing the geometry optimisation, another variable to consider is whether to optimise the crystal lattice parameters or only the internal atomic coordinates. For many MOFs, the experimentally determined crystal structure is reliable enough to permit fixing of the cell volume, avoiding further computational costs. Although this option is computationally faster, in certain cases the cell volume optimisation is not avoidable. For example, Ling and Slater40 analysed the band structure of the highly flexible M–MIL-53 (M = different metals) materials with large and narrow pore conformations. This MOF, a “breathing MOF”, has been shown to significantly change its conformation upon gas adsorption and/or varying pressure/temperature, thus changing its cell dimension and pore size. For such highly flexible MOFs, the geometry optimisation was carried out via accurate hybrid functional, HSE06,46 with relaxed lattice parameters.
To gain more insight into the electronic contributions of different MOF structural features, one can perform non-periodic DFT calculations on individual MOF molecular building blocks. The first important piece of information the building blocks could provide is the lowest energy conformation. For example, in the work of Sheberla et al.,45 the structure of HITP (hexaiminotriphenylene), a linker of a 2D Ni-based MOF was optimised using B3LYP level of theory calculations. The optimised HITP molecule was then inserted into the periodic structure in order to minimise the computational requirements, without reducing the accuracy of the calculations. Another useful property that can be obtained from MOF linkers is found via the characterisation of the highest occupied molecular orbital and the lowest unoccupied molecular orbital (HOMO–LUMO) gap. This approach is used when the interactions between building blocks are considered to manifest in the conductivity of the entire periodic structure: for example, in cases of strong π–π interactions between linkers, orbital overlap between functional groups, and/or the presence of guest molecules. For such studies, accurate geometry optimisation is a necessity. The basis set and the XC functional are usually selected by calculating specific properties (e.g. light absorption) and comparing the results obtained to known experimental values. Given that the geometry optimisation of non-periodic molecules is not as computationally intensive as periodic calculations, hybrid functionals (e.g. B3LYP)47,48 and meta-GGA functionals (e.g. M06)49 are often used. The most commonly used basis sets are the Pople basis sets50 with six primitive Gaussians comprising each core atomic orbital basis function (e.g. 6-311+G(d,p)). Non-periodic calculations are often performed using Gaussian09.
Band gap calculations
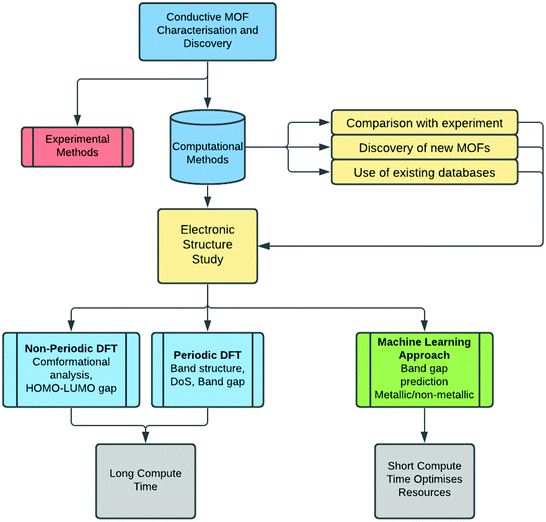
Once the MOF geometry is optimised, the band gap value can be obtained from the density of states (DoS) or from the band structure. The electronic band structure is a good way to investigate the energy states, and the band gap, as well as possible electronic transitions. MOFs that have localised charge often display flat electronic bands, and as a result, the conductivity is expected to be low, even for materials with no band gap. The band structure analysis can therefore be as important as the knowledge of the band gap itself. The DoS is a k-point point integrated version of the band structure, therefore it provides less information, but it is easier to interpret. It describes the number of electronic states available at different energy levels in a system, essential for determining the electron carrier concentrations and energy distributions within a semiconductor. When analysing the DoS, it is often useful to differentiate between individual contributions of atomic orbitals as this may provide more information about the underlying electron transport mechanism.In a recent contribution, Dou et al.51 reported a number of 2D conductive MOFs based on 2,3,7,8,12,13-hexahydroxy tetraazanaphthotetraphene (HHTT). Four MOFs were synthesised using the same HHTT linker and different metals (Ni, Cu, Co, Mg) which all showed zero band gap according to DFT predictions. The study of these MOFs is a good example of how the band structure and DoS can be analysed. As shown in Fig. 2, the band structure and the DoS are usually presented together. The band structure is centred on the Fermi level (see the red line in Fig. 2) and in this case, because the MOFs are essentially layered sheets, the band structure is divided into in-plane and out-of-plane (along the stacking direction) k-points. The DoS shows the contribution of each atom to the electronic states: neither MOF exhibits a band gap, indicating metallic behaviour. However, their electronic structures show different properties which can help further analyse their level of conductivity. Co–HHTT has low levels of DoS near the Fermi energy, indicating low availability of electrons, and it is mostly given by the C atoms. In Cu–HHTT, oxygen has a much higher contribution to the DoS, and the electronic bands of Cu–HHTT are more dispersed than those of Co–HHTT: an observation that can be related to higher conductivity, something that was indeed confirmed by experiments.
 | ||
| Fig. 2 Electronic band structures of Co–HHTT and Cu–HHTT. Both structures exhibit metallic electronic band structures, shown by the non-zero density of states at the Fermi level (indicated by the red line). The k-points are shown for the in plane and out of plane sections of both two-dimensional structures. Reproduced from ref. 51 with permission from Springer Nature, copyright 2020. | ||
Band gap calculations are often conducted using more accurate but computationally expensive hybrid functionals, usually Heyd–Scuseria–Ernzerhof HSE06 (or HSE0346). In fact, it is rather essential to use HSE when low band gap materials are studied.52 This is because LDA and GGA functionals severely underestimate band gap values. This underestimation arises from the self-interaction error39 caused by the use of approximations for the exchange and correlation energies. We note that the incorporation of substantial amounts of exact exchange (the nonlocal HF exchange) reduces this error. HSE functional can overcome this underestimation of the band gap. If HSE is used, a large number of k-points would require too much memory, so fewer k-points, or the Gamma-only approach is suggested. The HF contribution to the functional is what makes the hybrid functionals more expensive than low-level DFT calculations, therefore in some cases, different k-points are sampled for the HF and DFT approaches.53
As discussed above, system-specific correction schemes can be applied into DFT calculations. For example, the implementation of the Hubbard correction can optimise the Coulomb interaction potential which is not fully described by DFT. A good example of implementing DFT+U is the work of Zhang et al. where band gap values were calculated for MOF-74 materials.54 Values of U = 4 eV and J = 1 eV were selected according to previously published experiments,55 where the Hubbard correction was used on organometallic sheets. Another approximation algorithm to reduce the band gap error is the scissor operator used to match the computed band gap values with those obtained in experiments.56 In a recent work by Yang et al.,57 the band gap values (Eg) of UiO-66, -67 and -68 analogues were estimated using a scissor operator, whereby all computed values are scaled by a constant factor (1 + ε), written as:
| Eg ≈ (1 + ε)EDFTg |
We note that such error mitigation factors can be applied for MOFs with rather similar chemical properties, as the relative error is not comparable for MOFs with significantly different chemistries.
Finally, the GW15 approach is based on many-body perturbation theory where the generated energy levels are normally more reliable than DFT levels. Although the Kohn–Sham eigenvalues obtained from a DFT calculation can be interpreted as the energy needed to add or remove an electron from the system,58 strictly speaking, this is not true. DFT only finds the ground state electron density when the system is neutral. When adding or removing electrons, one charges the system and, consequently, other electrons redistribute to a new configuration. This is also why DFT tends to underestimate the band gap, as it does not consider the extra energy required to squeeze an extra electron into the real conduction band and the release of energy when removing an electron from the real valence band. We note that GW calculations are extremely computationally expensive – more expensive than hybrid functional DFT calculations – and are normally applied to MOFs with small unit cells. In this context, Huang et al.59 used G0W0, an approximation to GW, to find the corrections to the DFT band structure calculations. We refer the reader to the original publication for more details.
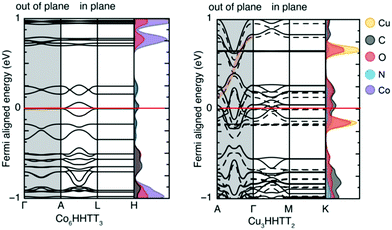
In addition to studying periodic structures of MOFs for band gap calculations, non-periodic building blocks of MOFs can be subjected to DFT investigations to gain insights into the electronic structure. One approach is the analysis of the HOMO–LUMO gap for studying the direct effect of organic linker modifications on band gap. This approach is useful for e.g. MOFs containing similar inorganic secondary building units but different linkers whose electronic properties can be calculated as individual molecules. Even though the HOMO–LUMO gap and the band gap cannot be directly compared, any correlation between different HOMO–LUMO gap values can tell if the linker has a significant influence on the overall band gap without the need to run prohibitively expensive periodic calculations. In a comparative study of different structural families of IRMOF-1, Pham et al.60 substituted some of the hydrogens in the BDC = benzenedicarboxylic acid linker with halogens and compared the DFT band gap values with those of HOMO–LUMO gap calculations from isolated linkers (Fig. 3a). Fig. 3b also reports the same study for IRMOF-20 in which the linker DHPDC (1,4-dihydropentalene-2,5-dicarboxylic acid) was modified using S and O. Interestingly, the trend of the HOMO–LUMO gap values is almost exactly that of the band gaps of the studied periodic MOFs.
 | ||
| Fig. 3 Conduction and valence bands (lines) and HOMO–LUMO values (red and blue dots) of halogen-substituted (a) IRMOF-1 and (b) IRMOF-20 with linker modifications. Reprinted with permission from ref. 60 Copyright (2014) American Chemical Society. | ||
With the help of post-processing DFT analysis tools, e.g. GaussView,61 one can generate and visualise molecular orbitals. Anh Tran et al.62 showed different metal-linker cluster models of ZIF-8 with their HOMO–LUMO orbitals (Fig. 4). In ZIF-8, the HOMO orbitals are localised on the imidazole rings, which are electron-rich, while the LUMO is localised on the Zn, which is electron deficient. Such visualisation techniques are useful in probing guest–host interactions in MOFs which can shed light on MOFs conductivity performance before and after e.g. gas adsorption in sensing applications.
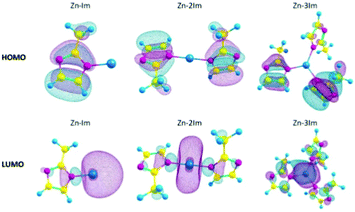 | ||
| Fig. 4 HOMOs and LUMOs of ZIF-8 cluster models with 1, 2 or 3 imidazole rings (Zn–Im, Zn–2Im, Zn3Im). Reproduced from ref. 62 with permission from Elsevier, copyright 2021. | ||
Band gap values: experiments vs. calculations
In Table 1, we present a comprehensive list of band gap values computed for MOFs and compare them with experimental values, where available. We envisage that this data establishes a baseline to compare the accuracy of low-level DFT methodologies (e.g. PBE), high-level hybrid functionals (e.g. HSE06), and experiments. Previous research suggests that the measured band gap values of MOFs can vary up to several tenths of an eV depending on the measurement technique, environment chemistry, synthesis, and post-treatment conditions, and the combination of such factors must be controlled for accurate and reproducible characterization.3,4,63,64 For example, several band gap values are reported for IRMOF-1 ranging from 3.4–4 eV, and these variations are attributed to the concentration of the reagents, synthesis temperature, and post-treatment methods.65,66 The presence of structural defects, a common attribute of MOFs chemistry, have also been reported to affect the band gap. Taddei et al.67 showed that the prototypical MOF, UiO-66, can be defect-engineered at different levels to generate a range of band gaps between 3.3 to 4.1 eV for the same material. In the same way, the choice of computational methods impacts band gap predictions and the quality of agreement with experiments. As mentioned earlier, PBE or other GGA functionals have a tendency to underestimate the band gap even when correction schemes are applied.43,52,68,69 Despite this underestimation, PBE functionals are frequently used for initial investigative calculations due to their scalability and lower computational cost, and are considered a sufficient benchmark to either motivate further high-level DFT calculations or experiments, or to disregard the material as a conductive candidate. It is worth noting that when large-scale calculations are carried out to identify conductive MOFs, such underestimation of bandgap may lead to false-positive band gap detection but not false-negatives. This means that the calculations will not discard “potentially” conductive materials at the exploratory screening stage. As shown in Table 1, in many MOF electronic studies such as those for Ni–HITP (HITP = hexaiminotriphenylene)70 and Cu–BHT (BHT = benzenehexathiol)71 materials, PBE predictions showed metallic behaviour corroborating experimental results. However, there are also a number of materials for which DFT calculations fail to accurately predict band gaps. In particular, the electronic structure for materials containing open-shell metals is difficult to be correctly described by most DFT functionals due to energy gaps between different spin states.72–75 We note that a hybrid DFT method is necessary to provide a more realistic description of the band gap especially in MOFs containing transition metals with unpaired electrons, e.g. Ti, V, and Fe.76–78Table 1 reports several HSE predicted band gaps that are within good agreement with experimental band gaps across a wide range of MOFs. A good example is UiO-66, where HSE calculation predicts a band gap of 4.03 eV, which is in excellent agreement with experimental values of ca. 3.94–4.07 eV. For the same structure, PBE underestimates the band gap by more than 1 eV (PBE band gap = 2.92 eV).53,67,79,80 All things considered, we encourage researchers working in the field to interpret both experimental and calculated band gap values for MOFs with appropriate considerations.| MOF name | Ref. code | Low-level DFT band gap (eV) | High level DFT band gap (eV) | Experimental band gap (eV) | Ref. |
|---|---|---|---|---|---|
| a Calculated with LDA. b Calculated with DFTB. c Calculated with B3LYP. d Calculated with PBE0. e Calculated with Grimme correction. f Calculated with Hubbard correction. g Calculated with PW-91. h Different modifications of similar MOFs reported in the paper. | |||||
| IRMOF-1 | SAHYIK | 3.4h | 4.6 | 3.4/4 | 81, 60 and 66 |
| IRMOF-8 | WORKOF | 2.91–2.83 | 3.27 | 82,83 | |
| IRMOF-7 | 2.77 | 83 | |||
| IRMOF-9 | WAKHUO | 3a | 3.42 | 82 | |
| M-IRMOF-10 | 2.8/3h | 84 | |||
| IRMOF-13 | 2.62 | 83 | |||
| M-IRMOF-14 | 2.4/2.5h | 85 | |||
| UiO-66 | RUBTAK, SURHEU03 | 2.92/2.8–2.2h | 4.03 | 4.07/3.94 | 53, 67, 79 and 80 |
| UiO-67 | WIZMAZ | 2.5–2.2h | 4.06/3.97c | 3.68/3.5 | 79 |
| UiO-68 | CEMBII | 2.4–2.2h | 3.2 | 79,86 | |
| HKUST-1 | FIQCEN | 1.8 | 3.8 | 3.6 | 87 |
| TCNQ@HKUST-1 | 1.4 | 88 | |||
| ZnBTC | 2.4h | 3.4 | 89 | ||
| NH2–ZnBTC | 1.9h | 2.8 | 89 | ||
| Ru3(BTC)2Cl1.5 | 2.06 | 90 | |||
| Cr–HITP | 1.15c | 91 | |||
| Cu–HITP | 0 | 92 | |||
| Ni–HITP | 0.12 | 0.2/0h | 92 | ||
| M–HHTT | 0 | 51 | |||
| Ln–HHTP | 0/1.2 | 93 | |||
| Cu–BHT | 0 | 71 | |||
| Fe2+/Fe3+(BDT) | 0.5 | 94 | |||
| Fe2+(BDT) | 2 | 94 | |||
| Fe–MOF-74 | 0.3–1.75fh | 1.38–2.44 | 2.1–1.3 | 54, 95 and 96 | |
| Co–MOF-74 | ORIWAP | 0.49–2fh | 2.76 | 54 and 97 | |
| Mg–MOF-74 | TODYUJ | 2.1 | 3 | 98 and 99 | |
| DSNDI–MOF-74 | 1.6 | 2.5 | 2.1 | 100 | |
| TTF–DSNDI–MOF-74 | 0.9 | 1.5 | 1 | 100 | |
| [CH3NH3][Ni(HCO2)3] | 1.8f | 101 | |||
| MFU-4 | IGOCOX | 2.52 | 3.43 | 3.08 | 102 and 103 |
| MIL-125 | 3.8 | 3.6 | 77 | ||
| Cu[Ni(PDT)2] | HIVPOU | 0.04 | 2.1de | 2 | 104 and 105 |
| MOF-177 | BABRII | 3.35b | 3.3 | 106 | |
| MOF–FMA | XOZXOA | 4.55 | 4.13 | 107 | |
| [Sr(HBTC)(H2O)]n | 2.3 | 102 | |||
| Zn2(TTFTB) | 1.75h | 108 | |||
| PCN-700 | RUBLAD | 4.19 | 109 | ||
| PCN-700–BDC | 4.11 | 109 | |||
| Ce–PCN-700–DHBQ | 2.1 | 109 | |||
| ZIF-67 | GITTOT02 | 1.98 | 110 | ||
| ZIF-8 | FAWCEN, OFERUN | 4.39 | 5.5–4.4c | 4.9 | 62, 98,1 05 and 111 |
| Zn5–BPDC | 2.93a | 3.36 | 82 | ||
| Zn–FDC | 1.87g | 112 | |||
| CPO-7 | 2.76 | 3.26 | 82 | ||
| Fe3(THT)2 | 0.35f | 113 | |||
| Co(THT)2 | 0 | 114 | |||
| Ni3(BHT)2 | 0 | 115 | |||
| Ni(HiIT) | 0 | 116 | |||
| Ni(HiAT) | 1.2 | 116 | |||
| MOF-650 | 0.9 | 117 | |||
| Zn-SURMOF 2 | 1.58b | 1.51d | 1.6 | 118 | |
| Cd–MOF-5 | 3.6 | 119 | |||
| NH2–MIL-101(Cr) | 2.65d | 2.3 | 120 | ||
| FeDSBDC | WUFXAY | 1.9 | 121 | ||
| Fe(1,2,3-triazolate) | 4.4–1.5h | 121 | |||
| Mn2(DSBDC) | 2.6 | 122 | |||
| Mn2(DOBDC) | 2.48h | 122 | |||
| Fe–MIL-53 | POJTUE | 2.734h | 2.72 | 40 and 123 | |
| Ce–UiO-66 | 3.04 | 2.8 | 124 | ||
| Ce–UiO-67 | 2.5 | 124 | |||
| Mn(BDT) | 0/1.54 | 125 | |||
| Ni(HIB) | 0 | 126 | |||
Let us further discuss notable materials from Table 1. An example of complementary use of PBE/HSE calculations and experiments is given by the Ni–HITP MOF and its analogues.92 This MOF was studied using the PBE functional and was found to have a 0.12 eV band gap. This small band gap prediction led to further calculations using HSE06, predicting a band gap of 0.2 eV, followed by the synthesis and experimental testing for sensing applications. This interesting discovery prompted substituition of the metals in M–HITP (M = metal), resulting in identification of additional conductive MOFs.91 This stimulated further work on structural analogues of the MOF with similar linkers, such as HHTT or HHTP (hexahydroxytriphenylene). All of these MOFs present bidimensional structures in which the high conductivity is attributed to in-plane conjugation between the linkers π orbitals and the metals’ d orbitals, or to the π–π stacking between the MOF planes: typical charge transfer pathways found in conductive MOFs developed so far. In another systematic study, Skorupskii et al.93 calculated the electronic structure of a number of lanthanide-based HHTP MOFs. Fig. 5 shows the band structure and DoS of La–HHTP. This MOF presents a band gap 1.5 eV in the in-plane direction, where the La orbitals show little conjugation with the ligand and contribute most to the valence and conduction band.
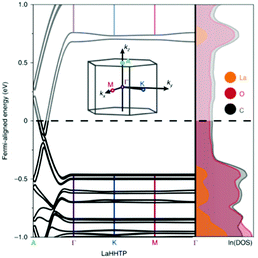 | ||
| Fig. 5 Band structure and DoS of La–HHTP. The inset shows the first Brillouin zone. Reproduced from ref. 93 with permission from Springer Nature, copyright 2020. | ||
On the contrary, due to the π–π stacking, there is no band gap along the out-of-plane direction and the bands are dispersed along the stacking direction of the 2D planes. When the metal is substituted for other lanthanides (Nd, Yb, Ho), the conductivity increases with the diminishing of the stacking distance, further evidence that the level of conductivity is attributed to the overlap of orbitals between the MOF planes.
Another group of MOFs worth highlighting is the M–MIL-53 (M = Ti, Fe, V, Sc, Cr, In, Ga, Al) isostructures.40 These MOFs are highly flexible and exhibit large pore (lp) and narrow pore (np) conformations under a variety of physical stimuli.127Fig. 6 compares the band gap values for eight MIL-53 materials (with different trivalent metal cations) in their lp and np forms. Given the presence of open shell metals, HSE06 calculations were deemed necessary to provide a faithful description of the electronic structures. Except for Ti–MIL-53, all other structures display considerable band gap changes when lp and np conformations are compared. In general, for all structures, lp M–MIL-53 conformations have a higher band gap compared to the np forms. For known MIL-53 materials, the difference in band gaps between np and lp conformations spans from 0.35 eV for V3+ to 1.39 eV for In3+. Narrow pores correspond to a smaller volume, which relates to stronger orbital overlap between neighbouring organic linkers and therefore producing lower band gaps. Given the ease of inducing structural transformations in MIL-53 by external stimuli, such as gas adsorption, temperature and pressure variations, their electronic properties can be tuned and exploited in applications such as resistive switching, phase-change memory, piezoresistor, gas sensing, and thermochromic materials.40
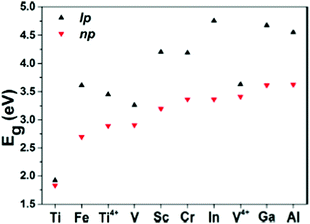 | ||
| Fig. 6 HSE06 predicted band gap values for M–MIL-53 with large pore (lp) and narrow pore (np). M = Different metals shown in the graph. Reprinted with permission from ref. 40. Copyright (2015) American Chemical Society. | ||
The electronic structure of UiO family of MOFs—characterised by the presence of the Zr6O4(OH)4 metal cluster—have been also studied in previous papers. In specific, UiO-66, -67 and -68 band structures have been systematically calculated after modifications of the linker and of the metal.79 UiO-66, 67, 68 are composed of the Zr–oxide cluster and BDC (benzene dicarboxylic acid), BPDC (biphenyl dicarboxylic acid) and TPDC (triphenyl dicarboxylic acid) linkers, respectively. The difference between these linkers is essentially the number of benzene rings in their ligands. These MOFs can exist in the hydroxylated and dehydroxylated forms which result in different band gap values as reported in Table 1. Another example is reported in Fig. 7, where UiO-66, modified with Ce, was recently synthesised and systematically functionalised.128 Such structural modification techniques enable systematic and clear band gap comparisons for MOFs with a similar parent structure but different functional groups. The study concludes that SH and NH functional groups are the most effective modifications to UiO-66(Ce) which narrows the band gap from 2.66 eV to 1 eV.
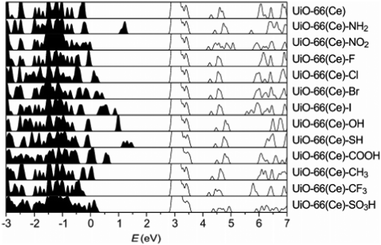 | ||
| Fig. 7 HSE06 calculated DoS of functionalised UiO-66(Ce). The conduction band minima are aligned. Reprinted with permission from ref. 128. Copyright (2018) American Chemical Society. | ||
We also note that the host–guest interaction is in certain MOFs accompanied by a formation of donor–acceptor pair between the MOF and the guest molecule, which may result in guest-induced electronic polarization and charge transfer. This means that the presence of e.g. residual solvent, adsorbed gas and doping agents can create new charge transport pathways influencing the band gap. Table 1 presents a few examples related to this phenomena. An important study is the work of Talin et al.129 on the infiltration of HKUST-1 by a redox-active molecule 7,7,8,8-tetracyanoquinododimethane (TCNQ) which resulted in significant increase in electrical conductivity of the material by six orders of magnitude to 7 × 10−2 S cm−1. UB3LYP/VTZP level of theory was applied for cluster models optimisation and PBEsol functional for periodic calculations to shed light on possible mechanism for the appearance of conductance in the doped material. The calculations showed that TCNQ molecules bridges HKUST-1's Cu dimer groups inserting unoccupied molecular orbitals into the MOF HOMO–LUMO gap, facilitating electronic coupling between HKUST-1 and TCNQ molecules.88 Similarly, another relevant case worth citing is the structure of MOF-74 analogue constructed from electron deficient naphthalenediimide (NDI) ligands with salicylic acid groups, DSNDI–MOF-74.100 The authors doped this structure with electron-rich tetrathiafulvalene (TTF) guests in order to suppress its band gap compared to that of the parent material. The electronic structure of DSNDI–MOF-74 was obtained via HSE06 and PBE calculations resulting in band gaps of 2.5 eV and 1.6 eV, respectively. More importantly, the HSE06 (PBE) predicted band gaps of TTF-doped DSNDI–MOF-74 were 1.5 (0.9) eV, nearly 1 eV smaller than that of the parent material. This reduction in the band gap was attributed to the formation of TTF/NDI stacks along the MOF promoting efficient π-donor/acceptor charge transfer interaction.
These case studies are examples of different computational approaches to modulate the band gap in MOFs. Organic linker functionalisation, metal substitution, guest molecules and variations in the cell volume or interlayer distance are all ways of tweaking the electrical conductivity. It is our hope that this overview of the reported band gap data can be used as a reference for future DFT studies and to further guide our intuition towards designing and discovering new electrically conductive MOFs.
Machine learning for characterisation of conductive MOFs
The aforementioned DFT calculations are essential to analyse the electronic structures of MOFs and their resulting conductivity, but they require considerable time and computational resources especially when high-throughput practices are considered. Computationally expensive many-atom MOFs could certainly benefit from the introduction of machine learning techniques,130 particularly for predicting electronic properties such as conductivity. Additionally, ML can help reduce the staggering ca. 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 existing MOF structures in the CSD MOF subset,2 to a more relevant and DFT manageable cluster of promising candidates and even accurately predict the band gap. Successful implementation of reliable ML MOF screening algorithms certainly has the potential to significantly expedite the discovery of new conductive MOFs.
000 existing MOF structures in the CSD MOF subset,2 to a more relevant and DFT manageable cluster of promising candidates and even accurately predict the band gap. Successful implementation of reliable ML MOF screening algorithms certainly has the potential to significantly expedite the discovery of new conductive MOFs.
The use of ML in the characterisation of MOFs electronic properties is still in its infancy. Initial ML approaches were developed to avoid high computational costs associated with DFT, even at PBE level. Presently, a number of ML models predict partial atomic charges of MOFs for the purpose of gas adsorption simulations.131,132 In a recent work by Raza et al., a message-passing neural network (MPNN) has been developed to assign partial point charges to each atom of a MOF structure with a computational cost ∼3 seconds per material. Additionally, Korolev et al.132 use a gradient boosting decision trees (GBDT) method, which provides feature importance, enabling one to study the contribution of individual features. Kancharpalli et al.133 trialled 4 new ML techniques, including random forest (RF) and linear regression (LR) approaches, notably on a set of neutral structures, in an attempt to further improve the reliability of ML. Techniques have also been demonstrated for covalent organic frameworks (COFs) as Deeg et al.134 developed a generic algorithm to derive accurate framework partial charges for COFs trained on a set of 98 structures. Semi-empirical methods are preferable with regards to computational cost; however, they often overestimate the value of point charges for certain elements. A commonly used training dataset is that compiled by Nazarian et al.135 which provides DFT calculated charge assignment for over 2000 MOFs. This set is publicly available for use as a supplement to the CoRE MOF database.136
The limitations of some of the studies thus far include many computationally developed MOFs due to the potential inclusion of rare features in hypothetical structures which are not present within this experimental training set (e.g. Se, Hf, Cs, Pu, and Ir appear in only one MOF). With most ML applications there is scope for improvement on any preliminary result if there are resources available to allow retraining on a more relevant, or diverse, dataset. Additional difficulties may occur due to periodicity and large MOF unit cells. However, the benefits of these emerging techniques include the ability to assign charges, or band gaps, to structures that contain thousands of atoms per unit cell, and which contain heavy elements (e.g. Tb and Eu) as these are often inaccessible for first-principle calculations. The ability to model structures containing these rare-earth elements widens the searching pool for desirable materials. As a result, there has been increased interest into the feasibility of ML techniques that can be applied directly to characterise MOFs conductive behaviour.
Using ML to predict the band gap of a material is not a new concept, there have been several studies into returning a reliable band gap prediction for inorganic materials.137–140 Applying ML in the search for conductive MOFs was first demonstrated in the work of He et al.141 At the time, a sufficiently large dataset of MOF band gap values was not available. As such, a transfer learning approach was taken, where four different ML models were trained to determine whether an inorganic solid was metallic or non-metallic. The training for the metallicity prediction of MOFs was performed upon the DFT+PBE-predicted band gaps of 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 inorganic materials.142 The models were then utilised in making predictions for a set of 2932 MOFs with unknown band gaps.135 In order to determine the metallic or insulating behaviour of a material, 45 material physical and chemical descriptors were generated. These included nine elemental properties: atomic number, group number, period number, electronegativity, electron affinity, melting temperature, boiling temperature, density, and ionisation energy. A flow diagram of the process used to predict these metallic MOFs is shown in Fig. 8. A band gap detected by the algorithm would trigger a binary output for metallic and non-metallic MOFs. A multi-voting scheme was implemented, where positive predictions by at least two models were required before structures would be accepted as metallic. After this initial screening, all positive metallic materials were then selected for further high-level DFT calculations.
300 inorganic materials.142 The models were then utilised in making predictions for a set of 2932 MOFs with unknown band gaps.135 In order to determine the metallic or insulating behaviour of a material, 45 material physical and chemical descriptors were generated. These included nine elemental properties: atomic number, group number, period number, electronegativity, electron affinity, melting temperature, boiling temperature, density, and ionisation energy. A flow diagram of the process used to predict these metallic MOFs is shown in Fig. 8. A band gap detected by the algorithm would trigger a binary output for metallic and non-metallic MOFs. A multi-voting scheme was implemented, where positive predictions by at least two models were required before structures would be accepted as metallic. After this initial screening, all positive metallic materials were then selected for further high-level DFT calculations.
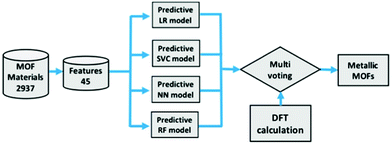 | ||
| Fig. 8 Screening process of MOFs using logistic regression (LR), support vector classification (SVC), neural network (NN), and random forest (RF) followed by high level DFT calculations. Reprinted with permission from ref. 141. Copyright (2020) American Chemical Society. | ||
The result of this investigation correctly predicted the existence of 6 metallic MOF structures from a total of 9 suggested candidates via ML. It is worth noting that these six materials are atypical of traditional MOFs due to a lack of hydrogen within the structures. These six structures were: (a) Mn8Re24C24S32N24 (EFOSUO), (b) Mn8Re24C24Se32N24 (EFOTEZ), (c) Mn8Re24C24Te32N24 (EFOTID), (d) Co4Hg4C16S16N16 (FEFZOF), (e) Cd2C8 (JUTCUW), and (f) Mn4Re12Te16C12N12 (NAMZIL). The authors reported a 67% accuracy rating, which could be increased by further ML training on exact MOF materials, to speed up the search for, and discovery of, metallic MOFs. An observation of the set notes that despite the presence of 196 Mn based MOFs, there were no positive metallic predictions. However, the presence of transition metal Re with Mn resulted in positive metallic predictions for all four occurrences of MOFs containing this metal cluster. It is also worth noting that due to the binary output technique, some potentially interesting semi-conducting MOFs are likely to have been screened out due to being non-metals, and having a non-zero predicted band gap. Additionally, the positive identification of a metallic structure by ML does not guarantee conductivity.
In an excellent contribution, Rosen et al.105 used several ML models for the prediction of DFT-computed band gaps, suggesting that it may be possible to avoid computationally expensive quantum-chemical calculations for screening thousands of structures. This approach attempts to rapidly predict DFT-computed band gaps from un-optimised experimental MOF crystal structures as a key contribution to the development of the new quantum-chemical database (QMOF) which contains not only values for band gaps, but partial charges, spin densities, bond orders, and other related structure properties. An initial dataset was constructed from 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 362 non-disordered MOFs taken directly from the CSD MOF subset, referred to as CSD-42362. This set was refined to entries with less than 150 atoms per primitive cell and as a result, a final set of 13
362 non-disordered MOFs taken directly from the CSD MOF subset, referred to as CSD-42362. This set was refined to entries with less than 150 atoms per primitive cell and as a result, a final set of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 058 non-duplicated structures were successfully optimised using periodic DFT+PBE VASP calculations to compute band gaps for all structures, returning values in the range of 0 eV to 6.45 eV. The QMOF database was developed for the function of training ML algorithms to predict the band gap of un-optimised structures, but may be used to aid development of many different structure–property predictors.
058 non-duplicated structures were successfully optimised using periodic DFT+PBE VASP calculations to compute band gaps for all structures, returning values in the range of 0 eV to 6.45 eV. The QMOF database was developed for the function of training ML algorithms to predict the band gap of un-optimised structures, but may be used to aid development of many different structure–property predictors.
Several techniques were used to approach this problem, notably the use of a crystal graph convolutional neural network (CGCNN143). CGCNN generates an approximate crystal graph for each MOF with nodes representing atoms, and edges as connecting bonds. This method of band gap prediction returned a mean absolute error (MAE) of 0.27 eV and an R2 value of 0.89. The result of this neural network technique for band gap prediction compared against more traditional DDEC computational methods can be seen in Fig. 9.
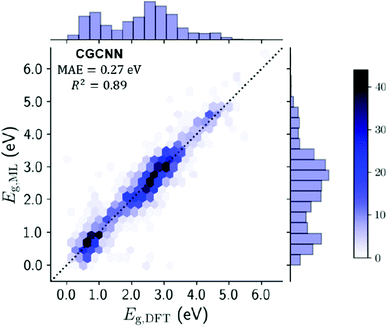 | ||
| Fig. 9 Testing set plot for the CGCNN model comparing the ML derived band gaps with the DFT derived band gaps. Gradient represents no. of MOFs in each hexagonal bin, with line of parity dashed. Histograms on x- and y-axes summarise band gap distribution. Reprinted with permission from ref. 105. | ||
The study reports a compute time of 7 minutes for 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 058 MOFs using the CGCNN model versus 1.5 million hours of computing time via DFT+PBE computation. This is an enormous resource-saving venture which can be used to create a set of preliminary structures for more detailed investigation in a single session using a laptop. Whilst it does require an initial computationally expensive database of post-calculation information to be created, the algorithm could be improved for use on new materials by increasing the size of the QMOF database. It would be expected that ML will be used for band gap predictions to be performed by researchers who are not familiar with, or do not have access to, high performance computing resources.
058 MOFs using the CGCNN model versus 1.5 million hours of computing time via DFT+PBE computation. This is an enormous resource-saving venture which can be used to create a set of preliminary structures for more detailed investigation in a single session using a laptop. Whilst it does require an initial computationally expensive database of post-calculation information to be created, the algorithm could be improved for use on new materials by increasing the size of the QMOF database. It would be expected that ML will be used for band gap predictions to be performed by researchers who are not familiar with, or do not have access to, high performance computing resources.
The performance of this CGCNN model can be compared to leading ML band gap models trained on other crystalline materials. The first CGCNN created by Xie et al.143 achieved a MAE of 0.39 eV on a training set of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 458 inorganic solids. Secondly, the MatErials Graph Network (MEGNet) created by Chen et al.144 reported a MAE of 0.38 eV on 36
458 inorganic solids. Secondly, the MatErials Graph Network (MEGNet) created by Chen et al.144 reported a MAE of 0.38 eV on 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 inorganic solids which was later improved to 0.33 after transfer learning. A global attention graph neural network (GATGNN) by Louis et al.145 pushed the average error achieved to MAEs of 0.32 eV and 0.31 eV using Open Quantum Materials Database (OQMD)142 and Materials Project146 datasets. Lastly, a weighted average smooth overlap of atomic positions (SOAP) based regression model by Olsthoorn et al.147 reported a MAE of 0.39 eV. Due to uncertainties in experimentally measured band gap values as previously discussed, an MAE less than 0.3 eV should be deemed as satisfactory for the purpose of screening materials, particularly if the nature of the search is aimed at semiconductors. Identification of low band gap MOFs enables the creation of a suitable set of candidates for trial in applications where electrical conductivity may be a necessity. The smaller pool of promising candidates can then be verified using higher level DFT calculations.
720 inorganic solids which was later improved to 0.33 after transfer learning. A global attention graph neural network (GATGNN) by Louis et al.145 pushed the average error achieved to MAEs of 0.32 eV and 0.31 eV using Open Quantum Materials Database (OQMD)142 and Materials Project146 datasets. Lastly, a weighted average smooth overlap of atomic positions (SOAP) based regression model by Olsthoorn et al.147 reported a MAE of 0.39 eV. Due to uncertainties in experimentally measured band gap values as previously discussed, an MAE less than 0.3 eV should be deemed as satisfactory for the purpose of screening materials, particularly if the nature of the search is aimed at semiconductors. Identification of low band gap MOFs enables the creation of a suitable set of candidates for trial in applications where electrical conductivity may be a necessity. The smaller pool of promising candidates can then be verified using higher level DFT calculations.
An additional method reported by Rosen et al. involved training models for composition-based features and representing these results using kernel ridge regression (KRR). The technique SOAP, was the best performer of all KKR models giving an MAE of 0.37 eV and R2 of 0.81, slightly underperforming compared to the CGCNN method. The 45-descriptor method used by He et al. was included in the study, but was well outperformed by both SOAP and CGCNN. Interestingly, the SOAP technique showed a significant improvement in learning rate compared to the top-performing CGCNN. However, the study was not extensive enough for these two methods to reach a learning plateau. There is scope, therefore, to extend these ML methods across a larger set of training materials, given sufficient time and information, with the aim of improving the accuracy of MOF band gap prediction.
Notable low band gap materials found via machine learning
Machine learning is capable of predicting band gaps not only for MOFs but for materials that exhibit some very similar properties. The CSD-42362 subset contains frameworks like RAXNEK, a Fe-containing material with a HSE06-D3(BJ) band gap of 1.06 eV.148 Many of these Fe-containing materials are yet to be investigated in depth to determine their potential as conductive materials but they are believed to be highly likely candidates for use in conductive applications.121 We note that a low band gap is not the only requirement for achieving good electrical conductivity. The presence of disorder and defects in experimentally synthesised structures can reduce the conductivity, in addition to unknown thermal contributions to the resistance.6 In general, it is ideal wherever possible to take into consideration both high-level DFT and experimental calculations when searching for conductivity.In the work of Rosen et al., the computational screening protocols performed on the CSD-42362 subset, predicted the lowest band gap material to be OTARUX, a 3D periodic structure. It was reported, after experimentation in 2011, that this is a conductive material that notably demonstrates unique non-linear current–voltage characteristics upon irradiation of Ag(DCl_2) crystals.149 A notable typical MOF structure flagged in this study was WAQMEJ,150 seen in Fig. 10, a 2-D non-catenated MOF, with a DFT+HSE06-D3(BJ) band gap value of 0.71 eV. In contrast, GUTYAW151 (a non-porous 3D periodic structure) was highlighted as the most insulating material, with a DFT+PBE predicted band gap of 6.27 eV which was then later refined to 8.36 eV after high level DFT+HSE06-D3(BJ) calculation.
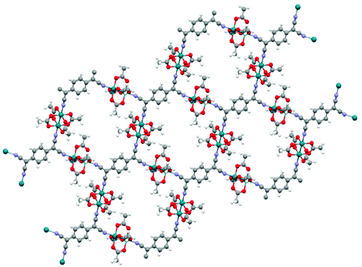 | ||
| Fig. 10 WAQMEJ, a rhodium oxide based MOF which expands into 2-dimensional sheets. with a reported band gap of 0.71 eV (key: red – O, turquoise – Rh, grey – C, white – H, purple – N). The Cambridge Structural Database.152 | ||
There is a wide-ranging selection of materials that have been screened out as potentially conductive due to their low band gaps, these include 7,7,8,8-tetracyano-quinodimethane (TCNQ) derivatives, fluorinated linker or metal fluoride species MOFs, polyoxovanadate-based MOFs, and molybdenum oxide-based frameworks. These notable structures are detailed in Table 2. The materials listed in this table were identified via ML, although their predicted band gaps have yet to be published for comparison with DFT results. These results suggest that transfer learning techniques are highly feasible for ML band gap prediction as there is significant, diverse, and successful identification of previously confirmed conductive structures. One of the more significant results of this work is the ability to search for a greater variety of semiconductive MOFs. The DFT+PBE predicted band gaps are reported for structures with solvents removed, as in the case of HIVPOU for example. However, the literature reports the band gap of a solvated material and concludes that the conductivity is very sensitive to the solvated state.104
| Name | CSD refcode | Metal | DFT+PBE predicted (eV) | Reported band gap (eV) | Method | Ref. | |
|---|---|---|---|---|---|---|---|
| Fe(bipydx)(Au(CN)2)2 | LOJLAZ | Fe/Au | 0.179 | 1.17 | HSE06-D3(BJ) | 105 and 153 | |
| Fe(squarate)(bpee)(H2O)2 | RAXNEK | Fe | 0.382 | 1.06 | HSE06-D3(BJ) | 153 | |
| Ag(DCl)2 | OTARUX | Ag | 0.045 | 149 | |||
| (TTF)[Rh2(CH3CO2)4]2TCNQ | WAQMEJ | Rh | 0.151 | 0.71 | HSE06-D3(BJ) | 150 | |
| Cu(TCNQCl2) | FAFJAZ | Cu | 0.009 | 0.032 | Experimental | 154 | |
| Ag(TCNQBr2) | BISVUW | Ag | 0.464 | 155 | |||
| Cu(Pz)(V4O10) | FEYCOE | Cu/V | 0.018 | 2.16 | Experimental | 156 | |
| Zn(C4H4N2)V4O20 | XEHYEP | Zn/V | 0.448 | 0.59 | Experimental | 157 | |
| Mo2O6(m-trtzH)(H2O)2 | LUYQUT | Mo | 2.963 | 158 | |||
| [ZnL(β-Mo8O26)0.5(H2O)]H2O | SASCIB | Zn/Mo | 1.947 | 159 | |||
| Cu[Ni(pdt)2] | HIVPOU | Ni/Cu | 0.039 | 2.1 | PBE0-D3 | 104 | |
| Cu[Cu(pdt)2] | WIHQEM | Cu | 0.240 | 0.193 | Experimental | 160 | |
| Cu2(bpe)(tfipa)(H2O) | MUQCEH | Cu | 0.924 | 161 | |||
| Co(p-F2-bdp) | HADMOR | Co | 0.762 | 162 | |||
| SIFSIX-1-Cu·C2D2 | EMEJAJ | Cu | 0.921 | 163 |
Conclusions
Computational studies are increasingly playing a fundamental role for the design and discovery of new functional materials. In the field of electrically conductive MOFs, most computational efforts have been focused on the calculation of band structure through quantum mechanical calculations. In this Review Article, we summarised the most common approaches to predict MOFs electronic properties with the aim of providing a global overview of the existing research and bringing together a unique record of preliminary knowledge for scientists working in the field of MOFs for electronic applications.Periodic DFT calculations are the most important and widely used methods in characterising electron charge transfer pathways, providing rich electronic structure details and datasets that provide atomistic insight into MOF conductivity. Band gap predictions are highly sensitive to the choice of DFT functional. DFT calculations using hybrid functionals (e.g. HSE06) often predict band gap values that are closer to experimental measurements, whereas LDA and GGA functional such as PBE show a strong tendency to underpredict the band gap. Measured band gap can also vary depending on the measurement technique, synthesis and post-treatment conditions. We, therefore, encourage theoreticians and experimentalists designing new conductive MOFs to collaborate more often, while considering the limitations of the techniques used.
A key advantage of computational modelling is the ability to design desirable structures before synthesis and laboratory testing. Usually, this is performed by either hypothesising entirely new materials or modifying existing structures to enhance the conductivity of MOFs. Effective structure modification strategies have been developed, in isolated case studies, by modulating the orbital overlap between metal cluster and organic ligands, the introduction of guest molecules as well as the incorporation of structural moieties to enhance redox activity and/or π⋯π interactions. Yet, there is clearly a lack of systematic investigation on the structural conductivity for a wide range of MOF chemistries which does not allow much rationalisation to develop a strong structure–conductivity correlation.
Given the rapidly increasing number of MOFs synthesised each year and advancements in computational resources, high-throughput DFT calculations are beginning to appear, typically employed to aid in the discovery of new conductive materials. Previous studies show that there is no “one size fits all” DFT functional that is suitable for accurate characterisation of band structure of MOFs and the application of such large screening practices will largely depend on computational resources available. An alternative approach is the application of machine learning to greatly speed up predictions of MOFs electronic properties. The use of such techniques allows us to narrow down the list of promising MOFs to a manageable number so that it is realistic to run high-level DFT calculations of their band structure. There are many positives to take away from the current foray into the use of machine learning, including the high predictive performance of both CGCNN and SOAP techniques used in band gap prediction. Although we are beginning to see an increase in the application of computer aided low computation searching, the full potential of machine learning for conductive MOFs discovery has yet to be realised. There is still an opportunity for further refinement for extensions of the training set to a chemically diverse set of MOFs as well as more efforts towards improvements in the accuracy of reference band gap calculations and improved methods to determine the uncertainty in the predictions. The availability of such comprehensive tools not only improves the power of DFT predictions but also increases the insight that it can provide to motivate experimentalists to design and discover new materials in the exciting field of electrically conductive MOFs.
Author contributions
F. Z. and L. G. contributed equally to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. Z. M. acknowledges funding from the Engineering and Physical Science Research Council (EPSRC) and the Cambridge Crystallographic Data Centre (CCDC) for the provision of PhD studentship funding to L. G. F. Z. thanks the University of Sheffield for funding her PhD program.References
- O. M. Yaghi, G. Li and H. Li, Nature, 1995, 378, 703–706 CrossRef CAS.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- L. Sun, M. G. Campbell and M. Dinca, Angew. Chem., Int. Ed., 2016, 55, 3566–3579 CrossRef CAS.
- I. Stassen, N. Burtch, A. Talin, P. Falcaro, M. Allendorf and R. Ameloot, Chem. Soc. Rev., 2017, 46, 3185–3241 RSC.
- A. Morozan and F. Jaouen, Energy Environ. Sci., 2012, 5, 9269–9290 RSC.
- L. S. Xie, G. Skorupskii and M. Dincă, Chem. Rev., 2020, 120, 8536–8580 CrossRef CAS.
- Y. Yan, R. Abazari, J. Yao and J. Gao, Dalton Trans., 2021, 50, 2342–2349 RSC.
- W.-H. Li, W.-H. Deng, G.-E. Wang and G. Xu, EnergyChem, 2020, 2(2), 100029 CrossRef.
- G. Wu, J. Huang, Y. Zang, J. He and G. Xu, J. Am. Chem. Soc., 2017, 139, 1360–1363 CrossRef CAS.
- A. M. Ullman, J. W. Brown, M. E. Foster, F. Leonard, K. Leong, V. Stavila and M. D. Allendorf, Inorg. Chem., 2016, 55, 7233–7249 CrossRef CAS PubMed.
- C.-K. Lin, D. Zhao, W.-Y. Gao, Z. Yang, J. Ye, T. Xu, Q. Ge, S. Ma and D.-J. Liu, Inorg. Chem., 2012, 51, 9039–9044 CrossRef CAS.
- D. Kedziera and A. Kaczmarek-Kedziera, in Handbook of Computational Chemistry, ed. J. Leszczynski, Springer, Netherlands, Dordrecht, 2012 DOI:10.1007/978-94-007-0711-5_3, pp. 55–93.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- M. S. a. L. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390–5413 CrossRef CAS.
- C. J. Cramer, Essentials of computational chemistry: theories and models, John Wiley & Sons, 2013 Search PubMed.
- A. D. Becke, J. Chem. Phys., 2014, 140, 18A301 CrossRef PubMed.
- J. Frank, Editorial Offices October, 1999.
- V. Fock, Z. Phys., 1930, 61, 126–148 CrossRef.
- D. R. Hartree, Math. Proc. Cambridge Philos. Soc., 1928, 24, 111–132 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- H. J. Monkhorst, Int. J. Quantum Chem., 2009, 12, 421–432 CrossRef.
- C. Friedrich and A. Schindlmayr, NIC Series, 2006, 31, 335 Search PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- T. D. Kuhne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schutt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borstnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Muller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Gloss, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef.
- B. Klahn, in Advances in Quantum Chemistry, ed. P.-O. Löwdin, Academic Press, 1981, vol. 13, pp. 155–209 Search PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- R. Dovesi, F. Pascale, B. Civalleri, K. a. H. Doll, M. Nicholas, I. Bush, P. D’arco, Y. Noel, M. Rerat and P. a. o. Carbonniere, J. Chem. Phys., 2020, 152, 204111 CrossRef CAS PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS.
- G. t. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- B. Hourahine, B. Aradi, V. Blum, F. Bonafe, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrica, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Kohler, T. Kowalczyk, T. Kubar, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Rezac, C. G. Sanchez, M. Sternberg, M. Stohr, F. Stuckenberg, A. Tkatchenko, V. W. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Computer program, 2016 Search PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- J. L. Bao, L. Gagliardi and D. G. Truhlar, J. Phys. Chem. Lett., 2018, 9, 2353–2358 CrossRef CAS.
- S. Ling and B. Slater, J. Phys. Chem. C, 2015, 119, 16667–16677 CrossRef CAS.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef.
- V. I. Anisimov, F. Aryasetiawan and A. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- D. Sheberla, L. Sun, M. A. Blood-Forsythe, S. Er, C. R. Wade, C. K. Brozek, A. Aspuru-Guzik and M. Dinca, J. Am. Chem. Soc., 2014, 136, 8859–8862 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- J. H. Dou, M. Q. Arguilla, Y. Luo, J. Li, W. Zhang, L. Sun, J. L. Mancuso, L. Yang, T. Chen, L. R. Parent, G. Skorupskii, N. J. Libretto, C. Sun, M. C. Yang, P. V. Dip, E. J. Brignole, J. T. Miller, J. Kong, C. H. Hendon, J. Sun and M. Dinca, Nat. Mater., 2021, 20, 222–228 CrossRef CAS PubMed.
- J. P. Perdew, Int. J. Quantum Chem., 1985, 28, 497–523 CrossRef.
- K. Hendrickx, D. E. Vanpoucke, K. Leus, K. Lejaeghere, A. Van Yperen-De Deyne, V. Van Speybroeck, P. Van Der Voort and K. Hemelsoet, Inorg. Chem., 2015, 54, 10701–10710 CrossRef CAS.
- Q. Zhang, B. Li and L. Chen, Inorg. Chem., 2013, 52, 9356–9362 CrossRef CAS PubMed.
- J. Zhou and Q. Sun, J. Am. Chem. Soc., 2011, 133, 15113–15119 CrossRef CAS.
- Z. H. Levine and D. C. Allan, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 4187 CrossRef CAS.
- L.-M. Yang, E. Ganz, S. Svelle and M. Tilset, J. Mater. Chem. C, 2014, 2, 7111–7125 RSC.
- R. Stowasser and R. Hoffmann, J. Am. Chem. Soc., 1999, 121, 3414–3420 CrossRef CAS.
- X. Huang, P. Sheng, Z. Tu, F. Zhang, J. Wang, H. Geng, Y. Zou, C.-a. Di, Y. Yi, T. Sun, W. Xu and D. Zhu, Nat. Commun., 2015, 6, 7480 CrossRef.
- H. Q. Pham, T. Mai, N.-N. Pham-Tran, Y. Kawazoe, H. Mizuseki and D. Nguyen-Manh, J. Phys. Chem. C, 2014, 118, 4567–4577 CrossRef CAS.
- R. Dennington, T. A. Keith and J. M. Millam, Gauss View, Version 5, Semichem Inc., Shawnee Mission KS, 2019 Search PubMed.
- V. Anh Tran, K. B. Vu, T.-T. Thi Vo, V. Thuan Le, H. H. Do, L. G. Bach and S.-W. Lee, Appl. Surf. Sci., 2021, 538, 148065 CrossRef CAS.
- J. Gascon, M. D. Hernández-Alonso, A. R. Almeida, G. P. M. van Klink, F. Kapteijn and G. Mul, ChemSusChem, 2008, 1, 981–983 CrossRef CAS PubMed.
- L. Sun, S. S. Park, D. Sheberla and M. Dincă, J. Am. Chem. Soc., 2016, 138, 14772–14782 Search PubMed.
- S. S. Kaye, A. Dailly, O. M. Yaghi and J. R. Long, J. Am. Chem. Soc., 2007, 129, 14176–14177 CrossRef CAS PubMed.
- J. Gascon, M. D. Hernandez-Alonso, A. R. Almeida, G. P. van Klink, F. Kapteijn and G. Mul, ChemSusChem, 2008, 1, 981–983 CrossRef CAS.
- M. Taddei, G. M. Schukraft, M. E. Warwick, D. Tiana, M. J. McPherson, D. R. Jones and C. Petit, J. Mater. Chem. A, 2019, 7, 23781–23786 RSC.
- B. Himmetoglu, A. Floris, S. De Gironcoli and M. Cococcioni, Int. J. Quantum Chem., 2014, 114, 14–49 CrossRef CAS.
- Á. Morales-García, R. Valero and F. Illas, J. Phys. Chem. C, 2017, 121, 18862–18866 CrossRef.
- E. M. Miner, S. Gul, N. D. Ricke, E. Pastor, J. Yano, V. K. Yachandra, T. Van Voorhis and M. Dincă, ACS Catal., 2017, 7, 7726–7731 CrossRef CAS.
- X. Huang, P. Sheng, Z. Tu, F. Zhang, J. Wang, H. Geng, Y. Zou, C. A. Di, Y. Yi, Y. Sun, W. Xu and D. Zhu, Nat. Commun., 2015, 6, 7408 CrossRef CAS PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz Jr, Phys. Rev. Lett., 1982, 49, 1691 CrossRef CAS.
- M. Reiher, CHIMIA, 2009, 63, 140–145 CrossRef CAS.
- K. Boguslawski, K. H. Marti, O. Legeza and M. Reiher, J. Chem. Theory Comput., 2012, 8, 1970–1982 CrossRef CAS PubMed.
- K. Boguslawski, C. R. Jacob and M. Reiher, J. Chem. Phys., 2013, 138, 044111 CrossRef PubMed.
- D. Danovich, S. Shaik and H. Chen, Comprehensive Inorganic Chemistry II: From Elements to Applications, 2013, vol. 9, pp. 1–57 Search PubMed.
- C. H. Hendon, D. Tiana, M. Fontecave, C. m. Sanchez, L. D’arras, C. Sassoye, L. Rozes, C. Mellot-Draznieks and A. Walsh, J. Am. Chem. Soc., 2013, 135, 10942–10945 CrossRef CAS PubMed.
- K. T. Butler, C. H. Hendon and A. Walsh, J. Am. Chem. Soc., 2014, 136(7), 2703–2706 CrossRef CAS PubMed.
- E. Flage-Larsen, A. Røyset, J. H. Cavka and K. Thorshaug, J. Phys. Chem. C, 2013, 117, 20610–20616 CrossRef CAS.
- L. Valenzano, B. Civalleri, S. Chavan, S. Bordiga, M. H. Nilsen, S. Jakobsen, K. P. Lillerud and C. Lamberti, Chem. Mater., 2011, 23, 1700–1718 CrossRef CAS.
- L.-M. Yang, G.-Y. Fang, J. Ma, E. Ganz and S. S. Han, Cryst. Growth Des., 2014, 14, 2532–2541 CrossRef CAS.
- C. K. Lin, D. Zhao, W. Y. Gao, Z. Yang, J. Ye, T. Xu, Q. Ge, S. Ma and D. J. Liu, Inorg. Chem., 2012, 51, 9039–9044 CrossRef CAS PubMed.
- A. Kuc, A. Enyashin and G. Seifert, J. Phys. Chem. B, 2007, 111, 8179–8186 CrossRef CAS PubMed.
- L.-M. Yang, P. Ravindran, P. Vajeeston and M. Tilset, RSC Adv., 2012, 2, 1618–1631 RSC.
- L. M. Yang, P. Ravindran, P. Vajeeston and M. Tilset, Phys. Chem. Chem. Phys., 2012, 14, 4713–4723 RSC.
- X. Ye and D. Liu, Cryst. Growth Des., 2021, 21(8), 4780–4804 CrossRef CAS.
- Z.-G. Gu, L. Heinke, C. Woll, T. Neumann, W. Wenzel, Q. a. F. Li, Karin, O. D. Gordan and D. R. Zahn, Appl. Phys. Lett., 2015, 107, 183301 CrossRef.
- C. H. Hendon and A. Walsh, Chem. Sci., 2015, 6, 3674–3683 RSC.
- G. D. Degaga, R. Pandey, C. Gupta and L. Bharadwaj, RSC Adv., 2019, 9, 14260–14267 RSC.
- T. Zhang, J.-W. Cao, X. Jiang, J. Chen, T. Wang and K.-J. Chen, Cryst. Growth Des., 2021, 21, 729–734 CrossRef CAS.
- M. E. Foster, K. Sohlberg, C. D. Spataru and M. D. Allendorf, J. Phys. Chem. C, 2016, 120, 15001–15008 CrossRef CAS.
- S. Chen, J. Dai and X. C. Zeng, Phys. Chem. Chem. Phys., 2015, 17, 5954–5958 RSC.
- G. Skorupskii, B. A. Trump, T. W. Kasel, C. M. Brown, C. H. Hendon and M. Dinca, Nat. Chem., 2020, 12, 131–136 CrossRef CAS PubMed.
- L. S. Xie, L. Sun, R. Wan, S. S. Park, J. A. DeGayner, C. H. Hendon and M. Dinca, J. Am. Chem. Soc., 2018, 140, 7411–7414 CrossRef CAS PubMed.
- L. Wei, B. Li, Q. Zhang, L. Chen and X. C. Zeng, J. Phys. Chem. C, 2016, 120, 26908–26914 CrossRef CAS.
- M. Märcz, R. E. Johnsen, P. D. Dietzel and H. Fjellvåg, Microporous Mesoporous Mater., 2012, 157, 62–74 CrossRef.
- J. A. Botas, G. Calleja, M. Sanchez-Sanchez and M. G. Orcajo, Int. J. Hydrogen Energy, 2011, 36, 10834–10844 CrossRef CAS.
- K. T. Butler, C. H. Hendon and A. Walsh, J. Am. Chem. Soc., 2014, 136, 2703–2706 CrossRef CAS PubMed.
- A. de Oliveira, G. F. de Lima and H. A. De Abreu, Chem. Phys. Lett., 2018, 691, 283–290 CrossRef CAS.
- Z. Guo, D. K. Panda, M. A. Gordillo, A. Khatun, H. Wu, W. Zhou and S. Saha, ACS Appl. Mater. Interfaces, 2017, 9, 32413–32417 CrossRef.
- S. G. Kang, Mater. Res. Bull., 2021, 138, 111239 CrossRef.
- M. Usman, S. Mendiratta and K.-L. Lu, Adv. Mater., 2017, 29, 1605071 CrossRef PubMed.
- P. Sippel, D. Denysenko, A. Loidl, P. Lunkenheimer, G. Sastre and D. Volkmer, Adv. Funct. Mater., 2014, 24, 3885–3896 CrossRef.
- M. L. Aubrey, M. T. Kapelewski, J. F. Melville, J. Oktawiec, D. Presti, L. Gagliardi and J. R. Long, J. Am. Chem. Soc., 2019, 141, 5005–5013 CrossRef CAS PubMed.
- A. Rosen, S. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. Notestein and R. Q. Snurr, Matter, 2021, 4, 1578–1597 CrossRef CAS.
- K. Leong, M. E. Foster, B. M. Wong, E. D. Spoerke, D. Van Gough, J. C. Deaton and M. D. Allendorf, J. Mater. Chem. A, 2014, 2, 3389–3398 RSC.
- J. H. Choi, Y. J. Choi, J. W. Lee, W. H. Shin and J. K. Kang, Phys. Chem. Chem. Phys., 2009, 11, 628–631 RSC.
- S. S. Park, E. R. Hontz, L. Sun, C. H. Hendon, A. Walsh, T. Van Voorhis and M. Dinca, J. Am. Chem. Soc., 2015, 137, 1774–1777 CrossRef CAS.
- S. Chong and J. Kim, Dalton Trans., 2020, 49, 102–113 RSC.
- H. Yang, X.-W. He, F. Wang, Y. Kang and J. Zhang, J. Mater. Chem., 2012, 22, 21849–21851 RSC.
- F. Wang, Z.-S. Liu, H. Yang, Y.-X. Tan and J. Zhang, Angew. Chem., 2011, 123, 470–473 CrossRef.
- D. Yan, R. Gao, M. Wei, S. Li, J. Lu, D. G. Evans and X. Duan, J. Mater. Chem. C, 2013, 1, 997–1004 RSC.
- R. Dong, P. Han, H. Arora, M. Ballabio, M. Karakus, Z. Zhang, C. Shekhar, P. Adler, P. S. Petkov, A. Erbe, S. C. B. Mannsfeld, C. Felser, T. Heine, M. Bonn, X. Feng and E. Canovas, Nat. Mater., 2018, 17, 1027–1032 CrossRef CAS PubMed.
- A. J. Clough, J. M. Skelton, C. A. Downes, A. A. De La Rosa, J. W. Yoo, A. Walsh, B. C. Melot and S. C. Marinescu, J. Am. Chem. Soc., 2017, 139, 10863–10867 CrossRef CAS PubMed.
- T. Kambe, R. Sakamoto, T. Kusamoto, T. Pal, N. Fukui, K. Hoshiko, T. Shimojima, Z. Wang, T. Hirahara, K. Ishizaka, S. Hasegawa, F. Liu and H. Nishihara, J. Am. Chem. Soc., 2014, 136, 14357–14360 CrossRef CAS PubMed.
- X. Sun, K. H. Wu, R. Sakamoto, T. Kusamoto, H. Maeda, X. Ni, W. Jiang, F. Liu, S. Sasaki, H. Masunaga and H. Nishihara, Chem. Sci., 2017, 8, 8078–8085 RSC.
- S. Yu, G. Jing, S. Li, Z. Li and X. Ju, Int. J. Hydrogen Energy, 2020, 45, 6757–6764 CrossRef.
- J. Liu, W. Zhou, J. Liu, I. Howard, G. Kilibarda, S. Schlabach, D. Coupry, M. Addicoat, S. Yoneda and Y. a. o. Tsutsui, Angew. Chem., Int. Ed., 2015, 54, 7441–7445 CrossRef PubMed.
- L.-M. Yang, P. Ravindran, P. Vajeeston, S. Svelle and M. Tilset, Microporous Mesoporous Mater., 2013, 175, 50–58 CrossRef.
- S. Abdpour, E. Kowsari, B. Bazri, M. R. A. Moghaddam, S. S. Tafreshi, N. H. de Leeuw, I. Simon, L. Schmolke, D. Dietrich and S. a. o. Ramakrishna, J. Mol. Liq., 2020, 319, 114341 CrossRef.
- L. Sun, C. H. Hendon, S. S. Park, Y. Tulchinsky, R. Wan, F. Wang, A. Walsh and M. Dinca, Chem. Sci., 2017, 8, 4450–4457 RSC.
- L. Sun, C. H. Hendon, M. A. Minier, A. Walsh and M. Dinca, J. Am. Chem. Soc., 2015, 137, 6164–6167 CrossRef CAS PubMed.
- J.-J. Du, Y.-P. Yuan, J.-X. Sun, F.-M. Peng, X. Jiang, L.-G. Qiu, A.-J. Xie, Y.-H. Shen and J.-F. Zhu, J. Hazard. Mater., 2011, 190, 945–951 CrossRef CAS PubMed.
- X. Qiu, Y. Zhu, X. Zhang, Y. Zhang, L. T. Menisa, C. Xia, S. Liu and Z. Tang, Sol. RRL, 2020, 4, 1900449 CrossRef CAS.
- M. Zhao, A. Wang and X. Zhang, Nanoscale, 2013, 5, 10404–10408 RSC.
- J. H. Dou, L. Sun, Y. Ge, W. Li, C. H. Hendon, J. Li, S. Gul, J. Yano, E. A. Stach and M. Dinca, J. Am. Chem. Soc., 2017, 139, 13608–13611 CrossRef CAS PubMed.
- J. Liang, X. Li, R. Xi, G. Shan, P.-Z. Li, J. Liu, Y. Zhao and R. Zou, ACS Mater. Lett., 2020, 2, 220–226 CrossRef CAS.
- X.-P. Wu, L. Gagliardi and D. G. Truhlar, J. Am. Chem. Soc., 2018, 140, 7904–7912 CrossRef CAS PubMed.
- A. A. Talin, A. Centrone, A. C. Ford, M. E. Foster, V. Stavila, P. Haney, R. A. Kinney, V. Szalai, F. El Gabaly and H. P. Yoon, Science, 2014, 343, 66–69 CrossRef CAS PubMed.
- S. Chong, S. Lee, B. Kim and J. Kim, Coord. Chem. Rev., 2020, 423, 213487 CrossRef.
- A. Raza, A. Sturluson, C. M. Simon and X. Fern, J. Phys. Chem. C, 2020, 124, 19070–19082 CrossRef.
- V. V. Korolev, A. Mitrofanov, E. I. Marchenko, N. N. Eremin, V. Tkachenko and S. N. Kalmykov, Chem. Mater., 2020, 32, 7822–7831 CrossRef.
- S. Kancharlapalli, A. Gopalan, M. Haranczyk and R. Q. Snurr, J. Chem. Theory Comput., 2021, 3052–3064 CrossRef PubMed.
- K. S. Deeg, D. Damasceno Borges, D. Ongari, N. Rampal, L. Talirz, A. V. Yakutovich, J. M. Huck and B. Smit, ACS Appl. Mater. Interfaces, 2020, 12, 21559–21568 CrossRef CAS PubMed.
- D. Nazarian, J. S. Camp and D. S. Sholl, Chem. Mater., 2016, 28, 785–793 CrossRef CAS.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, K. D. Vogiatzis, S. Ling, M. Milisavljevic, H. Zhang, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, J. Chem. Eng., 2019, 64(12), 5985–5998 CAS.
- P. Dey, J. Bible, S. Datta, S. Broderick, J. Jasinski, M. Sunkara, M. Menon and K. Rajan, Comput. Mater. Sci., 2014, 83, 185–195 CrossRef CAS.
- G. Pilania, J. E. Gubernatis and T. Lookman, Comput. Mater. Sci., 2017, 129, 156–163 CrossRef CAS.
- J. Lee, A. Seko, K. Shitara, K. Nakayama and I. Tanaka, Phys. Rev. B, 2016, 93, 115104 CrossRef.
- Y. Zhuo, A. Mansouri Tehrani and J. Brgoch, J. Phys. Chem. Lett., 2018, 9, 1668–1673 CrossRef CAS PubMed.
- Y. He, E. D. Cubuk, M. D. Allendorf and E. J. Reed, J. Phys. Chem. Lett., 2018, 9, 4562–4569 CrossRef CAS PubMed.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 1–15 Search PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef.
- S.-Y. Louis, Y. Zhao, A. Nasiri, X. Wang, Y. Song, F. Liu and J. Hu, Phys. Chem. Chem. Phys., 2020, 22, 18141–18148 RSC.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- B. Olsthoorn, R. M. Geilhufe, S. S. Borysov and A. V. Balatsky, Adv. Quantum Technol., 2019, 2, 1900023 CrossRef.
- S. C. Manna, E. Zangrando, J. Ribas and N. Ray Chaudhuri, Inorg. Chim. Acta, 2005, 358, 4497–4504 CrossRef CAS.
- T. Naito, A. Kakizaki, T. Inabe, R. Sakai, E. Nishibori and H. Sawa, Cryst. Growth Des., 2011, 11, 501–506 CrossRef CAS.
- Y. Sekine, M. Tonouchi, T. Yokoyama, W. Kosaka and H. Miyasaka, CrystEngComm, 2017, 19, 2300–2304 RSC.
- T. O. Salami, S. N. Patterson, V. D. Jones, A. Masello and K. A. Abboud, Inorg. Chem. Commun., 2009, 12, 1150–1153 CrossRef CAS.
- C. R. Groom and F. H. Allen, Angew. Chem., Int. Ed., 2014, 53, 662–671 CrossRef CAS PubMed.
- J. E. Clements, J. R. Price, S. M. Neville and C. J. Kepert, Angew. Chem., Int. Ed., 2014, 53, 10164–10168 CrossRef CAS PubMed.
- N. Lopez, H. Zhao, A. Ota, A. V. Prosvirin, E. W. Reinheimer and K. R. Dunbar, Adv. Mater., 2010, 22, 986–989 CrossRef CAS PubMed.
- Z. Zhang, H. Zhao, M. M. Matsushita, K. Awaga and K. R. Dunbar, J. Mater. Chem. C, 2013, 2, 399–404 RSC.
- S. Li, L. Zhang, B. Lu, E. Yan, T. Wang, L. Li, J. Wang, Y. Yu and Q. Mu, New J. Chem., 2018, 42, 7247–7253 RSC.
- B. Yan, J. Luo, P. Dube, A. S. Sefat, J. E. Greedan and P. A. Maggard, Inorg. Chem., 2006, 45, 5109–5118 CrossRef PubMed.
- A. B. Lysenko, G. A. Senchyk, K. V. Domasevitch, J. Hauser, D. Fuhrmann, M. Kobalz, H. Krautscheid, P. Neves, A. A. Valente and I. S. Gonçalves, Inorg. Chem., 2015, 54, 8327–8338 CrossRef PubMed.
- X.-L. Wang, S. Zhang, X. Wang, H.-X. Zhang, N. Xu and T.-J. Li, New J. Chem., 2017, 41, 2178–2185 RSC.
- Y.-L. Peng, T. Pham, P. Li, T. Wang, Y. Chen, K.-J. Chen, K. A. Forrest, B. Space, P. Cheng, M. J. Zaworotko and Z. Zhang, Angew. Chem., Int. Ed., 2018, 57, 10971–10975 CrossRef CAS PubMed.
- Y. Kobayashi, B. Jacobs, M. D. Allendorf and J. R. Long, Chem. Mater., 2010, 22, 4120–4122 CrossRef CAS.
- M. K. Taylor, T. Runčevski, J. Oktawiec, M. I. Gonzalez, R. L. Siegelman, J. A. Mason, J. Ye, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2016, 138, 15019–15026 CrossRef CAS PubMed.
- X. Cui, K. Chen, H. Xing, Q. Yang, R. Krishna, Z. Bao, H. Wu, W. Zhou, X. Dong, Y. Han, B. Li, Q. Ren, M. J. Zaworotko and B. Chen, Science, 2016, 353, 141–144 CrossRef CAS PubMed.
Footnote |
| † Equal contributions. |
| This journal is © The Royal Society of Chemistry 2021 |