Open Access Article
Open Access ArticleWhispering gallery mode resonators in continuous flow: spectral assignments and sensing with monodisperse microspheres†
Bryan C.
Paulus
 ,
Jenny K.
Banh
,
Jenny K.
Banh
 ,
Kirk D.
Rector
,
Kirk D.
Rector
 ,
Benjamin W.
Stein
,
Benjamin W.
Stein
 and
Laura M.
Lilley
and
Laura M.
Lilley
 *
*
Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA. E-mail: lilley@lanl.gov
First published on 4th April 2022
Abstract
Whispering gallery mode resonator (WGMR) microspheres yield highly structured optical spectra that are extremely sensitive to their environment and are of intense interest for use in a variety of sensing applications. Many efforts to leverage the unique sensitivities of WGMRs have relied on stringent experimental requirements to correlate specific spectral shifts/changes to an analyte/stimulus such as (1) precise positional knowledge, (2) reference spectra for each microsphere, and (3) high mechanical stability. Consequently, these factors can hinder adequate mixing or incorporation of analytes and can create challenges for remote sensing. This work describes a continuous flow technique for measuring whispering gallery mode (WGM) spectra of dye-doped microspheres suspended in solution and an accompanying analysis scheme that can extract the local refractive index without a priori knowledge of the microsphere size and position and without a reference spectrum. This measurement technique and analysis scheme was shown to accurately measure the refractive index of a range of alcohol and saline solutions down to a few thousandths of a refractive index unit (RIU). Additionally, a spectral clustering algorithm was applied to the fit results of two batches of microspheres suspended in water and was able to accurately assign spectra back to either batch of microspheres.
Introduction
Optical sensors have become an integral part of modern society, from raw materials production to fibre-optic communication. Driven by the need for miniaturized devices, many advances in optical sensing are focused on ways to amplify output signal as a function of input light. Microspherical whispering gallery mode resonators (WGMR) are a promising (and partially realized)1 technology for optical sensors. Trapping light within their spherical cavities via total internal reflection produces intense, sharp resonances—whispering gallery modes (WGMs)—that are highly sensitive to the resonator morphology and the contrast in refractive index between them and their environment.2 The outstanding sensitivity of WGMRs to chemical environment has been exploited for a variety of chemical3,4 and biological5–8 sensing applications. Further, they have been exploited to monitor a variety physical parameters including temperature9,10 and pressure.11,12 Many of these applications require that light is coupled directly into the resonator via a precisely aligned fibre taper such that spectra can be acquired both before and after the stimuli have been applied (referencing). This experimentally constrains WGM measurements by necessitating (1) high mechanical stability of the system to prevent movement of the light-coupling fibre taper and (2) the ability to retrace the location of specific WGMRs. These requirements make it challenging to adequately and efficiently incorporate the desired analyte onto the WGMR substrate and means that the user must have enough technical proficiency to correct finicky fibre alignment extempore. Alternatively, doping microspheres with a broadly emitting dye that can couple into WGMs offers numerous advantages. Dye mediated excitation removes many of the technical barriers inherent to fibre coupled systems while allowing for more efficient mixing of analyte and substrate. Furthermore, the easily excited dye opens the door for remote sensing.Towards this end, there have been several studies seeking to leverage dye-doped microspheres (active resonators) for sensing applications. With knowledge of the size distribution of a batch of commercial microspheres, Zijlstra et al.13 were able to use active WGMRs for refractometry without knowing the size of individual microspheres. However, some aspects of their analysis scheme rely on having a narrow size distribution, a quality not necessarily shared amongst all batches of WGMR microspheres. Weller et al.14 were able to determine the size of individual microspheres directly from their spectra but only when the microspheres were in air and they were not able to perform refractometry at the same time. Pang et al.15 utilized an approach whereby shifts in WGMs of individual resonators were referenced against resonance frequencies in solutions of known refractive index. Consequently, this requires that each sphere position remain traceable from one solution to the next. Perhaps most similar to the efforts described herein, Allen and co-workers have developed a reference-free analysis scheme for WGM spectra collected in free flowing solution7,8 or alongside a flow cytometry setup.16 In their analysis scheme, the entirety of the observed WGM spectral profile over a fixed wavelength region is compared to predicted spectra obtained from Chew's formalism of Mie theory.17,18 The technique described therein was successful both at identifying the refractive indices of various alcohol solutions and discriminating between biological analyte absorption and changes to the homogenous refractive index. However, the use of an area matching approach for spectral analysis means the fit results are sensitive to noise in the data and imperfections in the isolation of WGMs from the background emission spectrum.
Herein, we demonstrate a reference-free, continuous flow WGM measurement technique that is performed on free-flowing suspensions of microspheres in a range of solutions and highlight an analysis scheme whereby both individual microspheres and their surrounding environment can be characterized simultaneously without a priori knowledge of individual microsphere size or their size distribution. Further, we illustrate that microspheres of multiple types can be identified and characterized concurrently.
Methods
Continuous flow apparatus and sample measurements
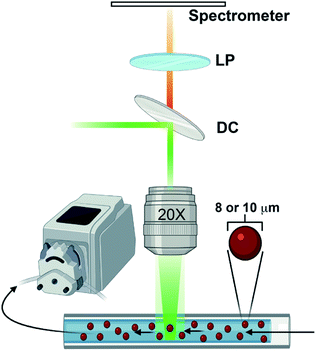
Emission spectra were acquired with a WITec Alpha 300R Raman microscope using the 532 nm laser line from a doubled Nd:Yag WITec laser fibre coupled through a Zeiss EC Epiplan 20× 0.4 NA objective. The resulting luminescence was collected by the objective in reflection geometry and delivered through a 100 μm fibre to a WITec UHTS300 spectrometer. The signal light was dispersed with a 600 g mm−1 500 nm blaze grating and recorded with an Andor Newton CCD camera thermoelectrically cooled to −60 °C. The instrument was controlled with WITec Control software v1.6 and saved to a standard personal computer. A small quantity of nominally 8 μm diameter polystyrene microspheres (Duke Scientific cat no. 36-3) or 10 μm polystyrene carboxylated microspheres (Spherotech cat no. CFP-10056-2) was suspended in a liquid of interest, loaded into a 100 μL borosilicate glass capillary tube (Corning cat no. 7099-S), and placed under the microscope objective. The sample was irradiated with roughly 10 mW of the 532 nm laser that was defocused enough to cover the entire cross-section of the capillary tube. The liquid suspension was drawn through the capillary tube via a peristaltic pump (ISAMATIC MCP) with a flow rate of 39.6 μL min−1 as spectra were acquired with 500 ms exposure times. A diagram of the experimental setup is shown in Fig. 1.Under optimal conditions that accounts for both the flow rate and exposure time, this continuous flow method can easily acquire ∼30 useable, unique spectra in roughly three minutes. When there is a low contrast in the refractive indices of the sphere material and its surroundings, however, there can be a significant quenching of the WGM intensity, making it more difficult to collect high quality spectra. Regardless, this method is considerably faster than finding an equivalent number of useable individual spheres sequentially by hand on a microscope slide. Since measurements are taken continuously, regardless of whether or not microsphere emission is being captured, adequate data processing schemes are needed to both parse out only the more useful data slices and prepare them for detailed analysis.
Data pre-processing
All data processing and analyses were performed in MATLAB software version 2020b on a personal computer. Once the data were uploaded, any baseline offset was removed by subtracting the average of the first 30 pixels in the spectral region blocked by the long pass filter and the data were processed using a Whittaker smoothing algorithm19 to reduce noise. Next, an initial data rejection step was implemented that discarded data which have a smoothed 2nd derivative with peaks below a certain specified, instrument dependent threshold magnitude. This removes spectra that are smooth and totally devoid of visible, sharp WGM resonances. Following data rejection, endpoints were automatically selected as the first point on each side of the spectrum that lay above a specified threshold value which should be optimized for the particular instrument in use. Next, an asymmetric least squares (AsLS) Whittaker smoothing algorithm20 was employed to fit the background emission spectrum that consists of any emission that is not coupled to WGMs. To perform this procedure, a Whittaker smoothing operation is first applied to the data according to eqn (1). Here, y and z are both column vectors containing the initial and smoothed data.| z = (W + λDTD)−1Wy | (1) |
The data weight matrix, W, is a square diagonal matrix containing the weight of each data point, wi, along the diagonal. Initially, each wi are set to one.
 | (2) |
The second order difference matrix, D, is shown in eqn (2). Finally, λ is a scalar smoothing parameter that adjusts the balance between how smooth the resulting profile is and how closely it resembles the original data. In this work, λ was set to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Once the smoothed profile has been generated, the data weights were redefined using an asymmetry parameter, p, as shown in eqn (3). Generally, it is recommended to set p between 0.001 and 0.1.20 In this work, p was set to 0.001.
000. Once the smoothed profile has been generated, the data weights were redefined using an asymmetry parameter, p, as shown in eqn (3). Generally, it is recommended to set p between 0.001 and 0.1.20 In this work, p was set to 0.001.
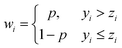 | (3) |
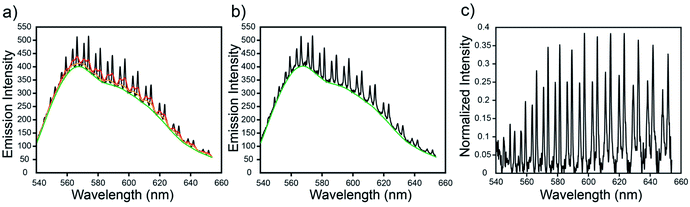
Eqn (1) was then solved again to acquire a new baseline, z. This process was repeated until the baseline stops changing (typically after around 10 iterations) or a set number of iterations (50) have completed. The baseline was subsequently subtracted from the total emission spectrum to isolate just the WGMs of interest. Each WGM was then rescaled by dividing by the newly found baseline. An example of this procedure is shown in Fig. 2.
In some instances, a single microsphere would linger in the detection region resulting in multiple acquisitions of the same spectrum. To identify these scenarios, the spectral similarity of each of the baseline corrected spectra were assessed via two methods: an area based metric commonly used for matching Raman spectra called the hit quality index (HQI)21 and a metric based on peak locations similar to an algorithm developed by Hansen and Smedsgaard,22 here referred to as the peak proximity index (PPI). Details of both similarity indices are included in the ESI.† The remaining WGM spectra were inspected with the aid of the HQI and PPI indices and a set of spectra was selected to save and further analyse. In the case where microspheres are stuck to the glass capillary tube in the detection region, the tube was either flushed with neat solvent or replaced with a clean tube.
Spectral fitting
A spectral fitting program written in MATLAB was used to assign peaks in the WGM spectrum to first order transverse electric (TE) or transverse magnetic (TM) modes. WGM resonances were labelled according to associated quantum numbers, l and i that determine their nodal structure, where l, the angular quantum number, determines how many angular nodes appear in the wave function around the circumference of the spherical resonator, and i, the radial quantum number, determines the number of radial nodes in the WGM wave function. In this work, only the most intense, first order (i = 1), modes were fit. From Mie theory, WGM resonance frequencies can be determined from a power series of ν−1/3 (with ν = l + 1/2) as seen in eqn (4):15,23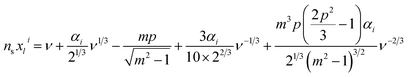 | (4) |
In general, the size and refractive indices of the spherical resonator and their surroundings cannot be explicitly solved for using eqn (4). Instead, the contrast ratio and the product of the resonator size and refractive index are attainable. If any of a, ns, or ne are known, however, the other two can be readily solved for. Thus, by calibrating against a solution of known refractive index, both the size and refractive index of individual microspheres can be discerned. In this work, ∼8 μm diameter dye-doped (Nile red) polystyrene microspheres from Duke Scientific (cat. no. 36-3) were calibrated against 18 MΩ deionized water (ne = 1.3324 at 589 nm)24 to determine an effective ns for this batch of spheres that could be used to parse out a and ne in future samples. It should be noted that the refractive index of a substance is inherently wavelength dependent, yet in this work a single value for the spherical resonator, the solution that it is suspended in, and the contrast ratio between those two quantities was used. Since the refractive index of the sphere material was referenced against the refractive index of water at 589 nm (the sodium D line), all further refractive indices obtained were reported against their literature values at 589 nm. The choice of reference wavelength, however, is arbitrary.
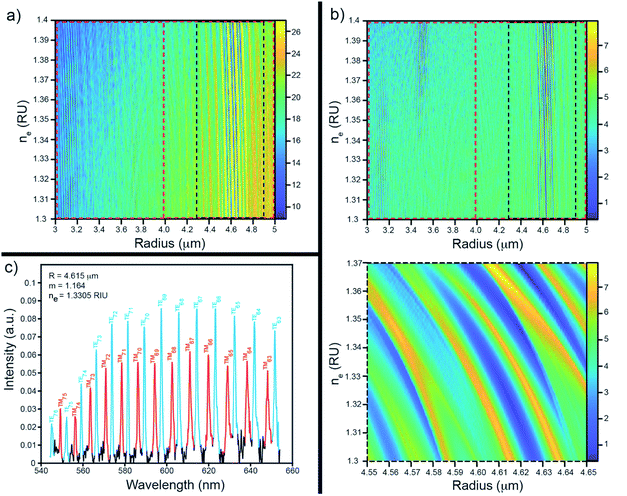
Since the refractive index of an unknown solution or the exact size of individual microspheres generating the WGM spectra are not known a priori, the first step to extracting relevant information from their spectra was to assign resonances to a particular mode type (i.e., TE or TM) and to their corresponding angular quantum number, l. To accomplish this, the position of each resonance was simulated for a range of l across an initial grid of sphere radii and plausible contrast ratios for a specified ns. Separately, the peaks in the experimental spectrum were located using a peak finding algorithm developed for MATLAB by Yoder.25 The predicted peaks were then uniquely matched to the observed peaks in the experimental spectrum (i.e. each peak in the observed spectrum may only be matched to a single peak in the predicted spectrum) to within a specified tolerance (2 nm in this study). The quality of the assignments were then judged by both the number of peaks from the experimental spectrum that could be matched and the error as defined by the sum of the square of the differences in their peak locations in nanometres. The set of (a, ne) pairs that yielded the highest number of matched peaks was searched for the lowest error to assign the best fit for that grid of radii and contrast ratios. If either a specified number of peaks were not yet matched or the error was above a specified threshold, the process was repeated over a new grid of (a, ne) pairs in which the new set of a searched over contained larger radii. This process was continued until an optimum (a, ne) pair was found that matched a sufficient number of peaks. From this point, a new, smaller range of a with finer point density were searched surrounding the previous optimum value and the resulting set of quantum numbers and their associated (a, ne) ordered pair was then fed into a non-linear solver to obtain a more refined radius and environmental refractive index. When the type of spheres under investigation and their RI was not known, a similar fitting procedure was performed to search instead for the resonator RI and radius product and the contrast ratio. In the latter case, the RI of the sphere material was not used as an input (Fig. 3).
Spectral clustering
Spectral clustering of the fit results was performed on data separately collected on two batches of microspheres (Duke Scientific cat no. 36-3 and Spherotech cat no. CFP-10056-2). Clustering was performed in a homebuilt MATLAB program based on the number of shared nearest neighbours spectral clustering (SC-nSNN) algorithm developed by Ye and Sakurai.26Broadly speaking, the goal of spectral clustering is to reduce the dimensionality of data by partitioning a set of n data points X = {x1, x2, …, xn} of arbitrary dimensionality into K clusters. To achieve this, a similarity graph of the data was first generated that depicts nodes (the data) and edges that connect them based on how similar they are. The similarity graph was then used to generate matrices that encode the connectivity of each data point and the corresponding eigenvalues and eigenvectors were used to identify clustering. In this work, data was clustered based on their (ns × a, m) ordered pairs. This algorithm first constructs a similarity matrix, S, based on the set of shared nearest neighbours of each pair of points, with a Euclidean distance metric. In simple terms, it measures the distance “the way the crow flies” between points. For Ni, the set of nearest neighbours of point xi that does not contain the point xi, let Ni ∩ Nj be defined as shown in eqn (5) where 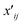 represents either xi as a nearest
represents either xi as a nearest
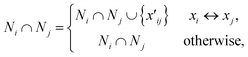 | (5) |
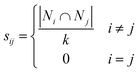 | (6) |
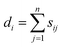 , was used to construct the symmetric normalized graph Laplacian matrix, L, as defined in eqn (7).
, was used to construct the symmetric normalized graph Laplacian matrix, L, as defined in eqn (7).| L = D−1/2(D − S)D−1/2 | (7) |
The first K eigenvectors of L were then calculated and used to form the matrix V = (vij)n×K with each eigenvector as a column. Each row of V was then normalized and represented as a point in RK-space. The set of these K-tuples were clustered into K groups according to the K-means method27 and each data point xi was ascribed to the same cluster as the ith row of V.
Results and discussion
Automatic baseline correction
An example of the automatic baseline correction algorithm used in this study can be seen in Fig. 2. This automated method is quick enough to process hundreds of spectra in roughly one second and can be written in just a few lines of MATLAB code. Furthermore, it reproduces the emission spectrum of the uncoupled dye. Thus, since the intensity of a WGM is proportional to the intensity of the incident light, the reproduction of the baseline emission spectrum allows one to rescale the WGM intensities by the magnitude of the emission spectrum so that their intensity is relatively constant across the measured spectral range, which is helpful for further analyses that involve peak fitting or peak finding. Moreover, this method has the added benefit that it does not rely on any mathematical model for describing the complex shape of an emission spectrum. It thus avoids the unnecessary complexities of functions meant for modelling arbitrary emission envelopes and removes the need to model with functions that are not physically relevant.Refractive index sensing
Whispering gallery modes are sensitive to the resonator's size, shape, and refractive index, and the refractive index of the surrounding media.28 While it can be helpful to leverage these sensitivities in a number of different ways, ultimately, most sensing applications of WGMRs rely on principles of refractometry.28 Here, we illustrate the capacity of continuous flow WGM measurements to detect the refractive indices of a range of saline and alcohol solutions.Typical refractive index sensing results obtained using the methods outlined in this paper can be seen in Table 1. Each experimental refractive index is within a few thousandths of a RIU of the corresponding literature value measured at 589 nm.24,29–32 It should be noted that the refractive index of a material is inherently wavelength dependent, with the refractive indices of some of the materials measured in this study varying by as much as a hundredth of a RIU over the wavelength range monitored in this work (∼540–700 nm). Despite this, the observed effective ne are in good agreement with values for RI of the studied solutions found in the literature. It is likely that the precision of these measurements could be improved further by taking the inherent wavelength dependence of the refractive index of materials into account, such as by incorporating a Cauchy33,34 or Sellmeier35 relationship into the fitting process, however this is beyond the scope of this paper. Additionally, while it is ideal to fit across as many peaks as possible, the spectral fitting algorithm employed here works with even a small number of visible peaks. Consequently, this means that even lower quality data that have only a few observable WGMs or spectra that have contributions from more than one microsphere can still be leveraged to obtain useful information. In contrast, these features are likely to prevent analogous area matching algorithms7,8,16 from performing well. Additionally, the ability to obtain information from spectra which arise from multiple WGMRs allows one to use a wide range of microsphere concentrations which is attractive for studying real world samples. Furthermore, coupled with the simple, affordable, and easily replaceable array of flow cell components described in this work, the ability to measure and analyse samples of high WGMR concentrations provides an important advantage over similar continuous flow methods utilizing flow cytometers16 which can be irreversibly damaged by using high concentration samples that tend to form large aggregates.
Microsphere identification and characterization
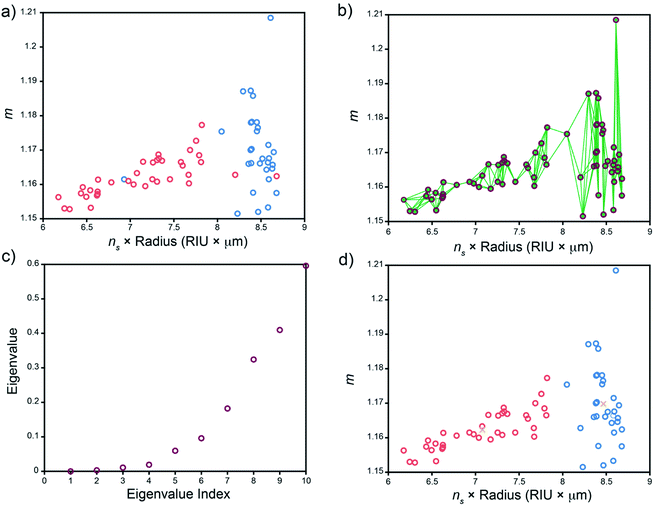
While WGM spectra are highly sensitive to the environment of the resonator, they are dependent on properties of the resonator itself and can thus provide valuable information on the WGMRs under study. This can be leveraged to identify and assign WGMRs to specific batches based on their emission spectra and lends utility towards tracking and tracing applications. We illustrate the utility of this here by comparing fit results on two batches of dye-doped microspheres: ∼8 μm diameter polystyrene spheres (Duke Scientific cat. no. 36-3) and ∼10 μm diameter polystyrene carboxylated spheres (Spherotech cat no. CFP-10056-2). Solutions containing a single type of sphere were used to collect WGM spectra and analysed as described vide supra to extract a set of (ns × a, m) ordered pairs for each type of sphere. It should be noted that while in principle, these spheres can be present in the same sample, we use separate solutions here to assess the quality of the sphere identification analysis. As can be seen in Fig. 4a, the fit results for each sphere type are not well separated, in part due to the relatively broad size distribution of the nominally 8 μm diameter unfunctionalized spheres, thus presenting a challenging exercise for microsphere identification using spectral fitting in conjunction with shared nearest neighbour spectral clustering (SC-nSNN).26Although we know a priori that there are two types of microspheres present, we can use the eigengap heuristic to identify how many clusters are readily identifiable to the clustering algorithm.36 In the eigengap heuristic, the goal is to choose the number of clusters, K, such that eigenvalues λ1, …, λK are close to zero but λK+1 is relatively large. The magnitude of these eigenvalues are dependent on characteristics of the data (i.e. the point density within a cluster as well as intercluster separation) and the number of nearest neighbours searched for when constructing the similarity graph, both of which determine the overall connectivity of the data.36,37 Thus, varying the number of nearest neighbours, k, searched for when constructing the similarity graph allows one to optimize the clustering performance. Fig. S3† shows a plot of the eigenvalue λ2 and the λ3 − λ2 eigengap across a range of k when performing the SC-nSNN algorithm on the data shown in Fig. 4a. We see that while the second eigenvalue is close to zero for each value of k ∈ [2,20] nearest neighbours, the λ3 − λ2 eigengap becomes larger and larger – a sign that intracluster connectivity is increasing while intercluster connectivity remains low. In this region, we begin to see nonzero λ3 − λ2 eigengaps when k is between 5 and 20, suggesting that the spectral clustering algorithm identifies two main clusters in this region. As k is increased further, the capacity for intracluster connectivity becomes exhausted because there are simply too few data points to connect. Consequently, the intercluster connectivity increases and each cluster becomes less defined. This manifests in larger λ2 − λ1 eigengaps and the clustering program effectively identifying only a single large cluster from the data. Thus, we can restrict our attempts at cluster identification to using smaller numbers of nearest neighbours, k, in the region from 5–20.
The results of SC-nSNN clustering using k = 5 nearest neighbours is shown in Fig. 4. A quick visual comparison of the color-coded fit results for each sphere type (Fig. 4a) and the spectral clusters identified by the SC-nSNN algorithm (Fig. 4d) shows that both sphere types can successfully be clustered and identified. Further, since the true identity of each sphere is known, we can quantitatively assess the clustering performance by calculating the normalized mutual information (NMI), a common metric for clustering performance.26,38 A detailed description of the NMI can be found in the ESI.† The NMI index has a range from 0 to 100% with 100% indicating perfect clustering performance. For the data set and clustering shown in Fig. 4a and d, only three out of the total 67 data points are miss assigned, yielding and NMI of 73.8%. Furthermore, we see good agreement in the ns × radius product and contrast ratio distributions for the known clusters of ∼8 and 10 μm microspheres and the clusters determined by the SC-nSNN algorithm (Table 2). The findings of the SC-nSNN algorithm are also quite robust, showing similar results when k is varied from 5–20 nearest neighbours (Fig. S3†).
| Cluster | Cluster size | n s × radius (RIU × μm) | Contrast ratio |
|---|---|---|---|
| Duke spheres | 37 | 7.2 ± 0.6 | 1.162 ± 0.006 |
| Spherotech spheres | 30 | 8.4 ± 0.3 | 1.170 ± 0.012 |
| SC-nSNN cluster 1 | 31 | 8.5 ± 0.1 | 1.170 ± 0.012 |
| SC-nSNN cluster 2 | 36 | 7.1 ± 0.5 | 1.162 ± 0.006 |
Conclusions
Here, we describe a continuous flow method for measuring spectra of dye-doped WGMRs and an accompanying analysis scheme was shown to accurately identify the refractive index of an array of alcohol and saline solutions down to within a few thousandths of a refractive index unit. By using a capillary tube as the flow cell, we have developed an efficient method for handling high-consequence or complex samples that does not require monodisperse microsphere solutions (overcoming a common issue with these types of measurements). This reference-free method allows us to extract useful information from free-flowing WGMRs in solution without a priori knowledge of the individual resonator sizes or their distribution, even when the spectra are of low quality. Given the ellipticity of the spheres used herein, we achieve lower apparent Q-factors and broader apparent peaks than other WGM detection methodologies. This, coupled with the indiscriminate excitation of the WGMs along multiple planes of the microsphere in dye-doped fluorescent resonators means that non-degenerate polar modes of elliptical microspheres remain unresolved in our experiments. However, by using the SC-nSNN clustering algorithm, spectral fitting results acquired from two batches of microspheres were clustered and accurately assigned to each batch of microspheres. This continuous flow approach thus provides a rapid, user-friendly method for accurately determining the composition of liquids and identifying solution phase analytes as well as discriminating against different WGMRs that might produce the desired signal, opening the door for remote sensing and tracking applications.Author contributions
Lead author Paulus designed the in-flow measurements, conducted data collection and processing, and wrote the MATLab codes used herein. Banh was responsible sample preparation and measurement collection. Rector helped conduct measurements on the WITec and was instrumental in writing. Stein provided help in ideation, funding acquisition, and writing. Lilley was responsible for project administration, experimental design, data visualization, and writing.Conflicts of interest
The authors declare that they have no known competing financial interests.Acknowledgements
This research was supported by LANL LDRD-ER (20210367ER). LANL, an affirmative action/equal opportunity employer, is managed by Triad National Security, LLC, for the NNSA of the U.S. Department of Energy (contract 89233218CNA000001).References
- Y. Zhang, T. Zhou, B. Han, A. Zhang and Y. Zhao, Nanoscale, 2018, 10, 13832–13856 RSC.
- Y. Q. Kang, A. François, N. Riesen and T. M. Monro, Sensors, 2018, 18, 2987 CrossRef PubMed.
- Y. Sun, S. I. Shopova, G. Frye-Mason and X. Fan, Opt. Lett., 2008, 33, 788–790 CrossRef CAS PubMed.
- Y. Sun, J. Liu, G. Frye-Mason, S. J. Ja, A. K. Thompson and X. Fan, Analyst, 2009, 134, 1386–1391 RSC.
- V. R. Dantham, S. Holler, C. Barbre, D. Keng, V. Kolchenko and S. Arnold, Nano Lett., 2013, 13, 3347–3351 CrossRef CAS PubMed.
- F. Vollmer, S. Arnold and D. Keng, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20701–20704 CrossRef CAS PubMed.
- M. Charlebois, A. Paquet, L. S. Verret, K. Boissinot, M. Boissinot, M. G. Bergeron and C. N. Allen, Nanoscale Res. Lett., 2010, 5, 524–532 CrossRef CAS PubMed.
- M. Charlebois, A. Paquet, L. S. Verret, K. Boissinot, M. Boissinot, M. G. Bergeron and C. N. Allen, IEEE Sens. J., 2013, 13, 229–233 Search PubMed.
- T. Munoz-Hernandez, E. Reyes-Vera and P. Torres, IEEE Sens. J., 2020, 20, 9170–9178 CAS.
- T. Ioppolo and M. Manzo, Appl. Opt., 2014, 53, 5065–5069 CrossRef PubMed.
- T. Ioppolo, U. K. Ayaz, M. V. Ötügen and V. Sheverev, Appl. Opt., 2008, 47, 3009–3014 CrossRef CAS PubMed.
- R. Madugani, Y. Yang, V. H. Le, J. M. Ward and S. N. Chormaic, IEEE Photonics Technol. Lett., 2016, 28, 1134–1137 Search PubMed.
- P. Zijlstra, K. L. Van Der Molen and A. P. Mosk, Appl. Phys. Lett., 2007, 90, 94–97 CrossRef.
- A. Weller, F. C. Liu, R. Dahint and M. Himmelhaus, Appl. Phys. B: Lasers Opt., 2008, 90, 561–567 CrossRef CAS.
- S. Pang, R. E. Beckham and K. E. Meissner, Appl. Phys. Lett., 2008, 92, 221108 CrossRef PubMed.
- R. Lessard, O. Rousseau-Cyr, M. Charlebois, C. Riviere, O. Mermut and C. N. Allen, Proc. SPIE, 2013, 8600, 86001Q CrossRef.
- H. Chew, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3410–3416 CrossRef CAS PubMed.
- H. Chew, J. Chem. Phys., 1987, 87, 1355–1360 CrossRef CAS.
- P. H. C. Eilers, Anal. Chem., 2003, 75, 3631–3636 CrossRef CAS PubMed.
- S.-J. Baek, A. Park, Y.-J. Ahn and J. Choo, Analyst, 2015, 140, 250–257 RSC.
- J. Park, A. Park, K. Yang and S. Baek, Analyst, 2017, 142, 380–388 RSC.
- M. E. Hansen and J. Smedsgaard, J. Am. Soc. Mass Spectrom., 2004, 15, 1173–1180 CrossRef CAS PubMed.
- C. C. Lam, P. T. Leung and K. Young, J. Opt. Soc. Am. B, 1992, 9, 1585–1592 CrossRef.
- G. M. Hale and M. R. Querry, Appl. Opt., 1973, 12, 555–563 CrossRef CAS PubMed.
- N. Yoder, Peakfinder (X0, Sel, Thresh, Extrema, IncludeEndpoints, Interpolate), MATLAB Central File Exchange, 2021 Search PubMed.
- X. Ye and T. Sakurai, ETRI J., 2016, 38, 540–550 Search PubMed.
- X. Wu, V. Kumar, Q. J. Ross, J. Ghosh, Q. Yang, H. Motoda, G. J. McLachlan, A. Ng, B. Liu, P. S. Yu, Z. H. Zhou, M. Steinbach, D. J. Hand and D. Steinberg, Knowl. Inf. Syst., 2008, 14, 1–37 CrossRef.
- M. R. Foreman, J. D. Swaim and F. Vollmer, Adv. Opt. Photonics, 2015, 7, 168–240 CrossRef CAS PubMed.
- H. El-Kashef, Phys. B, 2000, 279, 295–301 CrossRef CAS.
- J. Rheims, J. Köser and T. Wriedt, Meas. Sci. Technol., 1997, 8, 601–605 CrossRef CAS.
- I. Z. Kozma, P. Krok and E. Riedle, J. Opt. Soc. Am. B, 2005, 22, 1479–1485 CrossRef CAS.
- C. Y. Tan and Y. X. Huang, J. Chem. Eng. Data, 2015, 60, 2827–2833 CrossRef CAS.
- M. R. McGrory, M. D. King and A. D. Ward, J. Phys. Chem. A, 2020, 124, 9617–9625 CrossRef CAS PubMed.
- F. A. Jenkins and H. E. White, Fundamentals of Optics, McGraw-Hill Primis Custom Publishing, New York, 2010 Search PubMed.
- W. Sellmeier, Ann. Phys. Chem., 1871, 219, 272–282 CrossRef.
- U. Von Luxburg, Stat. Comput., 2007, 17, 395–416 CrossRef.
- A. Y. Ng, M. I. Jordan and Y. Weiss, Adv. Neural Inf. Process. Syst., 2001, 14, 849–856 Search PubMed.
- A. Strehl and J. Ghosh, J. Mach. Learn. Res., 2003, 3, 583–617 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ay00181k |
| This journal is © The Royal Society of Chemistry 2022 |