A graceful break-up: serendipitous self-assembly of a ferromagnetically coupled [Ni^II₁₄] wheel

Abstract

The complex [Ni^II₁₄(HL²)₁₂(HCOO)₁₄Cl₁₄(MeOH)(H₂O)] describes an aesthetically pleasing wheel displaying ferromagnetic nearest neighbour exchange.

---

Interest in the magnetic properties of polymetallic clusters of Ni^II began with the development of magneto-structural correlations of [Ni₂] dimers¹ and [Ni₄] cubanes² that revealed a dependence of the sign and magnitude of the exchange interaction on both the Ni–X–Ni bridging angle and the anisotropy of the Ni^II ion.³ The large axial zero-field splitting displayed by the latter in certain geometries also lends itself to the construction of both single-molecule magnets (SMMs)⁴ and single-ion magnets (SIMs)⁵ displaying slow relaxation of the magnetisation. Indeed, recent studies of Ni^II SIMs at both ambient and high pressure⁶ have revealed how magnetic anisotropy is extremely susceptible to even small structural distortions, in turn highlighting target geometries⁷ and directing the synthetic methodologies required to engineer molecules possessing giant magneto-anisotropies.⁸

Flexible N,O-bridging ligands have proved particularly successful in the construction of polymetallic clusters of Ni^II displaying a variety of topologies and nuclearities, including supertetrahedra,⁹ wheels,¹⁰ planar discs¹¹ and icosahedra.¹² The pro-ligand (3,5-dimethyl-1H-pyrazol-1-yl)methanol (HL¹) belongs in this family, having been employed to make both mono- and tetranuclear clusters of Ni^II.¹³ Here, we expand this chemistry to include the synthesis, structure and characterisation of [Ni₁₄(HL²)₁₂(HCOO)₁₄Cl₁₄(MeOH)(H₂O)]·4Me₂CO (1·4Me₂CO, HL² = 3,5-dimethylpyrazole), an aesthetically pleasing wheel formed serendipitously via the in situ transformation of HL¹ to HL².

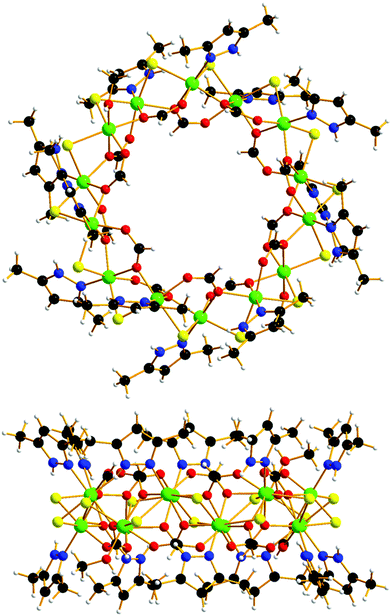
The reaction of NiCl₂·6H₂O and HL¹ in a basic MeOH solution heated at 65 °C for 40 minutes affords compound 1 (Fig. 1) upon diffusion of acetone into the cooled mother liquor (see the ESI† for full experimental details). Crystals of 1 are in a tetragonal cell and structure solution was performed in the space group P4₂/n (see the ESI† for full crystallographic details, Table S1 and Fig. S1). The asymmetric unit contains half the formula unit.

Fig. 1 Orthogonal views of the molecular structure of complex 1 viewed perpendicular (top) and parallel to the [Ni₁₄] ‘plane’. Colour code: Ni = green, O = red, N = blue, C = black, H = white, Cl = yellow. Acetone molecules of crystallisation are removed for clarity.

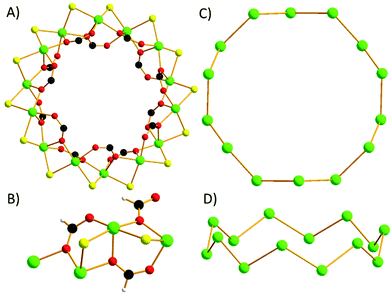
The metallic skeleton of 1 is a single stranded [Ni^II₁₄] wheel (Fig. 2A). The bridging between each pair of Ni^II ions is the same around the entire wheel and consists of one μ-Cl ion (Ni–Cl–Ni, ∼82.0–85.1°), one μ-O atom (Ni–O–Ni, ∼102.8–103.2°) and one μ-carboxylate which both derive from the syn, syn, anti-bridging formate (Fig. 2B). The six-coordinate Ni^II ions are all in distorted octahedral geometries with their {NiO₃Cl₂N} coordination spheres completed by a terminally bonded HL² ligand. The only exception to this is Ni₅, {NiO₄Cl₂}, in which there resides a disordered MeOH/H₂O molecule in place of the HL² ligand. The HL² ligands and the formate ions originate from the in situ reaction of HL¹.¹⁴

Fig. 2 (A) The magnetic core of 1. (B) Close-up of the bridging between neighbouring Ni^II ions. The metallic core viewed perpendicular (C) and parallel (D) to the [Ni₁₄] ‘plane’. Colour code: Ni = green, O = red, C = black, H = white.

The wheel is non-planar with nearest neighbour Ni^II ions being above and below the plane running through the middle of the fourteen metal ions, i.e., they form a zigzag/sinusoidal “up-down-up-down” motif as the wheel is circumnavigated (Fig. 2C and D). The approximate dimensions of the wheel are, Ni1⋯Ni1′, ∼12.7 Å.

The terminally bonded MeOH/H₂O molecules are H-bonded to acetone molecules of crystallisation (O(H)⋯O, ∼2.72 Å). Closest inter-cluster interactions are between neighbouring HL² ligands and between HL² ligands and the Cl ions (C/N⋯C/N/Cl > 3.6 Å). In the extended structure the wheels pack in eclipsed columns down the c-axis, with the remaining acetone molecules of crystallisation lying in a head-tail fashion in the voids between the wheels (O⋯C, ∼3.6 Å; Fig. S2, ESI†).

A subsequent investigation of reaction conditions does not reveal any simple relationship between reaction time, temperature and ligand degradation, but did reveal that 1 can be made directly from NiCl₂·6H₂O, formic acid (or sodium formate) and HL², and, perhaps unsurprisingly, in larger yields (see the ESI† for full details).

A search of the Cambridge Structural Database reveals that there are approximately thirty Ni wheels reported, ranging in nuclearity from [Ni₅] to [Ni₂₄].¹⁵ By far the most common are [Ni₆] and [Ni₁₂] wheels,¹⁶ with complex 1 being just the second example of a [Ni₁₄] wheel.¹⁷ The first example is a large (∼2 nm diameter) oval-shaped wheel in which neighbouring Ni ions are connected by artificial tripeptides (Ni⋯Ni, ∼8 Å). Compound 1 also represents the first Ni^II wheel built with 3,5-dimethylpyrazole (or 1H-pyrazole) and indeed is the largest nuclearity Ni cluster known with either ligand.

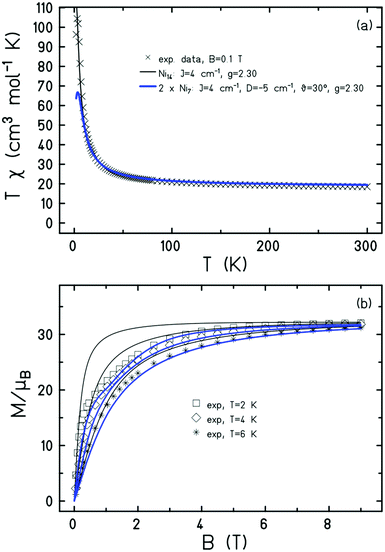
Dc magnetic susceptibility (χ) and magnetisation (M) measurements of 1 were taken in the T = 300–1.80 K, B = 0.1 T and T = 2.0–10 K and B = 0.5–9.0 T temperature and field ranges, respectively. These are plotted as the χT product versus T, and M versus B in Fig. 3 (and Fig. S3, ESI†). The T = 300 K value of χT = 18.5 cm³ K mol⁻¹ is equal to the value expected for fourteen non-interacting Ni^II ions with g = 2.30. Upon cooling the χT value remains relatively constant, increasing only very slowly to ∼24 cm³ K mol⁻¹ at 50 K before rising sharply to a maximum of ∼104 cm³ K mol⁻¹ at T = 3 K. The value then drops to ∼96 cm³ K mol⁻¹ at 2 K. The M vs. B data increases rapidly with increasing field, saturating at a value of M = 32.1 μ_B at T = 2 K and B = 9 T. The susceptibility and magnetisation data are therefore indicative of weak ferromagnetic nearest neighbour exchange and the stabilisation of an S = 14 ground state.

Fig. 3 (a) Magnetic susceptibility data potted as the χT product versus T measured in a field of B = 0.1 T between T = 300–2.0 K. Theory: black — isotropic model, blue – model with single-ion anisotropy. (b) M vs. B data in fields B = 0.5–9 T and temperature range T = 2–6 K. Theory curves: same colour as in (a), descending with higher temperatures. See the main text for details.

The magnetic susceptibility data can be simulated using exact diagonalisation¹⁸ and an isotropic spin-Hamiltonian 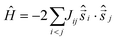with a coupling scheme that assumes just one independent exchange interaction between nearest neighbours, J = +4 cm⁻¹ with g = 2.30 (Fig. 3, black curve). The addition of a next nearest neighbour interaction makes no difference to the quality of the simulation. Given that this interaction is computed to be very weak and ferromagnetic by DFT (vide infra) this is to be expected. This simple isotropic model, however, does not explain the low temperature magnetisation data, which requires inclusion of the single ion anisotropy of the Ni ions, D(Ni), 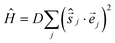, where e⃑_j = e⃑_j(θ_j, φ_j) is the direction of the local easy axis. Computational limitations direct us toward employing a [Ni₇] wheel, with the results multiplied by two to mimic the [Ni₁₄] wheel in order to assess the impact of anisotropy. The magnetisation data is simulated nicely with J = +4 cm⁻¹ and D(Ni) = −5 cm⁻¹ with the anisotropy axes tilted from the axis of the wheel by θ = 30°, φ_j = 2πj/7, in agreement with ab initio NEVPT2 calculations (Fig. 3, blue curves). The magenta curves in Fig. S3 (ESI†) demonstrate for the isotropic case that the substituted [Ni₇] model system is close to the original except for low temperatures where the S = 14 ground state obviously cannot be reproduced.

The ferromagnetic exchange in 1 is consistent with magneto-structural correlations developed for halide-bridged Ni^II dimers where the sign and magnitude of the interaction is dictated by the Ni–Cl–Ni angle – with a switch from antiferromagnetic to ferromagnetic occurring at approximately ≤102° and increasing with decreasing angle.¹⁹ Note the Ni–Cl–Ni angles in 1 are ∼82–85°. Alternating current (ac) susceptibility measurements between 50–3000 Hz under zero external dc field and an oscillating ac field of B_ac = 5 Oe were performed to investigate the relaxation dynamics of 1. A plot of 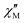versus frequency yielded temperature dependent maxima in the range 1.8–2.5 K (Fig. S4, ESI†).

To further understand the origin and sign of the magnetic coupling constants we have performed DFT calculations on models created from 1 (1A–C, Fig. S5 and Tables S2, S3, ESI†). All seven unique exchange interactions are in the range +1.7 ≤ J ≤ +3.9 cm⁻¹, consistent with the experimental values (Table S4, ESI†). The DFT calculated values for the seven crystallographically unique interactions also simulate the susceptibility well if they are scaled by a factor of 1.4 (ESI,† Fig. S3, red curve). The narrow range of values obtained can be attributed to the presence of similar structural parameters for each metal ion, with the relatively small Ni−μ-O/Cl–Ni angles resulting in ferromagnetic exchange (Table S4, ESI†).¹⁹ To further explore the origin of the sign and magnitude of these interactions we have performed overlap integral calculations^20–22 between the singly occupied molecular orbitals (SOMOs) of the Ni^II ions in a bimetallic model (1D) created from 1 (Fig. S6, ESI†). These calculations suggest competition between one moderate interaction [〈Ni(α)d_x²−y²||Ni(β)d_z²〉] and three weak interactions [〈Ni(α)d_x²−y²||Ni(β)d_x²−y²〉], [〈Ni(α)d_z²||Ni(β)d_x²−y²〉], [〈Ni(α)d_z²||Ni(β)d_z²〉]. The former contributes to the antiferromagnetic and the latter to the ferromagnetic part of the exchange. In this case, the three weak interactions dominate and the overall result is the observation of a weak ferromagnetic interaction. Spin density analysis suggests a strong spin delocalisation mechanism, with the spin densities on the Ni^II ions being between 1.668–1.682. Of the three different bridging moieties, the Cl ion has the largest spin density (0.122–0.141; Fig. S7, ESI†). To further investigate the contribution from the μ-Cl ion to the total magnetic exchange, we have replaced it with a point charge in model 1D. This results in an antiferromagnetic interaction, changing from +2.3 cm⁻¹ to −6.2 cm⁻¹, clearly suggesting the major ferromagnetic contribution to the exchange comes from the μ-Cl ion. Bearing in mind the connectivity of next-nearest neighbour Ni^II centres through a formate group, we have also estimated the next-nearest neighbour magnetic exchange interaction using model 1E (Fig. S8, ESI†). This is estimated to be very small and ferromagnetic, J = +0.5 cm⁻¹. All the Ni^II ions in 1 possess slightly distorted octahedral geometries (Table S5, ESI†) and are therefore expected to have axial zero-field splitting parameters of the order D ≤ −10 cm⁻¹. Ab initio NEVPT2 calculations performed using ORCA²³ reveal values in the range −1.9 ≤ D ≤ −6.5 cm⁻¹, with the major contribution arising from the d_xy → d_x²−y² electronic transition (Fig. S9 and Tables S6–S12, ESI†).²⁴ The D(Ni) axes are oriented approximately along the N(pyrazole)–Ni–O and O(MeOH)–Ni–O vectors, tilted at angles of θ = ∼32–37° from the axis of the wheel. This non-collinear nature of the easy axes explains why 1 is a relatively poor single-molecule magnet.

In summary, the in situ transformation of HL¹ to HL² and concurrent formation of formate anions results in the self-assembly of an aesthetically pleasing [Ni₁₄] wheel, with subsequent examination of reaction conditions leading to a more ‘rational’ synthetic procedure. Magnetic measurements reveal weak, ferromagnetic exchange interactions, with the susceptibility data simulated with a single exchange constant, J = +4 cm⁻¹. The DFT computed values also simulate the data well, albeit they need scaled by a factor of 1.4. The simulation of the magnetisation data requires inclusion of D(Ni) = −5 cm⁻¹ tilted at an angle θ = 30° with respect to the axis of the wheel. Theoretical calculations are in agreement with experimental observations, revealing the major contribution to the ferromagnetic exchange is mediated through the bridging Cl ions. Attempts to make analogues of compound 1 containing different M^II ions and other bridging halides, pseudohalides and carboxylates are underway.

This work was supported by The Leverhulme Trust (RPG-2021-176) and the European Union Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 832488. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) license to any Author Accepted Manuscript version arising from this submission.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) A. P. Ginsberg, R. L. Martin and R. C. Sherwood, Inorg. Chem., 1968, 7, 932–936; (b) A. P. Ginsberg, Inorg. Chim. Acta, Rev., 1971, 5, 45–68.
2. M. A. Halcrow, J.-S. Sun, J. C. Huffman and G. Christou, Inorg. Chem., 1995, 34, 4167–4177.
3. (a) A. Wilson, J. Lawrence, E.-C. Yang, M. Nakano, D. N. Hendrickson and S. Hill, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 140403; (b) J. P. S. Walsh, S. Sproules, N. F. Chilton, A. L. Barra, G. A. Timco, D. Collison, E. J. L. McInnes and R. E. P. Winpenny, Inorg. Chem., 2014, 53, 8464–8472.
4. J. Miklovič, D. Valigura, R. Boča and J. Titiš, Dalton Trans., 2015, 44, 12484–12487.
5. G. Aromí, S. Parsons, W. Wernsdorfer, E. K. Brechin and E. J. L. McInnes, Chem. Commun., 2005, 5038–5040.
6. R. Ruamps, R. Maurice, L. Batchelor, M. Boggio-Pasqua, R. Guillot, A. L. Barra, J. Liu, E.-E. Bendeif, S. Pillet, S. Hill, T. Mallah and N. Guihéry, J. Am. Chem. Soc., 2013, 135, 3017–3026.
7. K. E. R. Marriott, L. Bhaskaran, C. Wilson, M. Medarde, S. T. Ochsenbein, S. Hill and M. Murrie, Chem. Sci., 2015, 6, 6823–6828.
8. G. A. Craig, A. Sarkar, C. H. Woodall, M. A. Hay, K. E. R. Marriott, K. V. Kamenev, S. A. Moggach, E. K. Brechin, S. Parsons, G. Rajaraman and M. Murrie, Chem. Sci., 2018, 9, 1551–1559.
9. R. Shaw, I. S. Tidmarsh, R. H. Laye, B. Breeze, M. Helliwell, E. K. Brechin, S. L. Heath, M. Murrie, S. Ochsenbein, H.-U. Güdel and E. J. L. McInnes, Chem. Commun., 2004, 1418–1419.
10. A. J. Blake, C. M. Grant, S. Parsons, J. M. Rawson and R. E. P. Winpenny, J. Chem. Soc., Chem. Commun., 1994, 2363–2364.
11. S. T. Meally, G. Karotsis, E. K. Brechin, G. S. Papaefstathiou, P. W. Dunne, P. McArdle and L. F. Jones, CrystEngComm, 2010, 12, 59–63.
12. D. Geng, X. Han, Y. Bi, Y. Qin, Q. Li, L. Huang, K. Zhou, L. Song and Z. Zheng, Chem. Sci., 2018, 9, 8535–8541.
13. (a) V. M. Leovac, R. Petković, A. Kovács, G. Pokol and K. M. Szécsény, J. Therm. Anal. Calorim., 2007, 89, 267; (b) R. Touzani, M. Haibach, A. J. Nawara-Hultzsch, S. El Kadiri, T. J. Emge and A. S. Goldman, Polyhedron, 2011, 30, 2530; (c) J. Lim, G. Kim, K. Do, S. Lee, S. Ryu, D. Yoshioka and M. Mikuriya, X-Ray Struct. Anal. Online, 2015, 31, 49; (d) A. Mar, S. J. Retting, A. Storr and J. Trott, Can. J. Chem., 1988, 66, 101; (e) F. Paap, E. Bouwman, W. L. Driessen, R. A. G. de Graaff and J. Reedijk, J. Chem. Soc., Dalton Trans., 1985, 737.
14. W. L. Driessen, Recl. Trav. Chim. Pays-Bas, 1982, 101, 441–443.
15. See for example: (a) A. H. Mahmoudkhani and V. Langer, Inorg. Chim. Acta, 1999, 294, 83–86; (b) A. L. Dearden, S. Parsons and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2001, 40, 151–154.
16. See for example: (a) G. E. Lewis and C. S. Kraihanzel, Inorg. Chem., 1983, 22, 2895–2899; (b) A. J. Blake, C. M. Grant, S. Parsons, J. M. Rawson and R. E. P. Winpenny, J. Chem. Soc., Chem. Commun., 1994, 2363–2364.
17. R. Miyake, A. Ando, M. Ueno and T. Muraoka, J. Am. Chem. Soc., 2019, 141, 8675–8679.
18. (a) K. Bärwinkel, H.-J. Schmidt and J. Schnack, J. Magn. Magn. Mater., 2000, 212, 240–250; (b) R. Schnalle and J. Schnack, Int. Rev. Phys. Chem., 2010, 29, 403–452; (c) T. Glaser, V. Hoeke, K. Gieb, J. Schnack, C. Schröder and P. Müller, Coord. Chem. Rev., 2015, 289–290, 261–278.
19. A. Tamayo, L. Escriche, C. Lodeiro, J. Ribas-Ariño, J. Ribas, B. Covelo and J. Casabó, Inorg. Chem., 2006, 45, 7621–7627.
20. M. K. Singh, Dalton Trans., 2020, 49, 4539–4548.
21. M. K. Singh, A. Etcheverry-Berríos, J. Vallejo, S. Sanz, J. Martínez-Lillo, G. S. Nichol, P. J. Lusby and E. K. Brechin, Dalton Trans., 2022, 51, 8377–8381.
22. (a) C. Desplanches, E. Ruiz, A. Rodríguez-Fortea and S. Alvarez, J. Am. Chem. Soc., 2002, 124, 5197–5205; (b) M. K. Singh, N. Yadav and G. Rajaraman, Chem. Commun., 2015, 51, 17732–17735.
23. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
24. A. Sarkar, S. Dey and G. Rajaraman, Chem. – Eur. J., 2020, 26, 14036–14058.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures, characterisation details, computational methodology. CCDC 2169986. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2cc03445j

---