Very close I⋯As and I⋯Sb interactions in trimethylpnictogen-pentafluoroiodobenzene cocrystals†
Maciej
Bujak
 *ab,
Hans-Georg
Stammler
b,
Yury V.
Vishnevskiy
b and
Norbert W.
Mitzel
*ab,
Hans-Georg
Stammler
b,
Yury V.
Vishnevskiy
b and
Norbert W.
Mitzel
 *b
*b
aFaculty of Chemistry, University of Opole, Oleska 48, 45-052 Opole, Poland. E-mail: mbujak@uni.opole.pl
bLehrstuhl für Anorganische Chemie und Strukturchemie, Fakultät für Chemie, Universität Bielefeld, Universitätsstr. 25, 33615 Bielefeld, Germany. E-mail: mitzel@uni-bielefeld.de
First published on 23rd November 2021
Abstract
The cocrystals (CH3)3As·C6F5I (1) and (CH3)3Sb·C6F5I (2) were generated in situ from equimolar mixtures of their components. 1 and 2 show very close I⋯As and I⋯Sb directional intermolecular interactions. They are 0.5 and 0.7 Å shorter than the sums of van der Waals radii, respectively, and are the shortest C–I⋯As and C–I⋯Sb halogen bonds of this type found for experimentally characterized molecular (co)crystals. Comparisons of the packing motifs and contacts in 1 and 2 with those in (CH3)3As (3), (CH3)3Sb (4) and C6F5I (5) illustrate the occurrence and hierarchy of the specific interactions. The heteromolecular components in 1 and 2 are assembled by I⋯As, I⋯Sb and F⋯H interactions. There are no significant intermolecular As⋯As contacts in 3, but Sb⋯Sb interactions in 4. Molecules in 5 are mainly associated by I⋯F, F⋯F and F⋯C contacts. The intermolecular interactions observed in the (co)crystals correspond to the calculated electrostatic potentials.
Introduction
Chemical reactions carried out in research laboratories and chemical industry use the transformations of substrates that react with each other under specific conditions. Chemical transformations are in most cases performed in the liquid phase and involve breaking of chemical bonds and formation of new bonds. The obtained products are separated and purified, often using crystallization techniques. Cocrystallization has a lot in common with the broadly defined chemical transformations and syntheses. However, during cocrystal formation typical chemical bonds are neither broken nor formed, but rather the process involves the creation and balancing of subtle and specific attraction forces, i.e. typically weak intermolecular interactions formed between the cocrystal components. The products of cocrystallization show, similar to products of chemical reactions, unique physicochemical properties. The possible predictability of properties, on the basis of structural behaviour of the cocrystal components, as one of the benefit of cocrystallization should be mentioned. Therefore, cocrystals are not only interesting in terms of the molecular view of their growth, self-assembly, molecular recognition or polymorphism, but also from the point of view of (co)crystal engineering, i.e. the design of new materials including pharmaceuticals, with dedicated physicochemical properties.1 Structural chemistry abounds in a number of relatively recently discovered and described intermolecular interactions. So, not only hydrogen or halogen bonds, but also e.g. chalcogen, pnictogen, tetrel and regium bonds have been defined as attraction forces.2Cocrystals can be regarded as the products of processes involving the formation of heteromolecular interactions. One of the best models for the investigation of weak intermolecular interactions are cocrystals composed of simple and neutral molecules. Such components can form only a limited number of well-defined interactions. We have recently reported cocrystals of halogenated hydrocarbons, which are gases or liquids under ambient conditions, with benzene. These studies indicate that, although the molecular components form relatively weak heteromolecular interactions, they are strong enough to support the formation of cocrystal assemblies under the given thermodynamic conditions.3
Herein, we report the formation of the cocrystals (CH3)3As·C6F5I (1) and (CH3)3Sb·C6F5I (2) by the supramolecular reactions of the Lewis bases (CH3)3As (3) and (CH3)3Sb (4) with the halogen-bond donor Lewis acid C6F5I (5) and the identification of 1 and 2 by single-crystal X-ray diffraction. The structures of both pure components 3 and 4 were also investigated for comparison. Hirshfeld surface analysis and quantum-chemical calculations support the experimental study.
Results and discussion
Single-crystal samples of 1 and 2 were grown in situ at low temperatures in sealed capillaries from cryogenically loaded equimolar mixtures of the components. Their single-crystal structures were determined at several temperatures between 210 and 100 K. X-ray diffraction revealed that 1 and 2 crystallize in the monoclinic space groups C2/c and I2/a, respectively, with one (CH3)3As or (CH3)3Sb as well as one C6F5I molecule in the asymmetric units. There was no phase transition or symmetry change observed down to 100 K. Both cocrystals experience a similar contraction with decreasing temperature: the unit-cell volumes at 100 K are 3.2 and 3.1% less than those at 220 and 210 K for 1 and 2, respectively. All unit-cell parameters decrease upon cooling, except the unit-cell length c and angle β for 2, which increase. The largest decrease of 2.5% was found for the smallest length a in 1 (Tables S1 and S2, ESI†).Cocrystals 1 and 2 can be considered to consist of alternating molecular layers composed of their molecular components (Fig. 1). At 100 K, the C6F5I molecules in both cocrystals are basically planar with expected intramolecular dimensions.3b,4 The average E–C distances (E = As or Sb) within the (CH3)3E units in 1 and 2 at 100 K are 1.945 and 2.134 Å, whereas the C–E–C angles are 98.5 and 95.5°, respectively (Tables S5 and S6, ESI†). The difference between the E–C bond lengths of 1 and 2 corresponds to the difference in the covalent radii of As and Sb of ca. 0.2 Å.5 The ra-structures of the free molecules (CH3)3E (E = As, Sb) determined by gas electron diffraction show E–C distances of 1.968(3) and 2.163(3) Å and C–E–C angles of 96.1(5) and 94.1(5)°, respectively.6 This means that cocrystal formation with 5, leads to a shortening of the E–C distances by 0.023 and 0.029 Å, and a widening of the C–E–C angles by 2.4 and 1.4° for 1 and 2, respectively. Although these changes are close to the experimental errors, they are reasonable in terms of the valence shell electron pair repulsion (VSEPR) model.7 Both the above-mentioned intramolecular bond lengths and angles, for (CH3)3As and (CH3)3Sb in 1 and 2, respectively, are comparable to previous results obtained for analogous cocrystals.8
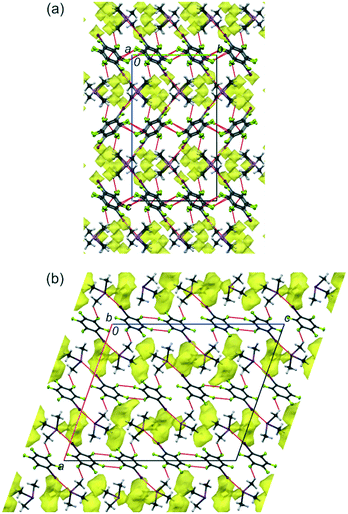 | ||
| Fig. 1 The structures of 1 (a) and 2 (b) at 100 K in views along the a (1) and b axes (2). The intermolecular voids accessible to a probing sphere of radius 0.65 Å and grid spacing of 0.6 Å are indicated in yellow. The void volumes are 2.0% (50.03 Å3, for 1) and 5.8% (154.04 Å3, for 2).9 The dotted red lines indicate the I⋯As, I⋯Sb, F⋯F, F⋯C and F⋯H intermolecular contacts. Displacement ellipsoids are plotted at the 25% probability level. | ||
For the purpose of comparing and better understanding the structural properties and interaction behaviour in 1 and 2, single crystals of the trimethylpnictogen components (CH3)3As (3) and (CH3)3Sb (4) were grown in situ at low temperatures. Their structures were determined at several temperatures between 170 and 100 K. 3 and 4 show orthorhombic and monoclinic symmetry in the space groups Cmc21 and P21/n, respectively. The asymmetric units contain half a (CH3)3As and one (CH3)3Sb molecule. 4 demonstrates a similar overall contraction with decreasing temperature as 1 and 2, whereas the contraction of 3 is weaker. The unit-cell volumes at 100 K for 3 and 4 are 1.3 and 2.8% less than those at 150 and 170 K, respectively. All unit-cell lengths, except the slight increase of the β angle for 4, shrink with decreasing temperature. The largest decrease of 1.2% was noticed for the smallest unit-cell parameter a in 4 (Tables S3 and S4, ESI†). Although 3 and 4 show different crystal structures, both can be regarded being composed of molecular layers (Fig. 2). As in 1 and 2, the difference in As–C (av. 1.963 Å) and Sb–C (av. 2.151 Å) bond lengths is ca. 0.2 Å at 100 K.5 The average C–As–C and C–Sb–C angles are 96.7° and 94.6°, respectively (Tables S7 and S8, ESI†). The values for the E–C distances and C–E–C angles are similar to those for the free molecules determined by gas electron diffraction6 (see above) and independently confirm the longer distances and wider angles in 1 and 2.
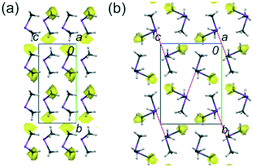 | ||
| Fig. 2 The structures of 3 (a) and 4 (b), at 100 K, along a axes. The intermolecular voids accessible to a probing sphere of radius 0.65 Å and grid spacing of 0.6 Å are indicated in yellow. The void volume is: 1.8% (9.64 Å3, for 3) and 1.1% (6.52 Å3, for 4).9 The dotted red lines indicate the Sb⋯Sb intermolecular contacts in 4. Displacement ellipsoids are plotted at the 25% probability level. | ||
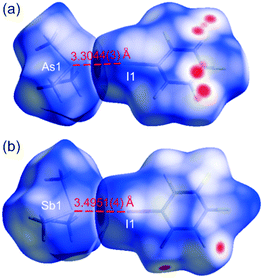
Both cocrystals, 1 and 2, show similar patterns of voids and interactions schemes9 that are dominated by the heteromolecular I⋯As and I⋯Sb, but also by weaker F⋯H contacts (Fig. 1, Tables S9 and S10, ESI†). In contrast, within the limits of van der Waals radii,103 does not show any pronounced intermolecular interactions (at 100 K the shortest are H⋯H distances of 2.62 Å, while the closest As⋯As separations are 5.172(1) Å), whereas the molecules in 4 are joined together only by Sb⋯Sb contacts (Fig. 2, Table S11, ESI†). Within the intermolecular distances the largest temperature-dependent differences were noted for the F⋯C and F⋯F contacts in 1 and 2, respectively; they become shorter both by ca. 0.07(1) Å upon cooling to 100 K. Simultaneously, the I⋯As and I⋯Sb distances contract by 0.063(1) and 0.051(1) Å, reaching 3.3044(3) and 3.4951(4) Å, respectively. These are the shortest C–I⋯E (E = As or Sb) halogen bonds of this type for experimentally studied molecular (co)crystals. On the basis of their geometrical parameters, the intermolecular interactions in cocrystals 1 and 2 can be classified as distorted electrostatically preferred type II halogen bonds for I⋯E, and type I dispersive forces for F⋯H contacts.2b,11
Among the properties of interactions that indicate their stabilizing role in (co)crystal structures are energy and related geometry as well as frequency of appearance. The geometry and relative distribution of interactions in 1 and 2 along with those in 3 and 4 were clarified and compared using the Hirshfeld surface analysis.12 This method covers all possible contacts including those with separations above the van der Waals radii regime10 and allows identifying particular types of contacts together with their impact on (co)crystal packing.
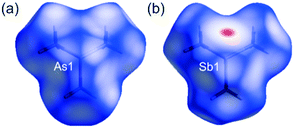
The Hirshfeld surfaces were independently generated for the molecular components in 1 and 2 as well as for the molecules in 3 and 4. The red regions, on the Hirshfeld surfaces, correspond to I⋯As and F⋯F/C contacts in 1, and I⋯Sb and F⋯F interactions in 2 (Fig. 3). The red zone marked on the Hirshfeld surface of (CH3)3Sb in 4 relates to the Sb⋯Sb contacts (Fig. 4).
Considering all possible contacts of the individual molecular (co)crystal components in the structures 1–4, it is obvious that the interactions involving H atoms should mainly contribute to the Hirshfeld surface area (Fig. 5 and S1, ESI†). The interactions in 3 and 4 are characterized by only three types of contacts: E⋯E, E⋯H and H⋯H (E = As for 3 and E = Sb for 4). The conversions 3 → 1 and 4 → 2 by formal incorporation of C6F5I molecules leads to a complete change in the interaction patterns. In both 1 and 2, the ‘new’ F⋯H, I⋯H and C⋯H contacts constitute ca. 51% of all cohesion forces. In addition, and most intriguingly, very short I⋯As and I⋯Sb interactions are introduced; their contribution is about 6%.
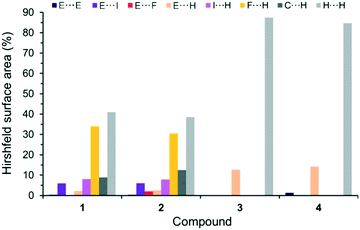 | ||
| Fig. 5 Distribution of contacts, on the basis of their relative contributions to the Hirshfeld surface area, for (CH3)3E molecules, in: 1–4 at 100 K. E = As for 1 and 3, and E = Sb for 2 and 4. | ||
A similar inspection of the formal conversions 5 → 1 and 5 → 2 by incorporation of (CH3)3E molecules into the known polymorphic forms 5-I4 and 5-II3b of C6F5I (5) leads to related observations (Fig. 6 and S2, ESI†). The dominating I⋯F, F⋯F and F⋯C contacts with the total average contribution of ca. 88% in 5-I and 5-II are reduced to an average ca. 43% in both 1 and 2. In turn, the input of above-mentioned ‘new’ F⋯H, I⋯H and C⋯H contacts constitute at least 51% of all cohesion forces in 1 and 2. Also, both cocrystals contain the important and strong contributions of the I⋯As and I⋯Sb interactions of ca. 5% on average.
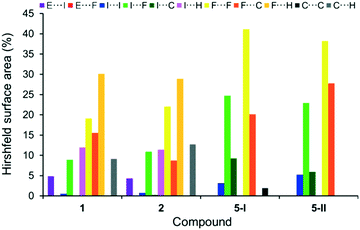 | ||
| Fig. 6 Distribution of contacts, on the basis of their relative contributions to the Hirshfeld surface area, for C6F5I molecules in 1 and 2 and two polymorphic forms of C6F5I 5-I4 at 150 K and 5-II3b at 100 K. E = As for 1, and E = Sb for 2. | ||
This analysis demonstrates that both the nature of molecular components and the distribution of particular interactions are the factors that are responsible for cocrystal formation. It also clearly shows the real possibility of a supramolecular engineering of dedicated interactions established by certain combinations of donor- and acceptor-type functions. Note that the contact distances, like in 3, do not have to be rigorously limited by the sums of the van der Waals radii of the relevant atoms13 as well as that the intermolecular distances are shortened upon decreasing the temperature. Moreover, the observed molecular aggregations in all studied compounds correlate with the calculated electrostatic potentials and polarizability of molecules (Fig. S3, ESI†).
To understand the nature of binding in the studied systems we applied an analysis using the local energy decomposition (LED) method.14 For this, we investigated the isolated molecules of 1–5 at the DLPNO-CCSD(T)/def2-QZVPP//PBE0-D3BJ/def2-QZVPP level of theory. This approximation was chosen after a calibration procedure using two model systems, H3As⋯ICH3 and H3Sb⋯ICH3. This procedure and other details of calculations are provided in the ESI.† The LED results are summarized in Table 1. Here we focus on the properties of the title systems in comparison to the other calculated molecular model systems including H3N⋯ClF, HF⋯HF and CH4⋯CH4, which represent dominating halogen, electrostatic and dispersion-type interactions, respectively. The two calibration systems H3As⋯ICH3 and H3Sb⋯ICH3 are also included for comparison.
| ΔEtotb | ΔEtot | ΔEint | ΔECint/ΔEint,g % | E C disp/ΔEint,h % | E C CT/ΔECint,i % | E C (T)/ΔECint,j % | |||
|---|---|---|---|---|---|---|---|---|---|
| ΔEintc | ΔEgeo-prepd | ΔEHFinte | ΔECintf | ||||||
| a Calculations are at the DLPNO-CCSD(T)/def2-QZVPP//PBE0-D3BJ/def2-QZVPP level. b Total binding energy. c Total interaction energy. d Geometry preparation energy (deformation energy). e Interaction energy at the HF level. f Total correlation part of the interaction energy. g Contribution of the correlation into the total interaction energy. h Contribution of the dispersion interaction into the total interaction energy. i Contribution of the charge transfer part of the correlation into the total correlation interaction energy. j Contribution of triple excitations into the total correlation interaction energy. | |||||||||
| (CH3)3As⋯IC6F5 | −4.96 | −5.59 | 0.63 | 0.83 | −6.42 | 115 | 95 | 152 | 28 |
| (CH3)3Sb⋯IC6F5 | −4.12 | −4.51 | 0.39 | 1.61 | −6.12 | 136 | 106 | 129 | 27 |
| H3As⋯ICH3 | −1.52 | −1.51 | 0.00 | 1.54 | −3.06 | 202 | 157 | 75 | 19 |
| H3Sb⋯ICH3 | −1.57 | −1.58 | 0.01 | 1.75 | −3.33 | 211 | 159 | 78 | 19 |
| H3N⋯ClF | −9.35 | −10.84 | 1.49 | −5.00 | −5.84 | 54 | 55 | 380 | 49 |
| HF⋯HF | −4.58 | −4.65 | 0.07 | −3.82 | −0.83 | 18 | 23 | 809 | 36 |
| CH4⋯CH4 | −0.47 | −0.47 | 0.00 | 0.37 | −0.84 | 179 | 173 | 13 | 15 |
The calculated systems are stabilized due to interactions between their components and, on the other hand, destabilized because of the geometrical deformation of their components during adduct formation. The latter is especially notable for (CH3)3E⋯IC6F5 (here and below E = As or Sb) and H3N⋯ClF. The total interaction energy is decomposed into Hartree–Fock (HF) and correlation (C) contributions. At the HF level the interaction in both (CH3)3E⋯IC6F5 systems is repulsive and the overall stabilization is solely due to electron correlation. This is also true for H3E⋯ICH3, in which the relative contribution of correlation in the total interaction energy is even larger (up to about 200% of the total interaction energy). H3N⋯ClF shows a different picture: it is already stable at the HF level and additionally stabilized to a similar extent by correlation effects. The smallest influence of the electron correlation on the binding energy is in HF⋯HF.
The energy attributed to dispersion interactions between the components can be separated from the correlation part of the interaction energy. Table 1 lists these values relative to the total interaction energy; this allows a simplified characterization of the interaction type. Values larger than 100% clearly indicate dispersion-driven interactions, values between 50 and 100% can be related to interactions with balanced contributions of dispersive and non-dispersive nature, while values below 50% are specific for cases with primarily non-dispersive types of interactions. In (CH3)3E⋯IC6F5 these values are 95 and 106% for E = As or Sb, respectively. This shows importance of dispersion interactions in the stabilization of these systems.
In addition, it is worth to discuss the contributions of charge transfer (CT), relative to the total correlation interaction energy. Note, in LED analysis only those CT components are calculated, which originate from the correlation part of the interaction. Our calculations show that for (CH3)3E⋯IC6F5 both, dispersion and charge transfer effects, are important. The latter is larger for the system with arsenic (152%) than that with antimony (129%). In the smaller H3E⋯ICH3 systems, the relative importance of these electronic effects is different. The dispersion contribution is significantly larger, while the CT is less pronounced. In H3N⋯ClF the contribution of dispersion is relatively small, 55% of the total interaction energy, whereas that of charge transfer is large, 380% of total correlation part of the interaction energy. The extreme example of this type of interaction is provided by the dimer HF⋯HF, showing very weak dispersion and very strong CT components. The obverse extreme example is the methane dimer, in which dispersion plays the most important role (173%), whereas the charge transfer contribution is very small (13%).
We also calculated the relative contributions of triple excitations within the correlation part of the interaction energy. They are the largest in the cases with dominant CT interactions, up to 49% in H3N⋯ClF, and far less important for systems with strong dispersion-type component. This can be taken into account in calculations of properties for other molecular systems.
I⋯As and I⋯Sb interactions on the basis of 6-OI-fulvene with pnictogen electron donors have been recently investigated theoretically by others.15 In this work the MP2 method was used for geometry optimizations and calculations of stabilization energies. It is known that this method is not suitable for an accurate description of systems with significant contribution of dispersion.16 Thus, the reported stabilization energies for the aforementioned I⋯As and I⋯Sb systems are likely to be overestimated. An approach to energy decomposition these systems was undertaken as part of an NBO analysis. We note, that in MP2 calculations the NBO analysis is performed for the HF part. As we demonstrate, this is the destabilizing part of the total energy, at least for 1 and 2. Thus, the analysis of the HF energy does give the understanding of the stabilization effects.
It is worth paying attention to the fact that the I⋯As interaction of 3.3044(3) Å, in 1 at 100 K, is the shortest one of this type found for any experimentally characterized molecular (co)crystal. A search (crystal structure data without errors) of the Cambridge Structural Database9,17 for the ‘I⋯As’ structural motif revealed only four compounds in which the contact distances between As and I are shorter than in 1, but they are either between As and isolated iodide ions18 or constitute a secondary bond within an [As2I8]2− anion.19 Also, a similar search of the structural fragment ‘I⋯Sb’ for contact distances that are shorter than that found in 2 at 3.4951(4) Å, resulted mainly in Sb–I secondary bonds in compounds showing polymeric {[SbI5]2−}n chains,20 interactions between Sb and isolated iodide ions21 or in I⋯Sb contacts in dialkylcarbamodithioato-iodo-antimony(III) complexes.22 There are two molecular crystals showing shorter interactions, one of them is described as a (CH3)3Sb·SbI2CH3 adduct with I⋯Sb distances of 3.400 and 3.479 Å,23 whereas the second one is (CH3)SbI2 with antimony-involving halogen bonds of 3.397 and 3.469 Å.24 The distorted type II I⋯Sb halogen bonds, similar to that in 2, were only found between (CH3)SbI2 molecules. The existence of intermolecular C–I⋯As and C–I⋯Sb metal-involving halogen bonds was described only for two systems, that are similar to 1 and 2.9,17 These are the products of cocrystallization of 1,3,5-trifluoro-2,4,6-triiodobenzene (tftib) with triphenylarsine and -stibine ((tftib)(AsPh3) and (tftib)-(SbPh3), respectively). In contrast to 1 and 2 the interactions in (tftib)(AsPh3) and (tftib)(SbPh3) are less linear and their separation distances I⋯As and I⋯Sb of 3.4211(3) and 3.5747(3) Å, respectively, are significantly longer (Fig. S5, ESI†).8
Conclusions
Investigating small and structurally similar molecular systems with a limited number of well-defined interaction types, we have shown a successful approach to supramolecular reactions and (co)crystal engineering – an engineering of the very close, directional interactions that control the organization of cocrystals. Both, (CH3)3E·C6F5I (E = As: 1 and E = Sb: 2), show very close I⋯As and I⋯Sb intermolecular interactions, that represent directional and the shortest C–I⋯As and C–I⋯Sb halogen bonds of this type for any experimentally characterized molecular (co)crystal. The analysis of the overall picture of interactions in 1 and 2, as well as in their molecular components 3–5 shows the significance of certain short heteromolecular contacts, mainly charge transfer (CT) and dispersion interactions, that can be considered as the main cohesion forces holding the cocrystal components together and determining their relative geometric and packing arrangements. This observation is supported by the Hirshfeld surface analysis and quantum-chemical calculations.Experimental
All chemicals were used as received from commercial sources. The single crystal samples of all (CH3)3As·C6F5I (1), (CH3)3Sb·C6F5I (2), (CH3)3As (3) and (CH3)3Sb (4) were obtained in the in situ low-temperature (co)crystallization experiments. A procedure of the in situ low-temperature (co)-crystallization technique was earlier reported and described in detail.3,25 The samples of 3 and 4 as well as 1 and 2 – equimolar mixtures of 3 and 4 with C6F5I (5), respectively, were cryogenically loaded, using the Schlenk technique, into thin-walled glass capillaries, ca. 0.3 mm in diameter. The liquid samples were cooled on the diffractometer, in a nitrogen gas stream of an Oxford Cryosystems cooler. The samples initially froze as milky polycrystalline materials, which were then slowly warmed close to their melting points to reduce the number of (co)crystal seeds. Then, by manual local warming, monitored under a microscope mounted on the diffractometer, everything but a few crystal seeds was melted followed by slow cooling (rate of 1–5 K h−1). This procedure was repeated until a single seed crystal could be selected and grown. First data sets were collected at the highest possible temperatures restricted by the melting points26 and stability of the studied samples, then the samples were successively cooled and the X-ray scattering intensity data were collected at one or two low-temperature points and finally at 100.0(1) K. There was no indication of any phase change/transition, from the collected diffraction patterns for all single (co)crystals 1–4.The low-temperature X-ray diffraction intensity data were gathered on a SuperNova diffractometer, with MoKα radiation (λ = 0.71073 Å). The reflections were measured using the ω-scan technique. All data were accounted for the Lorentz, polarization and sample absorption effects. The CrysAlisPro program was used for the data collection, unit-cell determination and data reduction processes.27 The structures were solved by direct methods and refined with SHELX.283 was refined as an inversion twin. All the non-hydrogen atoms, in the studied (co)crystals, were refined with anisotropic displacement parameters. All hydrogen atoms were located in the subsequent difference Fourier maps and then the riding model was applied (in the case of 3 the geometrical restrains were also used). The hydrogen atom displacement parameters were taken with coefficient being 1.5 times larger than the respective equivalent isotropic parameters of their carrier carbon atoms.
The selected crystal data and structure determination summary are listed in Tables S1–S4 in the ESI.† The bond lengths, angles and the shortest intermolecular contacts are gathered in Tables S5–S11, ESI.† The intermolecular contacts were compared using the Hirshfeld surface analysis provided by CrystalExplorer17.12 The structure drawings were prepared using Mercury.9 The details on quantum-chemical calculations are provided as a supplementary material in ESI.†
Author contributions
M. Bujak: (co)crystallization, structure determination, XRD data analysis, quantum-chemical calculations and analysis, writing, reviewing and editing the manuscript. H.-G. Stammler: (co)crystallization, structure determination. Yu. V. Vishnevskiy: quantum-chemical calculations and analysis, writing. N. W. Mitzel: sample preparation, writing, reviewing and editing the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We gratefully acknowledge financial support from Deutsche Forschungsgemeinschaft (DFG, grant MI477/28-2, project no. 271386299 and grant VI 713/1-3). We are also grateful to HPC facilities at the Universität zu Köln for providing computational time and programs. We thank T. Glodde (Universität Bielefeld) for laboratory assistance.Notes and references
- (a) C. Aakeröy, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 387–391 CrossRef; (b) S. Cherukuvada, R. Kaur and T. N. Guru Row, CrystEngComm, 2016, 18, 8528–8555 RSC; (c) M. Karimi-Jafari, L. Padrela, G. M. Walker and D. M. Croker, Cryst. Growth Des., 2018, 18, 6370–6387 CrossRef CAS; (d) L. Sun, W. Zhu, F. Yang, B. Li, X. Ren, X. Zhang and W. Hu, Phys. Chem. Chem. Phys., 2018, 20, 6009–6023 RSC; (e) O. N. Kavanagh, D. M. Croker, G. M. Walker and M. J. Zaworotko, Drug Discovery Today, 2019, 24, 796–804 CrossRef CAS PubMed.
- (a) G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond: In Structural Chemistry and Biology, Oxford University Press, Oxford and New York, 1999 Search PubMed; (b) G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS; (c) A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2016, 116, 2775–2825 CrossRef CAS PubMed; (d) W. Wang, B. Ji and Y. Zhang, J. Phys. Chem. A, 2009, 113, 8132–8135 CrossRef CAS PubMed; (e) S. Scheiner, Acc. Chem. Res., 2013, 46, 280–288 CrossRef CAS PubMed; (f) A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321 CrossRef; (g) G. Sánchez-Sanz, C. Trujillo, I. Alkorta and J. Elguero, ChemPhysChem, 2019, 20, 1572–1580 CrossRef.
- (a) M. Bujak, H.-G. Stammler, S. Blomeyer and N. W. Mitzel, Chem. Commun., 2019, 55, 175–178 RSC; (b) M. Bujak, H.-G. Stammler and N. W. Mitzel, Cryst. Growth Des., 2020, 20, 3217–3223 CrossRef CAS.
- H. J. Frohn, S. Görg, G. Henkel and M. Läge, Z. Anorg. Allg. Chem., 1995, 621, 1251–1256 CrossRef CAS.
- P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2009, 15, 186–197 CrossRef.
- R. Blom, A. Haaland and R. Seip, Acta Chem. Scand., 1983, 37, 595–599 CrossRef.
- (a) R. J. Gillespie and R. S. Nyholm, Q. Rev., Chem. Soc., 1957, 11, 339–380 RSC; (b) R. J. Gillespie, Coord. Chem. Rev., 2008, 252, 1315–1327 CrossRef CAS.
- K. Lisac, F. Topić, M. Arhangelskis, S. Cepić, P. A. Julien, C. W. Nickels, A. J. Morris, T. Friščić and D. Cinčić, Nat. Commun., 2019, 10, 61 CrossRef CAS PubMed.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- (a) A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS; (b) S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885 CrossRef CAS; (c) S.-Z. Hu, Z.-H. Zhou, Z.-X. Xie and B. E. Robertson, Z. Kristallogr., 2014, 229, 517–523 CrossRef CAS.
- (a) G. R. Desiraju and R. Parthasarathy, J. Am. Chem. Soc., 1989, 111, 8725–8726 CrossRef CAS; (b) A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524 CrossRef CAS PubMed.
- (a) M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, P. R. Spackman, D. Jayatalika and M. A. Spackman, Crystal Explorer17, University of Western Australia, Perth (Australia), 2017, http://hirshfeldsurface.net Search PubMed; (b) P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011 CrossRef CAS PubMed; (c) J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627–668 CrossRef PubMed; (d) J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816 RSC; (e) M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- (a) I. Dance, New J. Chem., 2003, 27, 22–27 RSC; (b) M. Bujak, M. Podsiadło and A. Katrusiak, CrystEngComm, 2011, 13, 396–398 RSC.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792 CrossRef CAS PubMed.
- M. Hou, Q. Li and S. Scheiner, ChemPhysChem, 2019, 20, 1978–1984 CrossRef CAS.
- (a) A. Tkatchenko, R. A. DiStasio Jr., M. Head-Gordon and M. Scheffler, J. Chem. Phys., 2009, 131, 094106 CrossRef; (b) S. M. Cybulski and M. L. Lytle, J. Chem. Phys., 2007, 127, 141102 CrossRef; (c) P. Jurečka, J. Šponer, J. Černý and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- (a) C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed; (b) I. J. Bruno, J. C. Cole, P. R. Edgington, M. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 389–397 CrossRef.
- (a) G. Beurskens, P. T. Beurskens, J. H. Noordik, J. Willemse and J. A. Cras, Recl.: J. R. Neth. Chem. Soc., 1979, 98, 416–419 CAS; (b) O. Blacque, H. Brunner, M. M. Kubicki, F. Leis, D. Lucas, Y. Mugnier, B. Nuber and J. Wachter, Chem. – Eur. J., 2001, 7, 1342–1349 CrossRef CAS; (c) J. W. Dube and P. J. Ragogna, Chem. – Eur. J., 2013, 19, 11768–11775 CrossRef CAS.
- J. Janczak and G. J. Perpétuo, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2006, 62, m45–m47 CrossRef.
- N. Louvain, N. Mercier and F. Boucher, Inorg. Chem., 2009, 48, 879–888 CrossRef CAS.
- J. W. Wielandt, S. Petrie, N. L. Kilah, A. C. Willis, R. D. Dewhurst, F. Belaj, A. Orthaber, R. Stranger and S. B. Wild, Aust. J. Chem., 2016, 69, 524–532 CrossRef CAS.
- O. S. Urgut, I. I. Ozturk, C. N. Banti, N. Kourkoumelis, M. Manoli, A. J. Tasiopoulos and S. K. Hadjikakou, Mater. Sci. Eng., C, 2016, 58, 396–408 CrossRef CAS.
- H. J. Breunig, M. Denker and K. H. Ebert, J. Chem. Soc., Chem. Commun., 1994, 875–876 RSC.
- H. J. Breunig, K. H. Ebert, S. Gülec, M. Dräger, D. B. Sowerby, M. J. Begley and U. Behrens, J. Organomet. Chem., 1992, 427, 39–48 CrossRef CAS.
- (a) M. A. Viswamitra and K. K. Kannan, Nature, 1966, 209, 1016–1017 CrossRef CAS; (b) D. Brodalla, D. Mootz, R. Boese and W. Osswald, J. Appl. Crystallogr., 1985, 18, 316–319 CrossRef CAS; (c) A. D. Bond, Chem. Commun., 2003, 250–251 RSC; (d) A. E. Goeta and J. A. K. Howard, Chem. Soc. Rev., 2004, 33, 490–500 RSC; (e) M. T. Kirchner, D. Bläser and R. Boese, Chem. – Eur. J., 2010, 16, 2131–2146 CrossRef CAS PubMed; (f) M. Bujak and A. Katrusiak, CrystEngComm, 2010, 12, 1263–1268 RSC; (g) R. Boese, Z. Kristallogr., 2014, 229, 595–601 CrossRef; (h) D. Li, J. Schwabedissen, H.-G. Stammler, N. W. Mitzel, H. Willner and X. Zeng, Phys. Chem. Chem. Phys., 2016, 18, 26245–26253 RSC; (i) D. Dey, S. K. Nayak and D. Chopra, Intermolecular Interactions in In situ Cryocrystallized Compounds, in Understanding Intermolecular Interactions in the Solid State – Approaches and Techniques, Monographs in Supramolecular Chemistry No. 26, ed. D. Chopra, The Royal Society of Chemistry, London, 2019 Search PubMed.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, Taylor and Francis, Boca Raton, FL, 87th Edition, 2007 Search PubMed.
- CrysAlisPro, Rigaku Oxford Diffraction, version 1.171.40.56a, Rigaku Corporation, The Woodlands TX (USA), 2019 Search PubMed.
- (a) G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS; (b) G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic details and quantum-chemical calculations. CCDC 2057063–2057076. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ce01268a |
| This journal is © The Royal Society of Chemistry 2022 |