Multi-component crystals containing urea: mechanochemical synthesis and characterization by 35Cl solid-state NMR spectroscopy and DFT calculations†
Cameron S.
Vojvodin
ab,
Sean T.
Holmes
ab,
Lara K.
Watanabe
 c,
Jeremy M.
Rawson
c,
Jeremy M.
Rawson
 c and
Robert W.
Schurko
c and
Robert W.
Schurko
 *ab
*ab
aDepartment of Chemistry & Biochemistry, Florida State University, Tallahassee, FL 32306, USA. E-mail: rschurko@fsu.edu
bNational High Magnetic Field Laboratory, Tallahassee, FL 32310, USA
cDepartment of Chemistry & Biochemistry, University of Windsor, Windsor, ON N9B 3P4, USA
First published on 22nd February 2022
Abstract
Mechanochemical synthesis provides new pathways for the rational design of multi-component crystals (MCCs) involving anionic or cationic components that offer molecular-level architectures unavailable to MCCs comprising strictly neutral components. Structural characterization of the products of mechanochemical syntheses is essential for divining clear relationships between the nature of coformers, milling conditions, reaction mechanisms, and intermolecular bonding. Notably, when powder X-ray diffraction and solid-state NMR (SSNMR) are combined with plane-wave density functional theory (DFT) calculations, they offer opportunities for NMR crystallographic solutions and structural refinements. Herein, we report mechanochemical syntheses of five urea-containing MCCs of the form NR4Cl:xUrea·yH2O (R = H, Et, n-Pr; x = 1, 2, 3; y = 0, 2), which can be made in high yields (> ca. 99%) and great rapidity (<40 minutes). We demonstrate the utility of 35Cl SSNMR for providing distinct fingerprints for each urea MCC and detecting chlorine-containing impurities. Dispersion-corrected plane-wave DFT-D2* calculations are used for structural refinement and relating 35Cl electric field gradient (EFG) tensors and chloride ion hydrogen bonding environments. Finally, ab initio molecular dynamics calculations are used to study the impact of molecular motions on 35Cl EFG tensors, and their concomitant use for site assignment and NMR crystallography. Together, these techniques show great promise for future development of crystal structure prediction protocols using NMR of quadrupolar nuclei.
1. Introduction
The rational design of single-phase multi-component crystals (MCCs) is a flourishing area in the fields of crystal engineering and pharmaceutical sciences.1,2 Solid forms of MCCs include solvates, salts, cocrystals, and combinations thereof; these are of particular interest to the pharmaceutical industry, as they can be made from an active pharmaceutical ingredient (API) and one or more pharmaceutically-acceptable coformers (i.e., pharmaceutical cocrystals, PCCs).3,4 By carefully selecting the appropriate constituents and mode(s) of preparation, it is possible to tailor the physicochemical properties (i.e., solubility, stability, and/or bioavailability) of MCCs for specific applications.5–8Mechanochemical synthesis (i.e., synthetic techniques that induce chemical changes with mechanical action) offers unique opportunities for the production of MCCs.9–11 One common mechanochemical synthetic methods is ball milling, where solid reagents are ground at a constant milling frequency using ball bearings in a sealed jar. Mechanochemical syntheses offers many advantages over crystallization from solution, including rapid production of solid-phase products in minutes (as opposed to days by crystallization), high yields, and potential production of novel solid forms that are either difficult or impossible to obtain by crystallization.9,10,12–16 Furthermore, mechanochemical synthesis adheres to many of the tenets of green chemistry, including minimal use of solvent, low energy input, atom economy, and reduction of waste and/or by-products.10,13,16–18
There are several techniques for characterizing products of mechanochemical syntheses, including X-ray diffraction (XRD), calorimetric analysis (i.e., thermogravimetric analysis and differential scanning calorimetry), vapour sorption analysis, vibrational spectroscopy (i.e., infrared and Raman spectroscopies), and solid-state NMR (SSNMR) spectroscopy.19 Single-crystal X-ray diffraction (SCXRD) generally has limited applicability for characterizing the products of mechanochemical syntheses, which tend to be microcrystalline powders (hence, powder XRD, PXRD, is more often used). Of these methods, SSNMR spectroscopy provides the most detailed information about molecular-level structure and dynamics for materials ranging in nature from highly crystalline to completely amorphous. Moreover, SSNMR is increasingly being used in the context of NMR crystallography,20–27 an important set of techniques that holds much promise for improving crystal structure prediction (CSP) methods.28–31
NMR crystallography utilizes SSNMR spectroscopy, XRD methods, and quantum chemical calculations to solve, refine, and/or validate crystal structures.20–27 Density functional theory (DFT) calculations of chemical shifts (i.e., most commonly 1H, 13C, and 15N) aid in structural refinements and can be used as a figure of merit for assessing the quality of structures of organic solids.32–41 However, there are many classes of organic solids with cationic or anionic species that have quadrupolar NMR-active nuclides (i.e., nuclear spin I > ½; e.g., 7Li, 23Na, 35/37Cl, 39K, 79/81Br, etc.). Acquisition of the SSNMR spectra of such nuclides permits the determination of their electric field gradient (EFG) tensors, which are extremely sensitive to even the most subtle structural changes or differences, as well as to longer-range interactions, providing a unique source of additional structural information.42–50 In turn, comparison of experimentally measured and computationally derived EFG tensors offers an alternative means of refining crystal structures (and possibly even identifying potential structures in conjunction with CSP methods) that do not depend solely on the measurement, assignment, and computation of chemical shifts. Moreover, quantum chemical calculations of EFG tensors are much less computationally expensive than those of chemical shifts, since the former depend only on the electronic ground state of the molecule. Furthermore, in certain situations, the calculation of both EFG and CS tensors can be a very powerful means of structural refinement, since their corresponding interactions have independent physical origins. As such, it is desirable to develop NMR crystallographic techniques that use quadrupolar parameters for crystal structure prediction, refinement, and validation.46,51–62
Of the commonly occurring quadrupolar nuclei in organic solids, 35Cl (I = 3/2) is the most widely explored from the perspective of structural refinements based on the measurement and computation of EFG tensors;45,47,56,59,63–69 this is due to both the preponderance of hydrochloride (HCl) salts of organic solids (such as APIs) and the relative ease of measurement of 35Cl SSNMR spectra of chloride ions. 35Cl SSNMR spectra feature central transition (CT, +½ ↔ −½) powder patterns that are influenced by the second-order quadrupolar interaction (SOQI) and chemical shift anisotropy (CSA). The magnitudes of the principal components of the 35Cl EFG tensor, as well as its orientation with respect to the molecular frame, are sensitive to the local electronic environment of the chloride ion. Slight differences in the hydrogen bonding environments of chloride ions have dramatic impacts on their 35Cl EFG tensors, resulting in distinct sets of quadrupolar parameters (i.e., the quadrupolar coupling constant, CQ, and the asymmetry parameter, ηQ) for even very small differences or changes in structure; as such, 35Cl SSNMR spectra often yield unique spectral fingerprints, making them useful for the differentiation of polymorphs, hydrates, solvates, and other solid forms of organic HCl salts, as well as the detection of impurity phases.42,45,47,56,59,63–68
In order to design an NMR crystallography protocol that can be used for solving crystal structures of MCCs involving cationic and/or ionic species, including PCCs, a series of simple candidate systems is required that meet the following criteria: (i) elementary chemical structures; (ii) small numbers of atoms in the asymmetric units; and (iii) abundance of useful NMR handles. One family of MCCs that meets these criteria is urea MCCs (i.e., MCCs comprised of urea molecules and other elementary ionic species). Urea remains a vital reagent in many areas of chemistry,70–76 and is able to form supramolecular assemblies such as inclusion compounds77–80 and cocrystals,72,73,81–84 which can be synthesized mechanochemically in some cases. Urea is an ideal molecule for investigation of the syntheses and structures of MCCs, as well as for benchmarking NMR crystallographic protocols, since it is small and has both hydrogen-bond donor and acceptor groups.
Herein, we discuss the mechanochemical preparation of urea MCCs and their structural characterization using 35Cl and 13C SSNMR spectroscopy, PXRD and/or SCXRD, and DFT calculations. Novel ball milling preparations of the MCCs NEt4Cl:2Urea, NEt4Cl:2Urea·2H2O, NPr4Cl:2Urea, NPr4Cl:3Urea, and NH4Cl:Urea, which are aimed at maximizing yield and optimizing efficiency, are described, and contrasted with previously-reported preparations featuring crystallization from solution. The identities and purities of the products of mechanochemical syntheses (i.e., MCCs, starting educts, and other potential impurities) are confirmed using 35Cl SSNMR and PXRD. Dispersion-corrected plane-wave DFT-D2* calculations58,85 are used to refine the crystal structures, assess the agreement between experimentally measured and theoretically derived 35Cl EFG tensors, and elucidate relationships between NMR parameters and molecular-level structure. Ab initio molecular dynamics (aiMD) simulations are used to probe the impact of molecular motions upon 35Cl EFG tensors, and to gauge the possibility of using such calculations for site assignments and NMR crystallographic analyses. Finally, we discuss the potential of these characterization methods for use in the design of NMR crystallographic-based CSP protocols for determining the structures of complex MCCs and PCCs.
2. Experimental and computational methods
2.1 Materials and syntheses
Ammonium chloride (NH4Cl), tetraethylammonium chloride monohydrate (NEt4Cl·H2O), tetra(n-propyl)ammonium chloride (NPr4Cl), urea, and solvents were purchased from Sigma Aldrich Canada Ltd. The solid educts were oven-dried prior to use at 110 °C for 16 hours, and their identities and purities verified using PXRD (Fig. S1†).Each MCC was prepared mechanochemically via ball milling of the dried reagents (and microliter quantities of H2O where indicated) in the appropriate molar ratios (Table S1†). These syntheses used a Retsch Mixer Mill 400, 10 mL stainless steel milling jars, and two 7 mm stainless steel ball bearings. The total mass of the solid reagents in each synthesis was scaled to ca. 200 mg. The maximum milling rate of 30 Hz was used for all syntheses. All syntheses were optimized to obtain maximum yield and optimized efficiency.
Crystals of NH4Cl:Urea, suitable for analysis by SCXRD, were grown by slow evaporation of an aqueous solution of equimolar NH4Cl and urea. Crystals of NPr4Cl were grown from a saturated DCM solution via slow diffusion of anhydrous pentane.
2.2 Powder X-ray diffraction
For all materials except NPr4Cl, PXRD patterns were acquired using a Rigaku MiniFlex benchtop diffractometer with a Cu Kα (λ = 1.541 Å) radiation source and a D/teX Ultra2 detector. Samples were packed in zero-background silicon wafers with a well size of 5 mm × 0.2 mm, and mounted on an eight-position autosampler. Experiments were conducted with an X-ray tube voltage of 40 kV, an amperage of 15 mA, 2θ angles ranging from 5–50°, a step size of 0.030°, and a dwell time of 5 s, resulting in an acquisition time of ca. 12 minutes per sample.For NPr4Cl, the PXRD pattern was acquired using a Rigaku Smartlab diffractometer with a Cu Kα radiation source and a D/teX Ultra2 detector. The sample was packed on a zero-background wafer and mounted in an air-tight sample holder. Experiments were conducted with an X-ray tube voltage 40 kV, an amperage of 44 mA, a length limiting slit of 5 mm, 2θ angles ranging from 5–50°, a step size of 0.030°, and a dwell time of 5 s, resulting in an acquisition time of ca. 12 minutes per sample.
The CrystalDiffract software package was used to simulate PXRD patterns for materials with known crystal structures.
2.3 Single-crystal X-ray diffraction
Crystals of NH4Cl:Urea or NPr4Cl were mounted on a cryoloop using paratone oil. Data were collected using φ and ω scans at a temperature of either 170(2) K or 150(2) K on a Bruker D8 Venture four-circle diffractometer equipped with a Photon 100 CCD detector using Mo Kα radiation (λ = 0.7107 Å). The temperature was controlled using an Oxford Cryosystems Cryostat (700 Series Cryostream Plus). An appropriate data collection strategy was determined using APEX III software,86 based on an initial cell indexing. The raw data were integrated and reduced using SAINT,86 and corrected for absorption effects using SADABS.86 Structures were solved using intrinsic phasing87 and refined against F2 with SHELXL88 within OLEX2.89 The positions of all non-hydrogen atoms were refined anisotropically. Hydrogen atoms were placed in idealized positions and refined using a riding model for NPr4Cl, or by Fourier difference maps and refined isotropically for NH4Cl:Urea. The structures of NPr4Cl and NH4Cl:Urea have been deposited on the Cambridge Structural Database [CSD deposition numbers 2120237 and 2120238, respectively].2.4 Solid-state NMR spectroscopy
2.5 Density functional theory calculations
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 total steps). The unit cell was altered from Pmna symmetry to a supercell with P1 symmetry, which increases the number of unique chlorine environments from two to eight. These calculations employed an SCF threshold of 2 × 10−6 eV atom−1, a plane-wave cutoff energy of 325 eV, and evaluated integrals over the Brillouin zone using a Monkhorst-Pack grid with a k-point spacing of 0.10 Å−1.
000 total steps). The unit cell was altered from Pmna symmetry to a supercell with P1 symmetry, which increases the number of unique chlorine environments from two to eight. These calculations employed an SCF threshold of 2 × 10−6 eV atom−1, a plane-wave cutoff energy of 325 eV, and evaluated integrals over the Brillouin zone using a Monkhorst-Pack grid with a k-point spacing of 0.10 Å−1.
3. Results and discussion
Here, we discuss (i) the characterization of the reagents NH4Cl, NPr4Cl, and NEt4Cl·H2O by 35Cl{1H} SSNMR spectroscopy, (ii) the synthesis and characterization of urea MCCs involving either NEt4Cl or NPr4Cl, as well as a comparison of their experimental and calculated 35Cl EFG tensors, and (iii) the synthesis and characterization of NH4Cl:Urea, which is distinct from all of the other systems, due to molecular-level motions that influence the measurement of 35Cl EFG tensors. PXRD and 13C SSNMR spectroscopy are used as supporting characterization techniques (Fig. S2 and S3, and Table S2†). We also report a novel crystal structure of NPr4Cl at 150 K and redetermine the crystal structure of NH4Cl:Urea at 170 K (Fig. S4 and Table S3†).In all cases, 35Cl SSNMR spectra were acquired at two distinct magnetic fields to aid in the precise determination of the principal components of the EFG and CS tensors, since the manifestations of the SOQI and CSA in CT powder patterns have distinct dependences on the strength of the magnetic field (i.e., the effects of the former and latter scale proportionally to B0−1 and B0, respectively, for most sets of Euler angles describing the relative orientation of the EFG and CS tensors, vide infra).95 Additionally, acquisition of 35Cl MAS NMR spectra allows for accurate determination of the δiso, CQ, and ηQ, due to the averaging of the 35Cl CSA (under a high enough MAS rate) and partial averaging of the SOQI; this aids in the fitting of the static NMR spectra using eight parameters, including the span (Ω), and skew (κ) of the CS tensor, and the aforementioned Euler angles (α, β, and γ) (see Table 1 for definitions of all parameters).
| Material (Cl site) | C Q (MHz) | η Q | δ iso (ppm) | Ω (ppm) | κ | α (°) | β (°) | γ (°) | |
|---|---|---|---|---|---|---|---|---|---|
| The experimental uncertainties in the last digit for each value are indicated in parentheses.a The principal components of the EFG tensors are ranked |V33| ≥ |V22| ≥ |V11|. The quadrupolar coupling constant and asymmetry parameter are given by CQ = eQV33/h, and ηQ = (V11 − V22)/V33, respectively. The sign of CQ cannot be determined from the experimental 35Cl spectra.b The principal components of the chemical shift tensors are defined using the frequency-ordered convention such that δ11 ≥ δ22 ≥ δ33. The isotropic chemical shift, span, and skew are given by δiso = (δ11 + δ22 + δ33)/3, Ω = δ11 − δ33, and κ = 3(δ22 − δiso)/Ω, respectively.c The Euler angles α, β, and γ define the relative orientation of the EFG and chemical shift tensors. Euler angles are reported using the ZY′Z″ convention.d The fits for these patterns were constrained using parameters obtained from DFT calculations.e Theoretical EFG and CS tensor parameters were obtained from calculations on XRD-derived structures and structures refined at the RPBE-D2* level.f The positions of hydrogen atoms were not reported in these crystal structures.g This parameter is not applicable or has little-to-no effect on the simulated 35Cl SSNMR pattern. | |||||||||
| NEt4Cl:2Urea | Exp. | 1.82(9) | 0.95(5) | 93(1) | 54(4) | 0.05(3) | 4(10) | 30(3) | 110(5) |
| DFT-D2* | −1.71 | 0.87 | 85 | 88 | −0.14 | 4 | 42 | 99 | |
| XRDe | 2.35 | 0.67 | 62 | 72 | −0.05 | 151 | 33 | 303 | |
| NEt4Cl:Urea·2H2O | Exp. | 2.88(4) | 0.95(2) | 61(2) | 78(10) | 0.51(8) | 82(6) | 3(5) | 173(9) |
| DFT-D2* | −3.27 | 0.88 | 53 | 73 | 0.57 | 76 | 2 | 36 | |
| XRDf | — | — | — | — | — | — | — | — | |
| NPr4Cl:2Urea | Exp. | 2.73(3) | 0.79(4) | 79(1) | 81(3) | 0.80(6) | 83(10) | 75(10) | 132(20) |
| DFT-D2* | 2.84 | 0.69 | 70 | 84 | 0.57 | 90 | 78 | 162 | |
| XRD | 2.75 | 0.47 | 48 | 74 | 0.6 | 90 | 70 | 190 | |
| NPr4Cl:3Urea | Exp. | 0.92(1) | 0.76(2) | 91(1) | 57(7) | 0.53(6) | 36(5) | 66(4) | 90(5) |
| DFT-D2* | −1.32 | 0.89 | 83 | 42 | 0.19 | 202 | 58 | 216 | |
| XRD | 2.10 | 0.25 | 57 | 36 | 0.34 | 179 | 34 | 200 | |
| NH4Cl:Urea (Cl1) | Exp. | 3.52(5) | 0.14(7) | 103(2) | 98(7) | 0.00(8) | 90(5) | 77(7) | 178(4) |
| DFT-D2* | −3.33 | 0.53 | 102 | 98 | −0.49 | 90 | 1 | 180 | |
| XRD | 3.39 | 0.74 | 71 | 88 | 0.13 | 90 | 58 | 180 | |
| NH4Cl:Urea (Cl2) | Exp. | 2.62(6) | 0.49(5) | 100(2) | 71(5) | 0.78(10) | 89(25) | 8(5) | 178(30) |
| DFT-D2* | 4.63 | 0.34 | 91 | 92 | 0.24 | 90 | 76 | 90 | |
| XRD | −2.50 | 0.90 | 74 | 86 | −0.44 | 90 | 11 | 90 | |
| NH4Cl | Exp. | < 0.03 | n/a | 120(1) | n/a | n/ag | n/a | n/a | n/a |
| DFT-D2* | 0 | n/a | 120 | 0 | n/a | n/a | n/a | n/a | |
| XRDf | — | — | — | — | — | — | — | — | |
| NPr4Cl | Exp. | 0.16(2) | 0d | 57(1) | 14(2) | −1.00d | 90d | 90d | 180d |
| DFT-D2* | 0.1 | 0 | 58 | 17 | −1.00 | 90 | 90 | 180 | |
| XRD | −0.05 | 0 | 44 | 17 | −1.00 | 90 | 90 | 180 | |
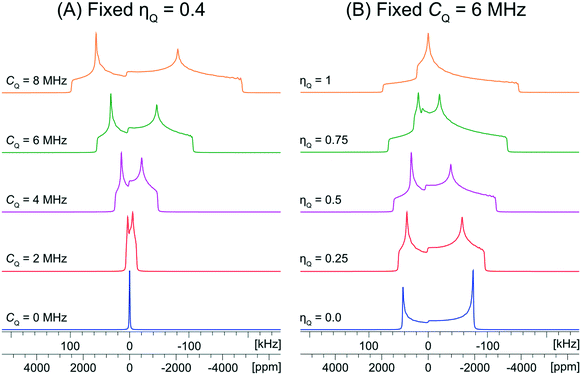
The values of the quadrupolar parameters determined from analysis of 35Cl CT patterns are of great value, since they are directly related to the principal components of the EFG tensor, which in turn provides information on the local ground state electron density about the chloride ions.111–113 Increased values of CQ, which result in broadening of the CT patterns (Scheme 1A), correspond to ground state electron distributions that increasingly depart from spherical (platonic) symmetry. For instance, if the electronic environment of a chloride ion is perturbed by hydrogen bonding, the absolute magnitude of CQ is generally observed to increase. On the other hand, values of ηQ, which produce patterns where the discontinuities adopt different relative positions (Scheme 1B), describe the axial symmetry of the EFG tensor, and correspondingly, the cylindrical symmetry of the ground state electron density (0 ≤ ηQ ≤ 1, where ηQ = 0 indicates perfect axial symmetry). For example, a Cl atom involved in a covalent C–Cl bond typically has an axially symmetric EFG tensor (ηQ = 0), whereas Cl− ions featuring multiple short H⋯Cl hydrogen bonds often have non-axially symmetric EFG tensors (ηQ ≠ 0). Unfortunately, interpretation of chlorine CS tensors is not as straightforward as this and relies heavily upon computationally expensive DFT calculations; hence, we will focus on exploring relationships between structure, symmetry, and 35Cl EFG tensors throughout this work.
3.1 Educts: NH4Cl, NPr4Cl, and NEt4Cl·H2O
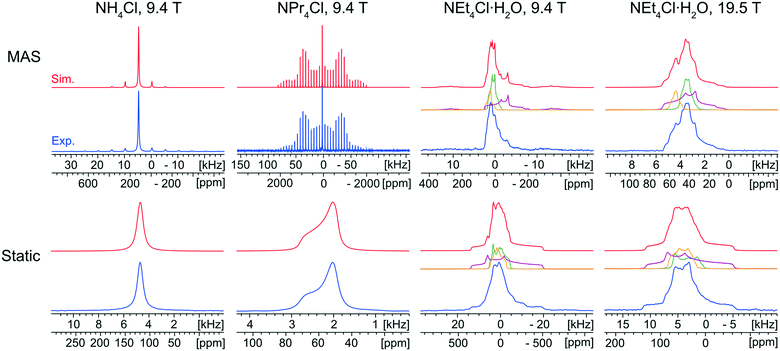
The characterization of the educts is important, primarily for the purpose of identifying their potential presence in the reaction products arising from either ball milling or recrystallization from solution. Fortunately, each of the ammonium chloride salts yields a distinct 35Cl NMR spectral fingerprint (Fig. 1).The static and MAS 35Cl{1H} SSNMR spectra (9.4 T) of NH4Cl are narrow and nearly featureless, indicating a single chlorine environment with negligible influence from the SOQI (CQ < 30 kHz) or CSA; this observation is consistent with the cubic space group of its crystal structure (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, Z′ = 1, Z = 1), in which the chloride ion sits at a site of local octahedral symmetry.114
m, Z′ = 1, Z = 1), in which the chloride ion sits at a site of local octahedral symmetry.114
The 35Cl{1H} MAS spectrum (9.4 T) of NPr4Cl is characterized by a sharp, featureless centerband corresponding to the CT, and a manifold of spinning sidebands (SSBs) arising from the satellite transitions (STs, ±3/2 ↔ ±1/2). Fitting this spectrum yields δiso = 57(1) ppm, CQ = 160(20) kHz, and ηQ = 0.0. The 35Cl static CT spectrum of NPr4Cl is dominated by the effects of CSA and characterized by Ω = 14(2) ppm and κ = −1.0. The CSA is small and has no observable influence on the SSBs in the MAS spectrum. The crystal structure of NPr4Cl is in the tetragonal space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) (Z′ = 0.25, Z = 2), with a single chlorine environment in the asymmetric unit. The magnitude of CQ is very small because the chloride ion, which is positioned on the C4 axis of the tetragonal unit cell, does not participate in hydrogen bonding with the surrounding NPr4+ ions (i.e., all H⋯Cl− distances are greater than 2.8 Å).115
(Z′ = 0.25, Z = 2), with a single chlorine environment in the asymmetric unit. The magnitude of CQ is very small because the chloride ion, which is positioned on the C4 axis of the tetragonal unit cell, does not participate in hydrogen bonding with the surrounding NPr4+ ions (i.e., all H⋯Cl− distances are greater than 2.8 Å).115
Finally, the 35Cl{1H} NMR spectra of NEt4Cl·H2O feature patterns that are substantially broader and more complex than those of the other educts, clearly indicating the effects of the SOQI. The NMR spectra are simulated with a minimum of three overlapping patterns, based upon the number of visible discontinuities in the MAS spectra, with values of CQ that are larger than those observed for NH4Cl and NPr4Cl (Table S4†). These broader patterns are clearly indicative of H⋯Cl− hydrogen bonds between the chloride ions and surrounding water molecules. The ratios of the integrated intensities for the three overlapping patterns are ca. 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (MAS) and 1
1 (MAS) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.4
4.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4 (static). Assuming the presence of only three patterns with distinct quadrupolar parameters, these spectra indicate the presence of three magnetically non-equivalent chloride ion sites. At first, this would seem to be inconsistent with the known crystal structure (C2/c, Z′ = 1, Z = 8), which comprises a single crystallographically distinct chloride ion. The presence of multiple patterns could arise from local disorder in the ethyl moieties (which is predicted in the crystal structure, and verified by the presence of eight distinct methyl peaks in the 1H→13C{1H} CP/MAS spectrum, Fig. S2A†).116 This system could be a subject for future investigations, but is beyond the scope of the current work – for now, the 35Cl CT patterns of NEt4Cl·H2O are strictly used to identify the presence of educt, if present.
1.4 (static). Assuming the presence of only three patterns with distinct quadrupolar parameters, these spectra indicate the presence of three magnetically non-equivalent chloride ion sites. At first, this would seem to be inconsistent with the known crystal structure (C2/c, Z′ = 1, Z = 8), which comprises a single crystallographically distinct chloride ion. The presence of multiple patterns could arise from local disorder in the ethyl moieties (which is predicted in the crystal structure, and verified by the presence of eight distinct methyl peaks in the 1H→13C{1H} CP/MAS spectrum, Fig. S2A†).116 This system could be a subject for future investigations, but is beyond the scope of the current work – for now, the 35Cl CT patterns of NEt4Cl·H2O are strictly used to identify the presence of educt, if present.
3.2 NR4Cl:xUrea·yH2O (R = Et, Pr; x = 1, 2, 3; y = 0, 2)
Mechanochemical syntheses of NEt4Cl:2Urea, NEt4Cl:Urea·2H2O, NPr4Cl:2Urea, and NPr4Cl:3Urea were all successful, as judged by comparison of PXRD patterns of the solid products with simulated PXRD patterns based on the known crystal structures (Fig. S5, Table S5†).117–119 It is noteworthy, however, that this does not preclude the presence of impurity phases, rather that the quantity of impurity phase(s) is low, typically <5–10%, vide infra.120 Initial trials revealed that all MCCs could be mechanochemically synthesized in 30–40 minutes, which is a significant improvement over growing single crystals via crystallization from solution, which can require several days.75 Remarkably, further optimizations revealed that most MCCs could be prepared much more quickly, with NEt4Cl:2Urea, NPr4Cl:2Urea, and NPr4Cl:3Urea taking only one minute (there was no reduction in preparation time for NEt4Cl:Urea·2H2O, which took 40 minutes, Table S1, Fig. S6–S10†). Some mechanochemical syntheses attempted with shorter milling times resulted in impurities that are detectable via PXRD (Fig. S6–S10†). Interestingly, the anhydrous NEt4Cl:2Urea and hydrated NEt4Cl:Urea·2H2O MCC products are dependent upon the ratio of urea to NEt4Cl·H2O educts (i.e., 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively). Preparations of NEt4Cl:Urea·2H2O with 0, 1, and 2 eq. of H2O yields products with similar pXRD patterns (Fig. S11†), indicating that in the case of the mechanochemical reaction with no additional liquid, water must come from the educt hydrate and the atmosphere.
1, respectively). Preparations of NEt4Cl:Urea·2H2O with 0, 1, and 2 eq. of H2O yields products with similar pXRD patterns (Fig. S11†), indicating that in the case of the mechanochemical reaction with no additional liquid, water must come from the educt hydrate and the atmosphere.
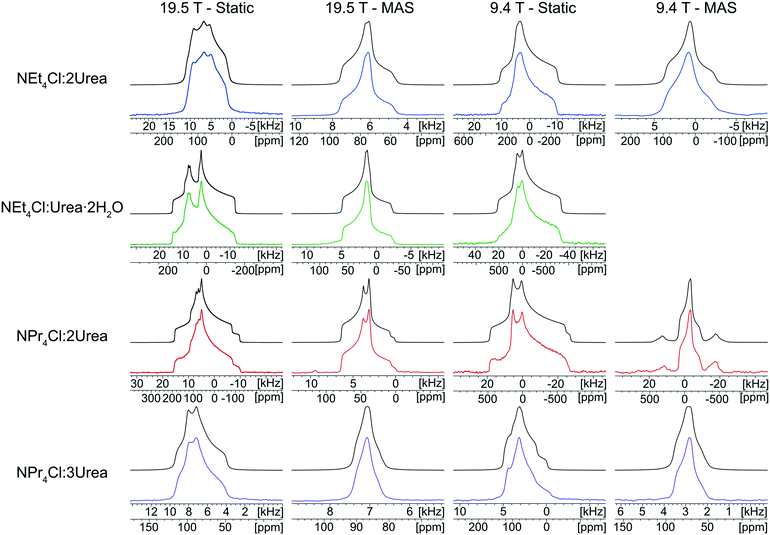
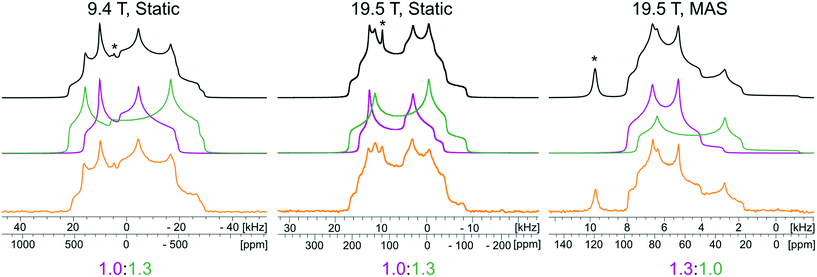
The 35Cl SSNMR spectra of these MCCs acquired under static and MAS conditions at 9.4 T and 19.5 T (Fig. 2) are distinct from those of the simple ammonium chloride salts (cf.Fig. 1), indicating that no impurity phases are present (N.B.: in many instances, carefully designed SSNMR experiments can quantitatively detect small amounts of impurities that are not always evident in PXRD patterns).38,64,121–124 In each spectrum, a CT pattern dominated by the SOQI is observed that corresponds to a single magnetically and crystallographically distinct chloride ion, in accordance with the reported crystal structures, where all four MCCs are reported to crystallize in either the monoclinic P21/c or P21/n space groups (Table S5†) and have one crystallographically distinct chloride ion in the asymmetric unit (Z′ = 1, Z = 4).117–119 The 35Cl EFG tensor parameters obtained from the analytical simulations feature values of CQ between 0.96(1) MHz and 2.88(4) MHz (Table 1), which are within the typical range observed for organic HCl salts.90 Additionally, the value of the asymmetry parameter is found to be high (ηQ ≥ 0.70) in each case.
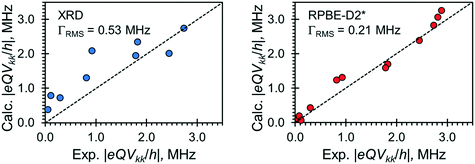
Relationships between the NMR parameters and crystal structures can be elucidated with quantum chemical calculations. Recent studies have demonstrated the use of plane-wave DFT calculations with semiempirical dispersion-corrected force-fields that result in higher quality crystal structures and more accurate predictions of EFG tensors than is possible from DFT calculations not employing these methods.41,57,58,85 This force-field correction, DFT-D2*, based on a modification on Grimme's two-body model,102 was developed through refinements of the crystal structures of various organic solids and subsequent calculations of 35Cl, 14N, and 17O EFG tensors.41,57,58,85 Structural models based on the reported crystal structures for each MCC were subjected to geometry optimizations using the DFT-D2* method. The 35Cl EFG tensors were calculated for both XRD-derived and DFT-D2* structural models and compared with experimentally determined tensors (Fig. 3). The RMS EFG distance58 is used as a figure of merit for assessing the agreement between calculated and experimental 35Cl EFG tensors. The DFT-D2* calculations result in better agreement between calculation and experiment, since the RMS EFG distance is ΓRMS = 0.53 MHz for the XRD-derived models, and much lower, ΓRMS = 0.21 MHz, for the DFT-D2* models (ESI† S2), which is consistent with our previous work.58,63 The structural models with atomic coordinates refined at the DFT-D2* level indicate that each chloride ion features between four and six H⋯Cl− contacts with urea and/or water molecules (Table 2) that are all greater than ca. 2.2 Å, which is consistent with the small magnitudes of CQ.45
| Material (Cl site) | Hydrogen bond typea | H⋯Cl− distanceb (Å) | X⋯Cl− distancec (Å) | X–H⋯Cl− angled (°) | δ iso (ppm) | C Q (MHz) | η Q |
|---|---|---|---|---|---|---|---|
| a The functional group involved in the H⋯Cl− hydrogen bond (e.g., H2O⋯Cl− signifies a hydrogen bond with a water molecule Urea⋯Cl− signifies a hydrogen bond with a urea molecule, and NH4+⋯Cl− signifies a hydrogen bond with an ammonium cation). b Hydrogen bonds (<2.6 Å), as determined from crystal structures refined at the DFT-D2* level. Two distances are listed for bidentate hydrogen bonds with urea molecules. c Distance between the chloride ion and the hydrogen-bond donor atom (X = N, O). Two distances are listed for bidentate hydrogen bonds with urea molecules. d Angle between the hydrogen-bond donor atom (X = N, O), the hydrogen atom, and the chloride anion. Two angles are listed for bidentate hydrogen bonds with urea molecules. | |||||||
| NEt4Cl:2Urea | Urea⋯Cl− | 2.318 | 3.276 | 173.2 | 85 | −1.71 | 0.87 |
| Urea⋯Cl− | 2.334 | 3.279 | 167.0 | ||||
| Urea⋯Cl− | 2.378 | 3.328 | 169.4 | ||||
| Urea⋯Cl− | 2.404 | 3.349 | 167.6 | ||||
| NEt4Cl:Urea·2H2O | H2O⋯Cl− | 2.236 | 3.145 | 165.7 | 53 | −3.27 | 0.88 |
| H2O⋯Cl− | 2.249 | 3.179 | 180.0 | ||||
| H2O⋯Cl− | 2.290 | 3.218 | 177.3 | ||||
| Urea⋯Cl− | 2.498 | 3.453 | 173.4 | ||||
| NPr4Cl:2Urea | Urea⋯Cl− | 2.415, 2.448 | 3.319, 3.345 | 156.9, 155.4 | 70 | 2.84 | 0.69 |
| Urea⋯Cl− | 2.433, 2.499 | 3.332, 3.383 | 155.8, 153.1 | ||||
| NPr4Cl:3Urea | Urea⋯Cl− | 2.402, 2.508 | 3.307, 3.381 | 157.4, 151.7 | 83 | −1.32 | 0.89 |
| Urea⋯Cl− | 2.441, 2.427 | 3.314, 3.320 | 155.1, 155.2 | ||||
| Urea⋯Cl− | 2.451, 2.539 | 3.355, 3.424 | 157.3, 153.9 | ||||
| NH4Cl:Urea (Cl1) | NH4+⋯Cl− | 2.265 | 3.229 | 169.3 | 102 | −3.33 | 0.53 |
| NH4+⋯Cl− | 2.265 | 3.229 | 169.3 | ||||
| Urea⋯Cl− | 2.302 | 3.257 | 175.6 | ||||
| Urea⋯Cl− | 2.319 | 3.270 | 172.3 | ||||
| Urea⋯Cl− | 2.536, 2.536 | 3.420, 3.420 | 153.9, 153.9 | ||||
| NH4Cl:Urea (Cl2) | NH4+⋯Cl− | 2.259 | 3.230 | 173.3 | 91 | 4.63 | 0.34 |
| NH4+⋯Cl− | 2.259 | 3.230 | 173.3 | ||||
| Urea⋯Cl− | 2.336 | 3.281 | 169.4 | ||||
| Urea⋯Cl− | 2.336 | 3.281 | 169.4 | ||||
| Urea⋯Cl− | 2.476, 2.548 | 3.369, 3.423 | 155.3, 152.5 | ||||
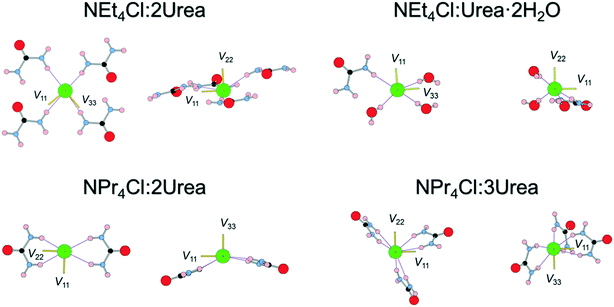
The orientations of the principal components of the 35Cl EFG tensors in their molecular frames give insight into the local chloride ion hydrogen-bonding environments (Fig. 4). For the purpose of this discussion, hydrogen bonds between chloride ions and nearby hydrogen atoms are defined as those with distances of 2.6 Å or less,115,125,126 whereas the term short contacts is used to refer to hydrogen bonds with distances of ca. 2.2 Å or less, based on earlier observations of their dominant influence on 35Cl EFG tensors.45 Although we have established relationships between 35Cl EFG tensor parameters and the local environments of chlorine ions featuring one or two short contacts,45 these relationships remain poorly understood for systems without short contacts, such as the urea MCCs, as well as for hydrates of organic HCl salts;45,90 as such, continued exploration of these relationships is warranted.
The chloride ions in NEt4Cl:2Urea feature four monodentate hydrogen bonds involving urea molecules. The largest principal component of the 35Cl EFG tensor, V33, is oriented near the bonding axis of the shortest hydrogen bond, ∠(H–Cl–V33) = 19.3°, whereas V22 is oriented perpendicular to the pseudo-plane in which the chloride ion and four urea molecules reside.
By contrast, three of the four hydrogen bonds in NEt4Cl:Urea·2H2O involve water molecules, and a fourth involves urea. V33 resides between the second- and third-shortest hydrogen bonds with water molecules (N.B.: these water molecules are crystallographically equivalent through inversion symmetry). In both cases, the sign of CQ is predicted to be negative (i.e., V33 is positive since Q(35Cl) = −8.165 fm2).45
NPr4Cl:2Urea has four H⋯Cl− hydrogen bonds, all of which are ca. 2.4 Å, stemming from bidentate interactions with two urea molecules, and resulting in a pyramidal Cl·(Urea)2− structural unit. V33 is oriented perpendicular to the bonding axis with the shortest contact, ∠(H–Cl–V33) = 99.4°, whereas V11 and V22 reside in the plane of the shortest contact (i.e., the EFGs are positive within this plane). The sign of CQ is predicted to be positive (i.e., V33 is negative), consistent with the orientation of V33 perpendicular to the shortest contacts.
Finally, the six hydrogen bonds in NPr4Cl:3Urea, which range from 2.40–2.54 Å, involve bidentate interactions with three urea molecules, forming a paddlewheel configuration about the chloride ion. For this chlorine site, which features the smallest value of CQ for any of the MCCs, the orientation of the 35Cl EFG tensor is not constrained by an apparent symmetry or pseudo-symmetry axis, and no simple relationships between tensor orientation or the sign of CQ (predicted to be negative) are apparent.
In summary, this series of model structures featuring chloride ions with no short contacts reveals a number of interesting relationships between local structures and 35Cl EFG tensor orientations, where in many instances, one or more principal components are found to align along or near key symmetry or pseudo-symmetry elements. Clearly, further investigations of more systems like these are likely to reveal EFG tensor-structure relationships that may greatly improve crystal structure prediction protocols.
Finally, the chlorine CS tensors for the four MCCs were calculated using the GIPAW approach (Fig. S12†). We find that refinement of the initial XRD-derived structures at the DFT-D2* level results in more accurate predictions of CS tensors than calculations on XRD-derived structures, which underestimate every principal component of the chlorine CS tensors, and are characterized by an RMS CS distance of ΔRMS = 32 ppm (ESI† S3).127 In contrast, calculations on the DFT-D2* refined structures do not feature this systematic error and are characterized by ΔRMS = 11 ppm. Unlike the EFG tensors, there are apparently no straightforward relationships between the chlorine CS tensors and the types, numbers, and spatial arrangements of hydrogen bonds that can be drawn; however, there is potential for chlorine CS tensor parameters to be used as additional constraints in NMR crystallographic protocols.
3.3 NH4Cl:Urea
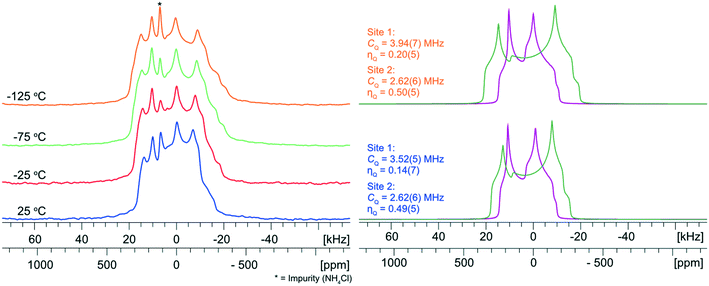
NH4Cl:Urea was synthesized using both crystallization from water (seven days to yield crystals suitable for analysis by SCXRD) and ball milling (10 minutes). Both preparations led to the formation of the same product, as indicated by their similar PXRD patterns; however, neither of these match the simulated PXRD patterns based on previously-reported crystal structures (Fig. S13†).128–130 In particular, these simulations indicate the presence of several low angle reflections (2θ < 12°) that are not detected in our experimental PXRD patterns. Single crystals of suitable size were grown for SCXRD analysis to determine if these differences arise from (i) an issue with the ball milling preparation method, (ii) production of a novel NH4Cl:Urea form, and/or (iii) problems with the previously-reported crystal structures.128–130Our new crystal structure of NH4Cl:Urea crystallizes in the orthorhombic space group Pmna, with Z′ = 1, Z = 8, unit cell parameters of a = 7.8835(4) Å, b = 17.0669(8) Å, and c = 8.0099(3) Å, and an asymmetric unit that has two crystallographically-distinct pairs of half molecules that are either bisected by a crystallographic C2 symmetry axis or feature a mirror plane in the plane of the molecule (see Table S3† for details). The simulated PXRD patterns based on this crystal structure match the experimental patterns of the solids from mechanochemical synthesis and crystallization from water. Additionally, our Pmna solution was subjected to a plane-wave DFT-D2* geometry optimization and was found to have a static lattice energy that agrees to within 0.7 kJ mol−1 of the previously-reported Pmna structures.129,130 A calculation was also attempted on the previously-reported Pcnm structure,128 though this did not converge.
The 35Cl SSNMR spectra feature three underlying patterns: two broad second-order quadrupolar patterns and one narrow pattern (Fig. 5). The two broad patterns correspond to the two crystallographically and magnetically distinct chloride ions, which are characterized by CQ = 3.52(5) MHz, ηQ = 0.14(8) and CQ = 2.62(6) MHz, ηQ = 0.49(5), respectively (Table 3). An additional sharp feature located at δiso = 120(1) ppm corresponds to a trace amount of unreacted NH4Cl, which is not detected in the corresponding PXRD patterns. There are three factors we consider in performing a quantitative Hahn echo NMR experiment on half-integer quadrupolar nuclei.131 First, we ensure the dataset was acquired with a sufficiently long recycle delay (in this case, 1 s) to allow for complete return to equilibrium magnetization.132 Second, we use CT-selective pulses, which result in uniform nutations of individual isochromats in the CT patterns, which ensures that integrated intensities can be regarded as quantitative.133–135 Finally, the effective T2’s (T2eff(35Cl)) for chloride ions in organic HCl salts are typically on the order of 2–20 ms; since an interpulse delay of 20 μs was used in the Hahn echo experiment, this has minor impact on the signal intensity collected after the refocusing pulse. Hence, we are able to reliably quantify not only the relative intensities of the two patterns corresponding to the chloride ions in the MCC (i.e., ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), but also the relative intensities of the patterns corresponding to NH4Cl and MCC (i.e., 2.5
1), but also the relative intensities of the patterns corresponding to NH4Cl and MCC (i.e., 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 97.5, or 1.9 ± 0.5 wt% NH4Cl).
97.5, or 1.9 ± 0.5 wt% NH4Cl).
| Cl site | C Q (MHz) | η Q | Γ RMS (MHz)c | |
|---|---|---|---|---|
| a Static calculations refer to a structural model derived from the crystal structure that was refined at the DFT-D2* level. b Dynamic calculations refer to an ensemble of 400 “snapshot” structures taken from the aiMD simulations, using the DFT-D2* structure as a starting point. c Γ m is the EFG distance for a single chlorine nucleus. See ESI† S2. | ||||
| Cl1 | Exp. | 3.52(5) | 0.14(8) | — |
| Static Calc.a | −3.33 | 0.53 | 0.35 | |
| Dynamic Calc.b | −3.98 | 0.23 | 0.33 | |
| Cl2 | Exp. | 2.62(6) | 0.49(5) | — |
| Static Calc. | 4.63 | 0.34 | 1.37 | |
| Dynamic Calc. | 2.91 | 0.47 | 0.20 | |
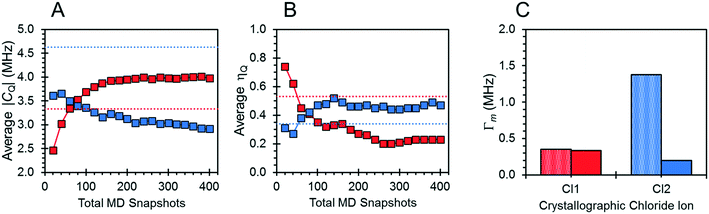
Unlike the other urea-containing MCCs, calculations of the 35Cl EFG tensors of NH4Cl:Urea do not result in good agreement with experimental values (Tables 3 and S6,† including calculations on geometry-optimized structural models based on our new crystal structure and those reported previously). The resulting EFG distances are large enough that no definitive assignment can be made for the two crystallographically distinct chloride ions. Their assignment is further complicated by the fact that both chloride ions have similar local environments (Fig. S14†), consisting of a bidentate hydrogen bond to one urea molecule, two monodentate hydrogen bonds with two additional urea molecules, and two hydrogen bonds with NH4+ ions; of these contacts, the hydrogen bonds to the NH4+ ions are the shortest (ca. 2.26 Å), and are therefore likely to exhibit the strongest influence on the calculated 35Cl EFG tensors (see Fig. S14† for EFG tensor orientations).
To explore the influence of molecular-level dynamics on the observed 35Cl EFG tensor parameters of NH4Cl:Urea, we measured variable-temperature (VT) 35Cl{1H} spectra between 25 and −125 °C at 14.1 T (Fig. 6). At all temperatures, the narrower pattern is characterized by CQ = 2.62(6) MHz and ηQ = 0.49(5) (i.e., no observable change in the EFG tensor with temperature). For the broader pattern, CQ increases from 3.52(5) MHz at 25 °C to 3.94(7) MHz at −125 °C, and the value of ηQ = 0.14(7) remains largely constant. The temperature-dependent variation of the 35Cl EFG tensor parameters of the broader pattern, and the fact that the crystal structure of NH4Cl:Urea does not change substantially over the same temperature range (i.e., the experimental unit cell volume increases by 1.6% at 298 K, relative to the structure at 170 K) suggest that molecular-level dynamics influence these values.
A growing body of work has demonstrated that certain NMR parameters are influenced by fast (femtosecond) time scale molecular-level motions that can be calculated using aiMD simulations;136–141 these effects can be modelled by averaging NMR interaction tensors over a representative sample of “snapshot” structures taken from an aiMD simulation. For example, Dračínský and Hodgkinson report that the effects of fast MD (i.e., vibrational motions, conformational averaging, molecular tumbling, etc.) can decrease the magnitudes of CQ(35Cl) in HCl salts by as much as 0.4 MHz.137 A similar analysis demonstrated that fast molecular motions have very little influence on the value of CQ(35Cl) for glycine HCl, whereas the magnitude of CQ(35Cl) in NaClO3, an inorganic solid, is decreased by ca. 1.6 MHz.140 Thus, it is possible that the poor agreement between experimental and calculated values of the 35Cl EFG tensors for the static structure of NH4Cl:Urea could be corrected by a model that accounts for the effects of fast molecular dynamics in the DFT calculations.
The effects of fast molecular dynamics have a substantial influence on the calculated 35Cl EFG tensor parameters of NH4Cl:Urea (Table 3). For the crystallographic sites Cl1 and Cl2, the aiMD simulations carried out at 300 K yield values of CQ = −3.98 MHz, ηQ = 0.23 and CQ = 2.91 MHz, ηQ = 0.47, respectively (Fig. 7). A definitive assignment of the two chlorine sites can be made based on comparison of the 35Cl EFG tensors measured at room temperature with those from aiMD simulations. The broader 35Cl CT powder pattern corresponds to Cl1, whereas the narrower pattern corresponds to Cl2.
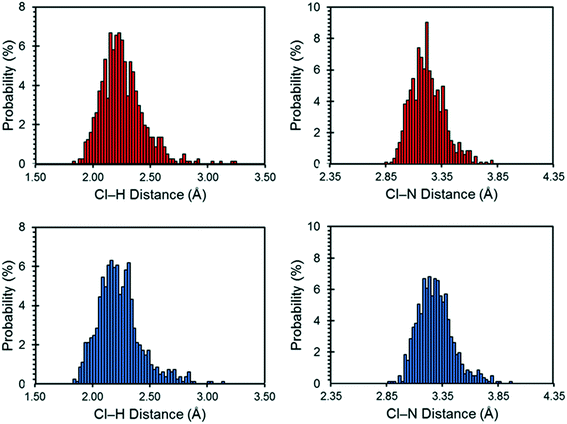
The motions of atoms in the vicinity of the chloride ions, especially those within the NH4+ ions, can have a substantial impact on the EFG tensors of the chloride ions – this hypothesis is further substantiated by calculations on the static DFT-D2* model of NH4Cl:Urea, for which V33 is predicted to reside either perpendicular to the plane formed by the two nearest NH4+ ions (Cl1) or within the plane (Cl2). The aiMD calculations reveal significant molecular-level motions of these atoms, as can be elucidated by examining the distributions of H⋯Cl and N⋯Cl internuclear distances (Fig. 8). The aiMD time-averaged H⋯Cl and N⋯Cl interatomic distances are nearly identical to those in the static DFT-D2* structure (i.e., these differences are less than 0.02 Å in all cases); however, the MD snapshot structures show large distributions for these distances. For both chloride ions, this analysis demonstrates that the motions of the NH4+ ions consist of two types: (i) vibrations of the ions around their equilibrium positions (indicated by the distribution of N⋯Cl distances), and (ii) random tumbling of the ions (indicated by the larger asymmetric distribution of H⋯Cl distances). Interestingly, the distribution of H⋯Cl distances for Cl2 is more heavily skewed toward longer bond lengths (i.e., weaker hydrogen bonds), which is consistent with the lower value of CQ observed for this site.
4. Conclusions
Herein, we have demonstrated novel mechanochemical preparations of five ammonium chloride urea MCCs, and their structural characterization by 35Cl and 13C SSNMR spectroscopy, PXRD and/or SCXRD, and plane-wave DFT calculations. These urea MCCs can be prepared mechanochemically with high purity and great rapidity, relative to crystallization from solution; this was confirmed using a combination of 35Cl SSNMR and PXRD data to validate the products, identify any impurities and/or leftover starting material, and optimize the experimental conditions for ball milling. In combination with DFT calculations, 35Cl EFG tensors can be used to validate and refine crystal structures, as well as to examine their relationship to structural features. aiMD simulations and VT-NMR indicate that the 35Cl EFG tensors for NH4Cl:Urea are significantly affected by fast molecular-level motions, and careful attention must be paid to systems with mobile functional groups and/or counterions. Together, these methods could be beneficial for designing new quadrupolar-based NMR crystallography techniques to validate, refine, and solve the crystal structures of a wide range of MCCs where traditional characterization methods are difficult or impossible.Finally, during the optimization of our ball milling routines, and the discovery of extremely short preparation times, we observed that the synthesis of certain ammonium chloride urea MCCs is possible with other green synthetic techniques, including accelerated aging.142 Since accelerated aging reactions progress slower than ball milling reactions (i.e., days versus minutes), they provide a unique opportunity to monitor reactions in situ, potentially allowing for the detection and identification of intermediate phases, and even providing a pathway for rational design of novel MCCs. Discussion of this exciting prospect is beyond the scope of this work, but explorations of these phenomena are already underway in our laboratory.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Genentech, The Florida State University, the National High Magnetic Field Laboratory, and the Natural Sciences and Engineering Research Council of Canada (NSERC Discovery grants 2016-06642 and 2020-04627 for R. S. and J. M. R. respectively) for funding this research. The National High Magnetic Field Laboratory is supported by the National Science Foundation through NSF/DMR-1644779 and the State of Florida. A portion of this research used resources provided by the X-ray Crystallography Center at the FSU Department of Chemistry and Biochemistry (FSU075000XRAY). We also acknowledge use of the SSNMR and SC-XRD facilities at the University of Windsor, supported by the Canadian Foundation for Innovation, Ontario Innovation Trust, and the University of Windsor.References
- G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967 CrossRef CAS PubMed.
- A. Karagianni, M. Malamatari and K. Kachrimanis, Pharmaceutics, 2018, 10, 1–30 Search PubMed.
- R. Thakuria, A. Delori, W. Jones, M. P. Lipert, L. Roy and N. Rodríguez-Hornedo, Int. J. Pharm., 2013, 453, 101–125 CrossRef CAS PubMed.
- M. Karimi-Jafari, L. Padrela, G. M. Walker and D. M. Croker, Cryst. Growth Des., 2018, 18, 6370–6387 CrossRef CAS.
- T. Friščić and W. Jones, J. Pharm. Pharmacol., 2010, 62, 1547–1559 CrossRef PubMed.
- D. P. McNamara, S. L. Childs, J. Giordano, A. Iarriccio, J. Cassidy, M. S. Shet, R. Mannion, E. O'Donnell and A. Park, Pharm. Res., 2006, 23, 1888–1897 CrossRef CAS PubMed.
- D. R. Weyna, T. Shattock, P. Vishweshwar and M. J. Zaworotko, Cryst. Growth Des., 2009, 9, 1106–1123 CrossRef CAS.
- G. Kuminek, F. Cao, A. B. O. da Rocha, S. G. Cardoso and N. Rodríguez-Hornedo, Adv. Drug Delivery Rev., 2016, 101, 143–166 CrossRef CAS PubMed.
- D. Tan and F. García, Chem. Soc. Rev., 2019, 48, 2274–2292 RSC.
- J. L. Howard, Q. Cao and D. L. Browne, Chem. Sci., 2018, 9, 3080–3094 RSC.
- T. Friščić, C. Mottillo and H. M. Titi, Angew. Chem., Int. Ed., 2020, 59, 1018–1029 CrossRef PubMed.
- T. Friščić, J. Mater. Chem., 2010, 20, 7599 RSC.
- D. Tan and T. Friščić, Eur. J. Org. Chem., 2018, 2018, 18–33 CrossRef CAS.
- D. Tan, L. Loots and T. Friščić, Chem. Commun., 2016, 52, 7760–7781 RSC.
- J. Andersen and J. Mack, Green Chem., 2018, 20, 1435–1443 RSC.
- S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Frišcic, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447 RSC.
- R. B. N. Baig and R. S. Varma, Chem. Soc. Rev., 2012, 41, 1559–1584 RSC.
- R. S. Varma, Green Chem., 2014, 16, 2027–2041 RSC.
- E. Pindelska, A. Sokal and W. Kolodziejski, Adv. Drug Delivery Rev., 2017, 117, 111–146 CrossRef CAS PubMed.
- F. Taulelle, in Encyclopedia of Magnetic Resonance, ed. R. K. Harris, R. E. Wasylishen and M. J. Duer, John Wiley & Sons, Ltd, Chichester, UK, 2009, pp. 1–14 Search PubMed.
- R. E. Wasylishen, R. K. Harris and M. J. Duer, NMR Crystallography, A Wiley & Sons, New York, NY, 2009 Search PubMed.
- S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204 RSC.
- C. Martineau, Solid State Nucl. Magn. Reson., 2014, 63–64, 1–12 CrossRef CAS PubMed.
- P. Hodgkinson, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10–53 CrossRef CAS PubMed.
- D. L. Bryce, IUCrJ, 2017, 4, 350–359 CrossRef CAS PubMed.
- C. Leroy and D. L. Bryce, Prog. Nucl. Magn. Reson. Spectrosc., 2018, 109, 160–199 CrossRef CAS PubMed.
- C. Martineau, J. Senker and F. Taulelle, NMR Crystallography, 2014, vol. 82 Search PubMed.
- C. J. Pickard, Nat. Rev. Mater., 2019, 4, 331–348 CrossRef.
- A. O. Lyakhov, A. R. Oganov and M. Valle, in Modern Methods of Crystal Structure Prediction, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2010, pp. 147–180 Search PubMed.
- Ş. Atahan-Evrenk and A. Aspuru-Guzik, Prediction and Calculation of Crystal Structures, Springer International Publishing, Cham, 2014, vol. 345 Search PubMed.
- A. R. Oganov, G. Saleh and A. G. Kvashnin, Computational Materials Discovery, Royal Society of Chemistry, Cambridge, 2018 Search PubMed.
- C. M. Widdifield, J. D. Farrell, J. C. Cole, J. A. K. Howard and P. Hodgkinson, Chem. Sci., 2020, 11, 2987–2992 RSC.
- J. R. Yates, S. E. Dobbins, C. J. Pickard, F. Mauri, P. Y. Ghi, R. K. Harris, L. D. M. De Paris, U. Pierre, P. Jussieu and C. Paris, Methods, 2005, 1402–1407 CAS.
- T. Pawlak, M. Jaworska and M. J. Potrzebowski, Phys. Chem. Chem. Phys., 2013, 15, 3137–3145 RSC.
- S. E. Soss, P. F. Flynn, R. J. Iuliucci, R. P. Young, L. J. Mueller, J. Hartman, G. J. O. Beran and J. K. Harper, ChemPhysChem, 2017, 18, 2225–2232 CrossRef CAS PubMed.
- K. Kalakewich, R. Iuliucci, K. T. Mueller, H. Eloranta and J. K. Harper, J. Chem. Phys., 2015, 143, 194702 CrossRef PubMed.
- A. Abraham, D. C. Apperley, T. Gelbrich, R. K. Harris and U. J. Griesser, Can. J. Chem., 2011, 89, 770–778 CrossRef CAS.
- A. E. Watts, K. Maruyoshi, C. E. Hughes, S. P. Brown and K. D. M. Harris, Cryst. Growth Des., 2016, 16, 1798–1804 CrossRef CAS.
- M. Baias, C. M. Widdifield, J.-N. Dumez, H. P. G. Thompson, T. G. Cooper, E. Salager, S. Bassil, R. S. Stein, A. Lesage, G. M. Day and L. Emsley, Phys. Chem. Chem. Phys., 2013, 15, 8069 RSC.
- J. D. Hartman, G. M. Day and G. J. O. Beran, Cryst. Growth Des., 2016, 16, 6479–6493 CrossRef CAS PubMed.
- S. T. Holmes, O. G. Engl, M. N. Srnec, J. D. Madura, R. Quiñones, J. K. Harper, R. W. Schurko and R. J. Iuliucci, J. Phys. Chem. A, 2020, 124, 3109–3119 CrossRef CAS PubMed.
- D. L. Bryce and G. D. Sward, Magn. Reson. Chem., 2006, 44, 409–450 CrossRef CAS PubMed.
- P. M. J. Szell and D. L. Bryce, in Annual Reports on NMR Spectroscopy, Elsevier Ltd., 1st edn, 2015, vol. 84, pp. 115–162 Search PubMed.
- Y. Xu, S. A. Southern, P. M. J. Szell and D. L. Bryce, CrystEngComm, 2016, 18, 5236–5252 RSC.
- M. Hildebrand, H. Hamaed, A. M. Namespetra, J. M. Donohue, R. Fu, I. Hung, Z. Gan and R. W. Schurko, CrystEngComm, 2014, 16, 7334–7356 RSC.
- K. M. N. Burgess, F. A. Perras, A. Lebrun, E. Messner-Henning, I. Korobkov and D. L. Bryce, J. Pharm. Sci., 2012, 101, 2930–2940 CrossRef CAS PubMed.
- D. L. Bryce, M. Gee and R. E. Wasylishen, J. Phys. Chem. A, 2001, 105, 10413–10421 CrossRef CAS.
- R. W. Schurko and M. J. Jaroszewicz, in Encyclopedia of Inorganic and Bioinorganic Chemistry, John Wiley & Sons, Ltd, Chichester, UK, 2015, pp. 1–56 Search PubMed.
- I. L. Moudrakovski, in Annual Reports on NMR Spectroscopy, Elsevier Ltd., 1st edn., 2013, vol. 79, pp. 129–240 Search PubMed.
- G. Wu and J. Zhu, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 61, 1–70 CrossRef CAS PubMed.
- S. T. Holmes, W. D. Wang, G. Hou, C. Dybowski, W. Wang and S. Bai, Phys. Chem. Chem. Phys., 2019, 21, 6319–6326 RSC.
- K. M. N. Burgess, Y. Xu, M. C. Leclerc and D. L. Bryce, Inorg. Chem., 2014, 53, 552–561 CrossRef CAS PubMed.
- K. E. Johnston, J. M. Griffin, R. I. Walton, D. M. Dawson, P. Lightfoot and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2011, 13, 7565 RSC.
- S. Sene, B. Bouchevreau, C. Martineau, C. Gervais, C. Bonhomme, P. Gaveau, F. Mauri, S. Bégu, P. H. Mutin, M. E. Smith and D. Laurencin, CrystEngComm, 2013, 15, 8763 RSC.
- C. Bonhomme, C. Gervais, N. Folliet, F. Pourpoint, C. Coelho Diogo, J. Lao, E. Jallot, J. Lacroix, J. M. Nedelec, D. Iuga, J. V. Hanna, M. E. Smith, Y. Xiang, J. Du and D. Laurencin, J. Am. Chem. Soc., 2012, 134, 12611–12628 CrossRef CAS PubMed.
- H. Hamaed, J. M. Pawlowski, B. F. T. Cooper, R. Fu, S. H. Eichhorn and R. W. Schurko, J. Am. Chem. Soc., 2008, 130, 11056–11065 CrossRef CAS PubMed.
- S. T. Holmes, R. J. Iuliucci, K. T. Mueller and C. Dybowski, J. Chem. Phys., 2017, 146, 064201 CrossRef PubMed.
- S. T. Holmes, C. S. Vojvodin and R. W. Schurko, J. Phys. Chem. A, 2020, 124, 10312–10323 CrossRef CAS PubMed.
- A. A. Peach, D. A. Hirsh, S. T. Holmes and R. W. Schurko, CrystEngComm, 2018, 20, 2780–2792 RSC.
- C. M. Widdifield, F. A. Perras and D. L. Bryce, Phys. Chem. Chem. Phys., 2015, 17, 10118–10134 RSC.
- C. Martineau, A. Cadiau, B. Bouchevreau, J. Senker, F. Taulelle and K. Adil, Dalton Trans., 2012, 41, 6232 RSC.
- C. M. Rice, Z. H. Davis, D. McKay, G. P. M. Bignami, R. G. Chitac, D. M. Dawson, R. E. Morris and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2020, 22, 14514–14526 RSC.
- S. T. Holmes, J. M. Hook and R. W. Schurko, Mol. Pharmaceutics, 2022, 19, 440–455 CrossRef CAS PubMed.
- D. A. Hirsh, S. T. Holmes, P. Chakravarty, A. A. Peach, A. G. Dipasquale, K. Nagapudi and R. W. Schurko, Cryst. Growth Des., 2019, 19, 7349–7362 CrossRef CAS.
- A. M. Namespetra, D. A. Hirsh, M. P. Hildebrand, A. R. Sandre, H. Hamaed, J. M. Rawson and R. W. Schurko, CrystEngComm, 2016, 18, 6213–6232 RSC.
- R. J. Attrell, C. M. Widdifield, I. Korobkov and D. L. Bryce, Cryst. Growth Des., 2012, 12, 1641–1653 CrossRef CAS.
- D. A. Hirsh, A. J. Rossini, L. Emsley and R. W. Schurko, Phys. Chem. Chem. Phys., 2016, 18, 1–34 RSC.
- F. G. Vogt, G. R. Williams and R. C. B. Copley, J. Pharm. Sci., 2013, 102, 3705–3716 CrossRef CAS PubMed.
- D. L. Bryce, G. D. Sward and S. Adiga, J. Am. Chem. Soc., 2006, 128, 2121–2134 CrossRef CAS PubMed.
- B. Sandhu, A. S. Sinha, J. Desper and C. B. Aakeröy, Chem. Commun., 2018, 54, 4657–4660 RSC.
- K. Honer, C. Pico and J. Baltrusaitis, ACS Sustainable Chem. Eng., 2018, 6, 4680–4687 CrossRef CAS.
- K. Honer, E. Kalfaoglu, C. Pico, J. McCann and J. Baltrusaitis, ACS Sustainable Chem. Eng., 2017, 5, 8546–8550 CrossRef CAS.
- L. Mazzei, V. Broll, L. Casali, M. Silva, D. Braga, F. Grepioni, J. Baltrusaitis and S. Ciurli, ACS Sustainable Chem. Eng., 2019, 7, 13369–13378 CrossRef CAS.
- P. Macfhionnghaile, C. M. Crowley, P. McArdle and A. Erxleben, Cryst. Growth Des., 2020, 20, 736–745 CrossRef CAS.
- L. Casali, L. Mazzei, O. Shemchuk, L. Sharma, K. Honer, F. Grepioni, S. Ciurli, D. Braga and J. Baltrusaitis, ACS Sustainable Chem. Eng., 2019, 7, 2852–2859 CrossRef CAS.
- P. A. Julien, L. S. Germann, H. M. Titi, M. Etter, R. E. Dinnebier, L. Sharma, J. Baltrusaitis and T. Friščić, Chem. Sci., 2020, 11, 2350–2355 RSC.
- K. D. M. Harris and J. M. Thomas, J. Chem. Soc., Faraday Trans., 1990, 86, 2985–2996 RSC.
- J. T. Zou, Y. S. Wang, W. M. Pang, L. Shi and F. Lu, Chin. J. Chem. Phys., 2013, 26, 198–202 CrossRef CAS.
- S. Thakral and A. K. Madan, J. Inclusion Phenom. Macrocyclic Chem., 2008, 60, 203–209 CrossRef CAS.
- I. J. Shannon, N. M. Stainton and K. D. M. Harris, J. Mater. Chem., 1993, 3, 1085–1090 RSC.
- A. Alhalaweh, S. George, D. Boström and S. P. Velaga, Cryst. Growth Des., 2010, 10, 4847–4855 CrossRef CAS.
- L. Casali, L. Mazzei, O. Shemchuk, K. Honer, F. Grepioni, S. Ciurli, D. Braga and J. Baltrusaitis, Chem. Commun., 2018, 54, 7637–7640 RSC.
- P. Cysewski, M. Przybyłek, D. Ziółkowska and K. Mroczyńska, J. Mol. Model., 2016, 22, 103 CrossRef PubMed.
- J. X. Song, Y. Yan, J. Yao, J. M. Chen and T. B. Lu, Cryst. Growth Des., 2014, 14, 3069–3077 CrossRef CAS.
- S. T. Holmes and R. W. Schurko, J. Phys. Chem. C, 2018, 122, 1809–1820 CrossRef CAS.
- Bruker, APEXIII, SAINT, SADABS, 2016, Madison, WI, USA.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- P. M. J. Szell and D. L. Bryce, Recent advances in chlorine, bromine, and iodine solid-state NMR spectroscopy, Elsevier Ltd., 1st edn, 2020, vol. 100 Search PubMed.
- Bruker, TopSpin Softw. Version 4.1, 2020, Ettlingen, Germany.
- S. G. J. van Meerten, W. M. J. Franssen and A. P. M. Kentgens, J. Magn. Reson., 2019, 301, 56–66 CrossRef CAS PubMed.
- M. E. Rose, Elementary Theory of Angular Momentum, Wiley, New York, NY, 1957 Search PubMed.
- M. Mehring, Principles of High Resolution NMR in Solids, Springer Berlin Heidelberg, Berlin, Heidelberg, 1983 Search PubMed.
- S. Adiga, D. Aebi and D. L. Bryce, Can. J. Chem., 2007, 85, 496–505 CrossRef CAS.
- A. Pines, M. G. Gibby and J. S. Waugh, Chem. Phys. Lett., 1972, 15, 373–376 CrossRef CAS.
- E. O. Stejeskal and J. Schaefer, J. Am. Chem. Soc., 1976, 98, 1031–1032 CrossRef.
- C. R. Morcombe and K. W. Zilm, J. Magn. Reson., 2003, 162, 479–486 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 1–11 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- T. A. Arias, M. C. Payne and J. D. Joannopoulos, Phys. Rev. Lett., 1992, 69, 1077–1080 CrossRef CAS PubMed.
- D. Alfè, Comput. Phys. Commun., 1999, 118, 31–33 CrossRef.
- B. Leimkuhler, E. Noorizadeh and F. Theil, J. Stat. Phys., 2009, 135, 261–277 CrossRef CAS.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- A. P. M. Kentgens, Geoderma, 1997, 80, 271–306 CrossRef CAS.
- J. W. Akitt and W. S. McDonald, J. Magn. Reson., 1984, 58, 401–412 CAS.
- O. Knop, E. M. Palmer and R. W. Robinson, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1975, 31, 19–31 CrossRef.
- G. Bartlett and I. Langmuir, J. Am. Chem. Soc., 1921, 43, 84–91 CrossRef CAS.
- G. Desiraju and T. Steiner, The Weak Hydrogen Bond, Oxford University Press, 2001, vol. 9 Search PubMed.
- M. Light, C. Haynes and P. A. Gale, CSD Commun., 2016 Search PubMed.
- Q. Li and T. C. W. Mak, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 180–192 CrossRef.
- Q. Li, W. H. Yip and T. C. W. Mak, J. Inclusion Phenom. Mol. Recognit. Chem., 1995, 23, 233–244 CrossRef CAS.
- Q. Li and T. C. W. Mak, J. Inclusion Phenom. Mol. Recognit. Chem., 1997, 28, 151–161 CrossRef CAS.
- C. F. Holder and R. E. Schaak, ACS Nano, 2019, 13, 7359–7365 CrossRef CAS PubMed.
- R. T. Berendt and E. J. Munson, J. Pharm. Sci., 2011, 100, 1879–1891 CrossRef CAS PubMed.
- K. D. M. Harris and J. M. Thomas, J. Solid State Chem., 1991, 94, 197–205 CrossRef CAS.
- D. V. Dudenko, P. A. Williams, C. E. Hughes, O. N. Antzutkin, S. P. Velaga, S. P. Brown and K. D. M. Harris, J. Phys. Chem. C, 2013, 117, 12258–12265 CrossRef CAS PubMed.
- F. G. Vogt, J. S. Clawson, M. Strohmeier, A. J. Edwards, T. N. Pham and S. A. Watson, Cryst. Growth Des., 2009, 9, 921–937 CrossRef CAS.
- S. Thomas, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef.
- T. Steiner, Chem. Commun., 1999, 313–314 RSC.
- D. W. Alderman, M. H. Sherwood and D. M. Grant, J. Magn. Reson., 1993, 101, 188–197 CrossRef CAS.
- A. Rimsky, Bull. Soc. Fr. Mineral. Cristallogr., 1960, 83, 187–200 CAS.
- B. Xue, M. Mao, Y. Liu, J. Guo, J. Li and E. Liu, J. Cryst. Growth, 2016, 442, 110–113 CrossRef CAS.
- Y. Wang, J. Han, A. Tudi, Z. Zhang, Z. Yang and S. Pan, CrystEngComm, 2019, 21, 6072–6079 RSC.
- D. A. Hirsh, Y. Su, H. Nie, W. Xu, D. Stueber, N. Variankaval and R. W. Schurko, Mol. Pharmaceutics, 2018, 15, 4038–4048 CrossRef CAS PubMed.
- M. J. R. Hoch, S. P. McAlister and M. I. Gordon, J. Phys. C: Solid State Phys., 1975, 8, 53–70 CrossRef CAS.
- A. J. Vega, in Encyclopedia of Magnetic Resonance, ed. D. M. Grant and R. K. Harris, John Wiley & Sons, Ltd, Chichester, UK, 2010, pp. 3869–3888 Search PubMed.
- P. P. Man, J. Klinowski, A. Trokiner, H. Zanni and P. Papon, Chem. Phys. Lett., 1988, 151, 143–150 CrossRef CAS.
- A. Samoson and E. Lippmaa, Phys. Rev. B, 1983, 28, 6567–6570 CrossRef CAS.
- M. Dračínský, H. M. Moller and T. E. Exner, J. Chem. Theory Comput., 2013, 9, 3806–3815 CrossRef PubMed.
- M. Dračínský and P. Hodgkinson, CrystEngComm, 2013, 15, 8705–8712 RSC.
- M. Dračínský and P. Hodgkinson, Chem. – Eur. J., 2014, 20, 2201–2207 CrossRef PubMed.
- M. Dračínský, P. Bour and P. Hodgkinson, J. Chem. Theory Comput., 2016, 12, 968–973 CrossRef PubMed.
- O. Socha, P. Hodgkinson, C. M. Widdifield, J. R. Yates and M. Dračínsky, J. Phys. Chem. A, 2017, 121, 4103–4113 CrossRef CAS PubMed.
- M. Dračínský, J. Vícha, K. Bártová and P. Hodgkinson, ChemPhysChem, 2020, 21, 2075–2083 CrossRef PubMed.
- M. J. Cliffe, C. Mottillo, R. S. Stein, D. K. Bučar and T. Friščić, Chem. Sci., 2012, 3, 2495–2500 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ce01610e |
| This journal is © The Royal Society of Chemistry 2022 |