Effect of substituents in novel bioactive tavaborole derivatives on the intermolecular interaction hierarchy

Abstract

Tavaborole, a molecule based on the benzoxaborole scaffold, is an effective antifungal drug marketed under the Kerydin® trademark. New tavaborole biologically active derivatives, namely 5-fluoro-3-morpholin-4-yl-2,1-benzoxaborol-1(3H)-ol and 5-fluoro-3-thiomorpholin-4-yl-2,1-benzoxaborol-1(3H)-ol have been synthesized and their crystal structures are discussed in comparison to the parent tavaborole and nonfluorinated benzoxaborole analogs. Our aim is to find the structural differences caused by the substitution with the fluorine atom, the introduction of a substituent at position 3, and its modification at a peripheral site. For this purpose, we have employed state-of-art tools using knowledge-based and quantum crystallography algorithms. Our study revealed that the presence of the fluorine atom reduces both the molecular dipole moment and the hydrogen bond acceptor abilities of a ring oxygen atom, hence affecting the structure of the main hydrogen-bonded motif. The analysis shows that in the new thiomorpholine derivative, the observed motif is not optimal, and thus other polymorphs might be sought. Hierarchical analysis of weak intermolecular interactions and elucidation of large supramolecular synthons allowed us to find similarities in the networks formed by 3-substituted derivatives and their different arrangement compared to unsubstituted benzoxaboroles. This approach gives an insight into weak interaction cooperativity and their exchange upon different substitutions. The results may serve as a basis for future search for new polymorphic forms and benzoxaborole derivative multicomponent crystals.

---

Introduction

Tavaborole (5-fluoro-1-hydroxy-3H-2,1-benzoxaborole, Tv in Scheme 1) is a novel antifungal drug approved to be used for the topical treatment of onychomycosis.¹ This small molecule was found to show a unique mechanism of action, named the oxaborole-tRNA-trapping mechanism.² It works by blocking the fungus' ability to produce proteins by interfering with the catalytic action of a cytoplasmic enzyme called leucyl-tRNA synthetase, which is involved in the translation process. This mechanism is attributed solely to the presence of the benzoxaborole fragment and related to its excellent sugar recognition properties.³ It is noteworthy that in many different derivatives of phenylboronic acids, the benzoxaboroles exhibit the highest reactivity,⁴ which might be related to their unbalanced coordination sphere, as shown in studies of a large group of such derivatives based on the bond-valence-vector (BVV) model.⁵ On the other hand, the lower activity of the unsubstituted benzoxaborole (Bx in Scheme 1) compared to tavaborole points out the significance of the presence of the fluorine atom.^6,7 Generally, it is considered that the effect of substitution by the fluorine atom on the action of drugs is complex and includes effects on acidity and lipophilicity, among others.⁸ Recent studies show that the presence of a fluorine atom at the position para to the boronic group enhances antifungal activity also in 3-substituted benzoxaboroles such as 5-fluoro-3-morpholin-4-yl-2,1-benzoxaborol-1(3H)-ol (TvO) and 5-fluoro-3-thiomorpholin-4-yl-2,1-benzoxaborol-1(3H)-ol (TvS), compared to their nonfluorinated analogs.⁹

Scheme 1 Tavaborole (Tv) and benzoxaborole (Bx) derivatives studied in this paper.

Surprisingly, so far, no structural studies have been published on any substitution of the tavaborole molecule (Cambridge Structural Database (CSD) version 5.43, update November 2021 (ref. 10)). The only modifications of tavaborole are described by MacGillivray et al.¹¹ They relate to tavaborole co-crystallization with selected 4-pyridyl-containing co-formers, thus altering the crystal structure, and not the tavaborole molecule itself. However, it has been found that the introduction of a strong hydrogen bond acceptor may change the position of the hydrogen atom bonded to the oxygen atom from the syn to anti conformation. According to the BVV model, the latter shows a higher degree of distortion at the boron coordination sphere. Also, the importance of C–H⋯F interactions in the co-crystal supramolecular architecture has been underlined.

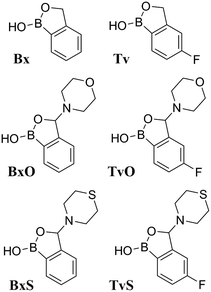
Herein, we present an analysis of crystal structures of two new tavaborole derivatives with a morpholine or thiomorpholine substituent at position 3 (TvO and TvS). We compare them with the tavaborole crystal structure (Tv) (CSD refcodes: IKACUT,¹² IKACUT01 (ref. 13)) as well as with structurally characterized analogous derivatives of unsubstituted benzoxaborole (Scheme 1), i.e. 1,3-dihydro-1-hydroxy-3-(morpholin-4-yl)-2,1-benzoxaborole, BxO (CSD refcode: DEBXIS¹⁴), and 1,3-dihydro-1-hydroxy-3-(thiomorpholin-4-yl)-2,1-benzoxaborole, BxS (CSD refcode: MACPUD¹⁵). Two polymorphic forms of unsubstituted benzoxaborole (1-hydroxy-3(1H)-1,2-benzoboroxole), Bx (CSD refcodes: LOQQEN,¹⁶ LOQQEN01 (ref. 17)) are discussed as well. We aim to find the structural differences caused by (a) the substitution with the fluorine atom, (b) the introduction of a substituent at position 3, and (c) changing the oxygen atom to the sulfur atom in the substituent.

Results and discussion

Molecular structure

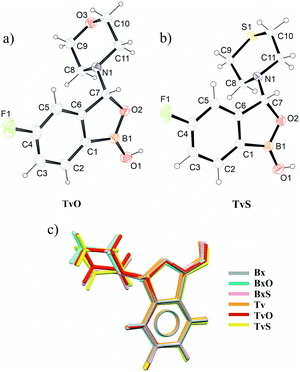
The crystal data for new structurally characterized molecules TvO and TvS are collected in Table 1. They crystallize in the centrosymmetric groups of triclinic and monoclinic systems, respectively, similar to their benzoxaborole analogs (BxO and BxS). It is noteworthy that these molecules are chiral, and thus both enantiomers are present in the crystals. Interestingly, Bx, an achiral molecule, crystallizes either in the centrosymmetric P1̄ (LOQQEN) or non-centrosymmetric P2₁ (LOQQEN01) space group. Both Bx polymorphic forms possess two molecules in the asymmetric unit, and the difference occurs in the main supramolecular motifs (described beneath). The records for tavaborole crystals deposited in the CSD cover data measured at room temperature (IKACUT01) or 100 K (IKACUT).

Table 1 Crystal data, data collection and refinement for new crystals

	TvO	TvS
Chemical formula	C11H13BFNO3	C11H13BFNO2S
Formula weight	237.03	253.09
Crystal system	Triclinic	Monoclinic
Space group	P1̄	P21/c
a/Å	6.1181(3)	9.0320(3)
b/Å	9.4155(4)	6.2712(3)
c/Å	10.1914(4)	21.3774(9)
α/°	99.383(3)	90
β/°	100.605(4)	99.420(4)
γ/°	91.220(4)	90
Unit cell volume/Å^3	568.53(4)	1194.52(9)
Temperature/K	293.15	293.0(2)
Z	2	4
Reflections collected	26 391	11 317
Independent reflections	2607	2966
R int	0.0342	0.0254
Final R1 values (I > 2σ(I))	0.0338	0.0413
Final wR(F^2) values (I > 2σ(I))	0.0866	0.0956
Final R1 values (all data)	0.0435	0.0572
Final wR(F^2) values (all data)	0.0922	0.1047
Goodness of fit on F^2	1.065	1.029
Largest diff. peak/hole/e Å^−3	0.23/−0.16	0.36/−0.38
CCDC no.	2152789	2152788

---

Primarily, in all analyzed molecules, the benzoxaborole scaffold (a fused 9-membered ring) is alike, with the OH group in the syn conformation and the tricoordinated boron atom (Fig. 1c, Table S1 in the ESI† file). The only difference that might be considered significant is the fold angle, i.e., the angle between planes containing 5-membered and 6-membered rings in the scaffold. Among the analyzed molecules, Bx, TvO, and TvS are almost perfectly flat with the average fold value of 0.4°, while the remaining ones are slightly bent with the fold angle ranging from 1.54(8) for Tv(rt) to 2.63(9)° for BxS (Table S1 in the ESI†). This parameter shows small and randomized variability; therefore, we can assume that the substitution by the fluorine atom as well as the morpholine/thiomorpholine substituent does not affect the molecular structure of the common benzoxaborole scaffold. It is worth mentioning that for all benzoxaborole structures found in the CSD, the fold does not exceed 5° (Fig. S1 in ESI†). Concerning the substituent at position 3, both morpholine and thiomorpholine rings adopt a chair conformation. They are similarly oriented towards the benzoxaborole fragment with an angle between the vector passing through the C7–N1 bond and normal to the substituent mean plane varying from 78.5(1)° for BxO to 87.0(1)° for TvS (Table S1†). On the other hand, introducing the fluorine atom in a para position towards the boron atom affects the dipole moment significantly. For Bx derivatives, the estimated values of μ (calculated in the CSD Mercury program¹⁸) are higher than for the Tv ones. For Bx it equals 4.8 D, while for tavaborole, it is only 1.1 D. In 3-substituted derivatives, the dipole moment for morpholine derivatives is bigger (BxO 4.3 and TvO 2.7) than for thiomorpholine analogs (BxS 3.0 and TvS 1.2). Considering that the dipole moment has been found to be a significant factor influencing the packing of fluorinated phenylboronic acid esters¹⁹ to assess the effect of the substituent, it is necessary to perform an in-detail analysis of the intermolecular interactions of the crystals in question.

Fig. 1 Ortep drawings of TvO (a) and TvS (b) molecules. Overlay of all six studied molecules (c).

Main supramolecular motifs

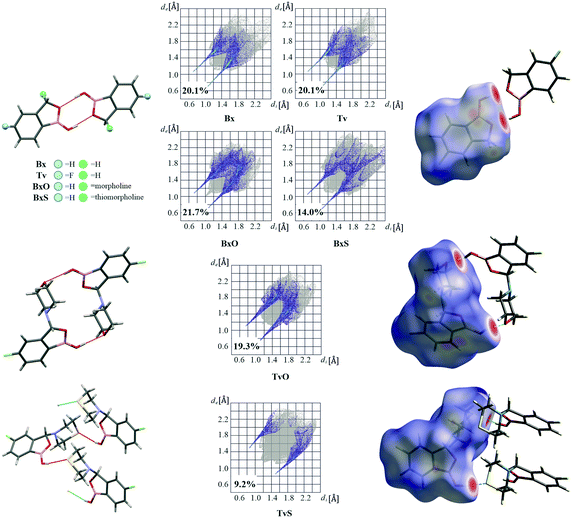
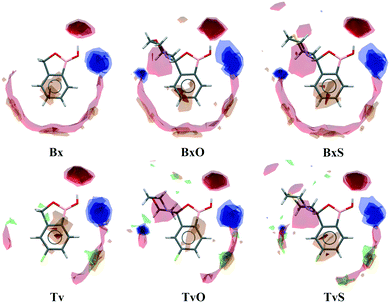
A basic motif observed in Tv, Bx, BxO and BxS crystals is a O1–H1⋯O2 hydrogen-bonded dimer described with the R²₂(8) graph-set.²⁰ To be precise, in the case of the non-centrosymmetric polymorph of Bx (LOQQEN01), the ring motif appears at the second level of the graph-set²¹ linking two crystallographically independent molecules. It should be noted that such an R²₂(8) dimeric motif is present in about half of the structurally characterized benzoxaboroles and topologically corresponds to the most common motif in carboxylic acids.²² In Fig. 2 (top row), this motif is visible on the molecular Hirshfeld surface²³ as two clear red regions; also the characteristic long whiskers appear on 2D-fingerprint Hirshfeld surface maps resolved to H⋯O/O⋯H contacts only.²⁴

Fig. 2 Main hydrogen bonded supramolecular motifs, Hirshfeld surface fingerprint plots decomposed to H⋯O/O⋯H (or H⋯S/S⋯H in TvS) contacts, and molecular Hirshfeld surfaces for tavaborole derivatives mapped with d_norm.

Interestingly, in the newly characterized molecules, different patterns were detected, and they may be explained based on the comparison of electrostatic potential (EP) map analysis (Fig. 3). The EP maps for benzoxaborole and tavaborole derivatives indicate that the fluorine substitution diminished the negative potential at O2 (Fig. 3). Hence, in Tv the O1 atom could potentially be a better acceptor leading to other polymorphs. However, in the CSD, there is only one example of the benzoxaborole derivative where the O1 atom plays the role of the H-bond acceptor (CSD refcode: HAWCEN²⁵), but in this case, the O1–H1 group is in the anti-conformation. As mentioned earlier, this orientation is relatively uncommon as it causes high stress in the benzoxaborole ring.

Fig. 3 Electrostatic potential isosurface calculated at 0.05 au using a B3LYP/6-31G(d,p) wavefunction. Blue and red regions around the atoms correspond to positive and negative potentials, respectively.

In the case of morpholine derivatives, the EP maps show that two additional acceptor regions appear at the substituent. They are located at nitrogen and O3 atoms, and the latter is substantially more negatively charged and accessible than the three others. This tendency is evident for the fluorinated TvO molecule (Fig. 3). Nevertheless, in BxO the R²₂(8) dimeric motif is retained, while in TvO, the substituents' oxygen atom plays the role of the H-bond acceptor, and the resulting motif is a centrosymmetric dimer described with an R²₂(18) graph (Fig. 2, middle row). The red spots on the Hirshfeld surface and associated H⋯O/O⋯H resolved fingerprint plots demonstrate that this motif is hierarchically the most important. Contrary to morpholine substituted molecules, in the case of thiomorpholine ones, the electrostatic potential maps show almost no negative region at the sulfur atom. In BxS, the dimeric motif with O1–H1⋯O2 bonds is observed, while in TvS, the influence of fluorine severely diminishes the abilities of all acceptor regions, and a new motif utilizing O1–H1⋯S1 hydrogen bonds is observed (Fig. 2, bottom row). It is an infinite chain running along the 2₁ screw axis and described with the C(9) graph-set. Interestingly, such a rearrangement from the R²₂(18) dimer in TvO to the C(9) chain in TvS corresponds to the similarity of carboxylic acid R²₂(8) dimers and C(4) catemers,²⁶ the latter are sparsely observed and with the necessary support of weaker C–H⋯O interactions.²⁷ Indeed, in TvS, the O1–H1⋯S1 hydrogen bonds are supported by C10–H10A⋯O2 short contacts (Table S2†). Also, in this case, the analysis of the Hirshfeld surface indicates the priority of this interaction over other contacts (Fig. 2). However, the comparison of interaction energies²³ estimated for the main motifs observed in the analyzed series (section 2.5, ESI†) revealed that in these O–H⋯S bonded chains, the energy value is approximately two times lower than for the O–H⋯O dimers. The latter shows the energy around 60 kJ mol⁻¹ despite the ring size, i.e., it is comparable for R²₂(8) and R²₂(18) motifs. Nevertheless, in all the above-mentioned interactions creating the main motifs, the electrostatic component is dominant (section 2.5, ESI†).

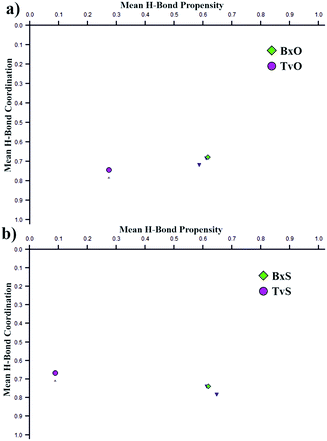
Curiously, the motifs observed in TvO and TvS are not optimal according to the CSD-Materials Polymorph Assessment module available in Mercury 4.0.¹⁸ We calculated the hydrogen bond propensity for all six compounds using specially defined probes, B–OH and B–O (instead of general OH and O). For 3-substituted derivatives, the additional default probes for tertiary amines and cyclic ethers or aliphatic thioethers were used. The results for 3-substituted derivatives are shown in Fig. 4, and details are gathered in section 2.3 in the ESI.† The plots depict the dependence of mean H-bond coordination (the higher, the better) and the H-bond propensity (the higher, the better). Each point corresponds to a different pair of possible interactions between the donor B–O1–H1 and one of the four acceptors: O1, O2, N1, O3, or S1, and as such represents different main motifs in potential polymorphs of TvO (Fig. 4a) and TvS (Fig. 4b). All the “classical” R²₂(8) dimers show high H-bond propensity and coordination values and thus should coincide with the lower energy polymorph. For TvO, however, the observed motif exhibits the worst H-bond propensity and simultaneously the best H-bond coordination value, the latter feature is consistent with the best acceptor properties of the O3 atom as shown in the electrostatic potential maps (Fig. 3). Meanwhile, the motif in TvS is the least favorable (purple circle at the left in Fig. 4b); hence, in our opinion, the search for a new polymorph might be worth trying.

Fig. 4 Polymorph assessment for TvO (a) and TvS (b). All points correspond to possible supramolecular motifs with different acceptors. The values for the observed motifs in 3-substituted tavaborole and benzoxaborole derivatives are purple and green.

Nevertheless, to be sure that the analyzed crystal structures of TvO and TvS correspond to the crystallized reaction products we performed powder X-ray diffraction studies (PXRD) and differential scanning calorimetry (DSC) measurements integrated with thermogravimetric analysis (TGA). The PXRD results confirmed the presence of one polymorphic form in each case and the samples' homogeneity. The obtained DSC–TG curves revealed no signs of temperature-induced polymorphic transitions and the samples decomposed just after melting.

Other supramolecular interactions

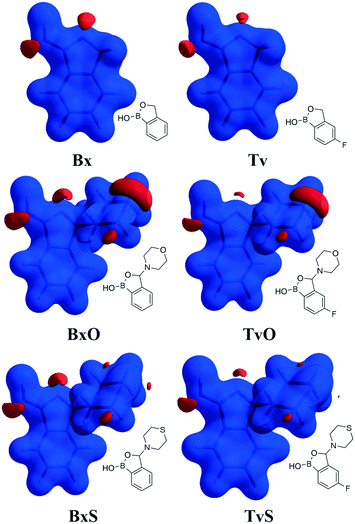
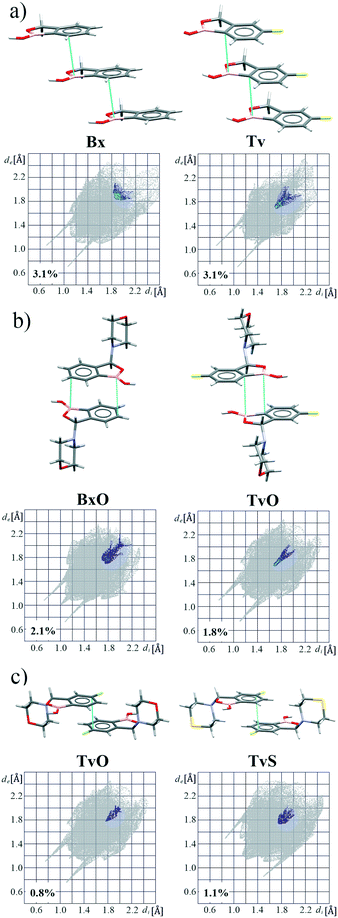
Except for influencing the main supramolecular motifs, the different substituents and the presence of the fluorine atom interfere with weaker intermolecular interactions. It is, therefore, worth exploring the types and motifs formed by such interactions in the analyzed series. The CSD Full Interaction Maps (FIMs) module, using a knowledge-based approach, is a convenient tool for assessing the types of non-covalent interactions.²⁸ We calculated the FIMs for each compound using standard probes such as uncharged NH nitrogen, carbonyl oxygen, and aromatic CH carbon atoms, and for tavaboroles, also the C–F fluorine atom. In Fig. 5, the maps for all compounds are shown. The most populated sites are the most likely interacting acceptors (red region) or donors (blue region). While the best acceptor site is evident, several possible donor sites are available. It is clear from the maps that the O1 atom is the best accessible H-bond acceptor (the most populated blue region near O1), and it is in line with electrostatic potential maps and the hydrogen bond propensity calculations, where the motifs with this acceptor were placed as the second best (section 2.3, ESI†).

Fig. 5 Full Interaction Maps. Blue and red regions show where potential hydrogen bond donors and acceptors, respectively, could be located. Orange and green surfaces correspond to the area for the most likely aromatic and organic fluorine atom interactions.

We found out that O1 is engaged in C–H⋯O interactions (Table S2†), mostly with hydrogen atoms bonded to the C7 atom (the motif C(5) in Fig. 6b) and also with aromatic C–H donors, for example, forming an R²₂(10) motif in TvO (Fig. 6a). It is worth noting that a small but highly populated area for external donors is near the N1 atom; however, no meaningful interactions have been detected with this acceptor in all analyzed structures (Table S2†). For fluoro-substituted derivatives, the green areas in FIMs stand for the possible spatial approach of C–F acceptors, and they are near aromatic C–H donors and near morpholine/thiomorpholine substituents. Indeed, in Tv, the C–H⋯F interactions form an R²₂(8) dimer (Fig. 6a), often observed in fluorinated benzene derivatives²⁹ as well as sustained in tavaborole co-crystals.¹¹ Meanwhile in substituted tavaborole derivatives, the aliphatic donors take part in C–H⋯F interactions, and R²₂(18) or R²₂(16) ring motifs are observed (Fig. 6b). The meaningful interactions are also formed with substituents' O3 and S1 atoms in BxO and BxS, respectively, (R²₂(16) motif in Fig. 6a), despite the areas near them are not visible on FIMs.

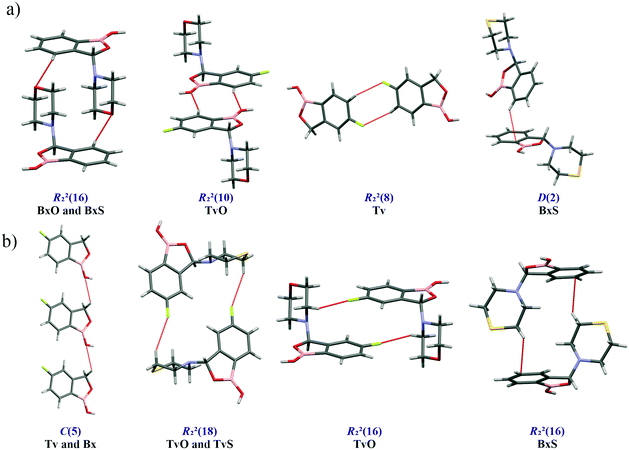Fig. 6 Structural motifs of C–H⋯X hydrogen bonds (X = O, S, F, π-electrons) involving aromatic (a) and aliphatic (b) C–H donors.

Most of the above-mentioned weak hydrogen bond interactions are in line with the FIMs, which show that both aliphatic and aromatic C–H donors are likely to participate in them. On the maps, there are also brown-colored areas pointing to the regions of various aromatic interactions (Fig. 5). The Aromatic Analyzer (AA) tool in Mercury 4.0, utilizing a neural network model, enables the quantitative assessment of such interactions between phenyl rings, both parallel and close-to-perpendicular (i.e., C–H⋯π hydrogen bonds). We focused only on contacts classified as strong, with “the score” above 7 within the scale of 0–10. Noteworthily, such aromatic interactions are present in all analyzed structures. In BxS, the C–H⋯π interactions between phenyl rings have been detected with a score of 8.5 (Fig. 6a, Table S18†). In this crystal structure, also a C–H⋯π interactions between thiomorpholine and phenyl rings are present (Fig. 6b), and they are substantially more robust than the one formed with the aromatic donor (see next paragraph and Table S10†). Interestingly, contrary to other structures in BxS there are no parallel π⋯π interactions. The latter are, in most cases, dominant in forming the next level of supramolecular architecture. In Bx and Tv structures, the interacting benzoxaborole 9-membered rings are stacked one above the other with a specific shift (Fig. 7a), with the AA score of 8.2 and 9.6 for Bx and Tv, respectively. In 3-substituted derivatives (except for BxS), the interacting rings have an antiparallel orientation, and two types of arrangement can be distinguished. In the first one (Fig. 7b), benzoxaborole rings are located so that the shortest distance is observed between boron and carbon atoms (see the associated fingerprint plots for C⋯B/B⋯C contacts detected on the Hirshfeld surface in Fig. 7b). Interestingly, in BxO, this contact is ascribed to the highest AA score of 9.8 with a B1⋯C3 distance of 3.475(3) Å, while in the fluorine substituted TvO the separation is 3.369(2) Å, but the contact is classified as moderate (the AA score 6.0). This difference may be an effect of a substantial slippage between phenyl rings and also the competing aromatic interactions. The second antiparallel motif is observed between fluorinated fragments of aromatic rings (Fig. 7c). In TvO, this interaction is given the AA score of 7.5, whereas, in TvS, it is classified as stronger with the AA score of 8.3.

Fig. 7 Examples of aromatic motifs and corresponding resolved fingerprint plots showing different arrangements of aromatic rings: (a) parallel, (b) antiparallel with short B⋯C contacts, and (c) antiparallel with short F–C⋯C–F contacts.

Large supramolecular synthons

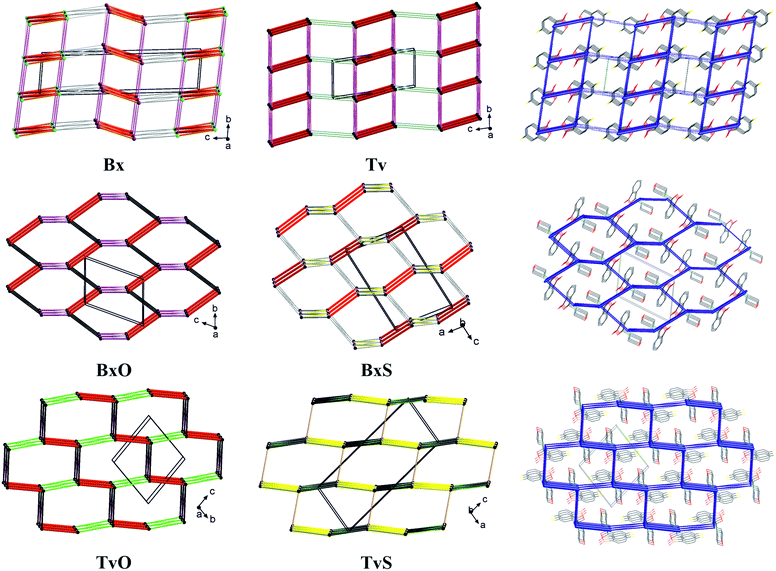
To summarize all the identified synthons and compare the crystal structures of the analyzed molecules, we describe the long-range synthon Aufbau modules (LSAMs) which are regarded as large supramolecular synthons composed of more than one type of intermolecular interaction.³⁰ For this purpose, we reduced every molecule to a node (its center of gravity) and drew lines between the nodes according to identified hydrogen bonds and aromatic interactions (Fig. 8). Further, we calculated the interactions energy in the Crystal Explorer program and based on that we could elucidate the hierarchy of the interactions and large synthons. First of all, it should be mentioned here that all the main motifs are 0D dimers (thick red lines in topological graphs in Fig. 8) except TvS, where the 1D chain with O–H⋯S interactions is the primary motif (thick yellow lines in Fig. 8).

Fig. 8 Simplified representation of the studied crystal structures in the form of topological graphs where a molecule is reduced to a node (its centre of gravity) and linkers are in line with the most important intermolecular interactions (red: O–H⋯O, yellow: O–H⋯S, pink: C–H⋯O, green: C–H⋯F, grey: interactions with aromatic rings). On the right, selected energy frameworks showing the total energy between molecular pairs in the form of tubes scaled according to the interaction energy values.

Hence, in both Bx and Tv, the aromatic π⋯π interactions join the dimers into 1D ladders, which extend along the [100] direction, i.e., the shortest unit cell vector (in Tv it is the most shrinking vector when lowering the temperature). The energy of these interactions is about 25 kJ mol⁻¹ and is the second highest after the interaction energy in the dimers. However, these ladders do not pack hexagonally as it would be expected for 1D entities being held in a crystal only by non-directional interactions. Hence, even though the subsequent identified interactions (the C–H⋯O hydrogen bonds from the aliphatic C7 atom to O1 atom) have an energy of 11–14 kJ mol⁻¹, they operate together and join the ladders into 2D layers (or more precisely, double layers) perpendicular to the longest unit cell vector (Fig. 8, top row). Such layers are observed in both polymorphs of Bx, and in the centrosymmetric one, the layers are built of one kind of molecules, while in the non-centrosymmetric one, two types of crystallographically independent molecules are in one layer (Fig. 8 and S2†). The layers in Tv and centrosymmetric Bx are related by translation only, while the mixed ones in the non-centrosymmetric polymorph of Bx are related by the 2₁ screw axis. In all cases, the energy of interactions between layers is around 6–8 kJ mol⁻¹, and it clearly shows the exchange of C–H⋯π interactions in both Bx structures for the C–H⋯F ones in Tv. Interestingly, in all co-crystals of Tv both C7–H⋯O1 and C–H(aromatic)⋯F interactions are present.¹¹ This regularity may open the path for obtaining new binary or ternary co-crystals of Tv or Bx.³¹ To sum up, the large synthon in unsubstituted derivatives can be assumed to be a 2D double-layer, and notably, the topology of the layer is reflected in the energy framework drawings (Fig. 8).

In BxO and TvO, the dimers, although different, are joined to form 1D chains via C–H⋯O3 and π⋯π interactions, respectively. These weaker interactions have approximately two times lower energy (∼30 kJ mol⁻¹) than the H-bonded main motifs. Again, these 1D entities do not pack hexagonally. What is more, the next identified synthons show the energy of approximately 20 kJ mol⁻¹ (section 2.5 in the ESI†); there are three such interactions in BxO (π⋯π, C7–H7⋯O1 and C–H⋯π) and two in TvO (C–H⋯F and C–H⋯B short contacts). As such, in both structures, they lead directly to 3D structures, and in our opinion, they should not be hierarchized. Similarly, in BxS, one might find 1D chains formed via C–H⋯π interactions (the one with the C–H donor from thiomorpholine), however, the remaining C–H⋯S, C–H⋯O and aromatic C–H⋯π interactions are only slightly weaker. Therefore, no large synthon should be distinguished in this case, and cooperative weak interactions lead directly from the 0D dimer to the 3D structure. In TvS, the main 1D motif made of O1–H1⋯S1 interactions with an energy ∼30 kJ mol⁻¹ is further joined by two types of interactions (π⋯π and C7–H7⋯O1, the energy around 22 kJ mol⁻¹) into a 2D supramolecular layer. The layers are parallel to (201) crystallographic planes, enforced by C–H⋯F interactions (∼15 kJ mol⁻¹). The interactions between the layers are of the C⋯O/B⋯O type and have an energy of 15 kJ mol⁻¹. They are visible in fingerprint plots as quite sharp lines (Fig. S4†), but their nature and the nature of C–H⋯B short contacts (Fig. S4†) need further discussion and investigation, presumably coming from the vague boron atom van der Waals radius.³² However, in all 3-substituted derivatives, the graph representation and the shape of the energy frameworks (Fig. 8) viewed along the shortest unit cell vector revealed the distorted honeycomb intersection of 3D frameworks. Remarkably, in new tavaborole derivatives, the hexagonal mesh is substantially flattened due to geometrical requirements for interactions of aliphatic donors from the substituent with a fluorine atom. As a result, the intersection more resembles a brick-wall arrangement.

It should be noted that the elucidated 2D large synthons in Tv and Bx exhibit a lattice energy substantially lower than the 3D frameworks in 3-substituted derivatives (Table S29†). This result is reasonable, considering that the interlayer C–H⋯F or C–H⋯π interactions have significantly lower energy. The 3D honeycomb structures in BxO and BxS show the highest lattice energy, but that in TvO is only slightly lower. Interestingly, in TvS, the lattice energy is midway in the series, either due to being more a 2D large synthon than a 3D framework or a suboptimal polymorph.

Conclusions

In the analyzed series, the molecular geometry is not influenced by either fluorine or morpholine/thiomorpholine substituents. However, the fluorine atom's presence reduces both the molecular dipole moment as well as the negative potential at the O2 atom, thus decreasing its hydrogen bond acceptor properties. This effect becomes even more pronounced when introducing the substituent at position 3, which results in the change of the main motif structure from the R²₂(8) O–H⋯O dimer in Tv to R²₂(18) dimer in TvO and the O–H⋯S C(9) chain in TvS. The latter, however, might not be the optimal polymorph as revealed by the hydrogen bond propensity analysis. On the other hand, the fluorine substituent does not influence the O1 atom acceptor ability. What is more, the full interaction and electrostatic potential maps as well as the hydrogen bond propensity calculations show that it is a very good hydrogen bond acceptor. Even though O1 does not participate in the formation of primary motifs (which probably would require the change of the boron hydrogen atom from the syn to anti conformation), it forms meaningful C–H⋯O interactions in all structures (and also in Tv co-crystals). Moreover, in 3-substituted derivatives, the analysis of intermolecular contacts and their energy revealed a similar pattern despite the different interaction types. In all of them, it is difficult to distinguish low dimensionality large synthons, however, the lattice energy differences might indicate a 2D structure in TvS. We expect that the presented way of analysis of the interaction hierarchy, using complementary methods based on knowledge-based and quantum crystallography algorithms, may help design new forms of benzoxaborole derivatives.

Experimental

TvO and TvS were synthesized according to the procedure recently described.⁹ The IR and Raman spectra of all studied compounds are given by Kaczorowska et al.³³ After several attempts, the best quality crystals were obtained from the 1 : 1 molar mixture of CH₂Cl₂ and hexane.

Programs for generating figures: Ortep-3 for Windows³⁴ (Fig. 1a and b), Mercury 4.0 (ref. 18) (Fig. 1c, 2 and 4–7), and Diamond v. 4.6.6 (ref. 35) (Fig. 8).

Single crystal X-ray diffraction

Single crystals suitable for X-ray diffraction studies were selected under a polarizing microscope, mounted on a capillary, and transferred to a diffractometer. Diffraction data for TvO (5-fluoro-3-morpholin-4-yl-2,1-benzoxaborol-1(3H)-ol) and TvS (5-fluoro-3-thiomorpholin-4-yl-2,1-benzoxaborol-1(3H)-ol) were collected on a Rigaku Oxford Diffraction Gemini A Ultra diffractometer with a fine-focus sealed X-ray tube using Mo Kα (λ = 0.71073) radiation at room temperature. Cell refinement and data collection and data reduction and analysis were performed with the CrysAlis^Pro 1.171.40.67a software.³⁶ Empirical absorption correction using spherical harmonics implemented in the SCALE3 ABSPACK scaling algorithm was used. The structures were solved with the SHELXT³⁷ structure solution program using direct methods and refined with the SHELXL³⁸ refinement package using the least-squares minimization procedure, both implemented in the Olex 2 1.3 suite.³⁹ All non-hydrogen atoms were refined with anisotropic temperature factors. The H-atoms were placed in calculated positions riding on their parent atom with fixed isotropic thermal parameters U_iso(H) = 1.2 × [U_eq(C)] for all C(H) and C(H,H) groups while hydrogen atoms in OH groups were freely refined with fixed U_iso(H) = 1.5 × [U_eq(O)].

Powder X-ray diffraction

Powder X-ray diffraction (PXRD) patterns for a bulk samples of TvO and TvS were recorded at room temperature on a Bruker Advance D8 diffractometer (Bruker, Billerica, MA, USA) equipped with a LYNXEYE position sensitive detector using CuKα radiation (λ = 0.15406 nm). The data were collected in the Bragg–Brentano (θ/θ) horizontal geometry (flat reflection mode) between 2° and 50° (2θ) in a continuous scan using 0.03° steps and 384 s per step. The diffractometer incident beam path was equipped with a 2.5° Soller slit and a 1.14° fixed divergence slit, while the diffracted beam path was equipped with a programmable anti-scatter slit (fixed at 2.20°), a Ni β-filter, and a 2.5° Soller slit.

The experimental diffraction patterns together with the patterns simulated from the scXRD final refinement data are presented in Fig. S5 in the ESI† file. The samples were pure and homogeneous.

Thermal analysis

The thermal behavior of TvO and TvS samples was examined using calorimetric studies carried out with differential scanning calorimetry (DSC) on a TA Instruments Q2000 apparatus and with thermogravimetric analysis (TGA) on a TA Instruments SDT Q600 apparatus. The heating rate in both cases was set to 10 K min⁻¹ and the pure nitrogen flow was set at 100 ml min⁻¹. The temperature range: from room temperature up to 550 °C. The results are presented in Fig. S6 and S7 in the ESI.†

In both cases after melting the samples decomposed with a considerable weight loss. No polymorphic transitions were detected.

Calculation details

CrystalExplorer software. All calculations were based on the CE-B3LYP/6-31G(d,p) model wavefunctions using the built-in Tonto program⁴⁰ embedded in CrystalExplorer21 (version 21.5).²³ The molecular and crystal geometries were taken directly from the cif files, with X–H bond lengths normalized to standard neutron diffraction values. The obtained Hirshfeld surfaces are presented (Fig. 2) using the d_norm property being a sum of normalized d_e (a distance of an external atom to the surface) and d_i (a distance of an internal atom to the surface) by the van der Waals radii of the atoms involved.²⁴ The red–white–blue coloring scheme corresponds to contacts shorter, equal, and longer than the sum of the van der Waals radii, respectively. The same scaling was set to all analyzed crystals. The fingerprint plots (Fig. 2 and 7) were resolved to the contacts of specified atoms outlined on the full map depicted in gray. The percentage values for specific contacts (both external and internal in the case of different atoms) are also given. Electrostatic potential surfaces (Fig. 3) were calculated at the isovalue of 0.05 a.u., and negative and positive potentials are represented on the surface by red and blue colors, respectively. Energy frameworks and lattice energies were calculated for a cluster of 20 Å radius around a central molecule.⁴¹ For Bv structures, the lattice energy is the average of the lattice sums for the two individual molecules. Energies between molecular pairs are represented as cylinders joining the centers of mass of the molecules (Fig. 8), with the cylinder radius proportional to the magnitude of the interaction energy. The energy scale factor was set to 40 for all structures and the energy threshold was 10 kJ mol⁻¹. Section 2.5 of the ESI† contains information about these calculations.

Mercury 4.0 software. Full interaction maps (FIMs), molecular dipole moments, polymorph assessment and hydrogen bond propensity, and the analysis of aromatic interactions have been calculated with Mercury 4.0 (version 2021.3.0) CSD-Materials module.¹⁸ Before any calculation, the molecules were standardized to Cambridge Structural Database conventions concerning the bond types. For calculations based on knowledge-based algorithms, CSD version 5.43 was used. For FIMs, standard probes such as uncharged NH nitrogen, carbonyl oxygen, and aromatic CH carbon atoms, and also the C–F fluorine atom have been used. The dipole moments were assessed using the Molecular Complementarity module.⁴² The Polymorph Assessment module, using both the hydrogen bond propensity calculations⁴³ and hydrogen-bond coordination analysis⁴⁴ was used with specially designed probes B–OH and B–O (instead of general OH and O) and default probes for tertiary amines and cyclic ethers or aliphatic thioethers. The H-bond distance was restricted not to be longer than the sum of vdW radii plus 0.05 Å. For the structures with the same substitution at position 3, the pairwise logistic regression models were used. In all cases, the number of true/false data was satisfactory and the area under the ROC curve was above 0.81 to verify that the model may be reliably used.⁴⁵ The Aromatic Analyzer module uses a neural network model to quantify the expected stabilizing interactions between the six-membered aromatic rings. The interactions are ranked on a scale of 0–10 as strong (10 → 7), moderate (7 → 3), and weak (3 → 0). The intramolecular contacts were excluded from the analysis. Section 2.4.3 of the ESI† contains the results for interactions classified as strong and moderate.

Author contributions

Anna M. Dąbrowska: conceptualization, crystallization, X-ray measurements and analysis, writing – original draft, figures and ESI† preparation, writing – review & editing. Agnieszka Adamczyk-Woźniak: synthesis & funding acquisition. Izabela D. Madura: conceptualization, methodology, resources, formal analysis, writing – original draft, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by Polish National Science Centre (NCN, grant no. 2016/23/B/ST5/02847). Authors would like to acknowledge Andrzej Ostrowski for PXRD as well as Tomasz Gołofit for DSC–TGA measurements.

Notes and references

1. A. K. Gupta and S. G. Versteeg, Expert Rev. Clin. Pharmacol., 2016, 9, 1145–1152.
2. F. L. Rock, W. Mao, A. Yaremchuk, M. Tukalo, T. Crépin, H. Zhou, Y. K. Zhang, V. Hernandez, T. Akama, S. J. Baker, J. J. Plattner, L. Shapiro, S. A. Martinis, S. J. Benkovic, S. Cusack and M. R. K. Alley, Science, 2007, 316, 1759–1761.
3. M. Dowlut and D. G. Hall, J. Am. Chem. Soc., 2006, 128, 4226–4227.
4. A. Adamczyk-Woźniak, K. M. Borys and A. Sporzyński, Chem. Rev., 2015, 115, 5224–5247.
5. K. Czerwińska, I. D. Madura and J. Zachara, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 241–248.
6. A. Adamczyk-Woźniak, O. Komarovska-Porokhnyavets, B. Misterkiewicz, V. P. Novikov and A. Sporzyński, Appl. Organomet. Chem., 2012, 26, 390–393.
7. A. Adamczyk-Woźniak, M. K. Cabaj, P. M. Dominiak, P. Gajowiec, B. Gierczyk, J. Lipok, Ł. Popenda, G. Schroeder, E. Tomecka, P. Urbański, D. Wieczorek and A. Sporzyński, Bioorg. Chem., 2015, 60, 130–135.
8. E. P. Gillis, K. J. Eastman, M. D. Hill, D. J. Donnelly and N. A. Meanwell, J. Med. Chem., 2015, 58, 8315–8359.
9. D. Wieczorek, E. Kaczorowska, M. Wiśniewska, I. D. Madura, M. Leśniak, J. Lipok and A. Adamczyk-Woźniak, Molecules, 2020, 25, 5999.
10. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
11. G. Campillo-Alvarado, C. A. Staudt, M. J. Bak and L. R. MacGillivray, CrystEngComm, 2017, 19, 2983–2986.
12. I. D. Madura, A. Adamczyk-Woźniak, M. Jakubczyk and A. Sporzyński, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2011, 67, o414–o415.
13. S. Sene, D. Berthomieu, B. Donnadieu, S. Richeter, J. Vezzani, D. Granier, S. Bégu, H. Mutin, C. Gervais and D. Laurencin, CrystEngComm, 2014, 16, 4999–5011.
14. A. Sporzyński, M. Lewandowski, P. Rogowska and M. K. Cyrański, Appl. Organomet. Chem., 2005, 19, 1202–1203.
15. A. Adamczyk-Woźniak, I. Madura, A. H. Velders and A. Sporzyński, Tetrahedron Lett., 2010, 51, 6181–6185.
16. V. V. Zhdankin, P. J. Persichini, L. Zhang, S. Fix and P. Kiprof, Tetrahedron Lett., 1999, 40, 6705–6708.
17. A. Adamczyk-Woźniak, M. K. Cyrański, M. Jakubczyk, P. Klimentowska, A. Koll, J. Kołodziejczak, G. Pojmaj, A. Zubrowska, G. Z. Zukowska and A. Sporzyński, J. Phys. Chem. A, 2010, 114, 2324–2330.
18. C. F. MacRae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235.
19. I. D. Madura, K. Czerwińska, M. Jakubczyk, A. Pawełko, A. Adamczyk-Woźniak and A. Sporzyński, Cryst. Growth Des., 2013, 13, 5344–5352.
20. M. C. Etter, J. C. MacDonald and J. Bernstein, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 256–262.
21. J. Bernstein, R. E. Davis, L. Shimoni and N.-L. Chang, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555–1573.
22. L. D'Ascenzo and P. Auffinger, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 164–175.
23. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011.
24. J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816.
25. V. L. Arcus, L. Main and B. K. Nicholson, J. Organomet. Chem., 1993, 460, 139–147.
26. P. Sanphui, G. Bolla, U. Das, A. K. Mukherjee and A. Nangia, CrystEngComm, 2013, 15, 34–38.
27. D. Das and G. R. Desiraju, CrystEngComm, 2006, 8, 674–679.
28. P. A. Wood, T. S. G. Olsson, J. C. Cole, S. J. Cottrell, N. Feeder, P. T. A. Galek, C. R. Groom and E. Pidcock, CrystEngComm, 2013, 15, 65–72.
29. V. R. Thalladi, H. C. Weiss, D. Bläser, R. Boese, A. Nangia and G. R. Desiraju, J. Am. Chem. Soc., 1998, 120, 8702–8710.
30. P. Ganguly and G. R. Desiraju, CrystEngComm, 2010, 12, 817–833.
31. S. Tothadi, A. Mukherjee and G. R. Desiraju, Chem. Commun., 2011, 47, 12080–12082.
32. M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812.
33. E. Kaczorowska, A. Adamczyk-Woźniak, G. Z. Żukowska, P. Kostecka and A. Sporzyński, Symmetry, 2021, 13, 1845.
34. L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854.
35. H. Putz and K. Brandenburg, Diamond, Crystal and Molecular Structure Visualization, Crystal Impact GbR, Kreuzherrenstr. 102, D-53227 Bonn, Germany.
36. CrysAlis^Pro 1.171.40.67a, Rigaku Oxford Diffraction, 2020.
37. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
38. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
39. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
40. D. Jayatilaka and D. J. Grimwood, Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), 2003, vol. 2660, pp. 142–151.
41. S. P. Thomas, P. R. Spackman, D. Jayatilaka and M. A. Spackman, J. Chem. Theory Comput., 2018, 14, 1614–1623.
42. L. Fábián, Cryst. Growth Des., 2009, 9, 1436–1443.
43. P. T. A. Galek, L. Fábián, W. D. S. Motherwell, F. H. Allen and N. Feeder, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 768–782.
44. P. T. A. Galek, J. A. Chisholm, E. Pidcock and P. A. Wood, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 91–105.
45. P. T. A. Galek, F. H. Allen, L. Fábián and N. Feeder, CrystEngComm, 2009, 11, 2634–2639.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary figures, geometrical parameters of the molecules, hydrogen bond geometry, hydrogen bond propensity calculation details, aromatic interaction geometry, Aromatic Analyzer calculation results, and calculated interaction energy details. CCDC 2152788 and 2152789. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce00279e

---