Unravelling conformational and crystal packing preferences of cyclohexane-5-spirohydantoin derivatives incorporating a halogenated benzoyl group†
Anita
Lazić
a,
Lidija
Radovanović
a,
Kristina
Gak Simić
a,
Jelena
Rogan
b,
Goran
Janjić
c,
Nemanja
Trišović
b and
Ivana
Đorđević
 *c
*c
aInnovation Centre of the Faculty of Technology and Metallurgy, Karnegijeva 4, 11120 Belgrade, Serbia
bUniversity of Belgrade, Faculty of Technology and Metallurgy, Karnegijeva 4, 11120 Belgrade, Serbia
cUniversity of Belgrade, Institute of Chemistry, Technology and Metallurgy, National Institute of the Republic of Serbia, Njegoševa 12, 11001 Belgrade, Serbia. E-mail: ivana.djordjevic@ihtm.bg.ac.rs
First published on 17th May 2022
Abstract
Two spirohydantoin derivatives, 3-(4-chlorobenzoyl)-1,3-diazaspiro[4.5]decane-2,4-dione (1) and 3-(4-bromobenzoyl)-1,3-diazaspiro[4.5]decane-2,4-dione (2), were synthesized and analyzed by single crystal X-ray diffraction, DFT and QTAIM calculations. Simple substitution of the benzoyl unit gave rise to different crystal structures. In 1, a parallel stack along the b-axis with alternating perpendicular separation is formed, while in 2 the R46(32) nets are joined together to form stacks which enclose linear channels. Hierarchical development of these crystal structures was analyzed through dimeric motifs associated with the presence of intermolecular interactions. By including the previously reported structurally-related spirohydantoin derivatives, we created a set of structures which enabled us to evaluate substituent effects on their conformational preferences, i.e., widening of the dihedral angle between the hydantoin and substituted benzoyl unit when going from F to Br. A conformational search revealed that the value of the torsion angle N3–C11–C12–C13 can be regarded as a compromise between the extended conjugation between the carbonyl and phenyl group and intramolecular C–H⋯O interaction between these two groups. This intramolecular effect is more pronounced on the torsion angle C2–N3–C11–C12, which defines the relative orientation between the hydantoin ring and the carbonyl bridge. The present work may provide a basis for design of new cyclohexane-5-spirohydantoins with potential for pharmaceutical applications both at the molecular and supramolecular level.
Introduction
Understanding the conformations and supramolecular arrangements of biologically active compounds is crucial for their applications as drugs. However, predictive power over these structural features still remains limited. Different modes of molecular aggregation are reflected in different crystal packings which influence the physico-chemical properties such as solubility and dissolution rate. Namely, low solubility usually leads to a slow dissolution and further to a limited bioavailability.1 Low solubility is also one of the dominant issues that affect the pharmaceutical processability, i.e., downstream operations such as filtration, drying and milling.2The conformational control is very important from the molecular-recognition and crystal-engineering point of view. Wassvik et al. used multivariate data analysis to identify features responsible for reduced solubility of marketed drugs.3 It was concluded that molecules with extended ring structures and large conjugated systems were less soluble, thus implying that features of the molecular structure which correspond to conformational rigidity and aromaticity cause solubility restricted by stable crystal structures. However, conformationally restricted biologically active compounds likely have increased affinity and selectivity of target binding, although the correlation between flexibility and promiscuity is still under debate.4
Conformational flexibility is additionally recognized as a potential obstacle to control the crystallization output in a purely chemical manner. When a molecule has several possible conformations, it does not necessarily adopt the lowest energy one in the crystal packing, but a higher energy conformation in order to balance inter- and intramolecular interactions.5 Thompson and Day demonstrated that high energy conformers are adopted when accessible surface area is increased, which results in the increased potential of the molecule to establish stabilizing intermolecular interactions.5a
The interpretation of the crystal packing is usually discussed in terms of directional intermolecular interactions of diverse strengths. Hydrogen bonding is a critical determinant of crystal packing and a favourite tool of crystal engineering, especially strong hydrogen bonds like O–H⋯O, N–H⋯O and O–H⋯N.6 Lo Presti questioned the relevance of weak hydrogen bonding between the C–H group and an electronegative atom and suggested that it is not expected to provide a significant thermodynamic drive toward a specific crystal form.7 Halogen bonding can also be as effective as hydrogen bonding and enables establishment of highly specific crystal packing motifs.8
The structural information for pharmaceutically relevant molecular fragments indicates the significance of intermolecular interactions that are relevant to the recognition events in chemical and biological systems and in solutions. Taking into account the complexity of the protein surroundings, however, understanding an individual intermolecular interaction, separated from other effects, with biological receptors is difficult.9 A comparison of the Cambridge Structural Database10 (CSD) and Protein Data Bank11 (PDB) statistical survey demonstrated some of the biases intrinsic to molecular conformations in the PDB which are consistent with protein-induced conformational perturbations.12 Mladenovic et al. showed that proteins can polarize molecules stronger than surroundings inside the crystals.13
Hydantoin represents an integral part of many natural products and marketed drugs. For example, conventional anticonvulsant drugs like phenytoin(5,5-diphenylhydantoin), fosphenytoin(3-((phosphonooxy)methyl)-5,5-diphenylhydantoin), mephenytoin(3-methyl-5-ethyl-5-phenylhydantoin) and ethotoin(3-ethyl-5-phenylhydantoin) have been widely used. Due to the presence of the N–H donors and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O acceptors, the rigid hydantoin framework is involved in hydrogen bonding. A statistical analysis of structures in the Cambridge Structural Database identified four main types of hydrogen bond motifs in hydantoin derivatives: R22(8)–1O–tape, R22(8)–2O–tape, R33(12)–2O–tape and R22(8)–dimer in network.14 Our group described several examples wherein halogen substitution in the phenyl ring separated from the hydantoin unit by a methylene or carbonyl spacer led to attractive supramolecular architectures through a remarkable diversity of intermolecular interactions involving even halogen bonding.15 Herein, we present the synthesis and determination of the crystal structure of two derivatives of cyclohexane-5-spirohydantoin bearing a 4-chlorobenzoyl or 4-bromobenzoyl group (1 and 2, Fig. 1). By taking into account previously reported analogues (3 and 4, Fig. 1),15b we created a series of compounds that enabled us to evaluate the effects of the halogen atom on the molecular conformation and the crystal packing. These compounds are suitably diverse to function as a reference because the torsional flexibility of the 4-substituted benzyl/4-substituted benzoyl group leads to the emergence of the various conformations. As already stated, this series also provides sufficient diversity in intermolecular interactions.
O acceptors, the rigid hydantoin framework is involved in hydrogen bonding. A statistical analysis of structures in the Cambridge Structural Database identified four main types of hydrogen bond motifs in hydantoin derivatives: R22(8)–1O–tape, R22(8)–2O–tape, R33(12)–2O–tape and R22(8)–dimer in network.14 Our group described several examples wherein halogen substitution in the phenyl ring separated from the hydantoin unit by a methylene or carbonyl spacer led to attractive supramolecular architectures through a remarkable diversity of intermolecular interactions involving even halogen bonding.15 Herein, we present the synthesis and determination of the crystal structure of two derivatives of cyclohexane-5-spirohydantoin bearing a 4-chlorobenzoyl or 4-bromobenzoyl group (1 and 2, Fig. 1). By taking into account previously reported analogues (3 and 4, Fig. 1),15b we created a series of compounds that enabled us to evaluate the effects of the halogen atom on the molecular conformation and the crystal packing. These compounds are suitably diverse to function as a reference because the torsional flexibility of the 4-substituted benzyl/4-substituted benzoyl group leads to the emergence of the various conformations. As already stated, this series also provides sufficient diversity in intermolecular interactions.
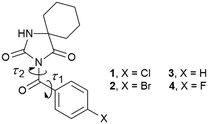 | ||
| Fig. 1 Chemical structures of the investigated compounds; τ1 and τ2 correspond to torsion angles N3–C11–C12–C13 and C2–N3–C11–C12, respectively, associated with the carbonyl bridge. | ||
Results and discussion
Molecular structure
Both 1 and 2 crystallize with Z = 2 in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . However, the unit cell parameters show some variations (Table 1) which indicates that these structures are not isostructural.
. However, the unit cell parameters show some variations (Table 1) which indicates that these structures are not isostructural.
| Compound | 1 | 2 |
|---|---|---|
| a w = 1/[σ2(Fo2) + (0.0457P)2 + 0.3053P] where P = (Fo2 + 2Fc2)/3. b w = 1/[σ2(Fo2) + (0.0494P)2 + 0.9158P] where P = (Fo2 + 2Fc2)/3. | ||
| Formula | C15H15ClN2O3 | C15H15BrN2O3 |
| Molecular weight/g mol−1 | 306.74 | 351.2 |
| Crystal system | Triclinic | Triclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| a/Å | 6.2836(13) | 6.6479(13) |
| b/Å | 10.928(2) | 10.089(2) |
| c/Å | 12.159(2) | 12.122(2) |
| α/° | 108.19(3) | 106.54(3) |
| β/° | 99.76(3) | 100.99(3) |
| γ/° | 104.73(3) | 91.53(3) |
| V/Å3 | 738.4(3) | 762.2(3) |
| Z | 2 | 2 |
| D c/g cm−3 | 1.38 | 1.53 |
| μ/mm−1 | 0.27 | 2.707 |
| F(000) | 320 | 356 |
| Crystal size/mm | 0.50 × 0.35 × 0.14 | 0.79 × 0.21 × 0.09 |
| θ range/° | 3.24–25.35 | 3.13–25.35 |
| Limiting indices | −7 ≤ h ≤ 7 | −8 ≤ h ≤ 8 |
| −13 ≤ k ≤ 13 | −12 ≤ k ≤ 12 | |
| −14 ≤ l ≤ 14 | −14 ≤ l ≤ 14 | |
| Measured reflections | 9756 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 556 556 |
| Independent reflections | 2707 | 2789 |
| Reflections with I > 2σ(I) | 1954 | 2112 |
| R int | 0.0272 | 0.0529 |
| Final R indices [I > 2σ(I)] | R 1 = 0.0548 | R 1 = 0.0563 |
| wR2 = 0.1157a | wR2 = 0.1194b | |
| R indices (all data) | R 1 = 0.0821 | R 1 = 0.0774 |
| wR2 = 0.1288 | wR2 = 0.1303 | |
| S | 1.031 | 1.032 |
| Parameters | 190 | 190 |
| Δρmax, Δρmin/e Å−3 | 0.241, −0.216 | 0.808, −0.737 |
| CCDC | 2156414 | 2156415 |
The ORTEP diagrams 1 and 2 are presented in Fig. 2a. The overlay of all structures (1–4) is shown in Fig. 2b and selected geometric parameters of 1 and 2 are collected in Table S1.†
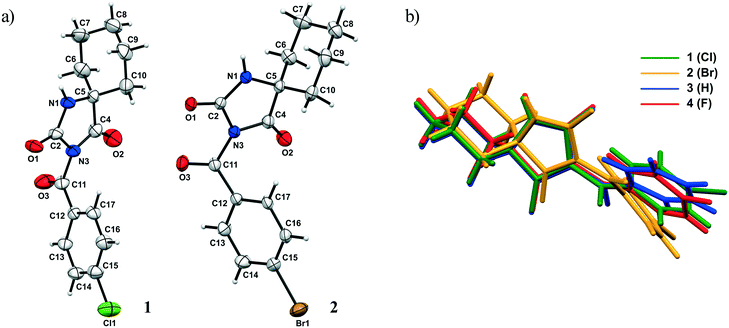 | ||
| Fig. 2 a) ORTEP diagram of 1 and 2 with the atom numbering scheme. The thermal ellipsoids are drawn at the 30% probability level; b) the overlay of structures 1–4 in the crystalline state. | ||
Firstly, the central hydantoin ring is basically planar and no significant effect on its structural features is exerted by the halogen atom X. The bond lengths and angles are in an agreement with those found in cycloalkane-5-spirohydantoins in the literature.15,16 On the other hand, the C11–N3 bond is longer and the C11–C12 bond is shorter in 1 than the corresponding ones in 2.
While the carbonyl spacer group is almost coplanar with the aryl ring in 1, the bending of this group out of the plane of the aryl ring by 26.16° is observed in 2. The exocyclic bond angles around the carbonyl spacer group are asymmetric; this asymmetry is somehow more pronounced in 2. As expected, the cyclohexyl ring adopts a chair conformation; thus, the hydantoin and cyclohexyl rings are almost perpendicular to each other. The most notable difference between the molecular conformations is manifested in widening of the dihedral angle between the hydantoin and aryl rings when going from F to Br. Namely, when the previously reported compound bearing the F atom is taken into account,15 a comparison of the dihedral angle shows that it varies from 81.9, 78.3 to 60.2° for F, Cl and Br, respectively. A possible explanation for the differences in the dihedral angles may lie in different crystal packings, i.e., different types and geometries of intramolecular interactions involving these rings. On the other hand, effects of intramolecular interactions on molecular conformation should not be excluded. This will be discussed in detail in the continuation of this paper.
Hirshfeld surface analysis
The Hirshfeld surface presents the shape of a molecule subjected to the intermolecular interactions with its surroundings.17Fig. 3 and 4 present the Hirshfeld surfaces for 1 and 2 mapped over a dnorm range from −0.5 to 1.7 Å. The N–H⋯O hydrogen bonds result in bright-red spots near the corresponding atoms. The faint-red spots near the O atom of the carbonyl bridge and the phenyl H atom provide a link between the molecules through a pair of comparatively weak C–H⋯O interactions. Furthermore, the faint-red spots near the carbonyl O atom of the hydantoin moiety and the cyclohexyl H atoms in the molecule of 2 indicate donors and acceptors of additional potential C–H⋯O interactions. The π⋯π stacking interactions (e.g., above the phenyl and heterocyclic ring) can be evidenced by the presence of a triangles pattern and a high planarity area in the shape-index and curvedness surface, respectively (Fig. S1 and S2†).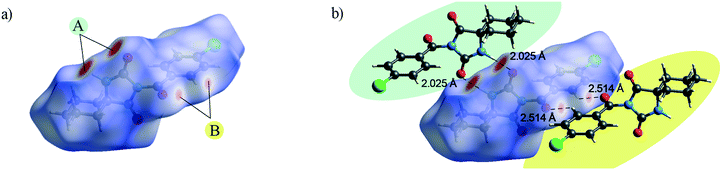 | ||
| Fig. 3 a) Hirshfeld surface generated on dnorm parameters and b) interactions of 1 with the generated Hirshfeld surface in 1. | ||
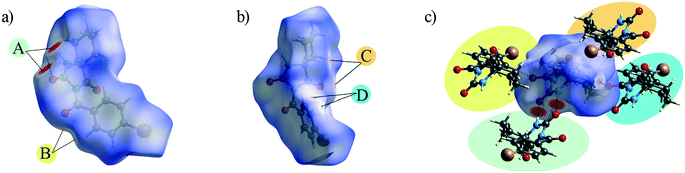 | ||
| Fig. 4 a) and b) Hirshfeld surface generated on dnorm parameters and c) interactions of 2 with the generated Hirshfeld surface in 2. | ||
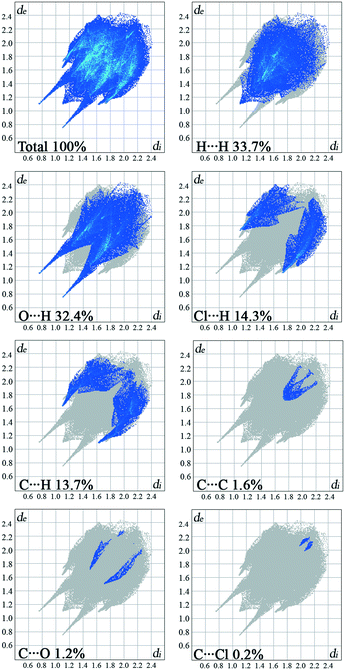
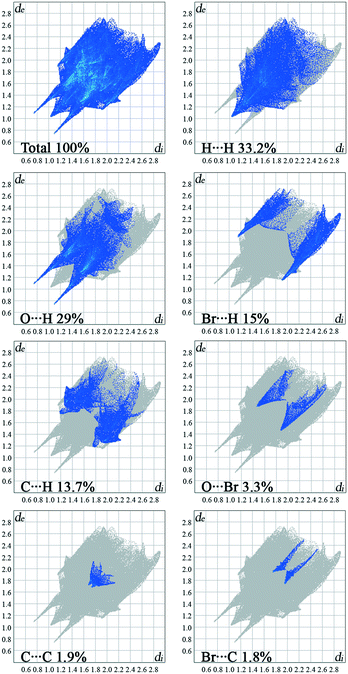
The overall Hirshfeld plots for 1 and 2 and those decomposed into the H⋯H, O⋯H/H⋯O, X⋯H/H⋯X, C⋯H/H⋯C, C⋯C, X⋯O/O⋯X and X⋯C/C⋯X contacts are shown in Fig. 5 and 6. From this simple analysis, it seems that the main contribution to the Hirshfeld surface results from the H⋯H contacts. A tip appears at de + di < 2.10 Å, i.e. less than two times the van der Waals radius of the H atom. In the fingerprint decomposed into the O⋯H/H⋯O contacts, a pair of overlapping spikes at de + di ∼ 1.9 Å results from the N–H⋯O hydrogen bonds, while a short spike with the tip at de + di ∼ 2.5 Å is due to the C–H⋯O interaction involving the carbonyl spacer group. As expected, the presence of the carbonyl spacer group increases contribution of the O⋯H/H⋯O contacts compared to the compounds with the methylene spacer group,15a thus reducing the contribution from the H⋯H contacts.
The wings at de + di ∼ 2.9 Å with a greater separation across the diagonal of the plot are attributable to short X⋯H/H⋯X contacts; these contacts comprise 15% of the Hirshfeld surface. The fingerprint plot decomposed into the C⋯H/H⋯C contacts shows a wing-like distribution of points with the edges at de + di ∼ 2.6 Å and indicates that the C–X⋯π interactions have a similar influence in both crystal packings.
Halogen bonding (X⋯O) makes a smaller contribution, i.e. 1.2%, to the Hirshfeld surface of 1 relative to 3.3% in 2. Interestingly, a contribution of the halogen bonding in 1 is smaller compared to the derivative bearing a methylene bridge between the hydantoin and phenyl ring.15a On the other hand, the contribution in 2 increases.
The π⋯π interactions between the phenyl rings make a small contribution from the C⋯C contacts to the overall surface. The X⋯π interactions resulting from X⋯C contacts are also indicated.
Supramolecular arrangement
The crystal packing can be analysed in terms of a number of simple dimeric motifs which are associated with different intermolecular interactions. In this context, the quantum chemical calculations at TPSSh-D3/def2TZVP level were performed in the Gaussian09 program. These dimeric motifs together with the corresponding interaction energies (ΔE) and the schematic presentation of the crystal packing are given in Fig. 7 and 8 for 1 and in Fig. 9 and 10 for 2.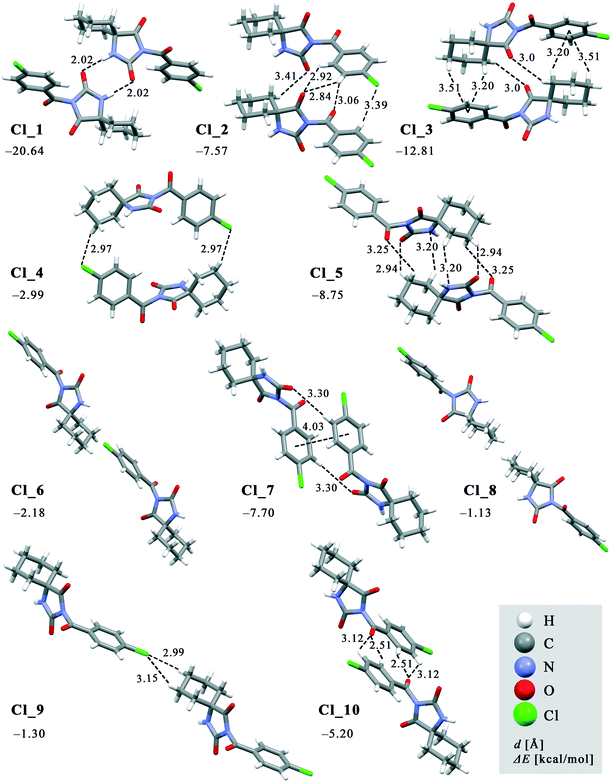 | ||
| Fig. 7 Dimeric motifs Cl_1–Cl_10 extracted from the crystal structure of 1 with their interaction energies. | ||
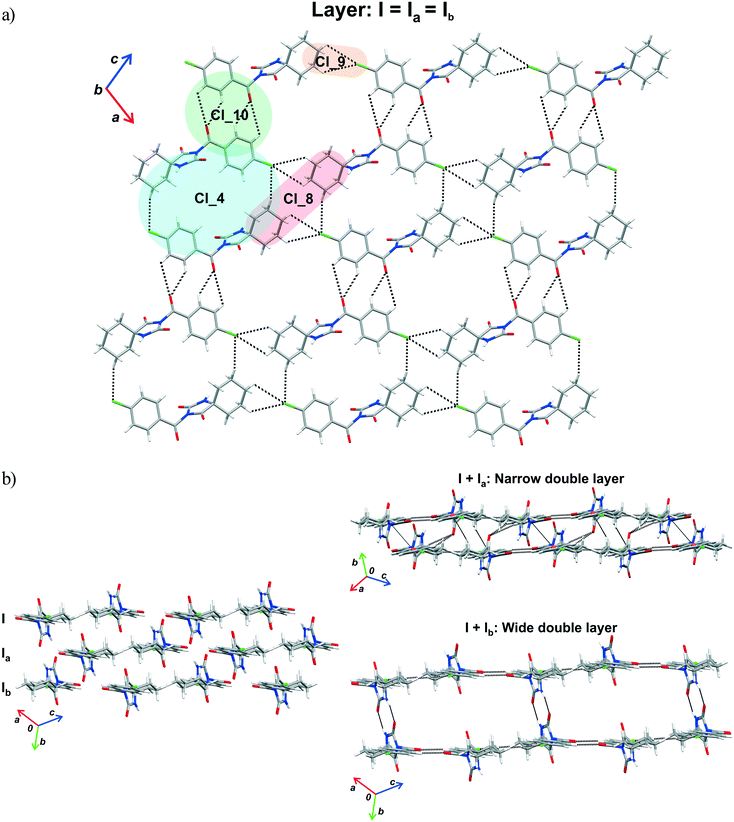 | ||
| Fig. 8 Part of the crystal structure of 1 showing formation of a) a layer and b) double layer arrangements. | ||
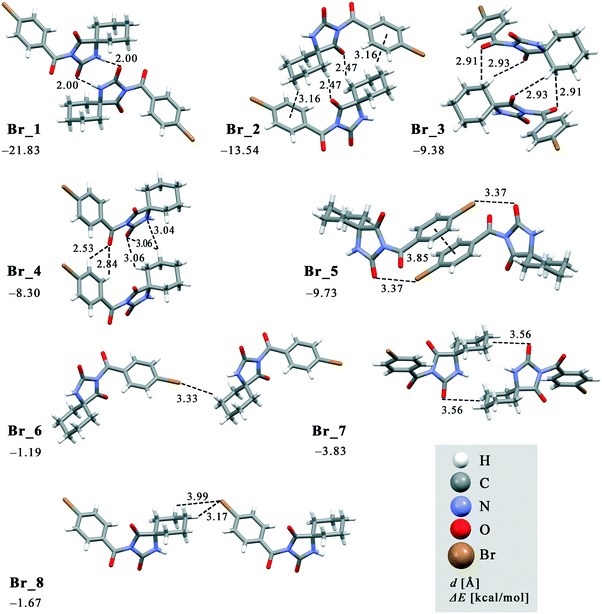 | ||
| Fig. 9 Dimeric motifs Br_1–Br_8 extracted from the crystal structure of 2 with their interaction energies. | ||
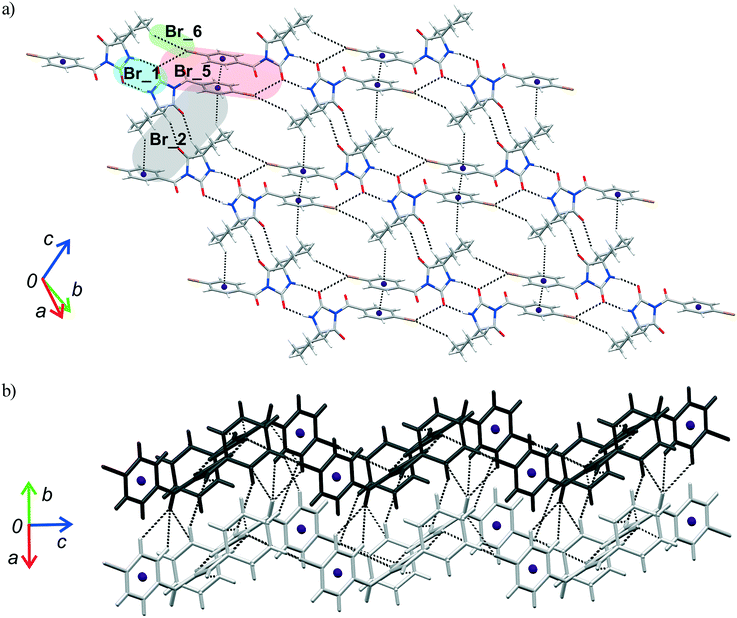 | ||
| Fig. 10 Part of the crystal structure of 2 showing formation of a) a two-dimensional net and b) intermolecular interactions between the adjacent nets. | ||
In both compounds, N–H⋯O hydrogen bonds connect pairs of molecules to form a cyclic dimer characterized by a centrosymmetric R22(8) motif in these crystal structures (motifs Cl_1 and Br_1 with ΔE being −20.64 and −21.83 kcal mol−1, respectively).
In 1, effects of interactions involving the Cl atom are twofold. Firstly, propagation of the C(sp3)–H⋯Cl interactions by translation generates a chain (motif Cl_9, ΔE = −1.30 kcal mol−1). On the other hand, the C(sp3)–H⋯Cl interactions of the motif Cl_4 form an isolated pair rather than part of a continuous chain, thus connecting the centrosymmetrically related chains into a double-chain (ΔE = −2.99 kcal mol−1). The double chains are weakly reinforced by hydrophobic interactions (motif Cl_8, ΔE = −1.13 kcal mol−1).
The motif Cl_10 (ΔE = −5.20 kcal mol−1) links together the double-chains into a layer (Fig. 8a). Regarding this motif, an interaction occurs through a side-on approach of the O atom of the carbonyl bridge of one molecule to the phenyl ring of the other and, hence, is characterized as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(lone-pair⋯π interaction. The motifs Cl_2, Cl_3, Cl_5, Cl_6 and Cl_7, the molecules of which belong to the neighbouring layers, serve to link them together into a narrow double layer. On the other hand, taking the motif Cl_1 as a starting motif, N–H⋯O hydrogen bonds connect every second layer into a wide double layer arrangement (Fig. 8b, bottom right).
O(lone-pair⋯π interaction. The motifs Cl_2, Cl_3, Cl_5, Cl_6 and Cl_7, the molecules of which belong to the neighbouring layers, serve to link them together into a narrow double layer. On the other hand, taking the motif Cl_1 as a starting motif, N–H⋯O hydrogen bonds connect every second layer into a wide double layer arrangement (Fig. 8b, bottom right).
In this way, a parallel stack with alternating perpendicular separation is formed (separation being about 6.5 Å between the layers within the wide double layer and about 3.5 Å between the narrow double layers). Regarding the motif Cl_2, the molecules related by translation are linked by a C(sp3)–H⋯O and three C(sp2)–H⋯O interactions (ΔE = −7.57 kcal mol−1). Within the pair of molecules forming a centrosymmetric ring motif of R22(10) type (motif Cl_3, ΔE = −12.81 kcal mol−1), there are two pairs of C–H⋯π interactions (Fig. 8b, upper right).
In addition to two pairs of C(sp3)–H⋯O in the motif Cl_5 (ΔE = −8.75 kcal mol−1), the N atom of the hydantoin ring acts as a hydrogen-bond acceptor of C(sp3)–H⋯N hydrogen bonds. Besides a pair of C(sp2)–H⋯O interactions, the phenyl rings in the molecules of the motif Cl_7 form a π⋯π stacking interaction (ΔE = −7.70 kcal mol−1). Hydrophobic interactions are also operative, as represented by the motif Cl_6 (ΔE = −2.18 kcal mol−1). Interestingly, significant halogen bonding was not observed in this case.
As previously stated, the crystal structure of 2 retains the motif commonly found in hydantoin derivatives wherein two molecules related by inversion are linked by a pair of N–H⋯O hydrogen bonds (motif Br_1). This motif is a part of two types of chain: a chain generated through alternation of the motifs Br_1 and Br_2 running along the b-axis and one with the altering motifs Br_1, Br_5 and Br_6. Within the motif Br_2 (ΔE = −13.54 kcal mol−1), the centrosymmetric rings formed by the action of C(sp3)–H⋯O interactions are of R22(10) type; this motif additionally features a pair of C(sp3)–H⋯π interactions. Regarding the motif Br_5 (ΔE = −9.73 kcal mol−1), an interaction between the O2 atom of one molecule and the Br atom of another can be identified, while their phenyl rings form an additional stacking interaction. Thus, C(sp3)–H⋯Br interactions enable formation of an additional motif Br_6 (ΔE = −1.19 kcal mol−1). The combination of all these motifs gives rise to a two-dimensional net built from R46(32) rings (Fig. 10a).
The two-dimensional nets are further joined together by intermolecular interactions, represented by the motifs Br_3, Br_4, Br_7 and Br_8, to form stacks which enclose linear channels. In the motif Br_3 (ΔE = −9.38 kcal mol−1), molecules related by inversion are linked by two pairs of C(sp3)–H⋯O hydrogen bonds. The motif Br_4 (ΔE = −8.30 kcal mol−1) features a pair of C(sp2)–H and C(sp3)–H groups donating to shared acceptor atoms O1 and O3, respectively; an additional C(sp3)–H⋯N interaction is also involved here. A pair of C(sp3)–H⋯O interactions connect molecules into dimer Br_7 (ΔE = −3.83 kcal mol−1), while a pair of C(sp3)–H⋯Br interactions is responsible for formation of dimer Br_8 (ΔE = −1.67 kcal mol−1).
Conformational search
To investigate the preferred conformations of the investigated compounds, the molecules extracted from the crystal structures were optimized at the TPSS-D3/def2tzvp level. The investigation of halogen effects on the phenyl group orientation was extended to include 3 and 4.15 An overlay of the molecules 1–4 showed that their conformations differ in the torsion angles τ1 and τ2 only (Fig. 1 and 2). The torsion angles τ1 and τ2 determined from the crystal structures and the TPSS-D3/def2tzvp calculations are given in Table 2. Evidently, there is no correlation between these values and the atomic number of X, although the trend in values of the torsion angles slightly changed after the optimization. The differences in the values of the torsion angle τ1 in the molecules extracted from the crystal structures and those optimized are not significant. This can be ascribed to the crystal packing effect, i.e., interactions of the substituted phenyl groups with the surrounding entities.| Torsion angle | Substituent X | H | F | Cl | Br |
|---|---|---|---|---|---|
| Compound | 3 | 4 | 1 | 2 | |
| τ 1 | Crystal structure | 10.5 | 7.9 | 4.1 | 26.6 |
| Optimized structure | 17.2 | 17.2 | 17.8 | 19.4 | |
| τ 2 | Crystal structure | 52.3 | 95.9 | 90.2 | 137.5 |
| Optimized structure | 56.3 | 55.0 | 54.4 | 140.0 |
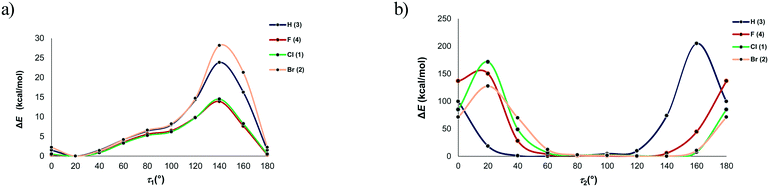
However, the optimized molecular structure is either the global minimum of the potential energy surface or one of the local minima. To verify whether a more stable conformation exists, the rotation of the substituted phenyl group with respect to the rest of the molecule was investigated by performing a series of calculations over the full range of values of the torsion angles τ1 and τ2 from 0 to 180° in intervals of 20°. The molecular structures extracted from the crystal structure served as the model structures and the energies relative to the most stable conformation are given in Fig. 11. In all four cases, the minimum corresponds to the value of the torsion angle τ1 of 20°, thus confirming that the optimized structures are the global minima. This further indicates that the conformation of the investigated compounds, i.e., the orientation of the substituted phenyl group relative to the carbonyl bridge, is determined rather by intramolecular interactions, while the contribution of intermolecular interactions is smaller. The energy profiles for the rotation of the phenyl group about the bond C11–C12 show that there is a free rotation of this group up to 60° (the energy barrier lower than 4.2 kcal mol−1), while the energy barrier rapidly increases after 100°. Considering the energy of intermolecular interactions within the dimeric motifs, it is evident that the energy barrier of 4.2 kcal mol−1 can be easily overcome, because a loss in energy due to a change in the torsion angle value can be compensated through intermolecular interactions with surrounding entities.
In all four cases, the most non-favourable orientation of the substituted phenyl group corresponds to the torsion angle value of 140°. The energy barrier increases with the halogen atom size, therefore rising from 4 (13.92 kcal mol−1) over 1 (14.51 kcal mol−1) to 2 (28.17 kcal mol−1). In this regard, the lowest energy barrier can be expected for 3, where the phenyl group is unsubstituted. However, it is evident that the energy barrier is similar for the fluorinated and chlorinated phenyl groups, but it is twice as high when the phenyl group is brominated. The energy barrier for the unsubstituted phenyl group is between those for the chlorinated and brominated phenyl groups (23.84 kcal mol−1). This implies that the energy barrier does not depend on the nature of the atom in the para position to the carbonyl bridge. An analysis of the intramolecular interactions involving the phenyl group shows that the ortho C–H groups form not only C–H⋯O interactions with the carbonyl bridge, but also C–H⋯π interaction with the hydantoin ring (Fig. S3†). Considering the intramolecular C–H⋯O interaction, the distance between the H atoms of the ortho C–H group in the phenyl ring and the O atom of the hydantoin ring ranges from 2.47 Å in 3 to 2.62 Å in 2. It is slightly shorter than the distance between the H atoms of the ortho C–H group in the phenyl ring and the O atom of the hydantoin ring featuring C–H⋯π interaction. The geometry of the C–H⋯π interaction is such that the ortho C–H group simultaneously makes contact with the C, N and O atom of the hydantoin ring (distance shorter than 3.5 Å). With exception of 3, the distance between the ortho C–H group and the N atom is the shortest.
Namely, differences in the energy barriers for rotation of the phenyl group about the bond C11–C12 cannot be simply explained on the basis of these intramolecular interactions. The model systems for C–H⋯O and C–H⋯π interactions showed that the interaction energies are close to each other and do not depend on the nature of the atom in the meta position to the donating C–H group. Considering C–H⋯O interactions, the aromatic C–H group interacts with the hydantoin C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, whereby the atoms within the interacting groups are linearly arranged and the ring planes are perpendicular to each other. In the model system for C–H⋯π interactions, the ring planes are also perpendicular to each other, whereas the C–H group is positioned above the N atom of the hydantoin ring (Fig. 12). The energy of C–H⋯O interaction is lower than 1 kcal mol−1 when the distance between the interacting atoms is shorter than 2.2 Å or longer than 3.2 Å (Table S2†). The minimum corresponds to the distance of 2.5 Å in all four cases, while the differences in energy minima are less than 0.5 kcal mol−1. The lowest interaction energy of C–H⋯O interaction was obtained for the unsubstituted phenyl ring (−1.48 kcal mol−1), while the higher values were obtained for 4 (−1.82 kcal mol−1) and 1 (−1.89 kcal mol−1) and 2 (−1.95 kcal mol−1). The energy of C–H⋯O interaction increases with increasing the atomic number of X. On the other hand, substituent effects on the energy of C–H⋯π interaction are smaller as the difference between the strongest and weakest interaction equals 0.08 kcal mol−1 (Table S3†). C–H⋯π interactions are slightly weaker than C–H⋯O interactions, but this difference is not of importance, because both interaction types are weak. The energy of C–H⋯π interaction is lower than 1 kcal mol−1 when the distance between the interacting atoms is shorter than 2.5 Å or longer than 3.2 Å. The energy minima correspond to the distance of 2.7 Å in all four cases and are as follows: −1.56 kcal mol−1 (X = H), −1.57 kcal mol−1 (X = F), −1.64 kcal mol−1 (X = Cl) and −1.64 kcal mol−1 (X = Br). Taking into account the geometry and the energy of C–H⋯O and C–H⋯π interactions involving the substituted phenyl groups (Fig. S3†) extracted from the crystal structures, it is evident that they cannot serve to explain the differences in the energy barriers for rotation of the phenyl group about the bond C11–C12 (Fig. 11).
O group, whereby the atoms within the interacting groups are linearly arranged and the ring planes are perpendicular to each other. In the model system for C–H⋯π interactions, the ring planes are also perpendicular to each other, whereas the C–H group is positioned above the N atom of the hydantoin ring (Fig. 12). The energy of C–H⋯O interaction is lower than 1 kcal mol−1 when the distance between the interacting atoms is shorter than 2.2 Å or longer than 3.2 Å (Table S2†). The minimum corresponds to the distance of 2.5 Å in all four cases, while the differences in energy minima are less than 0.5 kcal mol−1. The lowest interaction energy of C–H⋯O interaction was obtained for the unsubstituted phenyl ring (−1.48 kcal mol−1), while the higher values were obtained for 4 (−1.82 kcal mol−1) and 1 (−1.89 kcal mol−1) and 2 (−1.95 kcal mol−1). The energy of C–H⋯O interaction increases with increasing the atomic number of X. On the other hand, substituent effects on the energy of C–H⋯π interaction are smaller as the difference between the strongest and weakest interaction equals 0.08 kcal mol−1 (Table S3†). C–H⋯π interactions are slightly weaker than C–H⋯O interactions, but this difference is not of importance, because both interaction types are weak. The energy of C–H⋯π interaction is lower than 1 kcal mol−1 when the distance between the interacting atoms is shorter than 2.5 Å or longer than 3.2 Å. The energy minima correspond to the distance of 2.7 Å in all four cases and are as follows: −1.56 kcal mol−1 (X = H), −1.57 kcal mol−1 (X = F), −1.64 kcal mol−1 (X = Cl) and −1.64 kcal mol−1 (X = Br). Taking into account the geometry and the energy of C–H⋯O and C–H⋯π interactions involving the substituted phenyl groups (Fig. S3†) extracted from the crystal structures, it is evident that they cannot serve to explain the differences in the energy barriers for rotation of the phenyl group about the bond C11–C12 (Fig. 11).
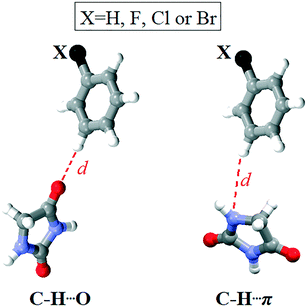 | ||
| Fig. 12 Model systems for C–H⋯O and C–H⋯π interactions involving the substituted phenyl group and the hydantoin unit. | ||
To explain the differences in heights of this barrier, we analysed intramolecular interactions involving the substituted phenyl group corresponding to the maxima on the energy profiles for the rotation of this group about the bond C11–C12. In the highest-energy conformation of all four compounds, the torsion angle τ1 is 140°. The distance between the ortho C–H group and the interacting O and N atoms increases through rotation. We noted new short contacts between the ortho C–H group and the hydantoin C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group of 2 and 3 (H⋯O distance being ca. 1.4 Å, Fig. S4†). In 1 and 4, this distance equals around 2.6 Å, thus corresponding to the optimum distance for C–H⋯O interaction (Table S2†).
O group of 2 and 3 (H⋯O distance being ca. 1.4 Å, Fig. S4†). In 1 and 4, this distance equals around 2.6 Å, thus corresponding to the optimum distance for C–H⋯O interaction (Table S2†).
Another ortho C–H group additionally forms C–H⋯O interaction with the carbonyl bridge at the distance from 2.68 to 2.85 Å (Fig. S4†), which is slightly larger than that in the crystal structure (Fig. S3†). The short H⋯O distances are clear evidence why the energy barriers are higher in the case of 2 and 3. Taking into account the geometry of intramolecular interactions involving the substituted phenyl group in 1 and 4 (Fig. S3†) and the interaction geometries corresponding to the conformations obtained by rotation of the substituted phenyl group for 140° (Fig. S4†) as well as the interaction energies (Tables S2 and S3†), their energy barriers are still high (14 kcal mol−1), but lower than those of 2 and 3. A potential explanation is deviation of the substituted phenyl group and the carbonyl bridge from co-planarity, which is necessary for the resonance stabilisation (Fig. S5†).
Although the most unstable conformations of all four compounds were obtained through rotation of the substituted phenyl group for 140°, short H⋯O distances are operative only in 2 and 3. However, the orientation of the phenyl group is also determined by rotation about the bond C11–N3, i.e., the value of the torsion angle τ2. In the crystal structure of 1 and 4, this angle is almost perpendicular, while the phenyl group in 2 and 3 is inclined toward the hydantoin C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, thus resulting in the torsion angle of 50° for 3 and 140° for 2. As previously stated, optimization of the molecular structures extracted from the crystal structures led to those with the torsion angle of around 55°, with the exception of 2 where this angle equals 140° (Table 2). We can conclude that the conformations of 2 and 3 are determined by intramolecular interactions, whereas the larger deviation of this torsion angle in 1 and 4 from the optimum values results from intermolecular interactions with surrounding entities.
O group, thus resulting in the torsion angle of 50° for 3 and 140° for 2. As previously stated, optimization of the molecular structures extracted from the crystal structures led to those with the torsion angle of around 55°, with the exception of 2 where this angle equals 140° (Table 2). We can conclude that the conformations of 2 and 3 are determined by intramolecular interactions, whereas the larger deviation of this torsion angle in 1 and 4 from the optimum values results from intermolecular interactions with surrounding entities.
A series of geometry calculations with different values of the torsion angle τ2 in intervals of 20° was performed. Fig. 11 shows that the relatively large freedom of rotation in 3 exists for the values of this torsion angle from 40 to 120°. In other compounds, this range is shifted from 60 to 140° (Table S4†). The high energy barriers for torsion angles smaller than 40° and larger than 120° result from very short contacts between the phenyl group and the hydantoin unit. The global minima on the potential energy surface correspond to the following torsion angles τ2 (Table S4†): 60° (3), 120° (4) and ca. 140° (1, 2). The torsion angles in the crystal structure conformation of 2 and 3 are close to the values corresponding to the global minima. On the other hand, these values deviate for 25° in 4 and 50° in 1. As already stated, these deviations originate from the crystal packing, i.e., effect on the interacting entities by surroundings. A loss in energy due to a change of the torsion angle is around 1 kcal mol−1 for 4 and 2.4 kcal mol−1 for 1. Evidently, this can be easily compensated through interactions with surrounding entities.
QTAIM analysis
The quantum theory of atoms in molecules (QTAIM) is the most common model to describe bonding interaction characteristics of molecular and condensed matter electronic systems. Atoms and bonds, as the fundamental parts of the molecular structure, represent a system's electron density distribution function. The electron density distribution of a molecule is the three-dimensional realspace probability distribution of the electronic charge in the attractive field exerted by the nuclei.Using QTAIM, it is possible to investigate and quantify changes in the electron density caused by the substitution of the H atom of an aryl group with a halogen atom. The introduction of a halogen atom in the aromatic ring has a twofold effect on the change in electron density. The resonance effect should increase the electron density in the aromatic ring (Fig. S5†), while a decrease in the electron density of the aromatic ring is expected due to greater electronegativity of the halogen atom and the inductive effect. The values of electron density (ρ(r)) in the center of the aryl group ((3, +1) ring critical point, RCP) are listed in Table 3. These values indicate that the substitution of the H with a halogen atom leads to a decrease in ρ in the center of the ring, and the decrease is the most pronounced in the brominated aryl group. Consequently, the energy density (H(r)) decreases in the series 3 > 4 > 1 > 2 at RCP of the aryl ring. The potential energy density (V(r)) and kinetic energy (G(r)) have trends similar to each other (3 > 1 > 4 > 2), but with the opposite sign, and when comparing their absolute values, kinetic energy (G(r)) has a slightly higher value.
| Critical point | Compound | Substituent X | ρ(r) (au) | ∇ 2 ρ(r) (au) | H(r) (au) | V(r) (au) | G(r) (au) | |H(r)|/ρ(r) |
|---|---|---|---|---|---|---|---|---|
| Aryl ring (ring) | 3 | H | 0.026271 | 0.161146 | 0.004763 | −0.030760 | 0.035523 | 0.181303 |
| 4 | F | 0.025993 | 0.158044 | 0.004711 | −0.030089 | 0.034800 | 0.181241 | |
| 1 | Cl | 0.026078 | 0.157980 | 0.004663 | −0.030170 | 0.034832 | 0.178810 | |
| 2 | Br | 0.025762 | 0.155209 | 0.004598 | −0.029607 | 0.034204 | 0.178480 | |
| C11–C12 (bond) | 3 | H | 0.270191 | −0.722605 | −0.250716 | −0.320781 | 0.070065 | 0.927921 |
| 4 | F | 0.288852 | −0.819879 | −0.283566 | −0.362162 | 0.078596 | 0.981700 | |
| 1 | Cl | 0.283662 | −0.792418 | −0.274054 | −0.350003 | 0.075949 | 0.966129 | |
| 2 | Br | 0.272978 | −0.738935 | −0.254533 | −0.324332 | 0.069799 | 0.932430 | |
| C11–N3 (bond) | 3 | H | 0.277047 | −0.766645 | −0.329847 | −0.468033 | 0.138186 | 1.190581 |
| 4 | F | 0.266110 | −0.699041 | −0.291543 | −0.408325 | 0.116783 | 1.095573 | |
| 1 | Cl | 0.267210 | −0.704201 | −0.293274 | −0.410496 | 0.117223 | 1.097541 | |
| 2 | Br | 0.280016 | −0.782802 | −0.338173 | −0.480645 | 0.142472 | 1.207692 |
The calculated parameters of electron density at the (3, −1) critical point corresponding to the bond C11–C12, around which the substituted phenyl group rotates, are listed in Table 3. Considering these ρ(r) values, it is clear that substitution of the H with a halogen atom causes an increase in electron density of the C11–C12 bond. This influence is the most pronounced when X = F and the smallest for X = Br, so the trend in ρ(r) is as follows: 4 > 1 > 2 > 3.
All ∇2ρ(r) values are negative and H(r) < 0, which indicates shared-shell nature of the bond C11–C12. Also, covalence of these bonds is indicated by the relation |V(r)| > G(r) and negative H(r) values for all compounds. The mentioned trend (4 > 1 > 2 > 3) is noticeable for the values of ∇2ρ(r), H(r), V(r) and G(r), suggesting that the C11–C12 bond of 4 has the greatest covalent character. When the absolute values of V(r) and G(r) are compared, dominance of potential V(r) over G(r) kinetic electron energy is obvious. The bond order (|H(r)|/ρ(r)) is close to 1 in all four cases and this trend is also noticeable.
However, when the value of the same parameter for the unsubstituted compound is subtracted from the values of the considered energy parameters (H(r), V(r) and G(r)) of halogen derivatives, the relative values of these three energy parameters (ΔH(r), ΔV(r), and ΔG(r)) are obtained. These changes are expressed in kcal mol−1 and are shown in Table S5.† The values of relative potential energy density (ΔV(r)) are: −25.97 kcal mol−1 for 4, −18.34 kcal mol−1 for 1 and −2.23 kcal mol−1 for 2. The values of relative kinetic energies (ΔG(r)) are of the opposite sign (except for 2) and are significantly lower: 5.35 kcal mol−1 for 4, 3.69 kcal mol−1 for 1, and −0.17 kcal mol−1 for 2. By adding these two terms, the total or relative energy density (ΔH(r)) is obtained, which in all three cases has a negative sign (stabilizing character). The highest value of ΔH(r) has 4 (−20.61 kcal mol−1), followed by 1 (−14.64 kcal mol−1), while 2 has the lowest value of this parameter (−2.40 kcal mol−1).
In contrast to the BCP of the bond C11–C12, replacing the H atom in the aromatic ring with a halogen has a twofold effect on the change in electron density at the BCP of the bond C11–N3 (Table 3). Namely, the electron density ρ(r) at the BCP decreases for 4 and 1, while increasing for 2. The trend of the ρ(r) values is as follows: 2 > 3 > 1 > 4. The same trend occurs in the values of ∇2ρ(r), H(r), V(r) and G(r) at the BCP of the bond C11–N3 and in the bond order (|H(r)|/ρ(r)), which is slightly higher than for the bond C11–C12.
Accordingly, relative energy density (ΔH(r)) is positive for 4 (24.04 kcal mol−1) and 1 (22.95 kcal mol−1), while negative (−5.22 kcal mol−1) for 3. This suggests that only the replacement of the H atom with a Br leads to the strengthening of the bond C11–N3. When the value of ΔH(r) is divided into the contributions of the relative potential ΔV(r) and the relative kinetic ΔG(r) component (Table S5†), the positive sign of the parameter ΔH(r) for 4 and 1 is due to the large positive value of the potential component ΔV(r) (37.47 and 36.11 kcal mol−1, respectively). In 2, this component has a negative sign (−7.91 kcal mol−1). On the other hand, 4 and 1 have negative values of the kinetic component ΔG(r) (−13.43 and −13.15 kcal mol−1), while 2 has a positive sign (2.69 kcal mol−1). This means that in the case of 4 and 1 the bond C11–N3 has higher mobility (indicates stretching or rotation) than in 2 and 3, which is in accordance with the data obtained from the crystal structures and the energy profile of the bond C11–N3. Namely, the values of τ2 in the crystal structures of 2 and 3 close to the values of this angle in structures corresponding to global minima are shown. On the other hand, the values of τ2 in the crystal structures of the 4 and 1 deviate by 25° and 50°, respectively, from the values of the angles in the structures corresponding to the global minima for these two derivatives.
Conclusions
The crystal structure investigation of the selected compounds, coupled with the quantum chemical calculations, provided several outcomes, based on effects of replacement of the H atom in the phenyl group by a halogen atom.The molecular overlay, when fixing the atoms in the hydantoin ring, identified the phenyl group orientation as the main structural difference. The conformational degrees of freedom are defined by the torsion angles τ1 and τ2; thus, effects of rotation about the C11–C12 and C11–N3 bonds on the molecular structure were investigated. As expected, the carbonyl bridge and the phenyl group are nearly co-planar. The value of the torsion angle τ1 can be regarded as a compromise between the extended conjugation between the carbonyl and phenyl group and intramolecular C–H⋯O interaction between these two groups. Although co-planarity is expected, the quantum chemical calculations showed that the phenyl group can undergo free rotation about the bond C11–C12 up to 60°. Evidently, this torsion angle is determined by intramolecular interactions. Since free rotation is possible, effect of interactions with the surrounding entities cannot be neglected.
This intermolecular effect is more pronounced at the torsion angle τ2, which defines the relative orientation between the hydantoin ring and the carbonyl bridge. The quantum chemical calculations showed a wide interval of the energetically favourable values for this angle in the case of the substituted phenyl group (from 50 to 140°), while this interval is shifted towards somehow lower values when the phenyl group is unsubstituted (from 40 to 120°). In the crystal structures, the torsion angle τ2 can be regarded as a compromise among the conjugation of the hydantoin amide group, intramolecular O⋯O interaction between the hydantoin ring system and the carbonyl bridge, as well as intramolecular C–H⋯π interaction between the hydantoin ring and the phenyl group. In this context, the investigated compounds can be divided into two groups. The carbonyl bridge and the hydantoin ring system are nearly perpendicular to each other in 1 and 4 (the torsion angle τ2 close to 90°), while this group is inclined towards the hydantoin ring system in 2 and 3. The torsion angle τ2 does not affect the orientation of the phenyl ring directly; however, the two torsion angles define the relative orientation of the hydantoin and phenyl rings cooperatively. Therefore, halogenation of the phenyl group does not affect significantly the interval of the energetically favourable values of the analysed torsion angle. Although the corresponding values in the crystal structures are within the favoured interval, the differences in the molecular structure cannot be solely attributed to the intermolecular effect, as the interval width is considerably large.
The contacts between the hydantoin ring and the phenyl group as well as those between the hydantoin ring and the cyclohexyl ring are the most numerous in the crystal structure of unsubstituted compound 3, while introduction of the fluorine atom in 4 resulted in an increase in overall number of contacts involving the phenyl group. Here, by contacts we mean a group of intermolecular interactions between two cyclic fragments, whereby those of the bridging carbonyl group are ascribed to the phenyl ring.15b Surprisingly, introduction of a Cl or Br atom in 1 and 2 did not increase the number of contacts between the cyclohexyl ring and the phenyl group nor of those between the cyclohexyl ring and the hydantoin ring. Regarding the type of intermolecular interactions in the crystal structures, C–H⋯O interactions are larger in number than the others.
Of intermolecular interactions involving the phenyl group in the crystal structures of 1 and 2, C–H⋯π interactions are the most numerous, although there is one stacking interaction in each structure. When it comes to intermolecular interactions involving halogen, the situation is different. Namely, C–H⋯Cl interactions occur in three dimeric motifs, whereas C–H⋯Br interactions are identified in only two dimeric motifs. This difference can be expected, because, with increasing the halogen atomic number, the electron density of the phenyl group lowers, thus decreasing its ability to form interactions where the π system has an accepting role.18a Although the Br atom participates in a smaller number of intermolecular interactions than the Cl atom, it additionally forms a Br⋯O interaction. An explanation lies in the difference in the size of the σ-hole of these atoms. According to the molecular electrostatic potential maps of halobenzenes,18b a σ-hole can be observed only along the extension of the C–X covalent bond (X = Cl, Br and I) and the size and positive potential of a σ-hole increase with increasing halogen atomic number (Cl < Br < I).
The present work is expected to help in developing a better understanding of correlation between the conformational and crystal packing preferences and the molecular recognition features. The free rotation of the phenyl group is important in this sense; however, it was indicated that halogenation does not have a significant effect on this rotation in the investigated compounds. The large free rotation enables the phenyl group to form different types of intermolecular interactions. A decrease in the electron density of the π system and an increase in the size of the σ-hole with increasing size of the halogen atom leads to a lower ability to form D–H⋯π and D–H⋯X interactions on one hand and a higher affinity towards aromatic⋯aromatic and σ-hole interactions on the other.
Experimental
All chemicals and solvents used for the synthesis were obtained from commercial sources and were used as received, without further purification. The investigated compounds were completely characterized by melting point determination, FT-IR, 1H and 13C NMR spectroscopy and elemental analysis. The melting point was measured on an electrothermal melting point apparatus without correction. The FT-IR spectra were measured using a Bomem MB spectrophotometer, while 1H and 13C NMR spectra were recorded on a Bruker AC 250 spectrometer. Elemental analyses were carried out using microanalyzer Elemental Vario EL III.Synthetic procedures
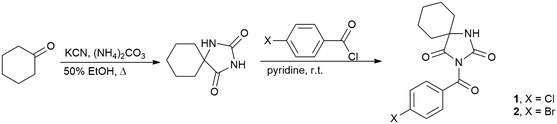
Synthetic details are illustrated in Scheme 1. Cyclohexane-5-spirohydantoin was synthesized by the method of Bucherer and Lieb19 and it was further acylated using the procedure described previously.15b Cyclohexane-5-spirohydantoin (0.84 g, 5.0 mmol) was suspended in dried pyridine (5 ml) and 4-substituted benzoyl chloride (5.0 mmol) was added dropwise to the mixture and stirred at room temperature overnight. After the completion of the reaction, pyridine was evaporated under vacuum and the residue was dissolved in ethyl acetate. The solution was washed with 5% NaOH and water and dried over anhydrous MgSO4. The residual solvent was removed and the crude product was purified by recrystallization from ethyl alcohol.Crystal structure determination
Single crystals suitable for an X-ray structure determination were obtained by slow evaporation of acetonitrile solutions at room temperature. Single-crystal X-ray diffraction data were collected at room temperature on an Oxford Gemini S diffractometer equipped with CCD detector using monochromatized MoKα radiation (λ = 0.71073 Å). Intensities were corrected for absorption using the multiscan method. The structures were solved by direct methods using SIR2014 (ref. 20) and refined on F2 by full-matrix least-squares using the programs SHELXL-2018/3 (ref. 21) and WinGX.22 All non-hydrogen atoms were refined anisotropically. The positions of the H atoms connected to the C and N atoms were calculated on geometric criteria and refined by the riding model with Uiso = 1.2Ueq(C, N). Selected crystal data and refinement results for 1 and 2 are listed in Table 1. CCDC 2156414 and 2156415 for 1 and 2, respectively, contain the supplementary crystallographic data for this paper.Quantum-chemical calculations
The Hirshfeld surface analysis and corresponding 2D fingerprint plots were mapped using CrystalExplorer 17.5.23 Calculations for Hirshfeld surface analysis were done at accurate B3LYP/6-31g(d,p) level of theory using the Gaussian 09 program package.24The geometry optimization and the interaction energies calculations were performed at TPSSh/def2TZVP level with Grimme's D3 correction as implemented in Gaussian 09 software. The crystal structures were used as initial models for optimization of all H atoms, while for non-hydrogen atoms the “freeze” procedure was applied. The interaction energies (ΔE) between the dimer were determined as the difference between the energy of the dimer and the sum of the monomer energies, corrected for basis set superposition error (BSSE) by the counterpoise method.25
Conformational searches of the preferred conformations of the investigated compounds were achieved after full optimization of the crystal structures at the TPSS-D3/def2tzvp level.
For QTAIM properties determination, the first order density matrices of the crystal structures calculations were used as input in the Multiwfn program.26
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia (Contract No. 451-03-68/2022-14/200135; 451-03-68/2022-14/200287 and 451-03-68/2022-14/200026).Notes and references
- (a) R. Paus, Y. Ji, F. Braak and G. Sadowski, Ind. Eng. Chem. Res., 2015, 54, 731 CrossRef CAS; (b) S. Jankovic, G. Tsakiridou, F. Ditzinger, N. J. Koehl, D. J. Price, A.-R. Ilie, L. Kalantzi, K. Kimpe, R. Holm, A. Nair, B. Griffin, C. Saal and M. Kuentz, J. Pharm. Pharmacol., 2019, 71, 441 CrossRef CAS PubMed; (c) C. Fink, D. Sun, K. Wagner, M. Schneider, H. Bauer, H. Dolgos, K. Mäder and S.-A. Peters, Clin. Pharmacol. Ther., 2020, 107, 650 CrossRef CAS PubMed.
- (a) N. Estime, S. Teychené, J. M. Autret and B. Biscans, Powder Technol., 2011, 208, 337 CrossRef CAS; (b) K. Göke, T. Lorenz, A. Repanas, F. Schneider, D. Steiner, K. Baumann, H. Bunjes, A. Dietzel, J. H. Finke, B. Glasmacher and A. Kwade, Eur. J. Pharm. Biopharm., 2018, 126, 40 CrossRef PubMed.
- C. M. Wassvik, A. G. Holmén, R. Draheim, P. Artursson and C. A. S. Bergström, J. Med. Chem., 2008, 51, 3035 CrossRef CAS PubMed.
- (a) M. W. He, P. S. Lee and Z. K. Sweeney, ChemMedChem, 2015, 10, 238 CrossRef CAS PubMed; (b) B. C. Doak, J. Zheng, D. Dobritzsch and J. Kihlberg, J. Med. Chem., 2016, 59, 2312 CrossRef CAS PubMed.
- (a) H. P. G. Thompson and G. M. Day, Chem. Sci., 2014, 5, 3173 RSC; (b) C. Greenwell and G. J. O. Beran, Cryst. Growth Des., 2020, 20, 4875 CrossRef CAS.
- (a) D. N. Chin, G. T. R. Palmore and G. M. Whitesides, J. Am. Chem. Soc., 1999, 121, 2115 CrossRef CAS; (b) C. Guzmán-Afonso, Y.-L. Hong, H. Colaux, H. Iijima, A. Saitow, T. Fukumura, Y. Aoyama, S. Motoki, T. Oikawa, T. Yamazaki, K. Yonekura and Y. Nishiyama, Nat. Commun., 2019, 10, 3537 CrossRef PubMed.
- L. Lo Presti, CrystEngComm, 2018, 20, 5976 RSC.
- (a) M. Saccone and L. Catalano, J. Phys. Chem. B, 2019, 123, 44 CrossRef PubMed; (b) L. González, S. Graus, R. M. Tejedor, A. Chanthapally, J. L. Serrano and S. Uriel, CrystEngComm, 2020, 22, 6010 RSC.
- E. Persch, O. Dumele and F. Diederich, Angew. Chem., Int. Ed., 2015, 54, 3290 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235 CrossRef CAS PubMed.
- K. A. Brameld, B. Kuhn, D. C. Reuter and M. Stahl, J. Chem. Inf. Model., 2008, 48, 1 CrossRef CAS PubMed.
- M. Mladenovic, M. Arnone, R. F. Fink and B. Engels, J. Phys. Chem. B, 2009, 113, 5072 CrossRef CAS PubMed.
- A. J. Cruz-Cabeza and C. H. Schwalbe, New J. Chem., 2012, 36, 1347 RSC.
- (a) A. Lazić, N. Trišović, L. Radovanović, J. Rogan, D. Poleti, Ž. Vitnik, V. Vitnik and G. Ušćumlić, CrystEngComm, 2017, 19, 469 RSC; (b) K. Gak Simić, I. Đorđević, A. Lazić, L. Radovanović, M. Petković-Benazzouz, J. Rogan, N. Trišović and G. Janjić, CrystEngComm, 2021, 23, 2606 RSC.
- (a) P. T. Todorov, R. N. Petrova, E. D. Naydenova and B. L. Shivachev, Cent. Eur. J. Chem., 2009, 7, 14 CAS; (b) B. Chattopadhyay, A. K. Mukherjee, N. Narendra, H. P. Hemantha, V. V. Sureshbabu, M. Helliwell and M. Mukherjee, Cryst. Growth Des., 2010, 10, 4476 CrossRef CAS; (c) B. A. Nogueira, A. Milani, G. O. Ildiz, J. A. Paixão, C. Castiglioni and R. Fausto, CrystEngComm, 2020, 22, 6347 RSC.
- (a) M. A. Spackman, J. J. McKinnon and D. Jayatilaka, CrystEngComm, 2008, 10, 377 CAS; (b) M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19 RSC.
- (a) J. D. Mottishaw, A. R. Erck, J. H. Kramer, H. Sun and M. Koppang, J. Chem. Educ., 2015, 92, 1846 CrossRef CAS; (b) M. A. A. Ibrahim and N. A. M. Moussa, ACS Omega, 2020, 5, 21824 CrossRef CAS PubMed.
- (a) H. T. Bucherer and V. A. Lieb, J. Prakt. Chem., 1934, 141, 5 CrossRef CAS; (b) I. A. Rivero, E. A. Reynoso and A. Ochoa-Teran, ARKIVOC, 2011, 260 Search PubMed; (c) R. Yousefi, D. C. Whitehead, J. M. Mueller, R. J. Staples and B. Borhan, Org. Lett., 2011, 13, 608 CrossRef CAS PubMed.
- M. C. Burla, R. Caliandro, B. Carrozzini, G. L. Cascarano, C. Cuocci, C. Giacovazzo, M. Mallamo and A. Mazzone, J. Appl. Crystallogr., 2015, 48, 306 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3 Search PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849 CrossRef CAS.
- M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, P. R. Spackman, D. Jayatilaka and M. A. Spackman, Crystal Explorer (Version 17), University of Western Australia, Pert, Australia, 2017 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, E. J. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09, Gaussian, Inc., Wallingford, 2009 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2156414 and 2156415. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce00376g |
| This journal is © The Royal Society of Chemistry 2022 |