Open Access Article
Open Access ArticleAccurate experimental characterization of the labile N–Cl bond in N-chloro-N′-(p-fluorophenyl)-benzamidine crystal at 17.5 K†
Riccardo
Destro
a,
Mario
Barzaghi
b,
Raffaella
Soave
c,
Pietro
Roversi
 de and
Leonardo
Lo Presti
de and
Leonardo
Lo Presti
 *af
*af
aUniversità degli Studi di Milano, Department of Chemistry, Via Golgi 19, 20133 Milano, Italy. E-mail: leonardo.lopresti@unimi.it
bConsiglio Nazionale delle Ricerche (CNR), Piazzale Aldo Moro 7, 00185 Roma, Italy
cConsiglio Nazionale delle Ricerche (CNR), Istituto di Scienze E Tecnologie Chimiche “Giulio Natta” (SCITEC), Via Golgi 19, 20133 Milano, Italy
dConsiglio Nazionale delle Ricerche (CNR), Istituto di Biologia e Biotecnologia Agraria (IBBA), Via Bassini 15, 20133 Milano, Italy
eLeicester Institute of Chemical and Structural Biology and Department of Molecular and Cell Biology, University of Leicester, Henry Wellcome Building, Lancaster Road, Leicester LE1 7HR, UK
fIstituto Nazionale di Fisica Nucleare (INFN), Laboratori Nazionali di Frascati, Frascati, Italy
First published on 17th August 2022
Abstract
N-Chloro-N′-(p-fluorophenyl)-benzamidine (NCLBA) is a N-halamine derivative which can easily release chlorine, for example when stimulated by high-energy photons. Despite the rich chemistry performed by N-halamines, the chemical properties of the N–Cl bond are poorly investigated. In this work, we determine the accurate charge density distribution of NCLBA by single crystal X-ray diffraction. A very low temperature (T = 17.5 K), coupled with the low X-ray flux of a fine-focus conventional source, allowed the specimen to survive for longer than 750 h of data acquisition without appreciable diffraction deterioration. Electronic and electrostatic properties of NCLBA are not significantly affected by the crystal field, enabling the derivation of molecular properties from the X-ray experimental data. The N–Cl bond in NCLBA is one of the longest reported to date in available structural studies. In general, the longer the N-halogen bond, the lower the amount of electron sharing in the internuclear region, with the bond approaching its homolytic dissociation limit. The synergy between accurately measured high-order data and low temperature enabled modelling of the residual thermal motion anharmonicity of the molecule's halogen atoms with refinement of Gram–Charlier thermal cumulants at the expense of large parameter correlations, as the data extension is rather short of the Kuhs empirical rule.
1. Introduction
In the last two decades, extremely brilliant X-ray sources enabled a revolution in solid state chemistry by putting within the reach of diffraction-based techniques the understanding of complex structures and dynamic phenomena, down to the femtosecond timescale.1 However, the high photon flux of modern high-brilliance facilities may degrade the sample within hours or even minutes,2 for example when protein crystals3 or reactive compounds4 are studied. The lost information can be retrieved, at least to some extent, by scaling and merging data from different fresh crystals, assuming that several high-quality5 samples are available. In any case, an accurate quantification of the radiation damage is mandatory6 to plan efficient data collection and reduction strategies. In contrast, datasets collected with in-home equipment can take advantage of both low T and lower photon flux, allowing to preserve the crystallographic integrity of the sample for very long periods. This is desirable, for example, if the aim of the experiment is to extract charge density-level information.In this work, we demonstrate that a combination of low X-ray flux and very low temperature is suitable to obtain the accurate experimental charge density distribution of a benzamidine derivative containing a reactive N–Cl covalent bond. The compound is N-chloro-N′-(p-fluorophenyl)-benzamidine (C13H10ClFN2, hereinafter NCLBA) and comes from the organic chemistry laboratory of professors Pocar and Stradi, who in the past extensively developed the N-haloamidines chemistry.7–9 The compound is an N-halamine, i.e. a compound containing one or more nitrogen–halogen covalent bonds, and usually formed by halogenation of imide, amide, or amine groups. The interest in the N–Cl bond is motivated by the very rich chemistry it deploys. Its uses range from being an internal oxidant for the construction of an isoquinoline skeleton10 to its cleavage in the Rh-catalyzed C–H amination of N-arylbenzamide with N-chloromorpholine,11 to the enantioselective oxidation by chiral compounds bearing N–Cl bond12 and to the antibacterial activity of N-halamines13,14 As reported in a review of the synthesis, characterization, and applications of antimicrobial N-halamine polymers and coatings,13 the oxidizing agent of molecules containing N–Cl bonds (usually chlorine) “can act through direct transfer of active element to the biological receptor or through dissociation to free halogen in aqueous media”.13 An early ab initio study15 showed that the N–Cl bond is rather weak, and a more recent high-level quantum chemical study16 highlights the effect of substituents on the strength of N–Cl bond dissociation energy. N–Cl bonds in N-halamine-based materials are not stable under UV light irradiation,17 and a reaction mechanism in which the N–Cl bond is cleaved by UV has been proposed for the transformation reaction of the micropollutant atenolol.18 To slow down the dissociation of the N–Cl bond in NCLBA, we performed the experiment at a very low temperature of 17.5 K, extracting a high-quality charge density distribution from the high-resolution diffraction pattern. A topological analysis of the experimental electron charge density according to the quantum theory of atoms in molecules (QTAIM)19 allowed us to go beyond purely structural analysis, providing insights into the real-space properties of the reactive N–Cl bond. Ultimately, we obtained experimentally derived information of clear chemical significance, including for example accurate in-crystal geometries and atomic displacement amplitudes, demonstration of the persistence of anharmonicity at very low T, and information on the effect of the crystal field on the molecular properties.
2. Methods
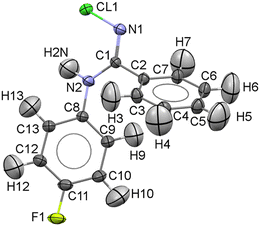
NCLBA crystallizes in the trigonal space group P31 (N. 144 in the International Tables20), with three molecules per cell. Table 1 reports the cell dimensions, crystal data and details of the data collection and refinement. A representation of the molecule, with numbering scheme, is shown in Fig. 1.| Sample information | |
|---|---|
| a Estimated standard deviations (esds) (in parentheses) on the last significant digit. b Cell dimensions at T = 290 K: a/Å = b/Å = 10.130(1), c/Å = 10.109(2), V/Å3 = 898.4(2). c Absorption coefficient times the crystal spherical ray (attenuation coefficient). d S α1–α2 is the Kα1–α2 separation in the intensity profile. | |
| Empirical formula | C13H10Cl F N2 |
| Formula wt/g mol−1 | 248.68 |
| Crystal system | Trigonal |
| Space group | P31 |
| Z | 3 |
| Crystal dimensions | Sphere of 0.5 mm in diameter |
| T/K | 17.5(9) |
| a/Å | 10.0227(3) |
| b/Å | 10.0227(3) |
| c/Å | 9.8795(4) |
| V/Å3 | 859.48(5) |
| D x /g cm−3 | 1.441 |
| F(000) | 384 |
| Absorp. coeff. μ mm−1 | 0.323 |
| μ R | 0.081 |
| Data collection | |
|---|---|
| Cryostat | He/closed cycle |
| Diffractometer | Home-modified Syntex P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| Monochromator | Graphite |
| λ/Å | 0.71073 |
(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ)max/Å−1 θ/λ)max/Å−1 |
1.144 |
| Scan technique | ω/2θ |
| Scan rate (2θ)/deg min−1 | 3.0 |
| Scan range/deg | 2.4 + Sα1–α2d |
| No. collected refln.s | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709 709 |
| No. unique refln.s | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 382 |
| No. obsd refln.s (I > 0, Nobs) | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309 309 |
2.1 Data collection
A total of about 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 X-ray diffracted intensities were measured at T = 17–19 K from two crystals mounted on a four-circle diffractometer equipped with a local version of the helium closed-cycle Samson cryostat,21,22 with cryo- and turbomolecular pumps, and a point-detector. More than 12
000 X-ray diffracted intensities were measured at T = 17–19 K from two crystals mounted on a four-circle diffractometer equipped with a local version of the helium closed-cycle Samson cryostat,21,22 with cryo- and turbomolecular pumps, and a point-detector. More than 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 measurements from the first sample, glued to the tip of a glass fiber and not encased into a protective medium, had to be discarded because a crystal fracture occurred during the data collection, causing irregular profiles and backgrounds. A second spherical sample, sealed into a Lindemann capillary, was then mounted and a new data collection was performed in three steps, with instrument maintenance in between. Accurate background and profile measurements were also carried out, as necessary for the subsequent treatment of truncation errors, according to the procedure regularly applied in our laboratory for accurate charge-density studies.22–27
000 measurements from the first sample, glued to the tip of a glass fiber and not encased into a protective medium, had to be discarded because a crystal fracture occurred during the data collection, causing irregular profiles and backgrounds. A second spherical sample, sealed into a Lindemann capillary, was then mounted and a new data collection was performed in three steps, with instrument maintenance in between. Accurate background and profile measurements were also carried out, as necessary for the subsequent treatment of truncation errors, according to the procedure regularly applied in our laboratory for accurate charge-density studies.22–27
The average temperature during the whole data collection from this crystal was T = 17.5 ± 0.9 K, and a total of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709 diffraction intensities were measured. At the two intermediate cryostat-maintenance openings, the crystal showed progressive color change, from colorless transparency to pale yellow and finally to brown. A detailed description of the data collection is reported as ESI† in section S1.
709 diffraction intensities were measured. At the two intermediate cryostat-maintenance openings, the crystal showed progressive color change, from colorless transparency to pale yellow and finally to brown. A detailed description of the data collection is reported as ESI† in section S1.
For an attenuation exponent μR of 0.081, in a spherical crystal the absorption correction A* varies, in the range θ = 0 to θ = 55, by ∼0.2% only.28 We did not apply such a correction to our data, that were instead corrected for scan-truncation errors,22–27 and then merged (Rmerge = 0.0286) to obtain a set of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 unique intensities. Those with I > 0, 14
382 unique intensities. Those with I > 0, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309 in number, were classed as observed.
309 in number, were classed as observed.
2.2 Multipole refinement
For the full-matrix least-squares refinement of the NCLBA low-T structure, multipolar scattering factors were used29–31 as implemented in the VALRAY program,32 to model the asphericity in the atomic electron density. Five different pseudo-atom models (labelled A–E, see Table S1 ESI†) were investigated. Model “A” included multipoles up to the octupole level for the C, N, Cl and F atoms, while in models B–E hexadecapole population coefficients were added to all non-H atoms. Multipolar expansion up to the quadrupole level was adopted for the ten H atoms. Positional parameters of the latter atoms were evaluated with the “polarized H atoms” option of VALRAY,32 and their anisotropic displacement parameters (ADPs) were estimated (and not refined) with the ADPH code of Roversi and Destro.33 The ADPs of the chlorine atom were modified in model “C” (an extension of model “B”) with the inclusion of the 10 third-order Gram–Charlier (GC) coefficients (Cijk's) for the Cl atom only; in model “D”, 15 fourth-order GC coefficients (Dijkl's) were added to the same atom. After the refinement of model “D”, attempts were made to optimize the κ parameters and the exponents α for single exponential functions of the five atomic species of NCLBA, but the α of the F atom refined to an unrealistic value, unless Cijk's and Dijkl's GC coefficients were added to the fluorine atom too. (Problems in the refinement of the α exponent of an F atom were encountered and discussed by Stewart, Larsen, and co-workers in a charge density study of tetrafluoroterephthalonitrile based on X-ray and neutron data34). After initial least-squares cycles of refinement to get the best estimates for the third- and fourth-order GC cumulants of the two halogen atoms, all 50 GC coefficients were kept fixed and ten radial parameters were least-squares optimized in model E. No symmetry constraints were imposed, as no compelling evidences can be found that the invariant harmonics (Y10 and Y30) under the point symmetry of the group are somewhat ill-determined.35 The results of the refinements are summarised in Table S1 ESI.†The analysis of the experimental ρ(r) in terms of topological features, nuclear-centred distributed multipole analyses (DMA) and derived electrostatic properties was carried out both with VALRAY32 and by means of the program PAMoC (an acronym for properties of atoms and molecules in molecular crystals),36 which retrieves all the required information from the binary checkpoint file produced by VALRAY.
2.3 Periodic quantum mechanical calculations
The quantum mechanical charge density distribution of crystalline NCLBA at the experimental geometry was estimated with a hybrid DFT PBE0 Hamiltonian37 corrected with the Grimme D3 functional38 to account for non-local dispersive interactions, as implemented in the CRYSTAL17 suite of programs.39 The all-electron pob-TZVP-rev2 triple-zeta valence plus polarization basis set proposed by Peintinger and co-workers,40 optimized for solid-state simulations, was used. The interested reader can find a full list of input instructions in section S3 ESI.† The TOPOND program41 was used throughout to perform the topological analysis of the ρ(r) scalar field.2.4 Gas-phase quantum mechanical calculations
Single point quantum calculations in the gas phase were also carried out with Gaussian16 (ref. 42) on 15 molecules bearing N–Cl moieties at their experimental geometries, as retrieved from the November, 2020 version of the Cambridge Structural Database (v5.42).43 Only organic molecular structures with one molecule in the asymmetric unit (Z′ = 1) and a reasonable level of accuracy were considered: mandatory inclusion criteria were: no errors, no disorder, crystallographic agreement factor R lower than 0.05. The list of these CCDC reference codes can be found in the ESI† (section S2†). Results from different levels of theory were compared, namely: MP2/6-31G(p,d), PBE0/6–311G(p,d) and PBE0/Peintinger,40 the latter chosen for comparison with solid state results (see above). DFT Hamiltonians were always corrected with the Grimme D3 functional.38 The local topological properties at relevant critical points were evaluated with PAMoC.363. Results and discussion
3.1 Radiation damage
A gradual browning of the crystal, which was originally colorless and transparent, was observed as the data collection proceeded (see also section S1 ESI†). Chlorine is probably released from the molecules following X-ray-induced breaking of the reactive N–Cl bond. To monitor the radiation-induced damage, three intense check reflections (namely (3 6 3), (1 1![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) and (3 1 0)) were selected and their diffraction intensities repeatedly recorded every 97 intensity measurements. The variation of these diffraction intensities in time suggests that the quality of the crystal was not appreciably reduced during data collection. The first check reflection (the stronger of the three) showed a decrease of 2.8%, corresponding to 10–11 esd's, after more then 750 hours of exposure to the X-rays; the second one remained practically unchanged (increase of 0.46%, i.e. about 1.3 esd's, at the end of the data collection); while the intensity of the third check reflection (the weakest of the three – about 80% of the most intense one) increased by 5%, corresponding to 6–7 esd's. We believe that this behavior was due to two effects: a genuine chemical transformation, as revealed by the color change, and, possibly to a minor extent, an instrumental instability (e.g. slight misplacement of the crystal), documented by the need of technical maintenance during data collection. In view of the relatively modest departure from the initial diffraction intensities, we decided to ignore the phenomena underlying crystal discoloration and proceed with the usual treatment of the data. A similar decision is reported in the literature in another case of contradictory behavior of the standards, (a charge density study of a thiapentalene compound at T = 11 K (ref. 44)).
) and (3 1 0)) were selected and their diffraction intensities repeatedly recorded every 97 intensity measurements. The variation of these diffraction intensities in time suggests that the quality of the crystal was not appreciably reduced during data collection. The first check reflection (the stronger of the three) showed a decrease of 2.8%, corresponding to 10–11 esd's, after more then 750 hours of exposure to the X-rays; the second one remained practically unchanged (increase of 0.46%, i.e. about 1.3 esd's, at the end of the data collection); while the intensity of the third check reflection (the weakest of the three – about 80% of the most intense one) increased by 5%, corresponding to 6–7 esd's. We believe that this behavior was due to two effects: a genuine chemical transformation, as revealed by the color change, and, possibly to a minor extent, an instrumental instability (e.g. slight misplacement of the crystal), documented by the need of technical maintenance during data collection. In view of the relatively modest departure from the initial diffraction intensities, we decided to ignore the phenomena underlying crystal discoloration and proceed with the usual treatment of the data. A similar decision is reported in the literature in another case of contradictory behavior of the standards, (a charge density study of a thiapentalene compound at T = 11 K (ref. 44)).
An approximate estimate of the total X-ray dose absorbed by the NCLBA crystals under the conditions here employed reads ∼9.5 × 106 Gy after 750 h (see section S4 ESI†), which is comparable with the absorbed dose in a few minutes of exposure using a synchrotron source45 and is enough to produce a detectable damage in biological samples.46 A calculation using RADDOSE-3D yields an estimate of 1.32 × 106 Gy.47 The take-home message is that X-ray low power, coupled with very low (<20 K) temperatures, can efficiently preserve the quality of the crystal even in the presence of photolabile N–Cl functional groups.
3.2 Crystal structure of NCLBA
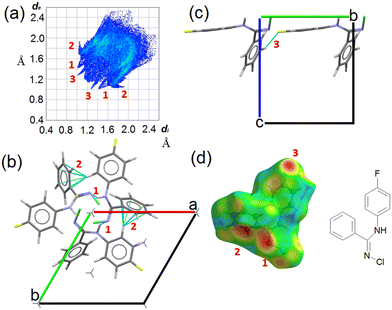
CCDC entry 2180453 contains the supplementary crystallographic data for this paper. In NCLBA crystals, two main directional interactions can be recognized. Neighbouring molecules are connected by NH⋯N hydrogen bonds and form parallel 31 helices along the c axis (Fig. 2). At the same time, the fluorinated phenyl ring establishes CH⋯π interactions with the unsubstituted phenyl group of the neighbouring molecule along the screw axis. These interactions correspond to the features marked as (1) and (2) in the Hirshfeld surface fingerprint plot48 (Fig. 2a). de is the distance from the Hirshfeld surface to the nearest nucleus outside the surface, and di is the corresponding distance to the nearest nucleus inside the surface: the fingerprint plot shows the frequency of interaction modes associated to specific (de, di) pairs. NH⋯N contacts occur as large spikes (1) at a minimum (de, di) distance of ∼ 2.4 Å, while in the CH⋯π system the proximity of the donor H to the carbon of the aromatic ring results in lateral H⋯C wings (2) with average distance of 2.6–2.8 Å. CH⋯F contacts are also present as long and sharp spikes at ∼ 2.3 Å (3) and mainly connect translation-related molecules along the b axis (Fig. 2c).All the closest contacts (1)–(3) are evident as hotspots when the de frequency is plotted onto the Hirshfeld surface of NCLBA (Fig. 2d). The chlorine atom is not involved in any obvious directional interaction, the only relevant close contacts being CH⋯Cl ones in the 2.8–3.2 Å H⋯Cl range of distances. Rather, the chlorine atom fits into the free space at different heights along the 31 axis (Fig. S1 ESI†). In general, CH⋯halogen contacts are not expected to provide significant contributions to crystal cohesion.49 We estimated the interaction energies (Eint) of closest molecular pairs in the crystal by classical atom–atom summations with the empirical UNI force field.50,51
Note that we do not intend to provide absolute estimates of molecule–molecule energies, but just to rank them on a relative scale. Results are summarized in Table 2 and Fig. S2 ESI.† The most tightly bonded pair involves both the NH⋯N and CH⋯π interactions, and the only direct CH⋯halogen contact belonging to a significantly stabilized pair (|Eint| > 2 kcal mol−1) is long and distorted (pair 3 in Table 2). On the contrary, the most favorable H⋯F interaction on geometrical grounds is established among translation-related molecules with the least negative Eint contribution (pair 5 in Table 2).
| Pair | Distancea/Å | E int/kJ mol−1 | Symmetry operation | Contacts(D–H⋯A) | D–H/Å | H⋯A/Å | D–A/Å | α DHA/deg |
|---|---|---|---|---|---|---|---|---|
| a Distance between the molecular centroids of coordinates. b The acceptor was taken as the centroid of the unsubstituted phenyl ring. c No significant directional atom-atom contacts in this pair. | ||||||||
| 1 | 6.8 | −40 | −x + y, −x, −1/3 + z | N2–H2N⋯N1 | 1.014 | 2.437 | 3.2926(3) | 141.6 |
| C13–H13⋯πb | 1.069 | 2.429 | 3.3968(2) | 149.9 | ||||
| 2 | 5.3 | −28 | −y, −1 + x − y, 1/3 + z | —c | —c | —c | —c | —c |
| 3 | 8.6 | −11 | −x + y, −1 − x, −1/3 + z | C3–H3⋯F1 | 1.081 | 2.738 | 3.7913(3) | 164.7 |
| 4 | 7.8 | −10 | 1 – x + y, −x, 2/3 + z | C5–H5⋯πb | 1.085 | 2.984 | 3.6711(2) | 121.6 |
| 5 | 10.1 | −8 | 1 + x, 1 + y, z | C6–H6⋯F1 | 1.078 | 2.289 | 3.2161(3) | 143.0 |
3.3 Multipole model
The resolution of our dataset (0.437 Å) would not afford modelling of low-T anharmonicities according to Kuhs' empirical criterion.53,54 However, we recently demonstrated25,27 that sidestepping the Kuhs' rule is possible, if the following requirements are fulfilled: high-quality crystals, accurate and statistically significant high-order data, and very low temperatures. This is the case of the present work (Table 1). Explicit inclusion of anharmonicity, in conjunction with radial scaling parameters, is necessary to have the molecular dipole comparable with its theoretical prediction, albeit still overestimated (see section 3.5 below). The Hamilton test55 is applied as a consistent adequacy criterion to check whether the introduction of Gram–Charlier coefficients grants a significant improvement of the quality of the charge density model. A similar strategy was used to estimate anharmonicity in an experimental charge-density study of tetra-fluoroterephthalonitrile34 and, more recently, of 2-mercaptopyridone.56Results are summarized in Table 3. In all cases, the improvement was significant at the confidence level 99.95%. The best model is E (Table S1 ESI†), with agreement factors on the whole set of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309 observed (I > 0) data as low as R(F) = 0.0159 and wR(F2) = 0.0274 and largest Fourier residuals not exceeding ±0.26 e Å−3 (see also Fig. 3a).
309 observed (I > 0) data as low as R(F) = 0.0159 and wR(F2) = 0.0274 and largest Fourier residuals not exceeding ±0.26 e Å−3 (see also Fig. 3a).
| Compared models | Aavs. Bb | Bbvs. Cc | Ccvs. Dd | Bbvs. Ee | |
|---|---|---|---|---|---|
| a Up to octupoles (lmax = 3) on non-H atoms, quadrupoles (lmax = 2) on H atoms. No Gram–Charlier coefficients. b Up to hexadecapoles (lmax = 4) on non-H atoms, quadrupoles (lmax = 2) on H atoms. No Gram–Charlier coefficients. c As model B, plus third-order Gram–Charlier coefficients on Cl. d As model B, plus third- and fourth-order Gram–Charlier coefficients on Cl. e As model B, plus third- and fourth order Gram–Charlier coefficients on Cl and F. In the last least-squares cycle, high-order cumulants are kept fixed while 10 radial parameters were activated (2 parameters per atomic species). f R b,n–m,α = (b/n–m × Fb,n–m,α + 1)1/2. Values of the F distribution were computed from online resources.59 | |||||
| b = dimension of the hypothesis | 670–517 = 153 | 680–670 = 10 | 695–680 = 15 | 680–670 = 10 | |
| n–m = degrees of freedom | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309–670 = 13 309–670 = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 639 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309–680 = 13 309–680 = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309–695 = 13 309–695 = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614 614 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309–680 = 13 309–680 = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
|
| Actual R-factor ratio R |
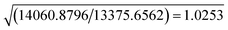
|
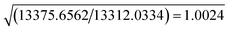
|
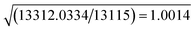
|
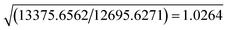
|
|
| SignificancefRb,n–m,α | α = 0.001 | 1.0078 | 1.0011 | 1.0014 | 1.0011 |
| α = 0.0005 | 1.0079 | 1.0012 | 1.0015 | 1.0012 | |
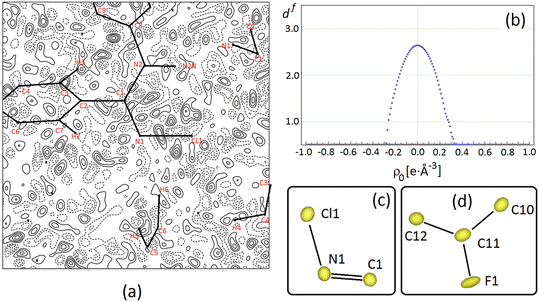 | ||
Fig. 3 (a) Difference Fourier density map, Δρ = 1/V∑hkl(Fohkl − Fchkl)·exp [−2πi(hx + ky + lz)], for NCLBA crystal at T = 17.5 K for the best multipole model E, where Fohkl and Fchkl are observed and calculated structure factor amplitudes (on the same scale), and V is the cell volume. The map is plotted in the Cl1–N1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1 plane and it is 9 × 9 Å wide, with the origin on N1. Contour levels are drawn in steps of 0.05 e Å−3 as full (dashed) lines if positive (negative) and range from −0.2 e Å−3 to +0.2 e Å−3. The minimum and maximum in Δρ are −0.25 e Å−3 and +0.26 e Å−3 respectively. The zero contour is omitted for the sake of clarity. (b) Distribution of Hausdorff fractal dimension for the experimental residual charge density in NCLBA at T = 17.5 K. (c) and (d) Joint probability density functions for halogens and their covalently connected atoms for NCLBA at T = 17.5 K, as computed through JANA2006 (ref. 60) from the best (E) multipole model. Black lines are only eyeguides. Anharmonic Gram–Charlier terms are included only for atoms Cl1 and F1. C1 plane and it is 9 × 9 Å wide, with the origin on N1. Contour levels are drawn in steps of 0.05 e Å−3 as full (dashed) lines if positive (negative) and range from −0.2 e Å−3 to +0.2 e Å−3. The minimum and maximum in Δρ are −0.25 e Å−3 and +0.26 e Å−3 respectively. The zero contour is omitted for the sake of clarity. (b) Distribution of Hausdorff fractal dimension for the experimental residual charge density in NCLBA at T = 17.5 K. (c) and (d) Joint probability density functions for halogens and their covalently connected atoms for NCLBA at T = 17.5 K, as computed through JANA2006 (ref. 60) from the best (E) multipole model. Black lines are only eyeguides. Anharmonic Gram–Charlier terms are included only for atoms Cl1 and F1. | ||
Model E includes third- and fourth-order cumulants on halogen atoms, plus hexadecapoles on non-H atoms and quadrupoles on hydrogens. Omitting high order cumulants on the F atom results in a largely overestimated radial parameter α for its valence functions (8 or 9 instead of 5.8(4) Å−1, section S6 ESI†) and a strongly biased molecular electrostatic dipole moment. This behaviour is due to the expected correlations34 among high order poles (l ≥ 3) and Gram–Charlier coefficients. In fact, the final least squares cycle comes from a block refinement where 2 radial parameters per atomic species were optimized, while keeping Gram–Charlier coefficients fixed (see Methods). Due to the rather limited resolution of the current dataset, short of the Kuhs' rule, the usual full least-squares matrix refinement could not be carried out.
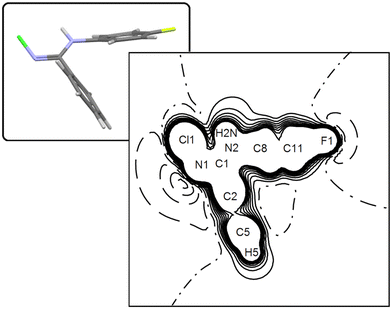
The quality of the multipole model is witnessed by the essentially featureless Fourier difference maps (see for example Fig. 3a), as well as by the fractal distribution of the charge density residuals, df(Δρ)57,58 (Fig. 3b). The latter quantity expresses the ability of specific Δρ isosurfaces to cover the whole space. The closer df(0) to 3, the better the Δρ = 0 isosurface covers the three–dimensional Euclidean manifold. In NCLBA, df(0) = 2.64, which is comparable with that estimated in our recent study on the experimental charge density of 1-methyluracil.27
As we illustrate in the next sections, the substantial agreement with quantum predictions on several key observables is even a stricter indicator of the quality of the “E” multipole model. In any case, anharmonic contributions determine only a small correction over the nuclear joint probability density (p.d.f.) surfaces of halogens, which remains very similar to the corresponding harmonic thermal ellipsoids (compare Fig. 3c and d with 1) as expected for residual anharmonicity at such low temperature.
3.4 The N–Cl bond
Owing the chemical importance of the N-halogen bond in N-halamines (see Introduction), and considering that the equilibrium length of any covalent bond is inversely related to its strength, the most relevant geometric parameter in NCLBA is just the length of the N–Cl bond. The X-ray estimate reads 1.7490(2) Å, which is 42% shorter than the corresponding van der Waals contact distance61 (3.02 Å). That said, this bond is among the longest N–Cl ones reported to date (see section S2 ESI†). All the low-R X-ray equilibrium structures we retrieved from the CSD (see sections 2.4 and S2 ESI†) bear one or more C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–Cl terminal groups, with the only exception of SEMHOI (N,N,N′-trichlorobenzamidine),62 which has also an asymmetric –NCl2 substituent (dN–Cl = 1.736 and 1.750 Å) attached to the imine carbon atom. The only other structure with a N–Cl bond longer than in NCLBA is RAQBIX (dN–Cl = 1.764 Å).63 Among substances not included in our selection, worth of note is N–chlorobenzamidine64 (BACTAE), which was reported to crystallize in P21/c with 4 molecules in the asymmetric unit and N–Cl distances ranging from 1.743(5) Å and 1.750(5) Å, that is, equivalent to our estimate within ∼1 standard deviation.
N–Cl terminal groups, with the only exception of SEMHOI (N,N,N′-trichlorobenzamidine),62 which has also an asymmetric –NCl2 substituent (dN–Cl = 1.736 and 1.750 Å) attached to the imine carbon atom. The only other structure with a N–Cl bond longer than in NCLBA is RAQBIX (dN–Cl = 1.764 Å).63 Among substances not included in our selection, worth of note is N–chlorobenzamidine64 (BACTAE), which was reported to crystallize in P21/c with 4 molecules in the asymmetric unit and N–Cl distances ranging from 1.743(5) Å and 1.750(5) Å, that is, equivalent to our estimate within ∼1 standard deviation.
On the computational side, it is known that the predicted length of the N–Cl bond depends on the level of theory.15 To estimate geometries fully compliant with the quantum mechanical potential, we also optimized the molecular structure in the solid state under fixed cell parameters (see Methods). The optimized N–Cl distance lengthened by 0.067 Å (3.8%). As demonstrated in the ESI† (section S7), this overestimate is an artefact due to the insufficient size of the basis set. The N–Cl bond length of the isolated NCLBA molecule converges to the experimental value as the size of the basis set increases, irrespective of the Hamiltonian and of the extension and nature of the basis set. This result is not surprising, and it applies to all pairs of bonded atoms (section S7 ESI†). To compare experiment and theory on the same grounds, hereinafter we focus on properties computed from the wavefunctions computed for atoms fixed at their X-ray geometries.
A neat linear correlation can be appreciated between the charge density at the N–Cl bond critical point and the geometrical bond length (Fig. 4a, Table S3 ESI†). NCLBA lies in the trend, irrespective of whether its charge density topology is evaluated on the molecule extracted from the crystal (blue dot at 1.749 Å) or within the crystal (periodic simulation, open red triangle). Interestingly, the experimental estimate (full red triangle) is within one estimated standard deviation from the value expected based on the quantum mechanical prediction.
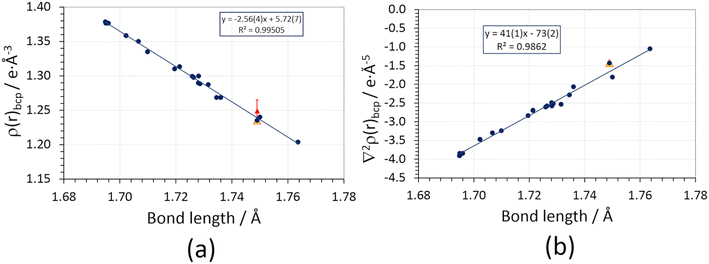 | ||
Fig. 4 (a) Charge density at the bond critical point (ρbcp) vs. geometric bond length of N–Cl covalent bonds in different compounds bearing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–Cl or C–NCl2 functional groups (section S2 ESI†). Blue circles: isolated molecules frozen at their in-crystal geometries, wavefunctions retrieved from D3 Grimme-corrected PBE0 calculations using a pob-TZVP-rev2 triple-zeta valence + polarization basis set. The blue line is the corresponding linear regression. Full red triangles: experimental multipole-based estimate of ρbcp, with error bars representing 1 estimated standard deviation (not included in the linear regression). Empty red triangles: periodic quantum simulations at the experimental crystal structure geometry (not included in the linear regression). (b) Same as (a), for the charge density Laplacian at the bond critical point (∇2ρbcp). The values corresponding to the experimentally derived multipole expansions are not shown (see text). N–Cl or C–NCl2 functional groups (section S2 ESI†). Blue circles: isolated molecules frozen at their in-crystal geometries, wavefunctions retrieved from D3 Grimme-corrected PBE0 calculations using a pob-TZVP-rev2 triple-zeta valence + polarization basis set. The blue line is the corresponding linear regression. Full red triangles: experimental multipole-based estimate of ρbcp, with error bars representing 1 estimated standard deviation (not included in the linear regression). Empty red triangles: periodic quantum simulations at the experimental crystal structure geometry (not included in the linear regression). (b) Same as (a), for the charge density Laplacian at the bond critical point (∇2ρbcp). The values corresponding to the experimentally derived multipole expansions are not shown (see text). | ||
The present analysis points out that an increase in covalent bond length implies a reduction of the formal bond order and thus of the bond strength, as it should be according to the QTAIM framework.19 However, we have no evidence that exposure to X-rays somehow weakened the N–Cl bond in the solid state. Note that this does not mean that exposure to high-energy photons has no effect at all: the observed discoloration of the crystal implies that interaction with X-rays creates some defects, which are likely related to the release of chlorine. However, such defects come unseen when the information throughout the crystal is merged through the diffraction pattern and a space–time average of the unit cell is produced by the multipole least-squares model. This likely implies that Cl-induced defects are randomly distributed and do not significantly affect the average crystallographic structure, as confirmed by the behavior of the check reflection intensities.
Agreement with our benchmark single point quantum mechanical PBE0/pob-TZVP-rev2 calculations supports the high quality of the experimental charge density distribution. Moreover, it implies that the observed properties of the N–Cl bond are genuinely molecular, i.e., they are not directly altered by the crystal field, at variance with other cases where the molecular bonding properties are significantly affected by the crystal lattice environment.65 An analogous but opposite linear trend is observed for the charge density Laplacian (Fig. 4b, Table S5 ESI†), ∇2ρbcp, which is invariably small and negative. As expected, the longer the bond, the less negative ∇2ρbcp is, suggesting that the amount of electron sharing is reduced as dN–Cl increases. It is worth noting that the experimental (multipole) estimate for ∇2ρbcp is off-trend and positive (+5.1(4) e Å−5). This discrepancy is due to the positive principal curvature (λ3), which is overestimated by the multipole expansion (Table S5 ESI†) owing to the so-called multipole model bias;66 the sign reversal is due to the low absolute value of the Laplacian in the N–Cl internuclear region.
The N–Cl bond has also a non-negligible electrostatic character: being N harder than Cl, Mulliken charges of the halogen are usually positive, and there is a strong inverse exponential correlation (R2 = 0.88) between the Cl charge and the bond length (Fig. S6 ESI†). In other words, higher positive charges on Cl contribute to stabilize short N–Cl bonds and this effect is less prominent in long N–Cl bonds. This is in keeping with N and Cl known electronegativity and with the observed correlation between bond length and the extent of electron sharing (longer N–Cl bonds being closer to their homolytic dissociation limit).
3.5 Electrostatic properties
Significant differences are apparent when the multipolar and QTAIM atomic charges are compared (Table S6 ESI†). This is not unexpected. Pseudoatom-centered electron density multipoles have boundaries that extend to infinity and overlap to each other as in a “fuzzy” flavor of charge density partitioning. This implies that electrostatic poles estimated from the Stewart's distributed multipole analysis (DMA) refer to the molecule extracted from the crystal. On the contrary, QTAIM moments derive from the full integration of the charge density over non-overlapping atomic basins bound by zero-flux surfaces of ∇ρ, which can be considered exact within the algorithm discretization error. Thus, the results from the QTAIM DMA depend on how the atomic boundaries are chosen. At variance with atomic charges, higher molecular moments are experimental observables and should be predicted equally well by both partitioning schemes. Once an isolated NCLBA molecule is simulated by artificially moving the atomic zero flux surfaces to infinity, this is exactly the case (Fig. 5, Table S7 ESI†).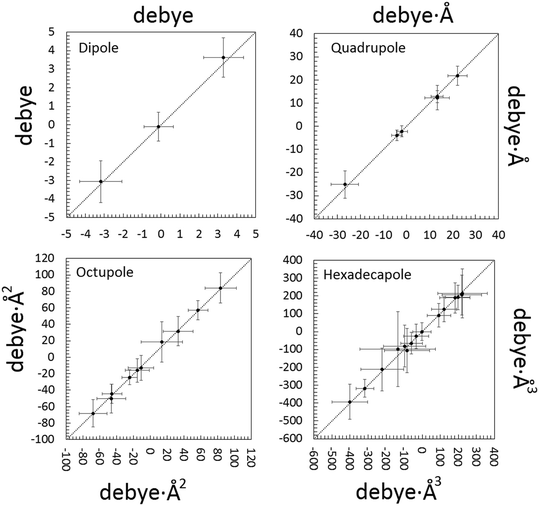 | ||
| Fig. 5 Correlation between electrostatic unabridged moments of the NCLBA molecule extracted from the crystal estimated by multipolar and QTAIM traceless Cartesian moments of pseudoatoms (x axis) vs. traceless Cartesian moments of QTAIM atoms (y axis). Origin: molecular centre of mass; reference system: inertial frame. Data points are represented by their error bars, corresponding to the pooled standard deviation. The dashed 45 deg lines represent perfect agreement. See Table S7 ESI† for the corresponding numerical entries. | ||
The molecular moments from the best model “E” are remarkably identical (within fractions of their pooled standard deviations) when evaluated from both the Stewart's and Bader's DMAs. NCLBA crystallizes in the acentric chiral P31 space group, which is compatible with a net in-cell polar field. Thus, molecular dipole moments are particularly relevant in this structure. The theoretical dipole moment magnitude of isolated NCLBA depends on the level of theory adopted. Analogously to what observed for the N–Cl distance (see above), the magnitude of the molecular dipole moment converges to 2.35–2.45 D as the size of the basis set increases (Fig. S7 and S8 ESI†).
Considering single-point calculations performed at the X-ray geometry, the PBE0 Hamiltonian predicts μ = 2.40 D or 2.93 D, depending on whether the Peintinger's or the standard 6-311G(p,d) basis set is used. These estimates should be compared with the MP2/6.31G(p) result of 2.62 D. Using the Mulliken fuzzy partitioning scheme in conjunction with the PBE0/Peintinger scheme, periodic simulations predict μ = 2.31 D for a molecule extracted from the crystal, that is, very similar to the gas phase estimate at the same theory level at the light of the precision expected on this quantity based on our experimental estimate. Switching to the in-crystal quantum-derived QTAIM DMA, the molecular dipole magnitude reads 3.09 D, to be compared with the 4.58(96) D (Stewart) or 4.74(60) D (QTAIM) values from the best experimental charge density model. Such a relatively low value of the molecular dipole moment module is understandable by looking at the distribution of the electrostatic potential (Fig. 6), where two opposite bay areas of negative potential are set up close to the N–Cl and C–F regions, respectively. Interestingly, the potential along the N–Cl axis is mainly positive, the largest negative contribution being related to the imine N lone pair. The harder nature of the fluorine substituent makes it more prone to attract electronic charge than chlorine, which in fact is predicted to bear a net positive charge by all the quantum models we tested (not only in NCLBA but also in all other molecules bearing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–Cl terminal groups (see Fig. S6 ESI†)).
N–Cl terminal groups (see Fig. S6 ESI†)).
It is worth noting that the differences among theoretical predictions are well below the capacity of the experiment to distinguish among them, as they lie below 1.5 experimental estimated standard deviations (e.s.d.’s) and are even lower than 1 e.s.d. in most cases. This implies that the crystal field does not influence the molecular dipole moment significantly. As a further check, we estimated the PBE0/6-311G(p,d) wavefunction of an isolated NCLBA molecule embedded in a crystal-like charge field. The latter was modelled by placing 4104 massless Mulliken-estimated charges at atomic positions in a 3 × 3 × 3 NCLBA supercell corresponding to the experimental structure at T = 17.5 K. The increment of the dipole magnitude in the reference molecule is insignificant (+0.047 D), implying that polarization effects are negligible, as we observed in other structures studied at very low temperatures.27 As remarked also by Spackman,67 great care should be paid when one claims to observe spectacular in-crystal enhancement of the molecular dipole moment, as it could be due to model inadequacies or to incorrectly applied partitioning criteria.
More interesting is perhaps the fact that individual dipole components sum up to a net moment of 2.73 D in the unit cell (periodic PBE0/Peintinger estimate), which runs parallel to the c axis (Fig. S9 ESI†). This suggests that NCLBA could possibly bear a measurable piezoelectric and pyroelectric response.68 Further studies are required to gain insights on this matter.
4. Conclusions
In this work, we determined the experimental charge density distribution in N-chloro-N′-(p-fluorophenyl)-benzamidine (NCLBA), a compound bearing a photolabile N–Cl bond. We demonstrated that the synergy of low X-ray flux and very low temperature (17.5 K), not so common in the charge density community, is able to reasonably preserve the sample integrity for very long times (>750 h), allowing one to obtain charge density-quality data without the need of repeatedly change the crystal or looking for fresh regions of the specimen not damaged yet by X-rays. Far be it from us to criticize modern data acquisition techniques using synchrotron facilities, whose merits in materials science and crystallography are there for all to see. However, we note that old-fashioned in-home apparatus can bring some pros sometimes, without giving up accuracy or rigorous practice in charge density analysis, even (or perhaps especially) in the case of radiation-sensitive compounds.This is true particularly in the present case, as the N–Cl bond in NCLBA is one of the longest (and labile) ones reported to date in X-ray diffraction studies. The topological analysis of the charge density according to QTAIM showed that the longer the N–halogen bond, the lower is the amount of electron sharing in the internuclear region. At the same time, long N–Cl bonds are closer to their homolytic dissociation limit.
Observable NCLBA electrostatic molecular properties do not seem to depend on the partitioning criterion used to define the distributed multipole analysis (DMA). There is a nice agreement among pseudoatom and QTAIM atom-derived electrostatic moments. For sure, electronic properties of NCLBA are not affected by the crystal field. Moreover, the present dataset is compatible with residual anharmonicity on the halogen atoms, even though explicit introduction of Gram–Charlier cumulants comes at the expense of a large increase in the estimated standard deviations of the refined multipole parameters. This problem may be possibly alleviated by collecting further high-order data at a resolution better than the actual one (0.44 Å). In any case, we think that necessary requirements to supersede the empirical Kuhs's criterion are the availability of high-quality crystals, statistically significant high-order data, and very low temperatures. Another point that is worth of note is that anharmonicity is likely more common than one usually believes, especially when dealing with organic crystals. It remains to see how the assumption of purely harmonic atomic vibrations impacts on the accuracy of X-ray determined geometrical parameters and Debye–Waller coefficients. Safe conclusions would come from the comparison of experimentally determined geometries with simulations, especially at room temperature. We foresee that computational and experimental crystallography will be more and more tightly intertwined in the next years.
Conflicts of interest
The authors have no conflict of interests to declare.Acknowledgements
Professors Donato Pocar and Riccardo Stradi (Università degli Studi di Milano) are warmly acknowledged for provision of crystals. The Authors thank Prof. Elspeth Garman for useful discussions. Università degli Studi di Milano is warmly acknowledged for providing funding for open access publishing.References
- H. Winick, in Proceedings of the 1997 Particle Accelerator Conference (Cat. No.97CH36167), IEEE, 2001, vol. 1, pp. 37–41 Search PubMed.
- L. Monico, M. Cotte, F. Vanmeert, L. Amidani, K. Janssens, G. Nuyts, J. Garrevoet, G. Falkenberg, P. Glatzel, A. Romani and C. Miliani, Anal. Chem., 2020, 92, 14164–14173 CrossRef CAS PubMed.
- E. de la Mora, N. Coquelle, C. S. Bury, M. Rosenthal, J. M. Holton, I. Carmichael, E. F. Garman, M. Burghammer, J. P. Colletier and M. Weik, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 4142–4151 CrossRef CAS PubMed.
- A. Al Hassan, J. Lahnemann, A. Davtyan, M. Al-Humaidi, J. Herranz, D. Bahrami, T. Anjum, F. Bertram, A. B. Dey, L. Geelhaar and U. Pietsch, J. Synchrotron Radiat., 2020, 27, 1200–1208 CrossRef CAS PubMed.
- R. Destro, L. Loconte, L. Lo Presti, P. Roversi and R. Soave, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, 60, 365–370 CrossRef PubMed.
- E. F. Garman and M. Weik, J. Synchrotron Radiat., 2021, 28, 1278–1283 CrossRef CAS PubMed.
- L. Citerio, D. Pocar, R. Stradi and B. Gioia, J. Chem. Soc., Perkin Trans. 1, 1978, 309–314 RSC.
- R. Stradi, G. Verga and B. Gioia, Synth., 1977, 1977, 688–690 CrossRef.
- L. Citerio, D. Pocar, R. Stradi and B. Gioia, Tetrahedron, 1979, 35, 69–76 CrossRef CAS.
- B. Qi, L. Fang, Q. Wang, S. Guo, P. Shi, B. Chu and J. Zhu, Tetrahedron Lett., 2020, 61, 151771 CrossRef CAS.
- Y. Yu, G. Luo, J. Yang and Y. Luo, Catal. Sci. Technol., 2020, 10, 1914–1924 RSC.
- H. İpek, A. Akdag, H. Ipek and A. Akdag, Phosphorus, Sulfur Silicon Relat. Elem., 2015, 190, 1285–1293 CrossRef.
- F. Hui and C. Debiemme-Chouvy, Biomacromolecules, 2013, 14, 585–601 CrossRef CAS PubMed.
- A. E. S. I. Ahmed, J. N. Hay, M. E. Bushell, J. N. Wardell and G. Cavalli, J. Appl. Polym. Sci., 2010, 116, 2396–2408 CAS.
- R. Destro, F. Merati and E. Ortoleva, Chem. Phys. Lett., 1988, 145, 193–199 CrossRef CAS.
- R. J. O'Reilly, A. Karton and L. Radom, J. Phys. Chem. A, 2011, 115, 5496–5504 CrossRef PubMed.
- D. Bu, N. Li, Y. Zhou, H. Feng, F. Yu, C. Cheng, M. Li, L. Xiao and Y. Ao, New J. Chem., 2020, 44, 10352–10358 RSC.
- J. Ra, H. Yoom, H. Son, T. M. Hwang and Y. Lee, Environ. Sci. Technol., 2019, 53, 7653–7662 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in molecules. A quantum theory, Oxford University Press, Oxford U.K., 1st edn, 1995 Search PubMed.
- T. Hahn, International Tables for Crystallography. Volume A: Space-group symmetry, International Union of Crystallography by Springer, Chester, England, Fifth Edit., 2006, vol. A Search PubMed.
- S. Samson, E. Goldish and C. J. Dick, J. Appl. Crystallogr., 1980, 13, 425–432 CrossRef CAS.
- R. Destro, Aust. J. Phys., 1988, 41, 503–510 CrossRef CAS.
- R. Destro and R. E. Marsh, Acta Crystallogr., Sect. A: Found. Crystallogr., 1987, 43, 711–718 CrossRef.
- R. Destro and R. E. Marsh, Acta Crystallogr., Sect. A: Found. Crystallogr., 1993, 49, 183–190 CrossRef.
- R. Destro, R. Ruffo, P. Roversi, R. Soave, L. Loconte and L. Lo Presti, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 722–736 CrossRef CAS PubMed.
- C. Gatti, E. May, R. Destro and F. Cargnoni, J. Phys. Chem. A, 2002, 106, 2707–2720 CrossRef CAS.
- R. Destro, P. Roversi, M. Barzaghi and L. Lo Presti, Molecules, 2021, 26, 3075 CrossRef CAS PubMed.
- E. N. Maslen, in International Tables for Crystallography Volume C: Mathematical, physical and chemical tables, International Union of Crystallography, Chester, England, 2006, pp. 599–608 Search PubMed.
- R. F. Stewart, J. Chem. Phys., 1969, 51, 4569–4577 CrossRef CAS.
- R. F. F. Stewart and IUCr, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 565–574 CrossRef.
- G. A. Jeffrey and J. F. Piniella, The Application of Charge Density Research to Chemistry and Drug Design, Springer US, Boston, MA, Nato Scien., 1991, vol. 250 Search PubMed.
- R. F. Stewart, M. A. Spackman and C. Flensburg, VALRAY User's Man., 2000, 1–134.
- P. Roversi and R. Destro, Chem. Phys. Lett., 2004, 386, 472–478 CrossRef CAS.
- H. O. Sorensen, R. F. Stewart, G. J. McIntyre and S. Larsen, Acta Crystallogr., Sect. A: Found. Crystallogr., 2003, 59, 540–550 CrossRef PubMed.
- P. Roversi and R. Destro, Symmetry, 2017, 9, 63 CrossRef.
- M. Barzaghi, PAMoC (version RV-2021) https://www.pamoc.it (accessed March 25, 2021)., 2021.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- R. Dovesi, A. Erba and R. Orlando, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- D. Vilela Oliveira, J. Laun, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2019, 40, 2364–2376 CrossRef CAS PubMed.
- C. Gatti and S. Casassa, TOPOND14 User's Man., 2017, 53.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian16 (Revision A.03), 2016.
- C. R. Groom and F. H. Allen, Angew. Chem., Int. Ed., 2014, 53, 662–671 CrossRef CAS PubMed.
- B. Fabius, C. Cohen-Addad, F. K. Larsen, M. S. Lehmann and P. Becker, J. Am. Chem. Soc., 1989, 111, 5728–5732 CrossRef CAS.
- R. L. Owen, E. Rudiño-Piñera and E. F. Garman, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 4912–4917 CrossRef CAS PubMed.
- H. Taberman, Crystals, 2018, 8, 157 CrossRef.
- C. S. Bury, J. C. Brooks-Bartlett, S. P. Walsh and E. F. Garman, Protein Sci., 2018, 27, 217–228 CrossRef CAS PubMed.
- M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392 RSC.
- L. Lo Presti, CrystEngComm, 2018, 20, 5976–5989 RSC.
- A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309–314 CrossRef CAS.
- A. Gavezzotti and G. Filippini, J. Phys. Chem., 1994, 98, 4831–4837 CrossRef CAS.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- W. F. Kuhs, Acta Crystallogr., Sect. A: Found. Crystallogr., 1992, 48, 80–98 CrossRef.
- W. F. Kuhs, Aust. J. Phys., 1988, 41, 369–382 CrossRef CAS.
- W. C. Hamilton, Acta Crystallogr., 1965, 18, 502–510 CrossRef CAS.
- M. Lutz, T. J. Smak and A. T. Sanderse, Crystals, 2022, 12, 338 CrossRef CAS.
- K. Meindl and J. Henn, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 404–418 CrossRef CAS PubMed.
- K. Meindl, R. Herbst-Irmer and J. Henn, Acta Crystallogr., Sect. A: Found. Crystallogr., 2010, 66, 362–371 CrossRef CAS PubMed.
- L. Casio Computer Co., Keisan Online Calculator, https://keisan.casio.com/exec/system/1180573187, (accessed 15 March 2022).
- V. Petrícek, M. Dušek and L. Palatinus, Z. Krist.-New Cryst. St., 2014, 229, 345–352 Search PubMed.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812 CrossRef CAS PubMed.
- T. Martinu and W. P. Dailey, J. Org. Chem., 2006, 71, 5012–5015 CrossRef CAS PubMed.
- Y. Ning, T. Fukuda, H. Ikeda, Y. Otani, M. Kawahata, K. Yamaguchi and T. Ohwada, Org. Biomol. Chem., 2017, 15, 1381–1392 RSC.
- R. A. Moss, J. Wlostowska, W. Guo, M. Fedorynski, J. P. Springer and J. M. Hirshfield, J. Org. Chem., 1981, 46, 5048–5050 CrossRef CAS.
- L. Lo Presti, A. M. Orlando, L. Loconte, R. Destro, E. Ortoleva, R. Soave and C. Gatti, Cryst. Growth Des., 2014, 14, 4418–4429 CrossRef CAS.
- L. Lo Presti and C. Gatti, Chem. Phys. Lett., 2009, 476, 308–316 CrossRef CAS.
- M. A. Spackman, P. Munshi and B. Dittrich, ChemPhysChem, 2007, 8, 2051–2063 CrossRef CAS PubMed.
- L. Lo Presti, M. Sist, L. Loconte, A. Pinto, L. Tamborini and C. Gatti, Cryst. Growth Des., 2014, 14, 5822–5833 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the data collection; list of Cambridge Structural Database reference codes employed to study the N–Cl bond; input stream for periodic quantum simulations (CRYSTAL code); estimation of the absorbed dose; details of crystal packing; results of multipole refinements; bond lengths; electrostatic properties. Archive crystal_data.zip: crystallographic information file, with the corresponding PLATON checkcif report. Archive NCLBA_VALRAY_FILES.zip: Valdat input, with the basis functions used to build the charge density, plus the full dataset; Vallsq output, with the least-squares details; fort7.txt file, with all geometrical, thermal and charge density parameters listed. CCDC 2180453. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce00957a |
| This journal is © The Royal Society of Chemistry 2022 |