Raman spectroscopy and DFT calculations of PEDOT:PSS in a dipolar field

Abstract

The conductive polymer–electrolyte interface plays an important role in many electrochemical devices. An unusual situation arises when a solvent-free ionic liquid (SF-IL) is used as the electrolyte because it behaves as a molten salt rather than an electrolyte solution. On the basis of Raman spectra, it was found that the presence of ion pairs of SF-IL in the vicinity of poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) results in a decrease in the oxidation level of the polymer and an increase in the HOMO–LUMO gap. The process of polymer “dedoping” and the modification of the electronic structure of the polymer are illustrated by quantum chemical calculations.

---

1 Introduction

The properties and functionality of electrochemical devices, such as electrolytic capacitors and supercapacitors, electrochemical diodes and transistors, electrochemical biological sensors, electrical switches, electrochemical solar cells, etc., are strongly influenced by the type of electrolyte. Frequently, the metal (semiconductor)–electrolyte interface plays an important role in these devices. LiClO₄ solution,¹ CaCl₂ water solution,² saturated KCl and NaCl aqueous solutions,³ LiClO₄ dissolved in high molecular weight polyethylene oxide,⁴ ion-gels,⁴ solid electrolytes, etc. are typically used as electrolytes. The organization of the solvent and ions in these electrolytic solutions and gels is described adequately by the Gouy–Chapman–Sterns model based on the Debye–Hückel theory for dilute electrolytes, assuming that the ions are well separated and non-interacting. Concerning the interface between the semiconductor (incl. organic semiconductors and conductive polymers) and electrolyte, it is usually assumed that an electric double layer is formed.⁵ Mixtures of room temperature ionic liquids (ILs) with organic solvents such as propylene carbonate are also occasionally used.^6,7 The application of ILs is attractive because of their negligible volatility, high electrochemical stability, and adequate conductivity. Charge transport is predominantly influenced by ions; ion pairs and ion aggregates do not participate in the conductive mechanism. Döbbelin et al.⁸ reported that the treatment of the conductive polymer poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) in ILs induced the formation of three-dimensional conducting networks in the polymer bulk with smaller PEDOT domains. Thus, the electrical conductivity and ionic character of the polymer films were significantly increased. Blending some IL additives into PEDOT:PSS increases the film conductivity to about 1000 S cm⁻¹, which is among others caused by the higher concentration of polarons; the Seebeck coefficient increases in some cases as well.⁹ The mixture of an IL with an insulating polymer such as poly(vinylidene fluoride) (PVDF) represents a different case. This ion gel contains both mobile anions and cations and these electrostatically neutral ion pairs can penetrate the channel of an organic mixed ionic–electronic device.¹⁰ Among others the mixture of PVDF and an IL can be used as a solid electrolyte in gas sensors.¹¹ The situation at the IL–semiconductive polymer interface is assumed to be more complicated. The discussions are usually concentrated on electrochemical or electrostatic doping in electrolyte-gated organic field-effect transistors and organic electrochemical transistors (OECTs) based on molecules and conductive polymers. The problem was addressed some time ago by Hamedi et al. in the context of the switching phenomenon.¹² On the basis of time-resolved electrical measurements they stated that the transistor channel forms in two steps: a first step attributable to the formation of an electric double layer (EDL), responsible for the electrostatic doping, followed by the second step attributable to the electrochemical doping. This study points to the possible co-existence of the two doping mechanisms: electrostatic and electrochemical. The chemical approach was published by Rawlings et al.¹³ They prepared two single-ion-conducting polymeric ionic liquids with opposite polarity, where either the anion or the cation was bound to the active polymer backbone. When employed with a p-type active layer, gating with the cation-bound polymer IL (CTPIL) results in electrochemical doping because the mobile anion can infiltrate the active layer to compensate positively charged holes. By contrast, the anion ATPIL gate results in interfacial electric double layer doping, where the polymer-bound anions are unable to infiltrate the semiconductor and the mobile cations migrate toward the gate electrode. However, practically, as mentioned by Giovanniti et al.,¹⁴ completely blocking the ion penetration in organic materials is difficult because of a relatively high free volume. Thus even materials designed to prevent ion penetration or form a double layer will often exhibit some degree of electrochemical doping when gated with an electrolyte. This process, including the formation of a barrier, induced charge transfer, stimulated charge injection and others, can influence the ion injection from the IL to the active semiconducting material. In addition, the doping can be affected by the intermolecular interactions between anions and cations constituting the IL.

Room temperature solvent-free ionic liquids (SF-ILs) represent a new class of electrolytes with specific properties. With respect to conductivity, we must regard these materials as molten salts. It is sometimes assumed that at the semiconductor–SF-IL interface a double layer is formed. However, in this case, the structure of the double layer should be different from that in conventional electrolytes, where the solvent molecules separate the semiconductor surface charges and electrolyte counterions.^15–17 This is definitely not the case with SF-ILs, as shown by nuclear magnetic resonance (NMR) and electrochemical impedance spectroscopy (EIS).¹⁸ The charge distribution extends into the bulk of the semiconductor (the space-charge region) and the double layer, if any, is formed within the solid part of the system. The high dipole moments of the ionic pairs in the SF-IL suggest that electron–dipole interactions cannot be neglected, as they can play an important role in electrochemical processes. This type of interface with the SF-IL is unusual and studies have mainly been focused on the modelling of metal–SF-IL structures¹⁹ (in the case of the SF-IL structure in the vicinity of the electrified metal not being greatly affected, the results can be extrapolated to the semiconductor–SF-IL interface). Baldelli used surface-specific vibrational spectroscopy and EIS for the detection and characterization of the possible double layer for several metals and SF-ILs.¹⁸ He found that the size of the molecules present in SF-ILs, their orientation, and the amount of charge at the interface are important.

Many previous studies have investigated the influence of dipolar fields on charge carrier transport and charge trapping in insulators.^20–24 In the present study, we employed Raman spectroscopy to investigate the influence of dipoles of the SF-IL 1-ethyl-3-methylimidazolium trifluoromethanesulfonate [EMIM]⁺[CF₃SO₃]⁻ on the electronic properties of the semiconductive polymer PEDOT:PSS. It was found that in the vicinity of dipolar species the level of oxidation of PEDOT:PSS decreases and the HOMO–LUMO gap increases. The results are supported by the quantum chemical calculations performed on the model complex EDOT (hexamer):SS (dimer).

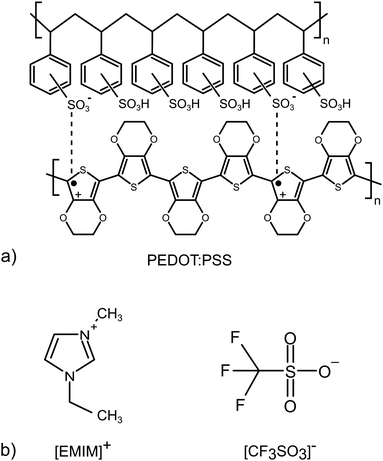
2 Materials and samples

The study was performed on the conductive polymer PEDOT:PSS (Clevios™ SV3) and a SF-IL (Merck) that consists of the [EMIM]⁺ cation and the [CF₃SO₃]⁻ anion. Both chemicals were used as received. Their chemical structures are shown in Fig. 1. The samples under study were prepared as follows: PEDOT:PSS layers were deposited on a silicon substrate by the doctor blade technique. Then, a very thin SF-IL film was deposited on these layers by dropping.

Fig. 1 Chemical structures of (a) poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS), (b) the 1-ethyl-3-methylimidazolium cation [EMIM]⁺ of the SF-IL (bottom left) and the trifluoromethanesulfonate anion [CF₃SO₃]⁻ of the SF-IL (bottom right).

It is assumed that the effect under study, i.e. the interaction between charge (PEDOT:PSS) and dipole (SF-IL), depends on the magnitude of the dipole moment. Therefore, the dipole moment of [EMIM]⁺[CF₃SO₃]⁻ was estimated. Izgorodina et al.²⁵ published values for the dipole moments of [EMIM]⁺ (m = 1.62 D) and [CF₃SO₃]⁻ (m = 4.02 D). The values were calculated at the MP2/aug-cc-pVTZ level. It should be noted that the calculated dipole moments can underestimate the true values due to the possibility that an induced contribution was not included. Thus, the real dipole moments are expected to be approximately 25% higher.²⁶ Taking into account the formula for the dipole moment m, specifically m² = m²(cation) + m²(anion), which is valid under the assumption that the dipole moments of individual ions align completely with the applied field, the overall dipole moment of [EMIM]⁺[CF₃SO₃]⁻ is 5.41 D (inclusive of the 25% correction). It should be noted that the use of the equation for calculating the overall dipole moment of the cation–anion configuration may be problematic, especially when cations interact with anions via hydrogen bonds. Such an interaction can be assumed here, as follows from Fig. 6c (orange rectangle, black dashed lines). Our calculation based on density functional theory (DFT) gives a value for the dipole moment of [EMIM]⁺[CF₃SO₃]⁻ equal to 10.77 D. It should be noted that the dipole moments of two conformers of [EMIM]⁺ were calculated. They are related to planar and nonplanar ethyl groups (for their chemical structures, see Fig. S1, ESI†) with respect to the imidazolium ring plane, the nonplanar [EMIM]⁺ giving the lower energy.²⁷ The dipole moments of both conformers were close to each other, those of the nonplanar one being a little higher, cf. 1.16 and 1.83 D (Hartree–Fock level ab initio calculations) and 1.13 and 1.64 D (B3LYP level ab initio calculations).²⁸

3 Experimental and computing procedure

3.1 Raman spectroscopy measurement

Raman spectra excited by means of a near-infrared diode laser (785 nm) were collected on a Renishaw inVia Reflex Raman microspectrometer. A research-grade Leica DM LM microscope with an objective magnification of ×50 was used to focus the laser beam onto the sample placed on an X–Y motorized sample stage. The scattered light was analysed using a spectroscope equipped with a holographic grating with 1200 lines mm⁻¹. A Peltier-cooled CCD (charge-coupled device) detector (576 × 384 pixels) registered the dispersed light.

3.2 Quantum chemical methods

The geometries of the 3,4-ethylenedioxythiophene hexamer in the (i) neutral EDOT⁰(6) and dication EDOT⁺²(6) state, (ii) styrenesulfonate dimer in the neutral SS⁰(2) and dianion SS⁻²(2) state, (iii) complex EDOT⁺²(6):SS⁻²(2) in the neutral state, where SO₃⁻ is in the anion state, and EDOT⁰(6):SS⁰(2), where SO₃H is in the neutral state, (iv) complex EDOT⁺²(6):SS⁻²(6), and (v) complex EDOT⁺²(6):SS⁻²(2) – n([EMIM]⁺[CF₃SO₃]⁻) (for n = 1, 2, 4, 6) were optimized using the DFT method (using the unrestricted Kohn–Sham equation) and B3LYP²⁹ functional including the D3 dispersion coefficient³⁰ in a vacuum. Here, the exponent means charge and the number within brackets means the number of monomer units. For the EDOT and EDOT:SS systems we used models similar to those described by Gangopadhyay et al.³¹ The 6-31G(d,p) basis set was used for all atoms.^32–36 EDOT⁺²(6):SS⁻²(2) and EDOT⁺²(6):SS⁻²(6) is the model system for PEDOT:PSS, and the complex EDOT⁺²(6):SS⁻²(2) – n([EMIM]⁺[CF₃SO₃]⁻) is the model for PEDOT:PSS including the ionic pairs of the SF-IL. Vibrational analysis was performed for all gradient-optimized structures. All DFT calculations were performed using the quantum chemical program Gaussian 09.³⁷ The transformation of molecular levels like the HOMO or LUMO to the density of states (DOS) was mathematically performed using the convolution process utilizing the Gaussian 09 and GaussSum 3.0 programs³⁸ with a full-width at half maximum (FWHM) of 0.3 eV of the Gaussian type of functions. Raman frequencies and intensities for geometrically optimized EDOT⁺²(6):SS⁻²(2) and EDOT⁺²(6):SS⁻²(2) – n([EMIM]⁺[CF₃SO₃]⁻) complexes (for n = 1, 2, 4, 6) were calculated by means of the numerical differentiation of dipole derivatives with respect to the electric field, as implemented in the Gaussian 09 program. To account for the solvent effect on Raman spectra, the polarizable continuum model (PCM)³⁹ was used and the PCM parameters were set for 2-methyl-1-propanol with a relative permittivity of 16.777, which is very close to the relative permittivity of [EMIM]⁺[CF₃SO₃]⁻ (16.5 ± 0.5)⁴⁰ for the EDOT⁺²(6):SS⁻²(2) computational model. The scaling factor was calculated as the ratio between the sum of the two main peaks in the experiment (one main peak from the PEDOT:PSS spectrum and one main peak from the spectrum of the SF-IL solvent) and the sum of the two main peaks based on the theoretically calculated Raman spectra (one main peak from the EDOT⁺²(6):SS⁻²(2) spectrum and one main peak from the EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻) spectrum). Finally, the DFT-calculated Raman wavenumbers were scaled by the constant 0.953. Raman spectra were displayed using a full width at half-maximum of 8 cm⁻¹. The dipole moments of SF-IL pairs in the investigated complexes were calculated using the SF-IL pair structures as geometrically optimized in the complex with EDOT⁺²(6):SS⁻²(2), and the origin of vectors representing the dipole moments was placed at the centre of mass of the IL pairs. The theoretical modelling was focused on the physiochemical properties of the PEDOT:PSS system (DOS, HOMO–LUMO gap) which are known to be closely related to the electrical conductance. We prepared several models of one PEDOT:PSS layer where the effect of stepwise added SF-IL units on its electronic structure was modelled. The calculated changes of the electronic structure indicate the changes in the level of oxidation of the PEDOT:PSS chain. Because the 3D atomistic structure of PEDOT:PSS layers including the SF-IL environment is currently unknown, the intermolecular charge transport was not studied. Note that the properties at the PEDOT:PSS–SF-IL interface can be also influenced by structure-related properties like the degree of crystallinity and the quality of crystal packing at the interface.⁴¹

4 Results and discussion

4.1 Raman spectra: experiment and modelling

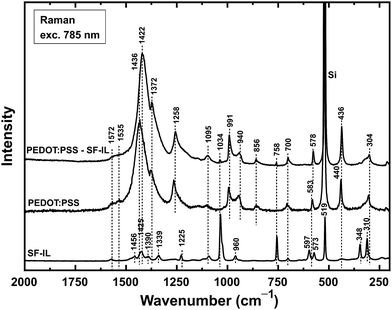
Raman spectra (excitation wavelength: 785 nm) for the systems under study are shown in Fig. 2. The characteristic peaks of the SF-IL observed at 1425, 1339, 1225, 1034, 960, 758, 597, 519, 348, and 310 cm⁻¹ were assigned mainly to the intramolecular vibrations of the nonplanar [EMIM]⁺ cation.⁴² The spectrum of PEDOT:PSS exhibits two weak bands, with maxima at 1572 cm⁻¹ (quinoid structure, see Fig. S2, ESI†) and 1535 cm⁻¹ (C_α′=C_β′ stretching, see Fig. S3, ESI†), one strong band at 1436 cm⁻¹ (symmetric C_α=C_β stretching vibrations) and one shoulder band at 1372 cm⁻¹ (C_β–C_β stretching). Other peaks with maxima at 1258 cm⁻¹ (C_α–C_α′ inter-ring stretching), 1095 cm⁻¹ (C–O–C deformation), 991 cm⁻¹ (oxyethylene ring deformation), 856 cm⁻¹ (C–H bending), 700 cm⁻¹ (symmetric S–S–C deformation), 583 cm⁻¹ (oxyethylene ring deformation), 440 cm⁻¹, and 304 cm⁻¹ were observed, in agreement with Chiu et al.⁴³ The band at 1436 cm⁻¹ is most significant since it reflects the level of oxidation (doping) of PEDOT:PSS.

Fig. 2 Raman spectra of a thin layer of PEDOT:PSS deposited on a silicon substrate, a PEDOT:PSS layer deposited on a Si substrate and covered by a film of SF-IL (PEDOT:PSS–SF-IL), and a thin film of SF-IL. The spectra are shifted in intensities owing to the better resolution.

The band for PEDOT:PSS at 1436 cm⁻¹ increased in intensity and was shifted to 1422 cm⁻¹ (Δ = 14 cm⁻¹, symmetric C_α=C_β stretching) when the PEDOT:PSS layer was covered with the SF-IL. It should be noted that a similar shift (Δ = 31 cm⁻¹) was also observed by Chiu et al. (a shift from 1445 to 1414 cm⁻¹ for the highly electrochemically oxidized/reduced PEDOT in a doped/undoped state).⁴³ According to these authors, the shift occurs because of a decrease in the ratio of oxidized to neutral structures within the PEDOT chain. This shift in band position due to oxidation/reduction was also observed for a treated PEDOT:PSS layer by Garreau et al. (laser excitation at both 514 and 1064 nm),⁴⁴ Lapkowski et al. (laser excitation at 1064 nm),⁴⁵ and McCarthy.⁴⁶ Another noticeable change in the spectrum was an increase in the intensity of the C_β–C_β stretching shoulder band at 1372 cm⁻¹. In accord with the literature, the position of this shoulder band remained unchanged but its intensity increased during the reduction process.⁴⁷ Besides the PEDOT bands mentioned above, we also detected some bands of the SF-IL at 1095, 1034, and 758 cm⁻¹ in the spectrum of PEDOT:PSS treated with the SF-IL. On the basis of experiments carried out on PEDOT:iodine samples, Chiu et al. suggested that the most intense band, assigned to the symmetric C_α=C_β stretching vibration, is a combination of two separate bands, one due to the symmetric C_α=C_β stretching vibration from the neutral PEDOT segments (centred at 1413 cm⁻¹) and the other to the symmetric C_α=C_β stretching vibration from the oxidized PEDOT segments (centred at 1444 cm⁻¹).^43,45 The integrated intensities of these bands vary with the degree of doping, i.e. the degree of oxidation in the PEDOT polymeric structure. This explains the shift in the wavenumbers and in the shape of the combined symmetric C_α=C_β stretching band when the doping level in the polymer is changed. As the level of doping becomes lower, the combined band should be dominated more by the neutral structure and move towards lower wavenumbers. Thus, the shift towards lower wavenumbers means that the PEDOT chain is less oxidized.

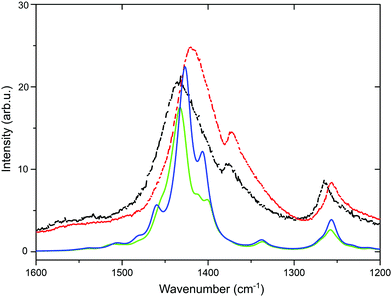
The experimental shift in the position of the symmetric C_α=C_β stretching vibration from 1436 to 1422 cm⁻¹ after the application of the SF-IL is shown in Fig. 3 (black and red dashed curves). Beside these measured curves, two other theoretical curves (green and blue) are presented. The calculation was performed on the hexamer (EDOT⁺²(6)) and dimer (SS⁻²(2)), as detailed in Section 3.2. At first glance, the theoretical DFT curves are narrower than the experimental ones, most likely due to sample inhomogeneity and possibly also to the gradient of SF-IL ions within the polymer bulk. Once the SF-IL ions penetrate the PEDOT:PSS bulk, a gradient towards the bulk arises, as can be inferred from the broadening of experimental spectra. In addition, theoretical spectra were calculated for the molecular models. According to DFT calculations, the occurrence of the SF-IL in the vicinity of the PEDOT:PSS chain results in a shift of the band maximum from 1503 (green line, doped oxidized state) to 1495 cm⁻¹ (blue line, undoped state). After scaling (using a scaling factor of 0.953), these wavenumbers were 1433 and 1425 cm⁻¹, respectively. Importantly, the direction of the calculated shift (Δ = 8 cm⁻¹) was in agreement with the direction of the experimental shift (Δ = 14 cm⁻¹). It should be noted that calculations were performed without solvation effects and for an equal number of SF-IL and ionized EDOT⁺²(6):SS⁻²(2) pairs. One effect regarding DFT calculations should be mentioned. The calculated shift of the peak maximum at 1433 cm⁻¹ towards lower wavenumbers was obtained only for a certain number of SF-IL units surrounding the EDOT⁺²(6):SS⁻²(2) framework (here two SF-IL units per two oxidized EDOT⁻²(2) units). For multiple SF-IL pairs the theoretical shift was the opposite, i.e. for 4 SF-IL pairs the band at 1503 cm⁻¹ shifted to 1513 cm⁻¹. The same trend was modelled due to the presence of solely PCM-implicit solvation employing the respective relative permittivity. For more SF-IL ion pairs, the Mulliken charge on both EDOT⁺²(6) and SS⁻²(2) decreased (e.g., for one SF-IL ion pair the Mulliken charge was 1.684 e and for four SF-IL ion pairs it was 1.593 e) and the charge transfer from both units to [EMIM]⁺ and [CF₃SO₃]⁻ was clearly visible (detailed results not presented here). Therefore, we can suggest that extended solvation by SF-IL pairs is not present in the experiment and that the surface properties of the PEDOT:PSS layer are more appropriately described by partial solvation of the EDOT⁺²(6):SS⁻²(2) system.

Fig. 3 Raman spectra in the region from 1600 to 1200 cm⁻¹. Black dashed line – PEDOT:PSS layer, experiment; red dashed line – PEDOT:PSS–SF-IL, experiment; full green line – PEDOT:PSS, DFT calculations; blue full line – PEDOT:PSS–SF-IL, DFT calculations.

4.2 Quantum chemical calculations

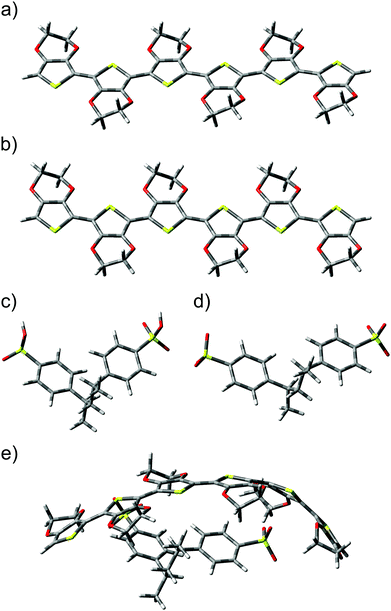
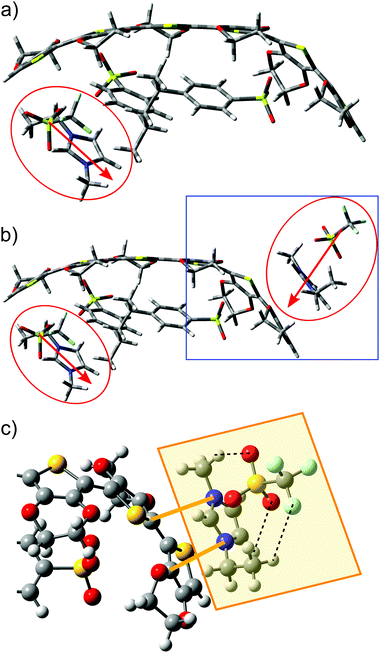
Calculations involving the 3,4-ethylenedioxythiophene hexamer EDOT⁺²(6) and the styrenesulfonate dimer SS⁻²(2) allowed the modelling of a bipolaron structure on the EDOT(6) chain.⁴⁸ Optimized geometries of (a) neutral EDOT⁰(6), (b) dicationic EDOT⁺²(6), (c) protonated SS⁰(2), (d) dianionic SS⁻²(2), and (e) the complex structure EDOT⁺²(6):SS⁻²(2) are presented in Fig. 4. It follows from this figure that the optimized structures of (a) neutral EDOT⁰(6) and (b) dicationic EDOT⁺²(6) are linear and nearly planar. Neutral protonated SS⁰(2) and dianionic SS⁻²(2) show similar relaxed structures (cf.Fig. 4c and d). In the case of EDOT⁺²(6):SS⁻²(2), the structure of EDOT⁺²(6) is bent in a concave manner to maximize the interaction with the anion SS⁻²(2) (see Fig. 4e). This indicates that PEDOT and PSS are not oriented parallel to each other. It should be noted that the degree of concavity is, among other effects, influenced by the length of the EDOT oligomer.⁴⁹ The bent concave structure and overall view of the relaxed structure consisting of the dicationic hexamer EDOT⁺²(6) and the dianionic hexamer SS⁻²(6) are shown in Fig. 5. Here, both the EDOT and the SS oligomer chains are visible.

Fig. 4 Geometries of optimized structures: (a) the neutral EDOT hexamer (EDOT⁰(6)), (b) the dication EDOT hexamer (EDOT⁺²(6)), (c) the protonated dimer (SS⁰(2)), (d) the dianion dimer (SS⁻²(2)), and (e) the complex of the dication hexamer EDOT⁺²(6) and the dianion dimer SS⁻²(2).

Fig. 5 Geometry of the optimized complex structure consisting of the dication hexamer EDOT⁺²(6) and the dianion hexamer SS⁻²(6). Yellow spheres – sulphur, black spheres – carbon, red spheres – oxygen, grey spheres – hydrogen.

When an ion pair of SF-IL ([EMIM]⁺[CF₃SO₃]⁻) is placed in the vicinity of EDOT⁺²(6):2SS⁻²(2), the structure of the dicationic EDOT⁺²(6) hexamer remains semi-planar and the geometry of dianionic SS⁻²(2) does not change very much. The geometry of the optimized structure of EDOT⁺²(6):(SS⁻²(2) – [EMIM]⁺[CF₃SO₃]⁻ is shown in Fig. 6a (a system with one ion pair of SF-IL) and Fig. 6b (a system with two ion pairs of SF-IL). The structures were optimized to the lowest energy. The distances between nitrogen atoms within the imidazolium ring and the selected carbon atoms of the thiophene rings are indicated by orange lines in Fig. 6c: from the top, 0.335 and 0.319 nm. The black dashed lines demonstrate the hydrogen bonds between [CF₃SO₃]⁻ and [EMIM]⁺. The inter-atomic distances influenced by the non-covalent interaction between the thiophene and imidazole rings are driven mostly by dispersion forces. Similar distances were measured between π–π stacked moieties, for example, those between the DNA base pairs⁵⁰ and also between PEDOT layers as was determined by the grazing-incidence wide-angle X-ray scattering (GIWAXS).⁴¹ We can assume that the dispersion forces owing to π–π stacking play a key role in the stabilization of these systems.

Fig. 6 Geometry of optimized structures: (a) EDOT⁺²(6):SS⁻²(2) – [EMIM]⁺[CF₃SO₃]⁻, the structure in red ellipse is [EMIM]⁺[CF₃SO₃]⁻, the red arrow indicates the direction of the dipole moment of [EMIM]⁺[CF₃SO₃]⁻; (b) EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻); (c) fraction of the EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻) structure marked by the blue rectangle in (b). Structure in the yellow rectangle is the SF-IL [EMIM]⁺[CF₃SO₃]⁻; characteristic distances of two nitrogen atoms of the imidazolium ring ([EMIM]⁺) from two selected carbon atoms of the thiophene rings are demonstrated by orange lines (from the top, 0.335 and 0.319 nm). The black dashed lines demonstrate the hydrogen bonds between [CF₃SO₃]⁻ and [EMIM]⁺. Yellow spheres – sulphur, black spheres – carbon, dark blue spheres – nitrogen, red spheres – oxygen, light blue spheres – fluorine.

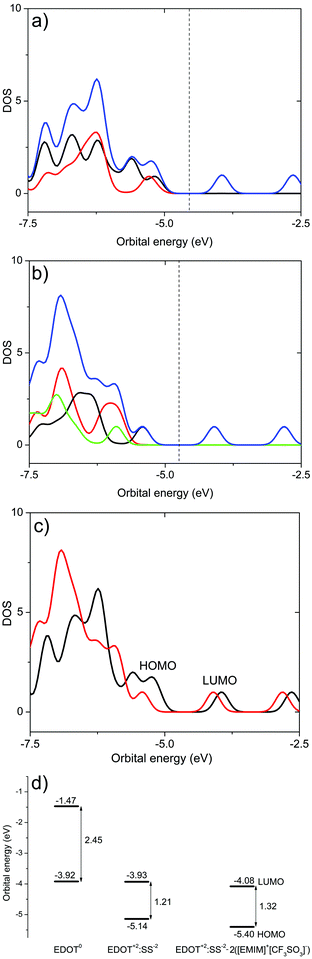
To acquire more information about the influence of the ion pairs of SF-IL on the charge distribution in EDOT⁺²(6):SS⁻²(2) – [EMIM]⁺[CF₃SO₃]⁻, the electronic structure was calculated. Let us first discuss the molecular orbitals and their energies and DOS. Fig. 7 and 8 show, respectively, the HOMO and LUMO molecular orbitals of (a) the hexamer EDOT⁰(6), (b) EDOT⁺²(6):SS⁻²(2), and (c) the complex structure EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻). Both the HOMO and LUMO of the hexamer EDOT⁰(6) show the extended conjugation of π-orbitals over the entire length of the molecule. The calculated HOMO–LUMO energy gap is 2.45 eV, with the HOMO and LUMO energies being −3.92 and −1.47 eV, respectively. This value decreases to 1.21 eV for the EDOT⁺²(6):SS⁻²(2) structure, with the HOMO and LUMO energies being −5.14 and −3.93 eV, respectively. For EDOT⁺²(6):SS⁻²(2), the HOMO is mainly localized on the EDOT (see Fig. 7b) with modest contributions owing to the presence of SO₃⁻ groups. The contribution of SO₃⁻ atomic orbitals to the HOMO was also calculated by Lenz et al.⁴⁹

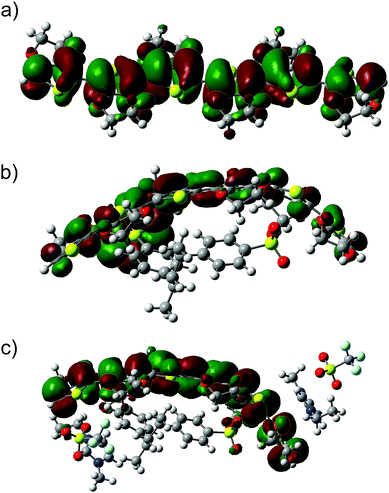Fig. 7 HOMOs of the investigated systems: (a) the neutral hexamer EDOT⁰(6), (b) EDOT⁺²(6):SS⁻²(2), and (c) the complex structure EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻).

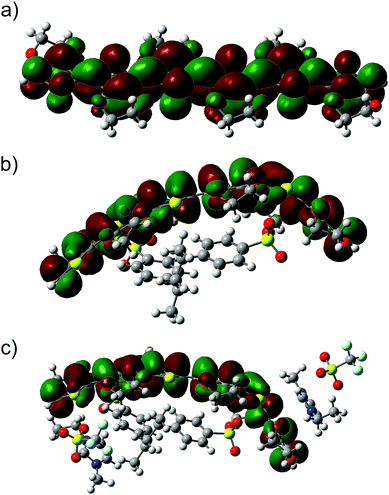Fig. 8 LUMOs of the investigated systems: (a) the neutral hexamer EDOT⁰(6), (b) EDOT⁺²(6):SS⁻²(2), and (c) the complex structure EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻).

The composition of the HOMO is consistent with the calculated density of states (DOS) (see Fig. 9a). In the presence of SF-IL pairs, the contribution to the HOMO decreases. However, π-conjugation of the extended HOMO is preserved. The HOMO–LUMO energy gap was calculated as 1.32 eV with the HOMO and LUMO energies being −5.40 and −4.08 eV, respectively. This energy gap is a little higher than that for EDOT⁺²(6):SS⁻²(2), which indicates that the electrical conductance of the de-doped system will be most likely lower.³¹ For all the systems, the LUMOs are primarily localized on the EDOT chain, as follows from Fig. 8. The presence of the SF-IL does not influence the conjugation. It is assumed that the wider HOMO–LUMO energy gap is a result of the dipolar interactions between the EDOT⁺²(6):SS⁻²(2) chain and SF-IL ion pairs (Fig. 6a and b). The total DOS (blue lines) values of (a) EDOT⁺²(6):SS⁻²(2) and (b) EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻) are shown in Fig. 9. The contributions by particular components owing to the presence of EDOT⁺²(6) (black line), SS⁻²(2) (red line), and 2([EMIM]⁺[CF₃SO₃]⁻) (green line) to the DOS are also presented. The comparison of the total DOS for EDOT⁺²(6):SS⁻²(2) and EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻) in Fig. 9c indicates that the total DOS close to the HOMO of EDOT⁺²(6):SS⁻²(2) is higher than that for EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻). This fact also implies the lower “conductance” of EDOT⁺²(6):SS⁻²(2) in the presence of [EMIM]⁺[CF₃SO₃]⁻. Fig. 9d shows the plot of the frontier orbital energies of the EDOT⁰(6), EDOT⁺²(6):SS⁻²(2), and EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻) structures, all in the neutral state. The total charge of the systems (in electrons (e)), the energies of frontier HOMO and LUMO (in (eV)), and the HOMO–LUMO gaps calculated for the systems under investigation are presented in Table 1. The HOMO–LUMO (H–L) gap calculated for the SS⁰(2) and SS⁻²(2) molecules was relatively high, regardless of their charge. This likely indicates the worse “conductance” of SS⁰(2) than that of EDOT. The HOMO–LUMO gap for neutral EDOT⁰(6) (2.45 eV) and the gap calculated for the dication EDOT⁺²(6) (1.26 eV) differed notably. The calculated energy gap suggests the larger “conductance” of the EDOT⁺²(6) dication than that of EDOT⁰(6), which is generally known. Similar energy gaps calculated for the dication EDOT⁺²(6) and EDOT⁺²(6):SS⁻²(2) indicate that the dication state of EDOT is most likely preserved, even in the presence of SS⁻²(2). On the other hand, the dication state of EDOT⁺²(6) owing to the presence of SS⁻²(2) can be turned off by the protonation of the SO₃⁻ group, as can be inferred from the increase in the HOMO–LUMO gap for EDOT⁰(6):SS⁰(2) (2.46 eV). We wish to underline that the energies were calculated for molecular models in a vacuum. No remarks can be made as regards the solid state problem due to the lack of information about the geometry of the multimolecular (crystalline) structure. At the molecular level, the interaction of the dipolar structures of the molten salt ([EMIM]⁺[CF₃SO₃]⁻) and EDOT⁺²(6):SS⁻²(2) results in a wider HOMO–LUMO gap and in a decrease in the DOS for the HOMO in EDOT⁺²(6):SS⁻²(2). Concerning PEDOT:PSS, we detected a decrease in the oxidation level. Generally, these effects are not strong, even with respect to the high dipole moment of [EMIM]⁺[CF₃SO₃]⁻ (here, 10.8 D).

Fig. 9 Calculated DOS as a function of orbital energy and graph of frontier orbital HOMO and LUMO energies. Total DOS (blue lines) of (a) EDOT⁺²(6):SS⁻²(2) and (b) EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻). Contributions of individual components: EDOT⁺²(6) (black lines), SS⁻²(2) (red lines), and EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻) (green lines). (c) Comparison of total DOS for EDOT⁺²(6):SS⁻²(2) (black line) and EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻) (red line). (d) Graph of the orbital energies of EDOT⁰(6), EDOT⁺²(6):SS⁻²(2), and EDOT⁺²(6):SS⁻²(2)–2([EMIM]⁺[CF₃SO₃]⁻). Dashed lines indicate the position of the midpoint of HOMO–LUMO gaps.

Table 1 Calculated total charge (in elementary charge, e), the orbital energies of the HOMO and LUMO (in eV), and the HOMO–LUMO gaps (H–L gap, in eV) of the systems under investigation

System	Charge (e)	HOMO (eV)	LUMO (eV)	H–L gap (eV)
SS^0(2)	0	−7.31	−1.39	5.92
SS^−2(2)	−2	−0.39	4.60	4.99
EDOT^0(6)	0	−3.92	−1.47	2.45
EDOT^+2(6)	2	−9.25	−7.99	1.26
EDOT^+2(6):SS^−2(2)	0	−5.14	−3.93	1.21
EDOT^0(6):SS^0(2)	0	−4.30	−1.84	2.46
EDOT^+2(6):SS^−2(2)–2([EMIM]^+[CF3SO3]^−)	0	−5.40	−4.08	1.32

---

5 Conclusions

In this paper, we present the results of studies concerning the interaction of the conductive polymer poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) with the room temperature solvent free ionic liquid (SF-IL) 1-ethyl-3-methylimidazolium trifluoromethanesulfonate ([EMIM]⁺[CF₃SO₃]⁻). The experiments were based on Raman spectroscopy. The obtained Raman spectra presented a complicated, though conventional, structure, including a strong band at 1436 cm⁻¹, assigned to symmetric C_α=C_β stretching vibrations within the five-membered ring of PEDOT, and a shoulder band at 1372 cm⁻¹, assigned to C_β–C_β stretching vibrations, both bands being sensitive to polymer oxidation. The band for PEDOT:PSS at 1436 cm⁻¹ increased in intensity and its maximum was shifted to 1422 cm⁻¹ in the presence of dipoles of the SF-IL. According to literature data (bulk electrochemical oxidation), this red shift corresponds to a decrease in the ratio of oxidized to neutral structures in the PEDOT chain. Concerning the band at 1372 cm⁻¹, during the reduction process its position remained unchanged but its intensity increased. A similar shift in the band was observed when a thin film of SF-IL was applied to the surface of the PEDOT:PSS layer. These processes suggest that in the vicinity of the dipolar field the oxidation level of PEDOT:PSS decreases. This idea was supported by quantum chemical calculations for the system 3,4-ethylenedioxythiophene hexamer in the dication EDOT⁺²(6) state and the styrenesulfonate dimer in the dianion SS⁻²(2) state. B3LYP DFT calculations confirmed the shifts of the spectral bands. The HOMO–LUMO gap increased, cf. the calculated value of 1.21 eV for EDOT⁺²(6):SS⁻²(2) and 1.32 eV in the presence of [EMIM]⁺[CF₃SO₃]⁻ dipoles. At the same time the DOS at the HOMO level decreases. These facts suggest that the “conductance” of PEDOT:PSS decreases in the vicinity of dipolar species. The effect at the molecular level is not strong, even in the case of high dipole moments (here, 10.8 D for [EMIM]⁺[CF₃SO₃]⁻).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the GACR under the project 20-03913S Organic gas sensors – novel structures, electrical parameters, properties and operation and under the project 18-14990S. The authors thank Prof. J. Sworakowski for his valuable comments.

References

1. G. Tarabella, F. Mahvash Mohammadi, N. Coppedè, F. Barbero, S. Iannotta, C. Santato and F. Cicoira, New opportunities for organic electronics and bioelectronics: ions in action, Chem. Sci., 2013, 4, 1395.
2. P. C. Hütter, A. Fian, K. Gatterer and B. Stadlober, Efficiency of the Switching Process in Organic Electrochemical Transistors, ACS Appl. Mater. Interfaces, 2016, 8, 14071–14076.
3. T. Amemiya, K. Hashimoto and A. Fujishima, Frequency-resolved faradaic processes in polypyrrole films observed by electromodulation techniques: electrochemical impedance and color impedance spectroscopies, J. Phys. Chem., 1993, 97, 4187–4191.
4. M. J. Panzer, C. R. Newman and C. D. Frisbie, Low-voltage operation of a pentacene field-effect transistor with a polymer electrolyte gate dielectric, Appl. Phys. Lett., 2005, 86, 103503.
5. M. J. Panzer and C. D. Frisbie, Exploiting Ionic Coupling in Electronic Devices: Electrolyte-Gated Organic Field-Effect Transistors, Adv. Mater., 2008, 20, 3177–3180.
6. J. Sayago, X. Meng, F. Quenneville, S. Liang, É. Bourbeau, F. Soavi, F. Cicoira and C. Santato, Electrolyte-gated polymer thin film transistors making use of ionic liquids and ionic liquid-solvent mixtures, J. Appl. Phys., 2015, 117, 112809.
7. A. Ispas, R. Peipmann, A. Bund and I. Efimov, On the p-doping of PEDOT layers in various ionic liquids studied by EQCM and acoustic impedance, Electrochim. Acta, 2009, 54, 4668–4675.
8. M. Döbbelin, R. Marcilla, M. Salsamendi, C. Pozo-Gonzalo, P. M. Carrasco, J. A. Pomposo and D. Mecerreyes, Influence of Ionic Liquids on the Electrical Conductivity and Morphology of PEDOT:PSS Films, Chem. Mater., 2007, 19, 2147–2149.
9. A. Mazaheripour, S. Majumdar, D. Hanemann-Rawlings, E. M. Thomas, C. McGuiness, L. D’Alencon, M. L. Chabinyc and R. A. Segalman, Tailoring the Seebeck Coefficient of PEDOT:PSS by Controlling Ion Stoichiometry in Ionic Liquid Additives, Chem. Mater., 2018, 30, 4816–4822.
10. T. J. Quill, G. LeCroy, A. Melianas, D. Rawlings, Q. Thiburce, R. Sheelamanthula, C. Cheng, Y. Tuchman, S. T. Keene, I. McCulloch, R. A. Segalman, M. L. Chabinyc and A. Salleo, Ion Pair Uptake in Ion Gel Devices Based on Organic Mixed Ionic–Electronic Conductors, Adv. Funct. Mater., 2021, 2104301, 1–10.
11. P. Kuberský, J. Altšmíd, A. Hamáček, S. Nešpůrek and O. Zmeškal, An Electrochemical NO₂ Sensor Based on Ionic Liquid: Influence of the Morphology of the Polymer Electrolyte on Sensor Sensitivity, Sensors, 2015, 15, 28421–28434.
12. M. Hamedi, L. Herlogsson, X. Crispin, R. Morcilla, M. Berggren and O. Inganös, Fiber-embedded electrolyte-gated field-effect transistors for e-Textiles, Adv. Mater., 2009, 21, 573–577.
13. D. Rawlings, E. M. Thomas, R. A. Segalman and M. L. Chabinyc, Controlling the Doping Mechanism in Poly(3-hexylthiophene) Thin-Film Transistors with Polymeric Ionic Liquid Dielectrics, Chem. Mater., 2019, 31, 8820–8829.
14. A. Giovannitti, D. T. Sbircea, S. Inal, C. B. Nielsen, E. Bandiello, D. A. Hanifi, M. Sessolo, G. G. Malliaras, I. McCulloch and J. Rivnay, Controlling the mode of operation of organic transistors through side-chain engineering, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12017–12022.
15. M. Lazzari, M. Mastragostino and F. Soavi, Capacitance response of carbons in solvent-free ionic liquid electrolytes, Electrochem. Commun., 2007, 9, 1567–1572.
16. V. Lockett, R. Sedev, J. Ralston, M. Horne and T. Rodopoulos, Differential Capacitance of the Electrical Double Layer in Imidazolium-Based Ionic Liquids: Influence of Potential, Cation Size, and Temperature, J. Phys. Chem. C, 2008, 112, 7486–7495.
17. M. M. Islam, M. T. Alam, T. Okajima and T. Ohsaka, Electrical Double Layer Structure in Ionic Liquids: An Understanding of the Unusual Capacitance−Potential Curve at a Nonmetallic Electrode, J. Phys. Chem. C, 2009, 113, 3386–3389.
18. S. Baldelli, Surface Structure at the Ionic Liquid−Electrified Metal Interface, Acc. Chem. Res., 2008, 41, 421–431.
19. A. A. Kornyshev, Double-Layer in Ionic Liquids: Paradigm Change?, J. Phys. Chem. B, 2007, 111, 5545–5557.
20. A. Dieckmann, H. Bässler and P. M. Borsenberger, An assessment of the role of dipoles on the density-of-states function of disordered molecular solids, J. Chem. Phys., 1993, 99, 8136–8141.
21. R. H. Young and J. J. Fitzgerald, Effect of polar additives on charge transport in a molecularly doped polymer: Evaluation of disorder models, J. Chem. Phys., 1995, 102, 9380–9391.
22. S. Nešpůrek, J. Sworakowski and A. Kadashchuk, The influence of dipolar species on charge carrier transport in a linear polysilicon, IEEE Trans. Dielectr. Electr. Insul., 2001, 8, 432–441.
23. S. Nešpůrek, H. Valerián, A. Eckhardt, V. Herden and W. Schnabel, Charge carrier transport in poly (methylphenyl silyene): The effect of additives, Polym. Adv. Technol., 2001, 12, 306–318.
24. J. Sworakowski, Current-voltage characteristics in organic field-effect transistors. Effect of interface dipoles, Chem. Phys., 2015, 456, 106–110.
25. E. I. Izgorodina, M. Forsyth and D. R. MacFarlane, On the components of the dielectric constants of ionic liquids: Ionic polarization?, Phys. Chem. Chem. Phys., 2009, 11, 2452–2458.
26. C. E. R. Prado, M. G. Del Pópolo, T. G. A. Youngs, J. Kohanoff and R. M. Lynden-Bell, Molecular electrostatic properties of ions in an ionic liquid, Mol. Phys., 2006, 104, 2477–2483.
27. E. A. Turner, C. C. Pye and R. D. Singer, Use of ab Initio Calculations toward the Rational Design of Room Temperature Ionic Liquids, J. Phys. Chem. A, 2003, 107, 2277–2288.
28. Y. Umebayashi, T. Fujimori, T. Sukizaki, M. Asada, K. Fujii, R. Kanzaki and S. Ishiguro, Evidence of Conformational Equilibrium of 1-Ethyl-3-methylimidazolium in Its Ionic Liquid Salts: Raman Spectroscopic Study and Quantum Chemical Calculations, J. Phys. Chem. A, 2005, 109, 8976–8982.
29. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
30. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
31. R. Gangopadhyay, B. Das and M. R. Molla, How does PEDOT combine with PSS? Insights from structural studies, RSC Adv., 2014, 4, 43912–43920.
32. R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724–728.
33. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements, J. Chem. Phys., 1982, 77, 3654–3665.
34. M. S. Gordon, J. S. Binkley, J. A. Pople, I. W. J. Pietro and W. J. Hehre, Self-consistent Molecular-Orbital Methods. 22. Small Split-Valence Basis Sets for Second-Row Elements, J. Am. Chem. Soc., 1982, 2657, 2797–2803.
35. P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222.
36. W. J. Hehre, R. Ditchfield and J. A. Pople, Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56, 2257–2261.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheesemann, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, S. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, P. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomenry Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09 Computer program, 2016.
38. N. M. O’boyle, A. L. Tenderholt and K. M. Langner, cclib: A library for package-independent computational chemistry algorithms, J. Comput. Chem., 2008, 29, 839–845.
39. J. Tomasi, B. Mennucci and R. Cammi, Quantum mechanical continuum solvation models, Chem. Rev., 2005, 105, 2999–3093.
40. M. M. Huang, Y. Jiang, P. Sasisanker, G. W. Driver and H. Weingärtner, Static relative dielectric permittivities of ionic liquids at 25 °C, J. Chem. Eng. Data, 2011, 56, 1494–1499.
41. J. Dong and G. Portale, Role of the Processing Solvent on the Electrical Conductivity of PEDOT:PSS, Adv. Mater. Interfaces, 2020, 7, 2000641.
42. E. R. Talaty, S. Raja, V. J. Storhaug, A. Dölle and W. R. Carper, Raman and Infrared Spectra and ab Initio Calculations of C2-4MIM Imidazolium Hexafluorophosphate Ionic Liquids, J. Phys. Chem. B, 2004, 108, 13177–13184.
43. W. W. Chiu, J. Travaš-Sejdić, R. P. Cooney and G. A. Bowmaker, Studies of dopant effects in poly(3,4-ethylenedioxythiophene) using Raman spectroscopy, J. Raman Spectrosc., 2006, 37, 1354–1361.
44. S. Garreau, G. Louarn, J. P. Buisson, G. Froyer and S. Lefrant, In Situ Spectroelectrochemical Raman Studies of Poly(3,4-ethylenedioxythiophene) (PEDT), Macromolecules, 1999, 32, 6807–6812.
45. M. Łapkowski and A. Proń, Electrochemical oxidation of poly(3,4-ethylenedioxythiophene) – ‘in situ’ conductivity and spectroscopic investigations, Synth. Met., 2000, 110, 79–83.
46. J. E. McCarthy, C. A. Hanley, L. J. Brennan, V. G. Lambertini and Y. K. Gun’Ko, Fabrication of highly transparent and conducting PEDOT:PSS films using a formic acid treatment, J. Mater. Chem. C, 2014, 2, 764–770.
47. Y.-K. Han, M.-Y. Chang, H.-Y. Li, K.-S. Ho, T.-H. Hsieh and P.-C. Huang, In situ synthesis and deposition of conducting PEDOT:PSS nanospheres on ITO-free flexible substrates, Mater. Lett., 2014, 117, 146–149.
48. J. Casado, V. Hernández, F. J. Ramírez and J. T. L. Navarrete, Ab initio HF and DFT calculations of geometric structures and vibrational spectra of electrically conducting doped oligothiophenes, THEOCHEM, 1999, 463, 211–216.
49. A. Lenz, H. Kariis, A. Pohl, P. Persson and L. Ojamäe, The electronic structure and reflectivity of PEDOT:PSS from density functional theory, Chem. Phys., 2011, 384, 44–51.
50. H. Lodish, A. Berk, C. A. Kaiser, M. Krieger, M. P. Scott, A. Bretscher, H. Ploegh and P. Matsudaira, Molecular Cell Biology, Palgrave Macmillan, 2008.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03899k

---