Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhanced sampling without borders: on global biasing functions and how to reweight them
Anna S.
Kamenik
 ,
Stephanie M.
Linker
,
Stephanie M.
Linker
 and
Sereina
Riniker
and
Sereina
Riniker
 *
*
Laboratory of Physical Chemistry, ETH Zurich, Vladimir-Prelog-Weg 2, 8093 Zurich, Switzerland. E-mail: sriniker@ethz.ch
First published on 14th December 2021
Abstract
Molecular dynamics (MD) simulations are a powerful tool to follow the time evolution of biomolecular motions in atomistic resolution. However, the high computational demand of these simulations limits the timescales of motions that can be observed. To resolve this issue, so called enhanced sampling techniques are developed, which extend conventional MD algorithms to speed up the simulation process. Here, we focus on techniques that apply global biasing functions. We provide a broad overview of established enhanced sampling methods and promising new advances. As the ultimate goal is to retrieve unbiased information from biased ensembles, we also discuss benefits and limitations of common reweighting schemes. In addition to concisely summarizing critical assumptions and implications, we highlight the general application opportunities as well as uncertainties of global enhanced sampling.
1 General introduction
Biomolecules in solution constantly fluctuate within an ensemble of conformational states with varying probability.1 Each of these conformational states exhibits (slightly) altered biophysical properties and provides different opportunities for interactions with surrounding molecules.2–5 The dynamic nature of biomolecules is thus essential to both fundamental and applied research, e.g. for drug discovery and lead optimization.1,3,6 However, even after several decades of research in this area, the complexity and longevity of the conformational rearrangements of biomolecules still poses substantial challenges for computational and experimental methods.4,7 The ideal technique would be a “molecular camera”, which records the time evolution of the motion of a single molecule in atomic resolution. Despite massive progress in the field of experimental integrative modeling, the tool that currently comes closest to this ideal of a molecular camera is molecular dynamics (MD) simulations.8,9 The theoretical framework as well as the implementation of MD simulations is built on numerous approximations to reduce the computational costs to a tractable level, which limits the accuracy of the resulting dynamic models.10–12 These approximations can be broadly divided into two categories: (i) inaccuracies in the underlying force field, and (ii) uncertainties due to limited phase-space exploration. Within this review, we will focus on the latter, which is traditionally also referred to as the “sampling problem”.A typical biomolecular system is characterized by a myriad of degrees of freedom, resulting in practically innumerable conformational and configurational states. This complex phase space translates into a free-energy surface that is vast and rugged. MD simulations offer the possibility to explore such free-energy landscapes with a resolution of nanometers and femtoseconds. However, in practice the system often gets trapped in a (local) minimum as high barriers to neighboring configurational states impose slow transition rates. With dedicated state-of-the-art hardware or exa-scale cloud-computing infrastructure, motions on the millisecond timescale can be observed for biomolecular systems of considerable size.13–15 Unfortunately, the general access to such supercomputing systems is limited. An alternative to brute force high-performance computing is to speed up the sampling process using enhanced sampling strategies.
Many different methodologies that fall into the category of enhanced sampling have been developed over the past decades (for previous reviews we refer the reader to ref. 16 and 17). Some of the most popular enhanced sampling strategies are pathway-dependent, meaning they rely on the definition of low-dimensional order parameters, also called reaction coordinates or collective variables (CVs). Methods such as local elevation18 or metadynamics,19 umbrella sampling20,21 or targeted MD22 increase sampling efficiency in a simulation by applying a bias along the selected CV. Consequently, identifying representative CVs is critical to the success of pathway-dependent enhanced sampling techniques, but reducing the complex dynamics of biomolecules to a few interpretable dimensions is far from trivial.23 Substantial research efforts are currently invested in the optimization and automatization of selecting appropriate CVs, e.g. with the aid of machine learning.24–26 Given relevant CVs, pathway-dependent methodologies can perform strikingly well, for example in modelling the activation of voltage-sensing domains of ion channels,27,28 the estimation of ligand koff rates,29 or membrane permeation probability calculations.30,31
Despite these successes, for many interesting biomolecular systems it is not straight-forward to derive a small number of representative observables as CVs. For example, when we simulate cyclic peptides in apolar environments, we usually observe one (or a few) well-defined “closed” structures. These closed conformational states can often be easily represented, e.g., via intramolecular hydrogen bond formation.32,33 However, when we study the same system in a polar environment, defining a unique representation immediately becomes more difficult. The ensembles of cyclic peptides in polar environments are generally much more diverse, and observables such as intramolecular hydrogen bonds or the radius of gyration fail to distinguish the conformational states. Other scenarios, which are challenging for CV-based pathway-dependent methods, include studies with the specific aim of identifying the most flexible domains of a biomolecule,34–36 or of discovering novel cryptic or allosteric binding sites.37–39 Whenever the goal is to explore and compare local flexibility patterns within one biomolecular system, a pathway-dependent bias should be avoided as it inherently steers the results towards the user-defined reaction coordinate.
Fortunately, also pathway-independent enhanced sampling techniques have been developed, which do not require the definition of CVs. Methods following the principles of hyperdynamics40 or parallel tempering41,42 add global biasing energies that act on the entire system simultaneously. Here, we provide an overview of currently available pathway-independent enhanced sampling methods, which we broadly categorize by whether the bias is defined via the potential or kinetic energy function. For each of the methodologies we describe in the following sections promising results that have been reported for various scientific problems. However, each approach also has its limitations. As we summarize benefits and pitfalls, we explain what can and cannot be expected from the different methods. Furthermore, we discuss the general and central challenge of extracting unbiased thermodynamic and kinetic information from biased ensembles. This process, typically referred to as reweighting, is in practice often decisive for the applicability of biasing methods.
2 Turning up the heat: biasing the kinetic energy
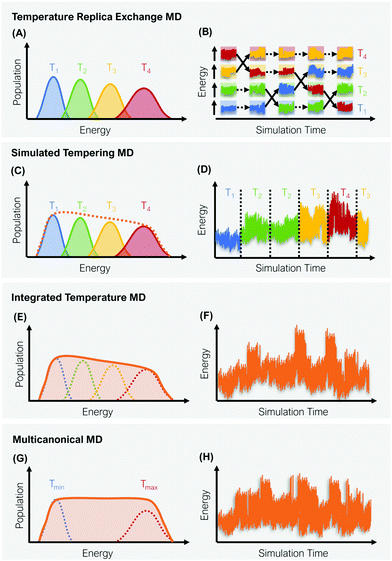
A straight-forward way to increase the velocity of motions in a simulated system is to elevate its temperature, i.e., to introduce a kinetic bias. At higher temperatures, the transition rates between local minima increase, thus a larger phase space can be explored in less computational time. Simulations at room temperature on the other hand ensure thorough sampling within the minima.43,44 The tempering approaches described below follow the same fundamental idea: Simulations at high and low temperatures are combined based on an energetic criterion, which retains the canonical ensemble (Fig. 1). Through this, conformational sampling is achieved more efficiently and more reliably than with conventional – single temperature – MD simulations. The practical implementation of this idea differs, however, greatly between individual enhanced sampling strategies, which we will outline in detail in the following paragraphs.2.1 Temperature replica exchange MD
In temperature replica exchange MD (T-REMD), also referred to as parallel tempering, multiple simultaneous simulations of identical systems are performed at varying temperatures.41,42 Exchanges between neighboring replicas are attempted at defined time intervals and accepted or rejected based on an energetic criterion, which retains the canonical distribution (Fig. 1A and B).45 Typically, this routine is based on a Metropolis criterion, where the exchange probability P(Tk → Tl) depends on the reference temperature of two replicas (Tk, Tl) and their potential energies (Vk, Vl):46, 47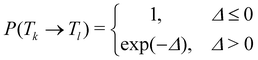 | (1) |
| Δ = (βk − βl)(Vk − Vl), | (2) |
Compared to serial simulated tempering (ST) simulations, T-REMD simulations have been found to converge slower at a higher computational cost,53 although depending on the studied system and simulation setup, T-REMD simulations could theoretically outperform ST simulations in terms of wall time. In practice, the use of T-REMD is notably more popular. This can most likely be attributed to its straight-forward implementation and the fact that no weighting factors need to be optimized.53 Furthermore, T-REMD simulations result in extensive sampling at different temperatures, which can provide valuable information beyond enhanced conformational sampling. Some of the most remarkable studies working with T-REMD include the first study of Sugita and Okomoto on the folding of Met-enkephalin,42 which was followed by numerous works using T-REMD to further elucidate the protein folding problem.54–58 Moreover, T-REMD has greatly aided the interpretation of experimental data from various sources.59–61 T-REMD simulations have also shown promising results in the area of cyclic peptides, generating ensembles that agree well with NMR interproton distances.62 In the study by Wakefield et al.,62 the authors were furthermore able to rationalize the varying binding affinities of the cyclic peptides through conformational pre-organization captured in T-REMD. In a different study, solvent induced conformational changes could be observed for cyclic tetrapeptides using T-REMD.63 Additionally, T-REMD simulations have shown valuable benefits in the parametrization of residue-specific force fields.64
2.2 Simulated tempering
ST simulations, also called serial tempering,44 follow a similar sampling strategy as T-REMD. In ST simulations, temperature switches are also accepted or rejected based on an energetic criterion. The major difference in the ST setup is, however, that only one continuous simulation is performed and the Hamiltonian becomes dependent on the system's reference temperature Ti in this single simulation (Fig. 1C and D).65,66 Let's consider a system where H(r) is the Hamiltonian of configuration r. As we choose a discrete set of temperatures T1 < … < TK, we define a generalized Hamiltonian44 to run the ST simulation:![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (r,k) = βkH(r) − gk, (r,k) = βkH(r) − gk, | (3) |
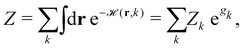 | (4) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) k→l(r)),66 where
k→l(r)),66 whereΔ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) k→l(r) := k→l(r) := ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (r, l) − (r, l) − ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (r, k) = (βl − βk) H(r) − (gl − gk). (r, k) = (βl − βk) H(r) − (gl − gk). | (5) |
Consequently, unbiased statistics of each temperature are collected for ST (as well as for T-REMD simulations), which do not need additional reweighting if analyzed individually. Achieving uniform sampling across the selected set of temperatures critically depends on the choice of the weighting coefficients gk. Optimization of these weights (and the automatization of it) is thus the main challenge in working with ST simulations.67 In practice, this is often a tedious task, which requires numerous short trial simulations as the weights are not known a priori.44,68 Nonetheless, ST simulations have been found to be quite robust across various computing environments as they only require a single computing node. The approach has already facilitated several studies which explore the free-energy landscapes of biomolecules (e.g. BPTI, Villin, Trp-cage, or fast folding WW-domain peptides) at low computational cost with speedups of several orders of magnitude.68,69 Further prominent examples for the application of ST simulations include folding dynamics of multiple mini-proteins in explicit solvent68,69 and Alzheimer related peptide aggregation.67
2.3 Integrated temperature sampling
Integrated temperature sampling (ITS) introduces a sum-over-temperature non-Boltzmann factor, which is essentially a linear combination of Boltzmann distributions at different temperatures.70,71 This means that the simulation is performed on a temperature-biased effective potential Ṽ(r), which is defined in the following manner for each configuration r: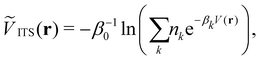 | (6) |
2.4 Multicanonical molecular dynamics
Multicanonical MD (McMD) simulations aim to uniformly sample the potential-energy surface (PES) between high temperature and low temperature regions (Fig. 1G and H).75,76 In other words, the aim is to derive a flat probability distribution function![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) McMD of the potential energy V:75
McMD of the potential energy V:75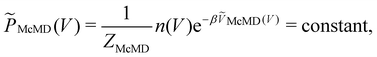 | (7) |
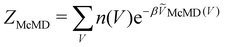 , n(V) is the density of states, and ṼMcMD(V) is the effective potential of the McMD simulation. ṼMcMD(V) is not known a priori and needs to be determined from a preceding conventional MD simulation as a function of its unbiased potential energy, V i.e.,77
, n(V) is the density of states, and ṼMcMD(V) is the effective potential of the McMD simulation. ṼMcMD(V) is not known a priori and needs to be determined from a preceding conventional MD simulation as a function of its unbiased potential energy, V i.e.,77ṼMcMD(V) = V + kBT0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(P(V, T0)), ln(P(V, T0)), | (8) |
3 Flooding valleys and shaving peaks: biasing the potential energy
More common than changing the kinetic component of the Hamiltonian is the introduction of a bias to the potential energy. Different algorithms have been developed, which decrease the barriers between conformational states either by “filling up” the minima or flattening the maxima of the PES. The varying benefits and limitations of the approaches described in the following paragraphs mostly stem from differences in the functional form of the implemented bias.3.1 Hyperdynamics
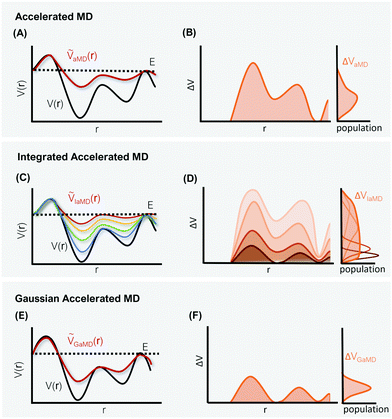
The general idea of distorting the PES with a global biasing potential was first introduced by Arthur Voter in 1997.40 The initial implementation of the approach required the calculation of the Hessian matrix to identify transition states, which inherently limited its applicability to relatively small systems. In further development, Hamelberg et al.84 reformulated the approach for large solvated biomolecular systems using a more simplistic biasing potential. From then on the approach became known as accelerated MD (aMD) simulations.In aMD simulations, a biasing term ΔVaMD(r) is added to the potential energy V(r), whenever it is below a certain threshold E. The effective potential ṼaMD(r) can thus be written as,
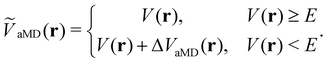 | (9) |
In the initial formulation of aMD, the biasing term ΔVaMD(r) – typically referred to as boosting potential – itself is defined as,
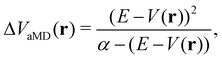 | (10) |
Since their introduction in 2004, aMD simulations have been employed to study a broad range of biomolecules. Some of the most notable applications include the work of Miao et al.,87,88 in which the free-energy surface of G-protein-coupled receptors was elucidated, as well as the investigation from Markwick et al.,89 where aMD predicted motions in protein GB3 on the millisecond timescale in agreement with NMR measurements. Generally, aMD has shown great potential in predicting, complementing, and refining NMR data for numerous biomolecular systems.86,90–94 In particular, aMD simulations have also been shown to produce reliable ensembles of macrocycles and cyclic peptides,94 which can be further utilized for drug optimization.95,96
The central challenge when working with aMD is to select appropriate values for the two acceleration parameters E and α. In double boost aMD,97 the variant of aMD that is probably most-widely used for biomolecules, all particles in the system are biased together with an extra boost on the dihedral terms. For this setup, four parameters need to be defined, i.e. threshold energy and smoothing parameters for both the dihedral terms (Edihed and αdihed) and the total potential energy (Etexttotal and αtexttotal). These values are typically derived from short conventional MD simulations based on empirically derived formulae that take into account the average total energy 〈Vtotal〉, the average dihedral energy 〈Vdihed〉, and the number of atoms natom and number of residues nres, respectively.85,98 To derive the dihedral biasing potential the following equations are commonly applied:
| Edihed = 〈Vdihed〉 + 4·nres | (11) |
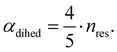 | (12) |
For the calculation of the total energy biasing potential, parameters can be calculated via
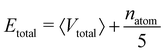 | (13) |
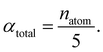 | (14) |
Despite these rules of thumb, choosing appropriate values for the acceleration parameters is far from trivial as the introduced bias should ideally increase sampling speed substantially without flattening the PES too severely. In our experience, it is usually worthwhile to start multiple short aMD simulation with different sets of parameters to assess the impact of the bias on the observed motions. If the PES becomes too distorted, the simulation mostly visits irrelevant high-energy states, which for proteins typically means irreversible unfolding. The latter scenario is probably one of the most dreaded risks of enhanced sampling in general, although seldom discussed in the literature. To circumvent the issue of manually selecting optimal parameters, a combination of aMD and replica exchange simulations (RE-aMD) has been proposed.99,100 Despite the advantages of RE-aMD, this approach has not found a great echo within the community. This might be due to the fact that RE-aMD requires replicas to be simulated in parallel, while one of the main selling points of the original aMD algorithm was that it can be carried out on a single computing node. This was a particularly intriguing feature in the early 2000s, when access to high-performance computing facilities was more scarce. Although the advances in computer power since then have worked in favor of parallel simulation techniques, the full potential of the RE-aMD approach has not yet been exploited, probably also due to several other intriguing advancements of aMD.
One of these more recent adaptations of the methodology is called integrated aMD (IaMD), which combines multiple aMD simulations with varying acceleration parameters into one trajectory by following the principle of ITS (Fig. 2).101–103 Here, the total boosting potential is defined as,
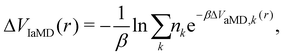 | (15) |
The probably most notable advancement of the aMD approach is termed Gaussian aMD (GaMD).108 The central idea in GaMD simulations is to inherently restrict the boosting potential in such a way that a Gaussian distribution is obtained (Fig. 2),
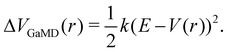 | (16) |
Again, this boosting potential is only applied when the system's potential energy is below a defined threshold energy E (see eqn (9)). In standard aMD simulations, the distribution of the boosting potential is often spread across a large energy range from tens to hundreds of kJ mol−1 in a non-Gaussian manner.109 This can lead to slow convergence as low-energy states are not sufficiently sampled, and additionally introduces severe difficulties for the subsequent reweighting procedure (see Section 4).45 By restricting the distribution of the boosting potential in GaMD, both of these issues can be circumvented. Nevertheless, also GaMD simulations require the definition of several parameters. These can again be optimized in an automated manner based on a short simulation preceding the production run. In this parameter optimization scheme, the threshold energy E is typically set to the system's maximum potential energy (while it can be freely chosen in aMD).108 The average boosting potential as well as its standard deviation have been shown to be lower compared to standard aMD.108 With the aid of GaMD simulations, large biomolecular systems have been studied, such as the CRISPR-Cas9 system,110 allergen-antibody complexes,111 or T-cell receptors binding to peptide-MHC complexes.112 For more details on the methodology and applications of GaMD, we recommend a recent and comprehensive review from the Palermo and Miao groups in ref. 113.
3.2 Hamiltonian replica exchange
Hamiltonian replica exchange MD (H-REMD) in principle also includes T-REMD, as temperature scaling inherently affects the full Hamiltonian.48 However, the term H-REMD is typically used to refer to methods, which alter the Hamiltonian via the potential-energy contribution. The replica exchange mechanism works as described for T-REMD, yet there is more freedom in the form of the implemented bias. This bias can act on selected force-field terms,114–117 or on the full energy function.100,118,119 One prominent example of a H-REMD approach is replica exchange with solute scaling (REST2).120 In the preceding version of this approach (i.e. replica exchange with solute tempering (REST1)), both the temperature and the potential energy vary between replicas.120,121 REST2 simulations, on the other hand, are carried out at a constant temperature T0, while the potential energy of each replica k is scaled via,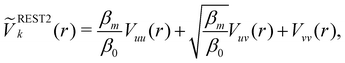 | (17) |
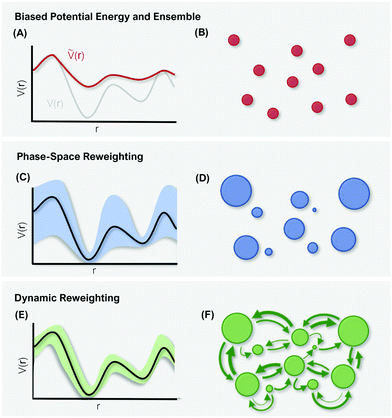
4 Reweighting
The purpose of MD simulations is typically to model the dynamic behavior of a system at experimental or physiological conditions. Yet, the bias introduced with enhanced sampling techniques – be it on the kinetic or potential energy - distorts the free-energy landscape and consequently does not allow direct comparison with experimental data.124 However, as the form and extent of the biasing potential is known at any given simulation step, the unbiased information can be retrieved using reweighting schemes.125, 126Thermodynamic quantities (e.g. free-energy differences or stationary distributions) are usually more easily accessible than kinetic information (e.g. transition rates), which are particularly challenging to recover.127,128 Therefore, different reweighting approaches have been developed that either focus on reconstruction of thermodynamic quantities, or additionally perform reweighting of the systems kinetics. In the following, we will discern between these two incentives as “phase-space reweighting” and “dynamic reweighting”. We are providing a condensed overview of both types of reweighting approaches, for a more detailed discussion we refer the interested reader to dedicated reviews and the original literature.124,127–129
4.1 Phase-space reweighting
Studies that leverage the sampling efficiency of a global biasing potential typically focus on the systems thermodynamics. For methods such as aMD, the most common way to reweight the trajectory data to the unbiased ensemble is to apply a Boltzmann-type reweighting (see the discussion in ref. 84 and 129). The probability of a configuration r on the unbiased PES V(r) is given by,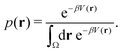 | (18) |
Accordingly, the probability of configuration r on the biased PES Ṽ(r) is,
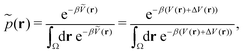 | (19) |
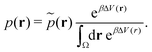 | (20) |
However, the biasing potential distribution is often very broad in practice, which means that the simulation often spends a substantial amount of time sampling high-energy states. As these high-energy states do not significantly contribute to the ensemble average, the reweighting is effectively based on a relatively small number of frames from the free-energy minima.124 Due to the nature of the exponential, the reweighting procedure only works well for comparably narrow distributions of the biasing potential (around 20kBT), and is known to be fairly inaccurate for large systems with broad bias distributions.129 This limitation has been bypassed by approximating the exponential term either by a Maclaurin series or cumulant expansion.129 The latter has been shown to provide the most reliable results, but is only applicable when the biasing potential follows a Gaussian distribution (which is enforced in the gaMD approach). Still, in particular around the transition regions, the biasing potentials are – by design – comparably small and in practice still vanish in the statistical noise (Fig. 3C). Consequently, relative differences in free energy can typically be reweighted to the unbiased ensemble with robust accuracy, while accurate estimations of barrier heights (i.e. kinetics) remain difficult or even inaccessible (Fig. 3).
A widely used approach that has been applied to reweight T-REMD simulations is the weighted histogram analysis method (WHAM).130 WHAM was originally defined for a joint analysis of independent simulations in the canonical ensemble and is similar to the Bennet acceptance ratio.131 However, advancements of the methodology allow now to generally combine multiple biased ensembles to retrieve a systems unbiased thermodynamics, e.g. from T-REMD simulations.132,133 Most notably Chodera et al.133 have introduced an extended WHAM workflow that explicitly considers the time correlation between configurations sampled in each replica. The estimation of the WHAM uncertainty is then corrected by adjusting the true number of independent samples.
The reweighting methods discussed above assume that the input data (i.e. the trajectory frames) are uncorrelated samples. However, in biomolecular systems with typically long correlation times this assumption does not necessarily hold.134 In particular, simulations of complex biomolecules often do not reversibly sample the equilibrium between different states. Even with enhanced sampling, transitions between conformational states may be observed rarely or only in one direction. Consequently, the proper equilibrium is not sampled and a critical assumption of WHAM is violated.
In summary, phase-space reweighting methods are straight-forward to implement and quickly produce an estimate of the thermodynamics of the system. In recent advances made to GaMD (i.e. Ligand-GaMD135 and Peptide GaMD136), also kinetic information was retrieved directly using Kramer's rate theory. The resulting (un)binding kinetics were found to be on the same order of magnitude with the experimental reference. However, to recover both thermodynamics and kinetics more accurately, the more costly dynamic reweighting methods need to be employed (Fig. 3E and F).
4.2 Dynamic reweighting
For unbiased MD simulations, the currently most widely used approach to retrieve robust estimates on a system's kinetics and thermodynamics is to construct a Markov state model (MSM).137–140 The same information can be obtained from biased simulation data using dynamic reweighting methods.141 The main advantage of MSMs is that the condition of local equilibrium within the simulation data is inherently enforced. The entire approach is based on transitions between states, and in theory only motions that show reversible exchanges between states are considered. Consequently, MSMs provide an ideal theoretical framework for dynamic reweighting strategies.In recent years, two main classes of dynamic reweighting methods have emerged, path-based and energy-based. The more recently developed path-based reweighting schemes include Weber–Pande reweighting142 and Girsanov reweighting.143 While their implementation is far from trivial, both have shown reliable results in reweighting dynamics, e.g. from umbrella sampling simulations.142, 143 The main challenge with path-based dynamic reweighting methods is that they are integrator-dependent, and in practice reweighting needs to be performed on-the-fly and not as a post-processing step.128 Energy-based reweighting algorithms, on the other hand, are agnostic to the simulation engine used as they only require information on the bias energy of each analyzed conformation. This less complex handling comes, however, at the price of accuracy – energy-based reweighting does not explicitly account for the possibility that different paths can contribute to the same transition probability. This issue becomes critical whenever the energy profile of the biased PES varies substantially between different pathways. Typically, such a behavior is inherent to pathway-dependent local biasing methodologies and not as pressing with global enhanced sampling techniques. However, in particular in studies on ligand (un)binding or protein folding mechanisms different pathways can lead to substantial deviations in the associated transition rates.104, 144 Hence, path-based reweighting might result in more accurate estimates even when a global bias is applied. Prominent examples for energy-based reweighting schemes include the dynamic histogram analysis method (DHAM),145 the transition-based reweighting analysis method (TRAM),134 and extensions thereof.146
While these dynamic reweighting methods were developed and implemented independently by different groups, we were recently able to demonstrate the relationship between them.128 In this work by Linker et al., we show that the path-independent DHAM equation is a special case of path-dependent dynamic reweighting. Additionally, we show that both dynamic reweighting families can be connected by introducing a path-correction term to the energy-based method. In doing so, the strongly limiting integrator-dependence of path-based reweighting is omitted, while retaining high accuracy and low parameter sensitivity.128
5 Conclusion
Enhanced sampling with global biasing functions has massively advanced the field of biomolecular simulations. The constant optimization and extension of promising algorithms has provided our community with the means to simulate large biomolecular complexes, and has opened the door to study conformational changes in the millisecond range. Nevertheless, a common theme for all methodologies is the challenge of choosing optimal parameters with as little pre-processing effort as possible. First attempts towards automated parameter optimization are already being developed, but will need further efficiency improvements for global enhanced sampling to reach its full potential in the study of large biomolecular systems.As important as the methods for enhanced phase-space exploration are the tools to reweight the biased simulation data to the unbiased canonical ensemble. The development of enhanced sampling techniques goes therefore hand in hand with that of reweighting methods. Over the past decade, multiple algorithms have been proposed that not only recover thermodynamic but also kinetic information from biased simulations. Most of these methods will require further refinement based on “real-world” complex biomolecular systems.
A general question in the application of the methods discussed above is how to validate the insights extracted from the simulations. Direct comparison with experiment is often challenging as techniques such as NMR, cryo-EM, or X-ray crystallography only provide ensemble-averaged data and cannot resolve high-energy states observed in MD simulations. Furthermore, they only provide limited information on a system's kinetics. While NMR (e.g. with relaxation dispersion experiments147,148) can provide dynamic information, the time scale is typically too long (hundreds of microseconds to milliseconds) even for enhanced sampling MD simulations. One promising strategy to generate reference data for the validation of global enhanced sampling techniques may be the combination of experimental data and MD simulations in integrative structural modeling studies.4 Information derived from experiments can be used to augment and guide MD simulations, which in turn provide a structural and dynamic explanation for the measured data.149,150
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support by the Swiss National Science Foundation (Grant Number 200021-178762), the Scholarship Fund of the Swiss Chemical Industry, the German National Academic Foundation PhD scholarship (granted to S. M. L.), and the Austrian Science Fund (Erwin Schrödinger fellowship no. J-4568 granted to A. S. K).References
- K. Henzler-Wildman and D. Kern, Nature, 2007, 450, 964–972 CrossRef CAS PubMed.
- G. Bhabha, J. T. Biel and J. S. Fraser, Acc. Chem. Res., 2015, 48, 423–430 CrossRef CAS PubMed.
- M. Fischer, R. G. Coleman, J. S. Fraser and B. K. Shoichet, Nat. Chem., 2014, 6, 575–583 CrossRef CAS PubMed.
- H. Van Den Bedem and J. S. Fraser, Nat. Methods, 2015, 12, 307–318 CrossRef CAS PubMed.
- G. Wei, W. Xi, R. Nussinov and B. Ma, Chem. Rev., 2016, 116, 6516–6551 CrossRef CAS PubMed.
- W. Pitsawong, V. Buosi, R. Otten, R. V. Agafonov, A. Zorba, N. Kern, S. Kutter, G. Kern, R. A. Pádua, X. Meniche and D. Kern, eLife, 2018, 7, e36656 CrossRef PubMed.
- M. Fischer, B. K. Shoichet and J. S. Fraser, ChemBioChem, 2015, 16, 1560 CrossRef CAS PubMed.
- T. Hansson, C. Oostenbrink and W. van Gunsteren, Curr. Opin. Struct. Biol., 2002, 12, 190–196 CrossRef CAS PubMed.
- W. F. van Gunsteren and H. J. Berendsen, Angew. Chem., Int. Ed. Engl., 1990, 29, 992–1023 CrossRef.
- W. Huang, Z. Lin and W. F. van Gunsteren, J. Chem. Theory Comput., 2011, 7, 1237–1243 CrossRef CAS PubMed.
- S. Riniker, J. Chem. Inf. Model., 2018, 58, 565–578 CrossRef CAS PubMed.
- W. F. van Gunsteren, X. Daura, N. Hansen, A. E. Mark, C. Oostenbrink, S. Riniker and L. J. Smith, Angew. Chem., Int. Ed., 2018, 57, 884–902 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, Science, 2011, 334, 517–520 CrossRef CAS PubMed.
- M. I. Zimmerman, J. R. Porter, M. D. Ward, S. Singh, N. Vithani, A. Meller, U. L. Mallimadugula, C. E. Kuhn, J. H. Borowsky, R. P. Wiewiora, M. F. D. Hurley, A. M. Harbison, C. A. Fogarty, J. E. Coffland, E. Fadda, V. A. Voelz, J. D. Chodera and G. R. Bowman, Nat. Chem, 2021, 13, 651–659 CrossRef CAS PubMed.
- K. J. Kohlhoff, D. Shukla, M. Lawrenz, G. R. Bowman, D. E. Konerding, D. Belov, R. B. Altman and V. S. Pande, Nat. Chem., 2014, 6, 15–21 CrossRef CAS PubMed.
- Y. Miao and J. A. McCammon, Mol. Simul., 2016, 42, 1046–1055 CrossRef CAS PubMed.
- R. C. Bernardi, M. C. Melo and K. Schulten, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 872–877 CrossRef CAS PubMed.
- T. Huber, A. E. Torda and W. F. Van Gunsteren, J. Comput.-Aided Mol. Des., 1994, 8, 695–708 CrossRef CAS PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- G. M. Torrie and J. P. Valleau, Chem. Phys. Lett., 1974, 28, 578–581 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- J. Schlitter, M. Engels, P. Krüger, E. Jacoby and A. Wollmer, Mol. Simul., 1993, 10, 291–308 CrossRef CAS.
- F. Noé and C. Clementi, Curr. Opin. Struct. Biol., 2017, 43, 141–147 CrossRef PubMed.
- J. M. L. Ribeiro, P. Bravo, Y. Wang and P. Tiwary, J. Chem. Phys., 2018, 149, 072301 CrossRef PubMed.
- M. M. Sultan and V. S. Pande, J. Chem. Phys., 2018, 149, 094106 CrossRef PubMed.
- Y. Wang, J. M. L. Ribeiro and P. Tiwary, Nat. Commun., 2019, 10, 3573 CrossRef PubMed.
- L. Delemotte, M. A. Kasimova, M. L. Klein, M. Tarek and V. Carnevale, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 124–129 CrossRef CAS PubMed.
- M. L. Fernández-Quintero, Y. El Ghaleb, P. Tuluc, M. Campiglio, K. R. Liedl and B. E. Flucher, eLife, 2021, 10, e64087 CrossRef PubMed.
- P. Tiwary, V. Limongelli, M. Salvalaglio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E386–E391 CrossRef CAS PubMed.
- M. Sugita, S. Sugiyama, T. Fujie, Y. Yoshikawa, K. Yanagisawa, M. Ohue and Y. Akiyama, J. Chem. Inf. Model., 2021, 61, 3681–3695 CrossRef CAS PubMed.
- M. Badaoui, A. Kells, C. Molteni, C. J. Dickson, V. Hornak and E. Rosta, J. Phys. Chem. B, 2018, 122, 11571–11578 CrossRef CAS PubMed.
- J. Witek, S. Wang, B. Schroeder, R. Lingwood, A. Dounas, H.-J. Roth, M. Fouché, M. Blatter, O. Lemke, B. Keller and S. Riniker, J. Chem. Inf. Model., 2018, 59, 294–308 CrossRef PubMed.
- T. Rezai, B. Yu, G. L. Millhauser, M. P. Jacobson and R. S. Lokey, J. Am. Chem. Soc., 2006, 128, 2510–2511 CrossRef CAS PubMed.
- J. E. Fuchs, S. von Grafenstein, R. G. Huber, H. G. Wallnoefer and K. R. Liedl, Proteins, 2014, 82, 546–555 CrossRef CAS PubMed.
- R. G. Weiß, M.-E. Losfeld, M. Aebi and S. Riniker, J. Phys. Chem. B, 2021, 125, 9467–9479 CrossRef PubMed.
- P. Winter, S. Stubenvoll, S. Scheiblhofer, I. A. Joubert, L. Strasser, C. Briganser, W. T. Soh, F. Hofer, A. S. Kamenik, V. Dietrich, S. Michelini, J. Laimer, P. Lackner, J. Horejs-Hoeck, M. Tollinger, K. R. Liedl, J. Brandstetter, C. G. Huber and R. Weiss, Front. Immunol., 2020, 11, 1824 CrossRef CAS PubMed.
- P. R. Markwick, R. B. Peacock and E. A. Komives, Biophys. J., 2019, 116, 49–56 CrossRef CAS PubMed.
- R. D. Smith and H. A. Carlson, J. Chem. Inf. Model., 2021, 61, 1287–1299 CrossRef CAS PubMed.
- T. Sztain, R. Amaro and J. A. McCammon, J. Chem. Inf. Model., 2021, 61, 3495–3501 CrossRef CAS PubMed.
- A. F. Voter, Phys. Rev. Lett., 1997, 78, 3908 CrossRef CAS.
- U. H. Hansmann, Chem. Phys. Lett., 1997, 281, 140–150 CrossRef CAS.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- D. J. Earl and M. W. Deem, Phys. Chem. Chem. Phys., 2005, 7, 3910–3916 RSC.
- S. Park and V. S. Pande, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 016703 CrossRef PubMed.
- L. Yang, Q. Shao and Y. Q. Gao, J. Chem. Phys., 2009, 130, 124111 CrossRef PubMed.
- T. Okabe, M. Kawata, Y. Okamoto and M. Mikami, Chem. Phys. Lett., 2001, 335, 435–439 CrossRef CAS.
- A. Patriksson and D. van der Spoel, Phys. Chem. Chem. Phys., 2008, 10, 2073–2077 RSC.
- H. Fukunishi, O. Watanabe and S. Takada, J. Chem. Phys., 2002, 116, 9058–9067 CrossRef CAS.
- A. Kone and D. A. Kofke, J. Chem. Phys., 2005, 122, 206101 CrossRef PubMed.
- N. Rathore, M. Chopra and J. J. de Pablo, J. Chem. Phys., 2005, 122, 024111 CrossRef PubMed.
- Temperature generator for REMD-simulations, http://virtualchemistry.org//remd-temperature-generator/index.php, accessed: 03.12.2021.
- R. Qi, G. Wei, B. Ma and R. Nussinov, Methods Mol. Biol., 2018, 1777, 101 CrossRef CAS PubMed.
- C. Zhang and J. Ma, J. Chem. Phys., 2008, 129, 134112 CrossRef PubMed.
- F. Rao and A. Caflisch, J. Chem. Phys., 2003, 119, 4035–4042 CrossRef CAS.
- D. A. Beck, G. W. White and V. Daggett, J. Struct. Biol., 2007, 157, 514–523 CrossRef CAS PubMed.
- P. Jiang, F. Yasar and U. H. Hansmann, J. Chem. Theory Comput., 2013, 9, 3816–3825 CrossRef CAS PubMed.
- F. Jiang and Y.-D. Wu, J. Am. Chem. Soc., 2014, 136, 9536–9539 CrossRef CAS PubMed.
- K. Jain, O. Ghribi and J. Delhommelle, J. Chem. Inf. Model., 2020, 61, 432–443 CrossRef PubMed.
- J. Chen, H.-S. Won, W. Im, H. J. Dyson and C. L. Brooks, J. Biomol. NMR, 2005, 31, 59–64 CrossRef PubMed.
- S. Gnanakaran, R. M. Hochstrasser and A. E. Garca, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9229–9234 CrossRef CAS PubMed.
- G. S. Jas and K. Kuczera, Biophys. J., 2004, 87, 3786–3798 CrossRef CAS PubMed.
- A. E. Wakefield, W. M. Wuest and V. A. Voelz, J. Chem. Inf. Model., 2015, 55, 806–813 CrossRef CAS PubMed.
- C. Merten, F. Li, K. Bravo-Rodriguez, E. Sanchez-Garcia, Y. Xu and W. Sander, Phys. Chem. Chem. Phys., 2014, 16, 5627–5633 RSC.
- H. Geng, F. Jiang and Y.-D. Wu, J. Phys. Chem. Lett., 2016, 7, 1805–1810 CrossRef CAS PubMed.
- E. Marinari and G. Parisi, Europhys. Lett., 1992, 19, 451 CrossRef CAS.
- E. Rosta and G. Hummer, J. Chem. Phys., 2010, 132, 034102 CrossRef PubMed.
- P. H. Nguyen, Y. Okamoto and P. Derreumaux, J. Chem. Phys., 2013, 138, 061102 CrossRef PubMed.
- T. Zhang, P. H. Nguyen, J. Nasica-Labouze, Y. Mu and P. Derreumaux, J. Phys. Chem. B, 2015, 119, 6941–6951 CrossRef CAS PubMed.
- A. C. Pan, T. M. Weinreich, S. Piana and D. E. Shaw, J. Chem. Theory Comput., 2016, 12, 1360–1367 CrossRef CAS PubMed.
- Q. Shao, J. Shi and W. Zhu, J. Chem. Theory Comput., 2017, 13, 1229–1243 CrossRef CAS PubMed.
- Y. I. Yang, Q. Shao, J. Zhang, L. Yang and Y. Q. Gao, J. Chem. Phys., 2019, 151, 070902 CrossRef PubMed.
- Y. Q. Gao, J. Chem. Phys., 2008, 128, 064105 CrossRef PubMed.
- C. D. Christ and W. F. van Gunsteren, J. Chem. Phys., 2007, 126, 184110 CrossRef PubMed.
- Q. Shao, J. Phys. Chem. B, 2014, 118, 5891–5900 CrossRef CAS PubMed.
- N. Nakajima, H. Nakamura and A. Kidera, J. Phys. Chem. B, 1997, 101, 817–824 CrossRef CAS.
- S. Ono, M. R. Naylor, C. E. Townsend, C. Okumura, O. Okada and R. S. Lokey, J. Chem. Inf. Model., 2019, 59, 2952–2963 CrossRef CAS PubMed.
- J. Higo, J. Ikebe, N. Kamiya and H. Nakamura, Biophys. Rev., 2012, 4, 27–44 CrossRef CAS PubMed.
- J. Higo, Y. Nishimura and H. Nakamura, J. Am. Chem. Soc., 2011, 133, 10448–10458 CrossRef CAS PubMed.
- B. A. Berg and T. Neuhaus, Phys. Rev. Lett., 1992, 68, 9 CrossRef PubMed.
- G.-J. Bekker, I. Fukuda, J. Higo, Y. Fukunishi and N. Kamiya, Sci. Rep., 2021, 11, 5046 CrossRef CAS PubMed.
- H. Shirai, N. Nakajima, J. Higo, A. Kidera and H. Nakamura, J. Mol. Biol., 1998, 278, 481–496 CrossRef CAS PubMed.
- G.-J. Bekker, I. Fukuda, J. Higo and N. Kamiya, Sci. Rep., 2020, 10, 1406 CrossRef CAS PubMed.
- S. Ono, M. R. Naylor, C. E. Townsend, C. Okumura, O. Okada, H.-W. Lee and R. S. Lokey, J. Chem. Inf. Model., 2021, 61, 5601–5613 CrossRef CAS PubMed.
- D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef CAS PubMed.
- L. C. Pierce, R. Salomon-Ferrer, C. Augusto, F. de Oliveira, J. A. McCammon and R. C. Walker, J. Chem. Theory Comput., 2012, 8, 2997–3002 CrossRef CAS PubMed.
- A. S. Kamenik, U. Kahler, J. E. Fuchs and K. R. Liedl, J. Chem. Theory Comput., 2016, 12, 3449–3455 CrossRef CAS PubMed.
- Y. Miao, S. E. Nichols, P. M. Gasper, V. T. Metzger and J. A. McCammon, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10982–10987 CrossRef CAS PubMed.
- Y. Miao, S. E. Nichols and J. A. McCammon, Phys. Chem. Chem. Phys., 2014, 16, 6398–6406 RSC.
- P. R. Markwick, G. Bouvignies and M. Blackledge, J. Am. Chem. Soc., 2007, 129, 4724–4730 CrossRef CAS PubMed.
- P. R. Markwick and J. A. McCammon, Phys. Chem. Chem. Phys., 2011, 13, 20053–20065 RSC.
- D. Bucher, B. J. Grant, P. R. Markwick and J. A. McCammon, PLoS Comput. Biol., 2011, 7, e1002034 CrossRef CAS PubMed.
- B. Fuglestad, P. M. Gasper, M. Tonelli, J. A. McCammon, P. R. Markwick and E. A. Komives, Biophys. J., 2012, 103, 79–88 CrossRef CAS PubMed.
- P. R. Markwick and M. Nilges, Chem. Phys., 2012, 396, 124–134 CrossRef CAS.
- A. S. Kamenik, U. Lessel, J. E. Fuchs, T. Fox and K. R. Liedl, J. Chem. Inf. Model., 2018, 58, 982–992 CrossRef CAS PubMed.
- H. Engelhardt, D. Boese, M. Petronczki, D. Scharn, G. Bader, A. Baum, A. Bergner, E. Chong, S. Doebel, G. Egger, C. Engelhardt, P. Ettmayer, J. E. Fuchs, T. Gerstberger, N. Gonnella, A. Grimm, E. Grondal, N. Haddad, B. Hopfgartner, R. Kousek, M. Krawiec, M. Kriz, L. Lamarre, J. Leung, M. Mayer, N. D. Patel, B. Peric Simov, J. T. Reeves, R. Schnitzer, A. Schrenk, B. Sharps, F. Solca, H. Stadtmüller, Z. Tan, T. Wunberg, A. Zoephel and D. B. McConnell, J. Med. Chem., 2019, 62, 10272–10293 CrossRef CAS PubMed.
- A. S. Kamenik, J. Kraml, F. Hofer, F. Waibl, P. K. Quoika, U. Kahler, M. Schauperl and K. R. Liedl, J. Chem. Inf. Model., 2020, 60, 3508–3517 CrossRef CAS PubMed.
- D. Hamelberg, C. A. F. de Oliveira and J. A. McCammon, J. Chem. Phys., 2007, 127, 10B614 CrossRef PubMed.
- J. Wereszczynski and J. A. McCammon, in Accelerated Molecular Dynamics in Computational Drug Design, ed. R. Baron, Springer New York, New York, NY, 2012, pp. 515–524 Search PubMed.
- M. Fajer, D. Hamelberg and J. A. McCammon, J. Chem. Theory Comput., 2008, 4, 1565–1569 CrossRef CAS PubMed.
- D. R. Roe, C. Bergonzo and T. E. Cheatham III, J. Phys. Chem. B, 2014, 118, 3543–3552 CrossRef CAS PubMed.
- D. Tworowski, A. V. Feldman and M. G. Safro, J. Mol. Biol., 2005, 350, 866–882 CrossRef CAS PubMed.
- X. Peng, Y. Zhang, Y. Li, Q. Liu, H. Chu, D. Zhang and G. Li, J. Chem. Theory Comput., 2018, 14, 1216–1227 CrossRef CAS PubMed.
- A. Wang, D. Zhang, Y. Li, Z. Zhang and G. Li, J. Phys. Chem. Lett., 2019, 11, 325–332 CrossRef PubMed.
- P. Lan, M. Tan, Y. Zhang, S. Niu, J. Chen, S. Shi, S. Qiu, X. Wang, X. Peng, G. Cai, H. Cheng, J. Wu, G. Li and M. Lei, Science, 2018, 362, eaat6678 CrossRef PubMed.
- P. R. Markwick, L. C. Pierce, D. B. Goodin and J. A. McCammon, J. Phys. Chem. Lett., 2011, 2, 158–164 CrossRef CAS PubMed.
- N. Gao, L. Yang, F. Gao, R. Kurtz, D. West and S. Zhang, J. Phys.: Condens. Matter, 2017, 29, 145201 CrossRef CAS PubMed.
- W. Sinko, C. A. F. de Oliveira, L. C. Pierce and J. A. McCammon, J. Chem. Theory Comput., 2012, 8, 17–23 CrossRef CAS PubMed.
- Y. Miao, V. A. Feher and J. A. McCammon, J. Chem. Theory Comput., 2015, 11, 3584–3595 CrossRef CAS PubMed.
- Y. Miao and J. A. McCammon, Annual Reports in Computational Chemistry, Elsevier, 2017, vol. 13, pp. 231–278 Search PubMed.
- G. Palermo, Y. Miao, R. C. Walker, M. Jinek and J. A. McCammon, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7260–7265 CrossRef CAS PubMed.
- M. L. Fernández-Quintero, J. R. Loeffler, F. Waibl, A. S. Kamenik, F. Hofer and K. R. Liedl, Protein Eng., Des. Sel., 2019, 32, 513–523 CrossRef PubMed.
- L. V. Sibener, R. A. Fernandes, E. M. Kolawole, C. B. Carbone, F. Liu, D. McAffee, M. E. Birnbaum, X. Yang, L. F. Su, W. Yu, S. Dong, M. H. Gee, K. M. Jude, M. M. Davis, J. T. Groves, W. A. Goddard III, J. R. Heath, B. D. Evavold, R. D. Vale and K. C. Garcia, Cell, 2018, 174, 672–687 CrossRef CAS PubMed.
- J. Wang, P. R. Arantes, A. Bhattarai, R. V. Hsu, S. Pawnikar, Y.-M. M. Huang, G. Palermo and Y. Miao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, e1521 Search PubMed.
- W. Kwak and U. H. Hansmann, Phys. Rev. Lett., 2005, 95, 138102 CrossRef PubMed.
- P. Liu, X. Huang, R. Zhou and B. J. Berne, J. Phys. Chem. B, 2006, 110, 19018–19022 CrossRef CAS PubMed.
- R. Affentranger, I. Tavernelli and E. E. Di Iorio, J. Chem. Theory Comput., 2006, 2, 217–228 CrossRef CAS PubMed.
- S. G. Itoh, H. Okumura and Y. Okamoto, J. Chem. Phys., 2010, 132, 134105 CrossRef PubMed.
- A. F. Voter and T. C. Germann, MRS Proc., 1998, 528, 221 CrossRef CAS.
- Y.-M. M. Huang, J. A. McCammon and Y. Miao, J. Chem. Theory Comput., 2018, 14, 1853–1864 CrossRef CAS PubMed.
- L. Wang, R. A. Friesner and B. Berne, J. Phys. Chem. B, 2011, 115, 9431–9438 CrossRef CAS PubMed.
- P. Liu, B. Kim, R. A. Friesner and B. Berne, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13749–13754 CrossRef CAS PubMed.
- J. Witek, B. G. Keller, M. Blatter, A. Meissner, T. Wagner and S. Riniker, J. Chem. Inf. Model., 2016, 56, 1547–1562 CrossRef CAS PubMed.
- J. Witek, M. Mühlbauer, B. G. Keller, M. Blatter, A. Meissner, T. Wagner and S. Riniker, ChemPhysChem, 2017, 18, 3309–3314 CrossRef CAS PubMed.
- T. Shen and D. Hamelberg, J. Chem. Phys., 2008, 129, 034103 CrossRef PubMed.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- A. M. Ferrenberg and R. H. Swendsen, Phys. Rev. Lett., 1989, 63, 1195 CrossRef CAS PubMed.
- S. Kieninger, L. Donati and B. G. Keller, Curr. Opin. Struct. Biol., 2020, 61, 124–131 CrossRef CAS PubMed.
- S. M. Linker, R. G. Weiß and S. Riniker, J. Chem. Phys., 2020, 153, 234106 CrossRef CAS PubMed.
- Y. Miao, W. Sinko, L. Pierce, D. Bucher, R. C. Walker and J. A. McCammon, J. Chem. Theory Comput., 2014, 10, 2677–2689 CrossRef CAS PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- M. R. Shirts and J. D. Chodera, J. Chem. Phys., 2008, 129, 124105 CrossRef PubMed.
- E. Gallicchio, M. Andrec, A. K. Felts and R. M. Levy, J. Phys. Chem. B, 2005, 109, 6722–6731 CrossRef CAS PubMed.
- J. D. Chodera, W. C. Swope, J. W. Pitera, C. Seok and K. A. Dill, J. Chem. Theory Comput., 2007, 3, 26–41 CrossRef CAS PubMed.
- H. Wu, F. Paul, C. Wehmeyer and F. Noé, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E3221–E3230 CrossRef CAS PubMed.
- Y. Miao, A. Bhattarai and J. Wang, J. Chem. Theory Comput., 2020, 16, 5526–5547 CrossRef CAS PubMed.
- J. Wang and Y. Miao, J. Chem. Phys., 2020, 153, 154109 CrossRef CAS PubMed.
- C. Schütte, A. Fischer, W. Huisinga and P. Deuflhard, J. Comp. Physiol., A, 1999, 151, 146–168 Search PubMed.
- W. C. Swope, J. W. Pitera and F. Suits, J. Phys. Chem. B, 2004, 108, 6571–6581 CrossRef CAS.
- J.-H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schütte and F. Noé, J. Chem. Phys., 2011, 134, 174105 CrossRef PubMed.
- J. D. Chodera and F. Noé, Curr. Opin. Struct. Biol., 2014, 25, 135–144 CrossRef CAS PubMed.
- J. D. Chodera, W. C. Swope, F. Noé, J.-H. Prinz, M. R. Shirts and V. S. Pande, J. Chem. Phys., 2011, 134, 06B612 CrossRef PubMed.
- J. K. Weber and V. S. Pande, J. Chem. Theory Comput., 2015, 11, 2412–2420 CrossRef CAS PubMed.
- L. Donati, C. Hartmann and B. G. Keller, J. Chem. Phys., 2017, 146, 244112 CrossRef CAS PubMed.
- N. Plattner and F. Noé, Nat. Commun., 2015, 6, 7653 CrossRef PubMed.
- E. Rosta and G. Hummer, J. Chem. Theory Comput., 2015, 11, 276–285 CrossRef CAS PubMed.
- L. S. Stelzl, A. Kells, E. Rosta and G. Hummer, J. Chem. Theory Comput., 2017, 13, 6328–6342 CrossRef CAS PubMed.
- J. P. Loria, M. Rance and A. G. Palmer, J. Am. Chem. Soc., 1999, 121, 2331–2332 CrossRef CAS.
- M. Akke and A. G. Palmer, J. Am. Chem. Soc., 1996, 118, 911–912 CrossRef CAS.
- S. Olsson, H. Wu, F. Paul, C. Clementi and F. Noé, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8265–8270 CrossRef CAS PubMed.
- S. Bottaro and K. Lindorff-Larsen, Science, 2018, 361, 355–360 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |