Open Access Article
Open Access ArticlePlanar in Brooker's mode and twisted in Reichardt's mode: defying the steric forces in biphenyl types of zwitterionic systems through metameric resonance stabilizations†
Sanyasi
Sitha
 *
*
Department of Chemical Sciences, University of Johannesburg, PO Box 524, Auckland Park, Johannesburg, 2006, South Africa. E-mail: ssitha@uj.ac.za
First published on 29th April 2022
Abstract
To be planar or to be twisted at the bridge junctions in biphenyls or biaryl types of molecular systems depends on two conflicting forces: (1) steric repulsions (destabilizations) and (2) conjugation assisted electron delocalizations (resonance stabilizations). This work reports an unfamiliar kind of behaviour shown by metamers of a zwitterionic biphenyl type of system, where the Reichardt's metamer was found to be in an usual twisted conformation (delicate balance of conflicting forces), but the Brooker's metamer was found to be in a fully planar conformation. Interestingly, at the ωB97xD/aug-cc-pVDZ level, energetically (ΔE) the planar Brooker's metamer was found to be 16.7 kcal mol−1 lower (22.9 kcal mol−1 lower in the CASSCF method) in energy (more stable) than the isoelectronic twisted Reichardt's metamer, and also thermodynamic ΔG values were found to be close to ΔE values for various methods (for example, 15.6 kcal mol−1 in the above case using the ωB97xD method). When the steric repulsions are in their full potentials at the ring junction site, attainment of a conformational planarity by any biaryl type of system has not been reported previously. Without reducing the steric constraints or even without inducing any attractive forces, determining what other factors were responsible for defying the steric forces is the main focus of this investigation. Using the results of quantum mechanical computations of NBO, rotational barriers, and other saddle points (metastable conformations in singlet and triplet surfaces) in the potential energy surfaces, the dominant contribution of the resonance stabilized quinonoid form to the ground state was delineated as the possible reason for this unusual behaviour.
1. Introduction
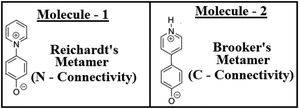
Biphenyl or biaryl types of molecular systems are known to show preferences for twisted conformations in the gas phases, over the fully planar conformations.1–8 While in a sterically constrained planar conformation, both the stabilizing conjugations and destabilizing steric repulsion factors can coexist simultaneously, and at the same time in the twisted conformation, one can see an interplay of adequate balances between the above two conflicting forces.9–12 In the gas phase behaviours, in the competition between the two opposing forces, steric repulsions (twisted forms) are known to always be the winners.13,14 Although these two factors are the main controlling factors, some other factors are also known to have effects on the conformational stabilities for biphenyl types of systems.15–17This work demonstrates a completely different aspect, which is the concept of isomerism (metamerism) on the conformational preferences for the biphenyl type of molecular systems. This work shows how two metamers (metamerism deals with the class of structural or constitutional isomerism, where two or more organic molecules have identical molecular formulas, but are different with respect to the order of connectivity of their atoms) can exhibit different conformations, even if the steric repulsions are prevalent at the bridge junction. To test this conjecture, the structures of two metameric zwitterionic molecules were investigated as shown in Fig. 1, where the steric constraints are prevalent in both cases (leaving no room for steric relaxations as the influential factor for conformational preferences).18–20 Two zwitterionic molecules have pyridinium (+vely charged) as the acceptor and phenolate (−vely charged) as the donor, but they differ with respect to the connectivity around the pyridinium N-atoms.18–20 Here, they are represented as the Reichardt's type metamer21 and Brooker's type metamer.22 Quantum chemical investigations on the structures of these two metameric zwitterion molecules were carried out using various well-known methodologies, and the possible reasons for the exhibition of such differential behaviours are outlined in this contribution.
 | ||
| Fig. 1 Schematic representations of the pyridinium phenolate types of zwitterionic systems as two metamers (molecular formula: C11H9NO). | ||
2. Computational methods
All the computations reported in this work were carried out using the Gaussian 09 program and the computed results were visualized using GaussView.23 Two metamers (Fig. 1) were fully optimized using various quantum mechanical methodologies like, HF,24,25 B3LYP,26,27 MP2,28 CASSCF(8,8),29 CAM-B3LYP30 and ωB97xD.31,32 For all these methods the 6-31G(d,p) basis set was used during the optimization processes. Then finally both the metamers were optimized with a larger basis set, aug-cc-pVDZ with the ωB97xD and MP2 methodologies. For other biaryl systems (non-zwitterionic), optimizations were carried out using the ωB97xD/6-31G(d,p) methodology with the 6-31G(d,p) basis set. During the minimum energy ground state conformational searches for the two metamers, no symmetry restrictions were imposed during the optimizations. From the computed vibrational frequencies, true local minimum with all positive frequencies or no negative eigen values in the Hessian was established for both the metamers (Fig. 1) and also for the other non-zwitterionic biaryl systems. Then for the two metamers, using their ωB97xD/6-31G(d,p) optimized geometries, NBO33–35 studies and rotational barrier estimations (rotational potential energy surfaces) were carried out at the same level of theory. Also, at the ωB97xD/6-31G(d,p) level, some of the other possible metastable (saddle point) conformations of both the molecules were located, in both singlet as well as triplet potential energy surfaces and analyzed. Energetics data were computed using the total energies of the stationary points and Gibbs’ free energy data were from thermochemistry computations.3. Results and discussion
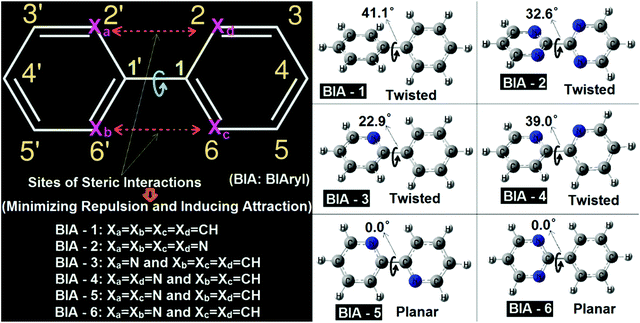
3.1. Conformational preferences in biaryl systems
In the biaryl types of systems, mainly for the biphenyl (either simple or substituted), which is capable of exhibiting conformational preferences, numerous reports exist in the literature.1–17,36–45 It is well known that a simple (unsubstituted) biphenyl is twisted in the ground state (gas phase).1–17,36–45 As discussed in the literature, ground state planar biaryl (gas phase) types of systems are mainly achieved (mostly) by minimizing steric repulsions (and at the same time by inducing simultaneous synchronized attractive interactions) at the bridge junction of the two aromatic rings.1–17,36–45 The types of systems reported in the literature and their corresponding optimized geometries are shown in Fig. 1. As many detailed reports already exist in the literature for these systems, a comprehensive discussion is not presented here. Rather, a qualitative picture of the nature of the interactions present in these molecular systems is discussed here in this contribution. In this work, all the biaryl systems (BIA-1 to 6) were investigated with the optimizations being carried out with the ωB97xD/6-31G(d,p) methodology (Fig. 2).As expected (and also previously reported), BIA-1 was found to be twisted at the bridge junction with a twist angle of 41.1°. A few recent reports related to studies on the nature of interactions existing at the bridge junction of the biphenyl system describe the cause and the twisting effect in great detail (with arguments and rebuttals). While with the Atoms-in-Molecules (AIM) analysis, Matta et al.44 argued for H–H bonding between two ortho-H atoms of the adjacent phenyl rings (possibilities of overlap of van der Waals surfaces46), at the same time with contradicting views Poater et al.43 advocated for the classical steric repulsions as the dominant cause for the twisted structure. Poater et al.43 also mentioned that when they investigated a derivative of biphenyl, where all four ortho-H atoms have been removed completely (like the case of molecule BIA-2), still the equilibrium structure was found to be twisted. In this report also, the equilibrium structure of BIA-2 was also found to be in twisted conformations, with a twist angle of 32.6°. It is interesting to note here that, without the substituents, in BIA-2, inter-ring repulsions are still prevalent, and are due to the repulsions coming from the interactions of the electron clouds of the N-atoms (lone pairs of the N-atoms: lone pair–lone pair or lp–lp repulsions) present at the bridge junctions of the two pyrimidine rings.47 As observed for the BIA-2, one can say that the lp–lp repulsion is lower (due to the compressibilities of the lone pairs: Mazzanti et al.47) compared to the H–H steric repulsions, resulting in a comparatively smaller twist in BIA-2 than in BIA-1.
While the two extreme cases of the biaryls (BIA-1 and BIA-2) showed twisting at the bridge junctions, still with fine tuning of the repulsions and compensating them with favorable attractions, one can easily move from a twisted biaryl to a planar biaryl type of conformation.40,41,48,49 A recent work of Bates et al.,40 described in detail the nature of interactions present in the bipyridine types of systems, and the interplays of twisted vs. planar conformations between the gauche bipyridine and s-trans bipyridine. In this work BIA-4 represents the gauche bipyridine and BIA-5 represents the s-trans bipyridine. The obtained equilibrium conformations were found to be twisted (39.0° twisting) and fully planar (0.0° twisting) respectively for BIA-4 and BIA-5, which agrees well with the reports of Bates et al.40 While, BIA-5 was found to be fully planar due to the stabilizing C–H⋯N interactions (H-atom and lone pair interactions), the twisted conformation of BIA-4 can be attributed to the lp–lp repulsions.47 It is interesting to note here that the observed twisting in BIA-4 was found to be slightly larger than that in BIA-2 and lower than that in BIA-1. This can be easily explained by considering the combined forms of H–H steric and lp–lp steric interactions, resulting in an intermediate twist angle for BIA-4, compared to BIA-1 and BIA-2.
I have also presented two well-known asymmetric biaryls, BIA-3 and BIA-6 (they are asymmetric in the sense that the two aromatic rings in each case are not the same). While BIA-3 is phenyl pyridine, BIA-6 is phenyl pyrimidine. Interestingly, in BIA-3, where the (H–H) steric repulsion is still present on one side of the junction, an induction of CH⋯N attractive interaction reduced the twisting (22.9°) drastically, compared to BIA-1, BIA-2 and BIA-4. On the other hand, the situation in BIA-6 is a case similar to BIA-5 (induction of two C–H⋯N interactions), resulting in a fully planar conformation. The difference between BIA-5 and BIA-6 is that while in the former case the attractive interactions are symmetrically present in both sides of the ring junction, on the other hand in the latter case the attractive interactions are found to be confined to one side of the bridge junction (asymmetric). For details of the interatomic distances and other structural parameters, optimized geometric data for BIA-1 to BIA-6 are provided in the ESI. As these types of systems have been previously discussed in detail in many earlier reports, other structural details are not discussed here.
All the above discussions clearly indicate that a fine balance between the attractive and repulsive forces present in biaryl types of systems is the determining factor for the observed conformational preference. From a search of all previous literature reports, I was not able to find a single case, where all the H–H steric repulsions are still present in the biphenyl types of systems, but the compoundexhibited a planar ground state equilibrium structure. From a thorough look at the numerous examples of biphenyl types of systems reported in the literature, I have observed one thing which is that when the biphenyls are para substituted (like donor–acceptor substituted or push–pull types of biphenyl systems), reduced values of twist angles are reported, compared to the unsubstituted biphenyl types of systems.50,51 Hence, one can say that chemical perturbation induced by donor/acceptor substitutions is capable of reducing the twist angle to some extent. Based on this observation I can conjecture that if large chemical perturbations (for example, charged donor/acceptor systems like zwitterions) can be induced in the biphenyl types of systems, then one can possibly be able to achieve planarity or pseudo planarity types of conformations. This was the motivation with which I have tried to investigate two well-known types of zwitterionic systems reported in the literature.
3.2. Conformational preferences in zwitterionic metamers
As discussed in the previous section for the biaryl types of systems, the main strategy was used to minimize the steric repulsions (and also simultaneously inducing attractive interactions) to achieve the conformation preferences for the planar conformation over the twisted conformation in the ground state (gas phase). But, with the steric interactions being prevalent (or intact), and at the same time without inducing any attractive interactions, achieving a fully planar gas phase ground state conformation can be believed to be impossible, and is also not mentioned anywhere in the literature. Based on my conjecture, I introduced the concept of metamerism to the biphenyl types of (zwitterionic) systems, and investigated the structures of two well-known zwitterionic metamers (as shown in Fig. 1: one is the Reichardt's type zwitterion21 and the other one is the Brooker's type zwitterion22). Also, the choice of the two metamers investigated in this contribution is based on the resonance (π-conjugation) assisted interplay of quinonoid and benzenoid forms as shown in Fig. 3.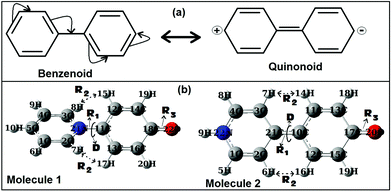 | ||
| Fig. 3 (a) Resonance assisted benzenoid and quinonoid representations of biphenyl. (b) ωB97xD/aug-cc-pVDZ optimized geometries of the two metamers, Molecules 1 and 2 (singlet states). | ||
From a first look at the Reichardt's type metamer and Brooker's type metamer, I can say that while the former resembles more the benzenoid form, the latter resembles more the quinonoid form. In a narrower sense I can say that, if the system prefers the benzenoid form, it can do so by avoiding the resonance to some extent, while on the other hand, if the system prefers a quinonoid form, then resonance is primary. Choices are made based on mere resemblances. Optimized geometries (from the ωB97xD/aug-cc-pVDZ method) of the two metamers are also shown in Fig. 3. It is also worth mentioning here that during the optimizations of the two metamers using various methodologies (HF, B3LYP, CAM-B3LYP, MP2 and ωB97xD with the 6-31G(d,p) basis set) and also with the ωB97xD/aug-cc-pVDZ method, no symmetry restrictions were imposed. Then, important optimized geometric parameters for the Reichardt's metamer and Brooker's metamer, computed with all these methodologies were analyzed and are shown in Table 1.
| Important geometric parameters | Metamers (Molecule #) | HF/6-31G(d,p) | B3LYP/6-31G(d,p) | CAM-B3LYP/6-31G(d,p) | ωB97xD/6-31G(d,p) | ωB97xD/aug-cc-pVDZ | CASSCF(8,8)/6-31G(d,p) | MP2/6-31G(d,p) | MP2/aug-cc-pVDZ |
|---|---|---|---|---|---|---|---|---|---|
| D | 1 | 41.5 | 29.5 | 30.7 | 33.0 | 33.1 | 45.5 | 29.2 | 27.7 |
| 2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 9.1 | 0.0 | |
| R 1 | 1 | 1.424 | 1.402 | 1.399 | 1.401 | 1.406 | 1.436 | 1.381 | 1.388 |
| 2 | 1.375 | 1.406 | 1.392 | 1.393 | 1.397 | 1.367 | 1.404 | 1.418 | |
| R 2 | 1 | 2.318 | 2.107 | 2.115 | 2.159 | 2.160 | 2.401 | 2.104 | 2.075 |
| 2 | 1.993 | 1.974 | 1.964 | 1.972 | 1.969 | 1.989 | 2.003 | 1.975 | |
| R 3 | 1 | 1.219 | 1.242 | 1.235 | 1.235 | 1.239 | 1.221 | 1.248 | 1.254 |
| 2 | 1.207 | 1.239 | 1.230 | 1.230 | 1.232 | 1.205 | 1.247 | 1.254 |
In all the methods, Molecule 1 was found to be in a twisted conformation. Another interesting observation for Molecule 1 was that the HF method predicted a larger value of twist angle (D: Fig. 3) of 41.5° (similar to non-zwitterionic biphenyls), while all other methods predicted it to be around 29–33°. Now for Molecule 2, except for the MP2 methods, all other methods showed it to be in a fully planar conformation. For the MP2 methods a small twist angle of 9.1° was observed, indicating the system to be close to planarity (or slightly twisted). The behavior shown here by the MP2 method was found to be quite unusual, whereas the ωB97xD method, which also accounts for both dispersion and long-range interactions, predicted a fully planar conformation for Molecule 2. To ascertain the claim of planarity for Molecule 2, I tried to optimize both the metamers using the CASSCF method (Complete Active Space Multi-Configuration, MC-SCF method) with the considerations of full configuration interactions (CI) involving (8,8) active space (8-orbitals and 8-electrons active space), using the 6-31G(d,p) basis set. The CASSCF method predicted a twisted conformation for Molecule 1 and a fully planar conformation for Molecule 2, and interestingly for both metamers the obtained geometries were found to be very similar to the HF method (Table 1). Hence, one can’t exclusively say that the HF method overestimates the twist angle. But it is worth noting here that the CASSCF method predicts a fully planar geometry for Molecule 2 like other methods and hence based on this observation we can say that the MP2/6-31G(d,p) method is not able to properly account for the geometries of the two zwitterionic metamers. To eliminate the possible inadequacy in basis set effects on such unusual behavior, I computed both the metamers using MP2/aug-cc-pVDZ. Surprisingly as anticipated the observed abnormality with the 6-31G(d,p) basis set was completely removed and Molecule 2 adopted a fully planar conformation (Table 1). This clearly indicates that for these kinds of zwitterionic systems, where conformational minimum is strongly influenced by internal rotational torsions, when dealing with the MP2 method, one needs to consider the computation with larger basis sets. However, for bigger molecular systems sometimes this will be computationally very expensive.
Though other structural parameters are also important, I have tried to look at the R2 (Fig. 3) values which are related to the H–H steric interactions. The two R2 values in both the molecules were found to be almost the same (showing the symmetrical nature of each zwitterion). As can be seen from Table 1, the inter-hydrogen distances for Molecule 1 in various methodologies were found to be slightly larger than for Molecule 2. This was expected due to the twisted structure of Molecule 1, but the differences were not so large. It is worth mentioning here that such distances were in the range of van der Waals distances for suitable interactions.46 But, surprisingly, Molecule 2 adopted a fully planar confirmation, whereas Molecule 1 adopted a twisted conformation. Hence, to determine the reasons for the possible origin of such a differential structural behavior, I have analyzed a few important properties related to the two metamers.
About the stability, with the 6-31G(d,p) basis set for all the methods, planar Brooker's metamer (Molecule 2) was found to be 24.1 kcal mol−1 (HF), 13.3 kcal mol−1 (B3LYP), 15.2 kcal mol−1 (CAM-B3LYP), 10.2 kcal mol−1 (MP2), 22.9 kcal mol−1 (CASSCF) and 15.1 kcal mol−1 (ωB97xD) more stable than those of Reichardt's metamer (Molecule 1). With the ωB97xD/aug-cc-pVDZ and MP2/aug-cc-pVDZ levels Molecule 2 was found to be 16.7 and 11.7 kcal mol−1 more stable than Molecule 1 respectively. It should be noted here that the energetics data (ΔE) presented here are based on the total energies of the stationary points. Instead of the ΔE values, when the ΔG (thermodynamic Gibbs free energies) were compared to assess the stabilities of both the metamers, similar trends were observed, where Molecule 2 was found to be more stable than Molecule 1 in all methodologies. With the 6-31G(d,p) basis set for all the methods, the ΔG values for the planar Brooker's metamer were found to be 23.9 kcal mol−1 (HF), 13.4 kcal mol−1 (B3LYP), 15.3 kcal mol−1 (CAM-B3LYP), and 15.2 kcal mol−1 (ωB97xD) more stable than those of the Reichardt's metamer. While the ωB97xD/aug-cc-pVDZ level ΔG value indicates that Molecule 2 was 15.6 kcal mol−1 more stable than Molecule 1.
3.3. Assessment of the behaviors
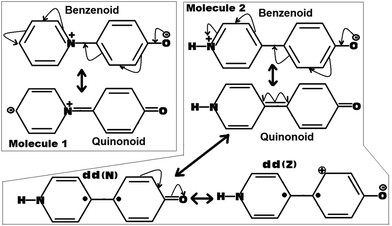 | ||
| Fig. 4 Possible resonance induced canonical structures of the molecules 1 and 2. Here the dd(N) represents the dot dot (Neutral)52,53 and the dd(Z) represents the dot dot (Zwitterionic)52,53 canonical structures related to the quinonoid form. | ||
As can be seen from Fig. 4, for Molecule 1, the obtained quinonoid form is zwitterionic in nature, whereas for Molecule 2, the obtained quinonoid form is fully neutral. As the localized zwitterionic quinonoid form (forced to adopt a planar structure) shown in the case of Molecule 1 can be believed to be highly unstable, it will have a very negligible contribution to the overall stability of the planar quinonoid form. This situation will not be able to force the molecule to adopt a planar ground state conformation by overcoming the prominent forces of steric repulsions present at the bridge junction. Such a thing was clearly observed in the case of Molecule 1, which adopted a twisted ground state conformation.
On the other hand, in the case of Molecule 2, the fully neutral, fully planar quinonoid type of canonical form can be believed to be highly stable. The obtained optimized structure for Molecule 2 was found to be clearly a mixture of both the benzenoid as well as the quinonoid forms (the fully planar quinonoid form would probably have the dominant contribution). One piece of evidence can be drawn from the observed dipole moment of Molecule 2, which was found to be slightly larger than that of Molecule 1 (for example, 13.1 D for Molecule 2 compared to 12.8 D for Molecule 1, in the ωB97xD/6-31G(d,p) method. We also observed similar trends for other methodologies investigated in this work). In an ideal situation, in view of the larger distance between the +ve and −ve charge centers as in the case of Molecule 2 compared to Molecule 1, one can expect a larger shift in the dipole moment value, but the observation was not the same as expected. This is a clear indication that the quinonoid form of Molecule 2 is not only very stable but also significantly contributing to the ground state stability of the molecule. Furthermore, regarding the stability of the quinonoid canonical form of Molecule 2, two more dot dot canonical forms dd(N) and dd(Z) (as shown in Fig. 4) can be expected to add more weightage.52,53 Here the dot dot canonical forms represent their biradical natures, obtained from the homolytic cleavage of the junction double bond (to be noted here in Molecule 1, such a cleavage can lead to more highly unstable diradical types of canonical forms). With this added stability of multiple other canonical forms to the overall stability of the quinonoid type of canonical form of Molecule 2, it was able to make a significant contribution to the ground state stability of Molecule 2. This situation is sufficiently capable of forcing the molecule to adopt a fully planar conformation by defying the counteracting steric forces. Thus I can say, that in the selective conformational preference of Molecules 1 and 2, the quinonoid type of canonical form plays a very significant role. In other words, the stability and relative contributions of the quinonoid form play a vital role in forcing Molecules 1 and 2 to adopt twisted and fully planar conformations respectively.
| NBO | Occupancy | LCAO coefficients | Hybrid | AO% | |
|---|---|---|---|---|---|
| Molecule 1 | σC11–N21 | 1.9824 | C11: 0.5879 | sp2.8 | s(26.29%) p(73.60%) d(0.11%) |
| N21: 0.8089 | sp1.8 | s(35.19%) p(64.79%) d(0.02%) | |||
| σ*C11–N21 | 0.0338 | C11: 0.8089 | sp2.8 | s(26.29%) p(73.60%) d(0.11%) | |
| N21: −0.5879 | sp1.8 | s(35.19%) p(64.79%) d(0.02%) | |||
| Molecule 2 | σC10–C21 | 1.9751 | C10: 0.6998 | sp1.8 | s(35.27%) p(64.70%) d(0.03%) |
| C21: 0.7144 | sp1.6 | s(37.98%) p(61.99%) d(0.03%) | |||
| πC10–C21 | 1.6955 | C10: 0.7573 | p1.0 | s(0.00%) p(99.98%) d(0.02%) | |
| C21: 0.6531 | p1.0 | s(0.00%) p(99.94%) d(0.06%) | |||
| σ*C10–C21 | 0.0238 | C10: 0.7144 | sp1.8 | s(35.27%) p(64.70%) d(0.03%) | |
| C21: −0.6998 | sp1.6 | s(37.98%) p(61.99%) d(0.03%) | |||
| π*C10–C21 | 0.3534 | C10: 0.6531 | p1.0 | s(0.00%) p(99.98%) d(0.02%) | |
| C21: −0.7573 | p1.0 | s(0.00%) p(99.94%) d(0.06%) |
| Donor(i) | Acceptor(j) | E (2) | E(j) − E(i) | F(i,j) | |
|---|---|---|---|---|---|
| Molecule 1 | σC11–N21 | σ*C1–C2 | 1.90 | 1.56 | 0.049 |
| σ*C2–N21 | 3.11 | 1.43 | 0.060 | ||
| σ*C3–C4 | 1.90 | 1.56 | 0.049 | ||
| σ*C3–N21 | 3.11 | 1.43 | 0.060 | ||
| σ*C11–C12 | 1.12 | 1.56 | 0.037 | ||
| σ*C11–C13 | 1.14 | 1.56 | 0.038 | ||
| σ*C12–C14 | 0.92 | 1.67 | 0.035 | ||
| σ*C13–C16 | 0.92 | 1.67 | 0.035 | ||
| Molecule 2 | σC10–C21 | σ*C1–C2 | 1.52 | 1.49 | 0.043 |
| σ*C2–C21 | 3.67 | 1.38 | 0.064 | ||
| σ*C3–C4 | 1.52 | 1.49 | 0.043 | ||
| σ*C3–C21 | 3.67 | 1.38 | 0.064 | ||
| σ*C10–C11 | 3.58 | 1.42 | 0.064 | ||
| σ*C10–C12 | 3.58 | 1.42 | 0.064 | ||
| σ*C11–C13 | 1.28 | 1.56 | 0.040 | ||
| σ*C12–C15 | 1.28 | 1.56 | 0.040 | ||
| πC10–C21 | π*C1–C2 | 15.30 | 0.38 | 0.070 | |
| π*C3–C4 | 15.30 | 0.38 | 0.070 | ||
| π*C10–C21 | 3.29 | 0.40 | 0.033 | ||
| π*C11–C13 | 26.09 | 0.44 | 0.100 | ||
| π*C12–C15 | 26.09 | 0.44 | 0.100 | ||
| π*C10–C21 | π*C11–C13 | 44.57 | 0.04 | 0.077 | |
| π*C12–C15 | 44.57 | 0.04 | 0.077 |
Analysis of the NBO data from Table 2 shows that the central junction bond for Molecule 1 is of purely σ-type (indicating a single bond characteristic), whereas for Molecule 2 it is a combination of both σ- and π-types (a double bond characteristic). Occupancy of the π-bond was found to be 1.6955 (slightly less than double electron occupation) thus indicating a partial double bond in nature, but at the same time, it also indicates a sense of strong delocalization happening through the central aryl–aryl junction bond. Added to this is the almost sp2 hybridization of both the junction C-atoms, and also a substantial partial occupancy (0.3534) of the π*-bond of Molecule 2. As the fully planar conformation of Molecule 2 is the stable structure, hence such a situation clearly indicates that the highly delocalized or the quinonoid form is the dominant form contributing to the ground state conformation of Molecule 2. At the same time, the absence of any π-type of bond for Molecule 1 clearly indicates that the benzenoid form is the dominant form contributing to its twisted conformations. Moreover, it can also be seen that for Molecule 1, the junction C-atom is sp3 hybridized and the N-atom is sp2 (indicating the single bond nature for the junction bond), supporting the dominance of the benzenoid form in its twisted ground state conformation. Then to account for the possible interactions of these central bonds of both the metamers with other bonds, second order perturbation theory analysis of the Fock matrix in the NBO basis was carried out and is shown in Table 3.
Analysis of the data from Table 3 shows that the stabilizing hyperconjugative energies (E(2)) are very large for the π-bond interactions of Molecule 2, whereas for Molecule 1, due to the absence of such interactions, stabilization energies were found to quite low. Very large stabilization energies (44.57 kJ mol−1) were obtained from the interactions of antibonding π*–C10–C21 with the two vicinal antibonding orbitals π*–C11–C13 and π*–C12–C15 (these two are in the donor side aromatic ring of Molecule 2). Also, energetically these interacting orbitals were found to be very close to each other (0.04 a.u.). Other strong stabilizing interactions were found to be the interactions of bonding π–C10–C21 with the antibonding orbitals π*–C11–C13 and π*–C12–C15 (donor side: 26.09 kJ mol−1), and interactions of bonding π–C10–C21 with the vicinal antibonding orbitals π*–C1–C2 and π*–C3–C4 (acceptor side: 15.30 kJ mol−1). All these stabilizing interactions clearly indicate that, not only is there strong delocalization in the case of Molecule 2, but they also significantly contribute to the stabilization of its fully planar quinonoid type of conformation.
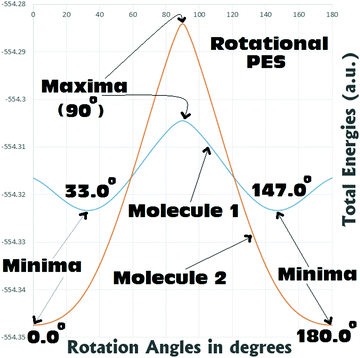
From Fig. 5 it can be seen that for both Molecules 1 and 2, the rotational barriers were found to be at the twist angle of 90.0° (where both the aryl units are mutually orthogonal to each other). For Molecule 1, this rotational barrier height was found to be approximately 11.9 kcal mol−1 above (higher in energy) the most stable twisted conformation (twist angle: 33.0°). At the same time the barrier height of rotation for Molecule 2 was found to be approximately 39.8 kcal/mol above (higher in energy) the most stable fully planar conformation (twist angle: 0.0°). Comparing the barrier heights, it can be seen that in the case of Molecule 2 the barrier to rotation is significantly (around 3–4 times) larger than that of Molecule 1. This gives a clear indication that the fully planar ground state obtained for Molecule 2 can be believed to be thermally quite stable. Whereas Molecule 1 may not be regarded as thermally very stable as it can easily reach the fully planar conformation (4.3 kcal mol−1 above the 33.0° twisted conformation) and the perpendicular conformation (11.9 kcal mol−1 above the 33.0° twisted conformation). Analysis of the rotational PES showed that there is a possibility of the existence of two metastable structures for Molecule 1 (0.0° and 90.0°), and only one for Molecule 2 (90.0°). Hence, a detailed search with full optimizations was carried out to locate these saddle points in the potential energy surfaces of both the metamers, and is discussed in the next section.
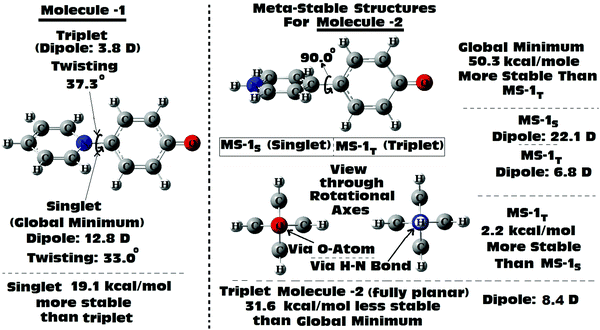
Scan of the complete singlet rotational PES of Molecule 1; the final conformation obtained in all the attempts was the same twisted conformation (twist angle: 33.0°). The situation was exactly the same, when the same was tried in the triplet PES. In the triplet PES all the attempts resulted in slightly different twisted conformations (twist angle: 37.3°) than the singlet global minimum. Also, the triplet minimum was found to be 19.1 kcal mol−1 higher in energy than the singlet global minimum (Fig. 6). The possible fully planar and the mutually perpendicular metastable conformation discussed in the previous section were not observed both in the singlet as well as triplet rotational potential energy surfaces. Now, as the triplet conformation of Molecule 1 was found to be a twisted conformation like the singlet conformation, any contribution from it, will not be able to induce substantial structural (conformational) changes to the ground state of the molecule.
But, in the case of Molecule 2, the complete scan of the singlet and triplet PESs resulted in a few metastable conformations (Fig. 6). For either the singlet or the triplet rotational PES scans with full optimizations, most of them converged to the fully planar singlet and triplet conformations respectively. The fully planar singlet state is the global minimum, whereas the fully planar triplet state was found to be 31.6 kcal mol−1 higher in energy than the global minimum. Other metastable conformations obtained in the potential energy surfaces were the fully (mutually) perpendicular conformations of Molecule 2, both in singlet and triplet surfaces. Interestingly in this structural orientation, the triplet metastable form (MS-1T) was found to be 2.2 kcal mol−1 more stable than the singlet metastable form (MS-1S). Also, MS-1S was found to be 52.5 kcal mol−1 (MS-1T: 50.3 kcal mol−1) higher in energy than the global minimum (singlet). Comparing this with the energy only computations of the rotational barrier (previous section: 39.8 kcal mol−1), the barrier can be imagined to be much larger. Based on the large energy differences for all the metastable conformations obtained for Molecule 2, they can be expected to have little contributions to the overall ground state conformation of it (which was already established from the NBO analysis as a mixed conformation of both benzenoid and quinonoid resonance forms, with the latter having the dominant contributions). Based on the close structural similarities between the singlet and triplet planar conformations of Molecule 2, a triplet planar conformation can be expected to have more contribution than the other metastable conformations. Also, from analysis of the dipole moment of the global minimum for Molecule 2 (13.1 D), the triplet conformations which were found to be showing low dipole moments, can be expected to have relatively more contributions to the ground state of Molecule 2.
4. Conclusions
In this work, detailed computational studies (using various methods) on the structures and conformational preferences of biaryl types of molecules were carried out. The results indicate that for simple biaryl types of systems, the conformational preference for either a twisted or a fully planar conformation is mostly dependent on factors like steric repulsions and conjugation assisted delocalizations. While the dominances of steric factors can result in a twisted type of conformation, on the other hand the dominances of resonance assisted conjugation delocalizations can stabilize a fully planar type of conformation. In this work it has been shown that to achieve the planar conformation through resonance stabilizations, complete eliminations of the H-atoms around the bridge junction may not be helpful. Rather inducing secondary stabilizing assistances from the C–H⋯N (or other hetero atoms) types of interactions, and getting a fine balance between the attractive and repulsive forces, can play vital roles in attaining fully planar types of conformations in biaryl types of molecular systems.Another part of this work, which is vital to this report, is about the conformational preference through metameric induction, which has not been investigated or reported previously. Investigations for two well-known zwitterionic biaryl types of metamers (Brooker's type and Reichardt's type metamers) showed very interesting results. While the Reichardt's type has shown preference for a twisted conformation (twisting at the aryl–aryl junction), at the same time Brooker's type metamer has shown preference for a fully planar conformation in the ground state. This observation was surprising as in both the metamers, the steric repulsion factors were still prevalent at their respective bridge junction sites, and were at their full potentials (as all four H-atoms at the bridge junctions in both the metamers were still intact) to force both the metamers into a twisted type of conformation. In fact, Reichardt's metamer was found to be surrendering the steric force and adopted a twisted conformation. But, Brooker's metamer by defying the steric force adopted a completely planar conformation. Detailed analysis indicates that unlike the cases of non-zwitterionic biaryls, where the secondary stabilizing interactions play vital roles in forcing them to adopt planar conformations, here in the zwitterion systems, the resonance assisted canonical quinonoid structure and its stability play the role of deciding force. In the case of Brooker's metamer, the observed planar conformation is attributed to the induced stability due to the fully neutral quinonoid form and partial contributions from the dot–dot (also other) canonical forms. Computed barriers of rotation, NBO studies and observations of various metastable conformations (in both singlet as well as triplet PESs) also strongly support the proposed conjecture of resonance induced stabilizations. I have discussed that these canonical forms significantly contribute to the ground state of the Brooker's metamer, and thus the mixtures of all these forms were able to induce the required stability that can defy the mighty steric forces. Moreover, due to this added stability, planar Brooker's metamer was found to be lower in energy compared to its isoelectronic metamer, the Reichardt's metamer.
Conflicts of interest
The author declares no competing financial interests.Acknowledgements
The authors would like to thank the University of Johannesburg for providing necessary facilities to carry out this work.References
- F. Grein, J. Phys. Chem. A, 2002, 106, 3823 CrossRef CAS.
- D. H. Barich, R. J. Pugmire, D. M. Grant and R. J. Iuliucci, J. Phys. Chem. A, 2001, 105, 6780 CrossRef CAS.
- S. Arulmozhiraja and T. Fujii, J. Chem. Phys., 2001, 115, 10589 CrossRef CAS.
- S. Tsuzuki, T. Uchimaru, K. Matsumura, M. Mikami and K. Tanabe, J. Chem. Phys., 1999, 110, 2858 CrossRef CAS.
- M. Rubio, M. Merchán and E. Ortí, Theor. Chim. Acta, 1995, 91, 17 CrossRef CAS.
- A. Almenningen, O. Bastiansen, L. Fernholt, B. N. Cyvin, S. J. Cyvin and S. Samdal, J. Mol. Struct., 1985, 128, 59 CrossRef CAS.
- O. Bastiansen and S. Samdal, J. Mol. Struct., 1985, 128, 115 CrossRef CAS.
- S. M.-G. Sanfeliciano and J. M. Schaus, PLoS One, 2018, 13, e0192974 CrossRef PubMed.
- M. P. Johansson and J. Olsen, J. Chem. Theor. Comput., 2008, 4, 1460 CrossRef CAS PubMed.
- R. Laplaza, R. A. Boto, J. Contreras-García and M. M. Montero-Campillo, Phys. Chem. Chem. Phys., 2020, 22, 21251 RSC.
- P. L.-A. Popelier, P. I. Maxwell, J. C.-R. Thacker and I. Alkorta, Theor. Chem. Acc., 2019, 138, 12 Search PubMed.
- B. Landeros-Rivera, V. Jancik, R. Moreno-Esparza, D. M. Otero and J. Hernández-Trujillo, Chem. – Eur. J., 2021, 27, 11912 CrossRef CAS PubMed.
- J. C. Sancho-García and J. Cornil, J. Chem. Theor. Comput., 2005, 1, 581 CrossRef PubMed.
- J. Jia, H.-S. Wu, Z. Chen and Y. Mo, Eur. J. Org. Chem., 2013, 611 CrossRef CAS.
- F. Morini, S. H.-R. Shojaei and M. S. Deleuze, J. Phys. B: Atom. Mol. Opt. Phys., 2014, 47, 225102 CrossRef.
- S. Jenkins, J. R. Maza, T. Xu, D. Jiajun and S. R. Kirk, Int. J. Quantum Chem., 2015, 115, 1678 CrossRef CAS.
- J. I. Wu, I. Fernandez, Y. Mo and P. V.-R. Schleyer, J. Chem. Theor. Comput., 2012, 8, 1280 CrossRef CAS PubMed.
- I. Zharinova, N. Saker Neto, T. C. Owyong, J. M. White and W. W.-H. Wong, Org. Mater., 2021, 03, 103 CrossRef CAS.
- A. Boeglin, A. Barsella, A. Fort, F. Mancois, V. Rodriguez, V. Diemer, H. Chaumeil, A. Defoin, P. Jacques and C. Carree, Chem. Phys. Lett., 2007, 442, 298 CrossRef CAS.
- E. A. Ribeiro and V. G. Machado, J. Brazilian Chem. Soc., 2021, 32, 1972 CAS.
- C. Reichardt, Chem. Rev., 1994, 94, 2319 CrossRef CAS.
- K. Brooker, et al. , J. Am. Chem. Soc., 1951, 73, 5326 CrossRef.
- M. J. Frisch, et al., Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- C. C.-J. Roothaan, Rev. Mod. Phys., 1951, 23, 69 CrossRef CAS.
- J. A. Pople and R. K. Nesbet, J. Chem. Phys., 1954, 22, 571–572 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275 CrossRef CAS.
- N. Yamamoto, T. Vreven, M. A. Robb, M. J. Frisch and H. B. Schlegel, Chem. Phys. Lett., 1996, 250, 373 CrossRef CAS.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1908, 102, 7211 CrossRef.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS.
- O. Potzel and G. Taubmann, Phys. Chem. Chem. Phys., 2013, 15, 20288 RSC.
- L. Zhang, G. H. Peslherbe and H. M. Muchall, Canadian J. Chem., 2010, 88, 1175 CrossRef CAS.
- L. F. Pacios, Struct. Chem., 2007, 18, 785 CrossRef CAS.
- L. F. Pacios and L. Gómez, Chem. Phys. Lett., 2006, 432, 414 CrossRef CAS.
- T. G. Bates, J. H. de Lange and I. Cukrowski, J. Comput. Chem., 2021, 42, e26491 CrossRef PubMed.
- I. Cukrowski, J. H. de Lange, D. M.-E. van Niekerk and T. G. Bates, J. Phys. Chem. A, 2020, 124, 5523 CrossRef CAS PubMed.
- N. A. Murugan, P. C. Jha, S. Yoshonath and S. Ramasesha, J. Phys. Chem. B, 2004, 108, 4178 CrossRef CAS.
- J. Poater, M. Solà and F. M. Bickelhaupt, Chem. – Eur. J., 2006, 12, 2889–2895 CrossRef CAS PubMed.
- C. F. Matta, J. Hernandez-Trujillo, T. H. Tang and R. F.-W. Bader, Chem. – Eur. J., 2003, 9, 1940 CrossRef CAS PubMed.
- J. Hernandez-Trujillo and C. F. Matta, Struct. Chem., 2007, 18, 849 CrossRef CAS.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806 CrossRef CAS PubMed.
- A. Mazzanti, L. Lunazzi, S. Lepri, R. Ruzziconi and M. Schlosser, Eur. J. Org. Chem., 2011, 6725 CrossRef CAS.
- A. Göller and U. W. Grummt, Chem. Phys. Lett., 2000, 321, 399 CrossRef.
- K. W. Dobbs and K. Sohlberg, J. Chem. Theor. Comput., 2006, 2, 1530 CrossRef CAS PubMed.
- D. Pant, N. Darla and S. Sitha, Comput. Theor. Chem., 2022, 113522 CrossRef CAS.
- D. Pant, N. Darla and S. Sitha, Comput. Theor. Chem., 2022, 113583 CrossRef CAS.
- M. Dekhtyar, W. Rettig, A. Rothe, V. Kurdyukov and A. Tolmachev, J. Phys. Chem. A, 2019, 123, 2694 CrossRef CAS PubMed.
- V. Kharlanov and W. Rettig, J. Phys. Chem. A, 2009, 113, 10693 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of all the molecules considered in this work from their ωB97xD/6-31G(d.p) optimizations. Optimized geometries from other methods can be obtained directly from the author through email request. See DOI: https://doi.org/10.1039/d1cp05372h |
| This journal is © the Owner Societies 2022 |