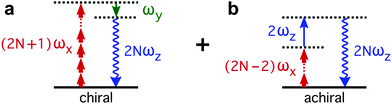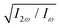Open Access Article
Open Access ArticleNew opportunities for ultrafast and highly enantio-sensitive imaging of chiral nuclear dynamics enabled by synthetic chiral light†
David
Ayuso
 ab
ab
aDepartment of Physics, Imperial College London, SW7 2AZ London, UK. E-mail: d.ayuso@imperial.ac.uk
bMax-Born-Institut, Max-Born-Str. 2A, 12489 Berlin, Germany
First published on 8th April 2022
Abstract
Synthetic chiral light [D. Ayuso et al., Nat. Photon., 2019, 13, 866–871] has opened up new opportunities for ultrafast and highly efficient imaging and control of chiral matter. Here we show that the giant enantio-sensitivity enabled by such light could be exploited to probe chiral nuclear rearrangements during chemical reactions in a highly enantio-sensitive manner. Using a state-of-the-art implementation of real-time time-dependent density functional theory, we explore how the nonlinear response of the prototypical chiral molecule H2O2 changes as a function of its dihedral angle, which defines its handedness. The macroscopic intensity emitted from randomly oriented molecules at even harmonic frequencies (of the fundamental) depends strongly on this nuclear coordinate. Because of the ultrafast nature of such nonlinear interactions, the direct mapping between the dissymmetry factor and the nuclear geometry provides a way to probe chiral nuclear dynamics at their natural time scales. Our work paves the way for ultrafast and highly efficient imaging of enantio-sensitive dynamics in more complex chiral systems, including biologically relevant molecules.
The 21st century has witnessed major advances in the emerging field of attochemistry1, the goal of which is to visualize and to control the motion of electrons and nuclei during chemical reactions. These include the observation of purely electronic motion in atoms,2–5 molecules6–11 and solids,12–16 as well as of highly correlated dynamics of electrons and nuclei in biologically relevant systems17, with unprecedented temporal resolution. However, despite these groundbreaking achievements, distinguishing ultrafast left- and right-handed chiral dynamics is still challenging.18,19
Chirality plays key roles in a number of scientific areas, from particle physics to pharmacy to astronomy. In general, an object is chiral if it cannot be superimposed to its mirror image. Chiral molecules appear in pairs of left- and right-handed enantiomers. Distinguishing them is vital, e.g. because they can present different biological activity.20 To this goal, we can make them interact with another chiral “object”, such as chiral light, and measure their enantio-sensitive response.
Well established optical methods for chiral recognition include optical rotation,21–25 photo-absorption circular dichroism23–37 and Raman optical activity,36–39 which address electronic21–30 and/or vibrational31–39 degrees of freedom. These techniques rely on weak chiro-optical effects that arise beyond the electric-dipole approximation, posing major challenges for time-resolved measurements of ultrafast chiral dynamics.18 Developing highly efficient all-optical approaches capable of tracking ultrafast chiral dynamics without relying on weak magnetic interactions is an important challenge that remains unsolved.
More sophisticated chiro-optical methods bypass the need of relying on non-electric–dipole interactions by analyzing enantio-sensitive vectorial observables.40 In photo-electron circular dichroism (PECD), this vectorial observable is the direction of the photoelectron current upon ionization with circularly polarized light,41–55 where the forward-backward asymmetry can reach values on the order of 10%. Such a strong enantio-sensitivity has enabled the determination of the enantiomeric excess of mixtures with precision below 1%50,51 as well as time-resolved measurements of ultrafast chiral dynamics.52,53 The recent application or tailored two-colour fields to PECD has led to the generation of highly enantio-sensitive tensorial observables.56–58 However, the total intensity signal in PECD (the total number of emitted photoelectrons) is barely enantio-sensitive, and this method requires angularly resolved measurements.
Using microwave radiation, Patterson and co-workers59 pioneered a highly efficient way of enantio-discrimination based on purely electric–dipole interactions. More recent achievements include driving enantio-sensitive population transfers between rotational states using fields with three non-coplanar frequency components,60–62 as well as the development of chiral optical centrifuges63,64 for enantio-separation. These approaches enable efficient control over the rotational degrees of freedom of chiral molecules in a highly enantio-sensitive way. However, achieving full control over chemical reactions using novel light sources – the ultimate goal of attochemistry – requires acting on the electronic degrees of freedom, on the attosecond to femtosecond time scales.
Synthetic chiral light65 enables all-optical imaging of chiral matter and ultrafast chiral dynamics at the level of electrons, with extreme enantio-efficiency. Such light is locally chiral: the tip of the electric-field vector draws a chiral, three-dimensional Lissajous figure in time, in every point in space. The enantio-sensitive response of chiral matter to this light arises within the electric–dipole approximation, and is orders of magnitude stronger than in traditional optical methods. We have recently shown that the application of synthetic chiral light65 to chiral high-harmonic generation can dramatically enhance the enantio-sensitivity of this emerging technique, which so far had relied on the interplay of the chiral molecules with the magnetic component of the light wave.66–70 We have also shown that the polarization of the driving field can be tailored in time and in space to encode the handedness of a chiral medium in the direction of emission of the harmonic light71 or in the polarization of the nonlinear response.72,73
The giant enantio-sensitivity enabled by synthetic chiral light opens up promising opportunities for ultrafast imaging and control of chiral matter. Can we exploit it to monitor, in real time, the nuclear rearrangements occurring during enantio-sensitive chemical reactions, with high enantio-sensitivity? Here we aim to provide (positive) answer this question.
This paper is organized as follows. First, we review the key aspects of synthetic chiral light, introduced in ref. 65. Second, we describe the numerical method that we have applied to compute ultrafast nonlinear dynamics in the prototypical chiral molecule H2O2, which is a convenient model to test our ideas. Third, we show how the enantio-sensitive response of this molecule depends strongly on its nuclear geometry, opening new opportunities for ultrafast imaging of chemical dynamics. We conclude by discussing these opportunities.
1 Synthetic chiral light
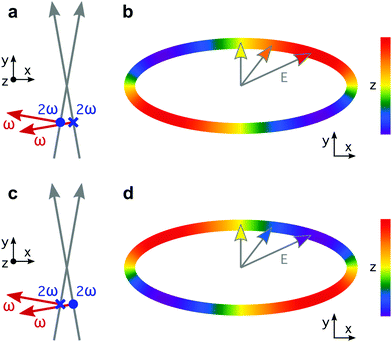
The recipe for creating synthetic chiral light65 has two main ingredients. The first one is related to the multi-colour nature of such fields: we need at least two phase-locked frequencies. Phase locking is key because the handedness of synthetic chiral light is sensitive to the multi-colour phase delays. The second one is a relatively strong longitudinal component, i.e. an electric field component in the propagation direction, which is absent in standard light, but appears naturally in non-collinear configurations or tightly focused beams.74 This longitudinal component allows the Lissajous curve of the field to be three-dimensional and chiral.Here we use the original configuration of synthetic chiral light, introduced in ref. 65. The proposed optical setup is depicted in Fig. 1. It requires two laser beams that propagate non-collinearly in the xy plane, creating small angles ±α with respect to the y direction, with propagation vectors
k1 = k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(α) sin(α)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + k + k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α)ŷ, cos(α)ŷ, | (1) |
k2 = −k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(α) sin(α)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + k + k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α)ŷ, cos(α)ŷ, | (2) |
E(n)ω(r, t) = A(n)ω(r, t) e−ρn2/w2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kn·r − ωt) ên, cos(kn·r − ωt) ên, | (3) |
E(n)2ω(r, t) = A(n)2ω(r, t) e−ρn2/w2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2kn·r − 2ωt − ϕ(n)ω) ẑ, cos(2kn·r − 2ωt − ϕ(n)ω) ẑ, | (4) |
ê1 = cos(α)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) − sin(α)ŷ, − sin(α)ŷ, | (5) |
ê2 = cos(α)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + sin(α)ŷ. + sin(α)ŷ. | (6) |
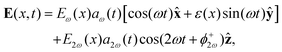 | (7) |
Eω(x) = 2e−x2/w2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α) cos(α)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kαx), cos(kαx), | (8) |
ε(x) = −tan(α)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(kαx), tan(kαx), | (9) |
E2ω(x) = 2e−x2/w2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2kαx + ϕ−2ω), cos(2kαx + ϕ−2ω), | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(α), and the two-colour phase delays that define the field's local handedness ϕ+2ω and ϕ−2ω are related to the two-colour phase delays in the individual beams (eqn 4) by
sin(α), and the two-colour phase delays that define the field's local handedness ϕ+2ω and ϕ−2ω are related to the two-colour phase delays in the individual beams (eqn 4) by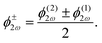 | (11) |
Locally chiral fields can drive strongly enantio-sensitive interactions at the single-molecule-response level, which are controlled and characterized via chiral correlation functions, see ref. 65. However, imprinting this microscopic response into the total macroscopic signal requires an additional condition: the field's handedness needs to be maintained in space, at least to certain extent over the interaction region. That is, synthetic chiral light also needs to be globally chiral. In our setup, this condition is fulfilled if ϕ(2)2ω = ϕ(1)2ω + π, as depicted in Fig. 1a and c. Then, by changing these phase delays synchronously, we can tailor the shape of the chiral Lissajous figure in a way that its handedness is maintained all over the interaction region. In particular, if we change these phase delays by π in both beams (Fig. 1c), we reverse the handedness of the chiral Lissajous figure (Fig. 1d). Synthetic chiral light that is locally and globally chiral enables the highest possible degree of control over the enantio-sensitive response of chiral matter: quenching the response in one molecular enantiomer while enhancing it in its mirror twin.
The proposed experimental setup to create synthetic chiral light with controlled handedness65 contains a nonlinear barium borate crystal which doubles the frequency of the fundamental beam, creating a second harmonic field with orthogonal polarization. It also includes calcite wedges, which allow us to control the two-colour the phase delay in the two beams independently. The target chiral medium could be in the gas phase or in a liquid microjet75, and it would be placed before the focus, as it is common in high harmonic generation experiments to favour phase-matching of the short trajectories.
The enantio-sensitive response of isotropic chiral matter to synthetic chiral light relies on the interference between chiral and achiral contributions to light-induced polarization. The multiphoton pathways describing these interactions in the perturbative regime are depicted in Fig. 2. The chiral contribution (Fig. 2a) involves absorption of 2N + 1 photons from the (x-polarized) strong-field component and emission of 1 photon into the (y-polarized) weak ellipticity component, leading to polarization at frequency 2Nω along z. This pathway is exclusive of chiral media, and the induced polarization is out of phase in media of opposite handedness. The achiral contribution (Fig. 2b) involves absorption of 2N − 2 photons from the strong-field component and absorption of 1 photon from the z-polarized 2ω-field, also leading to polarization at frequency 2Nω along z. As these two pathways lead to polarization at the same frequency and along the same axis, they interfere. This interference can be controlled and quantified via chiral correlation functions, see ref. 65.
2 Modeling the nonlinear response of H2O2 to synthetic chiral light
Hydrogen peroxide constitutes a convenient “toy model” to test the potential of synthetic chiral light as a tool to monitor enantio-sensitive nuclear dynamics in real time. The potential energy curve of the electronic ground state is shown in Fig. 3. It presents a double-well structure, with the two degenerate geometries associated with these wells being molecular enantiomers. Indeed, the molecular geometries with dihedral angles β and 360° − β are mirror twins. However, the energy barrier separating these two wells is small, around 0.5 eV, and thus the two enantiomers coexist in standard conditions. Still, from a computational perspective, the small size of this chiral molecule makes it an ideal candidate to test our ideas.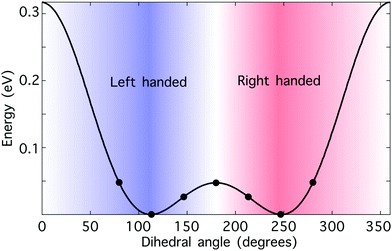 | ||
| Fig. 3 Hydrogen peroxide as a prototypical chiral molecule with reversible handedness. Potential energy curve of the electronic ground state of H2O2 as a function of the dihedral angle β calculated at the B3LYP theory level; the numerical values have been taken from ref. 76. The points indicate the values of the dihedral angle that we have considered in this work. The molecule is achiral if β = 0° or β = 180°, “left-handed” if 0° < β < 180°, and “right-handed” if 180° < β < 360°. The nuclear configurations with dihedral angles β and 360° − β correspond to molecular enantiomers. | ||
We have modelled the interaction of H2O2 with synthetic chiral light using the state-of-the-art implementation of real-time time-dependent density functional theory in Octopus,77–80 as described in the ESI.† To describe the physical situation of randomly oriented molecules, we calculated the time-dependent polarization driven by the field in different molecular orientations. The total polarization results from the coherent addition of the contribution from all possible orientations:
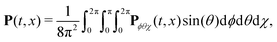 | (12) |
![[d with combining circumflex]](https://www.rsc.org/images/entities/b_char_0064_0302.gif) |Ψ(t)〉. We used the Lebedev quadrature81 of order 11 to integrate over ϕ and θ, using 50 points to sample the two angles. For each orientation, the laser field was defined in the molecular frame in a way that its strong-field component pointed along cos(ϕ)
|Ψ(t)〉. We used the Lebedev quadrature81 of order 11 to integrate over ϕ and θ, using 50 points to sample the two angles. For each orientation, the laser field was defined in the molecular frame in a way that its strong-field component pointed along cos(ϕ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)xM + sin(ϕ)
sin(θ)xM + sin(ϕ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)yM + cos(θ)zM, where xM, yM and zM are the molecular-frame axes. Thus, the orientation of the strong-field component of the laser did not depend on χ, which allowed us to reach convergence using only 4 points in χ in the trapezoidal numerical integration.
sin(θ)yM + cos(θ)zM, where xM, yM and zM are the molecular-frame axes. Thus, the orientation of the strong-field component of the laser did not depend on χ, which allowed us to reach convergence using only 4 points in χ in the trapezoidal numerical integration.
We have run numerical simulations for the left-handed configurations of H2O2 with dihedral angles 79°, 112° and 146° (see Fig. 3), as described in the ESI.† The results for the opposite right-handed configurations were obtained using symmetry considerations.
In the proposed implementation of synthetic chiral light (see Fig. 1), the longitudinal (y-polarized) component and the 2ω (z-polarized) component are sufficiently weak so the electronic response of the molecules along the y and z directions can be treated perturbatively. That is, the chiral pathway (Fig. 2a) is essentially unaffected by presence of the 2ω field, and the achiral pathway (Fig. 2b) is not modified by the weak ellipticity component. This allowed us to calculate the polarization associated with these pathways separately, see ESI.†
The far-field image was evaluated using the Fraunhofer diffraction equation, as in our previous works.65,71–73 The amplitude of harmonic emission at a given emission angle κ, or divergence, is given by
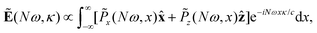 | (13) |
![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) =
= ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) x
x![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) +
+ ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) yŷ +
yŷ + ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) zẑ is the second derivative of the induced polarization in the frequency domain:
zẑ is the second derivative of the induced polarization in the frequency domain: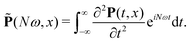 | (14) |
3 Numerical results
We have calculated the highly nonlinear response of different molecular geometries of H2O2 to the optical field presented in Fig. 1 using the procedure above described. Symmetry dictates that the enantio-sensitive harmonic signal is completely background free, separated from the non-enantio-sensitive signal in frequency, polarization and space65. The non-enantio-sensitive signal appears at odd harmonic frequencies and is polarized along x, whereas the enantio-sensitive response arises at even harmonic frequencies and is polarized along z. They are also emitted in different directions, as shown in our previous work.65Because our field is both locally and globally chiral, the total harmonic intensity, integrated over the emission angle κ, can be strongly enantio-sensitive. The emitted harmonic light has two polarization components which are orthogonal to each other (see eqn (13)), Ẽ = Ẽx![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + Ẽzẑ. For a better analysis, we decompose the total harmonic intensity into I = Ix + Iz, where
+ Ẽzẑ. For a better analysis, we decompose the total harmonic intensity into I = Ix + Iz, where
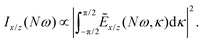 | (15) |
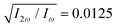 in both beams, and the relative phase delays to ϕ(1)2ω = 0.1π and ϕ(2)2ω = 1.1π, so the 2-colour phase delay of the locally chiral field was ϕ+2ω = 0.6π (eqn (7)) all over the interaction region.
in both beams, and the relative phase delays to ϕ(1)2ω = 0.1π and ϕ(2)2ω = 1.1π, so the 2-colour phase delay of the locally chiral field was ϕ+2ω = 0.6π (eqn (7)) all over the interaction region.
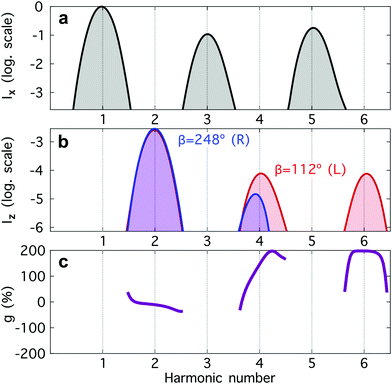 | ||
Fig. 4 Harmonic emission from the chiral equilibrium geometries of H2O2 driven by synthetic chiral light. (a) Non-enantio-sensitive x-polarized harmonic intensity emitted from the left-handed (β = 112°, see Fig. 3) and right-handed (β = 248°) equilibrium geometries. (b) Enantio-sensitive z-polarized harmonic intensity emitted from the left-handed (β = 112°, red) and right-handed (β = 248°, blue) equilibrium geometries. (c) Dissymmetry factor, see eqn (16). Laser parameters: fundamental wavelength λ = 400 nm, Iω = 2.5 × 1013 W cm−2 in each beam, 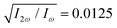 , α = ±10°, ϕ(1)2ω = 0.1π, ϕ(2)2ω = 1.1π, and w = 100 μm. , α = ±10°, ϕ(1)2ω = 0.1π, ϕ(2)2ω = 1.1π, and w = 100 μm. | ||
The non-enantio-sensitive (Fig. 4a) and enantio-sensitive (Fig. 4b) harmonic signals appear at different harmonic orders and are polarized orthogonal to each other, which makes the experimental detection easier. Fig. 4b shows that the enantio-sensitive (z-polarized) intensity emitted from the left- and right-handed enantiomers of H2O2 can be dramatically different. Here, we have tuned the relative amplitude and phase of the 2ω-field component to quench emission of harmonic 6 (H6) in the right-handed enantiomer, while maximizing it in the left-handed enantiomer.
The degree of enantio-sensitivity can be quantified using the dissymmetry factor:
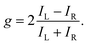 | (16) |
| IL = I(β), | (17) |
| IR = I(360° − β), | (18) |
An alternative expression of the dissymmetry factor can be defined using the intensity ratio between an enantio-sensitive even (z-polarized) harmonic and a reference odd (x-polarized) harmonic,
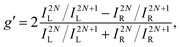 | (19) |
The enantio-sensitive response of isotropic chiral matter to synthetic chiral light relies on the interference between two contributions to light-induced polarization, as above discussed. The chiral contribution is out of phase in media of opposite handedness and is not affected by the 2ω-field component (Fig. 2a). The achiral contribution is identical in opposite enantiomers, and its intensity and phase can be fully controlled with the relative strength and phase of the 2ω-component of the driving field (Fig. 2b). Thus, by adjusting these parameters, we can achieve perfect constructive interference in one molecular enantiomer and perfect destructive interference the other. As we show in the following, this allows us to reach the limits of the dissymmetry factor (±200%) in any harmonic number and for any nuclear configuration.
Fig. 5 shows the dissymmetry factor for H2, H4 and H6, and for dihedral angles 79°, 112° and 146°, as a function of the relative strength and two-colour phase delay ϕ+2ω, for fixed ϕ−2ω = π/2. Note that varying ϕ+2ω while keeping ϕ−2ω constant means varying the two-colour delay in the individual beams synchronously, as ϕ(1)2ω = ϕ+2ω − ϕ−2ω and ϕ(2)2ω = ϕ+2ω + ϕ−2ω, see eqn (11). By keeping ϕ(2)2ω − ϕ(1)2ω = π (i.e. ϕ−2ω = π/2), we tailor the shape of the chiral Lissajous figure in a way that it has the same handedness in every point in space. As already anticipated, the dissymmetry factor reaches the limits of ±200% in all cases. Note that changing ϕ+2ω by π reverses the field's handedness. As a result, the values of ϕ+2ω that maximize the response of the left-handed enantiomer (g = 200%) and the right-handed enantiomer (g = − 200%) are always shifted by π. Furthermore, the phase of the achiral response depends linearly on ϕ+2ω (small variations are due to the shape of the pulse envelope). Thus, the nodal lines in Fig. 5, corresponding to g = 0, are shifted by π/2 with respect to the maximum and the minimum values of g. The specific features of these two-dimensional spectrograms record the nuclear configuration of the molecule.
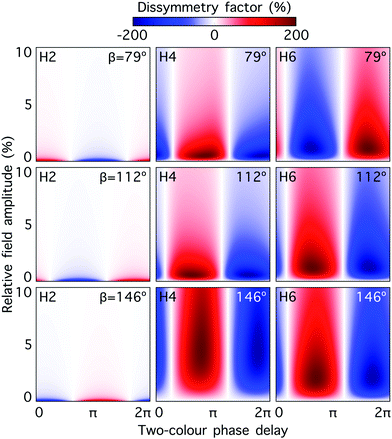 | ||
Fig. 5 Dissymmetry factor in the enantio-sensitive z-polarized harmonic intensity emitted from randomly oriented H2O2 molecules (see eqn (16)) as a function the two-colour phase delay ϕ+2ω and relative 2ω-field strength 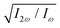 , for harmonic numbers 2 (left column), 4 (central column) and 6 (right column), and for dihedral angles 79° (upper row), 112° (central row), 146° (lower row). Here, we vary ϕ+2ω while keeping ϕ−2ω = π/2, i.e. we vary the two-colour delay in the individual beams synchronously, as ϕ(1)2ω = ϕ+2ω − π/2 and ϕ(2)2ω = ϕ+2ω + π/2, see eqn (11). This allows us to tailor the shape of the chiral Lissajous figure in a way that its handedness is maintained globally in space. , for harmonic numbers 2 (left column), 4 (central column) and 6 (right column), and for dihedral angles 79° (upper row), 112° (central row), 146° (lower row). Here, we vary ϕ+2ω while keeping ϕ−2ω = π/2, i.e. we vary the two-colour delay in the individual beams synchronously, as ϕ(1)2ω = ϕ+2ω − π/2 and ϕ(2)2ω = ϕ+2ω + π/2, see eqn (11). This allows us to tailor the shape of the chiral Lissajous figure in a way that its handedness is maintained globally in space. | ||
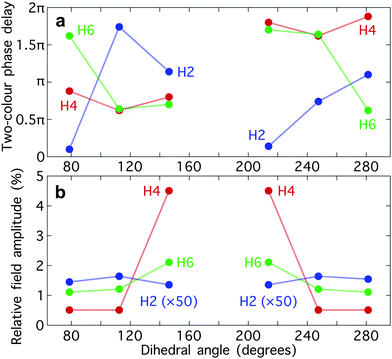
The optimum values of the relative field strength 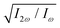 and two-colour phase delay ϕ+2ω which maximize the enantio-sensitive response of the left-handed enantiomer (g = 200% in Fig. 5) are presented in Fig. 6 as functions of the dihedral angle. They are different for each harmonic number, as they are associated with different multiphoton processes. Because the molecular susceptibilities change with the dihedral angle, these optimum parameters are also different for different molecular geometries.
and two-colour phase delay ϕ+2ω which maximize the enantio-sensitive response of the left-handed enantiomer (g = 200% in Fig. 5) are presented in Fig. 6 as functions of the dihedral angle. They are different for each harmonic number, as they are associated with different multiphoton processes. Because the molecular susceptibilities change with the dihedral angle, these optimum parameters are also different for different molecular geometries.
The strong modulation of the two spectroscopic parameters with the dihedral angle reveal that synthetic chiral light is indeed a flexible and powerful spectroscopic tool that allows us to image the nuclear configuration of the molecule in a highly enantio-sensitive manner. Because of the ultrafast nature of the nonlinear interactions responsible for the generation of the enantio-sensitive signal, synthetic chiral light seems to be ideally suited for monitoring chiral chemical reactions in real time.
Conclusions
Monitoring and controlling ultrafast chemical processes at their natural time scales are the ultimate goals of attochemistry. These goals are particularly challenging when dealing with chiral molecules, as the weak non-electric-dipole interactions make the response of left- and right-handed enantiomers to conventional light fields virtually identical. Synthetic chiral light, which is chiral already in the electric dipole approximation, overcomes this fundamental limitation. It creates a new way of imaging and controlling the electronic clouds in chiral molecules with extremely high enantio-sensitivity, introducing new opportunities to this emerging discipline.Here we have shown that the ultrafast electronic response of the prototypical chiral molecule H2O2 is highly sensitive to its nuclear geometry. Despite the simplicity of the molecular system, our numerical results validate the feasibility of synthetic chiral light as a tool for imaging enantio-sensitive chemical reactions in real time, which are ubiquitous in chemistry and of special relevance in biology. Further research should address more complex chiral systems, where synthetic chiral light may allow us to image and control the correlated interplay between electronic and nuclear degrees of freedom, which becomes particularly important in the vicinity of conical intersections.
The possibility of initiating highly enantio-sensitive dynamics in mixtures of left- and right-handed molecules using synthetic chiral light creates interesting opportunities in photo-chemistry, including the possibility of driving enantio-selective photo-chemical reactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
I am extremely grateful to Olga Smirnova and Misha Ivanov for their enormous support and guidance, for pushing me in the right direction, for highly stimulating discussions, and for being a constant source of inspiration. I acknowledge highly stimulating discussions with Andrés F. Ordoñez, expert advice from Oriana Brea in computing the geometry optimizations, and funding from the Royal Society URF\R1\201333 and the Deutsche Forschungsgemeinschaft SPP 1840 SM 292/5-2. I would also like to thank Rose Picciuto and Josh Vogwell for kindly reading the manuscript and providing useful feedback.References
- M. Nisoli, Opt. Photon. News, 2019, 30, 32–39 CrossRef.
- M. Hentschel, R. Kienberger, C. Spielmann, G. A. Reider, N. Milosevic, T. Brabec, P. Corkum, U. Heinzmann, M. Drescher and F. Krausz, Nature, 2001, 414, 509–513 CrossRef CAS PubMed.
- M. Drescher, M. Hentschel, R. Kienberger, M. Uiberacker, V. Yakovlev, A. Scrinzi, T. Westerwalbesloh, U. Kleineberg, U. Heinzmann and F. Krausz, Nature, 2002, 419, 803–807 CrossRef CAS PubMed.
- M. Uiberacker, T. Uphues, M. Schultze, A. J. Verhoef, V. Yakovlev, M. F. Kling, J. Rauschenberger, N. M. Kabachnik, H. Schröder, M. Lezius, K. L. Kompa, H.-G. Muller, M. J. J. Vrakking, S. Hendel, U. Kleineberg, U. Heinzmann, M. Drescher and F. Krausz, Nature, 2007, 446, 627–632 CrossRef CAS PubMed.
- C. Ott, A. Kaldun, L. Argenti, P. Raith, K. Meyer, M. Laux, Y. Zhang, A. Blättermann, S. Hagstotz, T. Ding, R. Heck, J. Madroñero, F. Martín and T. Pfeifer, Nature, 2014, 516, 374–378 CrossRef CAS PubMed.
- F. Martn, J. Fernández, T. Havermeier, L. Foucar, T. Weber, K. Kreidi, M. Schöffler, L. Schmidt, T. Jahnke, O. Jagutzki, A. Czasch, E. P. Benis, T. Osipov, A. L. Landers, A. Belkacem, M. H. Prior, H. Schmidt-Böcking, C. L. Cocke and R. Dörner, Science, 2007, 315, 629–633 CrossRef PubMed.
- O. Smirnova, Y. Mairesse, S. Patchkovskii, N. Dudovich, D. Villeneuve, P. Corkum and M. Y. Ivanov, Nature, 2009, 460, 972–977 CrossRef CAS PubMed.
- G. Sansone, F. Kelkensberg, J. F. Pérez-Torres, F. Morales, M. F. Kling, W. Siu, O. Ghafur, P. Johnsson, M. Swoboda, E. Benedetti, F. Ferrari, F. Lépine, J. L. Sanz-Vicario, S. Zherebtsov, I. Znakovskaya, A. L'Huillier, M. Y. Ivanov, M. Nisoli, F. Martín and M. J. J. Vrakking, Nature, 2010, 465, 763–766 CrossRef CAS PubMed.
- H. J. Wörner, J. B. Bertrand, D. V. Kartashov, P. B. Corkum and D. M. Villeneuve, Nature, 2010, 466, 604–607 CrossRef PubMed.
- F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. De Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martn and M. Nisoli, Science, 2014, 346, 336–339 CrossRef CAS PubMed.
- P. Peng, C. Marceau and D. M. Villeneuve, Nat. Rev. Phys., 2019, 1, 144–155 CrossRef.
- A. L. Cavalieri, N. Müller, T. Uphues, V. S. Yakovlev, A. Baltuška, B. Horvath, B. Schmidt, L. Blümel, R. Holzwarth, S. Hendel, M. Drescher, U. Kleineberg, P. M. Echenique, R. Kienberger, F. Krausz and U. Heinzmann, Nature, 2007, 449, 1029–1032 CrossRef CAS PubMed.
- M. Schultze, K. Ramasesha, C. Pemmaraju, S. Sato, D. Whitmore, A. Gandman, J. S. Prell, L. J. Borja, D. Prendergast, K. Yabana, D. M. Neumark and S. R. Leone, Science, 2014, 346, 1348–1352 CrossRef CAS PubMed.
- T. T. Luu, M. Garg, S. Y. Kruchinin, A. Moulet, M. T. Hassan and E. Goulielmakis, Nature, 2015, 521, 498–502 CrossRef CAS PubMed.
- Z. Tao, C. Chen, T. Szilvási, M. Keller, M. Mavrikakis, H. Kapteyn and M. Murnane, Science, 2016, 353, 62–67 CrossRef CAS PubMed.
- A. J. Uzan, G. Orenstein, Á. Jiménez-Galán, C. McDonald, R. E. F. Silva, B. D. Bruner, N. D. Klimkin, V. Blanchet, T. Arusi-Parpar, M. Krüger, A. N. Rubtsov, O. Smirnova, M. Ivanov, B. Yan, T. Brabec and N. Dudovich, Nat. Photonics, 2020, 14, 183–187 CrossRef CAS.
- D. Polli, P. Altoè, O. Weingart, K. M. Spillane, C. Manzoni, D. Brida, G. Tomasello, G. Orlandi, P. Kukura, R. A. Mathies, M. Garavelli and G. Cerullo, Nature, 2010, 467, 440–443 CrossRef CAS PubMed.
- M. Oppermann, J. Spekowius, B. Bauer, R. Pfister, M. Chergui and J. Helbing, J. Phys. Chem. Lett., 2019, 10, 2700–2705 CrossRef CAS PubMed.
- M. Schmid, L. Martinez-Fernandez, D. Markovitsi, F. Santoro, F. Hache, R. Improta and P. Changenet, J. Phys. Chem. Lett., 2019, 10, 4089–4094 CrossRef CAS PubMed.
- D. J. Abraham, T. J. Hagen and T. R. Helgren, Chirality and Drug Discovery, in Burger's Medicinal Chemistry and Drug Discovery, ed. D. J. Abraham, 2022 Search PubMed.
- P. L. Polavarapu and D. K. Chakraborty, J. Am. Chem. Soc., 1998, 120, 6160–6164 CrossRef CAS.
- P. Stephens, D. McCann, J. Cheeseman and M. Frisch, Chirality, 2005, 17, S52–S64 CrossRef CAS PubMed.
- J. A. Schellman, Chem. Rev., 1975, 75, 323–331 CrossRef CAS.
- D. M. McCann and P. J. Stephens, J. Org. Chem., 2006, 71, 6074–6098 CrossRef CAS PubMed.
- T. D. Crawford, M. C. Tam and M. L. Abrams, J. Phys. Chem. A, 2007, 111, 12057–12068 CrossRef CAS PubMed.
- F. Pulm, J. Schramm, J. Hormes, S. Grimme and S. D. Peyerimhoff, Chem. Phys., 1997, 224, 143–155 CrossRef CAS.
- N. Berova, L. D. Bari and G. Pescitelli, Chem. Soc. Rev., 2007, 36, 914–931 RSC.
- C. Toro, L. De Boni, N. Lin, F. Santoro, A. Rizzo and F. Hernandez, Chem. – Eur. J., 2010, 16, 3504–3509 CrossRef CAS PubMed.
- G. Pescitelli, L. Di Bari and N. Berova, Chem. Soc. Rev., 2011, 40, 4603–4625 RSC.
- C. Wolf and K. W. Bentley, Chem. Soc. Rev., 2013, 42, 5408–5424 RSC.
- L. A. Nafie, T. A. Keiderling and P. J. Stephens, J. Am. Chem. Soc., 1976, 98, 2715–2723 CrossRef CAS.
- T. A. Keiderling, Appl. Spectrosc. Rev., 1981, 17, 189–226 CrossRef CAS.
- P. J. Stephens, J. Phys. Chem., 1985, 89, 748–752 CrossRef CAS.
- T. B. Freedman, X. Cao, R. K. Dukor and L. A. Nafie, Chirality, 2003, 15, 743–758 CrossRef CAS PubMed.
- I. Dolamic, B. Varnholt and T. Bürgi, Nat. Commun., 2015, 6, 7117 CrossRef CAS PubMed.
- J. M. Batista Jr., E. W. Blanch and V. d. S. Bolzani, Nat. Prod. Rep., 2015, 32, 1280–1302 RSC.
- L. D. Barron and A. D. Buckingham, Chem. Phys. Lett., 2010, 492, 199–213 CrossRef CAS.
- J. Haesler, I. Schindelholz, E. Riguet, C. G. Bochet and W. Hug, Nature, 2007, 446, 526–529 CrossRef CAS PubMed.
- Y. He, B. Wang, R. K. Dukor and L. A. Nafie, Appl. Spectrosc., 2011, 65, 699–723 CrossRef CAS PubMed.
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2018, 98, 063428 CrossRef CAS.
- B. Ritchie, Phys. Rev. A, 1976, 13, 1411–1415 CrossRef.
- I. Powis, J. Chem. Phys., 2000, 112, 301–310 CrossRef CAS.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187–1190 CrossRef PubMed.
- G. A. Garcia, L. Nahon, M. Lebech, J.-C. Houver, D. Dowek and I. Powis, J. Chem. Phys., 2003, 119, 8781–8784 CrossRef CAS.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Köhler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS PubMed.
- C. S. Lehmann, N. B. Ram, I. Powis and M. H. M. Janssen, J. Chem. Phys., 2013, 139, 234307 CrossRef PubMed.
- G. A. Garcia, L. Nahon, S. Daly and I. Powis, Nat. Commun., 2013, 4, 2132 CrossRef PubMed.
- M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2014, 16, 856–871 RSC.
- C. Lux, M. Wollenhaupt, C. Sarpe and T. Baumert, ChemPhysChem, 2015, 16, 115–137 CrossRef CAS PubMed.
- A. Kastner, C. Lux, T. Ring, S. Züllighoven, C. Sarpe, A. Senftleben and T. Baumert, ChemPhysChem, 2016, 17, 1119–1122 CrossRef CAS PubMed.
- A. Comby, E. Bloch, C. M. M. Bond, D. Descamps, J. Miles, S. Petit, S. Rozen, J. B. Greenwood, V. Blanchet and Y. Mairesse, Nat. Commun., 2018, 9, 5212 CrossRef CAS PubMed.
- A. Comby, S. Beaulieu, M. Boggio-Pasqua, D. Descamps, F. Légaré, L. Nahon, S. Petit, B. Pons, B. Fabre, Y. Mairesse and V. Blanchet, J. Phys. Chem. Lett., 2016, 7, 4514–4519 CrossRef CAS PubMed.
- S. Beaulieu, A. Comby, B. Fabre, D. Descamps, A. Ferré, G. Garcia, R. Géneaux, F. Légaré, L. Nahon, S. Petit, T. Ruchon, B. Pons, V. Blanchet and Y. Mairesse, Faraday Discuss., 2016, 194, 325–348 RSC.
- S. Beaulieu, A. Comby, A. Clergerie, J. Caillat, D. Descamps, N. Dudovich, B. Fabre, R. Géneaux, F. Légaré, S. Petit, B. Pons, G. Porat, T. Ruchon, R. Taeb, V. Blanchet and Y. Mairesse, Science, 2017, 358, 1288–1294 CrossRef CAS PubMed.
- S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, A. G. Harvey, F. Légaré, Z. Masín, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Nat. Phys., 2018, 14, 484–489 Search PubMed.
- P. V. Demekhin, A. N. Artemyev, A. Kastner and T. Baumert, Phys. Rev. Lett., 2018, 121, 253201 CrossRef CAS PubMed.
- R. E. Goetz, C. P. Koch and L. Greenman, Phys. Rev. Lett., 2019, 122, 013204 CrossRef CAS PubMed.
- S. Rozen, A. Comby, E. Bloch, S. Beauvarlet, D. Descamps, B. Fabre, S. Petit, V. Blanchet, B. Pons, N. Dudovich and Y. Mairesse, Phys. Rev. X, 2019, 9, 031004 CAS.
- D. Patterson, M. Schnell and J. M. Doyle, Nature, 2013, 497, 475–477 CrossRef CAS PubMed.
- S. Eibenberger, J. Doyle and D. Patterson, Phys. Rev. Lett., 2017, 118, 123002 CrossRef PubMed.
- V. A. Shubert, D. Schmitz, C. Pérez, C. Medcraft, A. Krin, S. R. Domingos, D. Patterson and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 341–350 CrossRef CAS PubMed.
- C. Pérez, A. L. Steber, S. R. Domingos, A. Krin, D. Schmitz and M. Schnell, Angew. Chem., Int. Ed., 2017, 56, 12512–12517 CrossRef PubMed.
- A. Yachmenev, J. Onvlee, E. Zak, A. Owens and J. Küpper, Phys. Rev. Lett., 2019, 123, 243202 CrossRef CAS PubMed.
- A. A. Milner, J. A. M. Fordyce, I. MacPhail-Bartley, W. Wasserman, V. Milner, I. Tutunnikov and I. S. Averbukh, Phys. Rev. Lett., 2019, 122, 223201 CrossRef CAS PubMed.
- D. Ayuso, O. Neufeld, A. F. Ordonez, P. Decleva, G. Lerner, O. Cohen, M. Ivanov and O. Smirnova, Nat. Photonics, 2019, 13, 866–871 CrossRef CAS.
- R. Cireasa, A. E. Boguslavskiy, B. Pons, M. C. H. Wong, D. Descamps, S. Petit, H. Ruf, N. Thiré, A. Ferré, J. Suarez, J. Higuet, B. E. Schmidt, A. F. Alharbi, F. Légaré, V. Blanchet, B. Fabre, S. Patchkovskii, O. Smirnova, Y. Mairesse and V. R. Bhardwaj, Nat. Phys., 2015, 11, 654–658 Search PubMed.
- D. Ayuso, P. Decleva, S. Patchkowskii and O. Smirnova, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 06LT01 CrossRef.
- D. Ayuso, P. Decleva, S. Patchkowskii and O. Smirnova, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 124002 CrossRef.
- Y. Harada, E. Haraguchi, K. Kaneshima and T. Sekikawa, Phys. Rev. A, 2018, 98, 021401 CrossRef CAS.
- D. Baykusheva and H. J. Wörner, Phys. Rev. X, 2018, 8, 031060 CAS.
- D. Ayuso, A. F. Ordonez, P. Decleva, M. Ivanov and O. Smirnova, Nat. Commun., 2021, 12, 3951 CrossRef CAS PubMed.
- O. Neufeld, D. Ayuso, P. Decleva, M. Y. Ivanov, O. Smirnova and O. Cohen, Phys. Rev. X, 2019, 9, 031002 CAS.
- D. Ayuso, A. F. Ordonez, M. Ivanov and O. Smirnova, Optica, 2021, 8, 1243–1246 CrossRef.
- K. Y. Bliokh and F. Nori, Phys. Rep., 2015, 592, 1–38 CrossRef.
- G. Galinis, J. Strucka, J. C. T. Barnard, A. Braun, R. A. Smith and J. P. Marangos, Rev. Sci. Instrum., 2017, 88, 083117 CrossRef PubMed.
- U. Kuenzer and T. S. Hofer, Chem. Phys. Lett., 2019, 728, 195–200 CrossRef CAS.
- M. A. Marques, A. Castro, G. F. Bertsch and A. Rubio, Comput. Phys. Commun., 2003, 151, 60–78 CrossRef CAS.
- A. Castro, H. Appel, M. Oliveira, C. A. Rozzi, X. Andrade, F. Lorenzen, M. A. L. Marques, E. K. U. Gross and A. Rubio, Phys. Status Solidi B, 2006, 243, 2465–2488 CrossRef CAS.
- X. Andrade, D. Strubbe, U. De Giovannini, A. H. Larsen, M. J. T. Oliveira, J. Alberdi-Rodriguez, A. Varas, I. Theophilou, N. Helbig, M. J. Verstraete, L. Stella, F. Nogueira, A. Aspuru-Gzik, A. Castro, M. A. L. Marques and A. Rubio, Phys. Chem. Chem. Phys., 2015, 17, 31371–31396 RSC.
- N. Tancogne-Dejean, M. J. T. Oliveira, X. Andrade, H. Appel, C. H. Borca, G. Le Breton, F. Buchholz, A. Castro, S. Corni, A. A. Correa, U. De Giovannini, A. Delgado, F. G. Eich, J. Flick, G. Gil, A. Gomez, N. Helbig, H. Hübener, R. Jestädt, J. Jornet-Somoza, A. H. Larsen, I. V. Lebedeva, M. Lüders, M. A. L. Marques, S. T. Ohlmann, S. Pipolo, M. Rampp, C. A. Rozzi, D. A. Strubbe, S. A. Sato, C. Schäfer, I. Theophilou, A. Welden and A. Rubio, J. Chem. Phys., 2020, 152, 124119 CrossRef CAS PubMed.
- V. I. Lebedev and D. N. Laikov, Doklady Mathematics, 1999, 59, 477–481 Search PubMed.
- O. Smirnova and M. Ivanov, Multielectron High Harmonic Generation: Simple Man on a Complex Plane, John Wiley & Sons, Ltd, 2014, ch. 7, pp. 201–256 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1cp05427a |
| This journal is © the Owner Societies 2022 |