Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical predictions of phase stability for orthorhombic and hexagonal ternary MAB phases†
Adam
Carlsson
 ,
Johanna
Rosen
and
Martin
Dahlqvist
,
Johanna
Rosen
and
Martin
Dahlqvist
 *
*
Materials Design, Department of Physics, Chemistry and Biology (IFM), Linköping University, SE-581 83, Linköping, Sweden. E-mail: adam.carlsson@liu.se; martin.dahlqvist@liu.se
First published on 13th April 2022
Abstract
In the quest for finding novel thermodynamically stable, layered, MAB phases promising for synthesis, we herein explore the phase stability of ternary MAB phases by considering both orthorhombic and hexagonal crystal symmetries for various compositions (MAB, M2AB2, M3AB4, M4AB4, and M4AB6 where M = Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, and Co, A = Al, Ga, and In, and B is boron). The thermodynamic stability of seven previously synthesized MAB phases is confirmed, three additional phases are predicted to be stable, and 23 phases are found to be close to stable. Furthermore, the crystal symmetry preference for forming orthorhombic or hexagonal crystal structures is investigated where the considered Al-based MAB phases tend to favour orthorhombic structures whereas Ga- and In-based phases in general prefer hexagonal structures. The theoretically predicted stable MAB phases along with the structural preference is intended to both guide experimental efforts and to give an insight into the stability for different crystal symmetries of MAB phases.
Introduction
MAB phases are members of the nanolaminated crystal compound family. In addition to being layered borides, which, as of late, have attracted renewed interest due to their important properties, i.e., exfoliation potential towards two-dimensional (2D) materials,1 high melting points and high hardness.2 The mechanical properties of borides in general make them prominent candidates in application areas such as cutting tools3 and other wear-resistant coatings,4,5 which motivates the investigation of new stable MAB phases. The possibility of exfoliating MAB phases into their two-dimensional counterparts has been investigated theoretically.6–8 Experimentally, partial etching has been demonstrated,9–11 and only recently, Jie et al. successfully demonstrated the synthesis of a 2D transition metal boride Mo3/4B2−xTz by selectively etching Y and Al from the in-plane ordered (Mo2/3Y1/3)2AlB2 and Sc and Al from (Mo2/3Sc1/3)2AlB2.1 The discovery of Mo3/4B2−xTz boridene suggests a wealth of future 2D materials.Similar to MAB phases are the well-known nanolaminated MAX phases, where X, in contrast to B, refers to carbon and/or nitrogen.12 Like MAB phases, MAX phases are composed of alternating M–X layers interleaved by A-layers. These materials can be exfoliated into 2D MXenes with potential for use in energy storage and electromagnetic shielding.13,14
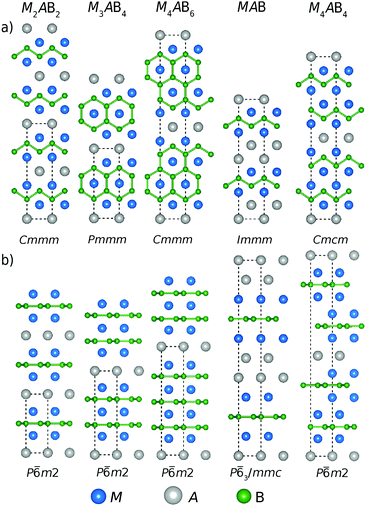
Both MAX and MAB phases were discovered in the 60s.15,16 MAX phases have since then been demonstrated to encompass a large variety of chemical compositions,17 in contrast to MAB phases which include fewer elemental combinations but with a larger structural variation. One of the general formulae of MAB phases is Mn+1AB2n which covers most compositions where M corresponds to a transition metal, A represents a Group 13 element, B is boron and n = 1, 2, and 3. Generally, MAB phases have alternating stacks of M–B layers interleaved by A-layers. However, additional multilayered compositions which do not fit this general formulation are MAB and M4AB4 comprised of double layers of A- and M-elements, respectively.
The stoichiometries considered in this work are based on the synthesized MoAlB and WAlB with orthorhombic space group symmetry (Cmcm); Cr2AlB2, Mn2AlB2 and Fe2AlB2 (Cmmm), Cr3AlB4 (Pmmm) and Cr4AlB6 (Cmmm), respectively.18 Additionally, in 2019, the field of ternary MAB phases expanded with the discovery of Cr4AlB4 with orthorhombic space group symmetry (Immm)19 and Ti2InB2 with hexagonal symmetry (P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2).10 The discovery of a hexagonal MAB phase demonstrated that hypothetical MAB phases may potentially crystallize in either orthorhombic or hexagonal symmetry depending on its composition. Our intention is to demonstrate that theory can be used to elucidate compositions favouring a certain symmetry and more importantly if it is stable and thus a suitable candidate for future synthesis.
m2).10 The discovery of a hexagonal MAB phase demonstrated that hypothetical MAB phases may potentially crystallize in either orthorhombic or hexagonal symmetry depending on its composition. Our intention is to demonstrate that theory can be used to elucidate compositions favouring a certain symmetry and more importantly if it is stable and thus a suitable candidate for future synthesis.
In this work we have performed a screening study on stability for various MAB phase compositions (MAB, M2AB2, M3AB4, M4AB4, and M4AB6) by considering both known and manually designed orthorhombic and hexagonal crystal structure symmetries. This is in order to reveal any possible expansion of the family of ternary MAB phases. The screening study includes metals M = Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, and Co and the A-elements A = Al, Ga, and In. We verify the stability for seven experimentally known MAB phases and predict the hypothetical Hf2InB2, Zr2InB2 and Mo4AlB4 to be stable. 23 additional phases are found to be close to stable.
Furthermore, additional pathways have previously been suggested as a substitute to thermodynamical stability calculations for identifying candidate MAB phases. Zhang et al. used descriptors like atomic size and electron concentration in an attempt to identify stable MAX phases.20 Shen et al. used a similar approach when investigating magnetic MAB phases.21 Additionally, similar methods have been used in an attempt to effortlessly identify the material properties.22–24 We challenge the use of such an approach since we find no distinct relation between the considered descriptors and their calculated phase stability.
Theoretical details
Density functional theory calculations
All first principles calculations were performed based on density functional theory (DFT) along with the projector augmented wave potential (PAW) method25,26 with a plane-wave cutoff energy set to 400 eV. The Vienna Ab Initio Simulation Package (VASP) version 5.4.1 was utilized27,28 with the electronic exchange–correlation interactions described by the generalized gradient approximation (GGA) as parameterized by Perdew–Burke–Ernzerhof (PBE).29 The use of different exchange correlation functionals has been demonstrated to have a minor influence on the formation enthalpy.30 Spin-polarization was considered for phases including Cr, Mn, Fe and Co elements in which all non-equivalent collinear magnetic spin configurations within the unit cell were considered for the competing phases. Magnetic spin configurations modelled for the MAB phase structures considered in this work are shown in Fig. S1–S4 (ESI†). The lowest energy spin configuration for each magnetic MAB phase is given in Table S1 (ESI†) where a majority of the phases (43 out of 60) are found to have an AFM configuration as the lowest energy. The identified spin configuration with the lowest energy represents the energy of the considered phase. It should be noted that a potential spin configuration of lower energy for the MAB phase will only stabilize the phase further, i.e., the stable MAB phase predicted here will remain stable even if the detailed magnetic ground state has not been identified. The Brillouin zone was sampled using the Monkhorst–Pack scheme with a k-point density of 0.1 Å−1.31 The chosen k-point density and cutoff energy is motivated from the formation enthalpy convergence calculations seen in Fig. S5 (ESI†). All structures were relaxed with respect to volume, shape, and internal atomic positions until an energy convergence of 10−6 eV per atom and a force convergence of 10−2 eV Å−1 was reached. Density of states (DOS) and crystal orbital Hamilton population (COHP) were calculated using the LOBSTER32–35 code where the calculated band-structure energy is reconstructed into orbital interactions. VESTA was used for visualizing the atomic structures.36The MAB compositions in focus are MAB, M2AB2, M3AB4, M4AB4 and M4AB6 in both orthorhombic and hexagonal space group symmetries, as shown in Fig. 1. The orthorhombic structures consist of the zigzag chains of boron while the hexagonal structures have boron in a flat honeycomb lattice. The hexagonal M3AB4, M4AB6, MAB and M4AB4 are hypothetical structures inspired symmetrically by the hexagonal Ti2InB2, where the considered composition and the stacking sequence is equivalent to their orthorhombic counterpart. The additional hypothetical hexagonal crystal structures of different stacking sequences were designed for the double layered MAB and M4AB4 compositions which can be observed in Fig. S6 (ESI†). The energy representing a specific phase is the crystal structure with the lowest energy. In this work we considered M from Groups 3 to 9; Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, and Co along with A elements; Al, Ga, and In, resulting in a total of 210 unique compositions and 420 MAB phases; i.e., at each composition the MAB phase is represented by both orthorhombic and hexagonal crystal structure symmetries. Additional information related to the considered crystal structures illustrated in Fig. 1 is found within Tables S2–S4 (ESI†).
Phase stability calculations
In this work, we express the stability of a MAB phases using two different variables evaluated at 0 K: formation energy37–40 and formation enthalpy.37–45 For a general MxAyBz phase, the formation energy, ΔEf is calculated using| ΔEf (MxAyBz) = E(MxAyBz) − xEM − yEA − zEB, | (1) |
The second approach builds on comparing the energy of a general MxAyBz phase with respect to all possible linear combinations of competing phases present in the ternary M–A–B material system using an energy convex hull construction. At a given MxAyBz composition, the convex hull consists of competing phases that have an energy lower than any other combination of phases. Note that by definition, MxAyBz is not part of the convex hull construction. This set of competing phases represents the most favourable decomposition and is identified using a linear optimization procedure. This approach has previously been successful, both confirming experimental known materials as well as predicting new materials.41–45 The set of most competing phases, commonly referred to as the equilibrium simplex, for a general MxAyBz composition, is obtained by solving
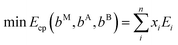 | (2) |
| ΔHcp(MxAyBz) = E(MxAyBz) − min Ecp, | (3) |
Results and discussion
Theoretical phase stability of MAB phases
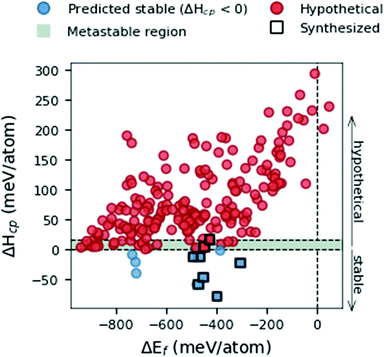
We start by evaluating different viewpoints for calculating stability at 0 K in Fig. 2 by comparing the formation energy, ΔEf (eqn (1)), and the formation enthalpy, ΔHcp (eqn (3)). The data represent the space group with the lowest energy for each MxAyBz composition. Experimentally synthesized phases are represented by black squares.Fig. 2 demonstrates the use of formation energy, ΔEf, to be a rather poor indicator when predicting thermodynamical stability, compared to the formation enthalpy, ΔHcp. Out of the 210 considered MAB phase compositions, all but two are found with ΔEf < 0. This indicates that 208 phases are stable with respect to decomposition into its constituent elements M, A and B. When formation enthalpy, ΔHcp, is considered, only 10 phases are identified as thermodynamically stable with ΔHcp < 0. It is apparent that even though ΔEf could indicate the stability of a phase it may be far from stable when compared to all competing phases in the material system. Out of the nine experimentally synthesized MAB phases, marked with black squares in Fig. 2, seven are found to be stable and two close to stable within 0 < ΔHcp < +17. We use this information to define a metastable region, represented by a grey area in Fig. 1, where the upper limit is decided by the experimentally verified Cr4AlB6 with ΔHcp = + 17 meV per atom. With this in mind, ΔHcp is motivated as the better descriptor to be used for predicting the phase stability of hypothetical MAB phases yet to be synthesized.
Formation enthalpies of the M2AB2, M3AB4 and M4AB6 systems
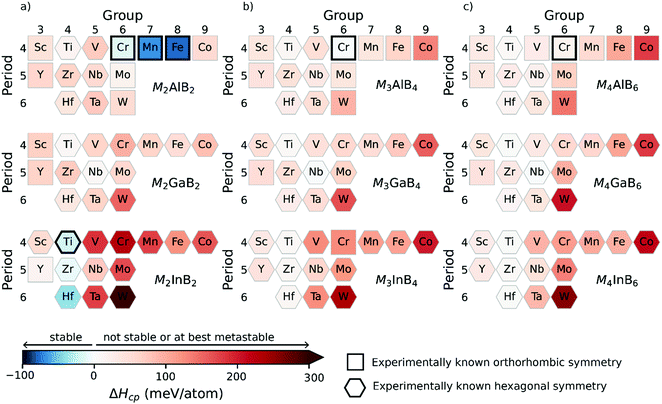
The considered MAB phases in this work, illustrated in Fig. 1, can be divided into two subgroups based on their structural appearance; (i) M2AB2, M3AB4 and M4AB6 which only differ in the thickness of the M–B layer and can thus be described with the general Mn+1AB2n formula where n = 1, 2, 3 and (ii) MAB and M4AB4 with double layers of A and M, respectively.We start by investigating the thermodynamic stability of the Mn+1AB2n phases with M = Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, Co and A = Al, Ga, and In. Both orthorhombic and hexagonal structures are considered (see Fig. 1). Fig. 3 shows an overview of the calculated formation enthalpy ΔHcp for Mn+1AB2n, with the corresponding identified equilibrium simplex listed in Table S5 (ESI†). The thermodynamic stability is visualized using a heat map where the background colour represents ΔHcp for the symmetry structure with the lowest energy where blue colour indicates a stable phase (ΔHcp < 0). A symbol representation is herein used to denote the structure of lowest energy; square for orthorhombic symmetry and hexagon for hexagonal symmetry. Experimentally synthesized phases are illustrated by a black square or a hexagon.
In Fig. 3a, we note that all experimentally known M2AB2 phases are found to be stable, i.e., the orthorhombic M2AlB2 with M = Cr, Mn, Fe and hexagonal Ti2InB2. In addition, two hypothetical phases are predicted to be stable with a hexagonal structure symmetry, Zr2InB2 and Hf2InB2. These predictions are consistent with ref. 50. Hence, experimental verification is encouraged. Furthermore, four additional phases of the M2AB2 composition are predicted to be close to stable, 0 < ΔHcp < 17 meV per atom, i.e., Ti2AlB2, Ti2GaB2, Nb2GaB2 and Y2InB2.
For M3AB4 and M4AB6 compositions in Fig. 3b and c, only two phases are experimentally known, Cr3AlB4 and Cr4AlB6. These are found to be close to stable with ΔHcp = 4 and 17 meV per atom, respectively. No phase is predicted stable, but 12 phases are found to be close to stable, 0 < ΔHcp < 17 meV per atom, and includes the hypothetical phases with the hexagonal symmetries: Ti4AlB6, Ti3GaB4, Ti4GaB6, Ti3InB4, Ti4InB6, Zr3InB4, Zr4InB6, Hf4AlB6, Hf4GaB6, H4InB6, Nb3GaB4, Nb4GaB6. This is in contrast to a previous study where Ti3AlB4, Ti3GaB4 and Ti3InB4 were reported as thermodynamical stable. This discrepancy, between our results with those in ref. 10, can be associated with the limited consideration of competing phases being A = Al, Ga, In, TiB, and Ti3B4 in ref. 10 whereas in this work all known phases within each ternary system are considered. This example demonstrates the importance of an extensive analysis including all competing phases for conclusive theoretical predictions.
In Fig. 3, M from Groups 3 to 5 mainly results in hexagonal symmetry with the lowest energy and this is for all considered A-elements and Mn+1AB2n compositions. Similar observations can be made for group 6 metals with A = Ga and In. Out of the 126 compositions in Fig. 3, 97 are identified with hexagonal symmetry of lowest energy. Orthorhombic symmetries are mainly found for A = Al.
Formation enthalpy of MAB and M4AB4 systems
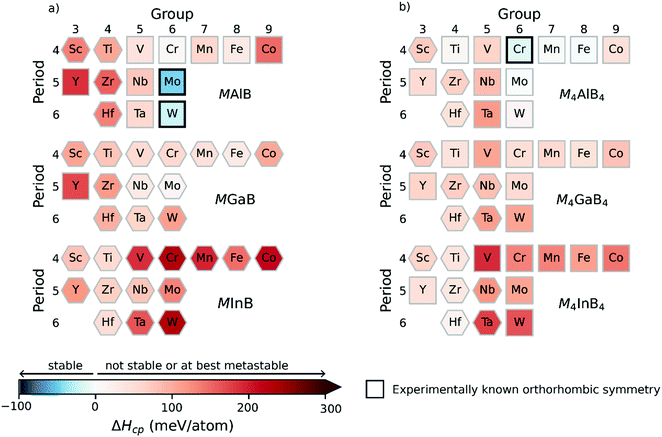
The following section focuses on the MAB phases with double layers of A and M, i.e., the MAB and M4AB4 compositions. Again, both orthorhombic and hexagonal symmetries are considered (see Fig. 1). Fig. 4 shows an overview of the calculated formation enthalpy ΔHcp for MAB and M4AB4, with the corresponding identified equilibrium simplex listed in Table S6 (ESI†). Again, the thermodynamic stability is visualized using a heat map with the background colour representing ΔHcp for the symmetry with the lowest energy, where the blue colour indicates thermodynamical stability (ΔHcp < 0), and the structure of lowest energy is represented by a square for orthorhombic symmetry and a hexagon for hexagonal symmetry. Experimentally synthesized phases are marked by a black square.In Fig. 4a, only two MAB phases are found to be stable, MoAlB and WAlB, both with orthorhombic symmetry, and formation enthalpies ΔHcp = −47 and ΔHcp = −22 meV per atom, respectively. Both MoAlB and WAlB have also been synthesized.18 Two additional phases, CrAlB and MoGaB, are found to be close to stable with ΔHcp = 9 and 13 meV per atom, respectively. Similar to Mn+1AB2n in Fig. 3, the majority of MAB phases are identified with the hexagonal symmetry as the energetically preferred crystal structure of the considered M4AB4 phases in Fig. 4b, only two are predicted to be stable, the already synthesized Cr4AlB4 of orthorhombic symmetry (ΔHcp = −12 meV per atom)19 and the hypothetical Mo4AlB4 (ΔHcp = −1 meV per atom). Five additional M4AB4 phases are identified to be close to stable, i.e., Ti4AlB4, W4AlB4, Mn4AlB4, Fe4AlB4, and Hf4InB4.
A noteworthy observation in Fig. 4b is the energetically preferred crystal structure for M4AB4 phases is dominated by the orthorhombic symmetry, in contrast to Mn+1AB2n and MAB where the majority of phases are found with hexagonal symmetry. This is observed for all A-elements. Fig. 4 shows that 46 out of the 84 considered phases resulted in a crystal structure of hexagonal symmetry with the lowest energy.
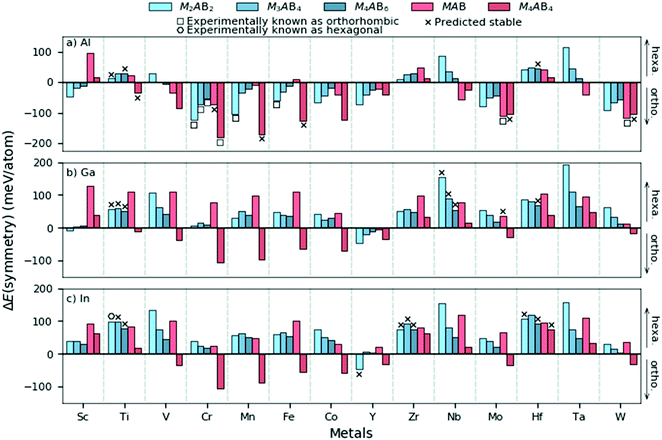
The general observation from Fig. 3 and 4 is that hexagonal symmetries are typically preferred for M of Groups 3 to 5 and orthorhombic symmetries for A = Al. However, it should be noted that the displayed information only represents the crystal symmetry with the lowest energy. We therefore choose to further inspect the difference in energy between the hexagonal and orthorhombic symmetries as a step towards attaining an understanding of the preferred symmetry with various compositions and chemistries. Fig. 5 demonstrates the energy difference, ΔE(symmetry) = E(ort) − E(hex), where ΔE > 0 indicates the hexagonal symmetry to be of lowest energy and is thus favoured whereas ΔE < 0 indicates the orthorhombic symmetry to be favoured.
In Fig. 5 we find that most structures with A = Al yields an orthorhombic symmetry with the lowest energy. This contrasts with A = Ga and In where the hexagonal symmetry is the dominating symmetry with the lowest energy. For Mn+1AB2n phases (blue colours), the energetic preference for the hexagonal symmetry is found to generally increase in the series Al–Ga–In. Phases with M from Group 4 and 5 for A = Ga and In always have the hexagonal space group symmetry with the lowest energy. The exception among the compositions considered here is found for M4AB4, where the orthorhombic symmetry is most common and this is true for all considered A-elements. Note that M4AB4 have double-layered M (see Fig. 1) and thus their layer sequence differs from the other considered compositions.
From the results in Fig. 5 we find some trends both among the structural compositions like Mn+1AB2n and for different M and A. One hypothesis for this may be related to their underlying binary substructures. A short survey of experimentally binary metal borides reveal that hexagonal structures are more common at high boron content while orthorhombic structures are mainly observed at lower boron content. A summary of experimentally metal boride binary phases and their space group symmetries are listed in Table S7 (ESI†). This underlying feature may in part explain the observed trends in Fig. 5. To reveal other tendencies which may explain the trends in Fig. 5, we try to find any correlation between ΔE(symmetry) and the atomic size, electron concentration and electronegativity. However, no clear correlation is found, as shown in Fig. S6 (ESI†). In an initial attempt to explain the results of the symmetry preference in Fig. 5, we performed a bonding analysis for a selected set of M2AB2 phases with M = Sc, Ti, V, and Cr and A = Al and In, considering both hexagonal and orthorhombic symmetries using the Local Orbital Hamiltonian Suit Towards Electronic Structure Reconstruction (LOBSTER) code.32–35 The total density of states (DOS) and its correlation with the total crystal orbital Hamiltonian population (COHP) for the considered M2AB2 phases is shown in Fig. S8 and S9 (ESI†). Furthermore, the total interaction within any of the considered orthorhombic symmetries is always greater than the hexagonal structure and this is independent of M or A, shown in Fig. S10 (ESI†). At this level, no distinct correlation between the populated anti-bonding and bonding states can be made in analogy with the symmetry preference in Fig. 5. A closer analysis of individual bonds, shown in Fig. S11 (ESI†), reveal stronger In–In bonds for the hexagonal structure as compared to the orthorhombic structure (∼2.5 eV stronger). For phases with A = Al, the M–A bonds seem to play a more significant role, especially in Sc2AlB2 and Cr2AlB2, which both favours the orthorhombic symmetry. The brief bonding analysis of the selected phases considered herein indicates that the A-element interactions to play a crucial role in the symmetry preference.
Further attempts to enlighten the symmetry preference is made by comparing the calculated DOS and COHP of hexagonal and orthorhombic symmetries for the Ti2InB2 and Cr2AlB2 phases, shown in Fig. S12 and S13 (ESI†) along with a detailed analysis. For Ti2InB2 we find that the major difference between considered symmetries is the location of the Fermi level, which is close to a minimum for the hexagonal structure. For the orthorhombic structure there are many antibonding states just below the Fermi level which costs energy. This indicates overall why the hexagonal symmetry is lower in energy as compared to the orthorhombic structure. For Cr2AlB2, with the orthorhombic symmetry of lower energy than the hexagonal one, we find that the Cr 3d states around the Fermi level are non-bonding for the orthorhombic structure while being antibonding for the hexagonal structure. The latter have a destabilizing impact on its energy. This analysis gives a first glimpse of the electronic and bonding differences of M2AB2 and could, at least in part, explain the difference between hexagonal and orthorhombic symmetries.
Prediction using atomic size and electron concentration
The procedure for evaluating the thermodynamical stability of a given phase requires comparison of energies with a set of competing phases and can thus be quite demanding, especially when multiple compositions and elemental combinations are to be investigated. In order to determine the stability of a certain phase, its energy must be compared with the energy of all competing phases as done in Fig. 3 and 4. This procedure may be considered to be computationally demanding. Hence, alternative routes may be tempting to use for fast discovery of new materials. One suggested approach is the so-called structure mapping methodology where the atomic size and electron concentration are used as descriptors for effortless predictions of a materials formability20,21 or its properties.22–24 Here we choose to test this hypothesis for predicting a material's possible existence or formability by using the same analysis as proposed in ref. 20 and 21. Adopted values of experimental atomic radii and number of valence/itinerant electrons for M, A, and B are retrieved from the ref. 51–53 and listed in Table S8 (ESI†).The atomic size ratio of M- and A-element for MxAyBz, as defined in ref. 20 is given by
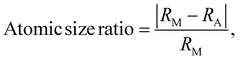 | (4) |
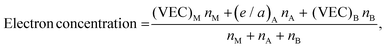 | (5) |
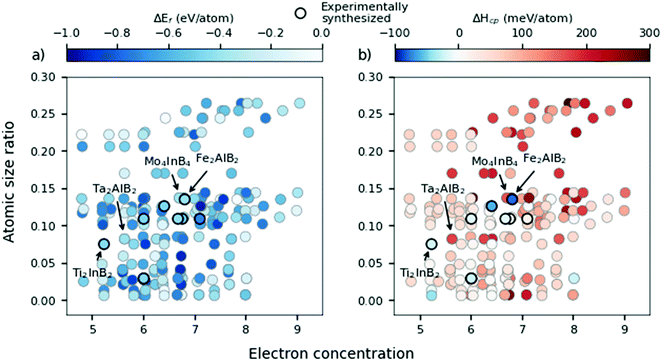
Fig. 6 shows the atomic size ratio as a function of electron concentration for all 210 compositions and where the difference between the two panels is how each data point is coloured. All experimentally synthesized phases are marked by black circles. In ref. 21, Shen et al. defined two lines to distinguish the most stable region, governed by 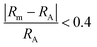 and an EC < 5.5, thus separating formable from non-formable phases which have been included within Fig. S7 (ESI†). Similarly, Zhang et al. introduced similar regions when investigating stability trends of MAX phases in ref. 20 As demonstrated in Fig. S14–S19 (ESI†) for each separate composition, using such lines is a rather crude approximation and do not give any valuable information.
and an EC < 5.5, thus separating formable from non-formable phases which have been included within Fig. S7 (ESI†). Similarly, Zhang et al. introduced similar regions when investigating stability trends of MAX phases in ref. 20 As demonstrated in Fig. S14–S19 (ESI†) for each separate composition, using such lines is a rather crude approximation and do not give any valuable information.
In Fig. 6a, the data points are correlated with the calculated formation energy (eqn (1)) represented by a blue colour scale depending on its value. Note that 208 out of 210 phases are considered stable according to the ΔEf approach. The large number of predicted stable phases in Fig. 6a in relation with the actual few experimentally synthesized phases indicate the ΔEf approach to be a very crude approximation to the phase stability. One may speculate that the different compositions and structures considered herein and in ref. 21, may have an impact on the uncorrelated results. Corresponding figures for each considered composition are shown in Fig. S14–S19 (ESI†) where tendencies for a decrease in ΔEf may correlate with a decrease of EC.
In Fig. 6b we include information from the calculated formation enthalpy (eqn (3)) to the atomic size ratio and the EC relationship. The corresponding colouring represents the value of ΔHcp and range from blue (stable) to red (not stable). The situation in Fig. 6b is very different as compared to Fig. 6a. There is no correlation at all between the predicted stability and the atomic size, in additon to the EC, which verifies the uncertainty of using structure mapping methodology for materials predictions, at least for MAB phases. This becomes even more clear in Fig. S12 and S13 (ESI†) showing individual plots for each unique MAB composition. The only distinct result found is that a large enough atomic size ratio 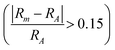 combined with a high EC (EC > 8) does result in phases far from being stable (ΔHcp > +140 meV per atom). Thus, the use of the structure mapping methodology for fast prediction of new materials gives misguiding information about possible phases suitable for future synthesis. This is explicitly demonstrated for two MAB phases of similar atomic size ratio and EC, Mo4InB4 and Fe2AlB2. Note that Fe2AlB2 is identified as stable (−78 meV per atom) indicated by the blue colour, and it has also been synthesized as indicated by the black circle. This is in contrast to the hypothetical Mo4InB4 which is far from being stable as indicated by the red colour (+107 meV per atom) yet has a similar size ratio and EC to Fe2AlB2. Additional contradictions between stable and unstable phases may be found within the M2AB2 system as demonstrated by comparing the experimentally verified Ti2InB2 (−21 meV per atom) and the far from stable Ta2InB2 (+177 meV per atom) both of which have similar size ratios and EC.
combined with a high EC (EC > 8) does result in phases far from being stable (ΔHcp > +140 meV per atom). Thus, the use of the structure mapping methodology for fast prediction of new materials gives misguiding information about possible phases suitable for future synthesis. This is explicitly demonstrated for two MAB phases of similar atomic size ratio and EC, Mo4InB4 and Fe2AlB2. Note that Fe2AlB2 is identified as stable (−78 meV per atom) indicated by the blue colour, and it has also been synthesized as indicated by the black circle. This is in contrast to the hypothetical Mo4InB4 which is far from being stable as indicated by the red colour (+107 meV per atom) yet has a similar size ratio and EC to Fe2AlB2. Additional contradictions between stable and unstable phases may be found within the M2AB2 system as demonstrated by comparing the experimentally verified Ti2InB2 (−21 meV per atom) and the far from stable Ta2InB2 (+177 meV per atom) both of which have similar size ratios and EC.
Based on the result shown in Fig. 6 and Fig. S12, S13 (ESI†), it is demonstrated here that even though it is tempting to use the structure mapping methodology for effortless predictions it does not reveal any valuable information about the possible existence or formability of MAB phases. It should be stressed that complete phase stability calculations, as shown in Fig. 3 and 4, are thus needed for reliable predictions of MAB phases, as demonstrated from verified stability for those already synthesized to date. Furthermore, the phase stability calculations also predict stable and close to stable phases not yet synthesized where experimental synthesis attempts are encouraged.
Conclusions
We have performed phase stability calculations on a total of 420 phases comprised of hexagonal and orthorhombic space group symmetries with MAB, M2AB2, M3AB4, M4AB4 and M4AB6 compositions where M = Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, and Co and A = Al, Ga, and In. The thermodynamical stability of the investigated compounds was evaluated in terms of both formation energy and formation enthalpy. The two alternative frameworks were compared and the formation enthalpy, ΔHcp, is demonstrated as a superior alternative when evaluating the thermodynamical stability. 10 phases are predicted to be thermodynamically stable, out of which seven have previously been synthesized while Zr2InB2, Hf2InB2 and Mo4AlB4 are awaiting experimental verification. An additional 23 phases are close to stable (0 < ΔHcp < 17 meV per atom). By comparing the energy of orthorhombic and hexagonal structures we find that the majority of the M1+nAB2n phases are found having the hexagonal symmetry of lowest energy when A = Ga and In while orthorhombic symmetry is of lowest energy when A = Al. Similar observations were made for the double layered MAB phases where the M4AB4 systems favour the orthorhombic symmetry. We have also critically examined the proposed structure mapping methodology for the fast prediction of new materials where the idea is to use the atomic size ratio and electron concentration as predictive descriptors. We conclude that it is an inappropriate approach which gives misguiding information about possible candidate phases for synthesis with no correlation at all to the calculated thermodynamical stability. This demonstrates the complexity of phase stability predictions and that shortcuts can give skewed results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. D. acknowledges support from the Swedish Research council through project 2019-05047. J. R. acknowledges funding from the Knut and Alice Wallenberg (KAW) Foundation for a Fellowship/Scholar Grant and Project funding (KAW 2020.0033). The calculations were carried out using the supercomputer resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Center (NSC), the High Performance Computing Center North (HPC2N), and the PDC Center for High Performance Computing, partially founded by the Swedish Research Council through grant agreement no. 2018-05973.References
- J. Zhou, et al., Boridene: two-dimensional Mo4/3B2−x with ordered metal vacancies obtained by chemical exfoliation., Science, 2021, 373(6556), 801–805 CrossRef CAS.
- S. Kota, M. Sokol and M. W. Barsoum, A progress report on the MAB phases: atomically laminated, ternary transition metal borides, Int. Mater. Rev., 2020, 65(4), 226–255 CrossRef CAS.
- A. Ahmed, et al., Belt abrasion resistance and cutting tool studies on new ultra-hard boride materials, Tribol. Int., 2009, 42(5), 706–713 CrossRef CAS.
- C. Martini, et al., Sliding and abrasive wear behaviour of boride coatings, Wear, 2004, 256(6), 608–613 CrossRef CAS.
- I. E. Campos-Silva and G. A. Rodríguez-Castro, in Boriding to improve the mechanical properties and corrosion resistance of steels, Thermochemical Surface Engineering of Steels, ed. E. J. Mittemeijer and M. A. J. Somers, Woodhead Publishing, Oxford, 2015, pp. 651–702 Search PubMed.
- M. Khazaei, et al., Novel MAB phases and insights into their exfoliation into 2D MBenes, Nanoscale, 2019, 11(23), 11305–11314 RSC.
- Z. Jiang, et al., MBene (MnB): a new type of 2D metallic ferromagnet with high Curie temperature, Nanoscale Horiz., 2018, 3(3), 335–341 RSC.
- X. Guo, et al., Establishing a Theoretical Landscape for Identifying Basal Plane Active 2D Metal Borides (MBenes) toward Nitrogen Electroreduction, Adv. Funct. Mater., 2021, 31(6), 2008056 CrossRef CAS.
- L. T. Alameda, et al., Topochemical Deintercalation of Al from MoAlB: Stepwise Etching Pathway, Layered Intergrowth Structures, and Two-Dimensional MBene, J. Am. Chem. Soc., 2018, 140(28), 8833–8840 CrossRef CAS PubMed.
- J. Wang, et al., Discovery of hexagonal ternary phase Ti2InB2 and its evolution to layered boride TiB, Nat. Commun., 2019, 10(1), 2284 CrossRef PubMed.
- H. Zhang, et al., Phase pure and well crystalline Cr2AlB2: a key precursor for two-dimensional CrB, J. Mater. Sci. Technol., 2019, 35(8), 1593–1600 CrossRef.
- M. W. Barsoum, The MN+1AXN phases: A new class of solids: Thermodynamically stable nanolaminates, Prog. Solid State Chem., 2000, 28(1), 201–281 CrossRef CAS.
- A. Vahid Mohammadi, J. Rosen and Y. Gogotsi, The world of two-dimensional carbides and nitrides (MXenes), Science, 2021, 372(6547), eabf1581 CrossRef CAS PubMed.
- M. Naguib, et al., Two-Dimensional Nanocrystals Produced by Exfoliation of Ti3AlC2, Adv. Mater., 2011, 23(37), 4248–4253 CrossRef CAS PubMed.
- I. E. B. Aronsson, X-ray investigations on Me–Si–B systems (Me = Mn, Fe, Co). II. Some features of the Fe–Si–B and Mn–Si–B systems, Acta Chem. Scand., 1960, 14, 1403–1413 CrossRef.
- H. Rohde and H. Kudielka, Strukturuntersuchungen an Carbosulfiden von Titan und Zirkon, Z. Kristallogr. - Cryst. Mater., 1960, 114(1–6), 447–456 CrossRef.
- M. Sokol, et al., On the Chemical Diversity of the MAX Phases, Trends Chem., 2019, 1(2), 210–223 CrossRef CAS.
- M. Ade and H. Hillebrecht, Ternary Borides Cr2AlB2, Cr3AlB4, and Cr4AlB6: The First Members of the Series (CrB2)nCrAl with n = 1, 2, 3 and a Unifying Concept for Ternary Borides as MAB-Phases., Inorg. Chem., 2015, 54(13), 6122–6135 CrossRef CAS PubMed.
- H. Zhang, et al., Crystal structure of Cr4AlB4: a new MAB phase compound discovered in Cr–Al–B system., J. Mater. Sci. Technol., 2019, 35(4), 530–534 CrossRef.
- Y. Zhang, et al., The role of Hume-Rothery's rules play in the MAX phases formability, Materialia, 2020, 12, 100810 CrossRef CAS.
- C. Shen, et al. Designing of Magnetic MAB Phases for Energy Applications, 2020, arXiv:2009.14543.
- X. Gu, et al., Sorting transition-metal diborides: new descriptor for mechanical properties, Acta Mater., 2021, 207, 116685 CrossRef CAS.
- D. V. Rybkovskiy, et al., Structure, Stability, and Mechanical Properties of Boron-Rich Mo–B Phases: A Computational Study, J. Phys. Chem. Lett., 2020, 11(7), 2393–2401 CrossRef CAS PubMed.
- K. Kádas,
et al., AlM2B2(M
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cr, Mn, Fe, Co, Ni): a group of nanolaminated materials, J. Phys.: Condens. Matter, 2017, 29(15), 155402 CrossRef PubMed.
Cr, Mn, Fe, Co, Ni): a group of nanolaminated materials, J. Phys.: Condens. Matter, 2017, 29(15), 155402 CrossRef PubMed. - P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- A. Poulou, T. A. Mellan and M. W. Finnis, Stability of Zr–Al–C and Ti–Al–C MAX phases: a theoretical study, Phys. Rev. Mater., 2021, 5(3), 033608 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations., Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13(12), 5188–5192 CrossRef.
- R. Nelson, et al., LOBSTER: Local orbital projections, atomic charges, and chemical-bonding analysis from projector-augmented-wave-based density-functional theory, J. Comput. Chem., 2020, 41(21), 1931–1940 CrossRef CAS PubMed.
- V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, Crystal orbital Hamilton population (COHP) analysis as projected from plane-wave basis sets, J. Phys. Chem. A, 2011, 115(21), 5461–5466 CrossRef CAS PubMed.
- R. Dronskowski and P. E. Bloechl, Crystal orbital Hamilton populations (COHP): energy-resolved visualization of chemical bonding in solids based on density-functional calculations, J. Phys. Chem., 1993, 97(33), 8617–8624 CrossRef CAS.
- S. Maintz, et al., Analytic projection from plane-wave and PAW wavefunctions and application to chemical-bonding analysis in solids, J. Comput. Chem., 2013, 34(29), 2557–2567 CrossRef CAS PubMed.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data., J. Appl. Crystallogr., 2011, 44(6), 1272–1276 CrossRef CAS.
- M. Ashton, et al., Computational discovery of stable M2AX phases., Phys. Rev. B, 2016, 94(5), 054116 CrossRef.
- D. Horlait, et al., Synthesis and DFT investigation of new bismuth-containing MAX phases, Sci. Rep., 2016, 6(1), 18829 CrossRef CAS PubMed.
- M. Khazaei, et al., Electronic properties and applications of MXenes: a theoretical review, J. Mater. Chem. C, 2017, 5(10), 2488–2503 RSC.
- Z. M. Wong, et al., Computational Discovery of Transparent Conducting In-Plane Ordered MXene (i-MXene) Alloys, Chem. Mater., 2019, 31(11), 4124–4132 CrossRef CAS.
- P. Eklund, et al., Discovery of the Ternary Nanolaminated Compound Nb2GeC by a Systematic Theoretical-Experimental Approach, Phys. Rev. Lett., 2012, 109(3), 035502 CrossRef PubMed.
- M. Dahlqvist and J. Rosen, Predictive theoretical screening of phase stability for chemical order and disorder in quaternary 312 and 413 MAX phases, Nanoscale, 2020, 12(2), 785–794 RSC.
- F.-Z. Dai, et al., M2M'AlB4 (M = Mn, Fe, Co, M′ = Cr, Mo, W): Theoretical predicted ordered MAB phases with Cr3AlB4 crystal structure, J. Mater. Sci. Technol., 2019, 35(7), 1432–1438 CrossRef.
- M. Dahlqvist, et al., Phase stability of Ti2AlC upon oxygen incorporation: a first-principles investigation, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(2), 024111 CrossRef.
- L. A. Hanner, et al., Synthesis, characterization and first principle modelling of the MAB phase solid solutions: (Mn1−xCrx)2AlB2 and (Mn1−xCrx)3AlB4, Mater. Res. Lett., 2021, 9(2), 112–118 CrossRef CAS.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD), JOM, 2013, 65, 1501–1509 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, The Materials Project: a materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- Springer Materials: The Landolt-Börnstein database.
- N. Miao, et al., Computational Prediction of Boron-Based MAX Phases and MXene Derivatives, Chem. Mater., 2020, 32(16), 6947–6957 CrossRef CAS.
- W. A. Deskin, Inorganic chemistry: principles of structure and reactivity (Huheey, James E.), J. Chem. Educ., 1973, 50(7), A379 CrossRef.
- N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, 2nd edn, 1997 Search PubMed.
- U. Mizutani and H. Sato, Determination of electrons per atom ratio for transition metal compounds studied by FLAPW-Fourier calculations, Philos. Mag., 2016, 96(29), 3075–3096 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1cp05750b |
| This journal is © the Owner Societies 2022 |