Open Access Article
Open Access ArticleNitrene formation is the first step of the thermal and photochemical decomposition reactions of organic azides†
Juan
Soto
 *a,
Manuel
Algarra
*a,
Manuel
Algarra
 b and
Daniel
Peláez
c
b and
Daniel
Peláez
c
aDepartment of Physical Chemistry, Faculty of Science, University of Málaga, E-29071 Málaga, Spain. E-mail: soto@uma.es
bINAMAT2 Institute for Advanced Materials and Mathematics, Department of Sciences, Campus de Arrosadia, 31006 Pamplona, Spain
cInstitut des Sciences Moléculaires d’Orsay (ISMO) - UMR 8214, Université Paris-Saclay, 91405 Orsay Cedex, Spain
First published on 31st January 2022
Abstract
In this work, the decomposition of a prototypical azide, isopropyl azide, both in the ground and excited states, has been investigated through the use of multiconfigurational CASSCF and MS-CASPT2 electronic structure approaches. Particular emphasis has been placed on the thermal reaction starting at the S0 ground state surface. It has been found that the azide thermally decomposes via a stepwise mechanism, whose rate-determining step is the formation of isopropyl nitrene, which is, in turn, the first step of the global mechanism. After that, the nitrene isomerizes to the corresponding imine derivative. Two routes are possible for such a decomposition: (i) a spin-allowed path involving a transition state; and (ii) a spin-forbidden one via a S0/T0 intersystem crossing. Both intermediates have been determined and characterised. Their associated relative energies have been found to be quite similar, 45.75 and 45.52 kcal mol−1, respectively. To complete this study, the kinetics of the singlet and triplet channels are modeled with the MESMER (Master Equation Solver for Multi-Energy Well Reactions) code by applying the RRKM and Landau–Zener (with WKB tunnelling correction) theories, respectively. It is found that the canonical rate-coefficients of the singlet path are 2-orders of magnitude higher than the rate-coefficients of the forbidden reaction. In addition, the concerted mechanism has been investigated that would lead to the formation of the imine derivative and nitrogen extrusion in the first step of the decomposition. After a careful analysis of CASSCF calculations with different active spaces and their comparison with single electronic configuration methods (MP2 and B3LYP), the concerted mechanism is discarded.
Introduction
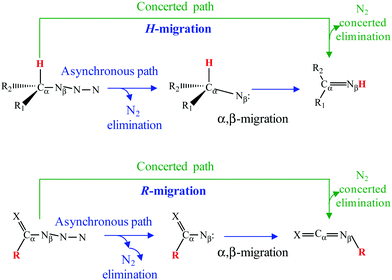
Organic azides (R–N3) play significant roles in a plethora of fields ranging from chemical synthesis, biological chemistry and pharmaceutics, to technological applications. For example, they are important components in click chemistry1–3 or synthesis of energetic materials.4–12 Most of these applications as well as their exceptional reactivity arise from their ability to generate nitrene intermediates after N2 extrusion.13–17 Although organic azides are known for more than a century,18 the decomposition reaction mechanism at an atomistic level is still under discussion. More specifically, there is a lack of agreement in the nature (concerted or asynchronous) of the so-called α,β-migration reaction in azides (Refs. 19 and 20 to cite both examples). In this process, a group attached to the neighboring Cα (for example an H-atom or another R-substituent, see Scheme 1) migrates to the Nβ. The presence of an intermediate would imply an asynchronous mechanism whereas a lack thereof would mean a concerted one (Scheme 1). To the best of our knowledge, such a controversy arises from two important sources: (i) the theoretical approach used to study the reaction; (ii) the energy barrier for α,β-migration starting at the nitrene intermediate is usually very low.19–23Hence, the main aim of this work is to shed some light on this issue. To reach this end, we have studied the reaction mechanism and kinetics of the thermal and photochemical decompositions of isopropyl azide [(CH3)2CHN3]. This alkyl azide has been selected for two reasons: (a) the thermolysis of this azide was experimentally studied by Bock and Dammel;24 (b) it has a unique migrating hydrogen atom. Unfortunately, to the best of our knowledge, there is no published data on the photochemistry of the title compound. Thus, the only available values are the calculated parameters (vertical excitations and oscillator strengths) by ourselves corresponding to the photochemical reaction of an analogous alkyl azide.19
In this work, we have performed a theoretical study using the complete active space self-consistent (CASSCF) method, which is compared with the data obtained from two commonly used single electronic configuration methods: (1) second order Møller–Plesset theory (MP2) and (2) density functional theory (DFT). Our results will demonstrate that the decomposition proceeds by a stepwise mechanism (asynchronous channel), whose initial step is the extrusion of N2 leading to the formation of the isopropyl nitrene intermediate. Furthermore, it is observed that two channels for nitrene formation exist: (i) via singlet and (ii) via triplet states. In addition, it will be shown through analysis of the kinetics of the singlet and triplet channels, and it is found that the formation of singlet nitrene is the main reaction channel in the decomposition of the studied azide.
Computational details
Multiconfigurational geometry optimizations of all the relevant species and intermediates of this work have been performed with the CASSCF25–33 method in conjunction with the ANO-RCC and ANO-R basis sets,34–36 as they are implemented in the MOLCAS 8.4 program.37,38 In addition, the energies of such species have been corrected by the multi-state second-order perturbation (MS-CASPT2)39,40 method by applying an imaginary shift equal to 0.1 in order to avoid the inclusion of intruder states, and the empirical correction (IPEA) was fixed at 0.25 in all the calculations. State average CASSCF calculations are denoted as SAn-CASSCF, where n denotes the number of states of a given symmetry included in the calculation. Spin–orbit coupling constants (SOCC) of intersystem crossing (ISC) have been computed with a spin–orbit Fock-type Hamiltonian.41–43Single electronic configuration calculations have been carried out with the Møller–Plesset (MP2)44 and DFT/B3LYP45 methods in conjunction with the def2-TZVPPbasis sets.46,47
Graphical analysis of the molecular geometries, vibrational normal modes and vectors defining the seam of crossing of minimum energy crossing points (MECP) has been performed with the program MacMolplt.48 Analysis of molecular orbitals have been carried out with the programs Gabedit49 and Molden.50
The labelling convention for the electronic states is based on their energetic ordering (S0, S1,…; T0, T1,…), where 0 denotes the lowest energy state in each spin state (singlet, S, or triplet, T). The construction of the potential energy curves (PECs) has been done with a linear interpolation method51–55 using the full space of non-redundant internal coordinates, which are built as follows. First, a common set of 3N-6 internal coordinates is defined for the target geometries, the reactants (R1) and the products (R2). Note that in the case of dissociation the fragments are separated by a physically reasonable distance [Δ(R2–R1)]. Our calculations show that a value of ∼4.7 Å for the dissociative bond (in this work, the N–N2) is enough to reach the asymptotic limit of the potential energy surface (PES) with respect to dissociation of the azide into nitrene and N2. This leads to an excellent agreement between the experimental and calculated enthalpies of dissociation.56,57 Second, the difference between R2 and R1 yields an interpolation vector (ΔR) that connects the reactants and products. Third, ΔR is divided into n segments. This parameter is chosen in order to ensure a smooth convergence of the CASSCF wavefunction upon a geometrical distortion following the ΔR hyperline. Consequently, each of the divisions constitutes an interpolation step corresponding to a given nuclear conformation on ΔR. The m-th one is given by Rm = R1 + (m/n) with m = 1,…,n. Given that our interpolation vectors result from the combination of valence coordinates (internuclear distances, valence bond and dihedral angles), we cannot give a unique unit for them and, in what follows, we will describe them as arbitrary units. Linear interpolations in internal coordinates present two main features that make them particularly appealing to these studies: (i) they are less expensive than scans with relaxation of geometry; (ii) all the points along the interpolation vector (reaction coordinate) are necessarily in a straight line within the set of defined coordinates hence providing a suitable set of coordinates for the representation of reduced dimensionality potential energy surfaces.
Finally, the rate constants associated with transition states (adiabatic reactions) as well as intersystem crossings (non-adiabatic reactions) have been determined with the program MESMER version 5.2.58–62 The microcanonical rate constants of transitions states have been computed using the Rice and Ramsperger–Kassel–Marcus (RRKM) theory63–66 and the microcanonical rate coefficients of ISCs have been calculated with the Landau–Zener67,68 model with inclusion of tunnelling corrections as described by Harvey and Aschi.69
Results and discussion
Selection of the active spaces of isopropyl azide
Given that we are interested in disentangling whether or not α,β-migration is involved in the initial step of the decomposition of azides, isopropyl azide has been studied with two active spaces of different sizes, including or not the bonding/antibonding pair or molecular orbitals (MOs) describing the σ(CH) bond (Cα in Scheme 1). These two active spaces have been carefully chosen in order to avoid misleading results.70–73 This, in turn, has allowed us to calibrate the reliability of our calculations. The largest active space comprises 16 electrons distributed in 14 MOs (Fig. 1). These correspond to: the 2s(N) of the N atom closest to Cα, the bonding/antibonding σ(CH) pair involving the Cα, and the migrating H, two bonding/antibonding σ(NNN) couples, two bonding/antibonding π(NNN) couples and one non-bonding π(NNN) orbital. The MOs included in the second smaller active space are the same as before except for the bonding/antibonding σ(CH) couple, as a consequence, it comprises 14 electrons and 12 orbitals.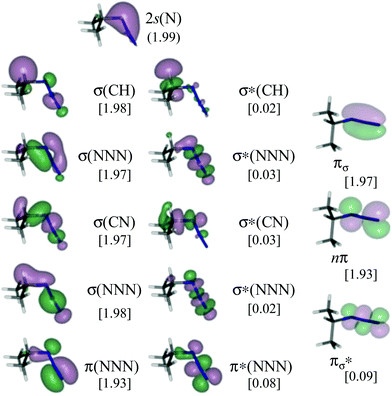 | ||
| Fig. 1 CASSCF/ANO-RCC natural orbitals included in the active space (16e, 14o) of isopropyl azide. In square brackets: occupation numbers of the natural orbitals. | ||
Mechanism of the dissociation of isopropyl azide from the CASSCF multiconfigurational perspective
In this section, we study the thermal and photochemical dissociation mechanisms of isopropyl azide in the ground and excited states, with special emphasis on the thermal reactions. Unless otherwise specified, all the calculations in this section have been performed under Cs symmetry with the CASSCF method and with an active space of 16 electrons and 14 orbitals. Thus, in a first stage, we have calculated (Table 1) the vertical excitation energies of the low-lying singlet and triplet states of the azide with respect to the minimum of the ground state (S0); in addition, Table 1 shows the character of the most relevant electronic configurations and the associated oscillator strengths of the singlet states or spin orbit coupling constants (Tn/S0: n = 0,1) for the triplet states, respectively. Vertically, the lowest excited state (4.19 eV: 97 kcal mol−1) corresponds to the first triplet state [T0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13A′′] and just above it (4.49 eV: 103 kcal mol−1), we have found the first excited singlet state [S1
13A′′] and just above it (4.49 eV: 103 kcal mol−1), we have found the first excited singlet state [S1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
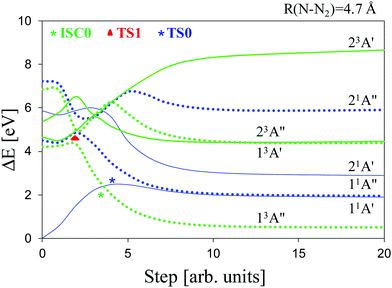
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11A′′], whose oscillator strength amounts to ∼9 10−4. Second, in accordance with the linear interpolation method (see above), we have determined the potential energy curves (PECs) for the dissociation processes of the electronic states of Table 1 that would lead to the formation of nitrene species and molecular nitrogen (Fig. 2). Furthermore, these PECs have provided a reasonable guess geometry for subsequent optimization of the critical points related to the sought dissociation channels in the relevant electronic states.
11A′′], whose oscillator strength amounts to ∼9 10−4. Second, in accordance with the linear interpolation method (see above), we have determined the potential energy curves (PECs) for the dissociation processes of the electronic states of Table 1 that would lead to the formation of nitrene species and molecular nitrogen (Fig. 2). Furthermore, these PECs have provided a reasonable guess geometry for subsequent optimization of the critical points related to the sought dissociation channels in the relevant electronic states.
| State | VE | f OSC | Configurationd | W |
|---|---|---|---|---|
| a C s MP2/def2-TZVPP optimized geometry. b SA2-CASSCF(16e, 14o)/ANO-RCC reference wave function, IPEA = 0.25. Imaginary shift = 0.1. c Oscillator strength. d MS-CASPT2 main electronic configurations of the excited states referred to the ground state configuration. e Weight of the configuration in %. Only contributions greater than 15% are included. f Spin orbit coupling constant in cm−1. | ||||
| 21A′ | 5.87 | 6.42 10−4 | [nπ]1[πσ*]1 | 39 |
| [π(NNN)]1[π*(NNN)]1 | 48 | |||
| 11A′′ | 4.49 | 8.68 10−-4 | [nπ]1[π*(NNN)]1 | 89 |
| 21A′′ | 7.22 | 5.94 10−3 | [π(NNN)]1[πσ*]1 | 89 |
| SOCf | ||||
| 13A′ | 4.66 | 0 | [nπ]1[πσ*]1 | 75 |
| [π(NNN)]1[π*(NNN)]1 | 15 | |||
| 23A′ | 5.36 | 0 | [nπ]1[πσ*]1 | 15 |
| [π(NNN)]1[π*(NNN)]1 | 73 | |||
| 13A′′ | 4.19 | 16.72 | [nπ]1[π*(NNN)]1 | 88 |
| 23A′′ | 6.85 | 16.52 | [π(NNN)]1[πσ*]1 | 89 |
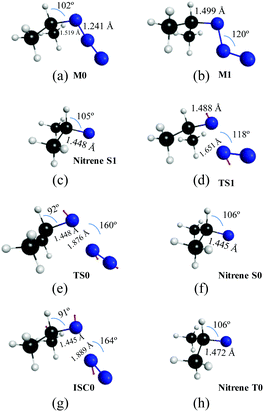
In Fig. 3 and 4, we display the geometries of the relevant critical points. The minimum energy geometry on the ground state S0 (M0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11A′) is represented in Fig. 3a. There also exists a minimum energy geometry on the surface of the first excited singlet S1 (M1
11A′) is represented in Fig. 3a. There also exists a minimum energy geometry on the surface of the first excited singlet S1 (M1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11A′′ [Fig. 3b]) state which lies 40.7 kcal mol−1 below the 11A′ → 11A′′ vertical excitation energy. Concerning the photochemistry of the molecules, the dissociation of the azide into isopropyl nitrene and N2 on the first excited singlet surface (11A′′) can occur after surmounting a small barrier to yield singlet nitrene (11A′′ [Fig. 3c]). The barrier corresponds to a transition state (TS1
11A′′ [Fig. 3b]) state which lies 40.7 kcal mol−1 below the 11A′ → 11A′′ vertical excitation energy. Concerning the photochemistry of the molecules, the dissociation of the azide into isopropyl nitrene and N2 on the first excited singlet surface (11A′′) can occur after surmounting a small barrier to yield singlet nitrene (11A′′ [Fig. 3c]). The barrier corresponds to a transition state (TS1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11A′′ [Fig. 3d]) that is 2.6 kcal mol−1 above M1 (S1 minimum). In contrast, the first excited triplet state does not present any minimum on the T0 surface around the Franck–Condon region, in fact, this state is dissociative. Concerning the thermal decomposition reaction, two channels for the generation of the nitrene intermediate have been determined: (i) a spin-allowed path, via a transition state on the S0 surface (TS0
11A′′ [Fig. 3d]) that is 2.6 kcal mol−1 above M1 (S1 minimum). In contrast, the first excited triplet state does not present any minimum on the T0 surface around the Franck–Condon region, in fact, this state is dissociative. Concerning the thermal decomposition reaction, two channels for the generation of the nitrene intermediate have been determined: (i) a spin-allowed path, via a transition state on the S0 surface (TS0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11A′ [Fig. 3e]) 45.8 kcal mol−1 above M0, which yields singlet nitrene (11A′: [Fig. 3f]); (ii) a spin-forbidden path, via an S0/T0 intersystem crossing process whose MECP lies 45.5 kcal mol−1 above M0 which is represented in Fig. 3g (ISC0
11A′ [Fig. 3e]) 45.8 kcal mol−1 above M0, which yields singlet nitrene (11A′: [Fig. 3f]); (ii) a spin-forbidden path, via an S0/T0 intersystem crossing process whose MECP lies 45.5 kcal mol−1 above M0 which is represented in Fig. 3g (ISC0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11A′/13A′′) and yields triplet nitrene (13A′′: [Fig. 3h]). It is worth noting that the spatial separation between TS0 and ISC0 is only 0.02 Å measured in Cartesian coordinates, a feature that should be important in the dynamics of dissociation through the spin-forbidden channel, given that this fact would imply an enhancement of the probability of intersystem crossing.74
11A′/13A′′) and yields triplet nitrene (13A′′: [Fig. 3h]). It is worth noting that the spatial separation between TS0 and ISC0 is only 0.02 Å measured in Cartesian coordinates, a feature that should be important in the dynamics of dissociation through the spin-forbidden channel, given that this fact would imply an enhancement of the probability of intersystem crossing.74
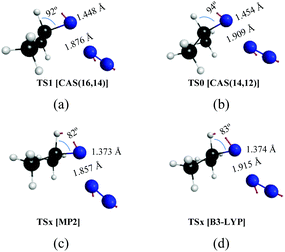 | ||
| Fig. 4 Transition states on the potential energy surfaces leading to dissociation of isopropyl azide into isopropyl nitrene and N2 obtained by different methods. | ||
The results obtained for the smaller active space are completely analogous to those reported in the previous paragraphs thus evidencing the robustness of our choice of active spaces. Specific data of these calculations are reported in the ESI† (Tables S1 to S8).
To finish this section, we give the main parameters, energetics and SOCC, calculated with the two basis sets and active spaces applied in this work (Table 2).
| BS1c | BS2d | BS3e | BS4f | |
|---|---|---|---|---|
| a Calculation referred to the same geometry used in Table 1. b Two-state average wave function. c CAS(16,14)/ANO-RCC. d CAS(14,12)/ANO-RCC. e CAS(16,14)/ANO-R. f CAS(14,12)/ANO-R. g Energy barrier height of the singlet channel. h Energy barrier height of the triplet channel. i Dissociation energy of the singlet channel. j Dissociation energy of the triplet channel. k Spin orbit coupling constant in cm−1. | ||||
| ΔE(S)g | 45.75 | 46.90 | 47.73 | 49.03 |
| ΔE(T)h | 45.52 | 46.39 | 47.34 | 48.46 |
| ΔE(DS)i | 43.52 | 43.54 | 46.01 | 46.22 |
| ΔE(DT)j | 11.11 | 11.19 | 13.49 | 13.76 |
| SOCCk | 49.05 | 47.02 | 46.40 | 46.33 |
Comparison of the decomposition mechanisms obtained from mono- and multiconfigurational methods
The reaction mechanism of the decomposition of isopropyl azide has been analyzed in the previous section. In here, we compare the CASSCF results with those that are obtained from MP2 and DFT/B3LYP calculations. As was noticed in the Introduction section, there are discrepancies among different theoretical approximations about the mechanism of the reaction (Scheme 1). To be specific, single electronic configuration methods, such as MP2 or DFT/B3LYP, predict a concerted mechanism for the dissociation of organic azides (profiles of the intrinsic reaction coordinates are given in Fig. S1, ESI†) leading to acetone imine formation as the main product. In contrast, multiconfigurational methods, such as CASSCF, yield an asynchronous mechanism in which isopropyl nitrene is the main intermediate of the first reaction step, but can be formed by two different channels: (i) spin-allowed and (ii) spin-forbidden. The geometries of the transition states for the first reaction step obtained with the four different approaches applied in this work are given in Fig. 4. Thus, Fig. 4a and b represent the structures calculated with the MP2 and DFT/B3LYP methods, respectively, and the geometries obtained from the two CASSCF calculations performed with two different active spaces are given in Fig. 4c d. The arrows in the structures depicted in Fig. 4 correspond to the normal mode of the imaginary frequency associated with the transition vector, which is parallel to the reaction coordinate. From the representation of the transition vectors of Fig. 4, it is clear that the α-H atom has an important contribution to the reaction coordinate of the MP2 and B3LYP calculations, while the CASSCF results indicate that such an atom does not significantly participate in the dissociation reaction, independent of whether the σ(CH) bonding/antibonding molecular orbitals were included or not in the CASSCF calculations. To obtain a quantitative estimation of the participation of each atom in the transition vector for each calculation, after performing the vibrational analysis of these transition states according to the GF method of Wilson,75,76 we have computed the potential energy distribution (PED) of the internal coordinates in each normal mode (Table S9, ESI†). Thus, the values shown in Tables S9 and S10 (ESI†) corroborate the previous assertion that was based on the pictorial representation of such transition vectors.Kinetics of the spin-allowed and spin-forbidden channels for isopropyl nitrene formation
Experimental decomposition of isopropyl azide was studied by Bock and Dammel.24 The pyrolysis of the azide was carried out under (nearly) unimolecular conditions (∼1 Pa). It was found that decomposition of the azide began above 600 K and was completed at 770 K. The main reaction products were the imine derivative and N2 In accordance with the experimental conditions, we have computed the coefficient rates for both channels (allowed and forbidden) in the 600–780 K range of temperatures. To achieve this end, we have modeled the kinetics of the dissociation reactions by calculating the reactions rates for the formation of singlet and triplet isopropyl nitrene from the parent azide with the program MESMER.51–55 The rate coefficients of the spin-allowed channel have been evaluated with the RRKM theory61–64 and the rate coefficients of ISC with the nonadiabatic transition state theory of the Landau–Zener67,68 model with inclusion of tunneling corrections.69 In Fig. 5, we present the canonical coefficient rates for both channels. The picture obtained from this graphic is crystal clear, and the predominant reaction channel corresponds to the spin-allowed channel whereas the triplet is 2 orders of magnitude lower.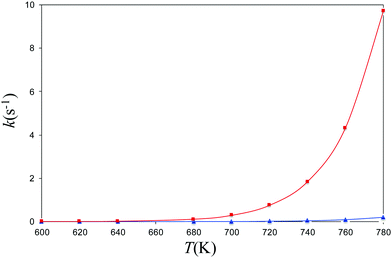 | ||
| Fig. 5 Canonical rate coefficients as a function of temperature of the singlet and triplet channels for the dissociation of isopropyl azide into isopropyl nitrene and N2. | ||
Concerning the calculations of density of states and vibrational partition functions for the MECP geometries, it is interesting to note that, in our calculations, there are two Hessians associated with each MECP (a singlet state Hessian H1 and a triplet state Hessian H2). To solve this complication, first, the effective Hessian matrix is introduced which is defined by eqn (1):77
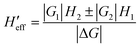 | (1) |
As usual, 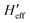 has been computed in Cartesian coordinates. This 3N × 3N matrix still contains 3N-6 vibrational degrees of freedom plus the six rotational-translational degrees of freedom (N being the number of atoms). Since the structures of the minimum energy crossing points (MECP) are not stationary points on any potential energy surface, the standard vibrational analysis is not valid at such crossing points. To do this properly, it is mandatory to project out from
has been computed in Cartesian coordinates. This 3N × 3N matrix still contains 3N-6 vibrational degrees of freedom plus the six rotational-translational degrees of freedom (N being the number of atoms). Since the structures of the minimum energy crossing points (MECP) are not stationary points on any potential energy surface, the standard vibrational analysis is not valid at such crossing points. To do this properly, it is mandatory to project out from 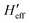 both the rotational-translational components as well as the gradient different vector. The projected matrix Heff is shown in eqn (2).23
both the rotational-translational components as well as the gradient different vector. The projected matrix Heff is shown in eqn (2).23
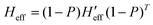 | (2) |
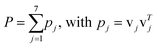 | (3) |
Conclusions
We studied the thermal and photochemical decomposition reactions of a prototypical alkyl azide, isopropyl azide, with emphasis on the thermal process. It is found that multiconfigurational methods (CASSCF in our case) are necessary to correctly describe the mechanism. We found that the first and rate-determining step of the reaction is the dissociation of the parent azide into isopropyl nitrene and molecular nitrogen. The prior assertion is applicable for both thermal and photochemical reactions.The photochemical reaction yields singlet nitrene. On the other hand, the formation of the nitrene intermediate in the thermal decomposition reaction can occur through two different mechanisms: one is a spin-allowed channel that passes through a conventional transition state on the S0 ground state surface yielding the singlet nitrene and the other mechanism is a spin-forbidden path which implies S0/T0 intersystem crossing yielding the triplet nitrene. The modelling of the kinetics of such paths gives the spin-allowed reaction as the major contribution to the formation of nitrene, as a consequence, the nitrene intermediate is formed in its singlet state. Afterwards, the singlet nitrene intermediate can isomerize to the imine derivative through an almost barrierless process. The estimated upper limit for nitrene–imine isomerization is less than 1 kcal mol−1 (Fig. S2, ESI†).
In contrast, the pictures obtained from single electronic methods, such as MP2 and B3LYP, are completely different, that is, both of them give a concerted mechanism in which imine formation is concurrent with elimination of molecular nitrogen.
However, in our opinion, the key point to give an appropriate answer to the problem under study lies in the electronic nature of the nitrene intermediate, which either in its triplet states or in its singlet states must be described by a multiconfigurational reference function. Thus, CASSCF seems to be a most suitable method to deal with the dissociation reaction of azides rather than MP2 or DFT/B3LYP methods.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work has been supported by projects UMA18-FEDER-JA-049 and P18-RT-4592 of Junta de Andalucía and FEDER founds. The authors thank R. Larrosa, D. Guerrero and F. Moreno for the technical support in running the calculations and the SCBI (Supercomputer and Bioinformatics) of the Univ. Málaga for computer and software resources.References
- A. Dehankar, T. Porter, J. A. Johnson, C. E. Castro and J. O. Winter, J. Chem. Phys., 2019, 151, 144706 CrossRef PubMed.
- M. Danese, M. Bon, G. M. Piccini and D. Passerone, Phys. Chem. Chem. Phys., 2019, 21, 19281–19287 RSC.
- P. J. Silva and C. E. P. Bernardo, J. Phys. Chem. A, 2018, 122, 7497–7507 CrossRef CAS PubMed.
- A. L. Shoaf and C. A. Bayse, New J. Chem., 2019, 43, 15326–15334 RSC.
- S. Kucher, S. Korneev, J. P. Klare, D. Klose and H.-J. Steinhoff, Phys. Chem. Chem. Phys., 2020, 22, 13358–13362 RSC.
- L. Bauer, M. Benz, T. M. Klapötke, T. Lenz and J. Stierstorfer, J. Org. Chem., 2021, 86, 6371–6380 CrossRef CAS PubMed.
- M. V. Gorn, N. P. Gritsan, C. F. Goldsmith and V. G. Kiselev, J. Phys. Chem. A, 2020, 124, 7665–7677 CrossRef CAS PubMed.
- Q. Liang, K. Hayashi, Y. Zeng, J. L. Jiménez-Santiago and D. Song, Chem. Commun., 2021, 57, 6137–6140 RSC.
- M. Schock and S. Bräse, Molecules, 2020, 25, 1009 CrossRef CAS PubMed.
- Q. Li, L. Yan, Z. Wang, Y. Lu, S. Wei, X. Liu and L. Wang, J. Chem. Phys., 2020, 152, 044704 CrossRef CAS PubMed.
- J. Li, M.-K. Liu, Q.-S. Li and Z.-S. Li, Phys. Chem. Chem. Phys., 2020, 22, 28317–28324 RSC.
- J. Y. Park, S. Mondal, H.-J. Kwon, P. K. Sahu, H. Han, K. Kwak and M. Cho, J. Chem. Phys., 2020, 153, 164309 CrossRef CAS PubMed.
- B. A. Shainyan, A. V. Kuzmin and M. Y. Moskalik, Comput. Theor. Chem., 2013, 1006, 52–61 CrossRef CAS.
- M. Schock and S. Bräse, Molecules, 2020, 25, 1009 CrossRef CAS PubMed.
- J. Soto and J. C. Otero, J. Phys. Chem. A, 2019, 123, 9053–9060 CrossRef CAS PubMed.
- D. Aranda, F. J. Avila, I. Lopez-Tocon, J. F. Arenas, J. C. Otero and J. Soto, Phys. Chem. Chem. Phys., 2018, 20, 7764–7771 RSC.
- J. Soto, J. C. Otero, F. J. Avila and D. Peláez, Phys. Chem. Chem. Phys., 2019, 21, 2389–2396 RSC.
- T. Curtius, Ber. Dtsch. Chem. Ges., 1890, 23, 3033–3041 CrossRef CAS.
- M. Algarra, J. Soto, L. Pinto da Silva, M. S. Pino-Gonzaĺez, J. E. Rodríguez-Borges, J. Mascetti, F. Borget, A. Reisi-Vanani and R. Luque, J. Phys. Chem. A, 2020, 124, 1911–1921 CrossRef CAS PubMed.
- J. F. Arenas, J. I. Marcos, J. C. Otero, A. Sanchez-Galvez and J. Soto, J. Chem. Phys., 1999, 111, 551–561 CrossRef CAS.
- J. F. Arenas, J. I. Marcos, J. C. Otero, A. Sanchez-Galvez and J. Soto, J. Chem. Phys., 1999, 111, 551–561 CrossRef CAS.
- M. Algarra and J. Soto, ChemPhysChem, 2020, 21, 1126–1133 CrossRef CAS PubMed.
- J. F. Arenas, J. I. Marcos, I. Lopez-Tocon, J. C. Otero and J. Soto, J. Chem. Phys., 2000, 113, 2282–2289 CrossRef CAS.
- H. Bock and R. Dammel, J. Am. Chem. Soc., 1988, 110, 5261–5269 CrossRef CAS.
- B. O. Roos, in Advances in Chemical Physics; Ab initio Methods in Quantum Chemistry II, ed. K. P. Lawley, John Wiley & Sons, Chichester, UK, 1987, ch. 69, p. 399 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- B. O. Roos, Int. J. Quantum Chem., 1980, 18, 175–189 CrossRef.
- P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, J Chem. Phys., 1981, 74, 2384–2396 CrossRef.
- H.-J. Werner and W. Meyer, J. Chem. Phys., 1980, 73, 2342–2356 CrossRef CAS.
- H.-J. Werner and W. Meyer, J. Chem. Phys., 1981, 74, 5794–5801 CrossRef CAS.
- J. Olsen, Int. J. Quantum. Chem., 2011, 111, 3267–3272 CrossRef CAS.
- D. A. Kreplin, P. J. Knowles and H.-J. Werner, J. Chem. Phys., 2019, 150, 194106 CrossRef PubMed.
- D. A. Kreplin, P. J. Knowles and H.-J. Werner, J. Chem. Phys., 2020, 152, 074102 CrossRef CAS PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 109, 6575–6579 CrossRef PubMed.
- J. P. Zobel, P. O. Widmark and V. Veryazov, J. Chem. Theory Comput., 2020, 16, 278–294 CrossRef PubMed.
- MOLCAS 8.4 V. Veryazov, P.-O. Widmark, L. Serrano-Andrés, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626–635 CrossRef CAS.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fernández. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, Molcas 8: New capabilities for multiconfigurational quantum chemical calculations across the periodic table, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- B. O. Roos, K. Andersson, M. P. Fülscher, P. Å. Malmqvist, L. Serrano-Andrés, K. Pierloot and M. Merchán, Adv. Chem. Phys., 1996, 93, 219–331 CAS.
- J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef.
- P. A. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- C. Ribbing, B. Gilliams, K. Pierloot, B. O. Roos and G. Karlström, J. Chem. Phys., 1998, 109, 3145–3152 CrossRef CAS.
- C. Møller and M. S. Plesser, Phys. Rev., 1934, 46, 618–622 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. R. Allouche, J. Comput. Chem., 2011, 32, 174–182 CrossRef CAS PubMed.
- G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134 CrossRef CAS PubMed.
- B. M. Bode and M. S. Gordon, J. Mol. Graphics Modell., 1998, 16, 133–138 CrossRef CAS PubMed.
- J. Soto, D. Peláez, J. C. Otero, F. J. Avila and J. F. Arenas, Phys. Chem. Chem. Phys., 2009, 11, 2631–2639 RSC.
- D. Pelaez, J. F. Arenas, J. C. Otero and J. Soto, J. Chem. Phys., 2006, 125, 164311 CrossRef PubMed.
- M. Algarra, V. Moreno, J. M. Lazaro-Martinez, E. Rodriguez-Castellon, J. Soto, J. Morales and A. Benitez, J. Colloid Interface Sci., 2020, 561, 678–686 CrossRef CAS PubMed.
- M. Louleb, L. Latrous, A. Rios, M. Zougagh, E. Rodriguez-Castellon, M. Algarra and J. Soto, ACS Appl. Nano Mater., 2020, 3, 8004–8011 CrossRef CAS.
- J. F. Arenas, J. C. Otero, D. Pelaez, J. Soto and L. Serrano-Andres, J. Chem. Phys., 2004, 121, 4127–4132 CrossRef CAS PubMed.
- J. Soto and M. Algarra, J. Phys. Chem. A, 2021, 125, 9431–9437 CrossRef CAS PubMed.
- J. Soto, D. Peláez and J. C. Otero, J. Chem. Phys., 2021, 154, 044307 CrossRef CAS PubMed.
- D. R. Glowacki, C. H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560 CrossRef CAS PubMed.
- P. Pokhilko, R. Shannon, D. Glowacki, H. Wang and A. I. Krylov, J. Phys. Chem. A, 2019, 123, 482–491 CrossRef CAS PubMed.
- L. Onel, R. Lade, J. Mortiboy, M. A. Blitz, P. W. Seakins, D. E. Heard and D. Stone, Phys. Chem. Chem. Phys., 2021, 23, 19415–19423 RSC.
- Z. S. Mir, T. R. Lewis, L. Onel, M. A. Blitz, P. W. Seakins and D. Stone, Phys. Chem. Chem. Phys., 2020, 22, 9448–9459 RSC.
- D. J. Medeiros, S. H. Robertson, M. A. Blitz and P. W. Seakins, J. Phys. Chem. A, 2020, 124, 4015–4024 CrossRef CAS PubMed.
- O. K. Rice and H. C. Ramsperger, J. Am. Chem. Soc., 1927, 49, 1617–1629 CrossRef CAS.
- (a) L. S. Kassel, J. Phys. Chem., 1928, 32, 225–242 CrossRef CAS; (b) L. S. Kassel, J. Phys. Chem., 1928, 32, 1065–1079 CrossRef CAS.
- R. A. Marcus and O. K. Rice, J. Phys. Colloid Chem., 1951, 55, 894–908 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 2658–2661 CrossRef CAS.
- C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702 Search PubMed.
- L. D. Landau, Phys. Z. Sov., 1932, 2, 46–51 CAS.
- J. N. Harvey and M. Aschi, Faraday Discuss., 2003, 124, 129–143 RSC.
- J. Soto, F. J. Avila, J. C. Otero and J. F. Arenas, Phys. Chem. Chem. Phys., 2011, 13, 7230–7231 RSC.
- F. Bernardi, M. Olivucci, M. A. Robb, T. Vreven and J. Soto, J. Org. Chem., 2000, 65, 7847–7857 CrossRef CAS PubMed.
- J. Zhang, J. Peng, D. Hu and Z. Lan, Phys. Chem. Chem. Phys., 2021, 23, 25597–25611 RSC.
- X.-L. Peng, A. Migani, Q.-S. Li, Z.-S. Li and L. Blancafort, Phys. Chem. Chem. Phys., 2018, 20, 1181–1188 RSC.
- D. R. Yarkony, J. Am. Chem. Soc., 1992, 114, 5406–5411 CrossRef CAS.
- E. B. Wilson, Jr., J. C. Decius and P. C. Cross, Molecular Vibrations, McGraw-Hills, New York, 1955 Search PubMed.
- J. F. Arenas, S. P. Centeno, J. I. Marcos, J. C. Otero and J. Soto, J. Chem. Phys., 2000, 113, 8472–8477 CrossRef CAS.
- A. O. Lykhin, D. S. Kaliakin, G. E. dePolo, A. A. Kuzubov and S. A. Varganov, Int. J. Quantum Chem., 2016, 116, 750–761 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tables of adiabatic excitation energies, relative energies, and of geometries in internal and cartesian coordinates, details of potential energy surfaces, and input files to MESMER (TAR.GZ). See DOI: 10.1039/d1cp05785e |
| This journal is © the Owner Societies 2022 |