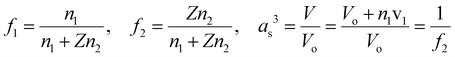Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamics of hydrogels for applications in atmospheric water harvesting, evaporation, and desalination†
Gang
Chen

Department of Mechanical Engineering, Massachusetts Institute of Technology, USA. E-mail: gchen2@mit.edu
First published on 19th April 2022
Abstract
Most thermodynamic modeling of hydrogels is built on Flory's theories for the entropy of mixing and rubber elasticity, and Donnan's equilibrium conditions if polyelectrolyte polymer and mobile ions are involved. The entropy of mixing depends on the number of solvent and polymer molecules while the configurational entropy depends on the volume the polymer occupied. Flory's theory treated these two entropy terms in the Gibbs free energy on an equal basis: using the molecular numbers as the variable. I argue that the molecular number and volume are two independent thermodynamic variables and reformulate Flory's classical hydrogel thermodynamic model by minimizing the Helmholtz free energy of a combined system consisting of the hydrogel and its environment. This treatment enables us to unequivocally state that the osmotic pressure is the thermodynamic pressure of the solvent inside the hydrogel and to unambiguously write down the chemical potential of each species. The balance of the chemical potentials of the mobile species, including both the solvent and the mobile ions gives a set of equations that can be simultaneously used to solve for the equilibrium volume of the hydrogel, the osmotic pressure, and the Donnan potential, including their coupling. The model is used to study the thermodynamic properties of both pure and salty water in non-electrolyte and electrolyte hydrogels such as (1) the latent heat of evaporation, (2) the ability of hydrogels to retain water and to absorb water from the atmosphere, (3) the use of hydrogels for desalination via solar or forward osmosis, (4) the antifouling characteristics of hydrogels, and (5) melting point suppression and boiling point elevation, and solubility of salts in hydrogels. These properties are of interest in solar-driven interfacial water evaporation for desalination and wastewater treatment, atmospheric water harvesting, and forward osmosis. The reformulated thermodynamic framework will also be useful for understanding polymer electrolytes and ion transport in electrochemical and biological systems.
1. Introduction
Hydrogels responsive to different stimuli such as temperature, pH, salt concentration, electrical field, and light have found a wide range of applications in biology, biomedical technology, environmental technology, and daily life (food, diapers, etc.).1,2 More recently, potential applications of hydrogels in desalination and atmospheric water harvesting have also drawn increasing attention with the demonstration of apparent reduction in latent heat3,4 during solar-driven interfacial water evaporation,5,6 hydrogel as a draw solution for forward osmosis,7,8 and adsorption of water from the atmosphere and regeneration of adsorbed water via phase separation with minimal energy input.9 Current studies are mostly experimental; understanding the thermodynamics underpinning these processes is of great interest for these applications and future advancements of these applications.Flory and Rehner developed a basic thermodynamic framework for analyzing hydrogel swelling,10,11 which served as the starting point for most subsequent developments. Their theory considered four additional contributions in the Gibbs free energy: the (1) entropy of mixing between the hydrogel polymers and the solvent molecules,12,13 (2) an enthalpic term due to binding of solvent molecules with the polymers, (3) an elastic energy term due to the configurational entropy change of the crosslinked polymer chains,14 and (4) for polyelectrolyte hydrogels, an ionic osmotic pressure term. Katchalsky and Michaeli15 further included the electrostatic interactions between charged polymers of a polyelectrolyte and surrounding ions in the Gibbs free energy based on the Debye–Huckel theory and their theory was later modified considering, for example, finite chain extensibility.16 English et al.17 developed a quasi-lattice model to account for charge on the polyelectrolyte and modified the Flory–Rehner theory correspondingly to model polyelectrolyte hydrogels. Bannon-Peppas and Peppas18 extended the Flory–Rehner theory to include the wet initial state of the hydrogel and the dissociation of ions from weak polyelectrolyte polymers. In analyzing the hydrogel's use in a power generation cycle based on a salinity gradient, Zhang et al.19 extended the previous thermodynamic models to include the effects of salts and fixed charge on a polymer. In general, ionization of weak polyelectrolyte is very complicated, as many studies based on modeling and simulations have shown.16,20–23 Hong et al.24 took a different approach, developing a field theory for hydrogel through analyzing the Helmholtz free energy under constraints at boundaries. In their derivation, the osmotic pressure emerges from a Lagrangian multiplier to the Helmholtz free energy due to the volume constraint, but its exact value changes with different choices of variables in the Helmholtz free energy.
Most applications of these thermodynamic models focused on the gel swelling ratio. For applications such as desalination,7,8 atmospheric water harvesting,9,25 and solar-driven evaporation,3–6 the thermodynamics of water in the hydrogel is of greater interest. Some experimental observations await explanations and call for deeper understanding of the water state inside the hydrogel from the thermodynamics perspective. For example, can water have reduced latent heat in hydrogel? And if yes, by how much?3 What kind of hydrogels can serve as draw solutions for forward osmosis?7 Why do hydrogels not get fouled under solar-driven interfacial evaporation of saline water?26 How can adding salt prevent hydrogels from drying up?27 Is there a thermodynamic basis for the classification of water in hydrogel into: bound, intermediate, and bulk water?28,29 Although thermodynamic analysis of water may not answer all these questions, especially considering how complex water is even in its pure bulk form,30,31 it will be interesting to examine what can be learnt from studying the thermodynamics of water in hydrogels.
In my attempt applying current models to explore answers to the above equations, I found that there are some flaws and ambiguities in the established classical approaches. For example, Donnan equilibrium32 is used to find out the concentrations of different ions inside and outside the gel, which are then used to compute part of the osmotic pressure. However, the classical Donnan equilibrium conditions neglected the pressure effect on ion concentration,37 whose inclusion effectively couples the electrostatic potential and the osmotic pressure. It also seems to me that Flory's treatment of the osmotic pressure term is a little bit ad-hoc, although his results are self-consistent. As I will discuss in detail, Flory did not clearly distinguish in his theory what are proper thermodynamic variables. Such ambiguities create confusion in the literature. For example, Lai et al.33 wrote “In the literature, however, it is less than clear, how swelling pressure, Donnan osmotic pressure or solid matrix stress are related to one another. For example, is the swelling pressure the same as the Donnan osmotic pressure for cartilage?”.
This paper has two objectives. The main goal is to reformulate Flory's thermodynamic model. The reformulation is based on minimizing the Helmholtz free energy of the combined system consisting of the hydrogel and its environment. This reformulation clearly shows that the thermodynamic pressure of the solvent inside the hydrogel is the osmotic pressure, which is at equilibrium with the tension from the polymer. The formulation allows unambiguous calculation of the chemical potentials of each species. At equilibrium, the chemical potential balance of the mobile species inside and outside hydrogels determines the equilibrium volume, the osmotic pressure, and the Donnan potential. My other goal is to apply the reformulated thermodynamic analysis to water in hydrogels to gain better insights related to hydrogel applications in solar-driven interfacial evaporation, atmospheric water harvesting, and forward osmosis desalination, and the reformulated thermodynamic framework will be used to examine these problems. The article starts with a brief review (Section 2) of Flory's classical model and some subsequent modifications of the model and points out existing confusions and deficiencies. Modifications to the models, for both non-electrolyte and polyelectrolyte hydrogels will be presented (Section 3) and applied to analyze water thermodynamic properties in hydrogels, including the latent heat of evaporation, atmosphere water absorption and water retention ability, antifouling characteristics, melting point suppression and boiling point elevation (Sections 4–6). Although the models on free energy and entropy terms I used are identical to what Flory used, and many subsequent studies had suggested improvements to these models, I believe that the reformulated thermodynamic approach is general and can be expanded readily to include more accurate descriptions of the polymers, the ions, and the solvent. The thermodynamic framework should be useful for related work in biological and biomedical applications for which osmosis and Donnan membrane equilibrium are widely used concepts.
2. Review of Flory's theories for hydrogel swelling
Flory's thermodynamic model is based on his derivations of the entropy of mixing between a solvent and a polymer and the configurational entropy for the polymer elasticity (see ESI†).10–12 Using these expressions, the change of the Gibbs free energy (the final state minus the initial state), ΔG, of the polymer–solvent system can be expressed as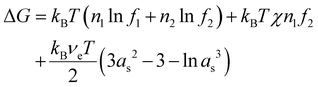 | (1) |
| νe = ν − 2n2 = ν(1 − 2n2/ν) = ν (1 − 2Mc/M) | (2) |
The change in the chemical potential for the solvent can be obtained from the change in Gibbs free energy by 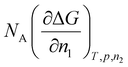 on a molar basis, where NA is the Avogadro number,
on a molar basis, where NA is the Avogadro number,
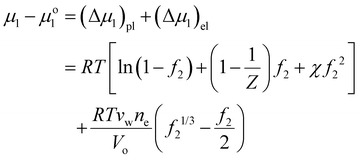 | (3) |
For polyelectrolyte hydrogels, Flory considered a strong polyelectrolyte that dissociates completely, yielding mobile anions Az−, where the superscript z− denotes the valence of the ion (and hence its charge is ez−), and fixed positive counterions i.e. per structural unit of the polymer with “i” as the valence of a monomer. The gel is in equilibrium with the surrounding solvent containing a strong electrolyte Mν+Aν− (z+ν+ = z−ν−) at concentration 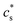 , where the superscript “*” denotes environment outside the gel. Since the gel initially contains no Mz+ cations, some of them will diffuse into the gel and some Az− will diffuse out. Because charge neutrality conditions should satisfy both inside and outside the gel, if cs [mole m−3] is the concentration of the Mν+Aν− salt inside the gel, the concentrations of mobile ions in the gel are c+ = ν+cs and c− = ν−cs + ic2/z−, where c2 is the concentration of the polymer with fixed charge per unit volume, c2 = f2/vu, and vu is the molar volume of a structural unit. The total mobile ion concentration (c+ + c−) inside the gel at equilibrium will inevitably exceed that in the external solution
, where the superscript “*” denotes environment outside the gel. Since the gel initially contains no Mz+ cations, some of them will diffuse into the gel and some Az− will diffuse out. Because charge neutrality conditions should satisfy both inside and outside the gel, if cs [mole m−3] is the concentration of the Mν+Aν− salt inside the gel, the concentrations of mobile ions in the gel are c+ = ν+cs and c− = ν−cs + ic2/z−, where c2 is the concentration of the polymer with fixed charge per unit volume, c2 = f2/vu, and vu is the molar volume of a structural unit. The total mobile ion concentration (c+ + c−) inside the gel at equilibrium will inevitably exceed that in the external solution 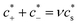 , where ν = ν+ + ν−. The osmotic pressure arising from the difference of the mobile ion concentration is
, where ν = ν+ + ν−. The osmotic pressure arising from the difference of the mobile ion concentration is
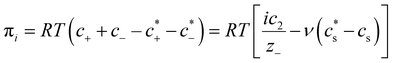 | (4) |
To determine 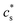 − cs, Flory used the typical Donnan equilibrium conditions,32
− cs, Flory used the typical Donnan equilibrium conditions,32
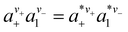 | (5) |
3. Reformulation of Flory's hydrogel thermodynamic model
There are some confusions in the Flory hydrogel model which persisted throughout subsequent developments. Some are as follows: (1) the Gibbs free energy expression in eqn (1) does not include pressure as its natural thermodynamic variable, (2) the volume variable in the configurational entropy is replaced by the molecule number variable, and (3) the enthalpy of mixing term does not explicitly include the pressure effect. Overall, the effect of pressure was included in ad-hoc ways, leading to confusions as reflected in the question asked by Lai et al.33 quoted before. We will show below that the first and the last term in eqn (1) should not be treated on an equal basis because they are governed by different natural thermodynamic variables: the molecular number for the entropy of mixing and the volume for the configurational entropy. Flory's theory neglected the electrostatic potential of the ions on the polyelectrolyte and interactions between the mobile ions and the polyelectrolyte, which subsequent studies tried to include. 17,19 These treatments, however, neglected the coupling between the Donnan potential and the osmotic pressure, a situation that persisted from Donnan's original treatment on the subject.32,37 In the following, I will present a reformulation of Flory's theory addressing the concerns raised here.A thermodynamic analysis typically starts with defining a system in contact with its environment under specified conditions. When the system is at equilibrium with the environment, its thermodynamic potential either maximizes or minimizes. For a system at constant temperature and pressure in equilibrium with its environment that it can exchange heat, force, and particle, its thermodynamic potential, the Gibbs free energy, is minimized and the natural thermodynamic variables are temperature and pressure. A system maintained at constant temperature and volume minimizes the Helmholtz free energy. For a hydrogel in equilibrium with its solvent, the problem is that its volume is not constrained, nor it is at the same pressure with the environment (due to osmotic pressure). We thus consider a combined system made of the gel and the ambient solvent as a closed system at constant temperature and volume. At equilibrium, the total Helmholtz free energy of this combined system is at its minimum.
The Helmholtz free energy, U-TS, of the hydrogel sub-system can be written as
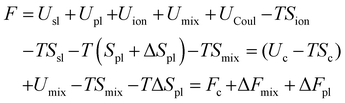 | (6) |
The natural variables for the Helmholtz free energy are T, Vt, φ, and ni, where φ is the electrostatic potential, ni the number of species i, and Vt total volume that is the sum of hydrogel volume V and the volume of the ambient solvent Ve. Assuming that the temperature remains constant through the combined system and with the environment, the change in the total Helmholtz free energy of the combined system can be written as ESI†
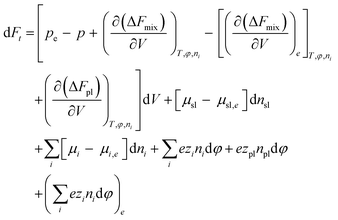 | (7) |
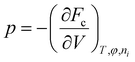 is the thermodynamic pressure acting on solvent, ions, and the polymer, pe is the pressure of the ambient solvent (which could also be extended to include externally applied pressure),
is the thermodynamic pressure acting on solvent, ions, and the polymer, pe is the pressure of the ambient solvent (which could also be extended to include externally applied pressure), 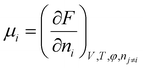 is the chemical potential of species i, and zi the valence of the ion denoted by the subscript.
is the chemical potential of species i, and zi the valence of the ion denoted by the subscript.
At equilibrium, dFt = 0, which leads to
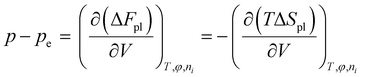 | (8) |
| μsl = μsl,e, μi = μi,e | (9) |
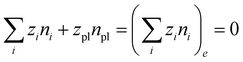 | (10) |
Flory's expression for the polymer Helmholtz free energy changes due to configurational entropy, i.e., the last term in eqn (1), can be expressed in terms of volume for isotropic swelling so that the Helmholtz free energy can be written as
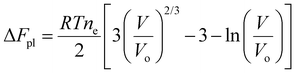 | (11) |
In a hydrogel, the solvent fills the empty space between polymer molecules such that V = Vo + n1v1. Flory used this relation to further write ΔFpl in terms of the solvent number n1. By doing so, the polymer tension due to configurational entropy change i.e., the 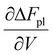 term in eqn (8), is grouped into the chemical potential term
term in eqn (8), is grouped into the chemical potential term 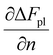 , as in eqn (3). Although Flory correctly pointed out that the mixing term, i.e., the first term in eqn (3), creates osmotic pressure, and the second term represents the polymer tension, the change of natural variable from V to n1 causes confusion since the polymer tension term becomes part of chemical potential. By using the volume as an independent variable (as in the case of rubber elasticity), we see clearly from eqn (7) that pressure p is the thermodynamic pressure acting on all components inside the hydrogel. From eqn (8), we see that the difference of p and pe, i.e., the osmotic pressure, balances the polymer tension created by the polymer configuration change. We will see later that p can be determined from the balance of chemical potentials as represented by eqn (9), rather than simply the first term in eqn (3). So, in answering Lai et al.'s question,33 the swelling pressure and the Donnan osmotic pressure are identical, while the solid matrix stress arises from different sources (the polymer configurational entropy change in Flory's model). They balance each other in mechanical equilibrium but can create motion in nonequilibrium situations.
, as in eqn (3). Although Flory correctly pointed out that the mixing term, i.e., the first term in eqn (3), creates osmotic pressure, and the second term represents the polymer tension, the change of natural variable from V to n1 causes confusion since the polymer tension term becomes part of chemical potential. By using the volume as an independent variable (as in the case of rubber elasticity), we see clearly from eqn (7) that pressure p is the thermodynamic pressure acting on all components inside the hydrogel. From eqn (8), we see that the difference of p and pe, i.e., the osmotic pressure, balances the polymer tension created by the polymer configuration change. We will see later that p can be determined from the balance of chemical potentials as represented by eqn (9), rather than simply the first term in eqn (3). So, in answering Lai et al.'s question,33 the swelling pressure and the Donnan osmotic pressure are identical, while the solid matrix stress arises from different sources (the polymer configurational entropy change in Flory's model). They balance each other in mechanical equilibrium but can create motion in nonequilibrium situations.
For a non-electrolyte hydrogel with pure solvent, we can write the extra molar-based Helmholtz free energy in Eqn (6) as
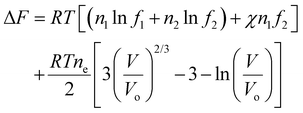 | (12) |
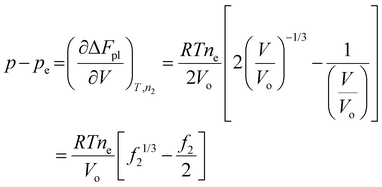 | (13) |
The chemical potential of the solvent is
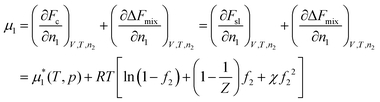 | (14) |
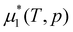 is the chemical potential of the pure solvent inside the gel at pressure p and temperature T. The 1/Z term in the above equation is often neglected as it is usually much smaller than 1. We will take this approximation in the rest of this paper.
is the chemical potential of the pure solvent inside the gel at pressure p and temperature T. The 1/Z term in the above equation is often neglected as it is usually much smaller than 1. We will take this approximation in the rest of this paper.
Since the chemical potentials are important for our analysis, we will elaborate a little more. We consider a solution consists of x1,…xi…xn mole fractions of components 1,…, i,…, n. We start from the definition of the chemical potential of component i on a molar basis38–40
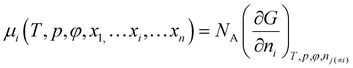 | (15) |
The derivative of the chemical potential can be written as
dμi(T, p, ϕ, x1,…xi,…xn) = vidp + ziFDdϕ + RTd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ai) ln(ai) | (16) |
μi(T, p, ϕ, x1,…xi,…xn, xs) = μoi(T, po) + vi(p − po) + ziFϕ + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γixi) ln(γixi) | (17) |
One question is how to include the activity coefficient into the entropy of mixing expression of Flory in eqn (1) for ionic species. This is necessary if we want to study the impact of different ions, for example, in the hydrogel water retention experiments.27 For a pure water–hydrogel system, we can get the water activity coefficient from eqn (14) and (17)
RT(ln(1 − f2) + f2 + χf22) = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γwxw) ln(γwxw) | (18) |
Ions in the hydrogel interact with both water and the polyelectrolyte polymer. Surrounding the charged polymer, ions can be immobilized, forming condensates as pictured in Manning's theory,43 in addition to the diffuse double layer as in the Debye–Huckel theory.44 The net effect of the electrostatic interactions of the charges along the chain among themselves and with the mobile ions is expressed in terms of free energy, for which different models have been developed.15–17 Given that the detailed mechanisms of ions in polymeric solutions remain an activity field of study due to their importance in biology and electrochemical technologies, I decide to include only the mixing term as Flory originally assumed, not because this is a better treatment, but is a reflection of my view of the large uncertainties in the current models. Using this approximation, the additional Helmholtz free energy change due to the mixing of ions with polymers can be expressed as
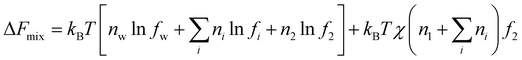 | (19) |
μw − μw*(T, p) = RT[ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fw + f2 + χf22] ≈ RT[ln(1 − f2) + f2 + χf22 + ln(γwxw)] fw + f2 + χf22] ≈ RT[ln(1 − f2) + f2 + χf22 + ln(γwxw)] | (20) |
μi − μi*(T, p) = RT[ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fi + f2 + χf22] ≈ RT[ln(1 − f2) + f2 + χf22 + ln(γixi)] fi + f2 + χf22] ≈ RT[ln(1 − f2) + f2 + χf22 + ln(γixi)] | (21) |
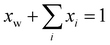 . In writing the second step in eqn (20), we have used the relation
. In writing the second step in eqn (20), we have used the relation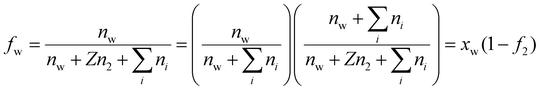 | (22) |
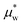 and
and 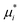 depend on pressure and electrostatic potential as shown in eqn (17). Although our numerical calculations will take activity coefficients as unity most of the time, we will include examples of different salts by using their actual activity coefficients to illustrate the impacts of nonunitary activity coefficients.
depend on pressure and electrostatic potential as shown in eqn (17). Although our numerical calculations will take activity coefficients as unity most of the time, we will include examples of different salts by using their actual activity coefficients to illustrate the impacts of nonunitary activity coefficients.
With the above approach, we have reformulated Flory's thermodynamic model under the Helmholtz free energy picture. The reformulation enables us to clearly define the thermodynamic pressure and relate its difference with the environmental pressure, i.e., the osmotic pressure, to that of the tension in the polymer. With the new formulation, we can express the chemical potentials of each species inside the hydrogel as exemplified in eqn (20) and (21). These chemical potentials depend on temperature, pressure, electrostatic potential, and composition. We will show next that the chemical potential balance between mobile species inside and outside determines the pressure, volume, composition, and electrostatic potential. We are interested in using the reformulated thermodynamic model to understand some recent experiments on using the hydrogel for solar-driven interfacial evaporation, atmospheric water harvesting, and forward osmosis desalination. It is difficult to do quantitative comparison with the experimental data because parameters needed for the model are usually unknown. Our focus is thus on the trend rather than trying to be quantitative. We will give below a summary of the experimental facts that serve as inspiration for our subsequent discussion.
Solar-driven interfacial evaporation uses sunlight to heat up a floating porous solar absorber to create a hot region on the water surface, which enhances the evaporation of water while the bulk water remains cold.5,6 This approach had drawn lots of interest due to its potential applications in desalination and waste water treatment. The theoretical thermal evaporation limit under standard 1 sun conditions is 1.45 kg m−2 h−1, assuming that the 1000 W m−2 solar energy in 1 sun is used to heat up and evaporate water from an ambient temperature of 25 °C to 40 °C. Yu's group9 used porous polyvinyl alcohol (PVA) hydrogels embedded with black absorbers and reported an evaporation rate as high as 4–5 kg m−2 h−1, followed by other similar reports using different hydrogels and even no hydrogels. The explanation for such a phenomenon championed by Yu's group was the existence of three kinds of waters in the hydrogel, the bound water, the intermediate water, and the free water.9,28,29 Some key evidence supporting this explanation is (1) latent heat reduction measured by differential scanning calorimetry experiments and (2) suppressed melting point of intermediate water up to −20 °C, also observed using differential scanning calorimetry (DSC) measurement.9,45 Another key experimental evidence is the Raman spectroscopy signatures of different waters. In some of the DSC latent heat measurement data, the end of the evaporation excursion curve exceeds the boiling point of pure water, which can be understood as the elevation of the boiling point. However, the maximal measured latent heat reduction with DSC is up to 30%, while experimentally, an evaporation rate about three times that of the thermal evaporation limit was reported. Another interesting observation is that in a solar-driven desalination experiment, salt does not seem to accumulate inside the hydrogel.46 We will show that the higher pressure of water inside a hydrogel can lead to reduced latent heat up to the order observed in the DSC experiment, but not to the same order observed in the solar-driven experiment. The thermodynamic model can also provide qualitative explanations for the experimental observation of freezing point depression and antifouling characteristics of a hydrogel. The results show that the DSC-based latent heat reduction and freezing point suppression do not provide sufficient proof that the experimental observations of a higher evaporation rate are due to the existence of the three types of water inside the hydrogel. Our recent experiments provide alternative explanations,47,48 which we will not discussed here since they are not related to the central topic of the paper.
When a hydrogel is placed in open air, it usually dries up over time. How to retain water is a challenge. Bai et al.27 tested the water retention capability of polyacrylamide (PAM) hydrogel impregnated with different salts such as sodium chloride (NaCl), lithium chloride (LiCl), magnesium chloride (MgCl2) and potassium acetate (KAc). They found for example, NaCl precipitates out, but LiCl can retain some water for a long time. While these experiments aim to retain water, adsorbing water from atmosphere is of interest in addressing the water shortage challenge in many regions. Adsorbents made of polyacrylamide (PAM) hydrogel composite with carbon nanotubes and CaCl2,49 and composite hydrogel made of poly N-isopropylacrylamide (PNIPAM) and chloride-doped polypyrole9 have shown promise. These examples also show the importance of ions for water adsorption. Hydrogel's water retention and adsorption capabilities depend on the relative humidity of the ambient air. We will examine the problem of water retention and atmospheric water extraction using the thermodynamic model, considering the effect of salts in both nonpolyelectrolytic and polyelectrolytic hydrogels. As we already mentioned before, ions in polyelectrolyte hydrogels are very complex. In fact, even without hydrogels, ion interaction with water is already complex. Our modeling did not include such complex interactions, as we aim at seeing the trend rather than being quantitative.
The ion concentrations in polyelectrolyte hydrogel in an electrolytic solution are usually modeled using the method originally developed by Donnan,32 as represented by eqn (4) and (5). Accompanying the Doannan equilibrium is the Donnan potential, a voltage difference between the hydrogel and the external electrolytic solution. The Donnan potential distribution across the hydrogel–solvent interface had been measured by Gong's group using a delicate electrolyte technique.50 I had shown in a previous paper37 that the traditional Donnan equilibrium neglected the coupling between the osmotic pressure and the Donnan potential. I will show using the reformulated hydrogel thermodynamic framework that the inclusion of this coupling leads to an additional potential which would not exist for a nonelectrolyte hydrogel immersed in a salt solution. There are no published results confirming this prediction. I learnt from private communication with members from Professor Gong's group that they had observed potentials drop in PVA hydrogels immersed in salt solutions.51
The reformulated thermodynamic model also makes it easy to calculate osmotic pressure which is relevant to the work in using hydrogels for forward osmosis-based desalination. In this technology, hydrogels with no or little water at the beginning but with a high osmotic pressure when at equilibrium are used to extract clean water from saline water separated using a semipermeable membrane.7,8 The osmotic pressure difference between the saline water and the water in the hydrogel drew clean water across the membrane to expand the hydrogel. In this case, the osmotic pressure of clean water in the hydrogel must be larger than that of the saline water. Li et al.7,8 tested different hydrogels such as poly(sodium acrylamide) (PSA), poly(sodium acrylate)-co-poly(N-isopropylacrylamide), PAM and poly(N-isopropylacrylamide) (PNIPAM), and found that PSA can draw most water. For such applications, no mobile ions exist in the hydrogel. In a different forward osmosis approach, Yu et al.52 directly immersed the hydrogel made of poly(sodium acrylate-co-hydroxyethyl methacrylate) in saline water containing NaCl, and squeezed out water inside the hydrogel with pressure. The recovered water contains less salt than the saline water. Thermodynamic analysis had been reported for such pressure-driven desalination cycle.53,54 Rud et al.55 simulated in detail the ion concentrations inside and outside the hydrogel using a Monte Carlo method motivated by Yu et al.'s experiment. I will use the thermodynamics model presented above to compare the osmotic pressure difference between saline water and water in hydrogel.
The above experiments will be discussed under three categories: (1) non-polyelectrolyte hydrogel such as PVA in equilibrium with pure water or humid air; (2) non-polyelectrolyte hydrogel in equilibrium with salty water or hydrogel impregnated with salt in equilibrium with humid air; and (3) polyelectrolyte hydrogel in equilibrium with salty water or humid air.
4. Non-electrolyte hydrogel in equilibrium with pure water or humid air
Expressing the chemical potential in eqn (20) at pressure p relative to ambient pressure pe as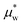 (T, p) =μow(T, pe) + vw(p − pe) and substituting the pressure difference using eqn (13), we get the chemical potential of water inside the hydrogel as
(T, p) =μow(T, pe) + vw(p − pe) and substituting the pressure difference using eqn (13), we get the chemical potential of water inside the hydrogel as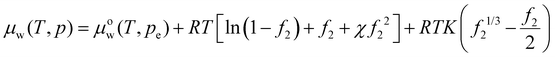 | (23) |
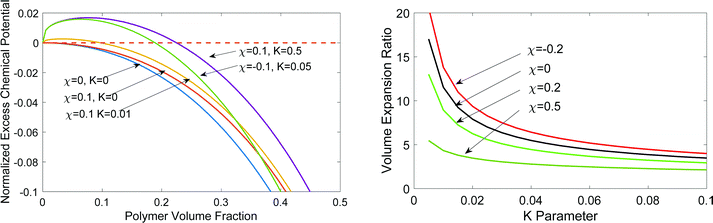
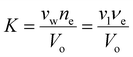 . Recall νe is the effective number of crosslinking unit, v1 is the volume of a single solvent molecule, and Vo is the initial dry volume of the polymer. So K is the ratio of the effective volume of the crosslinking node to that of the dry volume, and it can be controlled by the crosslinker concentration in hydrogel synthesis. Eqn (23) is identical to Flory's result except that the last term is due to the pressure dependence of the chemical potential of pure water. Fig. 1(a) plots the normalized excess chemical potential [μw(T, p) − μow(T, pe)]/(RT) as a function of the polymer volume fraction f2 at different χ and K values. We see that the excess chemical potential from the ambient water, μw(T, p) − μow(T, pe) could be positive between [0, f2,eq] under proper parameter combinations, which means that hydrogels are not stable and phase separation due to spinodal decomposition happens at f2,eq, where μ(f2 = 0) = μ(f2 = f2,eq), i.e., the polymer with some water (f2,eq = Vo/V) is in equilibrium with pure solvent. From eqn (23), at equilibrium, μw(T, p) = μow(T, pe), we have
. Recall νe is the effective number of crosslinking unit, v1 is the volume of a single solvent molecule, and Vo is the initial dry volume of the polymer. So K is the ratio of the effective volume of the crosslinking node to that of the dry volume, and it can be controlled by the crosslinker concentration in hydrogel synthesis. Eqn (23) is identical to Flory's result except that the last term is due to the pressure dependence of the chemical potential of pure water. Fig. 1(a) plots the normalized excess chemical potential [μw(T, p) − μow(T, pe)]/(RT) as a function of the polymer volume fraction f2 at different χ and K values. We see that the excess chemical potential from the ambient water, μw(T, p) − μow(T, pe) could be positive between [0, f2,eq] under proper parameter combinations, which means that hydrogels are not stable and phase separation due to spinodal decomposition happens at f2,eq, where μ(f2 = 0) = μ(f2 = f2,eq), i.e., the polymer with some water (f2,eq = Vo/V) is in equilibrium with pure solvent. From eqn (23), at equilibrium, μw(T, p) = μow(T, pe), we have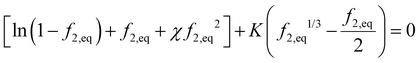 | (24) |
Fig. 1(b) shows the equilibrium volume expansion of a hydrogel as a function of K under different parameters. The smaller the K, i.e., the number of crosslinkers, the larger is the volume expansion due to the smaller tension of the polymers to counter the osmotic pressure of the solvent. We estimate that the PVA used in solar-driven interfacial evaporation4 has K ∼ 0.03 and V/Vo ∼ 10. The reported value of χ for PVA is ∼0.5,56 depending on temperature and volume fraction. The calculated volume expansion ratio values are of the same order as the experiment.
Latent heat of evaporation
Inside hydrogel, water is at a different pressure p and hence its latent heat will be different from that of the solvent at the ambient pressure pe. From the chemical potential of water, we derive that the latent heat of evaporation is (see ESI†)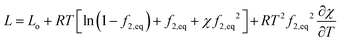 | (25) |
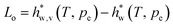 is the latent heat of evaporation of pure water at temperature T and environmental pressure
is the latent heat of evaporation of pure water at temperature T and environmental pressure 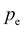 , and h is the enthalpy with the subscript w for water and additional subscript v representing the vapor phase.
, and h is the enthalpy with the subscript w for water and additional subscript v representing the vapor phase.
In Fig. 2, we plot the latent heat as a function of f2 for different χ values, assuming it is temperature independent. In reality, f2,eq is determined by χ and K as shown in Fig. 1b. During DSC or solar-driven interfacial evaporation experiments,3 hydrogel may not be in equilibrium and the solvent chemical potential may be higher than that of the surroundings. We can use eqn (25) to estimate the equivalent latent heat change as f2 varies from a small value to a large value (when the sample is close to dried up). We see that when f2 is large, the equivalent latent heat reduction change is appreciable. The latent heat reduction can be 1–5 × 105 J kg−1 for polymer volume fraction between 90 and 99%. Such a level of latent heat change could be seen in DSC measurements. However, in solar-driven interfacial evaporation experiments using hydrogel,3,4 the reported water evaporation rate can be ∼3 times that of the theoretical limit based on a nominal latent heat of 2.45 MJ, indicating a reduction of latent heat by 1.6 MJ, which is an order of magnitude larger than the pressure effect discussed here. The figure also shows that with increasing χ parameter, the latent reduction becomes smaller, because positive Flory–Huggins parameter indicates endothermic reaction when water binds to the polymer, reducing the impact of higher pressure inside the hydrogel. Hence, it does not seem that the pressure-change-caused evaporation latent heat reduction can explain the solar interfacial evaporation experimental results.
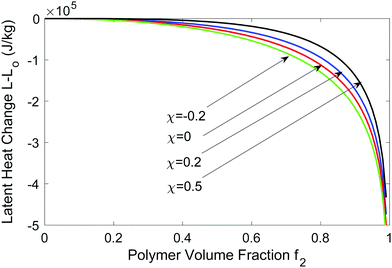 | ||
| Fig. 2 Latent heat reduction at T = 300 K at different χ values as a function of the polymer volume faction. | ||
The higher enthalpic state of water inside the hydrogel due to higher pressure also means that when water diffuses into the hydrogel, heat is absorbed at the interface despite the fact that binding of water with polymer is usually exothermic. If water enters the hydrogel from one surface and leaves from another surface, there is heat absorption at the interface where the water enters and heat release at the interface where the water leaves the hydrogel. The absorbed and rejected heat is given by the same expression as eqn (25). This is an effect analogous to the Peltier effect in thermoelectric materials, although the latter is due to the difference of electrons' entropy flux,57 while here it is due to the entropy difference of water molecules. In theory, a molecular Peltier cooling device can be built by allowing water to diffuse in from one side and diffuse out from the other through, for example, a pressure or thermal driven flow. On a per molecule basis, 105 J kg−1 heat absorbed is equivalent to 0.019 eV per molecule, or an effective Seebeck coefficient of 62.5 μV K−1. This is comparable to the typical electronic Seebeck coefficient. However, the value is not large enough to make such a cooling technology in a configuration similar to that of thermoelectric devices competitive because of the small flow rate of the molecules, i.e., the equivalent low molecular conductivity, compared to that of electrons, although the intrinsic low thermal conductivity of the hydrogel is an advantage.58 We had observed a small cooling effect when PVA hydrogels similar to that used in the reference solar-driven interfacial-evaporation experiment were first wetted with water, although we had not tested steady-state operation.
Freezing point depression and boiling point elevation
Next, we discuss the freezing point depression and the boiling point elevation; both were observed from DSC measurements on PVA hydrogels used in the solar-driven interfacial evaporation experiment.4,26 These observations can be explained based on the freezing point depression and boiling point elevation in solutions, typically called colligative properties for ideal cases when the ratios (melting point or boiling point) depend only on the concentration, and independent of the individual solute's chemical properties.39,40 In fact, Huggins34 had used the freezing point depression in developing his theory on polymer solutions. The standard approach in deriving the freezing point depression and boiling point elevation is to set the differentials of the chemical potential, i.e, the change in chemical potential of water inside the gel equaling that of the solid (for freezing point) or pure vapor (for boiling point), at which the activity can be taken as one. However, in typical DSC experiments, the hydrogel with water inside is taken out of the water bath. If one waits long enough, hydrogel will establish new equilibrium with the environment through volume change. The mechanical equilibrium with the environment at pressure po is ensured by eqn (24). The chemical equilibrium will be established by setting the water chemical potential equaling the chemical potential of water in the ambient gas (air or inert gas used in DSC measurements). We will discuss more of such equilibrium in the water adsorption section. For now, we will take f2 as a variable. At least in the DSC evaporation experiment, hydrogel is continuously evaporating and is not in chemical equilibrium with the environment.Following the standard approach as discussed above,38–40 we obtain the following expression for the freezing point ratio (see ESI†)
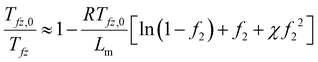 | (26) |
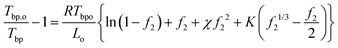 | (27) |
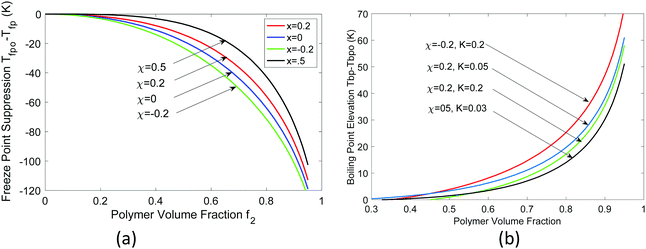 | ||
| Fig. 3 Calculated (a) freeze point depression from 0 °C and (b) boiling point elevation from 100 °C. | ||
In passing, we make the comment that if boiling happens inside the hydrogel, the vapor pressure will be even higher than p. One can combine the Laplace–Young equation for the vapor pressure and obtain corresponding boiling point inside the hydrogel following a similar approach.
Trapping water from air
Let us now consider if a hydrogel can trap water when it is placed in air. This is of interest for atmospheric water harvesting as well as to maintain functions of a hydrogel when it is exposed to air.9,27 The chemical potential of water vapor in air is related to water vapor's partial pressure pv relative to its saturation pressure ps at temperature T (assuming air is an ideal mixture),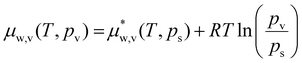 | (28) |
We equate the above chemical potential to water chemical potential inside the hydrogel, i.e., eqn (23), to get
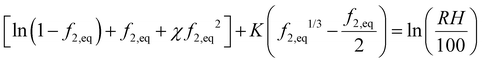 | (29) |
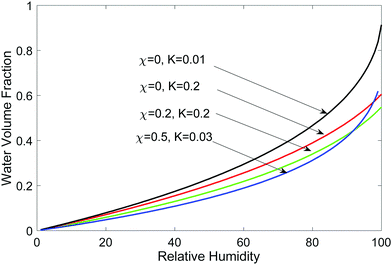 | ||
| Fig. 4 Water content (volume fraction) in the hydrogel as a function of relative humidity for different parameter combinations. | ||
5. Nonpolyelectrolyte hydrogels with salt in equilibrium with water or humid air
This topic is of interest for several applications we mentioned before. One of them is the solar-driven interfacial evaporation using hydrogels. It was found that there is no salt precipitation inside the hydrogel,3,4 an antifouling property. Another experimental observation is that by incorporating salt inside hydrogel, it is found that hydrogel does not dry out.27Salt content inside hydrogel in equilibrium with saline water outside
Let us consider first for simplicity that a symmetric monovalent salt such as NaCl salt is added to water outside the hydrogel. To find out the salt concentration inside the hydrogel at equilibrium, we start with eqn (21) to write down the chemical potential of Na+ and Cl− ions inside the hydrogel as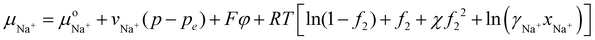 | (30) |
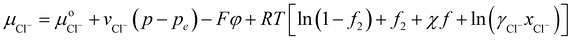 | (31) |
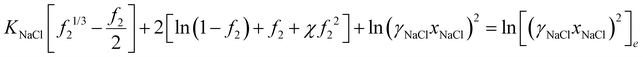 | (32) |
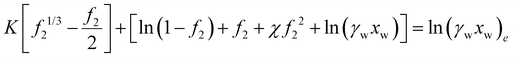 | (33) |
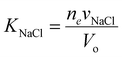 with vNaCl = vNa+ + vCl−, and subscript e represents external solution. Although we did assume that volume of ions equal to that of water molecule in the entropy of mixing expression in eqn (21), we will take here that KNaCl can differ from K for water as it is the case based on the molar volume measurements of salts.59–61 This is acceptable since for the entropy of mixing, water usually dominates over ions, while the ion volume directly enters the pressure term here.
with vNaCl = vNa+ + vCl−, and subscript e represents external solution. Although we did assume that volume of ions equal to that of water molecule in the entropy of mixing expression in eqn (21), we will take here that KNaCl can differ from K for water as it is the case based on the molar volume measurements of salts.59–61 This is acceptable since for the entropy of mixing, water usually dominates over ions, while the ion volume directly enters the pressure term here.
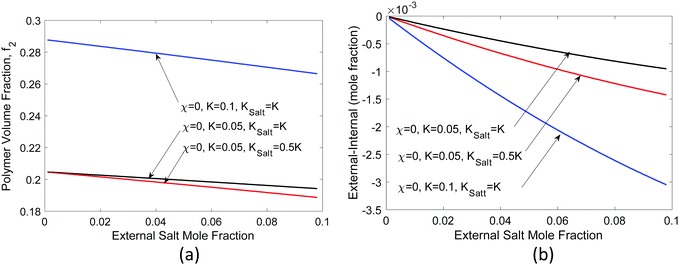
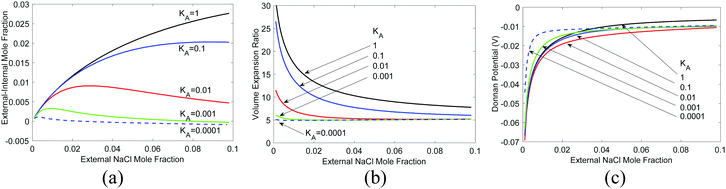
In Fig. 5(a), we show the equilibrium polymer volume fraction and in Fig. 5(b) the difference of the ion mole fraction between the external and the internal of the hydrogel, as a function of external ion mole fraction, varying different parameters but taking activity coefficient γ = 1 for all species. We see that as the external ion mole fraction increases, f2 decreases, i.e., the hydrogel expands (as long as KNaCl < 2KH2O, which is usually the case for ions). The external salt content is less than internal salt content [Fig. 5(b)]. One can prove this rigorously by multiplying eqn (33) by 2 and subtracting eqn (32) from it. In terms of a physical picture, in the current model, we see from eqn (19) and (32) that every NaCl-type of salt that enters the hydrogel is equivalent to two water molecules albeit with a different volume. The smaller the molar volume of the salt, the less is the pressure term contribution. More salt ions exist inside to counter the loss of pressure term contribution. More salts inside also create a higher osmotic pressure, which explains why the hydrogel expands.
However, real salts differ from each other. The difference is reflected in their activity coefficients, which vary with the salt concentration.41 In addition, the molar volume of salts also changes with concentration.61 For water, rather than the activity coefficient, the osmotic coefficient defined as the ratio of φ = ln(aw)/ln(xw) is often given. We took the measured62 activity coefficients of NaCl and LiCl salts in water and the corresponding osmotic coefficient [Fig. 6(a)], and recalculated the same quantities, as shown in Fig. 6(b) and (c). The partial molal volumes of NaCl and LiCl are 16.8 and 16.6 cm3 1−1 kg−1 and hence we took Ksalt/K = 0.3.59 We neglect the concentration dependence of the partial molar volume in these calculations. We see that LiCl has a higher activity coefficient and osmotic coefficient, which leads to larger volume expansion and concentration difference. For LiCl, internal salt concentration is higher for most concentrations, while for NaCl, the external salt concentration is higher for most concentrations.
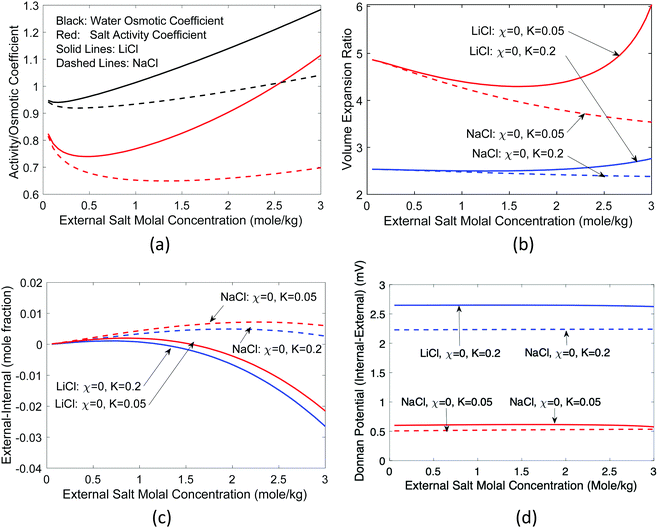 | ||
| Fig. 6 Impact of salt characteristics on volume expansion and salt concentration, (a) activity and osmotic coefficients of NaCl and LiCl (data from ref. 62), (b) volume expansion ratio, (c) salt concentration difference, and (d) Donnan potential as a function of the external salt molal concentration. Standard Donnan potential theory predicts a zero potential because there is no fixed charge. | ||
Also, in this case, a membrane potential might exist, which can be calculated from the following equation (see ESI†)
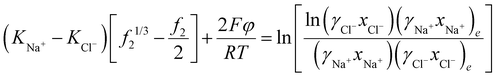 | (34) |
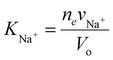 and
and 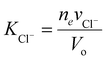 . Typically, the molar volumes of anions are larger than cations, and it is unlikely that first term on the left-hand side will exactly cancel the right hand side term, implying that a potential difference could develop between inside and outside hydrogel.37 We plot in Fig. 6(d) the potential difference between inside and outside the hydrogel. This potential difference should not exist under standard treatment of the Donnan potential since there are no fixed charge inside the gel. We predict the existence of a potential in this case because of the pressure difference between inside and outside the hydrogel. Although we have not found any publications reporting such a potential difference, I learnt from private communication that a potential indeed exists between nonelectrolyte hydrogels immersed in salt.51
. Typically, the molar volumes of anions are larger than cations, and it is unlikely that first term on the left-hand side will exactly cancel the right hand side term, implying that a potential difference could develop between inside and outside hydrogel.37 We plot in Fig. 6(d) the potential difference between inside and outside the hydrogel. This potential difference should not exist under standard treatment of the Donnan potential since there are no fixed charge inside the gel. We predict the existence of a potential in this case because of the pressure difference between inside and outside the hydrogel. Although we have not found any publications reporting such a potential difference, I learnt from private communication that a potential indeed exists between nonelectrolyte hydrogels immersed in salt.51
Trapping water from air
If a hydrogel impregnated with a salt is in equilibrium with air, the water chemical potential balance leads to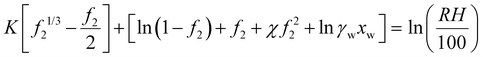 | (35) |
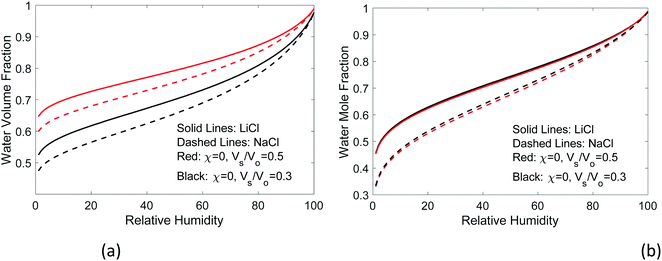
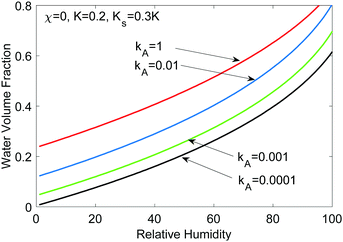
If the salt volume is Vs and the dry polymer volume is Vo, we can relate the salt mole fraction to the polymer volume fraction in expanded hydrogel as 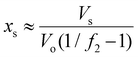 , where the approximate sign is due to our assumption of equal volume between water molecule and ions in the entropy of mixing formula. The water mole fraction is xw = 1 − 2xs, where the factor of 2 accounts for two different ions. We solved eqn (35) using the water osmotic coefficients for NaCl and LiCl and the results are shown in Fig. 7(a) and (b). Fig. 7(a) shows the amount of water as a function of the relative humidity. Compared to Fig. 4 for hydrogel not containing any salt, hydrogel with salt can absorb more water even at low humidity. Fig. 7(b) shows the water mole fraction. The solubility of salt determines the minimum humidity at which the salt will be dissolved in water. LiCl can maintain more water due to its (1) larger activity coefficient and (2) higher solubility. Bai et al.27 tested the water-retention ability of PAM hydrogel impregnated with LiCl and NaCl and found that NaCl precipitates out while LiCl impregnation can maintain hydrogel in the wet state. Our results here, together with the fact shown in Fig. 6(c) that there are more NaCl outside than inside in a solution, are consistent with the trends of experimental observations.
, where the approximate sign is due to our assumption of equal volume between water molecule and ions in the entropy of mixing formula. The water mole fraction is xw = 1 − 2xs, where the factor of 2 accounts for two different ions. We solved eqn (35) using the water osmotic coefficients for NaCl and LiCl and the results are shown in Fig. 7(a) and (b). Fig. 7(a) shows the amount of water as a function of the relative humidity. Compared to Fig. 4 for hydrogel not containing any salt, hydrogel with salt can absorb more water even at low humidity. Fig. 7(b) shows the water mole fraction. The solubility of salt determines the minimum humidity at which the salt will be dissolved in water. LiCl can maintain more water due to its (1) larger activity coefficient and (2) higher solubility. Bai et al.27 tested the water-retention ability of PAM hydrogel impregnated with LiCl and NaCl and found that NaCl precipitates out while LiCl impregnation can maintain hydrogel in the wet state. Our results here, together with the fact shown in Fig. 6(c) that there are more NaCl outside than inside in a solution, are consistent with the trends of experimental observations.
Solubility of salts inside hydrogel
The above analysis shows whether there is more salt inside or outside depends on the type of the salt: more NaCl outside while more LiCl inside. While this might explain the antifouling properties observed in the solar-driven hydrogel experiment because NaCl is the main salt in saline water, there are also two other possible mechanisms that can affect salt fouling: (1) mass transfer63 and (2) the salt might have higher solubility inside the hydrogel. The analysis of solubility is identical to that of the freezing point depression.38 One can think for example that a salt such as NaCl is at equilibrium between the pure solid and pure liquid form at its melting temperature Tm = 801 °C. It can be considered, from the fact that at room temperature there is equilibrium between solid NaCl in a solution, that the melting point depressed from Tm = 801 °C to room temperature. Following the established method, we obtain the following relation for solubility xNaCl (see ESI†):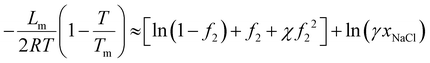 | (36) |
This equation is similar to freezing point depression eqn (26), except a factor of 2 due to the fact that Na+ and Cl+ ions are different and are treated separately. Comparing the above expression against the case f2 = 0, i.e., without the square bracket term on the right hand of the above equation, we see that the hydrogel increases the solubility of the salt since the square bracket term is negative. This increase at first might seem to be a little surprising. On the other hand, we can understand it as follows. As the temperature drops, the liquid phase Gibbs free energy will increase, this is why there is no liquid of NaCl at lower than the melting temperature. In a solution, the partial Gibbs free energy of the salt is reduced by the mixing term, which makes it possible for the solute to exist. With polymer, the solute entropy further increases, so more solute can exist, i.e., the solubility is higher.
Neglecting the activity coefficient dependence on concentration, the solubility ratio is
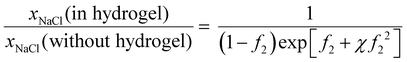 | (37) |
Fig. 8 shows the solubility ratio as a function of polymer volume f2. The increased solubility of the salt inside the hydrogel could further contribute to why hydrogel has antifouling properties, together with mass diffusion arising from the concentration difference.63
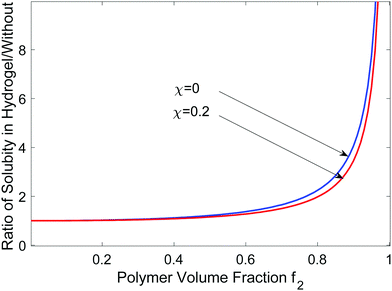 | ||
| Fig. 8 Ratio of solubility inside hydrogel vs. without hydrogel as a function of the polymer volume fraction. | ||
6. Polyelectrolyte hydrogels in equilibrium with water containing salt or humid air
Let us consider now a polyelectrolyte hydrogel, for example, poly sodium acrylate (PSA). Polyelectrolyte hydrogels had been used to extract water from the atmosphere9 and retain water in the hydrogel,27 and as a draw agent in forward osmosis for desalination applications. The forward osmosis application employs semipermeable membranes to separate ions. Here we first consider the case with no membranes, which will be of interest for solar evaporation and atmospheric water harvesting applications we discussed before.We assume that the equilibrium constant for the monomer dissociation
| CHCOONa → CHCOO− + Na+ | (38) |
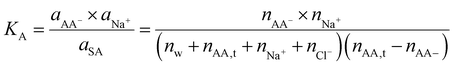 | (39) |
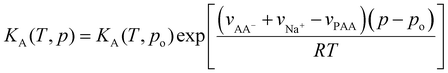 | (40) |
For the following, we neglect the pressure correction in the last term of eqn (40), which is reasonable if the molar volumes of dissociated ions do not differ from that of the non-dissociated monomers. From eqn (39), we have
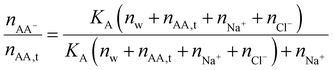 | (41) |
The chemical equilibrium in hydrogels is more complicated than modeled here because the ionized group AA− can also be neutralized by H+, which will set a limit to the dissociation of a weak polyelectrolyte. We refer readers to the literature considering such possibilities.21
Polyelectrolyte hydrogel in equilibrium with brine
Consider now that the hydrogel is in equilibrium with outside water containing the NaCl salt. Inside the hydrogel, we have fixed AA− ions and mobile Na+ and Cl− ions. Charge neutrality requires| nNa+ = nCl− + nAA− | (42) |
We assume that the equivalent volume of a monomer to water is y, then ynAA,t = Zn2. Dividing the above equation by nNa+ + nCl− +nw and using eqn (41), we arrive at,
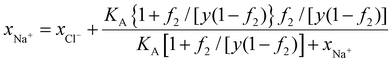 | (43) |
To find f2 and the salt concentration inside the hydrogel, we balance the chemical potential for each mobile species as in the previous section (see ESI†). Fig. 9 plots solutions for different equilibrium constant values while holding other parameters constant.
Compared to the case of non-polyelectrolyte hydrogels (Fig. 6) immersed in salty water, we see that with immobile ionized polymer chains inside the hydrogel, the salt is repelled from the hydrogel for most cases. When the external salt is less, i.e., the gel expands more. A peak can be observed in Fig. 9(a) for the difference of external to internal salt concentration when the equilibrium constant is small, i.e., the dissociated mobile ion concentration is low. This peak can be understood as follows: with more ionization of the polyelectrolyte and hence more fixed charge inside (KA large), salt is expelled. With less ionization of the polyelectrolyte, Fig. 5b shows there are more salt inside. These two different trends lead to the existence of the peak. The Donnan potential [Fig. 9(c)] is one order of magnitude larger than non-electrolyte hydrogel immersed in salt solution [Fig. 6(d)].
Polyelectrolyte hydrogel for water trapping from air
In terms of the capability of electrolyte hydrogel trapping water in air, eqn (35) is still applicable. For polyelectrolyte hydrogel, the dissociated ions (Na+ using the example we consider here) mix with water, which increases the entropy of the solution inside the hydrogel. Water mole fraction can be obtained from solving eqn (43) with xCl− = 0, which leads to the ionized sodium mole fraction and consequently the water mole fraction as,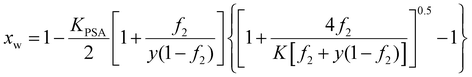 | (44) |
Fig. 10 shows the water volume at different parameter values obtained from solving eqn (35) and (44), focusing on changing the equilibrium constant. We can see that the larger the equilibrium constant, i.e, the more polyelectrolyte that can be ionized, the more water the hydrogel can contain. Compared to impregnate salt into non-electrolyte hydrogels (Fig. 6 and 7) which is limited by the salt solubility, using electrolyte hydrogels will be more effective in retaining water or extracting water from air. Strong polyelectrolyte with large equilibrium constant is desired.
Forward osmosis
Forward osmosis uses hydrogels or un-crosslinked polyelectrolytes as the draw solution.7,8 The osmotic pressure of hydrogel in fresh water at equilibrium inside the hydrogel should be larger than that of the salt water separated by a membrane. For polyelectrolyte hydrogel, its equilibrium volume can be obtained from solving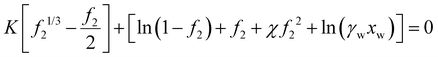 | (45) |
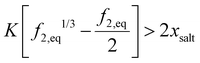 | (46) |
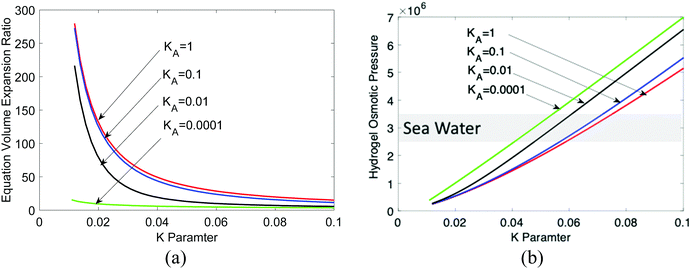
Fig. 11(a) shows the equilibrium hydrogel volume expansion ratio at different dissociation equilibrium constant values as a function of K, which can be controlled by crosslinking. Compared to non-electrolyte hydrogels, electrolyte hydrogels have a very large swelling ratio, a well-known fact. Fig. 11(b) shows the osmotic pressure. Sea water osmotic pressure is 25–35 bars, as marked in the shaded region. We can see that the osmotic pressure of electrolyte hydrogel can be much higher, suggesting that the electrolyte hydrogel can serve as a good draw medium for forward osmosis, which is consistent with the trend observed in experiments.7,8 The higher the KA value, the larger is the equilibrium volume, i.e., more clean water can be obtained. For regeneration of hydrogel, temperature sensitive hydrogel such as PNIPAM had been used,7,8 which can be modeled by including the temperature dependence of χ parameter.64
Multivalent ions
Although the examples we gave above considered monovalent symmetric salts, extension to unsymmetric and polyvalence ions is straightforward, which has been well-explained in textbooks.38,39 For MgCl2 salt, for example, for each mole of MgCl2 salt, there are two moles of Cl− ions and one mole of Mg+ ions (zi = 1 for Mg+ and 2 for Cl− in eqn (17). A similar operation as arriving at eqn (33) will lead to a term like ln(γMgCl22xMgCl2),3 in which the factor of 2 is due to the fact that the mole fraction of Cl− ions are twice that of xMgCl2. The factor 2 in front of the mixing term in eqn (32) will be replaced by 3.7. Summary
To summarize, we have reformulated Flory's thermodynamic model for hydrogels based on the minimization of Helmholtz free energy of the combined hydrogel and its environment. Our reformulation emphasizes the volume and molecular numbers as independent natural thermodynamic variables, which clarifies the roles of thermodynamic pressure. This formulation led to clear picture of the interplay between the osmotic pressure and the tension in polymer, and allows one to express the chemical potentials of the solvents and ions inside the hydrogel unambiguously. Relying on the chemical potential expressions, we examine water and ions in hydrogels related to applications in solar-driven interfacial evaporation, atmospheric water harvesting and hydrogel's water retention ability, and desalination. The chemical potentials of the solvent molecules and dissolved ions differ from that of their values in pure states, which lead to changes of the latent heat, boiling and freezing points, and solubility. The balances of each mobile species inside and outside the hydrogels determine the osmotic pressure, Donnan potential, the water and salt contents inside the hydrogel. Based on the trends predicted by the model, we can draw the following conclusions.Hydrogels have a reduced latent heat of evaporation, due to increased pressure of water inside the hydrogel. However, the reduction in the latent heat is not large enough to explain experimental observations. The melting point suppression and boiling point elevation phenomena as observed in DSC experiments can be explained similar to colligative properties observed in solutions, and they are caused by increased mixing entropy of water with polymer inside the hydrogel.
When nonelectrolyte hydrogel is placed in salty water, salt contents inside the hydrogel could be higher or lower than outside, depending on the salt's activity coefficient and concentration. Salts generally have higher solubility inside the hydrogel. Regular nonelectrolyte hydrogel can get completely dry in dry air. By impregnating salt, however, hydrogel can retain more water. Polyelectrolyte hydrogels have better ability to absorb water from moist air and retain water and such abilities increase with increasing ionization equilibrium constant. For electrolyte hydrogels immersed in salty water, the salt concentration inside is typically lower than that outside.
We should point out that although the thermodynamic approach we presented is general, the specific models we used for the Helmholtz free energy are simplified. We rely mainly on Flory's theories on the mixing entropy between the solvent and polymer molecules, and polymer's configurational entropy changes for the Helmholtz free energy. We did not consider the interaction between mobile ions and the fixed ions on the polymer, for which large amount of work has been done and different models exist. We only included polymer's configurational entropy changes, excluding the intermolecular force interactions along the chain which could be important in highly stretched polymers. We did not treat the dissociation of polyelectrolyte rigorously. All these details could be improved and indeed many studies had already been done as we cited along the way. The thermodynamic treatment we present however is general, and improvements in these details can be incorporated to make better predictions. However, the classical thermodynamic treatment is by nature a mean field theory.
Conflicts of interest
The author declares no conflict of interests.Acknowledgements
I would like to thank Dr. Xueyu Li and Dr. Honglei Guo for their attempts in measuring Donnan potential in a PVA hydrogel with salty environment and indeed observation of a potential difference. The author would like to thank Drs. Shaoting Lin, Jungwoo Shin, Yaodong Tu, and Mr. Simo Pajovic for helpful discussion, and to MIT for its support.References
- N. A. Peppas, J. Z. Hilt, A. Khademhosseini and R. Langer, Adv. Mater., 2006, 18, 1345–1360 CrossRef CAS.
- J. Y. Sun, H. X. Zhao, W. R.-K. Illeperuma, O. Chaudhuri, K. H. Oh, D. Mooney, J. J. Vlassak and Z. G. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed.
- F. Zhao, X. Y. Zhou, Y. Shi, X. Qian, M. Alexander, X. P. Zhao, S. Mendez, R. G. Yang, L. T. Qu and G. H. Yu, Nat. Nanotechnol., 2012, 13, 489–495 CrossRef PubMed.
- F. Zhao, Y. Guo, X. Zhou, W. Shi and G. Yu, Nat. Rev. Mater., 2020, 5, 388–401 CrossRef.
- H. Ghasemi, G. Ni, A. M. Marconnet, J. Loomis, S. Yerci, N. Miljkovic and G. Chen, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- P. Tao, G. Ni, C. Song, W. Shang, J. Wu, J. Zhu, G. Chen and T. Deng, Nat. Energy, 2018, 3, 1031–1041 CrossRef.
- D. Li, X. Y. Zhang, J. F. Yao, G. P. Simon and H. T. Wang, Chem. Commun., 2011, 47, 1710–1712 RSC.
- D. Li, X. Y. Zhang, J. F. Yao, Y. Zeng, G. P. Simon and H. T. Wang, Soft Matter, 2011, 7, 10048 RSC.
- F. Zhao, X. Y. Zhou, Y. Liu, Y. Shi, Y. F. Dai and G. H. Yu, Adv. Mater., 2019, 31, 1806446 CrossRef PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, NY, 1953 Search PubMed.
- P. J. Flory and J. Rehner, Jr., J. Chem. Phys., 1943, 11, 521–526 CrossRef CAS.
- P. J. Flory, J. Phys. Chem., 1942, 10, 51 CrossRef CAS.
- J. H. Hildebrand, J. Chem. Phys., 1947, 15, 225–228 CrossRef CAS.
- P. J. Flory and J. Rehner, Jr., J. Chem. Phys., 1942, 11, 512–520 CrossRef.
- A. Katchalsky and I. Michaeli, J. Polym. Sci., 1955, 15, 69–86 CrossRef CAS.
- P. Kosovan, T. Richter and C. Holm, Macromolecules, 2015, 48, 7698–7708 CrossRef CAS.
- A. E. English, S. Mafe, J. A. Manzanares, X. H. Yu, A. Y. Grosberg and T. Tanaka, J. Chem. Phys., 1996, 104, 8713–8720 CrossRef CAS.
- L. Bannon-Peppas and N. Peppas, Chem. Eng. Sci., 1991, 46, 715–722 CrossRef.
- S. Zhang, S. T. Lin, X. H. Zhao and R. Karnik, J. Appl. Phys., 2020, 128, 044701 CrossRef CAS.
- G. S. Longo, M. O. de la Cruz and I. Szleifer, Soft Matter, 2012, 8, 1344–1354 RSC.
- O. Rud, T. Richter, O. Borisov, C. Holm and P. Kosovan, Soft Matter, 2017, 13, 3264–3274 RSC.
- J. Landsgell and C. Holm, Macromolecules, 2019, 52, 9341–9353 CrossRef.
- C. Hofzumahaus, C. Strauch and S. Schneider, Soft Matter, 2021, 17, 6029 RSC.
- W. Hong, X. H. Zhao and Z. G. Suo, J. Mech. Phys. Solids, 2010, 58, 558–577 CrossRef CAS.
- H. Kim, S. Yang, S. R. Rao, S. Narayan, E. A. Kapustin, H. Furukawa, A. S. Umans, O. M. Yaghi and E. N. Wang, Science, 2017, 356, 430–434 CrossRef CAS PubMed.
- X. Y. Zhou, F. Zhao, Y. H. Guo, Y. Zhang and G. H. Yu, Energy Environ. Sci., 2018, 11, 1985–1992 RSC.
- Y. Y. Bai, B. H. Chen, F. Xiang, J. X. Zhou, H. Wang and Z. G. Suo, Appl. Phys. Lett., 2014, 105, 151903 CrossRef.
- M. S. Jhon and J. D. Andrade, J. Biomed. Mater. Res., 1973, 7, 509–522 CrossRef CAS PubMed.
- Y. Sekine and T. Ikeda-Fukazawa, J. Chem. Phys., 2009, 130, 034501 CrossRef PubMed.
- F. H. Stillinger, Science, 1980, 209, 451–457 CrossRef CAS PubMed.
- R. Ludwig, Angew. Chem., Int. Ed., 2001, 40, 1808–1827 CrossRef CAS.
- F. G. Donnan, Chem. Rev., 1924, 1, 73–90 CrossRef CAS.
- W. M. Lai, J. S. Hou and V. C. Mow, J. Biomech. Eng., 1991, 113, 245–258 CrossRef CAS PubMed.
- M. L. Huggins, J. Am. Chem. Soc., 1942, 64, 1712–1719 CrossRef CAS.
- M. S. Jhon and J. D. Andrade, J. Biomed. Mater. Res., 1973, 7, 509–522 CrossRef CAS PubMed.
- Y. Sekine and T. Ikeda-Fukazawa, J. Chem. Phys., 2009, 130, 034501 CrossRef PubMed.
- G. Chen, J. Micromech. Mol. Phys., 2022 DOI:10.1142/S2424913021420145.
- G. N. Lewis and M. Randall, Thermodynamics, McGraw-Hill, 2nd Ed., 1961 Search PubMed.
- H. DeVoe, Thermodynamics and Chemistry, v.10, 2nd edn, 2020, https://www.chem.umd.edu/thermobook Search PubMed.
- P. Ellgen, Thermodynamics and Chemical Equilibrium, LibreTexts™, https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Book%3A_Thermodynamics_and_Chemical_Equilibrium_(Ellgen).
- K. S. Pitzer, J. Phys. Chem., 1973, 77, 268–277 CrossRef CAS.
- O. Miyawaki, A. Saito, T. Matsuo and K. Nakamura, Biosci., Biotechnol., Biochem., 1997, 61, 466–469 CrossRef CAS.
- G. Manning, J. Chem. Phys., 1969, 51, 924–933 CrossRef CAS.
- P. Debye and E. Huckle, Phys. Z., 1923, 24, 185–206 CAS , translated and typeset by Bruas, M. J., 2020.
- X. Y. Zhou, Y. H. Guo, F. Zhao, W. Shi and G. H. Yu, Adv. Mater., 2020, 32, 2007012 CrossRef PubMed.
- X. Y. Zhou, F. Zhao, Y. H. Guo, Y. Zhang and G. H. Yu, Energy Environ. Sci., 2018, 11, 1985–1992 RSC.
- Y. D. Tu, J. W. Zhou, S. T. Lin, X. H. Zhao and G. Chen, 2022, arXiv:2201.10385.
- Y. D. Tu and G. Chen, 2022, arXiv:2202.10646.
- R. Y. Li, Y. Shi, M. Alsaedi, M. Wu, L. Shi and P. Wang, Environ. Sci. Technol., 2018, 52, 11367–11377 CrossRef CAS PubMed.
- H. L. Guo, T. Kurokawa, M. Takahata, W. Hong, Y. Katsuyama, F. Luo, J. Ahmed, T. Nakajima, T. Nonoyama and J. P. Gong, Macromolecules, 2016, 49, 3100–3108 CrossRef CAS.
- Private communication with X. Li and H. Guo, Dr Guo PhD thesis entitled “Establishment of Microelectrode Technique for Detecting the Spatial Distribution of Electrical Potential of Hydrogels”, Hokkaido University, 2016.
- C. Yu, Y. H. Wang, X. M. Lang and S. S. Fan, Environ. Sci. Technol., 2016, 50, 13024–13031 CrossRef CAS PubMed.
- T. Richter, J. Landsgell, P. Kosovan and C. Holm, Desalination, 2017, 414, 28–34 CrossRef CAS.
- O. Rud, O. Borisov and P. Kosovan, Desalination, 2018, 442, 32–43 CrossRef CAS.
- O. V. Rud, J. Landsgell, C. Holm and P. Kosovan, Desalination, 2021, 506, 114995 CrossRef CAS.
- N. A. Peppas and E. W. Merrill, J. Polym. Sci., 1976, 459–464 CAS.
- H. J. Goldsmid, Introduction to Thermoelectricity, Springer, 2010 Search PubMed.
- J. W. Zhou, S. T. Lin, H. X. Zeng, J. Liu, B. X. Li, Y. F. Xu, X. H. Zhao and G. Chen, Mater. Horiz., 2020, 7, 2936–2943 RSC.
- A. J. Ellis, J. Chem. Soc. A, 1966, 1570–1584 Search PubMed.
- E. Glueckauf, Trans. Faraday Soc., 1968, 64, 2423–2432 RSC.
- F. J. Millero, Chem. Rev., 1971, 71, 147–176 CrossRef CAS.
- M. E. Guendouzi, A. Dinane and A. Mounir, J. Chem. Thermodyn., 2001, 33, 1059–1072 CrossRef.
- G. Ni, S. H. Zandavi, S. M. Javid, S. V. Boriskina, T. A. Cooper and G. Chen, Energy Environ. Sci., 2018, 11, 1510–1519 RSC.
- S. Q. Cai and Z. G. Guo, J. Mech. Phys. Solids, 2011, 59, 2259–2278 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00356b |
| This journal is © the Owner Societies 2022 |