Open Access Article
Open Access ArticleUltrafast proton transfer of the aqueous phenol radical cation†
Muhammad Shafiq
Bin Mohd Yusof
a,
Hongwei
Song
 b,
Tushar
Debnath
a,
Bethany
Lowe
a,
Minghui
Yang
b,
Tushar
Debnath
a,
Bethany
Lowe
a,
Minghui
Yang
 bc and
Zhi-Heng
Loh
bc and
Zhi-Heng
Loh
 *a
*a
aDivision of Chemistry and Biological Chemistry, School of Physical and Mathematical Sciences, Nanyang Technological University, 21 Nanyang Link, Singapore 637371, Singapore. E-mail: zhiheng@ntu.edu.sg
bState Key Laboratory for Magnetic Resonance and Atomic and Molecular Physics, Wuhan Institute of Physics and Mathematics, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430071, China
cWuhan National Laboratory for Optoelectronics, Huazhong University of Science and Technology, Wuhan 430071, China
First published on 10th May 2022
Abstract
Proton transfer (PT) reactions are fundamental to numerous chemical and biological processes. While sub-picosecond PT involving electronically excited states has been extensively studied, little is known about ultrafast PT triggered by photoionization. Here, we employ femtosecond optical pump-probe spectroscopy and quantum dynamics calculations to investigate the ultrafast proton transfer dynamics of the aqueous phenol radical cation (PhOH˙+). Analysis of the vibrational wave packet dynamics reveals unusually short dephasing times of 0.18 ± 0.02 ps and 0.16 ± 0.02 ps for the PhOH˙+ O–H wag and bend frequencies, respectively, suggestive of ultrafast PT occurring on the ∼0.1 ps timescale. The reduced potential energy surface obtained from ab initio calculations shows that PT is barrierless when it is coupled to the intermolecular hindered translation between PhOH˙+ and the proton-acceptor water molecule. Quantum dynamics calculations yield a lifetime of 193 fs for PhOH˙+, in good agreement with the experimental results and consistent with the PT reaction being mediated by the intermolecular O⋯O stretch. These results suggest that photoionization can be harnessed to produce photoacids that undergo ultrafast PT. In addition, they also show that PT can serve as an ultrafast deactivation channel for limiting the oxidative damage potential of radical cations.
Introduction
Proton transfer reactions are ubiquitous in biological processes such as enzyme catalysis1,2 and the transport of ions through membranes.3 In addition, many biological redox reactions are facilitated by concomitant PT and electron transfer, as in proton-coupled electron transfer.4–7 Beyond PT reactions that occur in the electronic ground state, proton transfer can also involve electronically excited states. Excited-state proton transfer (ESPT) plays an important role in bioluminescence,8–10 as exemplified by the green fluorescent protein (GFP).11–13 Moreover, ESPT is also central to technologically important applications such as photoinitiated polymerization14,15 and photolithography.16Being triggered by light, ESPT reactions are particularly amenable to investigation by ultrafast spectroscopy.7,17,18 Previous time-resolved studies have elucidated ultrafast excited-state intramolecular proton transfer (ESIPT) that either occurs ballistically19 or is mediated by skeletal vibrational modes that modify the proton donor-acceptor distance.20,21 Ballistic PT occurs on timescales as short as ∼10 fs and exhibits pronounced H/D isotopic dependence whereas PT that is gated by structural deformations typically occur on timescales of ∼100 fs. Complementing molecules that undergo ESIPT is the class of molecules known as photoacids,18,22,23 which transfer a proton to a neighboring solvent molecule upon photoexcitation. Extensive studies of intermolecular excited–state proton transfer to solvent (ESPTS) have revealed a correlation between the PT rate and the acid dissociation constant of the electronically excited state, 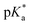 .24 The strongest photoacids, dubbed “superphotoacids”, have
.24 The strongest photoacids, dubbed “superphotoacids”, have 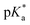 < −7 and exhibit proton transfer timescales of ∼100 fs, limited by the ∼100 cm−1 frequency of the intermolecular vibration between the proton donor and proton acceptor.25–28
< −7 and exhibit proton transfer timescales of ∼100 fs, limited by the ∼100 cm−1 frequency of the intermolecular vibration between the proton donor and proton acceptor.25–28
Aside from photoexcitation, photoionization can also lead to proton transfer. Ab initio simulations and experiments performed on ionized size-selected clusters, comprising the proton donor and a variable number of solvent molecules in the gas phase, have revealed spectroscopic signatures of the PT product.29–34 However, only a limited number of studies have shed light on the dynamics of PT induced by photoionization. Time-resolved mass spectrometry measurements performed on the gas-phase phenol–ammonia radical cation complex, PhOH•+–NH3, suggest that PT begins with the contraction of the intermolecular O⋯N distance within ∼0.1 ps followed by a ∼1 ps-long vibrational relaxation of the PT product.35,36 In the condensed phase, femtosecond soft X-ray absorption spectroscopy was recently revealed that the H2O˙+ radical cation, produced by the intense laser ionization of liquid water, undergoes PT on the ∼50 fs timescale.37 Beyond liquid water, however, the PT dynamics of ionized molecules in aqueous solution remains largely unexplored. It is important to note that ultrafast PT bears implications for the chemical reactivity of radicals. For example, the standard reduction potential of the H2O˙+ radical cation (3.8 V)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 is larger than that of the hydroxyl radical (OH˙) PT product (1.8 V).39 Within the context of radiation chemistry and radiation biology, the ultrashort lifetime of the H2O˙+ radical cation diminishes its potential for oxidative damage.
38 is larger than that of the hydroxyl radical (OH˙) PT product (1.8 V).39 Within the context of radiation chemistry and radiation biology, the ultrashort lifetime of the H2O˙+ radical cation diminishes its potential for oxidative damage.
Here, we employ optical pump–probe spectroscopy to resolve the ultrafast PT dynamics of the aqueous phenol radical cation, produced by the ionization of aqueous phenol. Our choice of phenol is motivated by its occurrence as the side chain of tyrosine (TyrOH), an amino acid whose redox activity is entwined with proton transfer.7,40 Oxidation of tyrosine requires a highly oxidizing potential of +1.46 V vs. NHE to give TyrOH˙+;41,42 this potential decreases to +0.94 V when deprotonation occurs in concert with oxidation to yield TyrO˙.43 Experimental and theoretical studies of microhydrated PhOH˙+–(H2O)n clusters in the gas phase show that PT only occurs when 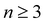 ,30–36 although the timescale for proton transfer remains unknown. Our experiments reveal ultrafast dephasing of the vibrational modes of the aqueous PhOH˙+ radical cation, suggestive of proton transfer occurring on the ∼0.1 ps timescale. These results are supported by quantum dynamics calculations.
,30–36 although the timescale for proton transfer remains unknown. Our experiments reveal ultrafast dephasing of the vibrational modes of the aqueous PhOH˙+ radical cation, suggestive of proton transfer occurring on the ∼0.1 ps timescale. These results are supported by quantum dynamics calculations.
Methods
Experimental
The experimental setup has been described in detail elsewhere.44 Briefly, the 4.4 mJ, 30 fs, 1 kHz output from an amplified Ti:sapphire laser system is focused into a helium-filled hollow-core fiber for spectral broadening followed by temporal compression using chirped mirrors. 80% of the compressed pulse energy is directed into a visible-NIR 4f-pulse shaper to correct for high-order dispersion to yield transform-limited, 6 fs pulses for strong-field photoionization of aqueous phenol (Fig. S1a and S2a, ESI†). 20% of the compressed pulse energy is sent to a 50 μm-thick Type I beta-barium borate (BBO) crystal for second-harmonic generation followed by chirped-mirror compression to generate near-UV probe pulses that span 360–470 nm (Fig. S1b, ESI†). The strong-field ionization pump pulses have a maximum pulse energy of 25 μJ and are focused to a beam waist of 80 μm (1/e2), giving a maximum peak intensity of 4 × 1013 W cm−2. On the other hand, the near-UV probe has a pulse energy of 100 nJ and is focused to a beam waist of 26 μm (1/e2), ∼3× smaller than that of the pump pulse to minimize the effects of spatial averaging. The instrumental response function is measured by difference-frequency mixing in a 10 μm-thick BBO crystal positioned at the sample target and is found to have a FWHM of 12 fs (Fig. S2b, ESI†). A synchronized optical chopper is positioned in the path of the pump beam to modulate the repetition rate of the pump beam at 0.5 kHz. The probe pulses that are transmitted through the sample are spectrally dispersed onto a 1024-element array detector with a read-out rate of 1 kHz, thus permitting the acquisition of the differential absorption (ΔA) spectrum from each successive pair of probe pulses. A reference spectrograph is used to eliminate noise caused by shot-to-shot fluctuations of the probe pulse.Phenol (Sigma-Aldrich, ≥99%), used as received without further purification, is dissolved in distilled water to produce a 0.20 M solution (pH ∼ 5.3). Deuterated phenol that is employed in the isotopic studies is prepared by dissolving phenol in deuterium oxide (D2O) (Cambridge Isotope Laboratories, Inc., 99.9%) to yield C6H5OD (PhOD). The aqueous phenol sample is delivered by a slit-type nozzle that is connected to a peristaltic pump and pulse dampener. The 7 μm thick jet is sufficiently thick to produce a sizeable ΔA signal while minimizing the dispersive broadening of the individual laser pulses as well as the group-velocity mismatch between pump and probe pulses in the liquid jet.
Theoretical calculations
The equilibrium molecular geometries of phenol and the phenol radical cation, as well as their associated vibrational frequencies, are obtained from DFT calculations performed with the GAUSSIAN 16 package.45 The calculations employ the hybrid exchange functional of Becke (B3),46 the correlation functional of Lee, Yang and Parr (LYP),47 and the 6-311G++(d,p) split-valence triple-ξ basis set. Three different models of phenol and the phenol radical cation are employed in the simulations. The first model is the isolated molecule, the second model is the molecule with three explicit water molecules of hydration, i.e., PhOH–(H2O)3 or PhOH˙+–(H2O)3, whereas the third model is the molecule with five explicit water molecules of hydration, i.e., PhOH-(H2O)5 or PhOH˙+–(H2O)5. All three models include a polarizable continuum (PCM) to mimic the dielectric environment of the water solvent.48 For PhOH–(H2O)3 or PhOH˙+–(H2O)3, the phenolic OH is directly hydrogen-bonded to all three water molecules, where one acts as the hydrogen bond acceptor and two act as hydrogen bond donors. For PhOH–(H2O)5 or PhOH˙+–(H2O)5, two additional hydrogen bond-accepting water molecules are coordinated to the proton-accepting H2O in PhOH–(H2O)3 and PhOH˙+–(H2O)3. The Cs point group symmetry, with the PhOH moiety residing within the reflection plane, is imposed during geometry optimizations. Each geometry optimization is followed by a vibrational frequency calculation to verify that the optimized geometry corresponds to a local minimum.To investigate the proton transfer dynamics, we construct the reduced potential energy surface (PES) along the intramolecular phenol O–H distance coordinate and the intermolecular OPh⋯Oa distance coordinate involving the phenol oxygen atom (OPh) and the oxygen atom of the proton-accepting water molecule (Oa). Since PhOH˙+–(H2O)3 does not support proton transfer, we employ PhOH˙+–(H2O)5 instead for the PES scan. The OPh⋯Oa distance is varied between 2.00–3.50 Å in steps of 0.05 Å while the phenol O–H distance is varied between 0.80–1.80 Å in steps of 0.05 Å; in addition, phenol O–H distances of 1.90 Å, 2.00 Å, 2.20 Å, and 2.40 Å are also included in the PES scan. The PES scan is repeated for neutral phenol, PhOH-(H2O)5, where the phenol O–H distance is varied from 0.79–1.49 Å and the OPh⋯Oa distance is varied between 2.04–3.54 Å, both with steps of 0.05 Å.
The resultant reduced PESs are fit by using the neural network method.49 The architecture of neural network is 2-20-40-1, giving a total of 941 parameters. The input layer consists of the two bond distances, the two hidden layers have 20 and 40 neurons, and the output layer has 1 potential energy. All fittings are carried out using the Levenberg–Marquardt algorithm50 and employ the root-mean-square error (RMSE) to assess the quality of each fit. To avoid overfitting, the data set is randomly divided into two groups, with 90% of the points as the training set and 10% as the validating set. The fits with the two sets that give similarly small RMSEs are thought to be reasonable. The total RMSEs of the final neutral and cationic PESs are 1.462 meV and 3.068 meV, respectively.
Quantum dynamics simulations employ the 2D Hamiltonian
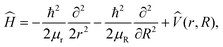 | (1) |
Results and discussion
Transient absorption of ionized aqueous phenol
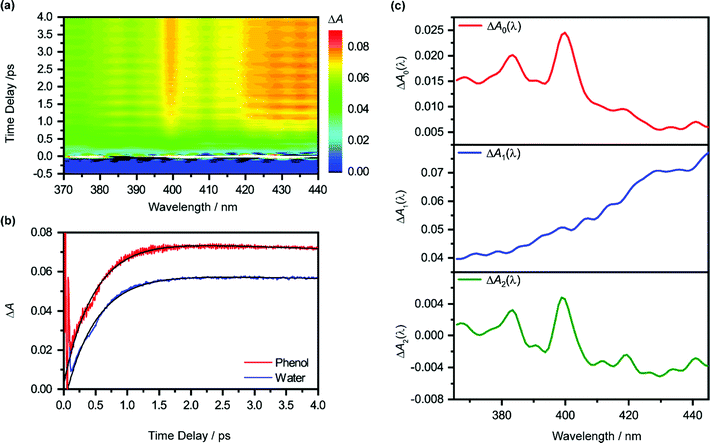
Pump-power dependence measurements show that the photoionization of phenol occurs via a four-photon process, corresponding to a total input energy of 7.8 eV (Fig. S3 and Section S1, ESI†). Considering the vertical ionization energy of 7.8 eV for aqueous phenol53 and the vertical electron affinity of ∼1 eV for liquid water,54 the 7.8 eV energy input is sufficient to eject an electron from phenol and inject it into the conduction band of liquid water. While a four-photon dependence could still result from a resonance-enhanced multiphoton ionization (REMPI) process in which the ionization step is not saturated, we consider such a scenario to be unlikely under our experimental conditions because any neutral electronically excited state that is populated via REMPI would be rapidly ionized in the presence of an intense laser field,55,56 thus saturating the ionization step and yielding a photon order lower than four. As such, we rule out any participation of intermediate electronically excited states in the multiphoton photoionization process. This contrasts with results obtained from previous studies, which reveal ionization of phenol following UV photoexcitation with photon energies spanning 4.6–6.2 eV, either by autoionization from electronically excited states to the solvent continuum54 or by O–H photodissociation along the repulsive 11πσ* potential57,58 followed by charge transfer to solvent.59 At the same time, we do not consider the possibility of accessing the first electronically excited state of PhOH˙+, located 0.8 eV above the electronic ground state, due to the propensity of strong-field ionization for producing ions in the electronic ground state.60–63The isotropic differential absorption (ΔA) spectrum of ionized aqueous phenol collected as a function of pump–probe time delay is shown in Fig. 1a. The increasing ΔA signal on the long-wavelength side of the probe spectral range is the absorption signature of the hydrated electron, formed from the conduction-band electron via electronic relaxation54,64 followed by vibrational cooling.65–71 In addition, the ΔA spectrum exhibits a pronounced absorption peak at 400 nm alongside a vibronic feature at 385 nm, indicative of the 2B1 ← 2B1 transition of the phenoxyl radical electronic ground state.72,73 The appearance of the absorption signature of the PhO˙ radical PT product on the sub-picosecond timescale indicates ultrafast PT.
The absorption signature of aqueous PhOH˙+, produced by the vertical ionization of phenol, appears to be missing from the ΔA spectra. In n-dodecane, cyclohexane, and 1,2-dichloroethane, the absorption maximum of the phenol radical cation is located at 430 nm, whereas the absorption maximum in n-butyl chloride is at 440 nm.74 These absorption maxima are broadened and red-shifted relative to the absorption maximum of the PhO˙ radical at 400 nm, recorded in the same solvents. In highly acidic aqueous solution (∼14 M H2SO4), an absorption peak at 419 nm (εmax = 1800 ± 150 M−1 cm−1), with a linewidth of 50 nm, has been attributed to the PhOH˙+ radical cation.75 The broad absorption feature of PhOH˙+ in both aqueous and nonaqueous solvents is also consistent with the broad, featureless electronic absorption spectra of gas-phase PhOH•+–(H2O)n (n = 1, 2), for which proton transfer does not occur;31 in comparison, the electronic absorption spectra of gas-phase PhOH˙+–(H2O)n (n = 3–6) show well-defined peaks that are characteristic of the PhO˙ radical proton transfer product.31 Interestingly, a recent study of aqueous phenol photoexcited at 200 nm attributed a weak and short-lived ΔA feature at 425 nm to aqueous PhOH˙+.73 Unfortunately, since the feature appears only within the 200 fs time resolution of the experimental setup, the decay constant of the feature, and hence presumably the lifetime of the phenol radical cation, could not be resolved. In our case, the time trace recorded at 425 nm does not reveal any additional ultrafast dynamics that can be ascribed to aqueous PhOH˙+ (Fig. 1b). It is possible that the broad absorption signature of the phenol radical cation is concealed by the prominent absorption of the hydrated electron75 (ε = 3148 M−1 cm−1 at 425 nm).76
Global analysis of the time-resolved ΔA spectra
To elucidate the timescales of the ultrafast dynamics encoded in the time-resolved ΔA spectra, we fit the ΔA time traces collected over the wavelength range of 365–450 nm and time delay range of 100–4455 fs to the function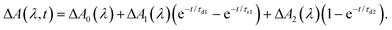 | (2) |
The form of eqn (2) is motivated by the following considerations. First, the component that appears immediately at time-zero should be identified; in eqn (2), this corresponds to the ΔA0(λ) term. Second, a term that accounts for the appearance and subsequent disappearance of the hydrated electron should be included; in eqn (2), this corresponds to the ΔA1(λ) term, with rise and decay time constants of τr1 and τd1, respectively. Finally, a term that accounts for the spectral evolution that is associated with vibrational cooling is included; in eqn (2), this corresponds to the ΔA2(λ) term, with an associated time constant τd2.
The global fit reveals that ΔA rises with a characteristic time constant τr1 = 0.51 ± 0.01 ps and decays with time constant τd1 ∼ 0.07 ns, much longer than the pump-probe time window sampled in our measurements; these time constants are consistent with those obtained from our experiments on pure liquid water, performed under identical experimental conditions. In the case of ionized phenol, an additional decay constant τd2 = 1.8 ± 0.1 ps is found. The time traces of ionized aqueous phenol and ionized liquid water at 425 nm, along with their respective fit functions, are shown in Fig. 1b. The decay associated difference spectra, ΔA1(λ) and ΔA2(λ), and the offset at time-zero, ΔA0(λ), are plotted in Fig. 1c.
The time constants τr1 and τd1 are assigned respectively to the timescales for the formation of the hydrated electron and its subsequent disappearance by geminate recombination.65,67,77–79 This assignment is supported by the similarity of the corresponding decay associated difference spectrum, ΔA1(λ), to the absorption spectrum of the hydrated electron. Multiphoton ionization of the phenol solute and the liquid water solvent injects electrons into the conduction band of liquid water. Subsequent trapping of the electrons followed by vibrational cooling yields hydrated electrons.65–71 The hydrated electrons can undergo geminate recombination with the phenoxyl (PhO˙) and hydroxyl (OH˙) radicals, produced via the ionization of phenol and water, respectively. Although germinate recombination is characterized by nonexponential kinetics,67,80 it can be approximated as an exponential decay in our analysis due to the narrow range of time delays (∼4 ps) sampled in our measurements.81,82
Fitting ΔA1(λ) to the reported molar extinction coefficients of the hydrated electron76 yields an initial concentration of 29.4 ± 0.1 mM for hydrated electrons produced from the ionization of aqueous phenol (Fig. S4a, ESI†). Repeating the same analysis for the pure liquid water sample, strong-field-ionized under experimental conditions identical to those of aqueous phenol, yields an initial hydrated electron concentration of 26.3 ± 0.1 mM (Fig. S4b, ESI†). Since hydrated electrons can be produced from the aqueous phenol sample by the ionization of both the phenol solute and the water solvent, and assuming that the electrons that are injected from solute and solvent into the conduction band of water have the same probability of producing hydrated electrons,83,84 the difference between the two concentrations corresponds to the concentration of the ionized phenol solute, c0(PhOH˙+) ∼ 3.1 ± 0.2 mM. From this concentration, we obtain an ionization fraction of ∼2%.
Aside from τr1 and τd1, global fitting also uncovers an additional time constant, τd2, for ionized aqueous phenol. The corresponding decay associated difference spectrum, ΔA2(λ), exhibits positive peaks at 384 nm and 399 nm (Fig. 1c), which coincide with the absorption maxima of the aqueous PhO˙ radical.72 The appearance of ΔA2(λ), with positive peaks superimposed on a broad, positive feature skewed towards the long-wavelength side, implies the growth of the PhO˙ radical absorption peaks and the decrease of the long-wavelength ΔA signal with time. Such a spectral evolution is suggestive of vibrational relaxation of the PhO˙ radical. As such, we tentatively assign τd2 to the timescale for vibrational relaxation. This timescale is comparable to τd2 = 0.93 ± 0.02 ps recently reported for the related tyrosyl radical anion, produced by the sub-6 fs photodetachment of the tyrosinate dianion.82
It is interesting to compare the vibrational relaxation timescales, τd2, for PhO˙ produced via two different routes: (1) the photoionization of phenol and (2) the photodetachment of phenoxide. The latter was the subject of a recent study;44 employing the data analysis procedure outlined here gives a vibrational relaxation time of 1.02 ± 0.03 ps. By comparison, the vibrational relaxation of PhO˙ produced via the photoionization of aqueous phenol is ∼2× slower. The difference in the vibrational relaxation times reflects the different precursors to PhO˙ formation for the two vibrational relaxation pathways. In the case of pathway 1, the Franck–Condon region corresponds to the equilibrium geometry of aqueous PhOH, whereas the Franck–Condon region for pathway 2 corresponds to the equilibrium geometry of the PhO− anion. Ab initio calculations of the equilibrium geometries of PhOH, PhO−, and PhO˙ (Fig. 2) show that pathway 1 is accompanied by a significantly larger extent of structural rearrangement than pathway 2 (Table 1). For example, the contraction of the C–O bond length increases by a factor of ∼2× on going from pathway 2 (ΔR = −5.8 pm) to pathway 1 (ΔR = –11.0 pm). It is conceivable that the larger extent of structural rearrangement leads to slower vibrational relaxation dynamics.
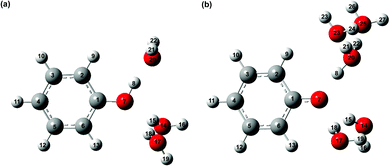 | ||
| Fig. 2 Equilibrium geometries of microhydrated phenol radical cations (a) PhOH˙+-(H2O)3 and (b) PhOH˙+-(H2O)5. | ||
| Bond | Bond length/pm | Difference/pm | |||
|---|---|---|---|---|---|
| Phenol (A) | Phenoxide anion (B) | Phenoxyl radical (C) | (C)–(A) | (C)–(B) | |
| C1–C2 | 139.6 | 141.7 | 144.8 | 5.2 | 3.1 |
| C2–C3 | 139.5 | 139.3 | 137.2 | −2.3 | −2.1 |
| C3–C4 | 139.5 | 139.8 | 141.1 | 1.6 | 1.3 |
| C4–C5 | 139.6 | 139.8 | 141.1 | 1.5 | 1.3 |
| C5–C6 | 139.3 | 139.3 | 137.2 | −2.1 | −2.1 |
| C1–C6 | 139.6 | 141.7 | 144.8 | 5.2 | 3.1 |
| C1–O7 | 137.8 | 132.6 | 126.8 | −11 | −5.8 |
Beyond the negative features located at 384 nm and 399 nm, the ΔA2(λ) spectrum also exhibits dips at 419 nm and 441 nm. These four features have a constant energy separation of 1135 ± 34 cm−1 (Fig. S5, ESI†) that is comparable to that observed in the 2B1 ← 2B1 absorption band of the aqueous PhO˙ radical,72 suggesting that they arise from the same vibronic progression. The dips at 419 nm and 441 nm appear in an overall positive region of the ΔA2(λ) spectrum, thus implying a decay, albeit with reduced decay amplitude. It should be noted that the 2B1 ← 2B1 absorption band of the vibrationally cold PhO˙ radical does not exhibit peaks at 419 nm and 441 nm;72 as such, their appearance in the ΔA2(λ) spectrum suggests that they are vibrationally hot bands, consistent with the PhO˙ radical being produced in a vibrationally excited state from the PhOH˙+ precursor.
According to eqn (2), the spectrum ΔA2(λ) in principle represents the ΔA spectrum recorded at 0 fs time delay. However, since global fitting is performed from 100 fs time delay onwards, it is more appropriate to consider ΔA0(λ) as the ΔA spectrum recorded in the first ∼100 fs. The appearance of spectral signatures of the PhO˙ radical absorption (at 383 nm and 400 nm) in ΔA0(λ) therefore suggests that proton transfer from PhOH˙+ occurs on the ∼100 fs timescale. The PhO˙ radical absorption sits atop an offset absorption that extends beyond the maximum wavelength of 450 nm probed in the experiments. This offset could be due to a combination of the absorption of the vibrationally hot PhO˙ radical and the PhOH˙+ radical cation. We note that the absorption at 425 nm that was previously attributed73 to PhOH˙+ is not observed in ΔA0(λ), perhaps due to the different ionization mechanisms. In ref. 73, PhOH˙+ is likely produced via autoionization following 6.2 eV excitation of PhOH, whereas the use of intense, few-cycle laser pulses in the present work is expected to drive vertical, multiphoton ionization of PhOH. While autoionization conceivably yields vibrationally cold PhOH˙+, vertical ionization results in vibrationally hot PhOH˙+. The excess vibrational energy that results from vertical ionization likely accelerates proton transfer, thus preventing the clear spectroscopic observation of the PhOH˙+ species in the present work. Aqueous PhOH˙+ is expected to yield a ΔA signal of ∼4 × 10−3 peaked at 419 nm, based on the concentration of ionized PhOH, c0(PhOH˙+) ∼3 mM, and both the molar extinction coefficient and the position of the absorption maximum of PhOH˙+ in concentrated aqueous acid (εmax = 1800 ± 150 M−1 cm−1 at 419 nm). Although the peak at 419 nm in ΔA0(λ) more likely originates from a hot band transition of the PhO˙ radical (see above) – it is too narrow to be attributed to the broad differential absorption expected for the PhOH˙+ radical cation – we cannot exclude the possibility of an underlying, broad absorption due to the PhOH˙+ radical cation.
Vibrational wave packet dynamics induced by the photoionization of aqueous phenol
Beyond the temporal evolution of the ΔA signal due to hydrated electron population dynamics and the vibrational relaxation of the PhO˙ radical, the time-resolved ΔA spectra also exhibit oscillatory features that encode vibrational wave packet dynamics. To analyze the wave packet dynamics quantitatively, we compute the spectral first-moment time trace E(t), given as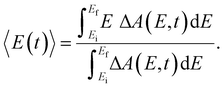 | (3) |
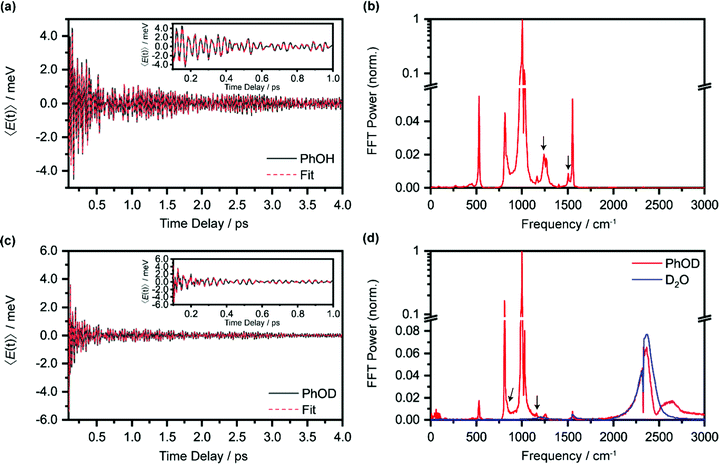
In the above expression, E represents the probe photon energy, t is the pump–probe time delay and 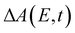 is the differential absorbance as a function of probe photon energy and pump–probe time delay. Ei and Ef define the spectral range over which 〈E(t)〉 is computed; in this case, Ei and Ef correspond to 2.95 eV (420 nm) and 2.88 eV (430 nm), respectively. To minimize possible contributions from coherent artifacts, 〈E(t)〉 is computed only from a time delay of 0.1 ps onward. The resultant 〈E(t)〉 trace is shown in Fig. 3a, with the inset showing a zoomed-in view of 〈E(t)〉 in the range of 0.1–1 ps. Fast-Fourier transform (FFT) of the 〈E(t)〉 trace yields its FFT power spectrum (Fig. 3b), from which the frequencies of vibrational modes that contribute to 〈E(t)〉 can be identified. To aid the assignment of the observed FFT frequencies, experiments were also performed on the isotopomer, phenol-OD (PhOD), dissolved in D2O. The 〈E(t)〉 time trace obtained for ionized aqueous PhOD and its corresponding FFT power spectrum are shown in Fig. 3c and d, respectively. Table 2 summarizes the FFT frequencies and normalized FFT powers for the peaks observed in the FFT power spectra.
is the differential absorbance as a function of probe photon energy and pump–probe time delay. Ei and Ef define the spectral range over which 〈E(t)〉 is computed; in this case, Ei and Ef correspond to 2.95 eV (420 nm) and 2.88 eV (430 nm), respectively. To minimize possible contributions from coherent artifacts, 〈E(t)〉 is computed only from a time delay of 0.1 ps onward. The resultant 〈E(t)〉 trace is shown in Fig. 3a, with the inset showing a zoomed-in view of 〈E(t)〉 in the range of 0.1–1 ps. Fast-Fourier transform (FFT) of the 〈E(t)〉 trace yields its FFT power spectrum (Fig. 3b), from which the frequencies of vibrational modes that contribute to 〈E(t)〉 can be identified. To aid the assignment of the observed FFT frequencies, experiments were also performed on the isotopomer, phenol-OD (PhOD), dissolved in D2O. The 〈E(t)〉 time trace obtained for ionized aqueous PhOD and its corresponding FFT power spectrum are shown in Fig. 3c and d, respectively. Table 2 summarizes the FFT frequencies and normalized FFT powers for the peaks observed in the FFT power spectra.
| Phenol | Phenol-OD | Calculated frequency (cm−1) | Assignment | ||
|---|---|---|---|---|---|
| Frequency (cm−1) | Power (norm.) | Frequency (cm−1) | Power (norm.) | ||
| a Vibrational mode of PhOH˙+ or PhOD˙+. | |||||
| 529 | 1.8 × 10−2 | 541 | CCC bend | ||
| 814 | 1.5 × 10−2 | 808 | 1.6 × 10−1 | 818 | Ring breath/CCC bend |
| 970 | 3.2 × 10−2 | 984 | 7.9 × 10−2 | 988 | CCC trig bend |
| 1002 | 1 | 1001 | 1 | 1006 | Ring breath/CH bend |
| 1025 | 8.2 × 10−2 | 1027 | 8.0 × 10−2 | 1007 | HCCH torsion |
| 1174 | 7.2 × 10−3 | 1164 | CH bend | ||
| 1268 | 3.2 × 10−3 | 1260 | 5.0 × 10−3 | 1295 | CC str/CH bend |
| 1228 | 8.3 × 10−3 | 835 | 1.6 × 10−2 | 1197 (870) | OH (OD) waga |
| 1502 | 7.0 × 10−2 | 1159 | 6.0 × 10−3 | 1414 (1170) | OH (OD) benda |
| 2364 | 6.5 × 10−2 | D2O OD stretch | |||
| 2469 | 4.7 × 10−3 | ||||
| 1557 | 1.1 × 10−2 | 1553 | 7.7 × 10−3 | O2 | |
| 2332 | 6.7 × 10−3 | 2328 | 6.7 × 10−3 | N2 | |
Our recent studies of the vibrational wave packet dynamics of radical species prepared by strong-field photoionization or photodetachment show that the displacive mechanism for the generation of vibrational coherences can be extended from photoexcitation to photoionization85,86 or photodetachment.82,87,88 According to this mechanism, wave packet motion is launched along vibrational modes for which the equilibrium geometries of the species before and after electron ejection are displaced. Extending this analysis to the present work would require us to consider the equilibrium geometries of neutral PhOH and the PhOH˙+ radical cation. However, since the time-resolved ΔA spectra recorded over 0.1–4 ps is dominated by the absorption signature of the PhO˙ radical, without any obvious sign of the PhOH˙+ radical cation absorption, we expect the observed vibrational wave packet dynamics to originate primarily from the PhO˙ radical as well. Table 2 gives the assignments of the observed vibrational frequencies obtained from DFT calculations. We note that there is no evidence of impulsive stimulated Raman scattering (ISRS) of phenol since the ΔA signal and its associated time-domain oscillations disappear when the ionizing-pump power is attenuated to suppress strong-field photoionization.
Wave packet dynamics could be initiated in PhO˙, the proton transfer product, via two possible pathways. First, ultrafast proton transfer from PhOH˙+ could serve as an impulse for generating vibrational coherences in PhO˙. In this mechanism, non-reactive vibrational modes of PhOH˙+, whose frequencies are lower than the reaction rate, are essentially frozen during an ultrafast chemical reaction. As a result, the vibrational probability densities of PhOH˙+ along these modes are projected onto the PES of PhO˙, thus yielding a nonstationary vibrational state. Such reaction-driven coherences have been observed in photofragments following ultrafast photodissociation.89,90 Second, vibrational wave packet motion could be launched in PhOH˙+ following the displacive mechanism uncovered in our recent work.82,85–87 Subsequent vibrational coherence transfer to the PhO˙ product is possible for vibrational modes that are weakly coupled to proton transfer and that exhibit minimal vibrational coordinate transformation between the PhOH˙+ reactant and the PhO˙ product. The transfer of vibrational coherence between different electronic states was recently observed in transition metal complexes after ultrafast intersystem crossing.91,92 As discussed below, our experimental results favor the mechanism involving vibrational coherence transfer.
To obtain further insight into the vibrational wave packet dynamics, we analyze the E(t) traces for photoionized aqueous PhOH and PhOD in the time domain by fitting them to a sum of exponentially damped cosine functions
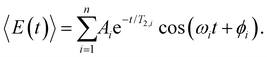 | (4) |
In the above expression, Ai, T2,i, ωi and ϕi are the amplitude, dephasing time, vibrational frequency and phase of the vibrational mode Qi, respectively. The fit parameters for PhOH and PhOD are summarized in Tables S1 and S2 (ESI†), respectively. Compared to FFT analysis, time-domain fitting directly furnishes the dephasing times of the vibrational modes. To gauge the accuracy of the time-domain fits, which employ a large number of fit parameters, we compute the FFT power spectra of the best-fit lines and compare them to the FFT power spectra of the data for both PhOH and PhOD (Figs. S7a and b, ESI†). The good agreement between the FFT power spectra suggests that the results obtained from the time-domain analysis are reliable.
While most of the vibrational frequencies have dephasing times on the order of a few hundred femtoseconds to a few picoseconds, some vibrational frequencies exhibit dephasing times of ∼0.1 ps (Table 3). With the aid of ab initio calculations, we assign these short-lived vibrational frequencies to the phenolic O–H (O–D) bend and wag modes of the PhOH˙+ (PhOD˙+) radical cation (see below). Support for our assignment comes from the observation that the O–H bend and wag frequencies are shifted upon deuteration to yield frequencies for the O–D bend and wag modes with similarly short dephasing times (∼0.1 ps). At the same time, we exclude the contribution of the C–O stretch, C–C stretch, and C–H bend modes, whose frequencies appear in a similar frequency range as the O–H bend and wag modes (Table S3), because these modes do not shift appreciably upon deuteration. We note that time-domain fitting does not yield the O–H and O–D stretching modes, predicted to be at 2593 cm−1 and 1909 cm−1, respectively. This peculiarity will be addressed below by examining the ab initio PES for proton transfer. Nevertheless, the ultrafast dephasing of the O–H and O–D bend and wag modes suggests that the PhOH˙+ and PhOD˙+ radical cations exhibit ultrafast proton transfer, which leads to their rapid depopulation, and hence, the rapid loss of vibrational coherence. The detection of vibrational coherences from transient species whose differential absorption signatures are not apparent is remarkable but not unprecedented – we recently demonstrated the possibility of resolving the vibrational wave packet dynamics of the tryptophan radical, prepared by the strong-field photodetachment of the aqueous tryptophan anion, even though its absorption signature in the visible region is obscured by the strong absorption band of the hydrated electron byproduct.87 We note that the linewidths of FFT spectral features that are assigned to the O–H and O–D modes appear narrower than expected – a dephasing time T2 is expected to yield a FWHM linewidth of 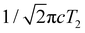 for the associated peak in the FFT power spectrum. We tentatively attribute this discrepancy to possible interference from nearby frequency components, which result in the narrowing of the lineshape.
for the associated peak in the FFT power spectrum. We tentatively attribute this discrepancy to possible interference from nearby frequency components, which result in the narrowing of the lineshape.
| Phenol | Phenol-OD | Calculated frequency (cm−1) | Assignment | ||
|---|---|---|---|---|---|
| Frequency (cm−1) | Dephasing time (ps) | Frequency (cm−1) | Dephasing time (ps) | ||
| 1246 ± 4 | 0.18 ± 0.02 | 839 ± 4 | 0.14 ± 0.02 | 1197 (870) | OH (OD) wag |
| 1497 ± 5 | 0.16 ± 0.02 | 1166 ± 6 | 0.07 ± 0.01 | 1414 (1170) | OH (OD) bend |
Interestingly, time-domain analysis of ionized PhOD reveals vibrational frequencies at 2373 ± 1 cm−1 and 2498 ± 2 cm−1, with comparable ultrafast dephasing times of 0.07 ± 0.01 ps and 0.06 ± 0.01 ps, respectively. In the FFT power spectrum (Fig. 3d), the 2373 cm−1 component appears as a peak whereas the 2498 cm−1 component appears as a dip, suggesting that these two frequency components do not oscillate in phase. The O–D stretch frequency for aqueous neutral PhOD93 of 2670 cm−1 excludes the possibility that these frequency components are produced via ISRS of aqueous neutral PhOD. Strong-field ionization of pure liquid D2O, however, yields an O–D stretch frequency of 2370 ± 2 cm−1 in both the time-domain analysis and the FFT power spectrum (Fig. S6, ESI†). This result suggests that the 2373 cm−1 component arises from the bulk D2O solvent response, whereas the 2498 cm−1 component is associated with the ionization of aqueous PhOD. The origin of the latter frequency requires further investigation. Here, we tentatively assign it to the O–D stretch of the D2O molecules that are hydrogen-bonded to the oxygen lone pairs of PhOD. Upon ionization to give PhOD˙+, the weakened intermolecular OPh⋯D2O hydrogen bond results in a blueshift of the intramolecular O–D stretch frequency of bulk D2O. Further support for this assignment comes from the ultrashort dephasing time of the 2498 cm−1 component, suggesting that it is associated with the solvent, albeit not in the bulk. Its observation suggests that the primary hydration shell of ionized molecules in aqueous solution also could undergo intramolecular structural rearrangement.
Estimated lifetime of the aqueous phenol radical cation
Following our tentative assignment of the vibrational frequencies listed in Table 3, we seek to estimate the lifetimes of the transient PhOH˙+ and PhOD˙+ radical cations from the measured dephasing times. Within the optical Bloch picture for a quantum beat involving states |a〉 and |b〉, the dephasing time T2 is related to the population lifetimes of the individual states, T1a and T1b, and the pure dephasing time,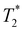 , via the relation94
, via the relation94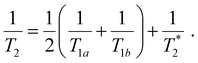 | (5) |
In the present context, |a〉 and |b〉 correspond to the vibrational ground and excited states of the vibrational modes of phenol radical cation with dominant OH or OD character. The vibrational coherent superposition leads to wave packet motion involving the phenolic OH or OD bond. These vibrational states undergo depopulation via proton transfer; in addition, the vibrationally excited state can also undergo intramolecular vibrational relaxation (IVR), i.e., 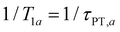 and
and 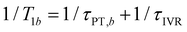 , where τPT,i is the proton transfer timescale for state |i〉 and τIVR is the IVR timescale (Fig. S8, ESI†). Hence, we obtain
, where τPT,i is the proton transfer timescale for state |i〉 and τIVR is the IVR timescale (Fig. S8, ESI†). Hence, we obtain
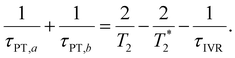 | (6) |
Eqn 6 can be further simplified by considering two limiting scenarios. First, in the limit that τPT,a ≫ τPT,b, i.e., the proton transfer reaction is greatly accelerated by vibrational excitation,95–98 we obtain the proton transfer time, τPT ∼ τPT,b, given by
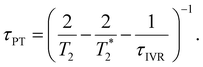 | (7) |
Second, when the proton transfer rate is independent of vibrational excitation, i.e., 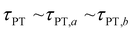 , a scenario that we deem unlikely, we obtain the proton transfer time
, a scenario that we deem unlikely, we obtain the proton transfer time
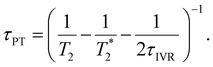 | (8) |
Eqn (7) and (8) imply lower bounds of T2/2 and T2, respectively, for τPT. The existence of two possible lower bounds arises from the unknown ratio of the two proton transfer time constants, 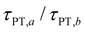 , a possible topic for future investigations. Here, we consider eqn (7) to furnish the lower bound, i.e., τPT > T2/2. Together with the typical ≳1 ps timescales for
, a possible topic for future investigations. Here, we consider eqn (7) to furnish the lower bound, i.e., τPT > T2/2. Together with the typical ≳1 ps timescales for 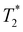 and τIVR,99,100 greater than the observed dephasing times T2, we obtain τPT ∼ T2/2. In this case, the timescale τPT ∼ 0.1 ps suggests that proton transfer cannot be the impulse for creating vibrational coherences in the PhO˙ product because it does not meet the criterion τPT < 2π/ωi, required to excite vibrational modes of frequency ωi observed in the FFT power spectra (Fig. 3b and d).
and τIVR,99,100 greater than the observed dephasing times T2, we obtain τPT ∼ T2/2. In this case, the timescale τPT ∼ 0.1 ps suggests that proton transfer cannot be the impulse for creating vibrational coherences in the PhO˙ product because it does not meet the criterion τPT < 2π/ωi, required to excite vibrational modes of frequency ωi observed in the FFT power spectra (Fig. 3b and d).
Ab initio vibrational frequency calculations
To compute the vibrational frequencies of the phenol radical cation by ab initio simulations, we first construct a model of the phenol radical cation in its non-proton transferred geometry. For this, we employ the microhydrated PhOH˙+–(H2O)3 model, comprising three water molecules directly hydrogen-bonded to the phenolic OH group, with one water molecule serving as a hydrogen bond acceptor and two water molecules serving as hydrogen bond donors. This microhydrated model is further embedded in a polarizable continuum to mimic the dielectric environment of the water solvent. The optimized geometry of PhOH˙+–(H2O)3 is shown in Fig. 2a. The O⋯O distance between PhOH˙+ and the hydrogen bond accepting H2O, OPh⋯Oa, is 2.533 Å, whereas the O⋯O distance between PhOH˙+ and the hydrogen bond donating H2O molecules, OPh⋯Od, is 3.269 Å. These O⋯O distances are consistent with those expected for hydrogen bonded systems.101,102 The phenol radical cation O–H bond length, OPh–H, is 1.030 Å, similar to OPh–H of 0.987 Å for neutral PhOH–(H2O)3 with the same hydrogen bonding configuration, confirming that proton transfer does not occur in PhOH˙+–(H2O)3. This result is supported by the calculated potential energy curve along the OPh–H coordinate (Fig. S9, ESI†) and is also consistent with previous ab initio calculations and experiments performed on the gas-phase PhOH˙+–H2O, which does not exhibit proton transfer.The absence of proton transfer in PhOH˙+–(H2O)3 suggests its possible use as a model for the transient aqueous phenol radical cation. The vibrational frequencies of PhOH˙+–(H2O)3 and PhOD˙+–(D2O)3, along with those obtained for isolated PhOH˙+ and PhOD˙+, in all cases with PCM solvation, are summarized in Table S3 (ESI†). Comparison of the vibrational frequencies obtained for the microhydrated and isolated species suggests that explicit solvation can lead to large changes in the calculated vibrational frequencies. The calculated O–H (O–D) bend and wag frequencies for PhOH˙+–(H2O)3 (PhOD˙+–(D2O)3), summarized in Table 3, are in good agreement with the frequencies of the short-lived vibrational modes obtained from time-domain analysis and assigned to the transient phenol radical cation. However, the O–H and O–D stretch frequencies, predicted to be at 2593 cm−1 and 1909 cm−1, respectively, are notably missing from the experimental data.
Ab initio calculation of ultrafast proton transfer
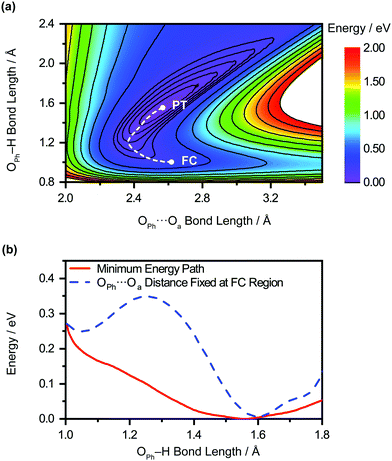
The unobserved vibrational coherences of the O–H and O–D stretches of the phenol radical cation are indicative of the coupling of these modes to the reaction coordinate for proton transfer, in analogy with the previously observed quenching of coherences along vibrational modes that drive internal conversion,103 intersystem crossing,104 electron transfer,105 and ESIPT.19 To explore this possibility, we employ DFT to calculate the reduced PES for proton transfer. Previous experimental and theoretical studies have shown that proton transfer occurs when the water molecule in PhOH˙+–H2O is further hydrogen-bonded to two hydrogen bond-accepting water molecules.32,33 In our work, we coordinate two water molecules to the hydrogen bond-accepting water molecule in PhOH˙+–(H2O)3, yielding PhOH˙+–(H2O)5. Its optimized geometry clearly reflects proton transfer (Fig. 2b): the OPh–H distance of 1.551 Å is elongated relative to 1.002 Å in neutral PhOH–(H2O)5. Using this model, we performed a 2D constrained geometry optimization along the OPh–H and OPh⋯Oa coordinates to generate a 2D PES. The choice of these coordinates is motivated by earlier studies of excess proton transport in water,106,107 which reveal the need to include both the O–H distance and the intermolecular proton donor–acceptor O⋯O distance in models of proton transfer. Moreover, an investigation of proton transfer in PhOH˙+–NH3 has shown that the modeling of ultrafast proton transfer must include changes in the intermolecular O⋯N distance.36The PES obtained from our 2D constrained geometry optimization is shown in Fig. 4a, where the dashed line denotes the minimum energy path. Fig. 4b shows the plot of the potential energy as a function of OPh–H distance along the minimum energy path as well as a section of the PES where the OPh⋯Oa distance is fixed at that of the Franck–Condon region (2.617 Å). Constraining the OPh–Oa distance in PhOH˙+–(H2O)5 to that of the Franck–Condon region yields a stabilization energy of 0.265 eV for proton transfer, albeit with a 99–meV-high barrier (Fig. 4b, dashed line). The minimum energy path, on the other hand, is barrierless and energetically downhill by 0.271 eV (Fig. 4b, solid line). The contraction of the OPh⋯Oa distance enroute to proton transfer along the minimum energy path – from 2.617 Å at the Franck–Condon region to 2.367 Å, where the proton transfer is barrierless, before reaching 2.565 Å in the proton-transferred form – is consistent with the results obtained from theoretical studies of excess proton transport in water.106,107 The coupling between OPh–H elongation and the intermolecular OPh⋯Oa hindered translational mode implies an OPh–H stretch frequency that changes with OPh⋯Oa distance, a condition that favors the ultrafast dephasing of vibrational wave packet motion along the OPh–H stretch coordinate. Other features of the ab initio PES that facilitate the rapid loss of phase coherence include the highly anharmonic nature of the OPh–H stretching mode itself, evident from comparing the potential energy curves of PhOH˙+–(H2O)3 (Fig. S9, ESI†) and PhOH˙+–(H2O)5, as well as the large possible displacement of the wave packet along the OPh–H coordinate, which enhances anharmonic coupling of the OPh–H stretch to other vibrational modes. Taken together, these factors promote the ultrafast dephasing of the OPh–H and OPh–D stretch, thus possibly accounting for the unobserved vibrational coherence of these modes.
Aside from its role in facilitating ultrafast dephasing, the concomitant contraction of the intermolecular OPh⋯Oa distance during OPh–H elongation also imposes a lower limit on the timescale for proton transfer. Fig. 4a shows that the OPh⋯Oa distance oscillates by approximately one period as the reaction proceeds from the Franck–Condon region (2.617 Å) to the proton-transferred form (2.565 Å) along the minimum-energy path. According to ab initio simulations of the PhOH˙+–(H2O)3 model, the vibrational frequency of the OPh–Oa hindered translation mode is 207 cm−1. The corresponding vibrational period of 161 fs is therefore expected to dictate the minimum timescale on which proton transfer occurs, consistent with the experimentally determined τPT ∼ 0.1 ps.
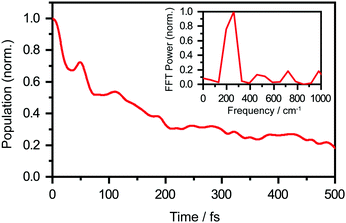
We perform quantum dynamics calculations on the reduced ab initio PES to compute the theoretical lifetime of the phenol radical cation. The calculated vibrational probability densities at 0, 100, and 200 fs are shown in Fig. 5a–c as contour plots. The vibrational probability density at 0 fs (Fig. 5a) corresponds to the wave packet in the Franck–Condon region, obtained by diagonalizing the 2D reduced Hamiltonian on the PhOH–(H2O)5 potential and projecting it onto the PhOH˙+–(H2O)5 radical cation surface. A secondary contour feature emerges at 100 fs (Fig. 5b), with OPh–H distances increasing to >1.5 Å and OPh⋯Oa distances decreasing to <2.4 Å, supporting the notion that proton transfer is promoted by the simultaneous contraction of the OPh⋯Oa intermolecular distance. Fig. 5c shows that the proton transferred form is the dominant species by 200 fs, with the vibrational probability density peaking at the OPh–H and OPh⋯Oa distances that correspond to the equilibrium PT geometry. To quantify the lifetime of the PhOH˙+ radical cation, we determine the population in the Franck–Condon region as a function of time. The resultant time trace shows that the population in the Franck–Condon region decreases rapidly, reaching its 1/e value in 193 fs (Fig. 6). This suggests a lifetime of 193 fs for the aqueous PhOH˙+ radical cation, consistent with our experimental results. Interestingly, inspection of the time-dependent population reveals a weak modulation with a frequency of 229 cm−1 (Fig. 6 inset), assigned to the vibrational frequency of the OPh⋯Oa intermolecular hindered translation mode, in good agreement with the frequency of 207 cm−1 obtained from ab initio vibrational frequency calculations.
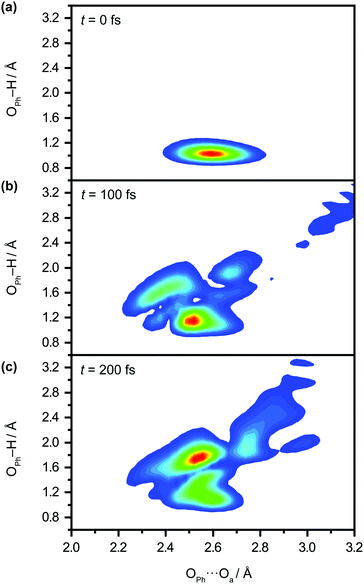 | ||
| Fig. 5 Quantum dynamics simulations of proton transfer in aqueous PhOH˙+ yields the time-dependent vibrational probability density at time delays of (a) 0 fs, (b) 100 fs, and (c) 200 fs. | ||
Conclusion
We have employed femtosecond optical pump-probe spectroscopy to investigate the ultrafast dynamics of ionized aqueous phenol. Intense laser pulses of sub-6 fs duration are used to drive the strong-field multiphoton ionization of aqueous phenol via a four-photon process. Global analysis of the resultant time-resolved ΔA spectra performed from 100 fs onwards does not reveal a clear spectral signature for the PhOH˙+ radical cation ionization product. Instead, the absorption signature of PhO˙ dominates the ΔA spectra, indicating the rapid depopulation of the PhOH˙+ radical cation by proton transfer. Time-domain analysis of the vibrational wave packet dynamics, however, reveals distinct vibrational frequencies that can be assigned to the O–H wag and bend modes of PhOH˙+. These assignments are supported by ab initio vibrational frequency calculations and isotopic substitution experiments performed on ionized aqueous PhOD in D2O. From the dephasing times of these vibrational frequencies, we obtain an estimated lifetime of ∼0.1 ps for the PhOH˙+ radical cation. The reduced PES obtained from ab initio calculations suggests that proton transfer is coupled to the intermolecular OPh⋯Oa hindered translation between PhOH˙+ and the neighboring proton-accepting water molecule. Contraction of the OPh⋯Oa distance leads to barrierless proton transfer, analogous to excess proton transport in water.106,107 As such, the frequency of this intermolecular motion, found to be 207 cm−1 according to ab initio calculations, dictates the timescale for proton transfer and is consistent with τPT ∼ 0.1 ps. This timescale is supported by quantum dynamics calculations, performed on the reduced ab initio PES, which yield a PhOH˙+ lifetime of 193 fs. Within the context of radiation damage induced by ionizing radiation, ultrafast proton transfer is an effective channel for diminishing the chemical reactivity of PhOH˙+ because the PT product, PhO˙, is a weaker oxidant [E0red(PhO˙) = 0.86 V vs. E0red(PhOH˙+) = 1.6 V; both potentials referenced to NHE].108It is instructive to compare the ultrafast proton transfer observed herein with intermolecular excited-state proton transfer to solvent (ESPTS). Previous extensive investigations of intermolecular ESPTS have correlated the timescale for proton transfer with 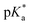 .24 The strongest photoacids have
.24 The strongest photoacids have 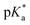 < −7 and exhibit τPT ∼ 100 fs, limited by the frequency of the intermolecular vibration between the proton donor and proton acceptor. Consistent with this classification, time-resolved fluorescence upconversion performed on the recently discovered superphotoacid, quinone cyanine 9 (QCy9), with a
< −7 and exhibit τPT ∼ 100 fs, limited by the frequency of the intermolecular vibration between the proton donor and proton acceptor. Consistent with this classification, time-resolved fluorescence upconversion performed on the recently discovered superphotoacid, quinone cyanine 9 (QCy9), with a 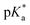 of −8.5, revealed proton transfer occurring on the ∼100 fs timescale;25 subsequent measurements with improved time resolution elucidated a biphasic proton transfer process, characterized by time constants of ∼40 fs and ∼200 fs.28 In the spirit of correlating the pKa to the timescale for proton transfer, we note that a recent study of the photodetached tryptophan anion revealed that the indole radical cation sidechain, with a pKa of 4.2,109–111 is stable with respect to PT on the few-picosecond timescale. In comparison, the phenol radical cation has a significantly lower pKa of –2.75.75 Our study reveals that PhOH˙+ exhibits the same intermolecular vibration-limited ultrafast proton transfer as QCy9, which in turn suggests the strong-field ionization of weak acids, such as PhOH, as a possible approach to generating strong acids that undergo ultrafast proton transfer.
of −8.5, revealed proton transfer occurring on the ∼100 fs timescale;25 subsequent measurements with improved time resolution elucidated a biphasic proton transfer process, characterized by time constants of ∼40 fs and ∼200 fs.28 In the spirit of correlating the pKa to the timescale for proton transfer, we note that a recent study of the photodetached tryptophan anion revealed that the indole radical cation sidechain, with a pKa of 4.2,109–111 is stable with respect to PT on the few-picosecond timescale. In comparison, the phenol radical cation has a significantly lower pKa of –2.75.75 Our study reveals that PhOH˙+ exhibits the same intermolecular vibration-limited ultrafast proton transfer as QCy9, which in turn suggests the strong-field ionization of weak acids, such as PhOH, as a possible approach to generating strong acids that undergo ultrafast proton transfer.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge financial support from the Ministry of Education, Singapore (grant no. RG1/20, RG105/17 and MOE2014-T2-2-052). M. S. B.M. Y. is supported by the Nanyang President's Graduate Scholarship. H. S. and M. Y. are supported by the National Natural Science Foundation of China (grant no. 21973109 to H. S., and 21773297, 21973108 and 21921004 to M.Y.).References
- J. H. Wang, Science, 1968, 161, 328–334 CrossRef CAS PubMed
.
- K. B. Schowen, H. H. Limbach, G. S. Denisov and R. L. Schowen, Biochim. Biophys. Acta, Bioenerg., 2000, 1458, 43–62 CrossRef CAS
.
- P. Mitchell, Nature, 1961, 191, 144–148 CrossRef CAS PubMed
.
- R. I. Cukier and D. G. Nocera, Annu. Rev. Phys. Chem., 1998, 49, 337–369 CrossRef CAS PubMed
.
- M. H.-V. Huynh and T. J. Meyer, Chem. Rev., 2007, 107, 5004–5064 CrossRef CAS PubMed
.
- S. Y. Reece and D. G. Nocera, Annu. Rev. Biochem., 2009, 78, 673–699 CrossRef CAS PubMed
.
- D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, A. Paul, D. H. Ess, D. G. McCafferty and T. J. Meyer, Chem. Rev., 2012, 112, 4016–4093 CrossRef CAS PubMed
.
- Y. Erez and D. Huppert, J. Phys. Chem. A, 2010, 114, 8075–8082 CrossRef CAS PubMed
.
- I. Presiado, Y. Erez, R. Simkovitch, S. Shomer, R. Gepshtein, L. Pinto da Silva, J. C.-G. Esteves da Silva and D. Huppert, J. Phys. Chem. A, 2012, 116, 10770–10779 CrossRef CAS PubMed
.
- P. Gosset, G. Taupier, O. Crégut, J. Brazard, Y. Mély, K.-D. Dorkenoo, J. Léonard and P. Didier, J. Phys. Chem. Lett., 2020, 11, 3653–3659 CrossRef CAS PubMed
.
- D. Stoner-Ma, A. A. Jaye, P. Matousek, M. Towrie, S. R. Meech and P. J. Tonge, J. Am. Chem. Soc., 2005, 127, 2864–2865 CrossRef CAS PubMed
.
- C. Fang, R. R. Frontiera, R. Tran and R. A. Mathies, Nature, 2009, 462, 200–204 CrossRef CAS PubMed
.
- Y.-H. Chen, R. Sung and K. Sung, J. Phys. Chem. A, 2018, 122, 5931–5944 CrossRef CAS PubMed
.
- R. M. Tarkka and S. A. Jenekhe, MRS Online Proc. Libr., 1995, 413, 97–102 CrossRef
.
- P. Jagadesan, G. Eder and P. L. McGrier, J. Mater. Chem. C, 2017, 5, 5676–5679 RSC
.
- H. Yeo and A. Khan, J. Am. Chem. Soc., 2020, 142, 3479–3488 CrossRef CAS PubMed
.
- E. M. Kosower and D. Huppert, Annu. Rev. Phys. Chem., 1986, 37, 127–156 CrossRef CAS
.
- L. M. Tolbert and K. M. Solntsev, Acc. Chem. Res., 2002, 35, 19–27 CrossRef CAS PubMed
.
- J. Lee, C. H. Kim and T. Joo, J. Phys. Chem. A, 2013, 117, 1400–1405 CrossRef CAS PubMed
.
- S. Takeuchi and T. Tahara, J. Phys. Chem. A, 2005, 109, 10199–10207 CrossRef CAS PubMed
.
- W. Heo, N. Uddin, J. W. Park, Y. M. Rhee, C. H. Choi and T. Joo, Phys. Chem. Chem. Phys., 2017, 19, 18243–18251 RSC
.
- J. C. Lennox, D. A. Kurtz, T. Huang and J. L. Dempsey, ACS Energy Lett., 2017, 2, 1246–1256 CrossRef CAS
.
- P. Zhou and K. Han, Acc. Chem. Res., 2018, 51, 1681–1690 CrossRef CAS PubMed
.
- R. Simkovitch, S. Shomer, R. Gepshtein and D. Huppert, J. Phys. Chem. B, 2015, 119, 2253–2262 CrossRef CAS PubMed
.
- R. Simkovitch, N. Karton-Lifshin, S. Shomer, D. Shabat and D. Huppert, J. Phys. Chem. A, 2013, 117, 3405–3413 CrossRef CAS PubMed
.
- R. Simkovitch, S. Shomer, R. Gepshtein, M. E. Roth, D. Shabat and D. Huppert, J. Photochem. Photobiol., A, 2014, 277, 90–101 CrossRef CAS
.
- R. Simkovitch, S. Shomer, R. Gepshtein, D. Shabat and D. Huppert, J. Phys. Chem. A, 2014, 118, 1832–1840 CrossRef CAS PubMed
.
- C. Lee, S. Chung, H. Song, Y. M. Rhee, E. Lee and T. Joo, ChemPhotoChem, 2021, 5, 245–252 CrossRef CAS
.
- S. K. Kim, S. Li and E. R. Bernstein, J. Chem. Phys., 1991, 95, 3119–3128 CrossRef CAS
.
- R. J. Stanley and A. W.-C. Jr., J. Chem. Phys., 1991, 94, 7744–7756 CrossRef CAS
.
- S. Sato and N. Mikami, J. Phys. Chem., 1996, 100, 4765–4769 CrossRef CAS
.
- T. Sawamura, A. Fujii, S. Sato, T. Ebata and N. Mikami, J. Phys. Chem., 1996, 100, 8131–8138 CrossRef CAS
.
- K. Kleinermanns, C. Janzen, D. Spangenberg and M. Gerhards, J. Phys. Chem. A, 1999, 103, 5232–5239 CrossRef CAS
.
- H. Ishikawa, I. Kurusu, R. Yagi, R. Kato and Y. Kasahara, J. Phys. Chem. Lett., 2017, 8, 2541–2546 CrossRef CAS PubMed
.
- C.-C. Shen, T.-T. Tsai, J.-W. Ho, Y.-W. Chen and P.-Y. Cheng, J. Chem. Phys., 2014, 141, 171103 CrossRef PubMed
.
- C.-C. Shen, T.-T. Tsai, J.-Y. Wu, J.-W. Ho, Y.-W. Chen and P.-Y. Cheng, J. Chem. Phys., 2017, 147, 164302 CrossRef PubMed
.
- Z.-H. Loh, G. Doumy, C. Arnold, L. Kjellsson, S. H. Southworth, A. A. Haddad, Y. Kumagai, M.-F. Tu, P. J. Ho, A. M. March, R. D. Schaller, M. S.-B. M. Yusof, T. Debnath, M. Simon, R. Welsch, L. Inhester, K. Khalili, K. Nanda, A. I. Krylov, S. Moeller, G. Coslovich, J. Koralek, M. P. Minitti, W. F. Schlotter, J.-E. Rubensson, R. Santra and L. Young, Science, 2020, 367, 179–182 CrossRef CAS PubMed
.
- F. Ambrosio and A. Pasquarello, Phys. Chem. Chem. Phys., 2018, 20, 30281–30289 RSC
.
- W. H. Koppenol and J. F. Liebman, J. Phys. Chem., 1984, 88, 99–101 CrossRef CAS
.
- J. Bonin and M. Robert, Photochem. Photobiol., 2011, 87, 1190–1203 CrossRef CAS PubMed
.
- M. Sjödin, S. Styring, H. Wolpher, Y. Xu, L. Sun and L. Hammarström, J. Am. Chem. Soc., 2005, 127, 3855–3863 CrossRef PubMed
.
- T. Irebo, S. Y. Reece, M. Sjödin, D. G. Nocera and L. Hammarström, J. Am. Chem. Soc., 2007, 129, 15462–15464 CrossRef CAS PubMed
.
- M. R. Defelippis, C. P. Murthy, M. Faraggi and M. H. Klapper, Biochemistry, 1989, 28, 4847–4853 CrossRef CAS PubMed
.
- T. Debnath, M. S.-B. Mohd Yusof, P. J. Low and Z.-H. Loh, Nat. Commun., 2019, 10, 2944 CrossRef PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed
.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed
.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed
.
-
L. Raff, R. Komanduri, M. Hagan and S. Bukkapatnam, Neural Networks in Chemical Reaction Dynamics, Oxford University Press, Oxford, 2012 Search PubMed
.
- M. T. Hagan and M. B. Menhaj, IEEE Trans. Neural Netw., 1994, 5, 989–993 CrossRef CAS PubMed
.
- Q. Hu, H. Song, C. J. Johnson, J. Li, H. Guo and R. E. Continetti, J. Chem. Phys., 2016, 144, 244311 CrossRef PubMed
.
- M. D. Feit, J. A. Fleck and A. Steiger, J. Comput. Phys., 1982, 47, 412–433 CrossRef CAS
.
- D. Ghosh, A. Roy, R. Seidel, B. Winter, S. Bradforth and A. I. Krylov, J. Phys. Chem. B, 2012, 116, 7269–7280 CrossRef CAS PubMed
.
- F. Ambrosio, Z. Guo and A. Pasquarello, J. Phys. Chem. Lett., 2018, 9, 3212–3216 CrossRef CAS PubMed
.
- R. J. Levis and M. J. DeWitt, J. Phys. Chem. A, 1999, 103, 6493–6507 CrossRef CAS
.
- J. E. Calvert, H. Xu, A. J. Palmer, R. D. Glover, D. E. Laban, X. M. Tong, A. S. Kheifets, K. Bartschat, I. V. Litvinyuk, D. Kielpinski and R. T. Sang, Sci. Rep., 2016, 6, 34101 CrossRef CAS PubMed
.
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2001, 105, 9275–9283 CrossRef CAS
.
- G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, J. Phys. Chem. Lett., 2012, 3, 348–352 CrossRef CAS PubMed
.
- D. Ayuso, M. Kimura, K. Kooser, M. Patanen, E. Plésiat, L. Argenti, S. Mondal, O. Travnikova, K. Sakai, A. Palacios, E. Kukk, P. Decleva, K. Ueda, F. Martín and C. Miron, J. Phys. Chem. A, 2015, 119, 5971–5978 CrossRef CAS PubMed
.
- J. H. Posthumus, Rep. Prog. Phys., 2004, 67, 623–665 CrossRef CAS
.
- V. I. Usachenko and S.-I. Chu, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 063410 CrossRef
.
- A.-T. Le, R. R. Lucchese and C. D. Lin, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 211001 CrossRef
.
- E. Yahel and A. Natan, Phys. Rev. A, 2018, 98, 053421 CrossRef CAS
.
- F. Ambrosio, G. Miceli and A. Pasquarello, J. Phys. Chem. Lett., 2017, 8, 2055–2059 CrossRef CAS PubMed
.
- C. Pépin, T. Goulet, D. Houde and J. P. Jay-Gerin, J. Phys. Chem. A, 1997, 101, 4351–4360 CrossRef
.
-
M. Mostafavi and I. Lampre, in Recent Trends in Radiation Chemistry, ed. J. F. Wishart, World Scientific, Singapore, 2010, ch. 2, pp. 21–58 Search PubMed
.
- R. A. Crowell and D. M. Bartels, J. Phys. Chem., 1996, 100, 17940–17949 CrossRef CAS
.
- C. Silva, P. K. Walhout, K. Yokoyama and P. F. Barbara, Phys. Rev. Lett., 1998, 80, 1086–1089 CrossRef CAS
.
- V. H. Vilchiz, J. A. Kloepfer, A. C. Germaine, V. A. Lenchenkov and S. E. Bradforth, J. Phys. Chem. A, 2001, 105, 1711–1723 CrossRef CAS
.
- M. S. Pshenichnikov, A. Baltuška and D. A. Wiersma, Chem. Phys. Lett., 2004, 389, 171–175 CrossRef CAS
.
- M. H. Elkins, H. L. Williams, A. T. Shreve and D. M. Neumark, Science, 2013, 342, 1496–1499 CrossRef CAS PubMed
.
- X. Chen, D. S. Larsen, S. E. Bradforth and I. H.-M. van Stokkum, J. Phys. Chem. A, 2011, 115, 3807–3819 CrossRef CAS PubMed
.
- T. A.-A. Oliver, Y. Zhang, A. Roy, M. N.-R. Ashfold and S. E. Bradforth, J. Phys. Chem. Lett., 2015, 6, 4159–4164 CrossRef CAS PubMed
.
- M. R. Ganapathi, R. Hermann, S. Naumov and O. Brede, Phys. Chem. Chem. Phys., 2000, 2, 4947–4955 RSC
.
- T. N. Das, J. Phys. Chem. A, 2005, 109, 3344–3351 CrossRef CAS PubMed
.
- F. Torche and J.-L. Marignier, J. Phys. Chem. B, 2016, 120, 7201–7206 CrossRef CAS PubMed
.
- A. Hertwig, H. Hippler and A.-N. Unterreiner, Phys. Chem. Chem. Phys., 1999, 1, 5633–5642 RSC
.
- J. Jortner, R. Levine, M. Ottolenghi and G. Stein, J. Phys. Chem., 1961, 65, 1232–1238 CrossRef CAS
.
- C. G. Elles, A. E. Jailaubekov, R. A. Crowell and S. E. Bradforth, J. Chem. Phys., 2006, 125, 044515 CrossRef PubMed
.
- J. A. Kloepfer, V. H. Vilchiz, V. A. Lenchenkov, A. C. Germaine and S. E. Bradforth, J. Chem. Phys., 2000, 113, 6288–6307 CrossRef CAS
.
- J. Peon, G. C. Hess, J.-M. L. Pecourt, T. Yuzawa and B. Kohler, J. Phys. Chem. A, 1999, 103, 2460–2466 CrossRef CAS
.
- M. S. Bin Mohd Yusof, Y. L. Lim and Z.-H. Loh, Phys. Chem. Chem. Phys., 2021, 23, 18525–18534 RSC
.
- F. H. Long, X. Shi, H. Lu and K. B. Eisenthal, J. Phys. Chem., 1994, 98, 7252–7255 CrossRef CAS
.
- E. R. Barthel, I. B. Martini, E. Keszei and B. J. Schwartz, J. Chem. Phys., 2003, 118, 5916–5931 CrossRef CAS
.
- Z. Wei, J. Li, L. Wang, S. T. See, M. H. Jhon, Y. Zhang, F. Shi, M. Yang and Z.-H. Loh, Nat. Commun., 2017, 8, 735 CrossRef PubMed
.
- Z. Wei, J. Li, H. Zhang, Y. Lu, M. Yang and Z.-H. Loh, J. Chem. Phys., 2019, 151, 214308 CrossRef PubMed
.
- M. S. Bin Mohd Yusof, T. Debnath and Z.-H. Loh, J. Chem. Phys., 2021, 155, 134306 CrossRef CAS PubMed
.
- M. S. Bin Mohd Yusof, J. X. Siow, N. Yang, W. X. Chan and Z.-H. Loh, Phys. Chem. Chem. Phys., 2022, 24, 2800–2812 RSC
.
- L. Zhu, J. Sage and P. Champion, Science, 1994, 266, 629–632 CrossRef CAS PubMed
.
- L. Zhu, A. Widom and P. M. Champion, J. Chem. Phys., 1997, 107, 2859–2871 CrossRef CAS
.
- R. Monni, G. Capano, G. Auböck, H. B. Gray, A. Vlček, I. Tavernelli and M. Chergui, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6396–E6403 CrossRef CAS PubMed
.
- P. Karak, K. Ruud and S. Chakrabarti, J. Phys. Chem. Lett., 2021, 12, 9768–9773 CrossRef CAS PubMed
.
- J. C. Evans, Spectrochim. Acta, 1960, 16, 1382–1392 CrossRef CAS
.
-
W. Demtröder, Laser Spectroscopy: Fourth Edition, 2008, vol. 1, pp. 1–457 Search PubMed
.
- S. Hammes-Schiffer and J. C. Tully, J. Phys. Chem., 1995, 99, 5793–5797 CrossRef CAS
.
- Y. Huang, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Science, 2000, 290, 111–114 CrossRef CAS PubMed
.
-
F. F. Crim,Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12654–12661 Search PubMed
.
- T. Michaelsen, B. Bastian, P. Strübin, J. Meyer and R. Wester, Phys. Chem. Chem. Phys., 2020, 22, 12382–12388 RSC
.
- J. C. Dean, S. Rafiq, D. G. Oblinsky, E. Cassette, C. C. Jumper and G. D. Scholes, J. Phys. Chem. A, 2015, 119, 9098–9108 CrossRef CAS PubMed
.
- S. Rafiq and G. D. Scholes, J. Phys. Chem. A, 2016, 120, 6792–6799 CrossRef CAS PubMed
.
-
G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York, 1997 Search PubMed
.
- P. Gilli, L. Pretto, V. Bertolasi and G. Gilli, Acc. Chem. Res., 2009, 42, 33–44 CrossRef CAS PubMed
.
- C. Lee, K. Seo, M. Kim and T. Joo, Phys. Chem. Chem. Phys., 2021, 23, 25200–25209 RSC
.
- J. Kim, D.-G. Kang, S. K. Kim and T. Joo, Phys. Chem. Chem. Phys., 2020, 22, 25811–25818 RSC
.
- Y. Yoneda, B. Kudisch, S. Rafiq, M. Maiuri, Y. Nagasawa, G. D. Scholes and H. Miyasaka, J. Am. Chem. Soc., 2021, 143, 14511–14522 CrossRef CAS PubMed
.
- D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604 CrossRef CAS
.
- D. Marx, ChemPhysChem, 2006, 7, 1848–1870 CrossRef CAS PubMed
.
- C. Li and M. Z. Hoffman, J. Phys. Chem. B, 1999, 103, 6653–6656 CrossRef CAS
.
- M. L. Posener, G. E. Adams, P. Wardman and R. B. Cundall, J. Chem. Soc., Faraday Trans. 1, 1976, 72, 2231–2239 RSC
.
- J. F. Baugher and L. I. Grossweiner, J. Phys. Chem., 1977, 81, 1349–1354 CrossRef CAS
.
- S. Solar, N. Getoff, P. S. Surdhar, D. A. Armstrong and A. Singh, J. Phys. Chem., 1991, 95, 3639–3643 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00505k |
| This journal is © the Owner Societies 2022 |