AuCo nanoparticles: ordering, magnetisation, and morphology trends predicted by DFT

Abstract

The rapid development of applications relying on magnetism at the nanoscale has put a spotlight on nanoparticles with novel morphologies that are associated with enhanced electronic and magnetic properties. In this quest, nanoalloys combining highly magnetic cobalt and weakly reactive gold could offer many application-specific advantages, such as strong magnetic anisotropy. In the present study, we have employed density functional theory (DFT) calculations to provide a systematic overview of the size- and morphology-dependence of the energetic order and magnetic properties of AuCo nanoparticles up to 2.5 nm in diameter. The core–shell icosahedron was captured as the most favourable morphology, showing a small preference over the core–shell decahedron. However, the magnetic properties (total magnetic moments and magnetic anisotropy) were found to be significantly improved within the L1₀ ordered structures, even in comparison to monometallic Co nanoparticles. Atom-resolved charges and orbital moments accessed through the DFT analysis of the electronic level properties permitted insight into the close interrelation between the AuCo nanoparticle morphology and their magnetism. These results are expected to assist in the design of tailored magnetic AuCo nanoalloys for specific applications.

---

Introduction

The relationship between the morphology and physical properties of nanoparticles (NPs) has been a focus of nanotechnology research in recent years, and it continues to attract significant interest as it enables continuous development of a suite of new materials with specific properties.^1–4 To date, most of the advances in metallic NPs have been made in single component monometallic systems.^5–9 However, synergistic effects captured within multimetallic alloys indicate that a vast new dimension of materials could emerge when two or more metals are combined at the nano-level. Furthermore, modern technology applications in the fields of biomedicine and catalysis have a limited tolerance in particle dimensions and surface chemistry, which makes it extremely challenging to access the desired material behaviour within a single component nanoscale system. To address the requirements of such applications, identifying the correlation between the physiochemical characteristics and geometrical relations of bi- and multi-metallic NPs is currently a hot topic, with modifications induced through the composition variations being especially intriguing.

Bimetallic (and multimetallic) NPs, often referred to as nanoalloys, present properties with a very high degree of tunability owing to the variety of morphologies they can adopt. This morphology is specified not only by the geometric structure, as in the case of monometallic systems, but also by the composition and chemical ordering of its components, giving a complex landscape of possible combinations. Nanoalloys of noble and transition metals (TM) have gathered considerable interest for cost reduction and improvement of catalytic properties compared to rare metal NPs, as well as for their capacity to stabilise ferromagnetic TM NPs from oxidation for use in magnetic data storage or biomedical applications. Although phase diagrams of many noble-TM systems indicate their immiscibility over wide composition ranges, there are indications of significant deviations from bulk mixing trends at the nanoscale originating from a size-modified electronic structure.

When the components are weakly miscible, core–shell arrangements are expected with the more cohesive element (usually TM) situated within the NP core. This trend has already been observed for many noble-TM NPs, giving stable nanomaterials with novel properties. Most of the AgNi/Co NPs were found to be phase segregated core–shell systems, owing to the very fast reduction potential of silver. Through global optimisation studies, the icosahedral morphology was indicated to be among the most stable geometries for sizes up to 10³ atoms. Magnetic and optical properties were also detected to depend strongly on the shape and placement of the Ni/Co cores.^10–13 2–5 nm AgNi/Co NPs with varying composition showed an enlarged, blue-shifted surface plasmon resonance compared to Ag NPs,¹⁴ whereas their electrocatalytic activity favours lower over-potentials and facilitates increased oxygen reduction kinetics over commonly employed Pt NPs.^15–17 Preferential Co/Ni core-Pt shell segregation was also clearly discerned in large Pt-rich clusters.^18–22 After the discovery of their outstanding reduction kinetics, which were measured to be as much as 90 times higher than that of the current state-of-art Pt catalysts, PtNi and PtCo NPs became a focus of many fuel cell studies.^23–27 For AuFe systems, it was found that nanoscale alloys retain in their entirety the optical and magnetic properties of the individual components.²⁸ Thus, AuFe NPs are particularly interesting in the context of MRI contrast agents, local heating, and drug delivery,^29–31 and they were found to adopt mostly icosahedral shapes with a homogeneous distribution of Fe and Au atoms, whereas annealing induces the formation of an Au-rich surface.^32,33 AuNi NPs are, on the other hand, promising catalysts for various chemical reactions,^34–36 with morphologies detected as core–shell, supersaturated, and Janus NPs.^37–39

Core–shell AuCo NPs have also been proposed for biomedical applications, such as hyperthermia or MRI, as their Co core with large magnetic moment is highly responsive to an externally applied magnetic field, and the Au shell, which is inert and biocompatible, allows for easy functionalisation. In accordance with the disproportionate radii and immiscibility predicted below 400 °C across all composition space,⁴⁰ theoretical studies reported structures that favour Au surface segregation and the formation of core–shell orderings.^41–43 A novel statistical-mechanics approach to determine the free energy cost of forming phase-separated aggregates developed by Ferrando et al. has shown that the decrease in cost is non-negligible for AuCo NPs with diameters up to 10 nm, thus indicating the permanence of an equilibrium miscibility gap at the nanoscale and the nonexistence of a critical size below which phase separation is impossible.⁴⁴ The global minimum geometries were corroborated by molecular dynamics studies, where rosette reconstructed icosahedra were found to be the most stable for systems with compact Co cores, whereas nanoparticles with larger Co core sizes adopted the shapes of regular Mackay icosahedra with central high-symmetry cores. Successful synthesis of AuCo NP has confirmed these predictions, and the core–shell NPs were found to have mostly icosahedral structure, although a novel morphology consisting of a Co icosahedron surrounded by fcc Au facets was recently described.^45–47 In addition, reports have indicated that the optical and magnetic properties may both be tuned by tailoring the size of the Co core.

However, the fact that the surface of the nanoalloy is expected to contain mostly noble metal atoms due to the atomic radius or surface energy, does not invariably determine the chemical ordering of such systems. The size, structure, and chemical arrangement of bimetallic NPs can be experimentally controlled throughout the synthesis protocol, allowing for metal species to intermix and maximise the synergistic benefits available through their alloying and interfaces. For example, physical methods were reported for the synthesis of AgNi ordered NPs, which exhibited substantial enhancement of their optical limiting efficiency.⁴⁸ Core–shell AuNi NPs with inverted segregation (Au cores covered by Ni) showed huge magnetisation, which was maintained even after the formation of NiO on the surface.⁴⁹ Furthermore, intermixed nanoalloys of magnetic 3d TM with Pt are potential materials to overcome the superparamagnetic limit due to their exceptional values of magnetic anisotropy, which can thus fulfil demanding requirements for high density information storage. Compared to the intermixed state of CoPt NPs, surface-segregated cuboidal counterparts have shown their magnetic moment reduced by 0.52 μ_B with a 19% reduction in magnetic anisotropy and, more pronouncedly, when adopting cuboctahedral morphology, reductions were of the order of 4.96 μ_B and 45%, respectively.⁵⁰ Distinct L1₀ orderings in CoPt systems have already shown how improved magnetic anisotropy can translate into superior catalytic performance in fuel cells,⁵¹ while a similar arrangement in FePt NPs indicated high anisotropy and promising integration in magnetic recording applications at room temperature.⁵²

The hybrid systems based on Au and Co nanoalloys are consequently also expected to offer unique properties in different chemical orderings because of the possible magnetoresistance effect and optical-magnetic bifunctionalities.⁵³ Although the limited literature on AuCo systems is almost exclusively focused on the core–shell structures, Marbella et al. have demonstrated the synthesis of discrete, composition-tuneable alloyed AuCo NPs with random ordering of Au and Co atoms, whose magnetic susceptibility can be tailored while maintaining almost identical particle size and surface chemistry.⁵⁴ Finally, a recent theoretical study has shown that magnetic effects can destabilise core–shell arrangements of AgCo and AuCo systems; their icosahedral structures remain preferential, but peculiar quantum effects reverse the energetics in favour of intermediate compositions, presenting a much more thorough intermixing of noble metal phases with the cobalt atoms.⁵⁵

Despite these previous efforts, the knowledge of AuCo binary nano-systems is still rather limited, since only a few confined sizes, compositions, and morphologies have been studied both theoretically and experimentally, with no systematic studies available. Since the physiochemical characteristics of bimetallic NPs depend distinctly on their structure, diameter, and chemical composition, the knowledge of magnetic and electronic properties, as well as the structural evolution with increasing size, is of crucial importance for further improvement of property-tuning strategies. This dependency is in no way trivial, and theoretical approaches can provide a useful contribution in this respect by narrowing down the structural candidates with application-specific properties.

To improve the comprehension of size and shape property alternations of AuCo NPs, the stabilities and structures of selected magic-numbered NPs with varying morphologies were probed with accurate DFT calculations. The electronic and magnetic properties of distinct orderings (core–shell, L1₀ ordered, and disordered NPs) were also predicted, including the atom-resolved magnetic orbital moments and magnetic anisotropy energies (MAE), thereby providing a detailed overview of morphology-specific AuCo NP features.

Computational details

The central difficulty in studying the morphological dependence of the properties of bimetallic NPs lies in the complexity of possible composition, geometry, and chemical ordering combinations. To simplify the task, computational studies often consider periodic slab models with dopants or monolayer coverages of a secondary metal to gain insight in the property changes.^56–59 This simplification is governed by two assumptions: (i) that the NP surface chemistry is dominated by the first two or three atomic layers, and (ii) that the chemistry of appearing NP crystal facets can be approximated by their respective single crystal surfaces. While periodic models can approximately resemble large particles with an appreciable share of facet areas, in most cases they cannot represent a realistic picture of NP systems, especially when it comes to NPs of a few nanometres in diameter. In such cases, the non-negligible portion of chemically under-saturated sites (steps, edges, vertices) significantly changes the NP reactivity and magnetic behaviour. Considering that the average size of NPs in many applications does not exceed a couple of nanometres, it is important to understand this simultaneous effect of NP size and surface structure, which has been demonstrated in the literature on examples of equilibrium configuration,⁶⁰ adsorption,^61–63 catalytic activity,^64,65 and magnetic properties.^66–69 For this reason, the calculations carried out here were performed using particle models.

The computational search for the low-energy geometric structures of a given NP size comprises an additional problem – the number of NP isomers (same size, different shape) increases drastically with the increase in the number of atoms. The addition of a secondary metal introduces further parameters of composition and ordering, and the number of NP homotops (same size and shape, different atom arrangement) quickly grows beyond the ability to consider each homotop separately. In addition, the term composomers has been introduced by Johnston and Belchior,⁷⁰ referring to compositional isomers (same size and geometry, but different composition). Hence, the systematic study of structurally and energetically favourable bimetallic NPs is, even within the single size or composition, extremely challenging. Several theoretical tools are available to at least partially reveal morphology preferences of certain nanoalloy systems. A thorough exploration of the potential energy surface was performed by molecular dynamics (MD) calculations for NPs of some metal pairs. However, the accuracy of available interatomic potentials is strictly system-dependent. In several cases, these potentials have proven to be a valuable method,^12,13,71 while in other instances, they tend to oversimplify the description of the alloy, leading to controversial results.^72–75 The challenge of developing efficient and accurate interatomic potentials for metal intermixing hence constitutes a rapidly progressing research field.^76,77 Although atomistic models can treat NPs of tens of thousands of atoms, far out of the reach of DFT calculations, ab initio methods still have an important role in the assessment of their properties.

However, open-shell magnetic compounds pose a challenge also for DFT methods, where the often employed generalized gradient approximation (GGA) exchange–correlation functional suffers from the over-delocalisation of the electrons in metal d orbitals, resulting in deficient descriptions of magnetic and electronic structures. This can be partially solved by introducing the Hubbard parameter (U), which localises the electrons on the d-metal atoms.⁷⁸ However, the localised formulation of DFT+U is constructed to impose a finite discontinuity to the exchange–correlation potential which is important in the description of semiconductors and insulators, but is in general not well suited to treat weakly correlated transition metals. Arguably the most important correlation effects in metals, namely fluctuation-induced mass renormalisation and itinerant exchange interactions, are hence missing, and excessive stabilisation of occupied states due to the +U corrective potential remains questionable in cases where the prediction of properties related to electronic localisation (such as magnetisation) cannot be accomplished without compromising the description of delocalised metal electrons.^79,80 Hybrid density functionals correct these errors by partially incorporating the exact exchange. Nevertheless, the main improvement of hybrid functionals is in the correct treatment of the valence bands near the Fermi level, again leading to improved localisation of the electrons mostly in semiconducting and insulating materials. If the determination of both geometry and electronic structure of transition metal NPs is to be achieved at the same level, which is desirable due to their strong interdependence, DFT has been proven to be a very efficient and reliable approach, although errors arising from d state over-delocalisation need to be taken into consideration.^81–85 Specifically for Co clusters, it has been shown that the lowest energy structures and magnetic properties are not as sensitive to the level of the exchange–correlation functional, and results indicate that the differences between GGA, GGA+U, and hybrid methods are purely an electronic effect.⁸⁶

The DFT systems of choice are usually driven by the well-known often occurring NPs with a complete, regular outer geometry designated as full-shell NPs. These sizes, known as magic numbers,^87,88 were the criteria implemented in this study on various fcc-based NP shapes, namely cuboctahedron, icosahedron, and Ino decahedron. The compositions were fixed to L1₀ ordered cuboctahedra with terminating Au layers, Fig. S1 of the ESI,† which are energetically more favourable than Co-terminated NPs. Such compositions deviate from perfectly ordered Ino decahedra, which were accordingly adapted with an excess of Co atoms distributed randomly over the Au anti-sites to allow direct comparison of their energetic and magnetic properties with icosahedra and cuboctahedra of the same sizes. With the central aim of identifying morphology trends, four magic sizes (N = 55, 147, 309, and 561 atoms) were considered.

The structural, energetic, and magnetic properties of AuCo NPs were determined by employing spin-polarised DFT calculations as implemented in the Vienna Ab initio Simulation Package (VASP).⁸⁹ GGA exchange–correlation functional developed by Perdew, Burke, and Ernzerhof (PBE)⁹⁰ has been used, since it has previously provided a satisfactory description of nanosized cobalt systems in good agreement with available experimental data.^91–95 The spatially confined core electrons were treated through the projector augmented wave (PAW) approach,⁹⁶ with the wave functions of the valence electrons expanded to an energy cut-off of 400 eV. The intrinsically non-periodic nature of NP systems, created by adding 12 Å of vacuum around each particle, restricted the Brillouin zone sampling to the Γ-point. Relaxations were carried out until a convergence criterion of 10⁻⁶ eV between consecutive steps was reached, without any structural, symmetry, or magnetic constraints.

The tendency of the two elements to mix (or segregate) within the given morphology was quantified through mixing energies, using the expression proposed by Jellinek and Krissinel.⁹⁷ Charge distribution was calculated using the Bader charge analysis approach of Henkelman et al.⁹⁸ Spin magnetic moments were determined iteratively through simultaneous optimisation during the self-consistent field (SCF) procedure. To predict spin–orbit-related properties (orbital magnetic moments and magnetic anisotropy energies), fully relativistic spin–orbit coupling (SOC) calculations^99,100 were performed within the non-collinear version of the VASP code developed by Hobbs et al. and Marsman and Hafner.^101,102 To satisfy the requirements of extremely well-converged wave functions and charge densities, the criteria for termination of the SCF cycles was tightened to 10⁻⁷ eV per cell and energy changes to less than a hundredth of a meV. Two sets of self-consistent SOC non-collinear calculations were performed, one for each easy and hard magnetisation axes, and the MAE was determined in terms of the difference in their total energies. In principle, such an approach, although time-consuming, is exact and straightforward.

Further details can be found in the ESI.†

Results

Energy trends

The structures of the studied bimetallic AuCo NPs are shown in Fig. 1, with the corresponding energetic evolution with respect to the increasing NP size captured in Fig. 2. The L1₀ ordered cuboctahedra were chosen as a reference point for each size. All remaining morphologies are located at negative energies, meaning that the L1₀ ordered cuboctahedron is the least favourable morphology across the whole size range. Relaxations of the NPs of the smallest size considered, N = 55 (d < 1 nm), led to significant structural changes due to the disproportionate radii of Au and Co atoms, resulting in energies which are difficult to relate directly to the energetic trends of larger NPs. For the NPs with diameters >1 nm, ordering within the icosahedral geometries showed improvement in stability over L1₀ cuboctahedra with energy differences of 0.050 eV per atom. Disordering of two metallic phases within the corresponding 147- and 309-atom NPs with icosahedral geometry showed further improvement in stability. L1₀ decahedra are energetically the most stable ordered AuCo NP structures, and calculated energy differences in reference to the L1₀ cuboctahedron are in the 0.062–0.075 eV per atom range, whereas, when disordered, the difference reduces to ∼0.040 eV per atom. This behaviour is in contrast to the results of the PtCo NP study,¹⁰³ where disordered mixing of the two elements was always found to be less favourable compared to ordered atomic arrangements.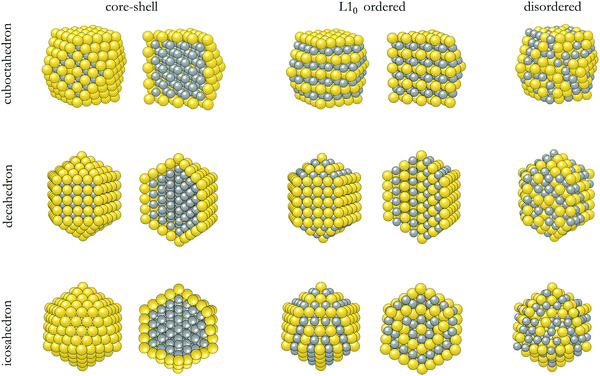

Fig. 1 Structures and cross sections showing outer and inner arrangement of Au and Co atoms in core–shell, L1₀ ordered, and disordered cuboctahedron, decahedron, and icosahedron AuCo bimetallic NPs.

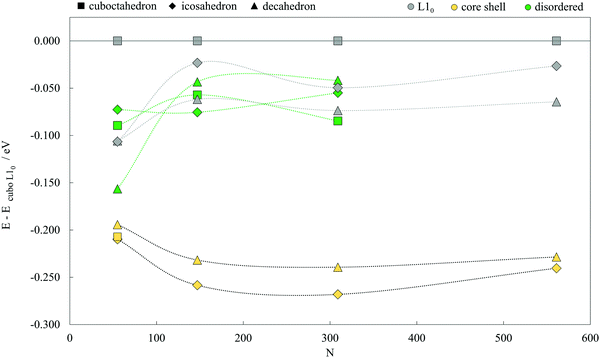Fig. 2 Energetics of AuCo NPs of varying morphologies (core–shell, L1₀ ordered, and disordered cuboctahedron, decahedron, and icosahedron) as a function of the NP size (N = 55, 147, 309, and 561). All energies are expressed per atom, in respect to the energy of the L1₀ cuboctahedron. Corresponding geometries can be found in Fig. 1.

Core–shell segregation is a dominant mechanism for all three geometries, similar to the PtCo icosahedra. Core–shell AuCo icosahedra have the most favourable energy difference with L1₀ cuboctahedra, between 0.210 and 0.268 eV per atom, followed by core–shell decahedra which are in the energy difference range of 0.194–0.239 eV per atom. The separation between the two geometries decreases with the increase in the NP size. Complete segregation of Au and Co phases in cuboctahedral NPs was observed to lead to a spontaneous transformation to the core–shell icosahedron for all except the smallest 55-atom NP,which, in turn, was significantly distorted after geometry optimisation, giving a core–shell/L1₀ energy difference of 0.207 eV.

Calculated mixing energies per atom are given in Table 1. Only core–shell morphologies show negative mixing energies, indicating spontaneous segregation of the Au and Co metallic phases. However, the extent of the convenient core–shell miscibility reduces as the NPs grow in size. There is an average 40% decrease in segregation favourability of icosahedral and decahedral core–shell AuCo NPs when going from a 1.0 nm to a 2.5 nm diameter. Additionally, positive mixing energies of 1.0 and 1.5 nm L1₀ decahedra (0.044–0.072 eV per atom) are only a small portion of the mixing energies of ordered icosahedra or cuboctahedra of the same size, which reach up to 0.283 eV per atom for the 561-atom L1₀ cuboctahedron.

Table 1 Mixing energies in eV per atom, E_mix, for differently sized AuCo NPs (N = 55, 147, 309, and 561) of varying morphologies (core–shell, L1₀ ordered, and disordered cuboctahedron, decahedron, and icosahedron)

E mix/eV per atom	Cuboctahedron			Decahedron			Icosahedron
	L10	Core–shell	Disordered	L10	Core–shell	Disordered	L10	Core–shell	Disordered
55	0.141	−0.066	0.051	0.070	−0.019	0.019	0.004	−0.099	0.038
147	0.199		0.142	0.044	−0.126	0.062	0.108	−0.127	0.056
309	0.258		0.174	0.072	−0.094	0.104	0.115	−0.103	0.110
561	0.283			0.087	−0.077		0.141	−0.073

---

In order to gain insight into the physical reasons behind the stark differences in the energies of varying AuCo NP morphologies, structural, electronic, and magnetic features were examined on the atom-decomposed level.

Structural parameters

By analysing the atomic distances in core–shell AuCo NPs, listed in Table 2, it can be seen that the average inter-shell nearest neighbour Co–Co distance is several percent shorter than the average Co–Co intra-shell distance for both icosahedral and decahedral NP geometries. This induced dense packing of Co shells allows the size mismatch between the atomic species to be compensated by radial accommodation of gold atoms on the surface and reduces the internal stress in comparison to the L1₀ ordering, where a certain portion of Au atoms is incorporated in the inner shells. The percentage difference in the inter- and intra-shell distances is greater in the icosahedron (3.8–5.7%) than in the decahedron NPs (0.7–1.3%), resulting in longer Co–Au distances and more favourable energetics.

Table 2 Average inter- and intra-shell atomic distances in AuCo NPs of core–shell ordered icosahedral (ico) and decahedral (deca) morphologies for varying NP sizes

d/Å		Inter-shell average		Intra-shell average
		Co–Co	Co–Au	Co–Co	Au–Au
55	Ico	2.412	2.727	2.524	2.774
	Deca	2.461	2.758	2.478	2.785
147	Ico	2.430	2.850	2.554	2.759
	Deca	2.480	2.744	2.512	2.775
309	Ico	2.423	2.846	2.562	2.788
	Deca	2.476	2.784	2.508	2.783
561	Ico	2.440	2.898	2.533	2.775
	Deca	2.475	2.810	2.498	2.802

---

Distances obtained for the L1₀ ordered morphologies are summarised in Table 3. In general, mixing of the two metallic phases within the inner shells of the NPs resulted in shorter average Co–Au and elongated inter-shell Co–Co distances compared to the core–shell counterparts. Single directional elongation of the decahedral geometry allowed for increased Co–Au distances in between the shells, which is possibly the most important contributor in the reduction of volumetric strain and leads to the improved stability over the L1₀ icosahedron and cuboctahedron. Owing to a particularly large difference in the radii of Co and Au atoms, it is not unusual that the mismatch in the average interatomic distances persists with the increase in the NP size.

Table 3 Average inter- and intra-shell atomic distances in AuCo NPs of L1₀ ordered icosahedral (ico), decahedral (deca), and cuboctahedral (cubo) morphologies for varying NP sizes

d/Å		Inter-shell average			Intra-shell average
		Co–Co	Co–Au	Au–Au	Co–Co	Co–Au	Au–Au
55	Ico	2.522	2.692	—	2.402	2.644	2.866
	Deca	2.525	2.728	—	2.622	2.651	2.773
	Cubo	2.539	2.647	—	2.504	2.689	2.891
147	Ico	2.507	2.666	2.684	2.456	2.742	2.826
	Deca	2.592	2.749	2.789	2.691	2.713	2.803
	Cubo	2.467	2.696	2.836	2.374	2.671	2.845
309	Ico	2.553	2.679	2.775	2.528	2.707	2.840
	Deca	2.527	2.698	2.787	2.704	2.694	2.807
	Cubo	2.592	2.673	2.845	2.493	2.680	2.856
561	Ico	2.575	2.680	2.798	2.530	2.699	2.865
	Deca	2.511	2.683	2.794	2.716	2.697	2.819
	Cubo	2.603	2.666	2.851	2.513	2.684	2.872

---

Electronic structure

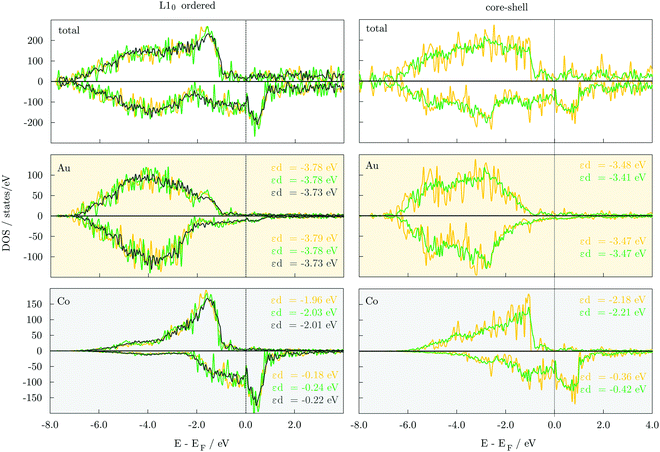
A qualitative understanding of energetic trends of distinct orderings can be gained through the analysis of electronic properties. Densities of state, DOS, of 147-atom L1₀ and core–shell structures, Fig. 3, show that both have the 3d majority-spin channel of Co atoms practically complete, which indicates that the stability difference comes from the filling up of the minority-spin channel and shifting of the contributions of the Co 3d states to lower energies. Calculated d-band energies of minority-spin Co 3d states are about two times lower in energy for the core–shell AuCo icosahedral and decahedral NPs (ε_d,ico = −0.36 eV, ε_d,deca = −0.42 eV) compared to the L1₀ counterparts (ε_d,ico = −0.18 eV, ε_d,deca = −0.24 eV). This improved filling of the Co minority-spin channel of the core–shell AuCo NPs reflects their increased stability. In addition, the Au 5d states of both spin channels within the L1₀ ordered structures are shifted to deeper energy levels, thereby decreasing the effective hybridisation with the Co 3d states as well as the exchange splitting of Au DOS. Differences in the DOS and d-band energies of varying L1₀ ordered AuCo NP geometries are less pronounced (Δε_d = 0.00–0.06 eV), providing only a general conclusion of the near degeneracy of L1₀ cuboctahedron, decahedron, and icosahedron. Similar behaviour is observed for core–shell icosahedral and decahedral AuCo NPs. DOS of disordered AuCo NP morphologies are presented in Fig. S2 (ESI†). Asymmetry of majority- and minority-spin channels of Co atoms is maintained throughout both the ordered and core–shell alloying with Au, indicating preserved magnetic moments. Minimal disruptions in the overlap of the two spin channels of Au were also captured.

Fig. 3 Total, 5d Au and 3d Co projected densities of state, DOS, of 147-atom cuboctahedron (grey), decahedron (green), and icosahedron (yellow) AuCo NPs of L1₀ (left) and core–shell (right) orderings. Both majority- and minority-spin states are shown. d-band energy centres, ε_d, are given for Au 5d and Co 3d states in corresponding colours.

In order to gain insight into the electron localisation, which can be correlated with variations in the reactivity of vertices, edges, and facets, Bader charges of Co and Au atoms have been analysed over different 147-atom AuCo NP morphologies, Table 4. The increased degrees of freedom on the NP surface naturally pull electrons from the core, whereas the difference in the electronegativity of Co and Au (χ_Co = 1.88, χ_Au = 2.54) additionally exacerbates this process, as is clearly reflected in the core–shell AuCo NPs, where Co cores show significant charge depletion (0.197 and 0.195 e⁻ per Co atom for icosahedron and decahedron, respectively). The difference in the charge transferred from Co core atoms to Au shell atoms between the two morphologies, namely decahedral and icosahedral AuCo NPs, is very small (0.001–0.002 e⁻), indicating only minimal dependence of the electron localisation on the NP geometry.

Table 4 Calculated Bader charge per atom, Δq, for Co and Au atomic species in 147-atom decahedron (deca), icosahedron (ico), and cuboctahedron (cubo) AuCo NPs with core–shell and L1₀ orderings. Charge contributions of atoms of each specie placed in the core and in the outer shell of the L1₀ NPs have also been assigned

Core–shell			L10 ordered
Δq/e^−	Core (Co)	Shell (Au)	Δq/e^−	Total Co	Total Au	Core Co	Shell Co	Core Au	Shell Au
Deca	0.195	−0.158	Deca	0.399	−0.328	0.407	0.388	−0.389	−0.292
Ico	0.197	−0.159	Ico	0.378	−0.311	0.396	0.362	−0.350	−0.294
			Cubo	0.370	−0.304	0.372	0.367	−0.337	−0.290

---

For the L1₀ ordered AuCo NPs, depletion of charge from the NP core and subsequent accumulation in the shell is even more pronounced, and calculated charge transfer between the two atomic species is two times larger than for the core–shell counterparts (0.378 and 0.399 e⁻ electron depletion per Co atom for L1₀ icosahedron and decahedron, respectively). In L1₀ structures, Co and Au atoms are both placed in the NP core as well as in the NP shell, and species-specific contributions have also been provided in Table 4. Core Co/Au atoms show increased levels of charge depletion/accumulation compared to those situated on the surface. The difference in charge per Co atom in the core and in the surface is 0.019 e⁻ for L1₀ decahedron, 0.034 e⁻ for L1₀ icosahedron, and 0.005 e⁻ for L1₀ cuboctahedron, whereas the gain of electrons on the core Au atoms is 0.097, 0.056, and 0.047 e⁻, respectively, in comparison to Au atoms in the NP shell. Nevertheless, surface Co atoms consistently showed electron loss, and significant charge transfer was captured to both core and shell Au atoms, indicating that, for the AuCo NPs, regardless the NP morphology or atomic arrangement, the difference in electronegativity is more influential than the surface effect. Finally, in correlation with the NP shape, variations in the charge transfer are relatively small (0.008–0.029 e⁻), similar to core–shell NPs, with a slight deviation of L1₀ decahedron possibly arising from the adaptation of excess Co atoms over Au anti-sites to comply with the chosen atomic composition.

Atom-decomposed local Bader charges, represented in Fig. S3 (ESI†), show an even distribution of negative charge amongst Au atoms of core–shell structures, together with a more prominent contribution of interface Co atoms over deeper, core-centred spheres. Intermixing of atomic species in L1₀ AuCo NPs resulted in a greater localisation of electrons over gold atoms which are more highly coordinated to Co. Similar behaviour is seen in the disordered decahedron, whose atom-decomposed charge transfer has also been shown.

Magnetic properties

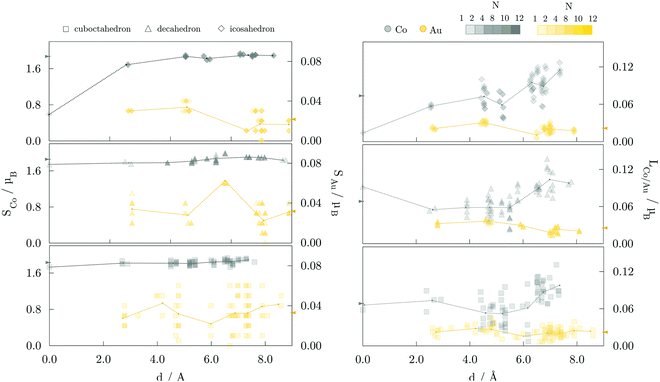
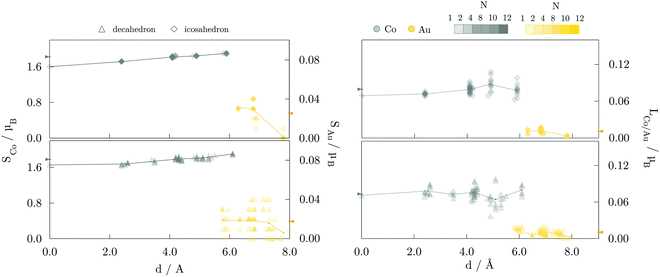
Average magnetic moments per atom for studied AuCo NP morphologies and sizes are plotted in Fig. 4. In general, the isomers are ferromagnetic with the average magnetic moments in the range of 0.80–0.90 μ_B, i.e. slightly lower than 1.12 μ_B averages obtained for CoPt NPs.¹⁰⁴ The highest deviations are encountered between the core–shell and L1₀ decahedra and icosahedra, where the core–shell mediated reduction mostly results from the lower magnetic moments of compressed centre-most neighbouring cobalt atoms and decreased magnetisation of shell-segregated gold atoms. For the largest sizes considered, this yields a total magnetic moment of L1₀ morphologies which is more than 30 μ_B higher than their core–shell counterparts.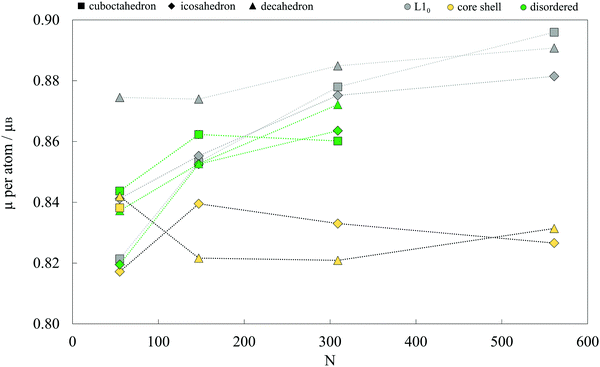

Fig. 4 Average magnetic moments per atom for various AuCo NP morphologies as a function of the NP size. Lines are to guide an eye only.

For the 147-atom L1₀ cuboctahedron, two antiferromagnetic variations of the magnetic structure were considered: a layered antiferromagnet, with Co and Au layers of alternating spin-up and spin-down orientation, and a staggered antiferromagnet, where the orientation of the atomic spins alternates between nearest neighbour pairs and thus the total magnetic moment is nearly cancelled within each layer. Both structures were allowed to relax, without restrictions on the orientation of the magnetic spins, upon which the layered antiferromagnetic structure spontaneously relaxed to the ferromagnetic ordering. This behaviour is likely due to the induced exchange splitting experienced by the naturally low magnetic Au sites. The structure with the staggered antiferromagnetism, Fig. S4 (ESI†), was found to be less stable than the original ferromagnetic NP by 0.034 eV per atom.

The site- and element-resolved distributions of the atomic spin magnetic moments for the 147-atom L1₀ ordered and core–shell morphologies are shown in Fig. 5 and Fig. 6, respectively. In all cases, Co atoms exhibit stable spin moments comparable to those of bulk phases. Site-dependency is most pronounced in the L1₀ icosahedron, where the centre atom experiences a substantial magnetic moment reduction, with a calculated spin magnetic moment of 0.59 μ_B compared to the NP average of 1.87 μ_B; the first complete shell surrounding the central Co atom has an average moment of 1.68 μ_B. There is a clear enhancement of spin magnetic moments in the surface Co atoms of around 0.1-0.3 μ_B, which is also reflected in the induced moments of the Au atoms. Gold atoms were shown to be more sensitive to the local environment, displaying a spread of spin magnetic moments for each morphology. The vertex Au atoms, i.e. the atoms positioned farthest from the NP centre, generally show below-average spin magnetic moments, which are already fairly low in the 0.018-0.033 μ_B range.

Fig. 5 Element-resolved spin, S_i, and orbital, L_i, magnetic moment as a function of the distance to the NP centre of 147-atom cuboctahedron (□), decahedron (Δ), and icosahedron (⋄) AuCo NPs with L1₀ ordering. Co magnetic moments are in grey, and Au in yellow. The number of overlapping symbols, arising from the NP symmetries, is represented by the saturation of colours as indicated in the top right. Dotted lines are connecting average moments for complete geometrical shells. The arrows denote the respective NP averages.

Fig. 6 Element-resolved spin, S_i, and orbital, L_i, magnetic moment as a function of the distance to the NP centre of 147-atom decahedron (Δ) and icosahedron (⋄) AuCo NPs with core–shell arrangements. Co magnetic moments are in grey, and Au in yellow. The number of overlapping symbols, arising from the NP symmetries, is represented by the saturation of colours as indicated in the top right. Dotted lines are connecting average moments for complete geometrical shells. The arrows denote the respective NP averages. Core–shell cuboctahedron is omitted because of the relaxation-induced rearrangement into icosahedral shape.

Average orbital magnetic moments of both Co and Au atoms within the core–shell orderings showed soothed site-dependence compared to the L1₀ ordered AuCo NPs for both icosahedron and decahedron. However, obtained averages of the Au orbital moments within the core–shell icosahedron and decahedron of 0.011 and 0.010 μ_B were found to be about half of those measured for the L1₀ orderings, namely 0.021 μ_B for the L1₀ icosahedron and 0.025 μ_B for the L1₀ decahedron. Averages for Co were, on the other hand, slightly higher for the core–shell icosahedron and decahedron NPs; 0.080 μ_B compared to the 0.074 μ_B obtained for the L1₀ icosahedron, and 0.073 μ_B compared to 0.068 μ_B calculated for the L1₀ decahedron. Despite the fluctuations in the average values with increasing distance from the central atom, the orbital contribution remains in the direction of spin magnetisation for all sites. The minimal variance in the orbital moments of Co atoms within the two distinct morphologies and the increase in the orbital moments of Au atoms situated in the L1₀ layers indicates the particular relevance of the incorporation of gold atoms in the non-surface positions in the NP anisotropy.

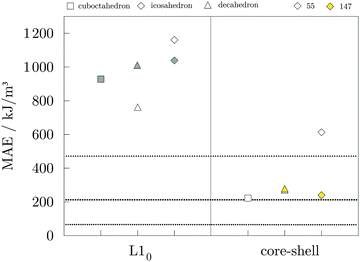
Magnetic anisotropy energies were calculated for the 55- and 147-atom AuCo core–shell and L1₀ ordered NPs of varying morphologies, and the results are presented in Fig. 7. In the case of core–shell AuCo NPs, considered directions of magnetisation were along the growth vectors of low Miller index facets and along the vertex sites. Both the core–shell icosahedron and decahedron were found to have the former as an easy magnetisation axis. For the L1₀ ordered AuCo NPs, the easy magnetisation axis is aligned perpendicular to the stacking of the Au and Co atomic layers, while the direction of the layer elongation forms a hard magnetisation plane. MAE values of corresponding 147-atom monometallic decahedron, icosahedron, and cuboctahedron Co NPs are 471.3, 65.6, and 211.8 kJ m⁻³, respectively, as presented in our previous work.¹⁰⁵ The core–shell arrangement within the icosahedral AuCo NP morphology more than triples the initial Co NP anisotropy to 239.9 kJ m⁻³, whereas the opposite effect is observed for the core–shell decahedron, which showed a reduced MAE value of 278.2 kJ m⁻³. L1₀ ordered AuCo NPs of all three morphologies showed an order of magnitude higher MAE, which is a substantial improvement of monometallic Co NP anisotropy energies. Calculated MAE for the 147-atom L1₀ AuCo NPs are 928.3 kJ m⁻³ for the cuboctahedral morphology, 1011.7 kJ m⁻³ for the decahedron, and 1038.2 kJ m⁻³ for the icosahedron. The 55-atom L1₀ decahedron and icosahedron NPs were also found to have very high MAE values of 762.1 and 1160.7 kJ m⁻³, respectively. The anisotropy of disordered alloy structures was calculated to be fairly low, e.g. 9.7 kJ m⁻³ for the disordered AuCo icosahedron, which is in agreement with the steep decrease in the optimum value of the MAE even with minimal reduction in the degree of order from 1.0 to 0.9, as found in both experimental and DFT studies.^106–108

Fig. 7 Magnetic anisotropy energy, MAE, of 55- (empty symbols) and 147-atom (coloured symbols) cuboctahedron (□), decahedron (Δ) and icosahedron (⋄) AuCo NPs with L1₀ (left, grey) and core–shell (right, yellow) ordering as calculated by DFT. MAE of pure 147-atom Co NPs are shown as ‘dotted’ lines in corresponding morphology symbols.

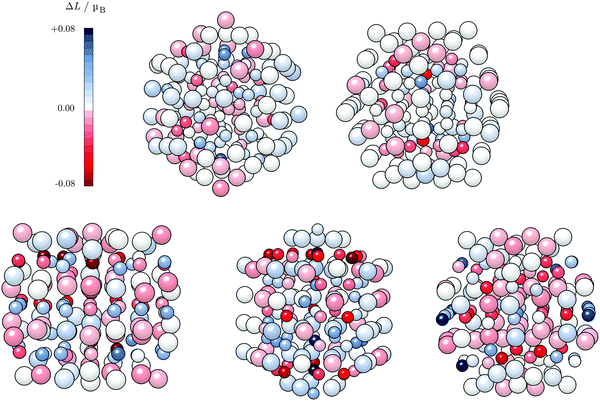
An important aspect is the intrinsic connection of the anisotropy energies with the local atomic anisotropies of the orbital magnetic moments, L_z − L_x ∝ E_z − E_x.¹⁰⁹ Although the direct proportionality between MAE and the orbital anisotropies from the monometallic case to the alloys containing heavy metals might not be completely confirmed,^110,111 this relationship can still give an indication on the sites which exhibit a pronounced dependence on the direction of magnetisation for varying AuCo NP morphologies. Atom-resolved orbital anisotropies are shown in Fig. 8. For core–shell AuCo NPs, the intermixing interface contains atoms with the highest ΔL values, whereas core Co atoms and under-coordinated Au atoms exhibit minimal orbital anisotropy. On the other hand, Co atoms populating the surface L1₀ sites of ordered AuCo NPs are the main contributors to the overall anisotropy.

Fig. 8 Atom-resolved local anisotropies of 147-atom AuCo NPs: core–shell decahedron and icosahedron (top panel) and L1₀ ordered cuboctahedron, decahedron, and icosahedron (bottom panel), in that order. Blue and red shades indicate positive and negative differences in the easy and hard magnetisation direction of orbital moments, respectively; a scale is provided on the top left. The larger spheres refer to Au atoms, while smaller ones denote Co atoms.

The MAE of the core–shell alloyed icosahedron is hence increased in comparison to the monometallic Co icosahedron owing to the induced orbital anisotropy at the Co–Au interface, in contrast to the almost complete lack of any anisotropy over the pure 55-atom Co NP (Fig. S5, ESI†). The contrast in behaviour of the decahedral core–shell alloyed AuCo NP is due to the highest local anisotropy present at under-coordinated surface sites of the 55-atom Co decahedron (Fig. S5, ESI†), which are saturated by the Au shell in AuCo NPs. This is not the case for L1₀ ordering, which allows for surface Co atoms to maintain their local anisotropy, at the same time facilitating the advantage of the Au–Co interface as an additional source of orbital anisotropy.

Conclusions

The interest in nanoalloys of noble and transition metals is associated with their enhanced electronic and magnetic properties, which could be valuable and tuneable assets in versatile applications. A combination of highly magnetic cobalt and inert and easy-to-functionalise gold could be an opportune solution for many magnetisation-based biomedical NP treatments. DFT calculations were performed to establish the relation between the morphology factors of AuCo NPs (NP geometry, size, and atomic arrangement) and their structural, energetic, and magnetic properties.

In particular, L1₀ ordered AuCo NPs of varying geometries (cuboctahedron, decahedron, and icosahedron) show high magnetic anisotropy energy in comparison to monometallic Co NPs, as well as a slight improvement of magnetic moments compared to the core–shell alloyed counterparts. However, analysis of the stability trends and mixing favourability highlighted the dominance of core–shell morphologies over a wide NP size range, especially that of the core–shell AuCo icosahedron, owing to the advantageous hybridisation of Au 5d and Co 3d states and low positioning of the minority spin channel centre. Nevertheless, energy separation between different morphologies can be reduced by embedding the NPs in a matrix or placing them in a carrier gas to facilitate diffusion processes during the NP growth. For example, a recent synthesis of 3 nm L1₀ CoPt NPs was achieved by creating samples of diluted CoPt layers embedded in amorphous carbon,¹¹² and the results provided here are expected to stimulate similar efforts in the synthesis of ordered AuCo NPs.

This DFT study has captured favourable magnetic properties of L1₀ ordered AuCo NPs, which are hence suggested to be promising candidates for applications such as magnetic nanoparticle hyperthermia. Further work on the passivation-mediated changes in the energetic and magnetic properties of AuCo NPs is our next step, whereas we trust that this work will encourage experimental research into AuCo NP synthesis.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

BF is grateful to Cardiff University for support through a Research Scholarship from the School of Chemistry. We acknowledge the Engineering and Physical Sciences Research Council (Grant No. EP/R512503/1 and EP/K009567/2) for funding. This work was performed using the computational facilities of the Advanced Research Computing @ Cardiff\(ARCCA) Division, Cardiff University. Via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work made use of the facilities of ARCHER, the UK's national high-performance computing service, which is funded by the Office of Science and Technology through EPSRC's High End Computing Programme. Information on the data underpinning the presented results, including how to access them, can be found in the Cardiff University data catalogue at DOI: http://10.17035/d.2022.0164147661.

References

1. A. Miyazaki, I. Balint and Y. Nakano, Morphology control of platinum nanoparticles and their catalytic properties, J. Nanopart. Res., 2003, 5, 69–80.
2. Y. Li, Q. Liu and W. Shen, Morphology-dependent nanocatalysis: Metal particles, Dalton Trans., 2011, 40, 5811–5826.
3. L. M. Liz-Marzán, Tailoring surface plasmons through the morphology and assembly of metal nanoparticles., Langmuir, 2006, 22, 32–41.
4. S. Cheong, J. D. Watt and R. D. Tilley, Shape control of platinum and palladium nanoparticles for catalysis, Nanoscale, 2010, 2, 2045–2053.
5. F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, Crossover among structural motifs in transition and noble-metal clusters, J. Chem. Phys., 2002, 116, 3856–3863.
6. B. Farkaš and N. H. de Leeuw, Towards a morphology of cobalt nanoparticles: size and strain effects, Nanotechnology, 2020, 31, 195711.
7. F. Baletto, C. Mottet and R. Ferrando, Growth simulations of silver shells on copper and palladium nanoclusters., Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155420.
8. R. C. Reuel and C. H. Bartholomew, Effects of support and dispersion on the CO hydrogenation activity/selectivity properties of cobalt., J. Catal., 1984, 85, 78–88.
9. G. Prieto, A. Martínez, P. Concepción and R. Moreno-Tost, Cobalt particle size effects in Fischer–Tropsch synthesis: Structural and in situ spectroscopic characterisation on reverse micelle-synthesised Co/ITQ-2 model catalysts, J. Catal., 2009, 266, 129–144.
10. F. Baletto, C. Mottet, A. Rapallo, G. Rossi and R. Ferrando, Growth and energetic stability of AgNi core–shell clusters, Surf. Sci., 2004, 566–568, 192–196.
11. I. Parsina and F. Baletto, Tailoring the structural motif of AgCo nanoalloys: Core/shell versus janus-like, J. Phys. Chem. C, 2010, 114, 1504–1511.
12. K. Laasonen, E. Panizon, D. Bochicchio and R. Ferrando, Competition between icosahedral motifs in AgCu, AgNi, and AgCo nanoalloys: A combined atomistic-DFT study, J. Phys. Chem. C, 2013, 117, 26405–26413.
13. D. Bochicchio and R. Ferrando, Size-dependent transition to high-symmetry chiral structures in AgCu, AgCo, AgNi, and AuNi nanoalloys, Nano Lett., 2010, 10, 4211–4216.
14. M. Gaudry, et al., Size and composition dependence in the optical properties of mixed (transition metal/noble metal) embedded clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 1–10.
15. F. H. B. Lima, J. F. R. de Castro and E. A. Ticianelli, Silver–cobalt bimetallic particles for oxygen reduction in alkaline media, J. Power Sources, 2006, 161, 806–812.
16. A. Holewinski, J. C. Idrobo and S. Linic, High-performance Ag–Co alloy catalysts for electrochemical oxygen reduction, Nat. Chem., 2014, 6, 828–834.
17. D. Wu and D. Cheng, Core/shell AgNi/PtAgNi nanoparticles as methanol-tolerant oxygen reduction electrocatalysts, Electrochim. Acta, 2015, 180, 316–322.
18. W. F. Hu, H. K. Yuan, H. Chen, G. Z. Wang and G. L. Zhang, Structural and magnetic properties of CoPt clusters, Phys. Lett. Sect. A Gen. At. Solid State Phys., 2014, 378, 198–206.
19. C. Cui, L. Gan, M. Heggen, S. Rudi and P. Strasser, Compositional segregation in shaped Pt alloy nanoparticles and their structural behaviour during electrocatalysis, Nat. Mater., 2013, 12, 765–771.
20. S. H. Noh, M. H. Seo, J. K. Seo, P. Fischer and B. Han, First principles computational study on the electrochemical stability of Pt–Co nanocatalysts, Nanoscale, 2013, 5, 8625–8633.
21. M. Heggen, M. Gocyla and R. E. Dunin-Borkowski, The growth and degradation of binary and ternary octahedral Pt–Ni-based fuel cell catalyst nanoparticles studied using advanced transmission electron microscopy, Adv. Phys. X, 2017, 2, 281–301.
22. G. Kovács, et al., Revealing chemical ordering in Pt–Co nanoparticles using electronic structure calculations and X-ray photoelectron spectroscopy, Phys. Chem. Chem. Phys., 2015, 17, 28298–28310.
23. N. M. Markovic, et al., Improved oxygen reduction activity on Pt₃Ni(111) via increased surface site availability, Science, 2007, 315, 493–497.
24. J. M. M. Tengco, et al., Synthesis and electrochemical evaluation of carbon supported Pt–Co bimetallic catalysts prepared by electroless deposition and modified charge enhanced dry impregnation, Catalysts, 2016, 6, 83.
25. I. Matanović, F. H. Garzon and N. J. Henson, Theoretical study of electrochemical processes on Pt–Ni alloys, J. Phys. Chem. C, 2011, 115, 10640–10650.
26. M. Asano, R. Kawamura, R. Sasakawa, N. Todoroki and T. Wadayama, Oxygen reduction reaction activity for strain-controlled Pt-based model alloy catalysts: Surface strains and direct electronic effects induced by alloying elements, ACS Catal., 2016, 6, 5285–5289.
27. S. Il Choi, et al., Synthesis and characterization of 9 nm Pt–Ni octahedra with a record high activity of 3.3 A/mgPt for the oxygen reduction reaction, Nano Lett., 2013, 13, 3420–3425.
28. H. L. Liu, J. H. Wu, J. H. Min and Y. K. Kim, Synthesis of monosized magnetic-optical AuFe alloy nanoparticles, J. Appl. Phys., 2008, 103, 07D529.
29. R. Sinclair, H. Li, S. Madsen and H. Dai, HREM analysis of graphite-encapsulated metallic nanoparticles for possible medical applications, Ultramicroscopy, 2013, 134, 167–174.
30. P. Srinoi, Y. T. Chen, V. Vittur, M. D. Marquez and T. R. Lee, Bimetallic nanoparticles: Enhanced magnetic and optical properties for emerging biological applications, Appl. Sci., 2018, 8, 1106.
31. A. Wijaya, K. A. Brown, J. D. Alper and K. Hamad-Schifferli, Magnetic field heating study of Fe-doped Au nanoparticles, J. Magn. Magn. Mater., 2007, 309, 15–19.
32. A. Naitabdi and B. Roldan Cuenya, Formation, thermal stability, and surface composition of size-selected AuFe nanoparticles, Appl. Phys. Lett., 2007, 91, 89–92.
33. V. Velasco, et al., On the stability of AuFe alloy nanoparticles, Nanotechnology, 2014, 25, 215703.
34. G. Darabdhara, et al., Au–Ni alloy nanoparticles supported on reduced graphene oxide as highly efficient electrocatalysts for hydrogen evolution and oxygen reduction reactions, Int. J. Hydrogen Energy, 2018, 43, 1424–1438.
35. X. Wang, S. Sun, Z. Huang, H. Zhang and S. Zhang, Preparation and catalytic activity of PVP-protected Au/Ni bimetallic nanoparticles for hydrogen generation from hydrolysis of basic NaBH₄ solution, Int. J. Hydrogen Energy, 2014, 39, 905–916.
36. P. He, X. Wang, Y. Liu, L. Yi and X. Liu, Reverse micelle synthesis of AuNi alloy as electrocatalyst of borohydride oxidation, Int. J. Hydrogen Energy, 2012, 37, 1254–1262.
37. G. Maduraiveeran, R. Rasik, M. Sasidharan and W. Jin, Bimetallic gold–nickel nanoparticles as a sensitive amperometric sensing platform for acetaminophen in human serum, J. Electroanal. Chem., 2018, 808, 259–265.
38. J. L. Rousset, et al., Comparative X-ray photoemission spectroscopy study of Au, Ni, and AuNi clusters produced by laser vaporization of bulk metals, J. Phys. Chem. B, 2000, 104, 5430–5435.
39. A. M. Molenbroek, J. K. Nørskov and B. S. Clausen, Structure and reactivity of Ni–Au nanoparticle catalysts, J. Phys. Chem. B, 2001, 105, 5450–5458.
40. H. Okamoto, T. B. Massalski, T. Nishizawa and M. Hasebe, The Au–Co (gold–cobalt) system, Bull. Alloy Phase Diagr., 1985, 6, 449–454.
41. X. Wu, Y. Sun, Z. Wei and T. Chen, Influence of noble metal dopants (M = Ag, Au, Pd or Pt) on the stable structures of bimetallic Co-M clusters, J. Alloys Compd., 2017, 701, 447–455.
42. D. Bochicchio and R. Ferrando, Morphological instability of core-shell metallic nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165435.
43. D. Nelli and R. Ferrando, Core–shell: Vs. multi-shell formation in nanoalloy evolution from disordered configurations, Nanoscale, 2019, 11, 13040–13050.
44. J. P. Palomares-Baez, E. Panizon and R. Ferrando, Nanoscale effects on phase separation, Nano Lett., 2017, 17, 5394–5401.
45. Y. Bao, H. Calderon and K. M. Krishnan, Synthesis and characterization of magnetic-optical Co–Au core-shell nanoparticles, J. Phys. Chem. C, 2007, 111, 1941–1944.
46. S. Mandal and K. M. Krishnan, Co core Au shell nanoparticles: Evolution of magnetic properties in the displacement reaction, J. Mater. Chem., 2007, 17, 372–376.
47. A. Mayoral, D. Llamosa and Y. Huttel, A novel Co@Au structure formed in bimetallic core@shell nanoparticles, Chem. Commun., 2015, 51, 8442–8445.
48. Z. Zhang, T. M. Nenoff, J. Y. Huang, D. T. Berry and P. P. Provencio, Room temperature synthesis of thermally tmmiscible Ag–Ni nanoalloys, J. Phys. Chem. C, 2009, 113, 1155–1159.
49. C. C. Kuo, C. Y. Li, C. H. Lee, H. C. Li and W. H. Li, Huge inverse magnetization generated by Faraday induction in nano-sized Au@Ni core@shell nanoparticles, Int. J. Mol. Sci., 2015, 16, 20139–20151.
50. Z. Liu, Y. Lei and G. Wang, Surface magnetism of L10 CoPt alloy: First principles predictions, J. Phys.: Condens. Matter, 2017, 29, 355801.
51. J. Li, et al., Hard-magnet L10–CoPt nanoparticles advance fuel cell catalysis, Joule, 2019, 3, 124–135.
52. A. Kabir, et al., Effect of structure on the magnetic anisotropy of L1₀ FePt nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 054424.
53. D. F. Zhang, et al., Low-temperature fabrication of Au–Co cluster mixed nanohybrids with high magnetic moment of Co, ACS Appl. Mater. Interfaces, 2012, 4, 5643–5649.
54. L. E. Marbella, et al., Gold–cobalt nanoparticle alloys exhibiting tunable compositions, near-infrared emission, and high T2 relaxivity, Adv. Funct. Mater., 2014, 24, 6532–6539.
55. R. Ferrando, A. Fortunelli and G. Rossi, Quantum effects on the structure of pure and binary metallic nanoclusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085449.
56. A. J. Logsdail, L. O. Paz-Bórbon and C. A. Downing, DFT-computed trends in the properties of bimetallic precious metal nanoparticles with core@shell segregation, J. Phys. Chem. C, 2018, 122, 5721–5730.
57. N. Zhang, et al., The activity origin of core–shell and alloy AgCu bimetallic nanoparticles for the oxygen reduction reaction, J. Mater. Chem. A, 2017, 5, 7043–7054.
58. G. Feng, et al., Atomically ordered non-precious Co3Ta intermetallic nanoparticles as high-performance catalysts for hydrazine electrooxidation, Nat. Commun., 2019, 10, 4514.
59. A. E. Russell, Electrocatalysis: Theory and experiment at the interface, Phys. Chem. Chem. Phys., 2008, 10, 3607–3608.
60. M. K. Alam, S. Saito and H. Takaba, Modeling of equilibrium conformation of Pt2Ru3 nanoparticles using the density functional theory and Monte Carlo simulations, J. Mater. Res., 2017, 32, 1573–1581.
61. S. Nigam and C. Majumder, Comparison between cluster and slab model for Pt-group atom adsorption on gold and silver substrate, Surf. Sci., 2014, 630, 78–84.
62. A. M. Pessoa, J. L. C. Fajín, J. R. B. Gomes and M. N. D. S. Cordeiro, Cluster and periodic DFT calculations of adsorption of hydroxyl on the Au(hkl) surfaces, J. Mol. Struct., 2010, 946, 43–50.
63. T. Jacob, R. P. Muller and W. A. Goddard, Chemisorption of atomic oxygen on Pt(111) from DFT studies of Pt-clusters, J. Chem. Phys. B, 2003, 107, 9465–9476.
64. A. Posada-Borbón, C. J. Heard and H. Grönbeck, Cluster size effects in ethylene hydrogenation over palladium, J. Phys. Chem. C, 2017, 121, 10870–10875.
65. S. M. Kozlov and K. M. Neyman, Insights from methane decomposition on nanostructured palladium, J. Catal., 2016, 337, 111–121.
66. Z. Liu and G. Wang, Shape-dependent surface magnetism of Co-Pt and Fe-Pt nanoparticles from first principles, Phys. Rev. B, 2017, 96, 224412.
67. B. Farkaš and N. H. De Leeuw, A perspective on modelling metallic magnetic nanoparticles in biomedicine: From monometals to nanoalloys and ligand-protected particles, Materials, 2021, 14, 3611.
68. Z. Liu, Y. Lei and G. Wang, First-principles computation of surface segregation in L10 CoPt magnetic nanoparticles, J. Phys.: Condens. Matter, 2016, 28, 266002.
69. P. Van Zwol, P. M. Derlet, H. Van Swygenhoven and S. L. Dudarev, BCC Fe surface and cluster magnetism using a magnetic potential, Surf. Sci., 2007, 601, 3512–3520.
70. R. A. Lordeiro, F. F. Guimarães, J. C. Belchior and R. L. Johnston, Determination of main structural compositions of nanoalloy clusters of Cu_xAu_y (x + y ≤ 30) using a genetic algorithm approach, Int. J. Quantum Chem., 2003, 95, 112–125.
71. E. Panizon, D. Bochicchio, G. Rossi and R. Ferrando, Tuning the structure of nanoparticles by small concentrations of impurities, Chem. Mater., 2014, 26, 3354–3356.
72. R. Ferrando, A. Fortunelli and R. L. Johnston, Searching for the optimum structures of alloy nanoclusters, Phys. Chem. Chem. Phys., 2008, 10, 640–649.
73. D. T. Tran and R. L. Johnston, Theoretical study of Cu_38−nAu_n clusters using a combined empirical potential-density functional approach, Phys. Chem. Chem. Phys., 2009, 11, 10340–10349.
74. E. Panizon and R. Ferrando, Strain-induced restructuring of the surface in core@shell nanoalloys, Nanoscale, 2016, 8, 15911–15919.
75. D. J. Borbón-González, et al., Global minimum Pt13M20 (M = Ag, Au, Cu, Pd) dodecahedral core–shell clusters, J. Phys. Chem. A, 2013, 117, 14261–14266.
76. S. M. Kozlov, G. Kovács, R. Ferrando and K. M. Neyman, How to determine accurate chemical ordering in several nanometer large bimetallic crystallites from electronic structure calculations, Chem. Sci., 2015, 6, 3868–3880.
77. J. Q. Goh, J. Akola and R. Ferrando, Geometric structure and chemical ordering of large AuCu clusters: A computational study, J. Phys. Chem. C, 2017, 121, 10809–10816.
78. S. L. Dudarev, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
79. A. G. Petukhov, I. I. Mazin, L. Chioncel and A. I. Lichtenstein, Correlated metals and the LDA+U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 153106.
80. M. Cococcioni and S. De Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the LDA+U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
81. D. Holec, F. D. Fischer and D. Vollath, Structure and surface energy of Au55 nanoparticles: An ab initio study, Comput. Mater. Sci., 2017, 134, 137–144.
82. T. M. Soini, et al., Extending the cluster scaling technique to ruthenium clusters with hcp structures, Surf. Sci., 2016, 643, 156–163.
83. G. L. Gutsev, C. W. Weatherford, K. G. Belay, B. R. Ramachandran and P. Jena, An all-electron density functional theory study of the structure and properties of the neutral and singly charged M12 and M13 clusters: M Sc-Zn, J. Chem. Phys., 2013, 138, 164303.
84. J. L. F. Da Silva, H. G. Kim, M. J. Piotrowski, M. J. Prieto and G. Tremiliosi-Filho, Reconstruction of core and surface nanoparticles: The example of Pt55 and Au55, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205424.
85. M. J. Piotrowski, P. Piquini and J. L. F. Da Silva, Platinum-based nanoalloys PtnTM55-n (TM = Co, Rh, Au): A density functional theory investigation, J. Phys. Chem. C, 2012, 116, 18432–18439.
86. M. J. Piotrowski, P. Piquini, L. Cândido and J. L. F. Da Silva, The role of electron localization in the atomic structure of transition-metal 13-atom clusters: The example of Co13, Rh13, and Hf13, Phys. Chem. Chem. Phys., 2011, 13, 17242–17248.
87. B. K. Teo and N. J. A. Sloane, Magic numbers in polygonal and polyhedral clusters, Inorg. Chem., 1985, 24, 4545–4558.
88. F. H. Kaatz and A. Bultheel, Magic mathematical relationships for nanoclusters, Nanoscale Res. Lett., 2019, 14, 150.
89. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
90. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
91. J. L. Rodríguez-López, F. Aguilera-Granja, K. Michaelian and A. Vega, Structure and magnetism of cobalt clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 174413.
92. S. Datta, et al., Structure, bonding, and magnetism of cobalt clusters from first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 014429.
93. C. Jo and J. Il Lee, Spin polarization and charge transfer of Co nanoclusters coated with CO molecules, J. Magn. Magn. Mater., 2009, 321, 47–51.
94. M. J. Piotrowski, P. Piquini and M. M. Odashima, & Da Silva, J. L. F. Transition-metal 13-atom clusters assessed with solid and surface-biased functionals, J. Chem. Phys., 2011, 134, 134105.
95. Y. Sun, S. Liu, X. Guo and S. Huang, Structural, magnetic and electronic properties of CunNi55−n (n = 0–55) nanoparticles: Combination artificial bee colony algorithm with DFT, Comput. Theor. Chem., 2019, 1154, 11–16.
96. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
97. J. Jellinek and E. B. Krissinel, NinAlm alloy clusters: Analysis of structural forms and their energy ordering, Chem. Phys. Lett., 1996, 258, 283–292.
98. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
99. R. Wu and A. J. Freeman, Spin–orbit induced magnetic phenomena in bulk metals and their surfaces and interfaces, J. Magn. Magn. Mater., 1999, 200, 498–514.
100. G. H. O. Daalderop, P. J. Kelly and M. F. H. Schuurmans, First-principles calculation of the magnetocrystalline anisotropy energy of iron, cobalt, and nickel, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 11919–11937.
101. D. Hobbs, G. Kresse and J. Hafner, Fully unconstrained noncollinear magnetism within the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 11556–11570.
102. M. Marsman and J. Hafner, Broken symmetries in the crystalline and magnetic structures of γ-iron, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 224409.
103. P. Entel and M. E. Gruner, Large-scale ab initio simulations of binary transition metal clusters for storage media materials, J. Phys.: Condens. Matter, 2009, 21, 064228.
104. M. E. Gruner, G. Rollmann, P. Entel and M. Farle, Multiply twinned morphologies of FePt and CoPt nanoparticles, Phys. Rev. Lett., 2008, 100, 087203.
105. B. Farkas and N. H. De Leeuw, Effect of coverage on the magnetic properties of –COOH, –SH, and –NH2 ligand-protected cobalt nanoparticles, Nanoscale, 2021, 13, 11844–11855.
106. S. Okamoto, et al., Chemical-order-dependent magnetic anisotropy and exchange stiffness constant of FePt(001) epitaxial films, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 024413.
107. J. B. Staunton, et al., Long-range chemical order effects upon the magnetic anisotropy of FePt alloys from an ab initio electronic structure theory, J. Phys.: Condens. Matter, 2004, 16, S5623.
108. A. Sakuma and Y. Kota, Relationship between magnetocrystalline anisotropy and orbital magnetic moment in L10-type ordered and disordered alloys, J. Phys. Soc. Jpn., 2012, 81, 84705.
109. M. Martins and W. Wurth, Magnetic properties of supported metal atoms and clusters, J. Phys.: Condens. Matter, 2016, 28, 503002.
110. O. Šipr, et al., Magnetic moments, exchange coupling, and crossover temperatures of Co clusters on Pt(111) and Au(111), J. Phys.: Condens. Matter, 2007, 19, 096203.
111. C. Andersson, et al., Influence of ligand states on the relationship between orbital moment and magnetocrystalline anisotropy, Phys. Rev. Lett., 2007, 99, 177207.
112. F. Tournus, et al., Evidence of L10 chemical order in CoPt nanoclusters: Direct observation and magnetic signature, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 144411.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00648k

---