Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ethanol electro-oxidation reaction on the Pd(111) surface in alkaline media: insights from quantum and molecular mechanics†
Jonathan
Campeggio
a,
Victor
Volkov
a,
Massimo
Innocenti
a,
Walter
Giurlani
a,
Claudio
Fontanesi
 b,
Mirco
Zerbetto
b,
Mirco
Zerbetto
 c,
Marco
Pagliai
c,
Marco
Pagliai
 a,
Alessandro
Lavacchi
d and
Riccardo
Chelli
a,
Alessandro
Lavacchi
d and
Riccardo
Chelli
 *a
*a
aDepartment of Chemistry “Ugo Schiff”, University of Florence, Via della Lastruccia 3, Sesto Fiorentino, 50019, Italy. E-mail: riccardo.chelli@unifi.it
bDepartment of Engineering “Enzo Ferrari”, University of Modena and Reggio Emilia, Via Università 4, Modena, 41121, Italy
cDepartment of Chemical Sciences, University of Padova, Via Marzolo 1, Padova, 35131, Italy
dCNR-ICCOM, Via Madonna del Piano 10, Sesto Fiorentino, 50019, Italy
First published on 21st April 2022
Abstract
The ethanol electro-oxidation catalyzed by Pd in an alkaline environment involves several intermediate reaction steps promoted by the hydroxyl radical, OH. In this work, we report on the dynamical paths of the first step of this oxidation reaction, namely the hydrogen atom abstraction CH3CH2OH + OH → CH3CHOH + H2O, occurring at the Pd(111) surface and address the thermodynamic stability of the adsorbed reactants by means of quantum and molecular mechanics calculations, with special focus on the effect of the solvent. We have found that the impact of the solvent is significant for both ethanol and OH, contributing to a decrease in their adsorption free energies by a few dozen kcal mol−1 with respect to the adsorption energy under vacuum. Furthermore, we observe that hydrogen atom abstraction is enhanced for those simulation paths featuring large surface–reactant distances, namely, when the reactants weakly interact with the catalyst. The picture emerging from our study is therefore that of a catalyst whose coverage in an aqueous environment is largely dominated by OH with respect to ethanol. Nevertheless, only a small amount of them, specifically those weakly bound to the catalyst, is really active in the ethanol electro-oxidation reaction. These results open the idea of a rational design of co-catalysts based on the tuning of surface chemical properties to eventually enhance exchange current density.
1 Introduction
In the last few years, fuel cells have emerged as a promising technology for clean power generation, because they can provide electric energy in an efficient way with negligible emission of polluting products and hence with a moderate impact on the environment.1–3 The nontoxicity, ease of storage and transport, carbon neutrality and relatively high energy content make ethanol (EtOH) more attractive than other fuels for large-scale energy production.In direct EtOH fuel cells, the EtOH oxidation at the anode is counterbalanced by the oxygen reduction at the cathode, generating a voltage of about 1.14 V. With respect to methanol, the complete oxidation of EtOH to CO2 gives a higher energy density, since it can deliver 12, against 6, electrons per molecule. However, optimal conditions for direct EtOH fuel cells have been obtained in alkaline media,4,5 where only 4 electrons per molecule are delivered, with EtOH being partially oxidized to acetate5–7
| CH3CH2OH + 5OH− → CH3COO− + 4H2O+ 4e− | (1) |
The EtOH oxidation reaction (EOR) into direct EtOH fuel cells occurs only if promoted by a catalyst. Among the large amount of catalysts tested for enhancing the EOR rate, those based on Pt, and especially on Pd into alkaline media, revealed surprisingly high electrocatalytic activity.5,8,9 Furthermore, alkaline electrolytes offer the advantage of providing an environment in which transition metals and rare-earth metals can be used as co-catalysts to promote the catalytic activity and functionality of Pd-based systems.5 In this respect, in the last few years much attention was attracted by Pd used synergistically with a ceria-based, CeO2, co-catalyst.10–15
The reaction mechanism leading from EtOH to acetate involves a number of elementary steps.5 In the literature, several hypotheses, based on experimental6,7,16–18 and theoretical6,19–24 studies, have been proposed. It has been shown that the Pd electrode reaches a peak performance for the EOR at very high pH values17,18 (greater than 13) forming acetate as a product, while, at pH values lower than 13, the EOR can also proceed towards the formation of CO2.
Concerning the first reaction steps of the EOR, different mechanisms have been proposed. Several authors invoked H-atom abstraction at the α-carbon site of EtOH as the first reaction step, followed by electron transfer from the adsorbed H,6,19,22–27 while other studies pointed to a determinant role of the adsorbed OH species in the H-atom abstraction process as follows20,21,27
| Pd(CH3CH2OH)ads + Pd(OH)ads → Pd(CH3CHOH)ads + Pd + H2O | (2) |
The above mechanisms, differing for the species acting as the H acceptor (the Pd surface or the OH), are not necessarily mutually exclusive, but can act synergistically to yield the H-atom abstraction,20 with a possible modulating effect of the pH.
A fundamental aspect concerning electrocatalytic reactions is the dramatic influence of the medium (aka the solvent) on the adsorption free energy of the reacting species.28 Addressing solvation in a rigorous way by using quantum mechanical simulations is difficult because these approaches may account for a very limited number of solvent molecules and the reduced sampling prevents accurate free energy calculations. Implicit-solvent models can be used to calculate configurational entropies, but they often provide inaccurate results when compared to explicit-solvent models. In our opinion, the most suitable techniques to obtain configurational entropies, and hence adsorption free energies, with explicit solvation are those based on the molecular dynamics (MD) simulations supplied with empirical force fields.29,30
In this work, we collect several results obtained from quantum mechanical calculations and classical MD simulations to provide some insight into the EOR mechanism, especially focusing on eqn (2). We combine several calculated quantities, such as the binding energies and the adsorption free energies of EtOH and OH− on the Pd(111) surface, to interpret the experimental data and to reveal a possible reaction pathway for the initial steps of EtOH oxidation. Adsorption free energies of OH− and EtOH are provided to assess separately the thermal and solvation effects on the binding of these species to the Pd surface. The present results are consistent with early studies of the EOR pathways and provide insightful suggestions for rational design of Pd based co-catalysts aimed at enhancing the electro-oxidation rate in direct EtOH fuel cells.
2 Methods and computational details
2.1 Quantum mechanical calculations
Quantum mechanical calculations have been carried out using density functional theory (DFT). In particular, we performed (a) single-point energy calculations of EtOH, OH−, OH and water onto the Pd(111) lattice aimed to model an empirical force field for the Pd interatomic interactions, (b) geometry optimizations to evaluate the adsorption energies of EtOH, OH and OH− and (c) Born–Oppenheimer MD simulations to identify dynamical paths for H-atom abstraction represented by the reaction of eqn (2). All calculations have been realized with the Quickstep31 module of the CP2K suite of programs.32The generalized gradient approximation of Perdew, Burke, and Erzenhorf33 was used to compute the exchange–correlation energy, while the dispersion interactions were accounted for by the Grimme D3 correction.34 Pseudopotentials were used through the parameterization proposed by Goedecker, Teter and Hutter:35,36 GTH-PBE-q6 for O, GTH-PBE-q4 for C, GTH-PBE-q1 for H and GTH-PBE-q18 for Pd. The wave function is expanded in the DZVP-MOLOPT-GTH Gaussian basis set. For Pd, the short-range version of this basis was used.37 The electron density was modeled by using the plane-wave cutoff and relative cutoff set to 500 Ry and 60 Ry, respectively. The smearing technique according to the Fermi–Dirac distribution (electronic temperature equal to 300 K) was adopted to handle the electronic properties. The number of additional molecular orbitals is 50.
The Pd(111) sample was prepared replicating a unit cell obtained by cutting the Pd(100) lattice with an experimental lattice constant of 3.89 Å.38 A slab with a periodicity of 9.528 × 8.252 Å, arising from a 2 × 3 unit cell replication, was built. The Pd lattices employed for DFT calculations are shown in Fig. S1 of the ESI.† Structural manipulation was carried out by using the VESTA package.39 In single-point energy calculations, in order to estimate the energy of the unbound states, the molecules were also placed far from the surface. To avoid possible spurious interactions of the molecules with atoms in the closest image of the cell, no periodic boundary conditions were applied along the normal to the surface. The same protocol was used for the geometry optimizations of OH, OH− and EtOH on the Pd surface. The problem of closest images along the normal to the surface is not present in the MD simulations, because the two reactants remain in close contact with the surface during the whole trajectory. This allows us to speed up the simulations adopting periodicity also along the normal to the surface (lattice period 30 Å).
In single-point calculations and geometry optimizations, the Pd lattice is assembled with four (111) layers, for a total of 48 atoms (left panel of Fig. S1 of the ESI†), while two layers were taken to build the samples for MD simulations (right panel of Fig. S1 of the ESI†). Simulations were carried out in the microcanonical ensemble. The simulation time step is 0.2 fs. The trajectories are about 100 fs long, a time ample enough to identify the occurrence of a reactive event. In order to reduce the computational cost, the plane wave cut-off was reduced to 400 Ry (the Gaussian basis set was not changed). The initial velocities of all atoms were set to zero. Additional technical details about the single-point calculations and the simulation setup are reported in Sections 3.1 and 3.3, respectively.
2.2 Classical MD simulations
Enhanced sampling simulations were performed to compute the potential of mean force (PMF, or free energy profile) of four systems: the Pd(111)/EtOH system, with and without the solvent, as a function of the Cα-surface distance and the Pd(111)/OH− system, with and without the solvent, as a function of the O-surface distance. Adsorption free energies were then computed exploiting the PMF as described in Section 3.2. To compute the PMF, multiple-window umbrella sampling in the framework of serial generalized ensemble approaches40,41 was employed, assuming, in turn, the aforementioned distances as collective variables. In this method, called MultiWindow tempering,41 several identical copies of the system (replicas) are simultaneously and independently simulated by adding an harmonic potential energy term (window potential) to the physical Hamiltonian. Such an additional potential can be centered at established values of the collective variable, z1, z2, etc., giving rise to a set of ensembles, each featured by a different value of zi. Thus, the ith ensemble is characterized by a window potential of the type k(z − zi)2, where z is the current value of the collective variable. The replicas are initially assigned to arbitrary ensembles. Then, for each replica, a switch zi → zi±1 is attempted at established time intervals (every 90 fs) according to a Monte Carlo-like criterion based on the free energies of the ensembles computed on the fly via the Bennett acceptance ratio. The instantaneous work, needed to compute the free energies of the ensembles, is collected from all replicas every 9 ps through a message passing interface protocol.40,41 In this way, the replicas have two kinds of dynamics, one in the space of atomic coordinates and the other through the ensembles. The latter dynamics forces the system to randomly explore the space of the collective variable. The PMF as a function of the collective variable is computed at the end of the simulation via the multistate Bennett acceptance ratio analysis.42 For all systems under study, we performed MultiWindow tempering simulations using 128 replicas. The centers of the window potentials are distributed along the collective variables as reported in Table S1 of the ESI.†The charge and Lennard-Jones parameters for OH− have been taken from the CHARMM force field.43 The SCP/E model44 was adopted for water. The AMBER-like ff99sb force field45 in combination with atomic charges computed through a RESP fit46 at the HF/6-31G* level of theory was used to model the EtOH molecule. The obtained atomic charges as well as the AMBER atom-types assigned to the atoms of the EtOH molecule are reported in ref. 47. For the interactions between Pd and the other atoms, an empirical force field based on Lennard-Jones interactions was built as described in the ESI.† Lorentz–Berthelot mixing rules were employed to account for the pairwise interactions between different atomic types.
The simulation box is orthorhombic and was prepared by extending the Pd unit cell along the (111) lattice plane to obtain a simulation-box face of 28.585 × 24.756 Å. The box side-length along the normal to the (111) lattice plane is set to 50 Å. Thus, nine Pd slabs were arranged in the box for a total of 972 atoms. In the empty region of the box, the EtOH or OH− molecule and 714 water molecules were randomly arranged. The simulation box is shown in Fig. S6 of the ESI.† The simulations for calculating the PMF in the absence of the solvent were performed with the same setup after removing the water molecules from the box.
All simulations were realized in the constant-volume, constant-temperature (canonical) thermodynamic ensemble under standard periodic boundary conditions. The temperature control (298 K) was achieved using the Nosé–Hoover thermostat.48 Electrostatic forces were treated with the smooth particle mesh Ewald method49 using a fourth order B-spline interpolation polynomial for the charges, an Ewald parameter of 0.43 Å−1 and a grid spacing smaller than 1 Å for the fast Fourier transform calculation of the charge weighted structure factor. The cut-off distance for the non-bonded interactions is 11.5 Å. A five time-step r-RESPA integrator50 was employed for integrating the equations of motion (with the largest time step of 9 fs). Constraints were enforced to covalent bonds involving H atoms. The Pd atoms were held fixed in the experimental arrangement during the entire duration of the simulations. Equilibration was obtained by scaling the atomic velocities in the first 100 ps and then freely relaxing the system for 1.8 ns. Data for the PMF calculation were obtained from production runs lasting for 3.6 and 1.5 ns for Pd/EtOH and Pd/OH−, respectively. MultiWindow tempering simulations were carried out with the ORAC program.41,51
3 Results and discussion
3.1 Adsorption energies of the reactants
The H-atom abstraction of eqn (2) was studied through ab initio MD simulations, as discussed in Section 3.3. Since eqn (2) involves adsorbed species, the binding between reactants and the Pd surface is a determinant factor entering the reaction process. Considering that the physisorption of OH− is prodromic to the formation of adsorbed OH, the thermodynamic stability of this adsorbed species is somehow correlated with the amount of OH present on the surface, and hence with the reaction rate. Clearly, also the stability of the adsorbed EtOH plays an important role. Before addressing adsorption free energies, in this section, we report on the stability of the OH−, OH and EtOH adsorbates from the quantum mechanical standpoint. Even if a thorough description of minimum energy structures is not the very aim of the present study, the data reported below will help us to rationalize and corroborate the outcomes concerning solvation and reactivity discussed in the following sections.On one hand, quantum mechanical methods can provide accurate estimates of binding energies related to minimum energy configurations, however, on the other hand, they omit, besides solvation, the configurational entropy arising from the possible presence of several competitive minimum energy states. In spite of this, the quantum mechanical calculations that we have carried out not only are a necessary input to model the empirical force field for classical MD simulations, but also give a reliable evaluation of the global stability of the adsorbates. In order to obtain a wide energetic panorama as well as a valid training set of energies/configurations to model the force field (see the ESI†), we opted to compute the energies of the Pd(111)/EtOH and Pd(111)/OH− systems for various arrangements of the adsorbed molecules, chosen heuristically to explore a variety of configurations (Fig. 1 and 2). For each configuration reported in the figures, the energy was determined for various arrangements obtained by translating rigidly the molecule along the normal to the surface, while keeping fixed the Pd surface, the molecular structure and the mutual arrangement of the surface and adsorbate as shown in Fig. 1 (for the EtOH-n, n = 1, 2,…, 5, configurations) and Fig. 2 (for the OH-1, OH-2 and OH-3 configurations). The DFT energies of the Pd(111)/EtOH and Pd(111)/OH− systems as a function of the adsorbate–surface distance are reported in Fig. 3. Clearly, we do expect that the binding energy Eb of each configuration, defined as the absolute value of the energy at the minimum (zero point energy correction is not considered), provides an underestimate of the value that would be obtained from an optimization procedure. Overall, all of the energy curves present a minimum, revealing a tendency of EtOH and especially of OH− to form a stable adsorbate with the Pd surface. In this respect, it is worth noting that the OH− anion (36 < Eb < 48 kcal mol−1) forms an adsorbate about 4 times more stable than EtOH (8.7 < Eb < 11.5 kcal mol−1). The comparable values of Eb obtained for radically different configurations in EtOH (the energies of all EtOH configurations fall within an interval of less than 3 kcal mol−1), suggest that van der Waals interactions contribute to adsorption more than the electrostatic dipolar ones.53
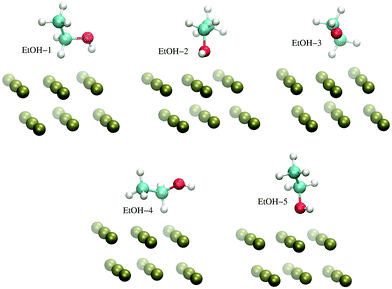 | ||
| Fig. 1 Configurations of the Pd(111)/EtOH system employed to model the empirical force field for the Pd–EtOH interactions, as described in the ESI.† For the sake of clarity, only a limited portion of the surface is reported. The VMD program52 was used for molecular graphics. | ||
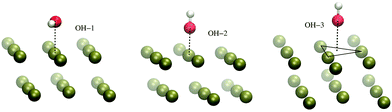 | ||
| Fig. 2 Configurations of the Pd(111)/OH− system employed to model the empirical force field for the Pd–OH− interactions, as described in the ESI.† For the sake of clarity, only a limited portion of the surface is reported. The black lines are drawn to make evident the OH− displacement with respect to the surface. The VMD program52 was used for molecular graphics. | ||
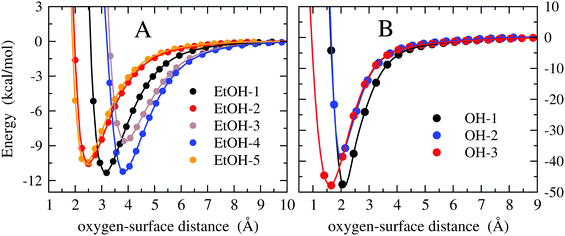 | ||
| Fig. 3 DFT energy of the Pd(111)/EtOH and Pd(111)/OH− systems (panels A and B, respectively) as a function of the O-surface distance. The energy plot for a given configuration is recovered by using structures where the atomic coordinates are obtained translating rigidly the molecule along the normal to the surface, while keeping fixed the arrangement as shown in Fig. 1 (for the EtOH-n, n = 1, 2,…, 5, configurations) and Fig. 2 (for the OH-1, OH-2 and OH-3 configurations). The zero energy is taken at the largest O-surface distance. The spline lines are guide for the eyes. Note that, in order to reveal the details of the curves, different scales have been used in the two panels. | ||
Geometry optimizations at the DFT level, as described in Section 2.1, were performed for both Pd(111)/EtOH and Pd(111)/OH− systems, obtaining binding energies of 19.0 and 56.2 kcal mol−1, respectively. The binding energy for EtOH is in fair agreement with the values of 19.6 kcal mol−1 obtained by Li and Henkelman54 and of 16.6 kcal mol−1 reported by Tereshchuk and Da Silva.53 Our calculation overestimates by about 7.2 kcal mol−1 the value obtained by the analysis of temperature-programmed desorption data.55 The binding energy of OH− is comparable to earlier calculations by Cao and Chen,56 who found 55.6 kcal mol−1 using a PW91 exchange–correlation functional. Moreover, the obtained molecular arrangements of EtOH53 and OH−56 are in perfect agreement with the data reported in the literature. Ball and stick representations of the minimum energy structures are reported in Fig. S2 and S3 of the ESI.†
It should be considered that, at the working cell voltage, the electrochemically favored form of the OH species is the radical one. Hence, the adsorption energy of OH is the actually relevant quantity in the context of the EOR. For the sake of comparison with the results obtained for the Pd(111)/OH− system (Fig. 3), in Fig. 4 we report the energy of the Pd(111)/OH system, where the OH is arranged as in the lowest-energy configurations observed for Pd(111)/OH−, namely OH-1 and OH-3. The most interesting feature of these data is that OH undergoes stabilization by more than 10 kcal mol−1 with respect to the anionic form and that such a stabilization occurs for both OH-1 and OH-3 configurations. The geometry optimization of OH provides a binding energy of 71.3 kcal mol−1, which is greater than the binding energy of OH− by about 15 kcal mol−1. Ball and stick views of the minimum energy structure are reported in Fig. S4 of the ESI.†
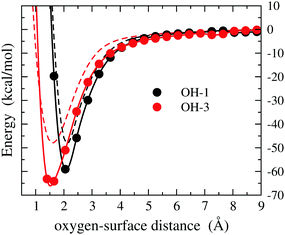 | ||
| Fig. 4 DFT energy of the Pd(111)/OH system as a function of the O-surface distance for the OH-1 and OH-3 configurations (circles). The energy plot for a given configuration is recovered by using structures where the atomic coordinates are obtained translating rigidly the molecule along the normal to the surface, while keeping fixed the arrangement as shown in Fig. 2. The zero energy is taken at the largest O-surface distance. The spline lines are guide for the eyes. The corresponding energies obtained for the anionic form (Fig. 3) are reported for comparison as dashed lines. | ||
The DFT data reported above reveal an energetic scenario in which the OH− species is much more strongly bonded to the Pd surface with respect to EtOH and its stabilization increases significantly upon oxidation to the radical form.
3.2 Adsorption free energies: thermal and solvation effects
An aspect often ignored in evaluating the stability of the adsorbed reactants is the solvating power of the medium. Here, we evaluate the impact of the solvent on the stability of OH− and EtOH adsorbates by computing their adsorption free energies in a water environment via classical MD simulations. While addressing OH− and EtOH is straightforward because of their molecular stability, the calculation on OH is unfeasible because it would require a quantum mechanical approach to account for its high reactivity. On the other side, using quantum mechanics would be too expensive computationally. Nevertheless, the effect of solvation on the OH− anion may provide semi-quantitative indications on the change in the stability of the adsorbed OH in an aqueous environment. The assumption of extending the trend of the solvation effect occurring in the Pd(111)/OH− system to the Pd(111)/OH system is supported by a Bader charge analysis,20 that revealed that the charge of adsorbed OH (−0.43 e) is similar to the charge of OH− in water (−0.62 e), indicating that OH preserves the characteristics of the anionic form in an aqueous solution. Thus, it is likely that OH and OH− might have similar intermolecular interactions with water and hence their adsorption free energies could show comparable changes when solvation is considered.Furthermore, in order to disentangle the thermal and solvation contributions to adsorption, we also determined the adsorption free energies at finite temperature in the absence of the solvent. In a liquid-surface environment, the formation of EtOH and OH adsorbates goes through a competition with other species present in the solution. Adsorption of other ions, in particular cations like Na+ or K+, can be considered almost irrelevant, given the positive potential of the metal surface.20,57
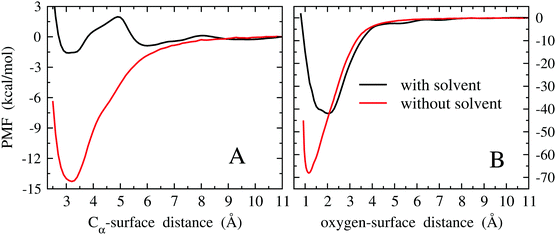
As described later in this section, the method employed to compute adsorption free energies is based on the evaluation of the PMF as a function of the adsorbate–surface distance. However, as we will see, the PMF minimum already gives a quantitative estimate of the adsorption free energy and hence we first discuss its behavior. The PMFs of the Pd(111)/EtOH system as a function of the Cα-surface distance and of the Pd(111)/OH− system as a function of the O-surface distance are reported in Fig. 5A and B, respectively.
The PMFs computed without the solvent show an almost regular behavior, with minimum values comparable to those obtained from quantum mechanical geometry optimizations. For EtOH, thermal effects contribute to a destabilization by about 5 kcal mol−1 with respect to the quantum mechanical minimum, while a stabilization of about 12 kcal mol−1 is obtained for OH−. In the latter case, it is probable that stabilization arises from overestimating the binding energy of the OH-3 configuration in the fit of the force field (see the energy curve of OH-3 in Fig. S8 of the ESI†). In fact, the minima of the PMF and of the energy curve of OH-3 both fall at the same oxygen-surface distance (∼1.2 Å).
As we can see from Fig. 5A, solvation leads to a further destabilization of the EtOH adsorbate by about 12.5 kcal mol−1 with respect to the under vacuum case. Moreover, some articulated modulation of the PMF profile is observed. Actually, such a solvation-induced destabilization is expected if we consider the polar nature of EtOH. A low PMF barrier of ∼3 kcal mol−1 at about 5 Å is noted. However, considering the moderate height of the barrier, it is unlikely that it plays a decisive role in the rate of the electro-oxidation process, limiting, for example, the delivery of EtOH towards the surface of the electrode. Also in the case of OH−1 (Fig. 5B), solvation leads to a significant destabilization of the adsorbate with respect to vacuum, amounting to ∼27 kcal mol−1. The larger destabilization observed for OH− with respect to EtOH can be ascribed to the larger solvation free energy of the former species. Moreover, the distance corresponding to the free energy minimum shifts from 1.2 to 2 Å, while it remains almost unchanged in the EtOH case. Also this feature can be explained considering the large solvation free energy of OH−.
If we assume that the decrease in stability observed for OH− upon solvation might be extended to OH as discussed above, then we would expect a PMF minimum for the radical species ranging around −55 kcal mol−1. In any case, the thermodynamic stability of adsorbed OH in an aqueous environment is expected to be comparable to that of its anionic form.
The PMF provides a quantitative estimate of the change of free energy by moving along an established collective variable, which, in the present context, is the distance between the molecule and the metal surface. Thus, the physically relevant quantity is related to differences between PMFs of two specific values of the collective variable. Strictly speaking, the PMF at the minimum referred to the PMF at infinite distance does not correspond exactly to the binding/adsorption free energy, because the extension of the PMF basin corresponding to the adsorbed state of the system is not accounted for. The adsorption free energy, namely the free energy difference between adsorbed and desorbed states, is related to the difference of specific PMF values computed for these states in a rather articulated way.58,59 Actually, this PMF difference provides the major contribution to the adsorption free energy, but it does not correspond exactly to it. According to ref. 58 and 59, the adsorption free energy can be expressed in terms of two quantities. One is the difference of the PMFs computed for two arbitrary values of the collective variable that must however represent the bound and unbound states of the system. In the present context, the collective variable is the Cα-surface distance for the Pd/EtOH system and the O-surface distance for the Pd/OH− system (Fig. 5). As values of the collective variable representative of the bound states, we have arbitrarily taken zb = 2 Å and zb = 3.3 Å for the Pd/OH− and Pd/EtOH systems in solution, respectively, that nearly correspond to the distances of the PMF minima. The collective variable associated with the unbound state corresponds to the distance at which the PMF is almost flat, namely zu = 11 Å for both systems. The PMF values corresponding to these collective variables are φ(zb) = −1.6 kcal mol−1 for Pd/EtOH and φ(zb) = −42 kcal mol−1 for Pd/OH−, while φ(zu) = 0 kcal mol−1 for both systems. The other quantity entering the adsorption free energy calculation is the probability density, ρ(zb), of finding the system at the chosen bound collective variable, zb, during the sampling of the bound state through an equilibrium MD simulation. MD simulations of the bound states led to ρ(zb) = 4.6 × 10−3 Å−3 and ρ(zb) = 1.9 × 10−3 Å−3 for Pd/OH− and Pd/EtOH systems, respectively. Given the quantities reported above, the adsorption free energy is computed as58
ΔGads = ϕ(zb) − ϕ(zu) +RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(ρ(zb)/C°) ln(ρ(zb)/C°) | (3) |
From the PMF curves shown in Fig. 5, we infer that the large difference in the stability of EtOH and OH−/OH may affect somehow the efficiency of a direct EtOH fuel cell. Specifically, the adsorption free energies of EtOH and OH− are expected to affect their optimal concentration ratio in solution, namely the concentration ratio providing the greatest efficiency of a fuel cell. To this regard, the effect of the concentration of the reactants on the direct EtOH fuel cell efficiency has been assessed experimentally. Liang et al.18 reported on the cyclic voltammetry measurements on an alkaline solution of EtOH upon varying, in turn, the concentrations of OH− and EtOH. Keeping fixed the concentration of KOH at 1 M, the oxidation current increases monotonically as the EtOH concentration increases from 0.25 to 2 M (at potentials smaller than −0.2 V; reference electrode Hg/HgO/KOH 1 M). At higher EtOH concentrations, specifically from 2 to 4 M, the electric current does not change significantly, showing an almost irrelevant decrease. On the basis of our results, the surface concentration of the OH species should be independent of the EtOH concentration in the solution, because of the large difference of the adsorption free energies of the two reactants. Therefore, on increasing the EtOH concentration, a greater quantity of EtOH can reach the electrode by simple diffusion, without affecting the surface concentration of OH. We notice that the low barrier observed in the PMF of Fig. 5A is not expected to slow down significantly the diffusion of EtOH towards the surface. Thus, the increasing delivery of EtOH to the surface yielded by the increase of concentration enhances the EOR rate, and hence the electric current. When the amount of EtOH at the electrode overcomes a given threshold, the EOR rate, and the electric current with it, becomes almost constant, because saturation of all active sites by OH and EtOH is reached.
On the other side, on fixing the EtOH concentration to 1 M, the electric current is found to increase as the KOH concentration increases from 0.01 to 1 M. In this case, in contrast to the trend observed by varying the EtOH concentration, a further increase in the OH− contents, specifically from 1 to 6 M, leads to a relevant electric current drop.18 We may argue that, at low OH− concentrations, an increase of concentration leads to an electric current growth because the added OH− are adsorbed and the amount of EtOH on the electrode is enough to allow the EOR to proceed quickly. Adsorption of OH− continues regularly by increasing its concentration owing to the large adsorption free energy and the low degree of surface coverage. Such a process is not affected by the presence of EtOH on the electrode, because of the large difference in the adsorption free energies of the two species. In this range of concentrations, EtOH is continuously replaced by OH−, while the EOR rate still continues to increase. The maximum electric current is reached at 1 M OH− concentration. Above this threshold, the coverage of the electrode by OH species is large enough to avoid a sufficient delivery of EtOH from the solution to the electrode. This replacement of EtOH in favor of OH species removes one reactant from the reaction environment, ultimately yielding an electric current drop.
3.3 Reaction pathways for H-atom abstraction of EtOH
The scenario emerging from the previous discussion highlights an unbalanced competition in the adsorption process completely in favor of the OH species against EtOH. This calls for an oxidation mechanism in which the reaction step leading from EtOH to CH3CHOH may not concern EtOH adsorbed species in the strict sense of the term, namely with the presence of a free energy well at the surface, but rather through a continuous delivery of EtOH from the solution to the surface according to a diffusive process. On such a basis, we suggest that the first H-atom abstraction step might take place without a really active participation of the catalyst on the side of EtOH. In this respect, assessing the propensity of eqn (2) in terms of mutual arrangement of the reactants and of the reactants with respect to the Pd surface can provide insightful information on the EOR mechanism.To study the possible EOR pathways and to obtain quantitative information on the energy barriers of the single reaction steps, including eqn (2), the most natural approach would be that of the minimum energy path. In this way, it is possible to obtain the energy profile as a function of some reaction coordinate, as well as the energies of reactants and products and those of the reaction intermediates.6,21 Here, we study the propensity of the reaction step of eqn (2) from the perspective of dynamical paths produced through ab initio MD simulations in which the reactants, specifically EtOH and OH, are arranged on the Pd surface according to the structural information obtained from the binding energy calculations of Section 3.1. Thus, the OH molecule is displaced almost parallel to the Pd(111) surface, while EtOH is oriented like in the EtOH-1 configuration shown in Fig. 1, with the hydroxyl H in the cis position with respect to the Cβ atom. One H atom, Hα, bonded to Cα points towards the O atom of OH, forming a Cα–Hα⋯O* angle of about 152 degrees (here and in the following the symbol * indicates that O belongs to the radical OH) and a Hα⋯O*–H angle of 92.4 degrees, much lower than the typical bonding angle of water. Several MD simulation paths have been realized as described in Section 2.1. The various paths differ only for the initial displacement of EtOH and OH. In particular, two generic initial configurations may differ for being the two reactants, considered as a unique assembly, rigidly shifted along the normal to the Pd(111) surface (vertical translation), and/or for being the EtOH molecule rigidly shifted along the Hα⋯O* direction, while keeping OH fixed (horizontal translation). Therefore, the paths are classified according to the initial values of the O*-surface distance (dv), denoting the vertical translation, and the Hα⋯O* distance (dh), denoting the horizontal translation. The dv distance can take discrete values from 1.8 to 3.3 Å, while dh can take discrete values from 1.5 to 1.9 Å. Smaller dh distances are not considered in this study to roughly preserve the individual molecular nature of the two reacting species in the initial state of the dynamical paths. The reference arrangement of the system, considered to build the initial configurations of the ab initio MD simulations, is shown in Fig. 6, together with the directions associated with the vertical and horizontal translations.
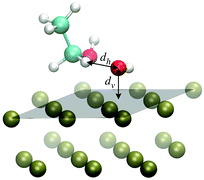 | ||
| Fig. 6 Arrangement of EtOH and OH over the Pd(111) surface adopted to build the initial configurations of the ab initio MD simulations. A system configuration is built by setting the distances dh and dv along the horizontal and vertical directions as indicated with left-right arrows. In particular, the molecules can be either shifted rigidly as a unique assembly along the normal to the surface by changing dv or the EtOH molecule can be rigidly shifted along the Hα⋯O* direction by changing dh, while keeping the OH molecule fixed. The reference plane taken to define the normal to the surface is drawn in gray transparency. The VMD program52 has been used for molecular graphics. | ||
We remark that, in all simulated reaction paths, the initial atomic velocities of EtOH and OH were set to zero without applying rescaling during the simulation. We point out that this kind of calculation is not addressed to quantify the energy barriers or to determine optimal reaction paths, but rather to evaluate if there is some evident dependence of the reactivity on the initial configuration, with special attention to the distance of the reactants from the catalyst.
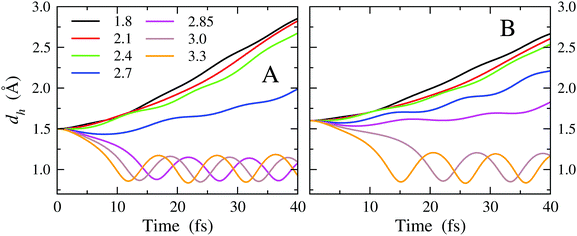
A total number of 35 MD trajectories have been carried out. For each trajectory, we have verified the occurrence of a reactive event leading to CH3CHOH and water, according to eqn (2). A trajectory is classified as reactive if the distance dh changes from the initial set value to values oscillating around 0.96 Å, namely the typical length of a covalent bond in water. As a confirmation criterion, we also checked the Hα⋯O*–H angle. When the reaction occurs, the angle is expected to vary from the initial value of 92.4 degrees to the typical bond angle of water. In this approach, the presence of an energy barrier is thus probed indirectly, evaluating the propensity of the reactants to form the products, upon enforcing initial molecular arrangements differing only in the dh and dv distances. A sort of bidimensional reaction map as a function of dh and dv, indicating when the reaction of eqn (2) takes place, is thus produced. The map is reported in Table 1. We remark that the simulation setup is not expected to be the optimal one to favor the reaction, neither in terms of structural arrangement nor in terms of atomic momenta, with the initial velocities of the reactants being set to zero. Hence, these results should be interpreted in a comparative fashion, trying to infer trends or systematic behaviors. First, we note that for dv = 1.8 Å, which almost corresponds to the distance of the binding-energy minimum of the Pd(111)/OH system and to the distance of the minimum PMF of the Pd(111)/OH− system (Fig. 5B), no reactive event is observed for all considered dh distances. It is worth noting that this behavior is common to all simulations performed with dv < 2.85 Å, namely distances to which OH is strongly bound to the surface. This means that, at short dv distances, an energy barrier, if any, should fall below dh = 1.5 Å. The data suggest that, when OH is strongly bound to the Pd surface, its reactivity against EtOH drops. This occurs because, in order to make OH available for reaction, energy should be spent to break the nearly covalent Pd–OH bond. Accordingly, for dv ≥ 2.85 Å, namely when the surface-OH bonding is weaker, reactive events are observed also for dh distances greater than 1.5 Å (see Table 1). For dv = 3.3 Å, the reaction is barrier-less even for dh = 1.8 Å. Here, we recall that O⋯H distances around 1.8 Å are typical of H-bonding. Therefore, considering that effective impacts in a chemical reaction are those for which the components of the atomic velocities along the collision direction are relevant and that, in our simulations, the initial velocities of EtOH and OH atoms are set to zero, the reactive events observed even at small dh may indicate a large propensity of the chemical reaction under consideration.
The general enhancement of the reactivity of OH vs. EtOH in consequence of an increase of the dv distance (and hence a weakening of the surface-OH bonding) inferred from the reaction map of Table 1 is more evident on inspecting the time dependence of the dh distance. In Fig. 7A and B, we report dh as a function of time obtained from MD simulations in which the initial value of dh is set to 1.5 and 1.6 Å, respectively (data obtained for dh = 1.7, 1.8 and 1.9 Å are reported in Fig. S5 of the ESI†). The curves obtained for all dv are drawn.
The trajectories leading to a reactive event are evident, as the dh distance shifts in a few fs from the initial value to values ranging around ∼1 Å, i.e., the typical covalent bond distance in water. Here, it is interesting to note that the oscillating behavior is reached earlier in simulations starting from larger dv, indicating greater reactivity when the surface-OH bonding is weaker. Vice versa, when the surface-OH bonding becomes stronger, which occurs by lowering dv, the MD trajectories appear gradually less reactive and the dh distance drifts towards large values.
Now the question is: why should the OH molecules strongly bonded to the Pd surface enter H-atom abstraction rather than remain peacefully bonded to the surface? To this regard, one should take into account that adsorbed OH are distributed at distances z from the surface according to a probability density dependent on the PMF as a function of z. The probability of finding a molecule at a distance z∈ [a,b] from the surface can be estimated through the relationship
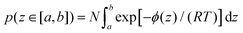 | (4) |
The same approach adopted for evaluating Pu/Pb provides a rough estimate of the ratio between reactive (weakly-bonded) and non-reactive (strongly-bonded) OH molecules according to the reaction of eqn (2). For this calculation, we should use, in principle, the PMF related to the Pd(111)/OH system, which is however unavailable. As a first approximation, we can resort, instead, to the PMF obtained for the Pd(111)/OH− system. On the basis of the simulated reaction paths (Table 1), we note that a reactive event may occur when the distance of the OH from the Pd surface is greater than the PMF-minimum distance, that is ∼2 Å. Therefore, indicating zreact as the distance threshold above which a OH becomes reactive, the probability of a bonded OH to be reactive is P(zreact) = p(z∈ [zreact,4])/p(z∈ [0,4]). Of course, such a probability depends critically on the threshold distance zreact. From our reaction paths (Table 1), we can roughly locate zreact between 2 and 2.85 Å; perhaps, zreact = 2.5 Å would be an effective value. In such a case, the probability of observing a reactive bonded molecule ranges from P(zreact = 2) ≃ 0.5 to P(zreact = 2.85) ≃ 10−15, with P(zreact = 2.5) ≃ 10−6. Such a value reveals that only a small amount of adsorbed OH could really be involved in reactive events. However, this is probably an underestimate, as we evaluated reactive paths (Table 1) through simulations enforcing suboptimal and hence unfavorable setup (think, for example, the initial atomic velocities which are zero).
4 Concluding remarks
The EOR catalyzed by Pd in alkaline media occurs through a sequence of reaction steps in which OH plays a fundamental role. In this study, we investigate the first step of the EOR, namely eqn (2), by means of quantum and molecular mechanical calculations. The effect of solvation on the adsorption of OH− and EtOH on the Pd surface has been investigated as well. We have found that both anion and radical OH are strongly adsorbed on the electrode, guaranteeing a significant surface coverage in this reactant. In contrast, EtOH, despite a non-negligible adsorption free energy under vacuum, shows a very modest affinity with the surface when solvation is accounted for. This implies that the role played by adsorbed EtOH could be almost irrelevant in the EOR, at least from the point of view of thermodynamics, thus suggesting that the electrode coverage in EtOH is dominated by diffusion processes. This picture is consistent with cyclic voltammetry measurements performed at different concentrations of EtOH and OH−. Furthermore, we have observed that the rate of the reaction step of eqn (2) depends critically on the distance of EtOH and OH from the Pd surface. In particular, we noted a rate enhancement when the distance of the two reactants from the surface increases and hence the adsorption strength, especially that of OH, decreases.The picture emerging from our study is that of an electrode surface rich in the OH species, owing to the large adsorption free energy, but only a small amount of them, specifically those weakly bound to the surface, are really active in the EOR. The concept that optimal performances of an electrocatalyst are obtained from a subtle balance between the requirements of having significant interactions between the reacting species and the electrode to allow electron transfer and of not having a really strong interaction with the electrode itself in order to make such species available for the reaction is not new in electrocatalysis. This is, for example, in close correlation with the volcano-type relationship existing between the exchange current density of the H evolution reaction on monometallic surfaces in alkaline media and the H binding energy on the metal.60,61 The aspect common to volcano-type relationships and our mechanism is that an excess binding energy might lead to a sort of passivation of the catalyst, making the adsorbed reactants not available for the reaction. The idea that the adsorption energy of the reactants can be used to identify the activity of electrocatalysts, not only in an average way, as revealed by volcano-type relationships,60 but also in a detailed way within a distribution of adsorbed molecules, as observed in the present study, suggests that the exchange current density could be tuned by modifying the surface chemical properties through, for example, the introduction of properly designed co-catalysts.10–15
Abbreviations
| EtOH | ethanol. |
| EOR | ethanol oxidation reaction. |
| MD | molecular dynamics. |
| DFT | density functional theory. |
| PMF | potential of mean force. |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Authors thank Prof. Gianni Cardini for helpful discussions. The research was realized within a PRIN 2017 Project funded by the MIUR-Italy (Grant No. 2017YH9MRK). We acknowledge the CINECA award under the ISCRA initiative, for the availability of high performance computing resources and support. We also acknowledge the support by the “Progetto Dipartimenti di Eccellenza 2018–2022” allocated to Department of Chemistry “Ugo Schiff” of the University of Florence.Notes and references
- L. An, T. S. Zhao and Y. S. Li, Renewable Sustainable Energy Rev., 2015, 50, 1462–1468 CrossRef CAS.
- S. Zhang, Y. Shao, G. Yin and Y. J. Lin, J. Mater. Chem. A, 2013, 1, 4631–4641 RSC.
- A. Heinzel, M. Cappadonia, U. Stimming, K. V. Kordesch and J. C. Tambasco de Oliveira, Ullmanns Encyclopedia of Industrial Chemistry, Wiley-VCH; Weinheim, Germany, 2010 Search PubMed.
- E. Antolini and E. R. Gonzalez, J. Power Sources, 2010, 195, 3431–3450 CrossRef CAS.
- E. A. Monyoncho, T. K. Woo and E. A. Baranova, Electrochemistry, 2019, 15, 1–57 CAS.
- E. A. Monyoncho, S. N. Steinmann, C. Michel, E. A. Baranova, T. K. Woo and P. Sautet, ACS Catal., 2016, 6, 4894–4906 CrossRef CAS.
- U. Martinez, A. Serov, M. Padilla and P. Atanassov, ChemSusChem, 2014, 7, 2351–2357 CrossRef CAS.
- F. P. Hu, C. L. Chen, Z. Y. Wang, G. Y. Wei and P. K. Shen, Electrochim. Acta, 2006, 52, 1087–1091 CrossRef CAS.
- P. K. Shen and C. W. Xu, Electrochem. Commun., 2006, 8, 184–188 CrossRef CAS.
- V. S. Pinheiro, F. M. Souza, T. C. Gentil, L. S. Parreira, B. L. Batista and M. C. Santos, Int. J. Hydrogen Energy, 2021, 46, 15896–15911 CrossRef CAS.
- M. Bellini, M. V. Pagliaro, A. Marchionni, J. Filippi, H. A. Miller, M. Bevilacqua, A. Lavacchi, W. Oberhauser, J. Mahmoudian, M. Innocenti, P. Fornasiero and F. Vizza, Inorg. Chim. Acta, 2021, 518, 120245 CrossRef CAS.
- G. Lu, H. Zheng, J. Lv, G. Wang and X. Huang, J. Power Sources, 2020, 480, 229091 CrossRef CAS.
- F. Wang, H. Yu, Z. Tian, H. Xue and L. Feng, J. Energy Chem., 2018, 27, 395–403 CrossRef.
- E. A. Monyoncho, S. Ntais, N. Brazeau, J.-J. Wu, C.-L. Sun and E. A. Baranova, ChemElectroChem, 2016, 3, 218–227 CrossRef CAS.
- V. Bambagioni, C. Bianchini, Y. Chen, J. Filippi, P. Fornasiero, M. Innocenti, A. Lavacchi, A. Marchionni, W. Oberhauser and F. Vizza, ChemSusChem, 2012, 5, 1266–1273 CrossRef CAS PubMed.
- Z.-Y. Zhou, Q. Wang, J.-L. Lin, N. Tian and S.-G. Sun, Electrochim. Acta, 2010, 55, 7995–7999 CrossRef CAS.
- X. Fang, L. Wang, P. K. Shen, G. Cui and C. Bianchini, J. Power Sources, 2010, 195, 1375–1378 CrossRef CAS.
- Z. X. Liang, T. S. Zhao, J. B. Xu and L. D. Zhu, Electrochim. Acta, 2009, 54, 2203–2208 CrossRef CAS.
- E. D. Wang, J. B. Xu and T. S. Zhao, J. Phys. Chem. C, 2010, 114, 10489–10497 CrossRef CAS.
- T. Sheng, W.-F. Lin, C. Hardacre and P. Hu, J. Phys. Chem. C, 2014, 118, 5762–5772 CrossRef CAS.
- G. Cui, S. Song, P. K. Shen, A. Kowal and C. Bianchini, J. Phys. Chem. C, 2009, 113, 15639–15642 CrossRef CAS.
- M. Li, W. Guo, R. Jiangs, L. Zhao and H. Shan, Langmuir, 2010, 26, 1879–1888 CrossRef CAS.
- W. Guo, M. Li, X. Lu, H. Zhu, Y. Li, S. Li and L. Zhao, Dalton Trans., 2013, 42, 2309–2318 RSC.
- J. E. Sutton and D. G. Vlachos, Ind. Eng. Chem. Res., 2015, 54, 4213–4225 CrossRef CAS.
- H.-F. Wang and Z.-P. Liu, J. Am. Chem. Soc., 2008, 130, 10996–11004 CrossRef CAS PubMed.
- H.-F. Wang and Z.-P. Liu, J. Phys. Chem. C, 2007, 111, 12157–12160 CrossRef CAS.
- R. Kavanagh, X.-M. Cao, W. Lin, C. Hardacre and P. Hu, J. Phys. Chem. C, 2012, 116, 7185–7188 CrossRef CAS.
- S. A. Akhade, N. Singh, O. Y. Gutiérrez, J. Lopez-Ruiz, H. Wang, J. D. Holladay, Y. Liu, A. Karkamkar, R. S. Weber, A. B. Padmaperuma, M.-S. Lee, G. A. Whyatt, M. Elliott, J. E. Holladay, J. L. Male, J. A. Lercher, R. Rousseau and V.-A. Glezakou, Chem. Rev., 2020, 120, 11370–11419 CrossRef CAS.
- C. J. Bodenschatz, S. Sarupria and R. B. Getman, J. Phys. Chem. C, 2015, 119, 13642–13651 CrossRef CAS.
- T. Xie, S. Sarupria and R. B. Getman, Mol. Simul., 2017, 43, 370–378 CrossRef CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- J. W. Arblaster, Platinum Met. Rev., 2012, 56, 181–189 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- R. Chelli, J. Chem. Theory Comput., 2010, 6, 1935–1950 CrossRef CAS.
- R. Chelli and G. F. Signorini, J. Chem. Theory Comput., 2012, 8, 830–842 CrossRef CAS.
- M. R. Shirts and J. D. Chodera, J. Chem. Phys., 2008, 129, 124105 CrossRef.
- A. D. MacKerell Jr., D. Bashford, M. Bellott, R. L. Dunbrack Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T.-K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef.
- H. J.-C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- A. de Oliveira Cavalcante and R. Chelli, J. Mol. Liq., 2021, 332, 115839 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- M. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001 CrossRef CAS.
- S. Marsili, G. F. Signorini, R. Chelli, M. Marchi and P. Procacci, J. Comput. Chem., 2010, 31, 1106–1116 CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- P. Tereshchuk and J. L.-F. Da Silva, J. Phys. Chem. C, 2012, 116, 24695–24705 CrossRef CAS.
- H. Li and G. Henkelman, J. Phys. Chem. C, 2017, 121, 27504–27510 CrossRef CAS.
- P. A. Redhead, Vacuum, 1962, 12, 203–211 CrossRef CAS.
- Y. Cao and Z.-X. Chen, Surf. Sci., 2006, 600, 4572–4583 CrossRef CAS.
- C. Bianchini and P. K. Shen, Chem. Rev., 2009, 109, 4183–4206 CrossRef CAS.
- E. Giovannelli, P. Procacci, G. Cardini, M. Pagliai, V. Volkov and R. Chelli, J. Chem. Theory Comput., 2017, 13, 5874–5886 CrossRef CAS PubMed.
- E. Giovannelli, M. Cioni, P. Procacci, G. Cardini, M. Pagliai, V. Volkov and R. Chelli, J. Chem. Theory Comput., 2017, 13, 5887–5899 CrossRef CAS PubMed.
- W. Sheng, M. Myint, J. G. Chen and Y. Yan, Energy Environ. Sci., 2013, 6, 1509–1512 RSC.
- J. Zheng, J. Nash, B. Xu and Y. Yan, J. Electrochem. Soc., 2018, 165, H27–H29 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00909a |
| This journal is © the Owner Societies 2022 |