Open Access Article
Open Access ArticleMolecular interactions in diffusion-controlled aldol condensation with mesoporous silica nanoparticles†
Yu Lim
Kim
ab,
James W.
Evans
ac and
Mark S.
Gordon
 *ab
*ab
aAmes Laboratory – US Department of Energy, Iowa State University, Ames, Iowa 50011, USA
bDepartment of Chemistry, Iowa State University, Ames, Iowa 50010, USA
cDepartment of Physics, Iowa State University, Ames, Iowa 50011, USA
First published on 11th April 2022
Abstract
The aldol reaction of p-nitrobenzaldehyde in amino-catalyzed mesoporous silica nanoparticles (MSN) has revealed varying catalytic activity with the size of the pores of MSN. The pore size dependence related to the reactivity indicates that the diffusion process is important. A detailed molecular-level analysis for understanding diffusion requires assessment of the noncovalent interactions of the molecular species involved in the aldol reaction with each other, with the solvent, and with key functional groups on the pore surface. Such an analysis is presented here based upon the effective fragment potential (EFP). The EFP method can calculate the intermolecular interactions, decomposed into Coulomb, polarization, dispersion, exchange-repulsion, and charge-transfer interactions. In this study, the potential energy surfaces corresponding to each intermolecular interaction are analyzed for homo- and hetero-dimers with various configurations. The monomers that compose dimers are five molecules such as p-nitrobenzaldehyde, acetone, n-hexane, propylamine, and silanol. The results illustrate that the dispersion interaction is crucial in most dimers.
1 Introduction
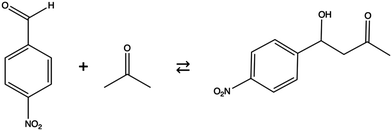
Mesoporous silica nanoparticles (MSNs) have been found to catalyze various chemical reactions selectively. The selectivity of this silica system is a result of the different types of functional groups available to be attached inside MSNs.1,2 Catalytic properties including selectivity of these nanostructured silica systems are determined by geometric features such as narrow pores and high surface areas, as well as by the formation of covalent and noncovalent interactions between reactant molecules and functional groups. In addition, it is possible to synthesize different MSN pore sizes. Other advantages of MSNs are stability and rigidity since they are resistant to heat, mechanical stress, and variations in pH.3 Therefore, MSNs are promising as heterogeneous catalysts that are selective and reusable.4Aldol condensation (See Scheme 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5–9) has been an important target for catalysis since this reaction forms new carbon–carbon bonds.10–14 To catalyze this reaction, aminoalkyls are commonly used as active sites on various kinds of heterogeneous catalysts.15–19 In a paper by Kandel et al.,5n-propylamine attached to MSNs (AP-MSNs) was used as a heterogeneous catalyst for the aldol reaction with p-nitrobenzaldehyde (PNB) and acetone as reactants in hexane solvent (Scheme 1). The heterogeneous reaction with a primary amine as the main catalyst was carried out for different MSN pore sizes. The reaction rate with the AP-MSN catalyst in hexane increases by 20 times when the pore diameter increases from 2.8 nm to 3.6 nm. This dramatic variation in reaction yield has been interpreted based upon infrared and NMR spectra suggesting that the Schiff-base formation between PNB and the aminopropyl group inhibits the aldol reaction. Therefore, the effective MSN diameter becomes smaller than 2.8 nm. This suggests that the diffusion of various species within the pore plays an important role in the catalytic process since the reactivity depends on the pore size. The initiation of a target reaction requires that reactant molecules diffuse inside the pore to active sites. In addition, multiscale modeling of the dependence of reactivity on the pore size of MSN reveals a strong impact of inhibited passing of the reactant and product inside the pore.20
5–9) has been an important target for catalysis since this reaction forms new carbon–carbon bonds.10–14 To catalyze this reaction, aminoalkyls are commonly used as active sites on various kinds of heterogeneous catalysts.15–19 In a paper by Kandel et al.,5n-propylamine attached to MSNs (AP-MSNs) was used as a heterogeneous catalyst for the aldol reaction with p-nitrobenzaldehyde (PNB) and acetone as reactants in hexane solvent (Scheme 1). The heterogeneous reaction with a primary amine as the main catalyst was carried out for different MSN pore sizes. The reaction rate with the AP-MSN catalyst in hexane increases by 20 times when the pore diameter increases from 2.8 nm to 3.6 nm. This dramatic variation in reaction yield has been interpreted based upon infrared and NMR spectra suggesting that the Schiff-base formation between PNB and the aminopropyl group inhibits the aldol reaction. Therefore, the effective MSN diameter becomes smaller than 2.8 nm. This suggests that the diffusion of various species within the pore plays an important role in the catalytic process since the reactivity depends on the pore size. The initiation of a target reaction requires that reactant molecules diffuse inside the pore to active sites. In addition, multiscale modeling of the dependence of reactivity on the pore size of MSN reveals a strong impact of inhibited passing of the reactant and product inside the pore.20
In addition, the silanol group from the surface of MSN plays an important role in supporting the catalytic effect by allowing proton transfer and providing the binding sites. Since solvent and reactant species attach to the MSN pore walls, the effective pore diameter is reduced relative to the measured pore size, as already noted above. For example, Schiff-base formation at the pore walls reduces the effective pore diameter by ∼1.5 nm.20 Even though the lengths of PNB reactant and the aldol product, about ∼1 nm, are smaller than the pore diameter, the pore size is too narrow for the product to pass reactant to exit the pore.20 Therefore, the molecular interactions between the main components during the reaction are therefore essential and necessary in all these processes. Consequently, the investigation of molecular interactions is fundamental, especially on the diffusion process which must have occurred before the complex catalytic chemical reaction.
Noncovalent interactions are important in chemistry, materials, and biology. For instance, noncovalent interactions contribute to the helical structure of DNA, they are a key factor for drug delivery, and they play a role in the secondary structure of proteins.21–23 In addition, nanomaterial self-assembly designs24,25 and some chemical reactions26,27 are affected by noncovalent interactions. For example, noncovalent interactions have been important in activating and controlling asymmetric catalysis such as the oxazaborolidine-catalyzed reactions28 and Noyori transfer hydrogenation29,30 The role of dispersion on structure stability has been reviewed in relation to chemical reactivity and catalysis.31 Furthermore, in condensed phases like liquids, noncovalent interactions largely determine the properties of the liquid, such as the density and the diffusion constant. Intermolecular interactions can also contribute to the reaction rate of a chemical reaction such as lowering the energy of transition states. Therefore, the investigations of noncovalent interactions are important for understanding diffusion mechanisms especially for narrow pore sizes.
This work is motivated by the role that noncovalent interactions, on the order of 10 kcal mol−1 or less, can play in the diffusion which has an impact on catalytic processes of reactants in solvent systems inside MSN pores, since the reactant, solvent, and product molecules must enter and move through the narrow pore to initiate the chemical reaction. It is therefore important to investigate the noncovalent intermolecular interactions between reactants, solvents, and MSN since diffusion is largely governed by intermolecular interactions. In this paper, the molecular interactions are examined between pairs of molecules that play a role in the diffusion processes in mesoporous silica nanoparticles rather than the effects of the pore structure. During diffusion, all molecules must move along the pore. Thus, a systematic analysis of the consequent intermolecular interactions is needed.
To examine the role of noncovalent interactions, it is necessary to investigate the full range of types of such interactions, including Coulomb (Coul), polarization/induction (pol), dispersion (disp), charge transfer (ct), and exchange repulsion (exrep). Each of these types of interaction can be important, depending on the types of molecules that are involved. For example, nucleotide bases can interact through strong hydrogen bonding interactions that are largely driven by electrostatic or via dispersion interactions that occur due to π stacking orientations.
The accurate analysis of noncovalent interactions is not trivial in computational chemistry. In general, a high level of ab initio electronic structure theory, for example, second-order perturbation theory (MBPT2) or coupled-cluster (CC) theory, is required. Symmetry adapted perturbation theory (SAPT)32,33 provides important insights into noncovalent interactions. However, all of these methods have unfortunate scaling (N5–N7) with system size and are therefore limited to systems of modest size. An appealing alternative is the effective fragment potential (EFP) method,34 a model potential that is derived entirely from first principles and which has been shown to provide intermolecular interaction energies that are comparable in accuracy to those obtained from second-order perturbation theory and coupled cluster [CCSD(T)] theory.35 Most dispersion-corrected density functional theory (DFT) methods are based on empirical components such as DFT-D3 that provide little insight. Even though there are nonempirical dispersion corrections for the DFT method such as vdW-DF, those methods need to be improved to describe intermolecular interactions.36 On the contrary, the main characteristic of the EFP method is that the EFP parameters are generated from first principles. The DLPNO-CCSD(T) is very promising since it scales comparably to DFT. However, the EFP method is orders of magnitude more computationally efficient than DFT.37 Slipchenko et al. have demonstrated, for example, that the EFP interaction energy of stacked benzene dimers is in good agreement with the interaction energies obtained from CCSD(T)/aug-cc-pVQZ calculations and that the decomposition of the interaction energies into their components are in reasonable agreement with SAPT.38 The EFP method has been applied to a broad range of noncovalent complexes, including DNA base pairs,39 dimers of substituted benzenes,40 water–benzene complexes,41 water–amino acid complexes42–44 and the S22 test set.45
The EFP interaction energy can be written as46,47
| EEFP = ECoul + Epol + Edisp + Eexrep + Ect |
Each energy term is divided into two groups depending on the interaction distance. The Coulomb, polarization, and dispersion terms have an R−n dependence and are long-range interactions, while the exchange repulsion and charge transfer terms are short-range interactions. The Coulomb potential is modeled with a distributed multipolar analysis (DMA),48 expanded through octopoles with expansion points located at each bond midpoint and nuclear center. The polarization interaction energy is formulated with localized molecular orbital (LMO) polarizability tensors and is iterated to self-consistency, thereby capturing many-body effects. The dispersion interaction between induced multipoles is calculated using LMO frequency-dependent polarizabilities in imaginary space.49,50 The exchange-repulsion term is expressed as a power series expansion in the intermolecular overlap. The intermolecular charge transfer term is derived using second order perturbation theory based on the interaction between the occupied orbitals on one fragment and the virtual orbitals on another fragment.47,51 The Coulomb, polarization, and dispersion terms are all damped in order to account for the use of semiclassical approximations.52 Because the EFP method has been shown to provide accurate intermolecular interaction energies, it is an attractive approach to analyze such interactions in terms of the component contributions summarized above.
This study investigates the interaction energies between the various molecules involved in the aldol reaction in mesoporous silica nanoparticles using the EFP method. This investigation provides chemical insights into the nature of the intermolecular interactions which control the diffusion-mediated aldol reaction in MSN, including the analysis of the relative importance of the five components of the interaction energy.
2 Computational details
All calculations have been performed with the quantum chemistry program GAMESS.53 The reactant molecules in the aldol reaction in the MSN pore are p-nitrobenzaldehyde (PNB) and acetone. A mixture of n-hexane (henceforth described as hexane) and acetone constitutes the solvent in the reaction. In this study, n-propylamine is used to represent the functional group attached to the MSN pore surface that acts as the catalyst. Also, silanol (SiH3OH) represents the silanol groups that also populate the MSN pore surface. Since this study represents the MSN model as the small molecule silanol, the pore itself is not explicitly included, so definitive conclusions regarding the impact of the pore cannot be drawn based on the calculations reported here. The analysis in this contribution will assess interactions between reactant and solvent molecules, as well as interactions between PNB and the species representing functional groups on the MSN pore surface. For each dimer combination, the decomposed molecular interactions will be discussed in the next section. Each molecule is optimized using the MP2/6-311++G(2d,2p) level of theory, and each molecule geometry is described in Fig. 1. For each monomer, stationary points were confirmed to be minima on the respective potential energy surfaces by calculating and subsequently diagonalizing the matrix of energy second derivatives (Hessians).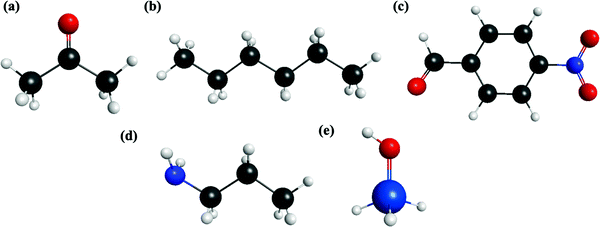 | ||
| Fig. 1 EFP monomer molecular geometry. (a) Acetone (b) hexane (c) p-nitrobenzaldehyde (PNB) (d) propylamine (e) silanol (SiH3OH). | ||
To generate the EFP parameters, the Pople basis set 6-311++G(3df,2p) is employed in the MAKEFP code in GAMESS at each optimized monomer geometry. The potential energy curve as a function of the distance between two of these molecules is performed by the EFP method using the internal geometries determined with MP2/6-311++G(2d,2p). The intermolecular distance is defined as the distance between the centers of mass of the two molecules except for parallel-displaced configurations. Since parallel-displaced arrangements have two different directions due to the nonsymmetrical geometry of each dimer, the intermolecular distances have positive or negative directions, which are explained in detail in each dimer Discussion section. All monomers have fixed internal coordinates during the EFP calculations. EFP single point dimer energies with fixed internal monomer geometries were calculated to generate the corresponding potential energy curves. The EFP interaction energy is obtained as the energy difference between dimer and two monomers. Multiple orientations of the molecular pairs were considered, and both homo-molecular and hetero–molecular pairs have been investigated. Since it is desirable to maintain each type of dimer arrangement (e.g., parallel displaced, T-shape), the EFP geometries are not fully optimized. The total EFP interaction energies are compared with the CCSD(T)/6-311++G(d,p) values at each minimum energy EFP geometry for each dimer. At the minimum energy on each EFP dimer potential energy curve, CCSD(T)/6-311++G(d,p) single point energy calculations were performed for comparison and the CCSD(T) intermolecular interaction energy is calculated by subtracting the two monomer energies from a dimer energy. The dimer geometries for the CCSD(T) calculations are obtained from the minimum energy structure on the EFP potential energy surface.
3 Results and discussion
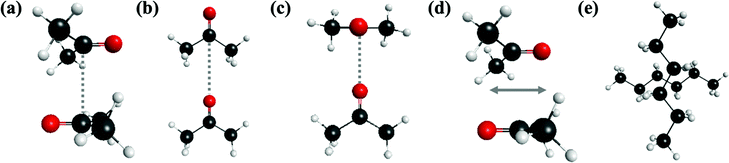
Diffusion of the reactant molecules (e.g., PNB and acetone) inside the MSN pore in the presence of a solvent is an important aspect of the catalyzed aldol reaction. Therefore, it is important to investigate the noncovalent intermolecular interactions of pairs of the molecules that are present in the pore. In the following subsections, the interactions between pairs of the same molecule (homo–molecular interactions) and between pairs of different molecules (hetero–molecular interactions) are considered.For the investigation of the accuracy of the EFP interaction energy, the total EFP dimer interaction energies are compared with the CCSD(T)/6-311++G(d,p) values for all molecular dimers in Table 1. The corresponding multiple dimer configurations are described in Fig. 2 using acetone dimer as an example. In the sandwich configuration illustrated in Fig. 2(a), there are two possible arrangements: In one of these (denoted trans-sandwich), the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups are oriented trans to each other; in the other, (denoted cis-sandwich) the two C
O groups are oriented trans to each other; in the other, (denoted cis-sandwich) the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups are oriented cis to each other. For the collinear configuration shown in Fig. 2(b), the C
O groups are oriented cis to each other. For the collinear configuration shown in Fig. 2(b), the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups in the two monomers are collinear with each other with their dipole moments aligned. For the T-shaped configuration in Fig. 2(c), the planes of the heavy atom backbones in the two molecules are orthogonal to each other. In the parallel-displaced configuration (Fig. 2(d)), one of the two molecules in a trans-sandwich arrangement has slipped relative to the other. The sandwich, T-shaped, and parallel-displaced configurations are similar to the analogous structures in, for example, the benzene dimer.40 Further details on specific dimers are described in later sections. To demonstrate the accuracy of the EFP interaction energies, the mean unsigned errors and the RMS errors for EFP relative to CCSD(T) are 0.8 kcal mol−1 and 1.0 kcal mol−1, respectively. In addition, the EFP energy order of the isomers for a given dimer pair reproduces the CCSD(T) order in most dimer pairs. This good agreement provides confidence in the reliability of the EFP method for assessing intermolecular interaction energies. One exception is the hexane homo-molecular dimer for which the EFP and CCSD(T) energy order differs. The largest absolute differences in interaction energies between EFP and CCSD(T) are 2–3 kcal mol−1. For acetone–acetone dimers, EFP generally overestimates the interaction energies compared to CCSD(T). This tendency is also observed for acetone–silanol dimer pairs. Overall, the EFP interaction energies are in good agreement with those obtained using CCSD(T).
O groups in the two monomers are collinear with each other with their dipole moments aligned. For the T-shaped configuration in Fig. 2(c), the planes of the heavy atom backbones in the two molecules are orthogonal to each other. In the parallel-displaced configuration (Fig. 2(d)), one of the two molecules in a trans-sandwich arrangement has slipped relative to the other. The sandwich, T-shaped, and parallel-displaced configurations are similar to the analogous structures in, for example, the benzene dimer.40 Further details on specific dimers are described in later sections. To demonstrate the accuracy of the EFP interaction energies, the mean unsigned errors and the RMS errors for EFP relative to CCSD(T) are 0.8 kcal mol−1 and 1.0 kcal mol−1, respectively. In addition, the EFP energy order of the isomers for a given dimer pair reproduces the CCSD(T) order in most dimer pairs. This good agreement provides confidence in the reliability of the EFP method for assessing intermolecular interaction energies. One exception is the hexane homo-molecular dimer for which the EFP and CCSD(T) energy order differs. The largest absolute differences in interaction energies between EFP and CCSD(T) are 2–3 kcal mol−1. For acetone–acetone dimers, EFP generally overestimates the interaction energies compared to CCSD(T). This tendency is also observed for acetone–silanol dimer pairs. Overall, the EFP interaction energies are in good agreement with those obtained using CCSD(T).
| Dimer | Geometry | CCSD(T)/6-311++G(d,p) | EFP |
|---|---|---|---|
| Acetone–acetone | trans-Sandwich | −5.7 | −8.4 |
| Linear | −2.5 | −3.5 | |
| T-shaped | −3.0 | −2.8 | |
| Parallel-displaced | −6.6 | −8.9 | |
| Acetone–amine | trans-Sandwich | −2.5 | −2.2 |
| Linear | −1.5 | −1.4 | |
| Parallel-displaced | −3.2 | −2.9 | |
| Acetone–silanol | trans-Sandwich | −2.8 | −3.5 |
| Linear | −2.5 | −3.3 | |
| T-shaped | −1.3 | −1.6 | |
| Parallel-displaced | −3.5 | −4.0 | |
| Acetone–hexane | Sandwich | −3.1 | −3.2 |
| Linear (1) | −1.8 | −1.6 | |
| Linear (2) | −1.4 | −1.0 | |
| Hexane–hexane | Sandwich | −3.9 | −3.8 |
| Cross | −4.4 | −3.0 | |
| T-shaped | −1.9 | −1.7 | |
| Hexane–amine | Sandwich | −3.6 | −4.0 |
| Hexane–silanol | Sandwich | −2.5 | −1.9 |
| T-shaped | −2.3 | −2.3 | |
| PNB–acetone | trans-Sandwich | −5.4 | −4.7 |
| cis-Sandwich | −4.4 | −3.1 | |
| Linear | −2.3 | −2.9 | |
| Parallel-displaced | −5.8 | −6.1 | |
| PNB–hexane | Sandwich | −7.3 | −6.6 |
| Cross | −6.5 | −3.9 | |
| T-shaped | −3.2 | −3.0 | |
| Parallel-displaced | −7.4 | −6.6 | |
| PNB–amine | trans-Sandwich | −5.0 | −3.5 |
| cis-Sandwich | −4.6 | −3.4 | |
| Linear | −1.1 | −0.6 | |
| Parallel-displaced | −5.6 | −5.0 | |
| PNB–PNB | trans-Sandwich | −9.6 | −8.7 |
| cis-Sandwich | −6.7 | −5.6 | |
| T-shaped | −5.4 | −3.4 | |
| Parallel-displaced | −10.3 | −10.0 | |
| PNB–silanol | trans-Sandwich | −4.0 | −3.3 |
| cis-Sandwich | −3.9 | −3.2 | |
| Linear (1) | −1.8 | −2.4 | |
| Linear (2) | −1.1 | −1.6 | |
| T-shaped | −2.0 | −1.7 |
3.1 Homo-molecular interactions
Three different types of homo-molecular dimers are investigated for acetone, hexane, and PNB which are the main reactant and solvent molecules. In the present work, silanol is used as a model for the MSN. Because siloxy groups are part of the pore, not detached molecules inside the pore, the silanol homo-molecular dimer is not considered here. The main catalyst group, n-aminopropyl, is covalently bound inside the MSN pore. Likewise, propylamine is represented as an n-aminopropyl group only for hetero–molecular dimers.Table 2 shows the components of the EFP interaction energies for the four acetone dimer configurations. Fig. 3 illustrates the potential energy surface for each arrangement. The trans-sandwich geometry has the acetone dimer ketone groups in a trans arrangement. This arrangement is electrostatically preferable to the aligned (cis) orientation due to the alignment of the monomer dipole moments. At the equilibrium geometry, the dispersion and Coulomb terms are the dominant interactions, both contributing ∼−7 kcal mol−1 to the net EFP interaction energy. The vertical intermolecular distance between monomers of the trans-sandwich geometry is 3.2 Å at the equilibrium point,37 in good agreement with the lowest energy geometry predicted by the MP2 level of theory.54 The potential energy surface of the antiparallel sandwich geometry in ref. 48 was investigated with MP2/6-31G(d) by moving the coordinates of the internally fixed acetone monomer relative to the second acetone molecule. At the most stable configuration of that study, the interaction energy is −4.85 kcal mol−1 when the acetone monomers are 3.2 Å apart. This MP2 interaction energy is about 1 kcal mol−1 smaller than the CCSD(T) value shown in Table 1. In the linear configuration, the Coulomb interaction is a bit larger in magnitude than is dispersion (∼−4 vs. ∼−2 kcal mol−1). The distance between the monomers in the linear arrangement is considerably larger than that in the trans-sandwich dimer. Consequently, the net EFP interaction energy is smaller in the linear isomer. In the T-shaped geometry, the Coulomb and dispersion interaction energies are similar to each other, ∼−3 kcal mol−1, again with a smaller net EFP interaction energy than in the trans-sandwich structure and comparable to that of the linear isomer. At the trans-sandwich configuration, since one oxygen atom forms a hydrogen bond with two hydrogen atoms on the other molecule, the acetone dimer stays in the equilibrium structure due to the presence of four hydrogen bonds. Therefore, the trans-sandwich alignment is the second lowest energy configuration among the acetone homo dimers. Only the parallel-displaced geometry has a stronger interaction.
| Distance (Å) | Coulomb (kcal mol−1) | Polarization (kcal mol−1) | Dispersion (kcal mol−1) | Exchange-repulsion (kcal mol−1) | Charge transfer (kcal mol−1) | Total EFP energy (kcal mol−1) | |
|---|---|---|---|---|---|---|---|
| Acetone dimer | |||||||
| trans-Sandwich | 3.2 | −7.0 | −0.9 | −7.2 | 6.9 | −0.3 | −8.4 |
| Linear | 4.9 | −3.7 | −0.6 | −2.1 | 3.0 | −0.0 | −3.5 |
| T-shaped | 4.2 | −2.7 | −0.7 | −2.5 | 3.1 | 0.0 | −2.8 |
| Parallel-displaced | −1.3 | −7.0 | −1.0 | −6.4 | 5.7 | −0.2 | −8.9 |
| Hexane dimer | |||||||
| Sandwich | 4.1 | −1.3 | 0.0 | −6.0 | 3.7 | 0.0 | −3.8 |
| Cross | 3.9 | −0.9 | 0.0 | −5.4 | 3.3 | 0.0 | −3.0 |
| T-shaped | 7.0 | −0.8 | 0.0 | −2.5 | 1.6 | 0.0 | −1.7 |
| PNB dimer | |||||||
| trans-Sandwich | 3.6 | −3.2 | −0.2 | −11.0 | 5.8 | 0.0 | −8.7 |
| cis-Sandwich | 3.7 | −0.1 | −0.2 | −9.8 | 4.6 | 0.0 | −5.6 |
| T-shaped | 6.4 | −1.5 | −0.4 | −3.7 | 2.2 | 0.0 | −3.4 |
| Parallel-displaced | 2.3 | −3.8 | −0.2 | −9.0 | 3.0 | 0.0 | −10.0 |
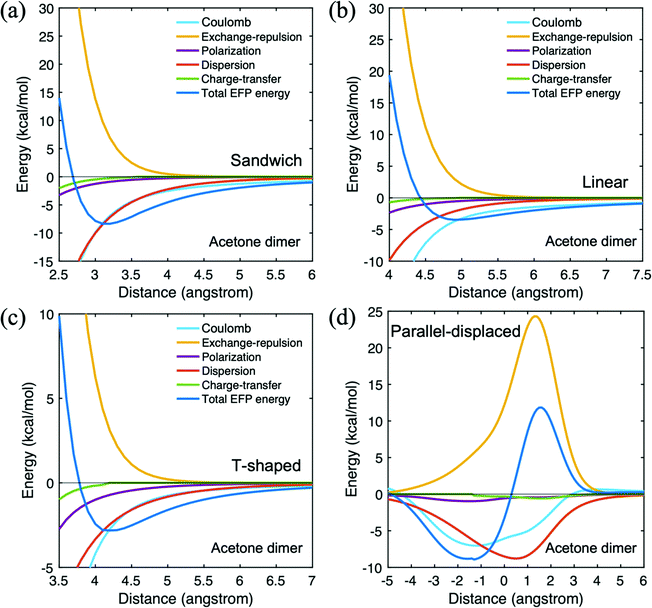 | ||
| Fig. 3 Potential energy surface for acetone dimer in four different configurations. (a) trans-Sandwich (b) linear (c) T-shaped (d) parallel-displaced. | ||
The parallel displaced structure is obtained by fixing the vertical intermolecular distance at the value for the sandwich configuration and then moving one of the monomers horizontally relative to the other. In Table 2, for the parallel displaced configuration, a negative (positive) distance means the upper acetone monomer moved to the left (right) relative to the reference monomer when the ketone group of the referenced bottom acetone towards the left side. The parallel displacement results in a small (0.5 kcal mol−1) increase in the magnitude of the interaction energy relative to the trans sandwich arrangement. Fig. 3(d) illustrates the potential energy surface for the acetone parallel displaced dimer. The most dominant contribution to the EFP interaction energy is the dispersion, but the Coulomb term clearly determines the direction of the displacement, as may be seen in Fig. 3(d).
The hexane dimer intermolecular interaction energies are summarized in Table 2. The cross configuration is illustrated in Fig. 2. As hexane is a nonpolar molecule, the Coulomb contribution to the interaction energy is relatively small. Indeed, all of the interaction terms are small, except for the dispersion, as one would expect for a nonpolar system, and the exchange repulsion. Because the dispersion dominates the hexane dimer interaction, the trend in the net EFP interaction energy follows the trend in the dispersion term: the sandwich dimer has the strongest interaction, followed closely by the cross configuration. The total EFP interaction energy of the T-shaped configuration is the smallest in magnitude, −1.7 kcal mol−1. The hexane potential energy surfaces are illustrated in Fig. 4. In all arrangements, the dispersion interaction is dominant throughout the potential energy surfaces. Because the contributions from the polarization and charge transfer terms are very small, these two contributions are omitted from the remaining tables.
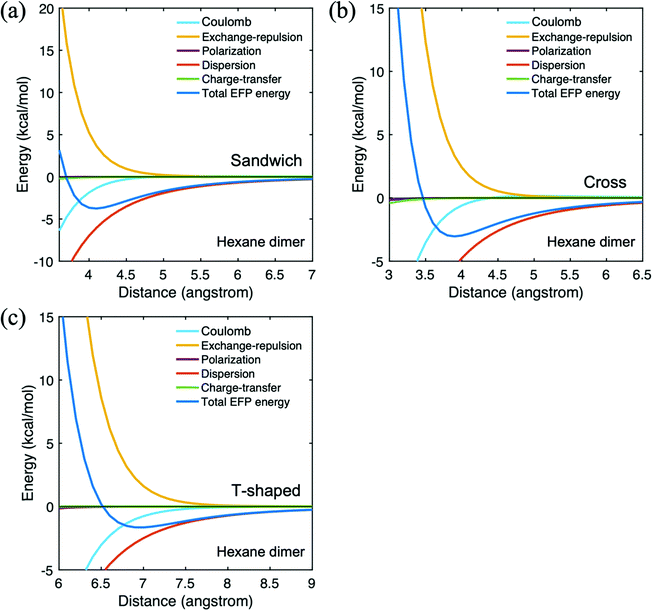 | ||
| Fig. 4 Potential energy surface for hexane dimer in three different configurations. (a) trans-Sandwich (b) T-shaped (c) cross. | ||
Finally, consider the dimers of p-nitrobenzaldehyde (PNB). As PNB is based on a benzene structure, π–π stacking interaction is expected to play an important role, especially in the sandwich structure. This is clear in Table 2, where one can see that the dispersion interaction is the dominant attractive term in all four structures, albeit smaller in the T-shaped arrangement. The polarization and charge transfer contributions are both small in all four species. The (attractive) Coulomb term makes modest contributions to the sandwich and parallel displaced structures and a significant contribution to the T-shaped arrangement where there are no π–π interactions.
The PNB trans-sandwich and cis-sandwich species differ in the orientation of the nitro groups: trans to each other in the trans-sandwich and cis to each other in the cis-sandwich. The trans nitro arrangement is preferred due to the more favorable dipole alignment. The parallel-displaced species is obtained starting from the trans-sandwich structure at a fixed vertical 3.6 Å equilibrium distance. If the upper PNB monomer moves to the right (as in Table 2), the distance is positive and vice versa when the nitro group toward to right side for the reference bottom PNB. As illustrated in Table 2, the displacement lowers the interaction energy by more than 1 kcal mol−1 relative to trans-sandwich, primarily due to more favorable Coulombic interactions and lower exchange repulsion. Fig. 5 shows the PNB dimer potential energy surfaces for the four configurations. The dispersion interaction is dominant throughout each PES. While the dispersion interaction in the parallel displaced species has the largest magnitude, the Coulomb term plays a role in determining the shape of the potential energy curve.
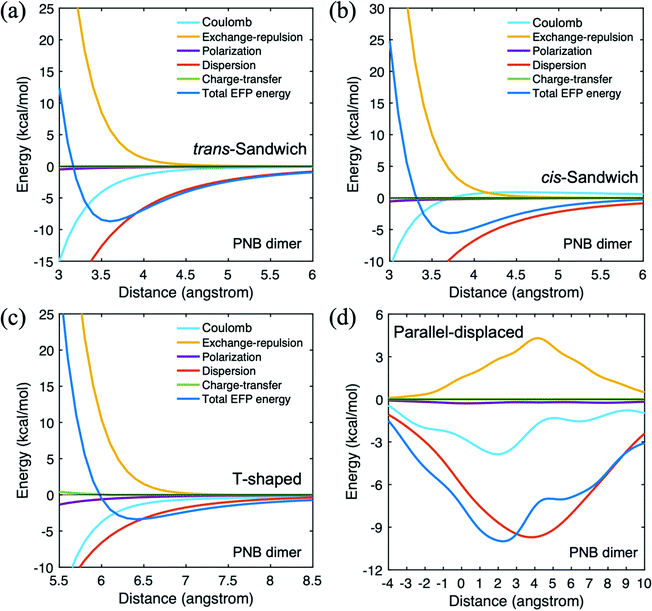 | ||
| Fig. 5 Potential energy surface for p-nitrobenzaldehyde (PNB) dimer in four different configurations. (a) trans-sandwich (b) cis-sandwich (c) T-shaped (d) parallel-displaced. | ||
3.2 Hetero-molecular interactions
For hetero intermolecular interactions, additional combinations of dimers are investigated with the EFP method. Besides the main reactants such as PNB, hexane, and acetone, propylamine representing the catalytic sites and silanol as a piece of the MSN are also included. In a nonpolar solvent like hexane, noncovalent interactions between the aminopropyl groups and silanol groups of the MSN can impact the diffusion process through the pore.55,56 The intermolecular interaction between PNB and acetone is summarized in Table 3. The parallel displaced arrangement is obtained in a manner analogous to that described above for the PNB dimer. A negative (positive) distance in Table 3 means the upper PNB monomer moved to the left (right) relative to the acetone monomer when the oxygen atom is towards the left side of the acetone. The parallel displaced configuration has the strongest interaction energy, dominated by the dispersion interaction, with a significant Coulomb contribution. The displacement from the trans-sandwich configuration lowers the exchange repulsion interaction energy, thereby contributing to the lower energy of the parallel displaced species. In the parallel displaced potential energy curve shown in Fig. 6(d), the dispersion is the most attractive interaction when the displacement is the smallest.| Distance (Å) | Coulomb (kcal mol−1) | Dispersion (kcal mol−1) | Exchange-repulsion (kcal mol−1) | Total EFP energy (kcal mol−1) | |
|---|---|---|---|---|---|
| PNB–acetone | |||||
| trans-Sandwich | 3.6 | −2.0 | −6.1 | 3.9 | −4.7 |
| cis-Sandwich | 3.7 | −0.6 | −5.4 | 3.4 | −3.1 |
| Linear | 7.1 | −2.9 | −2.2 | 2.4 | −2.9 |
| Parallel-displaced | −2.6 | −2.6 | −4.9 | 1.8 | −6.1 |
| PNB–hexane | |||||
| Sandwich | 3.8 | −3.2 | −9.9 | 6.7 | −6.6 |
| Cross | 3.8 | −0.8 | −7.0 | 4.0 | −3.9 |
| T-shaped | 6.4 | −1.8 | −3.9 | 2.9 | −3.0 |
| Parallel-displaced | −1.1 | −3.2 | −9.9 | 6.5 | −6.6 |
| PNB–silanol | |||||
| trans-Sandwich | 3.9 | −2.4 | −4.0 | 3.0 | −3.3 |
| cis-Sandwich | 3.8 | −2.1 | −4.1 | 3.0 | −3.2 |
| Linear (1) | 6.9 | −3.1 | −2.9 | 3.8 | −2.4 |
| Linear (2) | 7.5 | −1.8 | −1.9 | 2.3 | −1.6 |
| T-shaped | 7.1 | −2.0 | −2.0 | 2.7 | −1.7 |
| PNB–propylamine | |||||
| trans-Sandwich | 3.8 | −0.8 | −6.4 | 3.8 | −3.5 |
| cis-Sandwich | 3.9 | −0.4 | −5.5 | 2.6 | −3.4 |
| Linear | 8.6 | −0.4 | −1.1 | 0.9 | −0.6 |
| Parallel-displaced | −2.0 | −1.9 | −6.1 | 3.2 | −5.0 |
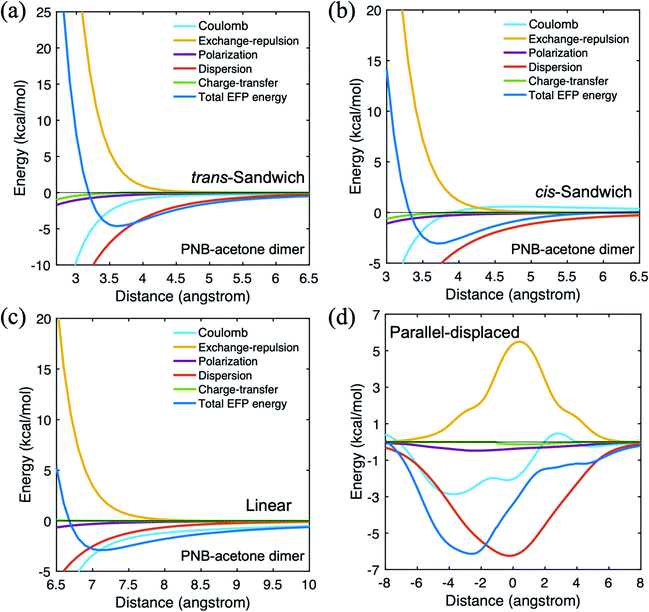 | ||
| Fig. 6 Potential energy surface for p-nitrobenzaldehyde(PNB)–acetone in four different configurations. (a) trans-Sandwich (b) cis-sandwich (c) linear (d) parallel-displaced. | ||
The trans-sandwich and cis-sandwich PNB-acetone configurations are distinguished by the alignment of the nitro group of PNB and the oxygen atom of acetone. The trans-sandwich structure has a more attractive EFP total binding energy than the cis-sandwich configuration. The dispersion contribution is the dominant attractive interaction for both the trans (−6.1 kcal mol−1) and cis (−5.4 kcal mol−1) sandwich arrangements owing to the π–π interactions of the benzene rings. Upon examining the potential energy curves in Fig. 6(a) and (b), it is clear that the dispersion term is most significant throughout the curves. Since nitro is a stronger electron-withdrawing group than the PNB carbonyl group, the trans-sandwich has a greater Coulombic contribution than the cis-sandwich. The more negatively charged PNB nitro group forms a strong attractive interaction with the positively charged hydrogen atoms of acetone. In the linear configuration, the PNB nitro group and the acetone oxygen atom are facing towards the same direction, so that the Coulomb interaction, −2.9 kcal mol−1, is most dominant due to the attractive dipolar interaction. The EFP total interaction energy in the lowest energy parallel-displaced configuration is −8.9 kcal mol−1 for acetone dimer and −10.0 kcal mol−1 for PNB dimer. Both interaction energies are lower than that of the PNB–acetone mixed dimer, −6.1 kcal mol−1.
Next, consider the PNB–hexane interaction summarized in Table 3. The parallel-displaced positive and negative distances are defined as discussed above: a negative (positive) distance means the upper PNB monomer moved to the left (right) relative to the hexane monomer when the nitro group of PNB is towards the right side. The corresponding potential energy curves are shown in the ESI.† Since PNB is the main reactant and hexane is the solvent in the aldol reaction, this interaction plays an important role in the diffusion process. As hexane is an alkane chain without functional groups, dispersion is expected to be important for the PNB–hexane interaction. The Coulomb contribution is also important due to the presence of the nitro and ketone groups in PNB. The sandwich and parallel displaced structures, both dominated by dispersion and with significant Coulomb contributions, have the largest magnitude total interaction energies. In the T-shaped configuration, there is a small polarization component since the PNB nitro group is oriented towards the hexane molecule, giving rise to an induced dipole. Still, the polarization component is minor compared to the dispersion and Coulomb contributions. The PNB–acetone interaction energy in the parallel-displaced configuration is −6.1 kcal mol−1, similar to the PNB–hexane value of −6.6 kcal mol−1. This suggests that the PNB reactant does not preferentially interact with either acetone or hexane in a mixed solvent.
The interaction between the reactant and the surface of MSN is represented as the dimer binding energy between PNB and silanol. Silanol is used to represent the MSN since silanol group is the main functional group on the surface of the MSN. It has been shown that silanol groups are important for initiating the aldol reaction.57 The PNB–silanol interactions are summarized in Table 3. The largest binding energy among the five different configurations is −3.3 kcal mol−1 for the trans-sandwich configuration with significant dispersion and Coulomb contributions. The trans-sandwich structure has a trans arrangement between the PNB nitro group and the silanol oxygen atom; the cis-sandwich structure has the corresponding cis alignment. The binding energies of the two arrangements differ by only 0.1 kcal mol−1. As shown in the table, the negatively charged silanol –OH group has a significant Coulomb interaction with the PNB electron-withdrawing groups. In the linear geometries, the silanol O atom and the PNB nitro group are either oriented in the same direction (linear (1)) or in the opposite direction (linear (2)). At their respective equilibrium geometries, linear (1) is nearly 1.0 kcal mol−1 more strongly bound, possibly due to the Coulombic interactions. The strongest PNB–silanol binding energy is −3.3 kcal mol−1 for the trans-sandwich structure, relatively small compared to other PNB hetero dimers. One could speculate that PNB consequently diffuses easily through the MSN pore.
The main features of the PNB–propylamine interaction are shown in Table 3. For the parallel-displaced configuration, a negative (positive) distance means the upper propylamine monomer moved to the left (right) comparable to the PNB monomer when the nitro group is on the left side of PNB. The strongest binding energy is found for the parallel displaced structure (∼5.0 kcal mol−1), followed by the cis- and trans-sandwich species (∼3.4–3.5 kcal mol−1). All three are clearly dominated by dispersion interactions. The linear structure, also predominantly dispersion, is more weakly bound, just over 1.0 kcal mol−1. The potential energy surfaces for these four arrangements are shown in Fig. 7. The curves for the two sandwich structures (Fig. 7a and b) are very similar to each other, suggesting that the orientation of the amine group has little impact. The weakly bound linear structure probably plays little role in the diffusion process. The shape of the parallel-displaced potential energy curve is similar to that of the Coulomb contribution, possibly due to the presence of the nitrogen atom in PNB. Nonetheless, the curve is dominated by dispersion at all intermolecular distances. Since the PNB–propylamine interaction is predicted to be stronger than the PNB–silanol interaction, it is likely that the former will play a more significant role in the diffusion process. It also suggests that a PNB molecule is more likely to interact with the catalytic group (represented by propylamine) than with the pore itself (represented by silanol). Interestingly, the binding of PNB to both acetone and hexane is somewhat stronger than their binding energy to propylamine.
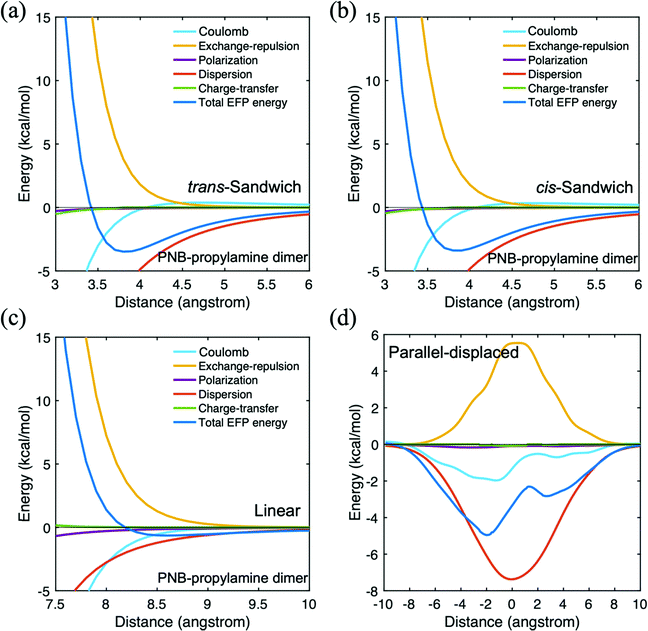 | ||
| Fig. 7 Potential energy surface for p-nitrobenzaldehyde (PNB)–propylamine in four different configurations. (a) trans-sandwich (b) cis-sandwich (c) linear (d) parallel-displaced. | ||
The molecular interaction between acetone and hexane is important for the diffusion process in MSN since hexane and acetone are relevant solvents that are often mixed in the experiments. In a previous paper, the interactions of the hexane–acetone sandwich configuration were part of a study of the diffusion coefficient based on EFP-MD simulations.37 It was concluded in that study that the permanent dipole of acetone exerts a strong acetone homo-molecular interaction. Therefore, the acetone–hexane interaction is weaker than the acetone homo–molecular interaction, thereby resulting in a higher self-diffusion coefficient for acetone in the acetone–hexane mixture than pure acetone. Table 4 presents the total acetone–hexane interaction energies of the sandwich and two linear structures. For the linear structures, when the acetone oxygen atom is oriented towards hexane, it is called linear (2) and vice versa. The sandwich binding energy is relatively small, and those of the linear species are even smaller. The previous EFP MD study37 indicates no aggregation of acetone molecules in an acetone–hexane 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio mixture. Based on the data in Table 3, the PNB–acetone and PNB–hexane interaction energies are very similar at the lowest energy parallel displaced arrangement. Therefore, it is likely that PNB molecules diffuse evenly in acetone–hexane mixed solvents.
1 volume ratio mixture. Based on the data in Table 3, the PNB–acetone and PNB–hexane interaction energies are very similar at the lowest energy parallel displaced arrangement. Therefore, it is likely that PNB molecules diffuse evenly in acetone–hexane mixed solvents.
| Distance (Å) | Coulomb (kcal mol−1) | Dispersion (kcal mol−1) | Exchange-repulsion (kcal mol−1) | Total EFP energy (kcal mol−1) | |
|---|---|---|---|---|---|
| Acetone–hexane | |||||
| Sandwich | 3.8 | −1.7 | −5.1 | 3.8 | −3.2 |
| Linear (1) | 5 | −0.8 | −2.8 | 2.1 | −1.6 |
| Linear (2) | 5 | −0.3 | −1.7 | 1.5 | −1.0 |
| Acetone–silanol | |||||
| trans-Sandwich | 3.4 | −3.0 | −4.3 | 4.3 | −3.5 |
| Linear | 4.9 | −4.1 | −2.0 | 3.5 | −3.3 |
| T-shaped | 4.4 | −0.7 | −2.4 | 1.7 | −1.6 |
| Parallel-displaced | 0.8 | −2.9 | −3.3 | 2.7 | −4.0 |
| Acetone–propylamine | |||||
| trans-Sandwich | 3.8 | −0.6 | −3.7 | 2.4 | −2.2 |
| Linear | 6.1 | −1.2 | −1.6 | 1.6 | −1.4 |
| Parallel-displaced | 1.6 | −1.1 | −2.7 | 1.1 | −2.9 |
| Hexane–silanol | |||||
| Sandwich | 4.0 | −1.1 | −3.2 | 2.4 | −1.9 |
| T-shaped | 4.3 | −1.4 | −3.9 | 3.0 | −2.3 |
| Hexane–propylamine | |||||
| Sandwich | 3.7 | −2.1 | −6.9 | 5.2 | −4.0 |
The contributions to the EFP acetone–silanol interaction energies are organized in Table 4. For the parallel-displaced configuration, a negative (positive) distance means the upper silanol monomer is shifted to the left (right) relative to the acetone monomer when the oxygen atom is on the right side of the acetone. The trans-sandwich, linear, and parallel displaced structures all have similar net interaction energies, from −3.3 (linear) to −4.0 kcal mol−1. In the trans-sandwich configuration, the dispersion is dominant as it is in other dimers as discussed above. For the linear configuration, the oxygen atoms of acetone and silanol are oriented in the same direction. The Coulomb contribution in the linear species is important due to the presence of the electronegative oxygen atom. The T-shaped arrangement has the smallest net interaction energy, with a very small Coulomb contribution because the C and Si are facing each other. Because the interaction energies of the acetone homo dimer or acetone–PNB are stronger than those of acetone–silanol, it is possible that acetone diffuses relatively unhindered inside MSN pores (i.e., diffusion is not inhibited by adsorption at the pore walls).
The interaction energies for the acetone–propylamine dimer are illustrated in Table 4. For the parallel-displaced configuration, a negative (positive) distance means the upper propylamine monomer moved to the left (right) relative to the acetone monomer when the oxygen atom is towards the right side of the acetone. In all configurations, dispersion is the largest contributor to the interaction energy, and the total EFP interaction energies are smaller in magnitude than −3.0 kcal mol−1. In comparison with the acetone–silanol interaction, the acetone–propylamine (representing the catalyst) interaction is weaker.
The interaction between hexane and MSN is described in Table 4 as the hexane–silanol dimer. In the sandwich arrangement, the total interaction energy is −1.9 kcal mol−1 with a dominant dispersion contribution. However, the T-shaped geometry has slightly stronger interaction energy (−2.3 kcal mol−1) at the equilibrium geometry, including −3.9 kcal mol−1 dispersion interaction energy. The molecular interaction energy of hexane–propylamine is summarized for the sandwich configuration which has a total interaction energy of −4.0 kcal mol−1 (Table 4). Since propylamine and hexane have carbon chain structures, dispersion dominates the interaction in the sandwich geometry. Hexane interacts more strongly with propylamine than with silanol. However, the interaction between hexane and propylamine is smaller than the interaction of PNB–propylamine, so hexane would not be an obstacle to initiating the aldol reaction in which PNB is the reactant.
4 Conclusion
This study has investigated the noncovalent interactions that may play an important role in the diffusion process which is important inside a narrow pore. The EFP method, which is based on first-principles quantum mechanics, has been validated through comparisons with the accurate CCSD(T) electronic structure method. The EFP method is used to analyze the competing interaction energies that might play a role in the aldol reaction with the PNB reactant in the MSN pore. Five molecules are relevant to this reaction: the PNB reactant, the solvents acetone and hexane, silanol representing the pore, and propylamine representing the catalyst group. For homo and heterodimers among five molecules, the decomposed intermolecular interactions are investigated by determining the potential energy surfaces to search the equilibrium structures in various arrangements. Although the internal geometries of the monomers are unlikely to change much during the diffusion process, the arrangements of monomers relative to each other may change more significantly from the equilibrium structure of each arrangement. By comparing all dimers, the EFP interaction energies of acetone dimer and PNB dimer are relatively large, −8.9 kcal mol−1 and −10.0 kcal mol−1, respectively. In addition, the interaction between PNB and propylamine, −5.0 kcal mol−1, is slightly stronger than acetone–propylamine or hexane–propylamine which is desirable for the initiations of the aldol reaction. In PNB-related dimers, the PNB-silanol interaction is noticeably small, −3.3 kcal mol−1, which could imply that diffusion of PNB molecules might not be inhibited inside the pore. Based on the decomposition of the EFP intermolecular energy into its components, in most dimers, dispersion has the largest attractive contribution. Therefore, the dispersion interaction is largely responsible for the location and the magnitude of the energy minima of the potential energy surfaces. This suggests that future computational studies of systems like the one presented here must provide accurate predictions of dispersion interactions for complex systems that dispersion is an important interaction to understand diffusion process.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Division of Chemical, Sciences, Geosciences, and Biological Sciences. MSG was supported by the Computational Chemical Sciences (CCS) project. YLK and JWE were supported by the Computational and Theoretical Chemistry (CTC) project. The work was performed at Ames Laboratory which is operated by Iowa State University under contract No. DE-AC02-07CH11358.References
- I. I. Slowing, J. L. Vivero-Escoto, B. G. Trewyn and V. S.-Y. Lin, J. Mater. Chem., 2010, 20, 7924–7937 RSC.
- I. Slowing, B. G. Trewyn and V. S.-Y. Lin, J. Am. Chem. Soc., 2006, 128, 14792–14793 CrossRef CAS PubMed.
- I. I. Slowing, J. L. Vivero-Escoto, C.-W. Wu and V. S.-Y. Lin, Adv. Drug Delivery Rev., 2008, 60, 1278–1288 CrossRef CAS PubMed.
- J. L. Vivero-Escoto, I. I. Slowing, C.-W. Wu and V. S.-Y. Lin, J. Am. Chem. Soc., 2009, 131, 3462–3463 CrossRef CAS PubMed.
- K. Kandel, S. M. Althaus, C. Peeraphatdit, T. Kobayashi, B. G. Trewyn, M. Pruski and I. I. Slowing, J. Catal., 2012, 291, 63–68 CrossRef CAS.
- N. Solin, L. Han, S. Che and O. Terasaki, Catal. Commun., 2009, 10, 1386–1389 CrossRef CAS.
- R. K. Zeidan and M. E. Davis, J. Catal., 2007, 247, 379–382 CrossRef CAS.
- B. Liu, S. Wu, X. Yu, J. Guan and Q. Kan, J. Colloid Interface Sci., 2011, 362, 625–628 CrossRef CAS PubMed.
- R. K. Zeidan, S. J. Hwang and M. E. Davis, Angew. Chem., 2006, 118, 6480–6483 CrossRef.
- H. Hattori, Chem. Rev., 1995, 95, 537–558 CrossRef CAS.
- K. K. Rao, M. Gravelle, J. S. Valente and F. Figueras, J. Catal., 1998, 173, 115–121 CrossRef CAS.
- H. Matsuhashi, H. Miyazaki, Y. Kawamura, H. Nakamura and K. Arata, Chem. Mater., 2001, 13, 3038–3042 CrossRef CAS.
- D. Tichit, B. Coq, S. Cerneaux and R. Durand, Catal. Today, 2002, 75, 197–202 CrossRef CAS.
- T. Gaydhankar, P. Joshi, P. Kalita and R. Kumar, J. Mol. Catal. A: Chem., 2007, 265, 306–315 CrossRef CAS.
- S.-E. Park, D.-S. Han, S.-C. Han, M.-J. Jin and T. Ohsuna, Chem. Commun., 2006, 4131–4133 Search PubMed.
- S. Luo, J. Li, L. Zhang, H. Xu and J. P. Cheng, Chem. – Eur. J., 2008, 14, 1273–1281 CrossRef CAS PubMed.
- X. Zheng, S. Luo, L. Zhang and J.-P. Cheng, Green Chem., 2009, 11, 455–458 RSC.
- T. M. Suzuki, M. Yamamoto, K. Fukumoto, Y. Akimoto and K. Yano, J. Catal., 2007, 251, 249–257 CrossRef CAS.
- S. Shylesh, A. Wagner, A. Seifert, S. Ernst and W. R. Thiel, Chem. – Eur. J., 2009, 15, 7052–7062 CrossRef CAS PubMed.
- A. García, I. I. Slowing and J. W. Evans, J. Chem. Phys., 2018, 149, 024101 CrossRef PubMed.
- C. A. Hunter, J. Singh and J. M. Thornton, J. Mol. Biol., 1991, 218, 837–846 CrossRef CAS PubMed.
- A. Anbarasu, S. Anand, M. M. Babu and R. Sethumadhavan, Int. J. Biol. Macromol., 2007, 41, 251–259 CrossRef CAS PubMed.
- C. A. Hunter and J. K. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- H. Fenniri, P. Mathivanan, K. L. Vidale, D. M. Sherman, K. Hallenga, K. V. Wood and J. G. Stowell, J. Am. Chem. Soc., 2001, 123, 3854–3855 CrossRef CAS PubMed.
- P. Kruse, E. R. Johnson, G. A. DiLabio and R. A. Wolkow, Nano Lett., 2002, 2, 807–810 CrossRef CAS.
- S. S. Sheiko, F. C. Sun, A. Randall, D. Shirvanyants, M. Rubinstein, H.-I. Lee and K. Matyjaszewski, Nature, 2006, 440, 191–194 CrossRef CAS PubMed.
- G. A. DiLabio, P. G. Piva, P. Kruse and R. A. Wolkow, J. Am. Chem. Soc., 2004, 126, 16048–16050 CrossRef CAS PubMed.
- E. Corey and T. W. Lee, Chem. Commun., 2001, 1321–1329 RSC.
- R. Noyori, Angew. Chem., Int. Ed., 2002, 41, 2008–2022 CrossRef CAS PubMed.
- P. I. Dalko, Comprehensive Enantioselective Organocatalysis: Catalysts, Reactions, and Applications, John Wiley & Sons, 2013, vol. 3 Search PubMed.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS PubMed.
- S. a. Rybak, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 1991, 95, 6576–6601 CrossRef CAS.
- P. Arrighini, Intermolecular forces and their evaluation by perturbation theory, Springer Science & Business Media, 2012 Search PubMed.
- M. S. Gordon, M. A. Freitag, P. Bandyopadhyay, J. H. Jensen, V. Kairys and W. J. Stevens, J. Phys. Chem. A, 2001, 105, 293–307 CrossRef CAS.
- J. C. Flick, D. Kosenkov, E. G. Hohenstein, C. D. Sherrill and L. V. Slipchenko, J. Chem. Theory Comput., 2012, 8, 2835–2843 CrossRef CAS PubMed.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- Y. L. Kim, Y. Han, J. W. Evans and M. S. Gordon, J. Phys. Chem. A, 2021, 125, 3398–3405 CrossRef CAS PubMed.
- L. V. Slipchenko and M. S. Gordon, J. Comput. Chem., 2007, 28, 276–291 CrossRef CAS PubMed.
- Q. A. Smith, M. S. Gordon and L. V. Slipchenko, J. Phys. Chem. A, 2011, 115, 11269–11276 CrossRef CAS PubMed.
- T. Smith, L. V. Slipchenko and M. S. Gordon, J. Phys. Chem. A, 2008, 112, 5286–5294 CrossRef CAS PubMed.
- L. V. Slipchenko and M. S. Gordon, J. Phys. Chem. A, 2009, 113, 2092–2102 CrossRef CAS PubMed.
- J. M. Mullin and M. S. Gordon, J. Phys. Chem. B, 2009, 113, 8657–8669 CrossRef CAS PubMed.
- J. M. Mullin and M. S. Gordon, J. Phys. Chem. B, 2009, 113, 14413–14420 CrossRef CAS PubMed.
- C. M. Aikens and M. S. Gordon, J. Am. Chem. Soc., 2006, 128, 12835–12850 CrossRef CAS PubMed.
- S. Kim, C. M. Kaliszewski, E. B. Guidez and M. S. Gordon, J. Phys. Chem. A, 2018, 122, 4076–4084 CrossRef CAS PubMed.
- M. S. Gordon, Fragmentation: toward accurate calculations on complex molecular systems, John Wiley & Sons, 2017 Search PubMed.
- H. Li, M. S. Gordon and J. H. Jensen, J. Chem. Phys., 2006, 124, 214108 CrossRef PubMed.
- A. J. Stone, Chem. Phys. Lett., 1981, 83, 233–239 CrossRef CAS.
- I. Adamovic and M. S. Gordon, Mol. Phys., 2005, 103, 379–387 CrossRef CAS.
- E. B. Guidez, P. Xu and M. S. Gordon, J. Phys. Chem. A, 2016, 120, 639–647 CrossRef CAS PubMed.
- P. Xu and M. S. Gordon, J. Chem. Phys., 2013, 139, 194104 CrossRef PubMed.
- L. V. Slipchenko and M. S. Gordon, Mol. Phys., 2009, 107, 999–1016 CrossRef CAS.
- G. M. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina and E. Guidez, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
- J. M. Hermida-Ramón and M. A. Ríos, J. Phys. Chem. A, 1998, 102, 2594–2602 CrossRef.
- J. D. Bass, A. Solovyov, A. J. Pascall and A. Katz, J. Am. Chem. Soc., 2006, 128, 3737–3747 CrossRef CAS PubMed.
- S. Nedd, T. Kobayashi, C.-H. Tsai, I. I. Slowing, M. Pruski and M. S. Gordon, J. Phys. Chem. C, 2011, 115, 16333–16339 CrossRef CAS.
- A. P. de Lima Batista, F. Zahariev, I. I. Slowing, A. A. Braga, F. R. Ornellas and M. S. Gordon, J. Phys. Chem. B, 2016, 120, 1660–1669 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00952h |
| This journal is © the Owner Societies 2022 |