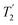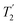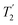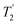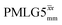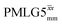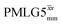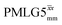Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optimisation of 1H PMLG homonuclear decoupling at 60 kHz MAS to enable 15N–1H through-bond heteronuclear correlation solid-state NMR spectroscopy†‡
Jacqueline
Tognetti
 ab,
W. Trent
Franks
ab,
W. Trent
Franks
 ab,
Józef R.
Lewandowski
ab,
Józef R.
Lewandowski
 a and
Steven P.
Brown
a and
Steven P.
Brown
 *b
*b
aDepartment of Chemistry, University of Warwick, Coventry CV4 7AL, UK
bDepartment of Physics, University of Warwick, Coventry CV4 7AL, UK. E-mail: S.P.Brown@warwick.ac.uk
First published on 26th July 2022
Abstract
The Lee–Goldburg condition for homonuclear decoupling in 1H magic-angle spinning (MAS) solid-state NMR sets the angle θ, corresponding to arctan of the ratio of the rf nutation frequency, ν1, to the rf offset, to be the magic angle, θm, equal to tan−1(√2) = 54.7°. At 60 kHz MAS, we report enhanced decoupling compared to MAS alone in a 1H spectrum of 15N-glycine with 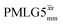 at θ = 30° for a ν1 of ∼100 kHz at a 1H Larmor frequency, ν0, of 500 MHz and 1 GHz, corresponding to a high chemical shift scaling factor (λCS) of 0.82. At 1 GHz, we also demonstrate enhanced decoupling compared to 60 kHz MAS alone for a lower ν1 of 51 kHz, i.e., a case where the nutation frequency is less than the MAS frequency, with θ = 18°, λCS = 0.92. The ratio of the rotor period to the decoupling cycle time, Ψ = τr/τc, is in the range 0.53 to 0.61. Windowed
at θ = 30° for a ν1 of ∼100 kHz at a 1H Larmor frequency, ν0, of 500 MHz and 1 GHz, corresponding to a high chemical shift scaling factor (λCS) of 0.82. At 1 GHz, we also demonstrate enhanced decoupling compared to 60 kHz MAS alone for a lower ν1 of 51 kHz, i.e., a case where the nutation frequency is less than the MAS frequency, with θ = 18°, λCS = 0.92. The ratio of the rotor period to the decoupling cycle time, Ψ = τr/τc, is in the range 0.53 to 0.61. Windowed  decoupling using the optimised parameters for a ν1 of ∼100 kHz also gives good performance in a 1H spin-echo experiment, enabling implementation in a 1H-detected 15N–1H cross polarisation (CP)-refocused INEPT heteronuclear correlation NMR experiment. Specifically, initial 15N transverse magnetisation as generated by 1H–15N CP is transferred back to 1H using a refocused INEPT pulse sequence employing windowed
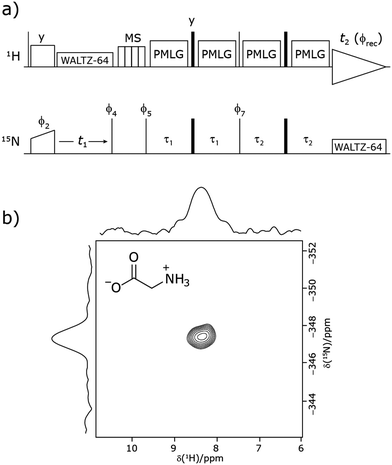
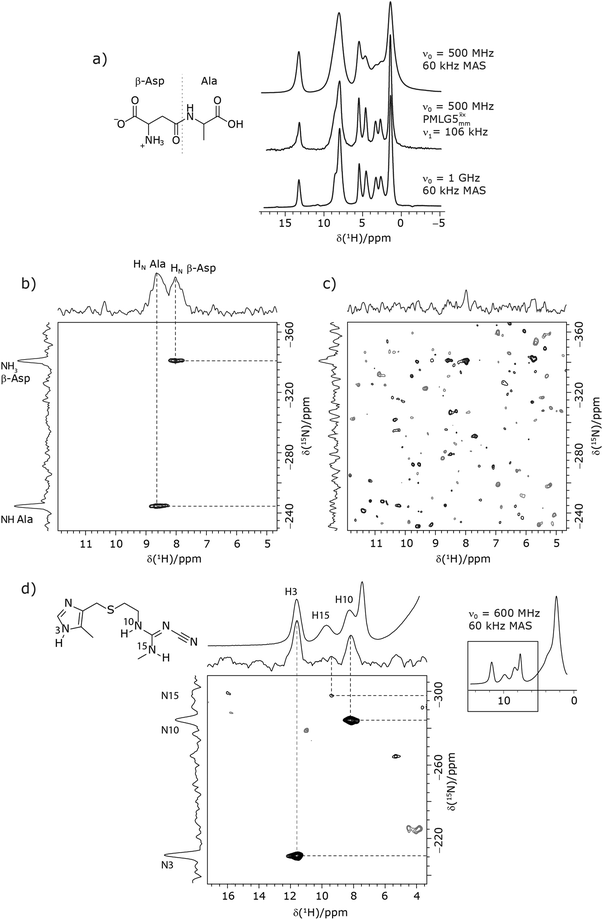
decoupling using the optimised parameters for a ν1 of ∼100 kHz also gives good performance in a 1H spin-echo experiment, enabling implementation in a 1H-detected 15N–1H cross polarisation (CP)-refocused INEPT heteronuclear correlation NMR experiment. Specifically, initial 15N transverse magnetisation as generated by 1H–15N CP is transferred back to 1H using a refocused INEPT pulse sequence employing windowed 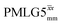 1H decoupling. Such an approach ensures the observation of through-bond N–H connectivities. For 15N-glycine, while the CP-refocused INEPT experiment has a lower sensitivity (∼50%) as compared to a double CP experiment (with a 200 μs 15N to 1H CP contact time), there is selectivity for the directly bonded NH3+ moiety, while intensity is observed for the CH21H resonances in the double CP experiment. Two-dimensional 15N–1H correlation MAS NMR spectra are presented for the dipeptide β-AspAla and the pharmaceutical cimetidine at 60 kHz MAS, both at natural isotopic abundance. For the dipeptide β-AspAla, different build-up dependence on the first spin-echo duration is observed for the NH and NH3+ moieties demonstrating that the experiment could be used to distinguish resonances for different NHx groups.
1H decoupling. Such an approach ensures the observation of through-bond N–H connectivities. For 15N-glycine, while the CP-refocused INEPT experiment has a lower sensitivity (∼50%) as compared to a double CP experiment (with a 200 μs 15N to 1H CP contact time), there is selectivity for the directly bonded NH3+ moiety, while intensity is observed for the CH21H resonances in the double CP experiment. Two-dimensional 15N–1H correlation MAS NMR spectra are presented for the dipeptide β-AspAla and the pharmaceutical cimetidine at 60 kHz MAS, both at natural isotopic abundance. For the dipeptide β-AspAla, different build-up dependence on the first spin-echo duration is observed for the NH and NH3+ moieties demonstrating that the experiment could be used to distinguish resonances for different NHx groups.
1. Introduction
Direct 1H detection is increasingly important for solid-state NMR study of pharmaceuticals1–4 and biological molecules.5–8 The availability of ever faster Magic Angle Spinning (MAS) frequencies reduces line broadening due to 1H homonuclear dipolar couplings.9–14 In particular, 1H detection is advantageous for the identification of specific correlations to nuclei with low gyromagnetic ratio, γ, such as the two natural-abundant isotopes of nitrogen, 14N and 15N. Our focus here is on the spin I = 1/2 15N, though it is to be noted that there is increasing application of 14N–1H experiments for the much higher natural abundance (99.6%) spin I = 1 nucleus.15–22 The low sensitivity of 15N, associated with its low natural abundance and gyromagnetic ratio, can be overcome by the use of 15N–1H correlation experiments with proton acquisition, thanks to the high natural abundance and γ that characterise protons, provided that fast MAS can achieve sufficient 1H line narrowing.23–26 We note that an 15N-detected MAS-J-HMQC 1H–15N two-dimensional spectrum has also been recorded at natural abundance and 12.5 kHz MAS using Frequency Switched Lee–Goldburg (FSLG) 1H homonuclear decoupling.271H-detected heteronuclear 15N–1H correlation experiments can be achieved by inverse polarization, CP, as applied to small molecules23,25,26,28–30 and 15N-labelled proteins as a hNH experiment.31–33 An alternative to CP-based dipolar-mediated through-space transfer is a J coupling mediated through-bond refocused INEPT solid-state NMR experiment.34–37 Specifically, we consider the CP-refocused INEPT correlation experiment,38,39 whereby J coupling mediated 15N–1H back-transfer, following CP to give maximum initial 15N magnetisation, ensures only the observation of peaks due to through-bond transfer in a 15N–1H spectrum.26 However, fast dephasing due to strong 1H homonuclear dipolar couplings shortens 1H coherence lifetimes, reducing sensitivity, making J coupling based experiments challenging. Even 60 kHz MAS is not sufficient to completely average out 1H homonuclear dipolar couplings.40 The application of 1H homonuclear decoupling41–44 under fast MAS during the 15N–1H coherence transfer improves sensitivity sufficiently for refocused INEPT transfer.26,39While a large number of 1H homonuclear decoupling schemes have been optimised under static conditions for operation at low (5–10 kHz) and moderate (∼15 kHz) MAS frequencies;41–54 there have only been a few papers presenting 1H homonuclear decoupling at faster MAS frequencies of (35+ kHz)55,56 and (60+ kHz).57–621H homonuclear decoupling is clearly not being applied under quasi-static conditions under such fast MAS and the performance is dependent upon the ratio between the rotor period, τr, and the cycle time of the 1H homonuclear decoupling, τc. Lee–Goldburg45,46,49,59 and DUMBO50,62 based decoupling are characterized by short cycle times which makes them compatible with faster MAS implementations. Nevertheless, a short cycle time means high 1H nutation frequencies, ν1, for the scheme which can be demanding on the instrumentation. In this work, we consider the application of phase-modulated Lee–Goldburg (PMLG)49 in a 1D 1H Combined Rotation and Multiple-Pulse Sequence (CRAMPS)63 experiment at 60 kHz MAS using relatively low nutation frequencies. The performance of PMLG depends on multiple factors such as the type of PMLG-block, frequency offset, and 1H nutation frequency;41,42,53,541H homonuclear decoupling sequences are usually evaluated through three principal parameters: the chemical shift scaling factor (λCS),57,58,64 and linewidth improvement reflected in sensitivity and resolution determined through observation of the chemical shift evolution,62 and extended coherence lifetimes as observed through spin-echo experiments.57 A bimodal Floquet theory analysis shows that 1H homonuclear decoupling requires a fine optimization at MAS above 40 kHz owing to the considerable number of zero- and first-order degeneracies.65 The two types of degeneracy arise when nνr + kνc = 0, where νr is the MAS spinning frequency and νc is the cycle frequency of the decoupling block, and n and k are integers. When these conditions are met, degeneracies occur within the diagonal block of the Floquet Hamiltonian and the effective Hamiltonian66 leading to dipolar line-broadening.
In this paper, we first demonstrate, at 60 kHz MAS, enhanced decoupling compared to MAS alone in a 1H solid-state NMR spectrum of 15N-glycine for an angle θ, corresponding to arctan of the ratio of the rf nutation frequency, ν1, to the rf offset, that is far from the ideal magic angle, θm, equal to tan−1(√2) = 54.7°. Moreover, the application of windowed 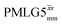 decoupling with parameters based on those optimised for the one-pulse spectrum gives enhanced dephasing times in a 1H spin-echo experiment. In this way, we systematically investigate the 1H homonuclear decoupling parameters that affect sensitivity in the 15N–1H CP-refocused INEPT experiment under 1H homonuclear decoupling and fast MAS. It is shown that optimized decoupling enables the recording of two-dimensional through-bond 15N–1H MAS NMR correlation spectra for moderately sized organic molecules such as the dipeptide β-AspAla and the pharmaceutical cimetidine.
decoupling with parameters based on those optimised for the one-pulse spectrum gives enhanced dephasing times in a 1H spin-echo experiment. In this way, we systematically investigate the 1H homonuclear decoupling parameters that affect sensitivity in the 15N–1H CP-refocused INEPT experiment under 1H homonuclear decoupling and fast MAS. It is shown that optimized decoupling enables the recording of two-dimensional through-bond 15N–1H MAS NMR correlation spectra for moderately sized organic molecules such as the dipeptide β-AspAla and the pharmaceutical cimetidine.
2. Experimental
15N-Labelled glycine, and natural abundance (NA) glycine, β-AspAla and cimetidine were purchased from Sigma Aldrich or Bachem (β-AspAla) and packed as received into 1.3 mm zirconia rotors. 15N-Glycine was packed into a restricted volume in the centre of the rotor using silicone spacers. 15N-Labelled glycine was used to optimise 1H homonuclear decoupling in 1D and 2D correlation experiments and the 2D 15N–1H CP-refocused INEPT experiment. Glycine, β-AspAla and cimetidine, all at natural abundance, were used to test the 15N–1H natural abundance CP-refocused INEPT correlation experiment.The experiments were performed on a Bruker Avance III (500 MHz) or Avance NEO (600 MHz, 1 GHz) spectrometer operating at a 1H Larmor frequency of ν0H = 500.13 MHz (11.7 T), 599.45 MHz (14.1 T), 1000.40 MHz (23.5 T) and sample spinning using a Bruker 1.3 mm HXY probe at 60 kHz. The 90° pulse duration of 2.5 μs (ν1 = 100 kHz) for 1H and 4 μs (ν1 = 62.5 kHz) or 3.5 μs (ν1 = 71.4 kHz, cimetidine) for 15N was calibrated using a one-pulse experiment and a CP followed by a 90° pulse experiment, respectively. A recycle delay of 3 s or 5 s (cimetidine) was used.
1H chemical shifts are externally referenced with respect to tetramethylsilane (TMS) viaL-alanine at natural abundance as a secondary reference (1.1 ppm for the CH31H resonance) corresponding to adamantane at 1.85 ppm.67,6815N chemical shifts are referenced relative to liquid CH3NO2 at 0 ppm,69 using the NH3+ peak of glycine (at natural abundance) at −347.4 ppm as a secondary reference. To convert to the chemical shift scale frequently used in protein NMR, where the alternative IUPAC reference (see Appendix 1 of ref. 70) is liquid ammonia at −50 °C, it is necessary to add 379.5 to the given values.711H and 15N chemical shifts can be experimentally determined to an accuracy of ±0.2 and ±0.1 ppm, respectively. The 15N RF transmitter frequency was centred at −304.5 ppm (or −291.5 ppm cimetidine). Where the 1H resonance offset is referred to, 0 kHz refers to on-resonance with the NH3+ peak of glycine at 8.4 ppm, with a positive resonance offset referring to a move of the RF transmitter frequency to higher ppm.
1D CRAMPS
The acquisition window was optimized to acquire 40 complex data points, each corresponding to 0.1 μs, with a ringdown delay of 1.0 μs and a deadtime optimized to be 2.2 μs, corresponding to a total acquisition window, τw, of 7.2 μs. The total acquisition time was 15 ms. Both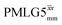 and
and 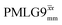 1H homonuclear decoupling schemes were optimized over a 1H nutation frequency, ν1(1H), range from ∼10 to ∼120 kHz.
1H homonuclear decoupling schemes were optimized over a 1H nutation frequency, ν1(1H), range from ∼10 to ∼120 kHz.
2D 15N–1H CP-refocused INEPT
Cross polarization (CP) from 1H to 15N was used for the initial excitation of 15N transverse magnetisation, where the 1H nutation frequency was ∼80 kHz (or ∼95 kHz for cimetidine) using a zero-quantum (ZQ) match condition;72,73 and a 15N nutation frequency of ∼20 kHz (or ∼25 kHz for cimetidine) with a linear ramp74 (70–100%) on the 15N channel (glycine and β-AspAla) or 1H (cimetidine). A CP contact time of 2 ms (or 4 ms for cimetidine) was used. The MISSISSIPPI suppression scheme75 was applied with a spinlock nutation frequency of ∼30 kHz for four intervals of 2 ms (or 5 ms for cimetidine) to remove residual 1H transverse magnetisation. Low-power76 heteronuclear 1H and 15N decoupling was applied during t1 evolution and 1H acquisition, respectively, using WALTZ6477,78 at a nutation frequency of ∼10 kHz. The pulse sequence used corresponds to a modified version of that presented by Althaus et al. (Fig. 1b).26Each 1H-detected FID was acquired for 30 ms with a spectral width of 80 ppm (or 40 ppm for cimetidine). The 15N dimension was acquired with 96 (glycine NA and β-AspAla) or 64 (cimetidine) t1 FIDs with a dwell time of 300 μs (glycine NA) or 142 μs (β-AspAla) or 160 μs (cimetidine), corresponding to a 15N spectral width of 66 ppm (glycine NA) or 138 ppm (β-AspAla) or 102 ppm (cimetidine) and a maximum t1 of 15 ms (glycine NA), 6.9 ms (β-AspAla), or 5.1 ms (cimetidine). The States-TPPI method was employed to achieve sign discrimination in the indirect dimension.
3. Results and discussion
3.1 15N–1H CP-refocused INEPT – pulse sequence and product operator analysis
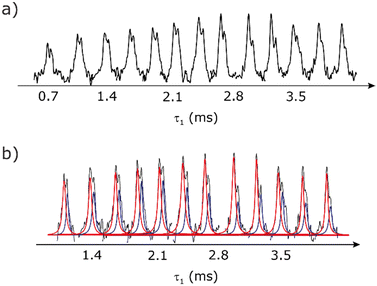
Our implementation of the 15N–1H CP-refocused INEPT experiment at 60 kHz MAS is shown in Fig. 1a. Note that the pulse sequence in Fig. 1a corresponds to a modified version of that used by Althaus et al. at νr = 40 kHz.26 The pulse sequence begins with an initial 1H to 15N CP transfer to provide the largest pool of polarization possible for the low-γ and natural abundance 15N nucleus. The 15N transverse magnetisation is allowed to evolve during t1. The desired magnetisation is stored during a z-filter period, in which 1H magnetisation suppression using the MISSISSIPPI sequence75 is implemented to remove the background proton signals. A 15N–1H refocused INEPT element is used to transfer the magnetization back to proton for acquisition. INEPT utilizes the 1H–15N J couplings to restrict the signals observed to those with direct one-bond H–N connections. Each spin-echo duration should be an integer number of rotor periods to ensure that the chemical shift anisotropy is completely averaged by MAS. Homonuclear 1H decoupling, here PMLG,49 is applied during the two spin-echoes of the refocused INEPT element. Under fast MAS, at a spinning frequency of 60 kHz in this work, low power heteronuclear decoupling,76 specifically WALTZ-6478 decoupling, is applied on 1H and 15N during t1 and t2, respectively. The resulting spectrum is a 2D 15N–1H through-bond correlation spectrum, as illustrated in Fig. 1b for natural abundance glycine.For a 15N–1H spin pair, a product-operator analysis (see Section S1,ESI‡) shows a product of sine terms dependence on the heteronuclear 15N–1H JIS coupling active during the two spin-echo (τ–π–τ) durations, τ1 and τ2:
| (NH) sin(2πJISτ2)sin(2πJISτ1) | (1) |
Analogously to the case of 29Si–1H J-couplings in SiHn moieties,82–84 there is a different dependence on the first spin-echo duration, τ1, for a NH3 moiety:
| (NH3) sin(2πJISτ2)[sin(2πJISτ1) + sin(6πJISτ1)] | (2) |
3.2 1H PMLG homonuclear decoupling under fast MAS
As noted in the above discussion of Fig. 1a, PMLG 1H homonuclear decoupling is employed during the two spin-echo durations of the refocused INEPT pulse sequence element that transfers magnetisation from 15N to 1H. Lee–Goldburg decoupling45 can be considered to be analogous to MAS where the sample is rotated around an axis inclined at the magic angle, θm, equal to tan−1(√2), to the external magnetic field in that the ratio of the nutation frequency, ν1, to the resonance offset, ΔνLG, is also set equal to tan−1(√2). This leads to an effective field, νeff_LG, that is given by Pythagoras’ theorem, as: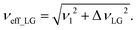 | (3) |
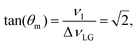 | (4) |
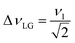 and
and 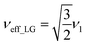 . In the PMLG implementation49 of the LG condition, rf irradiation is applied on resonance for a duration, τLG, that is the inverse of νeff_LG
. In the PMLG implementation49 of the LG condition, rf irradiation is applied on resonance for a duration, τLG, that is the inverse of νeff_LG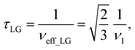 | (5) |
 over the duration, τLG, whereby ϕlast depends on ΔνLG according to:
over the duration, τLG, whereby ϕlast depends on ΔνLG according to: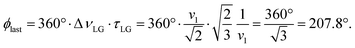 | (6) |
| ξLG = 360°·νeff_LG·τLG = 360°. | (7) |
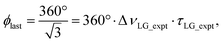 so that
so that 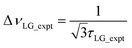 .
.
Nishiyama et al.57 have shown that this deviation from the ideal condition can be expressed in terms of how the angle, θ, deviates from the magic angle, θm:
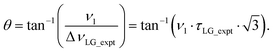 | (8) |
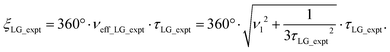 | (9) |
Following the notation of Leskes et al.85 a PMLG block is specified as 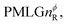 where: first, n is the number of finite pulses for each LG cycle, with n equal to 5 or 9 investigated here; second, R is the sense of the initial rotation for the phase steps, m for clockwise and p for counter-clockwise; and third, the initial phase, ϕ, is usually x or −x (denoted
where: first, n is the number of finite pulses for each LG cycle, with n equal to 5 or 9 investigated here; second, R is the sense of the initial rotation for the phase steps, m for clockwise and p for counter-clockwise; and third, the initial phase, ϕ, is usually x or −x (denoted ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ). As stated above (see eqn (7)) and as shown in Fig. 2a and b, τLG_expt is the time to sweep the phase over n discrete steps, i.e., as n finite pulses, from 0° to 207.8°. A single PMLG block,
). As stated above (see eqn (7)) and as shown in Fig. 2a and b, τLG_expt is the time to sweep the phase over n discrete steps, i.e., as n finite pulses, from 0° to 207.8°. A single PMLG block, 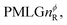 is of duration 2τLG with a 180° jump after n finite pulses in the first τLG followed by n finite pulses in the second τLG, whereby the phase steps are in the opposite direction. This corresponds to changing the sign of the equivalent resonance offset, as in the frequency-switched (FS) LG experiment, where rf irradiation is alternated between +ΔνLG and −ΔνLG.46,86,87 As further shown by Leskes et al.85 supercycling can be achieved as
is of duration 2τLG with a 180° jump after n finite pulses in the first τLG followed by n finite pulses in the second τLG, whereby the phase steps are in the opposite direction. This corresponds to changing the sign of the equivalent resonance offset, as in the frequency-switched (FS) LG experiment, where rf irradiation is alternated between +ΔνLG and −ΔνLG.46,86,87 As further shown by Leskes et al.85 supercycling can be achieved as 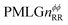 . Specifically, in this work, we use the
. Specifically, in this work, we use the 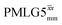 and
and 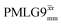 implementations.
implementations.
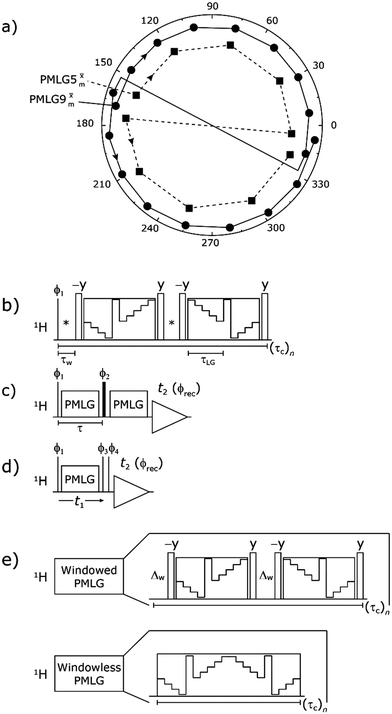 | ||
Fig. 2 (a) Representation of the phase rotation for 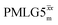 (dashed line, squares) and (dashed line, squares) and 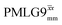 (solid line, circles). The phase increments are calculated according to ϕlast = 207.8° (see eqn (6)), divided by the number of steps. The starting point for both is −x. Pulse sequence for (b) a 1H 1D CRAMPS experiment with supercycled (solid line, circles). The phase increments are calculated according to ϕlast = 207.8° (see eqn (6)), divided by the number of steps. The starting point for both is −x. Pulse sequence for (b) a 1H 1D CRAMPS experiment with supercycled 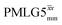 , where the asterisk represents an acquisition window, τw, (c) a 1H spin-echo and (d) a 2D 1H–1H correlation experiment. Thin lines and filled rectangles represent 90° and 180° pulses, respectively, while open rectangles denote tilt pulses. In (c) and (d), the block named PMLG can accommodate either (a and e) windowed, where τw is an equivalent period of free evolution, or a windowless sequence, whereby there is continuous rf irradiation during , where the asterisk represents an acquisition window, τw, (c) a 1H spin-echo and (d) a 2D 1H–1H correlation experiment. Thin lines and filled rectangles represent 90° and 180° pulses, respectively, while open rectangles denote tilt pulses. In (c) and (d), the block named PMLG can accommodate either (a and e) windowed, where τw is an equivalent period of free evolution, or a windowless sequence, whereby there is continuous rf irradiation during 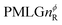 blocks, i.e., there are no tilt pulses and τw = 0. The following phase cycle is applied for (b) 1D CRAMPS: ϕ1 = {x, −x, −x, x}, ϕPMLG = {x, −x, −x, x} and acquisition ϕrec = {x, −x, −x, x}; (c) 1H spin-echo: ϕ1 = {x, −x}, ϕ2 = {y*2, x*2}, ϕPMLG = {x, −x} and acquisition ϕrec = {x, −x, −x, x}; (d) 1H–1H homonuclear correlation: ϕ1 = {x, −x}, ϕ3 = {−x*2, x*2}, ϕ4 = {x*4, y*4}, ϕPMLG = {x, −x} and acquisition ϕrec = {x, −x, −x, x, y, −y, −y, y}. blocks, i.e., there are no tilt pulses and τw = 0. The following phase cycle is applied for (b) 1D CRAMPS: ϕ1 = {x, −x, −x, x}, ϕPMLG = {x, −x, −x, x} and acquisition ϕrec = {x, −x, −x, x}; (c) 1H spin-echo: ϕ1 = {x, −x}, ϕ2 = {y*2, x*2}, ϕPMLG = {x, −x} and acquisition ϕrec = {x, −x, −x, x}; (d) 1H–1H homonuclear correlation: ϕ1 = {x, −x}, ϕ3 = {−x*2, x*2}, ϕ4 = {x*4, y*4}, ϕPMLG = {x, −x} and acquisition ϕrec = {x, −x, −x, x, y, −y, −y, y}. | ||
In the windowed implementation of PMLG88 acquisition windows of duration τW are placed between the 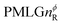 blocks (see Fig. 2b and e). In addition, tilt pulses of duration τtilt can be used.53,54,89–91 The cycle time for a complete
blocks (see Fig. 2b and e). In addition, tilt pulses of duration τtilt can be used.53,54,89–91 The cycle time for a complete 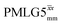 or
or 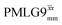 supercycle, τc, is:
supercycle, τc, is:
| τc = 2τw + 4τLG_expt + 4τtilt. | (10) |
3.3 Optimisation of CH2 and NH3 signal intensity in a 1D CRAMPS experiment of 15N-glycine
The optimization of the 1H nutation frequency and τLG_expt is performed differently for windowless and windowed sequences. In this paper, our focus is on windowed sequences that were optimized with a 1D CRAMPS experiment which gives both the chemical shift scaling factor λCS and the 1H linewidths in a few seconds for a particular combination of parameters. Specifically for windowed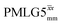 and
and 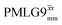 , a two variable optimization was performed over a range of 1H nutation frequencies between 0 and 110–120 kHz and τLG_expt between 3.5 and 7.5 μs for 15N labelled glycine – see Fig. 3a for
, a two variable optimization was performed over a range of 1H nutation frequencies between 0 and 110–120 kHz and τLG_expt between 3.5 and 7.5 μs for 15N labelled glycine – see Fig. 3a for 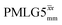 and Fig. S1 (ESI‡) with slices extracted at different peak intensities, hence with different resolution. (Note that the optimisation of the tilt pulses is discussed in Section S3 of the ESI‡.) For windowless sequences, a coarse optimization was performed, starting from optimised parameters from the 1D CRAMPS experiments, using a 1H spin-echo experiment (Fig. 2c) to find good candidate parameters which yield a long 1H coherence lifetime. As noted below, the 1H–1H correlation experiment (Fig. 2d) was used to determine the λCS of the candidate windowless sequences, but can only be used sparingly as the experimental time is relatively long (∼20 minutes for 4 co-added transients and 96 t1 FIDs for each combination of τLG_expt and ν1).
and Fig. S1 (ESI‡) with slices extracted at different peak intensities, hence with different resolution. (Note that the optimisation of the tilt pulses is discussed in Section S3 of the ESI‡.) For windowless sequences, a coarse optimization was performed, starting from optimised parameters from the 1D CRAMPS experiments, using a 1H spin-echo experiment (Fig. 2c) to find good candidate parameters which yield a long 1H coherence lifetime. As noted below, the 1H–1H correlation experiment (Fig. 2d) was used to determine the λCS of the candidate windowless sequences, but can only be used sparingly as the experimental time is relatively long (∼20 minutes for 4 co-added transients and 96 t1 FIDs for each combination of τLG_expt and ν1).
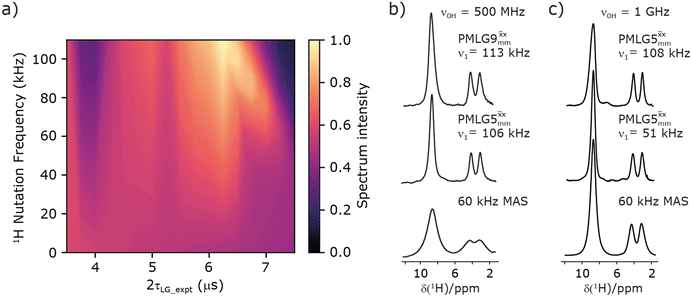 | ||
Fig. 3
1H MAS (νr = 60 kHz) NMR of 15N-labelled glycine. (a) 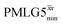 1D CRAMPS (see Fig. 2b, τtilt = 0.54 μs, Ω = −0.6 kHz) two-variable optimization (ν0 = 500 MHz) of both τLG_expt (in steps of 0.25 μs) and the 1H nutation frequency, ν1 (0–110 kHz) for the NH3+ peak intensity. (b) Comparison between 1H (ν0 = 500 MHz) 1D CRAMPS MAS NMR spectra acquired with windowed 1D CRAMPS (see Fig. 2b, τtilt = 0.54 μs, Ω = −0.6 kHz) two-variable optimization (ν0 = 500 MHz) of both τLG_expt (in steps of 0.25 μs) and the 1H nutation frequency, ν1 (0–110 kHz) for the NH3+ peak intensity. (b) Comparison between 1H (ν0 = 500 MHz) 1D CRAMPS MAS NMR spectra acquired with windowed 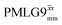 (ν1 = 113 kHz, τLG_expt = 2.92 μs, τtilt = 0.82 μs, Ω = −0.6 kHz), windowed (ν1 = 113 kHz, τLG_expt = 2.92 μs, τtilt = 0.82 μs, Ω = −0.6 kHz), windowed 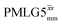 (ν1 = 106 kHz, τLG_expt = 3.1 μs, τtilt = 0.54 μs, Ω = −0.6 kHz), and a one-pulse MAS-alone experiment. (c) Comparison between 1H (ν0 = 1 GHz) 1D CRAMPS MAS NMR spectra acquired with windowed (ν1 = 106 kHz, τLG_expt = 3.1 μs, τtilt = 0.54 μs, Ω = −0.6 kHz), and a one-pulse MAS-alone experiment. (c) Comparison between 1H (ν0 = 1 GHz) 1D CRAMPS MAS NMR spectra acquired with windowed 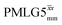 (ν1 = 108 kHz, τLG_expt = 3.10 μs, τtilt = 0.18 μs, Ω = −7.0 kHz), windowed (ν1 = 108 kHz, τLG_expt = 3.10 μs, τtilt = 0.18 μs, Ω = −7.0 kHz), windowed 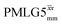 (ν1 = 52 kHz, τLG_expt = 3.63 μs, τtilt = 0.70 μs, Ω = −8.6 kHz), and a one-pulse MAS-alone experiment. 8 (a) or 32 (b and c) co-added transients were added for a recycle delay of 3 s. For all experiments, τw = 7.20 μs. (ν1 = 52 kHz, τLG_expt = 3.63 μs, τtilt = 0.70 μs, Ω = −8.6 kHz), and a one-pulse MAS-alone experiment. 8 (a) or 32 (b and c) co-added transients were added for a recycle delay of 3 s. For all experiments, τw = 7.20 μs. | ||
Fig. 3a reports on the NH3+ 1H resonance, noting its relevance in this paper for the 1H–15N refocused INEPT experiment. Fig. S2 (ESI‡) shows that optimum performance for the NH3+ 1H resonance (Fig. S2b, ESI‡) is closely matched by that for the CH21H resonances (Fig. S2a, ESI‡). 1D CRAMPS 1H NMR spectra of 15N-glycine for our best implementations of supercycled windowed 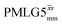 and
and 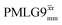 at ν0 = 500 MHz are shown in Fig. 3b, where enhanced resolution compared to MAS alone is evident. Moreover, both
at ν0 = 500 MHz are shown in Fig. 3b, where enhanced resolution compared to MAS alone is evident. Moreover, both 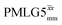 and
and 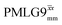 implemented at ν0 = 500 MHz (Fig. 3b) show better resolution than 60 kHz MAS alone at ν0 = 1 GHz (Fig. 3c). At ν0 = 1 GHz, optimised 1D CRAMPS 1H NMR spectra of 15N-glycine for windowed
implemented at ν0 = 500 MHz (Fig. 3b) show better resolution than 60 kHz MAS alone at ν0 = 1 GHz (Fig. 3c). At ν0 = 1 GHz, optimised 1D CRAMPS 1H NMR spectra of 15N-glycine for windowed 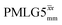 at a 1H nutation frequency of 108 and 51 kHz are presented in Fig. 3c that show enhanced resolution compared to MAS alone. Note that the latter case corresponds to the nutation frequency being less than the MAS frequency.
at a 1H nutation frequency of 108 and 51 kHz are presented in Fig. 3c that show enhanced resolution compared to MAS alone. Note that the latter case corresponds to the nutation frequency being less than the MAS frequency.
Table 1 compares the experimentally optimised τLG_expt values to the ideal τLG values: at ν0 = 500 MHz, the experimental values are less than half the ideal values, i.e., τLG_expt = 3.10 μs and 2.92 μs compared to 7.70 μs and 7.23 μs, respectively. As Table 1 further shows, with the corresponding changes in ΔνLG_expt and νeff_expt, the angle θ is 29.7°. While a very high nutation frequency of over 200 kHz has been used in the first experimental implementations of PMLG at 65 kHz MAS frequency59,65 resulting in a θ value of 61° for the spectrum presented by Leskes et al.,59 a similar value (of 31.2°) far from the magic angle has been reported by Nishiyama et al. for the implementation of windowed 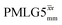 at an MAS frequency of 80 kHz and a 1H nutation frequency of 125 kHz.57 Moreover, the actual rotation, ξLG_expt, reported by Nishiyama et al. of 243° is similar to that of 239° for our implementation of both windowed
at an MAS frequency of 80 kHz and a 1H nutation frequency of 125 kHz.57 Moreover, the actual rotation, ξLG_expt, reported by Nishiyama et al. of 243° is similar to that of 239° for our implementation of both windowed 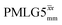 and
and 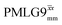 at a MAS frequency of 60 kHz (see Table 1). Table 1 also lists the implementations of
at a MAS frequency of 60 kHz (see Table 1). Table 1 also lists the implementations of 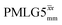 by Leskes et al. at 10 kHz MAS85 and Mao & Pruski at 12.5, 19.5, 25.0 and 41.7 kHz MAS:92 the angle θ is seen to vary between 45° and 64°. It is observed that an angle θ below and above the magic angle corresponds to an actual rotation, ξLG_expt, less than and more than the ideal 360°, respectively. For the good decoupling performance observed at ν0 = 1 GHz with windowed
by Leskes et al. at 10 kHz MAS85 and Mao & Pruski at 12.5, 19.5, 25.0 and 41.7 kHz MAS:92 the angle θ is seen to vary between 45° and 64°. It is observed that an angle θ below and above the magic angle corresponds to an actual rotation, ξLG_expt, less than and more than the ideal 360°, respectively. For the good decoupling performance observed at ν0 = 1 GHz with windowed 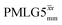 for a 1H nutation frequency of only 51 kHz (see Fig. 3c), the angle θ is only 17.6°.
for a 1H nutation frequency of only 51 kHz (see Fig. 3c), the angle θ is only 17.6°.
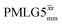 and
and 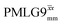 1H homonuclear decoupling: variation from the ideal Lee–Goldburg condition for this work and previous publications
1H homonuclear decoupling: variation from the ideal Lee–Goldburg condition for this work and previous publications
| Decoupling | ν r (kHz) | ν 1 (kHz) | τ LG (μs) | τ LG_expt (μs) | θ m (deg) | θ (deg) | ΔνLG (kHz) | ΔνLG_expt (kHz) | ν eff_LG (kHz) | ν eff_LG_expt (kHz) | ξ LG (deg) | ξ LG_expt (deg) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Parameters from this work for Fig. 3b and Table 3. b Parameters from this work for Fig. S3 (ESI). c Parameters from this work for Fig. 3c and Table 3. d Values extracted from Nishiyama et al. Fig. 2 and 3.57 e Values extracted from Leskes et al. Table 1.59 f Values extracted from Mao and Pruski,92 Fig. 3 and 2. g Values extracted from Leskes et al. Fig. 2.85 h Simulated values extracted from Leskes et al. Fig. 2.65 | ||||||||||||
Windowed 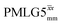 a (500 MHz) a (500 MHz) |
60.0 | 106 | 7.70 | 3.10 | 54.7 | 29.7 | 75.0 | 186.2 | 129.8 | 214.3 | 360.0 | 239.2 |
Windowless 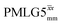 b (500 MHz) b (500 MHz) |
60.0 | 106 | 7.70 | 3.10 | 29.7 | 75.0 | 186.2 | 129.8 | 214.3 | 239.2 | ||
Windowed 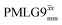 a (500 MHz) a (500 MHz) |
60.0 | 113 | 7.23 | 2.92 | 29.7 | 79.9 | 197.7 | 138.4 | 227.7 | 239.4 | ||
Windowless 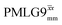 b (500 MHz) b (500 MHz) |
60.0 | 113 | 7.23 | 2.92 | 29.7 | 79.9 | 197.7 | 138.4 | 227.7 | 239.4 | ||
Windowed 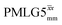 c (1 GHz, ν1 = 108 kHz) c (1 GHz, ν1 = 108 kHz) |
60.0 | 108 | 7.56 | 3.10 | 30.1 | 76.4 | 186.2 | 132.3 | 215.3 | 240.3 | ||
Windowed 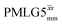 c (1 GHz, ν1 = 51 kHz) c (1 GHz, ν1 = 51 kHz) |
60.0 | 51 | 16.01 | 3.63 | 17.6 | 36.1 | 159.3 | 62.4 | 167.2 | 218.2 | ||
| Literature parameters | ||||||||||||
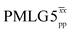 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
80.0 | 125 | 6.53 | 2.80 | 54.7 | 31.2 | 88.4 | 206.2 | 153.1 | 241.1 | 360.0 | 243.1 |
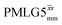
|
65.0 | 216 | 3.78 | 4.80 | 60.9 | 152.7 | 120.3 | 264.5 | 247.2 | 427.2 | ||
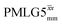
|
41.7 | 155 | 5.27 | 3.75 | 45.2 | 109.6 | 154.0 | 189.8 | 218.5 | 294.9 | ||
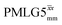
|
41.7 | 155 | 5.27 | 7.75 | 64.3 | 109.6 | 74.5 | 189.8 | 172.0 | 479.8 | ||
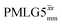
|
12.5 | 78 | 10.47 | 12.50 | 59.4 | 55.2 | 46.2 | 95.5 | 90.6 | 407.9 | ||
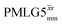
|
19.5 | 126 | 6.48 | 8.00 | 60.2 | 89.1 | 72.2 | 154.3 | 145.2 | 418.2 | ||
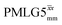
|
25.0 | 162 | 5.04 | 6.25 | 60.3 | 114.6 | 92.4 | 198.4 | 186.5 | 419.6 | ||
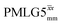
|
10.0 | 95 | 8.59 | 7.25 | 50.0 | 67.2 | 79.6 | 116.4 | 124.0 | 323.5 | ||
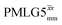
|
65.0 | 250 | 3.27 | 5.00 | 65.2 | 176.8 | 115.5 | 306.2 | 275.4 | 495.7 | ||
Table 2 states the τc values, as calculated from τLG_expt, τw and τtilt using eqn (10), for the implementations of 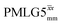 and
and 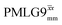 in this work, as well as that reported in the literature. An important parameter for predicting decoupling performance is the ratio, Ψ, of the MAS rotor period, τr, to the decoupling cycle time, τc, and vice versa, the ratio of the corresponding frequency, νc = 1/τc, to the MAS frequency, νr:65
in this work, as well as that reported in the literature. An important parameter for predicting decoupling performance is the ratio, Ψ, of the MAS rotor period, τr, to the decoupling cycle time, τc, and vice versa, the ratio of the corresponding frequency, νc = 1/τc, to the MAS frequency, νr:65
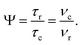 | (11) |
| nνr + kνr = 0, | (12) |
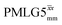 (Ψ = 1.34) and
(Ψ = 1.34) and 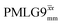 (Ψ = 1.43), are in line with the value of 1.40–1.60 reported by Mao et al. (in Tables 1 and 2 of their paper) for spectra acquired among a range of different spinning frequencies (12.5 kHz to 41.7 kHz) and 1H nutation frequencies (78–162 kHz).92 For windowed sequences, the Ψ value is usually lower. For the 1D CRAMPS spectra presented in Fig. 3b, Table 2 shows that Ψ equals 0.58 and 0.57 for windowed
(Ψ = 1.43), are in line with the value of 1.40–1.60 reported by Mao et al. (in Tables 1 and 2 of their paper) for spectra acquired among a range of different spinning frequencies (12.5 kHz to 41.7 kHz) and 1H nutation frequencies (78–162 kHz).92 For windowed sequences, the Ψ value is usually lower. For the 1D CRAMPS spectra presented in Fig. 3b, Table 2 shows that Ψ equals 0.58 and 0.57 for windowed 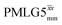 and windowed
and windowed 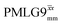 , respectively, at ν0 = 500 MHz, and 0.61 and 0.53 at ν0 = 1 GHz for a 1H nutation frequency of 108 and 51 kHz, respectively. These Ψ values are similar to the values of 0.60 and 0.63 for the experimental implementation of windowed
, respectively, at ν0 = 500 MHz, and 0.61 and 0.53 at ν0 = 1 GHz for a 1H nutation frequency of 108 and 51 kHz, respectively. These Ψ values are similar to the values of 0.60 and 0.63 for the experimental implementation of windowed 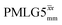 by Nishiyama et al. at an MAS frequency of 80 kHz and a 1H nutation frequency of 125 kHz57 and by Leskes et al. at an MAS frequency of 65 kHz and a 1H nutation frequency of 216 kHz,59 respectively.
by Nishiyama et al. at an MAS frequency of 80 kHz and a 1H nutation frequency of 125 kHz57 and by Leskes et al. at an MAS frequency of 65 kHz and a 1H nutation frequency of 216 kHz,59 respectively.
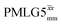 and
and 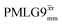 1H homonuclear decoupling: scaling factors and comparison of rotor period to cycle time for this work and previous publications
1H homonuclear decoupling: scaling factors and comparison of rotor period to cycle time for this work and previous publications
| τ LG_expt (μs) | τ w (μs) | τ tilt (μs) | τ c (μs) | τ r (μs) | Ψ | λ CS_calc | λ CS_expt | |
|---|---|---|---|---|---|---|---|---|
| a Parameters from this work for Fig. 3b and Table 3. b Parameters from this work for Fig. S5 (ESI). c Parameters from this work for Fig. 3c and Table 3. d Values extracted from Nishiyama et al. Fig. 2 and 3.57 e Values extracted from Leskes et al. Table 1.59 f Values extracted from Mao and Pruski,92 Fig. 3 and 2. g Values extracted from Leskes et al. Fig. 2.85 h Simulated values extracted from Leskes et al. Fig. 2.65 i λ CS is calculated with eqn (15) as stated in this paper, following from Nishiyama et al.57 j λ CS is calculated with eqn (16) as stated in this paper, following from Nishiyama et al.57 k Ψ is calculated with eqn (12), following from Leskes et al.65 | ||||||||
Windowed 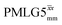 a (500 MHz) a (500 MHz) |
3.10 | 7.20 | 0.54 | 28.96 | 16.67 | 0.58 | 0.76j | 0.82 |
Windowless 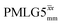 b (500 MHz) b (500 MHz) |
3.10 | — | — | 12.40 | 16.67 | 1.34 | 0.76i | 0.66 |
Windowed 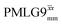 a (500 MHz) a (500 MHz) |
2.92 | 7.20 | 0.82 | 29.36 | 16.67 | 0.57 | 0.77j | 0.76 |
Windowless 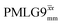 b (500 MHz) b (500 MHz) |
2.92 | — | — | 11.68 | 16.67 | 1.43 | 0.78i | 0.60 |
Windowed 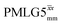 c (1 GHz, 108 kHz) c (1 GHz, 108 kHz) |
3.10 | 7.20 | 0.18 | 27.52 | 16.67 | 0.61 | 0.74j | 0.82 |
Windowed 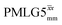 c (1 GHz, 51 kHz) c (1 GHz, 51 kHz) |
3.63 | 7.20 | 0.70 | 31.70 | 16.67 | 0.53 | 0.90j | 0.92 |
| Literature parameters | ||||||||
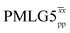 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
2.80 | 4.84 | — | 20.88 | 12.50 | 0.60 | 0.86i | 0.82 |
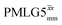
|
4.80 | 2.70 | — | 24.60 | 15.38 | 0.63 | 0.40i | 0.48 |
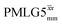
|
3.75 | — | — | 15.00 | 24.00 | 1.60 | 0.50i | 0.36 |
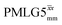
|
7.75 | — | — | 31.00 | 24.00 | 0.77 | 0.19i | 0.21 |
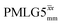
|
12.50 | — | — | 50.00 | 80.00 | 1.60 | 0.26i | — |
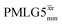
|
8.00 | — | — | 32.00 | 51.20 | 1.60 | 0.25i | — |
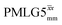
|
6.25 | — | — | 25.00 | 40.00 | 1.60 | 0.25i | — |
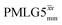
|
7.25 | 4.35 | — | 37.70 | 100.00 | 2.65 | 0.55i | 0.47 |
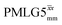
|
5.00 | — | — | 20.00 | 15.38 | 0.77 | 0.18i | — |
3.4 Windowed and windowless PMLG 1H decoupling, 1H spin-echo dephasing and scaling factors
It is well established that the application of rf 1H homonuclear decoupling leads to a chemical shift scaling: for a static sample, the chemical shift scaling factor, λCS, for perfect decoupling cannot exceed cos−1(θm) = 1/√3 = 0.577.64,95,96 The 1D 1H CRAMPS spectra presented in Fig. 3b and c have chemical shift axes that have been corrected for this scaling, i.e., a scaling is applied so as to ensure that the chemical shift separation between the NH3+ peak and the lower ppm CH2 peak corresponds to the MAS-only 1H chemical shifts, i.e., 8.4–3.0 = 5.4 ppm. The full width at half maximum, (FWHM), of the three 1H resonances before and after scaling for the spectra presented in Fig. 3b and c are presented in Table 3. Table 3 also states that λCS equals 0.82 and 0.76 for windowed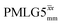 and windowed
and windowed 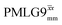 , respectively, at ν0 = 500 MHz, and 0.82 and 0.92 at ν0 = 1 GHz for a 1H nutation frequency of 108 and 51 kHz, respectively. Table 3 also reports, as a measure of decoupling efficiency, K, given by
, respectively, at ν0 = 500 MHz, and 0.82 and 0.92 at ν0 = 1 GHz for a 1H nutation frequency of 108 and 51 kHz, respectively. Table 3 also reports, as a measure of decoupling efficiency, K, given by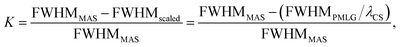 | (13) |
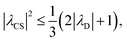 | (14) |
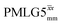 and
and 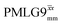 1H homonuclear decoupling efficiency for 1H (ν0 = 500 MHz and 1 GHz) CRAMPS NMR at νr = 60 kHz of 15N-glycinea
1H homonuclear decoupling efficiency for 1H (ν0 = 500 MHz and 1 GHz) CRAMPS NMR at νr = 60 kHz of 15N-glycinea
| δ (ppm) | FWHMMAS (Hz) | FWHMMAS (ppm) | FWHMPMLG (Hz) | FWHMPMLG (ppm) | FWHMscaled (Hz) | FWHMscaled (ppm) | Scaling factor, λCS | K | FWHMPMLG (Hz) | FWHMPMLG (ppm) | FWHMscaled (Hz) | FWHMscaled (ppm) | Scaling factor, λCS | K | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a See spectra in Fig. 3b (ν0 = 500 MHz) and Fig. 3c (ν0 = 1 GHz), for the pulse sequence in Fig. 2b and experimental parameters in Table 2. b Calculated with eqn (13). c FWHM extracted from the indirect dimension of a 2D 1H–1H correlation experiment with MAS alone, see Fig. S4 in the ESI. | |||||||||||||||
| ν 0 = 500 MHz |
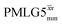 (ν1 = 106 kHz) (ν1 = 106 kHz) |
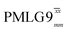 (ν1 = 113 kHz) (ν1 = 113 kHz) |
|||||||||||||
| NH3+ | 8.4 | 664 | 1.33 | 230 | 0.46 | 280 | 0.56 | 0.82 | 0.58 | 273 | 0.55 | 359 | 0.72 | 0.76 | 0.46 |
| CH2 | 4.2 | 800c | 1.60 | 217 | 0.43 | 264 | 0.53 | 0.67 | 213 | 0.43 | 280 | 0.56 | 0.65 | ||
| CH2 | 3.0 | 800c | 1.60 | 224 | 0.45 | 273 | 0.55 | 0.66 | 232 | 0.46 | 305 | 0.61 | 0.62 | ||
| ν 0 = 1 GHz |
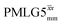 (ν1 = 108 kHz) (ν1 = 108 kHz) |
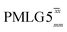 (ν1 = 51 kHz) (ν1 = 51 kHz) |
|||||||||||||
| NH3+ | 8.4 | 700 | 0.70 | 583 | 0.58 | 711 | 0.71 | 0.82 | −0.02 | 475 | 0.48 | 516 | 0.52 | 0.92 | 0.26 |
| CH2 | 4.2 | 740 | 0.74 | 346 | 0.35 | 422 | 0.42 | 0.43 | 448 | 0.45 | 487 | 0.49 | 0.34 | ||
| CH2 | 3.0 | 740 | 0.74 | 311 | 0.31 | 379 | 0.38 | 0.49 | 440 | 0.44 | 478 | 0.48 | 0.35 | ||
For 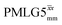 , Nishiyama et al. report a λCS of 0.82 at 80 kHz MAS and a 1H nutation frequency of 125 kHz. Nishiyama et al. further state equations for calculating λCS for
, Nishiyama et al. report a λCS of 0.82 at 80 kHz MAS and a 1H nutation frequency of 125 kHz. Nishiyama et al. further state equations for calculating λCS for 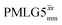 decoupling without and with tilt pulses:
decoupling without and with tilt pulses:
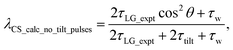 | (15) |
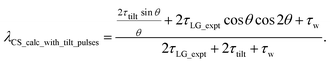 | (16) |
 in the literature, as well as
in the literature, as well as  and
and 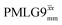 in this work. Deviation of the experimental scaling factor compared to theoretical behaviour can arise from phase transients that cause phase propagation delays.91,97
in this work. Deviation of the experimental scaling factor compared to theoretical behaviour can arise from phase transients that cause phase propagation delays.91,97
As well as scaling the chemical shifts, 1H homonuclear decoupling also scales evolution under a heteronuclear J coupling by the same factor.37,57,79 For magnetisation transfer from 15N to 1H during the spin echoes of the refocused INEPT pulse sequence element, the efficiency depends upon this scaling of the 15N–1H J couplings, but also the spin-echo dephasing time, 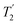 .92,98,99
.92,98,99
Fig. 4 compares spin-echo dephasing curves (see pulse sequence in Fig. 2c) for MAS alone to those for windowed and windowless 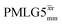 and
and 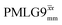 , with the values for experimental parameters and extracted
, with the values for experimental parameters and extracted 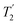 presented in Table 4. (Note that
presented in Table 4. (Note that 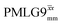 homonuclear decoupling was implemented with a slightly changed nutation frequency of ν1 = 109 kHz, as compared to ν1 = 113 kHz for the 1D CRAMPS spectrum in Fig. 3b). In windowless PMLG decoupling, there is continuous rf irradiation, i.e., there are no tilt pulses and τw = 0, while, in the windowed version, τw is replaced by a delay (Fig. 2e.) Note that the first implementation of PMLG was in the indirect dimension of a two-dimensional 1H–1H experiment where there is evolution under MAS alone in the direct dimension.49 Such a 2D experiment (see Fig. 2d) is used to measure λCS for our implementation of windowless
homonuclear decoupling was implemented with a slightly changed nutation frequency of ν1 = 109 kHz, as compared to ν1 = 113 kHz for the 1D CRAMPS spectrum in Fig. 3b). In windowless PMLG decoupling, there is continuous rf irradiation, i.e., there are no tilt pulses and τw = 0, while, in the windowed version, τw is replaced by a delay (Fig. 2e.) Note that the first implementation of PMLG was in the indirect dimension of a two-dimensional 1H–1H experiment where there is evolution under MAS alone in the direct dimension.49 Such a 2D experiment (see Fig. 2d) is used to measure λCS for our implementation of windowless 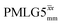 and
and 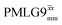 , as reported in Tables 2 and 4 (spectra are presented in Fig. S4, ESI‡).
, as reported in Tables 2 and 4 (spectra are presented in Fig. S4, ESI‡).
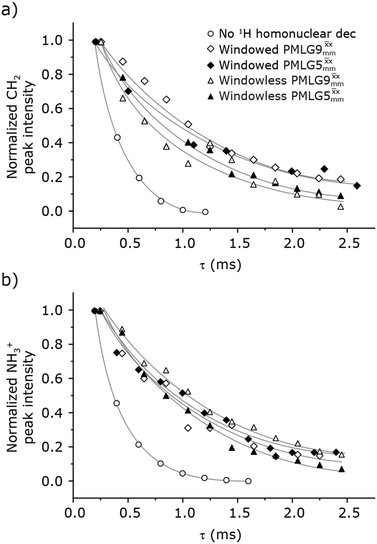 | ||
Fig. 4 Dephasing of the 15N-glycine (a) CH2 (the higher ppm 1H resonance is considered) and (b) NH3+ proton resonances as a function of the spin-echo (see Fig. 2c) duration, τ, with no 1H homonuclear decoupling (empty circles), windowed 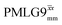 (empty diamonds), windowed (empty diamonds), windowed 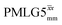 (full diamonds), windowless (full diamonds), windowless 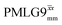 (empty triangles), and windowless (empty triangles), and windowless 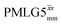 (full triangles) for nutation frequencies and resonance offsets as stated in Table 4. Fits to an exponential decay function are shown, with the spin-echo dephasing times, (full triangles) for nutation frequencies and resonance offsets as stated in Table 4. Fits to an exponential decay function are shown, with the spin-echo dephasing times, 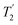 , as listed in Table 4. 16 transients were co-added for a recycle delay of 3 s. For all experiments with windowed 1H homonuclear decoupling, τw = 7.20 μs. , as listed in Table 4. 16 transients were co-added for a recycle delay of 3 s. For all experiments with windowed 1H homonuclear decoupling, τw = 7.20 μs. | ||
Considering Fig. 4 and Table 4, the 1H dephasing times, 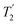 , for the CH2 (the higher ppm resonance is considered) and NH3+ peaks are 0.22 ms and 0.25 ms for 60 kHz MAS alone. With 1H homonuclear decoupling the 1H dephasing time for both groups increases. The longest CH2 dephasing time is observed for windowed
, for the CH2 (the higher ppm resonance is considered) and NH3+ peaks are 0.22 ms and 0.25 ms for 60 kHz MAS alone. With 1H homonuclear decoupling the 1H dephasing time for both groups increases. The longest CH2 dephasing time is observed for windowed 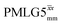 ,
, 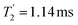 , slightly longer than for windowed
, slightly longer than for windowed 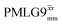 , where
, where 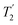 is equal to 1.10 ms. However, the scaling by λCS needs to be considered and Table 4 reports the product of λCS and
is equal to 1.10 ms. However, the scaling by λCS needs to be considered and Table 4 reports the product of λCS and 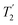 in each case. After this scaling (Table 4), windowed
in each case. After this scaling (Table 4), windowed 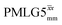 achieves an over 4 fold improvement with respect of MAS alone, compared to the slightly under 4 fold improvement of windowed
achieves an over 4 fold improvement with respect of MAS alone, compared to the slightly under 4 fold improvement of windowed 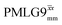 . A similar comparison can be made for the NH3+ peak, where windowless
. A similar comparison can be made for the NH3+ peak, where windowless 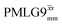 shows the longest
shows the longest 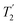 equal to 1.15 ms and the longest value of the product, λCS
equal to 1.15 ms and the longest value of the product, λCS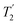 of 0.69 ms, thanks again to the large λCS; this corresponds to a just under 3 fold improvement with respect to MAS alone.
of 0.69 ms, thanks again to the large λCS; this corresponds to a just under 3 fold improvement with respect to MAS alone.
3.5 Optimisation of the 15N-glycine NH3+ signal intensity in a 1D-filtered CP-refocused INEPT NMR spectrum for PMLG 1H decoupling at 60 kHz MAS
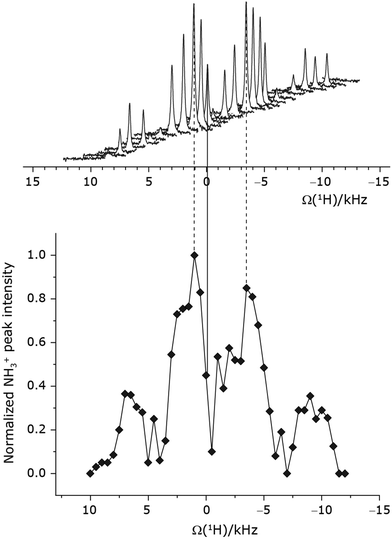
Under a 1H homonuclear decoupling sequence such as PMLG, the proton offset frequency influences the performance;53,54 this is linked to the overall z-rotation that the spins need under decoupling to avoid artifacts and RF imperfections.85 As shown by Leskes et al.,89 the non-supercycled m-block is particularly beneficial in narrowing lines of strong coupled spins, as for the CH2 groups of 15N-glycine, close to the on-resonance position. With the implementation of supercycled PMLG schemes,90 the sign of the offset is no longer a determining factor as the supercycle brings the effective rotation of the spins closer to the z-axis.100 However, the choice of the optimum offset still plays a significant role for achieving good decoupling performance, therefore it is necessary to investigate both positive and negative offsets. Here the optimization was performed directly on the 15N–1H CP-refocused INEPT experiment, where windowed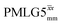 was applied over a wide range of offset values from ∼+10 kHz to −12 kHz, whereby on-resonance corresponds to the NH3+ peak. Fig. 5 shows that the best offsets in term of sensitivity are at +1 kHz and −3.5 kHz, highlighted by dashed vertical lines. Between the two best performing offsets, the sensitivity experiences a fluctuation (Fig. 5) corresponding to the on-resonance position (solid line), dropping to zero for a small negative offset of −0.5 kHz. It is then important to optimize the offset avoiding the on-resonance position. The need for a fine optimization of this parameter is emphasized by the considerable change in sensitivity that is observed for a small variation of the offset.53,54,95 For example, the relative sensitivity of the NH3+ peak falls from over 0.8 to 0.5 when switching the offset from ∼−3.5 to −2.5 kHz. In general, in Fig. 5 the offsets close to the on-resonance position yield better sensitivity symmetrically in a range between ±4 kHz, in agreement with the rotation improvement brought by the supercycled 1H homonuclear decoupling.89
was applied over a wide range of offset values from ∼+10 kHz to −12 kHz, whereby on-resonance corresponds to the NH3+ peak. Fig. 5 shows that the best offsets in term of sensitivity are at +1 kHz and −3.5 kHz, highlighted by dashed vertical lines. Between the two best performing offsets, the sensitivity experiences a fluctuation (Fig. 5) corresponding to the on-resonance position (solid line), dropping to zero for a small negative offset of −0.5 kHz. It is then important to optimize the offset avoiding the on-resonance position. The need for a fine optimization of this parameter is emphasized by the considerable change in sensitivity that is observed for a small variation of the offset.53,54,95 For example, the relative sensitivity of the NH3+ peak falls from over 0.8 to 0.5 when switching the offset from ∼−3.5 to −2.5 kHz. In general, in Fig. 5 the offsets close to the on-resonance position yield better sensitivity symmetrically in a range between ±4 kHz, in agreement with the rotation improvement brought by the supercycled 1H homonuclear decoupling.89
The same offset optimization was carried out on the different PMLG-block types, and similar trends were shown with a better sensitivity in the proximity of the on-resonance position. As stated in Table 4, the offsets which gave the maximum sensitivity were 0.75 kHz for windowed 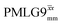 , −0.25 kHz for
, −0.25 kHz for 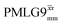 and +1 kHz for
and +1 kHz for 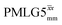 (the same as windowed
(the same as windowed 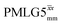 ) (see Fig. S5, ESI‡).
) (see Fig. S5, ESI‡).
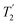 , and
, and 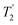 scaled by the experimental λCS, λCS
scaled by the experimental λCS, λCS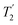 , as determined by a 1H spin-echo MAS NMR experimenta for 15N-glycine with optimised rf carrier offset and ν1
, as determined by a 1H spin-echo MAS NMR experimenta for 15N-glycine with optimised rf carrier offset and ν1
| Offset (kHz) | ν 1 (kHz) | λ CS | NH3+ (ms) | NH3+λCS (ms) | CH2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (ms) b (ms) |
CH2λCS (ms) | |
|---|---|---|---|---|---|---|---|
a
As implemented at ν0 = 500 MHz and νr = 60 kHz, see Fig. 4a for the CH2 resonance and Fig. 4b for the NH3+ peak. τtilt is equal to 0.54 μs for windowed 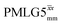 and 0.82 μs for windowed and 0.82 μs for windowed 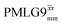 .
b For the CH2 group, the .
b For the CH2 group, the 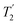 of the higher-ppm 1H resonance is stated. of the higher-ppm 1H resonance is stated.
|
|||||||
| No decoupling | 2 | — | 1 | 0.25 | 0.25 | 0.22 | 0.22 |
Windowed 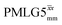 |
1 | 106 | 0.82 | 1.04 | 0.85 | 1.14 | 0.93 |
Windowed 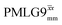 |
0.75 | 109 | 0.76 | 0.91 | 0.69 | 1.10 | 0.84 |
Windowless 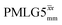 |
1 | 106 | 0.66 | 0.86 | 0.57 | 0.80 | 0.53 |
Windowless 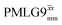 |
−0.25 | 109 | 0.60 | 1.15 | 0.69 | 0.78 | 0.47 |
The implementation of the 1H decoupling scheme into the heteronuclear correlation experiment required the further optimisation of the spin-echo durations during the refocused INEPT transfer. This was carried out separately for τ1 and τ2 (see pulse sequence in Fig. 1a) because, as stated in Section 3.1, for the two spin echoes, different spins are along the transverse plane, 15N for the first and 1H for the second spin echo. To ensure the best conditions, a double-optimisation of 1H homonuclear decoupling nutation frequency vs. τ1 and τ2 was carried out. Specifically, the two-variable optimisation was performed for 15N-labelled glycine for windowed or windowless 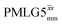 and
and 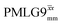 for the best offset (see Table 5) and the results are reported in Table 5. The dependence with respect to the second spin-echo duration, τ2, is presented in Fig. 6. Note from eqn (2), a sine dependence is expected from which the scaled J coupling could be extracted.
for the best offset (see Table 5) and the results are reported in Table 5. The dependence with respect to the second spin-echo duration, τ2, is presented in Fig. 6. Note from eqn (2), a sine dependence is expected from which the scaled J coupling could be extracted.
| 1H homonuclear decoupling | Offsetb (kHz) | λ CS | τ 1 (ms) | λ CS τ 1 (ms) | ν 1 (kHz) for τ1 | τ 2 (ms) | λ CS τ 2 (ms) | ν 1 (kHz) for τ2 | Relative intensityd |
|---|---|---|---|---|---|---|---|---|---|
a As implemented at ν0 = 500 MHz and νr = 60 kHz. τtilt is equal to 0.54 μs for windowed 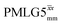 and 0.82 μs for windowed and 0.82 μs for windowed 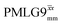 . See Fig. 6.
b Relative to the NH3+ 1H resonance.
c
τ
1 = nτc, τ2 = mτc, where n and m are positive integers.
d See Fig. 7. . See Fig. 6.
b Relative to the NH3+ 1H resonance.
c
τ
1 = nτc, τ2 = mτc, where n and m are positive integers.
d See Fig. 7.
|
|||||||||
| No decoupling | 2.00 | 1.00 | 1.600 | 1.600 | — | 0.300 | 0.300 | — | 0.08 |
Windowed 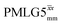 |
1.00 | 0.82 | 1.999 (69τc) | 1.639 | 106 | 1.391 (48τc) | 1.140 | 106 | 1.00 |
Windowed 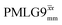 |
0.75 | 0.76 | 2.085 (71τc) | 1.585 | 104 | 1.498 (51τc) | 1.138 | 106 | 0.80 |
Windowless 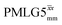 |
1.00 | 0.66 | 2.096 (169τc) | 1.383 | 102 | 0.496 (40τc) | 0.327 | 102 | 0.52 |
Windowless 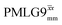 |
−0.25 | 0.60 | 2.091 (179τc) | 1.254 | 104 | 1.192 (102τc) | 0.715 | 102 | 0.48 |
Considering Table 5, the 1H nutation frequencies are in the range of 102–106 kHz for all the PMLG-block types, with a maximum of 2 kHz difference between that applied in τ1 and τ2 for the same PMLG block. For τ1, the optimum values for PMLG decoupling are 2.0 or 2.1 ms, as compared to 1.6 ms from MAS alone. However, as discussed in Section 3.4, it is the product λCS·τ, that needs to be considered, in which case similar values are obtained as compared to MAS alone. By comparison, a clear difference is observed for τ2, where the evolution of 1H coherence is markedly affected by the 1H–1H dipolar couplings. Indeed, the coherence transfer increases from 0.3 ms for MAS alone to 1.5 ms for windowed 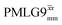 and 1.4 ms for windowed
and 1.4 ms for windowed 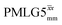 . After scaling, the product λCSτ2, 1.14 ms for both windowed
. After scaling, the product λCSτ2, 1.14 ms for both windowed 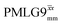 and
and 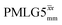 , are still ∼4 times longer than the optimum τ2 for MAS alone. We note a discrepancy for τ2 under windowless
, are still ∼4 times longer than the optimum τ2 for MAS alone. We note a discrepancy for τ2 under windowless 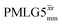 , which is considerably shorter (0.3 ms after scaling) with respect to the other 1H homonuclear implementations.
, which is considerably shorter (0.3 ms after scaling) with respect to the other 1H homonuclear implementations.
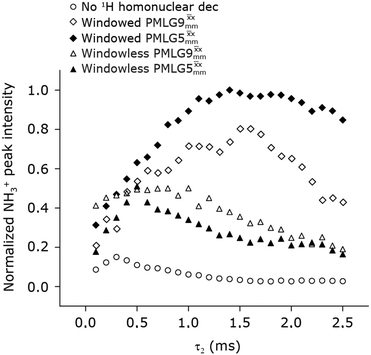
In Fig. 7, we compare the different peak intensities for the NH3+ peak of 15N-labelled glycine for the windowless and windowed implementation of 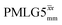 and
and 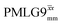 in a 15N–1H CP-refocused INEPT 1D filtered (t1 = 0) spectrum. The best performance is for our optimum implementation of windowed
in a 15N–1H CP-refocused INEPT 1D filtered (t1 = 0) spectrum. The best performance is for our optimum implementation of windowed 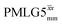 with a 12.5 times better relative sensitivity compared to MAS alone.
with a 12.5 times better relative sensitivity compared to MAS alone.
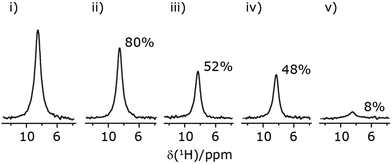 | ||
Fig. 7 Comparison of the sensitivity of 1D-filtered (t1 = 0) 15N–1H (ν0 = 500 MHz) CP (contact time = 2 ms)-refocused INEPT MAS (νr = 60 kHz) NMR spectra of 15N-glycine recorded with the application of different optimised PMLG 1H decoupling conditions, (i)–(iv) compared to MAS alone, (v): (i) windowed 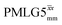 (τLG_expt = 3.1 μs, τtilt = 0.54 μs, τ1 = 1.999 ms (69τc) with ν1 = 106 kHz; τ2 = 1.391 ms (48τc) with ν1 = 106 kHz), (ii) windowed (τLG_expt = 3.1 μs, τtilt = 0.54 μs, τ1 = 1.999 ms (69τc) with ν1 = 106 kHz; τ2 = 1.391 ms (48τc) with ν1 = 106 kHz), (ii) windowed 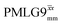 (τLG_expt = 2.92 μs, τtilt = 0.82 μs, τ1 = 2.085 ms (71τc) with ν1 = 104 kHz; τ2 = 1.498 ms (51τc) with ν1 = 106 kHz), (iii) windowless (τLG_expt = 2.92 μs, τtilt = 0.82 μs, τ1 = 2.085 ms (71τc) with ν1 = 104 kHz; τ2 = 1.498 ms (51τc) with ν1 = 106 kHz), (iii) windowless 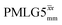 (τLG_expt = 3.1 μs, τ1 = 2.096 ms (169τc) with ν1 = 102 kHz; τ2 = 0.496 ms (40τc) with ν1 = 102 kHz), (iv) windowless (τLG_expt = 3.1 μs, τ1 = 2.096 ms (169τc) with ν1 = 102 kHz; τ2 = 0.496 ms (40τc) with ν1 = 102 kHz), (iv) windowless 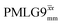 (τLG_expt = 2.92 μs, τ1 = 2.090 ms (179τc) with ν1 = 104 kHz; τ2 = 1.192 ms (102τc) with ν1 = 102 kHz), (v) no decoupling τ1 = 1.6 ms (96τr) and τ2 = 0.3 ms (18τr). For all experiments with windowed 1H homonuclear decoupling, τw = 7.20 μs. All the spectra were acquired with 16 coadded transients and the corresponding 1H transmitter offset reported in Table 5. (τLG_expt = 2.92 μs, τ1 = 2.090 ms (179τc) with ν1 = 104 kHz; τ2 = 1.192 ms (102τc) with ν1 = 102 kHz), (v) no decoupling τ1 = 1.6 ms (96τr) and τ2 = 0.3 ms (18τr). For all experiments with windowed 1H homonuclear decoupling, τw = 7.20 μs. All the spectra were acquired with 16 coadded transients and the corresponding 1H transmitter offset reported in Table 5. | ||
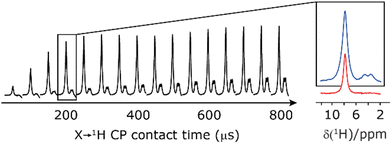
Finally, in this section, we compare the sensitivity and selectivity of the CP refocused INEPT experiment to that of a hNH double CP experiment. Specifically, the right-hand side of Fig. 8 compares 1D-filtered MAS NMR spectra of 15N-glycine recorded using the CP refocused INEPT experiment (red) or a hNH double CP experiment with a back (15N to 1H) CP contact time of 200 μs (blue). In both cases, the 1H to 15N CP contact time is 3.7 ms, i.e., CP is used initially to efficiently generate 15N transverse magnetisation. While the sensitivity of the CP refocused INEPT spectrum is half that of the double CP experiment, there is no intensity for the CH21H resonances. Fig. 8 also shows, for the double CP experiment, the dependence on the back (15N to 1H) CP contact time, with a plateau in intensity reached after 200 μs, though note that CH21H resonance signal is already evident from 100 μs.
3.6 2D 15N–1H CP-refocused INEPT NMR spectra with PMLG 1H decoupling at 60 kHz MAS of a dipeptide and a pharmaceutical at natural abundance
Due to the better sensitivity of windowed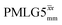 observed for glycine, it was selected as the 1H homonuclear decoupling sequence for a 15N–1H correlation experiment recorded for the β-AspAla dipeptide at natural isotopic abundance, with the improvement of resolution achieved in the 1D 1H CRAMPS compared here with a 1H one-pulse recorded at Larmor frequency of 500 MHz and 1 GHz (Fig. 9a). Note that a 15N CP MAS spectrum for the β-AspAla dipeptide has been presented in Tatton et al.22 The 15N–1H CP-refocused INEPT experiment was implemented with the offset and coherence transfer delays optimised for 15N-labelled glycine, as stated in Table 5, i.e., τLG_expt = 3.1 μs, τtilt = 0.54 μs, τ1 = 2.0 ms with ν1 = 106 kHz, v2 = 1.4 ms with ν1 = 106 kHz, and an offset of +1 kHz. High-performance 1H homonuclear decoupling achieved with a finely optimised implementation of windowed
observed for glycine, it was selected as the 1H homonuclear decoupling sequence for a 15N–1H correlation experiment recorded for the β-AspAla dipeptide at natural isotopic abundance, with the improvement of resolution achieved in the 1D 1H CRAMPS compared here with a 1H one-pulse recorded at Larmor frequency of 500 MHz and 1 GHz (Fig. 9a). Note that a 15N CP MAS spectrum for the β-AspAla dipeptide has been presented in Tatton et al.22 The 15N–1H CP-refocused INEPT experiment was implemented with the offset and coherence transfer delays optimised for 15N-labelled glycine, as stated in Table 5, i.e., τLG_expt = 3.1 μs, τtilt = 0.54 μs, τ1 = 2.0 ms with ν1 = 106 kHz, v2 = 1.4 ms with ν1 = 106 kHz, and an offset of +1 kHz. High-performance 1H homonuclear decoupling achieved with a finely optimised implementation of windowed 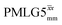 enables the recording at natural abundance of a 2D 15N–1H correlation spectrum at 60 kHz MAS with a through-bond back transfer (Fig. 9b). The sensitivity of the windowed
enables the recording at natural abundance of a 2D 15N–1H correlation spectrum at 60 kHz MAS with a through-bond back transfer (Fig. 9b). The sensitivity of the windowed 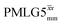 implementation is compared to a 15N–1H CP-refocused INEPT spectrum recorded with no decoupling at the optimum τ1 = 1.6 ms and τ2 = 0.3 ms values in Table 5 for 15N-labelled glycine; only noise is observed in Fig. 9c.
implementation is compared to a 15N–1H CP-refocused INEPT spectrum recorded with no decoupling at the optimum τ1 = 1.6 ms and τ2 = 0.3 ms values in Table 5 for 15N-labelled glycine; only noise is observed in Fig. 9c.
As noted in Section 3.1, there is a different dependence on the duration of the first spin echo, τ1, for a NH and NH3+ moiety, compare eqn (1) and (2). This is evident from Fig. 10 that shows the build-up of intensity in a 1D-filtered 15N–1H CP-refocused INEPT spectrum of the dipeptide β-AspAla. Two peaks are resolved for the higher-ppm NH and the lower-ppm NH3+ resonances (see deconvolution in Fig. 10b), and it is evident maximum intensity is reached at a shorter spin-echo duration for the lower-ppm NH3+ peak at ∼2.1 ms as compared to ∼3.5 ms for the higher-ppm NH peak. As shown in Fig. S7 of the ESI,‡ this is expected as based from a consideration of eqn (1) and (2). Such an experiment could hence be used to distinguish different NHx moieties, as for example has been demonstrated analogously for SiHx groups.82–84
Furthermore, windowed 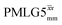 was employed to record a 2D 15N–1H CP-refocused INEPT spectrum of the pharmaceutical cimetidine at natural abundance (Fig. 9d), for which 1H, 15N CPMAS and 14N–1H spectra have been presented in ref. 101 and 102. (For comparison, note that in ref. 101, Tatton et al. use a simple 15N–1H heteronuclear spin echo with 1H homonuclear decoupling to demonstrate spectral editing.) In this case, spin-echo curves were recorded, because, as discussed above, the optimum τ1 and τ2 durations in the refocused INEPT pulse sequence element depends both on the J coupling between the involved nuclei and the 1H dephasing
was employed to record a 2D 15N–1H CP-refocused INEPT spectrum of the pharmaceutical cimetidine at natural abundance (Fig. 9d), for which 1H, 15N CPMAS and 14N–1H spectra have been presented in ref. 101 and 102. (For comparison, note that in ref. 101, Tatton et al. use a simple 15N–1H heteronuclear spin echo with 1H homonuclear decoupling to demonstrate spectral editing.) In this case, spin-echo curves were recorded, because, as discussed above, the optimum τ1 and τ2 durations in the refocused INEPT pulse sequence element depends both on the J coupling between the involved nuclei and the 1H dephasing 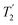 . The 1H coherence lifetime (see Fig. S6 and Table S1 (ESI‡) in comparison to Table 4) for two of the protons directly bonded to the nitrogens, N3 and N10, is longer than the NH3+
. The 1H coherence lifetime (see Fig. S6 and Table S1 (ESI‡) in comparison to Table 4) for two of the protons directly bonded to the nitrogens, N3 and N10, is longer than the NH3+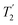 of 15N-glycine acquired with the same windowed
of 15N-glycine acquired with the same windowed 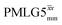 1H decoupling. In addition, considering the above discussion of Fig. 10 and eqn (1) and (2), note that for a NH group, a maximum signal is observed at a longer τ1 as compared to a NH3+ group. For this reason, τ1 and τ2 were increased to 2.5 ms and 2.0 ms, respectively. Note that weaker intensity is observed for the proton directly bonded to N15, where the respective 1H
1H decoupling. In addition, considering the above discussion of Fig. 10 and eqn (1) and (2), note that for a NH group, a maximum signal is observed at a longer τ1 as compared to a NH3+ group. For this reason, τ1 and τ2 were increased to 2.5 ms and 2.0 ms, respectively. Note that weaker intensity is observed for the proton directly bonded to N15, where the respective 1H 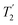 is ∼0.5 ms after scaling (Table S1, ESI‡). Further investigation is required to understand the shorter
is ∼0.5 ms after scaling (Table S1, ESI‡). Further investigation is required to understand the shorter 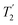 for this proton and the very weak signal for the N15–H15 cross peak in the 2D CP-refocused INEPT spectrum in Fig. 9d.
for this proton and the very weak signal for the N15–H15 cross peak in the 2D CP-refocused INEPT spectrum in Fig. 9d.
4. Conclusions and outlook
This paper has identified 1H homonuclear decoupling conditions for the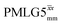 supercycle at 60 kHz MAS that give enhanced resolution in a 1D NMR spectrum as compared to MAS alone. At 1 GHz, we report what we believe to be the first example of effective homonuclear decoupling achieved by using a rf nutation frequency lower than the MAS frequency. The establishing of 2D 15N–1H heteronuclear correlation for natural abundance solids using a 1H detected CP-J coupling based refocused INEPT MAS NMR experiment26,38,39 has been demonstrated at 60 kHz MAS. The application of 1H homonuclear decoupling, specifically the
supercycle at 60 kHz MAS that give enhanced resolution in a 1D NMR spectrum as compared to MAS alone. At 1 GHz, we report what we believe to be the first example of effective homonuclear decoupling achieved by using a rf nutation frequency lower than the MAS frequency. The establishing of 2D 15N–1H heteronuclear correlation for natural abundance solids using a 1H detected CP-J coupling based refocused INEPT MAS NMR experiment26,38,39 has been demonstrated at 60 kHz MAS. The application of 1H homonuclear decoupling, specifically the 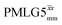 supercycle26,39,57,85 results in a factor of 12.5 sensitivity enhancement as compared to MAS alone. Notably, in our implementation at 500 MHz, a comparatively low 1H nutation frequency, for a 1.3 mm rotor, of 100 kHz was used, with this being associated with a high chemical shift scaling factor of 0.82 and a large deviation from the ideal Lee–Goldburg condition. Future work could further probe the suitability and optimisation of such windowed and windowless decoupling sequences for applications involving spin-echo evolution. In addition, nutation-frequency-selective pulses that reduce rf inhomogeneity could also be explored.103 The CP-refocused INEPT pulse sequence is complementary to dipolar coupling-based double CP or the use of symmetry-based decoupling to establish 15N–1H heteronuclear correlation under fast MAS.26,29,30,104 Note that the use of symmetry-based recoupling is more prone to t1 noise.105–107 In future work, the extension of our approach to 100+ kHz MAS could be considered, noting an increasing number of applications to pharmaceuticals and other small and moderately sized organic molecules.9,108–114
supercycle26,39,57,85 results in a factor of 12.5 sensitivity enhancement as compared to MAS alone. Notably, in our implementation at 500 MHz, a comparatively low 1H nutation frequency, for a 1.3 mm rotor, of 100 kHz was used, with this being associated with a high chemical shift scaling factor of 0.82 and a large deviation from the ideal Lee–Goldburg condition. Future work could further probe the suitability and optimisation of such windowed and windowless decoupling sequences for applications involving spin-echo evolution. In addition, nutation-frequency-selective pulses that reduce rf inhomogeneity could also be explored.103 The CP-refocused INEPT pulse sequence is complementary to dipolar coupling-based double CP or the use of symmetry-based decoupling to establish 15N–1H heteronuclear correlation under fast MAS.26,29,30,104 Note that the use of symmetry-based recoupling is more prone to t1 noise.105–107 In future work, the extension of our approach to 100+ kHz MAS could be considered, noting an increasing number of applications to pharmaceuticals and other small and moderately sized organic molecules.9,108–114
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. T. thanks Bruker and EPSRC for a PhD studentship through the EPSRC Centre for Doctoral Training in Molecular Analytical Science, grant number EP/L015307/1. The UK High-Field Solid-State NMR Facility used in this research was funded by EPSRC and BBSRC (EP/T015063/1), as well as, for the 1 GHz instrument, EP/R029946/1. The renewal of the 600 MHz solid-state NMR console (Avance NEO) was funded by BBSRC (BB/T018119/1), EPSRC and University of Warwick. We thank Dr Andrew P. Howes and Patrick Ruddy for supporting the operation of the Millburn House Magnetic Resonance Laboratory. Data for this study are provided as a supporting data set from the University of Warwick Research Datasets portal at https://wrap.warwick.ac.uk/166703/.References
- P. C. Vioglio, M. R. Chierotti and R. Gobetto, Adv. Drug Delivery Rev., 2017, 117, 86 CrossRef PubMed.
- E. Pindelska, A. Sokal and W. Kolodziejski, Adv. Drug Delivery Rev., 2017, 117, 111 CrossRef CAS PubMed.
- X. Lu, Y. Tsutsumi, C. Huang, W. Xu, S. R. Byrn, A. C. Templeton, A. V. Buevich, J.-P. Amoureux and Y. Su, Phys. Chem. Chem. Phys., 2020, 22, 13160 RSC.
- M. Li, W. Xu and Y. Su, Trac, Trends Anal. Chem., 2021, 135, 116152 CrossRef CAS.
- J. R. Lewandowski, J.-N. Dumez, Ü. Akbey, S. Lange, L. Emsley and H. Oschkinat, J. Phys. Chem. Lett., 2011, 2, 2205 CrossRef CAS.
- D. Lacabanne, J. Boudet, A. A. Malär, P. Wu, R. Cadalbert, L. Salmon, F. H.-T. Allain, B. H. Meier and T. Wiegand, J. Phys. Chem. B, 2020, 124, 11089 CrossRef CAS PubMed.
- V. Jirasko, A. Lends, N. A. Lakomek, M. L. Fogeron, M. E. Weber, A. A. Malär, S. Penzel, R. Bartenschlager, B. H. Meier and A. Böckmann, Angew. Chem., 2021, 133, 5399 CrossRef.
- S. Bahri, R. Silvers, B. Michael, K. Jaudzems, D. Lalli, G. Casano, O. Ouari, A. Lesage, G. Pintacuda, S. Linse and R. G. Griffin, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2114413119 CrossRef CAS PubMed.
- U. Sternberg, R. Witter, I. Kuprov, J. M. Lamley, A. Oss, J. R. Lewandowski and A. Samoson, J. Magn. Reson., 2018, 291, 32 CrossRef CAS PubMed.
- Y. Nishiyama, Solid State Nucl. Magn. Reson., 2016, 78, 24 CrossRef CAS PubMed.
- A. A. Malär, S. Smith-Penzel, G.-M. Camenisch, T. Wiegand, A. Samoson, A. Böckmann, M. Ernst and B. H. Meier, Phys. Chem. Chem. Phys., 2019, 21, 18850 RSC.
- M. Schledorn, A. A. Malär, A. Torosyan, S. Penzel, D. Klose, A. Oss, M. L. Org, S. Wang, L. Lecoq, R. Cadalbert, A. Samoson, A. Böckmann and B. H. Meier, ChemBioChem, 2020, 21, 2540 CrossRef CAS PubMed.
- Z. Zhang, A. Oss, M.-L. Org, A. Samoson, M. Li, H. Tan, Y. Su and J. Yang, J. Phys. Chem. Lett., 2020, 11, 8077 CrossRef CAS PubMed.
- E. C.-Y. Yuan, S.-J. Huang, H.-C. Huang, J. Sinkkonen, A. Oss, M.-L. Org, A. Samoson, H.-C. Tai and J. C. C. Chan, Chem. Commun., 2021, 57, 4110 RSC.
- Z. Gan, J. P. Amoureux and J. Trébosc, Chem. Phys. Lett., 2007, 435, 163 CrossRef CAS.
- S. Cavadini, S. Antonijevic, A. Lupulescu and G. Bodenhausen, J. Magn. Reson., 2006, 182, 168 CrossRef CAS PubMed.
- J. A. Jarvis, M. Concistre, I. M. Haies, R. W. Bounds, I. Kuprov, M. Carravetta and P. T. F. Williamson, Phys. Chem. Chem. Phys., 2019, 21, 5941 RSC.
- M. Grüne, R. Luxenhofer, D. Iuga, S. P. Brown and A.-C. Pöppler, J. Mater. Chem. B, 2020, 8, 6827 RSC.
- K. Bártová, I. Císařová, A. Lyčka and M. Dračínský, Dyes Pigm., 2020, 178, 108342 CrossRef.
- M. K. Pandey and Y. Nishiyama, Phys. Chem. Chem. Phys., 2018, 20, 25849 RSC.
- A. Pugliese, M. Toresco, D. McNamara, D. Iuga, A. Abraham, M. Tobyn, L. E. Hawarden and F. Blanc, Mol. Pharm., 2021, 18, 3519 CrossRef CAS PubMed.
- A. S. Tatton, J. P. Bradley, D. Iuga and S. P. Brown, Z. Phys. Chem., 2012, 226, 1187 CrossRef CAS.
- Y. Ishii and R. Tycko, J. Magn. Reson., 2000, 142, 199 CrossRef CAS PubMed.
- Y. Ishii, J. P. Yesinowski and R. Tycko, J. Am. Chem. Soc., 2001, 123, 2921 CrossRef CAS PubMed.
- D. H. Zhou, G. Shah, C. Mullen, D. Sandoz and C. M. Rienstra, Angew. Chem., Int. Ed., 2009, 48, 1253 CrossRef CAS PubMed.
- S. M. Althaus, K. Mao, J. A. Stringer, T. Kobayashi and M. Pruski, Solid State Nucl. Magn. Reson., 2014, 57–58, 17 CrossRef CAS PubMed.
- A. Lesage, P. Charmont, S. Steuernagel and L. Emsley, J. Am. Chem. Soc., 2000, 122, 9739 CrossRef CAS.
- T. Kobayashi, K. Mao, P. Paluch, A. Nowak-Król, J. Sniechowska, Y. Nishiyama, D. T. Gryko, M. J. Potrzebowski and M. Pruski, Angew. Chem., 2013, 125, 14358 CrossRef.
- S. L. Veinberg, K. E. Johnston, M. J. Jaroszewicz, B. M. Kispal, C. R. Mireault, T. Kobayashi, M. Pruski and R. W. Schurko, Phys. Chem. Chem. Phys., 2016, 18, 17713 RSC.
- C. Guzmán-Afonso, Y.-l Hong, H. Colaux, H. Iijima, A. Saitow, T. Fukumura, Y. Aoyama, S. Motoki, T. Oikawa, T. Yamazaki, K. Yonekura and Y. Nishiyama, Nat. Commun., 2019, 10, 3537 CrossRef PubMed.
- E. K. Paulson, C. R. Morcombe, V. Gaponenko, B. Dancheck, R. A. Byrd and K. W. Zilm, J. Am. Chem. Soc., 2003, 125, 15831 CrossRef CAS PubMed.
- V. Chevelkov, K. Rehbein, A. Diehl and B. Reif, Angew. Chem., Int. Ed., 2006, 45, 3878 CrossRef CAS PubMed.
- D. H. Zhou, G. Shah, M. Cormos, C. Mullen, D. Sandoz and C. M. Rienstra, J. Am. Chem. Soc., 2007, 129, 11791 CrossRef CAS PubMed.
- C. Fyfe, K. Wong-Moon, Y. Huang and H. Grondey, J. Am. Chem. Soc., 1995, 117, 10397 CrossRef CAS.
- O. Soubias, V. Réat, O. Saurel and A. Milon, J. Magn. Reson., 2002, 158, 143 CrossRef CAS PubMed.
- B. Alonso and D. Massiot, J. Magn. Reson., 2003, 163, 347 CrossRef CAS PubMed.
- B. Elena, A. Lesage, S. Steuernagel, A. Böckmann and L. Emsley, J. Am. Chem. Soc., 2005, 127, 17296 CrossRef CAS PubMed.
- K. Mao, J. W. Wiench, V. S.-Y. Lin and M. Pruski, J. Magn. Reson., 2009, 196, 92 CrossRef CAS PubMed.
- K. Mao and M. Pruski, J. Magn. Reson., 2009, 201, 165 CrossRef CAS PubMed.
- G. P. Holland, B. R. Cherry, J. E. Jenkins and J. L. Yarger, J. Magn. Reson., 2010, 202, 64 CrossRef CAS PubMed.
- P. K. Madhu, Solid State Nucl. Magn. Reson., 2009, 35, 2 CrossRef CAS PubMed.
- K. R. Mote, V. Agarwal and P. K. Madhu, Prog. Nucl. Magn. Reson. Spectrosc., 2016, 97, 1 CrossRef CAS PubMed.
- P. Hodgkinson, Annu. Rep. NMR Spectrosc., 2011, 72, 185 CrossRef CAS.
- E. Vinogradov, P. K. Madhu and S. Vega, New Techniques Solid-State NMR, 2005, p. 33 Search PubMed.
- M. Lee and W. I. Goldburg, Phys. Rev., 1965, 140, A1261 CrossRef.
- M. H. Levitt, A. C. Kolbert, A. Bielecki and D. J. Ruben, Solid State Nucl. Magn. Reson., 1993, 2, 151 CrossRef CAS PubMed.
- M. Hohwy and N. C. Nielsen, J. Chem. Phys., 1997, 106, 7571 CrossRef CAS.
- M. Hohwy, P. Bower, H. Jakobsen and N. Nielsen, Chem. Phys. Lett., 1997, 273, 297 CrossRef CAS.
- E. Vinogradov, P. K. Madhu and S. Vega, Chem. Phys. Lett., 1999, 314, 443 CrossRef CAS.
- D. Sakellariou, A. Lesage, P. Hodgkinson and L. Emsley, Chem. Phys. Lett., 2000, 319, 253 CrossRef CAS.
- P. K. Madhu, X. Zhao and M. H. Levitt, Chem. Phys. Lett., 2001, 346, 142 CrossRef CAS.
- M. E. Halse and L. Emsley, Phys. Chem. Chem. Phys., 2012, 14, 9121 RSC.
- F. M. Paruzzo and L. Emsley, J. Magn. Reson., 2019, 309, 106598 CrossRef CAS PubMed.
- C. Coelho, J. Rocha, P. K. Madhu and L. Mafra, J. Magn. Reson., 2008, 194, 264 CrossRef CAS PubMed.
- I. Schnell, S. P. Brown, H. Y. Low, H. Ishida and H. W. Spiess, J. Am. Chem. Soc., 1998, 120, 11784 CrossRef CAS.
- J.-P. Amoureux, B. Hu, J. Trébosc, Q. Wang, O. Lafon and F. Deng, Solid State Nucl. Magn. Reson., 2009, 35, 19 CrossRef CAS PubMed.
- Y. Nishiyama, X. Lu, J. Trebosc, O. Lafon, Z. Gan, P. K. Madhu and J.-P. Amoureux, J. Magn. Reson., 2012, 214, 151 CrossRef CAS PubMed.
- E. Salager, J.-N. Dumez, R. S. Stein, S. Steuernagel, A. Lesage, B. Elena-Herrmann and L. Emsley, Chem. Phys. Lett., 2010, 498, 214 CrossRef CAS.
- M. Leskes, S. Steuernagel, D. Schneider, P. K. Madhu and S. Vega, Chem. Phys. Lett., 2008, 466, 95 CrossRef CAS.
- J.-P. Amoureux, B. Hu and J. Trébosc, J. Magn. Reson., 2008, 193, 305 CrossRef CAS PubMed.
- Z. Gan, P. K. Madhu, J.-P. Amoureux, J. Trébosc and O. Lafon, Chem. Phys. Lett., 2011, 503, 167 CrossRef CAS.
- E. Salager, R. S. Stein, S. Steuernagel, A. Lesage, B. Elena and L. Emsley, Chem. Phys. Lett., 2009, 469, 336 CrossRef CAS.
- B. Gerstein, R. Pembleton, R. Wilson and L. Ryan, J. Chem. Phys., 1977, 66, 361 CrossRef CAS.
- E. Salager, J.-N. Dumez, L. Emsley and M. H. Levitt, J. Magn. Reson., 2011, 212, 11 CrossRef CAS PubMed.
- M. Leskes, P. K. Madhu and S. Vega, J. Magn. Reson., 2009, 199, 208 CrossRef CAS PubMed.
- R. Ramesh and M. S. Krishnan, J. Chem. Phys., 2001, 114, 5967 CrossRef CAS.
- S. Hayashi and K. Hayamizu, Bull. Chem. Soc. Jpn., 1991, 64, 685 CrossRef CAS.
- E. K. Corlett, H. Blade, L. P. Hughes, P. J. Sidebottom, D. Walker, R. I. Walton and S. P. Brown, CrystEngComm, 2019, 21, 3502 RSC.
- S. Hayashi and K. Hayamizu, Bull. Chem. Soc. Jpn., 1991, 64, 688 CrossRef CAS.
- R. K. Harris, E. D. Becker, S. M. C. De Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Pure Appl. Chem., 2008, 80, 59 CrossRef CAS.
- G. E. Martin and C. E. Hadden, J. Nat. Prod., 2000, 63, 543 CrossRef CAS PubMed.
- B. H. Meier, Chem. Phys. Lett., 1992, 188, 201 CrossRef CAS.
- S. Laage, J. R. Sachleben, S. Steuernagel, R. Pierattelli, G. Pintacuda and L. Emsley, J. Magn. Reson., 2009, 196, 133 CrossRef CAS PubMed.
- G. Metz, X. Wu and S. O. Smith, J. Magn. Reson. Ser. A, 1994, 110, 219 CrossRef CAS.
- D. H. Zhou and C. M. Rienstra, J. Magn. Reson., 2008, 192, 167 CrossRef CAS PubMed.
- M. Ernst, M. A. Meier, T. Tuherm, A. Samoson and B. H. Meier, J. Am. Chem. Soc., 2004, 126, 4764 CrossRef CAS PubMed.
- A. Shaka, J. Keeler and R. Freeman, J. Magn. Reson. (1969), 1983, 53, 313 CrossRef CAS.
- Z. Zhou, R. Kümmerle, X. Qiu, D. Redwine, R. Cong, A. Taha, D. Baugh and B. Winniford, J. Magn. Reson., 2007, 187, 225 CrossRef CAS PubMed.
- A. Lesage, S. Steuernagel and L. Emsley, J. Am. Chem. Soc., 1998, 120, 7095 CrossRef CAS.
- A. S. Tatton, I. Frantsuzov, S. P. Brown and P. Hodgkinson, J. Chem. Phys., 2012, 136, 084503 CrossRef PubMed.
- A. Lesage, L. Emsley, M. Chabanas, C. Coperet and J.-M. Basset, Angew. Chem., 2002, 114, 4717 CrossRef.
- M. P. Hanrahan, E. L. Fought, T. L. Windus, L. M. Wheeler, N. C. Anderson, N. R. Neale and A. J. Rossini, Chem. Mater., 2017, 29, 10339 CrossRef CAS.
- R. W. Dorn, E. A. Marro, M. P. Hanrahan, R. S. Klausen and A. J. Rossini, Chem. Mat., 2019, 31, 9168 CrossRef CAS.
- B. J. Ryan, M. P. Hanrahan, Y. Wang, U. Ramesh, C. K. A. Nyamekye, R. D. Nelson, Z. Liu, C. Huang, B. Whitehead, J. Wang, L. T. Roling, E. A. Smith, A. J. Rossini and M. G. Panthani, Chem. Mat., 2020, 32, 795 CrossRef CAS.
- M. Leskes, P. K. Madhu and S. Vega, Chem. Phys. Lett., 2007, 447, 370 CrossRef CAS.
- M. Mehring and J. S. Waugh, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 5, 3459 CrossRef.
- A. Bielecki, A. C. Kolbert and M. H. Levitt, Chem. Phys. Lett., 1989, 155, 341 CrossRef CAS.
- E. Vinogradov, P. K. Madhu and S. Vega, Chem. Phys. Lett., 2002, 354, 193 CrossRef CAS.
- M. Leskes, P. K. Madhu and S. Vega, J. Chem. Phys., 2006, 125, 124506 CrossRef PubMed.
- S. Paul, R. S. Thakur, M. Goswami, A. C. Sauerwein, S. Mamone, M. Concistre, H. Forster, M. H. Levitt and P. K. Madhu, J. Magn. Reson., 2009, 197, 14 CrossRef CAS PubMed.
- V. E. Zorin, M. Ernst, S. P. Brown and P. Hodgkinson, J. Magn. Reson., 2008, 192, 183 CrossRef CAS PubMed.
- K. Mao and M. Pruski, J. Magn. Reson., 2010, 203, 144 CrossRef CAS PubMed.
- S. Hafner and H. W. Spiess, J. Magn. Reson., Ser. A, 1996, 121, 160 CrossRef CAS.
- E. Vinogradov, P. K. Madhu and S. Vega, Chem. Phys. Lett., 2000, 329, 207 CrossRef CAS.
- A. Lesage, D. Sakellariou, S. Hediger, B. Eléna, P. Charmont, S. Steuernagel and L. Emsley, J. Magn. Reson., 2003, 163, 105 CrossRef CAS PubMed.
- J. S. Waugh, L. M. Huber and U. Haeberlen, Phys. Rev. Lett., 1968, 20, 180 CrossRef CAS.
- A. J. Vega, J. Magn. Reson., 2004, 170, 22 CrossRef CAS PubMed.
- A. Lesage, M. Bardet and L. Emsley, J. Am. Chem. Soc., 1999, 121, 10987 CrossRef CAS.
- V. E. Zorin, S. P. Brown and P. Hodgkinson, J. Chem. Phys., 2006, 125, 144508 CrossRef PubMed.
- L. Bosman, P. K. Madhu, S. Vega and E. Vinogradov, J. Magn. Reson., 2004, 169, 39 CrossRef CAS PubMed.
- A. S. Tatton, T. N. Pham, F. G. Vogt, D. Iuga, A. J. Edwards and S. P. Brown, CrystEngComm, 2012, 14, 2654 RSC.
- K. Maruyoshi, D. Iuga, A. E. Watts, C. E. Hughes, K. D. M. Harris and S. P. Brown, J. Pharm. Sci., 2017, 106, 3372 CrossRef CAS PubMed.
- K. Aebischer, N. Wili, Z. Tošner and M. Ernst, Magn. Reson., 2020, 1, 187 CrossRef.
- F. A. Perras, T. W. Goh, L.-L. Wang, W. Huang and M. Pruski, Solid State Nucl. Magn. Reson., 2019, 98, 12 CrossRef CAS PubMed.
- A. J. Robertson, M. K. Pandey, A. Marsh, Y. Nishiyama and S. P. Brown, J. Magn. Reson., 2015, 260, 89 CrossRef CAS PubMed.
- M. Shen, S. Wegner, J. Trébosc, B. Hu, O. Lafon and J.-P. Amoureux, Solid State Nucl. Magn. Reson., 2017, 87, 111 CrossRef CAS PubMed.
- A. Venkatesh, X. Luan, F. A. Perras, I. Hung, W. Huang and A. J. Rossini, Phys. Chem. Chem. Phys., 2020, 22, 20815 RSC.
- Y. Nishiyama, M. Malon, Y. Ishii and A. Ramamoorthy, J. Magn. Reson., 2014, 244, 1 CrossRef CAS PubMed.
- Y. Nishiyama, T. Kobayashi, M. Malon, D. Singappuli-Arachchige, I. I. Slowing and M. Pruski, Solid State Nucl. Magn. Reson., 2015, 66, 56 CrossRef PubMed.
- J. Struppe, C. M. Quinn, M. Lu, M. Wang, G. Hou, X. Lu, J. Kraus, L. B. Andreas, J. Stanek, D. Lalli, A. Lesage, G. Pintacuda, W. Maas, A. M. Gronenborn and T. Polenova, Solid State Nucl. Magn. Reson., 2017, 87, 117 CrossRef CAS PubMed.
- J. Struppe, C. M. Quinn, S. Sarkar, A. M. Gronenborn and T. Polenova, Mol. Pharm., 2019, 17, 674 Search PubMed.
- R. Zhang, Y.-l Hong, T. Ravula, Y. Nishiyama and A. Ramamoorthy, J. Magn. Reson., 2020, 313, 106717 CrossRef CAS PubMed.
- P. Moutzouri, F. M. Paruzzo, B. Simões de Almeida, G. Stevanato and L. Emsley, Angew. Chem., Int. Ed., 2020, 59, 6235 CrossRef CAS PubMed.
- P. Moutzouri, B. Simões de Almeida, D. Torodii and L. Emsley, J. Am. Chem. Soc., 2021, 143, 9834 CrossRef CAS PubMed.
Footnotes |
| † Dedicated to Shimon Vega (1943–2021). |
| ‡ Electronic supplementary information (ESI) available: Additional experimental solid-state NMR and simulated data. See DOI: https://doi.org/10.1039/d2cp01041k |
| This journal is © the Owner Societies 2022 |