Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Protonation and orientation: a computational approach to cocaine diffusion through a model membrane†
Sangwar Wadtey
Oung
 ab,
Nora
Kremer
ab,
Nora
Kremer
 a,
Safa
Ben Amara
c,
Ali
Zaidi
a,
Safa
Ben Amara
c,
Ali
Zaidi
 c and
Thorsten
Koslowski
c and
Thorsten
Koslowski
 *a
*a
aInstitut für Physikalische Chemie, Universität Freiburg, Albertstraße 21, 79104 Freiburg, Germany. E-mail: Thorsten.Koslowski@physchem.uni-freiburg.de
bInstitut für Physikalische und Theoretische Chemie, Technische Universität Braunschweig, Gaußstraße 17, 38106 Braunschweig, Germany
cLaboratoire de Spectroscopie Atomique Moléculaire et Applications, Université de Tunis El Manar, Faculté des Sciences de Tunis, Campus Universitaire El-Manar, 2092 El Manar Tunis, Tunisia
First published on 30th May 2022
Abstract
We study the diffusion of cocaine through a DMPC lipid bilayer as an example of a protonable, amphiphilic molecule passing a biological membrane. Using classical molecular dynamics simulations, the free energy surfaces are computed applying the umbrella sampling technique for the protonated and the neutral molecule. For the combined surface, we numerically solve the diffusion equation at constant flow and for time-dependent concentrations. We find a potential of mean force dominated by a barrier of 3.5 kcal mol−1 within the membrane, and a pH-dependent entry and exit barrier of 2.0 kcal mol−1 and 4.1 kcal mol−1, respectively. This behaviour can be rationalized chemically by the amphiphilic nature of the molecule and the change of its protonation state while passing the membrane. Diffusion through the barriers is 3.5 times slower than along the membrane, and the typical time scale of passage amounts to 0.1 ms. We discuss biochemical and medical implications of our findings, and comment on the mechanism of the drug passing the blood–brain barrier.
1. Introduction
Lipid bilayers are a fundamental structure in biological systems, as they maintain cell functionality by compartmentalizing reaction areas and act as selective barriers.1 Understanding these structures and their interaction with molecules or their aggregates – ranging from protons over the smallest signal molecules to protein complexes – is an important topic in biochemistry, biophysics and medicinal chemistry. In the past decade, transport through membranes has come into the focus of classical molecular dynamics computer simulations. This is due to an increase of computer power, the adaptation of program suites for GPU-based machines2,3 and the effective implementation of algorithms for the computation of free energy surfaces.4 As examples, we have the diffusion of medical drugs or drug-like compounds,5–7 small polymers,8 oligopeptides9 or particles that reach into the nanoscale.10,11 A recent review covers the state of the art in this field.12In our work, we focus on a single molecule passing a membrane, cocaine (2-(methoxycarbonyl)-3-(benzoyloxy)tropane).
It has been used as a local anesthetic,13 but is also a psychoactive, highly addictive drug. Its abuse has severe medical, social and economical implications.14 At synaptic clefts, it inhibits the reuptake of monoamine neurotransmitters, such as dopamine. In turn, the increasing concentration of dopamine in the synapses activates postsynaptic dopamine receptors, which is experienced as a constant reward while the drug is operative. To exert its effect, the drug has to cross the blood–brain barrier. This barrier is composed of endothelial cells that enable permeation either by passive diffusion through lipid membranes or by dedicated, substance-specific transport proteins. For cocaine, it has been assumed that the molecule can passively permeate the barrier in its unprotonated form due to its sufficient lipophilicity. This lipophilic character is attested by its solvation behaviour:15 the molecule is slightly soluble in water (1 g/600 ml), well soluble in alcohol (1 g/6.5 ml), chloroform (1 g/0.7 ml), ether (1 g/3.5 ml) and olive oil (1 g/12 ml), but to a much lesser extent in petrolatum (1 g per 30–50 ml). A curious clinical case report has been published by Jakkala-Saibaba et al.,16 who have successfully treated an overdose patient applying a lipid emulsion of soy bean oil (a total of 100 ml via 500 ml of 20% Fresenius Kabi Intralipid). This also highlights the lipophilic nature of the cocaine molecule.
However, at a pKa value of 8.61, cocaine in neutral aqueous solution acts as a weak base and is predominantly protonated, similar to nicotine and many neurotransmitters.17 It has been suggested that the molecule in its cationic form crosses the blood–brain barrier through active transport via a polyspecific H+-antiporter, which also recognizes the psychoactive molecules clonidine and nicotine.18 Effects hinting at active transport via an antiporter have been found in mouse hCMEC/D3 brain endothelial cells, which serve as a model system of the human blood–brain barrier. Here, a passage rate larger than anticipated by simple diffusion corresponds to a high synaptic activity. While an outline of possible features of the antiporter has been made recently19 the suggested protein complex or parts thereof have to the best of our knowledge neither been isolated nor characterized any further.
The question whether cocaine and related molecules cross the blood–brain barrier assisted by a protein or protein complex or by diffusion along a concentration gradient has an impact on addiction liability and treatment:18 a protein mediating the transport would present an additional target for medication via its inhibition. Furthermore, a genetic disposition towards an overexpression of the antiporter or mutations in this biochemical machine may be related to the sensitivity towards the drug.
As the pharmacological impact of cocaine is related to its molecular structure, the molecule has been approached by theoretical methods. An early attempt to describe the cocaine geometry and its energetics has been performed by Villar and Loew using molecular mechanics and semi-empirical calculations.20 Recently, Fagan et al. have combined chiroptical methods and DFT calculations to access the structure of cocaine in solution,21 and three of the present authors have studied the naturally occurring molecule and its diastereomers in detail.22
The remaining part of the article is organized as follows. In the next section, we describe the umbrella sampling setup and the resulting free energy surfaces. These are followed by the description of the unconstrained molecular dynamics simulations. The emerging results permit a chemical interpretation of the passage of the molecule through the membrane, and they provide the input parameters for the following two sections. In there, the diffusion equation is solved numerically at constant flow and for time-dependent concentrations, giving rise to an effective diffusion coefficient and the relevant time scales of the process. All results are subject to a final discussion and concluding remarks.
2. Umbrella sampling
2.1. Methods
The diffusion of molecules through liquid bilayers is usually outside the time scale of straightforward classical molecular dynamics simulations. In addition, to obtain a proper statistical basis, several hundred events have to be analyzed. Alternative setups at cyclic boundaries comprise two lipid bilayers and two water slabs with different initial concentrations of the diffusing molecule, they are subject to the same restrictions on the time scale.To simulate rare events such as membrane permeation, a series of harmonic restraints can be introduced, which are operative on the distance between the centers of mass of a molecule and selected atoms of the bilayer.4 As we center the membrane at the origin of the Cartesian coordinate system and arrange it in the xy-plane, the reaction coordinate simply equals z. The probability Pk(z) of finding the center of mass difference at z within a window k can be related to the free energy ΔGk of the system,
ΔGk(z) ≃ ΔAk(z) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pk(z) − wk(z) + Fk, Pk(z) − wk(z) + Fk, | (1) |
Force field parameters for cocaine in its neutral and its protonated form have been generated using the Amber antechamber utility.2 Input geometries stem from high-level quantum chemical computations,22,26 and we have also checked the resulting charge parameters stemming from the Austin model 1 calculations (with bond charge corrections, AM1-BCC) against this reference. The TIP3P force field has been used to describe the water molecules,27 and the lipid17 force field has been applied on the dimyristoylphosphatidylcholine (DMPC) molecules.28 Three system sizes have been studied, each containing a single cocaine molecule and (i) 50 lipid molecules and 1866 water molecules, (ii) 76 lipid molecules and 2918 water molecules and (iii) 196 lipid molecules and 7470 water molecules. The largest systems comprise 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581 atoms and have a dimension of ∼80 × 80 × 80 Å3. The systems have been generated using the PACKMOL-Memgen utility.29
581 atoms and have a dimension of ∼80 × 80 × 80 Å3. The systems have been generated using the PACKMOL-Memgen utility.29
The energy of the system was minimized for a total of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, switching from steepest descent to conjugate gradient minimization after 8000 cycles without the use of the SHAKE algorithm. The system was first brought to a temperature of 100 K, and in the second step to the production temperature (300 K) while the lipid molecules were restrained by a harmonic potential with a force constant of 10.0 kcal mol−1 Å−2. The simulation was run at constant volume. Bonds containing hydrogen atoms were restrained by the SHAKE algorithm. The externally coupled temperature was held constant by the Langevin thermostat with a collisional frequency of 1 ps. The system was equilibrated for 710 ps at constant pressure and with periodic boundary conditions. Constant pressure was enforced by applying semiisotropic pressure scaling and using a constant surface tension with the interfaces in the xy plane. The externally coupled temperature (300 K) was again held constant by the Langevin thermostat with a collisional frequency of 1 ps.
000 cycles, switching from steepest descent to conjugate gradient minimization after 8000 cycles without the use of the SHAKE algorithm. The system was first brought to a temperature of 100 K, and in the second step to the production temperature (300 K) while the lipid molecules were restrained by a harmonic potential with a force constant of 10.0 kcal mol−1 Å−2. The simulation was run at constant volume. Bonds containing hydrogen atoms were restrained by the SHAKE algorithm. The externally coupled temperature was held constant by the Langevin thermostat with a collisional frequency of 1 ps. The system was equilibrated for 710 ps at constant pressure and with periodic boundary conditions. Constant pressure was enforced by applying semiisotropic pressure scaling and using a constant surface tension with the interfaces in the xy plane. The externally coupled temperature (300 K) was again held constant by the Langevin thermostat with a collisional frequency of 1 ps.
Finally, the simulation was run under constant pressure and periodic boundary conditions. The cocaine molecule was pulled from the center of the lipid bilayer towards the water phase over a simulation time of 64 ns and with a pulling rate of 0.5 Å per ns. This trajectory was then split into 69 time windows, which were simulated for 100 ns each by applying a parabolic potential with a force constant of 2.5 kcal mol−1 Å−2 to the cocaine molecule. The output was analysed using the weighted histogram analysis method23,24 (WHAM), for which a program is included in the Amber 20 simulation package.2 The histograms are shown as ESI,† they exhibit a broad overlap, as essential for the resulting analysis. From the WHAM analysis, 680 data points were obtained, which are also presented in the ESI.†
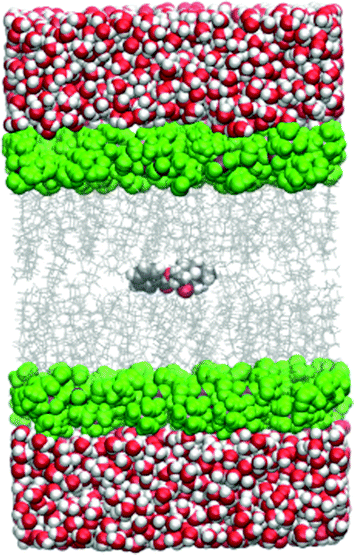
All the simulations within the umbrella sampling windows were run under periodic boundary conditions and the particle-mesh Ewald method was used for electrostatic interactions. The cutoff distance was 10.0 Å. The temperature was held constant by the Langevin thermostat and the pressure by the Berendsen barostat. A simulation snapshot is shown in Fig. 1.
2.2. Free energy surface
Utilizing the umbrella sampling method, we obtain two curves for the potential of mean force as a function of the coordinate, z, which points perpendicular to the lipid bilayer, and has its zero at the center of the bilayer. One set of data represents the protonated, the other the unprotonated form, the corresponding raw data are given as ESI.† As the membrane is symmetric w.r.t. an inversion of z, the curves have been recorded for positive values and mirrored. Using an empirical force field, it is not possible to determine the offset of the free energy curve between the protonated and the neutral form of the cocaine molecule. Nevertheless, they can be calibrated making use of the experimental pKa value of cocaine, 8.61. In the aqueous phase, we have| ΔG = 2.3kBT(pKa − pH) = 2.2 kcal mol−1, | (2) |
In Fig. 2, we show the free energy as a Boltzmann-weighted average of the calibrated cationic and the neutral curves:
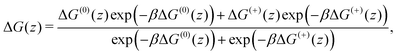 | (3) |
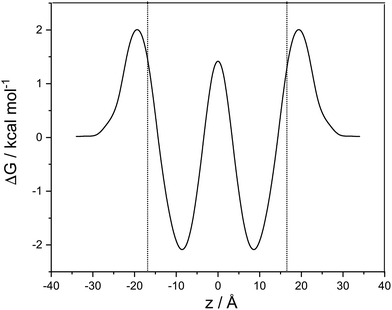
A cubic regression spline with 28 grid points has been applied to obtain a smooth curve. We observe two global minima at z = ±8.8 Å, which correspond to a localization of the neutral cocaine molecule within the membrane, cf.Fig. 2. The two minima are separated by a barrier of 3.5 kcal mol−1. Our conjecture about the nature of the molecule is a statistical one, the charged form is dominant in the aqueous phase, and the neutral molecule constitutes the majority form within the membrane.
Furthermore, we find an entry barrier of 2.0 kcal mol−1 and an exit counterpart of 4.1 kcal mol−1. These barriers depend on the pH value in the two aqueous phases: increasing the pH value shifts the protonated curve towards the unprotonated one on the free energy axis, and the point of crossover towards higher values of |z|, i.e. in the direction of the aqueous phase. The height of both the entry and the exit barrier increase. Lowering the pH value, this behaviour is reversed, and we have lower activation barriers for exit and entry. In a similar sense, this also holds for aqueous phases with different pH values. Partition coefficients stemming from experiments30 or reaction field computations31 can be used in a thermodynamic model to compute the pH-dependent distribution of anesthetics in detail.32 While we qualitatively discuss pH effects, the main focus of our work is on the transfer dynamics and its time scale. Below, we make use of the potential of mean force computed in this section and the diffusion coefficient parallel to the lipid layer – as estimated below – to address the time scales of transport in the following two sections.
Close to the center of the lipid membrane (<2.5 Å), we find a spurious effect in the potential of mean force of the protonated molecule. Its free energy is close to that of the neutral form, and the slope of the curve at z = 0 is not vanishing, as expected for a symmetric system. Inspecting snapshots of the simulations (see ESI†), we can attribute this behaviour to a cation that is globally, but not locally centered in the membrane, and locally deforms the bilayer and is in contact with the water phase. This does not change the thermodynamics, and – if not a simulation artefact – is relevant only on a minute fraction of the diffusion path.
3. Unconstrained molecular dynamics
3.1. Model and methods
Two series of simulations have been performed, one with an initial placement of the cocaine molecule in the aqueous phase, and one with an initial localization in the hydrophobic part of the liquid bilayer. System sizes were identical to those used for the umbrella sampling simulations.The energy of each system was minimized for a total of 5000 cycles, switching from a steepest descent to conjugate gradient procedure after 2500 cycles. Here, bonds involving hydrogen were not constrained. During the heating process, the system was brought to production temperature (300 K) at constant volume. Bonds with hydrogen were constrained applying the SHAKE algorithm. The system was equilibrated for 800 ps at constant pressure. A constant pressure was enforced by applying isotropic position scaling. In the production run, the system was simulated for 1000 ns at constant pressure. The coordinates were saved every 5000 steps for further analysis, the restart file was written every 5000 steps.
To determine the diffusion coefficient of cocaine in water, the R-cocaine molecule was solvated in 1000 water molecules in a simulation box of 40 × 40 × 40 Å3, and a molecular dynamics simulation was carried out. First, the energy of the system was minimized for a total of 5000 cycles, switching from steepest descent to conjugate gradient after 2500 cycles and without the use of the SHAKE algorithm. Then the system was brought to a production temperature of 300 K while being simulated under constant volume. Bonds including hydrogen were restrained by the SHAKE algorithm. The system was equilibrated for 800 ps at constant pressure by applying isotropic position scaling. Finally, the system was simulated for 2 ns at constant temperature and constant pressure.
If not stated otherwise, all the simulations described above were run under periodic boundary conditions and the particle-mesh Ewald method was used for electrostatic interactions. The cutoff distance was 10.0 Å. The temperature was held constant by the Langevin thermostat and the pressure by the Berendsen barostat. The diffusion coefficient of cocaine was determined by using the diffusion command included in the Amber 20 simulation package.2
3.2. Results
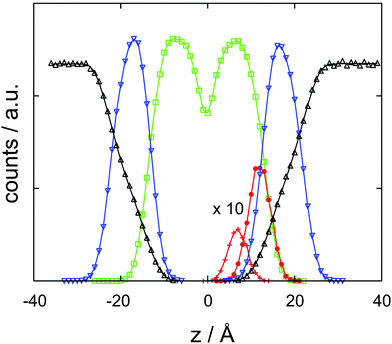
With the help of the concentration profile displayed in Fig. 3, the origin of the barrier finds a straightforward chemical interpretation. At a minimum, the neutral cocaine molecule is oriented with its hydrophobic phenyl ring embedded by likewise hydrophobic side chains. The tropane part of the molecule – with a stronger hydrophilic character – points towards the charged head groups of DMPC. Dragging the molecule deeper into the bilayer, this structural element now also experiences a purely hydrophobic environment, increasing the free energy. With due care and lacking a more appropriate terminology, we refer to this behaviour as amphiphilic, in line with recent literature.33 While oriented, the neutral cocaine molecule does not function as a detergent due to its small size. We will further discuss these orientational effects in connection with the findings from the diffusion computations in the final section of the paper.Trajectories from the simulation of a DMPC bilayer incorporating a cocaine molecule have been used to compute the diffusion coefficient parallel to the bilayer. Care has been taken to analyse a time window that shows a lower boundary that is sufficiently large to exclude cage effects, and an upper boundary that is small enough to be unaffected by the diffusion or undulations of the membrane. In two dimensions, we expect a dependence of the root mean square displacement as a function of time that follows rrmsd2 = 4Dt. To look for a potentially anomalous diffusion and spurious effects induced by the membrane, we have also interpreted the exponent as a variable and analyzed ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rrmsd2 = ln
rrmsd2 = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (4D)/2 + n
(4D)/2 + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t. We find n = 0.53 ± 0.03, still within the range of classical diffusion, and D = 2.7 ± 0.6 × 10−11 m2 s−1. This should be compared to a self-diffusion coefficient of D = 1 × 10−11 m2 s−1 obtained for DMPC by NMR spectroscopy.34 We note that the viscosity and diffusion coefficients for lipid bilayers comprise a range of several orders of magnitude, depending on the membrane composition and on the type of measurement.34–36
t. We find n = 0.53 ± 0.03, still within the range of classical diffusion, and D = 2.7 ± 0.6 × 10−11 m2 s−1. This should be compared to a self-diffusion coefficient of D = 1 × 10−11 m2 s−1 obtained for DMPC by NMR spectroscopy.34 We note that the viscosity and diffusion coefficients for lipid bilayers comprise a range of several orders of magnitude, depending on the membrane composition and on the type of measurement.34–36
We have also computed the diffusion constants for cocaine in a pure water environment. Minimization, equilibration and relaxation have been performed as described above. The diffusion coefficient amounts to ∼11 × 10−9 m2 s−1, with a correlation coefficient larger than or equal to 0.999.
4. Diffusion at stationary flow
Stationary flow between two reservoirs with fixed concentrations can be described by Fick's first law, relating the flow,![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) , to the concentration gradient, ∇c, with the diffusion coefficient, D, as a proportionality constant,
, to the concentration gradient, ∇c, with the diffusion coefficient, D, as a proportionality constant,![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) = D∇c = D∇c | (4) |
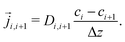 | (5) |
![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) i−1, i =
i−1, i = ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) i+1, i, leading to a tridiagonal system of equations for the unknown concentrations
i+1, i, leading to a tridiagonal system of equations for the unknown concentrations| Di−1,i(ci − ci−1) = Di,i+1(ci+1 − ci). | (6) |
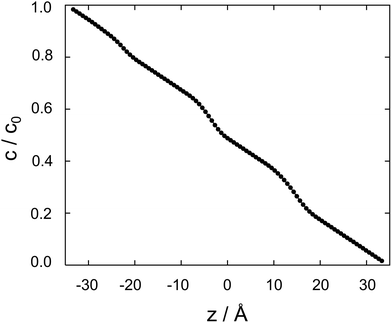 | ||
| Fig. 4 Cocaine concentration profile, c/c0 as a function z, the coordinate perpendicular to the membrane. The normalized concentration is dimensionless, z is in Ångstroms. | ||
Between two nodes, we can now readily compute the effective flow through the system, ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) = Di,i+1(ci − ci+1)/Δz and derive an effective diffusion coefficient for transfer along a system with a length L, Deff = c0|
= Di,i+1(ci − ci+1)/Δz and derive an effective diffusion coefficient for transfer along a system with a length L, Deff = c0|![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) |/L. For a linear arrangement of sites, as encountered here, computing the effective diffusion coefficient is equivalent to calculating the effective resistivity for a series of resistors. Thus,
|/L. For a linear arrangement of sites, as encountered here, computing the effective diffusion coefficient is equivalent to calculating the effective resistivity for a series of resistors. Thus, 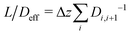 provides an alternative bypassing the solution of the system of equations formulated above. Numerically, we find Deff = 7.2 × 10−12 m2 s−1, a value that is considerably smaller than free diffusion parallel to the membrane, yet the two diffusion processes are not separated by an order of magnitude. We note that diffusion in spatially varying potentials has also been discussed by Livshits,38 who provided diffusion equations corrected for thermally activated processes.
provides an alternative bypassing the solution of the system of equations formulated above. Numerically, we find Deff = 7.2 × 10−12 m2 s−1, a value that is considerably smaller than free diffusion parallel to the membrane, yet the two diffusion processes are not separated by an order of magnitude. We note that diffusion in spatially varying potentials has also been discussed by Livshits,38 who provided diffusion equations corrected for thermally activated processes.
5. Time-dependent diffusion and rate theory
To explore the time scales involved in passing the membrane, we turn to time-dependent diffusion along the z coordinate, i.e. perpendicular to the lipid bilayer. We consider Fick's second law,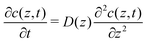 | (7) |
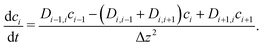 | (8) |
![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) (t) = (c1(t)…cn(t))T. As the dynamics of the system may cover several orders of magnitude, we set
(t) = (c1(t)…cn(t))T. As the dynamics of the system may cover several orders of magnitude, we set ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) (t) =
(t) = ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp
exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (λt), where
(λt), where ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) is independent of time. This approach is equivalent to a Laplace transform of the concentration in the time domain, and has e.g. been applied to problems in chemical kinetics by Cramer et al.39 or by Gellrich and co-workers.40
is independent of time. This approach is equivalent to a Laplace transform of the concentration in the time domain, and has e.g. been applied to problems in chemical kinetics by Cramer et al.39 or by Gellrich and co-workers.40
In this way, eqn (8) is transformed into a row of a real unsymmetric eigenvalue problem,
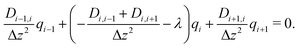 | (9) |
(D(Δz)−2) − λE)![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) = = ![[0 with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0030_20d1.gif) . . | (10) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) a, the concentrations as a function of time can be computed via
a, the concentrations as a function of time can be computed via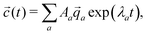 | (11) |
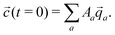 | (12) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) a are not necessarily orthogonal, so 〈
a are not necessarily orthogonal, so 〈![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) (t = 0)|
(t = 0)|![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) 〉 ≠ Aa holds in general.
〉 ≠ Aa holds in general.
We construct a three-layer system with the region for which the free energy curve displayed above (Fig. 2) lies in the center. To the left and to the right, it is extended by an aqueous layer containing 100 grid points each; we have a total of 301 grid points. Initially, the concentration in the leftmost part of the system (1 ≤ i ≤ 100) is set to c0 = 0.01 in arbitrary units. All eigenvalues are real, and the matrix is negative semidefinite with λ1 = 0 and λa < 0 for a > 1. The spectrum of nonzero eigenvalues ranges from −6 × 10−4 ns−1 to −23 ns−1.
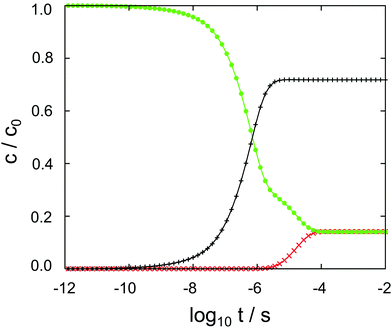
The results of the semi-analytical integration of the discretized diffusion equation is shown in Fig. 5. Here, the concentration of the molecule – either in its majority protonated or unprotonated form – is shown as a function of time for the aqueous layer, the central (membrane) part and the right aqueous layer, integrated over z for each of the regions. We denote these concentrations as cl, cc and cr, respectively. The diffusion process covers a time range from ∼10−11 to ∼10−4 s, or seven orders of magnitude. Retrospectively, this justifies the comparatively elaborate approach to the time evolution of the concentrations by eqn (9)–(11). For each of the three concentrations, we have typical time scales when c has been diminished to half of its initial value in the left region, or equals half its equilibrium value in the central or in the right region. Diffusion into the membrane takes slightly longer than 3 μs, and we find a time scale of 1 × 10−5 s for the penetration of the membrane. The latter is consistent with the eigenvalue spectrum discussed above, i.e. the smallest nonzero eigenvalue, (|λ|min)−1, gives rise to the largest time scale.
As discussed above, the point of the crossover between the protonated and the neutral molecule depends on the pH value. Here, we briefly discuss kinetic effects associated with protonation. Entering the membrane, a protonated cocaine molecule experiences a sufficient number of neighbour water molecules accepting the proton where the protonated and unprotonated free energy curves intersect, and we assume instant deprotonation. Leaving the membrane, however, the neutral molecule has to find a H3O+ cation in its vicinity as a proton donor, or continue its path on the POMF corresponding to the neutral molecule. As this is higher in free energy than the protonated curve once the aqueous phase is approached, it may slow down transfer from the membrane into the water layer.
In our numerical setup, equilibrium is reached at 10−4 s by the latest. Located at the interface between the polar head groups and the hydrophobic tails of the DMPC molecules, the neutral molecule is strongly localized in one of the two minima of the free energy surface. For the geometry used here, we find cc/cl = cc/cr ≃ 6 as the liquid–water partition coefficient.
Focussing on the rate-limiting exit of a molecule from the lipid to an aqueous phase with a small concentration and assuming fast, irreversible diffusion away from the membrane within the water phase, rate theory can be used. In the strongly damped, viscous regime that applies here, the exit rate can be estimated as (eqn (4.54) of ref. 42)
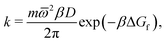 | (13) |
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) 2 = 0.2 kcal mol−1 Å−2 is geometric mean of the curvature of the POMF in its minimum and in the exit transition state, numerically calculated for the smoothed curve, D the diffusion constant parallel to the membrane, and ΔGf the height of the exit barrier. The obtained escape rate, k = 4 × 105 s−1, comes close to the numerical solution of the kinetics described above, which, however, also includes reversible back diffusion from the aqueous phase into the membrane into account.
2 = 0.2 kcal mol−1 Å−2 is geometric mean of the curvature of the POMF in its minimum and in the exit transition state, numerically calculated for the smoothed curve, D the diffusion constant parallel to the membrane, and ΔGf the height of the exit barrier. The obtained escape rate, k = 4 × 105 s−1, comes close to the numerical solution of the kinetics described above, which, however, also includes reversible back diffusion from the aqueous phase into the membrane into account.
In aqueous solution, substrate diffusion is believed to set a rate limit of ∼109 s−1 mol−1 to reactions catalyzed by an enzyme.43–45 For cocaine diffusion in water, we have computed a diffusion coefficient of the order of 10−10 m−2 s−1, a factor of ten smaller for diffusion parallel to the lipid bilayer, and an effective D that is again roughly four times smaller. Reactions of cocaine with a channel protein within the membrane or a receptor beyond the membrane are likely to be slowed down accordingly, if diffusion-controlled. In our calculations, the only process that is close to the water limit is the entry of cocaine into the membrane, cf.Fig. 5. Transfer across the membrane is about five orders of magnitude slower.
6. Discussion and conclusions
We have applied classical molecular dynamics simulations to address the question whether the cocaine molecule can permeate a model lipid bilayer. As the time scale of a crossing event exceeds that of typical simulations, we have computed the potential of mean force using the umbrella sampling technique, and addressed transport via a numerical solution of Fick's laws and rate theory based upon the free energy data and diffusion coefficients computed in the aqueous phase and in the bilayer. In addition, unconstrained simulations have been used to obtain a quantitative view of the molecule's orientation within the membrane.Umbrella sampling simulations have been performed both for the protonated and the neutral form of the molecule, and the free energy curves have been calibrated making use of the cocaine pKa value in the aqueous phase. From our computations, the following scenario emerges. Cocaine in its protonated form enters the hydrophilic part of the lipid bilayer by crossing a barrier of 2.0 kcal mol−1. In turn, it loses its proton and is located in a local minimum of the free energy surface. Here, it shows an orientation with the phenyl ring pointing towards the hydrophobic DMPC tails, and the polar part interacting with the heads of the lipid molecules. Moving to the second lipid layer, a barrier of 3.5 kcal mol−1 has to be overcome, and the orientation of the neutral molecule is reversed. Finally, release into the aqueous phase implies crossing a final barrier of 4.1 kcal mol−1 and the uptake of a proton. We note that orientational effects while crossing a membrane have been observed both in computer simulations and by NMR spectroscopy6 for clozapine and amitriptyline and that ROESY NMR provides an excellent experimental method to verify or to falsify the mechanism just outlined. Different penetration depths and orientational effects for the charged and the uncharged form of ibuprofen have also been reported,5 stemming from a combination of molecular dynamics and neutron diffraction studies. Like cocaine, the anesthetics lidocaine and articaine have a preference for the region close to the water–membrane interface.46,47
We acknowledge the complexity of the blood–brain barrier from the scale of cells down to the composition and organization of the endothelial cell membranes.48 At present, our computer models are limited to simulating what we assume to be the basic constituents of transfer. Taking into account membrane proteins, different lipid compositions or membrane asymmetry is likely to be in reach soon with increasing computer performance and progress in simulation algorithms.
The amphiphilic nature of the neutral cocaine molecule and its ability to further adapt to hydrophobic or hydrophilic environments by changing its protonation state leads to barriers of a few kBT for crossing a membrane, which is also manifested in a time scale of less than a millisecond. The process can be driven by a pH gradient, which lowers the rate-limiting exit barrier. As a consequence, a pH-dependent transport rate does not necessarily point at transfer mediated by a proton antiporter. It is interesting to note that the blockade of sodium channels – as relevant for cocaine as an anesthetic – also depends on the pH.49
As pointed out by Martinotti et al.,12 small molecules are ideal candidates for membrane permeation and fulfill one of Veber's empirical rules:50 the fewer rotatable bonds in a molecule, the higher its bioavailability. With two stereocenters, cocaine has 16 diastereomers, of which eight do not exhibit a serious sterical overlap or deformation. These stereoisomers exhibit a remarkable spectrum of dipole moments, ranging from 0.65 to 4.60 Debye.22 One may speculate whether these molecules show a different membrane permeation behaviour, and whether the effect of the naturally occurring R-cocaine may not only depend on the drug–receptor interaction, but also on the kinetics of transport. We are confident that future work will incorporate polarizable force fields51,52 and will benefit from recent developments in nonequilibrium methods suited to simultaneously compute the POMF and the friction while pulling a molecule.53,54
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft via the grant DFG 278002225/RTG 2202. We thank T. Hugel, B. Balzer, J. Haxhija, G. Stock and S. Wolf for fruitful discussions and helpful comments.References
- J. Kuriyan, B. Konforti and D. Wemmer, The Molecules of Life, W.W. Norton & Company, New York, 2012, ch. I.3 Search PubMed.
- D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, G. A. Cisneros, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, C. Jin, K. Kasavajhala, M. C. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. A. OHearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, Y. Xue, D. M. York, S. Zhao and P. A. Kollman, Amber 2021, University of California, San Francisco, California, 2021 Search PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Pall, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1-2, 19–25 CrossRef.
- J. Kästner, Umbrella sampling, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942 Search PubMed.
- M. B. Boggara and R. Krishnamoorti, Partitioning of Nonsteroidal Antiinflammatory Drugs in Lipid Membranes: A Molecular Dynamics Simulation Study, Biophys. J., 2010, 98, 586–595 CrossRef CAS PubMed.
- J. Ma, L. Domicevica, J. R. Schnell and P. C. Biggin, Position and orientational preferences of drug-like compounds in lipid membranes: a computational and NMR approach, Phys. Chem. Chem. Phys., 2015, 17, 19766–19776 RSC.
- R. P. Ribeiro, J. T.-S. Coimbra, M. J. Ramos and P. A. Fernandes, Diffusion of the small, very polar, drug piracetam through a lipid bilayer: an MD simulation study, Theor. Chem. Acc., 2017, 136, 1–10 Search PubMed.
- D. Bochicchio, E. Panizon, R. Ferrando, L. Monticelli and G. Rossi, Calculating the free energy of transfer of small solutes into a model lipid membrane: Comparison between metadynamics and umbrella sampling, J. Chem. Phys., 2015, 143, 144108 CrossRef PubMed.
- B. L. Lee, K. Kuczera, C. R. Middaugh and G. S. Jas, Permeation of the three aromatic dipeptides through lipid bilayers: Experimental and computational study, J. Chem. Phys., 2016, 144, 245103 CrossRef PubMed.
- T. H.-F. Thake, J. R. Webb, A. Nash, J. Z. Rappoport and R. Notman, Permeation of polystyrene nanoparticles across model lipid bilayer membranes, Soft Matter, 2013, 9, 10265 RSC.
- C.-F. Su, H. Merlitz, H. Rabbel and J.-U. Sommer, Nanoparticles of Various Degrees of Hydrophobicity Interacting with Lipid Membranes, J. Phys. Chem. Lett., 2017, 8, 4069–4076 CrossRef CAS PubMed.
- C. Martinotti, L. Ruiz-Perez, E. Deplazes and R. L. Mancera, Molecular dynamics simulation of the interaction of small molecules with biological membranes, ChemPhysChem, 2020, 21, 1486–1514 CrossRef CAS PubMed.
- Y. A. Ruetsch, T. Böni and A. Borgeat, From cocaine to ropivacaine: the history of local anesthetic drugs, Curr. Top. Med. Chem., 2001, 1, 175–182 CrossRef CAS PubMed.
- Division for Policy Analysis and Public Affairs, United Nations Office on Drugs and Crime, World Drug Report 2021, booklet 4, Drug Market Trends: Cocaine, Amphetamine-type Stimulants, United Nations publication, Sales No. E.21.XI.8, Viennna, 2021.
- The Merck Index – An Encyclopedia of Chemicals, Drugs, and Biologicals, ed. O'Neil M. J., Royal Society of Chemistry, Cambridge, 2013, p. 438 Search PubMed.
- R. Jakkala-Saibaba, P. G. Morgan and G. L. Morton, Treatment of cocaine overdose with lipid emulsion, Anaesthesia, 2011, 66, 1168–1170 CrossRef CAS PubMed.
- H. Lu, X. Chen and C.-G. Zhan, First-Principles Calculation of pKa for Cocaine, Nicotine, Neurotransmitters, and Anilines in Aqueous Solution, J. Phys. Chem. B, 2007, 111, 10599–10605 CrossRef CAS PubMed.
- H. Chapy, M. Smirnova, P. Andree, J. Schlatter, F. Chiadmi, P.-O. Couraud, J.-M. Scherrmann, X. Decleves and S. Cisternino, Carrier-Mediated Cocaine Transport at the Blood–Brain Barrier as a Putative Mechanism in Addiction Liability, Int. J. Neuropsychopharmacol., 2014, 1–10 Search PubMed.
- Y. Tega, H. Tabata, T. Kurosawa, A. Kitamura, F. Itagaki, T. Oshitari and Y. Deguchi, Structural Requirements for Uptake of Diphenhydramine Analogs into hCMEC/D3 Cells via the Proton-Coupled Organic Cation Antiporter, J. Pharm. Sci., 2021, 110, 397–403 CrossRef CAS PubMed.
- H. O. Villar and G. H. Loew, A conformational study of cocaine and its diastereomers, J. Comput. Chem., 1990, 11, 1111–1118 CrossRef CAS.
- P. Fagan, L. Kocourkova, M. Tatarkovic, F. Kralik, M. Kuchar, V. Setnicka and P. Bour, Cocaine hydrochloride structure in solution revealed by three chiroptical methods, ChemPhysChem, 2017, 18, 2258–2265 CrossRef CAS PubMed.
- S. ben Amara, T. Koslowski and A. Zaidi, Quantum Chemistry of Cocaine and its Isomers I: Energetics, Reactivity and Solvation, S. Afr. J. Chem., 2021, 75, 18–27 CAS.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- M. Souaille and B. Roux, Extension to the weighted histogram analysis method: Combining umbrella sampling with free energy calculation, Comput. Phys. Commun., 2001, 135, 40–57 CrossRef CAS.
- D. Chandler, Introduction to Modern Statistical Mechanics, Oxford University Press, New York, 1987, ch. 6.3 Search PubMed.
- S. Ben Amara, Theoretical study of the spectroscopic properties of the cocaine molecule and some derived alkaloid compounds, PhD thesis, University of Tunis El Manar, Tunis, Tunisia, 2021 Search PubMed.
- W. L. Jorgensen, J. Chandrasekhar and J. D. Madura, Comparison of Simple Potential Functions for Simulating Liquid Water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- C. J. Dickson, R. C. Walker and I. R. Gould, Lipid21: Complex Lipid Membrane Simulations with AMBER, J. Chem. Theory Comput., 2022, 18, 1726–1736 CrossRef CAS PubMed.
- S. Schott-Verdugo and H. Gohlke, PACKMOL-Memgen: A Simple-To-Use, Generalized Workflow for Membrane-Protein-Lipid-Bilayer System Building, J. Chem. Inf. Model., 2019, 59, 2522–2528 CrossRef CAS PubMed.
- G. R. Strichartz, V. Sanchez, G. R. Arthur, R. Chafetz and D. Martin, Fundamental properties of local anesthetics. II. Measured octanol: buffer partition coefficients and pKa values of clinically used drugs, Anesth. Analg., 1990, 71(2), 158–170 CrossRef CAS PubMed.
- H. Kavčič, N. Umek, D. Pregeljc, N. Vintar and J. Mavri, Local Anesthetics Transfer Across the Membrane: Reproducing Octanol-Water Partition Coefficients by Solvent Reaction Field Methods, Acta Chim. Slov., 2021, 68, 426–432 CrossRef.
- H. Kavčič, N. Umek, N. Vintar and J. Mavri, Local anesthetics transfer relies on pH differences and affinities toward lipophilic compartments, J. Phys. Org. Chem., 2021, 34, e4275 CrossRef.
- A. J. Johnston, S. Busch, L. C. Pardo, S. K. Callear, P. C. Biggin and S. E. McLain, On the atomic structure of cocaine in solution, Phys. Chem. Chem. Phys., 2016, 18, 991–999 RSC.
- A. Filippov, G. Orädd and G. Lindblom, The effect of cholesterol on the lateral diffusion of phospholipids in oriented bilayers, Biophys. J., 2003, 84, 3079 CrossRef CAS PubMed.
- A. Filippov, G. Orädd and G. Lindblom, Influence of Cholesterol and Water Content on Phospholipid Lateral Diffusion in Bilayers, Langmuir, 2003, 19, 6397–6400 CrossRef CAS.
- M. Nagao, E. G. Kelley, A. Faraone, M. Saito, Y. Yoda, M. Kurokuzu, S. Takata, M. Seto and P. D. Butler, Relationship between Viscosity and Acyl Tail Dynamics in Lipid Bilayers, Phys. Rev. Lett., 2021, 127, 078102 CrossRef CAS PubMed.
- J. J. Dongarra, J. R. Bunch, C. B. Moler and G. W. Stewart, LINPACK users' guide, Society for Industrial and Applied Mathematics, Philadelphia, 1979 Search PubMed.
- A. I. Livshits, The effect of spatial variation in potential energy on the diffusion in heterogeneous media, Phys. Lett. A, 2016, 380, 1891–1894 CrossRef CAS.
- T. Cramer, T. Steinbrecher, A. Labahn and T. Koslowski, Static and dynamic aspects of DNA charge transfer, Phys. Chem. Chem. Phys., 2005, 7, 4039 RSC.
- U. Gellrich, T. Koslowski and B. Breit, Full kinetic analysis of a rhodium-catalyzed hydroformylation: beyond the rate-limiting step picture, Catal. Sci. Technol., 2015, 5, 129 RSC.
- J. J. Dongarra, B. T. Smith and J. M. Boyle, Matrix eigensystem routines - EISPACK guide. Lecture notes in computer science, Springer, Berlin Heidelberg New York, 1988, vol. 6 Search PubMed.
- P. Hänggi, P. Talkner and M. Borkovec, Reaction-rate theory: fifty years after Kramers, Rev. Mod. Phys., 1990, 62, 251 CrossRef.
- R. A. Alberty and G. G. Hammes, Application of the Theory of Diffusion-controlled Reactions to Enzyme Kinetics, J. Phys. Chem., 1958, 2, 154–159 CrossRef.
- M. Eigen and G. G. Hammes, Advances in Enzymology and Related Areas of Molecular Biology, Wiley-Blackwell, Hoboken, 1963, pp. 1–38 Search PubMed.
- G.-Q. Zhou and W.-Z. Zhong, Diffusion-Controlled Reactions of Enzymes. A Comparison between Chou's Model and Alberty-Hammes-Eigen's Model, Eur. J. Biochem., 1982, 128, 383–387 CrossRef CAS PubMed.
- C. J. Högberg, A. Maliniak and A. P. Lyubartsev, Dynamical and structural properties of charged and uncharged lidocaine in a lipid bilayer, Biophys. Chem., 2007, 125, 416–426 CrossRef PubMed.
- M. Saeedi, A. P. Lyubartsev and S. Jalili, Anesthetics mechanism on a DMPC lipid membrane model: Insights from molecular dynamics simulations, Biophys. Chem., 2017, 226, 1–13 CrossRef CAS PubMed.
- P. Ballabh, A. Braun and M. Nedergaard, The blood–brain barrier: an overview: structure, regulation, and clinical implications, Neurobiol. Dis., 2004, 16, 1–13 CrossRef CAS PubMed.
- G. K. Wang and G. R. Strichartz, State-dependent inhibition of sodium channels by local anesthetics: a 40-year evolution, Biochem. (Moscow), Suppl. Ser., 2012, 6, 120–127 CrossRef PubMed.
- D. F. Veber, S. R. Johnson, H. Y. Cheng, B. R. Smith, K. W. Ward and K. D. Kopple, Molecular properties that influence the oral bioavailability of drug candidates, J. Med. Chem., 2002, 45, 2615–2623 CrossRef CAS PubMed.
- J. P.-M. Jämbeck and A. P. Lyubartsev, Implicit inclusion of atomic polarization in modeling of partitioning between water and lipid bilayers, Phys. Chem. Chem. Phys., 2013, 15, 4677 RSC.
- J. T.-S. Coimbra, P. A. Fernandes and M. J. Ramos, Revisiting Partition in Hydrated Bilayer Systems, J. Chem. Theory Comput., 2017, 13, 2290–2299 CrossRef CAS PubMed.
- S. Wolf and G. Stock, Targeted Molecular Dynamics Calculations of Free Energy Profiles Using a Nonequilibrium Friction Correction, J. Chem. Theory Comput., 2018, 14, 6175–6182 CrossRef CAS PubMed.
- M. Jäger, T. Koslowski and S. Wolf, Predicting ion channel conductance via dissipation-corrected targeted molecular dynamics and Langevin equation simulations, J. Chem. Theory Comp., 2021, 18, 494–502 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01140a |
| This journal is © the Owner Societies 2022 |