Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energetics and exchange of xenon and water in a prototypic cryptophane-A biosensor structure†
Perttu
Hilla
 * and
Juha
Vaara
* and
Juha
Vaara

NMR Research Unit, P.O. Box 3000, FI-90014 University of Oulu, Finland. E-mail: perttu.hilla@oulu.fi; juha.vaara@iki.fi
First published on 13th June 2022
Abstract
A microscopic description of the energetics and dynamics of xenon NMR biosensors can be experimentally difficult to achieve. We conduct molecular dynamics and metadynamics simulations of a prototypical Xe@cryptophane-A biosensor in an explicit water solvent. We compute the non-covalent Xe binding energy, identify the complexation mechanism of Xe, and calculate the exchange dynamics of water molecules between the solution and the host. Three distinct, hitherto unreported Xe exchange processes are identified, and water molecules initialize each one. The obtained binding energies support the existing literature. The residence times and energetics of water guests are reported. An empty host does not remain empty, but is occupied by water. The results contribute to the understanding and development of Xe biosensors based on cryptophane derivatives and alternative host structures.
Conventional nuclear magnetic resonance (NMR) is troubled by low sensitivity, requiring abundance of the target nuclei in the sample. Xe NMR biosensors1–4 (XBSs) are microscopic machines capable of molecular recognition at low concentration. The extremely sensitive electron cloud of 129Xe (ref. 5) and the ability to increase the Xe NMR signal intensity by several orders of magnitude6,7 by hyperpolarization8 and indirect detection9,10 enable accurate probing of low-concentration environments. In XBS, the Xe atom is encapsulated in a functionalized host molecule,1 and introduced as an exogenous agent to the sample. When the host binds to a target molecule with its molecule-selective antenna, a change is reported by the 129Xe NMR chemical shift.2,3
Cryptophanes11–14 (Crs) composed of two linked cyclotriveratrylene (CTV) bowls are currently a favorite category of XBS hosts. Their flexible, roughly spherical cavity is capable of molecular encapsulation via van der Waals forces. Crs meet the main requirements for potential hosts:2 (i) high affinity for Xe and (ii) suitable Xe exchange rate with the solvent. While (i) ensures that a sufficient amount of Xe is encapsulated, (ii) is essential for the Hyper-CEST technique,6,7 where hyperpolarized Xe enters the host, is depolarized by a frequency-swept irradiation at the resonance frequency in confinement, and is exchanged back to the solution. The resulting decrease of the bulk Xe NMR intensity as a function of the irradiation frequency is used to construct an indirect z-spectrum of sufficient intensity.
Host–guest systems are generally significant in chemical sensing and drug design.15–18 Gaining microscopic information on the non-covalent binding experimentally is challenging. Experiments on the energetics and dynamics of Xe@Cr complexes7,19–34 initially used an organic solvent.7,19–23,26,27,30,31,34 The introduction of water solubility-enhancing groups28 provided increased Xe affinity,24,25,28,29,32,33 with the Xe guest bound to the water-soluble Cr hosts by ca. 5–6 kcal mol−1.
Computational work on Xe@Cr systems includes the Xe chemical shift,35–40 affinity and dynamics,38,39,41 structural modifications of the host,35–38 and role of the solvent.39–41 The interior volume of the host is decisive for Xe affinity,14 and a dynamical cage allows an induced fit of the guest.29 The Xe@Cr binding energy, including some Cr derivatives, is ca. 4–17 kcal mol−1.38,39,41 Many of the studies do not include host dynamics or explicit solvent effects. Dispersion interactions have been found to be essential for these non-covalently bound systems.38,39,42 In ref. 41, the explicit solvent was found to be important, and correlation between the average number of encapsulated water molecules and Xe affinity was observed.
In this communication we study computationally the host–guest interactions between Xe and the simple, commonly used cryptophane-A (CrA) host, also known as Cr-222, in its natural solvent environment at room temperature. We focus on the Xe binding free energy, ΔABind, the mechanism of Xe complexation, as well as the role of solvent water. We attach no targeting or solubility-enhancing moieties, and hence the system can be viewed as a prototype XBS. Molecular dynamics (MD) and metadynamics (MTD)43,44 simulations are performed at the semiempirical GFN245 and GFN0,46 as well as at the GFN-FF47 force-field levels of theory within the xTB code.48,49 The Xe exchange rate between the solution and CrA has been experimentally estimated at ca. 102 s−1 (ref. 2, 3, 20, 21, 32 and 33). Hence, exchange events are rare in the molecular time scale. For this reason, Xe dissociation was modeled by MTD to enhance phase-space sampling. xTB employs the density-functional tight-binding approach,50,51 amenable for configurational and dynamical modeling of non-covalently bound systems over time scales and system sizes exceeding those possible entirely from first principles.
ΔABind was estimated by a thermodynamic cycle. Four distinct physical sites (Fig. 1) were simulated: (i) water only, (ii) Xe atom in water, (iii) CrA in water, and (iv) Xe@CrA in water. The averages 〈E〉 of the total energies of the different sites are subtracted as
| ΔEBound = 〈Eiv〉 − 〈Eiii〉, | (1) |
| ΔEFree = 〈Eii〉 − 〈Ei〉. | (2) |
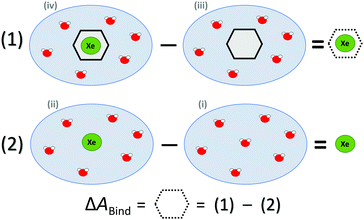 | ||
| Fig. 1 Thermodynamic cycle of the four sites (see text) simulated to access the free energy of Xe binding to the CrA host, ΔABind. Xe atom in green, water molecules in red, CrA cage in black. | ||
Hence, the free energy of Xe binding becomes
| ΔABind ≈ ΔEBound − ΔEFree | (3) |
The ESI† provides the technical details of the simulations. The results, –4.4 (1.2), –10 (4), and –21 (9) kcal mol−1 at the GFN-FF, GFN0, and GFN2 levels, respectively, all reproduce the correct, negative sign of ΔABind. The GFN-FF value is in good agreement with prior experiments, ca. 5–6 kcal mol−1. The larger ΔABind of GFN0 falls in the range of dispersion-corrected density-functional theory (DFT) data and the benchmark MP2 result of ref. 39, while GFN2 agrees with the even stronger binding produced by other DFT functionals.39 However, it should be noted that the first-principles calculations39 involved differences of potential energy minima at optimized geometries, whereas the present free-energy differences include the kinetic energy of the atoms. Our GFN-FF datum is expectedly in line with the earlier study41 that combined force-field MD with free energy perturbation methods. However, moieties increasing the water solubility of CrA, were included in ref. 41. The association constant Ka and the Eyring–Polanyi exchange rate ω,52,53
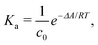 | (4) |
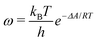 | (5) |
While ΔABind and the derived ω are relatively well reproduced by GFN-FF and GFN0, respectively, the GFN2 data appear to be overly attractive. This might be caused by several factors. According to a benchmark study,42 GFN2 systematically underestimates non-covalent repulsion. Secondly, site (iii) simulation started from an initially empty CrA and, with GFN2, did not proceed to encapsulate any water, unlike with GFN0 and GFN-FF. Presumably the GFN2 trajectory is too short (see ESI†). Hence, 〈Eiii〉 is higher than a system with encapsulated water would have had. This decreases ΔABind at the GFN2 level, rendering the host–guest interaction energetically too attractive. Additionally, the lack of solubility-enhancing units in our prototypic XBS can contribute to the discrepancy.
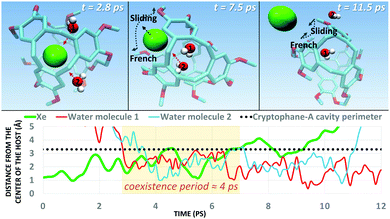
Next, we simulated the dissociation event by using MTD43,44 to push the Xe atom out from the CrA cavity, in site (iv). The association process would be much harder to simulate in practice, and is assumed to happen via the same path. Due to the computational requirements of the semiempirical methods, a sufficient number of long enough MTD simulations with GFN0/GFN2 was out of reach. Altogether, six of the MTD runs performed with GFN-FF produced dissociation, and always in two successive steps: (1) One or more H2O molecules enter the host cage and co-exist with Xe for a few ps, and (2) Xe exits, leaving one or more encapsulated waters behind. It is, hence, evident that water molecules play a crucial role in the Xe exchange. As expected, both the Xe guest and the water molecules are found to exit (and the H2O also enter) the cage via the portals between the three linkers (Fig. S1 in ESI†). In more detail, the simulated events can be classified into three categories (Fig. 2): (i) A water molecule enters, followed by the displacement of Xe. (ii) Two H2Os enter from different portals, followed by Xe exiting via the third portal. (iii) Two waters enter, one of them travels through the cage, and the other exits through the same portal it entered from. Two new waters enter, after which Xe exits as in (ii). Animations of the processes (i–iii) can be found in the ESI.†
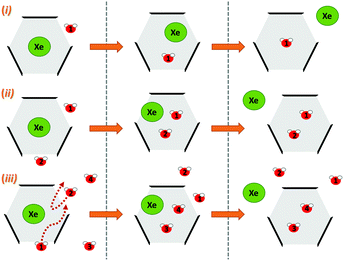 | ||
| Fig. 2 Three distinct Xe exit processes from CrA, each initialized by inclusion of water molecule(s) that displace Xe. | ||
In each process, the H2O molecules initialize the rare event, acting like a catalyst. The dissociation is analogous to a single displacement reaction. A schematic pathway of the process (ii) is presented in Fig. 3. Similar graphs on (i) and (iii) are shown in the ESI.† The conformation of the host changes in the Xe dissociation in a combination of the French door and sliding door gating mechanisms54 that open/close the portal. In the French door part (grey arrows in Fig. 3, top), the two OCH3 groups rotate away from the Xe dissociation pathway. In the sliding door part (grey dashed lines), the entire host structure opens by stretching the linkers that connect the CTV bowls.
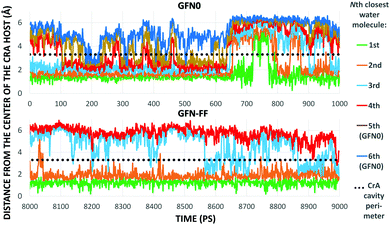
As Xe displacement is associated with the inclusion of water molecules, the energetics and dynamics of H2O in site (iii) were further simulated by MD. With GFN0 and GFN-FF, an initially empty, solvated CrA cage does not remain empty, but is eventually occupied by water molecules that undergo fast in-out exchange with the solution. At the GFN2 level this exchange was not observed (vide supra). The RMS distances of H2O molecules from the center of the host illustrate the exchange (Fig. 4). At the GFN0 level, the CrA cavity is occupied by at least three waters almost throughout the simulation. After ca. 700 ps, a short period of empty cavity is also seen. The exchange is markedly slower at the GFN-FF level. The host encapsulates an average of 3.32 and 2.25 water molecules at the GFN0 and GFN-FF levels, respectively.
The distribution of different cage occupation numbers NW is presented in Table 1. With GFN0, the broad distribution peaks around 3⋯5 water molecules, never exceeding six. In contrast, the GFN-FF occupation peaks sharply at 2, with the maximum NW = 4. After the initial equilibration there is always at least one H2O guest in the CrA cage at this level.
| Number of water molecules NW | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||
| a Relative occupation. b In units of kcal mol−1. | ||||||||
| GFN0 | RO (%)a | 4.5 | 11.9 | 12.3 | 24.4 | 17.2 | 24.6 | 5.2 |
| ΔAb | 0 | −0.58 | −0.60 | −1.01 | −0.80 | −1.02 | −0.09 | |
| ΔA/NWb | 0 | −0.58 | −0.30 | −0.34 | −0.20 | −0.20 | −0.02 | |
| GFN-FF | RO (%)a | — | 2.3 | 71.8 | 24.8 | 1.2 | — | — |
| ΔAb | — | 0 | −2.06 | −1.43 | 0.38 | — | — | |
| ΔA/NWb | — | 0 | −1.03 | −0.48 | 0.10 | — | — | |
In a two-state system, the relative binding energy ΔABA between the two states can be approximated by
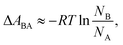 | (6) |
The exchange between encapsulated and bulk water molecules was studied by computing the survival probability function, P(t), of water inside the host. P(t) is the time correlation function of the number of molecules that remain in the cavity after the time t, with the value P(0) equaling the average occupation number. We approximate the mean residence time τ of water molecules through a single-exponential fit to 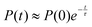 , as detailed in the ESI.† The results, τ = 198 (5) and 308 (8) ps at the GFN0 and GFN-FF levels, respectively, are consistent with the in-out exchange behavior of water (Fig. 4) and with the distribution of NW (Fig. S5, ESI†). Earlier force-field MD simulations41 for water-soluble CrA derivatives indicate a faster exchange by about one order of magnitude. The underlying force field used in ref. 41 is different from the present xTB Hamiltonians. Additionally, our prototypic CrA does not have the solubility enhancing moieties.
, as detailed in the ESI.† The results, τ = 198 (5) and 308 (8) ps at the GFN0 and GFN-FF levels, respectively, are consistent with the in-out exchange behavior of water (Fig. 4) and with the distribution of NW (Fig. S5, ESI†). Earlier force-field MD simulations41 for water-soluble CrA derivatives indicate a faster exchange by about one order of magnitude. The underlying force field used in ref. 41 is different from the present xTB Hamiltonians. Additionally, our prototypic CrA does not have the solubility enhancing moieties.
Conclusions
In summary, the behavior of a prototypic Xe biosensor, Xe@CrA, in an aqueous medium was studied by MD and MTD simulations. The correct, attractive sign for the Xe binding free energy could be reproduced in a thermodynamic cycle calculation. The binding energies agree well with earlier data, apart from a too attractive result obtained at the semiempirical GFN2 level. MTD simulations enabled the complexation mechanism and pathway of Xe to be identified for the first time. Three qualitatively different processes, each initialized by the inclusion of H2O molecules, were found. The host conformation changes prior to Xe dissociation in a combination of the French door and sliding door gating mechanisms. There might exist other possible exchange mechanisms, which could not be reproduced in the present, finite set of simulations. Despite the hydrophobic nature of the CrA interior, in an aqueous medium the host cavity is, on average, inhabited by 2–3 H2O molecules.Many of the earlier computational studies on XBSs were performed in vacuo and/or with static models, omitting the important dynamical and solvent effects modelled here. The present work sheds light on the microscopic description of the solvated Xe@CrA XBS core, supports the existing literature on the thermodynamics of the system, and paves the way for further studies. In addition, MTD is a promising method for the generation of non-covalent host–guest binding events that are out of reach for classical MD.
Author contributions
P. Hilla was responsible for data curation, general investigation, software coding, visualisation of methods and results, and writing of the original draft; J. Vaara supervised the entire work. Both authors contributed together to conceptualisation of the project and reviewing/editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Drs. V. -V. Telkki and P. Lantto, as well as Mr P. Mayorga Delgado (Oulu) are thanked for many useful discussions. We acknowledge funding from the Academy of Finland (Grant 331008) and U. Oulu (Kvantum Institute). Computations were carried out at CSC–the Finnish IT Centre for Science and the Finnish Grid and Cloud Infrastructure project (persistent identifier urn:nbn:fi:research-infras-2016072533).Notes and references
- M. Spence, S. Rubin, I. Dimitrov, J. Ruiz, D. Wemmer, A. Pines, S. Qin Yao, F. Tian and P. G. Schultz, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10654–10657 CrossRef CAS PubMed.
- P. Berthault, G. Huber and H. Desvaux, Progr. NMR Spectrosc., 2009, 55, 35–60 CrossRef CAS.
- L. Schröder, Phys. Med., 2013, 29, 3–16 CrossRef PubMed.
- S. Zemerov and I. Dmochowski, RSC Adv., 2021, 11, 7693–7703 RSC.
- B. Goodson, J. Magn. Reson., 2002, 155, 157–216 CrossRef CAS PubMed.
- L. Schröder, T. Lowery, C. Hilty, D. Wemmer and A. Pines, Science, 2006, 314, 446–449 CrossRef PubMed.
- M. Kunth, C. Witte and L. Schröder, J. Chem. Phys., 2014, 141, 1–9 CrossRef PubMed.
- T. Walker and W. Happer, Rev. Mod. Phys., 1997, 69, 629–642 CrossRef CAS.
- K. Ward, A. Aletras and R. Balaban, J. Magn. Reson., 2000, 143, 79–87 CrossRef CAS PubMed.
- E. Harel, L. Schröder and S. Xu, Annu. Rev. Anal. Chem., 2008, 1, 133–163 CrossRef CAS PubMed.
- J. Gabard and A. Collet, J. Chem. Soc., Chem. Commun., 1981, 21, 1137–1139 RSC.
- T. Brotin and J.-P. Dutasta, Chem. Rev., 2009, 109, 88–130 CrossRef CAS PubMed.
- T. Brotin, A. Martinez and J.-P. Dutasta, in Calixarenes and Beyond, ed. P. Neri, J. Sessler and M.-X. Wang, Springer, 2016, pp. 525–557 Search PubMed.
- G. El-Ayle and K. Travis, in Comprehensive Supramolecular Chemistry II, ed. J. Atwood, Elsevier, 2017, pp. 199–249 Search PubMed.
- J. Rebek, Angew. Chem., Int. Ed., 2005, 44, 2068–2078 CrossRef CAS PubMed.
- M. Liu, L. Zhang and T. Wang, Chem. Rev., 2015, 115, 7304–7397 CrossRef CAS PubMed.
- S. Barrow, S. Kasera, M. Rowland, J. del Barrio and O. Scherman, Chem. Rev., 2015, 115, 12320–12406 CrossRef CAS PubMed.
- L. Yang, X. Tan, Z. Wang and X. Zhang, Chem. Rev., 2015, 115, 7196–7239 CrossRef CAS PubMed.
- K. Bartik, M. Luhmer, J.-P. Dutasta, A. Collet and J. Reisse, J. Am. Chem. Soc., 1998, 120, 784–791 CrossRef CAS.
- T. Brotin, A. Lesage, L. Emsley and A. Collet, J. Am. Chem. Soc., 2000, 122, 1171–1174 CrossRef CAS.
- T. Brotin, T. Devic, A. Lesage, L. Emsley and A. Collet, Chem. – Eur. J., 2001, 7, 1561–1573 CrossRef CAS PubMed.
- T. Brotin and J.-P. Dutasta, Eur. J. Org. Chem., 2003, 973–984 CrossRef CAS.
- M. Spence, J. Ruiz, S. Rubin, T. Lowery, N. Winssinger, P. Schultz, D. Wemmer and A. Pines, J. Am. Chem. Soc., 2004, 126, 15287–15294 CrossRef CAS PubMed.
- G. Huber, T. Brotin, L. Dubois, H. Desvaux, J.-P. Dutasta and P. Berthault, J. Am. Chem. Soc., 2006, 128, 6239–6246 CrossRef CAS PubMed.
- A. Hill, Q. Wei, R. Eckenhoff and I. Dmochowski, J. Am. Chem. Soc., 2007, 129, 9262–9263 CrossRef PubMed.
- H. Fogarty, P. Berthault, T. Brotin, G. Huber, H. Desvaux and J.-P. Dutasta, J. Am. Chem. Soc., 2007, 129, 10332–10333 CrossRef CAS PubMed.
- G. Huber, L. Beguin, H. Desvaux, T. Brotin, H. Fogarty, J.-P. Dutasta and P. Berthault, J. Phys. Chem. A, 2008, 112, 11363–11372 CrossRef CAS PubMed.
- A. Hill, Q. Wei, T. Troxler and I. Dmochowski, J. Am. Chem. Soc., 2009, 131, 3069–3077 CrossRef PubMed.
- O. Taratula, A. Hill, N. Khan, P. Carroll and I. Dmochowski, Nat. Commun., 2010, 1, 148 CrossRef PubMed.
- R. Fairchild, A. Joseph, T. Holman, H. Fogarty, T. Brotin, J.-P. Dutasta, C. Boutin, G. Huber and P. Berthault, J. Am. Chem. Soc., 2010, 132, 15505–15507 CrossRef CAS PubMed.
- Y. Bai, A. Hill and I. Dmochowski, Anal. Chem., 2012, 84, 9935–9941 CrossRef CAS PubMed.
- S. Korchak, W. Kilian and L. Mitschang, Chem. Commun., 2015, 51, 1721–1724 RSC.
- S. Korchak, W. Kilian, L. Schröder and L. Mitschang, J. Magn. Reson., 2016, 265, 139–145 CrossRef CAS PubMed.
- P. Berthault, C. Boutin, E. Léonce, E. Jeanneau and T. Brotin, ChemPhysChem, 2017, 18, 1561–1568 CrossRef CAS PubMed.
- D. Sears and C. Jameson, J. Chem. Phys., 2003, 119, 12231–12244 CrossRef CAS.
- J. Ruiz, D. Sears, A. Pines and C. Jameson, J. Am. Chem. Soc., 2006, 128, 16980–16988 CrossRef PubMed.
- A. Bagno and G. Saielli, Chem. – Eur. J., 2012, 18, 7341–7345 CrossRef CAS PubMed.
- E. Dubost, J.-P. Dognon, B. Rousseau, G. Milanole, C. Dugave, Y. Boulard, E. Léonce, C. Boutin and P. Berthault, Angew. Chem., Int. Ed., 2014, 53, 9837–9840 CrossRef CAS PubMed.
- T. Demissie, K. Ruud and J. Hansen, J. Phys. Chem. A, 2017, 121, 9669–9677 CrossRef CAS PubMed.
- E. Léonce, J.-P. Dognon, D. Pitrat, J.-C. Mulatier, T. Brotin and P. Berthault, Chem. – Eur. J., 2018, 24, 6534–6537 CrossRef PubMed.
- L. Gao, W. Liu, O.-S. Lee, I. Dmochowski and J. Saven, Chem. Sci., 2015, 6, 7238–7248 RSC.
- K. Kříž, M. Nováček and J. Řezáč, J. Chem. Theory Comput., 2021, 17, 1548–1561 CrossRef PubMed.
- A. Laio and F. Gervasio, Rep. Progr. Phys., 2008, 71, 1–22 Search PubMed.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CAS.
- S. Grimme, S. Ehlert and C. Bannwarth, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef PubMed.
- P. Pracht, E. Caldeweyher, S. Ehlert and S. Grimme, ChemRxiv: A Robust Non-Self-Consistent Tight-Binding Quantum Chemistry Method for large Molecules, 2019.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 11, e01493 Search PubMed.
- GitHub: xTB, https://github.com/grimme-lab/xtb.
- J. Harris, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 1770–1779 CrossRef CAS PubMed.
- P. Koskinen and V. Mäkinen, Comput. Mater. Sci., 2009, 47, 237–253 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- M. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- K. Houk, K. Nakamura, C. Sheu and A. Keating, Science, 1996, 273, 627–629 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: ESI includes additional material illustrating the basic structure of Cr molecules and explaining the details of system preparation, on chosen MD and MTD parameters, error margin calculations, and numerical computations related to water dynamics are presented. Video examples of three Xe dissociation processes are also included. See DOI: https://doi.org/10.1039/d2cp01889f |
| This journal is © the Owner Societies 2022 |