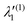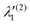The Jahn–Teller and pseudo-Jahn–Teller effects in the propyne radical cation†
Arun Kumar
Kanakati
,
Vadala Jhansi
Rani
and
S.
Mahapatra
 *
*
School of Chemistry, University of Hyderabad, Hyderabad 500 046, India. E-mail: susanta.mahapatra@uohyd.ac.in
First published on 20th June 2022
Abstract
The Jahn–Teller (JT) and pseudo-Jahn–Teller (PJT) effects in the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E, Ã2E and
2E, Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states of the propyne radical cation are investigated with the aid of ab initio quantum chemistry calculations and first principles quantum dynamics simulations. For the latter, both time-independent and time-dependent quantum mechanical methods are employed. Standard vibronic coupling theory is used to construct a symmetry consistent vibronic Hamiltonian in a diabatic electronic basis. Taylor series expansion of the elements of the diabatic electronic Hamiltonian is carried out and the parameters that appear in the expansion are derived from the ab initio calculated adiabatic electronic energies. It is found that the JT effect is weak in the
2A1 electronic states of the propyne radical cation are investigated with the aid of ab initio quantum chemistry calculations and first principles quantum dynamics simulations. For the latter, both time-independent and time-dependent quantum mechanical methods are employed. Standard vibronic coupling theory is used to construct a symmetry consistent vibronic Hamiltonian in a diabatic electronic basis. Taylor series expansion of the elements of the diabatic electronic Hamiltonian is carried out and the parameters that appear in the expansion are derived from the ab initio calculated adiabatic electronic energies. It is found that the JT effect is weak in the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state as compared to that in the Ã2E state. Because of large energy separation, the PJT coupling among the JT-split components of the
2E state as compared to that in the Ã2E state. Because of large energy separation, the PJT coupling among the JT-split components of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state with the neighboring states is also very weak. However, the PJT coupling of the
2E state with the neighboring states is also very weak. However, the PJT coupling of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 state with the JT split components of the Ã2E state has some impact on the dynamics in the coupled Ã2E–
2A1 state with the JT split components of the Ã2E state has some impact on the dynamics in the coupled Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states. The vibronic spectrum of each of these states is calculated and compared with the experimental results. The nonradiative internal conversion dynamics of excited cationic states is examined. Interesting comparison is made with the JT and PJT coupling effects in the nuclear dynamics of the
2A1 electronic states. The vibronic spectrum of each of these states is calculated and compared with the experimental results. The nonradiative internal conversion dynamics of excited cationic states is examined. Interesting comparison is made with the JT and PJT coupling effects in the nuclear dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E–Ã2E–
2E–Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2B2 electronic states of the isomeric allene radical cation.
2B2 electronic states of the isomeric allene radical cation.
1 Introduction
The Jahn–Teller (JT) effect,1–7i.e., the splitting of orbital degeneracy upon nuclear distortion, is a generic feature of nonlinear polyatomic molecules belonging to high symmetry point groups. Such a splitting of symmetry enforced degeneracy gives rise to vibronic coupling among the JT-split component states and leads to conical intersections (CIs) of electronic potential energy surfaces (PESs)8–16 of non-linear molecules. It is well known that the Born-Oppenheimer (BO)17 approximation breaks down in this situation and electronic and nuclear motion takes place concurrently. As a result of splitting, the equilibrium minimum of the degenerate state changes to a saddle point and new minima appear on the lower adiabatic sheet at a reduced symmetry.18 The JT-split component states may also undergo symmetry allowed coupling with other energetically close JT-split component states or a non-degenerate state. Such couplings are called pseudo-Jahn–Teller (PJT) coupling.18–21 The occurrence of JT and PJT couplings leads to multiple multi-dimensional CIs with different nonadiabatic coupling and highly complex nuclear dynamics.22,23Allene (H2CCCH2, propadiene), propyne (H3CCCH, methyl acetylene) and cyclopropene are the three stable isomers of C3H4. The former two isomers are important intermediates in combustion and astrochemistry.24–28 They are members of the cumulene series with odd number of carbon atoms. The radical cation of these isomers possesses degenerate electronic states and vibrational modes. Therefore, they provide a unique platform to investigate multimode JT and PJT effects in their ionic states. While the equilibrium configuration of allene belongs to the less common D2d symmetry point group, that of propyne belongs to the more common C3v symmetry point group. The non-degenerate vibrational modes of b1 and b2 symmetry are JT active in the degenerate ionic states of allene. On the other hand, the degenerate vibrational modes of e symmetry cause PJT coupling among the degenerate and non-degenerate ionic states of allene. Multimode JT and PJT interactions in the ionic states of allene have been extensively studied theoretically29–36 and also probed experimentally through photoelectron spectroscopy measurements.37–42 To the best of our knowledge, it is the first example treated with a higher-order vibronic coupling model in the literature.34 The PJT coupling in its Ã2E – ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2B2 electronic manifold was found to be extremely strong which leads to a broad and diffuse vibronic band structure at higher energies.
2B2 electronic manifold was found to be extremely strong which leads to a broad and diffuse vibronic band structure at higher energies.
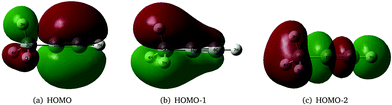
As stated above, the JT and PJT effects in the ionic states of propyne are not rigorously studied in the literature. It would therefore be interesting to study how these effects in the propyne radical cation differ as compared to those in the allene radical cation since they are isomeric in nature and have different JT and PJT coupling mechanisms. The first two valence molecular orbitals (MO) of propyne belong to e symmetry and possess π character [cf.Fig. 1(a and b)]. The third valence MO is of σ type and is of a1 symmetry [cf.Fig. 1(c)]. Ionization of an electron from these orbitals creates the propyne radical cation (CH3CCH˙+) in its electronic ground (![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E) and first two excited (Ã2E and
2E) and first two excited (Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1) electronic states, respectively.
2A1) electronic states, respectively.
The vibronic structure of the electronic states of CH3CCH˙+ was probed in photoelectron spectroscopy experiments.43–52 The He I and threshold photoelectron spectra43–45 revealed that the vibrational structure of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state consists of a strong origin band and weak progressions of C
2E state consists of a strong origin band and weak progressions of C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C and C–C stretching modes. This observation indicates that the equilibrium structure of the cationic ground state is similar to that of the neutral ground state and the JT effect is weak in the
C and C–C stretching modes. This observation indicates that the equilibrium structure of the cationic ground state is similar to that of the neutral ground state and the JT effect is weak in the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state. The photoelectron spectrum of CH3CCH has been recorded by Baker and Turner43 using the Helium 584 Å line. Among the first two bands in the ∼10–17 eV energy range, the second one revealed a highly overlapping vibronic structure. The first photoelectron (PE) band has a simple vibronic structure and appears at ∼10.3 eV. The maxima of the second band appear at ∼14.6 and ∼15.3 eV. This band is of particular interest as it apparently bears the signature of strong JT and PJT interactions in the excited electronic manifold of CH3CCH˙+. Matsui et al.49 recorded the photoelectron spectrum of CH3 CCH at higher energy resolution in a non-resonant two-photon pulsed-field ionization (PFI) Zero-Kinetic-Energy (ZEKE) measurement. They resolved spin–orbit (SO) structure in the rotational profile of the origin band of the
2E state. The photoelectron spectrum of CH3CCH has been recorded by Baker and Turner43 using the Helium 584 Å line. Among the first two bands in the ∼10–17 eV energy range, the second one revealed a highly overlapping vibronic structure. The first photoelectron (PE) band has a simple vibronic structure and appears at ∼10.3 eV. The maxima of the second band appear at ∼14.6 and ∼15.3 eV. This band is of particular interest as it apparently bears the signature of strong JT and PJT interactions in the excited electronic manifold of CH3CCH˙+. Matsui et al.49 recorded the photoelectron spectrum of CH3 CCH at higher energy resolution in a non-resonant two-photon pulsed-field ionization (PFI) Zero-Kinetic-Energy (ZEKE) measurement. They resolved spin–orbit (SO) structure in the rotational profile of the origin band of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state.
2E state.
Shieh et al.47 recorded the spectrum of propyne using the 2+1 resonance enhanced multi-photon ionization technique and obtained information on several Rydberg series of propyne. By extrapolating these series, they concluded that the SO splitting of the ground vibronic state of CH3CCH˙+ is less compared to that of the acetylene cation (∼30.91 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53). Xing et al.48 also recorded rotationally resolved spectra for CH3CCH˙+ (
53). Xing et al.48 also recorded rotationally resolved spectra for CH3CCH˙+ (![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E3/2,1/2, ν1+ = 1) and estimated SO coupling ∼−13.0 ± 0.2 cm−1, similar in magnitude to the value determined by Shieh et al.47 This is ∼60% smaller than that of the acetylene cation implying a quenching of SO coupling by the strong JT effect in the
2E3/2,1/2, ν1+ = 1) and estimated SO coupling ∼−13.0 ± 0.2 cm−1, similar in magnitude to the value determined by Shieh et al.47 This is ∼60% smaller than that of the acetylene cation implying a quenching of SO coupling by the strong JT effect in the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state of CH3CCH˙+ and contradicts the observation made by Matsui et al.49
2E state of CH3CCH˙+ and contradicts the observation made by Matsui et al.49
In order to resolve the ambiguity of the results of ref. 47–49, Marquez et al.50 performed high level ab initio quantum chemistry calculations including the vibronic and SO couplings. They found that the pure electronic SO coupling of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state of CH3CCH˙+ is ∼−28 cm−1, without including the JT interaction. This coupling is ∼18 cm−1 when the JT interaction was included. If the sign is ignored, this result is in qualitative agreement with the results of Shieh et al.47 and Xing et al.48 More recently, Jacovella et al.52 recorded the single photon PFI-ZEKE photoelectron spectrum of CH3 CCH at a resolution of ∼0.8 cm−1 and reported the partially resolved rotational structure of the origin band of the
2E state of CH3CCH˙+ is ∼−28 cm−1, without including the JT interaction. This coupling is ∼18 cm−1 when the JT interaction was included. If the sign is ignored, this result is in qualitative agreement with the results of Shieh et al.47 and Xing et al.48 More recently, Jacovella et al.52 recorded the single photon PFI-ZEKE photoelectron spectrum of CH3 CCH at a resolution of ∼0.8 cm−1 and reported the partially resolved rotational structure of the origin band of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state of CH3CCH˙+. Despite several experimental studies, a detailed theoretical study of multimode JT and PJT interactions in the electronic states of CH3CCH˙+ is missing in the literature. Theoretical calculations on the electronic structure and vertical ionization energies (VIEs) of CH3 CCH are reported.50,54
2E state of CH3CCH˙+. Despite several experimental studies, a detailed theoretical study of multimode JT and PJT interactions in the electronic states of CH3CCH˙+ is missing in the literature. Theoretical calculations on the electronic structure and vertical ionization energies (VIEs) of CH3 CCH are reported.50,54
In this article we therefore set out to carry out a detailed investigation of multimode JT and PJT effects in the first three electronic states of CH3CCH˙+. Among the three low-lying electronic states, the first two electronic states are doubly degenerate, which are prone to the JT distortion.1 The next higher electronic state is nondegenerate. The fifteen normal vibrational modes of propyne belong to the following irreducible representations of the C3v symmetry point group:
| Γvib = 5a1 + 5e. | (1) |
The direct product of E electronic representation and the direct product of E with A1 electronic representation in the C3v point group yield
| E ⊗ E = a1 + a2 + e. | (2) |
| E ⊗ A1 = e. | (3) |
We mention here that the symmetry of the electronic states and the vibrational modes is denoted by upper and lower case letters, respectively, throughout this paper. In the case of the E × e-Jahn–Teller problem the equivalency of the matrix elements in the detailed selection rule reduces eqn (2) to (E) 2 = a1 + e, the so-called symmetrized direct product.55 The elementary symmetry selection rules [cf.eqn (2) and (3)] suggest that the degenerate ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E and Ã2E electronic states of CH3CCH˙+ would undergo JT splitting in first-order when distorted along the degenerate vibrational modes of e symmetry [(E ⊗ e)-JT effect]. The JT split components of the two E states may also undergo PJT coupling through the vibrational modes of e symmetry. However, the
2E and Ã2E electronic states of CH3CCH˙+ would undergo JT splitting in first-order when distorted along the degenerate vibrational modes of e symmetry [(E ⊗ e)-JT effect]. The JT split components of the two E states may also undergo PJT coupling through the vibrational modes of e symmetry. However, the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E and Ã2E states of CH3CCH˙+ are energetically well separated and PJT coupling between them is not significant. The non-degenerate
2E and Ã2E states of CH3CCH˙+ are energetically well separated and PJT coupling between them is not significant. The non-degenerate ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 state undergoes PJT coupling with the components of the Ã2E state through vibrational modes of e symmetry [(E + A) ⊗ e -PJT effect] and these states are energetically close. The PJT coupling of these states is expected to yield multiple conical intersections and consequently the nuclear motion may become predominantly nonadiabatic. The totally symmetric a1 vibrational modes are Condon active in all three electronic states.
2A1 state undergoes PJT coupling with the components of the Ã2E state through vibrational modes of e symmetry [(E + A) ⊗ e -PJT effect] and these states are energetically close. The PJT coupling of these states is expected to yield multiple conical intersections and consequently the nuclear motion may become predominantly nonadiabatic. The totally symmetric a1 vibrational modes are Condon active in all three electronic states.
In the following a model Hamiltonian is constructed in a diabatic electronic basis and using the standard vibronic coupling theory.18 The elements of the electronic Hamiltonian are expanded in a Taylor series and the parameters are derived from the adiabatic electronic energies calculated ab initio, by both complete active space self-consistent field (CASSCF)-multi reference configuration interaction (MRCI)56–59 and equation of motion ionization potential coupled cluster singles and doubles (EOMIP-CCSD)60,61 methods. The quantum dynamical observables are calculated by solving the time-independent as well as time-dependent Schrödinger equations. In the time-independent case, the Lanczos algorithm62 is used to diagonalize the Hamiltonian matrix expressed on the basis of harmonic oscillator (HO) functions. This enables determination of the precise location of the vibronic energy levels and aids in their assignments. This method is computationally not affordable for systems with a large number of electronic and vibrational degrees of freedom (DOF). To calculate the broad band spectra, the time-dependent calculations are carried out by propagating wave packets (WPs) with the aid of the multi-configuration time-dependent Hartree (MCTDH) method developed at Heidelberg.63–66 The results are compared with the experimental findings and discussed. To this end, we note that alternative methods and algorithms are also developed in the literature to treat nonadiabatic dynamics of large systems from first principles in the past years with the aid of diabatic electronic states constructed from ab initio computed nonadiabatic coupling matrix elements (see ref. 67–69 for details).
2 Theoretical framework
2.1 The vibronic Hamiltonian
The photoionization to the first three low-lying![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E, Ã2E and
2E, Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states (hereafter these will be designated as
2A1 electronic states (hereafter these will be designated as ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ) of CH3CCH˙+ is examined theoretically. As stated in the introduction, each of the two degenerate electronic states undergoes JT splitting when CH3CCH˙+ is distorted along the degenerate vibrational modes of e symmetry. The symmetry selection rule [cf.eqn (2) and (3)] allows the JT split component states to undergo PJT coupling among themselves or with the nondegenerate electronic state. The PJT coupling of the
) of CH3CCH˙+ is examined theoretically. As stated in the introduction, each of the two degenerate electronic states undergoes JT splitting when CH3CCH˙+ is distorted along the degenerate vibrational modes of e symmetry. The symmetry selection rule [cf.eqn (2) and (3)] allows the JT split component states to undergo PJT coupling among themselves or with the nondegenerate electronic state. The PJT coupling of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state with the à and
state with the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) states is excluded on the energetic ground (we discussed more about this point in Section 3.2). There are five totally symmetric a1 vibrational modes that are Condon active in all three electronic states. In the following, we first resort to a diabatic electronic basis70–72 to treat this vibronic coupling problem. This is to avoid the numerical difficulties18 that arise due to the singular nature of the nonadiabatic coupling terms in an adiabatic electronic basis.17,18 The diabatic vibronic Hamiltonian is constructed in terms of the dimensionless normal coordinates of the vibrational modes of the electronic ground state of the neutral CH3 CCH. To a good approximation the vibrational motion in the latter state is treated as harmonic. In the following, we refer to Qi as the dimensionless normal coordinate of the vibrational mode νi with a harmonic vibrational frequency ωi. Actually, each Qi represents the normal displacement coordinate from the equilibrium configuration of the electronic ground state of CH3 CCH occurring at Q = 0. In the rest of the paper the totally symmetric (a1) vibrational modes are designated as ν1, ν2, ν3, ν4 and ν5 and the degenerate (e) vibrational modes as ν6, ν7, ν8, ν9 and ν10 in the order of decreasing frequency. With this description the diabatic vibronic Hamiltonian18 of the
states is excluded on the energetic ground (we discussed more about this point in Section 3.2). There are five totally symmetric a1 vibrational modes that are Condon active in all three electronic states. In the following, we first resort to a diabatic electronic basis70–72 to treat this vibronic coupling problem. This is to avoid the numerical difficulties18 that arise due to the singular nature of the nonadiabatic coupling terms in an adiabatic electronic basis.17,18 The diabatic vibronic Hamiltonian is constructed in terms of the dimensionless normal coordinates of the vibrational modes of the electronic ground state of the neutral CH3 CCH. To a good approximation the vibrational motion in the latter state is treated as harmonic. In the following, we refer to Qi as the dimensionless normal coordinate of the vibrational mode νi with a harmonic vibrational frequency ωi. Actually, each Qi represents the normal displacement coordinate from the equilibrium configuration of the electronic ground state of CH3 CCH occurring at Q = 0. In the rest of the paper the totally symmetric (a1) vibrational modes are designated as ν1, ν2, ν3, ν4 and ν5 and the degenerate (e) vibrational modes as ν6, ν7, ν8, ν9 and ν10 in the order of decreasing frequency. With this description the diabatic vibronic Hamiltonian18 of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) –Ö
–Ö![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) coupled electronic states of CH3CCH˙+ can be written as
coupled electronic states of CH3CCH˙+ can be written as![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 015 + Δ 015 + Δ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) . . | (4) |
In the above equation, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 (=
0 (=![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) N +
N + ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) 0) is the unperturbed Hamiltonian of the reference ground electronic state of CH3 CCH. Within the harmonic approximation its elements are given by
0) is the unperturbed Hamiltonian of the reference ground electronic state of CH3 CCH. Within the harmonic approximation its elements are given by
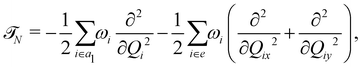 | (5) |
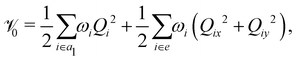 | (6) |
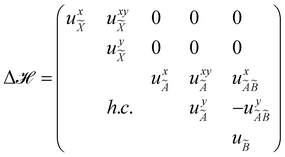 | (7) |
The quantity 15 in eqn (4) is a 5 × 5 diagonal unit matrix. The nuclear kinetic and potential energy operators of the reference state are denoted by ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) N and
N and ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) 0, respectively. The change of electronic energy upon ionization from this reference state is described by the electronic Hamiltonian matrix Δ
0, respectively. The change of electronic energy upon ionization from this reference state is described by the electronic Hamiltonian matrix Δ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) in eqn (7). The diagonal elements of this matrix represent the diabatic potential energies of the electronic states and the off-diagonal elements represent the coupling between them. The elements of Δ
in eqn (7). The diagonal elements of this matrix represent the diabatic potential energies of the electronic states and the off-diagonal elements represent the coupling between them. The elements of Δ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) are expanded in a standard Taylor series around the reference equilibrium geometry at Q = 0 in the following way:73–75
are expanded in a standard Taylor series around the reference equilibrium geometry at Q = 0 in the following way:73–75
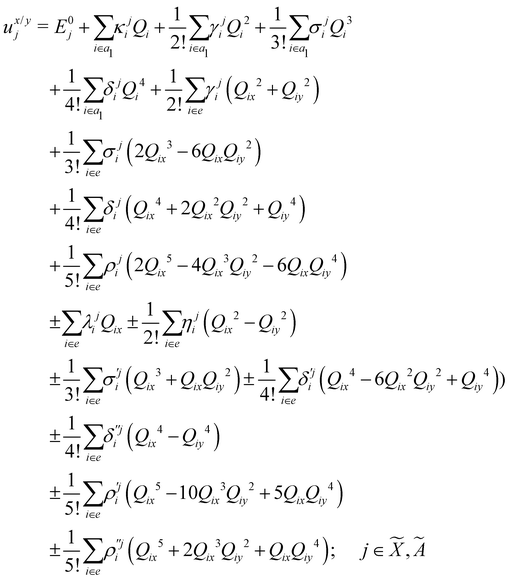 | (8) |
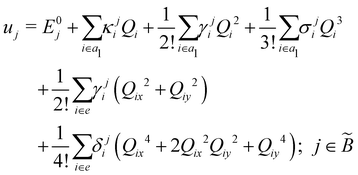 | (9) |
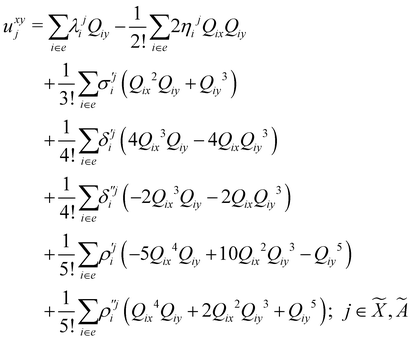 | (10) |
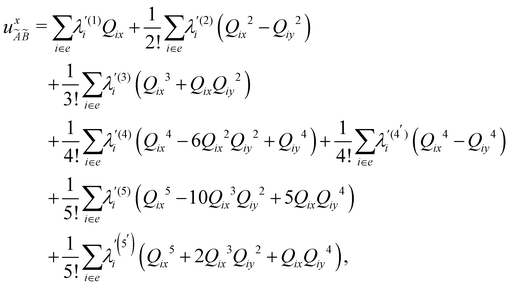 | (11) |
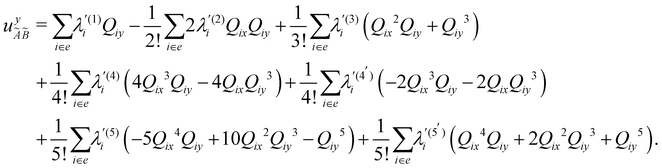 | (12) |
In the above equations, the two components of the degenerate electronic states and vibrational modes are identified with the labels x and y. The quantity E0j denotes the vertical ionization energy of the jth electronic state. The diagonal intra-state coupling parameters of the ith vibrational mode in the jth electronic state are given by κji (linear), γji (second-order), σji (third-order), δji (fourth-order), and ρji (fifth-order). The linear, second, third, fourth and fifth-order JT coupling parameters along the degenerate vibrational modes within the jth electronic state are given by λji, ηji, 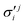 ,
, 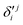 and
and 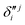 ,
, 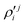 and
and 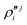 , respectively. The PJT coupling parameters between the Ã2E and
, respectively. The PJT coupling parameters between the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states along the degenerate vibrational modes are given by
2A1 electronic states along the degenerate vibrational modes are given by 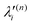 (i.e., nth order inter-state coupling constant). It is worth noting that the elements of the JT and PJT coupling matrices are of identical form and are only distinguished by different coupling constants. These parameters are derived by fitting the calculated adiabatic electronic energies to the adiabatic form of Δ
(i.e., nth order inter-state coupling constant). It is worth noting that the elements of the JT and PJT coupling matrices are of identical form and are only distinguished by different coupling constants. These parameters are derived by fitting the calculated adiabatic electronic energies to the adiabatic form of Δ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) . The summations in eqn (8)–(12) are carried out over the normal coordinate of all symmetry allowed vibrational modes. The plus and minus signs in eqn (8) are applicable to the x and y components of the degenerate electronic state, respectively. Note that the parameters of odd-order for the vibrational modes of e symmetry do not appear in eqn (9) in accordance with the symmetry selection rule.
. The summations in eqn (8)–(12) are carried out over the normal coordinate of all symmetry allowed vibrational modes. The plus and minus signs in eqn (8) are applicable to the x and y components of the degenerate electronic state, respectively. Note that the parameters of odd-order for the vibrational modes of e symmetry do not appear in eqn (9) in accordance with the symmetry selection rule.
2.2 Nuclear dynamics
The vibronic energy level structure of![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) states of CH3CCH˙+ is calculated by a time-independent matrix diagonalization approach.18,76 The spectral intensity, P(E), is calculated by Fermi's golden rule,
states of CH3CCH˙+ is calculated by a time-independent matrix diagonalization approach.18,76 The spectral intensity, P(E), is calculated by Fermi's golden rule,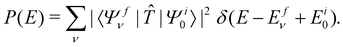 | (13) |
In the above equation, |Ψi0〉 represents the wave function of the initial vibronic ground state of the reference CH3 CCH with energy Ei0 and |Ψfν〉 is the vibronic wave function of the final (f) ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) –Ö
–Ö![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) coupled states of CH3CCH˙+ with energy Efν. The transition dipole operator
coupled states of CH3CCH˙+ with energy Efν. The transition dipole operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) describes the interaction of the 2e, 1e and 7a1 valence electrons of CH3 CCH with external radiation of energy E. The ground state |Ψi0〉 is assumed to be vibronically decoupled from the excited electronic states and can be written in a diabatic electronic basis as
describes the interaction of the 2e, 1e and 7a1 valence electrons of CH3 CCH with external radiation of energy E. The ground state |Ψi0〉 is assumed to be vibronically decoupled from the excited electronic states and can be written in a diabatic electronic basis as
| |Ψi0〉 = |Φi0〉|χi0〉 | (14) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 [cf.eqn (4)]. This is taken as the direct product of one-dimensional HO wave functions along the coordinates of all relevant vibrational modes. The final vibronic states of the
0 [cf.eqn (4)]. This is taken as the direct product of one-dimensional HO wave functions along the coordinates of all relevant vibrational modes. The final vibronic states of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states of CH3CCH˙+ can be expressed as
electronic states of CH3CCH˙+ can be expressed as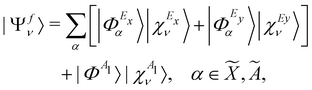 | (15) |
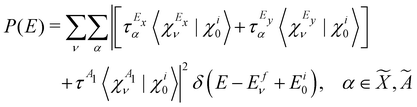 | (16) |
τm = 〈Φm|![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φi0〉 |Φi0〉 | (17) |
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E–Ã2E–
2E–Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 coupled electronic states of CH3CCH˙+. In rewriting eqn (16), the matrix elements of the transition dipole operator are considered to be weakly varying functions of the nuclear coordinates. These elements are treated as constants within the generalized Condon approximation applicable in a diabatic electronic basis.76
2A1 coupled electronic states of CH3CCH˙+. In rewriting eqn (16), the matrix elements of the transition dipole operator are considered to be weakly varying functions of the nuclear coordinates. These elements are treated as constants within the generalized Condon approximation applicable in a diabatic electronic basis.76
In order to solve the time-independent Schrödinger equation with the vibronic Hamiltonian [cf.eqn (4)], it is represented in the direct product HO basis of the reference state. In this situation the final vibronic state, |Ψfν〉, can be expressed as
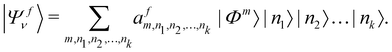 | (18) |
In the above equation, the quantum number of vibrational modes is identified by n and k represents the total number of such modes. The summation runs over the possible combination of vibrational quantum numbers and diabatic states. The vibrational basis is suitably truncated for each vibrational mode depending on its excitation strength, 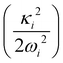 and
and 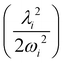 for the symmetric and degenerate vibrational modes, respectively. The Hamiltonian matrix acquires a sparse structure when expressed in a direct product HO basis. This sparse matrix is tridiagonalized employing the Lanczos algorithm62 prior to its diagonalization. The vibronic eigenvalues are precisely given by the diagonal elements and the squared first component of the Lanczos eigenvectors defines the intensity.77
for the symmetric and degenerate vibrational modes, respectively. The Hamiltonian matrix acquires a sparse structure when expressed in a direct product HO basis. This sparse matrix is tridiagonalized employing the Lanczos algorithm62 prior to its diagonalization. The vibronic eigenvalues are precisely given by the diagonal elements and the squared first component of the Lanczos eigenvectors defines the intensity.77
The spectral envelope can be obtained within the time-dependent quantum mechanical framework by Fourier transforming the time autocorrelation function of a WP evolving on the final electronic state as
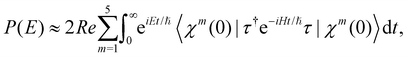 | (19) |
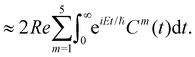 | (20) |
The WP propagation calculations are carried out within the framework of the MCTDH method63–65 implemented in the Heidelberg MCTDH suite of program developed by Meyer and co-workers.66 The latter utilizes a HO discrete variable representation for the primitive basis. The time-dependent single particle functions are represented in this basis to solve the equations of motion. Furthermore, the vibrational DOFs are combined using its multi-set ansatz to form single particles and to reduce the dimensionality problem in the multi-mode multi-state dynamics study. For more details of this method and algorithm, the readers are referred to the original research papers.63–65
3 Results and discussion
3.1 Electronic structure calculations
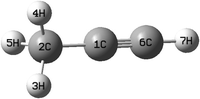
The equilibrium geometry of the CH3 CCH molecule belongs to the C3v symmetry point group in its electronic ground state. This geometry is optimized with the aid of the second order Møller-Plesset perturbation (MP2) method78 employing the augmented correlation-consistent polarized valence double zeta (aug-cc-pVDZ) basis set of Dunning.79 The Gaussian-09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 suite of program is used for this purpose. The optimized equilibrium geometry is shown in Fig. 2 with atom numbering and the corresponding geometry parameters are given in Table 1. The harmonic vibrational frequency (ωi) of the vibrational mode i at the reference equilibrium structure is calculated by diagonalizing the kinematic and ab initio force constant matrix at the same level of theory. The mass-weighted normal displacement coordinate of vibrational modes is calculated and transformed to the dimensionless form Qi by multiplying with
80 suite of program is used for this purpose. The optimized equilibrium geometry is shown in Fig. 2 with atom numbering and the corresponding geometry parameters are given in Table 1. The harmonic vibrational frequency (ωi) of the vibrational mode i at the reference equilibrium structure is calculated by diagonalizing the kinematic and ab initio force constant matrix at the same level of theory. The mass-weighted normal displacement coordinate of vibrational modes is calculated and transformed to the dimensionless form Qi by multiplying with 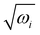 (in a.u., ħ =1). The harmonic frequencies of the vibrational modes and their symmetry are given in Table 2 along with the available literature data.81,82 It can be seen from Tables 1 and 2 that the theoretical results are in good accordance with the available literature data.
(in a.u., ħ =1). The harmonic frequencies of the vibrational modes and their symmetry are given in Table 2 along with the available literature data.81,82 It can be seen from Tables 1 and 2 that the theoretical results are in good accordance with the available literature data.
| Parameters | This work | Experiment94 |
|---|---|---|
| R(C1–C2), | 1.45 | 1.46 |
| R(C1–C6) | 1.20 | 1.20 |
| R(C2–H3, C2–H4, C2–H5) | 1.09 | 1.09 |
| R(C6–H7) | 1.06 | 1.06 |
| ∠(C1–C2–H3, C1–C2–H4, C1–C2–H5) | 110 | 110 |
| ∠(H3–C2–H4, H3–C2–H5, H4–C2–H5) | 107 | 108 |
| Symmetry | Modes | This work | Theory81 | Experiment81 | Experiment82 | Assignment |
|---|---|---|---|---|---|---|
| A 1 | ν 1 | 3471 | 3502/3618 | 3335 | Acetylene C–H str. | |
| ν 2 | 3028 | 2941/3180 | 2941 | Symm. methyl C–H str. | ||
| ν 3 | 2225 | 2138/2386 | 2138 | 1940 | C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C str. C str. |
|
| ν 4 | 1416 | 1385/1534 | 1385 | 1290 | Methyl deformation | |
| ν 5 | 941 | 930/972 | 930 | 940 | C–C str. | |
| E | ν 6 | 3084 | 2981/3246 | 2981 | Antisymm. methyl C–H str. | |
| ν 7 | 1479 | 1450/1600 | 1450 | Methyl skeletal deformation | ||
| ν 8 | 1058 | 1036/1152 | 1036 | Methyl skeletal rock | ||
| ν 9 | 672 | 628/792 | 628 | C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–H bend C–H bend |
||
| ν 10 | 347 | 327/386 | 327 | CC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bend C bend |
||
In order to study the nuclear dynamics, the PESs of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states of CH3CCH˙+ are calculated along the dimensionless normal displacement coordinates of the reference ground state. The adiabatic potential energies of these electronic states are calculated by both EOMIP-CCSD and CASSCF-MRCI methods using the aug-cc-pVDZ basis set. The EOMIP-CCSD and CASSCF-MRCI calculations are performed using the CFOUR83 and MOLPRO84 suite of programs, respectively. MOLPRO has no implementation of ionization problem. So, we used the CASSCF-MRCI method for ionization potential calculations. The adiabatic energies of the electronic states are calculated along the dimensionless normal displacement coordinate of each vibrational mode. The CASSCF-MRCI calculations are carried out with a (16,8) active space, which includes 8 valence occupied orbitals with sixteen electrons for the reference electronic ground state of CH3 CCH. The electronic states of CH3CCH˙+ have open shell configuration and a (15,8) active space is used. Test calculations are carried out with varying active space and the mentioned ones are found to yield the best results with an affordable computational cost. For all these calculations it took almost three months of CPU time on a “Intel(R) Xeon(R) CPU E5-2697 v3@2.60 GHz model with 28 cores, 56 processors” HPC cluster. The energy difference of the cationic states with the reference neutral ground state at the equilibrium configuration (at Q = 0) representing the VIEs is given in Table 3 along with the available literature data for comparison. In addition to the EOMIP-CCSD and CASSCF-MRCI results, the VIEs calculated by the Outer Valence Green's function (OVGF) method85 (using the Gaussian-09 program) are also given in Table 3. It can be seen from Table 3 that our theoretical results are in good accordance with the available experimental data. It can also be seen that at the vertical configuration the
electronic states of CH3CCH˙+ are calculated along the dimensionless normal displacement coordinates of the reference ground state. The adiabatic potential energies of these electronic states are calculated by both EOMIP-CCSD and CASSCF-MRCI methods using the aug-cc-pVDZ basis set. The EOMIP-CCSD and CASSCF-MRCI calculations are performed using the CFOUR83 and MOLPRO84 suite of programs, respectively. MOLPRO has no implementation of ionization problem. So, we used the CASSCF-MRCI method for ionization potential calculations. The adiabatic energies of the electronic states are calculated along the dimensionless normal displacement coordinate of each vibrational mode. The CASSCF-MRCI calculations are carried out with a (16,8) active space, which includes 8 valence occupied orbitals with sixteen electrons for the reference electronic ground state of CH3 CCH. The electronic states of CH3CCH˙+ have open shell configuration and a (15,8) active space is used. Test calculations are carried out with varying active space and the mentioned ones are found to yield the best results with an affordable computational cost. For all these calculations it took almost three months of CPU time on a “Intel(R) Xeon(R) CPU E5-2697 v3@2.60 GHz model with 28 cores, 56 processors” HPC cluster. The energy difference of the cationic states with the reference neutral ground state at the equilibrium configuration (at Q = 0) representing the VIEs is given in Table 3 along with the available literature data for comparison. In addition to the EOMIP-CCSD and CASSCF-MRCI results, the VIEs calculated by the Outer Valence Green's function (OVGF) method85 (using the Gaussian-09 program) are also given in Table 3. It can be seen from Table 3 that our theoretical results are in good accordance with the available experimental data. It can also be seen that at the vertical configuration the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state is energetically well separated from the à and
state is energetically well separated from the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states, whereas à and
electronic states, whereas à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) states are energetically close. Therefore, PJT coupling of the
states are energetically close. Therefore, PJT coupling of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state with à and
state with à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) states is expected to be insignificant. On the other hand, the interplay of JT and PJT coupling is expected to be strong in the Ö
states is expected to be insignificant. On the other hand, the interplay of JT and PJT coupling is expected to be strong in the Ö![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states.
electronic states.
| States |
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2
E
2
E
|
à 2 E |
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2
A
1
2
A
1
|
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 2
A
1
2
A
1
|
|
|---|---|---|---|---|---|
| VIE | 10.23 | 15.03 | 15.30 | 17.78 | OVGF |
| 10.40 | 15.09 | 15.31 | 17.68 | EOMIP-CCSD | |
| 10.28 | 15.40 | 15.75 | 18.29 | CASSCF-MRCI | |
| 10.37 | 14.4 | 15.13 | 17.2 | Expt.43 | |
| 10.37 | 14.6 | 15.3/15.5 | 17.4 | Expt.54 | |
| 10.54 | 14.60 | 15.4 | 17.4 | Expt.46 | |
| 10.36 | 13.69/14.70/15.30 | 15.8 | 17.49 | Expt.45 | |
| 10.37 | 13.69 | 15.2 | 17.2 | Expt.82 | |
| 10.37 | 14.70 | 15.50/15.80 | 17.49 | Expt.81 |
The adiabatic form of the 5 × 5 diabatic electronic Hamiltonian matrix [cf. Section 2.1] is fit to the ab initio adiabatic electronic energies by a nonlinear least-squares procedure to estimate the various coupling parameters of eqn (8)–(12). The Levenberg—Marquardt algorithm86,87 is used for the purpose. These coupling parameters are given in Tables 4 and 5 and the higher order coupling parameters are given in Tables S1 and S2 of the ESI.†
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E, Ã2E and
2E, Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states of CH3CCH˙+ derived from the EOMIP-CCSD electronic energy data. All quantities are in eV and the dimensionless Poisson parameters (
2A1 electronic states of CH3CCH˙+ derived from the EOMIP-CCSD electronic energy data. All quantities are in eV and the dimensionless Poisson parameters (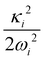 or
or 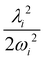 ) are given in parentheses
) are given in parentheses
| Mode |
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2
E
2
E
|
à 2 E | ||||
|---|---|---|---|---|---|---|
| κ i or λi | γ i | η i | κ i or λi | γ i | η i | |
| a 1 | ||||||
| ν 1 | 0.0003 (0.0000) | 0.0020 | — | 0.0318 (0.0027) | 0.0019 | — |
| ν 2 | −0.0320 (0.0035) | −0.0012 | — | −0.3779 (0.4921) | 0.0268 | — |
| ν 3 | 0.2184 (0.3442) | 0.0141 | — | −0.0644 (0.0299) | 0.0056 | — |
| ν 4 | 0.0452 (0.0342) | −0.0179 | — | −0.2606 (1.1359) | −0.0803 | — |
| ν 5 | −0.0194 (0.0136) | −0.0165 | — | 0.1027 (0.3835) | 0.0219 | — |
| e | ||||||
| ν 6 | 0.0266 (0.0023) | 0.0027 | 0.00011 | 0.2634 (0.2254) | −0.0249 | −0.0004 |
| ν 7 | 0.0439 (0.0289) | −0.0273 | 0.00004 | 0.4424 (2.9446) | −0.0856 | 0.0002 |
| ν 8 | 0.0462 (0.0638) | −0.0259 | 0.00020 | 0.2163 (1.3949) | −0.0553 | 0.0003 |
| ν 9 | 0.0101 (0.0108) | −0.0104 | −0.000003 | −0.0001 (0.00000) | −0.0479 | −0.0010 |
| ν 10 | 0.0119 (0.0656) | −0.0165 | −0.00020 | 0.0010 (0.00005) | −0.0609 | −0.0004 |
| Mode |
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2
A
1
2
A
1
|
Ã
2
E × ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 2A1 |
||||
|---|---|---|---|---|---|---|
| κ i | γ i | σ i | δ i | |||
| ν 1 | 0.1292 (0.0446) | −0.0351 | 0.0093 | 0.0028 | — | — |
| ν 2 | −0.0757 (0.0198) | −0.0129 | −0.0024 | — | — | — |
| ν 3 | −0.1311 (0.1240) | −0.0269 | 0.0030 | — | — | — |
| ν 4 | 0.4642 (3.6038) | −0.0262 | −0.0199 | — | — | — |
| ν 5 | 0.1729 (1.0866) | −0.0106 | −0.0023 | — | — | — |
| ν 6 | — | 0.05852 | — | −0.0206 | −0.0617 (0.0124) | 0.0478 |
| ν 7 | — | 0.02827 | — | −0.0241 | −0.0953 (0.1366) | 0.0756 |
| ν 8 | — | −0.0459 | — | −0.0015 | −0.0201 (0.0120) | 0.0210 |
| ν 9 | — | −0.0058 | — | 0.0036 | −0.0015 (0.0002) | 0.0038 |
| ν 10 | — | −0.0578 | — | 0.0049 | 0.0017 (0.0013) | −0.0019 |
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2
E
2
E
|
à 2 E | |||||
|---|---|---|---|---|---|---|
| Mode | κ i or λi | γ i | η i | κ i or λi | γ i | η i |
| a 1 | ||||||
| ν 1 | −0.0224 (0.0013) | 0.0037 | — | 0.0318 (0.0027) | 0.0028 | — |
| ν 2 | −0.0259 (0.0023) | −0.0011 | — | −0.4011 (0.5545) | 0.0280 | — |
| ν 3 | 0.2670 (0.5147) | 0.0142 | — | −0.0799 (0.0460) | 0.0084 | — |
| ν 4 | 0.0476 (0.0379) | −0.0148 | — | −0.2721 (1.2385) | −0.0853 | — |
| ν 5 | −0.0037 (0.0005) | −0.0165 | — | 0.1056 (0.4050) | 0.0245 | — |
| e | ||||||
| ν 6 | 0.0284 (0.0026) | 0.0027 | 0.000127 | 0.2562 (0.2254) | −0.1080 | 0.0042 |
| ν 7 | 0.0412 (0.0255) | −0.0248 | 0.000045 | 0.4199 (2.9446) | −0.1078 | 0.0001 |
| ν 8 | 0.0434 (0.0563) | −0.0244 | 0.000205 | 0.1966 (1.3949) | −0.0624 | 0.0003 |
| ν 9 | 0.0086 (0.0078) | −0.0063 | −0.000002 | −0.0023 (0.00000) | −0.0233 | −0.0016 |
| ν 10 | 0.0094 (0.0408) | −0.0263 | −0.000123 | 0.0002 (0.00005) | −0.0601 | −0.0004 |
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2
A
1
2
A
1
|
Ã
2
E × ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 2A1 |
|||||
|---|---|---|---|---|---|---|
| Mode | κ i | γ i | σ i | δ i | ||
| ν 1 | 0.1475 (0.0582) | −0.0467 | 0.0120 | 0.0033 | — | — |
| ν 2 | −0.0677 (0.0158) | −0.0132 | −0.0028 | — | — | — |
| ν 3 | −0.1415 (0.1445) | −0.0329 | 0.0038 | — | — | — |
| ν 4 | 0.4812 (3.8724) | −0.0272 | −0.0193 | — | — | — |
| ν 5 | 0.1901 (1.3136) | −0.0119 | −0.0023 | — | — | — |
| ν 6 | — | 0.2277 | — | −0.0588 | −0.0024 (0.00001) | 0.0515 |
| ν 7 | — | 0.0650 | — | −0.0389 | −0.1145 (0.19724) | 0.0895 |
| ν 8 | — | −0.0420 | — | −0.0039 | −0.0275 (0.02255) | 0.0274 |
| ν 9 | — | −0.0054 | — | 0.0004 | −0.0030 (0.00095) | 0.0115 |
| ν 10 | — | −0.0631 | — | −0.0021 | 0.0010 (0.00046) | 0.0020 |
3.2 Potential energy surfaces: the JT and PJT conical intersections
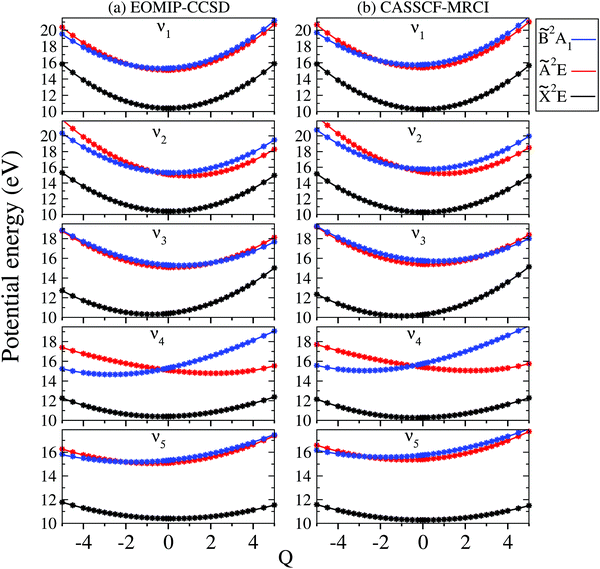
The adiabatic potential energy curves of the![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states of CH3CCH˙+ are shown and discussed in this section. The adiabatic potential energies of these states are plotted along the dimensionless normal displacement coordinates of the totally symmetric a1 vibrational modes (ν1–ν5) and the JT active e vibrational modes (ν6–ν8) in Fig. 3 and 4, respectively. The solid curves in these figures represent the potential energies obtained from the constructed theoretical model in Section 2.1 and the points superimposed on them are the computed ab initio adiabatic potential energies calculated by the EOMIP-CCSD (Fig. 3a and 4a) and CASSCF-MRCI (Fig. 3b and 4b) methods, discussed in Section 3.1. It can be seen that the calculated ab initio points are well reproduced by the present theoretical model. We note that up to a fourth- and fifth-order Taylor expansion of the electronic Hamiltonian along both a1 and JT active e vibrational modes is found to be necessary to represent the ab initio points extremely well. Also, these higher-order coupling parameters provide an accurate theoretical description of the JT split potentials and the associated vibronic spectrum. A second-order vibronic model is found to give rise to an inaccurate theoretical description. The totally symmetric vibrational modes do not lift the electronic degeneracy of the
electronic states of CH3CCH˙+ are shown and discussed in this section. The adiabatic potential energies of these states are plotted along the dimensionless normal displacement coordinates of the totally symmetric a1 vibrational modes (ν1–ν5) and the JT active e vibrational modes (ν6–ν8) in Fig. 3 and 4, respectively. The solid curves in these figures represent the potential energies obtained from the constructed theoretical model in Section 2.1 and the points superimposed on them are the computed ab initio adiabatic potential energies calculated by the EOMIP-CCSD (Fig. 3a and 4a) and CASSCF-MRCI (Fig. 3b and 4b) methods, discussed in Section 3.1. It can be seen that the calculated ab initio points are well reproduced by the present theoretical model. We note that up to a fourth- and fifth-order Taylor expansion of the electronic Hamiltonian along both a1 and JT active e vibrational modes is found to be necessary to represent the ab initio points extremely well. Also, these higher-order coupling parameters provide an accurate theoretical description of the JT split potentials and the associated vibronic spectrum. A second-order vibronic model is found to give rise to an inaccurate theoretical description. The totally symmetric vibrational modes do not lift the electronic degeneracy of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) and à states. They tune the electronic energy minimum of the cationic states relative to the equilibrium minimum of the electronic ground state of CH3 CCH (Q = 0) and therefore modify the vertical energy gap between the electronic states. It can be seen from Fig. 3 that the
and à states. They tune the electronic energy minimum of the cationic states relative to the equilibrium minimum of the electronic ground state of CH3 CCH (Q = 0) and therefore modify the vertical energy gap between the electronic states. It can be seen from Fig. 3 that the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state of CH3CCH˙+ is energetically well separated from the remaining two states. The latter states (à and
state of CH3CCH˙+ is energetically well separated from the remaining two states. The latter states (Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ) are vertically very close in energy [cf.Table 3] and undergo curve crossings in the near vicinity of reference equilibrium geometry at Q = 0 [cf.Fig. 3].
) are vertically very close in energy [cf.Table 3] and undergo curve crossings in the near vicinity of reference equilibrium geometry at Q = 0 [cf.Fig. 3].
Within a second-order coupling model and utilizing the parameters of Tables 2–5 the energetic minimum of the seam of CIs is calculated using a minimization algorithm employing Lagrange multipliers. The numerical tools available in MATHEMATICA88 are used for this purpose. The results are tabulated in a matrix array in Table 6. In the latter, the numbers in the diagonal represent the minimum of a state and those in the off-diagonal are the minimum of the intersection seam. It can be seen from Table 6 that the minimum of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state is energetically well separated from the à and
state is energetically well separated from the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) states. The intersection of the
states. The intersection of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state with the latter states occurs at very high energies and is not relevant for the present study. Using the EOMIP-CCSD (CASSCF-MRCI) electronic structure data the Ö
state with the latter states occurs at very high energies and is not relevant for the present study. Using the EOMIP-CCSD (CASSCF-MRCI) electronic structure data the Ö![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) intersection minimum is found at ∼14.80 eV (15.61 eV) and the minimum of the à state appears at ∼14.50 eV (14.87 eV). The energetic minimum of the
intersection minimum is found at ∼14.80 eV (15.61 eV) and the minimum of the à state appears at ∼14.50 eV (14.87 eV). The energetic minimum of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) state appears at ∼14.37 eV (14.71 eV). Vibronic coupling between the à and
state appears at ∼14.37 eV (14.71 eV). Vibronic coupling between the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states shifts the minimum of the
electronic states shifts the minimum of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) state at a distorted geometry. Among the five a1 vibrational modes, ν2, ν3, ν4 and ν5 shift the minimum of the
state at a distorted geometry. Among the five a1 vibrational modes, ν2, ν3, ν4 and ν5 shift the minimum of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states considerably away from the minimum of the neutral reference state occurring at Q = 0 [cf.Fig. 3].
electronic states considerably away from the minimum of the neutral reference state occurring at Q = 0 [cf.Fig. 3].
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) min (diagonal entries) and
min (diagonal entries) and ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) cmin (off-diagonal entries) of the electronic states of CH3CCH˙+ within a second-order coupling model, using the EOMIP-CCSD (CASSCF-MRCI) electronic energy data. All quantities are given in eV
cmin (off-diagonal entries) of the electronic states of CH3CCH˙+ within a second-order coupling model, using the EOMIP-CCSD (CASSCF-MRCI) electronic energy data. All quantities are given in eV
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2
E
2
E
|
à 2 E |
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2
A
1
2
A
1
|
|
|---|---|---|---|
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2
E
2
E
|
10.30 (10.14) | — | — |
| Ã 2 E | — | 14.50 (14.87) | 14.80 (15.53) |
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2
A
1
2
A
1
|
— | — | 14.37 (14.71) |
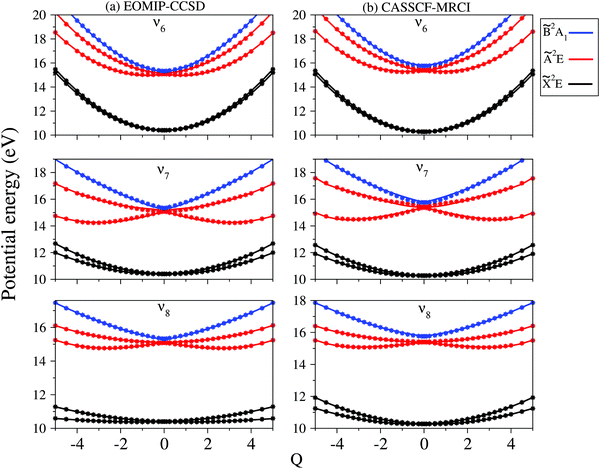
In contrast to the vibrational modes of a1 symmetry, the degenerate vibrational modes are JT active and lift the electronic degeneracy of ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) and à electronic states of CH3CCH˙+. The potential energy cuts along one component (say x) of a few JT active degenerate vibrational modes are shown in Fig. 4. It can be seen from Fig. 4 that the extent of splitting of electronic degeneracy of the
and à electronic states of CH3CCH˙+. The potential energy cuts along one component (say x) of a few JT active degenerate vibrational modes are shown in Fig. 4. It can be seen from Fig. 4 that the extent of splitting of electronic degeneracy of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state is small as compared to that of the à electronic state. The extent of splitting of the degeneracy depends on the JT coupling strength (λ2/2ω2) of the degenerate vibrational modes. It can be seen from Tables 4 and 5 that the vibrational modes ν7, ν8 and ν10 have moderate JT coupling strength [cf.Tables 4 and 5] than the other modes in the
state is small as compared to that of the à electronic state. The extent of splitting of the degeneracy depends on the JT coupling strength (λ2/2ω2) of the degenerate vibrational modes. It can be seen from Tables 4 and 5 that the vibrational modes ν7, ν8 and ν10 have moderate JT coupling strength [cf.Tables 4 and 5] than the other modes in the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state. In the case of the à electronic state, among the five degenerate vibrational modes, ν6, ν7 and ν8 have relatively large coupling strength [cf.Tables 4 and 5]. So, the extent of splitting of electronic degeneracy of the à state is more as compared to that of the
state. In the case of the à electronic state, among the five degenerate vibrational modes, ν6, ν7 and ν8 have relatively large coupling strength [cf.Tables 4 and 5]. So, the extent of splitting of electronic degeneracy of the à state is more as compared to that of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state.
state.
Using EOMIP-CCSD electronic structure data, we calculated the energetic minimum of the JT split lower adiabatic sheets and saddle points of both ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E and Ã2E electronic states using the following equations:89,90
2E and Ã2E electronic states using the following equations:89,90
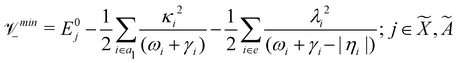 | (21) |
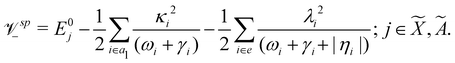 | (22) |
The minimum of the seam of CIs occurs at an energy
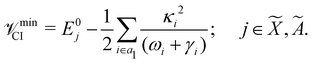 | (23) |
The JT stabilization energy is given by
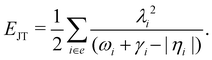 | (24) |
The mathematical steps to arrive at the above equations are discussed in the electronic supplementary information. In the case of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E electronic state, both energetic minimum and saddle points are found at ∼10.28 eV. This shows that the barrier to pseudo rotation is low. The energetic minimum and saddle points of the Ã2E state appear at ∼13.08 eV and ∼13.09 eV, respectively. The JT stabilization energies amount to ∼0.02 eV (∼160 cm−1) and ∼1.42 eV (∼11
2E electronic state, both energetic minimum and saddle points are found at ∼10.28 eV. This shows that the barrier to pseudo rotation is low. The energetic minimum and saddle points of the Ã2E state appear at ∼13.08 eV and ∼13.09 eV, respectively. The JT stabilization energies amount to ∼0.02 eV (∼160 cm−1) and ∼1.42 eV (∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 453 cm−1) for the
453 cm−1) for the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) and à electronic states, respectively. It is worthwhile to mention that the JT stabilization energy estimated above for the
and à electronic states, respectively. It is worthwhile to mention that the JT stabilization energy estimated above for the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state is in good agreement with the available theoretical data,50 ∼117 cm−1.
state is in good agreement with the available theoretical data,50 ∼117 cm−1.
Along with this, we have also calculated the SO coupling constant of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E electronic state. We obtained a value of ∼−28.60 cm−1 and ∼−28.83 cm−1, using EOMIP-CCSD and CASSCF-MRCI methods, respectively. This is in very good agreement with the value reported by Shieh et al.,47 Xing et al.,48 Marquez et al.50 and Jacovella et al.52
2E electronic state. We obtained a value of ∼−28.60 cm−1 and ∼−28.83 cm−1, using EOMIP-CCSD and CASSCF-MRCI methods, respectively. This is in very good agreement with the value reported by Shieh et al.,47 Xing et al.,48 Marquez et al.50 and Jacovella et al.52
3.3 Dynamical observables: vibronic spectra and time-dependent dynamics
The vibronic band structures of the![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states of CH3CCH˙+ are calculated with the aid of the theoretical formalism discussed above. Precise location of the vibrational energy levels of the uncoupled electronic states is calculated by the time-independent matrix diagonalization approach using the Lanczos algorithm.62 The HO basis functions used along each vibrational mode in these calculations are given in Table S3 of the ESI.† The first vibronic band due to the degenerate
electronic states of CH3CCH˙+ are calculated with the aid of the theoretical formalism discussed above. Precise location of the vibrational energy levels of the uncoupled electronic states is calculated by the time-independent matrix diagonalization approach using the Lanczos algorithm.62 The HO basis functions used along each vibrational mode in these calculations are given in Table S3 of the ESI.† The first vibronic band due to the degenerate ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) electronic state of CH3CCH˙+ is shown in Fig. 5. The vibronic spectra shown in panels b and c of this figure are obtained with the Hamiltonian parameters derived from the EOMIP-CCSD and CASSCF-MRCI electronic energies, respectively. The experimental
electronic state of CH3CCH˙+ is shown in Fig. 5. The vibronic spectra shown in panels b and c of this figure are obtained with the Hamiltonian parameters derived from the EOMIP-CCSD and CASSCF-MRCI electronic energies, respectively. The experimental ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) band is reproduced from ref. 43 and shown in panel a. Both the stick line spectra and the convoluted envelopes are shown in Fig. 5(b and c). The convergence of the stick spectrum is checked with respect to the size of the vibrational basis as well as number of Lanczos iterations. The stick spectrum is convoluted with the 30 meV full width at half maximum (FWHM) Lorentzian line shape function to generate the spectral envelopes shown in panels b and c. Five totally symmetric a1(ν1–ν5) and five degenerate JT active e (ν6–ν10) vibrational modes are included in the calculation of the spectrum in Fig. 5(b and c).
band is reproduced from ref. 43 and shown in panel a. Both the stick line spectra and the convoluted envelopes are shown in Fig. 5(b and c). The convergence of the stick spectrum is checked with respect to the size of the vibrational basis as well as number of Lanczos iterations. The stick spectrum is convoluted with the 30 meV full width at half maximum (FWHM) Lorentzian line shape function to generate the spectral envelopes shown in panels b and c. Five totally symmetric a1(ν1–ν5) and five degenerate JT active e (ν6–ν10) vibrational modes are included in the calculation of the spectrum in Fig. 5(b and c).
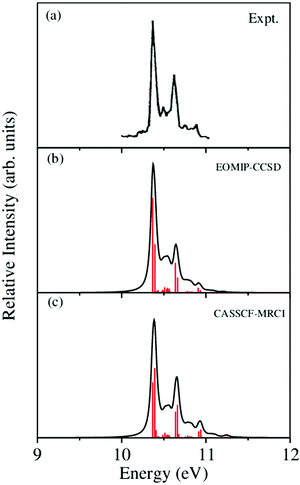 | ||
Fig. 5 The vibronic energy level spectrum of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) electronic state of CH3CCH˙+ obtained with the Hamiltonian parameters derived from the EOMIP-CCSD and CASSCF-MRCI electronic energies shown in panels (b) and (c), respectively. The experimental electronic state of CH3CCH˙+ obtained with the Hamiltonian parameters derived from the EOMIP-CCSD and CASSCF-MRCI electronic energies shown in panels (b) and (c), respectively. The experimental ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E band is reproduced from ref. 43 and shown in panel (a). Relative intensity (in arbitrary units) is plotted as a function of the energy (in eV). 2E band is reproduced from ref. 43 and shown in panel (a). Relative intensity (in arbitrary units) is plotted as a function of the energy (in eV). | ||
All five symmetric vibrational modes are excited in the spectrum of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state. Peak spacings of ∼3497 cm−1, ∼3067 cm−1, ∼2170 cm−1, ∼1328 cm−1 and ∼876 cm−1 (EOMIP-CCSD) and ∼3504 cm−1, ∼3067 cm−1, ∼2169 cm−1, ∼1341 cm−1 and ∼878 cm−1 (CASSCF-MRCI) due to the progression of ν1, ν2, ν3, ν4 and ν5 vibrational modes, respectively, are found. Among the five symmetric vibrational modes, ν3 (C
state. Peak spacings of ∼3497 cm−1, ∼3067 cm−1, ∼2170 cm−1, ∼1328 cm−1 and ∼876 cm−1 (EOMIP-CCSD) and ∼3504 cm−1, ∼3067 cm−1, ∼2169 cm−1, ∼1341 cm−1 and ∼878 cm−1 (CASSCF-MRCI) due to the progression of ν1, ν2, ν3, ν4 and ν5 vibrational modes, respectively, are found. Among the five symmetric vibrational modes, ν3 (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C stretching mode) is strongly excited in the
C stretching mode) is strongly excited in the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) state. The excitation of ν4, ν5 modes is weak and that of ν1, ν2 modes is very weak in accordance with their very low coupling strength [cf.Tables 4 and 5]. Among the JT active e vibrational modes, ν8 and ν10 are very weakly excited and the appearance of a relatively small number of lines in the spectrum is indicative of very weak JT coupling effects due to all five degenerate modes, as indicated by their coupling strength [cf.Tables 4 and 5].
state. The excitation of ν4, ν5 modes is weak and that of ν1, ν2 modes is very weak in accordance with their very low coupling strength [cf.Tables 4 and 5]. Among the JT active e vibrational modes, ν8 and ν10 are very weakly excited and the appearance of a relatively small number of lines in the spectrum is indicative of very weak JT coupling effects due to all five degenerate modes, as indicated by their coupling strength [cf.Tables 4 and 5].
The overlapping second photoelectron band of CH3 CCH in the ∼14–17 eV energy range is due to a transition to the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states of CH3CCH˙+.43 In order to systematically examine the vibronic structure of this band, we first focus on the results obtained for the JT active Ã2E electronic state. The calculations are carried out with both EOMIP-CCSD and CASSCF-MRCI Hamiltonian parameters and the resulting stick line spectra and convoluted envelopes are shown in panels (i) and (ii) of Fig. 6, respectively. In Fig. 6(a and b), the experimental Ã2E–
2A1 electronic states of CH3CCH˙+.43 In order to systematically examine the vibronic structure of this band, we first focus on the results obtained for the JT active Ã2E electronic state. The calculations are carried out with both EOMIP-CCSD and CASSCF-MRCI Hamiltonian parameters and the resulting stick line spectra and convoluted envelopes are shown in panels (i) and (ii) of Fig. 6, respectively. In Fig. 6(a and b), the experimental Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 band is reproduced from ref. 43. Panels (c) and (d) show the partial spectra of the à and
2A1 band is reproduced from ref. 43. Panels (c) and (d) show the partial spectra of the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states obtained with five symmetric vibrational modes, and panels (e) and (f) show the partial spectra of the à state obtained with four JT active degenerate vibrational modes. The symmetric mode spectrum of the à state in Fig. 6(c) and (d) reveals progressions of all five symmetric vibrational modes. Peak spacings of ∼3496 cm−1, ∼3178 cm−1, ∼2145 cm−1, ∼1304 cm−1 and ∼1024 cm−1 (EOMIP-CCSD) and ∼3499 cm−1, ∼3183 cm−1, ∼2156 cm−1, ∼1315 cm−1 and ∼1033 cm−1 (CASSCF-MRCI) due to ν1, ν2, ν3, ν4 and ν5, respectively, are estimated from the spectrum. Among the five symmetric vibrational modes, ν4 (methyl deformation) is strongly excited. The excitation of ν2 and ν5 vibrational modes is moderate and that of ν1 and ν3 modes is weak. In panels (c) and (d) of Fig. 6 the stick line spectrum and the convoluted envelope of the uncoupled
electronic states obtained with five symmetric vibrational modes, and panels (e) and (f) show the partial spectra of the à state obtained with four JT active degenerate vibrational modes. The symmetric mode spectrum of the à state in Fig. 6(c) and (d) reveals progressions of all five symmetric vibrational modes. Peak spacings of ∼3496 cm−1, ∼3178 cm−1, ∼2145 cm−1, ∼1304 cm−1 and ∼1024 cm−1 (EOMIP-CCSD) and ∼3499 cm−1, ∼3183 cm−1, ∼2156 cm−1, ∼1315 cm−1 and ∼1033 cm−1 (CASSCF-MRCI) due to ν1, ν2, ν3, ν4 and ν5, respectively, are estimated from the spectrum. Among the five symmetric vibrational modes, ν4 (methyl deformation) is strongly excited. The excitation of ν2 and ν5 vibrational modes is moderate and that of ν1 and ν3 modes is weak. In panels (c) and (d) of Fig. 6 the stick line spectrum and the convoluted envelope of the uncoupled ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic state are also shown. All five symmetric vibrational modes ν1–ν5 are found to contribute to the spectral progressions of the
electronic state are also shown. All five symmetric vibrational modes ν1–ν5 are found to contribute to the spectral progressions of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) state. Line spacings of ∼3332 cm−1, ∼3017 cm−1, ∼2018 cm−1, ∼1497 cm−1 and ∼917 cm−1 (EOMIP-CCSD) and ∼3279 cm−1, ∼3016 cm−1, ∼1996 cm−1, ∼1495 cm−1 and ∼914 cm−1 (CASSCF-MRCI) are obtained in this state. Dominant excitation of both ν4 and ν5 vibrational modes is found in this case. The symmetric vibrational modes excited in the
state. Line spacings of ∼3332 cm−1, ∼3017 cm−1, ∼2018 cm−1, ∼1497 cm−1 and ∼917 cm−1 (EOMIP-CCSD) and ∼3279 cm−1, ∼3016 cm−1, ∼1996 cm−1, ∼1495 cm−1 and ∼914 cm−1 (CASSCF-MRCI) are obtained in this state. Dominant excitation of both ν4 and ν5 vibrational modes is found in this case. The symmetric vibrational modes excited in the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states are assigned and given in Tables S4 and S5 of the ESI.† In the latter, the results of the present findings are compared to those available in the literature. It can be seen from Tables S4 and S5 of the ESI† that the present results compare well with various experimental findings in the literature.43,51
electronic states are assigned and given in Tables S4 and S5 of the ESI.† In the latter, the results of the present findings are compared to those available in the literature. It can be seen from Tables S4 and S5 of the ESI† that the present results compare well with various experimental findings in the literature.43,51
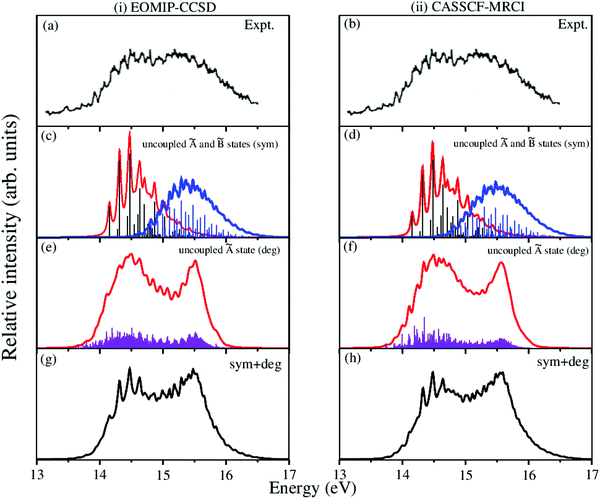 | ||
Fig. 6 Vibronic energy level spectra of the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states of CH3CCH˙+ obtained with the Hamiltonian parameters derived from the EOMIP-CCSD and CASSCF-MRCI electronic energies shown in columns (i) and (ii), respectively. The photoelectron bands of both Ã2E and 2A1 electronic states of CH3CCH˙+ obtained with the Hamiltonian parameters derived from the EOMIP-CCSD and CASSCF-MRCI electronic energies shown in columns (i) and (ii), respectively. The photoelectron bands of both Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states computed with five totally symmetric modes (ν1–ν5) are shown in panels (c) and (d). The partial spectrum of the Ã2E electronic state computed with four degenerate (ν6–ν9) vibrational modes is shown in panels (e) and (f). The composite Ã2E– 2A1 electronic states computed with five totally symmetric modes (ν1–ν5) are shown in panels (c) and (d). The partial spectrum of the Ã2E electronic state computed with four degenerate (ν6–ν9) vibrational modes is shown in panels (e) and (f). The composite Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 band obtained by convoluting the above two partial spectra (i.e., symmetric + degenerate) is shown in panels (g) and (h). The experimental Ã2E– 2A1 band obtained by convoluting the above two partial spectra (i.e., symmetric + degenerate) is shown in panels (g) and (h). The experimental Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 band is reproduced from ref. 43 and shown in panel (a) and panel (b). 2A1 band is reproduced from ref. 43 and shown in panel (a) and panel (b). | ||
The spectrum of the à state obtained with the JT active degenerate vibrational modes shown in Fig. 6 reveals progression of ν6, ν7 and ν8 vibrational modes. Peak spacings of ∼2110 cm−1, ∼711 cm−1 and ∼705 cm−1 (EOMIP-CCSD) and ∼2173 cm−1, ∼1442 cm−1 and ∼1428 cm−1 (CASSCF-MRCI), respectively, corresponding to these vibrational modes (in that order) are estimated from the spectrum. It can be seen from Tables 4 and 5 that the JT coupling due to ν7 and ν8 vibrational modes is relatively strong in the Ã2E electronic state. Because of the strong JT coupling, a bimodal structure is obtained for the spectrum of the JT modes in this case [cf.Fig. 6(e and f)]. This is in good agreement with the nature of the experimental band structure. The non-degenerate ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) state is vertically located ∼0.13 and ∼0.17 eV above the à state in the EOMIP-CCSD and CASSCF-MRCI electronic structure data [cf.Table 6], respectively. As a result of this energetic proximity the spectrum of the
state is vertically located ∼0.13 and ∼0.17 eV above the à state in the EOMIP-CCSD and CASSCF-MRCI electronic structure data [cf.Table 6], respectively. As a result of this energetic proximity the spectrum of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) state was found to be highly overlapping with the à band in the experiment. The spectrum of panels (g) and (h) of Fig. 6 is obtained by convoluting the partial stick spectra of uncoupled Ö
state was found to be highly overlapping with the à band in the experiment. The spectrum of panels (g) and (h) of Fig. 6 is obtained by convoluting the partial stick spectra of uncoupled Ö![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) states along symmetric (panels (c) and (d)) and degenerate vibrational modes (panels (e) and (f)). The energetic proximity of the à and
states along symmetric (panels (c) and (d)) and degenerate vibrational modes (panels (e) and (f)). The energetic proximity of the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states leads to the observed complex, diffuse and overlapping Ö
electronic states leads to the observed complex, diffuse and overlapping Ö![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) vibronic band. The minimum of the seam of the Ö
vibronic band. The minimum of the seam of the Ö![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) CIs is located ∼0.30 (EOMIP-CCSD) and ∼0.66 eV (CASSCF-MRCI) above the minimum of the à state [cf.Table 6]. Also, the energetic minimum of the
CIs is located ∼0.30 (EOMIP-CCSD) and ∼0.66 eV (CASSCF-MRCI) above the minimum of the à state [cf.Table 6]. Also, the energetic minimum of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) state is quasi-degenerate with that of the à state. This leads to a strong mixing of the vibronic levels of the
state is quasi-degenerate with that of the à state. This leads to a strong mixing of the vibronic levels of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) state with those of the à state. It can be seen from the bottom panels of this figure [cf. panels (g) and (h) of Fig. 6] that the convoluted spectrum is in good accordance with the experimental spectrum.
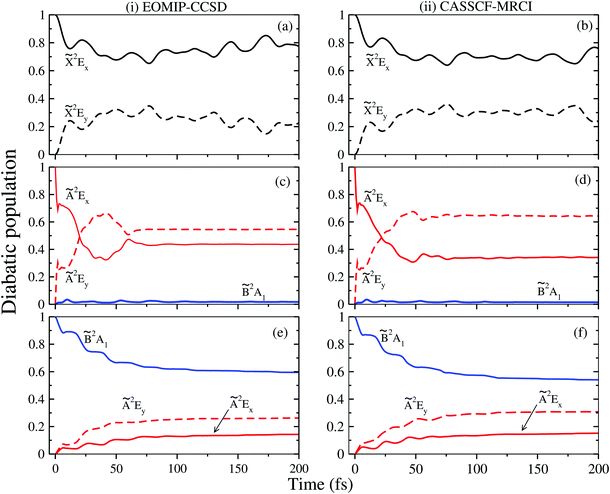
state with those of the à state. It can be seen from the bottom panels of this figure [cf. panels (g) and (h) of Fig. 6] that the convoluted spectrum is in good accordance with the experimental spectrum.
In addition to the energetic location and excitation strength analysis, the assignment of the peaks is also confirmed by examining the nodal pattern of the vibrational wave functions. These wave functions are calculated by a block-improved relaxation method as implemented in the MCTDH program module.91–93 In Fig. S1–S3 of the ESI† we present a few vibrational wave functions of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E, Ã2E and
2E, Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states. In these figures, the wave function probability density is plotted in a suitable reduced dimensional space of normal coordinates.
2A1 states. In these figures, the wave function probability density is plotted in a suitable reduced dimensional space of normal coordinates.
Finally, the complete vibronic band structure of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) –Ö
–Ö![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) electronic states is calculated by including the relevant coupling among them. Understandably, this exercise is beyond the capability of the matrix diagonalization method employed for the uncoupled states. This task is therefore accomplished by the time-dependent WP propagation method employing the MCTDH suite of programs.66 Because of large vertical energy separation of the
electronic states is calculated by including the relevant coupling among them. Understandably, this exercise is beyond the capability of the matrix diagonalization method employed for the uncoupled states. This task is therefore accomplished by the time-dependent WP propagation method employing the MCTDH suite of programs.66 Because of large vertical energy separation of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state from the Ã2E and
2E state from the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states, we have performed nuclear dynamical calculations for the
2A1 states, we have performed nuclear dynamical calculations for the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E and Ã2E–
2E and Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states separately. Both EOMIP-CCSD and CASSCF-MRCI Hamiltonian parameters are employed in the calculations. All 15 vibrational modes are included for the
2A1 electronic states separately. Both EOMIP-CCSD and CASSCF-MRCI Hamiltonian parameters are employed in the calculations. All 15 vibrational modes are included for the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state and 13 relevant vibrational modes are included for the Ã2E–
2E state and 13 relevant vibrational modes are included for the Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states. Five WP calculations are carried out by launching the initial WP on each of the five (two components of the JT split
2A1 states. Five WP calculations are carried out by launching the initial WP on each of the five (two components of the JT split ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) and à state plus the
and à state plus the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) state) electronic states separately. The details of the mode combination and the sizes of the basis sets are given in Table S6 of the ESI.† In each calculation WP is propagated for 200 fs. The time autocorrelation function is damped with an exponential function of relaxation time 33 fs for all electronic states, and then Fourier transformed to generate the spectrum. The results from five different calculations are combined with equal weightage to generate the composite theoretical band shown in Fig. 7, along with the available experimental results reproduced from ref. 43. It can be seen from the figure that the present theoretical results are in very good agreement with the experimental results.43 While the first band is formed by the
state) electronic states separately. The details of the mode combination and the sizes of the basis sets are given in Table S6 of the ESI.† In each calculation WP is propagated for 200 fs. The time autocorrelation function is damped with an exponential function of relaxation time 33 fs for all electronic states, and then Fourier transformed to generate the spectrum. The results from five different calculations are combined with equal weightage to generate the composite theoretical band shown in Fig. 7, along with the available experimental results reproduced from ref. 43. It can be seen from the figure that the present theoretical results are in very good agreement with the experimental results.43 While the first band is formed by the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state, the second band is formed by highly overlapping Ã2E and
2E state, the second band is formed by highly overlapping Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states.
2A1 electronic states.
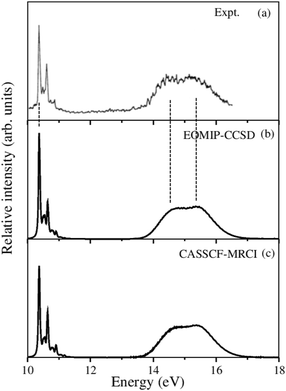 | ||
Fig. 7 Vibronic band structure of the coupled ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E–Ã2E– 2E–Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states of CH3CCH˙+. Relative intensity (in arbitrary units) is plotted as a function of the energy of the vibronic states of CH3CCH˙+. The experimental spectrum reproduced from ref. 43 is shown in panel (a). The present theoretical results obtained with the EOMIP-CCSD and CASSCF-MRCI Hamiltonian parameters are shown in panels (b) and (c), respectively. 2A1 electronic states of CH3CCH˙+. Relative intensity (in arbitrary units) is plotted as a function of the energy of the vibronic states of CH3CCH˙+. The experimental spectrum reproduced from ref. 43 is shown in panel (a). The present theoretical results obtained with the EOMIP-CCSD and CASSCF-MRCI Hamiltonian parameters are shown in panels (b) and (c), respectively. | ||
3.4 Diabatic electronic population
In order to understand the impact of complex nonadiabatic coupling on the dynamics of the![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E, Ã2E and
2E, Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states, the time-dependence of the diabatic electronic populations in the coupled (i.e.,
2A1 electronic states, the time-dependence of the diabatic electronic populations in the coupled (i.e., ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E–Ã2E–
2E–Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1) electronic states of CH3CCH˙+ is recorded and discussed in this section. The electronic populations obtained by initially locating the WP on two components of the JT split
2A1) electronic states of CH3CCH˙+ is recorded and discussed in this section. The electronic populations obtained by initially locating the WP on two components of the JT split ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E, Ã2E and the
2E, Ã2E and the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states are shown in columns (i) and (ii) of Fig. 8 calculated with the EOMIP-CCSD and CASSCF-MRCI parameters, respectively. It can be seen from panels (a) and (b) that when the WP is initially excited to the
2A1 states are shown in columns (i) and (ii) of Fig. 8 calculated with the EOMIP-CCSD and CASSCF-MRCI parameters, respectively. It can be seen from panels (a) and (b) that when the WP is initially excited to the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state the electronic population moves back and forth between its two components driven solely by the JT CIs and exhibits an exact mirror image behavior.
2E state the electronic population moves back and forth between its two components driven solely by the JT CIs and exhibits an exact mirror image behavior.
The population curve for an initial location of the WP on the Ã2E state is shown in panels (c) and (d) of Fig. 8. It can be seen that a very little amount (∼1%) of population is transferred to the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 state in this situation. This is due to the fact that the CI of the Ã2E state with the
2A1 state in this situation. This is due to the fact that the CI of the Ã2E state with the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 state is located at ∼0.3 eV above the minimum of the Ã2E state, and it is not accessible to the WP during its evolution on this state. Most of the population moves back and forth between the x and y component of the Ã2E state. Initially, the population decreases sharply within a short time of about ∼3 fs and then increases slightly. Again it decreases to ∼0.3 within a short time of about ∼40 fs and then increases slightly up to ∼60 fs. Then it remains constant between ∼0.4 and ∼0.6 at longer times. The population profiles provided in panels (c) and (d) of Fig. 8 are qualitatively the same, but quantitatively very different. This is because of quantitatively different coupling parameters that result from the EOMIP-CCSD and CASSCF-MRCI methods. The time-dependence of electronic populations for an initial location of the WP on the
2A1 state is located at ∼0.3 eV above the minimum of the Ã2E state, and it is not accessible to the WP during its evolution on this state. Most of the population moves back and forth between the x and y component of the Ã2E state. Initially, the population decreases sharply within a short time of about ∼3 fs and then increases slightly. Again it decreases to ∼0.3 within a short time of about ∼40 fs and then increases slightly up to ∼60 fs. Then it remains constant between ∼0.4 and ∼0.6 at longer times. The population profiles provided in panels (c) and (d) of Fig. 8 are qualitatively the same, but quantitatively very different. This is because of quantitatively different coupling parameters that result from the EOMIP-CCSD and CASSCF-MRCI methods. The time-dependence of electronic populations for an initial location of the WP on the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 state is shown in panels (e) and (f) of Fig. 8. In this case ∼40% of the population is transferred to both x and y components of the Ã2E state (i.e., internal conversion) via the PJT coupling and CI between Ã2E and
2A1 state is shown in panels (e) and (f) of Fig. 8. In this case ∼40% of the population is transferred to both x and y components of the Ã2E state (i.e., internal conversion) via the PJT coupling and CI between Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states. It can be seen that the PJT coupling effect between the à and
2A1 states. It can be seen that the PJT coupling effect between the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) states is not particularly strong. The complex band structure of the à and
states is not particularly strong. The complex band structure of the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) states arises solely from their energetic proximity.
states arises solely from their energetic proximity.
The behavior mentioned above is to be contrasted with the findings on the JT and PJT coupling effects in the isomeric allene radical cation.34 In the latter the PJT coupling between the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2B2 states is very strong. Due to this, ∼50% of the
2B2 states is very strong. Due to this, ∼50% of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2B2 state population decays within ∼5 fs when the WP is initially located on the
2B2 state population decays within ∼5 fs when the WP is initially located on the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2B2 state, and within ∼20 fs almost ∼90% of the population decays from this state [see Fig. 5 of ref. 34]. Therefore, while the strong PJT coupling between the Ã2E and
2B2 state, and within ∼20 fs almost ∼90% of the population decays from this state [see Fig. 5 of ref. 34]. Therefore, while the strong PJT coupling between the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2B2 states of the allene radical cation gives rise to broad and diffuse vibronic bands, the energetic proximity of the electronic states leads to the broad and diffuse vibronic bands in the isomeric propyne radical cation.
2B2 states of the allene radical cation gives rise to broad and diffuse vibronic bands, the energetic proximity of the electronic states leads to the broad and diffuse vibronic bands in the isomeric propyne radical cation.
4 Summary
The impact of JT and PJT interactions on the photo-ionization spectroscopy of CH3 CCH is examined in this article. The theoretical results are compared with the experimental recording by Baker et al.43 The equilibrium geometry of the reference electronic ground state of CH3 CCH is optimized at the MP2 level of theory. The potential energy surfaces of the![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E, Ã2E and
2E, Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states of the propyne radical cation are calculated along the dimensionless normal displacement coordinates of the electronic ground state of CH3 CCH (reference geometry) using both EOMIP-CCSD and CASSCF-MRCI ab initio quantum chemistry methods. With the aid of the electronic structure results, a higher-order model vibronic Hamiltonian is constructed in a diabatic electronic basis in terms of the dimensionless normal displacement coordinate of vibrational modes. It is found that the
2A1 electronic states of the propyne radical cation are calculated along the dimensionless normal displacement coordinates of the electronic ground state of CH3 CCH (reference geometry) using both EOMIP-CCSD and CASSCF-MRCI ab initio quantum chemistry methods. With the aid of the electronic structure results, a higher-order model vibronic Hamiltonian is constructed in a diabatic electronic basis in terms of the dimensionless normal displacement coordinate of vibrational modes. It is found that the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E electronic state is energetically well separated from the Ã2E and
2E electronic state is energetically well separated from the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states at the Franck–Condon geometry. Similar results were obtained for the allene radical cation.31–34 The curve crossings between the Ã2E and
2A1 states at the Franck–Condon geometry. Similar results were obtained for the allene radical cation.31–34 The curve crossings between the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states along the ν1–ν5 vibrational modes of the propyne radical cation are found.
2A1 electronic states along the ν1–ν5 vibrational modes of the propyne radical cation are found.
Nuclear dynamics calculations are carried out from first principles by time-independent and time-dependent methods. The individual vibronic bands are systematically analyzed. It is observed that the JT effect due to the e vibrational modes in the Ã2E electronic manifold of CH3CCH˙+ is stronger compared to the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state. The PJT coupling of e vibrational modes between the Ã2E and
2E state. The PJT coupling of e vibrational modes between the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states is weak. However, because of the energetic proximity the band structure of the Ã2E–
2A1 electronic states is weak. However, because of the energetic proximity the band structure of the Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states is highly overlapping and diffuse. In the first vibrational band due to the
2A1 electronic states is highly overlapping and diffuse. In the first vibrational band due to the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E state, C
2E state, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C stretching vibrational mode ν3 is strongly excited and the excitation of ν4 and ν5 vibrational modes is weak. Also, among the JT active e vibrational modes, ν8 and ν10 are weakly excited in this band and the JT coupling effect is weak in this band. The second photo-ionization band is due to the strongly overlapping Ã2E and
C stretching vibrational mode ν3 is strongly excited and the excitation of ν4 and ν5 vibrational modes is weak. Also, among the JT active e vibrational modes, ν8 and ν10 are weakly excited in this band and the JT coupling effect is weak in this band. The second photo-ionization band is due to the strongly overlapping Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states of CH3CCH˙+. In the case of the JT active Ã2E electronic state, ν4, ν7 and ν8 vibrational modes are strongly excited and the excitation of ν2, ν5 and ν6 modes is moderate. Because of the fairly strong JT coupling strength of the degenerate ν7 and ν8 vibrational modes, a bimodal structure of the Ã2E vibronic band is observed. This is in good agreement with the experimental band structure. Dominant excitation of both ν4 and ν5 vibrational modes is found in the
2A1 electronic states of CH3CCH˙+. In the case of the JT active Ã2E electronic state, ν4, ν7 and ν8 vibrational modes are strongly excited and the excitation of ν2, ν5 and ν6 modes is moderate. Because of the fairly strong JT coupling strength of the degenerate ν7 and ν8 vibrational modes, a bimodal structure of the Ã2E vibronic band is observed. This is in good agreement with the experimental band structure. Dominant excitation of both ν4 and ν5 vibrational modes is found in the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic state. The final theoretical results so obtained are in good agreement with the available experimental results. The close proximity of the minimum energies of both Ã2E and
2A1 electronic state. The final theoretical results so obtained are in good agreement with the available experimental results. The close proximity of the minimum energies of both Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states leads to broad, diffuse and overlapping vibronic bands for the Ã2E and
2A1 states leads to broad, diffuse and overlapping vibronic bands for the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 electronic states of CH3CCH˙+.
2A1 electronic states of CH3CCH˙+.
The time-dependence of the diabatic electronic population for an initial location of the WP on the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 state reveals that ∼40% of population is transferred to the Ã2E state via the PJT coupling and CI between Ã2E and
2A1 state reveals that ∼40% of population is transferred to the Ã2E state via the PJT coupling and CI between Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states. It is found that the PJT coupling between these states is not so strong. The complex band structure of the Ã2E and
2A1 states. It is found that the PJT coupling between these states is not so strong. The complex band structure of the Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states arises solely from their energetic proximity. This is in contrast to the effects in the vibronic band structure of the Ã2E–
2A1 states arises solely from their energetic proximity. This is in contrast to the effects in the vibronic band structure of the Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2B2 electronic states of the isomeric allene radical cation. In the latter, the PJT coupling among the Ã2E–
2B2 electronic states of the isomeric allene radical cation. In the latter, the PJT coupling among the Ã2E–![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2B2 states if particularly strong leading to a very fast decay of the population of the
2B2 states if particularly strong leading to a very fast decay of the population of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2B2 state and diffuse vibronic bands.
2B2 state and diffuse vibronic bands.
Author contributions
AKK: Conceptualization, data curation, formal analysis, investigation, methodology, software, writing – original draft, review and editing. VJR: together with AKK, data curation, formal analysis, investigation, methodology, software. SM: Conceptualization, project administration, supervision, validation, visualization, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AKK acknowledges the Council of Scientific and Industrial Research, New Delhi, for the doctoral fellowship. VJR acknowledges the Department of Science and Technology, India, for the INSPIRE fellowship. AKK thanks Dr Tanmoy Mondal and Dr Rajagopala Reddy for many helpful discussions during this work. This study is supported in part by a research grant (No. EMR/2017/004592) from the Department of Science and Technology, New Delhi. SM thanks the University Grants Commission, New Delhi, for a mid-career research award grant (F.19-231/2018(BSR). The computational facilities provided by the Translational Research Facility, UPE-II and the Centre for Modeling Simulation and Design at the University of Hyderabad are gratefully acknowledged.References
- H. A. Jahn and E. Teller, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235 CAS.
- U. Öpik and M. H. L. Pryce, Proc. R. Soc. London, Ser. A, 1957, 238, 425–447 Search PubMed.
- H. C. Longuet-Higgins, U. Öpik, M. H. L. Pryce and R. A. Sack, Proc. R. Soc. London, Ser. A, 1958, 244, 1–16 CAS.
- H. C. Longuet-Higgins, Adv. Spectrosc., 1961, 429 Search PubMed.
- R. Englman, The Jahn–Teller effect in molecules and crystals, Wiley-Interscience, New York, 1972 Search PubMed.
- I. B. Bersuker and V. Z. Polinger, Vibronic Interactions in Molecules and Crystals, Springer Berlin Heidelberg, 1987 Search PubMed.
- I. B. Bersuker, The Jahn-Teller effect and vibronic interactions in modern chemistry, Springer Science and Business Media, 2013 Search PubMed.
- E. Teller, J. Phys. Chem., 1937, 41, 109–116 CrossRef CAS.
- G. Herzberg and H. Longuet-Higgins, Discuss. Faraday Soc., 1963, 35, 77–82 RSC.
- T. Carrington, Faraday Discuss. Chem. Soc., 1972, 53, 27–34 RSC.
- D. R. Yarkony, Rev. Mod. Phys., 1996, 68, 985–1013 CrossRef CAS.
- D. R. Yarkony, Acc. Chem. Res., 1998, 31, 511–518 CrossRef CAS.
- S. Mahapatra, Int. Rev. Phys. Chem., 2004, 23, 483–512 Search PubMed.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- S. Mahapatra, Acc. Chem. Res., 2009, 42, 1004–1015 CrossRef CAS PubMed.
- W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325–352 CrossRef CAS PubMed.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457–484 CrossRef.
- H. Köppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 Search PubMed.
- I. B. Bersuker, Chem. Rev., 2001, 101, 1067–1114 CrossRef CAS PubMed.
- I. B. Bersuker, The Jahn–Teller Effect, Cambridge University Press, Cambridge, UK, 2006 Search PubMed.
- H. Köppel, L. S. Cederbaum and S. Mahapatra, Theory of the Jahn–Teller Effect in Handbook of high-resolution spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 3, pp. 1517–1550 Search PubMed.
- H. Köppel, L. S. Cederbaum and W. Domcke, J. Chem. Phys., 1988, 89, 2023–2040 CrossRef.
- M. Döscher and H. Köppel, Chem. Phys., 1997, 225, 93–105 CrossRef.
- A. Coustenis, A. Salama, B. Schulz, S. Ott, E. Lellouch, T. Encrenaz, D. Gautier and H. Feuchtgruber, Icarus, 2003, 161, 383–403 CrossRef CAS.
- R. I. Kaiser, Chem. Rev., 2002, 102, 1309–1358 CrossRef CAS PubMed.
- R. I. Kaiser, D. S. Parker and A. M. Mebel, Annu. Rev. Phys. Chem., 2015, 66, 43–67 CrossRef CAS PubMed.
- M. J. McEwan, G. B. Scott, N. G. Adams, L. M. Babcock, R. Terzieva and E. Herbst, Astrophys. J., 1999, 513, 287 CrossRef CAS.
- N. Hansen, J. A. Miller, P. R. Westmoreland, T. Kasper, K. Kohse-Höinghaus, J. Wang and T. A. Cool, Combust. Flame, 2009, 156, 2153–2164 CrossRef CAS.
- W. Von Niessen, G. Diercksen, L. S. Cederbaum and W. Domcke, Chem. Phys., 1976, 18, 469–476 CrossRef CAS.
- L. S. Cederbaum, W. Domcke and H. Köppel, Chem. Phys., 1978, 33, 319–326 CrossRef CAS.
- C. Woywod and W. Domcke, Chem. Phys., 1992, 162, 349–358 CrossRef CAS.
- S. Mahapatra, L. S. Cederbaum and H. Köppel, J. Chem. Phys., 1999, 111, 10452–10463 CrossRef CAS.
- G. A. Worth and L. S. Cederbaum, Chem. Phys. Lett., 2001, 348, 477–482 CrossRef CAS.
- S. Mahapatra, G. A. Worth, H.-D. Meyer, L. S. Cederbaum and H. Köppel, J. Phys. Chem. A, 2001, 105, 5567–5576 CrossRef CAS.
- A. M. Schulenburg and F. Merkt, J. Chem. Phys., 2009, 130, 034308 CrossRef CAS PubMed.
- S. Sardar, A. K. Paul and S. Adhikari, Mol. Phys., 2009, 107, 2467–2479 CrossRef CAS.
- P. Baltzer, B. Wannberg, M. Lundqvist, L. Karlsson, D. Holland, M. MacDonald and W. von Niessen, Chem. Phys., 1995, 196, 551–567 CrossRef CAS.
- R. K. Thomas and H. W. Thompson, Proc. R. Soc. London, Ser. A, 1974, 339, 29–36 CAS.
- F. J. Leng and G. L. Nyberg, J. Chem. Soc., Faraday Trans. 2, 1977, 73, 1719–1723 RSC.
- G. Bieri, F. Burger, E. Heilbronner and J. P. Maier, Helv. Chim. Acta, 1977, 60, 2213–2233 CrossRef CAS.
- A. C. Parr, A. J. Jason and R. Stockbauer, Int. J. Mass Spectrom. Ion Phys., 1978, 26, 23–38 CrossRef CAS.
- Z. Yang, L. Wang, Y. T. Lee, D. Shirley, S. Huang and W. Lester Jr, Chem. Phys. Lett., 1990, 171, 9–13 CrossRef CAS.
- C. Baker and D. W. Turner, Proc. R. Soc. London, Ser. A, 1968, 308, 19–37 CAS.
- A. C. Parr, A. J. Jason, R. Stockbauer and K. McCulloh, Int. J. Mass Spectrum., 1979, 30, 319–330 CrossRef CAS.
- G. H. Ho, M. S. Lin, Y. L. Wang and T. W. Chang, J. Chem. Phys., 1998, 109, 5868–5879 CrossRef CAS.
- G. Bieri and L. Åsbrink, J. Electron Spectrosc. Relat. Phenom., 1980, 20, 149–167 CrossRef CAS.
- J.-C. Shieh, J.-l Chang, J.-C. Wu, R. Li, A. Mebel, N. C. Handy and Y.-T. Chen, J. Chem. Phys., 2000, 112, 7384–7393 CrossRef CAS.
- X. Xing, M.-K. Bahng, B. Reed, C. S. Lam, K.-C. Lau and C. Y. Ng, J. Chem. Phys., 2008, 128, 094311 CrossRef PubMed.
- H. Matsui, Y.-F. Zhu and E. R. Grant, Laser Chem., 1996, 16, 151–156 CrossRef CAS.
- S. Marquez, J. Dillon and D. R. Yarkony, J. Phys. Chem. A, 2013, 117, 12002–12010 CrossRef CAS PubMed.
- U. Jacovella, D. M. P. Holland, S. Boyé-Péronne, D. Joyeux, L. E. Archer, N. de Oliveira, L. Nahon, R. R. Lucchese, H. Xu and S. T. Pratt, J. Chem. Phys., 2014, 141, 114303 CrossRef CAS PubMed.
- U. Jacovella and F. Merkt, Mol. Phys., 2018, 116, 3602–3606 CrossRef CAS.
- S. T. Pratt, P. M. Dehmer and J. L. Dehmer, J. Chem. Phys., 1993, 99, 6233–6244 CrossRef CAS.
- W. Ensslin, H. Bock and G. Becker, J. Am. Chem. Soc., 1974, 96, 2757–2762 CrossRef CAS.
- M. Hamermesh, Group Theory and Its Application to Physical Problems, Dover Publications, 1989 Search PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Theoret. Chim. Acta, 1992, 84, 95–103 CrossRef CAS.
- M. Musiał, S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 2003, 118, 1128–1136 CrossRef.
- Y. J. Bomble, J. C. Saeh, J. F. Stanton, P. G. Szalay, M. Kállay and J. Gauss, J. Chem. Phys., 2005, 122, 154107 CrossRef PubMed.
- J. Cullum and R. A. Willoughby, Lanczos Algorithms for Large Symmetric Eigenvalue Computations, Birkhäuser, Boston, 1985 Search PubMed.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS.
- U. Manthe, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1992, 97, 3199–3213 CrossRef CAS.
- M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- G. A. Worth, M. H. Beck, A. Jäckle and H.-D. Meyer, The MCTDH Package, Version 8.2, University of Heidelberg, Heidelberg, Germany, 2000, H.-D. Meyer, Version 8.3, 2002, Version 8.4, 2007. O. Vendrell and H.-D. Meyer, Version 8.5 2011, see http://mctdh.uni-hd.de.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- U. Manthe, J. Chem. Phys., 2008, 128, 164116 CrossRef PubMed.
- B. Mukherjee, K. Naskar, S. Mukherjee, S. Ghosh, T. Sahoo and S. Adhikari, Int. Rev. Phys. Chem., 2019, 38, 287–341 Search PubMed.
- W. Lichten, Phys. Rev., 1967, 164, 131 CrossRef CAS.
- F. T. Smith, Phys. Rev., 1969, 179, 111 CrossRef.
- T. Pacher, L. S. Cederbaum and H. Köppel, Adv. Chem. Phys., 1993, 84, 293–392 CAS.
- A. Viel and W. Eisfeld, J. Chem. Phys., 2004, 120, 4603–4613 CrossRef CAS PubMed.
- W. Eisfeld and A. Viel, J. Chem. Phys., 2005, 122, 204317 CrossRef PubMed.
- T. Zeng and I. Seidu, Phys. Chem. Chem. Phys., 2017, 19, 11098–11110 RSC.
- W. Domcke, H. Köppel and L. S. Cederbaum, Mol. Phys., 1981, 43, 851–875 CrossRef CAS.
- H. Köppel and W. Domcke, in Encyclopedia of Computational Chemistry, ed. P. von Ragué Schleyer, Wiley, New York, 1998, p. 3166 Search PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- M. H. Palmer, C. C. Ballard and I. C. Walker, Chem. Phys., 1999, 249, 129–144 CrossRef CAS.
- D. Frost, F. Herring, C. McDowell and I. Stenhouse, Chem. Phys. Lett., 1970, 4, 533–536 CrossRef CAS.
- J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews and P. G. Szalay, CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package, with contributions from A.A. Auer, R.J. Bartlett, U. Benedikt, C. Berger, D.E. Bernholdt, Y.J. Bomble, O. Christiansen, F. Engel, R. Faber, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, K. Klein, W.J. Lauderdale, F. Lipparini, T. Metzroth, L.A. Mück, D.P. O'Neill, D.R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J.D. Watts and the integral packages MOLECULE (J. Almlöf and P.R. Taylor), PROPS (P.R. Taylor), ABACUS (T. Helgaker, H.J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see http://www.cfour.de.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, version 2010.1, a package of ab initio programs, see https://www.molpro.net/ Search PubMed.
- L. S. Cederbaum and W. Domcke, Theoretical Aspects of Ionization Potentials and Photoelectron Spectroscopy: A Green's Function Approach, John Wiley & Sons, Ltd, 1977, pp. 205–344 Search PubMed.
- K. Levenberg, Quart. Appl. Math., 1944, 2, 164–168 CrossRef.
- D. W. Marquardt, J. Appl. Math., 1963, 11, 431–441 Search PubMed.
- Mathematica Version 11.1, Wolfram Research Inc., Champaign, Illinois, 2017 Search PubMed.
- S. Mahapatra, V. Vallet, C. Woywod, H. Köppel and W. Domcke, Chem. Phys., 2004, 304, 17–34 CrossRef CAS.
- R. Sarkar, S. Rajagopala Reddy, S. Mahapatra and H. Köppel, Chem. Phys., 2017, 482, 39–51 CrossRef CAS.
- H.-D. Meyer and G. A. Worth, Theor. Chem. Acc., 2003, 109, 251–267 Search PubMed.
- H.-D. Meyer, F. L. Quéré, C. Léonard and F. Gatti, Chem. Phys., 2006, 329, 179–192 CrossRef CAS.
- L. J. Doriol, F. Gatti, C. Iung and H.-D. Meyer, J. Chem. Phys., 2008, 129, 224109 CrossRef PubMed.
- J. Duncan, D. McKean, P. Mallinson and R. McCulloch, J. Mol. Spectrosc., 1973, 46, 232–239 CrossRef CAS.
Footnote |
† Electronic supplementary information (ESI) available: Formulation of eqn (21)–(24), the higher-order coupling parameters of the electronic Hamiltonian [cf.eqn (9) and (8)] of CH3CCH+ (Tables S1 and S2), vibrational energy levels and their assignments (Tables S4 and S5) and the numerical details of the calculations (Tables S3 and S6), and vibronic wave functions of ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E, Ã2E and 2E, Ã2E and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A1 states of CH3CCH+ (Figs. S1–S3)]. See DOI: https://doi.org/10.1039/d2cp01930b 2A1 states of CH3CCH+ (Figs. S1–S3)]. See DOI: https://doi.org/10.1039/d2cp01930b |
| This journal is © the Owner Societies 2022 |