Mode selective chemistry for the dissociation of methane on efficient Ni/Pt-bimetallic alloy catalysts
Sudipta
Roy
 and
Ashwani K.
Tiwari
and
Ashwani K.
Tiwari
 *
*
Department of Chemical Sciences, Indian Institute of Science Education and Research Kolkata, Mohanpur 741246, India. E-mail: ashwani@iiserkol.ac.in
First published on 24th June 2022
Abstract
The mode selectivity of methane dissociation is studied on three different Ni/Pt-bimetallic alloy surfaces using a fully quantum approach based on reaction path Hamiltonian. Dissociative sticking probability depends on the composition of alloying metals, excited vibrational mode, and symmetry of the reaction path about the plane perpendicular to the catalyst surface containing the carbon atom and two hydrogen atoms. Our calculations show that symmetry of the minimum energy reaction path depends on the surface alloy composition. In the transition state, the dissociating C–H bond elongates significantly for the dissociation of methane on these alloy systems. A significant decrease in the frequency of the symmetric stretching mode and the two bending modes near the transition state is observed on all the alloy surfaces. Under the vibrational adiabatic limit, excitation of these softened modes enhanced the dissociation probability compared to the ground vibrational state. The reaction probability values decrease abruptly at the incident energies less than the zero-point energy corrected barrier height. With the inclusion of non-adiabatic vibrational coupling terms, reaction probability in the low incident energy region increases to a greater extent, and mode selective behavior also becomes different from that observed within the vibrational adiabatic limit. Symmetric stretching mode displayed the highest reactivity on all the alloy surfaces. Overall, Ni8/Pt(111) is found to be the most reactive toward the methane dissociation.
1 Introduction
Steam reforming reaction is one of the major primary sources for producing molecular hydrogen and syngas. This reaction is always coupled with another industrially important reaction, the water-gas shift reaction.1 The rate limiting step of the steam reforming process is the dissociative chemisorption of methane on a catalyst surface. Therefore, the dissociative chemisorption reaction of CH4 on metal surfaces has been studied extensively by both theoreticians and experimentalists.2–11 Ni-Based catalysts are mainly used for industrial purposes due to their low cost and high reactivity. However, Ni-based catalysts are very much prone to coke formation, which deactivates the catalyst surfaces eventually.12,13 Pt, on the other hand, shows even higher reactivity towards methane dissociation compared to Ni,3,14 and is also more efficient towards coke resistance on its surface.15–18 However, it is challenging to use Pt as a catalyst for industrial purposes due to its higher cost. Therefore, an alternative approach is the formation of bimetallic alloys consisting of Ni and Pt,19 which is cost-effective and solves the coke formation process on the surface. In our previous work, using the DFT study, we have shown that by changing the surface composition of Ni/Pt bimetallic alloys the reactivity of the methane dissociation process can be enhanced with a reduction in the coke formation propensity.20This work aims to understand the dynamical aspects of CH4 dissociation on reactive and coke-resistant Ni/Pt bimetallic alloy surfaces. One important aspect of the methane dissociation reaction on metal surfaces is the non-statistical behavior with respect to the incident energy of the methane molecule.3,5–8,11,21–31 For the dissociation of methane on the Ni(100) surface, adding 0.36 eV of energy to the molecule by exciting the symmetric stretching mode leads to a greater increase in reactivity compared to adding the same amount of energy into the translational mode.7 But if a similar amount of energy is put into the asymmetric stretching mode, that leads to a smaller increase in reactivity compared to adding the same energy into the translation.23 These effects are expressed by the term vibrational efficacy. The formula and details of vibrational efficacy could be found elsewhere.32 Similar nonstatistical behavior of CH4 dissociation has been observed on Pt(110)(1 × 2),8,31 Pt(111),3,30 and Ni(111)3,25,26 surfaces also. Therefore, a mode selectivity is observed for the dissociation of CH4 on metal surfaces, where excitation of a certain vibrational mode shows higher reactivity than any other vibrational or translational mode. This non-statistical behavior of CH4 dissociation on a surface can vary from metal to metal for a given type of vibrational excitation. Therefore, it is necessary to examine the mode selectivity of CH4 dissociation reaction on our previously reported Ni/Pt bimetallic alloy surfaces. This will explain how mode selective behavior on the alloys differs from that of bare Ni and Pt surfaces and provide a deeper understanding of how alloying could affect the reactivity.
The non-statistical nature of this reaction emphasizes the significance of dynamical studies. In recent years, it has become possible to compute the dissociative sticking probability of methane on metal surfaces with a reasonable accuracy. Approaches based on classical mechanics14,33–37 could be used for the dynamical studies at high collision energies. Mode selectivity and intramolecular energy flow in CH4 dissociation have also been shown by ab initio direct dynamics methods.38,39 Guo et al. have shown that a simple transition state based model can rationalize the mode specific and bond selective behavior.40 At industrially relevant lower energies, quantum mechanical effects such as zero point energy (ZPE) and tunneling effects are important and need to be taken care of.41 Knowledge about the potential energy surface (PES) is essential for dynamical calculations. It is challenging to construct a full dimensional PES due to a very large number of degrees of freedom.42,43 Therefore, dynamical studies for the dissociation of CH4 on metal surfaces have been carried out, treating the molecule as pseudo-diatomic44–53 or in a lower dimension.54 However, significant progress has been made over the past several years in developing first-principle based multi-dimensional PESs.55 The first DFT-based 12-D global PES was developed by Guo and co-workers for CH4 dissociation on the Ni(111) surface.56 Using this PES for quasi-classical trajectory (QCT) studies, they have shown the alignment effect57 and the mode- and bond-selectivity58 in the dissociative chemisorption of methane. Shen et al. have fitted 13 and 15 dimensional PESs using neural networks (NNs)59,60 for the dissociative chemisorption of methane on Ni(111) and Ni(100)61–63 and reported 7-D and 9-D quantum dynamical results. More recently Jiang and co-workers have reported a QCT study for the dissociation of CH4 on the Ni(111) surface using a chemically accurate 15-D PES.64
The construction of high dimensional PESs is computationally very expensive,65,66 but necessary to understand the proper dynamical behaviors of the reaction. Therefore, a desirable method should be less computationally expensive but be able to capture the important details of the dynamical behaviors.67,68 One such approximate method was developed by Jackson and co-workers69,70 based on the reaction path Hamiltonian (RPH) method proposed by Miller et al.71 The reaction path is an abstract one dimensional path that connects the saddle point to the minima. Instead of a multidimensional PES, we have to determine a single dimensional reaction path in this method. As a result, the number of ab initio data points required to construct the PES is much less and thus computationally less expensive. Quantum formulation of the RPH method was used to carry out calculations for the dissociation of CH4 on bare Ni and Pt surfaces and successfully explained the mode specificity and bond selectivity.32,70,72–75
Methane activation by internal state averaged molecular beam studies showed modest surface temperature (Ts) dependence on Ni(111)76 and Ni(100)77,78 surfaces. In another study of methane dissociation on Ni(111) an 8 fold increase in reaction probability was observed as Ts increased from 90 K to 475 K at an incidence energy of 40 kJ mol−1.26 A stronger dependence of the dissociation probability on Ts was observed on Pt(111)2 and Ir(111)79 surfaces. The effect of surface temperature on the reactivity is more prominent at lower incident energy. At low incident energy, the surface temperature can cause the reaction probability to vary up to 2 orders of magnitude, depending on the surface temperature and incidence energy used for the calculation.50,80,81 Transition state calculations explored the role of surface phonon excitation in CH4 activation on metal surfaces. If the metal atom is allowed to relax in the presence of methane molecule, the metal atom beneath the molecule puckers out of the surface significantly.47,50,82 Therefore, surface phonon excitation changes the barrier height with more favorable energetic requirements. This strong molecule–phonon coupling leads to a significant variation of dissociation probability with surface temperature (Ts).32 Apart from this, an increase in Ts increases the energy available to the reaction, leading to a higher reactivity. It was found that for CH4 dissociation on a fully relaxed Ni(111) surface, at the transition state, the Ni atom directly beneath the carbon atom of CH4 puckers out of the surface by an amount of 0.23 Å, lowering the energy barrier by about 0.2 eV.44,83 To understand the effect of surface temperature (Ts) on dissociation probability, a ‘sudden model’ was used for the lattice motion calculation within the RPH framework.47,50
The details of methane dissociation on several Ni/Pt(111) close-packed alloys were reported in our previous study using DFT.20 It was found that Ni9/Pt(111) and Ni8/Pt(111) showed the highest reactivity towards CH4 dissociation with less coke formation. But these are costly alloys for being Pt-based. On the other hand, Ni-based subsurface-Pt9/Ni(111) is coke resistant, exhibits a lower energy barrier for CH4 dissociation compared to both bare Ni(111) and bare Pt(111), and is also cost-effective. Most of the available dynamical calculations for methane dissociation are on bare surfaces only. Recently, Kroes and co-workers have examined the dissociation of CH4 on a close-packed single atom alloy surface using the AIMD method.84 Here, we report RPH-based quantum dynamical calculations for the dissociation of methane on the three Ni/Pt-bimetallic alloy surfaces mentioned above. Change in mode selectivity and overall dissociation probability with the alloying are also reported.
The paper is organized as follows. Section 2 gives the details of electronic structure calculations and the wavepacket dynamics implementation on the reaction path potential. This section also describes the inclusion of lattice motion and harmonic energy shifting approximation. In Section 3, the results of dynamical calculations are presented and discussed. The paper concludes in Section 4.
2 Methods
The DFT based Vienna Ab initio simulation package (VASP)85–88 have been used to perform all total energy calculations. A plane wave basis set was used with a cut off energy of 400 eV. In all the calculations, spin polarization was included. Non-local exchange correlations are treated using the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional within the generalized gradient approximations.89,90 Interactions between the electrons and ionic cores are described by fully non-local optimized projector augmented-wave (PAW) potentials.91,92 A slab supercell with periodic boundary conditions was used to model the metal surfaces. Ni(111), Pt(111), and all the bimetallic surfaces are comprised of four layers within a 3 × 3 unit cell and were relaxed during structure optimization. A 16 Å vacuum space above the slab was maintained to avoid any interaction with the adjacent slabs along z-axis. Equilibrium lattice constant values of 3.52 Å for Ni and 3.97 Å for Pt surfaces are used as found from the bulk geometry optimization in VASP. Bimetallic surfaces are constructed by replacing surface (top) layer atoms one by one with foreign metal atoms, and sub-surface alloys are made by replacing the whole second layer from the top by foreign metal atoms. The 3 × 3 × 1 Γ-centred grid of k-points has been used for structure optimization. The convergence criterion for the optimization process is when forces on all the atoms are smaller than 0.01 eV Å−1. We did not consider the dispersion effect and Coulomb interaction of d electrons of the catalysts in our calculations. However, the inclusion of these effects may not qualitatively change the conclusion of this work, i.e., the trend and order of reactivity would remain same for all the Ni-based and Pt-based alloy surfaces. Previous theoretical calculations for the dissociation of methane on bare Ni(111)72 and Pt(111)75 and for the dissociation of H2O on Ni(111)93 without including these effects have been shown to match quite well with the experimental results.Molecular geometries for CH4 dissociation along the reaction path are identified by using climbing image-nudged elastic band (CI-NEB) method performed with a fixed surface.94 The convergence criterion of the CI-NEB calculation is when the forces are less than 0.05 eV Å−1. The distance between those points along the minimum energy path (MEP) is s, and 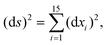 where xi are the mass-weighted Cartesian coordinates of the atoms of the methane molecule. s = 0 denotes the transition state, while the positive and negative values for s correspond to product and reactant states, respectively. We first compute the total energy V0 at various points along the reaction path to construct the 1D PES. Then the force constant matrix was diagonalised to find the normal mode coordinates Qk and the corresponding frequencies ωk(s) at these points. Normal mode coordinates Qk along with s form a new set of coordinates, which are related to the mass-weighted Cartesian coordinate xi through the eigenvectors Li,k by the following relation:
where xi are the mass-weighted Cartesian coordinates of the atoms of the methane molecule. s = 0 denotes the transition state, while the positive and negative values for s correspond to product and reactant states, respectively. We first compute the total energy V0 at various points along the reaction path to construct the 1D PES. Then the force constant matrix was diagonalised to find the normal mode coordinates Qk and the corresponding frequencies ωk(s) at these points. Normal mode coordinates Qk along with s form a new set of coordinates, which are related to the mass-weighted Cartesian coordinate xi through the eigenvectors Li,k by the following relation:
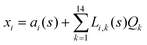 | (1) |
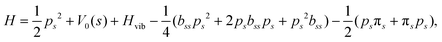 | (2) |
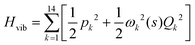 | (3) |
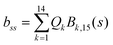 and
and 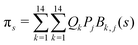 . Vibrationally nonadiabatic couplings are given by
. Vibrationally nonadiabatic couplings are given by 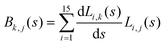 . Coriolis coupling Bk,j(s) described by the πs operator indicates the energy flow between the modes k and j. Operator bss on the other hand gives the coupling between the reaction path and vibrational mode, through the curvature effect Bk,15. The Hamiltonian in eqn (2) is expanded up to the first order in bss and πs,70,72,95 as higher order terms are not so important.41
. Coriolis coupling Bk,j(s) described by the πs operator indicates the energy flow between the modes k and j. Operator bss on the other hand gives the coupling between the reaction path and vibrational mode, through the curvature effect Bk,15. The Hamiltonian in eqn (2) is expanded up to the first order in bss and πs,70,72,95 as higher order terms are not so important.41
The total molecular wave function Ψ in the eigenfunctions of Hvib is written as
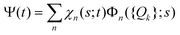 | (4) |
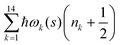 . Index n labels the vibrational state corresponding to the quantum numbers {nk}. For the given Hamiltonian of eqn (2) and the total molecular wave function of eqn (4), the coupled equation of motion for the wave packets χn(s;t) is defined by70
. Index n labels the vibrational state corresponding to the quantum numbers {nk}. For the given Hamiltonian of eqn (2) and the total molecular wave function of eqn (4), the coupled equation of motion for the wave packets χn(s;t) is defined by70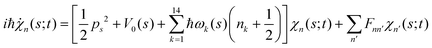 | (5) |
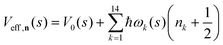 | (6) |
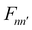 operator, which describes the transition among these vibrational states, contains bss and πs which couple vibrationally adiabatic states separated by one quantum and two quanta, respectively. The parametric dependence of Φn on s leads to the derivative coupling terms depending on the momentum and kinetic energy of the molecule. Therefore, the curve crossing between vibrationally adiabatic potential energy surfaces becomes more probable at higher velocity and for larger coupling values.41,72,73 The detailed expression for the equation of motion can be found elsewhere.93
operator, which describes the transition among these vibrational states, contains bss and πs which couple vibrationally adiabatic states separated by one quantum and two quanta, respectively. The parametric dependence of Φn on s leads to the derivative coupling terms depending on the momentum and kinetic energy of the molecule. Therefore, the curve crossing between vibrationally adiabatic potential energy surfaces becomes more probable at higher velocity and for larger coupling values.41,72,73 The detailed expression for the equation of motion can be found elsewhere.93
Twelve highest frequency modes near the transition state of a total fifteen modes are included in the vibrationally adiabatic basis set. The remaining two low frequency modes correspond to the translation parallel to the surface at s = −∞ and are treated differently. Given the equation of motion, standard techniques were used to evolve the wavepackets in time70,72 At large positive s, the reactive flux is Fourier transformed to give the vibrationally state resolved and energy resolved reaction probabilities,96,97 to get static surface reaction probability P0(Ei,n). The position of the molecule parallel to the surface (along the X and Y direction) for normal incidence conditions, changes little as it follows the minimum energy path up to the transition state. The rotational motion was treated adiabatically. The effect of lattice motion is important for the dissociation of methane,47,48,50 hydrogen,98–100 nitrogen,101 and water.93,102 In a recent perspective103 the importance of incorporating the lattice motion for the dissociative chemisorption of CH4, H2O, and CO2 on smooth and rough surfaces was examined. However, it is computationally expensive to carry out an explicit quantum dynamics calculation that includes the motion of the heavy lattice atoms on an exact multidimensional PES. Therefore, a physically meaningful ‘sudden model’ is used that includes the effect of surface temperature on the reactivity.48,50 The sudden model approach involves two coupling parameters, β (electronic coupling) and α (mechanical coupling). The coupling parameters are defined by ΔEbarrier = −βQ and ΔZbarrier = αQ, where Q is the lattice degrees of freedom. ΔEbarrier and ΔZbarrier are the change in the barrier height and relative position of the transition state along the z-axis, respectively, with the change in lattice atom position from its equilibrium position (Q = 0). The coupling parameters are calculated from the DFT calculations. For the dissociation of methane on close-packed Ni/Pt(111) bimetallic alloy surfaces, the TS is modified to a reasonable extent by the motion of the lattice atom over which methane dissociates. This implies that the force on the atom over which methane dissociates is significant compared to the other lattice atoms on the surface at the TS. The electronic coupling parameter β is the force felt by the lattice atom over which CH4 dissociates. A positive value of β indicates the puckering of the surface lattice atom out of the surface, and a decrease in the barrier height, whereas a negative value indicates its motion into the bulk and an increase in the barrier height. The dependence of the dissociation probability on the effective potential is calculated by Boltzmann averaging over all possible values of Q at a particular surface temperature (in our case it is 475 K and 600 K), using lattice distortion energy obtained from the DFT calculation. This dissociation probability improved further by including mechanical coupling parameter α and averaging over the lattice atom momentum P.50 The final dissociative sticking probability is calculated by averaging the reaction probabilities over impact sites X and Y away from the top site using an energy shifting approximation as
| P0(Ei,n0;X0,Y0) ≈ P0(Ei − ΔVXY(X0,Y0),n0;X0 = Y0 = 0) | (7) |
3 Results and discussion
In this work, we explain how the composition of Ni/Pt bimetallic alloy surfaces influences the reactivity and mode specificity for the dissociation of methane on the alloy surfaces. Jackson et al. and Guo et al. have calculated the dissociative sticking probability on bare Ni(111) and Pt(111) surfaces, respectively, using the same level of theory that we have used for both the energetics and dynamical studies. They were able to reproduce the available experimental results within a reasonable agreement.72,75 We have chosen Ni8/Pt(111), Ni9/Pt(111), and Sub-Pt9/Ni(111) alloys to study the reactivity and mode specificity as methane dissociation on these alloys exhibits lower activation energy barriers compared to both bare Ni(111) and Pt(111) surfaces. Furthermore, we explain how surface temperature (Ts) affects the reactivity by including a simple yet physically meaningful ‘sudden model’ into the RPH framework. Finally, the dissociative sticking probability is shown by including both the effect of surface temperature (Ts) and site averaging with the help of harmonic energy shifting approximation to account for the impact of site averaging.3.1 Reaction path and normal mode analysis
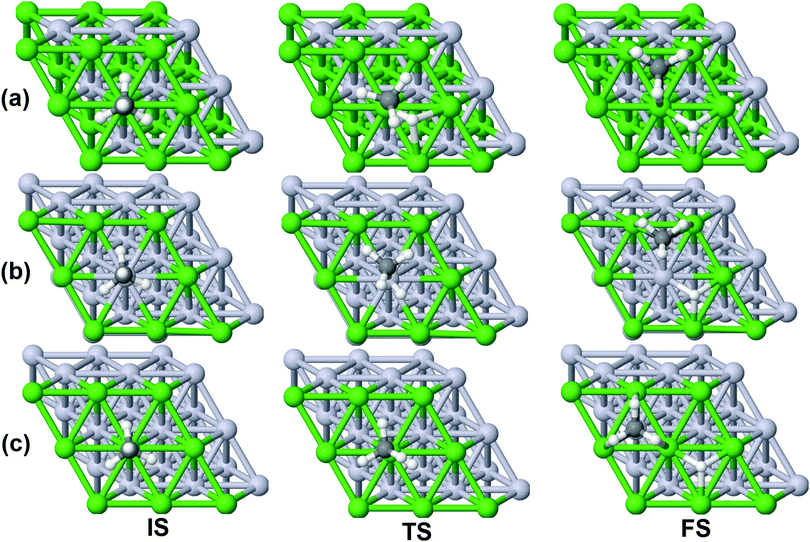
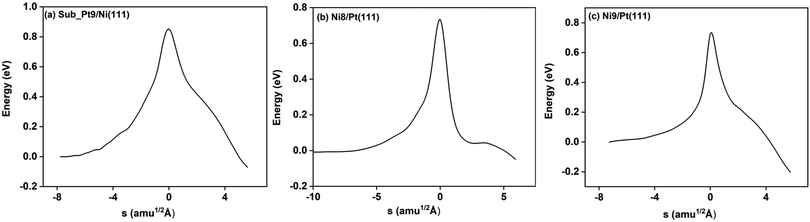
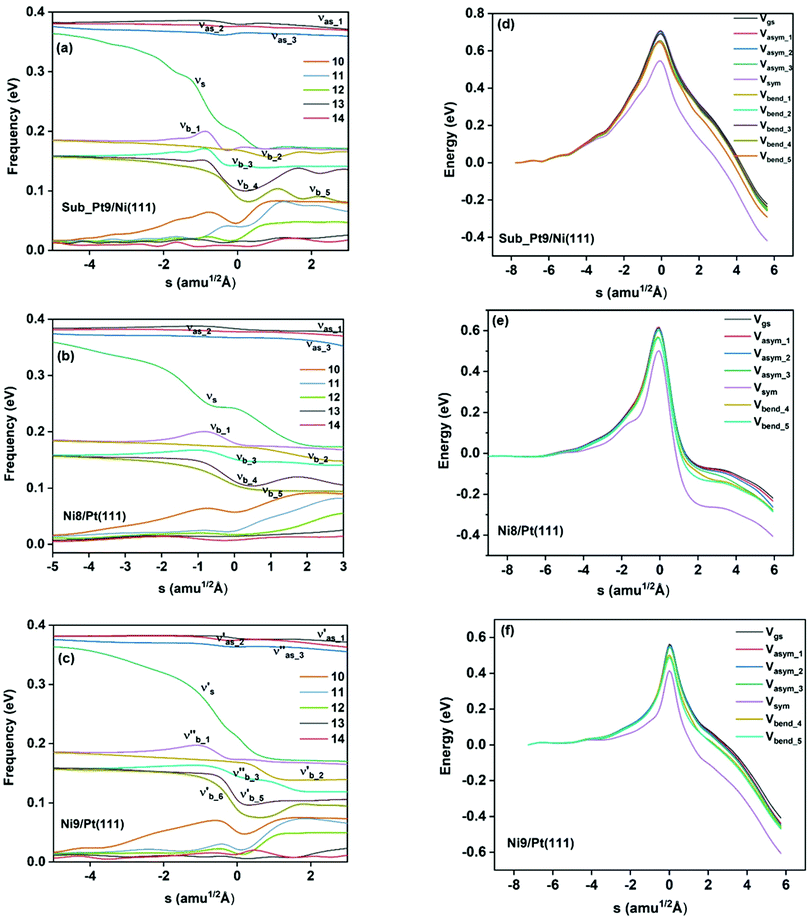
On all the three alloy surfaces, i.e., Sub-Pt9/Ni(111), Ni8/Pt(111), and Ni9/Pt(111), at the TS for CH4 dissociation, the carbon atom is nearly on the top site. The dissociating hydrogen atom is angled towards the surface, with an angle of 130.49°, 121.69°, and 126.83°, respectively, for Sub-Pt9/Ni(111), Ni8/Pt(111), and Ni9/Pt(111) from the surface normal. The non-reacting methyl group is angled away from the surface. In Fig. 1a–c, the optimized structures of initial, transition, and final states are shown for the dissociation of methane on Sub-Pt9/Ni(111), Ni8/Pt(111), and Ni9/Pt(111) alloy surfaces, respectively. The barrier heights for methane dissociation on these surfaces are V† = 0.84, 0.72, and 0.71 eV, respectively. The reaction path diagrams are plotted for all the three alloy surfaces in Fig. 2. On all the three surfaces, an elongation of the dissociating C–H bond is observed at the TS, and the bond distances are found to be 1.54, 1.54, and 1.59 Å on Sub-Pt9/Ni(111), Ni8/Pt(111), and Ni9/Pt(111) respectively. This elongation of bond distance at the TS suggests that vibrational excitation might increase the reactivity.32In Fig. 3a–c, the vibrational frequency of different normal modes along the reaction path for Sub-Pt9/Ni(111), Ni8/Pt(111), and Ni9/Pt(111) is plotted. When the methane molecule is far above the surface, the frequency of nine modes, viz., triply degenerate asymmetric stretching modes, νasym_1, νasym_2, νasym_3, symmetric stretching mode νsym, doubly degenerate bending modes, νbend_1, νbend_2, and another triply degenerate bending modes νbend_3, νbend_4, νbend_5, is non-zero. These frequency values of the nine vibrational modes far above the surface, i.e., at a large negative value of s, are comparable to the available theoretical107 and experimental108 results. Jackson and coworkers obtained similar frequency values for the dissociation of CH4 on Ni(111),72 Ni(100),69 Pt(111),75 and Pt(110)-(1 × 2)73 surfaces when the methane molecule is far above from the surface. The frequency of three degenerate asymmetric stretching modes remains constant throughout the reaction path, even after the molecule crosses the barrier. In the case of symmetric stretching mode, a significant decrease in frequency is observed near the TS. The symmetric stretching mode shows the highest decrease in frequency near the TS among all the normal modes. After the symmetric stretching mode, it is one of the triply degenerate bending modes (bend_5) that shows mode softening, followed by another bending mode (bend_4). As a result of this mode softening, the degeneracy of these triply degenerate bending modes gets removed near the TS. The remaining other bending mode of these triply degenerate bending modes, bend_3, and the doubly degenerate bending modes (bend_1 and bend_2) do not exhibit any significant change in frequency along the reaction path. Therefore, one would expect that excitation of the symmetric stretching mode, bend_4 mode, and bend_5 mode will increase the reactivity significantly, whereas excitation of the other six modes will not change the reactivity significantly as compared to the ground state reactivity. Except for these nine vibrational modes, other frequencies are zero when the molecule is far above the surface and correspond to molecular rotation and translation parallel to the surface. These frequencies become non-zero when the molecule approaches the surface, corresponding to hindered translational and rotational motions along the reaction path. Since we are concerned about the vibrational mode selectivity only, these frustrated modes are of not much importance for our study. From Fig. 3 and the discussion above, one can expect that within the vibrationally adiabatic approximation, excitation of the symmetric stretching mode should exhibit the highest reaction probability, followed by two bending modes, bend_4 and bend_5. One important point regarding the symmetric/antisymmetric nature of the reaction path needs to be discussed here. The only symmetry that is present along the reaction path, i.e., the molecular geometries for the dissociation of CH4 → CH3 + H through the transition state, is a mirror plane, perpendicular to the top layer of the alloy surface, which includes a row of atoms present on the surface, the C atom, the dissociating H atom, and another H atom from the non-reacting methyl group. We have shown this reflection plane in Fig. 4, where only the top layer of the Ni9/Pt(111) alloy is shown. All the normal modes that are symmetric with respect to the reflection through this plane are termed as A′. A′′ modes are antisymmetric with respect to the reflection through this plane. This symmetry is important since the non-adiabatic coupling terms, Bkjs, are non-zero only between the modes of same symmetry. Thus energy can be exchanged between the modes of the same symmetry, i.e., among A′ modes and the ground state, and among the A′′ modes, but not between A′ and A′′ modes.70 We have found that among the three alloy surfaces, only Ni9/Pt(111) exhibits such symmetry. In the case of Sub-Pt9/Ni(111) and Ni8/Pt(111) alloys the reaction path is not symmetric. Therefore, energy exchange could take place among all the modes and with the ground state.74 Due to the presence of this symmetry in Ni9/Pt(111) the frequency values (νs) shown in Fig. 3c are designated by either ν′ or ν′′ depending on whether the mode is symmetric or antisymmetric with respect to the reflection through the plane shown in Fig. 4. In the study of CH4 dissociation on bare Ni(111)72 and Pt(111),75 it was found that the reaction paths are symmetric for both the metal surfaces. In this work it has been reported that when the whole top layer of the alloy surfaces is consisting of guest metal atoms, i.e., Ni9/Pt(111) or Pt9/Ni(111) (not shown in this paper due to the very high energy barrier), then only the reaction path is symmetric in nature. Therefore, it can be concluded that the composition of alloy surfaces dictates whether the reaction path would be symmetric or not. In the case of Sub-Pt9/Ni(111), the top layer of the alloy consists of host metal atoms Ni only. Our calculations show that the minimum energy reaction path is not symmetric in that case.
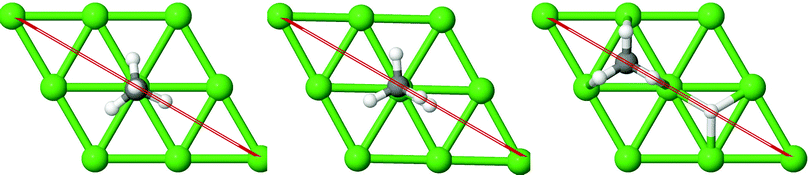 | ||
| Fig. 4 The plane perpendicular to the Ni9/Pt(111) alloy, containing the carbon atom, dissociating hydrogen atom and one of the methyl hydrogen atoms. It can be seen from this figure that the reaction path for the dissociation of CH4 is symmetric with respect to reflection through the plane shown in red. Here only the top layer of the alloy is shown. In Fig. 1(c) the optimized structures of Ni9/Pt(111) are shown with all the four layers as used in the calculation. Green balls in this figure refer to the nine Ni atoms present on the top layer of Ni9/Pt(111), and black and white balls refer to carbon and hydrogen atoms, respectively. | ||
In the right panel of Fig. 3(d–f) we have shown the ZPE corrected potentials of the ground vibrational state and vibrational state excited to one quantum in different vibrational modes for the dissociation of methane on three chosen alloy surfaces. Depending on the change in the frequency value along the reaction path, as shown in the left panel of Fig. 3(a–c), the ZPE corrected barrier heights for different vibrational modes would be different. For Sub-Pt9/Ni(111), the reaction path for the ground state and all nine vibrational modes is shown in Fig. 3d. This figure confirms our assumption for the reactivity based on the discussion of change of frequency values for different modes along the reaction path. It is evident from the right panel of Fig. 3 that the symmetric stretching mode shows the lowest ZPE corrected barrier, followed by bend_5 and bend_4 for all the three alloy surfaces. Three degenerate asymmetric stretching modes, two degenerate bending modes, bend_1 and bend_2, and one of the bending modes from triply degenerate bending modes, bend_3, show almost a similar energy barrier after ZPE correction. This order of ZPE corrected barrier heights for different vibrational modes is similar for all the alloy surfaces.72,75 For simplification, we have shown the potential of the ground vibrational state and six other vibrational states that show either high or low energy barrier on Ni8/Pt(111) (Fig. 3e) and Ni9/Pt(111) (Fig. 3f) alloys.
3.2 Reaction probabilities
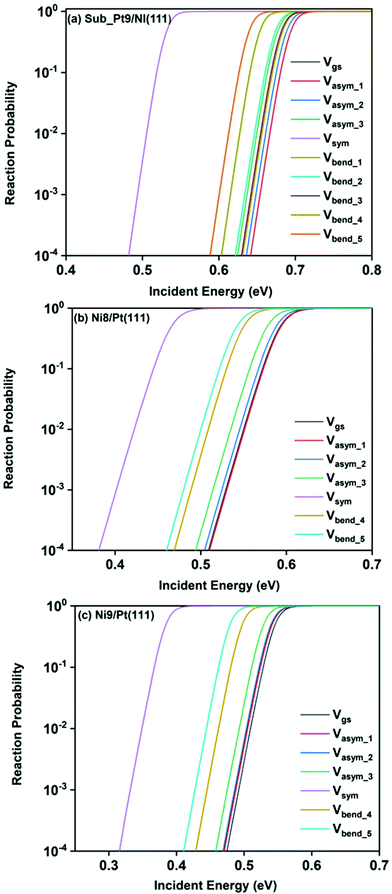
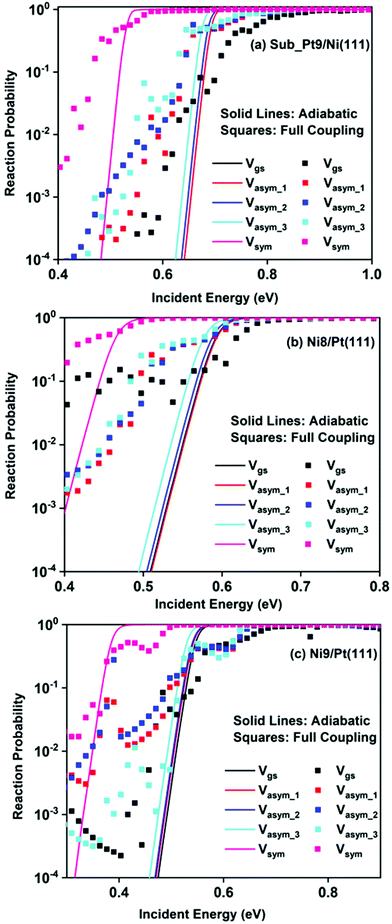
Static surface reaction probabilities within the vibrationally adiabatic limit for CH4 dissociation on Sub-Pt9/Ni(111), Ni9/Pt(111), and Ni8/Pt(111) are plotted as a function of incident energy, Ei, in Fig. 5. Under the vibrationally adiabatic approximation, the ground vibrational state shows the lowest reactivity on all the alloy surfaces. Among the one quantum excited modes, the symmetric stretching mode shows the highest reactivity. After the symmetric stretching mode, one of the triply degenerate bending modes, bend_5, shows the highest reactivity, followed by another one of the triply degenerate bending modes, bend_4. The asymmetric stretching modes, asym_1 and asym_2, exhibit the lowest reactivity. The asym_1 mode shows similar reactivity to that of the ground state. However, in the case of Ni9/Pt(111), the asym_1 stretching mode shows slightly higher reactivity than the ground state (Fig. 5c). For Sub-Pt9/Ni(111) (Fig. 5a), we have shown the reactivity for one-quantum excitation to all the nine vibrational modes in the plot. For Ni8/Pt(111) and Ni9/Pt(111), only the ground state and six other vibrational mode reactivity are shown (Fig. 5b and c). This behavior in the vibrational adiabatic limit, can be explained by the significant decrease of the barrier height with respect to the vibrationally ground state for one-quantum excited modes. A sudden fall in the reaction probability is observed at the incident energy just below the ZPE corrected barrier height, as the reaction proceeds only through the tunneling mechanism. We can correlate the order of reaction probability within the vibrationally adiabatic condition to the reactivity order that was obtained from the mode softening behavior of symmetric stretching, bend_5, and bend_4 modes. On the other hand, no appreciable mode softening was observed for asymmetric stretching modes and other three bending modes. Therefore, these modes show nearly similar or very little enhancement in the reactivity compared to that of the ground vibrational state. On all the alloy surfaces, the reactivity order in the vibrationally adiabatic limit is Vgs ≈ Vasym_1 < Vasym_2 < Vbend_1 < Vbend_3 < Vasym_3 < Vbend_2 < Vbend_4 < Vbend_5< Vsym.Removing the vibrational adiabaticity by switching on the coupling between different vibrational modes, Bk,j, and mode to the ground state, i.e., the curvature coupling Bk,15 alters the static surface reaction probability significantly. Jackson and co-workers have shown that for the CH4 dissociation process on bare Ni(111) and Pt(111), the asym_2 mode is as reactive as the symmetric stretching mode when the coupling between modes and mode to the reaction path is allowed.75 In Fig. 6, we plot the static surface reaction probability values computed with and without non-adiabatic couplings for the ground vibrational state, three asymmetric stretching modes, and the symmetric stretching mode. When the coupling is on between the modes and between the mode and the reaction path, excess vibrational energy after coupling among the states can be transferred into the motion along the reaction path, opening up over-the-barrier pathways for the reaction and allowing the reaction to occur even at lower incident energy values. However, under the adiabatic approximation, the reaction took place only through the tunneling mechanism at the lower incident energy. In our previous work, we have reported that the activation energy barrier of Ni8/Pt(111) and Ni9/Pt(111) is 0.72 eV and 0.71 eV, respectively.20 Therefore, from this energy barrier, one can expect that these two alloys will exhibit similar reactivity towards the methane dissociation. However, dynamical calculations reveal several interesting outcomes. In the vibrational adiabatic limit, Ni9/Pt(111) shows higher reactivity compared to Ni8/Pt(111). Overall, the mode-softening behavior is qualitatively similar on all the alloy surfaces.
In Table 1, the ZPE corrected barriers are given for the ground vibrational state and one-quantum excited vibrational states of the symmetric and the three degenerate asymmetric stretching modes. For the reason mentioned above, in the vibrationally adiabatic limit for the ground vibrational state or any of the one-quantum excited vibrational states, Ni9/Pt(111) is a better catalyst than Ni8/Pt(111). On the other hand, when we switch on the couplings, we find that Ni8/Pt(111) gives a higher reaction probability than that of Ni9/Pt(111) (Fig. 6b and c). This is due to the fact that in the case of Ni9/Pt(111), the reaction path is symmetric with respect to the reflection plane, as discussed in Section 3.1. Therefore, antisymmetric normal modes cannot be coupled with the symmetric normal modes and with the ground vibrational state.69 In the case of Ni8/Pt(111), the reaction path is not symmetric. As a result, all the nine vibrational modes can exchange energy among themselves and with the ground vibrational state. Therefore, it is quite natural that the reaction probability for the ground vibrational state or one-quantum vibrational excited state would be higher on Ni8/Pt(111) compared to that of Ni9/Pt(111), where energy exchange among the modes and reaction paths is restricted by the symmetry. Fig. 6c shows that dissociation probability values corresponding to the asym_3 mode are much less compared to asym_1 or asym_2 modes on Ni9/Pt(111) in the full coupling condition. However, in the adiabatic limit, the asym_3 mode is more reactive compared to the other two asymmetric stretching modes (i.e., asym_1 and asym_2). This is because the asym_3 mode is antisymmetric with respect to the reflection through the plane shown in Fig. 4. Being antisymmetric, it cannot transfer its excess energy to the reaction path, and therefore reactivity decreases. But asym_1 or asym_2 modes are symmetric with respect to the reflection and therefore transfer of energy among themselves or to any other symmetric mode present in the molecule, and to the reaction path is possible. Therefore, reaction probability gets increased for these modes. In the case of Ni8/Pt(111), on the other hand, all three asymmetric stretching modes show similar reaction probability as there is no restriction of energy flow from one mode to another or to the reaction path (Fig. 6b). The discussion of how the composition of alloy surfaces decides the symmetric nature of the minimum energy reaction path (Section 3.1) along with this discussion concludes that the reactivity and mode-selectivity depend strongly on the composition of alloy surfaces.
| System | V gs (eV) | V sym (eV) | V asym_1 (eV) | V asym_2 (eV) | V asym_3 (eV) |
|---|---|---|---|---|---|
| Ni8/Pt(111) | 0.612 | 0.498 | 0.612 | 0.607 | 0.597 |
| Ni9/Cu(111) | 0.562 | 0.415 | 0.557 | 0.555 | 0.545 |
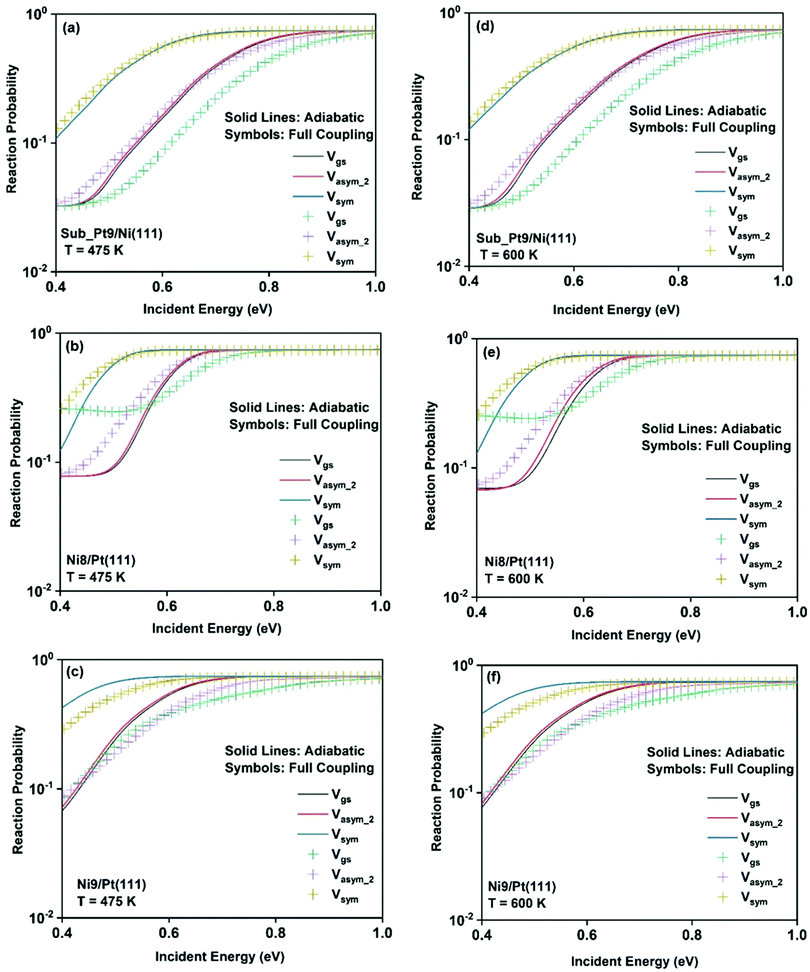
To understand the effect of surface temperature on the reactivity, in Fig. 7 we plot the dissociation probabilities as a function of incident energy at 475 K and 600 K surface temperatures. We have chosen these two surface temperatures because molecular beam studies for the dissociation of methane on bare Ni(111)24 and Pt(111)3 surfaces have been carried out at 475 K and 600 K surface temperatures, respectively. Since the increase in reactivity is similar for all the vibrational modes, we have shown the reactivity of the ground state and when the molecule is excited to two other stretching modes (symmetric and asym_2 stretching) as an illustrative example. The rigid surface dissociation probability was modified by including the two coupling parameters, β and α, using the sudden model.48 Due to the inclusion of lattice motion, for calculating the dissociation probability at a finite surface temperature, the reactivity increases significantly at all incident energies, especially at lower incident energy. The effect of both electronic (β) and mechanical (α) coupling parameters is discussed below. The electronic coupling parameter, β, is responsible for the change in reaction probability at the whole range of incident energy, more significantly at the lower incident energy, where lattice motion makes over-the-barrier pathways feasible for the reaction. On the other hand, the mechanical coupling parameter, α, further increases the reaction probability at the lower incident energy but decreases at higher incident energy. The main reason for this type of behavior of the mechanical coupling parameter, α, is its recoil effect. At higher incident energy of the incoming methane molecule, the surface lattice atom recoils and decreases the probability.32 The increase in surface temperature increases the dissociation probability on all the alloy surfaces. In Fig. 6, we have shown that the full coupling reaction probability for the symmetric stretching mode is quite large on Ni8/Pt(111) (Fig. 6b) compared to Ni9/Pt(111) (Fig. 6c). However, after the inclusion of lattice motion, still, the symmetric stretching mode on Ni8/Pt(111) displays higher reactivity, but the difference in reactivity between Ni8/Pt(111) and Ni9/Pt(111) becomes very less. This is due to the fact that the β value in Ni9/Pt(111) is larger than that of Ni8/Pt(111).20 Therefore, the effect of increasing surface temperature is more pronounced on the Ni9/Pt(111) alloy. At 475 K or 600 K surface temperature, the full coupling reactivity of Ni8/Pt(111) is the highest among all the alloy surfaces. However, under the vibrational adiabatic approximation the symmetric stretching mode of Ni9/Pt(111) exhibits the highest reactivity, as shown in Fig. 7c and f, due to the lowest ZPE corrected barrier height (cf.Table 1) and higher β values. The overall trend and pattern of reactivity are similar for both 475 K and 600 K surface temperatures. The reactivity at 600 K surface temperature (Fig. 7d–f) is slightly higher compared to that at 475 K surface temperature (Fig. 7a–c), as expected. We have observed that the effect of surface temperature in our case is much stronger than for the dissociation of water on metal surfaces.93,109,110
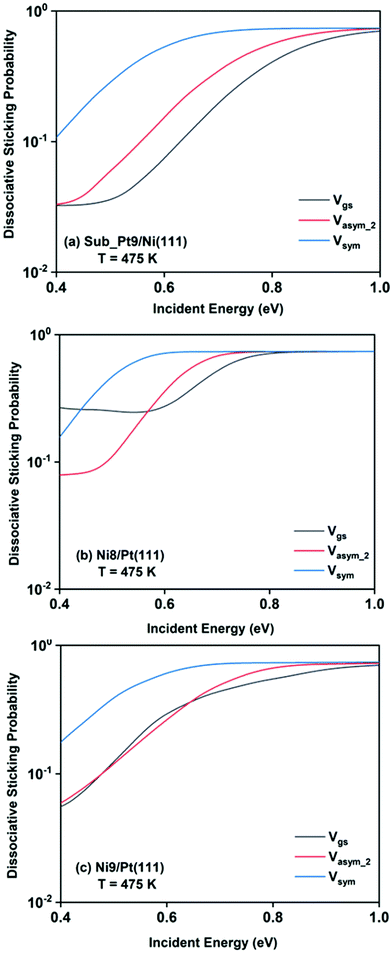
The final dissociative sticking probabilities were calculated by site averaging the dissociation probabilities at 475 K surface temperature. In Fig. 8, the full coupling dissociative sticking probability values of the ground vibrational state, and one-quantum excitation to asym_2 and symmetric stretching modes are shown for CH4 dissociation on the three alloy surfaces. The reaction probabilities decrease to some extent after the site averaging; as a consequence of that, the overall reactivity also decreases, at a finite surface temperature (in our case it is 475 K).
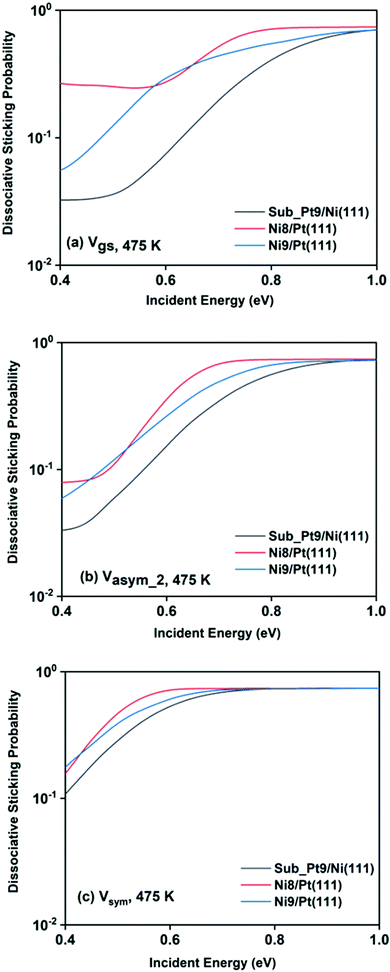
For a better understanding of the difference in reactivity between the three alloy surfaces, and how alloying alters the reactivity, full coupling dissociative sticking probabilities at 475 K surface temperature for the ground vibrational state and one-quantum excited states in symmetric and asym_2 stretching vibrational modes are plotted in Fig. 9. For the ground vibrational state at low incident energy, the reactivity on Ni8/Pt(111) is clearly much higher compared to the other alloy systems, as shown in Fig. 9a. The reactivity on Ni9/Pt(111) is notably low compared to Ni8/Pt(111) at low incident energy. With the increase in incident energy, dissociative sticking probability increases rapidly for Ni9/Pt(111), and at around 0.58 eV, the reactivity becomes similar to that of Ni8/Pt(111). On the other hand, on Ni8/Pt(111), the reactivity remains constant up to the incident energy, where its reactivity becomes similar to the Ni9/Pt(111) alloy (Fig. 9a). From this incident energy, the reactivity increases and finally gets saturated near 0.8 eV for Ni8/Pt(111). Nearly a similar trend of reactivity is observed for one-quantum excitation of the asym_2 stretching vibrational mode (Fig. 9b). However, for the asym_2 mode, the reactivity of Ni8/Pt(111) and Ni9/Pt(111) remains almost similar up to ∼0.52 eV of incident energy, with Ni8/Pt(111) exhibiting a slightly higher reactivity at around 0.4 eV. After 0.52 eV, Ni8/Pt(111) shows higher reactivity throughout the whole incident energy range, and at no incident energy, the reactivity of Ni8/Pt(111) and Ni9/Pt(111) becomes similar. In this case, reactivity on Ni8/Pt(111) saturates faster than that on Ni9/Pt(111). For the one-quantum excitation of the symmetric stretching mode, as shown in Fig. 9c, Ni8/Pt(111) exhibits higher reactivity than Ni9/Pt(111), although the difference of reactivities between these two Pt-based alloy surfaces is insignificant. Excitation of the symmetric stretching mode on the sub-Pt9/Ni(111) alloy displays the least reactivity among all the alloys, like the ground vibrational and asym_2 stretching mode. Overall, one-quantum excitation of the symmetric stretching mode for methane dissociation on Ni8/Pt(111) gives the highest reactivity, and the ground vibrational state of Sub-Pt9/Ni(111) exhibits the lowest reactivity at 475 K surface temperature. One could expect that this order of reactivity for the three alloy surfaces would be the same at 600 K surface temperature also, as in Fig. 7 we have already shown that the pattern and reactivity order on different alloy surfaces are similar at 475 K and 600 K surface temperatures.
4 Conclusions
Quantum dynamics study of methane dissociation was examined on two efficient Pt-based and one Ni-based alloy catalyst surfaces, using the reaction path Hamiltonian method. The minimum energy path was constructed for the dissociation of CH4 on all the three alloy surfaces, and normal mode analysis was performed along the reaction path. Normal mode analysis showed that the frequency of the symmetric stretching mode decreased significantly near the transition state, followed by two other bending modes. The remaining six vibrational modes did not change their frequency significantly along the reaction path. This decrease in vibrational frequency follows the same order on all the alloy surfaces. Within the vibrational adiabatic approximation, the excitation of the symmetric stretching mode exhibits the highest reactivity, followed by two of the triply degenerate bending modes. This order of reactivity arises directly from the mode softening behavior of the vibrational modes. One quantum excitation of the symmetric stretching mode and two of the triply degenerate bending modes reduce the effective barrier height significantly and resulted in a considerable enhancement in the reactivity, while three degenerate asymmetric stretching modes and three other bending modes slightly enhanced the reactivity compared to the ground vibrational state. Inclusion of the non-adiabatic coupling terms significantly alters the reactivity of different vibrational modes, depending on the coupling between the modes and mode to the ground vibrational state. As a result of these couplings, the reactivity increases to a greater extent, especially in the catalytically relevant low incident energy. The coupling behavior between modes and modes to the reaction path will become different if the reaction path is symmetric in nature with respect to the reflection through a mirror plane. Mode selective behavior was observed for all the studied alloy surfaces. The final dissociative sticking probability was calculated at a finite surface temperature by including the site averaging effect. An increase in the surface temperature increases the overall reaction probability. The nozzle temperature (Tn) used in the experimental studies also alters the reactivity. Just like the effect of surface temperature (Ts), reaction probability increases with the nozzle temperature (Tn).3,4 Site averaging decreases the reaction probability on all the alloy surfaces, for both the ground vibrational state and one-quantum excitation to the vibrational modes. This is due to the fact that on all the alloy surfaces, dissociation of the CH4 molecule takes place on the top site. Therefore the minimum energy path that we calculated was for dissociation over the top site only. The barrier to dissociation increases rapidly as the molecule moves away from the top site, and the net effect is a lowering of reaction probability at all incident energies. This implies that the reaction probability depends on the impact site of the catalyst surface.Although both Ni8/Pt(111) and Ni9/Pt(111) alloys exhibit similar activation energy barriers, from dynamical calculations we observe that the final dissociative sticking probability would be higher for the Ni8/Pt(111) alloy at a given surface temperature. Both the energetics and dynamics studies are necessary to elucidate the overall reactivity of a particular catalyst surface. Electronic energy dictates the activation energy barrier for the dissociation process on alloy surfaces. The distortion of the surface atom at the transition state is also explained by the electronic structure methods, which is important to calculate the effect of surface temperature on the reactivity.32 Apart from electronic energy, reaction probability depends strongly on the vibrational energy also. It has been shown that the dissociation of methane on all three alloy surfaces exhibits a late barrier-type reaction. Therefore, an increase in vibrational energy should increase the overall reactivity, compared to translational energy.111 Due to the non-statistical nature of the dissociative chemisorption of methane on metal surfaces, excitation of a given vibrational mode enhances the reactivity more compared to other vibrational modes. Overall, in our case the symmetric stretching mode of Ni8/Pt(111) displays the highest reactivity, and the ground vibrational state of Sub-Pt9/Ni(111) displays the lowest reactivity. Finally, along with the composition of the catalyst surface, which mode is being excited and also the symmetric or antisymmetric nature of the reaction path decide the overall reactivity for the dissociation process. It was found that the symmetric or antisymmetric nature of the low energy reaction path depends on the composition of alloy systems. Apart from these effects, the alignment of the reactant molecule along the reaction path also affects the dissociation probability. Yoder et al. have shown that the sticking probability was largest for the dissociation of methane on low index Ni surfaces if C–H stretch amplitude aligned parallel to the surface and lowest if perpendicular to the surface.112 This study is out of scope of the present work. We hope that our work will stimulate the molecular beam experiment of methane dissociation on alloy surfaces. This will increase our understanding of reaction dynamics at the gas metal alloy interface, and could suggest an alternate catalyst for industrial purposes with higher reactivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. R. thanks CSIR for the fellowship through file number 09/921(0126)/2015-EMR-I.Notes and references
- H. Bengaard, J. Nørskov, J. Sehested, B. Clausen, L. Nielsen, A. Molenbroek and J. Rostrup-Nielsen, J. Catal., 2002, 209, 365–384 CrossRef CAS.
- A. C. Luntz and D. S. Bethune, J. Chem. Phys., 1989, 90, 1274–1280 CrossRef CAS.
- R. Bisson, M. Sacchi, T. T. Dang, B. Yoder, P. Maroni and R. D. Beck, J. Phys. Chem. A, 2007, 111, 12679–12683 CrossRef CAS PubMed.
- D. J. Oakes, M. R. S. McCoustra and M. A. Chesters, Faraday Discuss., 1993, 96, 325–336 RSC.
- M. P. Schmid, P. Maroni, R. D. Beck and T. R. Rizzo, J. Chem. Phys., 2002, 117, 8603–8606 CrossRef CAS.
- R. D. Beck, P. Maroni, D. C. Papageorgopoulos, T. T. Dang, M. P. Schmid and T. R. Rizzo, Science, 2003, 302, 98–100 CrossRef CAS PubMed.
- P. Maroni, D. C. Papageorgopoulos, M. Sacchi, T. T. Dang, R. D. Beck and T. R. Rizzo, Phys. Rev. Lett., 2005, 94, 246104 CrossRef.
- R. Bisson, M. Sacchi and R. D. Beck, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 121404 CrossRef.
- H. Ueta, L. Chen, R. D. Beck, I. Colón-Dìaz and B. Jackson, Phys. Chem. Chem. Phys., 2013, 15, 20526–20535 RSC.
- P. M. Hundt, H. Ueta, M. E. van Reijzen, B. Jiang, H. Guo and R. D. Beck, J. Phys. Chem. A, 2015, 119, 12442–12448 CrossRef CAS PubMed.
- L. Chen, H. Ueta, R. Bisson and R. D. Beck, Faraday Discuss., 2012, 157, 285–295 RSC.
- Z. Wang, X.-M. Cao, J. Zhu and P. Hu, J. Catal., 2014, 311, 469–480 CrossRef CAS.
- J. Ni, L. Chen, J. Lin and S. Kawi, Nano Energy, 2012, 1, 674–686 CrossRef CAS.
- F. Nattino, H. Ueta, H. Chadwick, M. E. van Reijzen, R. D. Beck, B. Jackson, M. C. van Hemert and G.-J. Kroes, J. Phys. Chem. Lett., 2014, 5, 1294–1299 CrossRef CAS PubMed.
- C. Fan, Y.-A. Zhu, Y. Xu, Y. Zhou, X.-G. Zhou and D. Chen, J. Chem. Phys., 2012, 137, 014703 CrossRef PubMed.
- J. Niu, J. Ran, X. Du, W. Qi, P. Zhang and L. Yang, Mol. Catal., 2017, 434, 206–218 CrossRef CAS.
- M. García-Diéguez, I. Pieta, M. Herrera, M. Larrubia and L. Alemany, Appl. Catal., A, 2010, 377, 191–199 CrossRef.
- M. García-Diéguez, I. Pieta, M. Herrera, M. Larrubia and L. Alemany, J. Catal., 2010, 270, 136–145 CrossRef.
- J. Niu, Y. Wang, S. E. Liland, S. K. Regli, J. Yang, K. R. Rout, J. Luo, M. Rønning, J. Ran and D. Chen, ACS Catal., 2021, 11, 2398–2411 CrossRef CAS.
- S. Roy, S. Hariharan and A. K. Tiwari, J. Phys. Chem. C, 2018, 122, 10857–10870 CrossRef CAS.
- L. Juurlink, D. Killelea and A. Utz, Prog. Surf. Sci., 2009, 84, 69–134 CrossRef CAS.
- A. L. Utz, Curr. Opin. Solid State Mater. Sci., 2009, 13, 4–12 CrossRef CAS.
- L. B. F. Juurlink, P. R. McCabe, R. R. Smith, C. L. DiCologero and A. L. Utz, Phys. Rev. Lett., 1999, 83, 868–871 CrossRef CAS.
- R. R. Smith, D. R. Killelea, D. F. DelSesto and A. L. Utz, Science, 2004, 304, 992–995 CrossRef CAS PubMed.
- L. B. F. Juurlink, R. R. Smith, D. R. Killelea and A. L. Utz, Phys. Rev. Lett., 2005, 94, 208303 CrossRef CAS PubMed.
- D. R. Killelea, V. L. Campbell, N. S. Shuman, R. R. Smith and A. L. Utz, J. Phys. Chem. C, 2009, 113, 20618–20622 CrossRef CAS.
- D. R. Killelea, V. L. Campbell, N. S. Shuman and A. L. Utz, Science, 2008, 319, 790–793 CrossRef CAS PubMed.
- B. L. Yoder, R. Bisson and R. D. Beck, Science, 2010, 329, 553–556 CrossRef CAS PubMed.
- N. Chen, Y. Huang and A. L. Utz, J. Phys. Chem. A, 2013, 117, 6250–6255 CrossRef CAS PubMed.
- J. Higgins, A. Conjusteau, G. Scoles and S. L. Bernasek, J. Chem. Phys., 2001, 114, 5277–5283 CrossRef CAS.
- R. Bisson, M. Sacchi and R. D. Beck, J. Chem. Phys., 2010, 132, 094702 CrossRef PubMed.
- S. Nave, A. K. Tiwari and B. Jackson, J. Phys. Chem. A, 2014, 118, 9615–9631 CrossRef CAS PubMed.
- X. J. Shen, A. Lozano, W. Dong, H. F. Busnengo and X. H. Yan, Phys. Rev. Lett., 2014, 112, 046101 CrossRef CAS PubMed.
- F. Nattino, D. Migliorini, M. Bonfanti and G.-J. Kroes, J. Chem. Phys., 2016, 144, 044702 CrossRef PubMed.
- F. Nattino, D. Migliorini, G.-J. Kroes, E. Dombrowski, E. A. High, D. R. Killelea and A. L. Utz, J. Phys. Chem. Lett., 2016, 7, 2402–2406 CrossRef CAS PubMed.
- A. Lozano, X. Shen, R. Moiraghi, W. Dong and H. Busnengo, Surf. Sci., 2015, 640, 25–35 CrossRef CAS.
- D. Migliorini, H. Chadwick, F. Nattino, A. Gutiérrez-González, E. Dombrowski, E. A. High, H. Guo, A. L. Utz, B. Jackson, R. D. Beck and G.-J. Kroes, J. Phys. Chem. Lett., 2017, 8, 4177–4182 CrossRef CAS PubMed.
- M. Sacchi, D. J. Wales and S. J. Jenkins, Phys. Chem. Chem. Phys., 2012, 14, 15879–15887 RSC.
- M. Sacchi, D. J. Wales and S. J. Jenkins, J. Phys. Chem. C, 2011, 115, 21832–21842 CrossRef CAS.
- H. Guo and B. Jiang, Acc. Chem. Res., 2014, 47, 3679–3685 CrossRef CAS PubMed.
- M. Mastromatteo and B. Jackson, J. Chem. Phys., 2013, 139, 194701 CrossRef PubMed.
- G.-J. Kroes, Phys. Chem. Chem. Phys., 2012, 14, 14966–14981 RSC.
- G.-J. Kroes, Phys. Chem. Chem. Phys., 2021, 23, 8962–9048 RSC.
- S. Nave and B. Jackson, Phys. Rev. Lett., 2007, 98, 173003 CrossRef PubMed.
- S. Nave and B. Jackson, J. Chem. Phys., 2007, 127, 224702 CrossRef PubMed.
- S. Nave and B. Jackson, J. Chem. Phys., 2009, 130, 054701 CrossRef PubMed.
- S. Nave, A. K. Tiwari and B. Jackson, J. Chem. Phys., 2010, 132, 054705 CrossRef PubMed.
- A. K. Tiwari, S. Nave and B. Jackson, Phys. Rev. Lett., 2009, 103, 253201 CrossRef PubMed.
- A. Luntz and J. Harris, Surf. Sci., 1991, 258, 397–426 CrossRef CAS.
- A. K. Tiwari, S. Nave and B. Jackson, J. Chem. Phys., 2010, 132, 134702 CrossRef PubMed.
- M.-N. Carré and B. Jackson, J. Chem. Phys., 1998, 108, 3722–3730 CrossRef.
- Y. Xiang and J. Z. H. Zhang, J. Chem. Phys., 2003, 118, 8954–8959 CrossRef CAS.
- Y. Xiang, J. Z. H. Zhang and D. Y. Wang, J. Chem. Phys., 2002, 117, 7698–7704 CrossRef CAS.
- G. P. Krishnamohan, R. A. Olsen, G.-J. Kroes, F. Gatti and S. Woittequand, J. Chem. Phys., 2010, 133, 144308 CrossRef CAS PubMed.
- B. Jiang, M. Yang, D. Xie and H. Guo, Chem. Soc. Rev., 2016, 45, 3621–3640 RSC.
- B. Jiang, R. Liu, J. Li, D. Xie, M. Yang and H. Guo, Chem. Sci., 2013, 4, 3249–3254 RSC.
- B. Jiang and H. Guo, J. Phys. Chem. C, 2016, 120, 8220–8226 CrossRef CAS.
- B. Jiang and H. Guo, J. Phys. Chem. C, 2013, 117, 16127–16135 CrossRef CAS.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112 CrossRef PubMed.
- J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 204103 CrossRef PubMed.
- X. Shen, J. Chen, Z. Zhang, K. Shao and D. H. Zhang, J. Chem. Phys., 2015, 143, 144701 CrossRef PubMed.
- X. Shen, Z. Zhang and D. H. Zhang, J. Chem. Phys., 2016, 144, 101101 CrossRef PubMed.
- X. Shen, Z. Zhang and D. H. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 25499–25504 RSC.
- X. Zhou, F. Nattino, Y. Zhang, J. Chen, G.-J. Kroes, H. Guo and B. Jiang, Phys. Chem. Chem. Phys., 2017, 19, 30540–30550 RSC.
- B. Jiang and H. Guo, Phys. Rev. Lett., 2015, 114, 166101 CrossRef PubMed.
- B. Jiang, X. Ren, D. Xie and H. Guo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10224–10227 CrossRef CAS PubMed.
- H. Guo, Theor. Chem. Acc., 2012, 131, 1077 Search PubMed.
- K. Golibrzuch, N. Bartels, D. J. Auerbach and A. M. Wodtke, Annu. Rev. Phys. Chem., 2015, 66, 399–425 CrossRef CAS PubMed.
- S. Nave and B. Jackson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 233408 CrossRef.
- B. Jackson and S. Nave, J. Chem. Phys., 2011, 135, 114701 CrossRef PubMed.
- W. H. Miller, N. C. Handy and J. E. Adams, J. Chem. Phys., 1980, 72, 99–112 CrossRef CAS.
- B. Jackson and S. Nave, J. Chem. Phys., 2013, 138, 174705 CrossRef PubMed.
- D. Han, S. Nave and B. Jackson, J. Phys. Chem. A, 2013, 117, 8651–8659 CrossRef CAS PubMed.
- H. Guo and B. Jackson, J. Phys. Chem. C, 2015, 119, 14769–14779 CrossRef CAS.
- H. Guo and B. Jackson, J. Chem. Phys., 2016, 144, 184709 CrossRef PubMed.
- M. B. Lee, Q. Y. Yang and S. T. Ceyer, J. Chem. Phys., 1987, 87, 2724–2741 CrossRef CAS.
- P. M. Holmblad, J. Wambach and I. Chorkendorff, J. Chem. Phys., 1995, 102, 8255–8263 CrossRef CAS.
- A. C. Luntz, J. Chem. Phys., 1995, 102, 8264–8269 CrossRef CAS.
- D. C. Seets, C. T. Reeves, B. A. Ferguson, M. C. Wheeler and C. B. Mullins, J. Chem. Phys., 1997, 107, 10229–10241 CrossRef CAS.
- N. Gerrits, K. Shakouri, J. Behler and G.-J. Kroes, J. Phys. Chem. Lett., 2019, 10, 1763–1768 CrossRef CAS PubMed.
- V. L. Campbell, N. Chen, H. Guo, B. Jackson and A. L. Utz, J. Phys. Chem. A, 2015, 119, 12434–12441 CrossRef CAS PubMed.
- G. Henkelman and H. Jónsson, Phys. Rev. Lett., 2001, 86, 664–667 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, J. Chem. Phys., 2006, 124, 044706 CrossRef PubMed.
- N. Gerrits, D. Migliorini and G.-J. Kroes, J. Chem. Phys., 2018, 149, 224701 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- A. Farjamnia and B. Jackson, J. Chem. Phys., 2015, 142, 234705 CrossRef PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- B. Jackson, F. Nattino and G.-J. Kroes, J. Chem. Phys., 2014, 141, 054102 CrossRef PubMed.
- J. Dai and J. Z. H. Zhang, J. Phys. Chem., 1996, 100, 6898–6903 CrossRef CAS.
- D. H. Zhang, Q. Wu and J. Z. H. Zhang, J. Chem. Phys., 1995, 102, 124–132 CrossRef CAS.
- M. Bonfanti, C. Díaz, M. F. Somers and G.-J. Kroes, Phys. Chem. Chem. Phys., 2011, 13, 4552–4561 RSC.
- A. Marashdeh, S. Casolo, L. Sementa, H. Zacharias and G.-J. Kroes, J. Phys. Chem. C, 2013, 117, 8851–8863 CrossRef CAS.
- A. Mondal, M. Wijzenbroek, M. Bonfanti, C. Díaz and G.-J. Kroes, J. Phys. Chem. A, 2013, 117, 8770–8781 CrossRef CAS PubMed.
- L. Martin-Gondre, M. Alducin, G. A. Bocan, R. Díez Muiño and J. I. Juaristi, Phys. Rev. Lett., 2012, 108, 096101 CrossRef CAS PubMed.
- P. M. Hundt, B. Jiang, M. E. van Reijzen, H. Guo and R. D. Beck, Science, 2014, 344, 504–507 CrossRef CAS PubMed.
- H. Guo, A. Farjamnia and B. Jackson, J. Phys. Chem. Lett., 2016, 7, 4576–4584 CrossRef CAS PubMed.
- B. Jiang, Chem. Sci., 2017, 8, 6662–6669 RSC.
- B. Jiang, H. Song, M. Yang and H. Guo, J. Chem. Phys., 2016, 144, 164706 CrossRef PubMed.
- T. Liu, Z. Zhang, B. Fu, X. Yang and D. H. Zhang, Chem. Sci., 2016, 7, 1840–1845 RSC.
- I. M. Mills, Mol. Phys., 1958, 1, 107–122 CrossRef CAS.
- C. Li, W. Yan and Q. Xin, Catal. Lett., 1994, 24, 249–256 CrossRef CAS.
- S. Ghosh, D. Ray and A. K. Tiwari, J. Chem. Phys., 2019, 150, 114702 CrossRef PubMed.
- H. Seenivasan, B. Jackson and A. K. Tiwari, J. Chem. Phys., 2017, 146, 074705 CrossRef CAS PubMed.
- J. C. Polanyi, Science, 1987, 236, 680–690 CrossRef CAS PubMed.
- B. L. Yoder, R. Bisson, P. Morten Hundt and R. D. Beck, J. Chem. Phys., 2011, 135, 224703 CrossRef PubMed.
| This journal is © the Owner Societies 2022 |