Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic response properties of carbon nano-onions†
Mesías
Orozco-Ic
 * and
Dage
Sundholm
* and
Dage
Sundholm
 *
*
Department of Chemistry, Faculty of Science, University of Helsinki, P.O. Box 55, A. I. Virtasen aukio 1, FIN-00014 Helsinki, Finland. E-mail: mesias.orozcoic@helsinki.fi; dage.sundholm@helsinki.fi
First published on 9th September 2022
Abstract
The magnetic response of a number of double- and triple-layer carbon nano-onions (CNOs) is analyzed by calculating the magnetically induced current density and the induced magnetic field using the pseudo-π model. Qualitatively the same magnetic response was obtained in calculations at the all-electron level. The calculations show that the CNOs exhibit strong net diatropic (paratropic) ring currents when the external magnetic field points perpendicularly to one of the six-membered (five-membered) rings. They are deshielded inside and shielded outside the CNO; the latter dominates for larger CNOs. The magnetic response originates from a combination of spherical paratropic current densities on the inside of each carbon layer and diatropic current densities on the outside of them. The quantitative differences in the aromaticity of the CNOs as compared to single fullerenes are discussed in terms of ring-current strengths. The magnetic response of some of the CNOs is approximately the sum of the magnetic response of the individual layers, whereas deviations are significant for CNOs containing C80. For the largest CNOs, the deviation from the sum of the fullerene contributions is larger, especially when the external magnetic field is perpendicular to a six-membered ring.
1 Introduction
Aromaticity is commonly associated with properties of cyclic conjugated compounds such as high stability, high symmetry, low reactivity, and a diamagnetic response to external magnetic fields.1 Originally the aromaticity concept originates from planar organic compounds such as benzene.2 However, since the discovery of buckminsterfullerene (C60),3 aromaticity has been extended to non-planar molecular structures making its definition and quantification challenging. According to Hückel's rule a planar molecule is aromatic (antiaromatic) when it possesses 4n + 2 (4n) delocalized π electrons.4 For approximate spherical molecules such as fullerenes, Hirsch's rule predicts that those with 2(n+ 1)2 π electrons are spherically aromatic.5,6 However, it is not possible to judge whether a fullerene is aromatic only based on this electron-counting rule. Hirsch's rule suggests that C60 is non-aromatic, because it does not fulfil the rule.5The molecular magnetic response to an external magnetic field has been successfully used for elucidating and quantifying the aromatic character of planar and three-dimensional conjugated molecules. In aromatic molecules, the magnetic response is diamagnetic, characterized by a ring current flowing in the classical (diatropic) direction leading to a shielding of the external magnetic field. Paramagnetic response is associated with antiaromatic rings, which sustain a ring current in the opposite (paratropic) direction leading to a deshielding of the external magnetic field.7–9 For instance, C60 responds to an external magnetic field by sustaining spherical current densities flowing in opposite directions inside and outside the molecular surface.10 Integration of the ring-current strength in C60 yields a very small positive value when the external field points perpendicularly to a six-membered ring (6-MR), suggesting that it is weakly aromatic or non-aromatic.10,11 However, when the external magnetic field points perpendicularly to a five-membered ring (5-MR), the ring-current strength is paratropic suggesting that it is an antiaromatic compound.10,11 This has been confirmed by calculating the induced magnetic field, where the 6- and 5-MRs of fullerene have shielding and deshielding cones, respectively.12 The classification of the aromaticity in fullerenes is not unambiguous. We recently showed that the magnetic response of the π electrons of C60 has an antiaromatic character to the strong paratropic current density on the inside,11 which promotes a deshielding cone,11,12 whereas recent calculations point out that internal cage shielding seems to be caused by σ delocalization.13
Multilayer fullerenes, also known as carbon nano-onions (CNOs), are a class of concentric fullerenes with spacing distances between the carbon layers of about 3 to 4 Å.14–16 Since fullerenes have generally the 5-MRs surrounded by 6-MRs. The distance between the 5-MRs increases for larger fullerenes resulting in a pronounced sp2-hybridization of the carbon atoms.16 Recently, Hashmi and Lein scrutinized the structural properties of a number of double- and triple-layer CNOs.15 They suggested that the number of layers plays an important role for detecting these structures. They also noted that the highest occupied orbital (HOMO) and the lowest unoccupied orbital (LUMO) are alternately localized on different shells. The HOMO is located on an inner layer, while the LUMO is on an outer layer and they do not mix.15,17 The concentric structures allow rotation of the inner fullerenes with respect to the outer ones. This can be considered as a requirement for having a true CNO because when the distance between adjacent pairs is not large enough, C–C interlayer bonds can be formed.15
CNOs are of scientific interest due to their potential applications in electronic devices, in energy storage systems, as photosensors, as drug-deliverers, and as containers of heavy elements.14,18,19 Since magnetic interactions in CNOs are crucial for several of these applications, studying aromaticity by addressing the magnetic response of an external magnetic field is of interest.14,18–20 Here, we study the magnetic response properties of the CNOs proposed by Hashmi and Lein15 by calculating and visualizing magnetically induced current densities and the induced magnetic field. The studied CNOs are the C60@C180, C60@C240, and C60@C540 double-layer systems as well as the C60@C240@C540 and C80@C240@C540 triple-layer CNOs shown in Fig. 1.
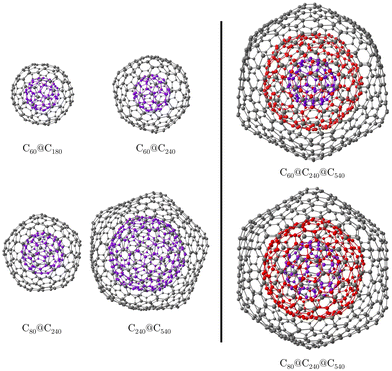 | ||
| Fig. 1 The molecular structures of the studied double- (left) and triple-layer (right) CNOs. Each layer is shown in a different color. | ||
Calculating the magnetic response is computationally demanding for large compounds as the studied CNOs. We therefore calculate the magnetic response using the pseudo-π model,21 which is computationally less demanding and has been found to yield accurate π-electron contributions to the magnetic response of organic and all-carbon structures.11,21–26 Calculations of the magnetic response of the π electrons is sufficient, because the π electrons provide the largest contribution to the global ring-current pathways.11
The calculations show that the CNOs have strong net diatropic (paratropic) ring currents when the external magnetic field is directed perpendicularly to the 6-MRs (5-MRs). The CNOs have a deshielding region inside and a shielding one outside, which dominates for the larger CNOs as a result of the inner spherical paratropic current density and the diatropic outer one of each carbon layer. The magnetic response of some CNOs is approximately the sum of the magnetic response of the individual layers. For the magnetic response of largest CNOs, the deviation from the added magnetic response of each layer is larger, especially when the external magnetic field is perpendicular to a 6-MR. The reason for this is probably due to stretching of the C–C bonds of the 6-MR leading to an increased diamagnetic response.
2 Computational details
It has recently been shown that density functional theory (DFT) calculations using long-range corrected hybrid functionals in combination with the D3(BJ) dispersion correction lead energies of stacked π–π structures that are in good agreement with results obtained in CCSD(T) calculations.27 These functionals correctly describe the molecular structures of large delocalized carbon structures.28,29 All molecular geometries were therefore fully optimized at the CAM-B3LYP-D3(BJ)/def2-SVP level.30–32 Magnetic properties calculated with hybrid functionals agree rather well with those calculated at the CCSD(T) and MP2 levels.33–36 Nuclear magnetic resonance (NMR) shieldings were therefore calculated at the CAM-B3LYP/def2-SVP level30,32 using gauge-including atomic orbitals (GIAOs).37,38The magnetic response was addressed by computing the magnetically induced current density (Jind),39–42 and the first derivative of the induced magnetic field43–45 (Bind) with respect to a uniform external magnetic field (Bext) in the zero-field limit. The electronic structure calculations were performed using the Turbomole program.46,47 In the calculations of the Jind and Bind we generally consider contributions from all electrons, i.e., the sum of the core-, σ-, π-contribution. However, in this work, the π-electron contribution to the magnetic response was calculated at the CAM-B3LYP/def2-SVP30–32 level using the inexpensive pseudo-π model.21 The current density (pπJind) and induced magnetic field (pπBind) were obtained with the pseudo-π model by calculating the magnetic response for a system where the carbon atoms are replaced by hydrogen atoms in the same positions. The pπJind and pπBind computations were performed using the gauge-including magnetically induced currents (GIMIC)39–41 and Aromagnetic48 programs, respectively. An external magnetic field (|Bext | = 1 T) can be considered to be applied parallel to the z axis and perpendicularly to the 6- or 5-MRs.49 The Bind analysis can then be made in terms of Bindz, which is equal to the zz component of the nucleus-independent chemical shift (NICSzz) index.50–52 Since three-dimensional molecules represent a challenge when using magnetic criteria that depend on the orientation of Bext with respect to the molecular ring(s), isotropic NICS50,51 calculations using the pseudo-π model were also performed (pπNICS). NICS values can be understood as the average strength of Bind using an external magnetic field in the three Cartesian directions. The GIMIC program is also able to integrate the strength of the current density (Jind) flowing through a plane intersecting one or more chemical bonds.39–41 The obtained strengths are particularly useful to quantify aromaticity in planar and three-dimensional molecules. Changes in the current-density flux along one coordinate of the integration plane can be determined by calculating current-strength profiles.41 The profiles show the derivative of Jind (dJind/dr) with respect to one of the coordinates of the integration plane (r). The r coordinate can in fullerenes be chosen to begin at the symmetry axis. The plane intersects the molecular surface and extends outside the molecule where the current density vanishes (see Fig. S1 in the ESI†). The area under the profile is the ring-current strength. The unit of the pseudo-π ring-current strengths is nA T−1, while pπNICS and pπBindz are given in ppm. For visualization purposes, the molecular structures shown in the figures of the pseudo-π magnetic response correspond to the original carbon structure.
3 Results and discussion
Single-layer fullerenes
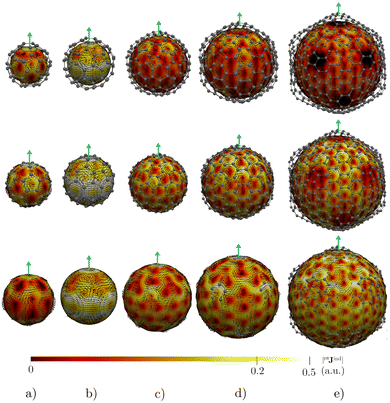
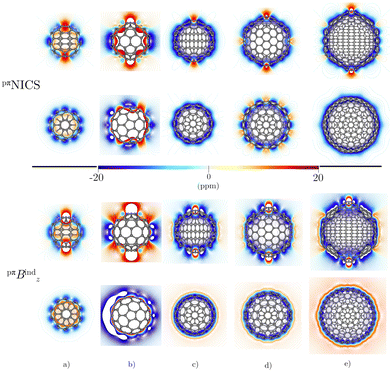
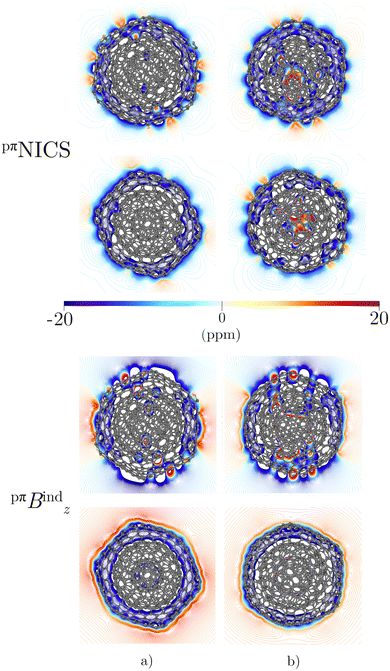
Before addressing the aromaticity of the CNOs, we consider the magnetic response of the single-layer fullerenes (C60, C80, C180, C240, and C540) to assess how their magnetic response changes when they are embedded in concentric CNO structures. None of the these fullerenes satisfies Hirsch's spherical aromaticity rule and to our knowledge no magnetic response calculations have been reported for the larger fullerenes. The exceptions are C60 and C80.10–12,23,53–55 The pseudo-π model offers the possibility to determine the current-density pathways and magnetic shielding without contamination from the core and σ electrons.11,21–26 Although the pseudo-π model was originally proposed to address the π magnetic response of planar systems,21 its applicability to non-planar structures is based on the fact that the carbon atoms in fullerenes do not significantly deviate from the sp2-hybridization.11,23,56C60 is the smallest molecule in our study. As reported in many studies,10–12,23,53,54 its magnetic response is characterized by paratropic ring currents flowing inside the cage, while diatropic (in the classical direction) ring currents appear outside it (see Fig. 2(a)). The paratropic ring current is represented as the negative region in the inner part of the ring-current profile leading to a pronounced minimum due to the local paratropic current in the 5-MR ring when Bext is perpendicular to the 5-MR ring (see Fig. 3). A deshielding zone appears therefore inside the fullerene. The 5-MRs sustain local paratropic ring currents that considerably distort the outer spherical current. C60 is characterized by positive pπBindz values inside the cage as well as near the 5-MRs as shown in Fig. 3(a). The NICS value calculated in the cage center is close to zero,53 whereas the π-component of NICS is deshielded with a value of about 20 ppm.53 This is confirmed by the pπBindz isolines shown in Fig. 4(a). The pπNICS function is similar to pπBindz because the z component dominates in Bind. In fact, the pπNICS and pπBindz values are identical (5.05 ppm) in the cage center.
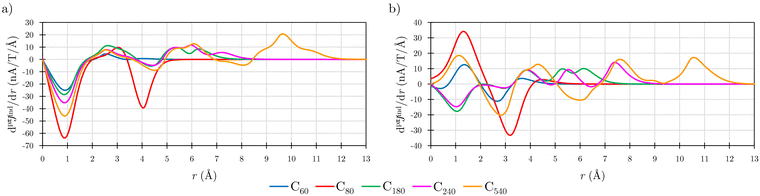 | ||
| Fig. 3 The pseudo-π ring-current strength profiles (dpπJind/dr) of the single-layer fullerenes when Bext is perpendicular to (a) 5-MR and (b) 6-MR calculated at the CAM-B3LYP/def2-SVP level. | ||
Previous magnetic shielding studies on C60 at the pseudo-π level revealed that the inside deshielding calculated with the pseudo-π model differs slightly from the one obtained in all-electron π-component calculations.22 The discrepancy originates from the close proximity of the 5-MRs in C60 leading to a strong overlapping and mixing of the local shielding and deshielding contributions in the inner region of the cage. Since deshielding contributions of antiaromatic rings are not very well described at the pseudo-π level,11,21,22 a quantitative better description is obtained for the larger fullerenes with the 5-MRs spaced farther apart. The current densities calculated at the pseudo-π level are though in qualitative and quantitative agreement with the current densities sustained by the π orbitals at the all-electron level.21,23 The ring-current strengths calculated at the pseudo-π level can be used for determining the degree of aromaticity of fullerenes, since similar ring-current strengths are obtained in all-electron calculations.11
Comparison of the ring current profile calculated at the pseudo-π model with that of the all-electron calculation shows that the profile is smoother at the pseudo-π level because contributions from the σ orbitals are not considered (see Fig. S2 in ESI†). The ring currents obtained at the two levels have the same tropicity with comparable strengths. Integration of the strength of the pseudo-π ring current results in a weak positive value of 2.37 nA T−1 when Bext points perpendicularly to one of the 6-MRs. When Bext is perpendicular to 5-MR, the integration yields a strong paratropic ring-current strength of −22.23 nA T−1, indicating local antiaromaticity (Table 1). These values are in qualitative agreement with the previously reported ring-current strengths of 3 nA T−1 and −15 nA T−1 that were obtained in all-electron (total) calculations with the magnetic field perpendicular to the 6-MR and 5-MR, respectively.10
| Molecule | Diatropic | Paratropic | Net |
|---|---|---|---|
| C60 | 10.23 (17.63) | −32.46 (−15.26) | −22.23 (2.37) |
| C80 | 17.60 (47.23) | −104.96 (−37.44) | −87.36 (9.78) |
| C180 | 37.38 (28.30) | −40.02 (−23.69) | −2.64 (4.61) |
| C240 | 40.14 (33.72) | −50.15 (−24.67) | −10.02 (9.04) |
| C540 | 70.38 (90.36) | −75.77 (−48.97) | −5.38 (41.38) |
Previous studies have shown that C80 has a singly occupied HOMO leading to a Jahn–Teller distortion of the structure and a triplet ground state.5,6,57,58 NICS(0) calculations yielded positive values in the middle of the 5-MRs and 6-MRs.5 Unconstrained structure optimization of the singlet state yielded a C2v structure with a HOMO-LUMO gap of 2.18 eV at the CAM-B3LYP-D3(BJ)/def2-SVP level. This isomer has been reported to be the second most stable singlet after the highly distorted D5d structure.57,58 The pπJind calculations reveal a strong paratropic current density flowing mainly at the equator of the fullerene both inside and outside the cage suggesting that it is antiaromatic (Fig. 2(b)) with a deep minimum in the ring-current profile originating from the local paratropic ring current of the 5-MRs. (Fig. (3)). Integration of the ring-current strength yields a value of −87.36 nA T−1 with a weak diatropic contribution. C80 is strongly deshielded both inside and outside the molecular surface (Fig. 4(b)). However, when Bext is perpendicular to a 6-MR, the ring current is diatropic with a strength of 9.78 nA T−1.
C180 and the larger single-layer fullerenes (C240 and C540) exhibit diamagnetic response inside the cage. They have a spherical paratropic inner ring-current and a diatropic outer one. The 5-MRs maintain local paratropic circulations. In the larger fullerenes, the diatropic current density near the equator outside the cage is more homogeneous than in the smaller ones (Fig. 2(c)–(e)). The current-density pathways are animated for some systems in the ESI.† Calculation of Bind yielded a more negative magnetic shielding than −20 ppm. The local ring-current loops at the 5-MRs give rise to small deshielding cones that are not able to suppress the overall diamagnetic response of the molecular cage (Fig. 4(c)–(e)). The ring-current profile has a positive maximum in the vicinity of the 6-MRs when Bext is perpendicular to a 6-MR (Fig. 3). The integration of the ring-current strengths, for a Bext perpendicular to a 5-MR, leads to the paratropic values of −2.64, −10.02, −5.38 nA T−1 for C180, C240, and C540, respectively (Table 1). When Bext is perpendicular to a 6-MR, the current strengths become positive with values of 4.61, 9.04, and 41.38 nA T−1 for C180, C240, and C540, respectively. The strengths of the diatropic and paratropic contributions that increase with the fullerene size almost cancel. The large fullerenes can still be considered non-aromatic, even though they shield the magnetic field inside the cage. However, C540 acts like a π-aromatic system when Bext is oriented perpendicular to a 6-MR. This is the only case where the diatropic component is very pronounced suggesting that the π delocalization increases as the fullerene size increases, at least for fullerenes belonging to the Ih point group.59 Since the distance between the 5-MRs substantially increases, large fullerenes can sustain strong spherical diatropic ring currents that are not significantly distorted by the local paratropic ring currents of the 5-MRs. Very large fullerenes will most likely be aromatic with dominating diatropic ring currents.
Double-layer CNOs
The layers of the CNOs are concentric with a distance of 3–4 Å between them. The interaction is then dominated by van der Waals forces. Short inter-layer distances may lead to covalent bonds between the layers, whereas when they are too far apart, the inner fullerene can move significantly away from the concentricity inside the cage. The system can then be considered as a molecule inside a nanoparticle. CNOs are the intermediate case where the layers can rotate with respect to each other while remaining practically concentric.15 The π–π stacking between the layers plays an important role for the stabilization of the structures, which might also be reflected in their magnetic response.The molecular structures of the CNOs deviate slightly from the Ih point group because the mimimun-energy structures have geometries whose symmetry axis of the 5-MRs and 6-MRs of different layers do not coincide. Thus, the symmetry axis cannot be aligned to a C5 or C3 axis as for single-layer fullerenes and Bext cannot be oriented parallel to a common symmetry axis. The magnetic response is therefore more qualitative than quantitative because the ring-current strengths slightly vary depending on how the layers of the CNO is oriented with respect to Bext.
For double-layer C60@C180 and C60@C240 CNOs, the pπJind pictures show that the inner layer has practically the same magnetic response as C60 (see Fig. 5). The spherical current density inside the cage is paratropic and outside it is diatropic. The same holds for the magnetic response of the outer C180 (or C240) layer. A strong diatropic current density appears outside the CNO. In the case of C60@C240, the diatropic contribution seems to dominate the global magnetic behavior.
Integration of pπJind through a plane that intersects both layers leads to a net ring-current strength of 28.68 and 1.10 nA T−1 for C60@C180 and C60@C240, respectively (Table 2). The diatropic component is larger. However, the paratropic one is also strong. We can associate the difference in the strengths for the different two-layered CNOs to their orientation with respect to Bext. The strong diatropic current density outside the CNO produces a shielding that practically covers the entire system as shown in Fig. 5. The small local paratropic circulations in the 5-MRs lead to local deshielding cones. Inside the innermost cage, the negative pπNICS and pπBindz values are small because the shielding from the outer layer is suppressed due to the inner deshielding caused by the inner C60 shell. The similarity between pπNICS and pπBindz in Fig. 5 shows that Bind is almost independent of the direction of Bext.
| CNO | Diatropic | Paratropic | Net |
|---|---|---|---|
| C60@C180 | 51.09 | −22.40 | 28.68 |
| C60@C240 | 59.94 | −58.84 | 1.10 |
| C80@C240 | 91.37 | −320.86 | −229.48 |
| C240@C540 | 103.47 | −51.22 | 52.25 |
| C60@C240@C540 | 126.33 | −78.80 | 47.52 |
| C80@C240@C540 | 226.63 | −167.45 | 59.18 |
The magnetic response of C80@C240 differs from the sum of the magnetic response of its layers. The current density is strongly paratropic at the C80 surface and diatropic at the C240 shell (Fig. 5 and 6) leading to a very strong paratropic ring current of −229.5 nA T−1.
| CNO | Diatropic | Paratropic | Net |
|---|---|---|---|
| C60@C180 | 47.2 (4.8) | −73.7 (−38.4) | −26.4 (6.5) |
| C60@C240 | 50.3 (63.9) | −82.8 (−50.1) | −31.9 (13.8) |
| C80@C240 | 121.2 (654.6) | −320.1 (−558.1) | −198.9 (96.4) |
| C240@C540 | 110.5 (133.7) | −125.6 (−50.5) | −15.1 (83.2) |
| C60@C240@C540 | 120.6 (157.2) | −158.0 (−87.3) | −37.5 (69.9) |
| C80@C240@C540 | 173.0 (273.6) | −446.0 (−184.8) | −273.0 (88.8) |
The magnetic response of C240@C540 originates from a paratropic current density inside and a diatropic one outside as shown in Fig. 5. The pπNICS and pπBindz calculations reveal a shielded CNO where the most negative values appear in the interior of C240 (Fig. 6). The ring-current strength integration yielded a strongly diatropic net value of 52.25 nA T−1.
The data in Table 2 show that it is not straightforward to find a clear trend and they could even be interpreted as the opposite to what the pπBindz analysis shows because the ring-current strengths depend on the orientation of the molecule relatively to Bext. Information about the cooperative magnetic response of the concentric CNOs is obtained by comparing the magnetic response of the CNOs with the sum of the magnetic response of the single-layer fullerenes. We oriented the fullerene layers such that their C5 (and C3) axes coincide and Bext is oriented parallel to a common symmetry axis. The symmetric structures are denoted C5-CNO and C3-CNO, respectively.
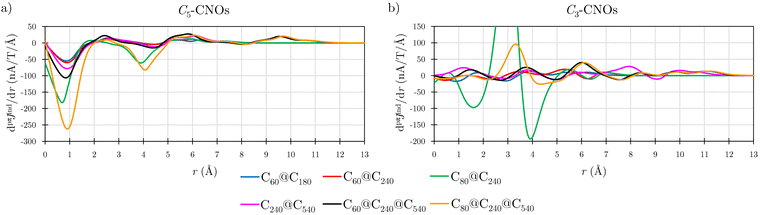
Details in the ring-current profiles are studied for the Cn-CNO structures (Fig. 7). The CNOs containing C60 have similar ring-current profiles in the C60 part of the CNOs. In C3-CNO, the paratropic component is sustained in the inner part of the structure due to C60, while at long distances the magnetic response is dominated by the one of the outer layer(s). The pseudo-π calculations show that pπJind of the Cn-CNOs qualitatively agrees with the one obtained in all-electron calculations. The profiles of the ring current of C60@C240 calculated at the two levels are shown in Fig. S2b of the ESI.† Integration of the two ring-current profiles yields ring-current strengths with the same tropicity and largely the same strengths. Despite the rapidly oscillating contributions from the σ orbitals to the ring-current profile in the all-electron calculation, the ring-current profiles calculated at the pseudo-π and all-electron levels display largely the same trend.
Integration of pπJind with planes that intersect the common 5-MRs and 6-MRs yielded the ring-current strengths of C3-CNO and C5-CNO shown in Table 3. The current density obtained with Bext along the C5 axis is paratopic for all double-layer CNOs, whereas the current density is diatropic when the Bext points along the C3 axis. The ring-current profile of C80@C240 has pronounced minima and maxima leading to a ring-current strength that differs significantly from the sum of the contributions of the individual fullerenes (Fig. 7). The integrated ring-current strength of the C3-CNO and C5-CNO structures of C80@C240 deviates by almost 100 nA T−1 from the sum of the ring-current strengths of the individual fullerenes (Table 3).
Calculations on the C3-CNO and C5-CNO structures of C240@C540 show that the ring-current strength can be expressed as the sum of the individual ring-current strengths when the magnetic field is oriented along the C5 axis of the C5-CNO, whereas the ring-current strength differs by about 30 nA T−1 in the corresponding calculation on the C3-CNO structure of C240@C540 (Table 4). The ring-current strengths of most of the C5-CNOs are almost equal to the sum of the single-layer components (Table 1). C5-C60@C240 has a net strength of −31.90 nA T−1, which agrees well with the sum of the ring-current strengths of C60 (−22.23 nA T−1) and C240 (−10.02 nA T−1). A small cooperative effect can also be seen in the almost vanishing difference in the ring-current profiles (Fig. S3 in ESI†). However, the magnetic response of C80@C240 differs completely from the magnetic response of the individual layers (Fig. S3, ESI†) probably because the position of the HOMO and LUMO orbitals do not alternate as the other CNOs.15 Similar additive features have been found in organic compounds where the global magnetic response could be reproduced by adding individual ring contributions.60,61 The cooperative magnetic response is larger for the C3-CNOs, whose Bext is oriented perpendicular to the 6-MRs maximizing their diamagnetic contribution to the magnetic response. The CNOs have longer C–C bonds in the 6-MRs than in fullerenes, whereas the 5-MRs have practically the same bond lengths as in the fullerenes.
| CNO | C 5-CNOs | Sum | C 3-CNOs | Sum |
|---|---|---|---|---|
| C60@C180 | −26.4 | −24.9 | 6.5 | 7.0 |
| C60@C240 | −31.9 | −32.2 | 13.8 | 11.4 |
| C80@C240 | −198.9 | −97.4 | 96.4 | 18.8 |
| C240@C540 | −15.1 | −15.4 | 83.2 | 50.4 |
| C60@C240@C540 | −37.5 | −37.6 | 69.9 | 52.8 |
| C80@C240@C540 | −273.0 | −102.8 | 88.8 | 60.2 |
Triple-layer CNOs
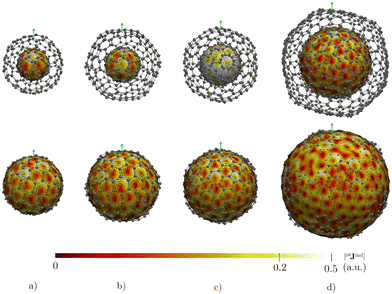
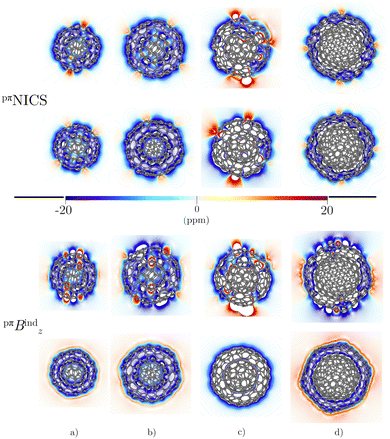
The triple-layer C60@C240@C540 is dominated by the diamagnetic response judged from the current density (Fig. 8(a)) and the magnetic shielding (Fig. 9(a)). Animation of pπJind confirms a bridging magnetic response between layers of large double- and triple-layer CNOs (see the ESI†). C60@C240@C540 is aromatic due to the enhanced diatropic contributions along the ring-current profile compared to sum of the individual fullerene contributions (Fig. 7(a)). For the C5-CNO and C3-CNO structures, the obtained ring-current strengths are −37.5 and 69.9 nA T−1, respectively. The sum of the ring-current strengths of the individual fullerenes yields the same ring-current strength as obtained for C5-CNO, whereas ring-current strength of the C3-CNO structure of C60@C240@C540 is 17 nA T−1 larger than the sum of the fullerene contributions. The deviation is also seen in the difference of the ring current profile (in Fig. S3, ESI†). C80@C240@C540 is deshielded inside the innermost layer, while the region between the second and third layers is shielded (Fig. 9(b)) because the C80 layer sustains a strong paratropic ring current near its surface, while the C240 and C540 layers are dominated by diatropic current densities. The ring-current strengths of the C5-CNO and C3-CNO structures (Table 3 and Fig. S3, ESI†) deviate significantly from the sum of the ring-current strengths of the individual layers (Table 1), which confirms that there is a strong interaction between the fullerenes in the CNO structures containing C80.4 Conclusions
We have studied the magnetic response of double- and triple-layer CNOs and the individual fullerenes by calculating magnetically induced current densities and the induced magnetic field using the pseudo-π model. We have considered CNOs consisting of C60, C80, C180, C240 and C540 fullerenes. Since each layer consists of pentagonal and hexagonal rings, the overall magnetic response of the single-layer fullerenes have significant paratropic and diatropic current-density contributions. The pentagonal rings sustain local paratropic ring currents. The fullerenes also sustain inner paratropic and outer diatropic spherical ring currents. The main exception is C80, which has a strong paramagnetic response because of the open–shell character of its ground state.The distance between the twelve pentagons increases with increasing size of the fullerenes leading to a dominating diatropic current density and diamagnetic response for the larger ones. The diatropic ring current is seen in the induced magnetic field, which is deshielding for C60 and C80. The larger ones are shielded on the inside and on the outside suggesting that the π delocalization increases as the fullerene size increases. In the limit of infinitely big fullerenes, the 6-MRs are connected by graphene-like flakes that are weakly perturbed near the 5-MRs.
Multilayer fullerenes that can be considered to be true CNOs must have an inter-layer distance that is large enough to prevent formation chemical bonds between them. The HOMO and LUMO are located in different layers allowing the layers to rotate with respect to each other.15 Fully optimization of the molecular structures of the CNOs does lead to layers whose pentagons coincide with the C5 symmetry axis. Therefore, we have also studied the magnetic response of CNOs whose pentagons are aligned and the external magnetic field is applied along the C5 and the C3 axis.
The weak coupling between the layers also results in a global magnetic response of the CNOs that can to first order be obtained by adding the magnetic response of the individual layers, especially when the magnetic field is oriented along the C5 axis. The magnetic coupling between the layers is stronger for the larger CNOs when the magnetic field is parallel to the C3 axis. The magnetic response of the CNOs containing C80 cannot be accurately expressed as the sum of the magnetic response of the individual fullerenes. It is hard to accurately assess the magnetic coupling based on calculated ring-current strengths because the ring-current strengths depend on the orientation of the layers with respect to the direction of the external magnetic field. For the largest CNOs, calculations on the fully optimized structures yield ring-current strengths in good agreement with the ones obtained for CNOs with symmetry aligned layers and the magnetic field along the C3 axis. Larger CNOs favor π delocalization giving rise to a pronounced diamagnetic response and a strong ring current.
The magnetic response of the CNOs containing C80 cannot be expressed as a sum of the magnetic response of the individual fullerenes. The magnetic coupling between C80 and the other fullerenes in the CNO is very strong suggesting that C80-containing CNOs cannot be considered as true CNOs. Thus, a weak magnetic coupling between the layers is an additional requirement for CNOs. The CNOs have longer C–C bonds in the hexagonal rings as compared to those of the corresponding fullerenes, whereas the pentagons have practically the same bond lengths as in the fullerenes.
Author contributions
M. O.-I. suggested pseudo-π current-density studies on CNOs. M. O.-I. and D. S. performed the calculations, discussed the results, and contributed to the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Academy of Finland through project numbers 314821 and 340583, by the Magnus Ehrnrooth Foundation, Waldemar von Frenckell's foundation, and the Swedish Cultural Foundation in Finland. We acknowledge computational resources from the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) and the CSC – IT Center for Science, Finland.Notes and references
- P. v R. Schleyer, Chem. Rev., 2001, 101, 1115–1118 CrossRef CAS.
- G. Merino and M. Solà, Phys. Chem. Chem. Phys., 2016, 18, 11587–11588 RSC.
- H. W. Kroto, J. R. Heath, S. C. O’Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- K. Yates, Hückel Molecular Orbital Theory, Academic Press, 2012 Search PubMed.
- A. Hirsch, Z. Chen and H. Jiao, Angew. Chem., Int. Ed., 2000, 39, 3915–3917 CrossRef CAS PubMed.
- Z. Chen, H. Jiao, A. Hirsch and W. Thiel, J. Mol. Model., 2007, 7, 161–163 CrossRef.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699–703 CrossRef CAS.
- J. A. Pople, Mol. Phys., 1958, 1, 175–180 CrossRef CAS.
- R. McWeeny, Mol. Phys., 1958, 1, 311–321 CrossRef CAS.
- M. P. Johansson, J. Jusélius and D. Sundholm, Angew. Chem., Int. Ed., 2005, 44, 1843–1846 CrossRef CAS PubMed.
- M. Orozco-Ic, M. Dimitrova, J. Barroso, D. Sundholm and G. Merino, J. Phys. Chem. A, 2021, 125, 5753–5764 CrossRef CAS PubMed.
- N. D. Charistos and A. Muñoz-Castro, J. Phys. Chem. C, 2018, 122, 9688–9698 CrossRef CAS.
- M. Orozco-Ic, N. D. Charistos, A. Muñoz-Castro, R. Islas, D. Sundholm and G. Merino, Phys. Chem. Chem. Phys., 2022, 24, 12158–12166 RSC.
- O. Mykhailiv, H. Zubyk and M. E. Plonska-Brzezinska, Inorg. Chim. Acta, 2017, 468, 49–66 CrossRef CAS.
- M. A. Hashmi and M. Lein, J. Phys. Chem. C, 2018, 122, 2422–2431 CrossRef CAS.
- M. Zeiger, N. Jäckel, V. N. Mochalin and V. Presser, J. Mater. Chem. A, 2016, 4, 3172–3196 RSC.
- J. A. Luque-Urrutia, A. Poater and M. Solà, Chem. – Eur. J., 2020, 26, 804–808 CrossRef CAS PubMed.
- M. E. Plonska-Brzezinska, ChemNanoMat, 2019, 5, 568–580 CrossRef CAS.
- V. Dhand, M. Yadav, S. H. Kim and K. Y. Rhee, Carbon, 2021, 175, 534–575 CrossRef CAS.
- A. I. Shames, V. Y. Osipov, A. Y. Vul, Y. Kaburagi, T. Hayashi, K. Takai and T. Enoki, Carbon, 2013, 61, 173–189 CrossRef CAS.
- P. W. Fowler and E. Steiner, Chem. Phys. Lett., 2002, 364, 259–266 CrossRef CAS.
- N. D. Charistos, A. Muñoz-Castro and M. P. Sigalas, Phys. Chem. Chem. Phys., 2019, 21, 6150–6159 RSC.
- A. Soncini, R. G. Viglione, R. Zanasi, P. W. Fowler and L. W. Jenneskens, C. R. Chim., 2006, 9, 1085–1093 CrossRef CAS.
- M. Antić, B. Furtula and S. Radenković, J. Phys. Chem. A, 2020, 124, 371–378 CrossRef.
- M. Orozco-Ic and G. Merino, Chemistry, 2021, 3, 1381–1391 CrossRef CAS.
- M. Orozco-Ic, R. R. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 6404–6409 RSC.
- S. Tsuzuki and T. Uchimaru, Phys. Chem. Chem. Phys., 2020, 22, 22508–22519 RSC.
- I. Casademont-Reig, R. Guerrero-Avilés, E. Ramos-Cordoba, M. Torrent-Sucarrat and E. Matito, Angew. Chem., Int. Ed., 2021, 60, 24080–24088 CrossRef CAS PubMed.
- D. W. Szczepanik, M. Solà, M. Andrzejak, B. Pawełek, J. Dominikowska, M. Kukułka, K. Dyduch, T. M. Krygowski and H. Szatylowicz, J. Comput. Chem., 2017, 38, 1640–1654 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- R. R. Valiev, H. Fliegl and D. Sundholm, Chem. Commun., 2017, 53, 9866–9869 RSC.
- R. R. Valiev, I. Benkyi, Y. V. Konyshev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2018, 122, 4756–4767 CrossRef CAS PubMed.
- L. N. Wirz, M. Dimitrova, H. Fliegl and D. Sundholm, J. Phys. Chem. Lett., 2018, 9, 1627–1632 CrossRef CAS PubMed.
- S. Lehtola, M. Dimitrova, H. Fliegl and D. Sundholm, J. Chem. Theory Comput., 2021, 17, 1457–1468 CrossRef CAS PubMed.
- R. Ditchfield, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 119, 8251–8260 CrossRef.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639 CAS.
- D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362–12378 RSC.
- G. Merino, T. Heine and G. Seifert, Chem. – Eur. J., 2004, 10, 4367–4371 CrossRef CAS PubMed.
- T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309 CrossRef CAS.
- R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, Cinvestav-Merida, Mexico, 2016 Search PubMed.
- F. A. L. Anet and D. J. OLeary, Concepts Magn. Reson., Part A, 1991, 3, 193–214 CrossRef CAS.
- P. v R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v R. Schleyer, Org. Lett., 2006, 8, 863–866 CrossRef CAS PubMed.
- Z. Chen, J. I. Wu, C. Corminboeuf, J. Bohmann, X. Lu, A. Hirsch and P. v R. Schleyer, Phys. Chem. Chem. Phys., 2012, 14, 14886–14891 RSC.
- R. Zanasi and P. W. Fowler, Chem. Phys. Lett., 1995, 238, 270–280 CrossRef.
- Z. Chen, J. Cioslowski, N. Rao, D. Moncrieff, M. Bühl, A. Hirsch and W. Thiel, Theor. Chem. Acc., 2001, 106, 364–368 Search PubMed.
- G. Monaco, F. F. Summa and R. Zanasi, J. Chem. Inf. Model., 2021, 61, 270–283 CrossRef CAS PubMed.
- C. Rios and R. Salcedo, Molecules, 2012, 17, 14588–14601 CrossRef CAS PubMed.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2001, 114, 10362–10367 CrossRef CAS.
- P. Calaminici, G. Geudtner and A. M. Köster, J. Chem. Theory Comput., 2009, 5, 29–32 CrossRef CAS PubMed.
- M. Orozco-Ic, J. Barroso, N. D. Charistos, A. Muñoz-Castro and G. Merino, Chem. – Eur. J., 2019, 26, 326–330 CrossRef.
- E. Paenurk and R. Gershoni-Poranne, Phys. Chem. Chem. Phys., 2022, 24, 8631–8644 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S3 contain a schematic representation of the integration planes, a comparison of the ring-current profiles calculated at the all-electron and pseudo-π levels, and the differences in the ring-current profiles of the carbon nano-onions and the sum of the ring current profiles of the individual fullerenes, respectively. Cartesian coordinates of the optimized molecular structures and the current-density animations for C60, C540, C240@C540 and C60@C240@C540. See DOI: https://doi.org/10.1039/d2cp02718f |
| This journal is © the Owner Societies 2022 |