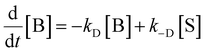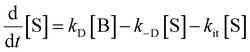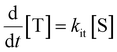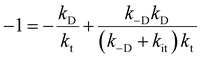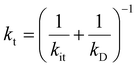Local charge carrier dynamics of a particulate Ga-doped La5Ti2Cu0.9Ag0.1O7S5 photocatalyst and the impact of Rh cocatalysts†
Tatsuya
Chugenji
a,
Zhenhua
Pan
 a,
Vikas
Nandal
a,
Vikas
Nandal
 b,
Kazuhiko
Seki
b,
Kazuhiko
Seki
 b,
Kazunari
Domen
b,
Kazunari
Domen
 *cd and
Kenji
Katayama
*cd and
Kenji
Katayama
 *a
*a
aDepartment of Applied Chemistry, Chuo University, Tokyo 112-8551, Japan. E-mail: kkata@kc.chuo-u.ac.jp; Tel: +81-3-3817-1913
bGlobal Zero Emission Research Center (GZR), National Institute of Advanced Industrial Science and Technology (AIST), Onogawa 16-1 AIST West, Tsukuba 305-8569, Japan
cResearch Initiative for Supra-Materials, Interdisciplinary Cluster for Cutting Edge Research, Shinshu University, Nagano 380-8553, Japan. E-mail: domen@chemsys.t.u-tokyo.ac.jp
dOffice of University Professors, The University of Tokyo, Tokyo 113-8656, Japan
First published on 1st July 2022
Abstract
Visible-light responsive photocatalytic materials are expected to be deployed for practical use in photocatalytic water splitting. One of the promising materials as a p-type semiconductor, oxysulfides, was investigated in terms of the local charge carrier behavior for each particle by using a home-built time-resolved microscopic technique in combination with clustering analysis. We could differentiate electron and hole trapping to the surface states and the following recombination on a micron-scale from the nanosecond to microsecond order. The map of the charge carrier type revealed that charge trapping sites for electrons and holes were spatially separated within each particle/aggregate. Furthermore, the effect of the rhodium cocatalyst was recognized as a new electron pathway, trapping to the rhodium site and the following recombination, which was delayed compared with the original electron recombination process. The Rh effect was discussed based on the phenomenological simulation, revealing a possible reason for the decay was due to the anisotropic diffusion of charge carriers in oxysulfides or the interfacial energy barrier at the interface.
Introduction
Solar-driven water splitting by a photocatalyst has been widely studied to obtain sustainable hydrogen energy.1,2 Nowadays, various oxide photocatalysts such as strontium titanium oxide (SrTiO3) have been developed and optimized for water splitting,3,4 but their solar conversion efficiencies are limited because they can only absorb ultra-violet light (λ < 400 nm), which covers only a small fraction of the solar spectrum. To this end, visible-light-responsive photocatalysts such as (oxy)nitrides and (oxy)chalcogenides have attracted increasing attention,5 together with doped SrTiO3, bismuth vanadate (BiVO4), hematite and copper oxide. While these photocatalysts can absorb more visible light in the solar spectrum and generate more charge carriers compared with oxide photocatalysts, their solar conversion efficiencies are still low because of the limited utilization of photo-generated charge carriers. The efficiency of a photocatalyst depends not only on the absorption wavelength range but also on the extraction efficiency of photo-excited charge carriers, which depends on the charge mobility and loss processes such as trapping and recombination. The physical properties of the charge carriers have been studied by understanding the dynamics involving generation, separation, transport of charge carriers, and their reactions at the interfaces. This understanding is a critical step to optimize the performance of a photocatalyst, but such studies on (oxy)nitride and (oxy)chalcogenide photocatalysts are still in progress.La5Ti2CuxAg1−xS5O7 (x = 0–1) are a series of oxysulfides that exhibit a strong absorption from approximately 550 to 750 nm. Since they are p-type semiconductors due to the presence of Cu species as an acceptor,6 they have been intensively studied for photoelectrochemical/photocatalytic H2 evolution.7–10 As an example, La5Ti2CuS5O7 has been used as a photocathode with an onset potential for hydrogen evolution as positive as + 0.9 V vs. RHE due to its one-dimensional conductivity along the long axis and a long diffusion length (∼μm) of charge carriers in this direction.7,11 Its photocatalytic ability was further enhanced by doping Ti with Ga to increase the electronic conductivity.12 The excellent photoelectrochemical performance of Ga-doped La5Ti2−xCuS5O7 (Ga-LTCA) promoted the introduction of this oxysulfide to tandem/parallel photoelectrochemical cells and photocatalyst sheets for unassisted water splitting.12,13 Cocatalysts are usually applied to enhance charge separation and catalyze surface reactions for photocatalytic water splitting.14–16 Various cocatalysts for H2 evolution have been tested on Ga-LTCA using various loading methods.12 A recent study revealed that Rh loading by impregnation provided the highest effect since highly dispersed and uniform-sized Rh particles can be firmly fixed on Ga-LTCA. Nevertheless, the optimized Rh/Ga-LTCA can only utilize ∼10% of the absorbed photons for photocatalytic H2 evolution.17,18 The detailed understandings of the deactivation processes of charge carriers are highly desirable to obtain clues on improving its photocatalytic performance, and, in particular, the spatial charge separation and the effect of the co-catalysts are not understood well for the micron-scale rod-like particles.
Recently, we have developed a time-resolved pattern-illumination phase microscopy (PI-PM) method for investigating the spatio-temporal dynamics of the charge carriers.19–21 In this method, photo-excited charge carriers are visualized via the refractive index change using phase-contrast imaging. The refractive index change is induced by the density change of photo-excited charge carriers, and the charge generation, transport, and decay processes can be imaged with a high time resolution same as the pulse width. The information of the charge carriers observed via the refractive index changes is different from those obtained by the conventional time-resolved techniques such as transient absorption and time-resolved photoluminescence methods, and non-radiative charge decay processes such as trapping and interfacial charge transfer have been frequently observed in the photovoltaic and photocatalytic processes.22–24
The temporal responses at all the pixels in a PI-PM image sequence are categorized in terms of the local charge carrier responses by clustering analysis.19 The similarities of the response shapes and intensities are used for the categorization of the types of charge carriers. The categorized map of the charge carrier types could reveal the structure-dependent charge carrier types from the comparison of the map with the optical image. This method was applied for a “Z-scheme” photocatalytic sheet consisting of Mo-doped BiVO4 (BVOM) for O2 evolution and Rh-doped SrTiO3 (STOR) for H2 evolution. The local sites that are active/inactive for water splitting reactions were mapped out based on the types of charge carriers.20 Moreover, we have recently modified the PI-PM method for the application to particulate samples. And, we could successfully distinguish the local charge carrier dynamics of photocatalytic particle samples such as BVOM and STOR.25 Besides, this technique was also applied to investigate a photovoltaic perovskite material for understanding the effect of methylammonium iodide (MAI) in terms of a passivation/deactivation effect. The local charge carrier dynamics revealed that excess MAI had a negative effect on the charge generation or transport, thus reducing the photo-conversion efficiency.21
In this study, we applied the PI-PM method to study the local charge carrier dynamics of a particulate Ga-LTCA. Several different types of charge carriers were assigned from the scavenger effect on the local charge carriers. Furthermore, the effect of cocatalysts was studied based on the types of charge carriers.
Experimental
Preparation of Ga-LTCA
Ga-LTCA was prepared using a solid-state-reaction method following a previous study.12 A precursor mixture including La2O3 (99.99%, high purity reagent, Kanto Chemical Co., Inc.), La2S3 (99.9%, High Purity Chemical Laboratory Co., Ltd), TiO2 (Rutile, 99.99%, Rare Metallic Co., Ltd), Cu2S (99%, High Purity Chemical Laboratory Co., Ltd), Ag2S (99%, High Purity Chemical Laboratory Co., Ltd), Ga2O3 (99.9%, Wako Pure Chemical Corporation) and sulfur (99.99%, High Purity Chemical Laboratory Co., Ltd) in a molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.96
3.96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.02
0.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.9
0.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 was prepared in a glovebox under a nitrogen atmosphere. La2O3 and TiO2 were annealed at 1273 K for 10 h and 1073 K for 1 h, respectively, just prior to mixing. Then, the precursor mixture was sealed in an evacuated quartz tube. The quartz tube was annealed in a muffle furnace with the following heating program: from room temperature to 473 K at 22 K min−1, from 473 to 673 K at 2 K min−1, from 673 to 1323 K at 0.2 K min−1, at 1273 K for 48 h, from 1273 to 773 K at 0.67 K min−1, and to ambient temperature naturally. After opening the sealed quartz tube, some bulk samples were obtained, and they were ground to powder.
0.5 was prepared in a glovebox under a nitrogen atmosphere. La2O3 and TiO2 were annealed at 1273 K for 10 h and 1073 K for 1 h, respectively, just prior to mixing. Then, the precursor mixture was sealed in an evacuated quartz tube. The quartz tube was annealed in a muffle furnace with the following heating program: from room temperature to 473 K at 22 K min−1, from 473 to 673 K at 2 K min−1, from 673 to 1323 K at 0.2 K min−1, at 1273 K for 48 h, from 1273 to 773 K at 0.67 K min−1, and to ambient temperature naturally. After opening the sealed quartz tube, some bulk samples were obtained, and they were ground to powder.
Cocatalyst deposition
Metallic Rh was loaded on Ga-LTCA particles using an impregnation-reduction method. First, Ga-LTCA particles were dispersed in an aqueous solution containing RhCl3·3H2O (99.9%, Wako Pure Chemical Industries). The amount of Rh was calculated to be 0.4 wt% with respect to the Ga-LTCA mass. Then, the obtained slurry was stirred with a glass rod and dried in a water bath. Finally, the product was annealed at 573 K for 1 h under a flow of H2 (20 mL min−1) and N2 (200 mL min−1) mixture.Characterization
The samples were characterized by X-ray diffraction (XRD, Rigaku Ultima III, Cu Kα), UV-visible-near infrared diffuse-reflectance spectroscopy (DRS. V-670, JASCO), scanning electron microscopy (SEM, Miniscope TM3030, HITACHI) and high-resolution SEM (HR-SEM, JSM-7001FA, JEOL).Photocatalytic hydrogen evolution
Photocatalytic H2 evolution was performed using a Pyrex top-irradiation cell connected with a glass closed gas circulation system. Prior to the H2-evolution reaction, the reaction vessel was evacuated three times to remove the ambient air and dissolved O2 in the reaction solution. Then, Ar was introduced to the cell until the background pressure reached 7 kPa. The cell was maintained at 285 K by cooling water. A 300 W Xe lamp (INOTEX, R300-3J) equipped with a dichroic mirror and an L42 cutoff filter (long pass filter >420 nm) was used as the light source. The amount of H2 was measured by gas chromatography (Shimadzu GC-8A) employing a thermal conductivity detector with 5 Å molecular sieve columns and Ar as the carrier gas.Sample preparation for analysis by time-resolved microscopic image sequences
Ga-LTCA or Rh/Ga-LTCA particles were immobilized on a glass substrate by two methods for measuring the average and local responses, differently. In general, for time-resolved measurements, it is preferred that a larger area is covered by particles for the average response to have a stronger signal intensity. On the other hand, good separation is expected for measurements of the local responses, even though the signal intensity is weaker. For the measurements of the average response, the samples were prepared using a particle-transfer method.26 Briefly, 10 mg of particles were dispersed in 450 μL of isopropanol by sonication. The suspension was drop-cast on a 1 × 3 cm glass substrate and then dried naturally in the air. Then, the particles on the glass substrate were covered with a layer of indium tin oxide (ITO, ∼2.5 μm) by sputtering. Another glass substrate with a transparent double-sided tape was used to peel off the ITO layer with the deposited LTCA particles. Finally, the obtained particle/ITO/tape/glass sample was sonicated in water for 10 s to remove the excessive particles without direct contact with the ITO layer. For measuring the local response, the samples were prepared by binding particles to a glass substrate with heat treatment. Briefly, 1 mg of particles were dispersed in isopropanol (100 μL) by sonication. Then the suspension was drop-cast on a glass substrate (1 × 3 cm) and dried naturally in the air. The particle/glass sample was annealed at 200 °C for 1 h under a flow of N2 (200 mL min−1). For both the average and local response measurements, a sample film on a substrate was sandwiched by another piece of a glass substrate with a 0.5 mm rubber spacer. A 0.15 mL of solvent was added into the gap. Each sample was measured in contact with acetonitrile (ACN) and methanol (MeOH). ACN was used as an inert solvent to prevent charge transfer to the solution side, and MeOH was used as a hole scavenger.PI-PM method
The PI-PM method was used for studying the microscopic charge carrier dynamics, and the basic principle of this technique is described in previous papers,19,27 and the optical configuration is shown in Fig. S1 in the ESI.† A pump light (355 nm, ∼1 mJ cm−2) pattern is illuminated on a sample for the photo-excitation of charge carriers. The charge carriers are generated and decay in time due to the charge trapping, recombination, and transfer, and the pattern of the charge carrier distribution is varied in time. The distribution of the photo-excited charge carriers is observed via the refractive index change by phase-contrast imaging using a CMOS camera. The refractive index was imaged by the self-imaging technique.27,28 In this setup, changes both in the refractive index change and absorption change are included in the images, but the absorption change was negligible for LTCA at the used wavelength. Pattern illumination is preferable for applying image recovery calculations, as described in a different paper.29 In this study, the image quality was recovered by the total variation regularization for the three-dimensional data consisting of a sequence of images in time.30 For the measurement of the average response, a ten-rectangle pattern as a pump light was used, and the center region of the sensor was cut off for analyses. The width and height of each rectangle were 25 and 60 μm, respectively. The full image size was 480.8 × 93.9 μm, corresponding to 1024 × 200 pixels. For the local response measurements, an arbitrary pattern was used. The pixel width corresponds to 469 nm.Results and discussion
Characterization of Ga-LTCA particles
Ga-LTCA particles prepared using the solid-state-reaction method were characterized by XRD as shown in Fig. S2(a) in the ESI,† which confirmed that they were composed of the same phase as that in a previous study.12 The light-absorption characteristics of these particles were further investigated by DRS as shown in Fig. S2(b) in the ESI,† showing an absorption edge around ca. 710 nm. The HR-SEM image in Fig. S3(a) in the ESI† shows that Ga-LTCA particles had a characteristic rod-like shape with a length of tens of micrometers, and Fig. S3(b) in the ESI† with a higher resolution shows that Ga-LTCA particles had a smooth surface. Rh loading did not change the morphology of Ga-LTCA particles (Fig. S3(c) in the ESI†), but Rh/Ga-LTCA particles had a rough surface due to the presence of Rh particles (Fig. S3(d) in the ESI†). The Rh/Ga-LTCA particles were used for photocatalytic H2 evolution in an aqueous solution containing Na2S and Na2SO3 as sacrificial reagents. As shown in Fig. S4 (ESI†), the H2-evolution rate was ∼1500 μmol h−1, similar to that reported in a previous study.18The optical microscopy and SEM images of the Ga-LTCA samples for the measurements of the average and local responses are shown in Fig. 1. The samples for the measurement of the average responses in the whole sample area were covered with a higher density of particles (Fig. 1(a)) compared with those for local measurements (Fig. 1(b)). The densely packed particles on a substrate could reduce the light scattering, leading to an improvement of the image quality. On the other hand, the particles in a rod shape with a length of 10–20 μm were dispersed on a glass substrate as shown in Fig. 1(b). The isolation of each particle was necessary to separate local charge responses at each location. No apparent change was observed by deposition of Rh.
 | ||
| Fig. 1 (A) Microscopy images and (B) SEM images of Ga-LTCA samples for the measurements of (a) average and (b) local responses. SEM was measured with a magnification of ×1000. | ||
Average charge carrier dynamics of Ga-LTCA
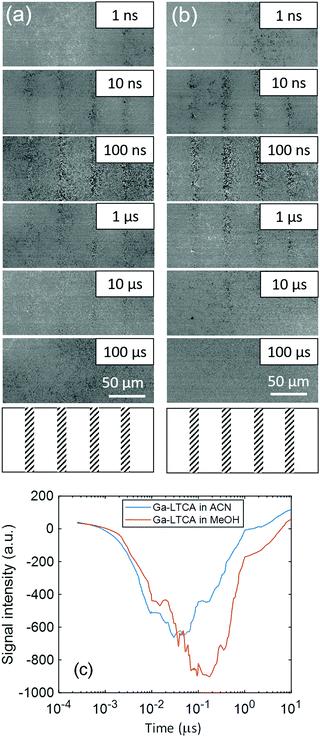
Time-resolved image sequences for Ga-LTCA in contact with two types of solvents (ACN and MeOH) were measured in the same region by the PI-PM method. ACN is an inert solvent for the interfacial charge transfer, while MeOH works as a hole scavenger. Fig. 2(a) and (b) shows the partial regions of the time-resolved images of the refractive index change (0 ns–10 μs). The pump light pattern on the sample is drawn at the bottom of Fig. 2. The photo-irradiated regions gradually became darker until 100 ns, followed by a decay until ∼10 μs. Compared with the contrast change in ACN (Fig. 2(a)) and MeOH (Fig. 2(b)), no apparent difference was recognized directly from the image sequences.Fig. 2(c) shows the average responses of Ga-LTCA in ACN and MeOH. The average response in the whole region was calculated by averaging the image intensities at all the pixels in the light irradiated regions. The response of Ga-LTCA in ACN showed a decay response until 10–20 ns, and followed by a recovery response until 800–900 ns. The average response of Ga-LTCA in MeOH was delayed compared with that of ACN for both the decay-and-recovery responses (time constants for the decay and recovery were 60–70 ns and 1–2 μs, respectively). The response shape did not depend on the pump intensity. Since holes are scavenged by MeOH, the extension of the response indicates that the recombination process was delayed due to fewer holes available. The decaying process corresponds to the charge carrier trapping to the surface states during diffusion, which has been observed via the refractive index change for various photocatalytic and photovoltaic materials, such as hematite, bismuth vanadate and SrTiO3,24 and it indicates that the observed response was due to the surface-trapped carriers. Overall, it is understood that photo-excited holes were scavenged, causing a longer time for charge carriers to be trapped at the surface states, and, as a result, the recombination of the surface-trapped charge carriers was delayed due to less availability of holes. However, each process was still not clear from the average response and we made the clustering analysis for local regions.
Local charge carrier dynamics of Ga-LTCA
Time-resolved image sequences for Ga-LTCA in ACN and MeOH were measured for a sparsely dispersed sample to study the local responses of charge carriers for each particle by the PI-PM method. Fig. 3 shows the partial regions of the time-resolved image sequences of the refractive index change (0 ns–10 μs). The pump light pattern on the sample surface is drawn at the bottom. The spotty contrast of the photo-irradiated region gradually became stronger until 100 ns, followed by a decay until several tens of microseconds. The sizes and shapes of these spots were well-matched with those for the Ga-LTCA particles (Fig. 1(b)), and it is reasonable to conclude that the image contrast was varied at the locations of Ga-LTCA particles. Since the contrast change was increased and decayed in time on the nanosecond to microsecond order and the response matched well with the result of the average response, the signal is supposed due to the generation and decay of the photo-excited charge carriers in each particle. Compared with the contrast change in ACN (Fig. 3(a)) and MeOH (Fig. 3(b)), no clear distinction was possible directly from the image sequences.We applied the clustering analysis for the photo-excited region to examine the types of charge carriers. In a previous study, we found that the effect of the scavenger worked locally on the micro-scale and the local charge carrier responses helped the assignment of the types of charge carriers by comparing the carrier type with and without the effect of the scavenger, instead that the average responses of the charge carriers are compared.25 For the differentiation of the charge carrier type, we calculated the similarity of the response shape and intensity at each pixel in regions 1–3 of Fig. 3 and divided the responses into several categories. The final number of categories was decided by comparing all the categorized responses.
Fig. 4 shows the categorized maps of the charge carrier responses for Ga-LTCA in ACN and MeOH, respectively, corresponding to region 1 in Fig. 3. It is noted that the average responses were made of three categories; a positive response (category 1), no response (category 2), and a negative response (category 3), as shown in Fig. 4(d). The positions of categories 1 and 3 showed a good agreement with the black regions of the optical images of Ga-LTCA (Fig. 4(a)), which indicated that the responses of categories 1 and 3 originated from the Ga-LTCA particles or aggregations. The responses of categories 1 and 3 in Fig. 4(d) had an opposite sign in the intensity. The signal with an opposite sign of the refractive index change indicates that the responses had a different origin of charge carriers. It is supposed that the anonymous shapes of the responses shown in Fig. 2(c) were due to the mixing of different components with opposite signs.
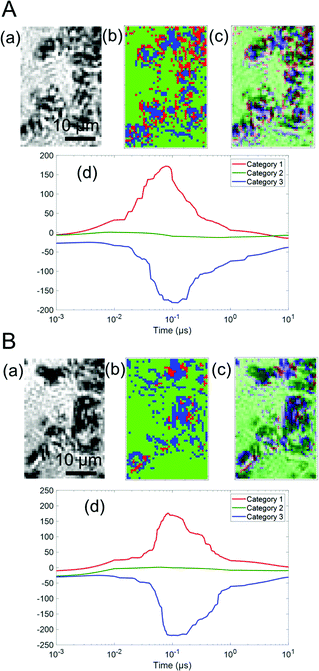 | ||
| Fig. 4 The categorized maps of the charge carrier responses of Ga-LTCA in (A) ACN and (B) MeOH in region 1 of Fig. 3. (a) A microscopic image, (b) the corresponding categorized map (c) an image of the overlap between (a) and (b). (d) The averaged responses for three categories. The ratios of categories 1–3 of (A) Ga-LTCA in ACN were 15, 65, and 21% and those of (B) Ga-LTCA in MeOH were 4, 76, and 20%, respectively. | ||
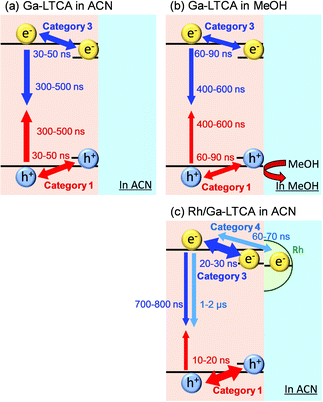
The ratios of categories 1–3 of Ga-LTCA in ACN (Fig. 4(A)) were 15, 65, and 21%, respectively, and those in MeOH were 4, 76, and 20% (Fig. 4(B)). The ratio of category 1 was decreased, and that of category 2 was increased in MeOH. Considering the effect of the hole scavenger (MeOH), category 1 was assigned as the hole response, and it is supposed that the hole-excited region was deactivated and converted into category 2. As a logical inference, category 3 was due to the counterpart of the holes, namely electrons.
In addition, the responses of categories 1 and 3 shown in Fig. 4(d) were delayed in MeOH. This tendency was similar to the average response shown in Fig. 2(c). The positions of categories 1 and 3 in ACN increased/decreased until 30–50 ns and decayed/recovered for 300–500 ns, respectively, and they were 60–90 ns and 400–600 ns in MeOH, respectively. Considering the discussions of the average responses, the responses of categories 1 and 3 correspond to the surface trapping and the following recombination of holes and electrons, respectively. The recombination was delayed for electrons by reducing the number of holes due to MeOH. It seems that the holes would decrease faster with MeOH, but the hole response also became slower. This is possibly because the observed holes were the ones trapped at the surface states and the response could be slower as a decrease in holes when the number of surface states is limited and occupied by the trapped holes. This is consistent that the increasing response (trapping to surface states) was also delayed, indicating that the trapping process was controlled by the holes at the valence band and the process became slower when the mobile holes were scavenged by MeOH. From the differentiation of the charge carrier types, it is noted that the positions of the surface-trapped electrons and holes were located differently, which indicated that the charge carriers were separated spatially in particles. The clustering results for the other regions are provided in Fig. S5 and S6 in the ESI.† These results showed the same tendency as region 1 (Fig. 4). The ratios of category 1 of Ga-LTCA in ACN were 16% (region 2) and 19% (region 3), and they decreased to 3% (region 2) and 8% (region 3) in MeOH, and those of category 2 increased from 61 (region 2) and 66% (region 3) to 77 (region 2) and 70% (region 3), respectively.
Effect of Rh cocatalysts on the charge carrier dynamics
The effect of Rh cocatalysts on the charge carrier dynamics of Ga-LTCA was investigated. Time-resolved image sequences for Rh/Ga-LTCA in ACN were measured by the PI-PM method. Fig. 5 shows the partial regions of the time-resolved image sequences of the refractive index change (0 ns–10 μs) for Rh/Ga-LTCA in ACN. The pump light pattern is indicated at the bottom. Similarly, as Ga-LTCA only, the spotty contrast gradually became stronger in the photo-irradiated region till 100 ns, followed by a decay until several tens of microseconds. The locations of the contrasted image matched well with those of the Rh/Ga-LTCA particles.Fig. 6 shows the categorized maps of the charge carrier responses of Rh/Ga-LTCA in ACN in region 3 of Fig. 5(b). We recognized four types of responses in Rh/Ga-LTCA in ACN, where an additional response with a negative intensity was found compared with the Ga-LTCA only. A positive response (category 1), no response (category 2), and two negative responses (categories 3 and 4) were categorized. The positions of categories 1, 3, and 4 showed good agreement with the dark regions of Fig. 6(a), and it indicates that these responses came from the Rh/Ga-LTCA particles. From the similarity of the responses between Rh/Ga-LTCA and Ga-LTCA and the scavenger effect by MeOH (the PI-PM image sequences are shown in Fig. S7 (ESI†), and the clustering analysis is provided in Fig. S8 and S9 in the ESI†), categories 1–3 were the same as those for Ga-LTCA; (category 1: surface-trapped holes, category 3: surface-trapped electrons). category 4 was a new component with a delayed response of category 3. (Sometimes, category 4 shows at non-particle areas and it is due to the smaller particles, which were ambiguous by the optical image. In Fig. 1, small particles were not clearly observed by an optical image due to the resolution).
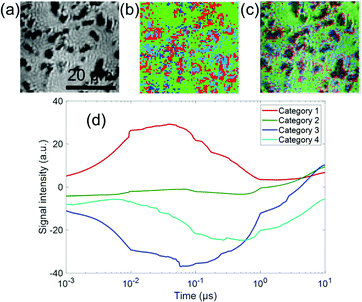 | ||
| Fig. 6 The categorized map of the charge carrier responses of Rh/LTCA in ACN in Fig. 5(a) (region 3). (a) A microscopic image and (b) the corresponding categorized map. (c) An image of the overlap between (a) and (b). (d) The averaged responses for three categories. The ratios of categories 1–4 were 20, 56, 5, and 19%, respectively. | ||
Rhodium acts as a cocatalyst by accumulating electrons. It was reported that the electron transfer to the cocatalyst occurs at least within microseconds.18 Based on this and the similarity between the response of categories 3 and 4, we speculated that the response of category 4 corresponds to the electrons trapped to the Rh sites.
The response of category 1 increased until 10–20 ns and decayed 500–600 ns (Fig. 6(d)). Compared with Ga-LTCA in ACN (Fig. 4), the response of category 1 shown in Fig. 6(d) became faster. On the other hand, the negative responses were separated into two types (one was similar to Ga-LTCA, and the other one was slower). The time constants of the fall-and-recovery component of category 3 were 20–30 ns and 700–800 ns, and those of category 4 were 60–70 ns and 1–2 μs. By adding a cocatalyst for electrons, the hole trapping process became faster, and some parts of the electrons were trapped to the Rh sites, which caused a delay in the electron response by accumulating them to the sites. These changes of the trapping and recombination processes indicated that the opposite sign of charge carriers and at different sites could affect each other. This result indicates that Rh does not only promote the charge separation but that it changes the quality of charge carriers (holes and electrons). In particular, the lifetime of the electrons was extended one order, which is preferable for the reduction reaction.
In region 3 of Fig. 6, categories 3 and 4 covered 24% in the whole area, and the ratio of them was 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8. The results in the other regions (regions 1 and 2) also showed similar ratios of categories 3 and 4, which were 3
8. The results in the other regions (regions 1 and 2) also showed similar ratios of categories 3 and 4, which were 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 and 3
7 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, respectively (Fig. S10 and S11 in the ESI†). It means that Rh worked as a cocatalyst for 70–80% of the excited electrons. Even though the amount of Rh deposition was optimized to obtain the highest efficiency, it is possible that some Rh could not cover all the electron-accumulating sites, or a part of Rh did not act as an electron mediator as a cocatalyst.
7, respectively (Fig. S10 and S11 in the ESI†). It means that Rh worked as a cocatalyst for 70–80% of the excited electrons. Even though the amount of Rh deposition was optimized to obtain the highest efficiency, it is possible that some Rh could not cover all the electron-accumulating sites, or a part of Rh did not act as an electron mediator as a cocatalyst.
The summary diagram of photo-excited charge carriers is shown in Fig. 7. For Ga-LTCA only, the surface trapping and the following recombination of holes and electrons were observed (Fig. 7(a)). We need to assume the surface-trapping and detrapping of the mobile charge carriers and the recombination was caused by the mobile charge carriers at the conduction and valence bands, for reproducing the rise-and-decay response, which is fully explained in the simulation. By the addition of methanol, the number of holes was reduced, and the hole trapping to the surface sites and the following recombination were delayed. Furthermore, the electron recombination was delayed due to the less availability of holes. The time required for trapping of electrons could be prolonged by scavenging holes when the trapping competes with recombination with holes because the recombination loss is suppressed by scavenging holes. On the other hand, the hole trapping was accelerated by the addition of a cocatalyst, which indicates that the holes could migrate faster due to the charge separation by the electron capture with Rh. 70–80% of the electrons were captured by the cocatalyst and the lifetime of the electrons became longer than the electrons without the cocatalyst.
Understanding of the delayed electron response due to the cocatalyst
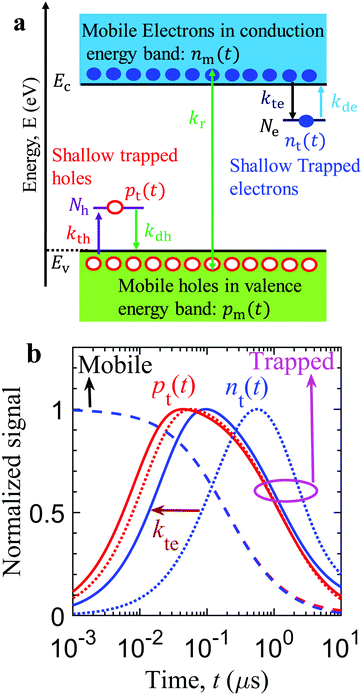
One of the key findings of the charge carrier dynamics of Rh-loaded Ga-LTCA is the delayed response of the electrons taking the pathway of the Rh cocatalyst. Numerical simulations are conducted to decipher the dominant charge carrier dynamics behind the kinetics of the response (Fig. 6(d)). The numerical simulations can reveal the origin of the increase and decrease of the measured response with time t, as well as provide the qualitative estimates of the governing material parameters to replicate the delayed negative response with the loading of the Rh co-catalyst.Fig. 8(a) shows the proposed numerical model, highlighting various relaxation processes of distinct charge species.31 After photo-excitation, densities of mobile electrons nm and holes pm are relaxed to the edge of the conduction Ec and valence energy bands Ev. These mobile charge carriers are subject to the competing processes of the band-to-band bimolecular recombination (with the rate constant kr) and the diffusion process before reaching the surface of the Ga-LTCA photocatalyst. The diffused electrons and holes get trapped and de-trapped in the shallow trap states at the Ga-LTCA surface and Rh co-catalyst, which are the key processes to explain the slow rise-and-decay response. The diffusion and charge transfer from the respective continuum trap-states to the surface or Rh states are encapsulated into the effective rate constants of the mobile charge carriers. The mobile electrons are trapped and de-trapped with the effective rate constant kte and kdevia. the shallow trap-states or Rh states (with density Ne and the representative energy depth Ete), respectively. Similarly, the mobile holes get trapped and de-trapped with the effective rate constants kth and kdh through the shallow trap-states (with density Nh and the representative energy depth Eth), respectively. Considering the above-mentioned relaxation processes, the evolution of the mobile electron density nm(t) with time t is dominated by
| dnm(t)/dt = – krpm(t)nm(t) − kte(Ne − nt(t))nm(t) + kde(Nc − nm(t))nt(t). | (1) |
| dnt(t)/dt = kte(Ne − nt(t))nm(t) − kde(Nc − nm(t))nt(t). | (2) |
Using the detailed balance condition,31 the rate constants satisfy kde = kte![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ete/kBT), where kB and T are the Boltzmann constant and temperature, respectively. Similarly, the dynamics of the mobile hole density pm(t) is controlled by
exp(−Ete/kBT), where kB and T are the Boltzmann constant and temperature, respectively. Similarly, the dynamics of the mobile hole density pm(t) is controlled by
| dpm(t)/dt = −krpm(t)nm(t) − kth(Nh − pt(t))pm(t) + kdh(Nv − pm(t))pt(t), | (3) |
| dpt(t)/dt = kth(Nh − pt(t))pm(t) − kdh(Nv – pm(t))pt(t), | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Eth/kBT) is required. The above-mentioned material parameters were unreported and tuned to adjust the model parameters with the measured peak positions of the signal in time t. Table 1 provides the adjusted material parameters of the Ga-LTCA photocatalyst. The initial boundary conditions were fixed at t = 0 ns such that the photon absorption produces the initial density of mobile electrons nm(0) and holes pm(0), but negligible trapped electrons nt(0) and holes nt(0) at the surface.
exp(−Eth/kBT) is required. The above-mentioned material parameters were unreported and tuned to adjust the model parameters with the measured peak positions of the signal in time t. Table 1 provides the adjusted material parameters of the Ga-LTCA photocatalyst. The initial boundary conditions were fixed at t = 0 ns such that the photon absorption produces the initial density of mobile electrons nm(0) and holes pm(0), but negligible trapped electrons nt(0) and holes nt(0) at the surface.
| Parameters, symbols | Numerical value |
|---|---|
| Effective density of states for the conduction and valence energy bands, Nc/v | 1020 cm−3 |
| Bi-molecular recombination rate constant, kr | 5 × 10−13 cm3 s−1 |
| Effective rate constant for hole trapping, kth | 4 × 10−11 cm3 s−1 at the surface |
| Effective rate constant for electron trapping, kte | 4 × 10−12 cm3 s−1 at the surface |
| 5 × 10−13 cm3 s−1 at the Rh site | |
| Trap state density, Ne/h | 4 × 1014 cm−3 |
| Energy depth of shallow trap states from continuum energy bands, Ete/th | 100 meV |
| Initial density of mobile electrons and holes, nm(0) = pm(0) | 1019 cm−3 |
| Initial density of trapped electrons and holes, nt(0) = pt(0) | 0 cm−3 |
Fig. 8(b) shows the simulated kinetics of charge carriers (mobile and trapped) of an LTCA photocatalyst. After photo-excitation, the mobile charges show unaffected decay kinetics with time t by the tapping rate constant kte, where the decay rate is limited primarily by the bi-molecular recombination rate constant kr. Despite the charge carrier trapping in the shallow states, such characteristics are caused by the relatively low trap density of the shallow trap-states in comparison to the initial photogenerated charge carriers nm(0) (refer to Table 1). Besides the recombination, the mobile charge carriers diffused and accumulated in the shallow states (near the valence and conduction energy bands) at the surface. As a result, the density of trapped charge species (pt(t): holes; nt(t): electrons) increases as time t. Concurrently, the available trap states for the diffused mobile charge carriers reduce with the accumulation of trapped charge carriers. Owing to the low energy depth of the shallow trap-states, the accumulated charge carriers (at the surface states) de-traps to the continuum energy bands (Ec/v). The de-trapping rate increases as the trapped carrier density increases. This leads to the saturation of the trapped charge carrier density (pt(t) and nt(t)) at a certain time tp. Beyond tp, the de-trapping process dominates over the trapping of charge carriers, which results in the decrease of the trapped charge carrier density. The trap-states close to the energy bands (with low energy depth) are crucial for the de-trapping of charge carriers, as the de-trapping rate constant kde/dh ∝ exp(−Eth/te/kBT). An increasing and decreasing trend similar to the measured signal with time t was simulated. This trapping/de-trapping model from the shallow trap-states was necessary to reproduce the slow rising and the delayed decay, different from the bi-molecular recombination process. (Separately, the refractive index change should be an increasing function of the trapped charge carrier density, confirmed from the reflectance change by photo-excitation.)
The similarity between the experimental and the simulated responses reassure that our model is appropriately assumed. This consideration suggests that the measured kinetics is proportional to the dynamics of trapped electrons and holes, not the mobile charge carriers at the conduction and valence bands. The parameters in Fig. 8(b) were adjusted to reproduce the experimental responses shown in Fig. 6. The peak positions of nte and pth were reproduced by varying the electron trapping rate constant, kte and kth. The results indicate that the position of the measured peak signal intensity in time corroborates well with the simulated tp of the respective trapped holes and electrons. The delayed peak responses due to the trapped electrons compared to that from the trapped holes were originated from the low kte (4 × 10−12 cm3 s−1 for surface states; 5 × 10−13 cm3 s−1 for Rh sites) in comparison to the (trapped holes) kth (4 × 10−11 cm3 s−1). The response for the trapped holes was not delayed much by reducing the electron trap rate constants.
The peak signal from trapped electrons was delayed by Rh loading. In our simulation, the effective trapping rate constant under Rh loading is approximately one order of magnitude smaller than that in the absence of Rh. It should be reminded that the effective trapping rate constants are phenomenological rate constants, which include the effect of diffusion to the surface besides trapping. If we denote the charge carrier density in bulk, at the surface, and at the surface trap-states by [B], [S], and [T], the phenomenological rate equations can be expressed as
by considering the kinetic processes,
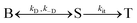 . kD and k−D represent the rate constants for the diffusion toward/from the surface and kit represents the intrinsic rate constant for trapping to the surface trap-states. The effective trapping rate constant is defined by
. kD and k−D represent the rate constants for the diffusion toward/from the surface and kit represents the intrinsic rate constant for trapping to the surface trap-states. The effective trapping rate constant is defined by 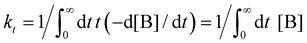 , where the initial conditions are given by [B] = 1, [S] = [T] = 0. By time-integration of rate equations, we obtain
, where the initial conditions are given by [B] = 1, [S] = [T] = 0. By time-integration of rate equations, we obtainand kt = [k−D/(kDkit) + 1/kD]−1. When kD = k−D, the effective trapping rate constant can be written as
The above phenomenological description of the effective trapping rate constant could be accurate in 3 dimensions, but less accurate as the dimensionality in diffusion is lowered. The final equation indicates that the lower effective trapping rate by Rh loading could be attributed to the lower rate of diffusion in bulk or the lower trapping rate constant to the trap-states. The latter could be attributed to the appearance of the barrier for trapping by Rh loading, which could modify the band bending and/or the activation energy barrier for the charge transfer. Diffusion might be the rate-determining process in LTCA owing to highly anisotropic diffusion with the dominant migration path along the long axis, and the Rh loading might influence the migration of carriers in LTCA. Further experimental and theoretical studies are required to discriminate between these two possible scenarios. In either scenario, the effective rate constants, kte, became smaller, and the electron trap to the Rh sites was delayed; concurrently, the de-trapping process was also delayed. By slowing down the electron accumulation at the Rh states, the effective time for the electrons with photocatalytic activity could be elongated by delaying the electron de-trapping process; as a result, the total photocatalytic activity is enhanced.
Conclusion
We could successfully distinguish different types of charge carriers of Ga-LTCA on a micro-scale by using the combination of the PI-PM method and clustering analysis. Furthermore, the effect of the cocatalyst, Rh, was clarified from the difference in the local charge carrier dynamics. We could recognize the charge carrier types by visualizing them on an optical image, and compare the maps with and without the scavenger effect. For Ga-LTCA, the trapping (<100 ns) and the following recombination (<1 μs) of photo-excited electrons and holes were categorized by the addition of a hole scavenger. We found that the surface-trapped electrons and holes were locally separated on a micron-scale in particles and aggregates. The effect of the Rh cocatalyst was clearly recognized from a different electron dynamics from the Ga-LTCA only. 70–80% of electrons took another pathway via the trapping to the Rh sites, extending their lifetimes. The delayed electron transfer to the Rh sites was analyzed by the phenomenological simulation, and the extension of the lifetime could be explained by the effect of Rh on either the charge transfer at the interface or the diffusion in the anisotropic material. Even though the amount of Rh deposition was optimized, there is still 20–30% space for the enhancement of the cocatalyst effect. From this strategy, we could fully understand the local charge carrier behavior of various photocatalytic particles or films and also could help in optimizing a mixture of the different materials such as overall photocatalytic materials, an amount of cocatalysts, defect passivation, etc.Author contributions
TC and KK designed the experiments and made measurements. PZ and KD designed and prepared the samples. VN and KS made simulation analysis of the data. TC and KK prepared the draft of the paper, and all the authors reviewed and discussed it.Conflicts of interest
I declare that the authors have no competing interests or other interests that might be perceived to influence the results and/or discussion reported in this article.Acknowledgements
This research was financially supported by the JST PRESTO (#JPMJPR1675), the JSPS Kakenhi (#22K05158) and the Institute of Science and Engineering, Chuo University.References
- T. Hisatomi, J. Kubota and K. Domen, Recent advances in semiconductors for photocatalytic and photoelectrochemical water splitting, Chem. Soc. Rev., 2014, 43(22), 7520–7535, 10.1039/C3CS60378D.
- T. Hisatomi and K. Domen, Reaction systems for solar hydrogen production via water splitting with particulate semiconductor photocatalysts, Nat. Catal., 2019, 2(5), 387–399, DOI:10.1038/s41929-019-0242-6.
- H. Kato, K. Asakura and A. Kudo, Highly efficient water splitting into H2 and O2 over lanthanum-doped NaTaO3 photocatalysts with high crystallinity and surface nanostructure, J. Am. Chem. Soc., 2003, 125(10), 3082–3089, DOI:10.1021/ja027751g.
- T. Takata, J. Jiang, Y. Sakata, M. Nakabayashi, N. Shibata, V. Nandal, K. Seki, T. Hisatomi and K. Domen, Photocatalytic water splitting with a quantum efficiency of almost unity, Nature, 2020, 581(7809), 411–414, DOI:10.1038/s41586-020-2278-9.
- Z. Pan, H. Yoshida, L. Lin, Q. Xiao, M. Nakabayashi, N. Shibata, T. Takata, T. Hisatomi and K. Domen, Synthesis of Y2Ti2O5S2 by thermal sulfidation for photocatalytic water oxidation and reduction under visible light irradiation, Res. Chem. Intermed., 2021, 47(1), 225–234, DOI:10.1007/s11164-020-04329-y.
- M. Katayama, D. Yokoyama, Y. Maeda, Y. Ozaki, M. Tabata, Y. Matsumoto, A. Ishikawa, J. Kubota and K. Domen, Fabrication and photoelectrochemical properties of La5Ti2MS5O7 (M = Ag, Cu) electrodes, Mater. Sci. Eng., B, 2010, 173(1), 275–278, DOI:10.1016/j.mseb.2009.12.021.
- J. Liu, T. Hisatomi, G. Ma, A. Iwanaga, T. Minegishi, Y. Moriya, M. Katayama, J. Kubota and K. Domen, Improving the photoelectrochemical activity of La5Ti2CuS5O7 for hydrogen evolution by particle transfer and doping, Energy Environ. Sci., 2014, 7(7), 2239–2242, 10.1039/C4EE00091A.
- T. Hisatomi, S. Okamura, J. Liu, Y. Shinohara, K. Ueda, T. Higashi, M. Katayama, T. Minegishi and K. Domen, La5Ti2Cu1−xAgxS5O7 photocathodes operating at positive potentials during photoelectrochemical hydrogen evolution under irradiation of up to 710 Nm, Energy Environ. Sci., 2015, 8(11), 3354–3362, 10.1039/C5EE02431E.
- G. Ma, Y. Suzuki, R. Balia Singh, A. Iwanaga, Y. Moriya, T. Minegishi, J. Liu, T. Hisatomi, H. Nishiyama, M. Katayama, K. Seki, A. Furube, T. Yamada and K. Domen, Photoanodic and photocathodic behaviour of La5Ti2CuS5O7 electrodes in the water splitting reaction, Chem. Sci., 2015, 6(8), 4513–4518, 10.1039/C5SC01344E.
- J. Liu, T. Hisatomi, M. Katayama, T. Minegishi, J. Kubota and K. Domen, Effect of particle size of La5Ti2CuS5O7 on photoelectrochemical properties in solar hydrogen evolution, J. Mater. Chem. A, 2016, 4(13), 4848–4854, 10.1039/C5TA10731H.
- D. H. K. Murthy, H. Matsuzaki, J. Liu, Y. Suzuki, T. Hisatomi, K. Seki, K. Domen and A. Furube, Transient absorption spectroscopy reveals performance-limiting factors in a narrow-bandgap oxysulfide La5(Ti0.99Mg0.01)2CuS5O6.99 photocatalyst for H2 generation, J. Phys. Chem. C, 2019, 123(23), 14246–14252, DOI:10.1021/acs.jpcc.9b02668.
- S. Sun, T. Hisatomi, Q. Wang, S. Chen, G. Ma, J. Liu, S. Nandy, T. Minegishi, M. Katayama and K. Domen, Efficient redox-mediator-free Z-scheme water splitting employing oxysulfide photocatalysts under visible light, ACS Catal., 2018, 8(3), 1690–1696, DOI:10.1021/acscatal.7b03884.
- T. Higashi, Y. Shinohara, A. Ohnishi, J. Liu, K. Ueda, S. Okamura, T. Hisatomi, M. Katayama, H. Nishiyama, T. Yamada, T. Minegishi and K. Domen, Sunlight-driven overall water splitting by the combination of surface-modified La5Ti2Cu0.9Ag0.1S5O7 and BaTaO2N photoelectrodes, ChemPhotoChem, 2017, 1(5), 167–172, DOI:10.1002/cptc.201600015.
- J. Yang, D. Wang, H. Han and C. Li, Roles of cocatalysts in photocatalysis and photoelectrocatalysis, Acc. Chem. Res., 2013, 46(8), 1900–1909, DOI:10.1021/ar300227e.
- Z. Pan, R. Yanagi, Q. Wang, X. Shen, Q. Zhu, Y. Xue, J. A. Röhr, T. Hisatomi, K. Domen and S. Hu, Mutually-dependent kinetics and energetics of photocatalyst/Co-catalyst/two-redox liquid junctions, Energy Environ. Sci., 2020, 13(1), 162–173, 10.1039/C9EE02910A.
- Z. Pan, J. A. Röhr, Z. Ye, Z. S. Fishman, Q. Zhu, X. Shen and S. Hu, Elucidating charge separation in particulate photocatalysts using nearly intrinsic semiconductors with small asymmetric band bending, Sustainable Energy Fuels, 2019, 3(3), 850–864, 10.1039/C9SE00036D.
- Z. Pan, Q. Xiao, S. Chen, Z. Wang, L. Lin, M. Nakabayashi, N. Shibata, T. Takata, T. Hisatomi and K. Domen, Synthesis of a Ga-doped La5Ti2Cu0.9Ag0.1O7S5 photocatalyst by thermal sulfidation for hydrogen evolution under visible light, J. Catal., 2021, 399, 230–236, DOI:10.1016/j.jcat.2021.05.015.
- Q. Xiao, J. Xiao, M. Vequizo, J. J. Hisatomi, T. Nakabayashi, M. Chen, S. Pan, Z. Lin, L. Shibata, N. Yamakata, A. Takata, T. Domen and K. Cocatalyst, Engineering of a narrow bandgap Ga-La5Ti2Cu0.9Ag0.1O7S5 photocatalyst towards effectively enhanced water splitting, J. Mater. Chem. A, 2021, 9(48), 27485–27492, 10.1039/D1TA08770C.
- M. Ebihara and K. Katayama, Anomalous charge carrier decay spotted by clustering of a time-resolved microscopic phase image sequence, J. Phys. Chem. C, 2020, 124(43), 23551–23557, DOI:10.1021/acs.jpcc.0c07609.
- M. Ebihara, T. Ikeda, S. Okunaka, H. Tokudome, K. Domen and K. Katayama, Charge carrier mapping for Z-scheme photocatalytic water-splitting sheet via categorization of microscopic time-resolved image sequences, Nat. Commun., 2021, 12(1), 3716, DOI:10.1038/s41467-021-24061-4.
- T. Chugenji, M. Ebihara and K. Katayama, Charge carrier inhomogeneity of MAPbI3 clarified by the clustering of the time-resolved microscopic image sequence, ACS Appl. Energy Mater., 2021, 4(7), 6430–6435, DOI:10.1021/acsaem.1c00258.
- S. Kuwahara, H. Hata, S. Taya, N. Maeda, Q. Shen, T. Toyoda and K. Katayama, Detection of non-absorbing charge dynamics via refractive index change in dye-sensitized solar cells, Phys. Chem. Chem. Phys., 2013, 15(16), 5975–5981, 10.1039/c3cp44597f.
- S. Kuwahara and K. Katayama, Distinction of electron pathways at titanium oxide/liquid interfaces in photocatalytic processes and co-catalyst effects, Phys. Chem. Chem. Phys., 2016, 18(36), 25271–25276, 10.1039/c6cp04016k.
- K. Katayama, T. Chugenji and K. Kawaguchi, Charge carrier trapping during diffusion generally observed for particulate photocatalytic films, Energies, 2021, 14(21), 7011, DOI:10.3390/en14217011.
- K. Kawaguchi, T. Chugenji, H. Tokudome, S. Okunaka and K. Katayama, Distinction and separation of different types of charge carriers from the time-resolved local charge carrier mapping for photocatalytic materials, J. Phys. Chem. C, 2022, 126(5), 6646–6652, DOI:10.1021/acs.jpcc.2c00798.
- T. Minegishi, N. Nishimura, J. Kubota and K. Domen, Photoelectrochemical properties of LaTiO2N electrodes prepared by particle transfer for sunlight-driven water splitting, Chem. Sci., 2013, 4(3), 1120–1124, 10.1039/C2SC21845C.
- K. Katayama, Photo-excited charge carrier imaging by time-resolved pattern illumination phase microscopy, J. Chem. Phys., 2020, 153(5), 054201, DOI:10.1063/5.0009312.
- M. Okuda and K. Katayama, Selective detection of real and imaginary parts of refractive index change in solutions induced by photoexcitation using near-field heterodyne transient grating method, Chem. Phys. Lett., 2007, 443(1–3), 158–162, DOI:10.1016/j.cplett.2007.06.056.
- M. Ebihara, W. Y. Sohn and K. Katayama, Lifetime mapping of photo-excited charge carriers by the transient grating imaging technique for nano-particulate semiconductor films, Rev. Sci. Instrum., 2019, 90(7), 073905, DOI:10.1063/1.5111418.
- X. Huang, J. Fan, L. Li, H. Liu, R. Wu, Y. Wu, L. Wei, H. Mao, A. Lal, P. Xi, L. Tang, Y. Zhang, Y. Liu, S. Tan and L. Chen, Fast, long-term, super-resolution imaging with hessian structured illumination microscopy, Nat. Biotechnol., 2018, 36, 451–459, DOI:10.1038/nbt.4115.
- V. Nandal, R. Shoji, H. Matsuzaki, A. Furube, L. Lin, T. Hisatomi, M. Kaneko, K. Yamashita, K. Domen and K. Seki, Unveiling charge dynamics of visible light absorbing oxysulfide for efficient overall water splitting, Nat. Commun., 2021, 12(1), 7055, DOI:10.1038/s41467-021-27199-3.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02808e |
| This journal is © the Owner Societies 2022 |