Q-Band relaxation in chlorophyll: new insights from multireference quantum dynamics†
Sebastian
Reiter‡
 a,
Lena
Bäuml‡
a,
Jürgen
Hauer
a,
Lena
Bäuml‡
a,
Jürgen
Hauer
 b and
Regina
de Vivie-Riedle
b and
Regina
de Vivie-Riedle
 *a
*a
aDepartment of Chemistry, Ludwig-Maximilians-Universität München, Butenandtstr. 11, 81377 Munich, Germany. E-mail: regina.de_vivie@cup.uni-muenchen.de
bDepartment of Chemistry, Technical University of Munich, Lichtenbergstr. 4, 85747 Garching, Germany
First published on 27th October 2022
Abstract
The ultrafast relaxation within the Q-bands of chlorophyll plays a crucial role in photosynthetic light-harvesting. Yet, despite being the focus of many experimental and theoretical studies, it is still not fully understood. In this paper we look at the relaxation process from the perspective of non-adiabatic wave packet dynamics. For this purpose, we identify vibrational degrees of freedom which contribute most to the non-adiabatic coupling. Using a selection of normal modes, we construct four reduced-dimensional coordinate spaces and investigate the wave packet dynamics on XMS-CASPT2 potential energy surfaces. In this context, we discuss the associated computational challenges, as many quantum chemical methods overestimate the Qx–Qy energy gap. Our results show that the Qx and Qy potential energy surfaces do not cross in an energetically accessible region of the vibrational space. Instead, non-adiabatic coupling facilitates ultrafast population transfer across the potential energy surface. Moreover, we can identify the excited vibrational eigenstates that take part in the relaxation process. We conclude that the Q-band system of chlorophyll a should be viewed as a strongly coupled system, where population is easily transferred between the x and y-polarized electronic states. This suggests that both orientations may contribute to the electron transfer in the reaction center of photosynthetic light-harvesting systems.
1 Introduction
Chlorophylls are a group of natural pigments that play a vital role in photosynthetic light-harvesting.1–3 There is a variety of differently substituted chlorophylls4 but in general, the absorption spectrum is dominated by two main bands in the visible range, labeled B- and Q-bands. While the B or Soret band appears as a strong absorption around 400 nm, the weaker Q band resides in the red part of the spectrum around 700 nm and exhibits an extensive pattern of vibrational side bands.Underlying both absorption bands are four excited states, labeled Qx/Qy and Bx/By, according to the polarization of the transition dipole moment vector (Fig. 1). These states have historically been characterized with the Gouterman model6,7 in terms of independent electronic transitions between the four frontier orbitals. In this context, Qy and By are both characterized mainly by the HOMO → LUMO and HOMO−1 → LUMO+1 excitations, albeit with different weights. Similarly, Qx and Bx are comprised mainly of the HOMO−1 → LUMO and HOMO → LUMO+1 excitations. However, this simplistic model does not explain the ultrafast internal conversion within the Q-bands,8–11 which plays an important role in energy and exciton transfer during photosynthetic light-harvesting.12 In particular, magnetic circular dichroism (MCD) and polarized fluorescence spectra of chlorophyll a exhibit not just one but two x-polarized bands, whose energetic positions are also strongly dependent on the solvent.8,13–16 Relative to the Qy 0–0 band maximum, the lower-energy component appears at 700 cm−1 (1100 cm−1) in diethylether (pyridine), while the higher-energy band occurs at 1700 cm−1 (2100 cm−1). Their assignment to an electronic state has been the subject of debate for several decades. The “traditional” assignment15,17 identifies the higher energy band as the Qx origin, while the “modern” assignment16,18 favors the lower energy component. Adding to the confusion, the historical assignment of the Qx state to the lower- or higher-energy band also changes with the solvent coordination pattern of the central magnesium ion.19 A recent re-evaluation of existing experiments in combination with vibronic coupling models8 indicated that the two transitions are better thought of as a single system of inseparably mixed vibronic states. The strong vibronic coupling between Qx and Qy spreads x-polarization across the whole Q band system and allows ultrafast population transfer on a timescale of 100 fs to 226 fs, depending on the solvent.8,20,21
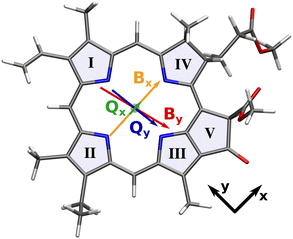 | ||
| Fig. 1 Transition dipole moments of the Q and B bands overlaid on the molecular structure of our chlorophyll model system. Arrows are scaled with the length of the respective transition dipole vector. Roman numerals signify the ring numbering convention used in this work.5 | ||
Here, high-level quantum mechanical calculations can complement experimental findings.8,22–24 In particular, non-adiabatic dynamics simulations can shed light on the mechanism behind the strong vibronic coupling. Most studies employ a semiclassical ansatz, where the internal molecular dynamics are modeled as point masses moving in a quantum mechanical electrostatic potential.9–11,25 While this approach is able to capture the molecular dynamics in full dimensionality, it is inherently limited by the need to calculate energy gradients in every time step for many trajectories with simulation times up to several picoseconds. These requirements limit the level of theory, as most multireference methods quickly become prohibitively expensive if gradients are involved. Moreover, a classical treatment of nuclear motion neglects the coherence of the wave packets in strongly coupled potentials as well as the interaction with the laser field.
In this paper, we therefore investigate the ultrafast relaxation within the Q-bands of a chlorophyll a analogue through the lens of wave packet quantum dynamics in reduced dimensionality. We first evaluate a variety of quantum chemical methods for their ability to adequately describe both states in question. Next, we present multiple two-dimensional coordinate spaces to construct XMS-CASPT2 potential energy surfaces (PESs), on which we model the ultrafast population transfer. We discuss the topography of the excited state potentials and its implications on the wave packet dynamics. In particular, we show how population can be transferred not only from the energetically higher Qx state to the lower Qy state, but also the other way round after laser excitation into vibrational side bands of Qy. Finally, the results are complemented by a simulation of the coupled nuclear and electron dynamics within the Q-band, using the NEMol ansatz.26–30 Our results shed light on the intimate coupling of the two Q states in chlorophyll and provide a reference for future theoretical and experimental studies.
2 Methods
All calculations in this work use a reduced model of chlorophyll a, where the phytyl chain is replaced by a methyl group. This reduces the number of atoms from 137 to 82 and speeds up the calculations at negligible errors in the absorption energies, which has been shown before5,31 and was validated again by us (Fig. S1, ESI†).Molecular visualizations within this work were created with VMD 1.9.3.32,33 Orbitals for CASSCF/-PT2 calculations were visualized with Luscus 0.8.6.34
2.1 Geometry optimizations
The ground state geometry of our chlorophyll model was optimized with the CAM-B3LYP density functional35 and the 6-311G(d) basis set36–38 using Gaussian 16.39 The Qy and Qx states were optimized with the same functional and basis set at the TDDFT level. Optimized geometries were verified as energy minima by the absence of imaginary vibrational frequencies.2.2 Excited state calculations
We tested a range of density functionals, namely CAM-B3LYP,35 ωB97X-D,40 ωB97X-D4,41 BHLYP,42,43 LC-ωHPBE44 and M062X45 to calculate chlorophyll excitation energies with a special focus on the Qx–Qy energy gap. These test calculations were conducted with Gaussian 16 and the 6-311G(d) basis set,36–38 with the exception of ωB97X-D4,41 which is implemented in Orca 5.046–48 and where the def2-TZVP basis49 was employed.While some of the density functionals gave promising results for the position of the Q-bands at the Franck–Condon (FC) geometry, investigating the ultrafast non-adiabatic population transfer requires the use of a multireference method. Therefore, we used the DFT/MRCI method50–52 with the redesigned R2018 Hamiltonian53 as a benchmark reference for all other methods. The Kohn–Sham reference orbitals were calculated at the BHLYP42,43/def2-SV(P)49 level of theory using the resolution of the identity approximation for Coulomb and exchange integrals54,55 (RI-JK) with the def2-SVP/C56 and def2/JK57 auxiliary basis sets, as implemented in Orca 4.2.46,47 An MRCI reference space was constructed iteratively for 50 roots, starting from a CISD expansion of four electrons in the four frontier orbitals, until the leading configurations of all roots were contained in the reference space. In the DFT/MRCI formalism, a parametrized damping function is applied to the MRCI matrix elements. This is done to avoid double counting of dynamic electron correlation, which has already been accounted for by the DFT part, and brings along an energy-based selection of configurations.52,53 In this work, we have used the short selection threshold of 0.8 Eh with the corresponding parameter set. The short MRCI expansion speeds up the calculations considerably, while providing an excellent absorption spectrum for our chlorophyll analogue.
CASSCF58 and (X)MS-CASPT259–64 calculations were conducted with OpenMolcas 19.1165,66 using the ANO-RCC-VDZP67–69 basis set. Great care must be taken in the selection of active spaces for multi-configurational approaches. Previous theoretical investigations have achieved reasonable results with small,70 medium-sized71,72 and very large22,23 active spaces. After initial testing, we settled on an active space of six electrons in six orbitals (Fig. 2) to construct a PES, as we will detail later.
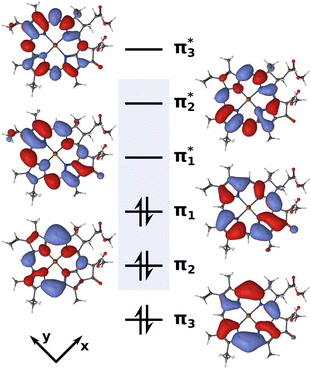 | ||
| Fig. 2 Active space of six electrons in six orbitals (isovalue 0.02) used for the XMS-CASPT2 calculations. The blue box highlights the four Gouterman orbitals. | ||
A balanced description of both Qy and Qx was achieved by state-averaging over six roots (SA6) in the CASSCF wave function and allowing all of them to mix in the subsequent XMS-CASPT2 calculation. Using both an IPEA and imaginary shift of 0.1, we obtained a Qx–Qy energy gap of 0.21 eV at the FC point, which matched the one calculated with DFT/MRCI (0.23 eV) almost exactly. However, this strategy turned out to be problematic for computing a PES. The higher excited states would cause rotations between active and inactive orbitals at geometries away from the FC region, thus introducing discontinuities in the PES. To mitigate this issue, we reduced the number of roots to four, resulting in an SA4-CASSCF(6,6) reference wave function. Here, the active space remained stable across the PES at the cost of strongly overestimating the Qx–Qy energy gap at the FC point with 0.54 eV. To get the best of both worlds, we calculated the CASSCF wave function in two steps. In the first step, the molecular orbitals were optimized in a SA4-CASSCF(6,6) scheme to arrive at a stable active space. In the second step, these orbitals were used in a SA6-CASCI(6,6) calculation where only the CI coefficients were re-optimized. Finally, all six roots were mixed in the subsequent XMS-CASPT2 calculation, using an IPEA73 and imaginary level shift74 of 0.1. In this way, we were able to stabilize the active space composition across the PES and still achieve a Qx–Qy gap of 0.39 eV, closer to the DFT/MRCI reference than in a pure SA4-XMS-CASPT2(4,4) scheme. Energies for both of the state-averaging schemes with various level shifts, along with an exemplary OpenMolcas input are provided in the ESI.† To account for the remaining deviation of the Qx–Qy gap from the DFT/MRCI reference, the calculated Qx PESs were finally shifted down by −0.16 eV.
2.3 Quantum dynamics
For the wave packet quantum dynamics, the time-dependent Schrödinger equation was solved on a spatial grid of 256 × 256 points, using the Chebyshev75 propagation scheme in a program of our own design. Energies, transition dipole moments and non-adiabatic coupling matrix elements (NACs) were calculated at 45 grid points (Fig. S5–S11, ESI†) and interpolated to the target grid with thin-plate splines.76 Since the use of XMS-CASPT2 gradients would have been too expensive, NACs were calculated in the SA4-CASSCF(6,6)/SA6-CASCI(6,6) scheme introduced above. To still account for the correct energy difference between the Qx and Qy state, we scaled the NACs with the ratio of the energy gap at the XMS-CASPT2 and the CASSCF level. Furthermore, the full-dimensional NAC vector was projected onto the respective 2D coordinate space. The kinetic energy in the reduced-dimensional coordinate space was expressed in the Wilson G-matrix formalism77–80 and matrix elements are provided in Table S9, ESI.† Vibrational eigenfunctions of the 2D potentials were calculated by propagation in imaginary time.812.4 Coupled nuclear and electron dynamics in molecules (NEMol)
The coupled nuclear and electron dynamics was determined using the NEMol ansatz26–30 developed in our group. Within this purely quantum-mechanical ansatz the electronic wave functions are propagated in the eigenstate basis and coupled to the nuclear wave packet propagated on coupled PESs. In this work a NEMol-grid29,30 of 45 grid points with the same dimensions and spacing as for the calculations of the energies, transition dipole moments and NACs was used. Using the NEMol ansatz, the coupled one-electron density is determined. Applying the NEMol-grid the integration over the full nuclear coordinate space is split up into segments. Summing up over the partial densities of all of these segments, the total electron density coupled to multiple nuclear grid points is obtained.3 Results and discussion
3.1 Assessment of quantum-chemical methods
The Q-band relaxation of chlorophyll strongly depends on the energy gap between the Qx and Qy state. Any theoretical investigation of the process therefore first requires a method which can adequately model both excited states and ideally also the rest of the observed spectrum. To assess different methods in this regard, we computed steady-state absorption spectra and compared them against an experimental spectrum82,83 for chlorophyll a measured in diethyl ether (Fig. 3a)).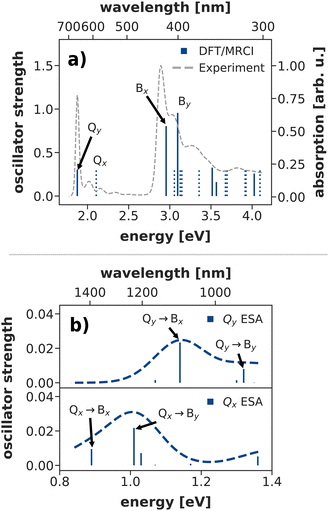 | ||
| Fig. 3 (a) Calculated steady state absorption spectrum of a chlorophyll model system at the DFT/MRCI level of theory, compared to an experimental spectrum of chlorophyll a in diethyl ether.82,83 The depicted absorption lines are red-shifted by 0.11 eV to the position of the experimental Qy band. (b) Excited state absorption spectra from the Q-bands at the DFT/MRCI level of theory (unshifted). | ||
We shall start our comparison with the DFT/MRCI method. Here, we only observe a small systematic blue-shift of the entire spectrum by 0.11 eV. The calculated absorption lines coincide well with the experimental band shape, even though the blue-shift is slightly stronger in the B bands. Both Qy and Qx exhibit a significant double excitation character of 9% and 12%, respectively. The contribution from double excitations only increases in the B band with 14% for Bx and 18% for By, highlighting the need for a multireference method. In contrast to earlier DFT/MRCI calculations,84 which report an additional doubly excited state in the visible region, we observe Bx as the third excited state. However, a dark state with 19% double-excitation character occurs at 392 nm, between Bx and By in our calculations. The difference may be due to our use of the revised R2018 DFT/MRCI Hamiltonian52 as well as a different optimized geometry.
To further assess the quality of DFT/MRCI for chlorophyll excitations, we computed transient spectra from both the Qx and Qy bands (Fig. 3b)). An experimental spectrum is available for a peridinin–chlorophyll-protein complex.85 After 0.5 ps, when all initial population in Qx should have decayed, it features an excited state absorption around 1290 nm which is consequently assigned to a series of transitions from Qy to energetically higher states.85 In comparison, the Qy absorption predicted by DFT/MRCI occurs at lower wavelengths around 1100 nm. The difference is in part due to the overestimation of the B–Q energy gap by DFT/MRCI, and partly due to protein–chlorophyll interactions that may shift the excited state absorption in the experiment.
Overall, the DFT/MRCI method is in excellent agreement with the experimental absorption spectrum and, most importantly, it provides a balanced description of the major absorption bands. From this we conclude that the position of the Qx band and thereby the Qx–Qy energy gap is correctly reproduced by DFT/MRCI. Therefore, we have used this method as a theoretical benchmark for all other methods in this work.
Apart from DFT/MRCI we also tested different density functionals and active space methods. The resulting vertical excitation energies are reported in Table 1. For the comparison of the different methods we mainly focused on the Qx–Qy energy gap, as this is the main parameter that determines the coupling between the two electronic states. In general, TDDFT considerably blue-shifts all vertical excitation energies, which has been observed before24 and is a result of neglecting double excitations. Consequently, the error increases with higher excited states, where the doubles' contributions become more important. All tested functionals apart from M062X are range-separated but the range-separation does not seem to be crucial for chlorophyll, as M062X stands out as one of the best functionals to describe the Qx–Qy gap at the TDDFT level. The consideration of London dispersion forces as in ωB97X-D and its more recent analogue ωB97X-D4 also does not lead to an improvement in accuracy and even further increases the Qx–Qy gap. Out of the tested functionals, M062X and CAM-B3LYP (Fig. 3) agree best with the DFT/MRCI results and experimental band assignments. However, all functionals significantly overestimate the Qx–Qy gap, which may be a problem for simulating the Q-band dynamics of chlorophyll at the TDDFT level.
| Qy | Qx | |Qx–Qy| | Bx | By | |
|---|---|---|---|---|---|
| a IPEA shift: 0.25, imaginary shift: 0.1. b IPEA shift: 0.1, imaginary shift: 0.1. c SA4-CASSCF/SA6-CASCI/XMS-CASPT2(6,6). d “modern” assignment in pyridine.16,19 e “modern” assignment in diethyl ether.16 f “traditional“ assignment in diethyl ether.15,17,19 | |||||
| CAM-B3LYP | 2.17 | 2.56 | 0.39 | 3.48 | 3.74 |
| wB97X-D | 2.09 | 2.71 | 0.62 | 3.58 | 3.92 |
| wB97X-D4 | 2.03 | 2.67 | 0.64 | 3.51 | 3.87 |
| BHandHLYP | 2.21 | 2.61 | 0.40 | 3.55 | 3.83 |
| LC-wHPBE | 2.06 | 2.79 | 0.73 | 3.61 | 3.97 |
| M062X | 2.21 | 2.59 | 0.38 | 3.48 | 3.72 |
| DFT/MRCI | 1.99 | 2.22 | 0.23 | 3.07 | 3.21 |
| SA4-XMS-CASPT2(6,6)a | 2.28 | 2.82 | 0.54 | — | — |
| SA6-XMS-CASPT2(6,6)b | 2.19 | 2.40 | 0.21 | 3.51 | 4.15 |
| SA6-XMS-CASPT2(6,6)a | 2.67 | 2.98 | 0.31 | 4.14 | 4.82 |
| SA6-XMS-CASPT2(8,8)a | 2.64 | 3.17 | 0.53 | 4.28 | 4.40 |
| SA6-XMS-CASPT2(10,10)a | 2.64 | 3.04 | 0.40 | 4.06 | 4.36 |
| SA6-MS-RASPT2(22,1,1;9,4,9)a | 2.34 | 2.74 | 0.40 | 3.39 | 4.00 |
| SA6-MS-RASPT2(22,2,2;9,4,9)a | 2.34 | 2.75 | 0.41 | 3.51 | 3.99 |
| SA4-/SA6-XMS-CASPT2(6,6)bc | 2.28 | 2.67 | 0.39 | 3.67 | 4.35 |
| Exp. (“modern”) | 1.85d/1.88e | 1.94d/2.00e | 0.09d/0.12e | — | — |
| Exp. (“traditional”) | 1.88f | 2.16f | 0.28f | 2.90 | 2.90 |
Even though DFT/MRCI provides excellent results in this regard, we did not use it to compute PESs modeling the Q-band dynamics, as it does not provide the gradients needed to construct the NAC between the two states. As an alternative, we investigated the CASSCF and (X)MS-CASPT2 methods. We compared the size and composition of the active space as well as the type and magnitude of applied level shifts with the goal to reproduce the Qx–Qy gap at a small enough computational cost to calculate PESs. In particular, we investigated four active spaces of different sizes. The smallest AS(6,6) contained the four Gouterman orbitals and a further pair of π/π*-orbitals, amounting to six electrons in six molecular orbitals (Fig. 2). The larger spaces AS(8,8) and AS(10,10) respectively contained one or two additional pairs of π/π*-orbitals (Fig. S2 and S3, ESI†) The largest space we tested featured 22 electrons in 22 orbitals in a restricted active space (RAS) scheme, with the four Gouterman orbitals in the RAS2 subspace, and nine π/π* orbitals each in the RAS1 and RAS3 subspaces (Fig. S4, ESI†). Excitations from RAS1 and into RAS3 were restricted to singles or doubles respectively, while all excitations were allowed within RAS2. All active space based approaches overestimate the experimentally determined excitation energies. While the Qy state is systematically stabilized when increasing the size of the active space, the Qx state and consequently the Qy–Qx energy gap do not follow this trend. Instead, adding orbitals to the active space favors one state over the other, depending on whether the additional orbitals are oriented more along the x or y molecular axis. The same behavior is observed for the Bx and By states. It is reminiscent of the La/Lb states in pyrene, which are also characterized by orthogonally polarized transitions and where a minimal active space proved beneficial for a balanced description of both states.86 This again highlights the fact that choosing an active space should not rely solely on size criteria.87,88 In light of these findings, we chose the small AS(6,6) for all further calculations to achieve a Qy–Qx energy gap that is close to the DFT/MRCI results at a reasonable computational cost. To keep this active space stable, also for geometries away from the FC region, we finally opted for a consecutive SA4-CASSCF/SA6-CASCI/XMS-CASPT2(6,6) scheme as outlined in the methods section.
Apart from the size and composition of the active space, the use of level shifts can strongly affect the results of CASPT2 calculations. Level shifts, particularly the IPEA73 and imaginary shift74 techniques, are a common way to remove intruder states. Indeed, using no level shift at all in the XMS-CASPT2(6,6) calculations introduces a spurious excitation from π3 to π1* as the first excited state. Therefore, we tested various combinations of IPEA and imaginary shifts to alleviate this issue (Tables S3–S6, ESI†). Applying any shift removes the intruder state, but the Qx–Qy gap is very sensitive to the exact combination of the two shift values. As the use of the IPEA shift is controversial,89–92 in particular for porphyrin-based systems,90,93 we tested applying only an imaginary shift. However, depending on the initial guess for the CASSCF reference, this leads to root-flipping at the FC point, such that Qy becomes the higher and Qx the lower energy excited state (Table S3, ESI†). Adding an IPEA shift helped resolve this issue and we therefore regard its use as justified in this case to preserve the correct state-ordering. In the end, combining an IPEA and imaginary shift of 0.1 emerged as a good choice to remove intruder states, ensure the correct state ordering across the PES and maintain a reasonable Qx–Qy gap.
3.2 Potential energy surfaces
Studying the quantum dynamics of the Q-band relaxation in chlorophyll requires not only an adequate method, but also a reduced-dimensional coordinate space, which can capture the essence of the relaxation process. To identify suitable coordinates, we calculated the overlap si of the normal modes qi (with i = 1,2,…,3N − 6) in mass-weighted Cartesian coordinates, and the normalized NAC vector f at the minimum geometry of the lower-energy state Qy: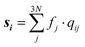 | (1) |
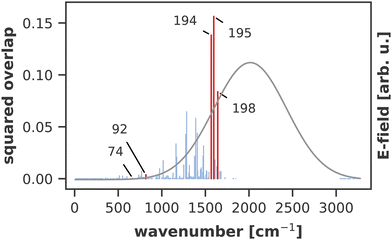
A similar technique has been used before in the context of semiclassical dynamics.10 As the normal modes span an orthogonal coordinate space, the squared overlap si2 corresponds to the percentage of non-adiabatic coupling contained in each mode 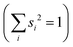 . A complete list of all normal modes, their respective squared overlap with the NAC vector and their harmonic vibrational frequency can be found in Table S10 in the ESI.†Fig. 4 illustrates the magnitude of si2 in each normal mode. We find that many modes are involved in the coupling but three modes stand out, together accounting for 38% of non-adiabatic coupling. The normal mode with the strongest overlap, mode 195 (s2 = 15.62%), describes an in-plane vibration of the entire porphyrin scaffold and appears at 1596 cm−1. A 1D potential along this mode (Fig. 5) reveals that the Qx and Qy state do not cross in an energetically accessible region of space. Instead, the two potentials run almost parallel to each other, facilitating non-adiabatic coupling across the coordinate space. This is further supported by the fact that the energetic order of the two states, computed at the DFT/MRCI level, is the same at the FC point as at their respective minimum geometries (Table S8, ESI†). So far, a true Qx/Qy conical intersection in chlorophyll-like systems has only been identified for free-base porphyrin.71 Its structure involves displacement of the pyrrolic protons – a coordinate which is not accessible in chlorophylls and other metal–porphyrins.
. A complete list of all normal modes, their respective squared overlap with the NAC vector and their harmonic vibrational frequency can be found in Table S10 in the ESI.†Fig. 4 illustrates the magnitude of si2 in each normal mode. We find that many modes are involved in the coupling but three modes stand out, together accounting for 38% of non-adiabatic coupling. The normal mode with the strongest overlap, mode 195 (s2 = 15.62%), describes an in-plane vibration of the entire porphyrin scaffold and appears at 1596 cm−1. A 1D potential along this mode (Fig. 5) reveals that the Qx and Qy state do not cross in an energetically accessible region of space. Instead, the two potentials run almost parallel to each other, facilitating non-adiabatic coupling across the coordinate space. This is further supported by the fact that the energetic order of the two states, computed at the DFT/MRCI level, is the same at the FC point as at their respective minimum geometries (Table S8, ESI†). So far, a true Qx/Qy conical intersection in chlorophyll-like systems has only been identified for free-base porphyrin.71 Its structure involves displacement of the pyrrolic protons – a coordinate which is not accessible in chlorophylls and other metal–porphyrins.
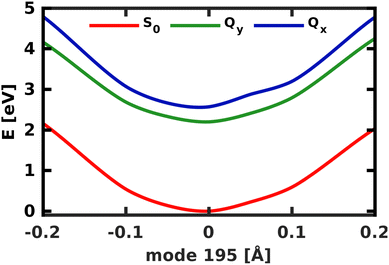 | ||
| Fig. 5 1D electronic potentials along normal mode 195. Qx and Qy do not cross but run almost parallel to each other. | ||
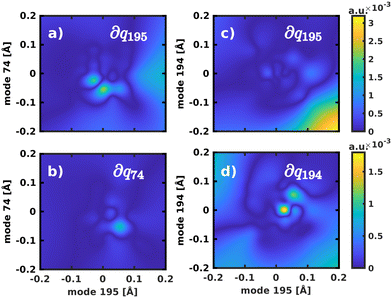
The normal mode with the second-highest overlap, mode 194 (s2 = 13.82%) appears at 1568 cm−1 and describes a similar collective in-plane vibration as mode 195. Given the strong coupling along these two modes, we used them to construct a 2D coordinate space for non-adiabatic quantum dynamics. To justify this choice of coordinates and to check whether our results also hold up in different coordinate spaces, we also tested three other 2D coordinate spaces between mode 195 and less strongly coupled modes from different spectral regions, namely modes 198 (s2 = 8.37%), 92 (s2 = 0.36%) and 74 (s2 = 0.005%).
For the 2D spaces spanned by modes 195/194 and 195/74 the NACs are visualized in Fig. 6 respectively to illustrate the extreme cases of strong and weak coupling. The weaker coupling in mode 74 is especially visible when comparing the projection of the NACs onto the respective second normal mode in Fig. 6b and d. However, in all tested coordinate spaces the non-adiabatic coupling is larger than zero across the PES, not localized at singular geometries as would be typical for a conical intersection.
3.3 Non-adiabatic quantum dynamics
To model the non-adiabatic dynamics within the Q-bands, we simulated the evolution of a nuclear wave packet in all four 2D coordinate spaces. For the following analysis, the excited state wave packet was prepared by placing the ground state vibrational eigenfunction of the S0 potential on the Qx surface. As we do not simulate coupling to environmental modes or decoherence effects, which take over at long time scales, we will restrict our analysis to the first 150 fs of the dynamics. The temporal evolution of the population in the two spaces 195/194 and 195/74 is illustrated in Fig. 7.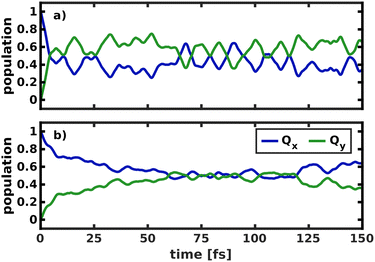 | ||
| Fig. 7 Population transfer between Qx and Qy in the 2D coordinate spaces spanned (a) by normal modes 195/194 and (b) by normal modes 195/74. | ||
The difference in the coupling strength is clearly reflected in the time it takes until half the population is transferred from Qx to Qy. In the strongly coupled 2D space 195/194, the transfer time is less than 10 fs, while in the weakly coupled space 195/74, it is 60 fs. The other weakly coupled 2D space we tested (195/92) fits into this trend with a transfer time of 25 fs. Only mode 198 appears to be more strongly coupled than the other modes, as indicated by higher NACs across the coordinate space (Fig. S9, ESI†), and yields a transfer time of <10 fs, only interrupted by strong back-coupling from Qx to Qy. The overall trends we observe in the population dynamics are consistent in all tested coordinate spaces and we therefore expect the results to be reliable. After half the population is transferred, back-coupling into Qx can be observed, as the wave packet cannot dissipate into other nuclear degrees of freedom in the quasi-harmonic 2D space on the Qy surface. For the same reason, the oscillations caused by this back-coupling do not decay in time. Given that the two potentials run mostly parallel to each other (Fig. 5), it is reasonable to assume a 50/50 population of both states at long time scales, under the assumption that energy is conserved within the Q-band system. If dissipation due to environmental coupling was included, the population would eventually decay to the vibrational ground state of Qy. These population dynamics are fully in line with the conclusions by Reimers et al., who argued that the Q-bands of chlorophyll should be regarded as an inseparably mixed system of two strongly vibronically coupled states.8
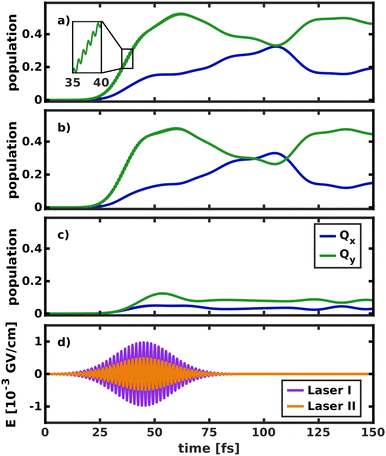
To simulate the wave packet dynamics after laser excitation, a pump pulse with a central frequency ω0 of 2.43 eV, a full width at half maximum (FWHM) of 30 fs and a maximum field strength of 4.9 × 10−3 GV cm−1 was used to excite the vibronic ground state eigenfunction in the space 195/194. As the zero-point vibrational energy in the 2D ground state potential is 0.19 eV, the energy of the laser pulse is tuned for excitation into the vibrational ground state of Qx at 2.62 eV. Its spectrum is broad enough to populate all the modes spanning the reduced-dimensional coordinate space (cf. grey line in Fig. 4). The temporal evolution of the population and the simulated laser pulse are depicted in Fig. 8.
Initially, the laser was allowed to interact with both electronic states (Fig. 8a), as would be the case in an experiment. The laser pulse starts to transfer population at 20 fs. Most of the population (52%) is initially transferred to Qy, as its transition dipole moment is significantly larger than that of Qx. In the first 40 fs of the excitation, fast oscillations at twice the frequency of the laser pulse can be observed in the Qy population curve, indicating that the intense laser field moves population back and forth between the ground and excited state. Immediately after the start of the laser pulse, population is also transferred into Qx. The population curves in Fig. 8b and c, where only one of the two states can interact with the laser, confirm that most of this population transfer into Qx does not stem from direct photo-excitation but from the vibronic coupling to Qy. Conversely, even if the transition dipole moment of Qy is explicitly turned off (Fig. 8c), such that the laser can only directly excite Qx, most of the population is instantly transferred into Qy. This is especially relevant to the assignment of the two experimentally observed absorption bands with x-polarization, because it means that even excitation into vibronic side bands of Qy immediately transfers population to Qx and vice versa. This again corroborates the position that Qx and Qy should not be regarded as independent electronic states but rather as a single, strongly coupled system of absorption bands, where x- and y-polarization is spread across the entire band.
The crossing point where half the population is transferred between the two states occurs at 105 fs, 25 fs after the laser field has decayed. This is around five times as long as in the delta pulse propagation in Fig. 7a and there are also fewer oscillations between the two states. There are two effects that can explain this behavior. First, the laser keeps transferring population into Qy while the vibronic coupling already populates Qx, thereby effectively smoothing the fast oscillations visible in Fig. 7a. Second, the laser energy and spectral width are tuned to match the vibrational ground state of Qx. In contrast, assuming a delta-pulse by placing an eigenfunction to the S0 potential on the Qx surface adds higher-energy components to the excited-state wave packet, which may induce faster oscillations in the population transfer.
To gain deeper insight into the processes after laser excitation, the nuclear wave packet in the Qy and Qx electronic potentials is visualized at different points in time in Fig. 9. In the Qy state (upper panel in Fig. 9), the wave packet exhibits one nodal plane during the laser excitation at 40 fs, barring interferences in regions of stronger vibronic coupling for the moment. It then proceeds to oscillate between two different orientations over time, corresponding to a superposition of the v = 1 and v = 2 eigenfunctions of the Qy potential. At 40 fs and 92 fs, the orientation of the wave packet resembles the v = 2 vibrational eigenfunction of the Qy PES, as the energy of this eigenstate matches the central frequency of the laser pulse and is nearly degenerate with the vibronic ground state of Qx (v = 0, Fig. 10). At 72 fs and 105 fs, the wave packet rotates to resemble the v = 1 eigenstate of Qy. The rotations decay over time and stop around 130 fs with a linear combination of the v = 1 and v = 2 eigenstates of Qy. On the Qx surface (bottom panel in Fig. 9), a wave packet corresponding to v = 0 appears immediately after laser excitation and increases in amplitude over time due to vibronic coupling to Qy. The region of stronger coupling around q195 = 0.025 Å/q194 = 0.025 Å (cf.Fig. 6d)) is clearly reflected in interferences in this part of the PES. Maintaining the coherence between the two electronic states, the Qx wave packet also rotates along with its counterpart on Qy. As back-coupling sets in around 50 fs, a second node appears on the Qy wave packet, corresponding to the current population in Qx.
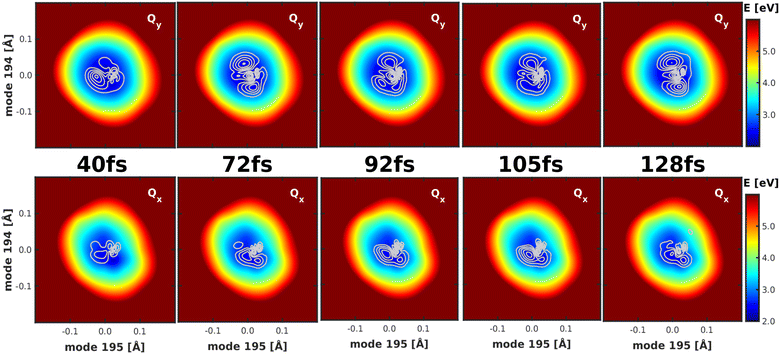 | ||
| Fig. 9 Visualization of the wave packet after laser excitation into the Qx state at four different points in time on the Qy (upper panel) and the Qx (lower panel) PES spanned by modes 195/194. | ||
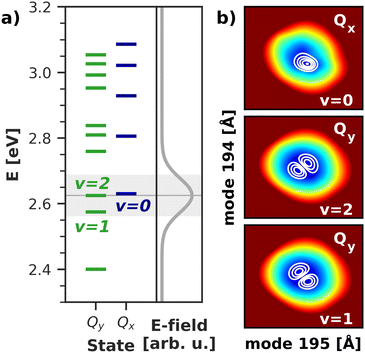 | ||
| Fig. 10 (a) Vibrational energy levels of the electronic Qy and Qx states in a 2D space spanned by normal modes 195/194. The highlighted area illustrates the spectral width (FWHM) of the simulated laser pulse. Energies are given relative to the energy of the electronic ground state. (b) Visualization of the relevant vibrational eigenfunctions in the Qx and Qy potentials. Axis ranges and color scheme are identical to those in Fig. 9. | ||
3.4 Coupling of nuclear and electronic dynamics
Applying the NEMol ansatz we are able to visualize not only the nuclear but also the coupled nuclear and electron dynamics. We performed this analysis for the propagation in the 2D space spanned by modes 195/194 by placing the ground state vibrational eigenfunction of the S0 potential onto the Qx surface. The corresponding population curve of the nuclear dynamics is shown in Fig. 7. Using the NEMol ansatz it would also be possible to study the excitation pulse induced dynamics, but as we are mainly interested in characterizing the coupling between Qx and Qy we have considered only the process after delta pulse excitation. The dipole moment induced by the electronic coherence is depicted in (Fig. 11a). It is calculated by taking the difference between the dipole moment obtained with and without electronic coherence and applying a Fourier transform of the obtained values. There is no dipole moment induced in the z-direction, whereas there are fast oscillations visible for both x- and y-component. They have a similar oscillation period with the ones of the y-component being slightly faster. As Qy is the lower electronic state, the wave packet can couple to more vibrational overtones, which also leads to faster oscillations in the coherence-induced dipole moment.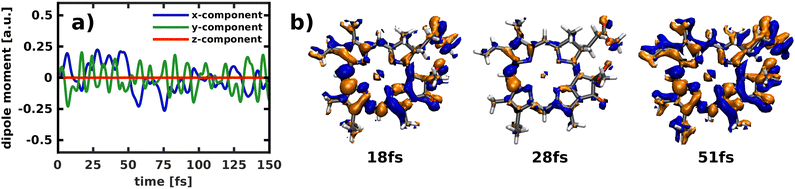 | ||
| Fig. 11 Temporal evolution of (a) the induced dipole moment obtained by building the difference between a calculation with and without electronic coherence and (b) the difference in density relative to the first frame of the simulation (isovalue: ±0.001). As the propagation starts in the Qx state, all non-vanishing difference density is indicative for population of the Qy state. Electron-gain is visualized in blue, electron-loss in orange. These results refer to the propagation after delta pulse excitation depicted in (Fig. 7a). | ||
Another way to visualize the oscillating dynamics between the two states is via the electronic difference densities shown in (Fig. 11b). They illustrate the difference between the electronic density at a point in time relative to the first frame of the simulation (t = 0). As the propagation starts in the Qx state, all non-vanishing difference density is indicative for population of the Qy state. The difference density at 51 fs shows the largest difference as the Qy states exhibits a maximum in population at this point in time. At 18 fs the Qy population in (Fig. 7a) exhibits a local maximum, which is also reflected in the difference density. In contrast, the frame at 28 fs shows smaller but still non-negligible differences to the Qx density, which corresponds well to the nearly equally population of both states at this point in time. The strongest feature in the difference density is the change at the bridging carbon between rings I and II, which is still present when Qx and Qy are equally populated. The more population is present in Qy the more changes also occur throughout the rest of the molecule, as is clearly visible in the snapshot at 51 fs. Using the difference density obtained with the NEMol ansatz therefore allows to visualize the electronic wave packet created due to the non-adiabatic coupling between the first two excited states, taking into account the quantum nature of both nuclear and electronic motion. Its long-lived coherence reaffirms the existence of a strongly coupled Qx/Qy system, rather than two independent electronic states.
4 Conclusions
We have simulated the internal conversion dynamics in the Q-bands of chlorophyll, fully taking into account the quantum nature of electronic and nuclear motion. This requires a computational method that reproduces the energy gap between the two excited states. Here, we are faced with the challenge of balancing computational cost with accuracy. Many affordable methods like TD-DFT overestimate the Qy–Qx gap, which may adversely affect the simulated coupling between the two states. Our tests once again24 highlight the need for high-level, ideally multireference methods like DFT/MRCI to capture the effect of higher-order excitations on the spectral features of chlorophylls.A conical intersection between Qx and Qy could not be found as the PESs studied along the selected normal mode coordinates run parallel to each other and the energetic state-ordering is retained upon relaxation in the excited states. Our results instead show the presence of strong vibronic coupling between Qy and Qx across the PES in multiple 2D coordinate spaces, due to strongly delocalized non-adiabatic coupling. A simple description of the Q-band system in terms of the Born-Oppenheimer approximation can therefore not be sufficient. In agreement with previous conclusions,8 but at a higher level of theory and from a different perspective, we conclude that the Q-band of chlorophyll is better thought of as a single system of strongly vibronically coupled states, where x-polarization can be spread across the vibronic side bands of Qy and vice versa. Using the NEMol ansatz, we could visualize how the electronic density, coupled to the nuclear motion, oscillates back and forth between x- and y-polarization. This strong mixing of the electronic states in chlorophyll a may have important implications for the charge transport in the reaction center of photosynthetic light-harvesting complexes. After excitation into the higher-energy absorption bands, the population will eventually decay into the Q-bands and from there facilitate electron transfer to neighboring pigments. This process may become more efficient if both x- and y-polarizations can contribute to it.
Author contributions
Sebastian Reiter: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review & editing; Lena Bäuml: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review & editing; Jürgen Hauer – funding acquisition, supervision, writing – review & editing; Regina de Vivie-Riedle – conceptualization, funding acquisition, project administration, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Eva Sextl for support in the preliminary test calculations. We gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the cluster of excellence e-conversion under Germany's Excellence Strategy – EXC 2089/1 – 390776260.Notes and references
- R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Wiley, 3rd edn, 2021 Search PubMed.
- A. N. Melkozernov, J. Barber and R. E. Blankenship, Biochemistry, 2006, 45, 331–345 CrossRef CAS PubMed.
- J. R. Reimers, M. Biczysko, D. Bruce, D. F. Coker, T. J. Frankcombe, H. Hashimoto, J. Hauer, R. Jankowiak, T. Kramer, J. Linnanto, F. Mamedov, F. Müh, M. Rätsep, T. Renger, S. Styring, J. Wan, Z. Wang, Z.-Y. Wang-Otomo, Y.-X. Weng, C. Yang, J.-P. Zhang, A. Freiberg and E. Krausz, Biochim. Biophys. Acta Bioenerg., 2016, 1857, 1627–1640 CrossRef CAS PubMed.
- M. Taniguchi and J. S. Lindsey, Photochem. Photobiol., 2021, 97, 136–165 CrossRef CAS PubMed.
- D. Sundholm, Chem. Phys. Lett., 2000, 317, 545–552 CrossRef CAS.
- M. Gouterman, J. Mol. Spectrosc., 1961, 6, 138–163 CrossRef CAS.
- M. Gouterman, G. H. Wagnière and L. C. Snyder, J. Mol. Spectrosc., 1963, 11, 108–127 CrossRef CAS.
- J. R. Reimers, Z.-L. Cai, R. Kobayashi, M. Rätsep, A. Freiberg and E. Krausz, Sci. Rep., 2013, 3, 1–8 Search PubMed.
- W. P. Bricker, P. M. Shenai, A. Ghosh, Z. Liu, M. G. M. Enriquez, P. H. Lambrev, H.-S. Tan, C. S. Lo, S. Tretiak, S. Fernandez-Alberti and Y. Zhao, Sci. Rep., 2015, 5, 13625 CrossRef PubMed.
- P. M. Shenai, S. Fernandez-Alberti, W. P. Bricker, S. Tretiak and Y. Zhao, J. Phys. Chem. B, 2016, 120, 49–58 CrossRef CAS PubMed.
- M. Fortino, E. Collini, J. Bloino and A. Pedone, J. Chem. Phys., 2021, 154, 094110 CrossRef CAS PubMed.
- M. Rätsep, J. M. Linnanto and A. Freiberg, J. Phys. Chem. B, 2019, 123, 7149–7156 CrossRef PubMed.
- F. Bär, H. Lang, E. Schnabel and H. Kuhn, Z. Elektrochem., Ber. Bunsenges. phys. Chem., 1961, 65, 346–354 Search PubMed.
- M. Gouterman and L. Stryer, J. Chem. Phys., 1962, 37, 2260–2266 CrossRef CAS.
- C. Weiss, J. Mol. Spectrosc., 1972, 44, 37–80 CrossRef CAS.
- M. Umetsu, Z.-Y. Wang, M. Kobayashi and T. Nozawa, Biochim. Biophys. Acta, Bioenerg., 1999, 1410, 19–31 CrossRef CAS.
- C. Houssier and K. Sauer, J. Am. Chem. Soc., 1970, 92, 779–791 CrossRef CAS.
- R. A. Avarmaa and K. K. Rebane, Spectrochim. Acta, Part A, 1985, 41, 1365–1380 CrossRef.
- L. L. Shipman, T. M. Cotton, J. R. Norris and J. J. Katz, J. Am. Chem. Soc., 1976, 98, 8222–8230 CrossRef CAS PubMed.
- Y. Shi, J.-Y. Liu and K.-L. Han, Chem. Phys. Lett., 2005, 410, 260–263 CrossRef CAS.
- E. Meneghin, C. Leonardo, A. Volpato, L. Bolzonello and E. Collini, Sci. Rep., 2017, 7, 11389 CrossRef PubMed.
- A. Anda, T. Hansen and L. De Vico, J. Chem. Theory Comput., 2016, 12, 1305–1313 CrossRef CAS PubMed.
- A. Anda, T. Hansen and L. De Vico, J. Phys. Chem. A, 2019, 123, 5283–5292 CrossRef CAS PubMed.
- A. Sirohiwal, R. Berraud-Pache, F. Neese, R. Izsák and D. A. Pantazis, J. Phys. Chem. B, 2020, 124, 8761–8771 CrossRef CAS PubMed.
- F. Zheng, S. Fernandez-Alberti, S. Tretiak and Y. Zhao, J. Phys. Chem. B, 2017, 121, 5331–5339 CrossRef CAS PubMed.
- D. Geppert, P. von den Hoff and R. de Vivie-Riedle, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 074006 CrossRef.
- P. von den Hoff, I. Znakovskaya, M. F. Kling and R. de Vivie-Riedle, Chem. Phys., 2009, 366, 139–147 CrossRef CAS.
- I. Znakovskaya, P. von den Hoff, S. Zherebtsov, A. Wirth, O. Herrwerth, M. J. J. Vrakking, R. de Vivie-Riedle and M. F. Kling, Phys. Rev. Lett., 2009, 103, 103002 CrossRef CAS PubMed.
- T. Schnappinger and R. de Vivie-Riedle, J. Chem. Phys., 2021, 154, 134306 CrossRef CAS PubMed.
- L. Bäuml, T. Schnappinger, M. F. Kling and R. de Vivie-Riedle, Front. Phys., 2021, 9, 1–12 Search PubMed.
- D. Sundholm, Chem. Phys. Lett., 1999, 302, 480–484 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Stone, An Efficient Library for Parallel Ray Tracing and Animation, Master’s thesis (M.S.), University of Missouri-Rolla, 1998, https://scholarsmine.mst.edu/masters_theses/1747 Search PubMed.
- G. Kovačević and V. Veryazov, J. Cheminf., 2015, 7, 16 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16, Revision A.03, Gaussian Inc., Wallingford CT, 2009, https://www.gaussian.com Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- A. Najibi and L. Goerigk, J. Comput. Chem., 2020, 41, 2562–2572 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- T. M. Henderson, A. F. Izmaylov, G. Scalmani and G. E. Scuseria, J. Chem. Phys., 2009, 131, 044108 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78 Search PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2022, e1606 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- M. Kleinschmidt, C. M. Marian, M. Waletzke and S. Grimme, J. Chem. Phys., 2009, 130, 044708 CrossRef PubMed.
- C. M. Marian, A. Heil and M. Kleinschmidt, WIREs Comput. Mol. Sci., 2018, 9, e1394 Search PubMed.
- A. Heil, M. Kleinschmidt and C. M. Marian, J. Chem. Phys., 2018, 149, 164106 CrossRef PubMed.
- F. Weigend, M. Kattannek and R. Ahlrichs, J. Chem. Phys., 2009, 130, 164106 CrossRef PubMed.
- S. Kossmann and F. Neese, Chem. Phys. Lett., 2009, 481, 240–243 CrossRef CAS.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed.
- B. O. Roos, in Advances in Chemical Physics, ed. K. P. Lawley, John Wiley & Sons, Ltd, 1987, pp. 399–445 Search PubMed.
- B. O. Roos, P. Linse, P. E. M. Siegbahn and M. R. A. Blomberg, Chem. Phys., 1982, 66, 197–207 CrossRef CAS.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- K. Andersson, P.-A. k Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- J. Finley, P.-A. k Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- T. Shiozaki, W. Györffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106 CrossRef PubMed.
- I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. A. P. Malhado, P. A. K. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. A. K. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117 CrossRef CAS PubMed.
- P.-O. Widmark, P.-A. k Malmqvist and B. O. Roos, Theoret. Chim. Acta, 1990, 77, 291–306 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-A. K. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- B. O. Roos, V. Veryazov and P.-O. Widmark, Theor. Chem. Acc., 2004, 111, 345–351 Search PubMed.
- J. Chmeliov, W. P. Bricker, C. Lo, E. Jouin, L. Valkunas, A. V. Ruban and C. D. P. Duffy, Phys. Chem. Chem. Phys., 2015, 17, 15857–15867 RSC.
- K. Falahati, C. Hamerla, M. Huix-Rotllant and I. Burghardt, Phys. Chem. Chem. Phys., 2018, 20, 12483–12492 RSC.
- V. V. Poddubnyy, M. I. Kozlov and I. O. Glebov, Chem. Phys. Lett., 2021, 778, 138792 CrossRef CAS.
- G. Ghigo, B. O. Roos and P.-A. K. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- N. Forsberg and P.-A. K. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204 CrossRef CAS.
- H. Tal-Ezer and R. Kosloff, J. Chem. Phys., 1984, 81, 3967–3971 CrossRef CAS.
- R. Franke, Comput. Math. with Appl., 1982, 8, 273–281 CrossRef.
- E. B. Wilson, J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover Publications, 1980 Search PubMed.
- L. J. Schaad and J. Hu, J. Mol. Struct. THEOCHEM, 1989, 185, 203–215 CrossRef.
- J. Stare and G. G. Balint-Kurti, J. Phys. Chem. A, 2003, 107, 7204–7214 CrossRef CAS.
- M. Kowalewski, J. Mikosch, R. Wester and R. de Vivie-Riedle, J. Phys. Chem. A, 2014, 118, 4661–4669 CrossRef CAS PubMed.
- R. Kosloff and H. Tal-Ezer, Chem. Phys. Lett., 1986, 127, 223–230 CrossRef CAS.
- M. Taniguchi, H. Du and J. S. Lindsey, Photochem. Photobiol., 2018, 94, 277–289 CrossRef CAS PubMed.
- M. Taniguchi and J. S. Lindsey, Photochem. Photobiol., 2018, 94, 290–327 CrossRef CAS PubMed.
- A. B. J. Parusel and S. Grimme, J. Phys. Chem. B, 2000, 104, 5395–5398 CrossRef CAS.
- D. Zigmantas, R. G. Hiller, V. Sundström and T. Polívka, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16760–16765 CrossRef CAS PubMed.
- M. K. Roos, S. Reiter and R. de Vivie-Riedle, Chem. Phys., 2018, 515, 586–595 CrossRef CAS.
- J. D. Coe and T. J. Martínez, J. Phys. Chem. A, 2006, 110, 618–630 CrossRef CAS PubMed.
- P. Chakraborty, Y. Liu, T. Weinacht and S. Matsika, J. Chem. Phys., 2020, 152, 174302 CrossRef CAS PubMed.
- C. Camacho, R. Cimiraglia and H. A. Witek, Phys. Chem. Chem. Phys., 2010, 12, 5058–5060 RSC.
- N. Ben Amor, A. Soupart and M.-C. Heitz, J. Mol. Model., 2017, 23, 53 CrossRef PubMed.
- J. P. Zobel, J. J. Nogueira and L. González, Chem. Sci., 2017, 8, 1482–1499 RSC.
- G. Giuliani, F. Melaccio, S. Gozem, A. Cappelli and M. Olivucci, J. Chem. Theory Comput., 2021, 17, 605–613 CrossRef CAS PubMed.
- A. Kerridge, Phys. Chem. Chem. Phys., 2013, 15, 2197–2209 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Details on the chosen methods with sample OpenMolcas input, optimized geometries and coordinate vectors, potential energy surfaces, non-adiabatic coupling matrix elements, transition dipole moments and additional quantum dynamics simulations. See DOI: https://doi.org/10.1039/d2cp02914f |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2022 |