Spin engineering of triangulenes and application for nano nonlinear optical materials design†
Cui-Cui
Yang
 a,
Xue-Lian
Zheng
a,
Jiu
Chen
a,
Wei Quan
Tian
a,
Xue-Lian
Zheng
a,
Jiu
Chen
a,
Wei Quan
Tian
 *a,
Wei-Qi
Li
*bcd and
Ling
Yang
*e
*a,
Wei-Qi
Li
*bcd and
Ling
Yang
*e
aChongqing Key Laboratory of Theoretical and Computational Chemistry, College of Chemistry and Chemical Engineering, Chongqing University, Huxi Campus, Chongqing 401331, China. E-mail: tianwq@cqu.edu.cn
bDepartment of Physics, Harbin Institute of Technology, Harbin 150001, China
cTechnology Innovation Center of Materials and Devices at Extreme Environment, School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China. E-mail: tccliweiqi@hit.edu.cn
dCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, P. R. China
eWenzhou Institute, University of Chinese Academy of Sciences, 1 Jinlian Street, Wenzhou 325001, China. E-mail: yangling@hit.edu.cn
First published on 19th July 2022
Abstract
The recently synthesized triangulenes with non-bonding edge states could have broad potential applications in magnetics, spintronics and electro-optics if they have appropriate electronic structure modulation. In the present work, strategies based on molecular orbital theory through heteroatom doping are proposed to redistribute, reduce or eliminate the spin of triangulenes for novel functional materials design, and the role of B, N, NBN, and BNB in such intended electronic structure manipulation is scrutinized. π-Extended triangulenes with tunable electronic properties could be potential nonlinear optical (NLO) materials with appropriate inhibition of their polyradical nature. The elimination of spin is achieved by B, N, NBN, and BNB doping with the intended geometric arrangement for enhanced polarity. Intended doping of BNB results in an optimal structure with large static first hyperpolarizability (〈β0〉) as well as strong Hyper–Rayleigh scattering (HRS) βHRS(−2ω; ω, ω) (ω = 1064.0 nm), TG7-BNB-ba with a large 〈β0〉 (18.85 × 10−30 esu per heavy atom) and βHRS (1.15 × 10−28 esu per heavy atom) much larger than that of a synthesized triangular molecule (1.12 × 10−30 esu of 〈β0〉 per heavy atom and 5.04 × 10−30 esu of βHRS per heavy atom). The strong second order NLO responses in the near-infrared and visible regions, particularly the strong sum frequency generation, make these B or (and) N doped triangulenes promising candidates for the fabrication of novel carbon-based optoelectronic devices and micro-NLO devices.
Introduction
The demands for nonlinear optical (NLO) materials with high stability and strong NLO responses have become significantly imperative in association with the developments of functional materials. Graphene fragments consisting of sp2 carbons, e.g., graphene nanoflakes (GNFs), have been attracting tremendous interest since the fabrication of graphene.1 The molecular sizes and shapes determine the electronic and magnetic properties of GNFs to a great extent.2,3 Among the GNFs with various possible shapes and sizes, zigzag-edged triangle-shaped GNFs with n fused hexagons at each side (denoted as [n]triangulenes where n is the number of hexagons at the edge) were predicted to show a radical nature (i.e., with unpaired or non-bonding π-electrons),4,5 which might allow their potential applications in energy storage devices,6 organic spintronics,7,8 bio-imaging,9 and nonlinear optics.10,11 The successful syntheses of [n]triangulenes (n = 2 to 5)4,12–14 make it possible to investigate its unique structures and peculiar characters at single molecule level. In [n]triangulenes (defined as TGn), the smallest triangulene, namely phenalenyl12 (i.e., TG2 in Fig. 1), has 13 carbon atoms and 13 π-electrons. The non-Kekulé structure in [n]triangulenes possesses one or more unpaired π-electrons with net spins according to the Ovchinnikov's rule.15 Approximately (n − 1) unpaired electrons localize along the zigzag edges rather than at the core of [n]triangulenes.5 In other words, the ground state of these [n]triangulenes shows an increasing open-shell nature with the increase of n (Table S1, ESI† and Fig. 1). However, the high chemical reactivity16 of the outer rims or the closeness of the flat band to the Fermi level2 causes the synthesis and isolation of extended triangulenes to be a big challenge,17 and finding an optimal means to functionalize triangulenes is a key factor for further applications.Efforts have been devoted to modulate the electronic state of carbon-based molecules, e.g., through steric hindrance,18,19 fusion with other aromatic skeletons,20 and introduction of heteroatoms.21 Incorporation of heteroatoms [e.g., boron (B), nitrogen (N), oxygen (O), or sulfur (S)] into the π-conjugated carbon skeleton is a promising strategy for such purposes.22 By virtue of the isoelectronic feature of B–N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, the introduction of BN into carbon-based nanomaterials (fullerenes, nanotubes, and graphenes)23–25 can break the symmetry of systems and polarize charge redistribution (enhance polarity), thereby generating even-order NLO responses. Doping of B or N atoms can also attenuate the net spin of zigzag-edged triangulenes with an edge size n = 6.26 On the other hand, the investigation of the second order NLO properties of octupolar molecules with a threefold symmetry axis has been extensively explored.27,28 Appropriate doping of B or (and) N in [n]triangulenes provides the possibility to “tune” the electronic structure and related properties for certain applications, e.g., in electro-optics or nonlinear optics.
C, the introduction of BN into carbon-based nanomaterials (fullerenes, nanotubes, and graphenes)23–25 can break the symmetry of systems and polarize charge redistribution (enhance polarity), thereby generating even-order NLO responses. Doping of B or N atoms can also attenuate the net spin of zigzag-edged triangulenes with an edge size n = 6.26 On the other hand, the investigation of the second order NLO properties of octupolar molecules with a threefold symmetry axis has been extensively explored.27,28 Appropriate doping of B or (and) N in [n]triangulenes provides the possibility to “tune” the electronic structure and related properties for certain applications, e.g., in electro-optics or nonlinear optics.
The present work employs molecular orbital theory (the electronic state – configuration state function – of a system is the linear combination of configurations) to analyse the spin distribution in triangulenes in combination with the Clar's rule, and then functionalize [n]triangulenes (n = 2 to 7) with B(N), i.e. spin engineering, for desired applications. In the present work, applications in the second order nonlinear optics are considered.
Model and computational details
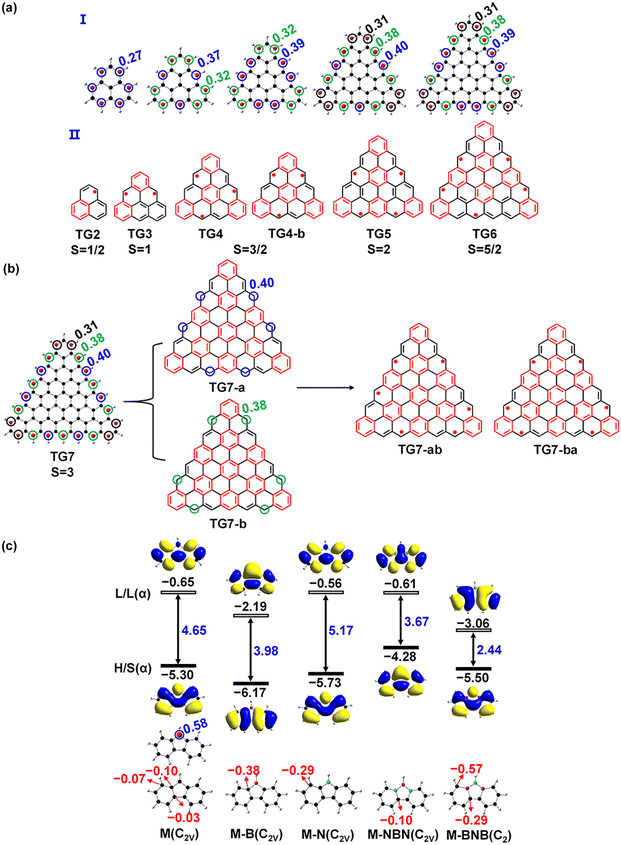
According to natural atomic spin distribution analyses on the optimized [n]triangulenes structures from density functional theory (DFT)29,30 based calculations with general gradient approximation of fundamental constant based exchange-correlation functionals PBE31 based hybrid method PBE032 and 6-31G(d,p) basis set,33,34 all the carbon atoms of CH groups at the three edges of those [n]triangulenes carry net spins (Fig. 1(a)-I) and those spins can be formally represented by non-Kekulé structures (Fig. 1(a)-II) according to the Clar's sextet theory.35 Taking TG7 as an example (Fig. 1(b) and the others are plotted in Fig. S1, ESI†), TG7 can be taken as a linear combination (or superposition) of two non-Kekulé structures (TG7-a and TG7-b). This is similar in the other triangulenes. The C atoms with unpaired electrons in those [n]triangulenes can be replaced with B or N to form a closed-shell electronic state. The non-centrosymmetric nature of second order nonlinear optical materials inspires a doping pattern with a combination of the doping sites in TG7-a and TG7-b resulting in a non-centrosymmetric hetero-triangulenes TG7-ab and TG7-ba (Fig. 2). Besides atoms B and N, NBN and BNB with the merits of polar BN being isoelectronic to CC could also be used to attenuate the edge spin while polarizing the charge distribution of [n]triangulenes. 9H-Fluorene-9-ylradical has an unpaired π-electron at the central C9 (Fig. 1(c)), and the doping of B and N, NBN and BNB at the C9 eliminates the net spin and leads to charge redistribution and the change of the energy gap Egap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). Thus, B and N, NBN and BNB are used to attenuate the net spin of those triangulenes and tune their NLO properties. All the designed hetero-TG7 and other hetero-triangulenes are shown in Fig. 2 and Fig. S1 (ESI†).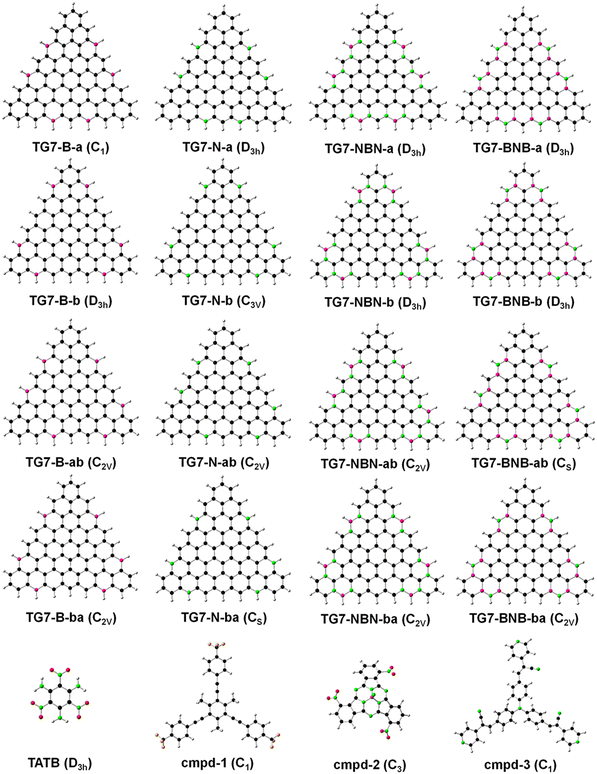 | ||
| Fig. 2 The structures of the TG7 series of molecules. The white, deep pink, black, green, red and orange denote the hydrogen, boron, carbon, nitrogen, oxygen and fluorine atoms, respectively. TATB, cmpd-1, cmpd-2 and cmpd-3 are from ref. 27, 56–58, respectively (cmpd refers to compound). | ||
In the present work, all the DFT calculations were carried out by using Gaussian 09.36 On the basis of optimized geometries, the electronic spectra of all systems were predicted with time-dependent CAM-B3LYP37 under the Franck-Condon principle, and the orientation averaged first hyperpolarizability (〈β〉) was calculated by using the LinSOSProNLO program38 based on the sum-over-states (SOS) model39,40 with improved computational efficiency.41 The predictions for the charge transfer based excitation by using CAM-B3LYP are in excellent agreement with the highly accurate multireference perturbation calculation with CASPT237 and charge transfer based excitations are common and also important to the NLO properties of the triangulenes studied in the present work. For π-conjugated systems with charge transfer based electron excitations, “it is mandatory to use range-separated hybrids (e.g., CAM-B3LYP) to reach physically meaningful estimates”42 according to the systematic studies on the performance of TDDFT based methods in electronic spectra predictions.42,43 Other studies found that different DFT methods have different performances on the prediction of electronic spectra of different systems.44,45
The calculations of the electronic spectra of the TGn (n = 2–6) series of molecules include all possible π-electrons involved in valence excitations, and the TG7 series are predicted with 576 excited states. The convergence of the static first hyperpolarizability (〈β0〉) with the number of excited states of TG7-BNB-ba indicates that 150 excited states are adequate to predict converged 〈β0〉 (Fig. S2, ESI†). The SOS model shows consistence in NLO properties (only the electronic contributions) predictions with the other methods or models, e.g., finite field,46,47 random phase approximation,48,49 and couple perturbed models.50
The orientation averaged first hyperpolarizability is obtained through the rewritten SOS formula40 as eqn (1)51
| 〈β〉 = (βx × rx + βy × ry + βz × rz)/(rx2 + ry2 + rz2)1/2 and βi = βiii + [βijj + βjij + βjji + βikk + βkik + βkki]/3 (i, j, k∈[x, y, z]) | (1) |
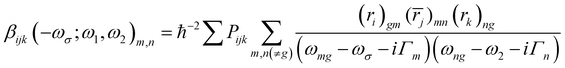 | (2) |
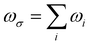 . (ri)gm = 〈g|ri|m〉 is the transition moment between the ground state g to the excited state m along the i direction and (
. (ri)gm = 〈g|ri|m〉 is the transition moment between the ground state g to the excited state m along the i direction and (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) j)mn = 〈m|rj|n〉 − 〈g|rj|g〉δmn is the dipole moment fluctuation. Γm (Γm = 0.01 × εm/ε2) is the damping factor of excited state m. ∑Pijk stands for a summation over all the terms obtained by permuting pairs of transition moment (or the dipole moment fluctuation) and the external field {e.g., [(ri)gm, −ωσ], [(
j)mn = 〈m|rj|n〉 − 〈g|rj|g〉δmn is the dipole moment fluctuation. Γm (Γm = 0.01 × εm/ε2) is the damping factor of excited state m. ∑Pijk stands for a summation over all the terms obtained by permuting pairs of transition moment (or the dipole moment fluctuation) and the external field {e.g., [(ri)gm, −ωσ], [(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) j)mn, ω1], and [(rk)ng, ω2]}. The transition moments and dipole moment of excited states were calculated with the Multiwfn program.52
j)mn, ω1], and [(rk)ng, ω2]}. The transition moments and dipole moment of excited states were calculated with the Multiwfn program.52
To quantify the dipolar (|βJ=1|) and octupolar contributions (|βJ=3|) to the NLO response, the relevant expressions53 [eqn (3) and (4)] can be written as follows:
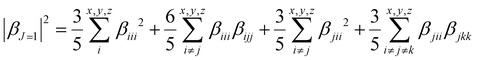 | (3) |
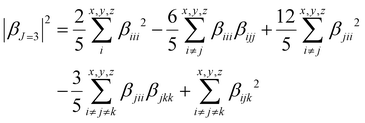 | (4) |
The Hyper–Rayleigh scattering (HRS)53,54 technique is a powerful means to explore the second harmonic generation (SHG) and the βHRS (−2ω; ω, ω) can be expressed as:53
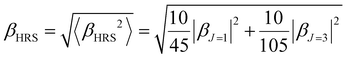 | (5) |
The molecular anisotropy ratio ρ [ρ = |βJ=3|/|βJ=1| runs from 0 (pure dipole) to ∞ (pure octupole)] and is used to evaluate the octupolar (ΦJ=3 = ρ/ρ + 1) and dipolar (ΦJ=1 = 1 − ΦJ=3) contributions to the first hyperpolarizability.
Furthermore, the polarization state of the incident light is determined by two angles (Ψ, δ). When a general elliptically polarized incident light propagates along the X direction, and the intensity of the harmonic light scatters at δ = π/2 along the Y direction, the vertically (V) polarized light along the Z axis can be given by the Bersohn's expression:55
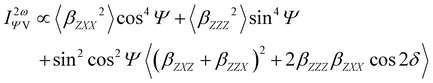 | (6) |
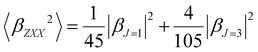 | (7) |
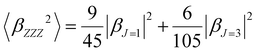 | (8) |
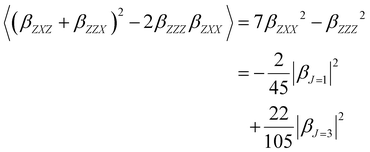 | (9) |
Note that linearly polarized incident lights are described by Ψ = 0 (horizontal, H) or Ψ = π/2 (V). The HRS intensity 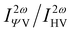 can exhibit different shapes through varying the polarization angle Ψ of the incident light.
can exhibit different shapes through varying the polarization angle Ψ of the incident light.
Results and discussion
Electronic properties tuned by spin engineering
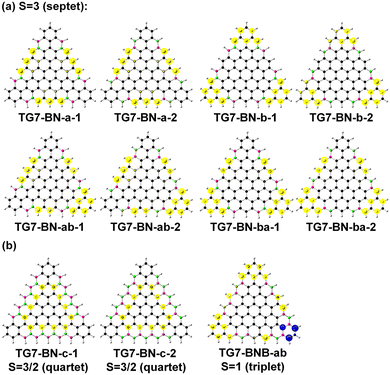
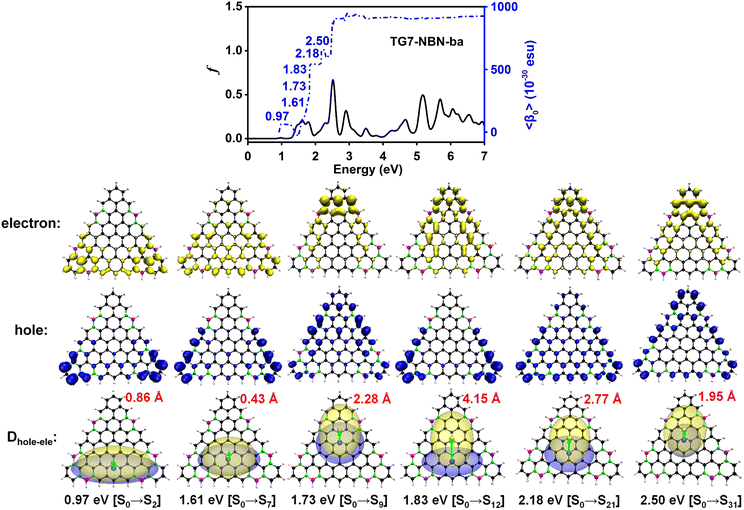
TG7 has a septet ground state (Table S1, ESI†), and the spin density mainly localizes at the zigzag edges (Fig. 1(b)). According to the molecular orbitals of BN doped heptene, the π orbital with a major contribution from the BN pair lies below the other π orbitals (Fig. S3, ESI†), thus the BN pair could be used to modify the π orbitals of graphene-based nano-systems. The intended introduction of BN pairs in the TG7 series redistributes the spin density with BN pairs (Fig. 3(a)). Spin reduction (e.g., from septet to quartet) can be modulated by a combination of B (or N) doping with BN pairs at the zigzag edges (i.e., TG7-BN-c1 and TG7-BN-c-2 in Fig. 3(b) and Table S1, ESI†) while making the spin density localized in the inner carbon atoms. Subtle adjustment of spin distribution can also be achieved by the different doping patterns of NB at the edges of triangulenes (TG7-BN-c1 and TG7-BN-c-2 in Fig. S4, ESI†). A specific arrangement of BNB doping can even create a localized region with a spin of different orientation (the blue region in TG7-BNB-ab in Fig. 3(b)). Such spin engineering of triangulenes renders those nanomaterials with potential applications in other fields, e.g., spintronics7 and magnetics.59 For applications of triangluenes in the fields requiring a closed-shell electronic state, the spin of triangulenes needs to be eliminated.As depicted in Fig. 2, different doping patterns in TG7 lead to different symmetries. Vibrational frequency calculation confirms that all [7]-triangulenes are minima on the potential energy surface (Table 1 and Table S1, ESI†). For the B, N or NBN series of TG7, the large relative electronic energy differences (ΔET–CS) [between triplet (T) and closed-shell singlet (CS), CS is taken as the reference] and the zero spin contamination of singlet indicate that closed-shell singlet is the ground state (Table 1). Remarkably, the polyradical nature in pristine triangulenes (n = 7) can be eliminated in those four series of triangulenes with appropriate doping patterns (i.e., TG7-ba series of molecules).
| Compound | ΔEOS–CS | ΔET–CS | 〈S2〉 | LVF | D g | E L | E H | E gap | 〈β0〉 | 〈β0〉/N |
|---|---|---|---|---|---|---|---|---|---|---|
| —: the 〈β0〉s of these molecules were not calculated because of their open-shell electronic ground states. | ||||||||||
| TG7 | −53.55 | −55.27 | 10.34 | 22.82 | 0.00 | −3.53 | −3.96 | 0.43 | — | — |
| TG7-B-a | 0.00 | 35.71 | 0.00 | 3.79 | 0.17 | −3.06 | −5.52 | 2.46 | −35.39 | −0.45 |
| TG7-B-b | 0.00 | 34.18 | 0.00 | 22.40 | 0.00 | −3.08 | −5.72 | 2.64 | 33.84 | 0.43 |
| TG7-B-ab | 0.00 | 29.44 | 0.00 | 9.62 | 5.21 | −3.10 | −5.42 | 2.32 | 358.73 | 4.60 |
| TG7-B-ba | 0.00 | 27.08 | 0.00 | 16.61 | 5.45 | −3.25 | −5.47 | 2.22 | 472.15 | 6.05 |
| TG7-N-a | 0.00 | 35.71 | 0.00 | 22.95 | 0.00 | −1.69 | −4.31 | 2.62 | −123.79 | −1.59 |
| TG7-N-b | 0.00 | 23.76 | 0.00 | 23.76 | 0.00 | −1.51 | −4.24 | 2.73 | −0.36 | −0.0046 |
| TG7-N-ab | 0.00 | 31.79 | 0.00 | 23.63 | 6.01 | −1.79 | −4.23 | 2.44 | 424.13 | 5.44 |
| TG7-N-ba | 0.00 | 29.72 | 0.00 | 24.13 | 6.21 | −1.74 | −4.04 | 2.30 | 484.84 | 6.22 |
| TG7-NBN-a | 0.00 | 5.29 | 0.00 | 24.31 | 0.00 | −2.10 | −3.69 | 1.59 | −439.17 | −5.63 |
| TG7-NBN-b | 0.00 | −0.58 | 0.00 | 25.16 | 0.00 | −2.09 | −3.65 | 1.56 | — | — |
| TG7-NBN-ab | −1.74 | 1.34 | 0.12 | 25.36 | 1.11 | −2.10 | −3.71 | 1.61 | — | — |
| TG7-NBN-ba | 0.00 | 19.70 | 0.00 | 25.31 | 1.31 | −2.14 | −3.67 | 1.53 | 915.73 | 11.74 |
| TG7-BNB-a | −7.27 | −8.80 | 6.90 | 4.47 | 0.00 | −3.66 | −5.04 | 1.38 | — | — |
| TG7-BNB-b | −8.18 | −4.92 | 6.23 | 12.13 | 0.00 | −3.68 | −5.11 | 1.43 | — | — |
| TG7-BNB-ab | −1.23 | −8.80 | 0.48 | 5.66 | 0.59 | −3.64 | −5.04 | 1.40 | — | — |
| TG7-BNB-ba | 0.00 | 13.27 | 0.00 | 7.06 | 0.82 | −3.68 | −5.06 | 1.38 | 1470.23 | 18.85 |
| TATB | 0.00 | 56.37 | 0.00 | 18.21 | 0.00 | −7.49 | −2.56 | 4.93 | −1.35 | −0.075 |
| cmpd-1 | 0.00 | 55.29 | 0.00 | 8.07 | 0.32 | −1.92 | −6.27 | 4.35 | 6.03 | 0.13 |
| cmpd-2 | 0.00 | 33.43 | 0.00 | 33.89 | 4.21 | −6.33 | −3.35 | 2.98 | 10.20 | 0.25 |
| cmpd-3 | 0.00 | 36.17 | 0.00 | 10.23 | 5.37 | −5.96 | −2.73 | 3.23 | 54.86 | 1.12 |
The HOMO–LUMO energy gap Egap and frontier molecular orbitals are used to not only characterize reactivity and electronic kinetic stability (feasibility of electron transition from occupied molecular orbitals to virtual molecular orbitals), but also qualitatively predict the optical and electrical properties of a molecule. For medium-sized π-systems, the Egap values predicted using hybrid density functional methods are in good agreement with the experimental excitation energies.60 The Egap of the triangulenes in the present work increases from 0.43 eV in TG7 to 2.46 eV in TG7-B-a by the introduction of B (Table 1). The unpaired π-electrons at the edges of the pristine triangulenes for example TG7, leads to small Egap (0.43 eV). The frontier molecular orbitals (including HOMO and LUMO) of these molecules clearly show charge redistribution upon the doping of heteroatoms. The incorporation of those dopants into pristine triangulenes diminishes or even eradicates the nonbonding orbitals formed by the unpaired π-electrons (Fig. S5, ESI†), and results in a low-lying HOMO or an elevating LUMO compared with that of TG7, i.e. a larger HOMO–LUMO energy gap. Compared with the B, N doped TG7 series, the doping of NBN and BNB in triangulenes leads to smaller Egap, in which the HOMO–LUMO gap of the TG7-ba series is slightly smaller than that of the TG7-ab series (Table 1).
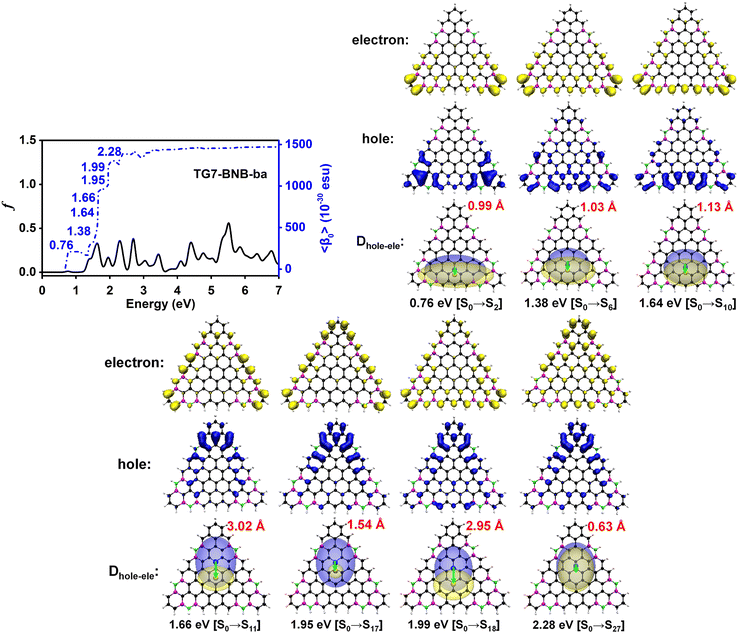
Electronic spectra and the 〈β0〉 of TG7-ba series of molecules
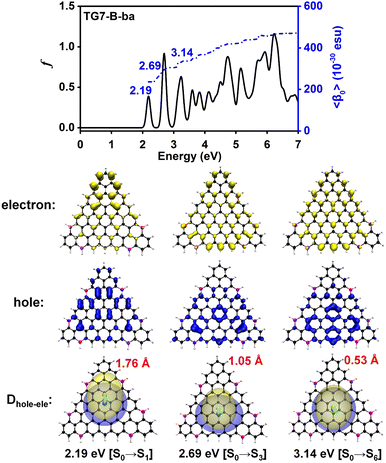
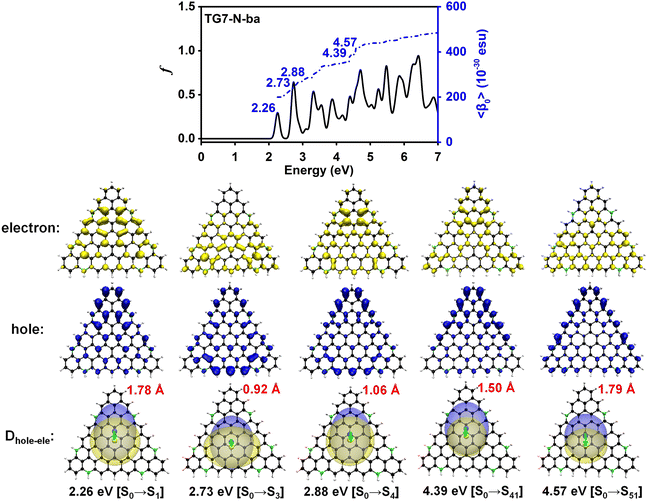
The doping patterns of B or (and) N in [n]triangulenes have significant effects on the electronic properties of these triangulenes, thereby leading to distinct static first hyperpolarizability (〈β0〉) (Table 1 and Table S2, ESI†), in which TG7-NBN-a has a relatively large 〈β0〉 per heavy atom (〈β0〉/N) (5.63 × 10−30 esu). Additionally, the (〈β0〉/N)s of the TG7-b series of molecules (with BN doped at the positions with the secondary largest spin densities) are weaker than that of the TG7-a series (Table 1). The TG7-ba series with mixed doping sites of TG7-a and TG7-b have large 〈β0〉. The 〈β0〉/N of TG7-BNB-ba reaches 18.85 × 10−30 esu, which is larger than that of TG7-NBN-ba (11.74 × 10−30 esu) and about three times that in TG7-NBN-a (5.63 × 10−30 esu) (Table 1).The evolution of 〈β0〉 with electron excitations provides information on the correlation between electronic structure and second order NLO properties of a system. The evolution of the 〈β0〉 with the major electron excitations in the four TG7-ba molecules (i.e., TG7-B-ba, TG7-N-ba, TG7-NBN-ba and TG7-BNB-ba) are investigated in this work to explore the effects of B or (and) N on the electronic properties of these triangulenes.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C unit with an X–B–X (X = O or N) unit, for instance OBO-doped nanographenes67 and double heliences,68,69 NBN-incorporated heterohelicenes70 and graphene nanoribbons,71 offer a possibility for the synthesis of novel hetero-triangulene NLO materials.
C–C unit with an X–B–X (X = O or N) unit, for instance OBO-doped nanographenes67 and double heliences,68,69 NBN-incorporated heterohelicenes70 and graphene nanoribbons,71 offer a possibility for the synthesis of novel hetero-triangulene NLO materials.
In summary, B, N, NBN, and BNB act as the spin eliminator and electrostatic potential modulator in tuning electron transitions among frontier molecular orbitals with conspicuous effects on the second order NLO responses. Compared with the doping of B or N, the NBN or BNB doping significantly polarizes charge distribution of the π-electrons of the pristine triangulene, thus inducing strong charge transfer based electron excitations in low energy regions, thereby bringing about large 〈β0〉/N of TG7-BNB-ba (18.85 × 10−30 esu). The NBN or BNB-doping in desired positions provides an opportunity to facilitate tuning triangulenes for their possible applications in triangulene-based nanoelectronic devices.
Hyper–Rayleigh scattering
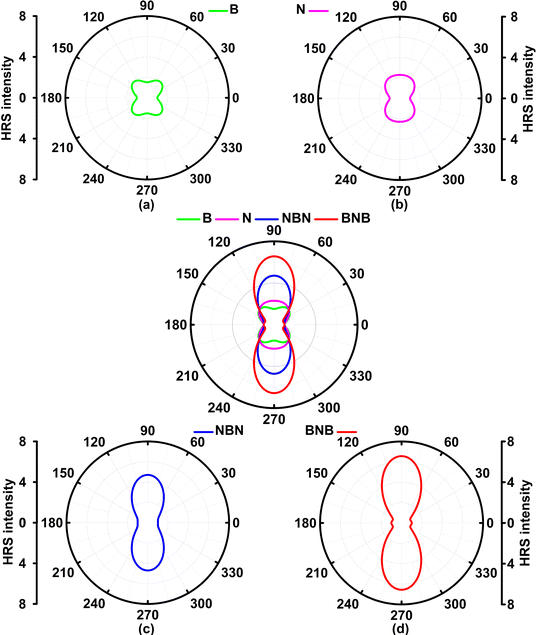
The Hyper–Rayleigh scattering (HRS) at the external field (0.0 nm or 1064.0 nm) and their corresponding dipolar (βJ=1) and octupolar (βJ=3) contributions to the NLO response of these four molecules are predicted with TD-CAM-B3LYP/6-31++G(d,p)-SOS (Table 2) for future possible measurement. The evolution of the HRS intensity with polarization angle also can reflect the structure-property correlation (Fig. 8), i.e. the HRS intensity (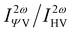 )53 (indication of polarization strength) can be regarded as a function of polarization angle at the designated incident wavelength.
)53 (indication of polarization strength) can be regarded as a function of polarization angle at the designated incident wavelength.
| Compound | β HRS(0; 0, 0) | β HRS(−2ω; ω, ω) | β ZZZ | β ZXX | |βJ=1| | |βJ=3| | ρ | Φ J=1 (%) | Φ J=3 (%) |
|---|---|---|---|---|---|---|---|---|---|
| TG7-B-ba | 182.72 | 498.33 | 386.95 | 314.01 | 104.57 | 1606.85 | 15.37 | 6.11 | 93.89 |
| TG7-N-ba | 188.29 | 959.26 | 800.68 | 528.28 | 1155.35 | 2558.75 | 2.21 | 33.23 | 66.77 |
| TG7-NBN-ba | 360.06 | 2827.45 | 2567.80 | 1183.60 | 5191.66 | 4588.16 | 0.88 | 53.19 | 46.81 |
| TG7-BNB-ba | 566.16 | 8931.65 | 8320.01 | 3248.34 | 17898.90 | 9492.14 | 0.53 | 65.36 | 34.64 |
| TATB | 0.82 | 7.20 | 5.85 | 4.20 | 6.78 | 20.90 | 3.08 | 24.51 | 75.49 |
| cmpd-1 | 9.56 | 33.53 | 28.57 | 17.55 | 46.08 | 82.76 | 1.80 | 35.71 | 64.29 |
| cmpd-2 | 10.29 | 79.25 | 62.24 | 49.06 | 39.76 | 249.52 | 6.28 | 13.74 | 86.26 |
| cmpd-3 | 79.30 | 246.86 | 210.66 | 128.68 | 342.41 | 605.21 | 1.77 | 36.10 | 63.90 |
The predicted βHRSs (−2ω; ω, ω) (ω = 0.0 nm or 1064.0 nm) follow a similar trend to the 〈β0〉 of these four molecules (Tables 1 and 2), i.e., in the order of TG7-BNB-ba > TG7-NBN-ba > TG7-N-ba > TG7-B-ba. TG7-B-ba and TG7-N-ba have a large |βJ=3| with the anisotropy ratio ρ > 1, and the proportions of the octupolar contributions (ΦJ=3) in the βHRS at 1064.0 nm of these two molecules are approximately 93.89% and 66.77% (Table 2) as depicted in Fig. 8. If triamino trinitrobenzene (TATB) is used as a representative reference for second order NLO properties of an octupolar molecule, TG7-B-ba and TG7-N-ba are good octupolar materials (Fig. 2 and Table 2). For the NBN or BNB doped triangulenes, the first hyperpolarizabilities of these molecules are dominated by a dipolar component with dipolar contribution (ΦJ=1) in the first hyperpolarizability of about 50.00–70.00%, and the reinforcement of dipolar character of the second order NLO response is also characterized by the decrease of the anisotropy ratio ρ from 15.37 (indicating a dominant octupolar character) to 0.53 (indicating a dominant dipolar character). Although the octupolar contributions of TG7-NBN/BNB-ba account for a small proportion of the total averaged first hyperpolarizability, the octupolar NLO responses of these triangulenes are significantly enhanced by the incorporation of NBN and BNB with respect to those of TG7-B-ba and TG7-N-ba (Table 2). The |βJ=1| of these four molecules significantly increases from TG7-B-ba to TG7-BNB-ba, and BNB or NBN polarizes charge redistribution (Fig. 3) thus enhancing the dipolar character, further verifying that the variation of dopants leads to a conspicuous change of polarization (Fig. 8). Compared with TG7-B-ba and TG7-N-ba, the strong HRS intensity of TG7-NBN-ba and TG7-BNB-ba is ascribed to the conspicuous contribution of diagonal terms (i.e., βZZZ) to the first hyperpolarizability (Fig. S11, ESI† and Table 2) (all triangulenes lie in the XZ plane). In summary, intended modification provides a promising means for stabilizing the radicals and also brings about an excellent NLO response (e.g. 8.93 × 10−27 esu of βHRS at 1064.0 nm in TG7-BNB-ba). The TG7-BNB-ba also has the largest βJ=1 (1.79 × 10−26 esu) and βJ=3 (9.49 × 10−27 esu) in all studied molecules, much larger than that of other triangular molecules (Fig. 2 and Table 2). This fine control of the ratio of dipolar/octupolar second-order NLO contribution opens interesting perspectives for applications in optoelectronic devices of carbon-based NLO materials.64,72
Two-dimensional second order NLO spectra
It is impractical, if not impossible, to measure the NLO responses of materials under all possible external fields in an experiment to find all possible applications in NLO. In this case, simulation of NLO responses of materials under all possible external fields is very helpful for this purpose. Two-dimensional (2D) second order NLO spectra73–75 encompass second order NLO responses of materials to external fields with all possible combinations of the two incident frequencies. The two-dimensional (2D) second order NLO spectra of four representative molecules (i.e., TG7-B-ba, TG7-N-ba, TG7-NBN-ba and TG7-BNB-ba) are investigated under external fields up to 7.00 eV with a scanning step size of 0.05 eV (Fig. 9 and Fig. S12, ESI†).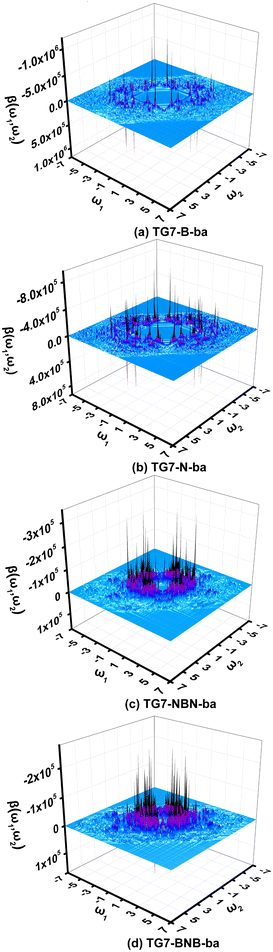 | ||
| Fig. 9 The two-dimensional second order nonlinear optical spectra (in 10−30 esu) of (a) TG7-B-ba, (b) TG7-N-ba, (c) TG7-NBN-ba, and (d) TG7-BNB-ba scanned up to 7.00 eV with a step size of 0.05 eV. | ||
The 2D second order NLO spectra landscapes of these four molecules reveal the intensity of NLO responses under external fields (Fig. 9). Overall, the landscape of the 2D second order NLO spectra of TG7-B-ba and TG7-N-ba is similar, and this is a similar case for TG7-BNB-ba and TG7-NBN-ba. For TG7-B-ba, the strong resonant response (different frequency generation – DFG) (1.08 × 10−24 esu) occurs at the external fields (3.25 eV, −1.05 eV) and (3.25 eV, −2.20 eV) (Fig. 9(a)), and fine scan with a step size of 0.005 eV finds the strongest NLO resonant (mainly with the electron excitation at 2.19 eV) response (1.78 × 10−24 esu) appearing at the external fields of (3.255 eV, −1.065 eV) and (3.255 eV, −2.190 eV) (Fig. S13a, ESI†). Similarly, strong sum frequency generation (SFG) (1.78 × 10−24 esu) with ω1 + ω2 = 3.255 eV (ω1, ω2 ∈ [0.000 eV, 3.255 eV]) is observed at the external field (2.190 eV, 1.065 eV) (Fig. S13b, ESI†). In the 2D second order NLO spectra of TG7-N-ba, there is a strong resonant response (8.46 × 10−25 esu) at the external field (2.25 eV, 1.05 eV) (Fig. 9(b)). Fine scanning with a step size of 0.005 eV locates the strongest SFG resonant response (1.28 × 10−24 esu) with ω1 + ω2 = 3.300 eV at the external field (2.255 eV, 1.045 eV) (Fig. S13c, ESI†), which may be caused by the resonance of external fields with the electron excitations at 2.26 eV and 3.30 eV (Fig. 5 and Table S3, ESI†). Strong DFG (1.28 × 10−24 esu) also occurs at the external fields (3.300 eV, −1.045 eV) and (3.300, −2.255 eV) (Fig. S13d, ESI†). Such strong resonant responses of SFGs and DFGs in the visible and near-infrared regions in TG7-B-ba and TG7-N-ba offer promising potential applications in studying the molecular structure and charging at interfaces76,77 or nonlinear nanophotonic devices.78
In TG7-NBN-ba, a strong resonant response (3.20 × 10−25 esu) at an external field (2.50 eV, −2.50 eV) is optical rectification (OR), and another strong one at (2.50 eV, 0.00 eV) with a single photon resonance at ω1 (ω2) = 2.50 eV is an electro-optical Pockels effect (EOPE) (Fig. 9(c)). Comparatively, another slightly strong NLO response (4.03 × 10−25 esu) occurs in the lower energy region (1.83 eV, −1.83 eV) (OR) and (1.83 eV, 0.00 eV) (EOPE) (Fig. S13e, ESI†). For TG7-BNB-ba, a strong resonant response (2.52 × 10−25 esu) occurs at the external fields (1.65 eV, 0.00 eV) and (1.65 eV, −1.65 eV) (Fig. 9(d)), and a fine scan with a step size of 0.005 eV locates the strongest response (3.19 × 10−25 esu) at external fields (1.66 eV, 0.00 eV) (EOPE) and (1.66 eV, −1.66 eV) (OR) (Fig. S13f, ESI†). Strong resonant response DFG (1.80 × 10−25 esu) is observed at a higher external field (1.95 eV, −1.55 eV), and a strong SFG (1.69 × 10−25 esu) with ω1 + ω2 = 1.95 eV appears at the external field (1.55 eV, 0.40 eV) (Fig. 9(d)). Likewise, strong resonant NLO responses (1.51 × 10−25 esu) OR and EOPE (Fig. 9(d)) occur at the external fields (1.95 eV, −1.95 eV) and (1.95, 0.00 eV). These strong ORs and EOPEs in TG7-BNB-ba and TG7-NBN-ba open the possibility for light tuning.
Conclusions
In this work, the spin distribution of triangulenes with a multi-radical character has been analyzed in the frame of molecular orbital theory and the Clar's sextet theory. Strategies for redistribution (by doping of BN pairs), reduction [by doping of B, N, BNB, NBN, and BN chains] and elimination (by doping of B, N, BNB and NBN) of the spin while polarizing the charge distribution of those triangulenes have been proposed. The doping sites are chosen as the combination of electronic configurations with different spin distributions for desired charge distribution. This proposed spin engineering based on molecular orbital theory on triangulenes based nanomaterials would broaden the applications of graphene in molecular magnetics, spintronics, and electro-optics. Such engineering strategies could also be applicable to other similar two-dimensional functional materials designs.Hole–electron distributions and electronic structure analyses on four TG7-ba molecules find that B essentially functions as an electron-acceptor while N acts as an electron-donor, while NBN and BNB make a concerted effect (combining BN with N or B) to bring about a smaller HOMO–LUMO energy gap and lead to charge redistribution, thus enhancing their second order NLO responses, e.g. the static first hyperpolarizability per heavy atom (〈β0〉/N) of TG7-BNB-ba reaches 18.85 × 10−30 esu in which BNB plays a more delicate role in both polarizing charge distribution and lowering electron excitation energies of the triangulene. The HRS response (βHRS) of TG7-BNB-ba at 1064.0 nm reaches 8.93 × 10−27 esu involving significant dipolar and octupolar NLO responses and is much larger than typical octupolar molecules. The strong second order NLO responses in the visible and near-infrared light regions, e.g., sum frequency generations and difference frequency generations, make these triangulenes potential NLO materials for applications in these regions. Intended heteroatom doping is an important means for improving the NLO response of carbon-based nanomaterials and shedding light on their promising applications, such as organic field-effect transistors,79 semiconductors,80 electromagnetics,81 photocatalysts for water splitting82 and the next generation of organic spintronic materials.7
The recent successful syntheses of BNB- or NBN-doped traiangulenes,83–85 [7]triangulene quantum rings,86 [7]triangulene87 and the advance in graphene nanosheets and nanoribbons syntheses88 certainly warrant future syntheses and applications of those proposed triangulenes in nano nonlinear optics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
YCC acknowledges the support from the graduate scientific research and innovation foundation of Chongqing, China (Grant No. CYB21042). This work is supported by the National Natural Science Foundation of China (21673025 and 11974091). The Open Projects of Key Laboratory of Polyoxometalate Science of Ministry of Education (NENU) and the State Key Laboratory of Supramolecular Structure and Materials (JLU) (SKLSSM2021020) are also acknowledged. The constructive comments and suggestions from the anonymous referees are acknowledged.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17954–17961 CrossRef CAS PubMed.
- K. Wakabayashi, M. Fujita, H. Ajiki and M. Sigrist, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8271–8282 CrossRef CAS.
- N. Pavliček, A. Mistry, Z. Majzik, N. Moll, G. Meyer, D. J. Fox and L. Gross, Nat. Nanotechnol., 2017, 12, 308–311 CrossRef PubMed.
- Q. Deng and J.-D. Chai, ACS Omega, 2019, 4, 14202–14210 CrossRef CAS PubMed.
- Y. Morita, S. Suzuki, K. Fukui, S. Nakazawa, H. Kitagawa, H. Kishida, H. Okamoto, A. Naito, A. Sekine, Y. Ohashi, M. Shiro, K. Sasaki, D. Shiomi, K. Sato, T. Takui and K. Nakasuji, Nat. Mater., 2008, 7, 48–51 CrossRef CAS PubMed.
- W. Han, R. K. Kawakami, M. Gmitra and J. Fabian, Nat. Nanotechnol., 2014, 9, 794–807 CrossRef CAS PubMed.
- J. Su, M. Telychko, S. Song and J. Lu, Angew. Chem., Int. Ed., 2020, 59, 7658–7668 CrossRef CAS PubMed.
- M. Rosenberg, K. R. Rostgaard, Z. Liao, A. Ø. Madsen, K. L. Martinez, T. Vosch and B. W. Laursen, Chem. Sci., 2018, 9, 3122–3130 RSC.
- J. D. Cox and F. J. García de Abajo, ACS Photonics, 2015, 2, 306–312 CrossRef CAS.
- J. D. Cox, I. Silveiro and F. J. García de Abajo, ACS Nano, 2016, 10, 1995–2003 CrossRef CAS PubMed.
- D. H. Reid, Tetrahedron, 1958, 3, 339–352 CrossRef CAS.
- S. Mishra, D. Beyer, K. Eimre, J. Liu, R. Berger, O. Gröning, C. A. Pignedoli, K. Müllen, R. Fasel, X. Feng and P. Ruffieux, J. Am. Chem. Soc., 2019, 141, 10621–10625 CrossRef CAS PubMed.
- J. Su, M. Telychko, P. Hu, G. Macam, P. Mutombo, H. Zhang, Y. Bao, F. Cheng, Z.-Q. Huang, Z. Qiu, S. J. R. Tan, H. Lin, P. Jelínek, F.-C. Chuang, J. Wu and J. Lu, Sci. Adv., 2019, 5, eaav7717 CrossRef CAS PubMed.
- A. A. Ovchinnikov, Theor. Chim. Acta, 1978, 47, 297–304 CrossRef CAS.
- D.-E. Jiang, B. G. Sumpter and S. Dai, J. Chem. Phys., 2007, 126, 134701 CrossRef PubMed.
- E. Clar and D. G. Stewart, J. Am. Chem. Soc., 1953, 75, 2667–2672 CrossRef CAS.
- X. Lu, S. Lee, Y. Hong, H. Phan, T. Y. Gopalakrishna, T. S. Herng, T. Tanaka, M. E. Sandoval-Salinas, W. Zeng, J. Ding, D. Casanova, A. Osuka, D. Kim and J. Wu, J. Am. Chem. Soc., 2017, 139, 13173–13183 CrossRef CAS PubMed.
- B. Tang, J. Zhao, J.-F. Xu and X. Zhang, Chem. Sci., 2020, 11, 1192–1204 RSC.
- A. Zhang, W. Jiang and Z. Wang, Angew. Chem., Int. Ed., 2020, 59, 752–757 CrossRef CAS PubMed.
- D. Shimizu, K. Furukawa and A. Osuka, Angew. Chem., Int. Ed., 2017, 56, 7435–7439 CrossRef CAS PubMed.
- M. Hirai, N. Tanaka, M. Sakai and S. Yamaguchi, Chem. Rev., 2019, 119, 8291–8331 CrossRef CAS PubMed.
- X. Zhou, W.-Q. Li, B. Shao and W. Q. Tian, J. Phys. Chem. C, 2013, 117, 23172–23177 CrossRef CAS.
- J. Gu, Y.-Q. Le, Y.-Y. Hu, W.-Q. Li and W. Q. Tian, ACS Photonics, 2014, 1, 928–935 CrossRef CAS.
- P. Karamanis, N. Otero and C. Pouchan, J. Am. Chem. Soc., 2014, 136, 7464–7473 CrossRef CAS PubMed.
- S. Yu, W. Zheng, C. Wang and Q. Jiang, ACS Nano, 2010, 4, 7619–7629 CrossRef CAS PubMed.
- C. G. Claessens, D. González-Rodríguez, T. Torres, G. Martín, F. Agulló-López, I. Ledoux, J. Zyss, V. R. Ferro and J. M. García de la Vega, J. Phys. Chem. B, 2005, 109, 3800–3806 CrossRef CAS PubMed.
- M. Moreno Oliva, J. Casado, J. T. López Navarrete, G. Hennrich, M. C. Ruiz Delgado and J. Orduna, J. Phys. Chem. C, 2007, 111, 18778–18784 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- E. Clar, The aromatic sextet, Wiley, New York, 1972 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- W. Q. Tian, LinSOSProNLO, V1.01. The linear scaling sum-overstates based program for nonlinear optics; Registration No. 2017SR526488 and classification No. 30219-7500. Copyright protection center of China: Beijing, China.
- B. J. Orr and J. F. Ward, Mol. Phys., 1971, 20, 513–526 CrossRef CAS.
- D. M. Bishop, J. Chem. Phys., 1994, 100, 6535–6542 CrossRef CAS.
- W. Q. Tian, J. Comput. Chem., 2012, 33, 466–470 CrossRef CAS PubMed.
- C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- D. Jacquemin, V. Wathelet, E. A. Perpete and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435 CrossRef CAS PubMed.
- V. Riffet, D. Jacquemin, E. Cauët and G. Frison, J. Chem. Theory Comput., 2014, 10, 3308–3318 CrossRef CAS PubMed.
- S. Alagawani, V. Vasilyev and F. Wang, arXiv e-prints, 2021 DOI:10.48550/arXiv.2112.03441.
- Z. Shuai and J. L. Brédas, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4395–4404 CrossRef CAS PubMed.
- L. Del Freo, F. Terenziani and A. Painelli, J. Chem. Phys., 2002, 116, 755–761 CrossRef CAS.
- S. A. Locknar, L. A. Peteanu and Z. Shuai, J. Phys. Chem. A, 1999, 103, 2197–2201 CrossRef CAS.
- R. R. Zope, T. Baruah, M. R. Pederson and B. I. Dunlap, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115452 CrossRef.
- N. Otero, P. Karamanis and M. Mandado, Phys. Chem. Chem. Phys., 2019, 21, 6274–6286 RSC.
- S. J. Lalama and A. F. Garito, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 1179–1194 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- F. Castet, E. Bogdan, A. Plaquet, L. Ducasse, B. Champagne and V. Rodriguez, J. Chem. Phys., 2012, 136, 024506 CrossRef PubMed.
- J. Zyss and I. Ledoux, Chem. Rev., 1994, 94, 77–105 CrossRef CAS.
- R. Bersohn, Y. H. Pao and H. L. Frisch, J. Chem. Phys., 1966, 45, 3184–3198 CrossRef CAS.
- O. Riant, G. Bluet, S. Brasselet, N. Druze, I. Ledoux, F. Lefloch, A. Skibniewski and J. Zyss, Mol. Cryst. Liq. Cryst., 1998, 322, 35–42 CrossRef CAS.
- G. Hennrich, I. Asselberghs, K. Clays and A. Persoons, J. Org. Chem., 2004, 69, 5077–5081 CrossRef CAS PubMed.
- R. D. Fonseca, M. G. Vivas, D. L. Silva, G. Eucat, Y. Bretonnière, C. Andraud, L. De Boni and C. R. Mendonça, J. Phys. Chem. C, 2018, 122, 1770–1778 CrossRef CAS.
- V. Sharma, N. Som, S. D. Dabhi and P. K. Jha, ChemistrySelect, 2018, 3, 2390–2397 CrossRef CAS.
- U. Salzner, J. B. Lagowski, P. G. Pickup and R. A. Poirier, J. Comput. Chem., 1997, 18, 1943–1953 CrossRef CAS.
- S. Yamaguchi and A. Wakamiya, Pure Appl. Chem., 2006, 78, 1413–1424 CrossRef CAS.
- L. Ji, S. Griesbeck and T. B. Marder, Chem. Sci., 2017, 8, 846–863 RSC.
- J. M. Farrell, C. Mützel, D. Bialas, M. Rudolf, K. Menekse, A.-M. Krause, M. Stolte and F. Würthner, J. Am. Chem. Soc., 2019, 141, 9096–9104 CrossRef CAS PubMed.
- S. K. Mellerup and S. Wang, Trends Chem., 2019, 1, 77–89 CrossRef CAS.
- T. Le Bahers, C. Adamo and I. Ciofini, J. Chem. Theory Comput., 2011, 7, 2498–2506 CrossRef CAS PubMed.
- S. Muhammad, H. Xu, Z. Su, K. Fukuda, R. Kishi, Y. Shigeta and M. Nakano, Dalton Trans., 2013, 42, 15053–15062 RSC.
- X. Y. Wang, A. Narita, W. Zhang, X. Feng and K. Mullen, J. Am. Chem. Soc., 2016, 138, 9021–9024 CrossRef CAS PubMed.
- X.-Y. Wang, T. Dienel, M. Di Giovannantonio, G. B. Barin, N. Kharche, O. Deniz, J. I. Urgel, R. Widmer, S. Stolz, L. H. De Lima, M. Muntwiler, M. Tommasini, V. Meunier, P. Ruffieux, X. Feng, R. Fasel, K. Müllen and A. Narita, J. Am. Chem. Soc., 2017, 139, 4671–4674 CrossRef CAS PubMed.
- Z. Zhou, X. Y. Wang, Z. Wei, K. Müllen and M. A. Petrukhina, Angew. Chem., Int. Ed., 2019, 58, 14969–14973 CrossRef CAS PubMed.
- Z. Sun, C. Yi, Q. Liang, C. Bingi, W. Zhu, P. Qiang, D. Wu and F. Zhang, Org. Lett., 2019, 22, 209–213 CrossRef PubMed.
- Y. Fu, H. Yang, Y. Gao, L. Huang, R. Berger, J. Liu, H. Lu, Z. Cheng, S. Du, H. J. Gao and X. Feng, Angew. Chem., Int. Ed., 2020, 59, 8873–8879 CrossRef CAS PubMed.
- S. Guo, X. Li, Z. Guo, X. Zhao, S. Meng and Z. Li, Nanomaterials, 2021, 11, 2559 CrossRef CAS PubMed.
- L. Lepetit, G. Chériaux and M. Joffre, J. Nonlinear Opt. Phys. Mater., 1996, 5, 465–476 CrossRef CAS.
- L. Lepetit and M. Joffre, Opt. Lett., 1996, 21, 564–566 CrossRef CAS PubMed.
- J. Chen, M. Q. Wang, X. Zhou, L. Yang, W. Q. Li and W. Q. Tian, Phys. Chem. Chem. Phys., 2017, 19, 29315–29320 RSC.
- S. Yamaguchi and T. Tahara, J. Phys. Chem. C, 2015, 119, 14815–14828 CrossRef CAS.
- G.-H. Deng, Y. Qian and Y. Rao, J. Chem. Phys., 2019, 150, 024708 CrossRef PubMed.
- J. He, H. Chen, J. Hu, J. Zhou, Y. Zhang, A. Kovach, C. Sideris, M. C. Harrison, Y. Zhao and A. M. Armani, Nanophotonics, 2020, 9, 3781–3804 CrossRef.
- J. P. Llinas, A. Fairbrother, G. Borin Barin, W. Shi, K. Lee, S. Wu, B. Yong Choi, R. Braganza, J. Lear, N. Kau, W. Choi, C. Chen, Z. Pedramrazi, T. Dumslaff, A. Narita, X. Feng, K. Müllen, F. Fischer, A. Zettl, P. Ruffieux, E. Yablonovitch, M. Crommie, R. Fasel and J. Bokor, Nat. Commun., 2017, 8, 633 CrossRef PubMed.
- Y. Jing and T. Heine, J. Am. Chem. Soc., 2019, 141, 743–747 CrossRef CAS PubMed.
- T. Wang, A. Berdonces-Layunta, N. Friedrich, M. Vilas-Varela, J. P. Calupitan, J. I. Pascual, D. Peña, D. Casanova, M. Corso and D. G. de Oteyza, J. Am. Chem. Soc., 2022, 144, 4522–4529 CrossRef CAS PubMed.
- Y. Jing, Z. Zhou, W. Geng, X. Zhu and T. Heine, Adv. Mater., 2021, 33, 2008645 CrossRef CAS PubMed.
- A. S. Scholz, J. G. Massoth, M. Bursch, J.-M. Mewes, T. Hetzke, B. Wolf, M. Bolte, H.-W. Lerner, S. Grimme and M. Wagner, J. Am. Chem. Soc., 2020, 142, 11072–11083 CrossRef CAS PubMed.
- M. Crumbach, O. Ayhan, L. Fritze, J. A. P. Sprenger, L. Zapf, M. Finze and H. Helten, Chem. Commun., 2021, 57, 2408–2411 RSC.
- M. Zhao and Q. Miao, Angew. Chem., Int. Ed., 2021, 60, 21289–21294 CrossRef CAS PubMed.
- J. Su, W. Fan, P. Mutombo, X. Peng, S. Song, M. Ondráček, P. Golub, J. Brabec, L. Veis, M. Telychko, P. Jelínek, J. Wu and J. Lu, Nano Lett., 2021, 21, 861–867 CrossRef CAS PubMed.
- S. Mishra, K. Xu, K. Eimre, H. Komber, J. Ma, C. A. Pignedoli, R. Fasel, X. Feng and P. Ruffieux, Nanoscale, 2021, 13, 1624–1628 RSC.
- A. Borissov, Y. K. Maurya, L. Moshniaha, W.-S. Wong, M. Żyła-Karwowska and M. Stępień, Chem. Rev., 2022, 122, 565–788 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02915d |
| This journal is © the Owner Societies 2022 |