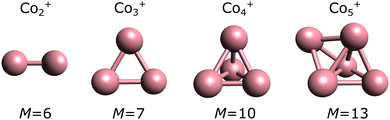The spin magnetic order of Co_n⁺ (n ≤ 5) clusters

Abstract

The magnetism of transition metal clusters has been for decades a complicated puzzle, with experimental results disagreeing with calculations performed within the density functional theory formalism. In this work, we provide a key to this puzzle by investigating the lowest-energy spin states of cobalt cluster, Co_n⁺ (n ≤ 5), using CASSCF/NEVPT2 calculations with very large active spaces. The geometries as well as the spin configurations adopted by the clusters in their ground-state are known from experiments, making Co_n⁺ clusters an ideal model system for theoretical investigation. Here, using the experimentally known geometries determined by far-infrared spectroscopy as inputs, we calculated the lowest-energy spin configurations of the clusters, revealing that the CASSCF/NEVPT2 formalism correctly predicts the preferred electronic configuration of the clusters known experimentally. This is in contrast to the widely used density functional theory, with results that depend on the selected exchange-correlation functional. The reasons for the failure of density functional theory, in opposition to CASSCF/NEVPT2, are discussed, providing a solid framework for investigating other transition metal and transition metal oxide clusters.

---

I. Introduction

The fascinating magnetism in transition metal clusters has been the center of intensive investigation for decades.^1–3 Early magnetic deflection experiments in molecular beams have shown a very rich but complicated zoo of magnetic orders in these clusters. For example, the magnetic moments per atom of neutral Ni_n, Co_n, and Fe_n clusters were seen to decrease with increasing cluster size, tending to the ferromagnetic bulk value in a very non-monotonic way.^4–6 Moreover, in Cr_n (n = 20–133)⁷ and Mn_n (n = 11–99)⁸ clusters, antiferromagnetic in the bulk, non-zero magnetic moments have been measured, as well as for Rh_n clusters, which is a paramagnetic bulk material. In more recent studies, the magnetic deflection technique has been applied to investigate bimetallic species, for instance Co_n(Mn,V)_m (n ≤ 60; m ≤ n/3)⁹ and (Fe)@Sn₁₂¹⁰ clusters. In general, the experimentally determined magnetic moments are in disagreement with theoretical predictions,^11,12 often performed with density functional theory (DFT), given the low computational cost and relatively high accuracy of this method. A common argument used for explaining the qualitative disagreement between experiments and simulations, is the observation that magnetic deflections are sensitive to the total magnetic moment of the clusters, thus spin plus orbital (J = S + L), while calculations consider spin only.¹³

Another approach used to experimentally determine the magnetic order in gas-phase clusters is a combination of infrared spectroscopy and DFT. In this method, the vibrational spectrum of a cluster is recorded and contrasted with simulated vibrational frequencies of different isomers, which in addition are computed for various spin states. Consequently, a specific configuration is assigned based on the experiment-theory agreement. Examples of this approach include studies on Co_n−1Cr⁺ (n = 3–5),¹⁴ Si_nMn⁺ (n = 6–16),¹⁵ and Co_xO_y⁺ (x = 3–6, y = 3–8)¹⁶ clusters. The drawback of this method, however, is the possibility that vibrational spectra are only weakly influenced by the spin state, making a proper assignment difficult. This has been seen often to be the case. Moreover, the technique heavily relies on the DFT calculations, with cases in which the assignment does not correspond to the lowest-energy configuration.¹⁶

A third possibility to experimentally access the magnetic order of gas-phase clusters is X-ray magnetic circular dichroism (XMCD) spectroscopy, where the spin and orbital contributions to the total magnetic moments can be deconvoluted. Since the technique uses an ion trap, it only works for charged particles. Different systems have been investigated by XMCD, for example, Fe_n⁺ (n = 2–9),¹⁷ Ni₂⁺,¹⁸ Co₃(benzene)_n⁺,¹⁹ Co_n⁺ (n = 4–9),²⁰ Co_n⁺ (n = 8–22)²¹ and (Co,Fe,Ni)_n⁺ (n = 10–15)²² clusters. In contrast to magnetic deflection and IRMPD, the results from XMCD experiments can be directly compared with DFT predictions, as the spin magnetic moments are determined alone, without contributions to the orbital magnetic moments or the geometry of the clusters. Nevertheless, in many cases the DFT calculations disagree with the experimental findings, even in these “clean” conditions, suggesting that the problems can be related to the theoretical formalism itself. For example, the predicted spin magnetic moments in (Co,Fe,Ni)_n⁺ (n = 10–15) clusters are underestimated with respect to the experimental values.²² In Co_n⁺ (n ≤ 8) clusters, the geometries adopted by the particles in molecular beams were assigned by IRMPD,²³ whereas XMCD measurements determined their spin states.²⁰ The lowest-energy spin configurations calculated by DFT, however, do not correspond to the measured configurations when the assigned geometries are used as inputs. This at least for the selected exchange-correlation functional in that study, i.e., the widely employed (GGA) PBE. Other studies employing DFT calculations have investigated the ground-state spin configurations of Co_n⁺, generally underestimating the measured multiplicities.^24,25 Beyond DFT, a few studies on transition metal-containing molecules have been performed, using either Coupled-Cluster or Density Matrix Renormalization Group calculations.^26–28

In this work, small Co_n⁺ clusters are selected as a study case, for which interesting physical and chemical properties have been observed. For example, the interaction strength of Co_n⁺ (n = 4–20) with CO was shown to be tunable by co-adsorbing H₂ molecules.²⁹ In Co_n⁺ (n = 1–6), the adsorption of NH₃ leads to dehydrogenation.³⁰ In the neutral Co_n (n = 9, 10, 13) clusters, a strong coupling between the vibrational and the electronic degrees of freedom have been observed,³¹ while for the cationic Co_n⁺ (n = 5–23) species, very high rates of radiation upon laser excitation have been quantified, attributed to the process of recurrent fluorescence.³² Moreover, as discussed, the geometries²³ and the spin states²⁰ adopted by the clusters in their lowest-energy configuration are known from experiments. Here, using as input the experimentally known geometries of the clusters, multiconfigurational calculations were performed in Co_n⁺ (n ≤ 5) clusters, specifically by the CASSCF plus NEVPT2 formalism, for which very large active spaces were employed. Therefore, we can deconvolute the effect of geometry in determining the preferred spin configuration of the clusters. Our advanced, however expensive, calculations correctly predict the lowest-energy spin configurations, in contrast with DFT, where energy orderings depend majorly on the applied exchange-correlation functional. Therefore, our work sheds some light on the reasons why many previous theoretical calculations have failed at explaining measured spin states of transition metal clusters, and provides a solid computational framework for future investigations in similar systems.

II. Methods

Multiconfigurational CASSCF and NEVPT2 calculations were performed for Co_n⁺ (n ≤ 5) clusters at various spin configurations, which throughout the text is described via the spin multiplicity M, defined as M = 2S + 1, with S the total spin. The experimentally known geometries of the clusters were used as inputs,²³vide infra. All calculations were conducted using the ORCA 5.0.2 software package,³³ employing the def2-TZVPP basis set with the addition of auxiliary basis sets for correlation and Coulomb fitting.^34,35 The “VERYTIGHTSCF” convergence criterion was selected for all CASSCF computations, as implemented in ORCA, without symmetry constraints applied during the optimizations. Moreover, all the electrons of cobalt were accounted implicitly, with scalar relativistic effects described by the zeroth order regular approximation (ZORA).³⁶ The employed active spaces depend on cluster size and therefore, are discussed case by case in the next section. For example, for the Co₁⁺ ion the active space includes eight electrons in six orbitals, i.e., CAS(8, 6), corresponding to all the electrons of cobalt in the 3d and 4s shells (one electron is subtracted from the total nine due to ionization). For increasing cluster size, however, more electrons distributed in more orbitals are required, as for Co₂⁺, where a CAS(17, 12) is needed when following the same procedure. To keep the computations manageable, some doubly occupied orbitals were removed from the active space for the n ≥ 3 clusters. In search for the ground-state energy, and given the significant computational cost of the calculations, a single root was computed. For Co⁺ and Co₂⁺, however, calculations with up to 10 roots were performed, showing no significant influence in the ground-state configuration.

The XYZ coordinates used in the CASSCF/NEVPT2 calculations were obtained by a combination of the previous infrared spectroscopy results²³ and DFT calculations. The experimentally known geometries identified in ref. 23 were optimized using the hybrid PBE0 functional and the def2-TZVPP basis set, for each of the different studied multiplicities, after which single-point calculations were conducted at the CASSCF/NEVPT2 level. In the ESI,† the accuracy of PBE0 is addressed by comparing the measured infrared spectrum of Co₄⁺ and Co₅⁺²³ with that computed with DFT, Table S1 (ESI†). For the DFT optimizations, all cobalt electrons were included implicitly, and scalar relativistic effects were accounted for by using the ZORA approximation. Direct geometry optimizations at the NEVPT2 level were nevertheless performed for the Co₂⁺ dimer, showing no effect on the energy ordering between its different spin configurations.

In addition to the CASSCF/NEVPT2 calculations, DFT computations employing exchange-correlation functionals of different complexity within Perdew's Jacob's Ladder³⁷ were performed with the ORCA 5.0.2 software package, to test the various spin configurations of the Co_n⁺ (n ≤ 5) clusters. These include the GGA PBE,³⁸ the meta-GGA TPSS,³⁹ the hybrids PBE0⁴⁰ and B3LYP,⁴¹ and the range-separated hybrid ωB97X-D3⁴² functionals. In the same way than for CASSCF, the DFT calculations were performed with all-electrons and the def2-TZVPP basis, together with the ZORA approximation. All employed XYZ coordinates are available in an open access repository (see the ESI†).

III. Results and analysis

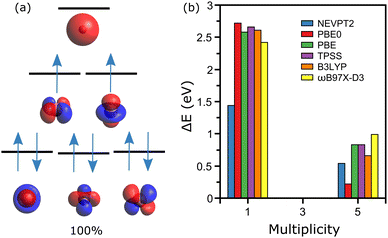
The simplest case is discussed first, namely the cobalt ion Co₁⁺, where geometry clearly does not play any role. From XMCD experiments, the lowest-energy configuration of this ion is known to be a triplet state,²⁰ hence M = 3 (M = 2S + 1). Given the electronic configuration of cobalt, [Ar]3d⁷4s², the CASSCF calculations were performed employing an active space composed of six orbitals (five 3d and one 4s), where eight electrons are distributed (one electron is subtracted as the atom is positively charged).

Within the selected active space there are three possible M values, 1, 3 and 5. The obtained active orbitals for Co₁⁺ together with the energy diagram of the electronic levels arranged in the M = 3 state are depicted in Fig. 1a. The qualitative diagram is constructed based on the energies of atomic orbitals. As expected, these orbitals have the symmetries of the 3d and 4s orbitals. For the experimentally determined triplet state, the obtained wavefunction is determined by a single determinant, with [222110] configuration as shown in Fig. 1a. The M = 1 calculation reveals a very multiconfigurational wavefunction, with almost equal contributions from the [222200], [222020] and [220220] configurations (∼29% each), and minor contributions from [202220] and [022220] (∼6% each). The M = 5 state, however, displays also a mono-determinant wavefunction with [221111] configuration.

Fig. 1 (a) Diagram of the electronic levels of the Co⁺ ion (not to scale), with a representation of the electron occupancies in the M = 3 ground-state. The determined wavefunction is mono-configurational, i.e., with a single determinant accounting for all the weight (100%). Below each energy level, the active orbitals are depicted. (b) Energy differences, with respect to the measured multiplicity state (M = 3), for calculations conducted at the NEVPT2, DFT(PBE0), DFT(PBE), DFT(TPSS) and DFT(ωB97X-D3) levels of theory.

Comparing total energies of the three spin configurations, after the NEVPT2 step is performed to account for dynamical correlation, gives a M = 3 ground-state, as determined experimentally. The M = 1 and M = 5 states are found 1.44 and 0.54 eV higher in energy than the M = 3 configuration. This analysis is presented in Fig. 1b, where additional DFT calculations employing different exchange-correlation functionals are given. For this simple system, all methods agree that M = 3 is the lowest-energy spin state. It is noteworthy that the energy difference between the M = 1 and M = 3 states is larger for the DFT calculations, which only considers a single determinant for describing the ion's wavefunction. Such formalisms cannot correctly describe the M = 1 configuration, which is thus found higher in energy.

From n ≥ 2, geometry is an important parameter in the calculations. As detailed in the Methods section, we adopted the geometries experimentally assigned in the work of ref. 23, followed by optimization at the PBE0 level. These geometries are presented in Fig. 2. The use of other functionals have little effect in the geometries, with only minor changes in bond lengths and angles. As an example, Fig. S1 in the ESI† shows a detailed comparison of the geometries optimized for Co₃⁺ in the M = 7 multiplicity (experimentally determined ground state). The geometry of Co₃⁺ is an (almost) equilateral triangle, while Co₄⁺ adopts a three-dimensional pyramidal structure. Co₅⁺ is a bipyramid.

Fig. 2 Geometries of Co_n⁺ (n = 2–5) clusters, optimized at the DFT level using the PBE0 functional. The multiplicities (M = 2S + 1) are depicted below each cluster, corresponding to the experimentally determined values.

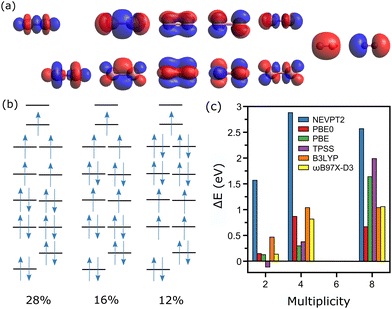
The analysis corresponding to the Co₂⁺ dimer is presented in Fig. 3, where for the CASSCF calculations 17 electrons are distributed among 12 active orbitals, hence CAS(17, 12). These molecular orbitals (MOs) are depicted in Fig. 3a, and can be rationalized as the bonding and antibonding combinations of 3d and 4s atomic orbitals of Co. The two lowest MOs are the bonding and antibonding combinations of 3d_z², followed by the bonding combinations of 3d_xz, 3d_yz, 3d_xy and 3d_x²−y², and the corresponding antibonding combinations of these orbitals, with lastly the bonding and antibonding combinations of the atomic 4s orbital.

Fig. 3 (a) Plot of the active orbitals in the CASSCF calculation of Co₂⁺, ordered from left to right in ascending order of energy. (b) Diagram (not to scale) of the electronic levels of the Co₂⁺ dimer, with a representation of the electron occupancies in the M = 6 ground-state. The three more relevant configurations are depicted, with their corresponding percentage labelled at the bottom. (c) Energy differences, with respect to the measured multiplicity state (M = 6), for calculations conducted at the NEVPT2, DFT(PBE0), DFT(PBE), DFT(TPSS), DFT(B3LYP) and DFT(ωB97X-D3) levels of theory.

For Co₂⁺, the experimentally determined spin state is M = 6.²⁰ In this spin configuration, the CASSCF calculation reveals a multiconfigurational wavefunction, with three dominant configurations, having percentages of 28, 16 and 12%. These three configurations are presented in Fig. 3b, although there are five other ones with percentages close to 8%. Three other spin states are considered for the CASSCF calculations, M = 2, 4 and 8. For M = 2, the wavefunction is composed of three main configurations, [222222221000], [222222201200] and [222222211100], having contributions of 37, 35 and 27%, respectively. The cases of M = 4 and 8, however, can be described essentially by a single determinant, with configurations of the active orbitals of [222222211100] and [222221111111], for M = 4 and 8, respectively. As shown in Fig. 3c, comparing total energies after the NEVPT2 step gives M = 6 as the lowest-energy state, as measured experimentally.

In contrast to the case of the Co⁺ ion, the single-point CASSCF calculations for Co₂⁺ require a specific bond length for the dimer. As was previously explained, the determination of the used XYZ coordinates was performed using the bond length calculated by DFT with the PBE0 functional. Such assumption is in principle not required for the dimer, as geometry optimizations are manageable at the CASSCF/NEVPT2 level. For the larger clusters, however, this is not computationally feasible. Accordingly, for consistency this simplification is applied for the entire n = 2–5 size range. Nevertheless, geometry optimizations at the CASSCF/NEVPT2 level were performed for the Co₂⁺ dimer, showing little influence on the energy ordering of the three considered spin states. Moreover, the bond length varied by only 0.01 Å, in comparison with the DFT optimization.

DFT calculations were also performed for the Co₂⁺ dimer, as is detailed in Fig. 3c. Here, except for TPSS, all functionals agree that M = 6 is the lowest-energy spin state. These calculations are therefore converging to the configuration with the higher contribution in CASSCF, namely [222222111110]. The prediction that M = 6 is the lowest-energy spin state by DFT has been seen in previous studies.^43,44 It is however noted that in general the CASSCF/NEVPT2 calculations predict a more stable M = 6 configuration than DFT (only with PBE as an exception). This can be related to the fact that the single-determinant nature of DFT cannot describe well the multiconfigurational M = 6 state of Co₂⁺, even though these methods are converging to the most dominant configuration. Hence, CASSCF/NEVPT2 predicts a more stable M = 6 state. Still, even for a dimer, which could be ascribed as a rather simple system, TPSS is predicting the wrong spin.

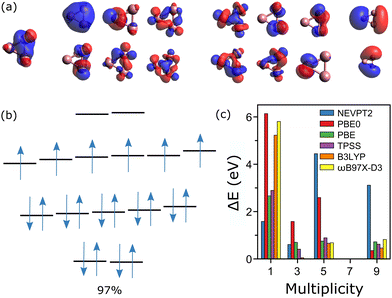
For Co₃⁺, an active space composed of all 3d and 4s orbitals would be composed of 18 orbitals and 26 electrons, too large to be computed. Thus, for the CASSCF calculations, three occupied orbitals were removed from the active space, one for each cobalt atom. This gives a nevertheless very large active space, composed of 20 electrons distributed in 15 orbitals, i.e., CAS(20, 15). The active orbitals are depicted in Fig. 4a, most of them being hybridized atomic d-orbitals. The measured spin state of Co₃⁺ is M = 7,²⁰ meaning that the two last orbitals are empty. The wavefunction calculated by CASSCF in the M = 7 state is essentially mono-determinant, with a main configuration having a weight of 97%, as depicted in Fig. 4b. The spin states M = 1, 3, 5 and 9 were also calculated, showing significant multiconfigurational character. For M = 1, there are five dominant configurations, with contributions of 26, 23, 21, 16 and 14%. In M = 3, the wavefunction is composed of four main configurations, having 27, 25, 24 and 23%. For M = 5, four configurations dominate, with 32, 23, 20 and 20%. Finally, in M = 9, there are three principal configurations, with contributions of 70, 15 and 7%.

Fig. 4 (a) Plot of the active orbitals in the CASSCF calculation of Co₃⁺, in ascending order of energy. (b) Diagram (not to scale) of the electronic levels of Co₃⁺, with a representation of the electron occupancies in the M = 7 ground-state. The determined wavefunction is essentially mono-configurational, i.e., with a single determinant accounting for most of the weight (97%). (c) Energy differences, with respect to the measured multiplicity state, for calculations conducted at the NEVPT2, DFT(PBE0), DFT(PBE), DFT(TPSS), DFT(B3LYP) and DFT(ωB97X-D3) levels of theory.

In Fig. 4c, the relative energies, with respect to the measured M = 7 state are presented for the CASSCF/NEVPT2 as well as the different DFT calculations. As can be seen, for Co₃⁺ all simulations agree on the lowest energy of the M = 7 state. Given that the M = 7 state of Co₃⁺ can be described by a wavefunction mostly composed of a single determinant, it is not surprising that the DFT calculations agree with CASSCF on the lowest-energy configuration, which is also the experimental result. Accordingly, up to n = 3, DFT is (mostly) able to correctly predict the spin order in Co_n⁺.

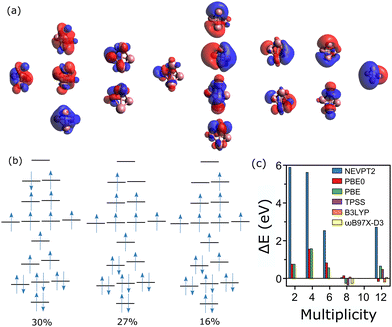
The situation, however, changes from n = 4. As for Co₃⁺, considering all the 3d and 4s orbitals of cobalt in the active space of Co₄⁺ is unfeasible, as it would correspond to 35 electrons in 24 orbitals. In this case, two more occupied orbitals of each Co atom are considered inactive orbitals, leaving a CAS(19, 16) calculation. The active orbitals of Co₄⁺ are presented in Fig. 5a. The wavefunction of the measured spin state, M = 10,²⁰ is highly multiconfigurational, with five configurations of significant contributions. The first three of them are depicted in Fig. 5b, having percentages of 30%, 27% and 16%. The extra two configurations also have large contributions, of 13% for [2222011111111120] and 12% for [2222101111111210].

Fig. 5 (a) Plot of the active orbitals in the CASSCF calculation of Co₄⁺, ordered in ascending order of energy. (b) Diagram (not to scale) of the electronic levels of Co₄⁺, with a representation of the electron occupancies in the M = 10 ground-state. The three more prominent configurations are depicted, with their corresponding percentage labelled at the bottom. (c) Energy differences, with respect to the measured multiplicity state (M = 10), for calculations conducted at the NEVPT2, DFT(PBE0), DFT(PBE), DFT(TPSS), DFT(B3LYP) and DFT(ωB97X-D3) levels of theory.

CASSCF calculations were also conducted for the M = 2, 4, 6, 8 and 12 multiplicities. Whereas for the M = 12 state the wavefunction can mostly be described by a single determinant, with a configuration of [2222111111111110] and a contribution of a 94%, the wavefunction of all other spin states is highly multiconfigurational. For M = 8, for example, five configurations contribute with more than 10%, with the most significant being [2222211111111100] with only a 19%. For M = 2, 4 and 6, the most significant configuration only contributes with a 12, 17 and 27%, respectively.

Given the multiconfigurational character of the wavefunctions describing the different spin states of Co₄⁺, it is not surprising the lack of predictability of DFT. As shown in Fig. 5c, CASSCF/NEVPT2 correctly predicts M = 10 as the lowest-energy spin state, opposite to the results from DFT, which are scattered for the different functionals. The lowest-energy spin states predicted by DFT are M = 12 (PBE0), M = 8 (PBE), M = 8 (TPSS), M = 12 (B3LYP) and M = 8 (ωB97X-D3). Hence, the results are highly functional-dependent and in fact, none of the functionals predict M = 10 as the lowest-energy state, which is the experimental value. Previous DFT studies employing the PBE functional have also been seen to underestimate the multiplicity of Co₄⁺,²³ consistent with our calculations. Importantly, the failure of DFT in predicting the magnetic order in Co₄⁺ seems to be more critical than simply due to an energy uncertainty given the approximations made in a DFT calculation. The calculated density of states of the M = 10 multiplicity with different functionals show significant differences, pointing that depending on the functional, the wavefunctions converge to different configurations.

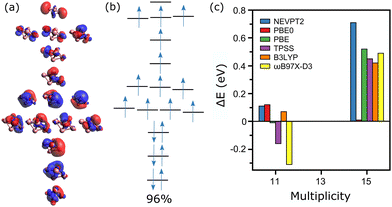
Finally, the Co₅⁺ cluster is analyzed, which is at the limit of what can be calculated at the CASSCF level. In total, 44 electrons in 30 orbitals should be considered in an active space to include all 3d and 4s orbitals. Instead, a CAS(16, 15) calculation is employed, corresponding to the larger active space computationally possible for this cluster size. Moreover, given the high computational cost of these calculations, only the spin states M = 11, 13 and 15 are considered, with M = 13 the experimental value. The active orbitals of the clusters are depicted in Fig. 6a. Again, CASSCF/NEVPT2 correctly predicts a lowest-energy spin state that agrees with the experimental result (M = 13). The wavefunction of this state is mostly mono-configurational, with a dominant configuration having a weight of 96% (Fig. 6b).

Fig. 6 (a) Plot of the active orbitals in the CASSCF calculation of Co₅⁺, ordered in ascending order of energy. (b) Diagram (not to scale) of the electronic levels of Co₅⁺, with a representation of the electron occupancies in the M = 13 ground-state. (c) Energy differences, with respect to the measured multiplicity state (M = 13), for calculations conducted at the NEVPT2, DFT(PBE0), DFT(PBE), DFT(TPSS), DFT(B3LYP) and DFT(ωB97X-D3) levels of theory.

In contrast, the wavefunction of M = 11 is highly multi-determinant, with several configurations with large contribution: [221111111111110] with 20%, [222111111111100] with 18%, [221211111111010] with 13%, [221121111110110] with 11%, [221101111112110] with 11%, [221011111111210] with 10% and [220111111111120] with 9%. The wavefunction of M = 15, instead, is composed by a single determinant, of configuration [211111111111111]. Therefore, overall, for the three considered spin states, the system is less multiconfigurational. Consequently, DFT does a better job for Co₅⁺ than it did for Co₄⁺. As presented in Fig. 6c, PBE0 and B3LYP correctly predict M = 13 as the lowest-energy configuration. Nevertheless, PBE, TPSS and in particular ωB97X-D3, wrongly assign the M = 11 multiplicity.

Hence, the past failure of DFT in predicting the experimentally determined spin multiplicities in Co_n⁺ clusters can be attributed to the multiconfigurational character of the wavefunction of these clusters. Such a problem is solved if a theoretical formalism that is multiconfigurational in nature is applied, such as CASSCF/NEVPT2. Similar problems with DFT have been seen in calculations of other transition metal clusters, as well as on transition metal oxides. Thus, our work provides a solid framework for investigating electronic-dependent properties of such systems.

IV. Conclusions

In this work, we have studied the preferred spin configurations of small cobalt cluster cations, Co_n⁺ (n ≤ 5), using a multiconfigurational quantum chemical approach, CASSCF combined with NEVPT2. Opposite to the conventional density functional theory, our calculations always obtain the spin multiplicity that has been determined experimentally as the lowest in energy. Therefore, our calculations solve a long-standing question about the magnetic order in these transition metal clusters, and provide a solid framework for future theoretical modelling of similar systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

P. F. acknowledges the Research Foundation – Flanders (FWO) for a senior postdoctoral grant. The work has been performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme; in particular, the author gratefully acknowledges the support of the Department of Inorganic and Organic Chemistry at the University of Barcelona, and the computer resources and technical support provided by the Barcelona Supercomputer Centre. S. G.-C. thanks Spanish Ministerio de Ciencia e Innovacion (grants PGC2018-093863-B-C21 and MDM-2017-0767 funded by MCIN/AEI/10.13039/501100011033) and Generalitat de Catalunya (grant SGR 2017-1289).

References

1. W. A. de Heer, Rev. Mod. Phys., 1993, 65, 661.
2. J. A. Alonso, Structure and properties of atomic nanoclusters, Imperial College Press; London, 2005.
3. R. L. Johnston, Atomic and Molecular Clusters, Taylor & Francis; London, 2002.
4. I. M. L. Billas, A. Châtelain and W. A. de Heer, Science, 1994, 265, 1682–1684.
5. S. E. Apsel, J. W. Emmert, J. Deng and L. A. Bloomfield, Phys. Rev. Lett., 1996, 76, 1441.
6. X. Xu, S. Yin, R. Moro and W. A. de Heer, Phys. Rev. Lett., 2005, 95, 237209.
7. F. W. Payne, W. Jiang and L. A. Bloomfield, Phys. Rev. Lett., 2006, 97, 193401.
8. M. B. Knickelbein, Phys. Rev. Lett., 2001, 86, 5255.
9. S. Yin, R. Moro, X. Xu and W. A. de Heer, Phys. Rev. Lett., 2007, 98, 113401.
10. U. Rohrmann and R. Schäfer, J. Phys. Chem. C, 2015, 119, 10958–10961.
11. F. W. Payne, W. Jiang, J. W. Emmert, J. Deng and L. A. Bloomfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 094431.
12. M. B. Knickelbein, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 014401.
13. A. Diaz-Bachs, L. Peters, R. Logemann, V. Chernyy, J. M. Bakker, M. L. Katsnelson and A. Kirilyuk, Phys. Rev. B, 2018, 97, 134427.
14. M. Jia, J. van der Tol, Y. Li, V. Chernyy, J. M. Bakker, L. N. Pham, M. T. Nguyen and E. Janssens, J. Phys.: Condens. Matter, 2018, 30, 474002.
15. V. T. Ngan, E. Janssens, P. Claes, J. T. Lyon, A. Fielicke, M. T. Nguyen and P. Lievens, Chem. – Eur. J., 2012, 18, 15788–15793.
16. C. N. van Dijk, D. R. Roy, A. Fielicke, T. Rasing, A. C. Reber, S. N. Khanna and A. Kirilyuk, Eur. Phys. J. D, 2014, 68, 357.
17. J. T. Lau, A. Föhlisch, R. Nietubyć, M. Reif and W. Wurth, Phys. Rev. Lett., 2002, 89, 057201.
18. V. Zamudio-Bayer, R. Lindblad, C. Bülow, G. Leistner, A. Terasaki, B. v Issendorff and J. T. Lau, J. Chem. Phys., 2016, 145, 194302.
19. S. T. Akin, V. Zamudio-Bayer, K. Duanmu, G. Leistner, K. Hirsch, C. Bülow, A. Ławick, A. Terasaki, B. v Issendorff, D. G. Truhlar, J. T. Lau and M. A. Duncan, J. Phys. Chem. Lett., 2016, 7, 4568–4575.
20. V. Zamudio-Bayer, K. Hirsch, A. Langenberg, A. Ławicki, A. Terasaki, B. von Issendorff and J. T. Lau, J. Phys.: Condens. Matter, 2018, 30, 464002.
21. S. Peredkov, M. Neeb, W. Eberhardt, J. Meyer, M. Tombers, H. Kampschulte and G. Niedner-Schatteburg, Phys. Rev. Lett., 2011, 107, 233401.
22. A. Langenberg, K. Hirsch, A. Ławicki, V. Zamudio-Bayer, M. Niemeyer, P. Chmiela, B. Langbehn, A. Terasaki, B. v Issendorff and J. T. Lau, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 184420.
23. R. Gehrke, P. Gruene, A. Fielicke, G. Meijer and K. Reuter, J. Chem. Phys., 2009, 130, 034306.
24. D. M. Kiawi, J. M. Bakker, J. Oomens, W. J. Buma, Z. Jamshidi, L. Visscher and L. B. F. M. Waters, J. Phys. Chem. A, 2015, 119, 10828–10837.
25. G. Martínez, E. Tangarife, M. Pérez and J. Mejía-López, J. Phys.: Condens. Matter, 2013, 25, 216003.
26. W. Hübner, Y. Pavlyukh, G. Lefkidis and J. Berakdar, Phys. Rev. B, 2017, 96, 184432.
27. D. A. Pantazis and J. Chem, Theory Comput., 2019, 15, 938–948.
28. M. Roemelt and D. A. Pantazis, Adv. Theory Simul., 2019, 2, 1800201.
29. I. Swart, A. Fielicke, D. M. Rayner, G. Meijer, B. M. Weckhuysen and F. M. de Groot, Angew. Chem., Int. Ed., 2007, 46, 5317–5320.
30. L. Geng, C. Cui, Y. Jia, H. Wu, H. Zhang, B. Yin, Z.-D. Sun and Z. Luo, J. Phys. Chem. A, 2020, 124, 5879–5886.
31. J. Jalink, J. M. Bakker, T. Rasing and A. Kirilyuk, J. Phys. Chem. Lett., 2015, 6, 750.
32. K. Peeters, E. Janssens, K. Hansen, P. Lievens and P. Ferrari, Phys. Rev. Res., 2021, 3, 033225.
33. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
34. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
35. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
36. C. van Wüllen, J. Chem. Phys., 1998, 109, 392.
37. J. P. Perdew, A. Ruzsinszky and J. Tao, J. Chem. Phys., 2005, 123, 062201.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
39. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
40. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982.
41. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
42. O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109.
43. C. Jamorski, A. Martinez, M. Castro and D. R. Salahub, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10905.
44. G. L. Gutsev and C. W. Bauschlicher, J. Phys. Chem. A, 2003, 107, 4755–4767.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03643f

---