Open Access Article
Open Access ArticleSimulating action-2D electronic spectroscopy of quantum dots: insights on the exciton and biexciton interplay from detection-mode and time-gating†
Matteo
Bruschi
 *a,
Federico
Gallina
*a,
Federico
Gallina
 a and
Barbara
Fresch
a and
Barbara
Fresch
 *ab
*ab
aDipartimento di Scienze Chimiche, Università degli Studi di Padova, via Marzolo 1, Padua, 35131, Italy. E-mail: matteo.bruschi@phd.unipd.it; barbara.fresch@unipd.it
bPadua Quantum Technologies Research Center, Università degli Studi di Padova, Italy
First published on 3rd November 2022
Abstract
Action-2D electronic spectroscopy is emerging as a powerful technique to investigate exciton dynamics in molecular aggregates and nanostructures. While maintaining the power of highlighting coherent evolution between the laser pulses, action detection is based on measuring the incoherent signal proportional to the excited-state populations generated by an additional laser pulse. Numerical simulations of the action signal play a crucial role in aiding the interpretation of the spectral features, which may differ from those of the analog coherent technique in a non-trivial way. We present a numerical investigation of the action response of a model of quantum dot as a case study to unravel the exciton and biexciton contributions in the 2D-spectra of nanostructures. The simulation protocol is based on a non-perturbative treatment of the light–matter interaction by solving the Lindblad quantum master equation and the different contributions to the non-linear response are disentangled using a phase-modulation scheme. We analyze how the relative weights of the exciton and biexciton signals determine the lineshape of the spectrum, how they depend upon the physical nature of the detected signal, i.e., fluorescence or photocurrent, and on the relaxation dynamics during the detection-time. Compatibly with the experimental conditions, the choice of the detection-mode and the use of time-gating may eventually facilitate the evaluation of relevant parameters, such as the biexciton binding energy and the timescale of the biexciton relaxation.
1 Introduction
Two-Dimensional Electronic Spectroscopy (2DES) probes the dynamics of excited-states by triggering a multitude of excitation pathways through a sequence of ultrafast laser pulses. The pivotal technique is represented by Coherent-2DES (C-2DES) based on the measurement of a coherent signal, proportional to the macroscopic polarization, resolved along specific wavevector-matching directions upon the interaction with three non-collinear laser pulses. Following its success in the study of exciton dynamics in molecular aggregates and nanostructures, modifications of the original set-up have been recently developed.1 Among the others, Action-2DES (A-2DES) has received increasing attention in the last decade.2 This technique relies on the detection of an incoherent signal, proportional to the fourth-order excited-state population, generated by the interaction with four fully-collinear laser pulses. The components of the optical response are resolved by manipulating the phases of the laser pulses, using phase-cycling3 or phase-modulation4 schemes.Depending on the nature of the measured signal, A-2DES allows to probe excited-state populations through the use of different detection-modes, i.e., fluorescence,4,5 photocurrent,6,7 photoions8 or photoelectron9 emission. These action signals offer a unique perspective to observe the connection between the ultrafast dynamics of the system and measurable properties, such as photoluminescence and photocurrent generation, opening up to the study of devices in operando conditions.10 Moreover, A-2DES can be combined with single-molecule and microscopy techniques to achieve a spatial resolution beyond the diffraction-limit,11–13 thus circumventing the inhomogeneities which intrinsically contributes to spectral broadening, especially in the case of nanostructures.14 A-2DES experiments have been performed on a variety of systems, such as atomic vapors,4,15,16 molecular dimers,5,17 dyads18 and aggregates,19 photosynthetic systems,12,20 metal-molecule interfaces,21 organic22,23 and perovskite24 solar cells, PbS7 and CdSe25 quantum dots.
Because of the high-informative content of these spectra, together with the plethora of dynamical processes influencing the response, theoretical simulations of model systems are crucial to disentangle and decipher spectral features.26 Previous theoretical works have analyzed the response of A-2DES by pointing out the necessity of carefully reconsidering the origin of the spectral features compared to its coherent analog, in order to avoid potential pitfalls in their interpretation.27–34 An important example was given by Malý and Mančal in ref. 30 by considering the role of cross-peaks in the optical response of a molecular hetero-dimer: while cross-peaks at zero waiting-time are a good witness of exciton delocalization in a C-2DES spectrum, the same spectral features in fluorescence-detected A-2DES may be present even in the case of weak-coupling between chromophores due to exciton–exciton annihilation active during the detection-time. The same annihilation process may cause the absence of spectral features typically due to Excited-State Absorption (ESA), i.e., the A-2DES spectrum results ESA-free.34 Kunsel et al.32 extended the analysis to multichromophoric systems such as LH2, shedding light on the interpretation of fluorescence-detected A-2DES experiments of these systems.12,20
While in molecular systems the presence of multiple excitations is extremely unstable, in nanostructures such as colloidal quantum dots (QD), they may play a crucial role in determining the action response. A pioneering demonstration was provided by Karki et al. who measured both photocurrent and fluorescence signals from samples of PbS quantum dots.7 More recently, multiple-quantum 2DES experiments by Mueller et al. have characterized the multiexciton photophysics in alloyed core-shell QDs using fluorescence detection.25
In this paper, we theoretically investigate the details of the non-linear action response of a minimal model of a semiconducting quantum dots sample. A theoretical analysis of the photocurrent response of an analogous system has been recently presented by Chen et al. pointing out the effects of the sample-electrode coupling in the photocurrent response.35 Here, we will focus on the interplay between the exciton and the biexciton contributions in shaping the total A-2DES spectra collected through different detection-modes, i.e., fluorescence and photocurrent detection. Such an interplay is a relevant case study for both conceptual and practical reasons. A first consideration refers to the already mentioned issue of understanding the differences between the C-2DES and the A-2DES response. At the level of perturbation theory, the interaction with the fourth pulse generates an additional ESA pathway which does not enter in the response of a C-2DES experiment.27 Therefore, while the biexciton would appear as a simple negative contribution in a C-2DES spectrum,36,37 its effect in A-2DES should be analyzed. The point is tightly connected to the study of the effects of exciton–exciton annihilation in interacting molecules which have been debated in previous works30,31,34 but with important distinct features. Differently from small organic chromophores, multiexciton states are quite commonly generated in QDs under photoexcitation independently of possible interdot coupling. In a QD, biexcitons are relatively stable38 and can contribute actively to the measured signal,39,40 especially in photocurrent detection when fast interfacial charge-separation can effectively compete with exciton–exciton recombination.7,41,42 We will discuss thoroughly how these processes determine the contributions of several optical pathways to the final spectrum. In essence, the biexciton recombination dynamics plays an analogous role to the exciton–exciton annihilation process in molecular aggregates, but it only depends on the internal system dynamics rather than on intermolecular coupling. As the generation of biexcitons naturally depends also on laser intensity, numerical simulation protocols going beyond the perturbative response function are better suited for the study of their spectral features.
Our simulation protocol, described in Section 2, is based on a non-perturbative approach to the light–matter interaction and it directly implements the phase-modulation scheme in close analogy with the experimental procedure.43 Besides the advantage of accounting for finite-bandwidth and pulse-overlap effects,44 it allows a flexible description of different relaxation pathways through the modeling of the dissipator of a Quantum Master Equation (QME) in the Lindblad form. This setting will allow us to naturally include the slow incoherent processes involved in the action-detection scheme in the simulation of the spectra. In Section 3.1, we will connect the fully dynamical picture given by the solution of the QME with the analysis of the spectra based on the contribution of different Feynman pathways from perturbative response theory.45,46 Building this connection will allow us to point out and discuss the effects of the detection-time dynamics on the 2D-spectrum obtained with different action signals. In Section 3.2, we will do so by isolating the effects of changing the detection-mode and of implementing time-gating of the collected signal. Time-gating of the fluorescence emission has been proposed as a useful technique to monitor the dynamics during the exciton–exciton annihilation process.30,32 Indeed, the timescale of the signal detection is definitely slower than the ultrafast timescale probed during photoexcitation and time-gating can be used to change the weights of different contributions to the total spectrum according to their dynamics. In Section 3.3, we show how controlling such weights is also the key to facilitating the reading of meaningful information from the analysis of the spectrum. For example, different optimal gating-time can be devised to estimate the biexciton binding energy, depending on the ratio of the exciton and the biexciton quantum yields. Furthermore, time-gating can be used to track the evolution of the relative amplitudes of spectral features providing information on the relaxation dynamics. In Section 4, we draw our conclusions and discuss the limitations of our analysis pointing out the directions for future work.
2 Theory and simulations
2.1 Model system
The electronic structure of nanocrystals can be described at different levels of theory. Here, we use the simplest picture explaining the absorption bands of small colloidal CdSe nanocrystals in the strong-confinement regime.47Upon photoexcitation, an electron (e) is promoted to the conduction-band and the corresponding hole (h) is created in the valence-band. The spherical symmetry of the confining potential leads to a hydrogen-like structure for the envelope function of the charge-carriers, labeled by a principal quantum number and the corresponding angular momentum (e.g., 1S, 2S, 1P, etc.). Due to the spin–orbit coupling, the valence-band which originates from the p orbitals of selenium atoms is further split according to the total angular momentum, with the state 1S3/2 being the lowest in energy. By explicitly considering the significant Coulomb interaction between hole and electron, we switch from the electron–hole basis to the excitonic basis, which is optically probed.48 In small CdSe QD, the two lowest energy excitons, conventionally named 1S and 2S, roughly correspond to the transitions 1S3/2(h) → 1S(e) and 2S3/2(h) → 1S(e) in the hole–electron picture. A more detailed description of the quantum mechanical interactions within the nanocrystal would reveal additional splitting of the bands, the so-called fine-structure of the excitons,38,49 however the coarse structure of the energy levels will suffice for the scope of this study.
Recently, Collini et al. presented a series of C-2DES spectra of samples of small CdSe QDs both in solution and in solid-state aggregates.50 We will refer to nanocrystals of the diameter of 2.8 nm and we will assume that the spectral bandwidth of the laser only covers the lowest energy exciton (1S) at around 2.34 eV, while the 2S manifold, lying more than 0.25 eV higher in energy, is excluded. The biexciton is generated from the band-edge exciton by the subsequent excitation of a second electron–hole pair. Since no other states are involved in the dynamics, this is the ideal setting to focus on the interplay between the exciton and the biexciton contributions to the A-2DES spectra.
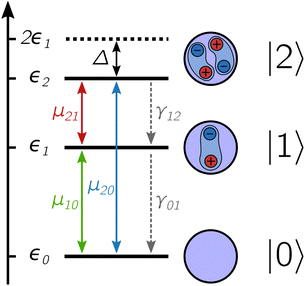
The energy structure of the QD nanocrystal is thus treated as a three-level system composed of the ground state |0〉, the band-edge exciton manifold |1〉 and the biexciton manifold |2〉 (Fig. 1). The corresponding Hamiltonian reads
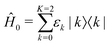 | (1) |
When the nanostructure interacts with the laser pulses, transitions between the different manifolds are induced according to the transition dipole moment operator:
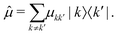 | (2) |
2.2 Action-2D electronic spectroscopy
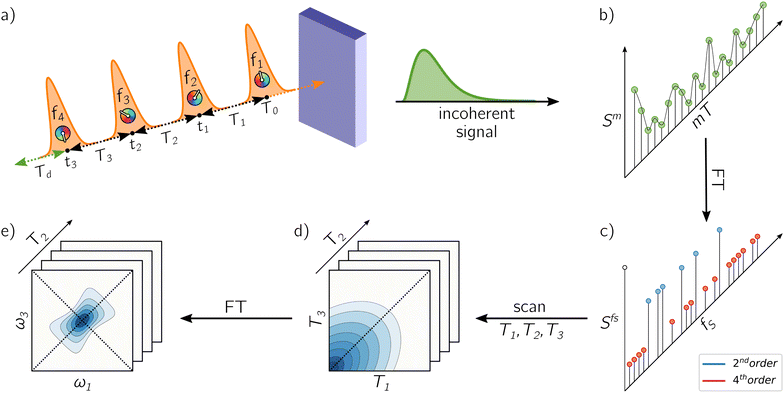
In the following, we introduce the working principles of A-2DES using a phase-modulation scheme. Fig. 2 outlines the main steps to obtain the 2D-spectra starting from the quantum dynamics triggered by the train of laser pulses. All these steps are implemented in the numerical simulation protocol in close analogy to the experimental procedure.Overall, the sample interacts with M + 1 trains of four laser pulses, separated by an intertrain delay-time T. In the phase-modulation protocol, the phase of each pulse, which can assume a finite set of values between 0 and 2π, is varied at a given modulation frequency. The m-th train, made of four collinear laser pulses (Fig. 2a), is written as:
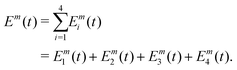 | (3) |
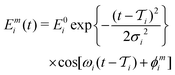 | (4) |
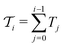 .
.
According to the non-linear response theory, the interaction with the former three pulses prepares the system into a coherent superposition of excited-states, which is then converted into an observable fourth-order population by the interaction with the last pulse.27 The incoherent signal, emitted during the detection-time Td, is thus proportional to the excited-state populations. Let us define  as the projection operator onto the k-th state and the coefficient γ(r)k as the rate of the relaxation event contributing to the signal, i.e., spontaneous emission for fluorescence and charge-separation for photocurrent detection. Typically, the timescale of the emitted signal is several orders of magnitude longer than the femtosecond timescale probed during photoexcitation. After the fourth pulse, the signal is obtained as the expectation value of the operator
as the projection operator onto the k-th state and the coefficient γ(r)k as the rate of the relaxation event contributing to the signal, i.e., spontaneous emission for fluorescence and charge-separation for photocurrent detection. Typically, the timescale of the emitted signal is several orders of magnitude longer than the femtosecond timescale probed during photoexcitation. After the fourth pulse, the signal is obtained as the expectation value of the operator 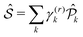 taken over the density matrix of the system, which leads to the explicit form of the time-resolved signal:
taken over the density matrix of the system, which leads to the explicit form of the time-resolved signal:
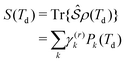 | (5) |
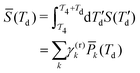 | (6) |
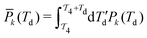 is the time-integrated population of the k-th state. Compared to C-2DES, the detection-time Td represents an additional dynamical variable in A-2DES. Furthermore, we emphasize that the incoherent signal depends parametrically, through the system density matrix, also on the phase-modulation index m and the set of delay-times as Sm(T1,T2,T3,Td). To disentangle the different contributions to the optical response, a phase-modulation scheme is employed.4 In practice, the phase of each pulse ϕmi = 2πmfiT is linearly modulated from a train to the following by varying the phase-modulation index m ∈ [0,M], where fi is the phase-modulation frequency of the i-th pulse and T is the intertrain delay-time, namely the time between the first pulse of two consecutive trains. For each set of delay-times and phase relations, the intensity of the signal obtained after excitation is stored as a function of the phase-modulation index and the intertrain delay-time mT (Fig. 2b). By taking the Fourier Transform along this variable, the Phase-Modulation Spectrum (PMS) is retrieved Sfs (Fig. 2c), which contains the various contributions to the optical response of the system. Each peak in the PMS is labeled by a certain modulation frequency fS given by the linear combinations of the modulation frequencies of each pulse fi:
is the time-integrated population of the k-th state. Compared to C-2DES, the detection-time Td represents an additional dynamical variable in A-2DES. Furthermore, we emphasize that the incoherent signal depends parametrically, through the system density matrix, also on the phase-modulation index m and the set of delay-times as Sm(T1,T2,T3,Td). To disentangle the different contributions to the optical response, a phase-modulation scheme is employed.4 In practice, the phase of each pulse ϕmi = 2πmfiT is linearly modulated from a train to the following by varying the phase-modulation index m ∈ [0,M], where fi is the phase-modulation frequency of the i-th pulse and T is the intertrain delay-time, namely the time between the first pulse of two consecutive trains. For each set of delay-times and phase relations, the intensity of the signal obtained after excitation is stored as a function of the phase-modulation index and the intertrain delay-time mT (Fig. 2b). By taking the Fourier Transform along this variable, the Phase-Modulation Spectrum (PMS) is retrieved Sfs (Fig. 2c), which contains the various contributions to the optical response of the system. Each peak in the PMS is labeled by a certain modulation frequency fS given by the linear combinations of the modulation frequencies of each pulse fi: 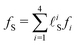 , where
, where ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) iS = 0, ±1, ±2, etc. The decomposition of the optical response in the PMS reflects the spatial decomposition of the polarization along the wavevector-matching directions in the non-collinear set-up of C-2DES.45 Each component in the PMS can be regarded as the signal related to a set of excitation pathways induced by a specific sequence of interactions with the laser pulses. Despite the cost of performing several phase realizations of the experiment, the phase-modulation protocol has the advantage of simultaneously obtaining the second-order response, i.e., linear absorption spectra, the fourth-order response, i.e., rephasing, non-rephasing and two-quantum signals, and even higher-order response in the light–matter coupling.
iS = 0, ±1, ±2, etc. The decomposition of the optical response in the PMS reflects the spatial decomposition of the polarization along the wavevector-matching directions in the non-collinear set-up of C-2DES.45 Each component in the PMS can be regarded as the signal related to a set of excitation pathways induced by a specific sequence of interactions with the laser pulses. Despite the cost of performing several phase realizations of the experiment, the phase-modulation protocol has the advantage of simultaneously obtaining the second-order response, i.e., linear absorption spectra, the fourth-order response, i.e., rephasing, non-rephasing and two-quantum signals, and even higher-order response in the light–matter coupling.
Both in the experiment and numerical simulation, the choice of the modulation frequencies is of key importance to isolate the components of interest. Also, notice that higher-order contributions can always enter at the same modulation frequency as lower-order contributions, therefore the strength of the excitation needs to be taken into account when interpreting the obtained spectra. From the numerical point of view, a suitable choice of modulation frequencies should also aim at minimizing the length of the phase-modulation sequence M in order to reduce the computational cost of running the dynamical evolution for each phase realization. By following these principles, we have selected the modulation frequencies reported in Table 1, together with the values of other specific parameters used for the simulations. The numerical values are compatible with the experimental set-up of ref. 23 and 50.
| Symbols | Meaning | Values |
|---|---|---|
| μ kk′ E 0 i | Light–matter coupling strength | 8 meV |
| σ i | Pulse duration | 5 fs |
| ħω i | Carrier-energy | 2.34 eV |
| T 0 | Center of the 1st pulse | 50 fs |
| M | Total phase-modulation index | 179 |
| f 1 | Modulation frequency 1st pulse | 0 Hz |
| f 2 | Modulation frequency 2nd pulse | 250 Hz |
| f 3 | Modulation frequency 3rd pulse | 600 Hz |
| f 4 | Modulation frequency 4th pulse | 1000 Hz |
| T | Intertrain delay-time | 1/3000 s |
At this point, by following the evolution of the components of the PMS as a function of the delay-times T1, T2 and T3, we obtain the time-dependent signal (Fig. 2d) and, by taking the Fourier Transform along suitable delay-times, the corresponding spectra are recovered (Fig. 2e). In general, the frequency axes chosen to display the 2D-map depend on the specific signal considered. In the case of the rephasing spectrum, the signal extracted from the PMS is Fourier transformed along the delay-times T1 and T3 to obtain a 2D-map as a function of the frequencies ω1 and ω3 for each value of T2. In Section 3, we will consider two classes of 2D-spectra characterized by the order of the coherences which are detected. The more common rephasing and non-rephasing signals are characterized by coherences between states that are separated by a single excitation, i.e., ground-exciton coherence or exciton-biexciton coherence. The second class is represented by two-quantum signals,51i.e., Two-Quantum-One-Quantum (2Q1Q) and One-Quantum-Two-Quantum (1Q2Q), which directly investigate also coherences between states separated by two excitations, i.e., ground-biexciton coherence. Their respective positions in the PMS are: rephasing at fS = −f1 + f2 + f3 − f4 = 150 Hz, non-rephasing at fS = f1 − f2 + f3 − f4 = 650 Hz, 2Q1Q at fS = 2f1 − f2 − f3 = 850 Hz and 1Q2Q at fS = −f1 − f2 + 2f3 = 950 Hz.
For the simulations, the delay-times have been scanned in steps of 10 fs from 0 to 300 fs, working in the rotating-frame at a frequency of ωRF = 3.56 [rad] fs−1 (doubled in the case of two-quantum signals). In order to smooth the spectra, each signal has been zero-padded in the time-domain. In the following, only the real part of each map is shown and the intensity is normalized relative to its absolute maximum/minimum. For the rephasing and non-rephasing signals, T1 and T3 are scanned while setting T2 = 0 fs. For 2Q1Q and 1Q2Q signals, T1 and T2 are scanned while setting T3 = 0 fs. Notice that the two-quantum signals correspond to the set of pathways where the system interacts twice with the first pulse (2Q1Q) or with the third pulse (1Q2Q) while there is no interaction with the fourth pulse.
2.3 Quantum dynamics
By avoiding the evaluation of the response function, non-perturbative approaches to the simulation of 2DES spectra rely on the explicit dynamics of the density matrix under the effect of the electric-field, at the cost of introducing an effective strategy to extract the pertinent component of the optical response.52,53In this context, the phase-modulation scheme is implemented to resolve the various components of the overall signal.43 Making use of the theory of open quantum system, the evolution of the density matrix during the experiment is obtained by solving the quantum master equation in the Lindblad form,54,55 assuming ħ = 1 in the following:
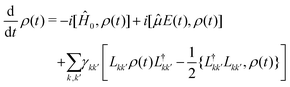 | (7) |
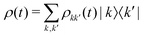 describes the state of the system, whose diagonal elements represent the populations of each excitonic state while the off-diagonal elements represent the coherences between them. In the QME, the first term accounts for the coherent evolution due to the system Hamiltonian (eqn (1)), the second term accounts for the light–matter interaction in the dipole-approximation (eqn (2) and (3)) and the last term accounts for the effects of the coupling with the environment, inducing decoherence and relaxation processes in the dynamics. An incoherent transition between states k′ and k is described by the Lindblad operator Lkk′ = |k〉〈k′| with an associated characteristic rate γkk′. Therefore, we define the relaxation mechanism as a cascade process from the biexciton to the exciton state, with L12 = |1〉 〈2|, and then from the exciton to the ground state, with L01 = |0〉〈1| (Fig. 1). The rates include all the decay channels, which may or may not contribute to the recorded signal, e.g., the transition from the biexciton to the exciton manifold can happen through radiative emission or fast Auger recombination. In addition, we introduce pure dephasing contributions through the Lindblad operators L00 = |0〉〈0|, L11 = |1〉〈1| and L22 = |2〉〈2|. Except otherwise stated, the characteristic relaxation times used in this work are γ01−1 = 10 ns and γ12−1 = 100 ps, while the decoherence time is γkk−1 = 100 fs. These parameters have been chosen in agreement with recent studies on similar systems.25
describes the state of the system, whose diagonal elements represent the populations of each excitonic state while the off-diagonal elements represent the coherences between them. In the QME, the first term accounts for the coherent evolution due to the system Hamiltonian (eqn (1)), the second term accounts for the light–matter interaction in the dipole-approximation (eqn (2) and (3)) and the last term accounts for the effects of the coupling with the environment, inducing decoherence and relaxation processes in the dynamics. An incoherent transition between states k′ and k is described by the Lindblad operator Lkk′ = |k〉〈k′| with an associated characteristic rate γkk′. Therefore, we define the relaxation mechanism as a cascade process from the biexciton to the exciton state, with L12 = |1〉 〈2|, and then from the exciton to the ground state, with L01 = |0〉〈1| (Fig. 1). The rates include all the decay channels, which may or may not contribute to the recorded signal, e.g., the transition from the biexciton to the exciton manifold can happen through radiative emission or fast Auger recombination. In addition, we introduce pure dephasing contributions through the Lindblad operators L00 = |0〉〈0|, L11 = |1〉〈1| and L22 = |2〉〈2|. Except otherwise stated, the characteristic relaxation times used in this work are γ01−1 = 10 ns and γ12−1 = 100 ps, while the decoherence time is γkk−1 = 100 fs. These parameters have been chosen in agreement with recent studies on similar systems.25
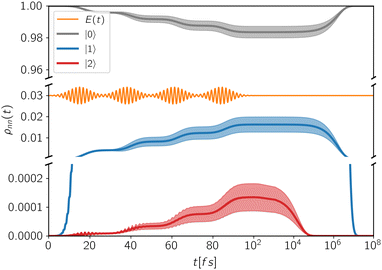
In Fig. 3 is reported the evolution of the diagonal elements of the density matrix induced by a train of pulses applied at regular delay-times. During each pulse, populations are coherently transferred between different states. The shaded area represents the variability of the population with respect to the specific phase realization of the pulses which is highly dependent on the decoherence time. Indeed, when the delay-times Ti exceeds the decoherence time γkk−1, no modulation of the final populations is observed. While decoherence primarily influences the system dynamics during photoexcitation, the relaxation mechanisms act on a slower timescale and become relevant especially during the detection-time Td.
Notice that according to eqn (7), in the absence of the external electric-field, the evolution of populations is decoupled from coherences. This means that, after the end of the fourth pulse, the dynamics of populations can be described in terms of a simple kinetic equation:
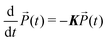 | (8) |
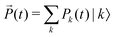 contains the occupation probability of each state and the kinetic matrix is defined by the rates of the relaxation processes connecting different diagonal elements of the density matrix, that is:
contains the occupation probability of each state and the kinetic matrix is defined by the rates of the relaxation processes connecting different diagonal elements of the density matrix, that is: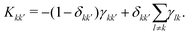 | (9) |
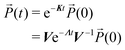 | (10) |
In the simulations, the Lindblad QME (eqn (7)) has been numerically integrated using the (4th order) Runge–Kutta method with a time-step of 0.1 fs from 0 fs until 100 fs after the center of the fourth pulse. Then, the kinetic scheme for the populations is solved by diagonalizing K and evolving using a time-step of 100 fs.
3 Results and discussion
3.1 Exciton and biexciton contributions to the A-2DES spectra
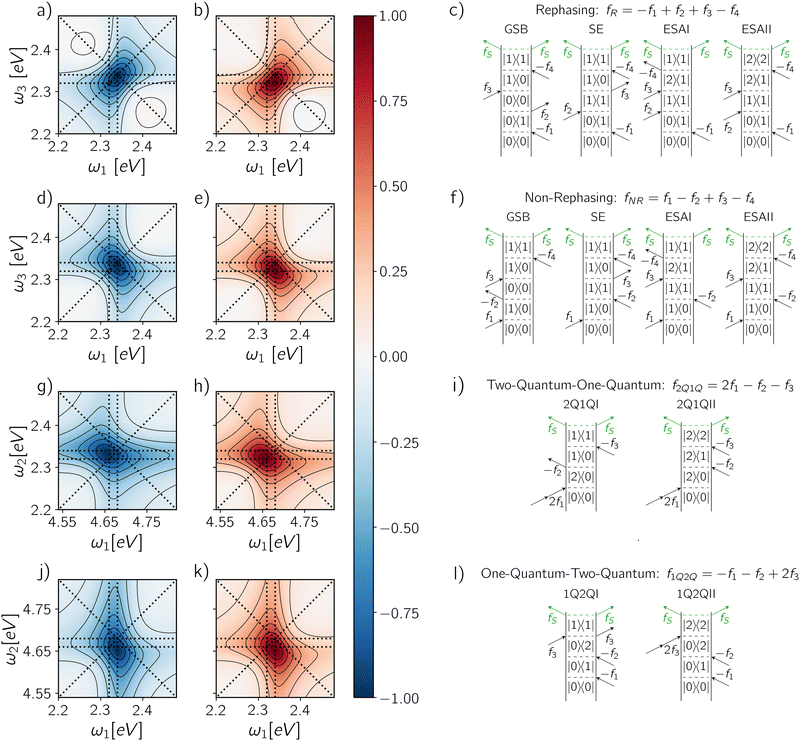
By applying the numerical procedure described in the previous section, we simulate the 2D-maps originating from the exciton and the biexciton states on the basis of the fourth-order population generated by the last pulse, ideally before any quantitative relaxation process occurs during Td. Although the non-perturbative solution of the system dynamics is a powerful method for the calculation of non-linear signals, the perturbative approach remains the key tool for the interpretation of the optical response in terms of different dynamical pathways. Accordingly, we will examine the exciton and biexciton contributions by using perturbative terminology45,46 to analyze how they combine in the total spectrum.We start by discussing the exciton and the biexciton contributions for the rephasing (Fig. 4a and b) and non-rephasing (Fig. 4d and e) signals along with the corresponding Feynman diagrams (Fig. 4c and f). Each Feynman diagram represents a dynamical pathway, specified by the sequence of coherence or population states of the system, induced by the interaction with the laser pulses. In the rephasing and non-rephasing signals, the system interacts once with each pulse, as represented by the four black arrows in a Feynman diagram. The incoherent signal, depicted as two green arrows, is due to the relaxation of the population generated by the fourth interaction. The sign by which a certain pathway contributes to the spectrum is given by the factor (−1)n, where n is the number of interactions on the bra side in the corresponding diagram. Depending on the sequence of interactions involved in a Feynman pathway, its contribution can be distinguished into Ground-State Bleaching (GSB), Stimulated Emission (SE) and Excited-State Absorption (ESA). The interaction with the first pulse prepares the system in a ground-exciton coherence oscillating during the delay-time T1. Then, the interaction with a second pulse generates a population that can be either in the ground or in the exciton state. The ground state population is associated with the GSB pathway upon the subsequent interaction with the last two pulses, while the exciton population follows the SE pathway, if the system emits upon interaction with the third pulse, or alternatively an ESA pathway, if it absorbs a photon from the third pulse. Whereas both GSB and SE pathways end in the exciton manifold, due to the interaction with the fourth pulse, two types of ESA pathways are possible in A-2DES: the ESAI, leading to a final population in the exciton manifold, and the ESAII, ending in a biexciton population.
It should be stressed that it is not possible to isolate the signal corresponding to a specific pathway (GSB, SE or ESA) from the full dynamical evolution of the density matrix since they represent just terms of a perturbative expansion.30 However, in principle, we can resolve the exciton and the biexciton contributions on the basis of the final population state from which the incoherent signal originates. Therefore, the exciton contribution results from the GSB, SE and ESAI pathways, while the biexciton contribution results from the ESAII pathway. Accordingly, the rephasing spectrum of the exciton manifold (Fig. 4a) shows a prominent negative peak along the diagonal at coordinates (ω10, ω10), corresponding to the GSB and SE pathways, and a less intense off-diagonal contribution from the ESAI centered at (ω10, ω21) which introduces an asymmetry in the peak leading to a lineshape elongated below the diagonal. On the other hand, the spectrum associated with the biexciton contribution (Fig. 4b) exhibits a positive off-diagonal peak at coordinates (ω10, ω21) related to the ESAII pathway. These contributions, which are defined based on the populations after the fourth pulse, are analogous to the corresponding terms of the perturbative response function reported in the ESI† (Fig. S1).
The opposite sign of the spectral contributions of the exciton and the biexciton is conserved also along other phase-modulation components. For example, within the same set of dynamical simulations, we can investigate less common contributions of the response, such as the Two-Quantum-One-Quantum (2Q1Q) and One-Quantum-Two-Quantum (1Q2Q) signals. The measurement of these components in an action-detected setting has been recently realized by Mueller et al.51,56 and applied to the study of QD nanocrystals.25 In this case, a two-quantum (2Q) coherence, i.e., coherence between states that are two excitations apart, is correlated with a one-quantum (1Q) coherence, i.e., coherence between states that are one excitation apart. In the following, we discuss the exciton and biexciton contributions in the 2Q1Q (Fig. 4g and h) and 1Q2Q (Fig. 4j and k) spectra along with the corresponding Feynman diagrams (Fig. 4i and l). The two signals are both characterized by only two Feynman diagrams, differing in the temporal sequence of the one- and two-quantum coherences. In 2Q1Q, the interaction of the system with the first pulse causes the absorption of two photons, generating a 2Q coherence between the ground and the biexciton states which evolves along T1. The subsequent interaction converts the state into a 1Q coherence: if the 1Q coherence which is established is a ground-exciton coherence, the signal is eventually emitted from the exciton manifold (2Q1QI), while in the case of an exciton-biexciton coherence, the signal is emitted from the biexciton state (2Q1QII). Similarly, for the 1Q2Q experiment, one pathway leads to the exciton population (1Q2QI), while the other leads to the biexciton population (1Q2QII) after the fourth pulse. The corresponding spectra are obtained by taking the Fourier Transform of the delay-times T1 and T2, directly correlating the two coherences. In the 2Q1Q map, the exciton and the biexciton contributions are centered respectively at two different spectral positions (ω20, ω10) and (ω20, ω21), while in the case of 1Q2Q map, they are found at the same coordinates (ω10, ω20).
Because the contribution of the biexciton is always of opposite sign than the exciton one, cancellation between different pathways takes place and the resulting spectral lineshape will crucially depend on their relative weights. Let us focus on the rephasing spectra, where the ESAI and ESAII pathways contribute in the same spectral location with opposite signs. To analyze the overall spectra, the contribution of different manifolds can be weighted by a phenomenological relative yield coefficient Γ, which quantifies the mean number of emitted photons in fluorescence detection, or charge-carriers in photocurrent detection, generated from the biexciton state relative to the average number generated from the exciton.7,27,30 The overall spectrum is then expressed in terms of exciton and biexciton contributions as follows
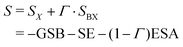 | (11) |
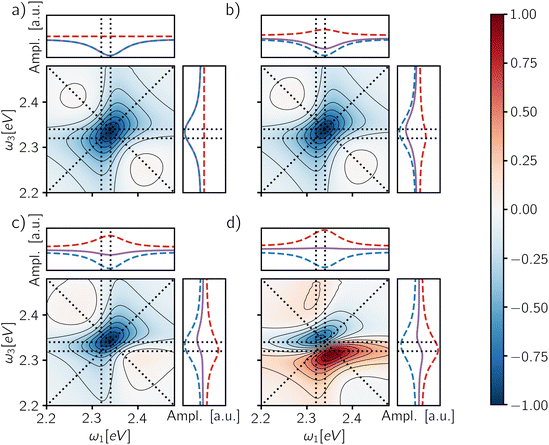 | ||
| Fig. 5 Rephasing maps calculated as a weighted sum of the exciton and biexciton contributions (eqn (11)) after the end of the fourth pulse for a phenomenological yield coefficient: (a) Γ = 0, (b) Γ = 1, (c) Γ = 2 and (d) Γ = 3. Each map is normalized to its absolute maximum/minimum. The panels on the top and the right of each map report the total signal (purple solid line), the isolated exciton contribution (blue dashed line) and the isolated biexciton contribution (red dashed line) averaged along ω3 and ω1 axes respectively. The signal has been integrated up to a detection-time Td = 1 ps. | ||
3.2 Effects of different detection-modes and time-gating
The special cases discussed in the previous section require strong assumptions on the relaxation dynamics of the excited manifolds of the system under consideration. While for molecular aggregates probed using fluorescence it is generally safe to assume a quantitative relaxation from the double-excited state to the single-excited state before signal detection,17,32 the biexcitons of QDs are characterized by a broader phenomenology which should be taken into account to correctly interpret the interplay between exciton and biexciton contributions in the total spectrum. In this section, we will answer the following questions: how can we determine the relative yield coefficient Γ from the relaxation rates governing the system dynamics (eqn (7))? Are there “experimental knobs” that can be used to control the relative weights of exciton and biexciton contributions in the final spectrum?We start by further specifying the total relaxation rates between two manifolds, γkk′ in eqn (7), in terms of a radiative (r) and a non-radiative (nr) contribution:
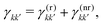 | (12) |
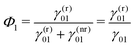 | (13) |
 | (14) |
By definition, the GQY is bounded: if the radiative contribution exceeds the non-radiative one 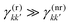 , the GQY is Φk → 1, otherwise for
, the GQY is Φk → 1, otherwise for 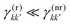 , the GQY is Φk → 0. Then, the signal in eqn (5) can be written in terms of the total relaxation rate, the GQY and the population of each state:
, the GQY is Φk → 0. Then, the signal in eqn (5) can be written in terms of the total relaxation rate, the GQY and the population of each state:
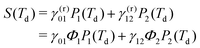 | (15) |
To proceed in our analysis, we assume that the ratio between the total relaxation rates γ12/γ01 is a constant that characterizes the system, while the Generalized Quantum Yields and the populations can be influenced, to some extent, by changing the settings of the spectroscopic experiment. Specifically, the ratio of the GQY Φ2/Φ1 strongly depends on the adopted detection-mode, while the ratio of the populations P2(Td)/P1(Td) depends on the detection-time. Fluorescence detection is typically associated with a low GQY ratio because higher excited-states mainly relax non-radiatively to the first excited state from which radiative emission occurs. However, while in molecular systems this ratio is commonly negligible, nanocrystals may exhibit a wider photophysical phenomenology with the GQY of the biexciton varying significantly in every single nanostructure and even approaching unity, when Auger decay channels are suppressed by thick shells.39,57–59 When the sample can be detected through photocurrent, the radiative contribution from multiexciton manifolds can be even higher, thus reversing the relative magnitude of the GQY of exciton and biexciton. When higher excitation frequencies are used, the presence of higher Quantum Yields may also depend on Multiple Exciton Generation (MEG).7
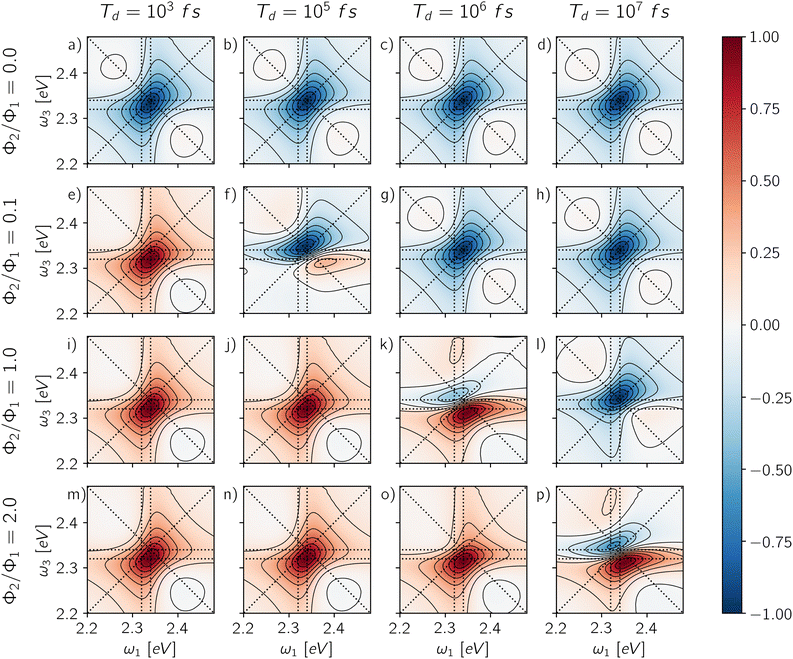
The last column of Fig. 6 shows the spectra obtained from the fully integrated signal for different GQY ratios. When the biexciton does not contribute directly to the detected signal (Φ2/Φ1 = 0), a quantitative relaxation of the biexciton to the exciton manifold takes place before emission. In this case, the signal originating from the ESAII pathway is transferred quantitatively to the exciton manifold during the detection-time and therefore it cancels exactly the ESAI signal. In other words, we realize the case of Γ = 1 (Fig. 5b) resulting in an ESA-free spectrum. In all the other cases, because the radiative decay of the biexciton is faster than the decay from the exciton manifold, we are in situations where Γ > 1 and the active contribution of the biexciton is observed in the off-diagonal position. Notice that the transfer of the ESAII contribution into the exciton manifold is a relatively slow dynamical process taking place during the detection-time Td.
The presence of a detection-time Td is another element of novelty of A-2DES compared to C-2DES and represents an additional experimental parameter influencing the optical response of the system. Time-gating techniques can be used, in principle, to resolve the emission in time by integrating the signal over a limited temporal window during detection. This technique has been already experimentally implemented in time-resolved fluorescence, photoluminescence60 and microscopy.61 Although the possibility to combine time-gating with fluorescence-detected A-2DES has been recently proposed,30,32 an experimental implementation is still lacking to our knowledge. While in fluorescence detection, time-gating may be achieved by photon-counting techniques, fast transient photocurrent measurements have also been reported in quantum dot assemblies.62
Through the choice of the detection-time, it is possible to parametrically control the ratio between biexciton and exciton populations P2(Td)/P1(Td). Therefore, the dynamics of the spectral features as a function of Td reflects the relaxation dynamics of the excited manifolds. The effect of changing the detection-time is reported in Fig. 6, where each row shows the spectra resulting from changing the integration window for each value of the GQY ratio. When the biexciton does not contribute actively to the signal for Φ2 = 0.0 (Fig. 6a–d), the biexciton contribution cannot become explicit and all the maps show a prominent negative diagonal feature mainly due to the GSB and SE pathways. However, for Td shorter than the biexciton recombination (Td < γ12−1), the spectra result slightly asymmetric, characterized by a counter-clockwise peak twist and a broadening below diagonal. Indeed, when the signal is collected before Auger relaxation, the ESA cancellation is not complete and the spectra reveal the off-diagonal feature at (ω10, ω21) corresponding to the ESAI pathway. As the detection-time increases (Td > γ12−1), the symmetry of the peak is restored because the biexciton converts to exciton and the ESAI pathway is completely canceled by the ESAII, resulting in the ESA-free spectrum.
When the biexciton contributes radiatively to the signal, the lineshape may change drastically as the Td proceeds. A similar trend is observed for all cases in which Φ2/Φ1 ≠ 0. In particular, at early Td, the main contribution to the spectra is the positive off-diagonal peak originating from the biexciton. Even in the case of a relatively small biexciton QY (Φ2/Φ1 = 0.1), the faster relaxation rate implies that the spectrum is dominated by the biexciton contribution at early detection-time. As the Td increases, the diagonal contribution from the exciton manifold gains intensity and because of cancellation effects, the map results in a dispersive lineshape. Due to the partial cancellation of positive and negative contributions, the maximum and the minimum do not fall at the same position as the isolated contributions, shown in Fig. 4, but the peaks are respectively red- and blue-shifted along the frequency axes.
In general, the details of the evolution of the overall spectral lineshape as a function of the detection-time depend on the kinetics of the populations relaxation (eqn (10)). In this case, we consider an idealized model where the non-radiative relaxation is characterized by a single rate. However, the kinetic scheme can be easily generalized by introducing other processes, notably hot-carrier relaxation and trapping due to surface effects, inducing more complex non-exponential behavior. Notice that a different dynamics during the detection-time implies a different combination of the exciton and biexciton contributions resulting in a different lineshape. Nonetheless, the individual contributions are defined prior to any relaxation dynamics (Section 3.1) and therefore, as long as the relaxation is slow compared to the timescale of the pulse train, they do not depend on the details of the relaxation processes.
We shall emphasize how the effects of the detection-mode and time-gating are in some sense complementary. Considering different combinations of the two parameters may produce similar results: isolating the exciton contribution (Fig. 6a–d, g, h and l), isolating the biexciton contribution (Fig. 6e, i, j and m–o) or featuring their simultaneous presence (Fig. 6f, k and p). The choice of the detection-mode and the use of time-gating may be used in combination to isolate specific contributions in the 2D-maps. Analogous combinations of the exciton and the biexciton signal determine the non-rephasing, 2Q1Q and 1Q2Q spectra, reported in the ESI† (Fig. S2–S4).
3.3 Signatures of binding energy and relaxation rates
In the previous section, we discussed how the combination of the exciton and the biexciton contributions gives rise to a variety of spectral shapes according to the specific system dynamics and experimental settings, such as the detection-mode and the time-gating. This diversity implies that the information about the system may be encoded in different spectral features. Now, we will focus on two parameters characterizing our simplified model of exciton and biexciton manifolds in nanocrystals, namely the biexciton binding energy and the biexciton relaxation rate, discussing their connection with spectral signatures.The biexciton binding energy gives a direct measurement of the correlation between two excitons in the QD and is defined by the difference between twice the exciton energy and the biexciton one, Δ = 2ε1 − ε2. Experimentally, it can be measured using pump–probe transient absorption spectroscopy, however, two-dimensional techniques offer the possibility to resolve the signal along two frequency axes and to operate at low excitation power, ideally limiting the number of overlapping processes in the signal.37,63–67 In 2DES experiments, the biexciton binding energy is obtained from a fitting procedure of the 2D-maps using a parameterized model. However, its quantification remains challenging and the sample inhomogeneities are detrimental.
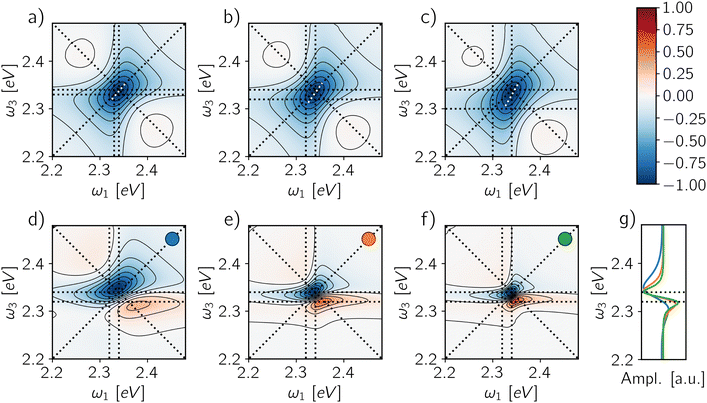
In this context, the possibility to combine A-2DES with single-molecule techniques to probe individual QDs is a promising route to characterize the biexciton manifold. The biexciton binding energy can be expressed in terms of the transition frequencies probed in the A-2DES rephasing spectra as Δ = ω10 − ω21. Therefore, the spectral position of the ESA feature is the key to evaluating the binding energy, either by directly considering its spectral coordinates (ω10, ω21) or by taking the distance of the ESA feature from the main diagonal peak located at (ω10, ω10) along the ω3 axis. Notice that in the cases where the biexciton manifold does not contribute directly to the signal (Φ2/Φ1 = 0) and the intensity is integrated over the detection-time, the spectrum is ESA-free and the information on the binding energy is completely lost. The only possibility to observe the effect of the biexciton is to avoid the cancellation of the ESAI pathway by employing a short time-gating window, as shown in Fig. 7a–c, where the maps are obtained by integrating the signal for 1 ps after the end of the fourth pulse. Even in this case, as long as the binding energy is smaller than the peak broadening, the ESAI contribution appears as a peak twist of the main diagonal contribution. As the value of Δ increases (Fig. 7a–c), the ESAI contribution is centered further apart from the diagonal, resulting in a more pronounced twist.
The situation changes when the biexciton gives a radiative contribution to the signal, as shown in Fig. 7d–f, where the spectra for a QY ratio Φ2/Φ1 = 0.1 and a time-gating window of 100 ps are reported for three different decoherence rates. In this case, the biexciton binding energy can be evaluated directly as the distance along ω3 between the negative and the positive spectral features. The projection of the lineshape profile along ω3 (Fig. 7g) shows how such an estimation is robust against the peak-shift of the exciton and biexciton contributions due to cancellation effects, even when the broadening is large. Indeed, the peak positions are more susceptible to variations along ω1 axis than ω3 for different weights of exciton and biexciton contributions. Moreover, since the phase-modulation protocol provides direct access to other components of the phase-modulation spectrum, the estimation of the biexciton binding energy can be checked by looking at other fourth-order signals, i.e., 1Q2Q and 2Q1Q. In these cases, the binding energy can be written in terms of one- and two-quantum transition frequencies as Δ = 2ω10 − ω20. Particularly convenient is the case of 1Q2Q spectra, where all the spectral contributions are centered at (ω10, ω20) (Fig. 4j and k). Therefore, in this situation, the main spectral peak allows a good estimation of the biexciton binding energy independently of the application of the time-gating.
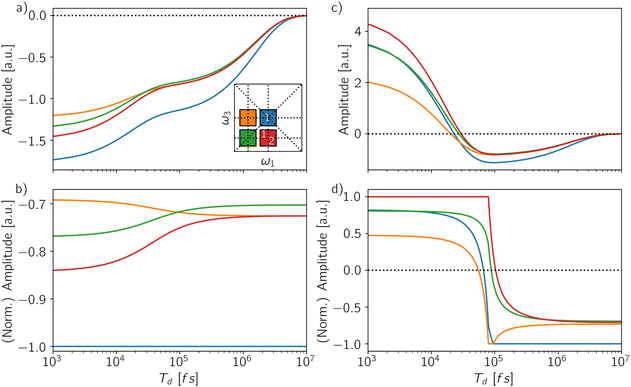
Besides varying the contribution of the biexciton, the detection-time can be understood as a further dimension to analyze, by monitoring how the spectral features change as a function of Td. Indeed, by time-gating the signal, one can in principle follow the incoherent dynamics connecting different manifolds. Let us pinpoint four different spectral positions in the rephasing map to define a square (inset of Fig. 8a): the diagonal peak at (ω10, ω10) (blue square) featuring the GSB and SE from the exciton, the off-diagonal peak at (ω10, ω21) (red square) featuring the interplay of the two Excited-State Absorption pathways from the exciton (ESAI) and the biexciton (ESAII), and two control positions, one above diagonal at (ω21, ω10) (orange square) and one on the diagonal at (ω21, ω21) (green square). We report the amplitude of these spectral positions as a function of the detection-time for two different QY ratios: Φ2/Φ1 = 0.0 (Fig. 8a and b) and Φ2/Φ1 = 0.1 (Fig. 8c and d). In Fig. 8a and c, we follow the instantaneous evolution according to eqn (5) without any integration step, while in Fig. 8b and d, the signal is integrated within a temporal window of increasing length (eqn (6)) and normalized with respect to the amplitude of the dominant peak. The instantaneous temporal profile of the spectral intensities directly reflects the dynamics of the populations showing two different relaxation timescales: the biexciton lifetime at Td ≈ 105 fs and the exciton relaxation at Td ≈ 107 fs. In the case of Φ2/Φ1 = 0.0 (Fig. 8a), the amplitudes are negative over the entire Td axis and the spectrum is always dominated by the diagonal peak (blue line). Because of the normalization to the main diagonal peak, the integrated signal (Fig. 8b) brings to evidence only the timescale of the biexciton relaxation. The biexciton lifetime controls the dynamics of the cancellation of the ESA pathways which is reflected by the decrease in amplitude of the off-diagonal feature below the diagonal (red line) to match the one of the control position above the diagonal (orange line) at Td ≈ 105 fs. For Φ2/Φ1 = 0.1 (Fig. 8c), the instantaneous amplitudes of the peaks change the sign from positive to negative along Td. At early detection-time, the spectrum is dominated by the biexciton contribution, related to the positive off-diagonal peak due to ESAII pathway (red line) while as the detection-time gets longer the biexciton relaxes and the main contribution in the spectra becomes the negative diagonal peak. Such a change of the dominant spectral contribution is even more evident in the integrated and normalized spectral amplitudes (Fig. 8d) where the inversion of the dominant peak offers a direct estimation of the biexciton lifetime. The evolution of the spectral features for other signals, i.e., 2Q1Q and 1Q2Q, as a function of the detection-time are reported in the ESI† (Fig. S5 and S6) and can be analyzed along the same line.
The availability of several contributions to the response representing the same relaxation dynamics in different spectral positions may be a valuable resource to resolve more complicated multiexciton dynamics in realistic systems.
4 Conclusions
Multiexciton states of QDs are at the heart of nanocrystal-based technology and A-2DES is a promising technique to study their properties. In this work, we have simulated and analyzed the role of the biexciton state in the action-response discussing how it depends on the detection-mode and the time-gating of the signal. Despite the simplicity of the model system, i.e., a three-level open quantum system, a variety of spectral shapes can be generated as the result of the interplay between the exciton and the biexciton contributions to the total spectrum. When the biexciton provides a non-vanishing contribution to the detected signal, the 2D-spectra at early gating-time is dominated by an off-diagonal positive feature originating from the biexciton, whose position depends on the binding energy. As the gating-time increases, a dispersive lineshape results from the interplay of the exciton and biexciton signals having opposite signs. When the signal is completely integrated along the detection-time, the generated spectra depend on the ratio between the quantum yields of the biexciton and the exciton, ranging from a fully diagonal (ESA-free) to a dispersive lineshape, as determined by the detection-mode.Amongst the other important applications, excitons in QD materials are candidate substrates for quantum technologies, including quantum computing.68,69 In this context, preparation and manipulation of exciton states can be achieved by optical pulses70–73 and the collinear geometry facilitates rapid data acquisition, making A-2DES a valuable test-bed for quantum information processing coupled with photocurrent readout.74 To assist developments in this direction, numerical simulation protocols going beyond the perturbative response function are needed. In this work, we adopted the non-perturbative simulation protocol developed in ref. 43 augmented with an explicit description of the detection-time dynamics. To focus on the internal recombination process, we have assumed non-interacting units in our simulations. Another crucial issue that needs to be investigated is related to interdot coupling, since charge and exciton migration may compete with the internal dynamics, especially in the solid-state.20,29 Moreover, strongly coupled dimers of colloidal QDs have been designed and the possibility of excitonic delocalization over the two units has been discussed, based on both theoretical and experimental evidences.50,75–79 How weak and strong-coupling are associated with specific spectral features in A-2DES maps is a critical issue which is left for future work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors want to thank Luca Bolzonello, Elisabetta Collini and Camilla Ferrante for many useful discussions. Computational work has been carried out on the C3P (Computational Chemistry Community in Padua) HPC facility of the Department of Chemical Sciences of the University of Padova. The partial support of the EC FET Project grant # 766563 is also acknowledged.References
- T. A. A. Oliver, R. Soc. Open Sci., 2018, 5, 171425 CrossRef PubMed.
- K. J. Karki and M. F. Ciappina, Adv. Phys.: X, 2022, 7, 2090856 Search PubMed.
- P. Tian, D. Keusters, Y. Suzaki and W. S. Warren, Science, 2003, 300, 1553–1555 CrossRef CAS PubMed.
- P. F. Tekavec, G. A. Lott and A. H. Marcus, J. Chem. Phys., 2007, 127, 214307 CrossRef PubMed.
- G. A. Lott, A. Perdomo-Ortiz, J. K. Utterback, J. R. Widom, A. Aspuru-Guzik and A. H. Marcus, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16521–16526 CrossRef CAS PubMed.
- G. Nardin, T. M. Autry, K. L. Silverman and S. T. Cundiff, Opt. Express, 2013, 21, 28617–28627 CrossRef PubMed.
- K. J. Karki, J. R. Widom, J. Seibt, I. Moody, M. C. Lonergan, T. Pullerits and A. H. Marcus, Nat. Commun., 2014, 5, 5869 CrossRef CAS PubMed.
- S. Roeding and T. Brixner, Nat. Commun., 2018, 9, 2519 CrossRef PubMed.
- D. Uhl, U. Bangert, L. Bruder and F. Stienkemeier, Optica, 2021, 8, 1316–1324 CrossRef.
- A. A. Bakulin, C. Silva and E. Vella, J. Phys. Chem. Lett., 2016, 7, 250–258 CrossRef CAS PubMed.
- M. Aeschlimann, T. Brixner, A. Fischer, C. Kramer, P. Melchior, W. Pfeiffer, C. Schneider, C. Strüber, P. Tuchscherer and D. V. Voronine, Science, 2011, 333, 1723–1726 CrossRef CAS PubMed.
- V. Tiwari, Y. A. Matutes, A. T. Gardiner, T. L. C. Jansen, R. J. Cogdell and J. P. Ogilvie, Nat. Commun., 2018, 9, 4219 CrossRef PubMed.
- V. Tiwari, J. Chem. Phys., 2021, 154, 230901 CrossRef CAS PubMed.
- H. Gattuso, R. D. Levine and F. Remacle, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21022–21030 CrossRef CAS PubMed.
- L. Bruder, M. Binz and F. Stienkemeier, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 053412 CrossRef.
- L. Bruder, A. Eisfeld, U. Bangert, M. Binz, M. Jakob, D. Uhl, M. Schulz-Weiling, E. R. Grant and F. Stienkemeier, Phys. Chem. Chem. Phys., 2019, 21, 2276–2282 RSC.
- P. Malý, J. Lüttig, S. Mueller, M. H. Schreck, C. Lambert and T. Brixner, Phys. Chem. Chem. Phys., 2020, 22, 21222–21237 RSC.
- V. Tiwari, Y. A. Matutes, A. Konar, Z. Yu, M. Ptaszek, D. F. Bocian, D. Holten, C. Kirmaier and J. P. Ogilvie, Opt. Express, 2018, 26, 22327–22341 CrossRef CAS PubMed.
- E. Gutiérrez-Meza, R. Malatesta, H. Li, I. Bargigia, A. R. S. Kandada, D. A. Valverde-Chávez, S.-M. Kim, H. Li, N. Stingelin, S. Tretiak, E. R. Bittner and C. Silva-Acuña, Sci. Adv., 2021, 7, eabi5197 CrossRef PubMed.
- K. J. Karki, J. Chen, A. Sakurai, Q. Shi, A. T. Gardiner, O. Kühn, R. J. Cogdell and T. Pullerits, Chem. Sci., 2019, 10, 7923–7928 RSC.
- M. Aeschlimann, T. Brixner, M. Cinchetti, M. Feidt, N. Haag, M. Hensen, B. Huber, T. Kenneweg, J. Kollamana, C. Kramer, W. Pfeiffer, S. Ponzoni, B. Stadtmüller and P. Thielen, Phys. Rev. B, 2022, 105, 205415 CrossRef CAS.
- Q. Bian, F. Ma, S. Chen, Q. Wei, X. Su, I. A. Buyanova, W. M. Chen, C. S. Ponseca, M. Linares, K. J. Karki, A. Yartsev and O. Inganäs, Nat. Commun., 2020, 11, 617 CrossRef CAS PubMed.
- L. Bolzonello, F. Bernal-Texca, L. G. Gerling, J. Ockova, E. Collini, J. Martorell and N. F. van Hulst, J. Phys. Chem. Lett., 2021, 12, 3983–3988 CrossRef CAS PubMed.
- N. Zhou, Z. Ouyang, J. Hu, O. F. Williams, L. Yan, W. You and A. M. Moran, J. Phys. Chem. Lett., 2020, 11, 4570–4577 CrossRef CAS PubMed.
- S. Mueller, J. Lüttig, L. Brenneis, D. Oron and T. Brixner, ACS Nano, 2021, 15, 4647–4657 CrossRef CAS PubMed.
- T. L. C. Jansen, J. Chem. Phys., 2021, 155, 170901 CrossRef CAS PubMed.
- A. Perdomo-Ortiz, J. R. Widom, G. A. Lott, A. Aspuru-Guzik and A. H. Marcus, J. Phys. Chem. B, 2012, 116, 10757–10770 CrossRef CAS PubMed.
- S. Mukamel, J. Chem. Phys., 2016, 145, 041102 CrossRef PubMed.
- P. Grégoire, A. R. Srimath Kandada, E. Vella, C. Tao, R. Leonelli and C. Silva, J. Chem. Phys., 2017, 147, 114201 CrossRef PubMed.
- P. Malý and T. Mancal, J. Phys. Chem. Lett., 2018, 9, 5654–5659 CrossRef PubMed.
- M. Schröter, T. Pullerits and O. Kühn, J. Chem. Phys., 2018, 149, 114107 CrossRef PubMed.
- T. Kunsel, V. Tiwari, Y. A. Matutes, A. T. Gardiner, R. J. Cogdell, J. P. Ogilvie and T. L. C. Jansen, J. Phys. Chem. B, 2019, 123, 394–406 CrossRef CAS PubMed.
- A. A. S. Kalaee, F. Damtie and K. J. Karki, J. Phys. Chem. A, 2019, 123, 4119–4124 CrossRef CAS PubMed.
- O. Kühn, T. Mancal and T. Pullerits, J. Phys. Chem. Lett., 2020, 11, 838–842 CrossRef PubMed.
- Q. Chen, Y. H. Kwok, W. Zhou, G. Chen and S. Mukamel, J. Chem. Phys., 2021, 155, 194113 CrossRef CAS PubMed.
- C. Y. Wong and G. D. Scholes, J. Lumin., 2011, 131, 366–374 CrossRef CAS.
- J. R. Caram, H. Zheng, P. D. Dahlberg, B. S. Rolczynski, G. B. Griffin, D. S. Dolzhnikov, D. V. Talapin and G. S. Engel, J. Chem. Phys., 2014, 140, 084701 CrossRef PubMed.
- V. I. Klimov, A. A. Mikhailovsky, D. W. McBranch, C. A. Leatherdale and M. G. Bawendi, Science, 2000, 287, 1011–1013 CrossRef CAS PubMed.
- J. Zhao, O. Chen, D. B. Strasfeld and M. G. Bawendi, Nano Lett., 2012, 12, 4477–4483 CrossRef CAS PubMed.
- G. Lubin, R. Tenne, A. C. Ulku, I. M. Antolovic, S. Burri, S. Karg, V. J. Yallapragada, C. Bruschini, E. Charbon and D. Oron, Nano Lett., 2021, 21, 6756–6763 CrossRef CAS PubMed.
- J. Huang, Z. Huang, Y. Yang, H. Zhu and T. Lian, J. Am. Chem. Soc., 2010, 132, 4858–4864 CrossRef CAS PubMed.
- S. Lian, J. A. Christensen, M. S. Kodaimati, C. R. Rogers, M. R. Wasielewski and E. A. Weiss, J. Phys. Chem. C, 2019, 123, 5923–5930 CrossRef CAS.
- F. A. Damtie, A. Wacker, T. O. Pullerits and K. J. Karki, Phys. Rev. A, 2017, 96, 053830 CrossRef.
- A. Anda and J. H. Cole, J. Chem. Phys., 2021, 154, 114113 CrossRef PubMed.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, 1995 Search PubMed.
- P. Hamm and M. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, 2011 Search PubMed.
- V. I. Klimov, Annu. Rev. Phys. Chem., 2007, 58, 635–673 CrossRef CAS PubMed.
- S. Palato, H. Seiler, H. Baker, C. Sonnichsen, P. Brosseau and P. Kambhampati, J. Chem. Phys., 2020, 152, 104710 CrossRef CAS PubMed.
- P. Kambhampati, Acc. Chem. Res., 2011, 44, 1–13 CrossRef CAS PubMed.
- E. Collini, H. Gattuso, Y. Kolodny, L. Bolzonello, A. Volpato, H. T. Fridman, S. Yochelis, M. Mor, J. Dehnel, E. Lifshitz, Y. Paltiel, R. D. Levine and F. Remacle, J. Phys. Chem. C, 2020, 124, 16222–16231 CrossRef CAS.
- S. Mueller, S. Draeger, X. Ma, M. Hensen, T. Kenneweg, W. Pfeiffer and T. Brixner, J. Phys. Chem. Lett., 2018, 9, 1964–1969 CrossRef CAS PubMed.
- T. Mancal, A. V. Pisliakov and G. R. Fleming, J. Chem. Phys., 2006, 124, 234504 CrossRef PubMed.
- B. Brüggemann, P. Kjellberg and T. Pullerits, Chem. Phys. Lett., 2007, 444, 192–196 CrossRef.
- G. Lindblad, Commun. Math. Phys., 1976, 48, 119–130 CrossRef.
- V. Gorini, A. Kossakowski and E. C. G. Sudarshan, J. Math. Phys., 1976, 17, 821–825 CrossRef.
- S. Mueller and T. Brixner, J. Phys. Chem. Lett., 2020, 11, 5139–5147 CrossRef CAS PubMed.
- F. García-Santamaría, Y. Chen, J. Vela, R. D. Schaller, J. A. Hollingsworth and V. I. Klimov, Nano Lett., 2009, 9, 3482–3488 CrossRef PubMed.
- Y.-S. Park, A. V. Malko, J. Vela, Y. Chen, Y. Ghosh, F. García-Santamaría, J. A. Hollingsworth, V. I. Klimov and H. Htoon, Phys. Rev. Lett., 2011, 106, 187401 CrossRef PubMed.
- H. Yang, L. Zhang, Y. Tang, W. Xiang, X. Wang, M. Xiao, Y. Cui and J. Zhang, J. Phys. Chem. C, 2021, 125, 10759–10767 CrossRef CAS.
- W. R. Algar, D. Wegner, A. L. Huston, J. B. Blanco-Canosa, M. H. Stewart, A. Armstrong, P. E. Dawson, N. Hildebrandt and I. L. Medintz, J. Am. Chem. Soc., 2012, 134, 1876–1891 CrossRef CAS PubMed.
- T. Zhao, J. S. Beckwith, M. J. Amin, M. Pálmai, P. T. Snee, M. Tien and H. Yang, J. Chem. Phys., 2021, 155, 164201 CrossRef CAS PubMed.
- J. Gao, L. Kidon, E. Rabani and A. P. Alivisatos, Nano Lett., 2019, 19, 4804–4810 CrossRef CAS PubMed.
- D. B. Turner, Y. Hassan and G. D. Scholes, Nano Lett., 2012, 12, 880–886 CrossRef CAS PubMed.
- T. A. Gellen, J. Lem and D. B. Turner, Nano Lett., 2017, 17, 2809–2815 CrossRef CAS PubMed.
- M. Righetto, L. Bolzonello, A. Volpato, G. Amoruso, A. Panniello, E. Fanizza, M. Striccoli and E. Collini, Phys. Chem. Chem. Phys., 2018, 20, 18176–18183 RSC.
- H. Seiler, S. Palato and P. Kambhampati, J. Chem. Phys., 2018, 149, 074702 CrossRef CAS PubMed.
- H. Seiler, S. Palato, C. Sonnichsen, H. Baker and P. Kambhampati, Nano Lett., 2018, 18, 2999–3006 CrossRef CAS PubMed.
- K. Komarova, H. Gattuso, R. D. Levine and F. Remacle, J. Phys. Chem. Lett., 2020, 11, 6990–6995 CrossRef CAS PubMed.
- D. Harankahage, J. Cassidy, M. Yang, D. Porotnikov, M. Williams, N. Kholmicheva and M. Zamkov, J. Phys. Chem. C, 2021, 125, 22195–22203 CrossRef CAS.
- T. P. Spiller, I. DAmico and B. W. Lovett, New J. Phys., 2007, 9, 20 CrossRef.
- B. Fresch, M. Cipolloni, T.-M. Yan, E. Collini, R. D. Levine and F. Remacle, J. Phys. Chem. Lett., 2015, 6, 1714–1718 CrossRef CAS PubMed.
- A. Smponias, D. Stefanatos and E. Paspalakis, Nanomaterials, 2021, 11, 1859 CrossRef CAS PubMed.
- E. Paspalakis, A. Smponias and D. Stefanatos, J. Appl. Phys., 2021, 129, 223104 CrossRef CAS.
- E. Collini, J. Phys. Chem. C, 2021, 125, 13096–13108 CrossRef CAS PubMed.
- M. Coden, P. De Checchi and B. Fresch, Nanoscale, 2020, 12, 18124–18136 RSC.
- J. Cui, Y. E. Panfil, S. Koley, D. Shamalia, N. Waiskopf, S. Remennik, I. Popov, M. Oded and U. Banin, Nat. Commun., 2019, 10, 5401 CrossRef CAS PubMed.
- C. N. Dibenedetto, E. Fanizza, R. Brescia, Y. Kolodny, S. Remennik, A. Panniello, N. Depalo, S. Yochelis, R. Comparelli, A. Agostiano, M. L. Curri, Y. Paltiel and M. Striccoli, Nano Res., 2020, 13, 1071–1080 CrossRef CAS.
- C. N. Dibenedetto, E. Fanizza, L. De Caro, R. Brescia, A. Panniello, R. Tommasi, C. Ingrosso, C. Giannini, A. Agostiano, M. L. Curri and M. Striccoli, Mater. Res. Bull., 2022, 146, 111578 CrossRef CAS.
- S. Koley, J. Cui, Y. E. Panfil, Y. Ossia, A. Levi, E. Scharf, L. Verbitsky and U. Banin, Matter, 2022, 5, 3997–4014 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04270c |
| This journal is © the Owner Societies 2022 |