Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic structure and bonding in endohedral Zintl clusters
John E.
McGrady†
 *a,
Florian
Weigend†
*a,
Florian
Weigend†
 *b and
Stefanie
Dehnen†
*b and
Stefanie
Dehnen†
 *b
*b
aPhysical and Theoretical Chemistry Laboratory, Department of Chemistry, University of Oxford, South Parks Road, OX1 3QZ, UK. E-mail: john.mcgrady@chem.ox.ac.uk
bFachbereich Chemie and Wissenschaftliches Zentrum für Materialwissenschaften, Philipps University Marburg, Hans-Meerwein-Straße 4, 35043 Marburg, Germany. E-mail: florian.weigend@chemie.uni-marburg.de; dehnen@chemie.uni-marburg.de
First published on 21st December 2021
Abstract
Endohedral Zintl clusters—multi-metallic anionic molecules in which a d-block or f-block metal atom is enclosed by p-block (semi)metal atoms—are very topical in contemporary inorganic chemistry. Not only do they provide insight into the embryonic states of intermetallic compounds and show promise in catalytic applications, they also shed light on the nature of chemical bonding between metal atoms. Over the past two decades, a plethora of endohedral Zintl clusters have been synthesized, revealing a fascinating diversity of molecular architectures. Many different perspectives on the bonding in them have emerged in the literature, sometimes complementary and sometimes conflicting, and there has been no concerted effort to classify the entire family based on a small number of unifying principles. A closer look, however, reveals distinct patterns in structure and bonding that reflect the extent to which valence electrons are shared between the endohedral atom and the cluster shell. We show that there is a much more uniform relationship between the total valence electron count and the structure and bonding patterns of these clusters than previously anticipated. All of the p-block (semi)metal shells can be placed on a ladder of total valence electron count that ranges between 4n+2 (closo deltahedra), 5n (closed, three-bonded polyhedra) and 6n (crown-like structures). Although some structural isomerism can occur for a given electron count, the presence of a central metal cation imposes a preference for rather regular and approximately spherical structures which maximise electrostatic interactions between the metal and the shell. In cases where the endohedral metal has relatively accessible valence electrons (from the d or f shells), it can also contribute its valence electrons to the total electron count of the cluster shell, raising the effective electron count and often altering the structural preferences. The electronic situation in any given cluster is considered from different perspectives, some more physical and some more chemical, in a way that highlights the important point that, in the end, they explain the same situation. This article provides a unifying perspective of bonding that captures the structural diversity across this diverse family of multimetallic clusters.
1. Introduction
1.1 Multimetallic clusters
Progress in (semi)metal cluster chemistry has been made on a number of fronts over the past few decades, and the field has seen major advances in synthesis, characterisation, and also materials chemistry.1–23 Multimetallic clusters may be viewed as embryonic states of intermetallic phase formation, and as such represent discrete molecular models that offer insight into the broad spectrum of chemical bonding between metal atoms. They are, however, much more than an appealing playground for theory: they can also be used as precursors to new (multi-)metallic solids as well as showing potential in bond-activation reactions.24–31The majority of experimental papers on multimetallic clusters are now complemented by theory, the broad aim of which is to rationalise structure and reactivity. The very fact that these clusters are of interest to both chemistry and physics communities makes it inevitable that different approaches to electronic structure have been adopted, using different methodologies and different scientific language to reflect the interests and priorities of the particular research teams. Whilst this diversity of perspectives has undoubtedly enhanced our understanding of the bonding, the rather different approaches have had the unfortunate side effect of obscuring important links between different classes of compound. A close inspection of the many reported examples reveals important repeating patterns that allow a classification of the known landscape into a few connected cluster families. It is the purpose of this review to explore the underlying relationships between so-called endohedral Zintl clusters, the electronic properties of which have been interpreted in many different ways, and to set out a framework for understanding the common features that link this fascinating class of compounds.
1.2 Endohedral Zintl clusters: the impact of interstitial atoms
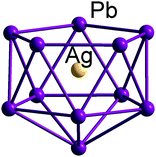
Our focus in this review will be firmly on endohedral Zintl clusters32–37 that are primarily the domain of synthetic inorganic chemistry and, very recently, materials science, but they have also been the subject of many theoretical and gas-phase spectroscopic studies.38–52 Generally, Zintl clusters are anionic molecules made up of atoms from p-block (semi)metals. More specifically, the title of this article narrows the focus further to endohedral clusters, in which a single atom or ion of the d- or f- block elements is encapsulated within a cluster shell comprising a much larger number of p-block (semi)metal atoms from groups 13 to 15. A classic examples of this kind would be [Pt@Pb12]2−,53 where the ‘@’ symbol is used to indicate endohedral encapsulation. Whilst the stability of these clusters is generally reliant on the presence of the metal in the sense that the corresponding ‘empty’ clusters do not exist (the exception being Pb102−), this does not necessarily mean that entirely different bonding models are required for homo- and heterometallic cases – by contrast, the concepts that have been developed for simple molecules and empty clusters of lighter atoms generally apply here, too. The critical question that we need to address is what is the role of the d or f electrons on the endohedral atom? We can easily identify some limits to the range of possible answers to this question. On the one hand, it is possible that the d/f electrons are entirely core-like and do not interact with the orbitals on the cage (the ‘non-interacting limit’). At this extreme, the endohedral atom is effectively acting as a noble gas atom trapped inside a cage only by the very large activation barrier required to pass through the walls; here, its role is that of a mere structural template, much like in the noble gas clathrates,54–57 for instance. At the opposite extreme, the endohedral metal could transfer all of its valence electrons to cage, which might then adopt a structure that reflects the presence of additional electron density in its frontier orbitals (the ‘fully-interacting limit’). In such cases, there are obvious analogies to back bonding in classic organometallic complexes: the presence of low-lying vacant orbitals on the cluster shell allows it to act, in effect, as an acceptor ligand. In between these two limits is a continuum of possibilities linked by different degrees of covalency, where the electrons are shared between inner metal and cage atoms. Within this continuum, we find examples where the cluster is only slightly distorted from the structure that we might have expected at the ‘non-interacting’ limit whereas in others we find a gross rearrangement to an entirely different structural type. We also find cases where the metal atom shell supports radical character (i.e. unpaired electron density), precisely as extended aromatic ligands do in many transition metal complexes. The diverse family of endohedral Zintl clusters therefore provides a uniquely rich platform for exploring different classes of chemical bonding. Ultimately, a close interplay between experiment and theory will be required to fully understand the chemistry of this intriguing family of clusters. In this review we will, for the most part, use examples of clusters with 12-vertex atoms to illustrate the key points, simply because this family is the most diverse, although we also bring in examples with other vertex counts.1.3 The correlation between valence electron count and structural features of simple metal clusters: early considerations and modern views.
The simplest cases of metal clusters, prominent examples of which are found in polyanions of group 15 (semi)metals like Sb73− or Bi113−, can be understood simply in terms of the 8 – N rule: each atom with a well-defined number of valence electrons, N, forms 8 − N 2-centre-2-electron (2c–2e) bonds to neighbouring atoms to complete its octet. Such clusters have 5n valence electrons and form the most symmetric cages that can be generated with the given number of three-bonded atoms. By contrast, clusters that are formally electron-deficient cannot be understood in terms of 2c–2e bonds. At a minimum number of 4n + 2 valence electrons, such as found in group 14 anions like Sn52− or Pb102−, they form spherical ‘closed’ deltahedral cages reminiscent of the (isoelectronic) boranes.58The seminal work of Wade and Mingos and Lipscomb in the 1970s that formulated a simple set of rules to account for structural trends across deltahedral clusters of different vertex count,59–62 and the later contributions of Mingos and Jemmis to this field,63–71 represent major landmarks in the sense that they brought order to an extensive body of structural data. It is remarkable how well these rules also apply to iso-valence-electronic p-block metal clusters. It is important to emphasise that much of the important insight from this early work emerged from relatively simple theoretical models—primarily a combination of symmetry-based arguments and tight-binding approaches such as the extended Hückel methodology pioneered by the Hoffmann school.72 These tools did not allow for the calculation of the total energy, let alone gradients, and so all of the very profound advances in this period came about without access to optimised geometries. In the modern age of density functional theory (DFT) and fast computers, many papers begin and sometimes also end with a set of optimised geometries, and the lesson we can learn from the work of Wade, Mingos and others is that it is the patterns and trends within these data, rather than the data themselves, which have real value. Moreover, these patterns should transcend the differences in methodology that complicate the comparison of different reports, particularly within the DFT literature. At the same time as the chemistry community was applying tight-binding models to these problems, the physics community took an alternative path, making extensive use of the jellium model to interpret the properties of small, typically gas-phase, clusters.73–75 The jellium model is also closely linked to ideas of shape and symmetry, although ‘shape’ in this sense relates to the approximate sphericality of the cluster, rather than the connectivity of individual vertices. The fact that the jellium model is, in some sense, less dependent on knowledge of precise atomic positions makes it a natural partner to gas-phase spectroscopy, where structural information can only be inferred from the interpretation of electronic, vibrational or rotational signatures. Closely linked to the jellium model is the concept of a ‘superatom’ pioneered by Castleman and others:76–82 the simple idea here is that closed electron shells in clusters mimic the well-defined atomic shells that give rise to Mendeleev's iconic periodic table of the elements. Some of the most famous endohedral ‘superatoms’ – albeit with an interstitial p-block metal atom – are Al13− (= [Al@Al12]−), and its isoelectronic analogues [B@Al12]−, [Si@Al12] and [P@Al12]+, which have been studied intensely using both spectroscopy and theoretical methods.37 All three have the ‘magic’ number of 40 valence electrons that corresponds to a shell closure and, as illustrated in Fig. 1, they have perfectly icosahedral structures and large HOMO–LUMO gaps. In contrast, clusters with higher or lower electron counts are distorted away from icosahedral symmetry and have substantially smaller HOMO–LUMO gaps.78
 | ||
| Fig. 1 Optimized structures of ‘superatoms’ [M@Al12]q (X = B, Al, Si, and P) with q = +1 (top), q = 0 (centre), and q = −1 bottom. The symmetry and HOMO–LUMO gaps (eV) are also shown. This figure has been reproduced from ref. 78 with permission from ACS, copyright 2013). | ||
The rather diverse array of theoretical models that have been used over the years is perhaps an inevitable reflection of the fact that cluster chemistry spans the traditional disciplines of inorganic chemistry, physical chemistry, physics itself and, most recently, materials science. We believe that many important links between clusters of different types have been obscured by differences in methodology, language and terminology used by different groups. Our aim in this review is to explore these links and cut through methodological issues to identify the important periodic trends that that control bonding in these clusters.
2. Endohedral Zintl clusters in experiment and theory
In this section we will present a brief overview of the most important experimental techniques that find use in the Zintl cluster field and the possible applications of the clusters. This is followed by an outline of the key theoretical methods that have been used to analyse their properties.2.1 Synthetic access of endohedral Zintl clusters
It is not our purpose here to present a detailed introduction into Zintl cluster synthesis and characterization because this has been reviewed extensively elsewhere in recent times.15,19,32,36 However, a few brief comments are necessary to give context to the subsequent discussion of structure and bonding, while we refer the interested reader to the literature for more detailed information.The most common approach to the synthesis of compounds containing endohedral Zintl clusters starts out from ‘Zintl salts’, i.e., compounds comprising sequestrated cations for the compensation of the anions’ charge (Scheme 1, top).
In the vast majority of cases, the cation is [K(crypt-222)]+ (crypt-222 = 4,7,13,16,21,24-hexaoxa-1,10-diazabicyclo-[8.8.8]hexacosane), favoured because of its superior ability to drive the crystallization of the large (and approximately spherical) cluster anions. However, some publications have also reported the use of mixtures of [K(crypt-222)]+ with unsequestrated K+ ions. Such salts are typically significantly soluble at room-temperature in highly polar solvents like ethane-1,2-diamine (en), liquid NH3, dimethylformamide (DMF), or pyridine (py), and so allow for wet-chemical reactions with d- or f-block organometallics or coordination compounds. This method works particularly well for ternary Zintl clusters that are obtained in reactions of salts of binary Zintl anions like (InBi3)2− or (Sn2Sb2)2−. A variation of this method involves the use of pristine Zintl phases, i.e., intermetallic compounds without cation sequestration like K4Ge9, K12Si17, or K5Bi4, which are extracted in situ into the solvent of choice (including liquid ammonia) in the presence of the cation-sequestration agent, and subsequently reacted with the d-/f-block metal compounds. In both cases, the products are relatively soluble salts of anionic Zintl clusters (Scheme 1, centre). An alternative strategy, which avoids the use of solvents, is solid state synthesis at high temperatures. The resulting compounds are typically ternary alloys, in which the Zintl clusters may carry much higher anionic charges and, as a consequence, typically have lower solubility (Scheme 1, bottom).
2.2 Experimental characterization of endohedral Zintl clusters.
The experimental characterization and further analysis of these compounds is generally done with X-ray diffraction for structure elucidation, often in combination with micro-X-ray fluorescence (μ-XRF) or energy-dispersive X-ray (EDX) spectroscopy to identify or corroborate the heavy-atom composition of the compounds.If the solubility of the salts and the stability of the anions permits, mass spectrometry has proven to be a valuable tool for very precise identification of anion composition, though it is important to emphasise that the transfer to the gas phase is usually accompanied by oxidation to lower-charge anions, and may also lead to fragmentation of the clusters. As a result, inferences about the composition of condensed phases from the analysis of mass spectrometric data must be done with some caution. In some cases complementary studies on solid samples or solutions using magnetometry or NMR, EPR, Mößbauer and infra-red/Raman spectroscopies have offered important insights into features like the protonation state of clusters, their solution dynamics, the metals’ valence states, or the magnetic ground states. These complementary methods are particularly important in cases where the interpretation of X-ray diffraction data is ambiguous, for example when clusters contain neighbouring elements in the periodic table with similar scattering factors, when extensive disorder of approximately spherical clusters complicates the structure determination, or when the cationic components cannot be localized from the structural data, leaving the total charge on the anionic component undetermined. Whilst the synergy between these different experimental techniques is obvious, it is only when combined with theory that the full information content of the data emerges. It is this synergy between experiment and theory that we emphasise throughout this article.
2.3 Chemical properties and potential use of Zintl clusters
Zintl clusters stand out not only for their structural aesthetics and their often remarkable bonding characteristics, which are the main scope of this review article, but also for their potential to display properties that may prove useful in future applications. The multitude of possible combinations of (semi)metal atoms in Zintl clusters means that properties such as reactivity and solubility can be finely tuned across a broad spectrum, with many important consequences. The most obvious of these is that the combination of reactivity and solubility determines the feasibility of being able to characterize and analyse a species and, ultimately, whether it is amenable to isolation. In addition, whilst chemical reactivity is typically interpreted to mean stability versus instability, it also gives an important indicator of the potential for bond activation in catalytic reactions. The majority of clusters discussed in this review are ‘naked’ metal particles, in the sense that they lack any organic substituents (although the chemistry of clusters with some organic shielding have also been developed in the past decade15,20,36), and so they typically show an intrinsic tendency to interact with other chemicals. The typically high anionic charges inhibit spontaneous agglomeration and/or the formation of metallic solids, but they also leave the cluster susceptible to electrophilic attack. The systematic exploration of the applications of Zintl clusters in bond activation reactions is thus one of the most significant recent developments in this field.26–31In contrast to molecules containing (mainly) non-metal atoms where 2-centre–2-electron (2c–2e) bonding dominates (aliphatic and non-aromatic carbon compounds, for example), the increasingly inert nature of the ns electrons in the heavier (semi)metal atoms in Zintl clusters tends to favour electron delocalization and multi-centre-bonding.83,84 While the finite size of known Zintl clusters (<50 atoms) prevents them from becoming truly metallic on a molecular scale, the typically intense colours (red to brownish black) of salts with sequestrated cations point to narrow HOMO–LUMO gaps. This small band gap can lead to applications in (photo)catalysis, and also makes Zintl clusters precursors of novel nanostructured or doped metals and intermetallic phases.24,25 This list of potential applications is far from exhaustive, but it highlights the point that the motivation for developing a deeper understanding of electronic structures and bonding goes far beyond the simple interest in novel (semi)metal nano-architectures.
2.4 Theoretical methods for the treatment of endohedral Zintl clusters
3. Concepts for the description of bonding in (multi)metallic clusters: how should we look at a cluster?
The preceding paragraphs have highlighted just some of the methodological choices that are available to the computational chemist when performing calculations on Zintl ions or indeed any other class of molecules. It is tempting, then, to see the identification of the minima (and in some cases the connecting transition states) as a goal in itself, and, all too often, the end point of the study. The longevity of the work of Longuet–Higgins, Wade, Mingos and others from the pre-DFT era58–67,69 shows us very clearly that the characterization of the structural minima should only be the starting point, from which we should seek to build an over-arching and qualitative model that unifies the properties of the clusters of interest. Ideally, one might hope to establish a single model that could encompass all clusters, but, more realistically, our present state of understanding allows only for the slightly less ambitious goal of bringing some semblance of order to different sub-families of closely related clusters, much as Wade did for the boranes almost half a century ago. Establishing links between the different families should, in the fullness of time, allow for a truly unifying model to emerge. The emphasis is therefore placed squarely on trends and patterns rather than on isolated results.As we have noted above, the choice of model used to describe the bonding in any particular context depends strongly on the field of expertise of the scientists involved, and very different approaches have evolved amongst the chemistry and physics communities as well as between different subsections of those two disciplines. To a certain degree these differences are only a matter of the scientific language, and the alternative perspectives reflect different views of the same underlying reality. One of the main goals of this review article is thus to cut through this diversity and to identify the unifying concepts that go beyond methodological preferences. A second goal is to show how clusters and concepts that appear, at first glance, to be very diverse, are in fact more congruent than might previously have been anticipated. A case in point is the close similarity between ‘empty’ and endohedrally filled clusters: the metal at the centre can be viewed as a source of additional electrons and also a spherically symmetric electrostatic potential, but the fundamental electronic requirements defined by the structure of the cluster shell remain unchanged.
3.1 Cluster orbitals and localized orbitals
At the most fundamental level, molecular orbitals (MOs) are the (approximate) solutions of the Schrödinger equation for molecules. Their energies are the eigenvalues which can be interpreted as ionization energies, at least in first order (Koopmans’ theorem102). For fundamental quantum mechanical reasons the corresponding eigenfunctions must transform according to the irreducible representations of the molecular point group, and in that sense they are necessarily delocalized. For spherical objects, the angular part of the wavefunction is identical to that for atoms, and for this reason, clusters that are approximately spherical generate MOs that resemble the atomic s, p, d, etc. orbitals. It is this analogy that gives rise to the term ‘superatom’. It is an obvious point that no molecule is truly spherical, so the interpretative power of the superatom approach depends very much on the extent to which the (necessarily) non-spherical arrangement of the nuclei perturbs the electron density distribution. It must also be stressed that approximate sphericality is a purely geometric phenomenon, and no conclusions concerning electron delocalization or aromaticity can or should be drawn from the simple observation that canonical orbitals with the same nodal structure as atomic s, p or d orbitals emerge! As an extreme case, one may consider an (approximately) spherical arrangement of a large number of (almost) non-interacting helium atoms, where the solution of the Schrödinger equation yields MOs that are linear combinations of the 1s atomic orbitals with the same nodal characteristics as atomic orbitals, purely for symmetry reasons. Nevertheless, the electronic density of such a system differs markedly from an equally spherical cluster of alkali or alkaline earth metal atoms, to which the ‘superatomic’ label is typically attached. In these alkali metal clusters, the relatively weak potential due to the ionic cores can be replaced by a uniform, positively charged background without significantly changing the electronic structure of the valence orbitals. This idea is the foundation of the so-called jellium model,73–75 which leads to energetically separated shells of cluster orbitals, and, ultimately, to the so-called ‘magic’ electron counts which correspond to electronic shell closures. For the He cluster, in contrast, all occupied shells of cluster orbitals are approximately energetically degenerate because the He atoms interact only very weakly.The difference between these two limiting cases (He and Na clusters) becomes evident when we attempt to localize the canonical orbitals which, as noted above, must reflect the point group symmetry of the cluster. Common localization procedures involve a unitary transformation of the MOs to obtain an alternative set of orbitals (localized orbitals, LMOs) which are individually localized on the smallest number of atoms possible. Popular criteria for the determination of these transformations have been proposed by Boys,103 Pipek and Mezey,104 and others. All such processes involve the minimisation of a particular physical quantity, and so absolutely perfect localization is, in principle, never possible: a small fraction of the electron density of each localized orbital is always located elsewhere in the molecule. Further, in contrast to the canonical orbitals, whose energies are eigenvalues that can be associated with ionization energies, the energies of localized orbitals are expectation values (a weighted average of eigenvalues) which cannot be measured, even in principle. Of course, there are technical alternatives to the ‘localize and search for multi-centre orbitals’ procedure: lone pairs and two-centre bonds may also be identified with Weinhold's natural bond orbital (NBO) analysis,105 and the residual density can then be identified by subtracting the lone pairs and bonds from the total density matrix. Boldyrev and coworkers106 have developed the AdNDP methodology, an extension of NBO for multicenter contributions, which presently requires a preceding NBO run from the Gaussian program suite. Results are usually qualitatively similar to Boys and Pipek–Mezey localization procedures (which are implemented in popular commercial and open access software). The extent to which orbitals can or cannot be localized into 1- and 2-centre components, in the entire system or in parts of it, is a very useful tool in categorizing cluster electronic structure. To come back to our example: in the Hen case, localization will restore a set of n well-localized, doubly occupied, 1s orbitals on the He atoms, while for an alkali metal cluster it will generate molecular orbitals that remain extensively delocalized over multiple centres.
In Zintl cluster chemistry, the completely delocalised and completely localized limits represent extremes of behaviour that are, in reality, never realised. However, the two extreme classes of clusters mentioned in the introductory section (electron-rich and electron-deficient) can be related directly to the concept of localizability: in a truly electron-precise situation a localization procedure will yield only 2c–2e bonds and lone pairs. Hund's localization condition107 must be fulfilled in these cases: for each atom, the number of electrons involved in bonding must be equal to the number of nearest neighbours, and also to the number of valence atomic orbitals involved in the bonding. These requirements lead to the formation of 8 – N bonds per atom where N is the number of valence electrons (not to be confused with n, which is used throughout this article to identify the number of vertices of a cluster). For an approximately spherical cluster with n vertices this corresponds to a total requirement of 5n valence electrons, where n is the number of vertices, as is found, for example, in tetrahedral clusters of the group 15 element atoms such as P4. For each atom, the lone pairs (localized on a single atom) carry the majority of the atomic s-orbital character while the p orbital character is localized primarily in the bonds to the three neighbouring atoms. The requirement to form precisely three bonds per p-block atom, and hence the total valence electron count of 5n, is a natural consequence of the fact that for a tetrahedral main group atom, a maximum of three hybrid orbitals are directed into the same hemisphere (Scheme 2).
Clusters like Sn94− or octahedral/icosahedral clusters, which contain hypercoordinated atoms that are connected to four or five neighbours in addition to their lone pair, do not conform to the 8 − N rule. Consequently, they can only be described in terms of multi-centre bonding, and localization procedures will always yield multi-centre contributions in addition to, or instead of, orbitals localized on one or two centres. Here, the Wade-Mingos rules provide a robust connection between the total electron count and the shape of the cluster.
Matters becomes somewhat less clear for clusters with endohedral d-block or f-block atoms: should their valence electrons be included in the total electron count or not? As we discuss in more details below, the role of the d/f electrons on the endohedral metal is a critical issue that can play a decisive role in the structural chemistry of the cluster. In a fully ionic description, the central atom can transfer all of its valence electrons to the cluster shell, allowing the latter to reach an electron-precise count. In reality, the transfer of electrons is not complete and so the LMOs representing two-centre bonds between atoms in the cluster shell usually also have small delocalization tails onto the endohedral atom. In such circumstances, whether the orbitals are regarded as 2-, 3- or multi-centred depends to a large extent on the chosen threshold for localisation.
3.2 Ring currents and the link to aromaticity
The majority of the systems discussed in this review are in some sense approximately ‘spherical’, and the nodal structure of the canonical orbitals resembles that of atomic orbitals: in this sense they could be considered to be ‘superatomic’. However, as we have noted above, important qualitative differences become evident when we attempt to apply localization procedures in the contrasting cases of Hen and Nan clusters. The presence of non-localizable molecular orbitals is a necessary precondition for (significant) magnetically induced ring currents, the intensity of which can be calculated from the magnetically perturbed electron density (available in most quantum chemical codes for the calculation of NMR shifts) by applying the Biot–Savart law. The gauge-including magnetically induced currents (GIMIC) program, for example,108 computes the total ring current by integration of the current density over a plane perpendicular to the bond axis of interest. Currents for electron-precise systems such as Hen are close to zero, while those in systems with non-localizable MOs such as Nan can be even larger than those in benzene, the prototype for a 2-dimensional aromatic ring system. This analogy has led to a set of criteria109 for classifying 3-dimensional molecules as aromatic (the existence of a diatropic ring current), anti-aromatic (a paratropic ring current) or non-aromatic (no significant ring current), which complement other measures such as resonance energies and equalization of bond lengths. The label ‘3-dimensional aromaticity’ has been coined to reflect the magnetic response properties in cluster structures exhibiting multi centre bonding, typically those which are well described by the Wade–Mingos rules. However, is should be noted that, the term aromaticity is reserved for the subset of cases where at least some of the canonical orbitals are not localizable so that the electrons produce a ring current. The term does not apply a priori to all cases where the canonical orbitals show the nodal characteristics of spherical symmetry.The so-called nucleus independent chemical shifts (NICS)110 offer a single parameter to measure the magnetic response at a particular point in space, and therefore ‘aromaticity’ in the sense defined above. This can be done by placing one or more (dummy) atoms (i.e., nuclei without nuclear charge) at the desired position, typically, a high-symmetry point where no atom is present. Both ring currents and NICS make use of the magnetically perturbed density, but the application of Biot–Savart's law for ring currents is replaced by the derivative with respect to the magnetic moment of the dummy atom in the case of NICS. It is important to bear in mind that, in contrast to ring currents, NICS are not measurable quantities, but they have nevertheless been used widely in the field of cluster chemistry. A classic example of the application of NICS come from the closo boranes [BnHn]2−, n = 5–16, all of which have large negative (diatropic) NICS values at the geometric centre of the cluster. However, the most symmetric of these clusters, [B6H6]2− and [B12H12]2−, stand out from their neighbours as the most aromatic by this measure. The applications of NICS data, together with the AdNDP methodology, in Zintl cluster chemistry has been reviewed in the recent literature.111 In the context of endohedral clusters, however, the use of NICS calculations is limited by the presence of an atom at the cluster centre. In contrast, calculation of ring currents remains possible even in in the presence of such an atom, although care must be taken in choosing integration boundaries to exclude the contribution of the central atom to the current.
4. The correlation of electron count with structural features and further properties of multi-metallic Zintl clusters
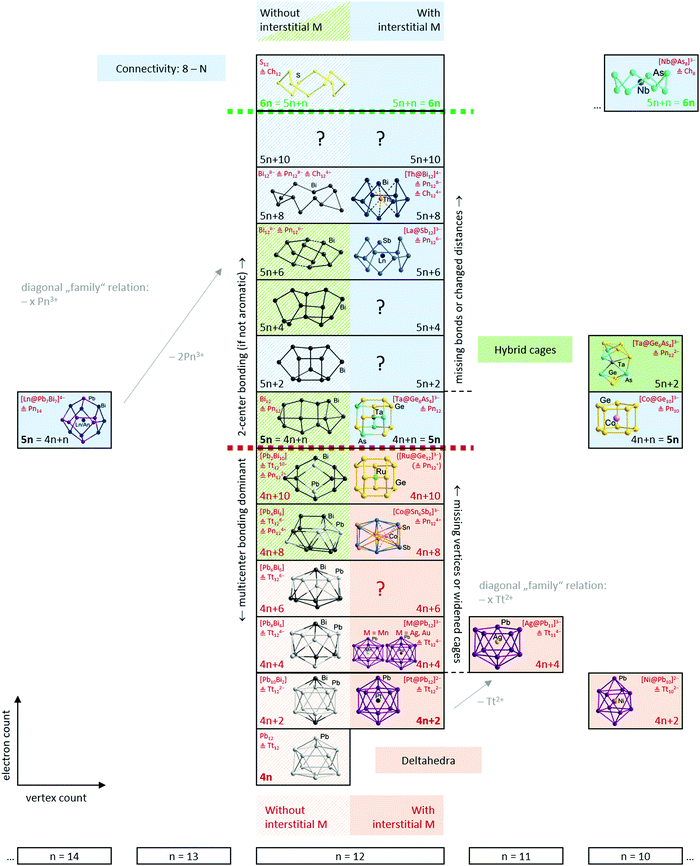
Having established the tools and paradigms that one might apply to understand the properties of Zintl clusters, we dedicate the remainder of this review to a discussion of examples that illustrate classical bonding paradigms (specifically, electron-precise and electron-deficient clusters). We will then attempt to establish links between the two paradigms, such that all clusters can be understood within a single continuous framework that is closely connected to the total valence electron count of the cluster shell. In the following sections we will illustrate these points using selected examples from the family of known metal clusters in general and multi-metallic Zintl clusters in particular. Throughout our discussion, we will use clusters or molecules without interstitial atoms as a reference point to the description of their endohedrally ‘filled’ analogues. In so doing, we emphasize the role of the endohedral atom as a stabilising template and, particularly towards the left of the periodic table, its ability to contribute to the total electron budget of the p-block atom shell encompassing it. We will also highlight a number of recent examples that appear to fall between the traditional classifications – we argue that the existence of these intermediate cases reflects the changing nature of the d/f orbitals on the central metal, from diffuse and high-lying in the electron poor transition metals to core-like (in both a spatial and energetic sense) in lanthanide and actinide atoms and towards the right of the transition series. It is not our intention to give an exhaustive coverage of all known clusters – this has been done in several excellent recent reviews. Rather it is our intention to highlight cases that establish different bonding paradigms, and also those that challenge them. We will draw most but by no means all of our examples from the family of 12-vertex clusters because this offers the most diversity, in terms of both composition and structure – and also because the ‘metalla-plumbaspherene’, [Pt@Pb12]2−, is an iconic example of an isolable endohedral Zintl cluster, reported for the first time by Eichhorn in 2004.53An overview of the ground to be covered is shown in Scheme 3. The horizontal axis defines the number of cluster vertices and, as noted above, our choice to emphasise the 12-vertex family reflects the great diversity to be found there. The vertical axis defines the valence electron count, ranging from highly electron-deficient (hypoelectronic) clusters with 4n valence electrons at the bottom to electron-precise crown-like clusters with 6n valence electrons at the top. This series, spanning 24 electrons in the 12-vertex family, captures the transition from highly delocalised multi-centre bonding at the bottom to localized 2c–2e bonding at the top. The 2-dimensional perspective reflects the diversity of models used to understand the relationship between structure and bonding: relationships between clusters with the same electron count but different number of vertices (diagonal relationships in the scheme), versus the development of the structures from deltahedra towards three-bonded polyhedra, and finally, crown-like structures on changing electron count within a fixed vertex count (vertical relationships in the scheme). Note that we focus on clusters with exclusively p-block (semi)metal shells, and, wherever applicable, we draw parallels between ‘empty’ clusters or other well-known molecules on the one hand and endohedral clusters on the other.
4.1 Electron-precise endohedral Zintl clusters: from 5n to 6n
We will illustrate the general concept for classical ‘empty’ examples first, before progressing to endohedral Zintl clusters that can also be considered as electron-precise. As a result of the division of the electron reservoir into 2n electrons for lone pairs (or exo bonds) and the remainder for cluster bonding, the natural structural preference is for each vertex to be bonded to precisely 8 − N others as observed in tetrahedral P4 or As4 (N = 5) or cyclic S8 (N = 6). The isoelectronic tetrahedral Tt44− anions Si44−, Ge44−, Sn44− and Pb44− are all known in Zintl phases or Zintl salts112 and also in discrete coordination compounds such as [Zn6(Ge4)4]4−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 and [Au(Sn4)2]7−.114 Several binary P4 analogues have also been reported as Zintl salts of anions (TrBi3)2− (Tr = Ga, In Tl), (Tt2Pn2)2− (Tt/Pn = Ge/P, Ge/As, Sn/Sb, Sn/Bi, Pb/Sb, Pb/Bi).115–122 Coordination compounds of some of them, (Ge2As2)2−, (Sn2Sb2)2−, or in situ-generated (Ge3P)3− and (Ge3As)3−, have also appeared in the recent literature:122–124 the gold cluster [Au6(Ge3As)(Ge2As2)3]3−,124 for example, is precisely isoelectronic with the aforementioned homonuclear [Zn6(Ge4)4]4−. The reduced anionic charge in the heteroatomic group 14/15 clusters confers significant advantages in terms of both stability and solubility, and these binary P4 analogues show great promise as synthons for the growth of larger, multinary clusters.19,21,36,121 One drawback, however, is that the characterisation of multi-metallic, as opposed to homo-nuclear, cluster units, is complicated by the difficulties associated with differentiating elements with similar atomic numbers using X-ray diffraction. In such circumstances, careful computational surveys of the potential energy surfaces have allowed the favoured positions of atoms that are neighbours in the periodic table to be established.125,126 The (pseudo-)tetrahedral units represent the only non-endohedral inorganic clusters that contain exactly 5n electrons; to find larger isolated examples, we have to move to the gas-phase or consider inherently unstable species such as prismane (C6H6, an isomer of benzene) and cubane (C8H8, an isomer of cyclooctatetraene). The stability of larger homo-nuclear analogues of the group 14 clusters is likely to be compromised severely by the ever higher negative charges required to attain the 5n electron count. This problem can, however, be mitigated to some extent by the incorporation of both group 14 and 15 elements in the same cluster, which lowers the charge (as described above for the Tt44− series and their binary analogues (Tt2Pn2)2−) or of endohedral atoms or ions that can contribute to the total electron count. Another strategy for lowering the overall charge on a cluster of group 14 element clusters with an electron count of 5n or more is to bind external counterions closely, for example in the formation of the 16-vertex Frank–Kasper polyhedron (Li4Ge12)8−.127 The presence of four Li+ cations intimately bound to the Ge1212− cage stabilises what would otherwise be a very unstable three-connected 5n-electron cluster (Fig. 2).
113 and [Au(Sn4)2]7−.114 Several binary P4 analogues have also been reported as Zintl salts of anions (TrBi3)2− (Tr = Ga, In Tl), (Tt2Pn2)2− (Tt/Pn = Ge/P, Ge/As, Sn/Sb, Sn/Bi, Pb/Sb, Pb/Bi).115–122 Coordination compounds of some of them, (Ge2As2)2−, (Sn2Sb2)2−, or in situ-generated (Ge3P)3− and (Ge3As)3−, have also appeared in the recent literature:122–124 the gold cluster [Au6(Ge3As)(Ge2As2)3]3−,124 for example, is precisely isoelectronic with the aforementioned homonuclear [Zn6(Ge4)4]4−. The reduced anionic charge in the heteroatomic group 14/15 clusters confers significant advantages in terms of both stability and solubility, and these binary P4 analogues show great promise as synthons for the growth of larger, multinary clusters.19,21,36,121 One drawback, however, is that the characterisation of multi-metallic, as opposed to homo-nuclear, cluster units, is complicated by the difficulties associated with differentiating elements with similar atomic numbers using X-ray diffraction. In such circumstances, careful computational surveys of the potential energy surfaces have allowed the favoured positions of atoms that are neighbours in the periodic table to be established.125,126 The (pseudo-)tetrahedral units represent the only non-endohedral inorganic clusters that contain exactly 5n electrons; to find larger isolated examples, we have to move to the gas-phase or consider inherently unstable species such as prismane (C6H6, an isomer of benzene) and cubane (C8H8, an isomer of cyclooctatetraene). The stability of larger homo-nuclear analogues of the group 14 clusters is likely to be compromised severely by the ever higher negative charges required to attain the 5n electron count. This problem can, however, be mitigated to some extent by the incorporation of both group 14 and 15 elements in the same cluster, which lowers the charge (as described above for the Tt44− series and their binary analogues (Tt2Pn2)2−) or of endohedral atoms or ions that can contribute to the total electron count. Another strategy for lowering the overall charge on a cluster of group 14 element clusters with an electron count of 5n or more is to bind external counterions closely, for example in the formation of the 16-vertex Frank–Kasper polyhedron (Li4Ge12)8−.127 The presence of four Li+ cations intimately bound to the Ge1212− cage stabilises what would otherwise be a very unstable three-connected 5n-electron cluster (Fig. 2).
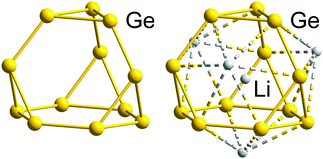 | ||
| Fig. 2 Molecular structure of the electron-precise Ge1212− skeleton (left), with 60 = 5n electrons found in the structure of the ternary alloy RbLi7Ge8, and that of the actual cluster stabilised by four outer and one inner Li+ cations in this phase, [Li+@(Li4Ge12)8−]7− (right), exhibiting a Frank–Kasper-type 16-vertex polyhedron with 64 = 4n electrons.127 | ||
In clusters with a 5n electron count, the canonical molecular orbitals typically show large HOMO–LUMO gaps. Localization algorithms then readily partition the density into lone pairs and orbitals localized over 2 centres, in accordance with the expectation of 2c–2e bonding in electron-precise clusters. For clusters where the electron count exceeds 5n, the additional electrons are accommodated in antibonding canonical orbitals, with the consequence that one or more bond is broken. In a localized ansatz, the combination of a bonding orbital and its antibonding counterpart that are both occupied generates lone pairs on two centres. From either perspective, clusters with more than 5n electrons are expected to adopt less symmetric structures with a mixture of 3-connected and 2-connected vertices.
A simple example of a more electron-rich cluster (with 5n + 2 = 22 electrons) is the butterfly-shaped Si46− anion found in Ba3Si4, where one of the six bonds of the Si44− tetrahedron has been broken, while two lone pairs are created at the respective Si atoms. This cluster and the isoelectronic borane B4H10 also highlight some of the ambiguities that emerge when considering different electron-counting schemes. The B4H10 cluster would conventionally be viewed as an arachno cluster in the Wade-Mingos terminology, with a characteristic total valence electron count of 4n + 6. Of course for n = 4, 4n + 6 = 5n + 2, and these clusters are rare examples where the structure can be understood from both perspectives, either as an ‘electron-precise’ or an ‘electron-deficient’ (arachno-type) cluster. As illustrated in Scheme 4, similar coincidences occur for n = 3 (6n = 4n + 6 = 18), n = 4 (5n = 4n + 4 = 20 and 5n + 2 = 4n + 6 = 22) and for n = 6 (5n = 4n + 6 = 30). In a similar vein, we can connect the apparently rather disparate triad of C8H8 (as the gyrobifastigium-type131 cuneane isomer), S4N4, S82+ and S8 by noting that their respective electron counts are 40 (= 5n), 44 (= 5n + 4), 46 (= 5n + 6), and 48 (= 5n + 8 = 6n for n = 8), so they have 12, 10, 9 and 8 bonding pairs, respectively.
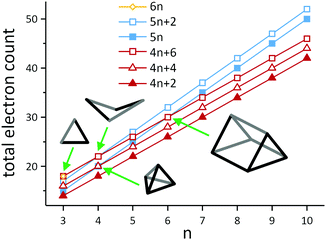 | ||
| Scheme 4 Illustration of the development of total electron counts in electron-deficient clusters with 4n + 2 (closo-type), 4n + 4 (nido-type) and 4n + 6 (arachno-type) electrons on the one hand (red) and electron-precise clusters with 5n or 5n + 2 electrons (blue) or 6n electrons (yellow) on the other hand. Note that the lines only serve as a guide to the eye. The structural diagrams represent the four types of clusters, in which the families overlap. The triangle (n = 3) lies at the intersection of 6n = 18 and 4n + 6 = 18 electrons, hence it can be viewed as an electron-precise cluster or an arachno-type cluster (trigonal bipyramid minus two vertices; example: Pn33− (Pn = Sb, Bi);128,129 the butterfly structures (n = 4) can be either understood as an electron-precise cluster with 5n + 2 = 22 electrons or as an arachno-type cluster with 4n + 2 = 22 electrons (octahedron minus two vertices; example: Si46−); a trigonal pyramid (n = 4) corresponds either to an electron-precise cluster with 5n = 20 electrons or to a nido-type cluster with 4n + 4 = 20 electrons (trigonal pyramid minus one vertex; example: Sn44−); the trigonal prism (n = 6) can be described as either an electron-precise cluster with 5n = 30 electrons or an arachno-type cluster with 4n + 6 = 30 electrons (trigonal dodecahedron minus two vertices; example: Te66+).130 | ||
Polyphosphide chemistry also provides us with many prominent examples of clusters possessing 5n + x electrons, for instance, the nor-tricyclane-type P73− and the ‘ufosane’-type P113− clusters. All heavier homologues of both Pnx3− anions with Pn = As, Sb, Bi are also well established.132,133 In these clusters, the neutral Pn atoms, with 5 valence electrons have 8 − N = 3 nearest neighbours and one lone pair (as for P4 above), while the three negatively charged Pn− centres (isoelectronic with S) have 6 valence electrons and consequently form only 8 − N = 2 bonds, along with two lone pairs. Charged centres can be considered as pseudo-atoms of the neighbouring group in the periodic table, which, in the case of P73−, highlights the structural correspondence with P4S3 and P4Se3. For P4S3, for example, the total number of valence electrons is 38, with 4·7 − 19 = 9 bonding pairs and 38 − 4·7 = 10 lone pairs. In principle, all isoelectronic systems should behave in this way, although the absolute structures cannot be predicted a priori, particularly for larger systems where more than one isomer may satisfy the equations for B and Lp indicated above. The ufosane-type P113− anion represents the largest known ‘spherical’ Zintl-ion cluster in the electron-precise category; beyond this size, catenation of distinct cluster units is the dominant growth pattern rather than further expansion into larger, still approximately spherical, clusters. Examples include larger polyphosphides or -arsenides and binary anions like (Ga4Bi14)4− or (Ga2Bi16)4−.134,135
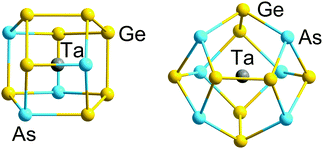 | ||
| Fig. 3 Structures of 12-vertex and 14-vertex clusters [Ta@Ge8As4]3− (left) and [Ta@Ge8As6]3− (right) with 5n valence electrons (60 or 70) in their binary cluster shells.121 | ||
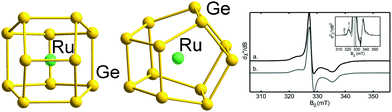 | ||
| Fig. 4 Structure of the binary cluster [Ru@Ge12]3− with 59 (5n − 1) valence electrons (left and centre, two views), and the measured and simulated EPR signals indicating the radical character (right). The graphic on the right hand side has been reproduced from ref. 136 with permission from ACS, copyright 2014. | ||
Finally, we note that whilst our emphasis has been on 12-vertex clusters, 3-connected architectures have also been identified in smaller clusters of germanium, notably pentagonal prismatic (D5h) [Fe@Ge10]3− and [Co@Ge10]3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 137,138 with total valence electron counts of 51 and 52, respectively, compared to a 5n count of 50. In this case, however, the excess electrons (1 and 2, respectively) are localised in a metal dz2 orbital which is non-bonding with respect to the 50-electron cage. Therefore, these clusters are considered to be electron-precise, too, in agreement with a three-bonded nature of the Ge atoms (with somewhat longer distances between the two pentagonal Ge5 faces, 2.608 Å on average, than within the faces, 2.517 Å on average). The significant contribution of Co(3d) orbitals to the bonding MOs is elegantly illustrated in real-space by the electron localization function (ELF) shown in Fig. 5.139
137,138 with total valence electron counts of 51 and 52, respectively, compared to a 5n count of 50. In this case, however, the excess electrons (1 and 2, respectively) are localised in a metal dz2 orbital which is non-bonding with respect to the 50-electron cage. Therefore, these clusters are considered to be electron-precise, too, in agreement with a three-bonded nature of the Ge atoms (with somewhat longer distances between the two pentagonal Ge5 faces, 2.608 Å on average, than within the faces, 2.517 Å on average). The significant contribution of Co(3d) orbitals to the bonding MOs is elegantly illustrated in real-space by the electron localization function (ELF) shown in Fig. 5.139
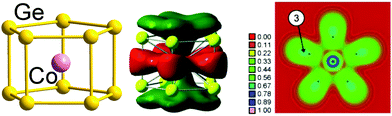 | ||
| Fig. 5 Structure (left), one of the bonding MOs (centre) and plot of the electron delocalization function (ELF; right). The figure has been adopted from ref. 138 with permission from Wiley VCH, copyright 2009. | ||
An even more electron-rich situation is found in endohedral clusters of the type [Ln@Sb12]3− (Ln = Y, La, Ho, Er, Lu),140 which formally contain an Ln3+ ion at their geometric centre, encapsulated by a doughnut-shaped 66-electron Sb126− anion based on three linked 4-membered rings. The electron count sits precisely midway between 5n and 6n (thus, 5n + 6), and the resultant combination of 2- and 3-connected vertices (6 of each type) in the doughnut-type p-block atom shell is fully consistent with the 8 − N rule, and all available electrons can again be localized in 2c–2e bonds (Fig. 6). Notably, the electrostatic stabilisation by a central metal ion is crucial here, which becomes obvious when comparing the structure with that of (hypothetical) ‘Bi126−’ anion (see Scheme 3), where the absence of a metal centre leads to a more oblate geometry.
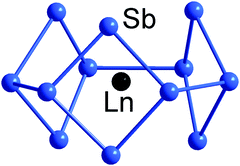 | ||
| Fig. 6 Structure of [La@Sn12]3− with 5n + 6 = 66 valence electron in its 12-vertex shell.140 | ||
A further 2 or 3 additional valence electrons are accommodated in the related clusters [Th@Bi12]4− (Fig. 7) and [U@Bi12]3−.83,141 As for the lanthanide-centred analogues, the endohedral atoms favour 3-dimensional structures which minimise the distance between the metal cation and the formally anionic (2-bonded) Bi− vertices. The first two additional electrons fill the LUMO of ‘Bi126−’, which then becomes the HOMO for the ‘Bi128−’ unit, and the third additional electron in the uranium cluster enters a 5f orbital. The HOMO for [Th@Bi12]4− displayed in Fig. 7 shows extensive π-delocalization and, in contrast to all other molecular orbitals, is inherently not localizable. For these 2π-systems, quantum chemical studies indicate the presence of remarkably strong ring currents, 24.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nA
nA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T−1 for [Th@Bi12]4− (Fig. 7). This value is similar to that in 26π-aromatic porphine (25.3
T−1 for [Th@Bi12]4− (Fig. 7). This value is similar to that in 26π-aromatic porphine (25.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nA
nA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T−1), despite the much lower number of π-electrons involved. The occupation of the delocalized orbital in the actinide compounds also introduces a π component to the Bi–Bi bonds between the four-membered rings, which leads to a significantly narrower range of Bi–Bi bond lengths for these compounds (Bi–Bi = 3.04–3.13
T−1), despite the much lower number of π-electrons involved. The occupation of the delocalized orbital in the actinide compounds also introduces a π component to the Bi–Bi bonds between the four-membered rings, which leads to a significantly narrower range of Bi–Bi bond lengths for these compounds (Bi–Bi = 3.04–3.13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å for [Th@Bi12]4−) compared to the Sb–Sb bonds in [La@Sb12]3− (2.80–3.04 Å).
Å for [Th@Bi12]4−) compared to the Sb–Sb bonds in [La@Sb12]3− (2.80–3.04 Å).
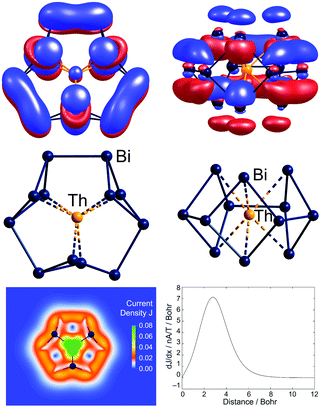 | ||
| Fig. 7 The non-localisable HOMO of [Th@Bi12]4−, accommodating the additional electron pair of the total of 5n + 8 valence electrons (top, two views) and the structure in its 12-vertex shell (centre, two views). The inherent non-localizability of the HOMO causes a significant ring current of this 2π–aromatic cluster (bottom). This figure has been adopted from ref. 83 with permission from Springer-Nature, copyright 2021. | ||
This comparison highlights the close connection between aromaticity and the lack of dispersion of bond lengths. The structural contrast between these clusters and the ‘empty’ (and unknown) ‘Bi128−’ anion is again striking – the absence of an endohedral metal ion causes the cluster to open out into an oblate crown-like geometry that maximises the distances between the anionic pseudo-group 16 Bi− centres (see Scheme 3).
A further increase in electron count (relative to 5n) leads to an even greater dominance of 2-connected over 3-connected vertices. One of the limiting cases is the (idealized) D3d-symmetric Sn612− ring in [Sn6{Nb(η6-C6H5Me)}2]2−, although this cluster is probably best considered as an inverted sandwich-type structure rather than an interstitial cluster.142 However, (formal) transfer of all 5 valence electrons from both Nb atoms increases the valence electron count at the polystannide crown to 36 (= 6n), and the arrangement of Sn atoms similar to a chair-like conformation of C6H12 cyclohexane or S6, where all electrons can be localized into lone pairs or 2e–2c bonds. One further examples where the group 5 metal donates (at least formally) all 5 of its valence electrons to the cluster electron count is the D4d-symmetric 48 (= 6n)-electron [Nb@As8]3− anion, where all 8 vertices are bonded to 2 others in a crown, isostructural and isoelectronic to S8.143
4.2 A close-up of the nature and role of the endohedral atom
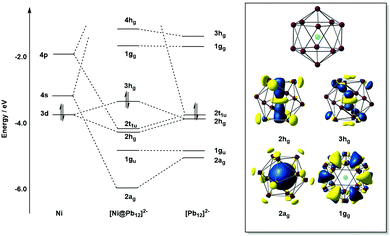
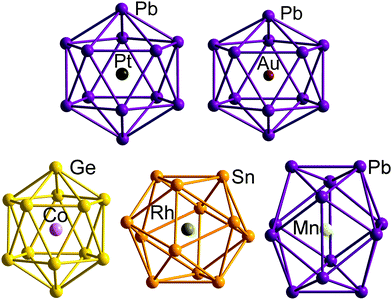
The electron counts reported in the previous paragraphs have been based on the assumption that all of the transition metal d electrons contribute to the electron count at the cluster. It is, then, no coincidence that all of the transition metals involved (Nb, Ta, Ru, Fe, Co) are relatively early in the transition series, and all, with the possible exception of Fe and Co, have relatively accessible higher oxidation states. Whilst the formulation of [La@Sb12]3− (Fig. 6) as La3+ and Sb126− is uncontroversial, and [Ta@Ge8As4]3− (Fig. 3) as Ta5+ and (Ge8As4)8− is plausible in light of the known oxidation states of the elements involved, it is less realistic to think of [Ru@Ge12]3− (Fig. 4) as containing Ru8+ and Ge1211−. Nevertheless, the covalent interactions between the cluster orbitals and the d orbitals on the metal are clearly sufficient to allow the d electron density to imprint itself on the cluster shell, forcing it to adopt a structure that, in the absence of the metal, would be characteristic of a much higher negative charge. This, then, immediately raises the question of what happens when the d electrons on the transition metal become less accessible, as they inevitably must as we move towards the right hand side of the transition series. An important illustration for this case comes from the comparison of [Ta@Ge8As4]3− (Fig. 3 left) with [Ni@Pb12]3−:144 both would have 5n = 60 valence electrons if all metal d electrons were included in the count, which amounts to the assumption that the interstitial ions adopt Ta5+ and Ni10+ oxidation states, respectively. The unrealistic nature of the latter has the consequence that [Ni@Pb12]2−, like all filled metallaspherenes, is icosahedral rather than D2d-symmetric – in full agreement with the more chemically reasonable idea of the Ni atom retaining all of its valence electrons in a d10 shell and transferring none of them to the p-block atoms (Ni0). The deltahedral structure, based on triangular faces, is highly characteristic of electronic-deficient clusters with 5n − 10 = 50 = 4n + 2 valence electrons (for n = 12), familiar to many readers through Wade's classic work on boranes.4.3 Electron-deficient endohedral Zintl clusters: from 4n to 5n − 2
The adoption of deltahedral structures with triangular faces is, in fact, highly characteristic of a broad class of ‘electron-deficient’ clusters, i.e, those with fewer than 5n valence electrons. [B12H12]2−, for example, has 50 (= 5n − 10 = 4n + 2 for n = 12) valence electrons, so is manifestly more ‘electron-deficient’ than [Ta@Ge8As4]3−, with 60 valence electrons in the 12-vertex cluster shell. The icosahedron is a relatively common motif in Zintl-ion chemistry but Zintl-ion analogues of the smaller boranes such as [B6H6]2− are rare. One beautiful example, however, is the [Sn6{Cr(CO)5}]2− cluster reported by Huttner and co-workers,145 which contains an octahedral [Sn6]2− core, isolobal with [B6H6]2−, with 4n + 2 = 26 valence electrons. The 4n + 2 count is generally characteristic of ‘closo’ structures where the atoms sit at the vertices of a perfect deltahedron such as an octahedron or icosahedron. The ‘magic’ stability of the 4n + 2 electron count can be rationalised by noting that each vertex bears an exo-type B–H bond (or a lone pair in the case of Zintl-ions), accounting for 2n = 12 of the electrons in the octahedral clusters and 2n = 24 in an icosahedron. This then leaves 4n + 2 − 2n = 2n + 2 = 14 valence electrons (the so-called skeletal electrons) to form the bonds that bind the B6 or Sn6 cluster units. Two of these 14 electrons occupy a totally symmetric combination of atomic orbitals directed inwards to the centre of the cluster while the remaining 2n occupy a further n bonding combinations of orbitals that are oriented around the surface of the cluster, tangential to the surface norm. These n + 1 bonding (and occupied) MOs are well separated from the 2n – 1 antibonding (and unoccupied) MOs, emphasising the imbalance between occupied and vacant orbitals that is characteristic of electron-deficiency. The real power of the Wade–Mingos model lies in its ability to (a) establish a conceptual connection between clusters which share the same skeletal electron count but differ in the number of vertices, and (b) allow a transfer of the electron-count/structure correlation to other isoelectronic (or isolobal) atoms or groups, and hence also to p-block atoms of any kind. As an illustration, we can highlight the progression from [B6H6]2− to C4v-symmetric nido-B5H9, a square pyramidal structure with a total valence electron count of 4n + 4 = 24, and to the ‘butterfly’ structure of arachno-B4H10, with a total count of 4n + 6 = 22. In the Zintl-ion domain, we can trace the same progression from Sn62− to the (as yet unknown) Sn54− (24 electrons), and to the 22-electron Si46− anion found in Ba3Si4. We have highlighted above the ambiguities that emerge when different paradigms intersect, as they do for B4H10 and Si46−, where the total valence electron count of 22 equals both 4n + 6 and 5n + 2.
The structures of many Zintl clusters, both with and without endohedral metal atoms, can be understood in terms of Wade's rules, and in fact the vast majority fall into the closo category. Rather like the electron-precise family, empty clusters (i.e., those without an endohedral metal) are common for smaller species, the smallest example being the trigonal prismatic tetrelide anions Tt52− (Tt = Si, Ge, Sn, Pb),146–150 and their isostructural analogues Tl57− and Bi53+,151–153 with total electron counts of 22 (= 4n + 2). 9-Vertex nido-clusters such as Tt92− (Tt = Si, Ge)154–156 are well known, and the bicapped square antiprismatic closo-Pb102− anion has also been isolated and unambiguously characterised crystallographically,157 while the still elusive Ge102− anion was found to coordinate an {Mn(CO)4} fragment in [Ge10Mn(CO)4]3−.158 The larger Sn122− and Pb122− clusters have been observed in the gas phase by Wang,159,160 but could not be isolated in the condensed phase. Whilst this may reflect crystallization issues for the generally robust 12-vertex clusters (according to DFT studies, see Scheme 3), it may also signal the collapse of clusters with large central cavities into more compact globular clusters. Comprehensive DFT calculations using a genetic algorithm on ‘empty’ 12-vertex clusters running from Pb12 through mixed Pb12−xBix species (x = 1–11) to Bi12, spanning electron counts of 4n to 5n valence electrons, indicated that in the absence of a central atom, cluster architectures other than the deltahedron are the global minima (see Scheme 3).161 The only global minimum that corresponds to an experimentally known geometry is found for (hypothetical) Pb10Bi2, a closo-type structure with 4n + 2 valence electrons. All other clusters, including the 12-vertex structure of (hypothetical) Bi12 with a 5n valence electron count, require the presence of a central atom – either for electrostatic stabilisation or covalent bonding, or a mixture of both.
For all isolated cases of electron-deficient metal clusters, the minimum number of electrons is 4n + 2. The lower 4n electron count – associated with the label pre-closo or hypoelectronic – has been reported for small monovalent clusters of group 13 atoms such as the boron subchlorides, (BCl)n (n = 4, 8, 9)162–164 the related aluminium clusters (AlCp*)4 (Cp* = C5Me5), and Tl77−,165 which actually possess closo-type architectures.10–12 According to DFT calculations on ‘empty’ Pb12 the 4n-electron species undergoes a distortion to a compressed icosahedron (see Scheme 3).161
Proceeding in the opposite direction, a stepwise increase of the total number of valence electrons above 4n + 2, generates structures that resemble fragments of deltahedra, with one (nido), two (arachno), or even three vertices (hypho) missing relative to a (hypothetical or existing) closo cluster deltahedron. The descriptor ‘nido’ is typically applied to clusters with a 4n + 4 count to reflect their ‘nest-like’ structure while ‘arachno’ captures the resemblance to a spider's web shown by the 4n + 6 family. Generally, this pattern holds for electron deficient Zintl anions but, in contrast to the many examples of closo Zintl-ion clusters, analogues of the nido, arachno and hypho clusters that dominate the chemistry of the boranes are relatively scarce. Amongst the family of empty Zintl ions, the 9-vertex Tt94− clusters (Tt = Si, Ge, Sn, Pb) have been studied extensively.166 They possess 40 = 4n + 4 valence electrons and adopt a capped square anti-prismatic geometry typical of nido clusters. Moreover, they are sufficiently stable to be used as a starting materials in the synthesis of larger Zintl cluster compounds. The 8-vertex [Sn5Sb3]3− has also been reported very recently, with a structure that is unknown in borane chemistry but is consistent with an arachno (4n + 6 = 38) electron count. A detailed survey of the potential energy surface for this anion reveals three distinct low-lying isomers for the 8-vertex, 38-electron cluster, all of which can be derived from the 10-vertex closo bicapped square antiprism via the loss of two vertices. The isomer observed for the binary Zintl anion is described as iso-arachno with respect to the borane analogue, highlighting an important difference between non-metal and metal clusters. The boranes comply strictly with Wade's rules, i.e., they release neighbouring corners when going from closo to arachno cages in order to retain a maximum number of triangular faces for efficient multi-centre bonding. Metal clusters, in contrast, can also tolerate other forms of cluster deconstruction where mutually trans vertices are removed. Square antiprismatic Sn86− (in Rb4Li2Sn8),167 for example, can be derived formally from an E102− parent structure by removal of two opposing vertices. The higher negative charge and greater degree of electron delocalization in metal clusters, along with their ability to form intimate contacts to counterions such as Li+, gives access to a wider range of structural alternatives.
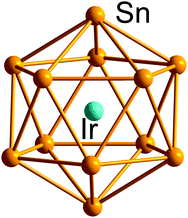 | ||
| Fig. 8 Structure of the archetypical 12-vertex closo-type icosahedron in [Ir@Sn12]3−.170 | ||
Detailed photo-electron spectroscopic (PES) measurements have been made on a number of these clusters, including the [M@Sn12]− systems (M = Cu, Ni, Co, Fe, Cr, V, Tl, Au, Pt, Nb).39 The spectra are illustrated in Fig. 9. The rather invariant orbital energies of the hg, t1u, and gu bands, and the resemblance of the measured spectrum to the eigenvalue spectrum of the computed canonical orbitals (Fig. 10) is striking, as is the similarity between [M@Pb12]2− and the empty Pb122− cage. The latter point highlights the relatively clean separation between orbitals localized on the metal and those localized on the cage.
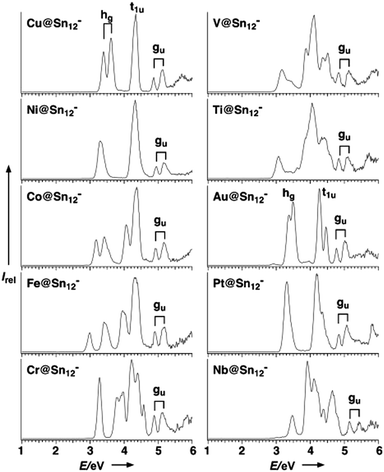 | ||
| Fig. 9 Photoelectron spectra (PES) of gas-phase species [M@Sn12]− at 193 nm (6.424 eV). The signals that stem from the three highest occupied orbitals (hg, t1u, gu) are depicted; note that the 1− charge of these clusters does not necessarily represent the original charge of the species in the condensed phase, as they easily undergo oxidation reactions in the gas phase. This figure has been reproduced from ref. 39 with permission from Wiley-VCH, copyright 2007. | ||
In comparison to both boranes and the ‘empty’ metal polyanions and polycations, endohedral Zintl clusters appear to show a much reduced propensity to adopt classically nido-type cluster structures. Instead, they prefer somewhat expanded and distorted versions of more spherical geometries that might be thought typical of a closo electron count. A striking example is the family of endohedral clusters, [M@Sn9]q− (M/q = Co/5, Ni/4, Cu/3), studied extensively by Fässler, Sevov, Corbett and others, all of which can be formulated as [M@Sn94−]q− with M being a neutral or charged d10 metal atom (Co−, Rh2−, Ni, Cu+).172–174 This work highlights the important point that the monocapped square antiprism, the classic nido-type structure, is very similar in energy to a tricapped trigonal prism (the structure expected for a closo electron count), albeit with elongated edges. Clearly, the precise structure adopted in any given case is very sensitive to the surrounding crystalline lattice as a result of rather weak metallic bonds and the soft vibrational modes that allow for small deformations. There are a number of possible reasons for this general preference for approximately spherical (albeit distorted) geometries over genuinely nido alternatives. One is that the cage is intrinsically more flexible in Zintl ions compared to boranes, due to the different characteristics of metal–metal vs. B–B bonding. The other relates to the nature of the interaction between the interstitial d-block or f-block atom with the p-block (semi)metal atoms of the cluster shell. The endohedral metal atom generates a spherical potential at the centre of the cluster which will inevitably favour approximately spherical arrangements of atoms over non-centrosymmetric isomers where one face is exposed. We have noted similar trends in the structural chemistry of [An@Bi12]4− compared to empty ‘Bi128−’, where the presence of a central metal ion favours a more compact geometry that maximises electrostatic attractions. A rare example of a genuinely endohedral cluster with a nido geometry is the C5v-symmetric [Ag@Pb11]3− (Fig. 11) with a total electron count of 48 (= 4n + 4).175 The structure shows the classic open face typical of this electron count and, although Cu and Au analogues have not been isolated, they have been proposed as intermediates in the growth of larger clusters such as [Cu4Pb22]4−, [Au8Pb33]6− and [Au12Pb44]8−.175
 | ||
| Fig. 11 Molecular structure of the nido-type endohedral Zintl cluster [Ag@Pb11]3−.175 | ||
A number of recent examples from the 12-vertex family with which we are primarily concerned in this review highlight the tendency to retain centrosymmetric geometries despite having electron counts that would be consistent with nido geometries.169,176–178 The [Au@Pb12]3− cluster is a particularly interesting example:176 if we assume that the Au 5d electrons do not contribute to the total electron count, the skeletal electron count of 52 = 4n + 4 suggests that a nido geometry should be adopted, just as it is for [Ag@Pb11]3−. Instead, the X-ray structure reveals a highly distorted icosahedron, compressed along one C3 axis to give D3d-symmetry (Fig. 12, top right). The HOMO of [Au@Pb12]3− (with a2g symmetry in the D3d-symmetric structure, see Fig. 13) has zero amplitude on the Au 6s, 5d or 6p orbitals, and its nodal characteristics are identical to those of one component of the gg-symmetric LUMO of [Ni@Pb12]2− shown in Fig. 10. This shows that the additional 2 electrons, above and beyond the 50-electron closo count, occupy an orbital localised on the Pb12 cage, and suggests that the most appropriate formulation of this cluster is [Au+@Pb124−]3−. The driving force for the observed compression along a 3-fold axis of the icosahedron is then a first-order Jahn–Teller instability within the gg2 configuration.
 | ||
| Fig. 12 Structure of the undistorted endohedral Zintl cluster [Pt@Pb12]2−with 50 = 4n + 2 valence electrons (top left)158 compared to other [M@E12]q− clusters that do exhibit distorted, yet still near-icosahedral structures: Au/Pb/3 (4n + 4 electrons, D3d symmetry, top right),176 Co/Ge/3 (4n + 2electrons, approximate D5d symmetry, bottom right),177 Rh/Sb/3 (4n + 2 electrons, D3d-symmetry, bottom centre),169 Mn/Pb/3 (4n − 2 electrons, D2h symmetry, bottom left).178 | ||
 | ||
| Fig. 13 Canonical orbitals calculated for [Au@Pb12]3− by means of DFT methods. Only one of the twofold degenerate LUMO orbitals are drawn. This figure has been reproduced from ref. 176 with permission from RSC, copyright 2017. | ||
The fact that [Ag@Pb11]3− favours a nido structure while [Au@Pb12]3− prefers a distorted icosahedron, despite both having classically nido electron counts of 4n + 4, probably reflects the absence of a highly symmetric ‘closo’ E11 geometry analogous to the icosahedron. A closely-related example of a distorted icosahedron, the [Co@Ge12]3− anion, merits comment in this context (Fig. 12, bottom left).177 Despite having exactly the same 50-electron (closo) count as perfectly icosahedral [M@Pb12]2− (M = Ni, Pd, Pt), the icosahedron in [Co@Ge12]3− is significantly elongated along one 5-fold axis. Sun, Boldyrev and co-workers argued that size drives this distortion: the (formally negatively charged) Co atom is simply too large to fit inside the cavity of a Ge122− icosahedron. Alternatively, a second-order Jahn–Teller instability caused by the energetic proximity of the metal 3d orbitals (hg symmetry in an icosahedron) and the gg LUMO of the Ge122− cage can drive a lowering of symmetry to D5d which allows the flow of electron density from four of the metal 3d orbitals into the four components of the LUMO of the cage (now a pair of e1g-symmetric orbitals) (Fig. 14). The relationship to [Ru@Ge12]3−, which was discussed in the context of electron-precise clusters, is significant here: the driving force for transfer of electron density outwards from the metal d orbitals to the cage is, in [Co@Ge12]3−, sufficient to distort the icosahedron via 2nd order Jahn–Teller effects, but not sufficient to force a wholesale rearrangement to the 3-connected architecture found in [Ru@Ge12]3−. The greater availability (in both spatial and energetic senses) of the 4d orbitals of Ru compared to the 3d orbitals of Co is therefore the key driver for the different cluster geometries of [Co@Ge12]3− and [Ru@Ge12]3−. An extension of this argument also allows us to rationalise the striking D2h-symmetric distortion observed in [Mn@Pb12]3−, which is elongated along one 2-fold rotation axis of the icosahedron (Fig. 12, bottom right).178 [Mn@Pb12]3− can be formulated as [Mn−@Pb122−]3− and the (high-spin) d8 configuration at Mn can be stabilised by allowing electron transfer from the spin-β components of the three doubly occupied Mn 3d orbitals to the (gg) LUMO of cage. The favoured distortion is therefore one which stabilises precisely three, rather than four, of the components of the gg-symmetric LUMO of the icosahedron, and this is precisely the situation engineered by the elongation along a 2-fold axis (Fig. 14, right). In the limit that one spin-β electron was transferred entirely to each of the three stabilised components of the cage LUMO, the Mn atom would achieve a stable half-filled (d5) configuration and the effective electron count at the cage would increase to 53. The common theme that unites the structural chemistry of this trio of clusters is therefore the flow of electrons from metal to the 4-fold degenerate LUMO of the icosahedral cage, whether it be driven by 1st-order Jahn–Teller instabilities ([Au@Pb12]3−), 2nd-order Jahn–Teller instabilities ([Co@Ge12]3−), or the stability of the half-filled d shell on the metal ([Mn@Pb12]3−). A summary of the distortions, along with the corresponding changes in the frontier orbitals, is given in Fig. 14. Although this spectrum of bonding situations is most well characterised within the 12-vertex family, the same pattern of increasing participation of metal d electron density can also be identified in the 10-vertex analogues [Ni@Pb10]2−, marginally distorted but still deltahedral [Fe@Sn10]3− and the 3-connected [Co@Ge10]3− cluster discussed above.
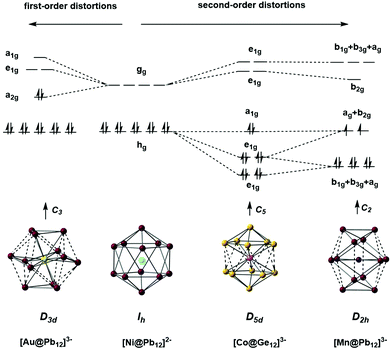 | ||
| Fig. 14 The origin of distortions in approximately icosahedral clusters [Ni@Pb12]2−, [Au@Pb12]3−, [Co@Ge12]3−, and [Mn@Pb12]3−. | ||
There remains one further arrangement of 12 atoms in an electron deficient polyhedron around a single endohedral atom, the ternary cluster anion [Co@Sn6Sb6]3− (Fig. 15)179 where two face-sharing square antiprisms form a (Sn6Sb6)2− cluster shell that encapsulates one Co− in one of the square antiprisms (the lower one in Fig. 15). The lower square antiprism is significantly expanded to accommodate the Co atom, such that the distances between the lower and middle squares (3.45 Å on average) are at least 0.4 Å larger than all other interatomic distances (on average: 3.06 Å between the upper and middle square, 3.14 within the middle square, 2.87 Å within the upper and lower squares).
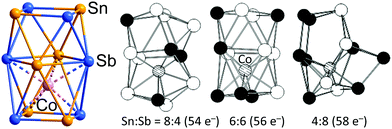 | ||
| Fig. 15 Structure of the [Co@Sn6Sb6]3− cluster (left), and illustration of the effect of decreasing or increasing electron numbers on the structure of the 12-vertex cluster shell (DFT; centre and right). This figure has been adopted from ref. 179 with permission from Wiley-VCH, copyright 2018. | ||
The Co centre could, therefore, also be regarded as 8-coordinate in a square antiprismatic array defined by two 4-membered rings, one of which is shared with the residual unbound Sn2Sb2 square. This binary (Sn6Sb6)2− shell has an electron count of 56 electrons, so either 4n + 8 or 5n − 4, depending on whether we choose to start from the electron-deficient or electron-precise limit. The cluster shows characteristics of both the 4n and the 5n limits, with both deltahedral and square faces. The intermediate electron count of 56 means that neither the icosahedron characteristic of 50-electron [M@Pb12]2− nor the 3-connected architecture adopted by 60-electron [Ta@Ge8As4]3− are viable structural choices. The division of the (Sb6Sn6)2− cluster into a 38-electron, 8-vertex arachno (Sb4Sn4)2− unit and a planar 18-electron Sb2Sn2 unit which is a 2π electron aromatic, isolobal with (C4H4)2+, then partitions the electron density in such a way that two stable units emerge. An argument in favour of this interpretation is the fact that, if all eight atoms contribute 2 electrons to the Co–(Sn, Sb) interactions, the Co atom would adopt an 18-electron noble-gas configuration. However, as related clusters exist where two Co− ions or two Ni atoms are accommodated in both hemispheres of the 12-vertex shell, which are more regular in shape, one can also think of a special kind of an endohedral cluster without partition into said substructures. Detailed DFT studies of the total electron count actually indicate that the architecture behaves like a closely interconnected assembly of 12 atoms: when adding electrons (by replacing Sn with Sb atoms), the cluster shell as a whole undergoes deformation.
To summarize the essence of Chapters 4.1–4.3, we emphasize that – like Zintl anions without an endohedral guest – endohedral Zintl clusters can be understood as belonging to one large family, the structural characteristics of which are dominated by the total valence electron count of the cluster shell. There is thus no general difference in how to interpret clusters that have valence electron counts between 4n and 5n or between 5n and 6n; it is necessary only to understand how the clusters manage an excess/deficit of electrons relative to the ideal number of 5n for a spherical, highly symmetrical cluster with three-bonded atoms. Highly symmetric clusters are reached at the bottom or top of the ‘ladder’ of possible electron counts (except for the minimum number being 4n + 2 instead of 4n due to the presence of the strongly bonding totally symmetric MO that is common to all). The crucial question, which tips the scales, is how the endohedral d-block or f-block atom interacts with the p-block metal shell, and whether the electrons in these shells contribute to the overall electron count or not. Unlike the boranes (and most of the known Zintl anions), endohedral Zintl clusters tend to retain centrosymmetric closo-like structures despite having nido-like or even higher electron counts, as a result of the spherically symmetric potential imposed by the atom at the centre of the cluster. This point marks the most significant difference between endohedral and non-endohedral clusters, but thorough analyses of the electronic structures are usually essential to rationalise a given structural preference.
4.4 Steps towards cluster growth: fused clusters
The very extensive chemistry of boranes based on two or more fused closo polyhedra is not mirrored in the Zintl-ion domain, where there are still relatively few examples of fused cluster units. The dearth of these larger clusters probably reflects the coulomb explosion associated with the linking of subunits which typically carry a high negative charge. Amongst those that are known, the majority contain closed-shell (d10) transition metal ions that are well separated from each other, with little or no potential for metal–metal bonding. Examples of clusters of this type include [Co2@Ge16]4−,180 [M2@Sn17]4− (M = Ni, Pt)181,182 or [Pd2@Tt18]4− (Tt = Ge, Sn),183,184 based on the vertex sharing of two Sn9 units, the C3v-symmetric [Rh3@Sn24]5− cluster where three Sn9 units share common edges around a central trigonal prism, and [Au3Ge45]9− that has the same (idealized) symmetry, yet is based on four Ge94− units, one of which is extended to an unusual Ge18 unit.185 The ideas that underpin the Wade-Mingos rules have been extended to clusters containing two or more fused deltahedral units through Jemmis’ ‘mno’ rules that include the impact of fusion via vertices, edges or faces.70,71 The same ideas can also be applied to the fused Zintl-ion clusters: the [Ni2Sn17]4− cluster, for example, can be rationalised in terms of a total count of 2(m + n + o) = 40, where m is the number of condensed polyhedra (2), n the number of vertices (17) and o the number of shared single vertices (1). It is important to emphasise, however, that NMR studies have shown that Zintl-ion clusters (whether with one or more endohedral metal ions) are typically very fluxional, suggesting a rather flat potential energy surface connecting multiple minima. This, along with the very high negative charges associated with the ions, means that the cationic lattice may exert a very substantial influence on structure (so-called ‘packing effects’ in the crystal). In such circumstances, it is not obvious that a direct correlation between structure and the intrinsic electron count of the isolated anion should be expected. In addition to the examples where the transitions metal ions are effectively ‘dilute’ (which led to the alternative terminology of ‘intermetalloid clusters’)32 there is a small number of examples where direct metal–metal bonding cannot be neglected. In the majority of these cases, transition metal ions occupy vertices of the polyhedral as well as the endohedral sites, allowing them to bridge multiple polyhedral. The [Ni3@Ge18]4− cluster reported by Sevov and Goicoechea is a prominent example of this kind, with a linear Ni3 chain and Ni–Ni distances of 2.49 Å.1865. Conclusions and outlook
In this article we have tried to bring together a diverse body of structural data to identify the underlying patterns and trends that drive structural change as a function of electron count. In so doing, we encounter a wide range of bond types, from localised 2c–2e bonding in electron-precise clusters through to highly delocalised multi-centre bonds in their more electron-deficient counterparts. Rather different theoretical paradigms are typically applied to these distinct scenarios, and we have tried to cut through these distinctions to reveal relationships between apparently rather different cluster species. Perhaps the most critical issue is the role of the electrons on the endohedral metal: at one limit they can be entirely core-like while at the other they can interact strongly with the orbitals on the shell, effectively raising the cluster electron count. Thus a careful consideration of the role of the metal d or f electrons is critical to understanding the structural diversity within this family.Our emphasis has been primarily on the 12-vertex family, simply because this offers the greatest diversity. Within this family we find numerous examples of icosahedral cages characteristic of multi-centre bonding, low (50) electron counts and essentially core-like metal d electrons. At the opposite extreme, electron-poor transition metal atoms such as Ta contribute all of their valence electrons to the cage to give a total count of 60, driving the adoption of 3-connected structures that are more characteristic of electron precise counts and 2c–2e bonding. The cases that fall between these limits are perhaps the most fascinating of all: the cluster can accommodate changes in electron count either through subtle distortions of the icosahedron, or, in more extreme cases, by sub-dividing the 12-vertex cluster into electronically distinct sub-units. For electron counts above 60, the structural trends can be understood in a localized context, where successive 2-electron increments in the count drive the cleavage of bonds and hence the adoption of structures with 2-connected vertices.
Perhaps the most important point that emerges from this survey is that the structural chemistry of this seemingly unconnected set of compounds can be understood within a single continuous framework defined by the total electron count at the cluster (shell). Unlike the boranes or empty Zintl ions, however, the electron count is not always a priori obvious—it depends critically on the characteristics of the transition metal or f-block element at the centre of the cluster. Capturing these characteristic properties of d- and f-electrons presents a very substantial challenge to theory, and it should therefore come as little surprise that the structural predictions in this field are often highly dependent on choice of methodology. This dependence highlights the importance of trends and patterns in data rather than isolated data points – only when we consider the body of data as a whole can we truly appreciate the connections that unify the field.
This article is dedicated to Professor D. M. P. Mingos in recognition of his extraordinary contributions to the field of cluster chemistry, and in particular in identifying the links between electronic and geometric structure.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the German Research Society (Deutsche Forschungsgemeinschaft, DFG) and the Alexander von Humboldt Foundation.Notes and references
- Metal Clusters, ed. W. Ekardt, John Wiley & Sons Ltd, 1st edn, 1999 Search PubMed.
- Metal Clusters in Chemistry, ed. P. Braunstein, L. A. Oro and P. R. Raithby, Wiley-VCH, 1st edn, 1999 Search PubMed.
- T. Tsukuda and H. Häkkinen, Front. Nanosci, 2015, 9, 1–7 CrossRef.
- T. P. Fehlner, in Cluster Compounds: Inorganometallic Compounds Containing Transition Metal & Main Group Elements, in Encyclopedia of Inorganic Chemistry, ed. R. B. King, R. H. Crabtree, C. M. Lukehart, D. A. Atwood and R. A. Scott, 2006 DOI:10.1002/0470862106.ia097.
- F. Weigend and R. Ahlrichs, Phil. Trans. R. Soc. A, 2010, 368, 1245–1263 CrossRef CAS PubMed.
- Clusters – Contemporary Insight in Structure and Bonding, in Structure and Bonding, ed. S. Dehnen, Springer, 1st edn, 2017 Search PubMed.
- P. Braunstein and A. A. Danopoulos, Chem. Rev., 2021, 121, 7346–7397 CrossRef CAS PubMed.
- S. Takano and T. Tsukuda, J. Am. Chem. Soc., 2021, 143, 1683–1698 CrossRef CAS PubMed.
- T. Tsukamoto, T. Kambe, T. Imaoka and K. Yamamoto, Nat. Rev. Chem, 2021, 5, 338–347 CrossRef CAS.
- A. Purath, R. Köppe and H. Schnöckel, Angew. Chem., Int. Ed., 1999, 38, 2926–2928 CrossRef CAS PubMed.
- A. Schnepf and H. Schnöckel, Angew. Chem., Int. Ed., 2002, 41, 3532–3554 CrossRef CAS PubMed.
- H. Schnöckel, Chem. Rev., 2010, 110, 4125–4163 CrossRef PubMed.
- C. Döring, A.-M. Dietel, M. V. Butovskii, V. Bezugly, F. R. Wagner and R. Kempe, Chem. – Eur. J, 2010, 16, 10679–10683 CrossRef PubMed.
- S. Gonzalez-Gallardo, G. Prabusankar, T. Cadenbach, C. Gemel, M. von Hopffgarten, G. Frenking and R. A. Fischer, Struct. Bond., 2010, 136, 147–188 CrossRef CAS.
- S. Scharfe, F. Kraus, S. Stegmaier, A. Schier and T. F. Fässler, Angew. Chem., Int. Ed., 2011, 50, 3630–3670 CrossRef CAS PubMed.
- Zintl Phases – Principles and Recent Developments, in Structure and Bonding, ed. T. F. Fässler, Springer, 1st edn, 2011 Search PubMed.
- S. González-Gallardo, T. Bollermann, R. A. Fischer and R. Murugavel, Chem. Rev., 2012, 112, 3136–3170 CrossRef PubMed.
- B. Oelkers, M. V. Butovskii and R. Kempe, Chem. – Eur. J, 2012, 18, 13566–13579 CrossRef CAS PubMed.
- B. Weinert and S. Dehnen, Struct. Bond., 2017, 174, 99–134 CrossRef.
- K. Mayer, J. Weßing, T. F. Fässler and R. A. Fischer, Angew. Chem., Int. Ed., 2018, 57, 14372–14393 CrossRef CAS PubMed.
- B. Weinert, S. Mitzinger and S. Dehnen, Chem. – Eur. J., 2018, 24, 8470–8490 CrossRef CAS PubMed.
- R. J. Wilson, B. Weinert and S. Dehnen, Dalton Trans, 2018, 47, 14861–14869 RSC.
- B. Peters, N. Lichtenberger, E. Dornsiepen and S. Dehnen, Chem. Sci, 2020, 11, 16–26 RSC.
- R. E. Benfield, D. Grandjean, M. Kröll, R. Pugin, T. Sawitowski and G. Schmid, J. Phys. Chem. B, 2001, 105, 1961–1970 CrossRef CAS.
- M. M. Bentlohner, M. Waibel, P. Zeller, K. Sarkar, P. Müller-Buschbaum, D. Fattakhova-Rohlfing and T. F. Fässler, Angew. Chem., Int. Ed., 2016, 55, 2441–2445 CrossRef CAS PubMed.
- Z. Luo, A. W. Castleman, Jr. and S. N. Khanna, Chem. Rev., 2016, 116(23), 14456–14492 CrossRef CAS PubMed.
- P. Ferrari, J. Vanbuel, E. Janssens and P. Lievens, Acc. Chem. Res., 2018, 51, 3174–3182 CrossRef CAS PubMed.
- Y.-X. Zhao, Z.-Y. Li, Y. Yang and S.-G. He, Acc. Chem. Res., 2018, 51, 2603–2610 CrossRef CAS PubMed.
- O. P. E. Townrow, C. Chung, S. A. Macgregor, A. S. Weller and J. M. Goicoechea, J. Am. Chem. Soc., 2020, 142, 18330–18335 CrossRef CAS PubMed.
- C. Dong, Y. Li, D. Cheng, M. Zhang, J. Liu, Y.-G. Wang, D. Xiao and D. Ma, ACS Catalysis, 2020, 10, 11011–11045 CrossRef CAS.
- G.-L. Hou, E. Faragó, D. Buzsáki, L. Nyulászi, T. Höltzl and E. Janssens, Angew. Chem., Int. Ed., 2021, 60, 4756–4763 CrossRef CAS PubMed.
- T. F. Fässler and S. D. Hoffmann, Angew. Chem., Int. Ed., 2004, 43, 6242–6247 CrossRef PubMed.
- J. M. Goicoechea and J. E. McGrady, Dalton Trans, 2015, 44, 6755–6766 RSC.
- X. Jin, V. Arcisauskaitea and J. E. McGrady, Dalton Trans, 2017, 46, 11636–11644 RSC.
- X. Jin and J. E. McGrady, Adv. Inorg. Chem., 2019, 73, 265–304 CrossRef CAS.
- R. J. Wilson, N. Lichtenberger, B. Weinert and S. Dehnen, Chem. Rev., 2019, 119, 8506–8554 CrossRef CAS PubMed.
- J. Zhao, Q. Du, S. Zhou and V. Kumar, Chem. Rev., 2020, 120, 9021–9163 CrossRef CAS PubMed.
- J. P. Dognon, C. Clavaguéra and P. Pyykkö, Angew. Chem., Int. Ed., 2007, 46, 1427–1430 Search PubMed.
- L.-F. Cui, X. Huang, L.-M. Wang, J. Li and L.-S. Wang, Angew. Chem., Int. Ed., 2007, 46, 742–745 CrossRef CAS PubMed.
- A. Grubisic, Y. J. Ko, H. Wang and K. H. Bowen, J. Chem. Phys., 2008, 129, 054302 CrossRef PubMed.
- A. Grubisic, Y. J. Ko, H. Wang and K. H. Bowen, J. Am. Chem. Soc., 2009, 131, 10783–10790 CrossRef CAS PubMed.
- A. Grubisic, H. Wang, X. Li, Y.-J. Ko, F. S. Kocak, M. Pederson, K. Bowen and B. Eichhorn, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 14757–14762 CrossRef CAS PubMed.
- H. G. Xu, X. Y. Kong, X. J. Deng, Z. G. Zhang and W. J. Zheng, J. Chem. Phys., 2014, 140, 024308 CrossRef PubMed.
- X. J. Deng, X. Y. Kong, H. G. Xu, X. L. Xu, G. Feng and W. J. Zheng, J. Phys. Chem. C, 2015, 119, 11048–11055 CrossRef CAS.
- X. J. Li, P. Claes, M. Haertelt, P. Lievens, E. Janssens and A. Fielicke, Phys. Chem. Chem. Phys., 2016, 18, 6291–6300 RSC.
- S. J. Lu, L. R. Hu, X. L. Xu, H. G. Xu, H. Chen and W. J. Zheng, Phys. Chem. Chem. Phys., 2016, 18, 20321–20329 RSC.
- X. J. Deng, X. Y. Kong, X. Q. Liang, B. Yang, H. G. Xu, X. L. Xu, G. Feng and W. J. Zheng, J. Chem. Phys., 2017, 147, 234310 CrossRef PubMed.
- X. Q. Liang, X. J. Deng, S. J. Lu, X. M. Huang, J. J. Zhao, H. G. Xu, W. J. Zheng and X. C. Zeng, J. Phys. Chem. C, 2017, 121, 7037–7046 CrossRef CAS.
- H. Tsunoyama, H. Akatsuka, M. Shibuta, T. Iwasa, Y. Mizuhata, N. Tokitoh and A. Nakajima, J. Phys. Chem. C, 2017, 121, 20507–20516 CrossRef CAS.
- M. Shibuta, T. Niikura, T. Kamoshida, H. Tsunoyama and A. Nakajima, Phys. Chem. Chem. Phys., 2018, 20, 26273–26279 RSC.
- H. G. Yang, X. L. Xu, W. J. Xu and J. Zheng, J. Phys. Chem. A, 2018, 122, 9886–9893 CrossRef PubMed.
- V. Fries, M. P. Klein, A. Steiner, M. H. Prosenc and G. Niedner-Schatteburg, Phys. Chem. Chem. Phys., 2021, 23, 11345–11354 RSC.
- E. N. Esenturk, J. Fettinger, Y.-F. Lam and B. Eichhorn, Angew. Chem., Int. Ed., 2004, 43, 2132–2134 CrossRef CAS PubMed.
- P. Villard, C. R. Hebd. Seances Acad. Sci., 1896, 123, 377 CAS.
- R. de Forcrand, C. R. Hebd. Seances Acad. Sci., 1923, 176, 355 CAS.
- R. de Forcrand, C. R. Hebd. Seances Acad. Sci., 1923, 181, 15 Search PubMed.
- D. Londono, W. F. Kuhs and J. L. Finney, Nature, 1988, 332, 141 CrossRef CAS.
- H. C. Longuet-Higgins and R. P. Bell, J. Chem. Soc., 1943, 250–255 RSC.
- K. Wade, J. Chem. Soc. D, 1971, 792–793 RSC.
- D. M. P. Mingos, Nat. Phys. Sci., 1972, 236, 99–102 CrossRef CAS.
- K. Wade, Adv. Inorg. Chem. Radiochem., 1976, 18, 1–66 CrossRef CAS.
- W. N. Lipscomb, Science, 1977, 196, 1047–1055 CrossRef CAS PubMed.
- D. M. P. Mingos, J. Chem. Soc., Chem. Commun., 1983, 706–708 RSC.
- D. M. P. Mingos and D. G. Evance, J. Organometal. Chem, 1983, 251, C13–C16 CrossRef CAS.
- D. M. P. Mingos, Acc. Chem. Res., 1984, 17, 311–319 CrossRef CAS.
- D. M. P. Mingos and J. Modrego, New J. Chem, 1991, 15, 9–16 CAS.
- D. M. P. Mingos, Pure Appl. Chem., 1991, 63, 807–812 CAS.
- D. M. P. Mingos, Chimia, 2019, 73, 152–164 CrossRef CAS PubMed.
- D. M. P. Mingos and D. J. Wales, Introduction to Cluster Chemistry, Prentice Hall, Englewood Cliffs, New Jersey, 1990 Search PubMed.
- E. D. Jemmis, M. M. Balakrishnarajan and P. D. Pancharatna, J. Am. Chem. Soc., 2001, 123, 4313–4323 CrossRef CAS PubMed.
- E. D. Jemmis, M. M. Balakrishnarajan and P. D. Pancharatna, Chem. Rev., 2002, 102, 93–144 CrossRef CAS PubMed.
- R. Hoffmann, J. Chem. Phys., 1963, 39, 1397–1412 CrossRef CAS.
- M. Brack, Rev. Mod. Phys., 1993, 65, 677–732 CrossRef CAS.
- Z. Lin, T. Slee and D. M. P. Mingos, Chem. Phys., 1990, 142, 321–334 CrossRef CAS.
- W. A. de Heer, W. D. Knight, M. Y. Chou and M. L. Cohen, Solid State Phys, 1987, 40, 93–182 CAS.
- A. W. Castleman, Jr. and S. N. Khanna, J. Phys. Chem. C, 2009, 113(7), 2664–2675 CrossRef.
- P. Jena, J. Phys. Chem. Lett., 2013, 4, 1432–1442 CrossRef CAS PubMed.
- T. Iwasa and A. Nakajima, J. Phys. Chem. C, 2013, 117, 21551–21557 CrossRef CAS.
- X. Z. Luo and A. W. Castleman, Acc. Chem. Res., 2014, 47, 2931–2940 CrossRef PubMed.
- J. U. Reveles, P. A. Clayborne, A. C. Reber, S. N. Khanna, K. Pradhan, P. Sen and M. R. Pederson, Nat. Chem, 2009, 1, 310–315 CrossRef CAS PubMed.
- D. A. Tomalia and S. N. Khanna, Chem. Rev., 2016, 116, 2705–2774 CrossRef CAS PubMed.
- A. C. Reber and S. N. Khanna, Acc. Chem. Res., 2017, 50, 255–263 CrossRef CAS PubMed.
- A. R. Eulenstein, Y. J. Franzke, N. Lichtenberger, R. J. Wilson, L. Deubner, F. Kraus, R. Clérac, F. Weigend and S. Dehnen, Nat. Chem, 2021, 13, 149–155 CrossRef CAS PubMed.
- A. R. Eulenstein, Y. J. Franzke, P. Bügel, W. Massa, F. Weigend and S. Dehnen, Nat. Commun., 2020, 11, 5122 CrossRef CAS PubMed.
- R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1988 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129 CrossRef CAS.
- P. Pyykkö, Chem. Rev., 1988, 88, 563–594 CrossRef.
- X. Cao and M. Dolg, Chem Rev, 2012, 112, 403–480 CrossRef PubMed.
- W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102 CrossRef PubMed.
- Y. J. Franzke and F. Weigend, J. Chem Theory Comput, 2019, 15, 1028–1043 CrossRef PubMed.
- Y. J. Franzke, F. Mack and F. Weigend, J. Chem. Theory Comput., 2021, 17, 3974–3994 CrossRef CAS PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans., 1993, 2, 799–805 RSC.
- M. Bühl and A. Hirsch, Chem. Rev., 2001, 101, 1153–1184 CrossRef PubMed.
- E. Hückel, Z. Phys, 1931, 70, 204–286 CrossRef.
- T. Koopmans, Physica, 1934, 1, 104–113 CrossRef.
- S. F. Boys, Rev. Mod. Phys., 1960, 32, 296–299 CrossRef CAS.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916–4926 CrossRef CAS.
- W. Kutzelnigg, Einführung in die Theoretische Chemie, Wiley-VCH, 2002, vol. 2, pp. 210–211 Search PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–846 CrossRef CAS.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- D. Sundholm, H. Fliegl and R. J. Berger, Wiley Interdiscip. Rev. Comput. Mol. Sci, 2016, 6, 639–678 CrossRef CAS.
- A. D. McNaught and A. Wilkinson, Compendium of Chemical Terminology, ed. S. J. Chalk, Blackwell Scientific Publications, 2nd edn, 1997, online version 2019 Search PubMed.
- P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed.
- C. Liu, I. Popov, Z. Chen, A. Boldyrev and Z. Sun, Chem. – Eur. J., 2018, 24, 14583–14597 CrossRef CAS PubMed.
- I. F. Hewaidy, E. Busmann and W. Klemm, Z. Anorg. Allg. Chem., 1964, 328, 283–293 CrossRef CAS.
- H.-L. Xu, I. A. Popov, N. V. Tkachenko, Z.-C. Wang, A. Muñoz-Castro, A. I. Boldyrev and Z.-M. Sun, Angew. Chem., Int. Ed., 2020, 59, 17286–17290 CrossRef CAS PubMed.
- C. B. Benda, M. Waibel, T. Köchner and T. F. Fässler, Chem. – Eur. J, 2014, 20, 16738–16746 CrossRef CAS PubMed.
- S. C. Critchlow and J. D. Corbett, Inorg. Chem., 1982, 21, 3286–3290 CrossRef CAS.
- S. C. Critchlow and J. D. Corbett, Inorg. Chem., 1985, 24, 979–981 CrossRef CAS.
- G. Cordier and W. Blase, Z. Kristallogr., 1991, 196, 207–211 CrossRef.
- L. Xu and S. C. Sevov, Inorg. Chem., 2000, 39, 5383–5389 CrossRef CAS PubMed.
- F. Lips, I. Schellenberg, R. Pöttgen and S. Dehnen, Chem. – Eur. J, 2009, 15, 12968–12973 CrossRef CAS PubMed.
- R. Ababei, J. Heine, M. Holyńska, G. Thiele, B. Weinert, X. Xie, F. Weigend and S. Dehnen, Chem. Commun., 2012, 48, 11295–11297 RSC.
- S. Mitzinger, L. Broeckaert, W. Massa, F. Weigend and S. Dehnen, Nat. Commun., 2016, 7, 10480–10490 CrossRef CAS PubMed.
- S. Mitzinger, J. Bandemehr, K. Reiter, J. S. McIndoe, X. L. Xie, F. Weigend, J. F. Corrigan and S. Dehnen, Chem. Commun., 2018, 54, 1421–1424 RSC.
- F.-X. Pan, L.-J. Li and Z.-M. Sun, Chin. J. Struct. Chem., 2016, 35, 1099–1106 CAS.
- F. Pan, L. Guggolz, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2020, 59, 16638–16643 CrossRef CAS PubMed.
- F. Weigend, C. Schrodt and R. Ahlrichs, J. Chem. Phys., 2004, 121, 10380–10384 CrossRef CAS PubMed.
- F. Weigend and C. Schrodt, Chem. – Eur. J, 2005, 11, 3559–3564 CrossRef CAS PubMed.
- S. Bobev and S. C. Sevov, Angew. Chem., Int. Ed., 2001, 40, 1507–1510 CrossRef CAS PubMed.
- F.-X. Pan, L.-J. Li, Y.-J. Wang, J.-C. Guo, H.-J. Zhai, L. Xu and Z.-M. Sun, J. Am. Chem. Soc., 2015, 137, 10954–10957 CrossRef CAS PubMed.
- R. Ababei, W. Massa, K. Harms, X. Xie, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2013, 52, 13544–13548 CrossRef CAS PubMed.
- J. Barr, R. J. Gillespie, G. P. Pez, P. K. Ummat and O. C. Vaidya, J. Am. Chem. Soc., 1970, 92, 1081–1082 CrossRef CAS.
- C. Nicolas, G. Bernardinelli and J. Lacour, J. Phys. Org. Chem., 2010, 23, 1080–1087 CrossRef.
- R. S. P. Turbervill and J. M. Goicoechea, Chem. Rev., 2014, 114, 10807–10828 CrossRef CAS PubMed.
- B. van IJzendoorn and M. Mehta, Dalton Trans, 2020, 49, 14758–14765 RSC.
- R. J. Wilson and S. Dehnen, Angew. Chem., Int. Ed., 2017, 56, 3098–3102 CrossRef CAS PubMed.
- F. Pan, S. Wei, L. Guggolz, A. Eulenstein, F. Tambornino and S. Dehnen, J. Am. Chem. Soc., 2021, 143, 7176–7188 CrossRef CAS PubMed.
- G. Espinoza-Quintero, J. C. A. Duckworth, W. K. Myers, J. E. McGrady and J. M. Goicoechea, J. Am. Chem. Soc., 2014, 136(4), 1210–1213 CrossRef CAS PubMed.
- B. Zhou, M. S. Denning, D. L. Kays and J. M. Goicoechea, J. Am. Chem. Soc., 2009, 131, 2802–2803 CrossRef CAS PubMed.
- J.-Q. Wang, S. Stegmaier and T. F. Fässler, Angew. Chem., Int. Ed., 2009, 48, 1998–2002 CrossRef CAS PubMed.
- A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1992, 31, 187–188 CrossRef.
- X. Min, I. A. Popov, F.-X. Pan, L.-J. Li, E. Matito, Z.-M. Sun, L.-S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2016, 55, 5531–5535 CrossRef CAS PubMed.
- N. Lichtenberger, R. J. Wilson, A. R. Eulenstein, W. Massa, R. Clérac, F. Weigend and S. Dehnen, J. Am. Chem. Soc., 2016, 138, 9033–9036 CrossRef CAS PubMed.
- B. Kesanli, J. Fettinger and B. Eichhorn, Angew. Chem., Int. Ed., 2001, 40, 2300–2302 CrossRef CAS PubMed.
- H.-G. von Schnering, J. Wok, D. Weber, R. Ramirez and T. Meyer, Angew. Chem., Int. Ed. Engl., 1986, 25, 353–354 CrossRef.
- E. N. Esenturk, J. Fettinger and B. Eichhorn, J. Am. Chem. Soc., 2006, 128, 9178–9186 CrossRef CAS PubMed.
- B. Schiemenz and G. Huttner, Angew. Chem., Int. Ed. Engl., 1993, 32, 297–298 CrossRef.
- J. M. Goicoechea and S. C. Sevov, J. Am. Chem. Soc., 2004, 126, 6860–6881 CrossRef CAS PubMed.
- J. Campbell and G. J. Schrobilgen, Inorg. Chem., 1997, 36, 4078–4081 CrossRef CAS.
- C. Suchentrunk and N. Korber, New J. Chem., 2006, 30, 1737–1739 RSC.
- P. A. Edwards and J. D. Corbett, Inorg. Chem., 1977, 16, 903–907 CrossRef CAS.
- M. Somer, W. Carrillo-Cabrera, E. M. Peters, K. Peters, M. Kaupp and H. G. von Schnering, Z. Anorg. Allg. Chem., 1999, 625, 37–42 CrossRef CAS.
- Z. Dong and J. D. Corbett, J. Am. Chem. Soc., 1994, 116, 3429–3435 CrossRef CAS.
- Z.-C. Dong and J. D. Corbett, Inorg. Chem., 1996, 35, 3107–3112 CrossRef CAS PubMed.
- S. Ulvenlund, K. Stahl and L. Bengtsson-Kloo, Inorg. Chem., 1996, 35, 223–230 CrossRef CAS PubMed.
- J. M. Goicoechea and S. C. Sevov, Inorg. Chem., 2005, 44, 2654–2658 CrossRef CAS PubMed.
- C. H. E. Belin, J. D. Corbett and A. Cisar, J. Am. Chem. Soc., 1977, 99, 7163–7169 CrossRef CAS.
- J. Akerstedt, S. Ponou, L. Kloo and S. Lidin, Eur. J. Inorg. Chem, 2011, 3999–4005 CrossRef.
- A. Spiekermann, S. D. Hoffmann and T. F. Fässler, Angew. Chem., Int. Ed., 2006, 45, 3459–3462 CrossRef CAS PubMed.
- D. Rios and S. C. Sevov, Inorg. Chem., 2010, 49(14), 6396–6398 CrossRef CAS PubMed.
- L.-F. Cui, X. Huang, L.-M. Wang, J. Li and L.-S. Wang, J. Phys. Chem. A, 2006, 110(34), 10169–10172 CrossRef CAS PubMed.
- L.-F. Cui, X. Huang, L.-M. Wang, D. Y. Zubarev, A. I. Boldyrev, J. Li and L.-S. Wang, J. Am. Chem. Soc., 2006, 128, 8390–8391 CrossRef CAS PubMed.
- C. Seifried, L. Longo, P. Pollak and F. Weigend, J. Chem. Phys., 2017, 146, 034304 CrossRef PubMed.
- M. Atoji and W. N. Lipscomb, J. Chem. Phys., 1953, 21, 172 CrossRef CAS.
- R. A. Jacobson and W. N. Lipscomb, J. Am. Chem. Soc., 1958, 80, 5571–5572 CrossRef CAS.
- M. B. Hursthouse, J. Kane and A. G. Massey, Nature, 1970, 228, 659–660 CrossRef CAS PubMed.
- S. Kaskel and J. D. Corbett, Inorg. Chem., 2000, 39, 778–782 CrossRef CAS PubMed.
- S. C. Sevov and J. M. Goicoechea, Organometallics, 2006, 25(24), 5678–5692 CrossRef CAS.
- S. Bobev and S. C. Sevov, Angew. Chem., Int. Ed., 2000, 39, 4108–4110 CrossRef CAS PubMed.
- E. N. Esenturk, J. Fettinger and B. Eichhorn, Chem. Commun., 2005, 247–249 RSC.
- C. Liu, X. Jin, L.-J. Li, J. Xu, J. E. McGrady and Z.-M. Sun, Chem. Sci, 2019, 10, 4394–4401 RSC.
- J.-Q. Wang, S. Stegmaier, B. Wahl and T. F. Fässler, Chem. – Eur. J., 2010, 16, 1793–1798 CrossRef CAS PubMed.
- Z. C. Dong and J. D. Corbett, J. Am. Chem. Soc., 1995, 117, 6447–6455 CrossRef CAS.
- B. J. L. Witzel, W. Klein, J. V. Dums, M. Boyko and T. F. Fässler, Angew. Chem., Int. Ed., 2019, 58, 12908–12913 CrossRef CAS PubMed.
- M. M. Gillett-Kunnath, J. I. Paik, S. M. Jensen, D. T. Jacob and S. C. Sevov, Inorg. Chem., 2011, 50, 11695–11701 CrossRef CAS PubMed.
- S. Scharfe, T. F. Fässler, S. Stegmaier, S. D. Hoffmann and K. Ruhland, Chem. – Eur. J, 2008, 14, 4479–4483 CrossRef CAS PubMed.
- C.-C. Shu, H. W. T. Morgan, L. Qiao, J. E. McGrady and Z.-M. Sun, Nat. Commun., 2020, 11, 3477 CrossRef CAS PubMed.
- L.-J. Li, F.-X. Pan, F.-Y. Li, Z.-F. Chen and Z.-M. Sun, Inorg. Chem. Front, 2017, 4, 1393–1396 RSC.
- V. Liu, L.-J. Li, I. A. Popov, R. J. Wilson, C.-Q. Xu, J. Li, A. I. Boldyrev and Z.-M. Sun, Chin. J. Chem, 2018, 36, 1165–1168 CrossRef.
- B. Zhou, T. Krämer, A. L. Thompson, J. E. McGrady and J. M. Goicoechea, Inorg. Chem., 2011, 50, 8028–8037 CrossRef CAS PubMed.
- R. J. Wilson, F. Hastreiter, K. Reiter, P. Büschelberger, R. Wolf, R. Gschwind, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2018, 57, 15359–15363 CrossRef CAS PubMed.
- C. Liu, I. A. Popov, L. J. Li, N. Li, A. I. Boldyrev and Z. M. Sun, Chem. – Eur. J, 2018, 24, 699–705 CrossRef CAS PubMed.
- E. N. Esenturk, J. C. Fettinger and B. W. Eichhorn, J. Am. Chem. Soc., 2006, 128(1), 12–13 CrossRef CAS PubMed.
- B. Kesanli, J. E. Halsig, P. Zavalij, J. C. Fettinger, Y.-F. Lam and B. W. Eichhorn, J. Am. Chem. Soc., 2007, 129(15), 4567–4574 CrossRef CAS PubMed.
- Jose M. Goicoechea and Slavi C. Sevov, J. Am. Chem. Soc., 2005, 127, 7676–7677 CrossRef CAS PubMed.
- Z.-M. Sun, H. Xiao, J. Li and L.-S. Wang, J. Am. Chem. Soc., 2007, 129, 9560–9561 CrossRef CAS PubMed.
- A. Spiekermann, S. D. Hoffmann, T. F. Fässler, I. Krossing and U. Preiss, Angew. Chem., Int. Ed., 2007, 46, 5310–5313 CrossRef CAS PubMed.
- J. M. Goicoechea and S. C. Sevov, Angew. Chem., Int. Ed., 2005, 44, 4026–4028 CrossRef CAS PubMed.
Footnote |
| † All three authors contributed equally and co-wrote the article. |
| This journal is © The Royal Society of Chemistry 2022 |