Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metallosupramolecular cages: from design principles and characterisation techniques to applications
Anna J.
McConnell

Otto Diels Institute of Organic Chemistry, Christian-Albrechts-Universität zu Kiel, Kiel 24098, Germany. E-mail: amcconnell@oc.uni-kiel.de
First published on 31st March 2022
Abstract
Although metallosupramolecular cages are self-assembled from seemingly simple building blocks, metal ions and organic ligands, architectures of increasingly large size and complexity are accessible and exploited in applications from catalysis to the stabilisation of reactive species. This Tutorial Review gives an introduction to the principles for designing metallosupramolecular cages and highlights advances in the design of large and lower symmetry cages. The characterisation and identification of cages relies on a number of complementary techniques with NMR spectroscopy, mass spectrometry, X-ray crystallography and computational methods being the focus of this review. Finally, examples of cages are discussed where these design principles and characterisation techniques are put into practice for an application or function of the cage.
Key learning points(1) The directional bonding, symmetry interaction and molecular panelling approaches for the design of metallosupramolecular cages via coordination-driven self-assembly.(2) The complexity of the self-assembly process and the role of factors from building block design (e.g. metal ion and ligand geometries), solvent and the presence of templates on the outcome on self-assembly. Thermodynamic and stereochemical considerations are also discussed. (3) The approach to the characterisation of unknown cages and the use of complementary techniques, such as NMR spectroscopy, mass spectrometry, X-ray crystallography and computational studies. (4) The implementation of these design principles and characterisation techniques to the design of cages for applications from catalysis to the stabilisation of reactive species. |
1. Introduction
Metallosupramolecular cages are a class of molecular containers or flasks1 that are self-assembled from metal ions and organic ligands by coordination-driven self-assembly exploiting the reversibility of the metal–ligand bond.2–7 The interest in this class of supramolecular architectures comes not only from the synthetic challenge of their rational design, particularly for cages with increased size and complexity, but also their host–guest chemistry; their well-defined three-dimensional cavities can bind guest molecules, potentially with high affinity and selectivity. Thus, these cages find application in cavity-directed reactions,1 the stabilisation of reactive species,8 catalysis,9 and molecular separations.10 As a result, the field has evolved from establishing fundamental design principles in pioneering examples of cages11–14 to designing cages for tailored functionality in applications.This Tutorial Review will give an introduction to the design principles as well as characterisation techniques for newcomers to the field and furthermore, demonstrate how they underpin the design and characterisation of metallosupramolecular cages for particular applications. For simplicity, metallosupramolecular cages will be referred to as cages throughout the review and while the focus of this review is cages, examples of helicates will also be included to illustrate key points. This Tutorial Review is not intended to be a comprehensive review, but rather illustrate concepts and in particular, highlight recent advances. More comprehensive reviews will be included in each section for readers interested in further information about the topic.
2. Design principles
2.1 Directional bonding, symmetry interaction and molecular panelling approaches
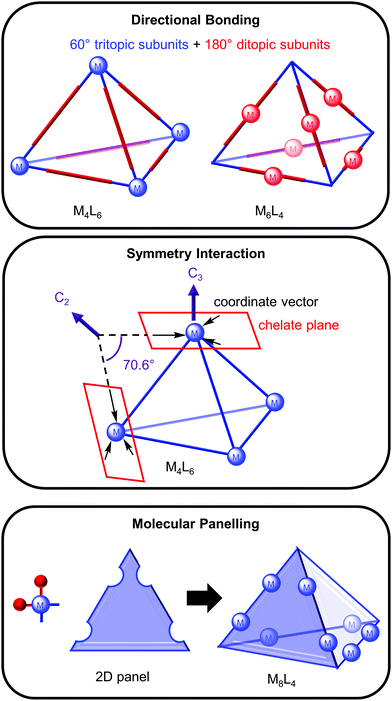
The architectures of many metallosupramolecular cages resemble Platonic or Archimedean solids and different approaches have been used to rationally design them from their constituent building blocks, metal ions (M) and organic ligands (L). Three approaches—directional bonding,6 symmetry interaction7 and molecular panelling3—will be briefly overviewed using a tetrahedron as an example to demonstrate each approach.In the directional bonding approach described by Stang and co-workers, the three-dimensional cage is described by tritopic and ditopic subunits; for example, a tetrahedron can be broken down into four 60° tritopic (blue) and six 180° ditopic (red) subunits (Fig. 1, top).6 When the tritopic subunit represents the metal complex on the vertices and the ditopic subunit the ligand on the edges of the tetrahedron, this gives a M4L6 tetrahedron. Conversely, a M6L4 tetrahedron would result from linear metal complexes (ditopic subunit) on the tetrahedron's edges and tritopic ligand subunits on the vertices.
In the symmetry interaction approach (Fig. 1, middle), Raymond and co-workers defined the symmetry of the cage in terms of the geometric relationship between the metal and ligand, as represented by the coordinate vector (from the interaction between the metal and ligand) and chelate plane (defined by the plane in which the coordinate vectors of the chelating ligands lie).7 For a M4L6 tetrahedron, the three coordinate vectors of each metal complex form a chelate plane containing a C3 axis and an angle of 70.6° is required between the coordinate vectors within each ligand to bridge the metal centres.
Finally, the molecular panelling approach3 developed by Fujita and co-workers constructs polyhedral cages from square planar complexes with a 90° angle (achieved by blocking two of the coordination sites with another cis-coordinating ligand, e.g. ethylenediamine) and 2D panels (e.g. triangles, squares and pentagons) representing the organic ligands (Fig. 1, bottom). A M8L4 tetrahedron can be designed from four triangular panels and 8 cis-protected square planar complexes linked together in an antiparallel fashion.3 Alternatively, a M8L4 cone results from linking the panels together in a parallel fashion.3
2.2 Coordination-driven self-assembly of metallosupramolecular cages
Using design principles such as those described in Section 2.1, geometric information for the cage is encoded into the building blocks so that the cage can be self-assembled via coordination-driven self-assembly. Highly symmetrical, rigid ligands are typically employed as well as metal ions with predictable coordination geometries since they provide well-defined geometries for the improved rational design of cages.It is important that the self-assembly process is under thermodynamic control so that the metal–ligand bonds can break and form reversibly; this ensures that error-checking can take place so that the thermodynamically most stable structure(s) results.7 A subset of coordination-driven self-assembly, subcomponent self-assembly,2 relies not only the reversible formation of metal–ligand bonds but also dynamic covalent bonds; the ligand, typically a pyridyl imine, forms in situ from aldehyde- and amine-functionalised subcomponents templated by the metal ion.
Thus, the choice of metal ion is important not only in terms of its coordination geometry but also its kinetic lability for error-checking during the self-assembly process. For this reason, octahedral (e.g. GaIII, TiIV, FeII, CoII, ZnII, CdII, NiII)2,7 and square planar (e.g. PdII and PtII)4,5 metal ions are typically used. Lanthanide ions can also be used for self-assembly since they are kinetically labile, however, the variable coordination number and geometry can complicate rational design.15 Nevertheless, the number of lanthanide-based cages is increasing and various architectures including M3L2, tetrahedra, cubes and more recently, a hexameric cage self-assembled from helicates have been reported.15–17 The counterion of the metal salt can also influence the self-assembly process as a template (see Section 2.2.1) and recently, Reek and co-workers reported halide impurities in metal salts play a catalytic role in the self-assembly of a variety of PdII, PtII and NiII cages;18 these impurities are proposed to reduce the energy required to convert kinetically trapped species to the thermodynamically favoured cage.
Examples of homometallic cages self-assembled from kinetically inert metal ions, such as RuII and IrIII, are rarer since self-assembly is under kinetic rather than thermodynamic control, although metal building blocks exploiting the trans effect can labilise the metal–ligand bond.19 To circumvent this problem of kinetic inertness, Lusby and co-workers exploited the kinetic lability of CoII to self-assemble a CoII4L6 cage that was “locked” through chemical oxidation to the kinetically inert CoIII4L6 cage.20
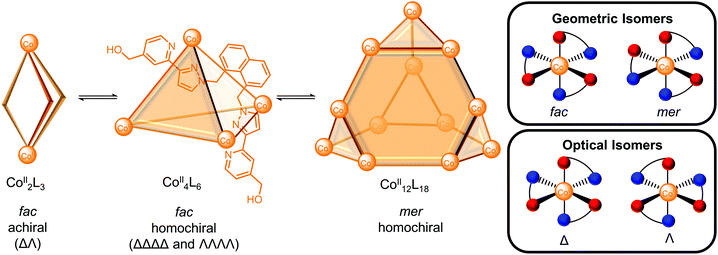
In many cases, multiple architectures can be self-assembled from the same building blocks and therefore, various outcomes can be envisaged based on the relative energies of the possible self-assemblies: (a) a single cage when it is the thermodynamically most stable structure; (b) a mixture of cages as the thermodynamic products with the distribution reflecting the relative energies of the cages; (c) a dynamic combinatorial library with a large number of interconverting species in equilibrium. In an interconverting mixture of three architectures in D2O, Ward and co-workers reported the smaller Co2L3meso-helicate and Co4L6 tetrahedron were favoured at higher temperature and lower concentration on entropic grounds, whereas the larger Co12L18 truncated tetrahedron was favoured at higher concentration and lower temperature (Fig. 2).22 The hydrophobic effect was proposed to be the driving force for the self-assembly of the larger Co12L18 cage in spite of unfavourable electrostatic and entropic effects since the hydrophobic surfaces of the ligand could be more effectively buried away from water. Indeed, the smaller Co2L3 helicate predominated following equilibration of the mixture in MeNO2 where the hydrophobic effect is absent (for a more detailed discussion of the solvent effects of water and the hydrophobic effect for self-assembly and host–guest binding see ref. 23 and 24).
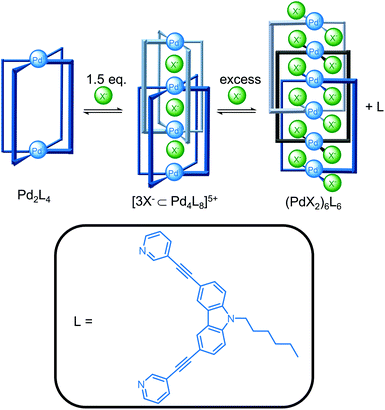
Guest binding can also template the self-assembly of cages (Fig. 3). Clever and co-workers reported the addition of 1.5 equivalents of halide ions templated the formation of the [3X−⊂Pd4L8]5+ interpenetrated double cage from the [Pd2L4](BF4)4 cage since the smaller halide ions could fit within the binding pockets, whereas the BF4− anions were too large.25 The double cage was in equilibrium with the Pd2L4 cage and free ligand and addition of excess halide ions to increase conversion resulted, however, in competing coordination of the halide to the metal centre and decomposition of the double cage with release of free ligand. The triply catenated (PdBr2)6L6 structure crystallised from the mixture containing excess bromide ions.
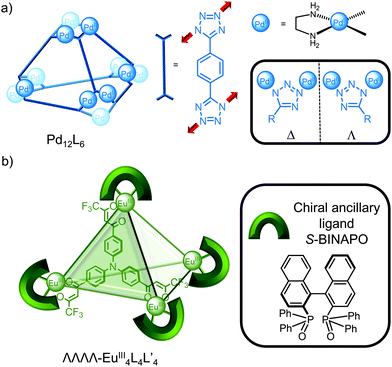
While cages based on PtII and PdII tend to be highly symmetric due to the square planar coordination and achiral unless a chiral ligand is incorporated, Mukherjee and co-workers recently reported the unusual self-assembly of a homochiral Pd12L6 cage from achiral building blocks (Fig. 4a); symmetry breaking of the ligand upon metal coordination to the 1- and 3-nitrogens of the tetrazole ligand results in either a Δ or Λ configuration (Fig. 4a, inset) with all the metal centres within the cage having the same handedness.26 Enantiopure cages were self-assembled extending this strategy by using an enantiopure cis-blocked Pd complex27 or through resolution of the enantiomeric cages via encapsulation of a chiral guest.28
While the stereoselective self-assembly of enantiopure cages29 often employs enantiopure ligand building blocks, Li and co-workers exploited the variable coordination number of lanthanide metal centres to introduce a chiral ancillary ligand (S-BINAPO) to self-assemble the enantiopure cage using an achiral triphenylamine-based ligand (Fig. 4b).17 Furthermore, exchange of the chiral ancillary ligand for an achiral one resulted in stereochemical memory so that the enantiopure cage was obtained even in the absence of the chiral information.
Using the second approach, Fujita and co-workers have demonstrated that a series of spherical PdnL2n cages4 of increasing size from the 3.5 nm Pd12L24 cuboctahedron33 to the 8 nm M30L60 icosidodecahedron34 can be self-assembled by tuning the bend angle (θ) between the donor sites in the ligand from 127° to approx. 150° (Fig. 5).33–35 A key challenge to the successful self-assembly of the M30L60 cage was balancing the ligand flexibility; kinetically trapped smaller species self-assembled with more flexible ligands but some flexibility was necessary to overcome the angle mismatch of the 90° square planar complex with the 60° and 108° angles required for the triangular and pentagonal faces, respectively, of the cage.34 Increasing the bend angle to 152° gave a new class of cage, Pd30L60 (Fig. 5) and Pd48L96 Goldberg polyhedra with square and triangular faces, rather than the expected M60L120 rhombicosidodecahedron.36
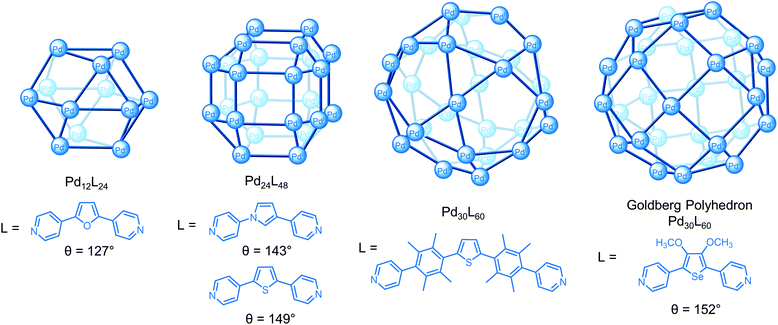 | ||
| Fig. 5 Series of PdnL2n spherical cages reported by Fujita and co-workers where the bend angle (θ) between the donor sites influences the size of the architecture. | ||
In a new approach to access larger cages with higher complexity, Domoto and Fujita recently reported that (M3L2)n cages (where n = 2, 4, 6, 8) can be constructed by molecular entanglement where the M3L2 building blocks oligomerise via metal–acetylene interactions37,38 and the (M3L2)8 truncated cube can be self-assembled from the (M3L2)2 cage by anion exchange of BF4− for NO3−.37 In a similar hierarchical self-assembly approach, Sun and co-workers reported EuIII2L3 helicates self-assemble into a hexameric cage with a 4 nm diameter in the presence of anions.16
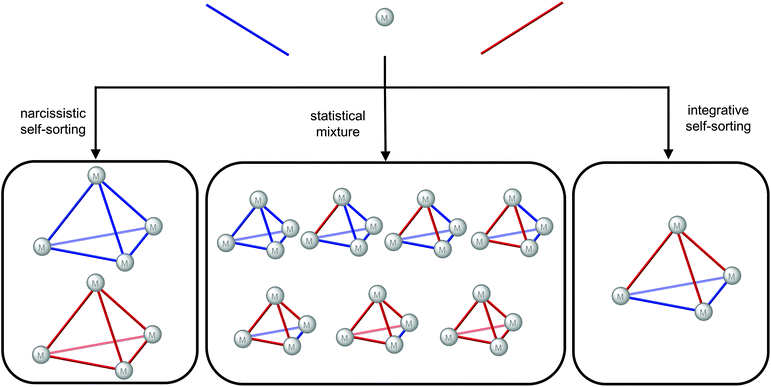
For self-assembly with a mixture of ligands, three outcomes can be envisaged based on the self-sorting, or lack thereof (Fig. 6): narcissistic self-sorting giving homoleptic cages with one ligand type in each cage; a statistical mixture where both ligands are incorporated into the cages according to their statistical distribution; integrative self-sorting where a non-statistical distribution of heteroleptic cages results. The key challenges to the design of heteroleptic cages via integrative self-assembly40 are, therefore, stabilisation of the heteroleptic cage/s relative to the homoleptic cages and biasing the system away from the statistical mixture. Various strategies have been successfully employed including the use of templates, steric effects, complementarity of the ligands’ geometries, ligand interactions and control of the metal's coordination sphere.40
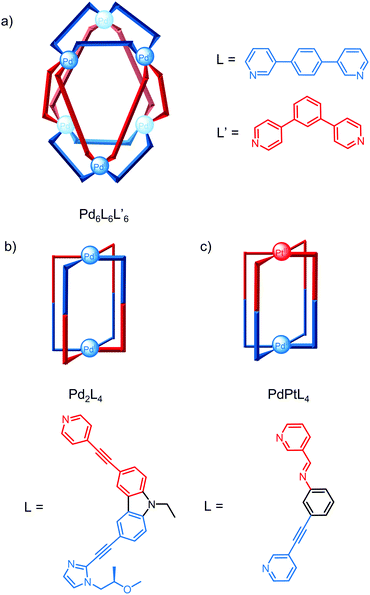
Severin and co-workers exploited a selection approach to identify heteroleptic cages by screening six ligands with a sub-stoichiometric amount of a Pd salt in a virtual combinatorial library;41 although a large number of species are theoretically possible, the most thermodynamically stable self-assemblies were selected by competition for the metal salt. Using this approach, the Pd6L6L′6 cage with an unusual trigonal antiprismatic architecture was identified, even though none of the ligands screened form hexanuclear cages and ligands L and L′ form Pd4L8 and Pd12L′24 homoleptic cages, respectively (Fig. 7a).
Non-symmetric ligands have also been used to access lower symmetry cages and similar approaches such as the use of templates and ligand geometry complementarity have been exploited to induce integrative self-sorting.42 Yuasa and co-workers reported the self-assembly of an open Pd2L4 cage from a ligand containing pyridine and imidazole binding sites.43 Despite the three potential conformations of the two coordination motifs (perpendicular, parallel and antiparallel) and four possible isomers for the open cage depending on the relative orientations of the ligand in the parallel conformation, only one isomer formed (Fig. 7b); DFT calculations revealed this isomer was 61–204 kcal mol−1 more stable than the other isomers.
The self-assembly of heterometallic cages relies on the different coordination preferences of the metals and while there are a number of examples of heterometallic cages, the majority have symmetric cavities.44,45 Crowley and co-workers recently reported a rare example of a lower symmetry heterobimetallic PdPtL4 cage where guest binding induces loss of the cage's four-fold symmetry and desymmetrisation of the 2,6-diaminoanthraquinone guest (Fig. 7c).46
3. Characterisation techniques
While the cage architecture can, in many cases, be successfully predicted using the design principles above (see Section 2), this is not always the case given the complexity of the self-assembly process. This section will introduce the approach for characterising and identifying an unknown cage(s) and studying its host–guest chemistry, discuss recent technique advances/developments as well as highlight challenges to characterisation.Characterisation47 is reliant on a number of techniques and this section will focus on the three most commonly used techniques—NMR spectroscopy, mass spectrometry (MS) and X-ray crystallography—since these provide complementary information; NMR spectroscopy reveals the symmetry of the resulting self-assembled architecture(s) through the number of ligand environments, mass spectrometry the stoichiometry of the metal ion and organic ligand building blocks and X-ray crystallography the 3-dimensional connectivity of the building blocks within the cage. Finally, advances in computational methods for aiding cage characterisation and design will be discussed.
3.1 NMR spectroscopy
There are a number of excellent reviews on the NMR characterisation of supramolecular structures in general.47–50 This section will be divided into the NMR characterisation of the: (a) self-assembly process; (b) resulting cage(s); (c) host–guest chemistry.Nevertheless, Hiraoka and co-workers have developed an NMR-based method, quantitative analysis of self-assembly process (QASAP),51 to indirectly quantify these species over time by monitoring the NMR-detectable species (free ligand, cage and metal containing a 1H NMR active ligand such as pyridine). QASAP as well as NASAP (numerical analysis of self-assembly process)52 also developed by Hiraoka and co-workers, have been used to provide insight into the self-assembly pathway of cages under thermodynamic and kinetic control; in the self-assembly of a Pd6L8 cage, QASAP revealed the final intramolecular ligand exchange of pyridine (Py) in [Pd6L8Py1]12+ was the rate-determining step with further evidence from the detection of this species by mass spectrometry.51
In contrast, the shortened relaxation times from the presence of paramagnetic metal centres such as CoII, NiII and high spin FeII limits the number of NMR techniques for characterisation. Furthermore, the structural information cannot be as readily extracted since: (a) the NMR signals can be found over a much wider chemical shift range due to large paramagnetic shifts; (b) integration is less reliable when there is non-uniform excitation over this wider chemical shift range; (c) the NMR signals have broad linewidths, resulting in loss of the coupling information; (d) in some cases, signals with very short relaxation times and/or broad linewidths can be missing entirely (Fig. 8).54,55 On the other hand, the shorter relaxation times allow the acquisition of more scans in a shorter amount of time from reduction of the acquisition times and recycle delays and this can lead to increased sensitivity.54,56,57
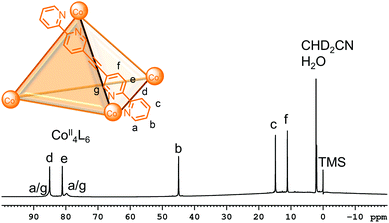 | ||
| Fig. 8 1H NMR spectrum of a CoII4L6 cage showing the characteristic large paramagnetic shifts and broad linewidths resulting from the presence of paramagnetic centres. The assignments were made using the paramagnetic NMR toolbox reported by McConnell and co-workers. Adapted with permission from ref. 54. Copyright 2020 Wiley-VCH. | ||
Previously, the above challenges often limited characterisation of paramagnetic cages to 1H NMR spectroscopy only or in some cases, assignment using the Solomon equation, which relates T1 relaxation times to metal–proton distances from an X-ray crystal structure (see Section 3.3 for challenges with obtaining these).56,57 However, McConnell and co-workers recently optimised a paramagnetic NMR toolbox that enables detailed structural characterisation of paramagnetic cages in solution using a combination of 1D (e.g.1H, proton-coupled 13C, selective 1H decoupling 13C, steady state NOE) and 2D (COSY, NOESY and HMQC) NMR techniques.54 While its use is still in its infancy with application to the characterisation of highly symmetric tetrahedral cages thus far (Fig. 8), optimisation studies using mononuclear complexes demonstrated its potential for the characterisation of more complex systems (e.g. mixtures of cages or lower symmetry cages).54
Analysis of the 1D and 2D NMR data indicates whether a discrete cage, mixture of cages or a dynamic combinatorial library result from the self-assembly. In the case of a discrete cage or a mixture of cages, analysis provides information about the symmetry of the resulting self-assembled architecture(s) through the number of ligand environments. This combined with a knowledge of the design principles (see Section 2) can allow proposal of the cage architecture(s).
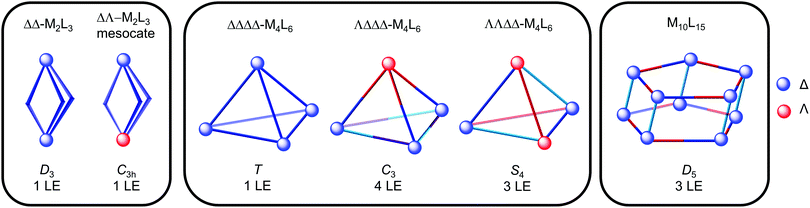
Fig. 9 shows the idealised symmetry of M2L3, M4L6 and M10L15 architectures and corresponding number of ligand environments (LE), provided the ligand is symmetric and there is no symmetry breaking upon coordination. The T-, C3- and S4-diastereomers of M4L6 tetrahedra can be differentiated on the basis of the number of ligand environments (1, 4 and 3, respectively). Furthermore, cages containing mer octahedral metal complexes such as the Co12L18 truncated tetrahedron22 (Fig. 2) and M10L15 pentagonal prism (Fig. 9) have three ligand environments, whereas the T-symmetric M4L6 tetrahedron with fac octahedral complexes only has one. Highly symmetrical architectures often result since highly symmetrical building blocks are typically used and multiple architectures with the same number of ligand environments could be possible from the same building blocks e.g. a M2L3 helicate and T-symmetric M4L6 tetrahedron, each with one ligand environment. Thus, these architectures cannot be distinguished on the basis of NMR spectroscopy alone and other techniques, such as mass spectrometry and X-ray crystallography, are necessary (see Sections 3.2 and 3.3).
Diffusion ordered spectroscopy (DOSY) can be useful in these circumstances and for general characterisation since it provides information about the size and shape of the cage.48 Firstly, DOSY indicates whether the signals assigned to the cage have the same diffusion coefficient and therefore, most likely belong to the same species. This caveat is necessary since architectures with similar molecular weights can be difficult to distinguish by DOSY, particularly when their chemical shifts are similar and in this case, a 2–3 fold difference in diffusion coefficient is recommended.49 For example, Fujita's Goldberg polyhedral M30L60 (Fig. 5) and M48L96 cages could not be separated by DOSY since the signals of the two species were broad and overlapping.36
Secondly, the diffusion coefficient obtained from DOSY can be used to give an estimation of the cage's size. For example, the Pd24L48 cage in Fig. 5 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D = −10.49) has a smaller diffusion coefficient than the smaller Pd12L24 cage (log
D = −10.49) has a smaller diffusion coefficient than the smaller Pd12L24 cage (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D = −10.3).35 The hydrodynamic radius of the cage can be calculated from the diffusion coefficient using the Stokes–Einstein equation.48 This equation assumes a hard sphere is diffusing in a continuum fluid and the contributions from solvent and ion-pair interactions are neglected. While these approximations appear valid for spherical cages, they may not be for non-spherical cages. In those cases, the modified Stokes–Einstein equation is more appropriate since it takes into account shape and size factors.48
D = −10.3).35 The hydrodynamic radius of the cage can be calculated from the diffusion coefficient using the Stokes–Einstein equation.48 This equation assumes a hard sphere is diffusing in a continuum fluid and the contributions from solvent and ion-pair interactions are neglected. While these approximations appear valid for spherical cages, they may not be for non-spherical cages. In those cases, the modified Stokes–Einstein equation is more appropriate since it takes into account shape and size factors.48
The use of DOSY has been largely limited to diamagnetic rather than paramagnetic cages due to the large paramagnetic shifts and broad linewidths. However, the recent report of paramagnetic DOSY for first row transition metal complexes by Byers and co-workers55 demonstrates the potential for more widespread use of DOSY for paramagnetic cages. Indeed, the hydrodynamic radius determined by DOSY for a trigonal bipyramidal cage incorporating iron in three different spin states reported by Riddell and co-workers showed good agreement with the diameter obtained from the X-ray crystal structure.58
Initial evidence for encapsulation comes from changes to the chemical shifts of the cage as well as guest signals. These shifts can be observed by 1H NMR spectroscopy but also other types of NMR spectroscopy when the guest and/or cage contain NMR active nuclei such as 19F and 31P. Two situations can be envisaged based on the rate of guest exchange compared to the NMR time-scale: slow exchange where two sets of signals are observed, corresponding to the empty cage (or alternatively, the free guest) and host–guest complex; fast exchange so only one set of signals is observed reflecting the average of the empty cage and host–guest complex signals.
The magnitude of the chemical shift changes upon guest encapsulation is dependent on a number of factors since not only the ligand but also the metal can influence the environment of the cavity. In many cases, the cavity is enclosed by ligands containing aromatic groups. Therefore, guest signals typically shift upfield as a result of shielding, reflecting the weaker field the guests experience compared to the applied magnetic field.61 For example, the signals of encapsulated NEt4+ (marked with *) within the GaIII4L6 tetrahedral cage reported by Raymond and co-workers are in slow exchange and shifted compared to the “free” guest (marked with #, Fig. 10).62 In contrast, Nitschke and co-workers recently reported a FeII4L6 tetrahedral cage containing antiaromatic walls and the signals of polyaromatic hydrocarbon guests were observed to shift up to 15 ppm downfield due to deshielding.61
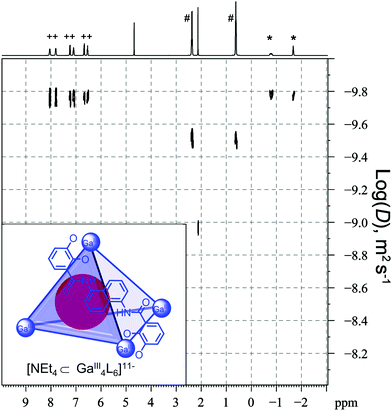 | ||
| Fig. 10 1H and DOSY spectra of Raymond's [NEt4⊂GaIII4L6]11− host–guest complex where the encapsulated NEt4+ guest is in slow exchange with “free” NEt4+. Signals marked with + correspond to the cage, * the encapsulated NEt4+ guest and # the “free” NEt4+. Adapted with permission from ref. 62. Copyright 2008 American Chemical Society. | ||
Large shifts of the guest signals upon encapsulation are also observed with paramagnetic cages, facilitating detection of host–guest binding.56,57 Furthermore, the potential for increased scanning due to the shorter relaxation times can lead to improved sensitivity. For example, Nitschke and co-workers reported trace impurities of cis-decalin in a sample of commercial trans-decalin could be detected through the formation of its host–guest complex with a high spin FeII4L4 tetrahedral cage.57
For host–guest complexes in slow exchange, DOSY can provide further evidence for guest encapsulation since the cage and encapsulated guest will have the same diffusion coefficient that is distinct from the “free” guest (Fig. 10). The observed diffusion coefficients, however, can be affected by ion-pairing with Raymond and co-workers reporting a decrease in the diffusion coefficient of a GaIII4L6 cage with an increasing amount of the NEt4+ guest but addition of a second countercation K+ disrupted ion-pairing leading to an increase of the diffusion coefficient for “free” NEt4+.62
Chemical exchange saturation transfer (CEST)60 NMR methods can be used to study host–guest systems in slow exchange, particularly when there is line broadening of the NMR signals from exchange and undetectable signals due to weak guest binding.50 In a CEST experiment the bound guest is selectively “labelled” with a saturation pulse so that it has no magnetisation. Since these “labelled” bound guests exchange with the free guest population, the signal for the free guest decreases in intensity. Thus, CEST techniques can amplify the signal of the lower concentration species (the host–guest complex), which may not be detectable, by exploiting the sensitivity of the higher concentration species (the free guest).
Despite its increased sensitivity, there are relatively few examples of CEST experiments for characterising the host–guest complexes of cages. 129Xe hyper-CEST experiments increase the sensitivity of detection by combining hyperpolarisation and CEST with Dmochowski and co-workers reporting that a [Xe⊂Co4L6]4− host–guest complex could be detected at a concentration of 100 pM.63 Furthermore, hyper-CEST enabled detection of a mixture of [Xe⊂ConFe4−nL6]4− host–guest complexes when these species could not be simultaneously measured directly by hyperpolarised 129Xe NMR spectroscopy due to weak signals and exchange between the different species (Fig. 11).64
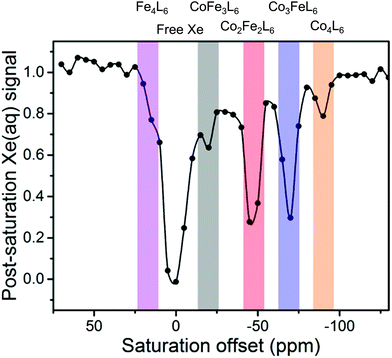 | ||
| Fig. 11 CEST spectrum reported by Dmochowski and co-workers of a mixture of [Xe⊂ConFe4−nL6]4− host–guest complexes detected using hyperCEST. Adapted with permission from ref. 64. Copyright 2020 American Chemical Society. | ||
Although it has yet to be applied to the characterisation of metallosupramolecular cages, an emerging new tool in the detection of host–guest interactions by CEST is 19F guest exchange saturation transfer (GEST) reported by Bar-Shir and co-workers since it can amplify undetectable host–guest complex signals and quantify guest exchange.50 Furthermore, various guest molecules incorporate a 19F atom and thus, the guest is not restricted to Xe like hyper-CEST.
3.2 Mass spectrometry
For a general introduction to instrumentation and the study of supramolecules by mass spectrometry, the reader's attention is turned to reviews by Schalley.65,66 For metallosupramolecular cages, mass spectrometry provides complementary information to NMR spectroscopy regarding the number of each building block within the structure and this can confirm the type of architecture proposed from the symmetry observed by NMR spectroscopy. There are a number of caveats, however, when comparing information obtained from mass spectrometry and NMR spectroscopy. Firstly, the mass spectrometric measurements take place at much lower concentrations (typically μM range) than NMR spectroscopy and thus, other species including fragments may be present in the more dilute sample due to the change in the equilibrium. Secondly, mass spectrometric measurements take place in the gas phase where the cage is no longer solvated and in equilibrium with its constituent building blocks and therefore, different properties of the cage may be observed in the gas phase versus solution.65 Finally, the intensity of the peaks in the mass spectrum does not correlate with their concentration.65 Therefore, NMR assignment of signals to a particular architecture in a mixture of cages cannot be made on the basis of the relative peak intensities of the architectures in the mass spectrum.Cages are typically characterised by electrospray ionisation (ESI) mass spectrometry since this uses relatively mild ionisation conditions.66 Nevertheless, characterisation can be challenging due to the relatively weak metal–ligand coordinative bonds; the cages can be prone to fragmentation under not only the ionisation conditions (e.g. heat from the desolvation chamber) but also due to the low μM concentration. Increased concentrations (100–300 μM) can lead to spectra with fewer fragments, although this is at the expense of increased ion source cleaning.66 For particularly labile cages where ESI mass spectrometry is not suitable, Yamaguchi, Fujita and co-workers have reported coldspray ionisation (CSI) mass spectrometry as a variant of ESI mass spectrometry where both the cage solution and ion source are cooled to reduce fragmentation.67
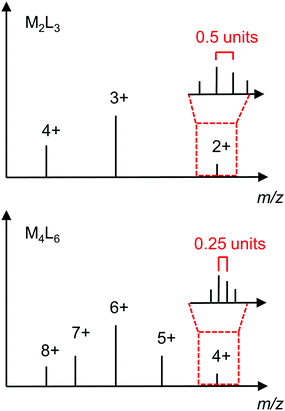 | ||
| Fig. 12 Idealised mass spectra of M2L3 and M4L6 structures showing how they can be differentiated on the basis of the series of ion peaks and isotope pattern for a particular m/z ratio. | ||
Mass spectrometry is particularly important for determining the composition of cages that cannot be differentiated on the basis of their NMR spectra alone, e.g. a [M2L3]4+ helicate and T-symmetric [M4L6]8+ tetrahedron (see Section 3.1.2). Fig. 12 shows idealised mass spectra for these two architectures to illustrate how they can be distinguished; while there are several ion peaks in common (i.e. at the same m/z ratio), the ion peaks corresponding to the odd charges of the M4L6 are not present for the M2L3. Furthermore, the difference in charge is evident in the isotope patterns with a spacing of 0.5 units and 0.25 units for the [M2L3]2+ and [M4L6]4+, respectively.
Mass spectroscopy can, however, provide more information than just the number of each building block within a cage and techniques such as tandem MS/MS65,66 and ion mobility mass spectrometry66,68,69 also play a role in the characterisation of cages and their host–guest complexes. While the discussion thus far has pointed out the challenges associated with characterisation due to undesired cage fragmentation, tandem MS/MS experiments exploit fragmentation of a mass-selected ion peak of the cage to provide additional structural information. For example, Schalley, Nitschke and Sanders used infrared-multiphoton dissociation experiments to distinguish specific from non-specific binding of crown ethers (C) in a Fe4L6C6 tetrahedral polycatenane by comparing the fragmentation of the [Fe4L6C6]8+ and [Fe4L6C7]8+ ions, respectively.70
Ion-mobility mass spectrometry selects ions based on their m/z ratio and separates them according to their collision cross section in a drift tube with a low electric field; the collision cross section is used as a measure of the ion size and ions with larger collision cross sections undergo more collisions, resulting in longer arrival times at the detector. Thus, ion-mobility mass spectrometry can be used to separate ions with the same m/z ratio but different sizes. This is particularly useful when cages cannot be distinguished by other techniques, such as NMR spectroscopy. For example, Clever and co-workers demonstrated that 10 heteroleptic cages a–i including two isomeric cages generated from PdII ions and four different ligands could be differentiated by their collision cross sections (Fig. 13).71
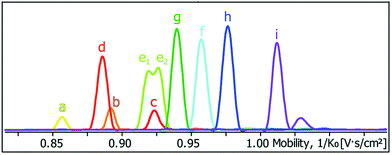 | ||
| Fig. 13 Mobilogram of a mixture of 10 heteroleptic cages (a–i) reported by Clever and co-workers depicting the differentiation of the cages on the basis of their collision cross section (increasing from left to right) by trapped ion mobility mass spectrometry. Reproduced from ref. 71 with permission from the Royal Society of Chemistry. | ||
3.3 X-Ray crystallography
X-Ray crystallography is a powerful characterisation technique, providing the three-dimensional connectivity of the metal ions and ligands within a cage and in some cases, evidence of guest encapsulation. Given the nanomolecular size of cages, there are a number of challenges associated with obtaining a single crystal of sufficient quality that diffracts well in addition to refining the crystal structure due to disorder from the cage, solvent, guest molecules and counterions.72 Numerous crystallisation conditions are typically screened to obtain suitable crystals and synchrotron radiation is used in many cases to improve the resolution for weakly diffracting crystals.Despite these challenges, X-ray crystallography is instrumental in the characterisation of cages, particularly for those where other techniques give ambiguous structural assignments or cannot be used. For example, the Goldberg polyhedral Pd48L96 cage could not be distinguished from the smaller Goldberg polyhedral Pd30L60 cage by DOSY (see Section 3.1.2) or be detected by mass spectrometry.36 While both cages crystallise, a single crystal X-ray structure with 2.85 Å resolution was obtained of the Pd48L96 cage by collecting data for more than 10 crystals with different cell parameters to the Pd30L60 cage.
Since crystallisation is driven by solubility and crystal packing effects, the X-ray structure does not necessarily reflect the major species in solution as it is determined from a single crystal in the solid state. Bloch and co-workers recently demonstrated that three isomers of a cage can be selectively crystallised via self-sorting from a dynamic combinatorial library and DFT calculations revealed that the crystallised isomers were not the thermodynamically most stable isomer.73
The crystallisation of host–guest complexes has the additional challenge that crystals of the cage can be obtained with solvent in the cavity rather than the guest or the guest is too disordered to model in the X-ray crystal structure of the host–guest complex.74 Ward and co-workers have reported improved crystallisation of host–guest complexes using Fujita's “crystalline sponge” method75 where crystals of the cage are soaked in the guest rather than crystallising the cage from solution in the presence of the guest.74
Surprisingly, X-ray crystal structures of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host–guest complexes of a Co8L12 cage were obtained where the guests occupy up to 87% of the cage's cavity volume (Fig. 14) when solution studies indicated the formation of a 1
2 host–guest complexes of a Co8L12 cage were obtained where the guests occupy up to 87% of the cage's cavity volume (Fig. 14) when solution studies indicated the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 host–guest complex.74 This apparent violation of the Rebek 55% rule for optimal binding is attributed to the use of a large excess of guest (i.e. non-equilibrium conditions) and favourable interactions, such as π–π stacking between guests and hydrogen bonding between the guest and cage. Furthermore, solution experiments at higher concentrations also indicated the formation of the 1
1 host–guest complex.74 This apparent violation of the Rebek 55% rule for optimal binding is attributed to the use of a large excess of guest (i.e. non-equilibrium conditions) and favourable interactions, such as π–π stacking between guests and hydrogen bonding between the guest and cage. Furthermore, solution experiments at higher concentrations also indicated the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host–guest complex, showing the importance of using complementary techniques.
2 host–guest complex, showing the importance of using complementary techniques.
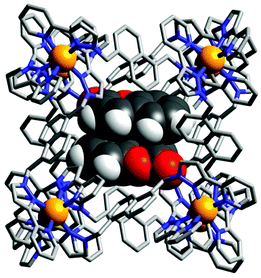 | ||
| Fig. 14 X-Ray crystal structure of [(coumarin)2⊂Co8L12]16+ reported by Ward and co-workers where the cage is depicted as a wireframe and the two guests in spacefilling. Reproduced with permission from ref. 74. Copyright 2020 Wiley-VCH. | ||
3.4 Computational studies
Computational studies are playing an increasingly large role in both the design and characterisation of metallosupramolecular cages. Duarte and co-workers reported cgbind, an open source Python module and web app, for generating three-dimensional structures of cages from their metal ion and organic ligand building blocks, predicting binding affinities for guests and calculating properties of the cages such as their electrostatic potential, cavity size and pore size.76 Furthermore, it has been applied to provide insight into the catalytic activity of a Pd2L4 cage (see Section 4).77Lewis and Jelfs have recently proposed a high-throughput screening method employing the supramolecular toolkit (stk) for identifying low-symmetry Pd2L4 cages.78 The potential of this approach to facilitate cage discovery was demonstrated through the screening of 60 unsymmetrical ligands for the energies of the four possible Pd2L4 isomers and 5 ligands were identified for synthetic experiments; of these, four self-assembled into a single isomer of a heteroleptic cage, whereas one produced a mixture of isomers.
Computational methods also have the potential to make the host–guest screening more efficient. Using the protein/ligand docking GOLD program, Ward, Hunter and co-workers optimised a scoring function for a water soluble Co8L12 cage using a dataset of experimental binding affinities and in silico screening of a library of 3000 guests identified 15 previously unknown guests, predicting their binding affinities within an order of magnitude.79 It is proposed this approach can be applied to other rigid cages and for host–guest binding in solvents other than water, provided there is an X-ray structure/model of the cage and a large enough dataset of experimental binding affinities for optimising the scoring function.79
4. Applications
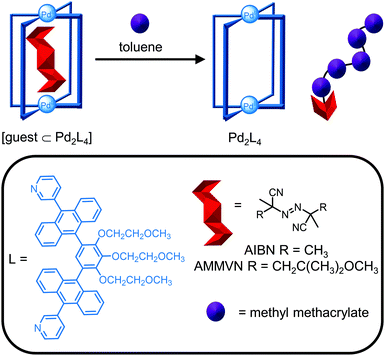
Metallosupramolecular cages are employed in a variety of applications including exploiting the confined space within the cavity for modulating the properties of encapsulated molecules. Given the breadth of applications from catalysis to molecular separations, it is not possible to give a detailed description and therefore, this section will focus on three examples to illustrate the synergy between design (Section 2) and characterisation techniques (Section 3) in the development of cages for tailored functionality in applications.Reactive species can be stabilised upon encapsulation and subsequently released exploiting the host–guest chemistry of the cage. Yoshizawa and co-workers reported the photochemical stability of the radical initiator 2,2′-azobisisobutyronitrile (AIBN) is increased by >380 times when bound within a Pd2L4 cage due to light absorption by the ligands’ large aromatic panels (Fig. 15).80 Host–guest complex formation was confirmed by mass spectrometry and the methyl protons of AIBN were observed to desymmetrise and shift significantly upfield by almost 4 ppm upon encapsulation. The X-ray crystal structure also revealed the S-shaped trans configuration of AIBN in the cavity. While the thermal stability of AIBN was not improved by encapsulation, the thermal stability of the larger analogue AMMVN increased 645 times, attributed to a tighter size fit in the cavity. The reactivity of the radical initiators was restored upon its release from the cage in toluene, as evidenced by the thermal and photochemical polymerisation of methyl methacrylate (Fig. 15).
A new approach in cavity-directed reactions1 is the use of cages as supramolecular masks to control the regioselectivity of reactions. While the functionalisation of C60 leads to complex mixtures of adducts, von Delius, Ribas and co-workers recently reported the formation of the trans-3 bis-adduct only from a Bingel cyclopropanation reaction in a ternary complex consisting of a Pd-based tetragonal prismatic cage, [10]cycloparaphenylene ([10]CPP) and C60 (Fig. 16).81 The reaction in the presence of [10]CPP or cage alone gave mixtures of the trans and e,e bis-adducts, respectively, demonstrating the formation of the ternary complex is key to the regioselectivity. The crystal structures of the ternary complexes [C60⊂[10]CPP⊂CuII4L2L′4] and [trans-3-C60⊂[10]CPP⊂CuII4L2L′4] with the CuII analogue of the cage provided an explanation for the observed selectivity; although the formation of the e,e bis-adduct would be expected based on the 90° angle between the cage windows, the tilt of the [10]CPP ring relative to the porphyrin faces of the cage blocks the approach of the dialkyl bromomalonate so that bis-functionalisation occurs at an angle of 120° only. The increased steric bulk from functionalisation resulted in desymmetrisation of the cage signals and a decrease in the binding affinity so that trans-3-C60 could be removed by solvent washing and addition of C60.
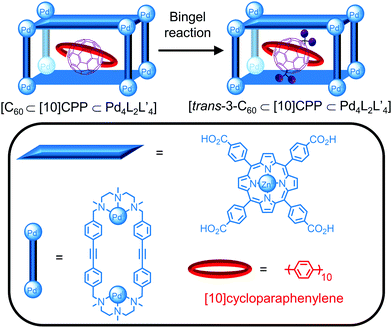 | ||
| Fig. 16 Regioselective functionalisation of C60 reported by von Delius, Ribas and co-workers within a ternary complex consisting of C60, [10]cycloparaphenylene and a Pd4L2L′4 cage. | ||
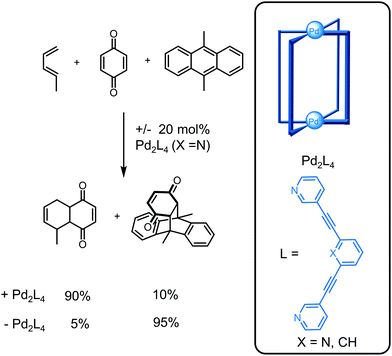
With the increasing number of catalytically active cages, computational studies are providing complementary insights to experimental studies for the improved rational design of catalytic systems. Lusby and co-workers reported the Pd2L4 cage (X = N) catalyses Diels–Alder reactions between a bound quinone substrate and diene (Fig. 17).82 Through confinement, the chemoselectivity is reversed so that the smaller but less reactive 1,3-pentadiene reacts preferentially with the bound quinone compared to the larger but more reactive 9,10-dimethylanthracene, unlike the uncatalysed reaction. Furthermore, subtle changes to the cage such as a replacement of a pyridine (X = N) with a benzene ring (X = CH) resulted in no catalytic activity even though the quinone is bound more strongly. Computational studies provided insight into the cause of this change in catalytic activity;77 although both cages activate the dienophile by lowering the LUMO, the energetic cost to distort the cage for favourable transition state binding was higher for the less flexible cage with X = CH and thus, this cage was not catalytically active. This highlights the synergistic roles experimental and computational studies play in the design of cages for applications and also the need for the development of new computational methods, particularly those that are inexpensive in terms of computational time but accurate.
5. Conclusions
This Tutorial Review has introduced the different approaches (directional bonding, symmetry interaction and panelling) to the design of metallosupramolecular cages as well as the various factors influencing the self-assembly process from the building block design to the choice of solvent and presence of guests. In many cases, cages can be rationally designed with an understanding of these design principles, however, serendipity can also play a role in the discovery of new and unexpected architectures. In either case, a range of complementary characterisation techniques are necessary to identify the cage, particularly when multiple architectures are possible from the same building blocks.NMR spectroscopy, mass spectrometry, X-ray crystallography and increasingly computational studies are the workhorses of cage characterisation, each with their strengths and challenges. While NMR spectroscopy and mass spectrometry are primarily used to provide information about the symmetry and composition of the cage, respectively, they can also give insight into the size and shape of the cage and its host–guest complexes through DOSY and ion-mobility mass spectrometry. This information can also be obtained by X-ray crystallography from the three-dimensional structure of the cage. As less computationally expensive but accurate computational methods are being developed to rationalise experimental findings, there is the opportunity to exploit them as prediction tools to facilitate cage design, discovery and application.
From the initial pioneering self-assembly of metallosupramolecular cages, the field has evolved from understanding the fundamentals to applying this knowledge to the design of cages for applications. As the boundaries of self-assembly are pushed and the size and complexity of the cages increase, the toolbox of design principles will be expanded and this will allow not only more complex functionality for applications but also drive the development of new characterisation techniques.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Deutsche Forschungsgemeinschaft (DFG, project numbers 413396832 and 429518153) is gratefully acknowledged.Notes and references
- M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418–3438 CrossRef CAS PubMed and references cited therein.
- T. K. Ronson, S. Zarra, S. P. Black and J. R. Nitschke, Chem. Commun., 2013, 49, 2476–2490 RSC and references cited therein.
- M. Fujita, K. Umemoto, M. Yoshizawa, N. Fujita, T. Kusukawa and K. Biradha, Chem. Commun., 2001, 509–518 RSC and references cited therein.
- K. Harris, D. Fujita and M. Fujita, Chem. Commun., 2013, 49, 6703–6712 RSC and references cited therein.
- Y. Sun, C. Chen, J. Liu and P. J. Stang, Chem. Soc. Rev., 2020, 49, 3889–3919 RSC and references cited therein.
- R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810–6918 CrossRef CAS PubMed and references cited therein.
- D. L. Caulder and K. N. Raymond, Acc. Chem. Res., 1999, 32, 975–982 CrossRef CAS and references cited therein.
- A. Galan and P. Ballester, Chem. Soc. Rev., 2016, 45, 1720–1737 RSC and references cited therein.
- Y. Fang, J. A. Powell, E. Li, Q. Wang, Z. Perry, A. Kirchon, X. Yang, Z. Xiao, C. Zhu, L. Zhang, F. Huang and H.-C. Zhou, Chem. Soc. Rev., 2019, 48, 4707–4730 RSC and references cited therein.
- D. Zhang, T. K. Ronson, Y.-Q. Zou and J. R. Nitschke, Nat. Rev. Chem., 2021, 5, 168–182 CrossRef CAS and references cited therein.
- T. Beissel, R. E. Powers and K. N. Raymond, Angew. Chem., Int. Ed. Engl., 1996, 35, 1084–1086 CrossRef CAS.
- R. W. Saalfrank, A. Stark, K. Peters and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1988, 27, 851–853 CrossRef.
- M. Fujita, D. Oguro, M. Miyazawa, H. Oka, K. Yamaguchi and K. Ogura, Nature, 1995, 378, 469–471 CrossRef CAS.
- B. Olenyuk, J. A. Whiteford, A. Fechtenkötter and P. J. Stang, Nature, 1999, 398, 796–799 CrossRef CAS PubMed.
- L.-L. Yan, C.-H. Tan, G.-L. Zhang, L.-P. Zhou, J.-C. Bünzli and Q.-F. Sun, J. Am. Chem. Soc., 2015, 137, 8550–8555 CrossRef CAS PubMed.
- X.-Q. Guo, L.-P. Zhou, S.-J. Hu, L.-X. Cai, P.-M. Cheng and Q.-F. Sun, J. Am. Chem. Soc., 2021, 143, 6202–6210 CrossRef CAS PubMed.
- Y. Zhou, H. Li, T. Zhu, T. Gao and P. Yan, J. Am. Chem. Soc., 2019, 141, 19634–19643 CrossRef CAS PubMed.
- E. O. Bobylev, B. de Bruin and J. N. H. Reek, Inorg. Chem., 2021, 60, 12498–12505 CrossRef CAS PubMed.
- D. Rota Martir and E. Zysman-Colman, Chem. Commun., 2019, 55, 139–158 RSC and references cited therein.
- P. R. Symmers, M. J. Burke, D. P. August, P. I. T. Thomson, G. S. Nichol, M. R. Warren, C. J. Campbell and P. J. Lusby, Chem. Sci., 2015, 6, 756–760 RSC.
- R. Kramer, J. M. Lehn and A. Marquis-Rigault, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 5394–5398 CrossRef CAS PubMed.
- W. Cullen, C. A. Hunter and M. D. Ward, Inorg. Chem., 2015, 54, 2626–2637 CrossRef CAS PubMed.
- A. J. McConnell and M. Lehr, in Supramolecular Chemistry in Water, ed. S. Kubik, Wiley-VCH, 2019, pp. 249–284 and references cited therein Search PubMed.
- E. G. Percástegui, T. K. Ronson and J. R. Nitschke, Chem. Rev., 2020, 120, 13480–13544 CrossRef PubMed and references cited therein.
- R. Zhu, J. Lübben, B. Dittrich and G. H. Clever, Angew. Chem., Int. Ed., 2015, 54, 2796–2800 CrossRef CAS PubMed.
- P. Howlader and P. S. Mukherjee, Chem. Sci., 2016, 7, 5893–5899 RSC.
- P. Howlader, E. Zangrando and P. S. Mukherjee, J. Am. Chem. Soc., 2020, 142, 9070–9078 CrossRef CAS PubMed.
- P. Howlader, S. Mondal, S. Ahmed and P. S. Mukherjee, J. Am. Chem. Soc., 2020, 142, 20968–20972 CrossRef CAS PubMed.
- L.-J. Chen, H.-B. Yang and M. Shionoya, Chem. Soc. Rev., 2017, 46, 2555–2576 RSC and references cited therein.
- A. V. Virovets, E. Peresypkina and M. Scheer, Chem. Rev., 2021, 121, 14485–14554 CrossRef CAS PubMed and references cited therein.
- S. M. Jansze, M. D. Wise, A. V. Vologzhanina, R. Scopelliti and K. Severin, Chem. Sci., 2017, 8, 1901–1908 RSC.
- S. M. Jansze, D. Ortiz, F. Fadaei Tirani, R. Scopelliti, L. Menin and K. Severin, Chem. Commun., 2018, 54, 9529–9532 RSC.
- M. Tominaga, K. Suzuki, M. Kawano, T. Kusukawa, T. Ozeki, S. Sakamoto, K. Yamaguchi and M. Fujita, Angew. Chem., Int. Ed., 2004, 43, 5621–5625 CrossRef CAS PubMed.
- D. Fujita, Y. Ueda, S. Sato, H. Yokoyama, N. Mizuno, T. Kumasaka and M. Fujita, Chem, 2016, 1, 91–101 CAS.
- Q.-F. Sun, J. Iwasa, D. Ogawa, Y. Ishido, S. Sato, T. Ozeki, Y. Sei, K. Yamaguchi and M. Fujita, Science, 2010, 328, 1144–1147 CrossRef CAS PubMed.
- D. Fujita, Y. Ueda, S. Sato, N. Mizuno, T. Kumasaka and M. Fujita, Nature, 2016, 540, 563 CrossRef CAS PubMed.
- Y. Domoto, M. Abe and M. Fujita, J. Am. Chem. Soc., 2021, 143, 8578–8582 CrossRef CAS PubMed.
- Y. Domoto, M. Abe, T. Kikuchi and M. Fujita, Angew. Chem., Int. Ed., 2020, 59, 3450–3454 CrossRef CAS PubMed.
- L. R. Holloway, P. M. Bogie and R. J. Hooley, Dalton Trans., 2017, 46, 14719–14723 RSC and references cited therein.
- W. M. Bloch and G. H. Clever, Chem. Commun., 2017, 53, 8506–8516 RSC and references cited therein.
- S. Sudan, R.-J. Li, S. M. Jansze, A. Platzek, R. Rudolf, G. H. Clever, F. Fadaei-Tirani, R. Scopelliti and K. Severin, J. Am. Chem. Soc., 2021, 143, 1773–1778 CrossRef CAS PubMed.
- J. E. M. Lewis and J. D. Crowley, ChemPlusChem, 2020, 85, 815–827 CrossRef CAS PubMed and references cited therein.
- D. Ogata and J. Yuasa, Angew. Chem., Int. Ed., 2019, 58, 18424–18428 CrossRef CAS PubMed.
- M. Hardy and A. Lützen, Chem. – Eur. J., 2020, 26, 13332–13346 CrossRef CAS PubMed and references cited therein.
- Y.-Y. Zhang, W.-X. Gao, L. Lin and G.-X. Jin, Coord. Chem. Rev., 2017, 344, 323–344 CrossRef CAS and references cited therein.
- L. S. Lisboa, J. A. Findlay, L. J. Wright, C. G. Hartinger and J. D. Crowley, Angew. Chem., Int. Ed., 2020, 59, 11101–11107 CrossRef CAS PubMed.
- N. Geue, R. E. P. Winpenny and P. E. Barran, Chem. Soc. Rev., 2022, 51, 8–27 RSC and references cited therein.
- L. Avram and Y. Cohen, Chem. Soc. Rev., 2015, 44, 586–602 RSC and references cited therein.
- Y. Cohen, S. Slovak and L. Avram, Chem. Commun., 2021, 57, 8856–8884 RSC and references cited therein.
- L. Avram and A. Bar-Shir, Org. Chem. Front., 2019, 6, 1503–1512 RSC and references cited therein.
- Y. Tsujimoto, T. Kojima and S. Hiraoka, Chem. Sci., 2014, 5, 4167–4172 RSC.
- Y. Matsumura, S. Hiraoka and H. Sato, Phys. Chem. Chem. Phys., 2017, 19, 20338–20342 RSC.
- M. Foroozandeh, G. A. Morris and M. Nilsson, Chem. – Eur. J., 2018, 24, 13988–14000 CrossRef CAS PubMed.
- M. Lehr, T. Paschelke, E. Trumpf, A.-M. Vogt, C. Näther, F. D. Sönnichsen and A. J. McConnell, Angew. Chem., Int. Ed., 2020, 59, 19344–19351 CrossRef CAS PubMed.
- M. P. Crockett, H. Zhang, C. M. Thomas and J. A. Byers, Chem. Commun., 2019, 55, 14426–14429 RSC.
- S. Turega, M. Whitehead, B. R. Hall, A. J. H. M. Meijer, C. A. Hunter and M. D. Ward, Inorg. Chem., 2013, 52, 1122–1132 CrossRef CAS PubMed.
- A. J. McConnell, C. M. Aitchison, A. B. Grommet and J. R. Nitschke, J. Am. Chem. Soc., 2017, 139, 6294–6297 CrossRef CAS PubMed.
- L. L. K. Taylor, I. J. Vitorica-Yrezabal, I. Borilović, F. Tuna and I. A. Riddell, Chem. Commun., 2021, 57, 11252–11255 RSC.
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC and references cited therein.
- P. C. M. van Zijl and N. N. Yadav, Magn. Reson. Med., 2011, 65, 927–948 CrossRef CAS PubMed and references cited therein.
- M. Yamashina, Y. Tanaka, R. Lavendomme, T. K. Ronson, M. Pittelkow and J. R. Nitschke, Nature, 2019, 574, 511–515 CrossRef CAS PubMed.
- M. D. Pluth, B. E. F. Tiedemann, H. van Halbeek, R. Nunlist and K. N. Raymond, Inorg. Chem., 2008, 47, 1411–1413 CrossRef CAS PubMed.
- K. Du, S. D. Zemerov, S. Hurtado Parra, J. M. Kikkawa and I. J. Dmochowski, Inorg. Chem., 2020, 59, 13831–13844 CrossRef CAS PubMed.
- K. Du, S. D. Zemerov, P. J. Carroll and I. J. Dmochowski, Inorg. Chem., 2020, 59, 12758–12767 CrossRef CAS PubMed.
- D. P. Weimann, M. Kogej and C. A. Schalley, in Analytical Methods in Supramolecular Chemistry, ed. C. A. Schalley, Wiley VCH, 2012 and references cited therein Search PubMed.
- Z. Qi, T. Heinrich, S. Moorthy and C. A. Schalley, Chem. Soc. Rev., 2015, 44, 515–531 RSC and references cited therein.
- S. Sakamoto, M. Fujita, K. Kim and K. Yamaguchi, Tetrahedron, 2000, 56, 955–964 CrossRef CAS.
- E. Kalenius, M. Groessl and K. Rissanen, Nat. Rev. Chem., 2019, 3, 4–14 CrossRef CAS and references cited therein.
- O. H. Lloyd Williams and N. J. Rijs, Front. Chem., 2021, 9 DOI:10.3389/fchem.2021.682743 and references cited therein.
- S. P. Black, A. R. Stefankiewicz, M. M. J. Smulders, D. Sattler, C. A. Schalley, J. R. Nitschke and J. K. M. Sanders, Angew. Chem., Int. Ed., 2013, 52, 5749–5752 CrossRef CAS PubMed.
- K. E. Ebbert, L. Schneider, A. Platzek, C. Drechsler, B. Chen, R. Rudolf and G. H. Clever, Dalton Trans., 2019, 48, 11070–11075 RSC.
- K. Rissanen, Chem. Soc. Rev., 2017, 46, 2638–2648 RSC and references cited therein.
- A. W. Markwell-Heys, M. L. Schneider, J. M. L. Madridejos, G. F. Metha and W. M. Bloch, Chem. Commun., 2021, 57, 2915–2918 RSC.
- C. G. P. Taylor, S. P. Argent, M. D. Ludden, J. R. Piper, C. Mozaceanu, S. A. Barnett and M. D. Ward, Chem. – Eur. J., 2020, 26, 3054–3064 CrossRef CAS PubMed.
- M. Hoshino, A. Khutia, H. Xing, Y. Inokuma and M. Fujita, IUCrJ, 2016, 3, 139–151 CrossRef CAS PubMed and references cited therein.
- T. A. Young, R. Gheorghe and F. Duarte, J. Chem. Inf. Model., 2020, 60, 3546–3557 CrossRef CAS PubMed.
- T. A. Young, V. Martí-Centelles, J. Wang, P. J. Lusby and F. Duarte, J. Am. Chem. Soc., 2020, 142, 1300–1310 CrossRef PubMed.
- A. Tarzia, J. E. M. Lewis and K. E. Jelfs, Angew. Chem., Int. Ed., 2021, 60, 20879–20887 CrossRef CAS PubMed.
- W. Cullen, S. Turega, C. A. Hunter and M. D. Ward, Chem. Sci., 2015, 6, 2790–2794 RSC.
- M. Yamashina, Y. Sei, M. Akita and M. Yoshizawa, Nat. Commun., 2014, 5, 4662 CrossRef CAS PubMed.
- E. Ubasart, O. Borodin, C. Fuertes-Espinosa, Y. Xu, C. García-Simón, L. Gómez, J. Juanhuix, F. Gándara, I. Imaz, D. Maspoch, M. von Delius and X. Ribas, Nat. Chem., 2021, 13, 420–427 CrossRef CAS PubMed.
- V. Martí-Centelles, A. L. Lawrence and P. J. Lusby, J. Am. Chem. Soc., 2018, 140, 2862–2868 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2022 |