Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
DiSCoVeR: a materials discovery screening tool for high performance, unique chemical compositions
Sterling G.
Baird
 *a,
Tran Q.
Diep
*a,
Tran Q.
Diep
 b and
Taylor D.
Sparks
b and
Taylor D.
Sparks
 a
a
aDepartment of Materials Science and Engineering, University of Utah, Salt Lake City, UT 84108, USA. E-mail: sterling.baird@utah.edu; sparks@eng.utah.edu
bDepartment of Chemical Engineering, Brigham Young University, Provo, UT 84604, USA
First published on 7th February 2022
Abstract
We present Descending from Stochastic Clustering Variance Regression (DiSCoVeR) (https://www.github.com/sparks-baird/mat_discover), a Python tool for identifying and assessing high-performing, chemically unique compositions relative to existing compounds using a combination of a chemical distance metric, density-aware dimensionality reduction, clustering, and a regression model. In this work, we create pairwise distance matrices between compounds via Element Mover's Distance (ElMD) and use these to create 2D density-aware embeddings for chemical compositions via Density-preserving Uniform Manifold Approximation and Projection (DensMAP). Because ElMD assigns distances between compounds that are more chemically intuitive than Euclidean-based distances, the compounds can then be clustered into chemically homogeneous clusters via Hierarchical Density-based Spatial Clustering of Applications with Noise (HDBSCAN*). In combination with performance predictions via Compositionally-Restricted Attention-Based Network (CrabNet), we introduce several new metrics for materials discovery and validate DiSCoVeR on Materials Project bulk moduli using compound-wise and cluster-wise validation methods. We visualize these via multi-objective Pareto front plots and assign a weighted score to each composition that encompasses the trade-off between performance and density-based chemical uniqueness. In addition to density-based metrics, we explore an additional uniqueness proxy related to property gradients in DensMAP space. As a validation study, we use DiSCoVeR to screen materials for both performance and uniqueness to extrapolate to new chemical spaces. Top-10 rankings are provided for the compound-wise density and property gradient uniqueness proxies. Top-ranked compounds can be further curated via literature searches, physics-based simulations, and/or experimental synthesis. Finally, we compare DiSCoVeR against the naive baseline of random search for several parameter combinations in an adaptive design scheme. To our knowledge, this is the first time automated screening has been performed with explicit emphasis on discovering high-performing, novel materials.
1. Introduction
Guided materials discovery examples have been increasingly prevalent in the literature. Some of these are experimental1–9 and computational10,11 adaptive design (AD) schemes using high-throughput experimental5,12–19 or computational (e.g. density functional theory (DFT)20–29 and finite element modeling30,31) methods. Such materials discovery projects generally rely on the backbone of a regression model. A non-exhaustive list ordered from oldest to newest by journal publication year is given: GBM-Locfit,32 CGCNN,33 MEGNet,34 wren,35 GATGNN,36 iCGCNN,27 Automatminer,37 Roost,38 DimeNet++,39 Compositionally-Restricted Attention-Based Network (CrabNet),40 and MODNet,41 each with varying advantages and disadvantages.Extraordinary predictions, or predictions which perform close to or better than top performers in the training data are rare.42–44 Many of the algorithms used for materials discovery in the literature are Euclidean-based Bayesian optimization schemes which seek a trade-off between high-performance and high-uncertainty regions,4,9,11,29,44–51 thereby favoring robust models and discovery of better candidates. These models have born many fruits in materials discovery including the discovery of extraordinary materials, though often for initially small datasets.
Kauwe et al.52 describe how it is even rarer to discover materials that are fundamentally (as opposed to incrementally) different from existing materials, i.e. discover new chemistries. For traditional Euclidean-based Bayesian optimization algorithms, while high uncertainty may be correlated with novelty, they do not explicitly favor discovery of novel compounds.
Kim et al.53 introduced two metrics for materials discovery: predicted fraction of improved candidates and cumulative maximum likelihood of improvement. These metrics are geared at identifying “discovery-rich” and “discovery-poor” design spaces, but again, in the context of high-performance rather than chemical distinctiveness.
In summary, there is a lack of materials discovery algorithms and metrics that explicitly favor the discovery of novel compounds.
In this work, we introduce the Descending from Stochastic Clustering Variance Regression (DiSCoVeR) algorithm, which unlike previous methods, screens candidates that have a high probability of success while enforcing – through the use of novel loss functions (i.e. metrics) – that the candidates exist beyond typical materials landscapes and have high performance. In other words, DiSCoVeR acts as a multi-objective screening where the promise of a compound depends on both having desirable target properties and existing in sparsely populated regions of the cluster to which it's assigned. This approach then favors discovery of novel, high-performing chemical families as long as embedded points which are close together or far apart exhibit chemical similarity or chemical distinctiveness, respectively.
2. Methods
The novelty of the DiSCoVeR algorithm consists largely of connecting recent, existing tools (Section 2.1) in conjunction with new proxies for chemical uniqueness (Section 2.2). DiSCoVeR depends on clusters exhibiting homogeneity with respect to chemical classes, which we enforce via a recently introduced distance metric: Element Mover's Distance (ElMD).54 Dimensionality reduction algorithms such as Uniform Manifold Approximation and Projection (UMAP)55 or t-distributed stochastic neighbor embeddings56 can then be used to create low-dimensional embeddings suitable for clustering algorithms such as Hierarchical Density-based Spatial Clustering of Applications with Noise (HDBSCAN*)57 or k-means clustering.58Finally, these can be fed into density estimator algorithms such as Density-preserving Uniform Manifold Approximation and Projection (DensMAP)59 a UMAP variant or kernel density estimation60,61 where density is then used as a proxy for chemical uniqueness. In this work, we use DensMAP in place of UMAP to obtain density estimations directly within the dimensionality reduction step.
Additionally, we describe our data and validation methods (Section 2.3). By combining a materials suggestion algorithm and DiSCoVeR, it is possible to assess the likelihood of a new material existing relative to known materials.
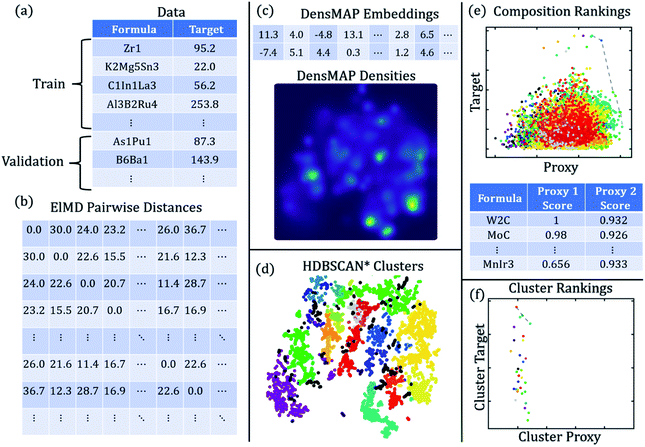
The workflow for creating chemically homogeneous clusters is shown in Fig. 1, and a description of methods and each method's role is given in Table 1.
| Method | What is it? | What is its role in DiSCoVeR? |
|---|---|---|
| a A Pareto front is more information-dense than a proxy score in that there are no predefined relative weights for performance vs. uniqueness proxy. Compounds that are closer to the Pareto front are better. The upper areas of the plot represent a higher weight towards performance while the right-most areas of the plot represent a higher weight towards uniqueness. | ||
| CrabNet40 | Composition-based property regression | Predict performance for proxy scores |
| ElMD54 | Composition-based distance metric | Supply distance matrix to DensMAP |
| DensMAP59 | Density-aware dimensionality reduction | Obtain densities for density proxy |
| HDBSCAN*57 | Density-aware clustering | Create chemically homogeneous clusters |
| Peak proxy | High performance relative to nearby compounds | Proxy for “surprising” high performance |
| Density proxy | Sparsity relative to nearby compounds | Proxy for chemical novelty |
| Peak proxy score | Weighted sum of performance and peak proxy | Used to rank compounds |
| Density proxy score | Weighted sum of performance and density proxy | Used to rank compounds |
| Pareto front | Optimal performance/uniqueness trade-offs | Visually screen compounds (no weightsa) |
2.1. Chemically homogeneous clusters
How are chemically homogeneous clusters achieved? The key is in the dissimilarity metric used to compute distances between compounds. Recently, ElMD54 was developed based on earth mover's or Wasserstein distance; ElMD calculates distances between compounds in a way that more closely matches chemical intuition. For example, compounds with similar composition templates (e.g. XY2 as in SiO2, TiO2) and compounds with similar elements are closer in ElMD space. In other words, clusters derived from this distance metric are more likely to exhibit in-cluster homogeneity with respect to material class which in turn allows in-cluster density estimation to be used as a proxy for novelty.In this work, we use DensMAP for dimensionality reduction and HDBSCAN* for clustering similar to the work by Hargreaves et al.54† which successfully reported clusters of compounds that match chemical intuition. Removal of the DensMAP step result in a much higher proportion of points classified as “noise” in the clustering results‡ and precludes the use of density-based proxies unless other suitable density estimation algorithms are used.
2.2. Proxies for chemical uniqueness
It is relatively straightforward (albeit computationally costly) to obtain a DFT-calculated bulk modulus value, but this speaks little to chemical uniqueness. Experimental synthesis and characterization would likewise provide information about the chemical, structural, and performance properties, but not chemical uniqueness. Finally, what might be considered “chemically unique” today could be considered “run-of-the-mill” a decade later based on the progress in the field, and so the metric is also largely dependent on what's considered to be in the “training” dataset. Thus, we rely on a dissimilarity metric (ElMD) for which at least some scientists agree that it “intuitively” encodes chemical similarity, and we determine our training dataset based on what is available in a recent snapshot of the Materials Project database.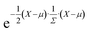 | (1) |
The covariance matrix used in this work is given by eqn (2):
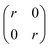 | (2) |
We evaluate the sum of densities contributed by all training points evaluated at each of the validation locations (eqn (3)):
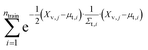 | (3) |
We refer to this as “train contribution to validation density” which acts as a proxy for chemical uniqueness relative to existing materials. Validation points with a low training contribution to the density exist in sparse regions of the embedded space, whereas validation points with a high training contribution to the density exist in densely populated regions of the embedded space.
It is significant that the proxy for a given validation point does not consider the density contribution from other validation points. To illustrate, consider training and validation datasets containing 1000 and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points, respectively. In this case, the training data are considered “existing” compounds (i.e. low novelty) with a known performance measurement (e.g. bulk modulus), and the validation points are considered “unknown” in the sense that the performance and novelty are unknown. If the density contributions from both training and validation points are considered, the proxy then depends on the size and distribution of the validation dataset which can be arbitrarily large, small, sparse, or dense (e.g. by the fineness of sampling possible compositions). In other words, for density to act as a proxy for novelty, it need consider (and only consider) how far it is from existing, low-novelty materials (i.e. training data).
000 points, respectively. In this case, the training data are considered “existing” compounds (i.e. low novelty) with a known performance measurement (e.g. bulk modulus), and the validation points are considered “unknown” in the sense that the performance and novelty are unknown. If the density contributions from both training and validation points are considered, the proxy then depends on the size and distribution of the validation dataset which can be arbitrarily large, small, sparse, or dense (e.g. by the fineness of sampling possible compositions). In other words, for density to act as a proxy for novelty, it need consider (and only consider) how far it is from existing, low-novelty materials (i.e. training data).
By combining high-fidelity CrabNet predictions of bulk modulus with DensMAP validation densities, we extract a list of promising compounds at the Pareto front – the line or “front” at which the trade-off between performance and chemical uniqueness is optimal. CrabNet predictions have been shown to be comparable to state-of-the-art composition-based materials regression schemes, and since structure is often not known during a materials discovery search, CrabNet is a reasonable model choice. One partial workaround for the limitation of structure being unknown a priori has been explored in the Bayesian optimization with symmetry relaxation algorithm,63 which may be of interest to incorporate into DiSCoVeR in future work.
Additionally, by performing leave-one-cluster-out cross-validation (LOCO-CV),64 we accurately sort the list of validation clusters by their average performance with a scaled sorting error of approximately 1%. This proof-of-concept strongly suggests that DiSCoVeR will successfully identify the most promising compounds when supplied with a set of realistic chemical formulae that partly contains out-of-class formulae produced via a suggestion algorithm. To our knowledge, this is a novel approach that has never been used to encourage new materials discovery as opposed to incremental discoveries within known families.
Because it is based on nearest neighbors rather than a defined radius, compounds which are in relatively sparse UMAP areas may have neighbors from a chemically distant cluster. In this case, if all kNNs come from the same cluster, and this cluster exhibits similar properties, this can skew the measure to some extent. This artifact can be avoided by instead using a defined radius and a variable number of kNNs while ignoring compounds which have no kNNs within the specified radius.
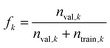 | (4) |
Cluster target mean is given by eqn (5):
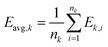 | (5) |
2.3. Data and validation
As a proof of concept, we use 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 583 unique chemical formulae and associated bulk moduli from Materials Project65,66 to test whether DiSCoVeR can find new classes of materials with high performance. In accordance with materials informatics best practices,67 we also sanitize the data. Materials are filtered to exclude noble gases, Tc-containing compounds, and compounds with an energy above hull (e_above_hull) value greater than 500 meV. The highest bulk modulus is chosen when considering identical formulae. The motivation here is to ensure that the highest-performing materials are not overlooked; however, this can bias the model towards more difficult to synthesize and/or less stable allotropes (e.g. diamond vs. carbon). We use CrabNet40 as the regression model for bulk modulus which depends only on composition to generate machine learning features; however, a different composition-based model mentioned in Section 1 could have been used instead.
583 unique chemical formulae and associated bulk moduli from Materials Project65,66 to test whether DiSCoVeR can find new classes of materials with high performance. In accordance with materials informatics best practices,67 we also sanitize the data. Materials are filtered to exclude noble gases, Tc-containing compounds, and compounds with an energy above hull (e_above_hull) value greater than 500 meV. The highest bulk modulus is chosen when considering identical formulae. The motivation here is to ensure that the highest-performing materials are not overlooked; however, this can bias the model towards more difficult to synthesize and/or less stable allotropes (e.g. diamond vs. carbon). We use CrabNet40 as the regression model for bulk modulus which depends only on composition to generate machine learning features; however, a different composition-based model mentioned in Section 1 could have been used instead.
We split the data into training and validation sets using a 0.8/0.2 train/val split as well as via LOCO-CV. We report two types of validation tests as summarized in Table 2. One of the validation methods uses a weighted root-mean-square error (RMSE) of various multi-objective Pareto front properties (target vs. chemical uniqueness proxy). The target is weighted against the proxy property (eqn (6)):
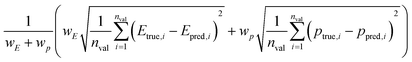 | (6) |
| Method | Splits | Notion of best fit | Property |
|---|---|---|---|
| a This density is the sum of all training densities evaluated at the validation location in the embedded DensMAP space. For the k-neighbors data, the average of the 10 nearest neighbor properties were used as a proxy. b Cluster validation fraction refers to the ratio of number of validation points within a cluster (as opposed to training points) to the total number of points in the cluster. DensMAP densities and cluster fractions are determined simultaneously for both validation and training sets during the DensMAP embedding resulting in computational throughput restrictions. In other words, “predicted” and “true” are identical due to implementation of DiSCoVeR at the time of writing. We plan to address this in future work. | |||
| Train/val | 0.8/0.2 | Weighted RMSE | Target vs. densitya |
| Train/val | 0.8/0.2 | Weighted RMSE | Target vs. k-neighbors average |
| Train/val | 0.8/0.2 | Weighted RMSE | Target vs. cluster validation fractionb |
| LOCO-CV | 25 clusters | Weighted CDF distance | Cluster target mean |
In the current implementation, however, the chemical uniqueness proxy is determined a priori and simultaneously using the full dataset; thus, the error contribution from the chemical uniqueness proxy is zero. In other words, while Etrue,i (DFT calculation) and Epred,i (CrabNet prediction) vary, ptrue,i and ppred,i are identical. This approach is reasonable for small to medium-sized datasets (e.g. less than 100 000), but can quickly become intractable for large datasets due to memory constraints. We plan to modify DiSCoVeR to be compatible with large datasets (∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) by utilizing the ElMD metric directly within DensMAP rather than computing a pairwise distance matrix in advance.
000) by utilizing the ElMD metric directly within DensMAP rather than computing a pairwise distance matrix in advance.
Likewise, the score for each compound is a weighted sum of the robust-scaled§ target and proxy properties (eqn (7)):
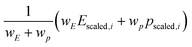 | (7) |
Without a “true” chemical uniqueness dataset, it's up to the scientist to decide how important performance is relative to the uniqueness proxy. This could take the form of trial-and-error and evaluating the ranked results based on chemical intuition or interactively exploring the Pareto front plot to decide what areas “seem” most interesting (and finding a suitable weight that favors that area). In other words, it's subjective. The results are also affected by the choice of “Scaler” (e.g. MinMaxScaler vs. RobustScaler) in how outliers are dealt with during scaling.
The other validation method is a LOCO-CV approach using cumulative density function (CDF) distance (i.e. earth mover's or Wasserstein distance) as a metric to determine the sorted similarity of a predicted cluster property vs. a true cluster property using scipy.stats.wasserstein_distance()68 as follows¶:
3. Results and discussion
One of the primary difficulties in validating a materials discovery tool that considers chemical uniqueness is that while scientists might agree that discovering chemically unique (rather than incrementally different) materials is important, the interpretation of chemical uniqueness can vary significantly. The natural result is a lack of any curated data of “true” chemical uniqueness which makes it difficult to validate the tool in the conventional sense. Where possible, we present validation results; however, the results of DiSCoVeR in this work are largely focused on visualizations that can help to guide the discovery process and generation of rankings for each uniqueness proxy that are actionable, yet subjective.First, we present characteristics of the DensMAP embedding and clustering scheme (Section 3.1) followed by compound-wise (Section 3.2) and cluster-wise (Section 3.3) Pareto front results. We also discuss results of the LOCO-CV scheme. Finally, we discuss how to use DiSCoVeR in a practical materials discovery scheme (Section 3.4).
3.1. Density-preserving uniform manifold approximation and projection characteristics
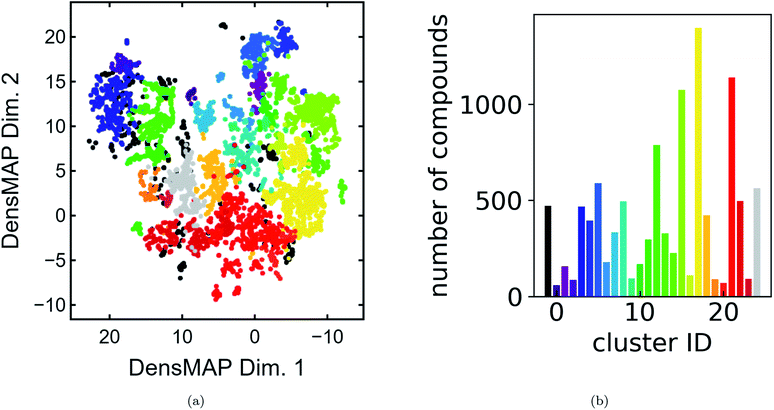
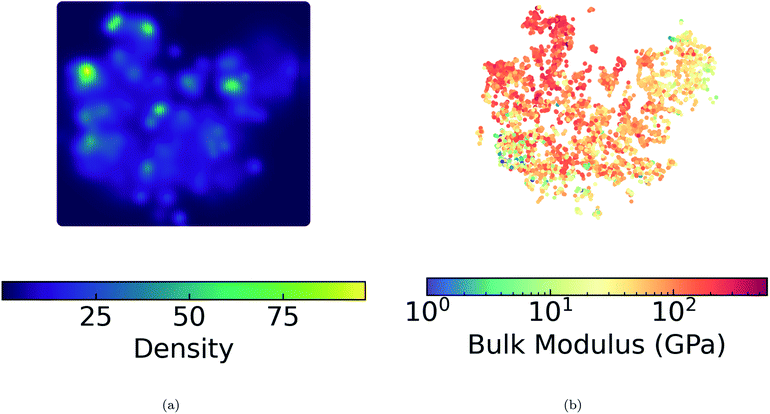
We present a DensMAP clustering of ElMD distances between all pairs of compounds (Fig. 2a) and plot the cluster count histogram (Fig. 2b). We then sum densities at equally spaced locations across DensMAP space (Fig. 3a) and color the points according to bulk modulus values (Fig. 3b).We obtain a total of 25 clusters, plus a non-cluster of unclassified points comprising a small percentage of the data (∼5%). The number of clusters gives an estimation of the number of distinct chemical classes present in the dataset and is also affected by DensMAP and HDBSCAN* model parameters such as local density regularization strength (dens_lambda), minimum cluster size (min_cluster_size), and distance threshold for merging clusters (cluster_selection_epsilon). The unclassified points are typically isolated points in DensMAP space. In other words, unclassified points will likely exhibit high chemical contrast relative to other compositions via a low-density proxy. In other cases, unclassified points seem to appear “within” a cluster; however, this likely arises from the use of a density-based clustering algorithm rather than a manifold partitioning clustering algorithm. In other words, the density is low, but appears high when visualized with thousands of points in a 2D plot due to “low magnification”. We further discuss results related to the density proxy in Section 3.2.
A summary of the computational runtimes of the various methods is given in Table 3. Computation of the full pairwise distance matrix takes ∼18 s, which is quite fast due to use of a CUDA/Numba69 version of the Wasserstein distance that we developed for this work. An NVIDIA GeForce RTX 2060 is used for GPU computations, and an Intel® Core™ i7-10750H CPU @ 2.60 GHz is used for CPU computations. All non-GPU calculations are single-threaded.
| Procedure | Time (s) | GPU |
|---|---|---|
| CrabNet | 91 | Y |
| ElMD | 18 | Y |
| Cluster DensMAP | 137 | N |
| Vis. DensMAP | 47 | N |
| HDBSCAN* | 0.14 | N |
| 100 × 100 grid | 11 | N |
| Density-proxy | 2.7 | N |
| Total | 296 | — |
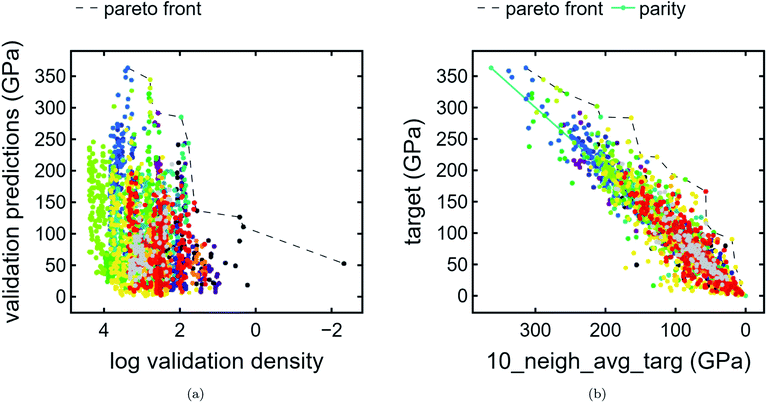
3.2. Compound Pareto fronts
We present compound-wise Pareto fronts—a common technique used in multi-objective optimization—with predicted bulk modulus as the ordinate and one of two compound-wise proxies as the abscissa: train contribution to validation log density (Fig. 4a) and kNN average (Fig. 4b) as described in Section 2.2.On the other hand, kNN average acts as a poor man's gradient – in other words, used in conjunction with target predictions, it emphasizes compounds which have much higher predicted bulk modulus than that of its neighbors. In addition to the Pareto front, a parity line is also plotted. Compounds which are far above the parity line are high-performing relative to the surrounding neighborhood.
In terms of discovering materials which are chemically distinct from existing materials, train contribution to validation log density is the preferred proxy. We note that each of the proxies produce distinct plots. In the case of Fig. 4a, clusters tend to be stratified horizontally, whereas in Fig. 4b, cluster shapes exhibit similar orientations. As expected (Section 3.1), unclassified points appear frequently at or near the first Pareto front owing to the fact that unclassified points are likely to have a lower density proxy and therefore higher score. By contrast, unclassified points appear infrequently at or near the latter Pareto front. Additionally, the unique list of clusters present at the Pareto front are different for each plot. In other words, these are two types of chemical uniqueness – the first emphasizing chemical “distance” from other compounds and the latter emphasizing performance superiority over chemically similar compounds. We believe that either may be successfully used in the domain of materials discovery.
Compounds were assigned scaled discovery scores as described in Section 2.3 for each of the chemical uniqueness proxies. The top-10 ranked candidates for the density and peak proxies are given in Tables 4 and 5, respectively. An outer merge of these two lists is given in Table 6.
| Formula | E pred | ρ | s ρ |
|---|---|---|---|
| ReB2 | 344.735 | 16.167 | 2.738 |
| B2W | 331.170 | 16.183 | 2.604 |
| UB2Os3 | 285.076 | 7.146 | 2.546 |
| MoN | 322.441 | 16.586 | 2.500 |
| TaN | 321.934 | 16.827 | 2.485 |
| BMo | 315.166 | 16.625 | 2.427 |
| Co(BW)2 | 311.329 | 15.935 | 2.419 |
| B2Mo | 310.618 | 16.044 | 2.408 |
| Re3W | 363.181 | 29.179 | 2.349 |
| TaMoN | 291.558 | 13.128 | 2.348 |
| Formula | E pred | E pred,kNN | s kNN |
|---|---|---|---|
| WO2 | 283.530 | 27.270 | 5.457 |
| UO3 | 166.335 | 11.264 | 5.443 |
| NiH | 185.373 | 19.595 | 4.830 |
| V2O3 | 221.155 | 11.704 | 4.415 |
| FeF2 | 158.245 | 33.249 | 4.328 |
| Mg(MoO2)2 | 162.200 | 18.138 | 4.255 |
| ZrSiO | 191.061 | 12.789 | 4.238 |
| PaB3 | 188.567 | 11.816 | 3.966 |
| NiHO2 | 148.222 | 41.454 | 3.827 |
| CrOF3 | 90.328 | 15.092 | 3.773 |
| Formula | s ρ | s kNN |
|---|---|---|
| ReB2 | 2.738 | 1.795 |
| B2W | 2.604 | 2.145 |
| UB2Os3 | 2.546 | 3.239 |
| MoN | 2.500 | −0.117 |
| TaN | 2.485 | 2.471 |
| BMo | 2.427 | −0.484 |
| Co(BW)2 | 2.419 | 0.519 |
| B2Mo | 2.408 | 1.162 |
| Re3W | 2.349 | 1.373 |
| TaMoN | 2.348 | 1.991 |
| V2O3 | 1.717 | 4.415 |
| WO2 | 1.649 | 5.457 |
| PaB3 | 1.391 | 3.966 |
| ZrSiO | 1.373 | 4.238 |
| UO3 | 1.196 | 5.443 |
| NiH | 1.018 | 4.830 |
| Mg(MoO2)2 | 0.854 | 4.255 |
| CrOF3 | 0.280 | 3.773 |
| FeF2 | 0.153 | 4.328 |
| NiHO2 | −0.306 | 3.827 |
It is interesting to note the lack of shared compounds between the top-10 lists of the two proxies. By contrast, in previous tests, we found that increasing the weight of Epred (wE = 2) led to significant overlap between the two lists, although with differing priority (i.e. the order of the rankings was different). Because the weights used can have a significant effect on the rankings, it may be worth probing several values for a given study to elucidate and assess behaviors. Indeed, as wE grows larger, it tends towards a classic approach of searching for high-performance candidates only, yet for very small values of wE, the performance of the top-ranked compounds may be too low to be of utility in real-world applications.
The weighted RMSE for the validation data is 26.5 GPa; however, as mentioned in Section 2.3, the proxy error contribution is zero in this work.
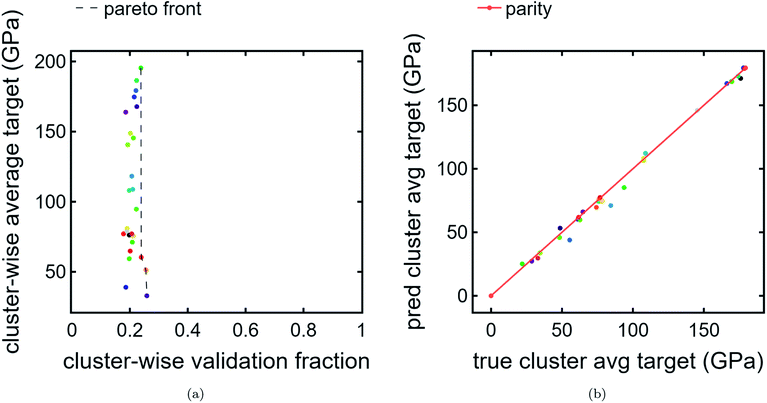
3.3. Cluster Pareto front and leave-one-cluster-out cross-validation
We also present a Pareto front for cluster-wise properties. For the ordinate, we use predicted cluster average bulk modulus Fig. 5a. For the abscissa, we use cluster validation fraction as a proxy for chemical distinctiveness of a cluster. In this example, the data is clustered tightly in the abscissa due to a the train/val split being applied randomly without regard to cluster. In a more realistic scenario with much more validation data than training data, where the validation encompasses previously unexplored chemical spaces, there is likely to be a larger spread. Indeed, such a use-case is the intention for this visualization tool. There is a much wider spread in the ordinate, indicating an interesting feature of the clustering results: compositions which are chemically similar to each other also tend to have, on average, similar bulk moduli. This is reasonable, especially since the regression model used is based purely on composition.In future work, it may be interesting to replace average bulk modulus with best-in-cluster bulk modulus to explore a different type of high-ranking clusters.
Finally, we perform LOCO-CV to evaluate the utility of the DiSCoVeR method in identifying clusters with high average cluster bulk modulus. A LOCO-CV parity plot is given in Fig. 5. We accurately sort the list of validation clusters by their average performance with a weighted scaled sorting error (Section 2.3) of ∼1.4%. In other words, the out-of-cluster regression is very accurate. This suggests that CrabNet can successfully extrapolate performance predictions for new chemical spaces in accordance with the goal of DiSCoVeR. In future work, we plan to also test the out-of-cluster extrapolation performance for chemical uniqueness proxies (Section 2.3).
3.4. Practical materials discovery
While we believe the results generated by DiSCoVeR to be useful for screening for high-performing, novel materials, it is up to the scientist to manually curate and act on the results. A practical materials discovery approach with examples is summarized in Table 7.| Step | Example(s) |
|---|---|
| (1) Obtain training data (chemical formula, properties) | Stable Materials Project chemical formulas with bulk modulus |
| (2) Obtain validation data (chemical formula) | Stable Materials Project chemical formulas without bulk modulus |
| (3) Rank validation formulas by score | Use top-100 ranked validation formulas from DiSCoVeR |
| (4) Literature search | https://citrination.com, Synthesis Explorer,70 MatScholar,71 MPDS72 |
| (5) Physics-based simulation | Pymatgen elastic tensor calculations (requires CIF inputs) |
| (6) Synthesis | Arc-melting, high-pressure synthesis, solid-state, etc. |
| (7) Post-processing | Powderization or polishing, annealing (reduce surface strain) |
| (8) Characterization | X-ray diffraction, nanoindenter hardness, diamond anvil/synchrotron |
Obtaining the training and validation data (steps 1 and 2) should be guided by materials informatics best practices.67 Interactively exploring the Pareto front plots can aid in the choice of hyperparameters such as the performance and uniqueness weights during validation scoring (step 3). The literature search helps in determining which compounds have already been synthesized and how, and which compounds have already been characterized and how. This helps prevent unnecessary repetition of work. Physics-based simulations (step 5) can help to eliminate candidates with unrealistically high property predictions. Synthesis, post-processing, and characterization (steps 6–8) are in a sense the pinnacle of materials discovery for practical applications. These steps appear last in part because they typically represent the highest cost-per-datapoint out of all other steps.
While these steps represent a single materials discovery iteration, the approach can also be modified into an AD scheme. For example, this could mean iteratively moving newly simulated validation data into the training dataset and swapping certain steps based on time and resource constraints (e.g. perform literature search after simulation-based AD).
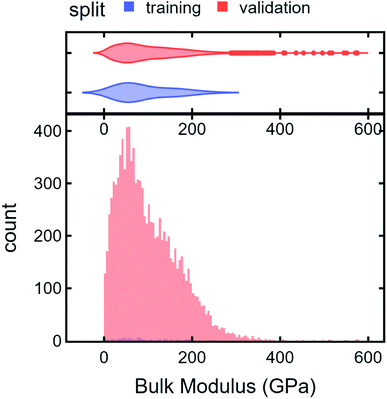
To illustrate an AD scheme and elucidate the effect of DiSCoVeR weighting parameters, we perform a closed-loop AD validation study to compare random search with three DiSCoVeR performance/proxy weighting combinations. We begin by holding out the top 2% of highest-performing bulk modulus Materials Project compounds out of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 582 candidates. From the non-extraordinary compounds, we randomly select 100 chemical formulas as training data which are fixed across each of the comparisons. The remainder, including the held out “extraordinary” compounds, comprise the validation set or pool of possible candidates. Histograms of the “extraordinary” training/validation split are given in Fig. 6.
582 candidates. From the non-extraordinary compounds, we randomly select 100 chemical formulas as training data which are fixed across each of the comparisons. The remainder, including the held out “extraordinary” compounds, comprise the validation set or pool of possible candidates. Histograms of the “extraordinary” training/validation split are given in Fig. 6.
For random search, a new chemical formula is selected at random during each AD iteration and added to the training set. For the novelty-only (no performance contribution), equal, and performance-only (no novelty contribution) weighting combinations, scores are assigned per Section 2.3 and the top-ranked candidate is chosen and added to the training set during each AD iteration.
During the first iteration, the performance and proxy Scaler+ objects are fixed, facilitating gradually increasing emphasis on performance as high-novelty candidates are explored and eliminated and as higher targets are discovered. This mimics the usually desired behavior of Bayesian optimization acquisition functions such as expected improvement which favor exploration during early iterations and exploitation during later iterations.
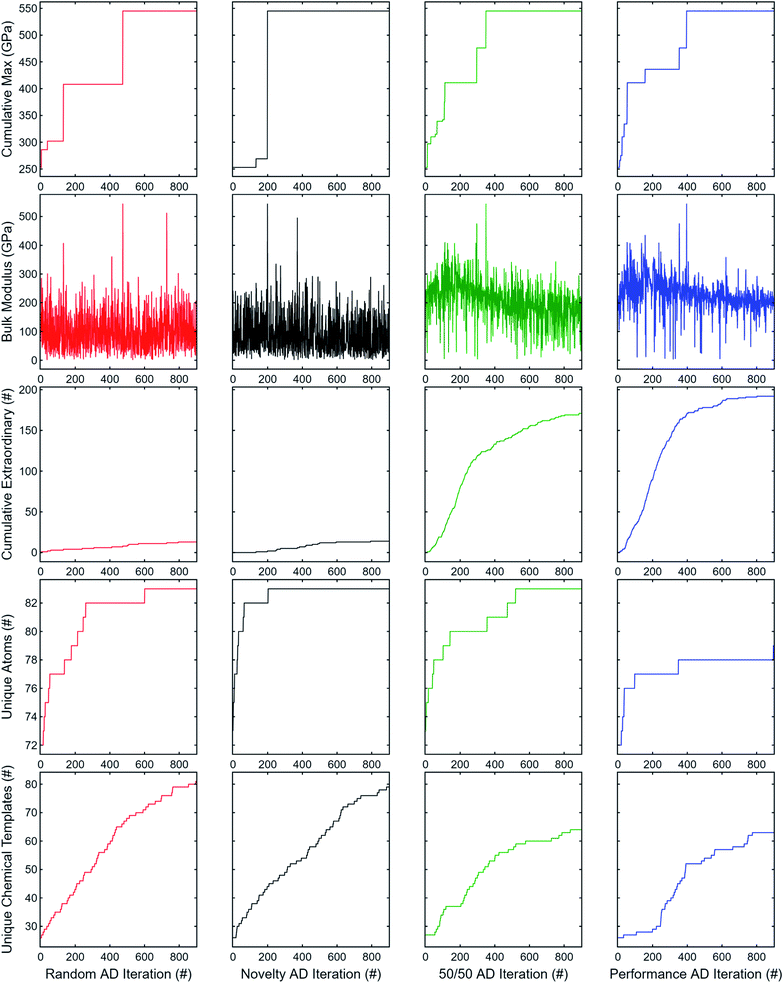
Five properties are used to assess the performance and novelty of the explored compounds: the best observed bulk modulus, the currently observed bulk modulus, the total number of observed “extraordinary” compounds (top 2%), and the total number of additional unique atoms and chemical formulae templates added. In other words:
(1) What's the best bulk modulus observed so far?
(2) What bulk modulus was observed during this iteration?
(3) How many “extraordinary” compounds have been observed so far?
(4) How many unique atoms have been explored so far, not counting atoms already in the starting 100 formulas?
(5) How many unique chemical templates (e.g. A2B3, ABC, ABC2) have been explored so far, not counting templates already in the starting 100 formulas?
We note that unlike ElMD, added number of unique atoms and unique chemical templates does not capture the interplay between each other; despite being somewhat naive, we employ these because they are reasonably straightforward and visualizable measures of novelty.
The results for 900 subsequent AD iterations are summarized in Fig. 7. Random search exhibits good explorability, at least for the dataset used; however, the novelty-only weighting produces a much steeper rise in unique atoms explored while retaining a similar rise in unique chemical templates. Neither random search nor novelty-only consistently produce observations of extraordinary compounds. On the other hand, the performance-only weighting has worse explorability, but significantly better exploitation having observed nearly all extraordinary candidates by the end of the 900 iterations. The equal weighting combination offers a good trade-off between performance (properties 1–3) and novelty (properties 4 and 5) such that new elements and chemical templates are explored initially while retaining a high rate of extraordinary discovery nearly comparable to the performance-only results.
4. Conclusion
We embedded ElMD distances in DensMAP space and clustered via HDBSCAN* to identify chemically similar clusters for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 583 compositions. We introduced new proxies (i.e. metrics) for uniqueness-based materials discovery in the form of train contribution to validation log density, k-neighbor averages, and cluster validation fraction. By pairing these with the CrabNet regression model, we visualize Pareto plots of predicted bulk modulus vs. uniqueness proxy and obtain weighted uniqueness/performance rankings for each of the compounds. This reveals a new way to perform materials discovery with a focus towards identifying new high-performing, chemically distinct compositions.
583 compositions. We introduced new proxies (i.e. metrics) for uniqueness-based materials discovery in the form of train contribution to validation log density, k-neighbor averages, and cluster validation fraction. By pairing these with the CrabNet regression model, we visualize Pareto plots of predicted bulk modulus vs. uniqueness proxy and obtain weighted uniqueness/performance rankings for each of the compounds. This reveals a new way to perform materials discovery with a focus towards identifying new high-performing, chemically distinct compositions.
Data availability
The raw data required to reproduce these findings is available to download from https://www.materialsproject.org. A snapshot of the data as obtained via the MPRester API on October 15, 2021 is provided in CrabNet/data/materials_data/elasticity/train.csv. See generate_elasticity_data.py78 for the MPRester implementation. The processed data required to reproduce these findings is available to download from figshare with DOI: 10.6084/m9.figshare.16786513.v2.79 The code required to reproduce these findings is hosted at https://github.com/sparks-baird/mat_discover with DOI: 10.5281/zenodo.5594678.80 The version of the code employed for this study is v1.2.1 with DOI: 10.5281/zenodo.5594679.78 The code is also packaged on PyPI and Anaconda. GPU and CPU “playground” environments are hosted on Google Colab and Binder, respectively,80 and a reproducible Code Ocean capsule is published with DOI: 10.24433/CO.8463578.v1.81 Finally, interactive Pareto front plots are available.82Author contributions
Sterling G. Baird: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization. Taylor D. Sparks: supervision, project administration, funding acquisition, conceptualization, formal analysis, resources, writing – review & editing. Tran Q. Diep: conceptualization, methodology, software, formal analysis.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors thank Dr Anna Little for useful discussions regarding density- and distance-preserving dimensionality reduction techniques and Anthony Wang for assistance with the CrabNet repository. The authors thank the reviewers for feedback which has led to significant improvements in the manuscript. Plots were produced via either Matplotlib73 or Plotly,74 several tables were formatted via an online formatter https://www.tablesgenerator.com/,75 and equations were typeset using the Mathematica76https://github.com/sgbaird/TeXport functionality of https://github.com/sparks-baird/auto-paper.77 This work was supported by the National Science Foundation under grant no. DMR-1651668 and DMR-1950589.References
- P. V. Balachandran, B. Kowalski and A. Sehirlioglu, et al., Experimental search for high-temperature ferroelectric perovskites guided by two-step machine learning, Nat. Commun, 2018, 9, 1668, DOI:10.1038/s41467-018-03821-9.
- B. Cao, L. A. Adutwum, A. O. Oliynyk, E. J. Luber, B. C. Olsen, A. Mar and J. M. Buriak, How to Optimize Materials and Devices via Design of Experiments and Machine Learning: Demonstration Using Organic Photovoltaics, ACS Nano, 2018, 12(8), 7434–7444, DOI:10.1021/acsnano.8b04726 , ISSN 1936086X..
- Y. Chen, Y. Tian, Y. Zhou, D. Fang, X. Ding, J. Sun and D. Xue, Machine Learning Assisted Multi-Objective Optimization for Materials Processing Parameters: A Case Study in Mg Alloy, J. Alloys Compd., 2020, 844, 156159, DOI:10.1016/j.jallcom.2020.156159 , ISSN 09258388..
- K. Homma, Y. Liu, M. Sumita, R. Tamura, N. Fushimi, J. Iwata, K. Tsuda and C. Kaneta, Optimization of a Heterogeneous Ternary Li3PO4-Li3BO3-Li2SO4 Mixture for Li-Ion Conductivity by Machine Learning, J. Phys. Chem. C, 2020, 124(24), 12865–12870, DOI:10.1021/acs.jpcc.9b11654 , ISSN 19327455..
- Z. Hou, Y. Takagiwa, Y. Shinohara, Y. Xu and K. Tsuda, Machine-Learning-Assisted Development and Theoretical Consideration for the Al2Fe3Si3 Thermoelectric Material, ACS Appl. Mater. Interfaces, 2019, 11(12), 11545–11554, DOI:10.1021/acsami.9b02381 , ISSN 19448252..
- X. Li, Z. Hou, S. Gao, Y. Zeng, J. Ao, Z. Zhou, B. Da, W. Liu, Y. Sun and Y. Zhang, Efficient Optimization of the Performance of Mn2+-Doped Kesterite Solar Cell: Machine Learning Aided Synthesis of High Efficient Cu2(Mn,Zn)Sn(S,Se)4 Solar Cells, Sol. RRL, 2018, 2, 1800198, DOI:10.1002/solr.201800198.
- P. Raccuglia, K. C. Elbert, P. D. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Machine-Learning-Assisted Materials Discovery Using Failed Experiments, Nature, 2016, 533(7601), 73–76, DOI:10.1038/nature17439 , ISSN 14764687..
- A. Sakurai, K. Yada, T. Simomura, S. Ju, M. Kashiwagi, H. Okada, T. Nagao, K. Tsuda and J. Shiomi, Ultranarrow-Band Wavelength-Selective Thermal Emission with Aperiodic Multilayered Metamaterials Designed by Bayesian Optimization, ACS Cent. Sci., 2019, 5(2), 319–326, DOI:10.1021/acscentsci.8b00802 , ISSN 2374-7943, 2374-7951..
- Y. K. Wakabayashi, T. Otsuka, Y. Krockenberger, H. Sawada, Y. Taniyasu and H. Yamamoto, Machine-Learning-Assisted Thin-Film Growth: Bayesian Optimization in Molecular Beam Epitaxy of SrRuO3 Thin Films, APL Mater., 2019, 7(10) DOI:10.1063/1.5123019 , ISSN 2166532X..
- S. Ju, T. Shiga, L. Feng, Z. Hou, K. Tsuda and J. Shiomi, Designing Nanostructures for Phonon Transport via Bayesian Optimization, Phys. Rev. X, 2017, 7(2), 021024, DOI:10.1103/PhysRevX.7.021024 , ISSN 2160-3308..
- A. Talapatra, S. Boluki, T. Duong, X. Qian, E. Dougherty and R. Arróyave, Autonomous Efficient Experiment Design for Materials Discovery with Bayesian Model Averaging, Phys. Rev. Mater., 2018, 2(11) DOI:10.1103/PhysRevMaterials.2.113803 , ISSN 24759953..
- M. W. Gaultois, T. D. Sparks, C. K. Borg, R. Seshadri, W. D. Bonificio and D. R. Clarke, Data-Driven Review of Thermoelectric Materials: Performance and Resource Considerations, Chem. Mater., 2013, 25(15), 2911–2920, DOI:10.1021/cm400893e , ISSN 08974756..
- M. W. Gaultois, A. O. Oliynyk, A. Mar, T. D. Sparks, G. J. Mulholland and B. Meredig, Perspective: Web-based Machine Learning Models for Real-Time Screening of Thermoelectric Materials Properties, APL Mater., 2016, 4(5) DOI:10.1063/1.4952607 , ISSN 2166532X..
- A. M. Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper, F. Lin, L. Miyagi, T. D. Sparks and J. Brgoch, Machine Learning Directed Search for Ultraincompressible, Superhard Materials, J. Am. Chem. Soc., 2018, 140(31), 9844–9853, DOI:10.1021/jacs.8b02717 , ISSN 15205126..
- C. Wen, Y. Zhang, C. Wang, D. Xue, Y. Bai, S. Antonov, L. Dai, T. Lookman and Y. Su, Machine Learning Assisted Design of High Entropy Alloys with Desired Property, Acta Mater., 2019, 170, 109–117, DOI:10.1016/j.actamat.2019.03.010 , ISSN 13596454..
- D. Xue, D. Xue, R. Yuan, Y. Zhou, P. V. Balachandran, X. Ding, J. Sun and T. Lookman, An Informatics Approach to Transformation Temperatures of NiTi-based Shape Memory Alloys, Acta Mater., 2017, 125, 532–541, DOI:10.1016/j.actamat.2016.12.009 , ISSN 13596454..
- Z. Zhang, A. M. Tehrani, A. O. Oliynyk, B. Day and J. Brgoch, Finding the Next Superhard Material through Ensemble Learning, Adv. Mater., 2020, 2005112, DOI:10.1002/adma.202005112 , ISSN 0935-9648, 1521-4095..
- Y. Iwasaki, R. Sawada, V. Stanev, M. Ishida, A. Kirihara, Y. Omori, H. Someya, I. Takeuchi, E. Saitoh and S. Yorozu, Identification of Advanced Spin-Driven Thermoelectric Materials via Interpretable Machine Learning, npj Comput. Mater., 2019, 5(1), 6–11, DOI:10.1038/s41524-019-0241-9 , ISSN 20573960..
- F. Ren, L. Ward, T. Williams, K. J. Laws, C. Wolverton, J. Hattrick-Simpers and A. Mehta, Accelerated Discovery of Metallic Glasses through Iteration of Machine Learning and High-Throughput Experiments, Sci. Adv., 2018, 4(4) DOI:10.1126/sciadv.aaq1566 , ISSN 23752548..
- P. V. Balachandran, D. Xue, J. Theiler, J. Hogden and T. Lookman, Adaptive Strategies for Materials Design Using Uncertainties, Sci. Rep., 2016, 6(1), 19660, DOI:10.1038/srep19660 , ISSN 2045-2322..
- P. V. Balachandran, Data-Driven Design of B20 Alloys with Targeted Magnetic Properties Guided by Machine Learning and Density Functional Theory, J. Mater. Res., 2020, 35(8), 890–897, DOI:10.1557/jmr.2020.38 , ISSN 20445326..
- P. V. Balachandran, J. Young, T. Lookman and J. M. Rondinelli, Learning from Data to Design Functional Materials without Inversion Symmetry, Nat. Commun., 2017, 8 DOI:10.1038/ncomms14282 , ISSN 20411723..
- P. V. Balachandran, T. Shearman, J. Theiler and T. Lookman, Predicting Displacements of Octahedral Cations in Ferroelectric Perovskites Using Machine Learning, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 962–967, DOI:10.1107/S2052520617011945 , ISSN 20525206..
- S. Lu, Q. Zhou, Y. Ouyang, Y. Guo, Q. Li and J. Wang, Accelerated Discovery of Stable Lead-Free Hybrid Organic-Inorganic Perovskites via Machine Learning, Nat. Commun., 2018, 9(1), 3405, DOI:10.1038/s41467-018-05761-w , ISSN 2041-1723..
- A. Mannodi-Kanakkithodi, G. Pilania, T. D. Huan, T. Lookman and R. Ramprasad, Machine Learning Strategy for Accelerated Design of Polymer Dielectrics, Sci. Rep., 2016, 6(1), 20952, DOI:10.1038/srep20952 , ISSN 2045-2322..
- B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. W. Doak, A. Thompson, K. Zhang, A. Choudhary and C. Wolverton, Combinatorial Screening for New Materials in Unconstrained Composition Space with Machine Learning, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(9), 094104, DOI:10.1103/PhysRevB.89.094104 , ISSN 1098-0121, 1550-235X..
- C. W. Park and C. Wolverton, Developing an Improved Crystal Graph Convolutional Neural Network Framework for Accelerated Materials Discovery, Phys. Rev. Mater., 2020, 4(6), 063801, DOI:10.1103/PhysRevMaterials.4.063801 , ISSN 2475-9953..
- A. Seko, H. Hayashi, H. Kashima and I. Tanaka, Matrix- and Tensor-Based Recommender Systems for the Discovery of Currently Unknown Inorganic Compounds, Phys. Rev. Mater., 2018, 2(1), 013805, DOI:10.1103/PhysRevMaterials.2.013805 , ISSN 2475-9953..
- A. D. Sendek, Q. Yang, E. D. Cubuk, K. A. N. Duerloo, Y. Cui and E. J. Reed, Holistic Computational Structure Screening of More than 12 000 Candidates for Solid Lithium-Ion Conductor Materials, Energy Environ. Sci., 2017, 10(1), 306–320, 10.1039/c6ee02697d , ISSN 17545706..
- B. B. Hoar, S. Lu and C. Liu, Machine-Learning-Enabled Exploration of Morphology Influence on Wire-Array Electrodes for Electrochemical Nitrogen Fixation, J. Phys. Chem. Lett., 2020, 11(12), 4625–4630, DOI:10.1021/acs.jpclett.0c01128 , ISSN 19487185..
- B. Yan, R. Gao, P. Liu, P. Zhang and L. Cheng, Optimization of Thermal Conductivity of UO2-Mo Composite with Continuous Mo Channel Based on Finite Element Method and Machine Learning, Int. J. Heat Mass Transfer, 2020, 159, 120067, DOI:10.1016/j.ijheatmasstransfer.2020.120067 , ISSN 00179310..
- M. de Jong, W. Chen, R. Notestine, K. Persson, G. Ceder, A. Jain, M. Asta and A. Gamst, A Statistical Learning Framework for Materials Science: Application to Elastic Moduli of k-Nary Inorganic Polycrystalline Compounds, Sci. Rep., 2016, 6(1), 34256, DOI:10.1038/srep34256 , ISSN 2045-2322..
- T. Xie and J. C. Grossman, Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties, Phys. Rev. Lett., 2018, 120(14), 145301, DOI:10.1103/PhysRevLett.120.145301 , ISSN 0031-9007, 1079-7114..
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals, Chem. Mater., 2019, 31(9), 3564–3572, DOI:10.1021/acs.chemmater.9b01294 , ISSN 0897-4756, 1520-5002..
- R. E. A. Goodall, A. S. Parackal, F. A. Faber and R. Armiento, Wyckoff Set Regression for Materials Discovery, in Neural Information Processing Systems, 2020, 7 Search PubMed.
- S.-Y. Louis, Y. Zhao, A. Nasiri, X. Wang, Y. Song, F. Liu and J. Hu, Graph Convolutional Neural Networks with Global Attention for Improved Materials Property Prediction, Phys. Chem. Chem. Phys., 2020, 22(32), 18141–18148, 10.1039/D0CP01474E , ISSN 1463-9076, 1463-9084..
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, Benchmarking Materials Property Prediction Methods: The Matbench Test Set and Automatminer Reference Algorithm, npj Comput. Mater., 2020, 6(1), 138, DOI:10.1038/s41524-020-00406-3 , ISSN 2057-3960..
- R. E. A. Goodall and A. A. Lee, Predicting Materials Properties without Crystal Structure: Deep Representation Learning from Stoichiometry, Nat. Commun., 2020, 11(1), 6280, DOI:10.1038/s41467-020-19964-7 , ISSN 2041-1723..
- J. Klicpera, S. Giri, J. T. Margraf and S. Günnemann, Fast and Uncertainty-Aware Directional Message Passing for Non-Equilibrium Molecules, 2020, arXiv:2011.14115 [physics], http://arxiv.org/abs/2011.14115.
- A. Y.-T. Wang, S. K. Kauwe, R. J. Murdock and D. Sparks, Compositionally-Restricted Attention-Based Network for Materials Property Predictions, npj Comput. Mater., 2021, 33, DOI:10.1038/s41524-021-00545-1.
- P.-P. De Breuck, G. Hautier and G.-M. Rignanese, Materials Property Prediction for Limited Datasets Enabled by Feature Selection and Joint Learning with MODNet, npj Comput. Mater., 2021, 7(1), 83, DOI:10.1038/s41524-021-00552-2 , ISSN 2057-3960..
- A. O. Oliynyk, L. A. Adutwum, B. W. Rudyk, H. Pisavadia, S. Lotfi, V. Hlukhyy, J. J. Harynuk, A. Mar and J. Brgoch, Disentangling Structural Confusion through Machine Learning: Structure Prediction and Polymorphism of Equiatomic Ternary Phases ABC, J. Am. Chem. Soc., 2017, 139(49), 17870–17881, DOI:10.1021/jacs.7b08460 , ISSN 15205126..
- J. M. Rickman, H. M. Chan, M. P. Harmer, J. A. Smeltzer, C. J. Marvel, A. Roy and G. Balasubramanian, Materials Informatics for the Screening of Multi-Principal Elements and High-Entropy Alloys, Nat. Commun., 2019, 10(1), 1–10, DOI:10.1038/s41467-019-10533-1 , ISSN 20411723..
- D. Xue, P. V. Balachandran, R. Yuan, T. Hu, X. Qian, E. R. Dougherty and T. Lookman, Accelerated Search for BaTiO3-based Piezoelectrics with Vertical Morphotropic Phase Boundary Using Bayesian Learning, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(47), 13301–13306, DOI:10.1073/pnas.1607412113 , ISSN 10916490..
- M. Asahara and R. Fujimaki, An Empirical Study on Distributed Bayesian Approximation Inference of Piecewise Sparse Linear Models, IEEE Trans. Parallel Distrib. Syst., 2019, 30(7), 1481–1493, DOI:10.1109/TPDS.2019.2892972 , ISSN 1045-9219, 1558-2183, 2161-9883..
- T. Baldacchino, E. J. Cross, K. Worden and J. Rowson, Variational Bayesian Mixture of Experts Models and Sensitivity Analysis for Nonlinear Dynamical Systems, Mech. Syst. Signal Process., 2016, 66–67, 178–200, DOI:10.1016/j.ymssp.2015.05.009 , ISSN 08883270..
- R. Eto, R. Fujimaki, S. Morinaga and H. Tamano, Fully-Automatic Bayesian Piecewise Sparse Linear Models, in International Conference on Artificial Intelligence and Statistics, 2014, 9 Search PubMed.
- W. Hashimoto, Y. Tsuji and K. Yoshizawa, Optimization of Work Function via Bayesian Machine Learning Combined with First-Principles Calculation, J. Phys. Chem. C, 2020, 124(18), 9958–9970, DOI:10.1021/acs.jpcc.0c01106 , ISSN 19327455..
- T. Ueno, T. D. Rhone, Z. Hou, T. Mizoguchi and K. Tsuda, COMBO: An Efficient Bayesian Optimization Library for Materials Science, Mater. Discov., 2016, 4, 18–21, DOI:10.1016/j.md.2016.04.001 , ISSN 23529245..
- H. Wahab, V. Jain, A. S. Tyrrell, M. A. Seas, L. Kotthoff and P. A. Johnson, Machine-Learning-Assisted Fabrication: Bayesian Optimization of Laser-Induced Graphene Patterning Using in Situ Raman Analysis, Carbon, 2020, 167, 609–619, DOI:10.1016/j.carbon.2020.05.087 , ISSN 00086223..
- Y.-F. Lim, C. K. Ng, U. Vaitesswar and K. Hippalgaonkar, Extrapolative Bayesian Optimization with Gaussian Process and Neural Network Ensemble Surrogate Models, Adv. Intell. Syst., 2021, 2100101, DOI:10.1002/aisy.202100101 , ISSN 2640-4567, 2640-4567..
- S. K. Kauwe, J. Graser, R. Murdock and T. D. Sparks, Can Machine Learning Find Extraordinary Materials?, Comput. Mater. Sci., 2020, 174, 109498, DOI:10.1016/j.commatsci.2019.109498 , ISSN 09270256..
- Y. Kim, E. Kim, E. Antono, B. Meredig and J. Ling, Machine-Learned Metrics for Predicting the Likelihood of Success in Materials Discovery, npj Comput. Mater., 2020, 6(1), 131, DOI:10.1038/s41524-020-00401-8 , ISSN 2057-3960..
- C. J. Hargreaves, M. S. Dyer, M. W. Gaultois, V. A. Kurlin and M. J. Rosseinsky, The Earth Mover's Distance as a Metric for the Space of Inorganic Compositions, Chem. Mater., 2020, 32(24), 10610–10620, DOI:10.1021/acs.chemmater.0c03381 , ISSN 0897-4756, 1520-5002..
- L. McInnes, J. Healy and J. Melville, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, 2020, arXiv:1802.03426 [cs, stat], http://arxiv.org/abs/1802.03426.
- L. van der Maaten and G. Hinton, Visualizing Data Using T-SNE, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed , ISSN 1532-4435, https://www.webofscience.com/wos/woscc/full-record/WOS:000262637600007..
- L. McInnes, J. Healy and S. Astels, Hdbscan: Hierarchical Density Based Clustering, J. Open Source Softw., 2017, 2(11), 205, DOI:10.21105/joss.00205 , ISSN 2475-9066..
- S. Lloyd, Least Squares Quantization in PCM, IEEE Trans. Inf. Theory, 1982, 28(2), 129–137, DOI:10.1109/TIT.1982.1056489 , ISSN 0018-9448..
- A. Narayan, B. Berger and H. Cho, Density-Preserving Data Visualization Unveils Dynamic Patterns of Single-Cell Transcriptomic Variability, bioRxiv 2020.05.12.077776, 2020, DOI:10.1101/2020.05.12.077776.
- E. Parzen, On Estimation of a Probability Density Function and Mode, Ann. Math. Stat., 1962, 33(3), 1065–1076, DOI:10.1214/aoms/1177704472 , ISSN 0003-4851, 2168-8990..
- M. Rosenblatt, Remarks on Some Nonparametric Estimates of a Density Function, Ann. Math. Stat., 1956, 27(3), 832–837, DOI:10.1214/aoms/1177728190 , ISSN 0003-4851, 2168-8990..
- M. Ester, H.-P. Kriegel, J. Sander and X. Xu, A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise, in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, KDD’96, AAAI Press, Portland, Oregon, 1996, pp. 226–231 Search PubMed.
- Y. Zuo, M. Qin, C. Chen, W. Ye, X. Li, J. Luo and S. P. Ong, Accelerating Materials Discovery with Bayesian Optimization and Graph Deep Learning, Mater. Today, 2021, 51, 126–135, DOI:10.1016/j.mattod.2021.08.012 , S1369702121002984, ISSN 13697021..
- B. Meredig, E. Antono, C. Church, M. Hutchinson, J. Ling, S. Paradiso, B. Blaiszik, I. Foster, B. Gibbons, J. Hattrick-Simpers, A. Mehta and L. Ward, Can Machine Learning Identify the next High-Temperature Superconductor? Examining Extrapolation Performance for Materials Discovery, Mol. Syst. Des. Eng., 2018, 3(5), 819–825, 10.1039/C8ME00012C , ISSN 2058-9689..
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. a. Persson, The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 1(1), 011002, DOI:10.1063/1.4812323 , ISSN 2166532X..
- M. de Jong, W. Chen, T. Angsten, A. Jain, R. Notestine, A. Gamst, M. Sluiter, C. Krishna Ande, S. van der Zwaag, J. J. Plata, C. Toher, S. Curtarolo, G. Ceder, K. A. Persson and M. Asta, Charting the Complete Elastic Properties of Inorganic Crystalline Compounds, Sci. Data, 2015, 2(1), 150009, DOI:10.1038/sdata.2015.9 , ISSN 2052-4463..
- A. Y.-T. Wang, R. J. Murdock, S. K. Kauwe, A. O. Oliynyk, A. Gurlo, J. Brgoch, K. A. Persson and T. D. Sparks, Machine Learning for Materials Scientists: An Introductory Guide toward Best Practices, Chem. Mater., 2020, 32(12), 4954–4965, DOI:10.1021/acs.chemmater.0c01907.
- M. G. Bellemare, I. Danihelka, W. Dabney, S. Mohamed, B. Lakshminarayanan, S. Hoyer and R. Munos, The Cramer Distance as a Solution to Biased Wasserstein Gradients, 2017, arXiv:1705.10743 [cs, stat], http://arxiv.org/abs/1705.10743.
- S. K. Lam, A. Pitrou and S. Seibert, Numba: A LLVM-based Python JIT Compiler, in Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, LLVM’15, Association for Computing Machinery, New York, NY, USA, 2015, pp. 1–6, ISBN 978-1-4503-4005-2, DOI:10.1145/2833157.2833162.
- O. Kononova, H. Huo, T. He, Z. Rong, T. Botari, W. Sun, V. Tshitoyan and G. Ceder, Text-Mined Dataset of Inorganic Materials Synthesis Recipes, Sci. Data, 2019, 6(1), 203, DOI:10.1038/s41597-019-0224-1 , ISSN 2052-4463..
- L. Weston, V. Tshitoyan, J. Dagdelen, O. Kononova, A. Trewartha, K. A. Persson, G. Ceder and A. Jain, Named Entity Recognition and Normalization Applied to Large-Scale Information Extraction from the Materials Science Literature, J. Chem. Inf. Model., 2019, 59(9), 3692–3702, DOI:10.1021/acs.jcim.9b00470 , ISSN 1549-9596, 1549-960X..
- MPDS Materials Platform, https://mpds.io/, 2021 Search PubMed.
- J. D. Hunter, Matplotlib: A 2D Graphics Environment, Comput. Sci. Eng., 2007, 9(3), 90–95, DOI:10.1109/MCSE.2007.55 , ISSN 1558-366X..
- P. T. Inc., Collaborative Data Science, https://plot.ly, 2015 Search PubMed.
- Create LaTeX Tables Online – TablesGenerator.Com, https://www.tablesgenerator.com/, 2021 Search PubMed.
- W. R. Inc., Mathematica, Version 12.2, 2020 Search PubMed.
- Auto-Paper, sparks-baird, https://github.com/sparks-baird/auto-paper, 2021 Search PubMed.
- S. Baird and C. Hargreaves, Sparks-Baird/Mat_discover: Release v1.2.1, Zenodo, 2021, DOI:10.5281/zenodo.5594679.
- S. Baird, T. Diep and T. Sparks, Trained Discover Class for Materials Discovery, 2021, DOI:10.6084/m9.figshare.16786513.v2.
- S. Baird and C. Hargreaves, Sparks-Baird/Mat_discover, Zenodo, 2021, DOI:10.5281/zenodo.5594678.
- S. G. Baird, T. Q. Diep and T. D. Sparks, High Performance, Chemically Unique Materials Discovery for Elasticity, 2021, DOI:10.24433/CO.8463578.v1.
- S. Baird, Interactive DiSCoVeR Figures, https://mat-discover.readthedocs.io/en/latest/figures.html, 2021 Search PubMed.
Footnotes |
| † In Hargreaves et al.,54 density-based spatial clustering of applications with noise62 was used instead of HDBSCAN*. We use HDBSCAN* because it is generally regarded as a more sophisticated algorithm in that it requires less hyperparameter tuning (https://hdbscan.readthedocs.io/en/latest/how_to_use_epsilon.html) and can be less susceptible to noise. |
| ‡ We clustered without DensMAP dimensionality reduction and found that the number of clusters increased from 24 to 44. As might be expected (https://umap-learn.readthedocs.io/en/latest/clustering.html), the percentage of unclassified points increases from 4.8% to 23.2%, highlighting the difficulty of using density-based clustering algorithms with sparse, high-dimensional data. |
| § See sklearn.preprocessing.RobustScaler. |
| ¶ The code was formatted in Black code style via an online formatter: https://black.vercel.app/. |
| This journal is © The Royal Society of Chemistry 2022 |