Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting compositional changes of organic–inorganic hybrid materials with Augmented CycleGAN†
Qianxiang
Ai
 a,
Alexander J.
Norquist
a,
Alexander J.
Norquist
 b and
Joshua
Schrier
b and
Joshua
Schrier
 *a
*a
aDepartment of Chemistry, Fordham University, 441 E. Fordham Rd, The Bronx, New York 10458, USA. E-mail: jschrier@fordham.edu
bDepartment of Chemistry, Haverford College, 370 Lancaster Ave, Haverford, PA 19041, USA
First published on 1st March 2022
Abstract
Despite its simplicity, the composition of a material can be used as input to machine learning models to predict a range of materials properties. However, many property optimization tasks require the generation of novel but realistic materials compositions. In this study, we describe a way to generate compositions of hybrid organic–inorganic crystals through adapting Augmented CycleGAN, a novel generative model that can learn many-to-many relations between two domains. Specifically, we investigate the problem of composition change upon amine swap: for a specific chemical system (set of elements) crystalized with amine A, how would the product chemical compositions change if it is crystalized with amine B? By training with limited data from Cambridge Structural Database, our model can generate realistic chemical compositions for hybrid crystalline materials. The Augmented CycleGAN model can also utilize abundant unpaired data (compositions of different chemical systems), a feature that traditional supervised methods lack. The generated compositions can be used for many tasks, for example, as input fed to a classifier that predicts structural dimensionality.
1. Introduction
Organic–inorganic hybrid crystalline materials are a wide class of functional materials that encompasses halide perovskites,1–3 metal organic frameworks (MOFS),4,5 and templated metal oxides.6 The subclass of amine-templated metal oxides (ATMOs) have been a research focus of structural chemistry owing to the intricate interactions between their inorganic building units and amine templates.7–11 The great structural diversity found in ATMOs (exemplified by the amine-templated zinc phosphate structures of four different dimensionalities), can only be matched by their compositional diversity (71 elements, 25 main group building units, and 349 amines as of 2021).12 This immense chemical space, along with various types of possible interactions, makes it extremely challenging to predict the properties of novel ATMOs.Since the seminal works on generative adversarial networks13 (GAN) and variational autoencoder14 (VAE) in 2014, generative models have proliferated in multiple disciplines, including biology,15 geology,16 and meteorology.17 Chemistry is no exception: exploring the virtually infinite chemical space requires efficient methods and representations. A variety of architectures, such as generative adversarial networks,18 recurrent neural networks,19 and variational autoencoders20 have been applied to a wide range of substances, including drug-like small molecules,21,22 chemical formulations,23 and crystalline reticular materials.24 The generators can be conditioned such that the generated samples have desired properties, enabling their use for inverse design.25
Most chemical generative models focus on molecules, which can be represented as molecular graphs. Representations for periodic crystalline materials typically require coordinate information, which is considerably more difficult. To represent crystal structures, a common practice is to define a parameterized structural model and to represent the structure in this parameter space.26,27 Recent studies also explored representation learning. Noh et al. proposed a VAE based framework (iMatGen) which learns a latent space from 3D images with predefined composition (V–O system).28 This method was also used in the Bi–Se binary system.29 A framework similar to iMatGen was proposed by Hoffmann et al. with a U-Net segmentation model to assign atomic species from decoded images.30 Court et al. used a similar VAE/U-Net framework based on electron-density map for cubic structures.31
Using structural representations for crystalline materials is not always necessary: compositional information alone can have excellent predictive power for a wide range of properties, such as formation energy,32 band gap33 and thermal hysteresis.34 For inverse design, the immense space of chemical composition35 requires efficient sampling methods to guide materials discovery. Sawada et al. used conditional VAE and GAN to generate inorganic composition with bag-of-atom representations, however, it appears that their models could not generate compositions with properties outside the training domain, possibly owing to the use of property descriptors in the encoding process.36 Dan et al. proposed a GAN model using a 2D encoding of composition information. While this model returns chemically plausible compositions with high novelty, the encoding method used can only represent composition of integer element fraction.37 Furthermore, only inorganic materials were investigated in these studies.
In this study, we describe the generation of ATMO compositions through Augmented CycleGAN,38 a novel generative model that can learn many-to-many relations between two domains through unpaired data. Given observed compositions, our model predicts a distribution of possible compositions when the amine is changed. Our model takes composition information as the only input, and thus can be readily generalized to other types of materials. To showcase its application, the generated compositions were passed to an inorganic framework dimensionality classifier, providing a dense sampling of different structural dimensionality in the chemical space.
2. Composition translation
Image translation is the problem of how to transform images from one domain to another,39 for example, the task of transforming pictures of horses to pictures of zebra without altering the background or pose of the animal.40 In this study, we focus on an analogous composition translation problem for amine-templated metal oxides (ATMO, see Methods for detailed definitions): given the chemical compositions of structures containing amine A, can we learn a function that transforms them to compositions of structures containing amine B? As a specific example, we chose amine A and amine B to be N-methylmethanamine (SMILES: CNC) and ethane-1,2-diamine (SMILES: NCCN), respectively, as they are the two amines found most frequently (in 314 and 427 structures, respectively) in the Cambridge Structural Database (CSD) as of 2021. The popularity provides more data points for training and more paired data for testing, which allows us to better characterize the performance of our model. Throughout this paper, chemical compositions of CNC-templated structures and NCCN-templated structures will be referred to as CA and CB, respectively, and are encoded as normalized 1D vectors of elemental mole fractions [C = (x1, x2,…) and Σixi = 1 where xi is the mole fraction of the ith element, see Fig. 1 for an example].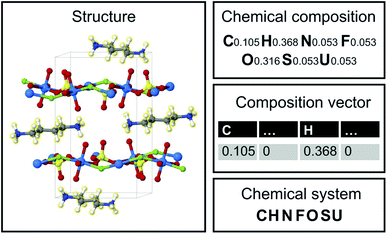 | ||
| Fig. 1 Structure, chemical composition, composition vector and chemical system of an amine-templated uranium sulfate (CCDC identifier: FAHYOD).41 | ||
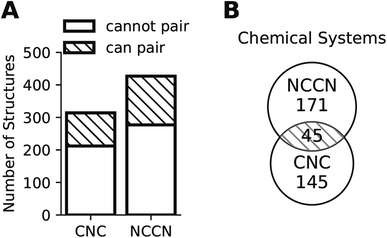
Composition translation is not a formal chemical reaction, as it does not specify the amounts of each reagent that are incorporated into the final product. Consequently, it need not conserve the total number of atoms of each type. However, it should conserve the types of elements present, because the inorganic reagents remain the same. We define a chemical system as the set of unique elements in a chemical composition, and impose the requirement that the translation model only map an input in a given chemical system to an output of the same chemical system. Such conservation also greatly reduces the number of datapoints available for supervised learning. As shown in Fig. 2, only a portion of all compositions can form a pair of the same chemical system (35.1% of CA and 32.5% of CB), and most chemical systems found in a structure group cannot be found in the other structure group. The lack of paired data is analogous to the horse to zebra image translation problem: there are virtually no real horse–zebra image pairs where the pose and background are identical. Fig. 2 also suggests the limitation of training a generator on one structure group (CA or CB) only: such a generator would not be able to generate compositions of chemical systems that are absent in this structure group. Using data from two (or multiple) structure groups, extrapolations can be made to chemical systems that are absent in one particular structure group.
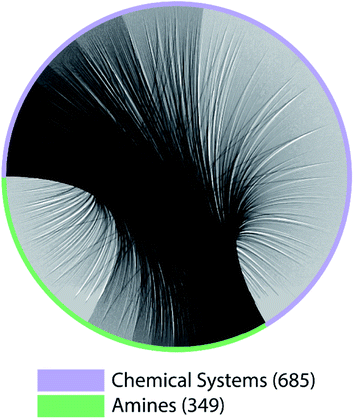
The lack of paired data is not unique to CNC and NCCN. Out of the 10 pairs of amines from the most popular 5 amines as of 2020 in the CSD, for 7 of them, the number of shared chemical systems is less than the unshared (Fig. S1†). The pairing between chemical systems and amines can be described by a bipartite graph whose edges are the observed structures. Two noteworthy features of this bipartite graph (Fig. 3) are that: the number of observed chemical systems (685, the purple arc) is much larger than that of amines (349, the green arc),12 and, more importantly, connections are concentrated on a small portion of all available nodes for both chemical systems and amines. Only 22.64% of all amine pairs are connected, and there is only a small probability (1.03%) to find an edge between a randomly chosen chemical system–amine pair. Such concentrated connections are consistent with a preferential attachment type of discovery process,42 and are not unique to organic templated oxides but also present in other fields of chemistry, such as organic reactions: in the network where reactants (nodes) connected by reactions (edges), some reactants are much more likely to be in a reaction than others.43
We aim to generate hypothetical CB (which will be referred to as 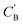 ) regardless of the popularity of its chemical system in observed amine A-templated structures. For a specific chemical system, the absence of different amine-directed structures in crystallographic databases merely indicates they have not been attempted or reported, but is not a strong indication that they cannot be synthesized. In fact, previous studies have found that there are no meaningful differences in the synthetic feasibility for popular and unpopular amines within a chemical system.42
) regardless of the popularity of its chemical system in observed amine A-templated structures. For a specific chemical system, the absence of different amine-directed structures in crystallographic databases merely indicates they have not been attempted or reported, but is not a strong indication that they cannot be synthesized. In fact, previous studies have found that there are no meaningful differences in the synthetic feasibility for popular and unpopular amines within a chemical system.42
3. CycleGAN and Augmented CycleGAN
3.1 CycleGAN
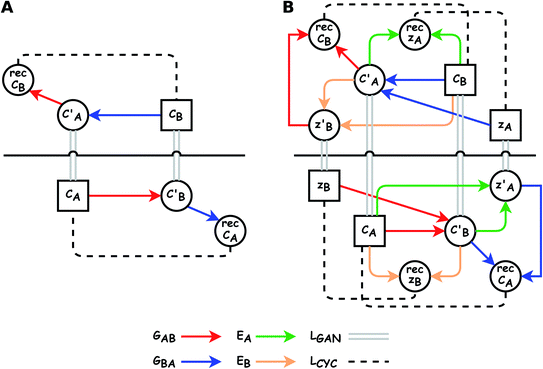
The small number of paired examples precludes a supervised approach relying on paired data. Instead we propose a composition translation model based on CycleGAN,44 a generative model originally developed for image translation. It does not require a predefined similarity measure, and, more importantly, can be trained with unpaired data. Its training process, shown in Fig. 4A, consists of two cycles starting from CA and CB, both encoded as normalized 1D vectors of elemental mole fractions. Randomly selected pairs (CA, CB) are passed to two residual network45 generators, GAB and GBA. GAB takes a composition vector of amine A (CA) and translates it to a composition vector of amine B (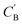 ). A prime is used to denote generated composition vectors throughout this paper. Similarly, GBA translates CB to
). A prime is used to denote generated composition vectors throughout this paper. Similarly, GBA translates CB to 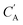 . Filters were added to the generators to avoid generating compositions of a different chemical system.
. Filters were added to the generators to avoid generating compositions of a different chemical system.
A CycleGAN model is trained by the CycleGAN loss LCycleGAN:
| LCycleGAN = LGAN−A + LGAN−B + λcycLcyc | (1) |
that has three contributions and a hyperparameter λcyc. The first two terms are the LS-GAN46 objective functions. The second term is:
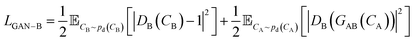 | (2) |
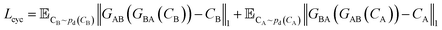 | (3) |
3.2 Augmented CycleGAN
While CycleGAN can utilize unpaired data, its cycle-consistency loss forces a one-to-one mapping between domains. This is appropriate for image translation (each horse image corresponds to a single zebra image), but problematic for chemical compositions. A chemical system may have multiple compositions (determined by stoichiometric ratios, polymorphism, etc.) necessitating a many-to-many relation. To address this, we adapted the Augmented CycleGAN model38 which connects the original CycleGAN model with two latent spaces ZA and ZB. This allows generation of multiple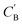 from one CA by sampling ZB and vice versa, which cannot be realized in the original CycleGAN.
from one CA by sampling ZB and vice versa, which cannot be realized in the original CycleGAN.
As shown in the lower part of Fig. 4B, the generator GAB now takes an additional vector, zB, sampled from a prior on ZB to generate 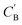 . An autoencoder EA is used to encode
. An autoencoder EA is used to encode 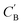 and CA to
and CA to 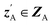 , which is used to reconstruct CAvia GBA (rec CA). The number of elements in an ATMO composition ranges from 5 to 7. To avoid generating mappings solely rely on zA and zB, the dimensions of both ZA and ZB should be smaller than 5. We set the dimensions to be one to lower the computation cost of optimizing zA and zB.
, which is used to reconstruct CAvia GBA (rec CA). The number of elements in an ATMO composition ranges from 5 to 7. To avoid generating mappings solely rely on zA and zB, the dimensions of both ZA and ZB should be smaller than 5. We set the dimensions to be one to lower the computation cost of optimizing zA and zB.
The total loss function for Augmented CycleGAN is:
| Laug−CycleGAN = λaug−cyc[Laug−cyc−A + Laug−cyc−B + λaug−cyc−z(Laug−cyc−zA + Laug−cyc−zB)] + Laug−GAN | (4) |
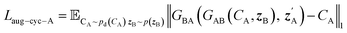 | (5) |
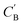 and CA, which gives another cycle-consistency loss term Laug−cyc−zB:
and CA, which gives another cycle-consistency loss term Laug−cyc−zB: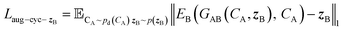 | (6) |
Similarly, we can construct the other cycle with Laug−cyc−B and Laug−cyc−zA. Two training cycles are connected by the adversarial loss:
| Laug−GAN = Laug−GAN−A + Laug−GAN−B + Laug−GAN−zA + Laug−GAN−zB | (7) |
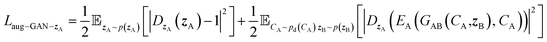 | (8) |
4. Composition translation with augmented CycleGAN
Given NA examples of CA and a potentially smaller test set of CB that have a corresponding CA, a latent vector zB (just a number since we set the dimension of ZB to be one), sampled from a Gaussian prior on ZB, is used to generate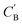 through Augmented CycleGAN. To compare two compositions
through Augmented CycleGAN. To compare two compositions 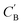 ,CB of the same chemical system, we define the average elemental mole fraction difference
,CB of the same chemical system, we define the average elemental mole fraction difference 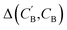 as:
as: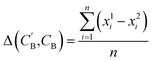 | (9) |
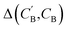 :
:
(1) Δsample: for each CB, what is the minimum 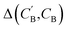 obtained after sampling the prior on ZB for Nsample times for each CA?
obtained after sampling the prior on ZB for Nsample times for each CA?
(2) Δopt: for each CB, what is the minimum 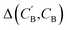 obtained after optimizing zB for each CA?
obtained after optimizing zB for each CA?
For comparison, two baseline methods were used:
(1) Identity baseline Δidentity: the generated  is a copy of CA.
is a copy of CA.
(2) Random baseline Δrandom: the generated  is a randomly selected vector from a uniform distribution in the subspace of CB vectors. The vector is normalized such that the sum of its elements is one.
is a randomly selected vector from a uniform distribution in the subspace of CB vectors. The vector is normalized such that the sum of its elements is one.
Distributions of Δopt, Δsample and Δidentity for compositions were generated using three independently trained models (three-fold splitting of CB, see Methods for more details). Augmented CycleGAN results are shown in Fig. 5. The distribution of Δrandom is too broad to be included. Comparing with both baseline methods, Augmented CycleGAN model generates more realistic compositions, with mean values of Δopt, Δsample, Δidentity and Δrandom being 0.0123, 0.0147, 0.0338 and 0.1395, respectively. The distribution of Δsample is a function of Nsample, as enlarging sample size naturally improves the best result of that batch. The mean value of Δsample, as a function of Nsample, converges at Nsample = 50 (Fig. S2†) with a cutoff of 0.001. While previous studies suggest the earth mover's distance (EMD) a good distance function for chemical compositions,48,49 changing the L1 loss function in eqn (3) to EMD of modified Pettifor scale48 does not improve results.
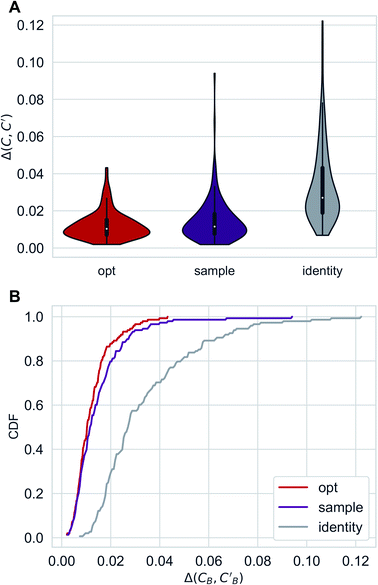 | ||
| Fig. 5 Distributions of Δopt, Δsample(Nsample = 50) and Δidentity for compositions generated using Augmented CycleGAN. (A) Violin graph. (B) Cumulative density function. | ||
Augmented CycleGAN captures information from unpaired data to generate realistic samples. Fig. 6 shows the cross-validated results Augmented CycleGAN trained either with or without unpaired data. The X-axis indicates the proportion of can-pair B used in training as the total number of can-pair B is a fixed number (see Fig. 2A caption for the definition of can-pair). When trained with only unpaired data (i.e., no can-pair B in training), the mean value of Δsample is 0.0206 (already smaller than the identity baseline of 0.0338). It can be further lowered by adding paired data to training. Without unpaired data, the mean value of Δsample becomes larger and more dependent on the amount of paired data. It also exhibits greater variation in cross-validation than models trained with unpaired data. This may come from the narrower distribution of B samples when unpaired data are excluded. These results indicate that our model is particularly useful when paired data is absent or rare.
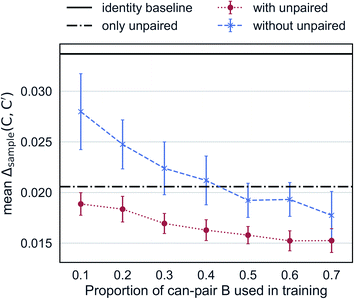 | ||
| Fig. 6 Mean Δsample as a function of the amount of paired data in training. Error bars indicate standard deviation over 10 trained models from randomly selected can-pair B samples. | ||
In addition to the quantitative analyses based on 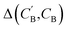 , we qualitatively assess the validity of generated compositions by comparing features of generated compositions to that of real samples. One approach is to compare compositions in a low-dimensional space. With UMAP dimensionality reduction, both real and generated compositions are mapped to a 2D space, as shown in Fig. 7. Augmented CycleGAN compositions generated from sampling a prior with Nsample = 5 cover most real compositions, while the identity baseline method covers much fewer real compositions. This demonstrates that our model generates diverse compositions spanning the observed diversity. A second approach is to determine if the distribution of element ratios in generated compositions is similar to the real observations. Fig. 8A shows the distribution of C/N element fraction ratios in generated compositions, which reflects the ratios found in real compositions (Fig. 8B). The distribution centers at 1.0. This is expected as for most (85.1%) of NCCN templated structures, C and N only come from amine templates. Values other than 1.0 come from inclusion of non-amine building units containing C/N, such as nitrate or carboxylate ions. This demonstrates that our model generates reasonable compositions by learning the characteristics of CB.
, we qualitatively assess the validity of generated compositions by comparing features of generated compositions to that of real samples. One approach is to compare compositions in a low-dimensional space. With UMAP dimensionality reduction, both real and generated compositions are mapped to a 2D space, as shown in Fig. 7. Augmented CycleGAN compositions generated from sampling a prior with Nsample = 5 cover most real compositions, while the identity baseline method covers much fewer real compositions. This demonstrates that our model generates diverse compositions spanning the observed diversity. A second approach is to determine if the distribution of element ratios in generated compositions is similar to the real observations. Fig. 8A shows the distribution of C/N element fraction ratios in generated compositions, which reflects the ratios found in real compositions (Fig. 8B). The distribution centers at 1.0. This is expected as for most (85.1%) of NCCN templated structures, C and N only come from amine templates. Values other than 1.0 come from inclusion of non-amine building units containing C/N, such as nitrate or carboxylate ions. This demonstrates that our model generates reasonable compositions by learning the characteristics of CB.
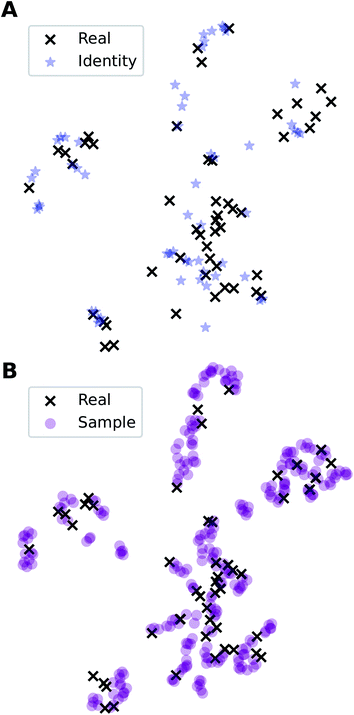 | ||
Fig. 7 Visualization of CA (blue star, identity baseline), CB (black cross, real samples), and  (purple circle, generated samples) using UMAP with Minkowski distance function (p = 1),50 where (purple circle, generated samples) using UMAP with Minkowski distance function (p = 1),50 where  were generated by sampling a prior with Nsample = 5 (i.e. from every CA, five were generated by sampling a prior with Nsample = 5 (i.e. from every CA, five 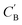 were generated). were generated). | ||
 | ||
| Fig. 8 (A) Distribution of C/N ration in generated compositions using Augmented CycleGAN with a Gaussian prior on ZB. (B) Bar chart illustrating the distribution of C/N ratio in real compositions. | ||
As amine identity plays a role in the structure formation of ATMOs, a new Augmented CycleGAN should be trained if a different amine pair is selected. A more general solution for generating ATMO compositions would be a generative model conditioned on both amine identity and chemical system (in contrast to the current model, which is conditioned by the chemical system of input compositions). One challenge is the highly imbalanced ATMO dataset: while there are 349 different amines in our dataset, the 5 amines that appear most frequently account for around 35% of all reported structures, 243 amines (nearly 70% of all amines in the dataset) appear in fewer than 5 structures each, and 159 amines (around 46% of all amines) have only one reported structure. Furthermore, the underrepresented amines (e.g., porphyrin, found in only 8 structures) can be chemically very different from the popular ones (the 5 most frequent amines are short, aliphatic amines). This raises the possible concern that such a general generator model, trained on this severely imbalanced dataset, may not learn from the minority classes, and for this reason we have not studied this more general problem in the current paper.
5. Dimensionality prediction with generated compositions
Recent studies have demonstrated promising results for composition-based model in property prediction.32–34 As an example application for the composition generation models, we use the outputs generated by Augmented CycleGAN as inputs to a composition-based inorganic framework dimensionality classifier. This allows us to explore potential structural outcomes of swapping amine templates. This is particularly useful for studying structural diversity of a specific chemical system (set of elements). We note that inorganic framework dimensionality is just one of many properties can be predicted through compositional information.We first trained the classifier using observed structures in the CSD. K-nearest neighbor, logistic regression, and random forest were tested for dimensionality classification using chemical compositions as input (represented as 75-element 1D vectors for each of the 75 unique elements found in ATMOs). All results are cross-validated through 5-fold train-test splitting (Fig. 9), and the baseline accuracy is 37.4% (predicting the majority class, 0D). The best classifier is the random forest model with an accuracy of 77.6 ± 1.3%. Surprisingly, a high accuracy of (73.9 ± 1.6%) can be reached with a simple 1-nearest neighbor model (1NN) using Manhattan distance. The high performance of 1NN model suggests the dataset may be fitted through memorization.51 Different distance functions (Euclidean and Chebyshev distances) do not have significant impact on classification accuracy.
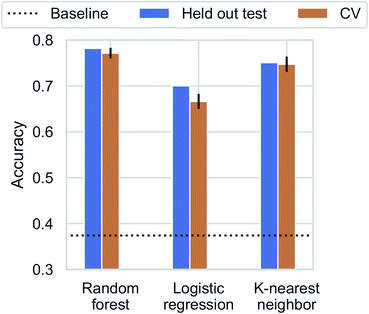 | ||
| Fig. 9 Classification accuracy for dimensionality prediction. Horizontal dotted line indicates the baseline prediction of predicting the majority class (0D). | ||
The dimensionality predictor can be used to explore the outcomes of amine swap for a specific chemical system. Using Al–C–H–N–O–P system as an example, from the chemical compositions of CNC-templated structures (CA), compositions of NCCN-templated structures ( ) are generated through Augmented CycleGAN. The generated compositions, after dimensionality reduction, are shown as transparent circles in Fig. 10, while real compositions as solid rectangles (used in training Augmented CycleGAN) or triangles (not used in Augmented CycleGAN). These compositions are colored by their dimensionalities, as predicted by the random forest dimensionality classifier. Fig. 10 illustrates that the generated compositions provide a dense sampling over the realistic chemical space that can be exploited to reach desired properties. The overall dimensionality trend is correlated to continuous changes of Al
) are generated through Augmented CycleGAN. The generated compositions, after dimensionality reduction, are shown as transparent circles in Fig. 10, while real compositions as solid rectangles (used in training Augmented CycleGAN) or triangles (not used in Augmented CycleGAN). These compositions are colored by their dimensionalities, as predicted by the random forest dimensionality classifier. Fig. 10 illustrates that the generated compositions provide a dense sampling over the realistic chemical space that can be exploited to reach desired properties. The overall dimensionality trend is correlated to continuous changes of Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio in compositions (Fig. S3†), and, from a fixed CA, generated
O ratio in compositions (Fig. S3†), and, from a fixed CA, generated  can have various Al
can have various Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O values that cover the values in CB (Fig. S4†). For the twelve NCCN-containing structures reported in the CSD, the proportions of 0D, 1D, 2D and 3D structures are 8.3% (1/12), 8.3% (1/12), 58.3% (7/12) and 25% (3/12), respectively. From generated compositions, the proportions are 0%, 17.7%, 33%, and 49%, indicating there could be more 3D compounds accessible by changing reaction parameters. These results suggest that our model can generate diverse, realistic compositions that can be used to explore structural properties of ATMOs.
O values that cover the values in CB (Fig. S4†). For the twelve NCCN-containing structures reported in the CSD, the proportions of 0D, 1D, 2D and 3D structures are 8.3% (1/12), 8.3% (1/12), 58.3% (7/12) and 25% (3/12), respectively. From generated compositions, the proportions are 0%, 17.7%, 33%, and 49%, indicating there could be more 3D compounds accessible by changing reaction parameters. These results suggest that our model can generate diverse, realistic compositions that can be used to explore structural properties of ATMOs.
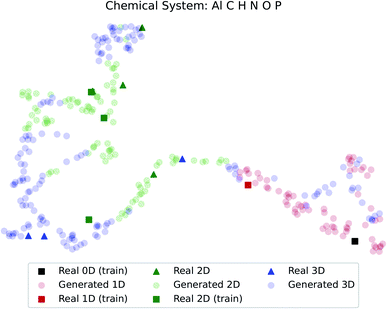 | ||
| Fig. 10 Predicted dimensionality of real and generated compositions. Dimensionality reduction follows the method used in Fig. 7. | ||
6. Perspective: unpaired data in materials chemistry
A strength of the Augmented CycleGAN approach is its ability to generate predictions about hypothetical pairs when trained with few (or no) observed pairs. Many datasets have a popularity imbalance—in our case some amines and chemical systems are reported disproportionately often, as illustrated in the concentrated connections in a bipartite graph (Fig. 3)—which leads to the prevalence of unpaired data over paired data. This is a general problem that arises in chemistry and materials systems that involve a pairing of items from two disjoint sets, such as binary molecular cocrystals. For donor–acceptor cocrystals in organic electronics, while in theory a specific molecule can be electron donor or acceptor, in practice the sets of molecular donors and acceptors barely overlap.52–54 Some donors/acceptors are much more popular than others, e.g. a search in CSD returns 215 binary cocrystal structures of tetrathiafulvalene (TTF), while many donors like dithienophenazine (DTPhz) have been only used once.55 Pharmaceutical cocrystals are often made by crystalizing one molecule from the set of active pharmaceutical ingredients (APIs) and one molecule from the (disjoint) set of pharmaceutically accepted coformers that improve the solubility/stability of the resulting cocrystals. Again, some APIs/coformers are more popular than others.56,57 With appropriate representations, Augmented CycleGAN can be used to transform cocrystals of, for example, TTF-TCNQ to that of DTPhz-TCNQ.The disjoint sets to pair need not be at the level of molecules, but could also be at the level of molecular substructures. For example, one approach to the design of organic semiconductors, is to functionalize an electronically active chromophore (e.g., acene, thiophene oligomer) with an electronically inert side groups that direct solid-state packing.58,59 Here too, there is a disparity in observed pairs, with crystals of functionalized thiophene oligomers having relatively low side-group diversity and functionalized acenes having high side-group diversity. By using a suitable molecular graph representation, an Augmented CycleGAN approach could be used to generate and explore the missing links between unpopular components.
7. Conclusion
We studied the composition translation problem of amine swap in amine-templated metal oxides. Specifically, we focused the task of generating chemical compositions of NCCN-templated metal oxides from that of CNC-templated oxides. The two key challenges are the lack of paired data and the many-to-many relations among chemical compositions. To address these challenges, an image translation model, Augmented CycleGAN, was adapted to generated chemical compositions from composition vectors (element mole fractions) without any data augmentation. Through a series of qualitative and quantitative analyses, it is demonstrated that the generative models can generate realistic, diverse chemical compositions of NCCN-templated metal oxides from CNC-templated compositions by utilizing unpaired data. We demonstrated a possible application to property exploration by connecting the composition generation models with a dimensionality classifier. Finally, potential applications of Augmented CycleGAN in other fields of materials chemistry were discussed.8. Methods
8.1 Dataset preparation
Crystal structures of amine-templated metal/metalloid oxides (ATMO) were collected from Cambridge Structure Database (CSD, version 5.41) following the procedures described in our previous study.12 Briefly, a structure is considered as an ATMO if it (1) contains amine cations all of which can be neutralized to one type of amine (quaternary ammonium cations are therefore excluded), (2) contains at least one metal/metalloid atom bonded to three oxygen atoms, and (3) metal/metalloid atoms in the structure are bonded to oxygen/halogen only. Their chemical compositions were extracted using CSD API (the formula property of ccdc.crystal.Crystal), and were normalized to element fractions (sum to 1).Dimensionalities of inorganic components in ATMO structures are determined using the implementation in matminer (version 0.6.4),60 which employs the algorithm by Larsen et al.61 based on predefined connectivity. More details regarding dimensionality determination are available in Methods section of our previous study.12
8.2 Augmented CycleGAN
The model is implemented following the original study by Almahairi et al.38 using PyTorch version 1.9.0.62 Major modifications include: (1) a filter is appended to the RESNET generator to avoid appearance of new elements; (2) 2D convolution layers are replaced with 1D linear layers; (3) grid search is used to optimize zB. A high-level overview is shown in Fig. 3B, more details regarding generators and discriminators can be found in the model summary file available at https://github.com/qai222/CompAugCycleGAN/blob/main/scripts/model_summary.txt. Composition data are encoded as 1D vectors of element fractions. In training, all CA are used as pool A, and pool B consists of all CB that cannot pair and a proportion pB of CB that can pair (see Fig. 2 caption regarding pairing). pB is set to be 2/3, and three-fold cross validation is done by splitting the set of CB that can pair. One exception case is Fig. 6: (1) pB is varied from 0 to 0.7; and, (2) when the model is trained without unpaired data, both pool A and pool B contain only samples that can pair.For a sample in pool A, one sample is randomly selected from pool B, and these two samples are passed to GAB and GBA, respectively. For each batch, every sample in pool A is selected once, but this is not true for samples in pool B due to randomness. Adam optimizer is used throughout the training process.63
All hyperparameters are tuned against the mean value of Δsample with Nsample = 50 (three-fold cross validated) through gaussian processes implemented in scikit-optimize (version 0.8.1) after 50 iterations.64 The tuned hyperparameters are shown in Table 1. The learning rate for all generators is set to be 0.0002.
| Hyperparameter | Comment | Tuned |
|---|---|---|
| g_block | Number of RESNET blocks in generators | 20 |
| lr_divider | Learning rate of generators divided by learning rate of discriminators | 2 |
| lr_slowdown_param | The learning rate is changed every 50 epochs by multiplying this factor | 0.9806 |
| cyc_weight | λ aug−cyc in eqn (1) | 1.0 |
| lambda_z | λ aug−cyc−z in eqn (4) | 0.1 |
Data availability
The source code for data processing and model construction, along with the amine-templated metal oxide dataset, can be found at https://github.com/qai222/CompAugCycleGAN. A release of the source code can also be found at https://doi.org/10.5281/zenodo.6227643. The pretrained models are available at https://doi.org/10.5281/zenodo.5721355. A notebook illustrating dataset generation and model training is included in the repository at https://github.com/qai222/CompAugCycleGAN/blob/main/scripts/tutorial.ipynb. Testing scripts are placed at https://github.com/qai222/CompAugCycleGAN/tree/main/scripts.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support from the National Science Foundation (Grant No. DMR-1928882) and the Henry Dreyfus Teacher-Scholar Award (Grant No. TH-14-010). Computational resources were provided in part by the MERCURY consortium (http://mercuryconsortium.org/) under NSF grants CNS-2018427.References
- A. K. Jena, A. Kulkarni and T. Miyasaka, Halide Perovskite Photovoltaics: Background, Status, and Future Prospects, Chem. Rev., 2019, 119(5), 3036–3103, DOI:10.1021/acs.chemrev.8b00539
.
- W.-J. Yin, J.-H. Yang, J. Kang, Y. Yan and S.-H. Wei, Halide Perovskite Materials for Solar Cells: A Theoretical Review, J. Mater. Chem. A, 2015, 3(17), 8926–8942, 10.1039/c4ta05033a
.
- A. Walsh, Principles of Chemical Bonding and Band Gap Engineering in Hybrid Organic–Inorganic Halide Perovskites, J. Phys. Chem. C, 2015, 119(11), 5755–5760, DOI:10.1021/jp512420b
.
- H.-C. “Joe” Zhou and S. Kitagawa, Metal–Organic Frameworks (MOFs), Chem. Soc. Rev., 2014, 43(16), 5415–5418, 10.1039/c4cs90059f
.
- M. O'Keeffe, M. Eddaoudi, H. Li, T. Reineke and O. M. Yaghi, Frameworks for Extended Solids: Geometrical Design Principles, J. Solid State Chem., 2000, 152(1), 3–20, DOI:10.1006/jssc.2000.8723
.
- A. K. Cheetham, G. Férey and T. Loiseau, Open-Framework Inorganic Materials, Angew. Chem., Int. Ed., 1999, 38(22), 3268–3292, DOI:10.1002/(sici)1521-3773(19991115)38:22<3268::aid-anie3268>3.0.co;2-u
.
- J. H. Olshansky, K. J. Wiener, M. D. Smith, A. Nourmahnad, M. J. Charles, M. Zeller, J. Schrier and A. J. Norquist, Formation Principles for Vanadium Selenites: The Role of pH on Product Composition, Inorg. Chem., 2014, 53(22), 12027–12035 CrossRef CAS PubMed
.
- K. B. Chang, D. J. Hubbard, M. Zeller, J. Schrier and A. J. Norquist, The Role of Stereoactive Lone Pairs in Templated Vanadium Tellurite Charge Density Matching, Inorg. Chem., 2010, 49(11), 5167–5172 CrossRef CAS PubMed
.
- H. S. Casalongue, S. J. Choyke, A. N. Sarjeant, J. Schrier and A. J. Norquist, Charge Density Matching in Templated Molybdates, J. Solid State Chem., 2009, 182(6), 1297–1303 CrossRef CAS
.
- A. K. Stover, J. R. Gutnick, A. N. Sarjeant and A. J. Norquist, [Mo16O53F2]12-: A New Polyoxofluoromolybdate Anion, Inorg. Chem., 2007, 46(11), 4389–4391 CrossRef CAS PubMed
.
- D. J. Hubbard, A. R. Johnston, H. S. Casalongue, A. N. Sarjeant and A. J. Norquist, Synthetic Approaches for Noncentrosymmetric Molybdates, Inorg. Chem., 2008, 47(19), 8518–8525 CrossRef CAS PubMed
.
- Q. Ai, D. M. Williams, M. Danielson, L. G. Spooner, J. A. Engler, Z. Ding, M. Zeller, A. J. Norquist and J. Schrier, Predicting Inorganic Dimensionality in Templated Metal Oxides, J. Chem. Phys., 2021, 154(18), 184708, DOI:10.1063/5.0044992
.
-
I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. BengioGenerative Adversarial Nets, in Proceedings of the 27th International Conference on Neural Information Processing Systems, NIPS'14, Montreal, Canada, 2014, vol. 2, pp. 2672–2680 Search PubMed
.
- D. P. Kingma and M. Welling, Auto-Encoding Variational Bayes, arXiv:1312.6114 [cs, stat], 2014 Search PubMed.
-
A. Osokin, A. Chessel, R. E. Carazo Salas and F. Vaggi, GANs for Biological Image Synthesis, in Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 2233–2242 Search PubMed
.
- L. Mosser, O. Dubrule and M. J. Blunt, Stochastic Seismic Waveform Inversion Using Generative Adversarial Networks as a Geological Prior, Math. Geosci., 2020, 52(1), 53–79 CrossRef
.
- S. Ravuri, K. Lenc, M. Willson, D. Kangin, R. Lam, P. Mirowski, M. Fitzsimons, M. Athanassiadou, S. Kashem, S. Madge, R. Prudden, A. Mandhane, A. Clark, A. Brock, K. Simonyan, R. Hadsell, N. Robinson, E. Clancy, A. Arribas and S. Mohamed, Skilful Precipitation Nowcasting Using Deep Generative Models of Radar, Nature, 2021, 597(7878), 672–677, DOI:10.1038/s41586-021-03854-z
.
- A. Kadurin, S. Nikolenko, K. Khrabrov, A. Aliper and A. Zhavoronkov, DruGAN: An Advanced Generative Adversarial Autoencoder Model for de Novo Generation of New Molecules with Desired Molecular Properties in Silico, Mol. Pharmaceutics, 2017, 14(9), 3098–3104 CrossRef CAS PubMed
.
- F. Grisoni, M. Moret, R. Lingwood and G. Schneider, Bidirectional Molecule Generation with Recurrent Neural Networks, J. Chem. Inf. Model., 2020, 60(3), 1175–1183, DOI:10.1021/acs.jcim.9b00943
.
-
W. Jin, R. Barzilay and T. Jaakkola, Junction Tree Variational Autoencoder for Molecular Graph Generation, in International conference on machine learning, PMLR, 2018, pp. 2323–2332 Search PubMed
.
- D. C. Elton, Z. Boukouvalas, M. D. Fuge and P. W. Chung, Deep Learning for Molecular Design—a Review of the State of the Art, Mol. Syst. Des. Eng., 2019, 4(4), 828–849, 10.1039/c9me00039a
.
- C. Shen, M. Krenn, S. Eppel and A. Aspuru-Guzik, Deep Molecular Dreaming: Inverse Machine Learning for de-Novo Molecular Design and Interpretability with Surjective Representations, arXiv:2012.09712 [physics], 2020 Search PubMed.
- E. Sevgen, E. Kim, B. Folie, V. Rivera, J. Koeller, E. Rosenthal, A. Jacobs and J. Ling, Toward Predictive Chemical Deformulation Enabled by Deep Generative Neural Networks, Ind. Eng. Chem. Res., 2021, 60(39), 14176–14184, DOI:10.1021/acs.iecr.1c00634
.
- Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha, R. Q. Snurr and A. Aspuru-Guzik, Inverse Design of Nanoporous Crystalline Reticular Materials with Deep Generative Models, Nat. Mach. Intell., 2021, 3(1), 76–86, DOI:10.1038/s42256-020-00271-1
.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse Molecular Design Using Machine Learning: Generative Models for Matter Engineering, Science, 2018, 361(6400), 360–365 CrossRef CAS PubMed
.
- A. Nouira, N. Sokolovska and J.-C. Crivello, CrystalGAN: Learning to Discover Crystallographic Structures with Generative Adversarial Networks, arXiv:1810.11203 [cs, stat], 2019 Search PubMed.
- V. Fung, J. Zhang, G. Hu, P. Ganesh and B. G. Sumpter, Inverse Design of Two-Dimensional Materials with Invertible Neural Networks, npj Computational Materials, 2021, 15 DOI:10.1038/s41524-021-00670-x
.
- J. Noh, J. Kim, H. S. Stein, B. Sanchez-Lengeling, J. M. Gregoire, A. Aspuru-Guzik and Y. Jung, Inverse Design of Solid-State Materials via a Continuous Representation, Matter, 2019, 1(5), 1370–1384, DOI:10.1016/j.matt.2019.08.017
.
- T. Long, N. M. Fortunato, I. Opahle, Y. Zhang, I. Samathrakis, C. Shen, O. Gutfleisch and H. Zhang, Constrained Crystals Deep Convolutional Generative Adversarial Network for the Inverse Design of Crystal Structures, npj Comput. Mater., 2021, 7(1), 1–7, DOI:10.1038/s41524-021-00526-4
.
- J. Hoffmann, L. Maestrati, Y. Sawada, J. Tang, J. M. Sellier and Y. Bengio, Data-Driven Approach to Encoding and Decoding 3-D Crystal Structures, arXiv:1909.00949 [cond-mat, physics:physics, stat], 2019 Search PubMed.
- C. J. Court, B. Yildirim, A. Jain and J. M. Cole, 3-D Inorganic Crystal Structure Generation and Property Prediction via Representation Learning, J. Chem. Inf. Model., 2020, 60(10), 4518–4535, DOI:10.1021/acs.jcim.0c00464
.
- D. Jha, L. Ward, A. Paul, W. Liao, A. Choudhary, C. Wolverton and A. Agrawal, ElemNet: Deep Learning the Chemistry of Materials From Only Elemental Composition, Sci. Rep., 2018, 8(1), 17593, DOI:10.1038/s41598-018-35934-y
.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A General-Purpose Machine Learning Framework for Predicting Properties of Inorganic Materials, npj Comput. Mater., 2016, 2(1), 1–7, DOI:10.1038/npjcompumats.2016.28
.
- S. Liu, B. B. Kappes, B. Amin-ahmadi, O. Benafan, X. Zhang and A. P. Stebner, Physics-Informed Machine Learning for Composition – Process – Property Design: Shape Memory Alloy Demonstration, Appl. Mater. Today, 2021, 22, 100898, DOI:10.1016/j.apmt.2020.100898
.
- D. W. Davies, K. T. Butler, A. J. Jackson, A. Morris, J. M. Frost, J. M. Skelton and A. Walsh, Computational Screening of All Stoichiometric Inorganic Materials, Chem, 2016, 1(4), 617–627, DOI:10.1016/j.chempr.2016.09.010
.
- Y. Sawada, K. Morikawa and M. Fujii, Study of Deep Generative Models for Inorganic Chemical Compositions, arXiv:1910.11499 [cond-mat, physics:physics], 2019 Search PubMed.
- Y. Dan, Y. Zhao, X. Li, S. Li, M. Hu and J. Hu, Generative Adversarial Networks (GAN) Based Efficient Sampling of Chemical Composition Space for Inverse Design of Inorganic Materials, npj Comput. Mater., 2020, 6(1), 1–7, DOI:10.1038/s41524-020-00352-0
.
- A. Almahairi, S. Rajeswar, A. Sordoni, P. Bachman and A. Courville, Augmented CycleGAN: Learning Many-to-Many Mappings from Unpaired Data, arXiv:1802.10151 [cs], 2018 Search PubMed.
- Y. Pang, J. Lin, T. Qin and Z. Chen, Image-to-Image Translation: Methods and Applications, arXiv:2101.08629 [cs], 2021 Search PubMed.
- P. Isola, J.-Y. Zhu, T. Zhou and A. A. Efros, Image-to-Image Translation with Conditional Adversarial Networks, arXiv:1611.07004 [cs], 2018 Search PubMed.
- M. B. Doran, B. E. Cockbain, A. J. Norquist and D. O'Hare, The Effects of Hydrofluoric Acid Addition on the Hydrothermal Synthesis of Templated Uranium Sulfates, Dalton Trans., 2004, 22, 3810–3814 RSC
.
- X. Jia, A. Lynch, Y. Huang, M. Danielson, I. Lang’at, A. Milder, A. E. Ruby, H. Wang, S. A. Friedler, A. J. Norquist and J. Schrier, Anthropogenic Biases in Chemical Reaction Data Hinder Exploratory Inorganic Synthesis, Nature, 2019, 573(7773), 251–255, DOI:10.1038/s41586-019-1540-5
.
- B. A. Grzybowski, K. J. M. Bishop, B. Kowalczyk and C. E. Wilmer, The “wired” Universe of Organic Chemistry, Nat. Chem., 2009, 1(1), 31–36, DOI:10.1038/nchem.136
.
-
J.-Y. Zhu, T. Park, P. Isola and A. A. Efros, Unpaired Image-To-Image Translation Using Cycle-Consistent Adversarial Networks, in Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 2223–2232 Search PubMed
.
-
K. He, X. Zhang, S. Ren and J. Sun, Deep Residual Learning for Image Recognition, in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, Las Vegas, NV, USA, 2016, pp. 770–778, DOI:10.1109/cvpr.2016.90
.
-
X. Mao, Q. Li, H. Xie, R. Y. K. Lau, Z. Wang and S. P. Smolley, Least Squares Generative Adversarial Networks, in 2017 IEEE International Conference on Computer Vision (ICCV), 2017, pp. 2813–2821, DOI:10.1109/iccv.2017.304
.
- E. Hosseini-Asl, Y. Zhou, C. Xiong and R. Socher, Augmented Cyclic Adversarial Learning for Low Resource Domain Adaptation, arXiv:1807.00374 [cs, stat], 2019 Search PubMed.
- H. Glawe, A. Sanna, E. K. U. Gross and M. A. L. Marques, The Optimal One Dimensional Periodic Table: A Modified Pettifor Chemical Scale from Data Mining, New J. Phys., 2016, 18(9), 093011, DOI:10.1088/1367-2630/18/9/093011
.
- C. J. Hargreaves, M. S. Dyer, M. W. Gaultois, V. A. Kurlin and M. J. Rosseinsky, The Earth Mover's Distance as a Metric for the Space of Inorganic Compositions, Chem. Mater., 2020, 32(24), 10610–10620, DOI:10.1021/acs.chemmater.0c03381
.
- L. McInnes, J. Healy and J. Melville, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, arXiv:1802.03426 [cs, stat], 2020 Search PubMed.
- I. Wallach and A. Heifets, Most Ligand-Based Classification Benchmarks Reward Memorization Rather than Generalization, J. Chem. Inf. Model., 2018, 58(5), 916–932, DOI:10.1021/acs.jcim.7b00403
.
- K. P. Goetz, D. Vermeulen, M. E. Payne, C. Kloc, L. E. McNeil and O. D. Jurchescu, Charge-Transfer Complexes: New Perspectives on an Old Class of Compounds, J. Mater. Chem. C, 2014, 2(17), 3065–3076 RSC
.
- L. Fábián, Cambridge Structural Database Analysis of Molecular Complementarity in Cocrystals, Cryst. Growth Des., 2009, 9(3), 1436–1443, DOI:10.1021/cg800861m
.
- M. J. Mnguni, J. P. Michael and A. Lemmerer, Binary Polymorphic Cocrystals: An Update on the Available Literature in the Cambridge Structural Database, Including a New Polymorph of the Pharmaceutical 1:1 Cocrystal Theophylline–3,4-Di-hydroxy-benzoic Acid, Acta Crystallogr., Sect. C: Struct. Chem., 2018, 74(6), 715–720, DOI:10.1107/s2053229618006861
.
- Q. Ai, Y. A. Getmanenko, K. Jarolimek, R. Castañeda, T. V. Timofeeva and C. Risko, Unusual Electronic Structure of the Donor–Acceptor Cocrystal Formed by Dithieno[3,2-a:2′,3′-c]Phenazine and 7,7,8,8-Tetracyanoquinodimethane, J. Phys. Chem. Lett., 2017, 8(18), 4510–4515, DOI:10.1021/acs.jpclett.7b01816
.
- N. K. Duggirala, M. L. Perry, Ö. Almarsson and M. J. Zaworotko, Pharmaceutical Cocrystals: Along the Path to Improved Medicines, Chem. Commun., 2015, 52(4), 640–655, 10.1039/c5cc08216a
.
- D. D. Gadade and S. S. Pekamwar, Pharmaceutical Cocrystals: Regulatory and Strategic Aspects, Design and Development, Adv. Pharm. Bull., 2016, 6(4), 479–494, DOI:10.15171/apb.2016.062
.
- Q. Ai, V. Bhat, S. M. Ryno, K. Jarolimek, P. Sornberger, A. Smith, M. M. Haley and J. E. Anthony, Risko, C. OCELOT: An Infrastructure for Data-Driven Research to Discover and Design Crystalline Organic Semiconductors, J. Chem. Phys., 2021, 154(17), 174705, DOI:10.1063/5.0048714
.
- J. E. Anthony, J. S. Brooks, D. L. Eaton and S. R. Parkin, Functionalized Pentacene: Improved Electronic Properties from Control of Solid-State Order, J. Am. Chem. Soc., 2001, 123(38), 9482–9483, DOI:10.1021/ja0162459
.
- L. Ward, A. Dunn, A. Faghaninia, N. E. R. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom, M. Dylla, K. Chard, M. Asta, K. A. Persson, G. J. Snyder, I. Foster and A. Jain, Matminer: An Open Source Toolkit for Materials Data Mining, Comput. Mater. Sci., 2018, 152, 60–69, DOI:10.1016/j.commatsci.2018.05.018
.
- P. M. Larsen, M. Pandey, M. Strange and K. W. Jacobsen, Definition of a Scoring Parameter to Identify Low-Dimensional Materials Components, Phys. Rev. Mater., 2019, 3(3), 034003, DOI:10.1103/physrevmaterials.3.034003
.
-
A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, PyTorch: An Imperative Style, High-Performance Deep Learning Library, in Advances in Neural Information Processing Systems 32, ed. Wallach, H., Larochelle, H., Beygelzimer, A., Alché-Buc, F. d', Fox, E. and Garnett, R., Curran Associates, Inc., 2019, pp. 8024–8035 Search PubMed
.
- D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, arXiv:1412.6980 [cs], 2017.
-
T. Head, G. L. MechCoder and I. Shcherbatyi, Scikit-Optimize/Scikit-Optimize: V0.8.1. Zenodo, 2021, DOI:10.5281/zenodo.4014775
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1dd00044f |
| This journal is © The Royal Society of Chemistry 2022 |