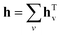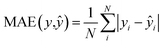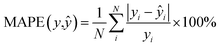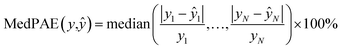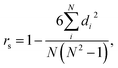3D chemical structures allow robust deep learning models for retention time prediction†
Received
26th March 2022
, Accepted 27th August 2022
First published on 30th August 2022
Abstract
Chromatographic retention time (RT) is a powerful characteristic used to identify, separate, or rank molecules in a mixture. With accumulated RT data, it becomes possible to develop deep learning approaches to assist chromatographic experiments. However, measured RT values strongly vary with respect to the different chromatographic conditions, thus, limiting the applicability of the deep learning models. In this work, we developed a robust deep learning method (CPORT) to predict RTs based on the 3D structural information of the input molecules. When trained on the METLIN dataset comprising ∼80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RTs measured under specific chromatographic conditions and applied for 47 datasets corresponding to different chromatographic conditions, we observed a strong positive correlation (|rs| > 0.5) between the predicted and measured retention times for 30 experiments. CPORT is fast enough both for the fine-tuning, allowing absolute RT value prediction, and for the large-scale screening of small molecules.
000 RTs measured under specific chromatographic conditions and applied for 47 datasets corresponding to different chromatographic conditions, we observed a strong positive correlation (|rs| > 0.5) between the predicted and measured retention times for 30 experiments. CPORT is fast enough both for the fine-tuning, allowing absolute RT value prediction, and for the large-scale screening of small molecules.
1 Introduction
The problem of identification and separation of components in a mixture arises in many areas, from the oil and gas industry1 to doping2 and drug3 detection. Chromatography is one of the most powerful and widespread methods of compound separation, and measured RTs serve as the discriminate characteristics of molecules.4 Many separation techniques have been developed for liquid chromatography, here we considered reversed-phase liquid chromatography (RPLC), hydrophilic interaction liquid chromatography (HILIC), and ion chromatography (IC), which are mainly used in untargeted small-molecule applications. For instance, RPLC is more suitable for separation of hydrophobic compounds, while HILIC and IC are more suitable for highly polar compounds.5–7 However, liquid chromatography experiments are often tedious, resource-consuming, and require a precise experimental setup, including correct composition of the stationary and mobile phases and obtaining reference RT values for pure chemical compounds, as well as the flow rate, temperature, and many other parameters.4 With the progress in machine learning applied to chemical science, it becomes possible to assist chromatographic experiments,8–10 and many supervised learning algorithms were developed to predict RTs.11–16 Recently large scale RT measurements resulted in the massive commercial dataset of ∼100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chemicals (NIST17) and publicly available dataset of ∼80
000 chemicals (NIST17) and publicly available dataset of ∼80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chemicals (METLIN18) for the gas and reversed-phase liquid chromatography, respectively, let alone the peptide-specific dataset of ∼140
000 chemicals (METLIN18) for the gas and reversed-phase liquid chromatography, respectively, let alone the peptide-specific dataset of ∼140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 peptides.19,20 These opened opportunities to apply deep learning approaches to predict RTs; the first fully connected neural network (DNN) trained on the molecular fingerprint representation of small molecules from METLIN showed 6.8% and 4.5% mean and median absolute percentage errors, respectively.18 Finally, 1D and graph convolutional neural networks, that do not rely on hand-crafted features, demonstrated superior performance compared to the classical deep learning approach.21,22 In this study we present the first structure-based deep learning approach, that directly relies on 3D atomic coordinates for RT prediction of small molecules, which is robust with respect to various chromatographic conditions. Our approach, dubbed CPORT (Conformation-based Prediction Of Retention Time), operates with 3D chemical structures as with 3D images, namely, a 40 × 40 × 40 voxel grid representation of a molecule, comprising information about physicochemical properties of a molecule in seven different channels. We demonstrated that CPORT learns relevant information about the chromatography, rather than overfit to the training set, by directly applying it to 47 RPLC chromatography experiments, including two in-house RT measurements of ∼500 drug-like molecules. For 30 out of 47 experiments, we observed a positive correlation between the predicted and measured retention times, outperforming the state-of-the-art counterparts. Finally, we showed that CPORT is applicable to predict RTs for various chromatographic conditions by means of transfer learning. CPORT is fast and suitable for the large-scale predictions of RTs; more specifically, screening of 1
000 peptides.19,20 These opened opportunities to apply deep learning approaches to predict RTs; the first fully connected neural network (DNN) trained on the molecular fingerprint representation of small molecules from METLIN showed 6.8% and 4.5% mean and median absolute percentage errors, respectively.18 Finally, 1D and graph convolutional neural networks, that do not rely on hand-crafted features, demonstrated superior performance compared to the classical deep learning approach.21,22 In this study we present the first structure-based deep learning approach, that directly relies on 3D atomic coordinates for RT prediction of small molecules, which is robust with respect to various chromatographic conditions. Our approach, dubbed CPORT (Conformation-based Prediction Of Retention Time), operates with 3D chemical structures as with 3D images, namely, a 40 × 40 × 40 voxel grid representation of a molecule, comprising information about physicochemical properties of a molecule in seven different channels. We demonstrated that CPORT learns relevant information about the chromatography, rather than overfit to the training set, by directly applying it to 47 RPLC chromatography experiments, including two in-house RT measurements of ∼500 drug-like molecules. For 30 out of 47 experiments, we observed a positive correlation between the predicted and measured retention times, outperforming the state-of-the-art counterparts. Finally, we showed that CPORT is applicable to predict RTs for various chromatographic conditions by means of transfer learning. CPORT is fast and suitable for the large-scale predictions of RTs; more specifically, screening of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules took about 1 day on a single GPU.
000 molecules took about 1 day on a single GPU.
2 Results and discussion
We trained a 3D convolutional neural network, that takes the 3D representation of a molecule as input and estimates its RT value as output, and Fig. 1 schematically shows the CPORT's workflow. When trained on the METLIN dataset, CPORT showed the mean (MAE) and median (MedAE) absolute and percentage (MAPE and MedAPE) errors of 44 (5.5%) and 26 (3.4%) seconds, respectively (see Table S1†) (Fig. 2). It is important to note that random train and test split often yields over-optimistic results;23 as for the retention time prediction problem, Domingo-Almenara reported that the presence of at least one highly similar molecule in the training set noticeably decreases the prediction error for a molecule.18 Therefore we also tested CPORT using the scaffold split,24 that guarantees no similar molecules shared between the train and test sets. The scaffold split typically results in worse performance metrics for quantitative–structure–activity(property)–relationship (QSA(P)R) models, compared to the random split;25 accordingly, we observed 2–4 (0.2–0.5%) and 1–5 (0.2–0.6%) seconds drop in terms of the mean and median absolute and percentage errors, respectively, for CPORT as well as the deep neural network (DNN)18 and graph convolutional neural network (GNN).21 To demonstrate that CPORT learns essential information about molecules with respect to the chromatographic retention time prediction problem, rather than overfit to the METLIN dataset, we directly applied CPORT to the datasets collected with another experimental setup and environment. For this blind test, we used 45 RPLC and 9 HILIC external datasets. Note that the elution order is typically highly conserved between chromatography systems of the same type and between chromatography systems of two different types, the elution order is not identical, but some patterns still exist, for instance, highly polar compounds are expected to be amongst the first analytes in RPLC, while will be usually retained for a longer time in HILIC. Therefore, the rank-based performance metrics, such as Spearman's rank correlation coefficient, should be used to compare the predicted and experimental values with respect to the different experimental setups. On the one hand, an ideal model trained on METLIN, as on the RPLC dataset, should demonstrate positive correlation with respect to the other RPLC datasets. On the other hand, although retention in RP and HILIC has different nature, one may expect negative correlation between the corresponding measurements. We want to emphasize that we did not fine-tune the model on the external datasets but directly applied CPORT, as it is, and calculated Spearman's rank correlation coefficient between the measured and predicted retention time values for molecules from the external datasets. Remarkably, for 22 and 30 out of 45 RPLC datasets we observed strong positive correlation in terms of Spearman's correlation coefficient (rs > 0.5) for the CPORT models trained using random and scaffold splits, respectively (see Fig. 3 and Table S4†). Note that for six and five datasets, no models, trained on random and scaffold splits, respectively, show strong correlation.
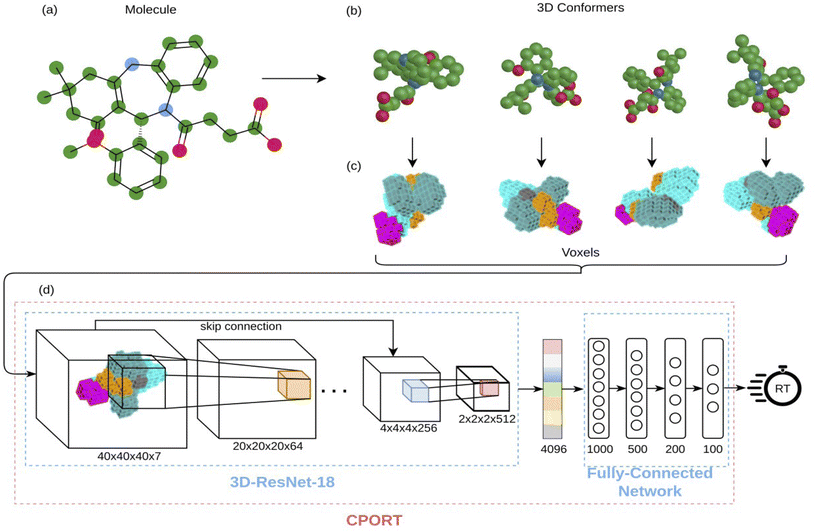 |
| | Fig. 1 Illustration of the CPORT pipeline. (a) The input molecule; (b) different 3D conformations generated for the input molecule; (c) 3D image representations of the conformations; (d) neural network architecture consisting of 3D convolutional layers and fully-connected layers. | |
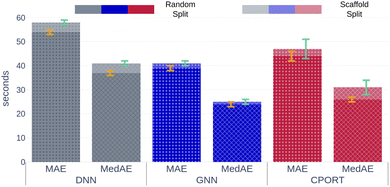 |
| | Fig. 2 Mean and median absolute errors for each model. Gray, blue, and red bars correspond to the DNN,18 GNN,21 CPORT models, respectively. Opaque and transparent bars stand for models trained using random and scaffold splits, respectively. Orange and cyan error bars correspond to the standard deviation of the metrics for models trained using random and scaffold splits, respectively. | |
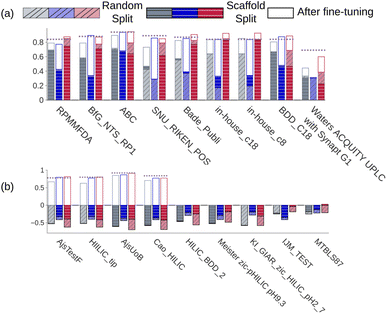 |
| | Fig. 3 Spearman's rank correlation coefficients calculated for (a) seven external RPLC and two in-house datasets and (b) for 9 HILIC datasets. Gray, blue, and red bars correspond to the DNN,18 GNN,21 and CPORT models, respectively. Bar outlines with the corresponding colors stand for the performance of the fine-tuned models. Opaque and transparent bars stand for models trained using random and scaffold splits, respectively. Violet dashed lines correspond to the XGBoost models. | |
We observed that CPORT substantially outperformed the DNN and GNN models on 10 and 23 out of 45 RPLC datasets for models trained on random and scaffold splits, respectively, and demonstrated on par performance on the remaining datasets (see the Methods). We also noticed that GNN often predicts unfeasible retention times (>2000 seconds), while the largest value in METLIN is <1500 seconds; moreover, it was observed for highly similar to METLIN molecules (the Tanimoto similarity coefficient between the ECFP2 fingerprints26 >0.7). As for CPORT, all its predictions that are out of the METLIN dataset range correspond to the highly hydrophobic molecules, which is in full accordance with RPLC experiments (see Fig. S4†). In the HILIC case we observed substantial outperforming of CPORT with |rs| > 0.5 for 5 out of 9 cases using the scaffold splits, and inferior performance compared to the DNN model for two cases using the random split. Note that all the models did not show strong correlation for two and three datasets using random and scaffold splits, respectively. Notably, the experimental correlation between HILIC and RPLC data calculated for the intersection of the HILIC_tip and the METLIN datasets (42 molecules) is similar to that observed with the predicted values (rsexp = −0.45). As for the absolute RT value prediction, CPORT supports the transfer learning approach. To show this, we considered six RPLC and five HILIC datasets with more than 400 molecules, separately fine tuned CPORT on 75% of molecules of each dataset, and applied the fine-tuned models on the remaining 25% of molecules. To investigate whether the transfer learning approach may outperform direct training with classical machine learning methods, we additionally trained the XGBoost27 models on eleven external and two in-house datasets, as it follows (see the Methods). As one can see from Fig. 3, the fine-tuned CPORT models slightly outperformed the starting models and have adapted retention time characteristics corresponding to the different chromatographic conditions (see also Fig. S5†). Remarkably, the fine-tuned CPORT models performed on par or better compared to the XGBoost models in all, but two cases and outperformed the fine-tuned GNN21 and DNN18 models for ten out of eleven cases. Table S3† lists the performance metrics calculated for the fine-tuned CPORT, DNN,18 GNN,21 and XGBoost models.
Finally, to demonstrate feasibility of the proposed approach in a real chromatographic setup, we collected two in house datasets of RT values measured using C8 and C18 chromatographic columns. The RT values were measured for ∼500 molecules corresponding to the drug-like molecules and pesticides, and the median similarity with respect to METLIN is ∼0.5 in terms of the Tanimoto coefficient (see Fig. S6†). CPORT substantially outperforms the other methods showing Spearman's rank correlation coefficients of 0.83/0.84, compared to 0.64/0.64 for DNN18 and 0.33/0.18 for GNN21 when trained with the random or scaffold split, respectively (see Fig. 4). Remarkably, with fine-tuning we observed only minor improvement in the correlation metric, while the distribution of the predicted RT values was shifted towards the experimental ones (see Fig. 4 and S6†), justifying the robustness of the CPORT model. The fine-tuned CPORT model also outperformed the fine-tuned DNN18 and GNN21 models, and Table S3† lists the corresponding performance metrics. Therefore, it is possible to use CPORT in practice for both the elution order and retention time predictions by means of fine tuning the original CPORT model, given relatively small amounts of compounds with measured RTs. Computational speed is another important aspect in a real chromatographic setup, and CPORT is fast and suitable for the large-scale RT assessment. Indeed, calculation of RTs for a batch of 128 molecules takes ∼0.4 seconds on a single GPU. As for the full pipeline, including molecule preprocessing along with the RT prediction, on a workstation with ten CPUs and one GPU it took ∼26 hours to screen 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules (see Fig. S8†). Note, however, that such a large screen is possible only with a fast conformation generator, such as RDKit, that takes ∼0.3 seconds on a single CPU to produce conformers for a single molecule. As for the fine-tuning process, it took only ∼20 minutes to fine-tune the model using RT measurements for 1000 molecules on a single GPU (GeForce GTX 1080Ti). The web-server implementation of the CPORT pipeline is available at https://sites.skoltech.ru/imolecule/tools/cport, and the source code to fine-tune CPORT on a custom dataset is available at https://github.com/i-Molecule/cport.
000 molecules (see Fig. S8†). Note, however, that such a large screen is possible only with a fast conformation generator, such as RDKit, that takes ∼0.3 seconds on a single CPU to produce conformers for a single molecule. As for the fine-tuning process, it took only ∼20 minutes to fine-tune the model using RT measurements for 1000 molecules on a single GPU (GeForce GTX 1080Ti). The web-server implementation of the CPORT pipeline is available at https://sites.skoltech.ru/imolecule/tools/cport, and the source code to fine-tune CPORT on a custom dataset is available at https://github.com/i-Molecule/cport.
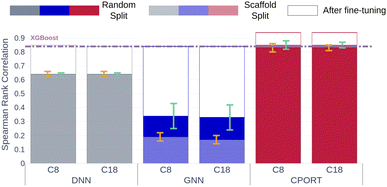 |
| | Fig. 4 Spearman's coefficients between predicted and measured RTs for in-house datasets with C8 and C18 columns. Gray, blue, and red bars correspond to the DNN,18 GNN,21 CPORT models, respectively. Opaque and transparent bars stand for models trained using random and scaffold splits, respectively. Bar outlines with the corresponding colors stand for the performance of the fine-tuned models. Orange and cyan error bars correspond to the standard deviation of the metrics for models trained using random and scaffold splits, respectively. Violet dashed lines correspond to the XGBoost models. | |
3 Conclusion
To conclude, in this study we demonstrated that structural information allows derivation of deep learning methods to predict the chromatographic retention time for small molecules, which are robust with respect to different chromatographic conditions. The proposed approach, dubbed CPORT, outperformed state-of-the-art neural network models in the elution order prediction problem on 28 and 36 out of 45 external RPLC benchmarks using the random and scaffold splits, respectively. CPORT supports domain adaptation with respect to various chromatographic conditions (both RPLC and HILIC), as we showed for 11 external and two in house datasets.
4 Methods
4.1 Training and test sets
We used the METLIN dataset of 80, 038 small molecules along with the retention time values (RTs) obtained from the reverse-phased chromatography experiment.18 Briefly, the pure standard materials for the 80, 038 molecules were analyzed in batches composed of mixtures of 100 molecules with different molecular weights by HPLC on an Agilent 1100/1200 series LC system coupled to a quadrupole-time of flight mass spectrometer G6538A using a Zorbax Extend-C18 reverse-phase column. During prepossessing, we discarded non-retained molecules with RT ≤ 200 seconds, the duplicated entries, most of which corresponded to stereoisomers, and molecules for which we could not generate feasible 3D conformers, resulting in 77, 318 compounds. We also discarded molecules that do not fit into the 20 Å × 20 Å × 20 Å cube, as they are too large for our method (see below). To train and validate the deep learning model, we used 4-fold cross-validation with the random split (57, 988 and 19, 330 small molecules for training and validation, respectively) similarly to the existing methods,18,21 and the scaffold split with the same ratio. The scaffold splits were obtained using the DeepChem Library28 with additional shuffling in order to achieve more similar distributions between the train and test partitions (see Fig. S9†). Further to evaluate the generalization ability of the derived models, we considered 9 HILIC and 87 RPLC datasets corresponding to different chromatographic conditions retrieved from the PredRet database.29 We discarded datasets with inconsistencies between the molecular names and molecular formulae or containing less than 50 molecules, after removing duplicates and molecules with molecular weights greater than 900 daltons, resulting in 45 RPLC and 9 HILIC datasets (see Table S4†). Additionally we collected two in-house datasets of 499 small molecules (drugs and pesticides) to evaluate the model with commercially available standards or standard mixtures (Sigma-Aldrich, Agilent Technologies Inc.). For this, we measured the RT values using an ACQUITY UPLC system (Waters Corp.) coupled with a QExactive Orbitrap mass spectrometer (Thermo Scientific Inc.). Separation was achieved on the ACQUITY UPLC BEH C18 column (2.1 × 100 mm, 1.7 μ, Waters Corp.) and ACQUITY UPLC BEH C8 column (2.1 × 100 mm, 1.7 μ, Waters Corp.) with the following gradient: 5% mobile phase B at 0–5 min, 5% to 75% mobile phase B at 5–25 min, 75% to 100% mobile phase B at 25–26 min, 100% mobile phase B at 26–33 min, 100% to 5% mobile phase B at 33–35 min and 5% mobile phase B at 35–40 min. The flow rate was set at 0.4 mL min−1. Water and acetonitrile with the addition of 0.1% formic acid were used as mobile phases A and B respectively. Chromatograms were processed via the peak picking approach, and the compounds were confirmed by using accurate mass and fragmentation spectra.
4.2 3D conformers
For each molecule in a dataset, we generated the 3D conformers with RDKit30 based on the experimental-torsion knowledge distance geometry (ETKDG) algorithm.30,31 More precisely, we converted SMILES into the RDKit molecule objects and explicitly added hydrogens to heavy atoms. Then for each molecule we generated eight conformers using ‘EmbedMultipleConfs’ utility of RDKit's ‘AllChem’ module, and we kept conformer with the lowest energy estimated with the universal force field.32 We repeated this procedure to obtain up to four different conformers for each molecule. In addition, we generated conformations using molecular dynamics simulations in Gromacs,33 as it follows. Firstly, we converted molecules from sdf to mol2 formats using the AmberTools20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 antechamber package, that assigns atom types according to GAFF2 (General Amber Force Field),35,36 and calculated the partial charges on each atom, using the AM1-BCC37 semi-empirical algorithm. Next, we generated the frcmod files using the AmberTools20 prmchk2 package; we discarded molecules, for which these procedures failed. The water molecules were prepared in the same manner. This was followed by the parameterization of molecules in GAFF2 in water using the AmberTools20 tleap package, resulting in the prmtop topology files; we converted the AmberTools20's prmtop files to the Gromacs's top files using the parmed package.38 The pdb files of water and solute simulation boxes were generated using the packmol software.39 The solute was fixed in the center of the box, and then the box was packed with solvent molecules to circumvent water density of 1.0 g mL−1. Note that we did not intend to mimic real chromatographic conditions, such as composition of the mobile phase, but to explore if using of more comprehensive conformation generation pipeline could boost the model's performance. Given that eluent compositions used in RP and HILIC mostly contain water as a weak or strong eluent component, we chose water as a solvent for the MD simulations. We set the box size to 40 Å × 40 Å × 40 Å, such that the distance from any solute atom is at least 10 Å to any point on the box boundary for all the molecules in the dataset. Given the top and pdb files for every molecule in water, we run molecular dynamics simulations in Gromacs according to the standard pipeline: the energy minimization (EM) was performed (using the steepest descent algorithm with the force limit of 10 kJ mol−1 nm−1), followed by the NVT run (300 K, 100 ps), the NPT (i.e. isothermal-isobaric ensemble) run (300 K, 100 ps), and the MD production run (300 K, 1 ns with 2 fs step size). Finally, we centered the obtained molecular trajectory frames around the solute molecules using the Gromacs's gmx trjconv utility, and selected four (out of 21 stored frames) the most dissimilar frames in terms of pair-wise RMSD calculated with the mdanalysis package.40 It is important to note that the conformer generation with RDKit is very fast, allowing large-scale molecule screening. Indeed, generation of one conformer with RDKit using a single CPU takes ∼0.3 seconds. On the other hand, conformation generation with molecular dynamics is much slower: on average 1 nanosecond of simulation took ∼15 seconds per molecule using eight CPUs. Also note that RDKit is more fail-safe compared to the MD pipeline: we could not generate conformations for only 43 molecules with RDKit and for 490 molecules with MD.
34 antechamber package, that assigns atom types according to GAFF2 (General Amber Force Field),35,36 and calculated the partial charges on each atom, using the AM1-BCC37 semi-empirical algorithm. Next, we generated the frcmod files using the AmberTools20 prmchk2 package; we discarded molecules, for which these procedures failed. The water molecules were prepared in the same manner. This was followed by the parameterization of molecules in GAFF2 in water using the AmberTools20 tleap package, resulting in the prmtop topology files; we converted the AmberTools20's prmtop files to the Gromacs's top files using the parmed package.38 The pdb files of water and solute simulation boxes were generated using the packmol software.39 The solute was fixed in the center of the box, and then the box was packed with solvent molecules to circumvent water density of 1.0 g mL−1. Note that we did not intend to mimic real chromatographic conditions, such as composition of the mobile phase, but to explore if using of more comprehensive conformation generation pipeline could boost the model's performance. Given that eluent compositions used in RP and HILIC mostly contain water as a weak or strong eluent component, we chose water as a solvent for the MD simulations. We set the box size to 40 Å × 40 Å × 40 Å, such that the distance from any solute atom is at least 10 Å to any point on the box boundary for all the molecules in the dataset. Given the top and pdb files for every molecule in water, we run molecular dynamics simulations in Gromacs according to the standard pipeline: the energy minimization (EM) was performed (using the steepest descent algorithm with the force limit of 10 kJ mol−1 nm−1), followed by the NVT run (300 K, 100 ps), the NPT (i.e. isothermal-isobaric ensemble) run (300 K, 100 ps), and the MD production run (300 K, 1 ns with 2 fs step size). Finally, we centered the obtained molecular trajectory frames around the solute molecules using the Gromacs's gmx trjconv utility, and selected four (out of 21 stored frames) the most dissimilar frames in terms of pair-wise RMSD calculated with the mdanalysis package.40 It is important to note that the conformer generation with RDKit is very fast, allowing large-scale molecule screening. Indeed, generation of one conformer with RDKit using a single CPU takes ∼0.3 seconds. On the other hand, conformation generation with molecular dynamics is much slower: on average 1 nanosecond of simulation took ∼15 seconds per molecule using eight CPUs. Also note that RDKit is more fail-safe compared to the MD pipeline: we could not generate conformations for only 43 molecules with RDKit and for 490 molecules with MD.
4.3 Voxelization
To obtain fixed-sized tensor-based representation of molecules, we voxelized each 3D conformer using HTMD,41 resulting in 40 × 40 × 40 voxels, where each voxel corresponds to the 0.5 × 0.5 × 0.5 Å−3 cube. The center of the voxel grid corresponds to the geometrical center of a 3D conformer. We observed that most of the small molecules in datasets fit into such a grid; note, however, that this restricts our method towards the molecules less than 20 angstroms in size. A voxel stores seven channels corresponding to the physicochemical properties of small molecules (hydrophobicity, aromaticity, h-bond donor, h-bond acceptor, positive ionizable, negative ionizable, and occupancy) of the nearest to the voxel's center atom according to:| | 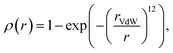 | (1) |
where rVdW is the van der Waals radius of the corresponding atom.
4.4 Neural network architecture
We used the 3D analog of the ResNet18 neural network architecture42,43 with added stacked dense layers. More precisely, the neural network comprises 17 convolutional blocks with skip connections between each two consecutive blocks (see Fig. S1†). The skip connections mitigate the vanishing gradient problem and effectively preserve low-level semantic features extracted from the input. Then the flattened output is fed to five stacked dense layers with 1000, 500, 200, 100, and 1 neurons. We also tested the SqueezeNet44 and CNN architectures with no skip-connections but obtained inferior performance, compared to the 3D ResNet18 analog; stacking more dense layers neither improves the model. We used the RMSprop optimizer45 with the decaying learning rate, the mean squared error (MSE) and boxed mean squared error(bMSE) as the loss functions, the batch size of 128, the number of epochs 240, the ReLU activation function for all, but the last layer, and the L2 regularization of the dense layers, but the last one. For the transfer learning the number of epochs was set to 60.| | 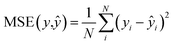 | (2) |
| | 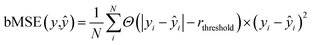 | (3) |
where Θ(x) is the Heaviside step function which equals one only if x is positive, otherwise zero; rthreshold – is the error threshold introduced to not penalize predicted retention times close to the experimental values. It has been noticed that 3D CNNs are not invariant with respect to the input orientation of a molecule, and to improve the robustness of a model, it is possible to augment the input with rotated molecules.46 Accordingly, each step during training, we randomly oriented voxel grids, and for the testing, we averaged the predicted retention times over 24 possible orientations of the input voxel grid.47 We observed ∼10(1.6%) seconds improvement in the RT prediction due to random orientation during training and ∼1.5(0.3%) seconds additional improvement due to the averaging over the 24 predictions corresponding to different grid orientations. To evaluate the robustness with respect to the different conformations of a molecule, we calculated the normalized standard deviation from the predictions obtained for four different conformers of each molecule m in the train and test sets:| | 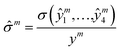 | (4) |
where σ is the standard deviation, and y and ŷi are true and predicted values, respectively. For most of the molecules the calculated ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e111.gif) m < 0.02, and only for 72 and 27 molecules for the train and test sets, respectively,
m < 0.02, and only for 72 and 27 molecules for the train and test sets, respectively, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e111.gif) m > 0.1 (see Fig. S7†). Note that we used averaged RT values over 4 conformers for each molecule, as the final predictions.
m > 0.1 (see Fig. S7†). Note that we used averaged RT values over 4 conformers for each molecule, as the final predictions.
In addition, we tested if the orientation along the principal axis could help increase the model's accuracy but observed slightly inferior performance compared to the best model.
For comparison we used the fully connected deep neural network (DNN)18 and the graph neural network(GNN).21 Briefly, the DNN relies on the extended connectivity fingerprints(ECFP)26 calculated by RDKit30 as on the feature vectors. The feature vectors are fed into five stacked dense layers with 1000, 500, 200, 100 and 1 neurons. All but the last dense layer has a ReLU function as an activation function. The model was trained for 20 epochs with a batch size of 35. The mean squared error with the L2 regularization term (α = 0.0001) was used as a loss function. The Adam optimizer with a learning rate of 0.01 was used for training. For transfer learning the number of epochs was only 5.
As for the GNN, it relies on molecular graph G with corresponding adjacency matrix A and pre-computed node features xv. The first stage consists of T = 6 steps of updating the hidden states htv of each node gathering the information from the neighbouring atoms. At step zero hv equals xv and then it is updated according to the following equation:
| | | ht+1v = htv + F(Wthtv) × A, | (5) |
where
Wt is a matrix on step
t with learnable coefficients and
F is the ReLU activation function. Once updating is finished the resulting hidden vector of a molecular graph is computed by summation of hidden states of all nodes:
| | 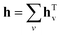 | (6) |
Then the hidden vector of a graph(h) is fed to 6 stacked dense layers with 48 neurons with ReLU as an activation function. Finally, the resultant vector is fed to the last layer with 1 neuron and with the linear activation function. For training and transfer learning of DNN and GNN we used the source code provided by authors.
We also trained XGBoost models for eleven external and two in-house datasets, as it follows. Firstly, we calculated physicochemical descriptors for the molecules using RDKit30 to form the feature vectors (see Table S6†). Then for each dataset we used the same train-test partition, as for the transfer learning approach. Next, for every dataset we dropped correlated (Pearson's correlation coefficient is larger than 0.95) and constant features based on the train set. In the next step we used 4-fold cross-validation in order to find optimal hyperparameters for the XGBoost regression model (see Table S7†). Finally, we trained separate models for each dataset with the corresponding optimal parameters and evaluated its performances on the test sets. To evaluate a model, we used the mean absolute error, the mean absolute percentage error, the median absolute error, the median absolute percentage error, and Spearman's rank correlation coefficient as the performance metrics:
| | 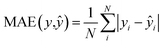 | (7) |
| | 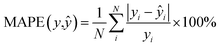 | (8) |
| | | MedAE(y,ŷ) = median(|y1 − ŷ1|,…,|yN − ŷN|) | (9) |
| | 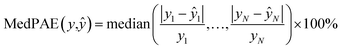 | (10) |
| | 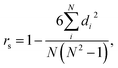 | (11) |
where
di is the difference between the two ranks of each observation. When comparing two models we defined substantial difference in their performance, if [
μ1 −
σ1,
μ1 +
σ1] ∩ [
μ2 −
σ2,
μ2 +
σ2] =
∅, where
μ and
σ are the mean and standard deviation corresponding to the 4-fold cross-validation metrics and on par performance, otherwise.
4.5 Best model selection
It is important to note that a molecule can adopt different conformations; thus, a method used to generate conformers is essential. Moreover, the lowest energy conformations in different media, for example, water and vacuum, can differ dramatically. To investigate the influence of the conformation generation on the model's performance, we compared the performance metrics on a model trained on “vacuum” conformations, generated with RDKit, and a model trained on “water” conformations, generated with full-atom molecular dynamics. Interestingly, the models trained on the RDKit conformations showed better performance, which could be explained by the less feasible conformations of the hydrophobic molecules formed in water, compared to the RDKit conformations (see Fig. S3†). We also tested if adding several different conformations of the same molecule would improve the performance. Finally, to consider the non-zero experimental error of the true RT values, we introduced a modification of mean squared error, such that there is no penalty for errors below a certain threshold. Overall, we varied: (i) the number of conformations per molecule (1, 2, or 4), (ii) the conformation generator (RDkit or molecular dynamics in water), (iii) initial orientation (random or aligned along the principal axes), and (iv) allowed errors with respect to the experimental value (15 and 45 seconds), resulting in 24 different models (Table S2† lists the performance for each tested model). We also performed the ablation study by removing each of the channels from the input. We observed drop in the performance metrics for all the cases, indicating that each channel positively contributes to the final model (see Table S5†). Interestingly, removal of the h-bond acceptor channel or the aromatic channel provided the largest impact on the performance metrics. The drop in terms of the MAE (MAPE) and MedAE (MedAPE) is 27 (2.8%) and 23 (3.2%) for the h-bond acceptor channel, and 26 (3.4%) and 25 (3.2%) for the aromatic channel. The best model was trained using 2 randomly rotated conformations generated by RDKit and the box mean squared error with 15s rthreshold, resulting in the mean and median errors of 43(5.4%) and 28 (3.5%), respectively.
Data availability
The source code required to reproduce the results presented in this work can be obtained at https://github.com/i-Molecule/cport. The web-server implementation of the CPORT pipeline is available at https://sites.skoltech.ru/imolecule/tools/cport.
Author contributions
M. Z., P. P. – formal analysis, investigation, validation; M. Z., I. B., P. P. – data curation, methodology, software; S. O., Y. K., and E. N. – validation, resources, P. P. – conceptualization, project administration, supervision; all authors – writing manuscript.
Conflicts of interest
There are no conflicts to declare.
References
-
D. van Herwerden, B. W. Pirok and P. J. Schoenmakers, Analytical Techniques in the Oil and Gas Industry for Environmental Monitoring, 2020, pp. 225–258 Search PubMed.
-
B. D. Ahrens, B. Starcevic and A. W. Butch, in LC-MS in Drug Analysis, Springer, 2012, pp. 115–128 Search PubMed.
-
G. Yagihashi, T. Tarui, H. Miyagi, H. Ohnishi, T. Watanabe and Y. Yamaguchi, Acute medicine & surgery, 2020, vol. 7, p. e487 Search PubMed.
-
R. Ardrey, Liquid Chromatography – Mass Spectrometry: An Introduction, 2003 Search PubMed.
- R. Malviya, V. Bansal, O. P. Pal and P. K. Sharma, J. Global Pharma Technol., 2010, 2, 22–26 CAS.
- C. Bryant, A. Adam, D. Tayior and R. Rowe, Anal. Chim. Acta, 1994, 297, 317–347 CrossRef CAS.
- O. Coskun, North. Clin. Istanb., 2016, 3, 156 Search PubMed.
- E. Bach, S. Szedmak, C. Brouard, S. Böcker and J. Rousu, Bioinformatics, 2018, 34, i875–i883 CrossRef CAS PubMed.
- L. Bijlsma, R. Bade, A. Celma, L. Mullin, G. Cleland, S. Stead, F. Hernandez and J. V. Sancho, Anal. Chem., 2017, 89, 6583–6589 CrossRef CAS PubMed.
- S. Osipenko, I. Bashkirova, S. Sosnin, O. Kovaleva, M. Fedorov, E. Nikolaev and Y. Kostyukevich, Anal. Bioanal. Chem., 2020, 412, 7767–7776 CrossRef CAS PubMed.
- L. Moruz, D. Tomazela and L. Käll, J. Proteome Res., 2010, 9, 5209–5216 CrossRef CAS.
- B. Lei, S. Li, L. Xi, J. Li, H. Liu and X. Yao, J. Chromatogr. A, 2009, 1216, 4434–4439 CrossRef CAS PubMed.
- M. Song, C. M. Breneman, J. Bi, N. Sukumar, K. P. Bennett, S. Cramer and N. Tugcu, J. Chem. Inf. Comput. Sci., 2002, 42, 1347–1357 CrossRef CAS PubMed.
- F. Luan, C. Xue, R. Zhang, C. Zhao, M. Liu, Z. Hu and B. Fan, Anal. Chim. Acta, 2005, 537, 101–110 CrossRef CAS.
- J. Chen, T. Yang and S. M. Cramer, J. Chromatogr. A, 2008, 1177, 207–214 CrossRef CAS PubMed.
- P. J. Eugster, J. Boccard, B. Debrus, L. Bréant, J.-L. Wolfender, S. Martel and P.-A. Carrupt, Phytochemistry, 2014, 108, 196–207 CrossRef CAS PubMed.
-
NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. Linstrom and W. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 2021 Search PubMed.
- X. Domingo-Almenara, C. Guijas, E. Billings, J. R. Montenegro-Burke, W. Uritboonthai, A. E. Aisporna, E. Chen, H. P. Benton and G. Siuzdak, Nat. Commun., 2019, 10, 1–9 CrossRef PubMed.
- C. Ma, Y. Ren, J. Yang, Z. Ren, H. Yang and S. Liu, Anal. Chem., 2018, 90, 10881–10888 CrossRef CAS PubMed.
- G. Rosenberger, C. C. Koh, T. Guo, H. L. Röst, P. Kouvonen, B. C. Collins, M. Heusel, Y. Liu, E. Caron and A. Vichalkovski,
et al.
, Sci. Data, 2014, 1, 1–15 Search PubMed.
- Q. Yang, H. Ji, H. Lu and Z. Zhang, Anal. Chem., 2021, 93, 2200–2206 CrossRef CAS PubMed.
- E. S. Fedorova, D. D. Matyushin, I. V. Plyushchenko, A. N. Stavrianidi and A. K. Buryak, J. Chromatogr. A, 2021, 462792 Search PubMed.
- R. P. Sheridan, J. Chem. Inf. Model., 2013, 53, 783–790 CrossRef CAS PubMed.
- G. W. Bemis and M. A. Murcko, J. Med. Chem., 1996, 39, 2887–2893 CrossRef CAS PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley and M. Mathea,
et al.
, J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef CAS.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
-
T. Chen and C. Guestrin, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 2016, pp. 785–794 Search PubMed.
-
B. Ramsundar, P. Eastman, P. Walters, V. Pande, K. Leswing and Z. Wu, Deep Learning for the Life Sciences, O'Reilly Media, 2019 Search PubMed.
- J. Stanstrup, S. Neumann and U. Vrhovsek, Anal. Chem., 2015, 87, 9421–9428 CrossRef CAS PubMed.
-
G. Landrum, rdkit/rdkit: 2021_03_3 (Q1 2021) Release, 2021, DOI:10.5281/zenodo.4973812.
- S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574 CrossRef CAS.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
-
Gromacs, https://www.gromacs.org/ Search PubMed.
-
AmberTools20, https://ambermd.org/AmberTools.php Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- D. Vassetti, M. Pagliai and P. Procacci, J. Chem. Theory Comput., 2019, 15, 1983–1995 CrossRef CAS.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS.
- M. R. Shirts, C. Klein, J. M. Swails, J. Yin, M. K. Gilson, D. L. Mobley, D. A. Case and E. D. Zhong, J. Comput.-Aided Mol. Des., 2017, 31, 147–161 CrossRef CAS.
-
Packmol, https://www.ime.unicamp.br/martinez/packmol/userguide.shtml Search PubMed.
-
R. J. Gowers, M. Linke, J. Barnoud, J. Tyler. E. Reddy, M. N. Melo, S. L. Seyler, D. Jan, D. L. Dotson, S. Buchoux, I. M. Kenney and B. Oliver, Proceedings of the 15th Python in Science Conference, 2016, pp. 98–105 Search PubMed.
- S. Doerr, M. Harvey, F. Noé and G. De Fabritiis, J. Chem. Theory Comput., 2016, 12, 1845–1852 CrossRef CAS PubMed.
-
K. He, X. Zhang, S. Ren and J. Sun, Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778 Search PubMed.
-
T. He, Z. Zhang, H. Zhang, Z. Zhang, J. Xie and M. Li, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 558–567 Search PubMed.
-
F. N. Iandola, S. Han, M. W. Moskewicz, K. Ashraf, W. J. Dally and K. Keutzer, 2016, arXiv preprint arXiv:1602.07360.
-
Hinton's lectures, https://www.cs.toronto.edu/tijmen/csc321/slides/lecture_slides_lec6.pdf Search PubMed.
- I. Kozlovskii and P. Popov, Commun. Biol., 2020, 3, 1–12 CrossRef PubMed.
- D. V. Zankov, M. Matveieva, A. V. Nikonenko, R. I. Nugmanov, I. I. Baskin, A. Varnek, P. Polishchuk and T. I. Madzhidov, J. Chem. Inf. Model., 2021, 4913–4923 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Sergey
Osipenko
,
Sergey
Osipenko
 ,
Yury
Kostyukevich
,
Evgeny
Nikolaev
and
Petr
Popov
,
Yury
Kostyukevich
,
Evgeny
Nikolaev
and
Petr
Popov
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RTs measured under specific chromatographic conditions and applied for 47 datasets corresponding to different chromatographic conditions, we observed a strong positive correlation (|rs| > 0.5) between the predicted and measured retention times for 30 experiments. CPORT is fast enough both for the fine-tuning, allowing absolute RT value prediction, and for the large-scale screening of small molecules.
000 RTs measured under specific chromatographic conditions and applied for 47 datasets corresponding to different chromatographic conditions, we observed a strong positive correlation (|rs| > 0.5) between the predicted and measured retention times for 30 experiments. CPORT is fast enough both for the fine-tuning, allowing absolute RT value prediction, and for the large-scale screening of small molecules.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chemicals (NIST17) and publicly available dataset of ∼80
000 chemicals (NIST17) and publicly available dataset of ∼80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chemicals (METLIN18) for the gas and reversed-phase liquid chromatography, respectively, let alone the peptide-specific dataset of ∼140
000 chemicals (METLIN18) for the gas and reversed-phase liquid chromatography, respectively, let alone the peptide-specific dataset of ∼140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 peptides.19,20 These opened opportunities to apply deep learning approaches to predict RTs; the first fully connected neural network (DNN) trained on the molecular fingerprint representation of small molecules from METLIN showed 6.8% and 4.5% mean and median absolute percentage errors, respectively.18 Finally, 1D and graph convolutional neural networks, that do not rely on hand-crafted features, demonstrated superior performance compared to the classical deep learning approach.21,22 In this study we present the first structure-based deep learning approach, that directly relies on 3D atomic coordinates for RT prediction of small molecules, which is robust with respect to various chromatographic conditions. Our approach, dubbed CPORT (Conformation-based Prediction Of Retention Time), operates with 3D chemical structures as with 3D images, namely, a 40 × 40 × 40 voxel grid representation of a molecule, comprising information about physicochemical properties of a molecule in seven different channels. We demonstrated that CPORT learns relevant information about the chromatography, rather than overfit to the training set, by directly applying it to 47 RPLC chromatography experiments, including two in-house RT measurements of ∼500 drug-like molecules. For 30 out of 47 experiments, we observed a positive correlation between the predicted and measured retention times, outperforming the state-of-the-art counterparts. Finally, we showed that CPORT is applicable to predict RTs for various chromatographic conditions by means of transfer learning. CPORT is fast and suitable for the large-scale predictions of RTs; more specifically, screening of 1
000 peptides.19,20 These opened opportunities to apply deep learning approaches to predict RTs; the first fully connected neural network (DNN) trained on the molecular fingerprint representation of small molecules from METLIN showed 6.8% and 4.5% mean and median absolute percentage errors, respectively.18 Finally, 1D and graph convolutional neural networks, that do not rely on hand-crafted features, demonstrated superior performance compared to the classical deep learning approach.21,22 In this study we present the first structure-based deep learning approach, that directly relies on 3D atomic coordinates for RT prediction of small molecules, which is robust with respect to various chromatographic conditions. Our approach, dubbed CPORT (Conformation-based Prediction Of Retention Time), operates with 3D chemical structures as with 3D images, namely, a 40 × 40 × 40 voxel grid representation of a molecule, comprising information about physicochemical properties of a molecule in seven different channels. We demonstrated that CPORT learns relevant information about the chromatography, rather than overfit to the training set, by directly applying it to 47 RPLC chromatography experiments, including two in-house RT measurements of ∼500 drug-like molecules. For 30 out of 47 experiments, we observed a positive correlation between the predicted and measured retention times, outperforming the state-of-the-art counterparts. Finally, we showed that CPORT is applicable to predict RTs for various chromatographic conditions by means of transfer learning. CPORT is fast and suitable for the large-scale predictions of RTs; more specifically, screening of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules took about 1 day on a single GPU.
000 molecules took about 1 day on a single GPU.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules (see Fig. S8†). Note, however, that such a large screen is possible only with a fast conformation generator, such as RDKit, that takes ∼0.3 seconds on a single CPU to produce conformers for a single molecule. As for the fine-tuning process, it took only ∼20 minutes to fine-tune the model using RT measurements for 1000 molecules on a single GPU (GeForce GTX 1080Ti). The web-server implementation of the CPORT pipeline is available at https://sites.skoltech.ru/imolecule/tools/cport, and the source code to fine-tune CPORT on a custom dataset is available at https://github.com/i-Molecule/cport.
000 molecules (see Fig. S8†). Note, however, that such a large screen is possible only with a fast conformation generator, such as RDKit, that takes ∼0.3 seconds on a single CPU to produce conformers for a single molecule. As for the fine-tuning process, it took only ∼20 minutes to fine-tune the model using RT measurements for 1000 molecules on a single GPU (GeForce GTX 1080Ti). The web-server implementation of the CPORT pipeline is available at https://sites.skoltech.ru/imolecule/tools/cport, and the source code to fine-tune CPORT on a custom dataset is available at https://github.com/i-Molecule/cport.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 antechamber package, that assigns atom types according to GAFF2 (General Amber Force Field),35,36 and calculated the partial charges on each atom, using the AM1-BCC37 semi-empirical algorithm. Next, we generated the frcmod files using the AmberTools20 prmchk2 package; we discarded molecules, for which these procedures failed. The water molecules were prepared in the same manner. This was followed by the parameterization of molecules in GAFF2 in water using the AmberTools20 tleap package, resulting in the prmtop topology files; we converted the AmberTools20's prmtop files to the Gromacs's top files using the parmed package.38 The pdb files of water and solute simulation boxes were generated using the packmol software.39 The solute was fixed in the center of the box, and then the box was packed with solvent molecules to circumvent water density of 1.0 g mL−1. Note that we did not intend to mimic real chromatographic conditions, such as composition of the mobile phase, but to explore if using of more comprehensive conformation generation pipeline could boost the model's performance. Given that eluent compositions used in RP and HILIC mostly contain water as a weak or strong eluent component, we chose water as a solvent for the MD simulations. We set the box size to 40 Å × 40 Å × 40 Å, such that the distance from any solute atom is at least 10 Å to any point on the box boundary for all the molecules in the dataset. Given the top and pdb files for every molecule in water, we run molecular dynamics simulations in Gromacs according to the standard pipeline: the energy minimization (EM) was performed (using the steepest descent algorithm with the force limit of 10 kJ mol−1 nm−1), followed by the NVT run (300 K, 100 ps), the NPT (i.e. isothermal-isobaric ensemble) run (300 K, 100 ps), and the MD production run (300 K, 1 ns with 2 fs step size). Finally, we centered the obtained molecular trajectory frames around the solute molecules using the Gromacs's gmx trjconv utility, and selected four (out of 21 stored frames) the most dissimilar frames in terms of pair-wise RMSD calculated with the mdanalysis package.40 It is important to note that the conformer generation with RDKit is very fast, allowing large-scale molecule screening. Indeed, generation of one conformer with RDKit using a single CPU takes ∼0.3 seconds. On the other hand, conformation generation with molecular dynamics is much slower: on average 1 nanosecond of simulation took ∼15 seconds per molecule using eight CPUs. Also note that RDKit is more fail-safe compared to the MD pipeline: we could not generate conformations for only 43 molecules with RDKit and for 490 molecules with MD.
34 antechamber package, that assigns atom types according to GAFF2 (General Amber Force Field),35,36 and calculated the partial charges on each atom, using the AM1-BCC37 semi-empirical algorithm. Next, we generated the frcmod files using the AmberTools20 prmchk2 package; we discarded molecules, for which these procedures failed. The water molecules were prepared in the same manner. This was followed by the parameterization of molecules in GAFF2 in water using the AmberTools20 tleap package, resulting in the prmtop topology files; we converted the AmberTools20's prmtop files to the Gromacs's top files using the parmed package.38 The pdb files of water and solute simulation boxes were generated using the packmol software.39 The solute was fixed in the center of the box, and then the box was packed with solvent molecules to circumvent water density of 1.0 g mL−1. Note that we did not intend to mimic real chromatographic conditions, such as composition of the mobile phase, but to explore if using of more comprehensive conformation generation pipeline could boost the model's performance. Given that eluent compositions used in RP and HILIC mostly contain water as a weak or strong eluent component, we chose water as a solvent for the MD simulations. We set the box size to 40 Å × 40 Å × 40 Å, such that the distance from any solute atom is at least 10 Å to any point on the box boundary for all the molecules in the dataset. Given the top and pdb files for every molecule in water, we run molecular dynamics simulations in Gromacs according to the standard pipeline: the energy minimization (EM) was performed (using the steepest descent algorithm with the force limit of 10 kJ mol−1 nm−1), followed by the NVT run (300 K, 100 ps), the NPT (i.e. isothermal-isobaric ensemble) run (300 K, 100 ps), and the MD production run (300 K, 1 ns with 2 fs step size). Finally, we centered the obtained molecular trajectory frames around the solute molecules using the Gromacs's gmx trjconv utility, and selected four (out of 21 stored frames) the most dissimilar frames in terms of pair-wise RMSD calculated with the mdanalysis package.40 It is important to note that the conformer generation with RDKit is very fast, allowing large-scale molecule screening. Indeed, generation of one conformer with RDKit using a single CPU takes ∼0.3 seconds. On the other hand, conformation generation with molecular dynamics is much slower: on average 1 nanosecond of simulation took ∼15 seconds per molecule using eight CPUs. Also note that RDKit is more fail-safe compared to the MD pipeline: we could not generate conformations for only 43 molecules with RDKit and for 490 molecules with MD.
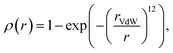
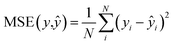
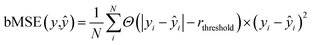
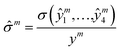
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e111.gif) m < 0.02, and only for 72 and 27 molecules for the train and test sets, respectively,
m < 0.02, and only for 72 and 27 molecules for the train and test sets, respectively, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e111.gif) m > 0.1 (see Fig. S7†). Note that we used averaged RT values over 4 conformers for each molecule, as the final predictions.
m > 0.1 (see Fig. S7†). Note that we used averaged RT values over 4 conformers for each molecule, as the final predictions.