A smile is all you need: predicting limiting activity coefficients from SMILES with natural language processing

Abstract

The knowledge of mixtures’ phase equilibria is crucial in nature and technical chemistry. Phase equilibria calculations of mixtures require activity coefficients. However, experimental data on activity coefficients are often limited due to the high cost of experiments. For an accurate and efficient prediction of activity coefficients, machine learning approaches have been recently developed. However, current machine learning approaches still extrapolate poorly for activity coefficients of unknown molecules. In this work, we introduce a SMILES-to-properties-transformer (SPT), a natural language processing network, to predict binary limiting activity coefficients from SMILES codes. To overcome the limitations of available experimental data, we initially train our network on a large dataset of synthetic data sampled from COSMO-RS (10 million data points) and then fine-tune the model on experimental data (20 870 data points). This training strategy enables the SPT to accurately predict limiting activity coefficients even for unknown molecules, cutting the mean prediction error in half compared to state-of-the-art models for activity coefficient predictions such as COSMO-RS and UNIFAC_Dortmund, and improving on recent machine learning approaches.

---

1 Introduction

With over 500 000 molecules registered even in the CAS common chemicals database,¹ the chemical design space of molecules is substantially larger than our capacity to measure their thermodynamic property data. This gap further increases when considering that properties usually depend on temperature and pressure, and even more for mixtures due to combinatorics and dependency on mixture composition. Binary activity coefficients are of particular interest in chemical engineering, as activity coefficients govern the phase equilibria in distillation and extraction, the key separations of many chemical processes. However, even large property databases, such as the Dortmund Datenbank (DDB), only hold experimental data for the activity coefficients of 31 000 binary systems, a tiny fraction of all possible molecular combinations.²

To overcome the inherent lack of experimental data, predictive thermodynamic property models have been developed over recent decades for many molecular properties, e.g., COSMO-RS,³ COSMO-SAC,⁴ SAFT-γ Mie,⁵ and UNIFAC.⁶ These models can predict thermodynamic properties with increasing accuracy and are therefore particularly beneficial for molecule mixtures with missing experimental data. However, despite the vital advantages of predictive thermodynamic models, these models come with shortcomings. For example, calculating the surface charges of molecules for COSMO models is time-consuming, whilst UNIFAC is limited to known functional groups parametrized to experimental data. Moreover, these physically based predictive models are still less accurate than experiments.⁷

Computationally efficient alternatives to physically based predictive models are data-driven models using machine learning. Machine learning is currently a rising topic in chemical engineering, as summarized in multiple recent reviews^8–10 that identify challenges in many areas such as optimal decision making, introduction and enforcing of physics, information and knowledge representation, and safety and trust.¹¹ The application of machine learning has also already led to recent advances in thermodynamic property prediction. Alshehri et al.¹² developed a data-driven model to predict 25 pure component properties based on a Gaussian process. The developed model surpasses classical group contribution models in accuracy. Chen et al.¹³ use a transformer-convolutional model to predict the sigma profiles of pure components with high accuracy.

To predict activity coefficients, matrix completion methods have been recently proposed that represent the limiting activity coefficient of binary mixtures as a matrix. In matrix completion methods, all mixtures are sorted into a solvent-by-solute matrix. Known mixtures are used to learn embeddings for each solvent/solute, which then can be used to fill the matrix by interpolating towards unknown combinations. Jirasek et al.¹⁴ proposed a matrix completion method to predict the limiting activity coefficients of binary mixtures at 298.15 K that exceeded the accuracy achieved by UNIFAC. Recently, Damay et al.¹⁵ extended the method of Jirasek et al.¹⁴ to capture temperature dependencies. The proposed model has a higher accuracy for the temperature-dependent prediction of limiting activity coefficients than UNIFAC. Chen et al.¹⁶ developed an approach to extend the UNIFAC-Il model¹⁷ for predicting limiting activity coefficients in ionic liquids by combining matrix completion with convolutional networks. These proposed approaches exceed the accuracy of the widely employed UNIFAC model in predicting limiting activity coefficients. Moreover, matrix completion approaches do not require any characterization of the molecules to train the model and predict thermodynamic properties, as the model solely learns from the correlations within the matrix. However, their lack of molecular characterization prevents matrix completion methods from extrapolating beyond the space of molecules available for training. Recently, Sanchez Medina et al.¹⁸ developed a graph neural network to predict limiting activity coefficients at constant temperature. In principle, this graph neural network is capable of extrapolating to unknown solvents and solutes, but the extrapolatory capabilities of the network were not tested. Thus, it is still unclear how well machine learning methods can extrapolate out of the realm of training data onto unknown solutes and solvents.

Here, we present a SMILES-to-property-transformer (SPT), a data-driven model with high accuracy for interpolation and extrapolation that can predict temperature-dependent limiting activity coefficients from nearly arbitrary SMILES, based on natural language processing and a transformer architecture.¹⁹ Due to their ability to learn structural relationships, transformer models have recently shown to be successful in predicting the pure component properties of various molecules and pharmaceuticals.^20,21 However, transformer models require large amounts of training data, which is typically unavailable for thermodynamic properties from experiments. To overcome the lack of experimental training data, we propose a two-step approach: first, the model is trained on a large amount of synthetic data from a physically based predictive model for limiting activity coefficients to convey the grammar of SMILES and the underlying physics of activity coefficients to the model. Second, the pretrained model is fine-tuned using available experimental data to improve accuracy and reduce the systematic errors of physically based predictive models. We compare the SPT model to state-of-the-art predictive thermodynamic models and ML approaches and demonstrate its high accuracy for predicting the temperature-dependent limiting activity coefficients of unknown molecules after fine-tuning.

2 Transformer-based method for thermodynamic property prediction

The SPT model predicts the temperature-dependent limiting activity coefficients of binary mixtures from the SMILES codes of the mixture components. For this purpose, we apply a transformer model. For machine learning, two major characteristics are vital for success: the model’s architecture and the training data. We first describe our model architecture (Section 2.1) and subsequently discuss the datasets used for training and validation of the model (Section 2.2), data augmentation (Section 2.3) and model parametrization (Section 2.4).

2.1 Architecture of the SMILES-to-property-transformer

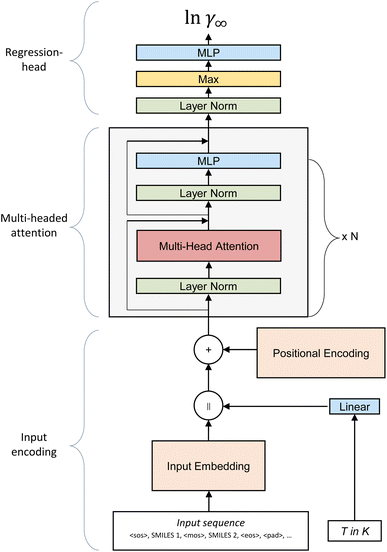
The SPT model is based on the transformer architecture developed by Vaswani et al.¹⁹ for natural language processing. Since its conception in 2017, the transformer architecture has proven to be applicable to many tasks beyond natural language processing, such as image generation or classification.^22,23 For molecular property prediction, the transformer model has been successfully applied to predict pure component properties for various pharmaceuticals by Lim and Lee²⁴ or generate novel molecules with specific target properties.²⁵ However, to the best of the authors’ knowledge, the transformer model has not yet been applied to predict the thermodynamic properties of binary mixtures.

As the backbone of the SPT, we adopt a GPT-3 architecture decoder-only transformer²⁶ as implemented by Karpathy²⁷ in MinGPT with changes to the input encoding and regression-head section of the model (Fig. 1). The GPT-3 architecture shows higher accuracy than, e.g., the transformer implementation of PyTorch,²⁸ most likely due to the use of a Post-LN transformer instead of a Pre-LN transformer.²⁹

Fig. 1 Architecture of the SPT to predict limiting binary activity coefficients from SMILES codes. The model takes the input sequence consisting of the SMILES of the solvent and solute and the temperature as input. In the input encoding section of the model, the information about the entering SMILES, the temperature and the position of tokens is all compiled into a single matrix. The multi-headed attention section performs the main work of the model by transmitting information between different parts of the molecules. The head section reduces the multidimensional output of the model to a single value.

2.1.1 Input encoding. Calculating the temperature-dependent limiting activity coefficients of a solute in a solvent requires information about the structure of both molecules and the temperature. In our model, the molecules are represented by SMILES codes. The simplified molecular-input line-entry system code, abbreviated to SMILES, was introduced in 1988 by Weininger³⁰ as a method to represent complex molecules in a single line of text. Since then, the SMILES code has been used in many applications and has developed into one of the standard ways to represent molecules. In SMILES, heavy atoms are represented as their periodic table symbol, e.g., C for carbon, while hydrogen atoms are implicitly assumed, e.g., ethane has the SMILES code CC. For single bonds, atoms are simply chained together, while double or triple bonds are represented by = and #, respectively. Branching arms of a molecule are contained within brackets, and for rings, numbers are used to show the joining points of a ring. Thus, the molecule 2-methyl phenol can be represented by the following SMILES: Oc1c(C)cccc1. Since SMILES essentially possesses a grammar to convey the structure of a molecule in a linear form, it can be understood by natural language processing. Thus, SMILES has shown to be a suitable input for deep learning models that predict molecular properties.^31,32

In the first step of our model, only the molecule’s structural information is passed to the model by constructing an input sequence from the SMILES of the solute and the solvent. Four special characters are used to signal (1) the start of the first molecule, <SOS>, (2) the middle between both molecules <MOS>, (3) the end of the second molecule <EOS>, and (4) the padding <PAD> to fill the input sequence to a fixed length of n_seq, e.g.:

<SOS>,SMILES_solute,<MOS>,SMILES_solvent,<EOS>,<PAD>,… (1)

Next, the input sequence is tokenized by assigning a number to each unique character of the SMILES code. In general, each token could be longer than a single character per encoding. However, a single character is used in this work for simplicity. Consequently, the vocab contains the following tokens: <SOS>, <MOS>, <EOS>, and <PAD>, characters that can be contained in a SMILES code adapted from Kim et al.²⁵ and a special token for water to clearly distinguish between pure water (SMILES “O”) and oxygen groups on hydrocarbons. Not all tokens included in the vocab are part of the molecules of our training data. Thus, the embedding of some tokens remains untrained in our final model. Including these untrained tokens makes the model easily expandable for more complex structures in later fine-tuning steps. However, evaluating SMILES that contain untrained tokens leads to unreliable results. The overall vocab and a list of trained and untrained tokens are available in ESI S1.†

After tokenizing the input sequence characterizing the solute and solvent, the input matrix X is constructed from the input sequence and the embedding matrix E. The embedding matrix E contains a learned vector of length d_emb for each token. The input matrix X is constructed by concatenating the embedding vectors belonging to the input tokens resulting in an n_seq × d_emb matrix. Next, temperature information is incorporated into the model by projecting the temperature into the embedding space via a linear layer and concatenating it to the right of the input matrix. Therefore, the input matrix size is expanded to n_seq+1 × d_emb. The input matrix now contains information about the tokens making up the molecules of the mixture and the temperature. At this stage, all tokens of the same type, e.g., ‘C’, are represented by the same token encoding, independent of their position in the molecule. However, information about the position of each token is crucial for the prediction of molecular properties. This positional information of the tokens is incorporated into the input matrix in the next step by adding the learned positional encoding matrix D of size n_seq+1 × d_emb to the input matrix X. As the vector in the first position of D is always added to the first token, the second vector of D to the second token, and so forth, these vectors can learn specific properties of their position over time and combine them with the token information. After the positional encoding is incorporated into the input matrix, it is passed to the transformer block, the heart of the model.

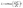2.1.2 Transformer block: multi-headed attention. In the transformer block, the inputs are normalized via a layer norm and then passed to the multi-headed attention block. On a high-level, multi-headed attention allows the model to move information from one token to another. For molecular property prediction, multiple attention-heads enable each attention-head’s attention to focus on different features. This attention mechanism can learn complex structures of molecules even when represented as a linear string. On a mathematical level, the output of a single attention-head i, Z_i, is defined as:with the query matrix Q_i, the key matrix K_i, and the value matrix V_i, and d_k = d_emb/n_head, where n_head is the number of attention-heads.

The query, key, and value matrices are calculated by multiplying the input matrix X with the learned matrices W_i^Q, W_i^k, and W_i^V. The matrices Q_i, K_i, and V_i have the size n_seq+1 × d_k. The product of Q_i and K_i can be interpreted as the relative importance of each token to another token. This result is normalized by the square root of the key dimension d_k and passed to a softmax function returning the attention from each token to each other token. The value matrix is then multiplied with the attention, leading to the matrix Z_i of size n_seq+1 × d_k, which contains for each token information of other tokens weighted by their importance.

The attention operation is repeated for each attention-head. The resulting output matrices Z_i of each attention operation are concatenated and projected to the input size of n_seq+1 × d_embvia a linear layer. Finally, the data are passed through a multilayer perceptron (MLP) layer containing a GeLu non-linearity, concluding the transformer block. In the first MLP layer, the size of the model is increased by a factor of four for the embedding dimension; the second linear layer of the MLP projects it back down to the input size. Residual connections connect the input and output of the attention and MLP block, including their respective layer norms. Multiple transformer blocks can be stacked consecutively to increase the depth of the model. In this work, we use two consecutive transformer blocks. For a more in-depth and visual explanation, the reader is referred to the blog of Alammar.³³

2.1.3 Regression-head. The output of the transformer blocks needs to be projected to a single value. This projection is performed in the last part of the model, the regression-head. The regression-head first applies a max function along the sequence dimension that reduces the size from n_seq+1 × d_emb to 1 × d_emb, followed by one MLP that reduces the size from 1 × d_emb to 1 × 1. The resulting single output value represents the molecular properties of interest, i.e., the limiting activity coefficient in our work.

2.2 Property data for training and validation

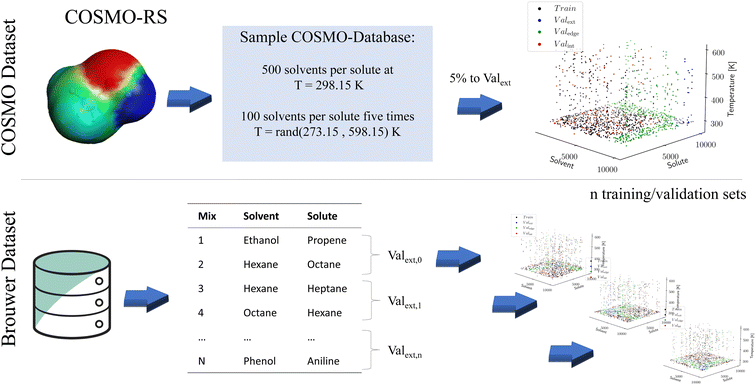
While machine learning models have proven to be powerful tools capable of astonishing predictions, their training requires large amounts of data. Such large amounts of data are typically unavailable for binary property data. Two options have emerged to pretrain language models for molecular property prediction: unsupervised pretraining is based on auto-translation tasks that first teach the models about the grammar of SMILES before property data are introduced in a subsequent step Honda 12.11.2019.³⁹ In contrast, supervised pretraining employs synthetic data Vermeire 2021.⁴⁰ To our knowledge, the relative performance of both approaches has not yet been compared. In this work, we follow the supervised approach and pretrain using synthetic data for the molecular properties of interest. Subsequently, we use experimental data for the fine-tuning of the model. The definition of the training and validation sets for pretraining and fine-tuning is shown in Fig. 2 and explained in the following section.

Fig. 2 Creation of the synthetic dataset from COSMO used for pretraining and sampling procedures for the experimental data from Brouwer used for fine-tuning. For the COSMO dataset, 5% of the solvents and solutes are removed from the training set constructing Val_ext, for which neither solvent nor solute is known, and Val_edge for which either solvent or solute is known. Furthermore, 5% of the remaining training data are sampled randomly and moved into the training set Val_int. Due to the smaller size of the Brouwer dataset, n-fold cross-validation is used. N mixtures are selected and moved into Val_ext,i, resulting in n = 1000 validation sets. The remaining mixtures are sorted into Val_edge,i and Train_i depending on the occurrence of their constitutes in Val_ext,i. Finally, 5% of mixtures are removed from Train_i to Val_int,i, and the set of all mixtures is reassessed.

2.2.1 Synthetic data for pretraining. For the pretraining of our model, we generate a large amount of synthetic data using the established thermodynamic model COSMO-RS.³ The advantage of COSMO-based models is that they can predict activity coefficients for arbitrary molecules from the molecular structure and are not limited to specific functional groups such as UNIFAC (Fredenslund et al.⁶). Thus, training data can be generated from a more diverse set of molecules, increasing the machine learning model’s ability to extrapolate. Furthermore, an extensive database and infrastructure to sample COSMO-RS are available from our previous work.³⁴

To generate the synthetic data, we use the COSMObase 2020 database. This database contains around 10 000 molecules resulting in more than 100 million possible binary combinations for solutes and solvents. Calculating activity coefficients for all combinations is computationally intractable. Thus, for each of the 10 000 solutes, 500 random solvents are sampled at a temperature of T = 298.15 K, resulting in around 5 million solvent/solute combinations. Furthermore, 100 of the 500 random solvents per solute are sampled at five random temperatures between 273.15 K and 598.15 K to provide temperature-dependent data. In total, around 10 million data points are sampled for pretraining, referred to as the COSMO dataset. We use the TZVDP-FINE parametrization and a maximum of 3 conformers for calculating the limiting activity coefficient of each data point.

To validate the performance of our machine learning model during the pretraining, the COSMO dataset is split into three validation sets. For this purpose, 5% of the solvents and solutes are initially removed from the training set (see Fig. 2). Crucially, preliminary tests showed that water cannot be entirely removed from the training set to ensure an accurate prediction for this notable molecule. Removing solvents and solutes from the training set enables the creation of two validation sets: first, a validation set containing the cross-section of the excluded solvent and solutes, where the training data contain neither the solvent nor the solute. This validation set tests the extrapolation accuracy of the model for entirely unknown solute/solvent combinations and is referred to as Val_ext. Second, a validation set is created where either solvent or solute is contained in the training set, but not both. This validation set tests the extrapolation capability of the model for one unknown molecule while the other one is known. Since the validation set tests the edge of known structures, we call it Val_edge. Finally, an additional 5% of the remaining solute–solvent combinations are randomly removed from the training set. If a solute–solvent combination exists for more than one temperature, the combination is removed for all temperatures. The resulting third validation set, so-called Val_int, tests the interpolation capabilities of the model when solvent and solute are known in other combinations but not in precisely this combination. This validation set is most comparable to the matrix completion approaches discussed earlier, where both mixture components have to be known.

2.2.2 Experimental data for fine-tuning. In the second step, the model pretrained on the COSMO dataset is fine-tuned to experimental data. To increase the reproducibility and accessibility of our model, we solely use publicly available data on limiting activity coefficients. Furthermore, using open-source experimental data enables an open benchmark to compare other methods.

To our knowledge, the largest publicly available dataset on limiting activity coefficients was published recently by Brouwer et al.³⁵. This dataset contains 77 173 limiting activity coefficients for various solute/solvent combinations and temperatures gathered from the literature. However, from the 77 173 data points, around 52 000 data points use ionic liquids or deep eutectic solvents as solvents and are thus excluded. Additionally, we excluded impure substances such as sunflower oil, solvents with specific phase orientations (nematic phase and isotropic phase), and uranium complexes. For 10 solvents/solutes, no SMILES code could be identified. Furthermore, some errors in the data by Brouwer et al.³⁵ were corrected, such as wrong exponents, ln γ^∞ instead of γ^∞, misclassification, or data entered in the wrong row. A list of all changes and an updated data table can be found in ESI S2.† Overall, 20 870 suitable data points are identified and used for the fine-tuning of our model. The resulting data set for the fine-tuning contains 349 solvents and 373 solutes in 6416 unique combinations in a temperature range from 250 K to 555.6 K. The distribution of the data in ln γ^∞ and T is shown in ESI S3.† In the following, the dataset is referred to as the Brouwer dataset.

To test the performance of the fine-tuning, again, three validation sets are defined as for the pretraining. Due to the much smaller amount of data available from experiments, n-fold cross-validation is used to determine the accuracy of the network. Due to the small sample size of a single validation set, this approach would be expected to have a high variance (Fig. 2). To construct the training and validation sets, all solute/solvent combinations without water are split into 1000 subsets, each constructing one Val_ext,i. The solute/solvent combinations not part of Val_ext,i are assigned either to the edge validation set Val_edge,i, or to the training set Train_i depending on whether one or none of the two components are part of the Val_ext,i. Subsequently, 5% of the training set Train_i is randomly sampled to yield the validation set Val_int,i used to test the interpolation capability. Finally, all data points are reassessed to determine whether they have to be moved to another validation set due to the removal of Val_int,i from Train_i. A large number of splits is required since to test for extrapolation both solvents and solutes must be excluded from the training set. Due to the uneven distribution of the training data, moving to many mixtures into the validation set Val_ext makes it very unlikely that common molecules such as ethanol or hexane ever appear in the training data as they are nearly always moved into Val_edge. If many of these common molecules are excluded from the training, the training data set becomes prohibitively small. For example, using 5 splits leaves only 500–600 of 21 000 data points remaining in the training set (2%).

Solvent–solute combinations with water are excluded from Val_ext,i for two main reasons: first, the unique nature of water makes it challenging to extrapolate water properties when only organic compounds are known within the training set. Second, we believe that applications are rare where the limiting activity coefficient of the unknown and unmeasured molecule water must be predicted. While water is excluded from the validation set Val_ext, the validation set Val_edge still contains combinations with water as a known solvent and an unknown organic solute, which we envisage as likely use-cases. The results for the validation set Val_int and Val_edge, including only combinations with water, are available in ESI S6.†

Due to the varying number of data points for each solute/solvent combination, the size of the training sets varies. The sizes range between 15 000 and 19 270 for Train, 6 and 69 for Val_ext, 640 and 5000 for Val_edge, and 640 and 1200 for Val_int.

2.3 Data augmentation

We increase the variety of the data provided to the model by generating up to 9 equivalent SMILES for each input molecule using the tool of Bjerrum.³⁶ During training, one of the resulting 10 SMILES is randomly selected each time an input sequence is constructed. Thus, during training, all different variations of the SMILES are shown to the model at some point. During validation, the initially assigned SMILES are used to increase reproducibility.

2.4 Training and hyperparameter tuning

Identifying good hyperparameters is vital for the performance of machine learning models. We select hyperparameters by conducting a manual scan on the COSMO dataset, considering the embedding size, number of attention-heads, number of attention layers, dropout, batch size, and learning rate. The loss function is fixed to mean-squared-error (MSE) loss. The Adam optimizer and cosine annealing with linear warmup are used as a learning rate schedule with a warmup time of 5 epochs. For the hyperparameter tuning, training was stopped after 20 epochs, while the final pretraining ran for 50 epochs. The model is trained in mixed precision with the PyTorch autocast function to reduce the training time. A detailed hyperparameter table is available in ESI S4.†

3 Results: predicting limiting activity coefficients

Our machine learning model STP is trained on synthetic and experimental data to predict limiting activity coefficients, as described in Section 2.2. In this section, we first introduce the results of the pretraining to synthetic data (Section 3.1). Then, we discuss the final results based on fine-tuning to experimental data (Section 3.2).

3.1 Pretraining

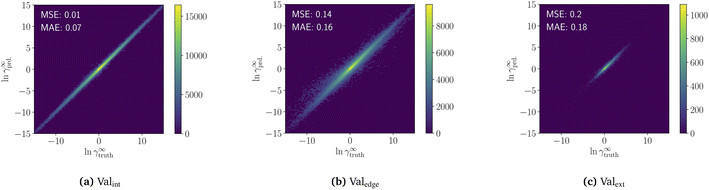
The pretraining of the model on the COSMO dataset takes 34 h on an RTX 2080 Ti. The resulting model predictions of the three validation sets are shown in a heatmap in Fig. 3. For interpolation (Val_int), the pretrained model achieves high accuracy with a mean-squared-error of MSE = 0.01 and a mean-absolute-error of MAE = 0.06. For edge extrapolation (Val_edge), the pretrained model has an MSE of 0.13 and MAE of 0.15, and for extrapolation (Val_ext), an MSE of 0.2 and an MAE of 0.18. The progression of validation and training loss during the pretraining is available in the ESI S5.†

Fig. 3 Heatmap of predicted limiting activity coefficients ln γ_pred.^∞vs. the validation data ln γ_COSMO.^∞ for the pretrained model in the three validation datasets Val_ext (a), Val_edge (b), and Val_int (c). Mean squared error (MSA) and mean average error (MAE) are shown in the top left corner of every diagram.

The result highlights the high interpolation and extrapolation capabilities of our pretrained model for predicting temperature-dependent limiting activity coefficients generated from COSMO-RS. Furthermore, the machine learning model is very fast, predicting around 3000 limiting activity coefficients per second on an RTX 2080 Ti without requiring precalculation of sigma surfaces. This high speed should remove property prediction as a bottleneck and allow for the exploration of larger spaces when searching for new components.

3.2 Fine-tuning

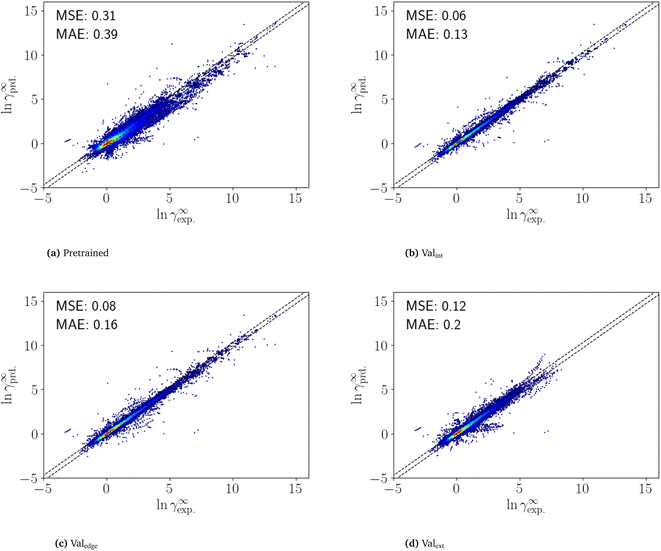
The fine-tuning was performed on an RTX 2080 Ti and took 6 min for an individual dataset and 100 h for all 1000 datasets. The high speed of fine-tuning one dataset enables fine-tuning with single datasets even without a GPU. Fine-tuning on a CPU is expected to be around 200 times slower, thus taking about 20 h to fine-tune one dataset.

To analyze the performance of the fine-tuned SPT model, the Brouwer dataset is first predicted using the pretrained model (Fig. 4a). The pretrained model achieves an MSE of 0.32 and MAE of 0.39, which is comparable to the accuracy of COSMO-RS for the same dataset (MSE 0.36 and MAE 0.38).

Fig. 4 Predicted vs. experimental limiting activity coefficients from the pretrained model (a), and for the fine-tuned models, Val_int (b),Val_edge (c) and Val_ext (d). For the fine-tuned model, multiple instances of the same molecule can occur in different iterations of Val_int,i and Val_edge,i. For this case, the mean of all predictions is shown.

The results of the n-fold cross-validation of the fine-tuned SPT are shown in Fig. 4. For interpolation (Val_int), the fine-tuned SPT archives an MSE of 0.06 and an MAE of 0.13 (Fig. 4b) and for edge extrapolation (Val_edge), an MSE of 0.08 and an MAE of 0.16 (Fig. 4c). Thus, the prediction of the fine-tuned SPT model for interpolation (Val_int) and edge extrapolation (Val_edge) is close to an experimental accuracy of between 0.1 and 0.2.¹⁵ However, this high accuracy is only achieved if at least one of the mixture components is included in the training set. Still, for the extrapolation (Val_ext), the MSE and MAE are only slightly higher with values 0.12 and 0.20, respectively (Fig. 4d). Notably, even in Val_ext, the SPT outperforms COSMO-RS (MSE_SPT 0.12 vs. MSE_COSMO-RS 0.36) (see Section 4).

The highest errors are mainly obtained for mixture compounds containing nitrogen and silicon. However, only a few data points are contained in the training data with molecules containing silicon. Thus, the prediction might improve with more training data. Overall, the fine-tuning improves the already high accuracy of the pretrained model for all validation sets, leading to a highly accurate prediction of temperature-dependent limiting activity coefficients. Some artifacts seen in Fig. 4 might also be the result of faulty measurements, as they come from few publications. More curated training and validation data thus might still improve prediction. The results highlight the advantages of combining synthetic and experimental data for predicting thermodynamic properties using deep learning.

4 Comparison to other models

To assess the performance of the SPT model discussed in Section 3, we benchmark our model against competing models from the literature. We first compare our model on temperature-dependent data with the predictive physical models COSMO-RS, UNIFAC, and the recent machine learning approach based on matrix completion by Damay et al.¹⁵ (Section 4.1). A comparison to COSMO-SAC implementations is available in ESI S7.† Subsequently, we compare the inter- and extrapolation capabilities of the SPT to the graph neural network by Sanchez Medina et al.¹⁸ on an isothermal dataset by Sanchez Medina et al.¹⁸ (Section 4.2). Following Damay et al.¹⁵, we use the percentage of data points with |Δln γ^∞| < 0.3 as our primary quality measure for the comparison. The percentage of data with |Δln γ^∞| < 0.3 as well as the mean average error (MAE) and mean squared error (MSE) are summarized in Table 1.

Table 1 Mean average error (MAE), mean square error (MSE), and the percentage of data with |Δln γ^∞| < 0.3 of the assessed models COSMO-RS, UNIFAC, Damay et al.,¹⁵ Sanchez Medina et al.,¹⁸ and the SPT on the common Brouwer and Medina datasets. For performance on all data points see ESI S9. Generally all models perform slightly worse when considering all datapoints with UNIFAC performing significantly worse. The model of Damay et al.¹⁵ does not include the MAE and MSE as they are not disclosed in the original publication, and the model is not available for reproduction

Dataset	Brouwer			Medina
Error	MAE	MSE	|Δln γ^∞| < 0.3	MAE	MSE	|Δln γ^∞| < 0.3
COSMO-RS	0.36	0.29	60.6%	0.31	0.23	64.5%
UNIFAC	0.35	0.45	63.9%	0.28	0.33	74.9%
Damay et al. (on DDB)	—	—	(76.6%)
Medinaext				0.47	0.52	51.1%
Medinaedge				0.28	0.20	67.7%
Medinaint				0.19	0.10	82.8%
SPText	0.17	0.09	85.8%	0.25	0.17	74.7%
SPTedge	0.13	0.06	92.5%	0.16	0.07	86.1%
SPTint	0.11	0.05	94.0%	0.13	0.05	92.5%

---

4.1 Comparison on the Brouwer dataset

For the comparison on the Brouwer dataset, we calculate all solute/solvent combinations of the Brouwer dataset available in COSMO-RS using the COSMO-RS database 2020 with TZVDP-fine parametrization and up to 3 conformers. For UNIFAC, we used the UNIFAC_Dortmund implementation by Bell and contributers³⁷ with 2019 parameters and UNIFAC groups by Müller.³⁸ For a consistent comparison, the results show only the 9625 combinations available in all compared sets, i.e., COSMO-RS database, UNIFAC, and Val_int, Val_edge, and Val_ext (Fig. 5a). For Val_int and Val_edge the mean of the n-fold validation is used for each mixture.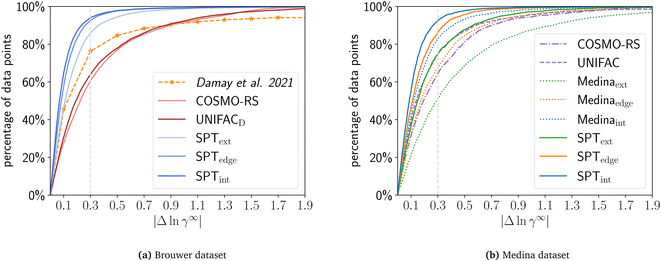

Fig. 5 Cumulative distribution of the prediction error for COSMO-RS, UNIFAC, SPT_ext, SPT_edge, SPT_int, Medina_ext, Medina_edge, and Medina_int using a common subset of the (a) Brower or (b) Medina dataset. For Val_edge and Val_int the mean of the n-fold cross-validation is used. Data for Damay et al.¹⁵ are approximated from their publication and were evaluated on a different dataset.

The physical models, UNIFAC and COMSO-RS, have very similar performance, with UNIFAC surpassing COSMO-RS slightly with 63.9% of data below an error of 0.3 compared to 60.5% for COSMO-RS on the common dataset. COSMO-SAC-based models perform substantially worse than COSMO-RS and UNIFAC (38% for COSMO-SAC₂₀₀₂ and 50% for COSMO-SAC_dsp, see ESI S7†). The SPT achieves higher accuracy than COSMO-RS and UNIFAC, even for extrapolation Val_ext: Val_ext predicts 85.8% of all data points with |Δln γ^∞| < 0.3 for the compared mixtures. The validation sets Val_int and Val_edge achieve even higher accuracies with |Δln γ^∞| < 0.3 for 94.0% and 92.5% of all combinations, respectively. While our ML model relies on the COSMO models to generate initial data for pretraining, the fine-tuning step on experimental data allows it to surpass the accuracy of the original COSMO models.

In a further analysis, we compare the SPT to the machine learning-based model from Damay et al.¹⁵. The authors use matrix completion and train the model to predict limiting activity coefficients from the commercial database DDB. The resulting model yields higher accuracy than the reference model UNIFAC for data taken from the DDB. The authors report that 76.6% of all data points are within |Δln γ^∞| < 0.3 when using leave-one-out validation. For qualitative comparison, the results of Damay et al. (Fig. 10 of Damay et al.¹⁵) are shown in Fig. 5a. This result is most comparable to our validation set Val_int (94.0% with |Δln γ^∞| < 0.3) since matrix completion only allows interpolation when both molecules are contained within the training. However, since the authors used another non-public dataset for training (DDB), these results are not directly comparable to our results. Comparing UNIFAC to both datasets, Damay et al. report a higher accuracy of UNIFAC on the DDB dataset than we obtain for UNIFAC on the Brouwer dataset (71% with |Δln γ^∞| < 0.3 for UNIFAC on DDB vs. 63% for Brouwer). This result can indicate that the data in the DDB are of better quality. Thus, SPT’s performance may be improved when fine-tuned on the DDB data.

In contrast to matrix completion, the SPT allows for extrapolating unseen and partly unseen solute/solvent combinations. The (edge) extrapolation capacity of our model indicates a high accuracy even if compared to the interpolation accuracy of the matrix completion model proposed by Damay et al.¹⁵ with 85.8% and 92.5% of all data points with |Δln γ^∞| < 0.3, respectively. While evaluation took place on different datasets and thus results are not directly comparable, these results still strongly suggest that the SPT can achieve higher accuracies in predicting limiting activity coefficients than matrix completion, though coming at a higher computational effort.

4.2 Comparison on the Medina dataset

Sanchez Medina et al.¹⁸ proposed a graph neural network for predicting limiting activity coefficients at 298.15 K. An extension for temperature dependency is proposed in the outlook but not yet available in the model. The authors tested the model using random splits, resulting in sets most comparable to our Val_int set. Thus, the extrapolation capabilities of the model proposed by Sanchez Medina et al.¹⁸ are unknown.

For a consistent comparison of the SPT model and the Medina model, we split the dataset from Sanchez Medina et al.¹⁸ (Medina dataset) into 200 training and validation sets according to our validation strategy discussed in Section 2.2.2. Subsequently, we train the Medina model and our model on the resulting 200 training sets (ESI S8†). Due to the lack of a test set to stop training and adjust the learning rate, we use the performance on Val_ext to set the learning rate and select the epoch with the lowest mean validation MSE out of the 200 training epochs across the 200 datasets for each validation set (Val_ext = 117, Val_edge = 135, and Val_int = 163). For the SPT, we use the performance at the final epoch (50) as previously. As in Section 4.1, for Val_int and Val_edge, the mean of the n-fold validation is calculated and used for each unique mixture. For the Medina model, training failed on the sets 87, 115, 149 and 182 for unknown reasons, and these sets are excluded.

The MSE and MAE of the Medina model on Val_int as calculated by us (MSE: 0.10 and MAE: 0.19) reproduce the MSE and MAE reported by Sanchez Medina et al.¹⁸ using random splitting (MSE: 0.10 and MAE: 0.18) (Table 1). This result indicates that random splitting results in a test set that is similar to our Val_int set and random splitting is thus not suitable to assess the extrapolation capabilities of models.

Fig. 5b shows the prediction error of COSMO-RS, UNIFAC_Dortmund, the Medina model, and the SPT model fine-tuned on the Medina dataset. The Medina dataset is reduced from 2810 mixtures to 2469 mixtures that all models can calculate.

The SPT generally outperforms the Medina model on all validation sets. For Val_int, 92.5% of the data points are with |Δln γ^∞| < 0.3 for the SPT compared to 82.8% for the Medina model. For Val_edge, 86.1% and 67.7%, and for Val_ext, 74.9% and 51.1% of data points are with |Δln γ^∞| < 0.3 for the SPT and the Medina model, respectively. The MAE of the SPT is about half the MAE of the Medina model for each validation set. Particularly, the vast difference in performance for (edge) extrapolation highlights the effective performance of the SPT when predicting new molecules. As for the Brouwer dataset (Section 4.1), the SPT outperforms COSMO-RS and UNIFAC on the Medina dataset even for extrapolation. Similarly, the Medina model outperforms COSMO-RS and UNIFAC for interpolation tasks, but performs similarly to COSMO-RS and worse than UNIFAC on edge extrapolation and is surpassed for extrapolation by both COSMO-RS and UNIFAC. Please note that it is very likely that UNIFAC parameters were fitted to mixtures contained in the Medina dataset, likely improving the UNIFAC performance for this dataset.

The results highlight the advantage of our pretraining on synthetic data to exploit scarce experimental data and extend the extrapolative abilities of our model. The obtained data-driven model shows a good understanding of molecular properties. Overall, the SPT performs slightly worse on the Medina dataset than on the Brouwer dataset, likely due to the smaller total amount of training data (2810 vs. 20 870). Therefore, we analyze the data scaling of our SPT model in more detail in Section 5.

In addition to the increased accuracy, our SPT model requires 45 s to fine-tune for 50 epochs on the Medina dataset, while the Medina model requires around 4 min for 50 epochs on an RTX 2080 Ti, even though the Medina model has much fewer parameters (21 000 vs. 6.5 million). The shorter training time can be vital if no GPU is available. However, the training time of the Medina model would likely be improved with the use of mixed-precision training, and the SPT requires lengthy pretraining before fine-tuning.

5 Data scaling of the model

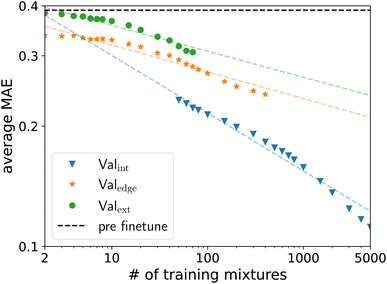
In Section 3, the SPT model was trained using on average 17 370 data points from the Brouwer dataset. Machine learning models are well known for increasing their performance with larger amounts of training data. Conversely, for many thermodynamic properties, less experimental data is available than for limiting activity coefficients. Thus, this section gives insight into SPT’s data scaling to estimate model improvements with larger datasets and the expected model performance when less experimental data is available for fine-tuning.

To determine the scaling of the fine-tuning of the SPT model, we create 200 training datasets, each containing n_train random unique solute/solvent combinations from the Brouwer dataset for n_train between 2 and 5000 solute/solvent combinations excluding water. The remaining solute/solvent combinations in the Brouwer dataset are then sorted into the validation sets Val_ext, Val_edge, and Val_int. For large numbers n_train, only a few solute/solvent combinations remain in Val_ext and Val_edge, since common molecules are likely to be included in the training dataset and thus necessarily excluded from the validation sets Val_ext and Val_edge. For example, for 5000 training mixtures, only 17 unique solute/solvent combinations remain in the validation set Val_ext, across all 200 training datasets. Moreover, many of the 200 training datasets do not have a single solute/solvent combination in the validation set Val_ext. This small number of solute/solvent combinations for the validation set Val_ext leads to high variance. Thus, we only consider validation sets Val_ext and Val_edge, where more than 17 500 of the 18 348 solute/solvent combinations are still present. The cutoff point is n_train = 80 for Val_ext and n_train = 500 for Val_edge. For Val_int the reverse is the case. Here, small n_train leads to unreliable results and thus, no n_train below 50 is considered.

The MAE of Val_ext and Val_edge decreases linearly with the size of the training dataset in the log–log space (Fig. 6). The MAE of Val_int decreases with a steeper slope, indicating that interpolation might be easier to learn. Furthermore, there is some indication the slope is increasing for even larger training sets. For the investigated training sizes, no saturation is visible in any validation set, indicating that the accuracy of the machine learning model still improves for increasing amounts of experimental data for fine-tuning. Following this prediction, between 10 000 and 20 000 solute/solvent combinations would be needed for training to reach an average MAE of lower than 0.15 for Val_ext, which is within experimental accuracy. The amount of required data would thus be smaller than the 31 000 unique solute/solvent combinations available in the commercial database DDB, indicating that high-quality prediction of limiting activity coefficients is in reach.

Fig. 6 Scaling behavior of SPT’s average MAE for the data sets Val_ext, Val_edge and Val_int as a function of available experimental data for fine-tuning. The solid line indicates the performance of the pretrained model without fine-tuning.

Even small amounts of experimental data used for fine-tuning lead to substantial improvements in the validation set Val_edge. The SPT should thus require only a few experimental data points for fine-tuning for accurate predictions around specific data points. The high performance of the SPT, even for limited experimental data available, originates from the pretraining to synthetic data, which enables learning the underlying grammar of the molecular representation and the physics provided by the predictive thermodynamic model used to generate the synthetic data. The capability of our model to accurately predict similar mixtures with only a few experimental data points could be used to guide experiments by measuring and predicting in tandem, narrowing down a target region.

6 Conclusions

One of the main roadblocks to the widespread application of deep learning in chemical engineering is the availability of training data. Particularly, for predicting thermodynamic mixture properties, often only a limited amount of experimental data is available. This work tackles the challenge of scarce data availability for thermodynamic property prediction based on deep learning by combining synthetic data with experimental data. For this purpose, we introduce a SPT model, which we pretrain to synthetic data generated using COSMO-RS and subsequently fine-tune the model using experimental data. Therefore, we achieve a highly accurate prediction of temperature-dependent limiting activity coefficients solely from SMILES codes.

The SPT machine learning model surpasses the accuracy of conventional predictive thermodynamic models such as COSMO-SAC, COSMO-RS, and UNIFAC and recently proposed machine learning approaches based on matrix completion and graph neural networks.

Combining synthetic data with scarce experimental data opens new possibilities for the training of deep learning models for thermodynamic property prediction. Even small amounts of experimental data points already lead to significant improvements in the prediction quality of the SPT. Furthermore, the main computational effort is in the pretraining of the model to synthetic data, while the fine-tuning is computationally efficient. The efficient fine-tuning opens up possibilities to combine deep learning with automated experiments, where a model is continuously refined with experimental data while providing predictions of new promising candidates to measure. Such workflows could generate machine learning models that are highly accurate in specific domains.

During the pretraining, the model builds an inherent understanding of molecules. Preliminary tests show that this understanding allows the model to learn molecular properties other than limiting activity coefficients with little experimental data. This flexibility could turn the SPT into a Swiss-army knife of molecular property prediction applicable to many tasks.

Data availability statement

Code: https://github.com/Bene94/SMILES2PropertiesTransformer

Datasets and trained models https://www.polybox.ethz.ch/

Author contributions

Benedikt Winter: conceptualization, data curation, formal analysis, investigation, methodology, visualization, writing – original draft, and writing – review & editing. Clemens Winter: conceptualization, methodology, resources, software, and writing – review & editing. Johannes Schilling: writing – review & editing, conceptualization, methodology, and supervision. André Bardow: writing – review & editing, conceptualization, methodology, supervision, resources, and funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was created as part of NCCR Catalysis (grant number 180544) a National Centre of Competence in Research funded by the Swiss National Science Foundation.

Notes and references

1. CAS, 2022, https://commonchemistry.cas.org/.
2. Dortmund Datenbank, 2022, https://www.ddbst.com/.
3. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
4. S.-T. Lin and S. I. Sandler, Ind. Eng. Chem. Res., 2002, 41, 899–913.
5. T. Lafitte, A. Apostolakou, C. Avendaño, A. Galindo, C. S. Adjiman, E. A. Müller and G. Jackson, J. Chem. Phys., 2013, 139, 154504.
6. A. Fredenslund, R. L. Jones and J. M. Prausnitz, AIChE J., 1975, 21, 1086–1099.
7. T. Brouwer and B. Schuur, Ind. Eng. Chem. Res., 2019, 58, 8903–8914.
8. A. S. Alshehri and F. You, Curr. Opin. Chem. Eng., 2022, 36, 100752.
9. M. Haghighatlari and J. Hachmann, Curr. Opin. Chem. Eng., 2019, 23, 51–57.
10. M. R. Dobbelaere, P. P. Plehiers, R. van de Vijver, C. V. Stevens and K. M. van Geem, Engineering, 2021, 7, 1201–1211.
11. A. M. Schweidtmann, E. Esche, A. Fischer, M. Kloft, J.-U. Repke, S. Sager and A. Mitsos, Chem. Ing. Tech., 2021, 93, 2029–2039.
12. A. S. Alshehri, A. K. Tula, F. You and R. Gani, AIChE J., 2021, 68(6), e17469.
13. G. Chen, Z. Song and Z. Qi, Chem. Eng. Sci., 2021, 246, 117002.
14. F. Jirasek, R. A. S. Alves, J. Damay, R. A. Vandermeulen, R. Bamler, M. Bortz, S. Mandt, M. Kloft and H. Hasse, J. Phys. Chem. Lett., 2020, 11, 981–985.
15. J. Damay, F. Jirasek, M. Kloft, M. Bortz and H. Hasse, Ind. Eng. Chem. Res., 2021, 60, 14564–14578.
16. G. Chen, Z. Song, Z. Qi and K. Sundmacher, AIChE J., 2021, 67, e17171.
17. S. Nebig and J. Gmehling, Fluid Phase Equilib., 2010, 294, 206–212.
18. E. I. Sanchez Medina, S. Linke, M. Stoll and K. Sundmacher, Digital Discovery, 2022, 1, 216–225.
19. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser and I. Polosukhin, Attention Is All You Need, 2017, https://arxiv.org/pdf/1706.03762.
20. Y. Rong, Y. Bian, T. Xu, W. Xie, Y. Wei, W. Huang and J. Huang, 2020, arxiv.2007.02835v2.
21. M. A. Skinnider, F. Wang, D. Pasin, R. Greiner, L. J. Foster, P. W. Dalsgaard and D. S. Wishart, Nat. Mach. Intell., 2021, 3, 973–984.
22. N. Parmar, A. Vaswani, J. Uszkoreit, Ł. Kaiser, N. Shazeer, A. Ku and D. Tran, 2018, arxiv:1802.05751.
23. A. Dosovitskiy, L. Beyer, A. Kolesnikov, D. Weissenborn, X. Zhai, T. Unterthiner, M. Dehghani, M. Minderer, G. Heigold, S. Gelly, J. Uszkoreit and N. Houlsby, An Image is Worth 16 x 16 Words: Transformers for Image Recognition at Scale, 2020, arxiv:2010.11929v2.
24. S. Lim and Y. O. Lee, 2020 25th International Conference on Pattern Recognition (ICPR), 2021, pp. 3146–3153.
25. H. Kim, J. Na and W. B. Lee, J. Chem. Inf. Model., 2021, 61, 5804–5814.
26. T. B. Brown, B. Mann, N. Ryder, M. Subbiah, J. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell, S. Agarwal, A. Herbert-Voss, G. Krueger, T. Henighan, R. Child, A. Ramesh, D. M. Ziegler, J. Wu, C. Winter, C. Hesse, M. Chen, E. Sigler, M. Litwin, S. Gray, B. Chess, J. Clark, C. Berner, S. McCandlish, A. Radford, I. Sutskever and D. Amodei, Language Models are Few-Shot Learners, 2020, arxiv:2005.14165v4.
27. A. Karpathy, minGPT, 2021, https://github.com/karpathy/minGPT/blob/master/LICENSE.
28. PyTorch, 2021, https://pytorch.org/docs/stable/generated/torch.nn.Transformer.html.
29. R. Xiong, Y. Yang, Di He, K. Zheng, S. Zheng, C. Xing, H. Zhang, Y. Lan, L. Wang and T.-Y. Liu, 2020, arxiv:2002.04745v2.
30. D. Weininger, J. Chem. Inf. Model., 1988, 28, 31–36.
31. I. V. Tetko, P. Karpov, R. van Deursen and G. Godin, Nat. Commun., 2020, 11, 5575.
32. S. Wang, Y. Guo, Y. Wang, H. Sun and J. Huang, Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, New York, NY, USA, 2019, pp. 429–436.
33. J. Alammar, The Illustrated Transformer, 2018, https://jalammar.github.io/illustrated-transformer/.
34. J. Scheffczyk, C. Redepenning, C. M. Jens, B. Winter, K. Leonhard, W. Marquardt and A. Bardow, Chem. Eng. Res. Des., 2016, 115, 433–442.
35. T. Brouwer, S. R. Kersten, G. Bargeman and B. Schuur, Sep. Purif. Technol., 2021, 272, 118727.
36. E. J. Bjerrum, SMILES Enumeration as Data Augmentation for Neural Network Modeling of Molecules, 2017, arxiv:1703.07076.
37. C. Bell and Contributers, Thermo: Chemical properties component of Chemical Engineering Design Library (ChEDL), 2016–2022, https://github.com/CalebBell/thermo.
38. S. Müller, J. Cheminf., 2019, 11, 57.
39. S. Honda, S. Shi and H. R. Ueda, SMILES Transformer: Pre-trained Molecular Fingerprint for Low Data Drug Discovery, 2019, http://arxiv.org/pdf/1911.04738v1.
40. F. H. Vermeire and W. H. Green, Chem. Eng. J., 2021, 418, 129307.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2dd00058j

---