Open Access Article
Open Access ArticleFast exploration of potential energy surfaces with a joint venture of quantum chemistry, evolutionary algorithms and unsupervised learning†
Giordano
Mancini
 *a,
Marco
Fusè
*a,
Marco
Fusè
 b,
Federico
Lazzari
a and
Vincenzo
Barone
b,
Federico
Lazzari
a and
Vincenzo
Barone
 a
a
aScuola Normale Superiore, Piazza dei Cavalieri, 56125, Pisa, Italy. E-mail: giordano.mancini@sns.it
bUniversità di Brescia, DMMT-sede Europa, Viale Europa 11, 25121 Brescia, Italy
First published on 16th September 2022
Abstract
Contemporary molecular spectroscopy allows the study of flexible molecules, whose conformational behavior is ruled by flat potential energy surfaces (PESs) involving a large number of energy minima with comparable stability. Under such circumstances assignment and interpretation of the spectral signatures can strongly benefit from quantum chemical computations, which face, however, several difficulties. In particular, the mandatory characterization of all the relevant energy minima leads to a huge increase in the number of accurate quantum chemical computations (which may even hamper the feasibility of a study) and the intricate couplings among several soft degrees of freedom can defy simple heuristic approaches and chemical intuition. From this point of view, the exploration of flat PESs is akin to other optimization problems and can be tackled with suitable metaheuristics, which can drive QC computations by reducing the number of necessary calculations and providing effective routes to sample the most relevant regions of the PES. Unfortunately, in spite of the significant reduction of the number of QC calculations, a brute-force approach based on state-of-the-art methods remains infeasible. This problem can be solved effectively by multi-level strategies combining methods of different accuracy in the first PES exploration, refinement of the structures of the most important stationary points and computation of spectroscopic parameters. Building on previous experience, in this contribution we introduce new improvements in an evolutionary algorithm based method using curvilinear coordinates for both intra- and inter-molecular interactions. Two test cases will be analyzed in detail, namely aspartic acid in the gas-phase and the silver cation in aqueous solution. Comparison between fully a priori computed spectroscopic parameters and the experimental counterparts will provide an unbiased validation of the proposed strategy.
1 Introduction
In the last 30 years the application of artificial intelligence (AI) and machine learning (ML) methods has grown exponentially in most sectors of industrial and academic research. Three technological breakthroughs are at the heart of this trend: (i) the availability of a huge amount of data sources e.g. from mobile devices and low cost sensors1 (since the very definition of a learning algorithm is based on increasing the performance when additional data are used in training2), (ii) the availability of cheap storage devices (to process data we need to have available space) and (iii) the availability of terrific processing power particularly suited for ML applications (FPGAs and GP-GPUs).3,4 The application of ML methods such as artificial neural networks (ANNs),5 cluster analysis6 or genetic algorithms7 in computational chemistry dates back to the last years of the past century and its exponential growth is mirrored by the number of publications including ML keywords8 and/or the number of reviews and special topics devoted to AI and ML in computational chemistry journals.9–12Here we focus on a specific field of AI, known as scruffy AI,13 which includes metaheuristics,14 that is, the application of algorithms loosely inspired by concepts such as natural selection or collective intelligence (as manifested in bird flocks or fish schools) to solve complex problems. In particular, we are concerned with the use of metaheuristics in the exploration of potential energy surfaces (PESs) of flexible molecular systems of medium size (roughly containing less than 100 atoms). In previous contributions15–17 we have proposed and validated the application of one such algorithm, namely the (λ + μ) island model evolutionary algorithm (IM-EA hereafter), to the investigation of the conformational landscape of biomolecule building blocks18 or relatively simple organometallic systems.19 The present contribution presents a number of relevant improvements to the IM-EA method: (i) in the previous contribution we simply checked the capabilities of the method in exploring PESs of flexible systems with the goal of completeness without an in depth discussion of the importance of various components in the method, which is presented in this manuscript; (ii) we previously limited the exploration to dihedral angles of isolated flexible systems, whereas here we present also a new set of operators based on quaternions20,21 able to deal with inter-molecular interactions; (iii) we add a number of improvements to the method, with new mutation operators and the hall of fame mechanism (see section 2.1) and (iv) introduce effective unsupervised clustering of candidate structures in order to reduce as much as possible the number of expensive quantum chemical (QC) computations; neither the computer code, nor the case studies discussed below were presented before. Once again, we carry out an in depth benchmark study of several semi empirical (SE) methods22–25 in the exploration step and of last-generation methods rooted in the density functional theory (DFT) for the exploitation of the above results to compute accurate structural and spectroscopic parameters.
Metaheuristics have been previously applied to the exploration of intra-molecular PESs,26–30 whereas the inter-molecular counterparts are usually explored by techniques rooted in the molecular dynamics (MD) approach, thanks to the simplified topological description that underpins the use of Cartesian coordinates. While the method and the underlying coordinates are not formally connected since one could propagate the equations of motion employing different sets of (possibly curvilinear) coordinates, in practice, the overwhelming majority of MD simulations are carried out in Cartesian coordinates. However, we argue that suitable internal coordinates (IC) (also including mixed IC/Cartesian sets) are more tightly connected to the chemistry of a system and can strongly reduce the couplings between stiff and soft degrees of freedom, thus allowing reduced-dimensionality explorations of the space ruling the phenomenon under investigation. We also make extensive use of several unsupervised learning11 (UL hereafter) tools, including clustering and non linear dimensionality reduction methods (see section 2.6), between the exploration step of the procedure (carried out with relatively cheap SE methods) and the subsequent refinement steps to analyze the results provided by different tests and to reduce the number of the more accurate (and costly) electronic structure computations.
Based on these premises, we introduce in this contribution some improvements of our general IM-EA platform including a set of specialized genetic operators (GOs) purposely tailored for describing the soft coordinates of flexible systems. The potentialities of the new engine will be illustrated by two prototypical case studies, namely the conformational landscape of aspartic acid in the gas-phase31,32 and the first coordination sphere of the silver cation in aqueous solution.33
Several approaches have been proposed to compute the spectroscopic outcome of flexible molecules in terms of averages among the spectra of significantly populated structures.34,35 However, high-resolution (especially microwave) spectroscopy in the gas-phase requires the accurate individual properties of those low-lying structures unable to relax to more stable energy minima under the experimental conditions.36 The current standards for the study of biomolecule building blocks in the gas phase (see e.g. ref. 31, 32, 36–41) do not permit the a priori prediction of the relative energies, interconversion barriers and spectroscopic outcome with sufficient accuracy, but only the a posteriori interpretation of experimental results in terms of the agreement with the computed spectroscopic parameters for a predefined number of conformers without explicit reference to their computed relative stability and possible relaxation. We have, instead, performed a comprehensive study of aspartic acid with the aim of obtaining an unbiased a priori description of its conformational landscape to be validated only in a second step by the comparison of computed and experimental rotational spectroscopic parameters for the most stable conformers separated from each other by sufficiently high energy barriers.
Aqua ions are another paradigmatic model for computational chemistry for reasons analogous to those mentioned above for biomolecule building blocks in the gas-phase. Their structure and dynamics can be studied by neutron diffraction (ND)42 and X-ray absorption spectroscopy (XAS),43 but an unbiased interpretation of the experimental data in structural terms is still challenging for computational simulations both from the point of view of exhaustive explorations of different coordination modes44 and of the reliability of the underlying force fields.45 In the specific case of the silver cation in aqueous solution we tried to stress the limits of EA’s ability to escape from local minima by starting from plainly wrong initial conditions. At the same time, we investigated the ability of semiempirical methods to reproduce the preference for a quasi linear coordination obtained from refined QM simulations33 and the relative weight of first-shell and bulk solvent effects in tuning the preferred coordination geometry.
The paper is organized as follows: we start with a brief recap of the IM-EA method and then proceed to illustrate the new features of the computational engine. Next, we provide the main computational details of the selected quantum chemical methods and electronic structure codes (ESCs) and discuss how the results of the searches can be rationalized by means of unsupervised learning methods. In section 3 the essential details of the case studies are given. The next section starts with an analysis of the results obtained for aspartic acid using different SE methods and an improved version of the IM-EA, together with a comparison with the well-known CREST46 software. Then, we analyze in a similar way the Ag+ ion in aqueous solution providing also an explanation for the unusual shape of its first coordination sphere. The main conclusions and perspectives are summarized in the last section.
2 Methods
2.1 The IM-EA engine
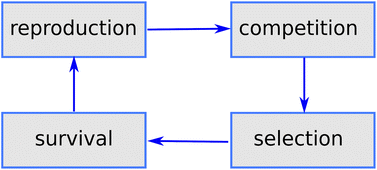
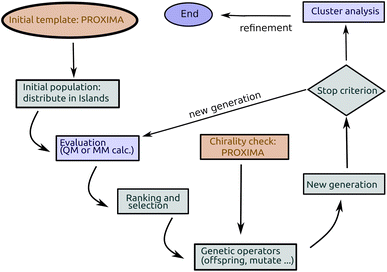
Genetic algorithms (GAs) were first proposed by John Holland47 in the 70's and are among the earliest metaheuristics. The idea was to mimic the mechanisms of Darwinian selection, inheritance and sexual reproduction to explore a search space: a starting set of candidate solutions are allowed to mate and change selecting at each step only the best ones (survival of the fittest); repeated application of this mechanism finally yields a set of solutions which are optimal (fit) for the problem under consideration (see Fig. 1).In short (see Fig. 2), a basic implementation of a GA begins with the (random) generation of a set of candidate solutions (the initial population). Each member of the population (chromosome or specimen) is described by a set (genome) of values (alleles) of the independent variables (genes), which are changed during optimization, and by a fitness value. Until some stopping criterion is met (e.g. the number of cycles or generations) a new population is formed by applying, with a predefined probability (see Table 1), genetic operators namely mutation (changing one or more variables for a chromosome with some stochastic rule), selection (giving high fitness individuals a higher chance of mating i.e. propagating their features to the next generation) and crossover (interpolating the genomes of parents i.e. chromosomes selected for mating to create new ones i.e. the offspring or children). In GAs, the mutation and crossover operators take care of different aspects of the search: mutation is an exploration operator which enforces random changes in the population, whereas selection + crossover is an exploitation operator which builds improved solutions by mixing existing ones. The relative importance of these two steps is still a matter of discussion in different applications: Brain and Addicoat26 argued that mutation is by far the most important operator for PES exploration, whereas crossover is usually the driving operator in other applications, like, e.g., combinatorial optimization problems.
| Parameter | Value |
|---|---|
| a LH was used in all explorations, except those run purposely to test the effect of its absence. b In no crossover runs. c In no mutation runs. | |
| Initial pop. | LH/no LHa |
| Population size | 100 |
| Number of generations (max) | 50 |
| Selection rate | 0.5 |
| Selection method | Tournament (first 90% gen.) |
| Selection method | Rank (last 10% gen.) |
| Tournament size | 2 |
| Crossover method | SBX |
| Crossover probability | 0.6/0b |
| Mutation rate (parents) | 0.3/0c |
| Mutation rate (children) | 0.5/0c |
| Number of islands | 4 |
| Migration frequency | 4 |
| Migration size | 0.05 |
| Hall of fame size | 0.1 |
The extreme flexibility and high level formulation of GAs have prompted their widespread application and the development of several variants.48 In the (λ + μ) evolutionary algorithm (EA), at each generation μ parents generate λ offspring; then survival occurs and the population size is reduced back to μ. In our implementation, we add the selection rate (s) parameter, i.e., the number of new offspring that will be created at each generation; μ/2 pairs of existing specimens always generate λ/2 pairs of different offspring i.e. we employ a unitary λ/μ ratio and λ = s × P where s is the selection rate and P the population size. In other words, the population size P becomes (1 + s) × P when offspring is generated and it is shrunk back to P when the worst s specimens (parents and offspring) are eliminated. The rationale behind the choice of this specific method is related to the high cost of evaluating the fitness of a new individual, which implies a (costly) electronic structure calculation (see section 2.2): high fitness individuals are then worth being preserved in the population until some really improved individual is found. The island model49 is another variant of a GA in which the operators (competition, selection, survival and reproduction) act separately on suitable sub-populations (islands), which are mixed only at predefined intervals by a dedicated operator (migration). The underlying idea is that for flexible systems the positions of atoms belonging to different moieties can to some extent be relaxed separately (in the GA language these would correspond to low-order non related schemata50). The most important choices that must be made when applying a GA are the types of selection + crossover and mutation. For selection we have used the same approach presented in our previous work i.e. we use tournament selection (with a tournament size of 2) to ensure a balance between diversity and fitness of parents and then switch to elitism for the last 5% of planned generations if the search has not yet stopped.15 For the former choice, one possibility is to interpolate the alleles with the simulated binary crossover (SBX) approach,27 which employs the so-called β factor, defined in terms of a uniformly distributed random number μ and a spread factor η (the latter is proportional to how much offspring alleles will resemble those of the parents):
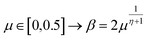 | (1) |
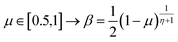 | (2) |
In a second step β is employed to interpolate the parent's coordinates:
| C1 = 0.5[(1 + β)P1 − (1 − β)P2] | (3) |
| C2 = 0.5[(1 + β)P2 + (1 − β)P1] | (4) |
2.2 Manipulation of molecular structures
In computational chemistry terms a specimen in a GA is a molecular structure whose genes are the set of coordinates being used in the search and the alleles are the specific values of those coordinates, which identify a structure in the PES together with its fitness (here its SE or DFT energy). Hence, crossover implies mixing the coordinates of two parent structures to generate new ones, while mutation changes the value of one coordinate moving the structure to a new region of the PES. The best specimens are those with the lowest absolute energy, which can be part of the hall of fame and/or can be selected to generate offspring. Obviously, the manipulation of structures must avoid the generation of atomic clashes or unphysical structures. For intra-molecular conformational searches crossover works in the following way: (i) starting from the first gene (a dihedral angle value) the mean value of the parents’ alleles is calculated; (ii) a stepwise rotation is performed around the selected dihedral angle towards each parent (since two offspring are generated) until no clashes are present (up to using the parent allele); the step size depends on the number of allowed attempts (default = 20). Mutation works similarly: after a gene and new allele have been generated, the dihedral angle is rotated from the new value towards the old value until clashes are solved. To detect clashes we use the same criterion used by the Proxima52 library for detecting covalent bonds.2.3 Mutation and crossover for non-covalent interaction
When inter-molecular interactions are considered, it becomes necessary to decide which parts of the system can move, i.e. to take into account topological changes. In a forthcoming release of the IM-EA code we will integrate completely the Proxima python API52 (PyProxima) to detect topological changes on the fly, but for the present case (Ag+ in aqueous solution) the presence of just two different molecular species allowed us to use a fixed topology with distinct fragments. To manipulate fragment coordinates, instead of working with Cartesian coordinates, we adopted a rigid body description based on quaternions21 for most transformations. Mutation happens then in the following way: first, a fragment is selected; then, with user defined probabilities, one operator is selected among a panel of six choices (note that any move can be excluded by setting its probability to 0):(1) rattle applies a Gaussian displacement to each atom in the selected fragment;
(2) rotate rotates the fragment by a random quaternion around an axis passing through the center of mass;
(3) swap swaps the center of mass of the fragment with another one in a defined pool;
(4) mirror reflects the coordinates of a given fragment through a random plane (set to 0 when chirality has to be preserved);
(5) orbit rotates a whole fragment by a random quaternion around an axis passing through the center of mass of the system;
(6) displace translates a whole fragment along a random axis passing through the center of mass of the system.
To mix parents’ genes we tried to apply SBX. However, for very mobile fragments such as water molecules this choice generated too many clashes or forced to have small steps in dry runs. Therefore, we applied the following checks before the crossover operation: for each fragment in parent a the (same topology) fragments in parent b are ordered with respect to the center of mass distances; for each involved fragment new trial coordinates are generated by interpolation (with SBX) between the coordinates in a and those of a fragment in b (starting with the first one) if the RMSD between the two is below a given threshold (here 1 Å).
2.4 Generation of the starting population
In the original implementation15 we randomly sampled the initial alleles (starting dihedral angles) in the interval [ − π, π] with a resolution of 30° and a Gaussian distribution with a standard deviation of 10° for conformational searches. However, a key factor for the exhaustive exploration of a given space by EA methods is a sufficient diversity of the population. This is accounted for by using the IM during the EA runs, but not in the creation of the initial population. Hence, in this work we have tried to improve this feature by imposing that each starting individual had different alleles. To this end, we generated alleles from a Latin Hypercube sampling53 (LHS hereafter), which is a form of stratified sampling used to generate controlled random ensembles. In a one dimensional LHS if we have to extract N samples from a distribution we divide it into N evenly spaced regions and then pick a value from each region with uniform probability; in other words we get one ensemble of N points. Scaling to two variables we divide the space of each variable into N intervals and thus we get an N by N squared grid from which we can get one set of N points (with the requirement that they will not be neighbours or touch at a vertex). With m variables the procedure is similar and there will be just one sampling point for each m-dimensional interval. This procedure is repeated for each specimen that must be generated in the initial population. For molecular clusters, such as the silver ion in aqueous solution, LH samplings for displacements and rotations of the different fragments are generated and then all the operators described in section 2.3 are applied to an initial template.2.5 Quantum chemistry
All the IM-EA conformational searches were carried out within the flexible rotor approximation, i.e. optimizing all the other degrees of freedom at given values of dihedral angles (EA genes). DFTBA,22 PM7 (ref. 23) or GFN2-xTB24 (XTB hereafter) semi-empirical methods were employed for the exploration. Higher level calculations were carried out at the B3LYP/6-311G++(d,p)54 (hereafter B3), PW6B95/jul-cc-pVDZ55–57 (hereafter PW6), and rev-DSD-PBEP86/jun-cc-pVTZ56–58 (hereafter rDSD) levels, also including, unless explicitly stated, empirical dispersion.59 In the case of the silver cation we also performed BLYP60,61 computations in order to permit a more direct comparison with previous Car–Parrinello simulations.33 The cc-pVTZ basis set56 was used for hydrogen and oxygen, whereas the core electrons of the silver ion were described by pseudopotentials,62,63 and the valence electrons by the corresponding basis sets.64 Furthermore, bulk solvent effects were taken into account by embedding the Ag(H2O)6 cluster in a continuum starting 6 Å from the center of mass of the cluster and represented by the conductor version of the polarizable continuum model (CPCM).65 IM-EA searches were performed by an in house program, which calls either the Gaussian66 or XTB24 codes for electronic energy evaluations. CREST simulations were, instead, performed with the corresponding software.462.6 Analysis of the obtained structures
Comparison against a reference data set composed of Nstruct structures was based on the full (weighted) root mean square distance (RMSD) matrix of atomic positions between different structures (excluding non-polar H atoms) and checking that all structures in the reference set had at least one neighbour within a given threshold (0.2 Å here25,46). The structures of the Ag(H2O)6 cluster to be further optimized at higher computational levels were obtained by a cluster analysis of all frames within 25 kJ mol−1 above the global energy minimum (GEM). Based on previous experience,15,67,68 we used the partition around medoids (PAM) algorithm69 selecting the best number (k) of clusters by using the consensus of four internal validation scores:70 within sum of squares (WSS), silhouette coefficient (SC), Calinski–Harabasz score (pSF) and Dunn score (DS) available in the Scikit-Learn library71 or implemented in purposely written scripts. The feature space was built using the Ultrafast Shape Recognition72 method (USR hereafter) and the L1 distance, which we already applied in the clustering of MD trajectories.73 The surfaces sampled by different SE methods were plotted by means of the t-distributed stochastic neighbor embedding74 (tSNE) method as implemented in the Scikit-Learn library.71 A quantitative (albeit approximate) measure of the different distributions of low- and high-energy structures yielded by SE methods was obtained by using the Gini coefficient: | (5) |
Using the energy difference of a given structure with respect to the GEM: Emax − ΔEGEM. The source code for clustering and other analyses is available under the GPL3 license at https://github.com/tuthmose/Clustering.
3 Case studies
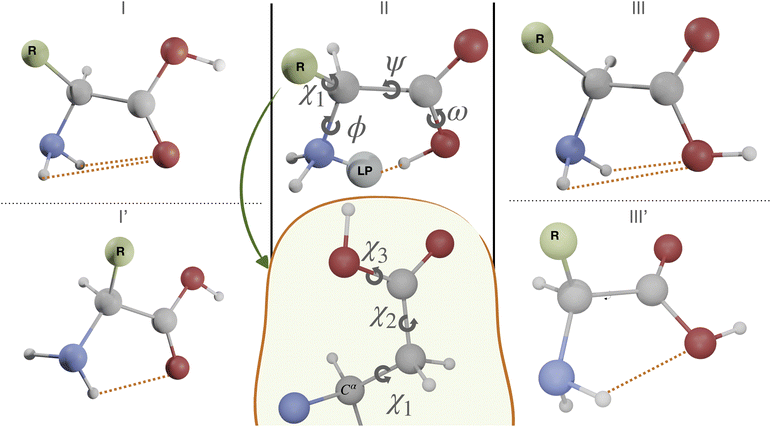
The first case study is the gas phase conformational landscape of aspartic acid, which is the smallest proteinogenic α-amino acid involving a carboxylic group in the side chain. Its conformational behavior is ruled by the six dihedral angles shown in Fig. 3. Three of them belong to the backbone (ϕ, ψ, and ω) and the other three to the side-chain (χi,i = 1,3). The conventional labels c, g−, g and t are used to indicate cis, gauche, or trans conformations of each χ dihedral angle, whereas the non-planarity of the NH2 moiety suggests replacing the customary ϕ dihedral angle (HNCC) by ϕ′ = LP–C–C–C = ϕ + 120° (LP is the nitrogen lone-pair). The only conformers observed experimentally for amino acids are stabilized by hydrogen bonds between the amine and carboxyl moieties of the backbone, which can be either bifurcated (e.g., type I, NH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, ϕ′ ≈ 180°, ψ ≈ 180°, and ω ≈ 180°), or conventional (e.g., type II, N⋯H(O),ϕ′ ≈ 0°, ψ ≈ 0°, and ω ≈ 0°). Additional conformers are observed when polar side chains are present, which involve both intra-backbone and backbone-side chain hydrogen bonds. In particular, starting from type I structures, rotation of the NH2 moiety by about 90° allows its involvement in two different H-bonds (I′ conformer, ϕ′ ≈ 90°, ψ ≈ 180°, and ω ≈ 180°). Conformers involving the backbone OH oxygen as the acceptor and the NH2 moiety as the donor (type III, bifurcated, ϕ′ ≈ 180°, ψ ≈ 0°, and ω ≈ 180° or type III′, single, ϕ′ ≈ 180°, ψ ≈ 90°, and ω ≈ 180°) have also been observed in some cases, but they are always the least populated.75
C, ϕ′ ≈ 180°, ψ ≈ 180°, and ω ≈ 180°), or conventional (e.g., type II, N⋯H(O),ϕ′ ≈ 0°, ψ ≈ 0°, and ω ≈ 0°). Additional conformers are observed when polar side chains are present, which involve both intra-backbone and backbone-side chain hydrogen bonds. In particular, starting from type I structures, rotation of the NH2 moiety by about 90° allows its involvement in two different H-bonds (I′ conformer, ϕ′ ≈ 90°, ψ ≈ 180°, and ω ≈ 180°). Conformers involving the backbone OH oxygen as the acceptor and the NH2 moiety as the donor (type III, bifurcated, ϕ′ ≈ 180°, ψ ≈ 0°, and ω ≈ 180° or type III′, single, ϕ′ ≈ 180°, ψ ≈ 90°, and ω ≈ 180°) have also been observed in some cases, but they are always the least populated.75
The aim of the study is, therefore, twofold: on one hand it is necessary to find all the conformers lying within a pre-defined energy threshold. On the other hand, the most stable ones must be ordered, characterized and, finally, their computed spectroscopic parameters must be compared with those of their experimental counterparts. Concerning the first aspect, extensive enhanced sampling classical simulations with different force fields followed by QC geometry optimizations at the B3LYP/6-311++ G(d,p) and MP2/6-311++G(d,p) levels by Comitani et al.32 identified 19 distinct minima covering an energy range of 42.6 kJ mol−1. Concerning the second aspect, the rotational constants and nitrogen quadrupole couplings of six conformers were measured by Sanz et al.31
The second test case is the silver cation in aqueous solution, which was recently studied by X-ray absorption spectroscopy (XAS), large-angle X-ray scattering (LAXS) and Car–Parrinello molecular dynamics.33 It was found that, at variance with the previously accepted tetrahedral coordination, the first shell quasi-linear structure obtained from CPMD simulations (two water molecules showing Ag–O distances of 2.34 Å and an O–Ag–O angle between 150° and 180°) was in better agreement with the experiment.
4 Results and discussion
4.1 Aspartic acid
In this section we analyze (i) the role of crossover and mutation operators on the performance of the IM-EA using a large population and (ii) the effect of the new features added in the exploration step. All these tests were run with the XTB SE method and, unless explicitly specified, using four replicas. To judge the results of these trials we checked the number of calculations needed to obtain at least one structure with an RMSD within 0.2 Å (heavy atoms) from each of the MP2 structures of the data set provided by Comitani et al.32 For each test we ran four replicas employing the parameters shown in Table 1. Next, we compared different exploration strategies (IM-EA vs. CREST) employing the same electronic Hamiltonian (XTB) or different semi-empirical methods (XTB, DFTBA and PM7) employing the same exploration strategy (IM-EA).| Run | # calc. | # miss | RMSDmin (Å) | ΔE(kJ mol−1) |
|---|---|---|---|---|
| No LH | 4300 | 2 | 0.2012 | 26.022 |
| No LH | 4100 | 0 | NA | NA |
| No LH | 4000 | 1 | 0.2174 | 30.936 |
| No LH | 2300 | 2 | 0.2026 | 21.956 |
| LH | 2800 | 0 | NA | NA |
| LH | 3500 | 2 | 0.2298 | 21.956 |
| LH | 4000 | 1 | 0.2286 | 26.002 |
| LH | 3800 | 1 | 0.2381 | 54.229 |
| HOF | 2000 | 1 | 0.2308 | 26.002 |
| HOF | 3300 | 0 | NA | NA |
| HOF | 2600 | 0 | NA | NA |
| HOF | 3400 | 0 | NA | NA |
It is apparent that LH speeds up the convergence as the chromosomes start exploring different regions of the search space. Concerning the hall of fame mechanism, the significant improvement yielded by its inclusion matches very well the “hill climber” picture (see the ESI†): since a mutation induced by a stochastic force can either improve or worsen a specimen's fitness by keeping the few best specimens in the population untouched, ensuring that they will continue to contribute to the gene pool. This is particularly important for the island model where the gene pool of each island is small as compared to the whole populations. The results obtained by excluding one of the main operators and adding the hall of fame prompted us to perform further experiments with the mutation operator. First of all, when mutating a gene, we impose that the difference between the old and new allele is larger than the spread of the normal distributions used to generate new moves (5° and 10°, respectively). The generation of starting structures by the LH ensures that random changes do not compromise the diversity of the population. In addition, we change the values of either one or two dihedral angles with equal probability. In this set of tests performed with XTB we also run four searches with CREST (Fig. 5).46
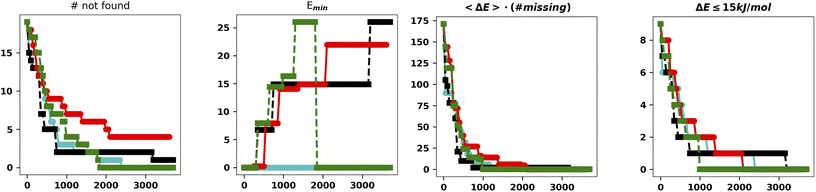 | ||
| Fig. 5 Summary of the results for the IM-EA searches with the new mutation operator. The panels are analogous to those of Fig. 4. | ||
This is the only set of four replicas used so far that does not miss any minimum with an RMSD from any reference structure of 0.18 Å. Another approach to mutation, which tries to change the current allele by a small value30 or to use a combination of smaller and larger changes, did improve the performances (data not shown). It is worth observing that, at variance with the benchmark purposes of the present study, in real world cases one generally wants to find all the statistically relevant structures, which, for different applications, may imply an 8–15 kJ mol−1 cutoff from the global energy minimum. These structures are often retrieved already in a single run and always found when considering at least three replicas. Hence, the recommendation for real world applications is to use replicated runs for a limited number of generations.
From another point of view, it is noteworthy that all the CREST searches provide a structure with a nearly constant RMSD (about 0.3 Å) from the missed energy minimum (J-4TcT2 in the nomenclature of Comitani et al.32). CREST employs enhanced sampling MD and a crossover type operator. If the effect of the two types of coordinate interpolations is roughly comparable, the metadynamics part has the same effect as the mutation operator, but the collective variables used are unable to approach the J-4TcT2 structure more closely. The other culprit could be the filtering procedure, if other generated neighbours of J-4TcT2 were higher in energy. In any case, it must be observed that (i) all the missing structures (both for CREST and IM-EA) lie more than 20 kJ mol−1 above the GEM, thus having (at least with XTB energies) negligible statistical relevance, (ii) while reasonable, the choice of the cutoff (0.2 Å in the present context) remains arbitrary and (iii) we are directly comparing geometries obtained at the XTB and MP2 levels (even if MP2 is not our reference level as discussed in section 4.1.2) without taking into account higher-level relaxation. This was done intentionally because the purpose of the paper was to analyze both the exploration algorithm and the quantum chemical model. It is also noteworthy that the χ3 dihedral angle of the most elusive structure is close to 0° at variance with the value of ≈180° characterizing all the most stable conformers. Since the barrier ruling the χ3 torsion is quite high and its coupling with other degrees of freedom is huge when using Cartesian coordinates, short MD runs and collective variables ruled by Cartesian coordinates could be unable to reach the secondary minimum at χ3 ≈ 0° (see Fig. 6). In this connection, use of curvilinear (internal) coordinates permits a strong reduction of couplings between stiff and soft degrees of freedom, with the consequent increased efficiency of any exploration strategy.
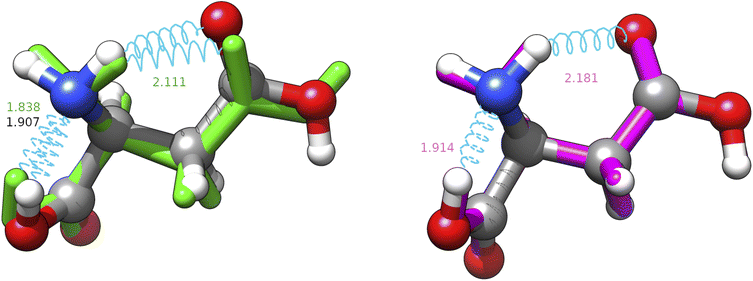 | ||
| Fig. 6 Superposition between the MP2 geometry (ball and stick, conventional atomic colours) of structure J-4TcT2 and its nearest neighbours in the replica of searches shown in Table 3 with CREST (green, licorice) and IM-EA (magenta, licorice). Intramolecular H-bonds are shown by cyan springs and the corresponding distances (in Å) are annotated; for the CREST and IM-EA geometries fonts are in their atomic representation colour. The corresponding heavy atom RMSDs are 0.3094 and 0.0700 Å, respectively. | ||
Another relevant aspect concerns the use of energy gradients. While they must be used systematically in any MD algorithm, EAs are in principle derivative-free methods. We do, however, make use of gradients since (with the exception of generation 0) each specimen is partially relaxed within the flexible rotor approximation. The reason is that stiff degrees of freedom (bond lengths and valence angles) are absent in the genotype and hence cannot be used in the search. The choice of including or not including stiff degrees of freedom in the problem representation is related to the ratio between the cost of computing gradients and that of computing an increased number of energies characterizing the schemata to be compared by the EA (in addition to the practical issue of defining the proper operators, as the next case study will show). A direct comparison of the computational cost of the procedures is difficult since the IM-EA uses wrapper and template input file trading performance with flexibility while CREST uses function calls to use GFN2-XTB or molecular mechanics. However, the computational cost depends mainly on the number of energy/gradient evaluations carried out in the two procedures which (i) in the IM-EA is the number of generated structures (ii) in CREST is the number of total MD steps and crude + tight optimizations carried out between MD iterations. Looking at the four replicated runs carried out for aspartic acid (with the run parameters set automatically by the application itself) we have 2 MTD iterations of 1000 steps each plus about 3000 optimizations which is roughly twice the number of geometry optimizations needed by the IM-EA with optimal settings (note, however, that we let CREST set most of its run parameters which may have led to conservative values in some cases). Finally, it can be observed that, in general, any claim about the greater effectiveness of the IM/EA vs. CREST and/or vs. a third method would be at least problematic according to the “No Free Lunch Theorem”,76 which states that it is not possible to find a single algorithm showing the best performance for any class of problems. Thus, a wise approach to explore very rugged surfaces would be to compare the ensembles generated by different methods in addition to using short replicated runs (Table 3).
| Run | # calc. | # miss | RMSDmin (Å) | ΔE(kJ mol−1) |
|---|---|---|---|---|
| New mut. | 1900 | 0 | NA | NA |
| New mut. | 2700 | 0 | NA | NA |
| New mut. | 1500 | 0 | NA | NA |
| New mut. | 2900 | 0 | NA | NA |
| CREST | 107/127 | 1 | 0.3108 | 32.185 |
| CREST | 107/127 | 1 | 0.3094 | 32.185 |
| CREST | 108/125 | 1 | 0.3133 | 32.185 |
| CREST | 104/121 | 1 | 0.3106 | 32.185 |
Finally, Table 4 shows the results obtained with DFTBA using the latest settings of the IM-EA, whereas Fig. S1† in the ESI shows the descriptive statistics for the best DFTBA replica.
| Run | # calc. | # miss | RMSDmax (Å) | ΔE(kJ mol−1) |
|---|---|---|---|---|
| DFTBA | 2500 | 5 | 0.207 | 0.220 |
| DFTBA | 2600 | 5 | 0.210 | 0.228 |
| DFTBA | 2500 | 6 | 0.204 | 0.0 |
| DFTBA | 2800 | 6 | 0.205 | 7.901 |
Apparently, XTB outperforms DFTBA since none of the DFTBA replicas is able to retrieve all of the 19 reference structures: in one case the GEM is missing and in the other two cases the lowest lying missing conformer is within 1 kJ mol−1 from it. However, a closer look shows that the RMSD of the missing conformers has, across replicas, an upper bound of 0.21 Å. Clearly, DFTBA is indeed sampling structures that are likely to collapse into the nearest reference ones after geometry refinement. However, it is worth investigating in deeper detail why XTB geometries are closer to the MP2 references than the DFTBA counterparts. One reason may be the different relative energy differences between the two SE models. Table 5 shows the Gini coefficients for the Emax − ΔE difference in XTB and DTFBA runs. It is apparent that the DFTBA values are consistently larger, meaning that these searches produce a larger number of high-energy structures with respect to the XTB counterparts. This different distribution of relative energies can be visually appreciated by looking at Fig. 7, which shows the 2D t-SNE projections of the USR feature space for all points sampled by the best XTB and DFTBA replicas. In this figure the size of dots is inversely proportional to ΔEGEM; clearly, the XTB plots show a higher number of connected low-lying structures as compared to DFTBA, which increases the chances of finding nearby minima and increases the effectiveness of crossover operations. While it is true that the IM-EA (or even a simple Monte Carlo search) does not need to cross barriers, the survival probability of each structure is still related to its relative energy. The presence of a smaller number of low-energy structures in the DFTBA generation limits the diversity of the gene pool, thereby slowing down the search. More in detail, the particular settings of our procedure (island model and hall of fame) are likely to be much more advantageous for a model like XTB, which tends to underestimate energy differences.
| Run | GI |
|---|---|
| XTB | 0.3715 |
| XTB | 0.3688 |
| XTB | 0.2960 |
| XTB | 0.2961 |
| DFTBA | 0.4753 |
| DFTBA | 0.3848 |
| DFTBA | 0.4334 |
| DFTBA | 0.4113 |
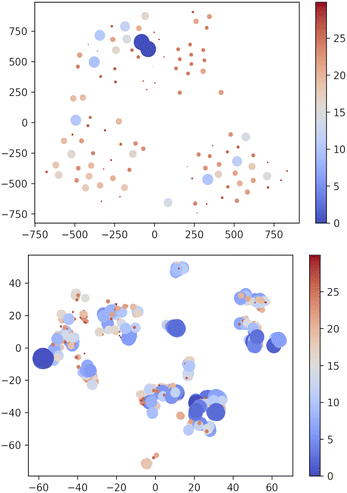 | ||
| Fig. 7 Two-dimensional TSNE plot of the USR phase space72 using PM7 and XTB methods. Points with ΔEGEM ≥ 30 kJ mol−1 are not included. The size and colour of dots are scaled as (Emax − ΔE) × 2/4 with Emax = 30. i.e. bigger blue shifted points correspond to low-lying structures. Note that t-SNE is a method oriented to conserve the local structure (rather than the global one privileged by the principal component analysis) and thus positions in the projected space depend on the local neighbourhood for each point, which accounts for the different scales in the axes of the two panels. | ||
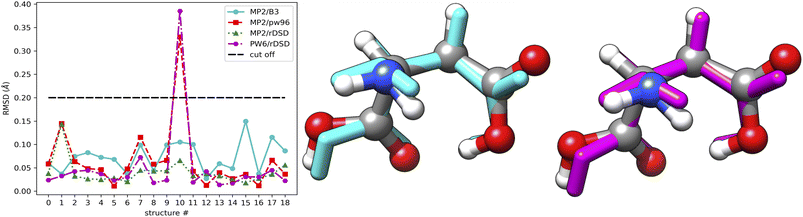
For purposes of illustration, the reference MP2 geometries of the 19 structures mentioned above are compared with their B3, PW6 and rDSD counterparts, as shown in Fig. 8. The left panel shows that the RMSD of the double-hybrid rDSD functional is always smaller than those of the hybrid functionals (B3 and PW6). A superposition of the different geometries for the structure showing the largest RMSD is shown in the middle and right panels of Fig. 8, which clearly points out that most of the difference is related to a tilting of the side chain carboxyl group.
To this end, starting from the 4000 candidates found in each GFN2-xTB replica, a first reduction to about 1000 structures is obtained by applying a threshold of 25 kJ mol−1 with respect to the absolute energy minimum. These candidates were compared with each other in terms of the root-mean-square deviations of heavy atom positions and the rotational constant. The 300 structures remaining after this selection are further reduced to about 30 by the clustering procedures described in the methods section and subsequent full geometry optimization at the B3 level leads to 12 conformers lying within 16 kJ mol−1. The structures of this final panel of candidates were finally refined at the rDSD level. This composite strategy allows the number of costly geometry optimizations by using hybrid and, especially, double-hybrid functionals to be strongly reduced and to end up with 10 conformers lying within 12 kJ mol−1 above the absolute energy minimum. Next, we proceed from electronic energy differences to the corresponding free energies at room temperature (ΔG°), with rDSD harmonic frequencies being employed to compute zero point energies (ZPEs) and vibrational partition functions. This step leads to significant changes in the trend arising from relative electronic energies and, in particular, to the destabilization of all the conformers showing type II hydrogen bridges (see Table 6).
| Conformer | IIgtt | IIg−tt | Igtt | III′gtt | I′g−tt | Ig−gc |
|---|---|---|---|---|---|---|
| Experimental | ||||||
| A c0 | 2612.20878(26) | 3416.43489(66) | 2553.85523(70) | 2651.953(31) | 3378.20873(26) | 3198.861(19) |
| B c0 | 1191.01132(17) | 902.904474(79) | 1205.08478(10) | 1183.51697(30) | 907.373507(28) | 945.84803(7) |
| C c0 | 1057.33169(16) | 764.631177(96) | 1069.14318(10) | 1054.98929(34) | 780.042139(32) | 781.75139(18) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Computed | ||||||
| A c0 | 2607.9 | 3412.3 | 2546.8 | 2643.8 | 3372.8 | 3192.2 |
| B c0 | 1188.9 | 900.4 | 1202.1 | 1182.9 | 904.2 | 943.8 |
| C c0 | 1057.1 | 762.5 | 1067.2 | 1055.9 | 778.1 | 781.4 |
| ΔEel | 0.0 | 1.6 | 3.5 | 4.2 | 5.7 | 4.1 |
| ΔG0 | 0.0 | 0.2 | 0.8 | 1.6 | 2.1 | 3.8 |
Together with the rDSD geometries (straightforwardly providing equilibrium rotational constants) and harmonic frequencies, anharmonic contributions, required for going from equilibrium to effective rotational constants,80,81 were also computed at the B3 level. More accurate structures, and thus improved equilibrium rotational constants, were obtained by correcting the rDSD geometrical parameters with the so-called linear regression approach (LRA).80 Within the latter, systematic errors affecting bond lengths and valence angles are corrected based on linear regressions, whose parameters were derived from a large database of accurate semi-experimental equilibrium geometries.81
Since six conformers were detected in the microwave study of aspartic acid,31 and in Table 6 we collect the computed spectroscopic parameters of the six conformers having the lowest free energies at room temperature according to rDSD computations. The final match between the spectroscopic parameters of the six most stable conformers and the experimental counterparts is indeed quite impressive. MP2/6-311++G(d,p)31 computations forecast that one or two different conformers should be experimentally detected and the spectroscopic constants obtained at that level show maximum and average absolute errors w.r.t. the experiment (29.2 and 10.6 MHz) much more than three times larger than those of their rDSD-LRA counterparts (8.2 and 3.1 MHz), with the latter value (smaller than 0.2%) approaching the accuracy of state-of-the-art composite methods for small semi-rigid molecules82 and permitting an unbiased assignment of any microwave spectrum.83
In summary, the proposed exploration strategy in conjunction with an exploitation step employing last-generation double-hybrid density functionals and an appropriate account of anharmonic contributions paves the way toward the ful a priori disentanglement of rugged conformational landscapes and the resulting prediction of accurate spectroscopic signatures.
4.2 Silver ions in aqueous solution
The paradigmatic case of a silver ion in aqueous solution was selected to test the capability of genetic operators to drive the system toward the most stable structure employing the same SE models (XTB and PM7) employed for the intra-molecular searches. To this end, we selected a very small model system containing, together with Ag+, just six water molecules and ran only two replicas with different initial starting conditions. In particular, we selected either the most symmetric arrangement of the water molecules (an octahedron) or a very unlikely fully planar structure (see Fig. S2† of the ESI). The IM-EA run parameters were those which have provided the best performances for aspartic acid and the probability with which the different mutation operators could be applied are shown in Table 7:| Mutation type | Probability |
|---|---|
| rattle | 0.15 |
| rotate | 0.15 |
| swap | 0.15 |
| mirror | 0.15 |
| orbit | 0.20 |
| displace | 0.20 |
Since this kind of system is often investigated by means of MD,84,85 we performed some CREST searches as well. At the end of each search all the obtained structures were analyzed as explained in section 2.6. To get an approximate coordination number (CN hereafter, to be used simply as a descriptor in the tables) we calculated the distribution of ion-water distances in all the generated geometries and then (i) checked if the corresponding histogram was mono- or multi-variate and (ii) calculated the number of molecules within the distance corresponding to the boundary of the first region. Table 8 summarizes the characteristics of the different searches performed. The distance distributions for the first CREST and IM-EA replicas are shown in Fig. S3† of the ESI.
| Search type | n | k | n cl1 | 〈CN〉 | CNcl1 | CNGEM | ΔEGEM−M1 (kJ mol−1) |
|---|---|---|---|---|---|---|---|
| a Planar template. b Octahedral template. | |||||||
| CREST | 32 | 4 | 10 | 5.63 | 6 | 6 | 1.862 |
| CREST | 20 | 3 | 8 | 5.8 | 6 | 6 | 1.854 |
| IM-EA/XTBa | 2499 | 4 | 2188 | 5.75 | 6 | 6 | 0.0577 |
| IM-EA/XTBb | 2404 | 3 | 2261 | 5.88 | 6 | 6 | 0.1928 |
| IM-EA/PM7 | 40 | 3 | 13 | 5.5 | 5 | 5 | 37.099 |
| IM-EA/B3SC | 851 | 5 | 485 | 3.24 | 3 | 3 | 0.0516 |
The first observation that can be drawn from these results is that the feature space selected by USR (which was originally devised for covalent bonds) is able to produce big clusters, whose medoids are also very similar to the structure of the GEM. Furthermore, the computed CNs suggest that none of the searches employing SE Hamiltonians leads to structures close to those produced by CPMD simulations or by the fitting of XAS data. This is confirmed by the medoids obtained from one of the IM-EA/XTB searches and shown in Fig. 9 (the corresponding validation score graphs are shown in Fig. S4† of the ESI).
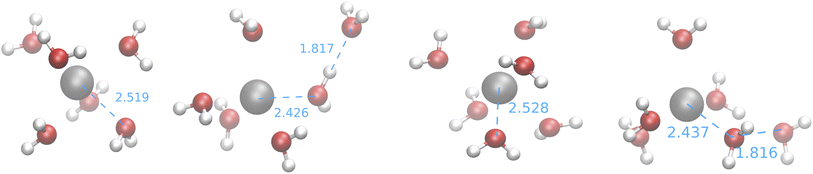 | ||
| Fig. 9 Medoids obtained from the first IM-EA/XTB search (see Table 8). Selected Ag–O and O–H distances are shown in Å. | ||
The medoids and validation scores obtained from the first CREST search are shown in Fig. 4 and 5 in the ESI† for the sake of comparison. It is apparent that all the obtained structures resemble distorted antiprisms (CN = 6) or square pyramids (CN = 5) with ion-oxygen distances in the 2.4–2.6 Å range.
We run different searches and geometry optimizations using the two different functionals and pseudopotentials, which will be referred to as B3SC, B3LC, BSC and BLC, respectively, with an obvious notation. In particular, we run an IM-EA/B3SC search and re-optimized all the medoids obtained from the first IM-EA/XTB search at the B3SC, B3LC, BSC and BLC levels. Given the high computational cost of this exploration we squeezed the number of generations, population size and number of islands to 30, 40 and 2, respectively.
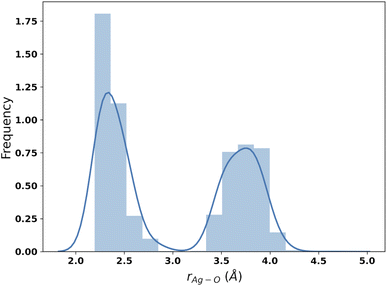
The results of the B3SC search are summarized in the last row of Table 8. The distribution of Ag–O distances is shown in Fig. 10 and this is the only case in which the histogram has a bivariate distribution where a first and second hydration shell are clearly visible. The structures sampled in this search have a larger spread and a lower CN than their SE counterparts. The corresponding medoids are shown in Fig. 11 and their clustering validation scores, in Fig. S7† in the ESI.
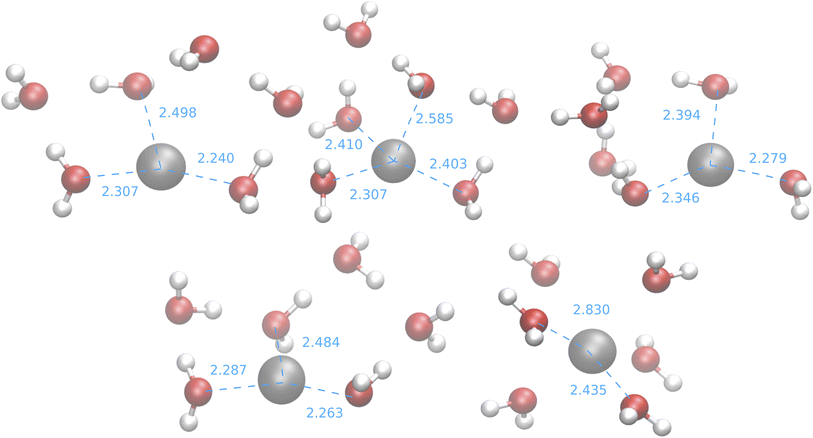 | ||
| Fig. 11 Medoids from the IM-EA/B3SC search. Dashed lines indicate selected ion-oxygen distances in Å. | ||
With the exception of the last medoid, which resembles the geometries obtained using SE methods (and which is associated with a cluster including only 20 points), the other four structures show two water molecules in the first coordination shell, an ‘intermediate’ water molecule and the last three water molecules in the second coordination sphere. In particular, medoid 4 features the two closest water molecules at 2.26 and 2.28 Å and forming an O–Ag–O angle of about 150°. This structure (but the others are not very different) is quite similar to those predicted by the CPMD simulation and observed in XAS experiments:33 the XAS Ag–O distance falls in the range of 2.34–2.36 Å whereas that of the CPMD counterpart is 2.29 Å with an O–Ag–O angle lying between 150° and 180°. The presence of the third water molecule marks a difference with respect to the XAS results, which were interpreted in terms of a non negligible contribution of a “2 + 2” distorted tetrahedral structure. The asymmetric hydrogen-bond network and the lack of contributions from the second hydration shell in the Ag+–(H2O)6 cluster can explain the distortion. However, the main features of the CPMD and XAS results are well reproduced already in the first generation (i.e., after the first set of 40 single point calculations), thus strongly reducing the computational cost of the simulation. On these grounds, it can be concluded that the reduced CN and symmetry of the coordination sphere of the silver cation with respect to typical ‘hard’ ions (e.g., Na+) are intrinsic properties of the metal ion and do not depend on collective solvent properties. Therefore, the problems of the previous searches are indeed related to the limited accuracy of the SE Hamiltonians.
Two aspects remain to be clarified at this point, namely (i) the origin of the limited accuracy of SE models and (ii) the possibility of replacing the entire search effort by straightforward geometry optimizations.
The first question is settled by the B3SC and B3LC calculations carried out on the IM-EA/XTB medoids, which are summarized in Fig. 12 and S8† of the ESI. It is apparent that the B3LC structures more closely resemble the SE than their B3SC counterparts, even if a displacement of water from the neighbourhood of the ion is also observed for these clusters. More importantly, the optimization of medoid 3 at the B3SC level (Fig. 12) results in an almost linear geometry (about 9° from linearity) with highly symmetrical distances in very good agreement with XAS and CPMD. The same coordinates optimized at the B3LC level lead to a more compact geometry closer to the starting point and with a CN close to 4 (or, better a “2 + 2” model). The same behaviour (actually with an even stronger tendency towards linearity) is obtained by refining those same medoids at the BLC and BSC levels (see Fig. S9 and S10† in the ESI). From these results it is clear that, at variance with hard cations, the coordination of the soft silver cation cannot be described by simple spherical models and requires a proper account of inner (mainly 4d) electrons.
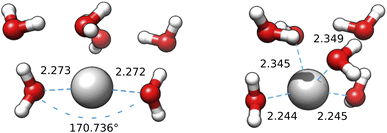 | ||
| Fig. 12 Medoid 3 from the first IM-EA/XTB search re-optimized at the B3SC (left) and B3LC (right) levels. The first shell O–Ag–O angle is shown for the first geometry. | ||
Concerning the second point, even if the higher level optimizations cause relevant deformations, the optimized structures are not (and could not be) completely different from the starting ones. Therefore, the exploration performed by the EA (or MD) is critical to produce (even if among others) structures not too far from the GEM. In any case, the high-level searches (followed by geometry optimizations) remain much more efficient (and cheaper) than a complete CPMD simulation.
5 Conclusions
In this paper, a general strategy aimed at the accurate computational characterization of potential energy surface features ruling intra- and inter-molecular large amplitude motions has been further improved and its capabilities have been illustrated by two prototypical examples.For flexible molecules containing a significant number of soft dihedral angles, crucial information in the field of molecular spectroscopy is the number and type of conformers contributing to the experimental spectra. This requires. first of all, an effective exploration of the PES that can be performed by genetic algorithms driving local geometry optimizations with last-generation semi-empirical methods. Further refinement of the “surviving” species by means of geometry optimizations using double-hybrid functionals and incorporation of vibrational and thermal effects on energetics complete the procedure. Subsequently, for each energy minimum, accurate spectroscopic parameters can be computed resorting to last-generation double-hybrid functionals, possibly integrated with linear regression corrections.81 Concerning inter-molecular interactions, the same exploration strategy based on suitable curvilinear coordinates can be profitably used provided that the underlying electronic Hamiltonian is sufficiently accurate. In this case, the resulting structures permit an unbiased interpretation of neutron or X-ray diffraction experiments. In our opinion this shows the potential and the robustness of the IM-EA method, which can be safely applied to different systems and problems.
Concerning future developments, in our opinion priority should be given to processes involving topology changes through complete integration with the PyProxima library52 and the inclusion of knowledge-based steps in the workflow along lines already followed, for instance, in the Torsiflex87 software. Another useful development is the implementation of a distributed version of the IM-EA to exploit the GA’s inherent parallelism (this is critical for searches carried out with high-level quantum chemical models) and the very limited communication requirements for fitness calculations running on different machines. Last, but not least, implementation of consistent documentation and user-friendly interfaces (either of the command line (CLI) or graphical user (GUI) type) would also allow the widespread use of the developed tool by non specialists.
Data availability statement
The code developed for this study is available on GitHub (see section 2) under the GPL3 license. It is based on our previous work15 which was not released previously. XTB and Gaussian 16 electronic structure calculations have been carried out with standard keywords/parameters available in the codes. Example bash scripts for submission of searches, template input files for Gaussian and XTB ESC and Gaussian 16 input files for LC/SC calculations are provided in the ESI.† Examples of ensembles obtained with IM-EA/XTB for aspartic acid and with IM-EA/XTB for the silver aqua ion are available for download in the ESI† section.Author contributions
GM wrote part of the article and contributed to the revision of the final text, developed the GA software and performed the PES explorations; MF wrote part of the article and performed the QC computations; FL designed the PROXIMA library, managed its integration and contributed to the revision of the paper; VB supervised the project, wrote part of the paper and revised the final text. All authors have read and approved the final manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The financial funding from the Italian Ministry of University and Research (Grant 2017A4XRCA) and the Italian Space Agency (ASI; ‘Life in Space’ project, N. 2019-3-U.0) is gratefully acknowledged. We also thank the technical staff at SNS' SMART Laboratory for managing the computational facilities.References
- W. Zhao, A. Bhushan, A. Santamaria, M. Simon and C. Davis, Algorithms, 2008, 1, 130–152 CrossRef CAS PubMed.
- A. L. Samuel, IBM J. Res. Dev., 1959, 3, 210–229 Search PubMed.
- V. Sze, Y.-H. Chen, J. Emer, A. Suleiman and Z. Zhang, 2017 IEEE Custom Integrated Circuits Conference (CICC), 2017, pp. 1–8 Search PubMed.
- M. Pandey, M. Fernandez, F. Gentile, O. Isayev, A. Tropsha, A. C. Stern and A. Cherkasov, Nat. Mach. Intell., 2022, 4, 211–221 CrossRef.
- J. Gasteiger and J. Zupan, Angew. Chem., Int. Ed., 1993, 32, 503–527 CrossRef.
- A. Li and V. Daggett, Proc. Natl. Acad. Sci., 1994, 91, 10430–10434 CrossRef CAS PubMed.
- N. Nair and J. M. Goodman, J. Chem. Inf. Comput. Sci., 1998, 38, 317–320 CrossRef CAS.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed.
- T. Zubatiuk and O. Isayev, Acc. Chem. Res., 2021, 54, 1575–1585 CrossRef CAS PubMed.
- M. Kulichenko, J. S. Smith, B. Nebgen, Y. W. Li, N. Fedik, A. I. Boldyrev, N. Lubbers, K. Barros and S. Tretiak, J. Phys. Chem. Lett., 2021, 12, 6227–6243 CrossRef CAS PubMed.
- A. Glielmo, B. E. Husic, A. Rodriguez, C. Clementi, F. Noé and A. Laio, Chem. Rev., 2021, 121, 9722–9758 CrossRef CAS PubMed.
- M. Ceriotti, C. Clementi and O. Anatole von Lilienfeld, J. Chem. Phys., 2021, 154, 160401 CrossRef CAS PubMed.
- B. Gonçalves and F. G. Cozman, in Intelligent Systems, ed. A. Britto and K. Valdivia Delgado, Springer International Publishing, Cham, 2021, vol. 13074, pp. 177–192 Search PubMed.
- J. Brownlee, Clever algorithms: nature-inspired programming recipes, LuLu.com, s.l., Revision 2 edn, 2012 Search PubMed.
- G. Mancini, M. Fusè, F. Lazzari, B. Chandramouli and V. Barone, J. Chem. Phys., 2020, 153, 124110 CrossRef CAS.
- V. Barone, C. Puzzarini and G. Mancini, Phys. Chem. Chem. Phys., 2021, 23, 17079–17096 RSC.
- S. Potenti, L. Spada, M. Fusè, G. Mancini, A. Gualandi, C. Leonardi, P. G. Cozzi, C. Puzzarini and V. Barone, ACS Omega, 2021, 6(20), 13170–13181 CrossRef CAS.
- G. Ceselin, Z. Salta, N. Tasinato and V. Barone, J. Phys. Chem. A, 2022, 126, 2373–2387 CrossRef CAS PubMed.
- U. Cosentino, A. Villa, D. Pitea, G. Moro, V. Barone and A. Maiocchi, J. Am. Chem. Soc., 2002, 124, 4901–4909 CrossRef CAS PubMed.
- C. F. Karney, J. Mol. Graphics Modell., 2007, 25, 595–604 CrossRef CAS PubMed.
- G. Mancini, S. Del Galdo, B. Chandramouli, M. Pagliai and V. Barone, J. Chem. Theory Comput., 2020, 16, 5747–5761 CrossRef CAS PubMed.
- D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947–12957 CrossRef CAS PubMed.
- J. J. P. Stewart, J. Mol. Graphics, 2007, 13, 1173–1213 CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- B. Chandramouli, S. Del Galdo, M. Fusè, V. Barone and G. Mancini, Phys. Chem. Chem. Phys., 2019, 19921–19934 RSC.
- Z. E. Brain and M. A. Addicoat, J. Chem. Phys., 2011, 135, 174106 CrossRef.
- J. L. Llanio-Trujillo, J. M. C. Marques and F. B. Pereira, J. Phys. Chem. A, 2011, 115, 2130–2138 CrossRef CAS PubMed.
- L. B. Vilhelmsen and B. Hammer, J. Chem. Phys., 2014, 141, 044711 CrossRef PubMed.
- J. Zhao, R. Shi, L. Sai, X. Huang and Y. Su, Mol. Simul., 2016, 42, 809–819 CrossRef CAS.
- M. J. Vainio and M. S. Johnson, J. Chem. Inf. Model., 2007, 47, 2462–2474 CrossRef CAS.
- M. E. Sanz, J. C. López and J. L. Alonso, Phys. Chem. Chem. Phys., 2010, 12, 3573–3578 RSC.
- F. Comitani, K. Rossi, M. Ceriotti, M. E. Sanz and C. Molteni, J. Chem. Phys., 2017, 146, 145102 CrossRef PubMed.
- M. Busato, A. Melchior, V. Migliorati, A. Colella, I. Persson, G. Mancini, D. Veclani and P. D'Angelo, Inorg. Chem., 2020, 59, 17291–17302 CrossRef CAS PubMed.
- S. Grimme, C. Bannwarth, S. Dohm, A. Hansen, J. Pisarek, P. Pracht, J. Seibert and F. Neese, Angew. Chem., Int. Ed., 2017, 56, 14763–14769 CrossRef CAS PubMed.
- F. Bohle, J. Seibert, S. Grimme and S. Grimme, J. Org. Chem., 2021, 86, 15522–15531 CrossRef CAS PubMed.
- E. R. Alonso, I. León and J. L. Alonso, Intra- and Intermolecular Interactions Between Non-Covalently Bonded Species, Elsevier, 2020, pp. 93–141 Search PubMed.
- P. D. Godfrey and R. D. Brown, J. Am. Chem. Soc., 1998, 120, 10724–10732 CrossRef CAS.
- G. M. Florio, R. A. Christie, K. D. Jordan and T. S. Zwier, J. Am. Chem. Soc., 2002, 124, 10236–10247 CrossRef CAS PubMed.
- S. Grimme and M. Steinmetz, Phys. Chem. Chem. Phys., 2013, 15, 16031–16042 RSC.
- T. Risthaus, M. Steinmetz and S. Grimme, J. Comput. Chem., 2014, 35, 1509–1516 CrossRef CAS.
- H. V. L. Nguyen and I. Kleiner, Phys. Sci. Rev., 2020, 20200037 Search PubMed.
- G. Herdman and G. Neilson, J. Mol. Liq., 1990, 46, 165–179 CrossRef CAS.
- J. Evans, in X-Ray Absorption Spectroscopy for the Chemical and Materials Sciences, John Wiley & Sons, Ltd, Chichester, UK, 2017, pp. 1–8 Search PubMed.
- G. Mancini, G. Brancato and V. Barone, J. Chem. Theory Comput., 2014, 10, 1150–1163 CrossRef CAS.
- F. Fracchia, G. Del Frate, G. Mancini, W. Rocchia and V. Barone, J. Chem. Theory Comput., 2017, 14, 255–273 CrossRef PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- J. H. Holland, Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence, MIT Press, Cambridge, Mass, 1st edn, 1992 Search PubMed.
- Evolutionary computation, ed. D. B. Fogel, T. Bäck and Z. Michalewicz, Institute of Physics Publishing, Bristol, Philadelphia, 2000 Search PubMed.
- D. Whitley, S. Rana and R. B. Heckendorn, J. Comp. Inf. Tech., 1998, 7, 1 Search PubMed.
- D. E. Goldberg, Genetic algorithms in search, optimization, and machine learning, Addison-Wesley Pub. Co, Reading, Mass, 1989 Search PubMed.
- E. Wirsansky, Hands-On Genetic Algorithms with Python: Applying genetic algorithms to solve real-world deep learning and artificial intelligence problems, Packt Publishing Ltd, Birmingham, 2020 Search PubMed.
- F. Lazzari, A. Salvadori, G. Mancini and V. Barone, J. Chem. Inf. Model., 2020, 60, 2668–2672 CrossRef CAS PubMed.
- A. Olsson, G. Sandberg and O. Dahlblom, Struct. Saf., 2003, 25, 47–68 CrossRef.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- G. Santra, N. Sylvetsky and J. M. L. Martin, J. Phys. Chem. A, 2019, 123, 5129–5143 CrossRef CAS PubMed.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS PubMed.
- R. Sure and S. Grimme, J. Comput. Chem., 2013, 34, 1672–1685 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3098–3100 CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- D. Figgen, G. Rauhyt, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227 CrossRef CAS.
- P. Fuentalba, H. Stoll, L. v. Szentpaly, P. Schwerdtfeger and H. Preuss, J. Phys. B, 1983, 16, L323 CrossRef.
- J. M. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408–3420 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. M. Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.01, Gaussian Inc., Wallingford CT 2016 Search PubMed.
- G. Mancini and C. Zazza, PLoS One, 2015, 10, e0137075 CrossRef PubMed.
- G. Mancini, M. Fusè, F. Lipparini, M. Nottoli, G. Scalmani and V. Barone, J. Chem. Theory Comput., 2022, 18, 2479–2493 CrossRef CAS PubMed.
- L. Kaufmann and P. Rousseeuw, Data Analysis based on the L1-Norm and Related Methods, 1987, pp. 405–416 Search PubMed.
- J. Han and M. Kamber, Data mining: concepts and techniques, Elsevier, 3rd edn, 2011 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- P. J. Ballester, I. Westwood, N. Laurieri, E. Sim and W. G. Richards, J. R. Soc. Interface, 2010, 7, 335–342 CrossRef CAS PubMed.
- D. Licari, M. Fusè, A. Salvadori, N. Tasinato, M. Mendolicchio, G. Mancini and V. Barone, Phys. Chem. Chem. Phys., 2018, 20, 26034–26052 RSC.
- L. van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- J. L. Alonso and J. C. López, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, Springer, 2015, pp. 335–401 Search PubMed.
- D. H. Wolpert and W. G. Macready, IEEE Trans. Evol. Comput., 1997, 1, 67–82 CrossRef.
- T. Fornaro, D. Burini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 4224–4236 CrossRef CAS PubMed.
- C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191 CrossRef CAS PubMed.
- V. Barone, G. Ceselin, M. Fusè and N. Tasinato, Front. Chem., 2020, 8, 584203 CrossRef CAS.
- M. Piccardo, E. Penocchio, C. Puzzarini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 2058–2082 CrossRef CAS.
- G. Ceselin, V. Barone and N. Tasinato, J. Chem. Theory Comput., 2021, 17, 7290–7311 CrossRef CAS.
- A. G. Watrous, B. R. Westbrook and R. Fortenberry, J. Phys. Chem. A, 2021, 125, 10532–10540 CrossRef CAS.
- F. Xie, M. Fusè, A. S. Hazrah, W. Jaeger, V. Barone and Y. Xu, Angew. Chem., Int. Ed., 2020, 59, 22427–22430 CrossRef CAS.
- O. Crescenzi, M. Pavone, F. de Angelis and V. Barone, J. Phys. Chem. B, 2005, 109, 445–453 CrossRef CAS PubMed.
- G. Mancini, N. Sanna, V. Barone, V. Migliorati, P. D'Angelo and G. Chillemi, J. Phys. Chem. B, 2008, 112, 4694–4702 CrossRef CAS.
- C. Adamo, A. di Matteo and V. Barone, Adv. Quantum Chem., 1999, 36, 45–76 CrossRef CAS.
- D. Ferro-Costas, I. Mosquera-Lois and A. Fernández-Ramos, J. Cheminf., 2021, 13, 100 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2dd00070a |
| This journal is © The Royal Society of Chemistry 2022 |