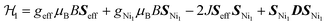Strong magnetic exchange coupling in a radical-bridged trinuclear nickel complex

Abstract

Reaction of 2,3,6,7,10,11-hexaaminotriphenylene hexahydrochloride (HATP·6HCl) and (Tp^PhNi)Cl (Tp^Ph = tris(3,5-diphenyl-1-pyrazolyl)borate) produces the radical-bridged trinickel complex [(Tp^PhNi)₃(HITP)] (HITP³⁻˙ = 2,3,6,7,10,11-hexaiminotriphenylene). Magnetic measurements and broken-symmetry density functional theory calculations reveal strong exchange coupling persisting at room temperature between HITP³⁻˙ and two of the three Ni²⁺ centers, a rare example of strong radical-mediated magnetic coupling in multimetallic complexes. These results demonstrate the potential of radical-bearing tritopic HITP ligands as building blocks for extended molecule-based magnetic materials.

---

Introduction

Radical-mediated coupling of paramagnetic spin centers is an effective strategy for developing molecule-based magnetic materials, including high-temperature multifunctional magnets,^1–3 switchable porous magnetic sensors,^4,5 and low-dimensional compounds with slow relaxation dynamics,^6,7 because coupling in such compounds can give rise to strong and long-range magnetic interactions through the direct exchange mechanisms.^3,8 To date, many ditopic radical-containing ligand bridges have been reported to mediate strong coupling persistent at room-temperature in transition-metal complexes.^9–13 In comparison, trimetallic complexes with tritopic radical bridges, a common topological component for solid-state magnets as well as high-spin-state molecular magnets, are rare and often experience weaker coupling.^3,6,14–16 One promising candidate for a tritopic radical bridge that could mediate strong coupling through π-type delocalized radicals is the trianionic 2,3,6,7,10,11-hexaiminotriphenylene (HITP³⁻˙),¹⁷ a tritopic congener of the radical anion o-benzosemiquinone diimine (BQDI) that is known for strong magnetic exchange coupling with transition metal centers.⁶

Here, we report the synthesis of [(Tp^PhNi)₃(HITP³⁻˙)], 1 (Tp^Ph = tris(3,5-diphenyl-1-pyrazolyl)borate), a trimetallic cluster containing Ni²⁺ centers and an HITP-centered radical. Notably, magnetic measurements reveal strong Ni–HITP coupling between HITP³⁻˙ and two Ni²⁺ spins that persists at room temperature. This interaction is much stronger than the previously reported metal–ligand spin coupling in the oxygen analogs, [(Tp^PhNi)₃(HOTP³⁻˙)] (2)¹⁸ and [(Me₃TPANi)₃(HOTP³⁻˙)] (3)¹⁹ (Me₃TPA = N,N,N-tris[(6-methyl-2-pyridyl)methyl]amine), and is attributed to strong orbital delocalization between Ni²⁺ and the nitrogen atoms on HITP. These results provide inspiration for the rational design of new room-temperature magnetic materials.

Results and discussion

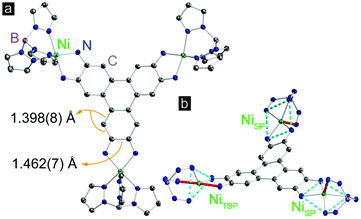
Complex 1 was synthesized by deprotonation of 2,3,6,7,10,11-hexaaminotriphenylene hexahydrochloride with tetrabutylammonium hydroxide under an atmosphere of N₂, followed by reaction with (Tp^PhNi)Cl in air in a dichloromethane–methanol mixture. Dark purple crystals were obtained in 45% yield by layering n-hexane onto a solution of 1 in dichloromethane (Scheme S1†). High resolution electrospray ionization/mass spectrometry (ESI/MS) revealed an M⁺ peak at m/z = 2496.8, which together with microelemental analysis confirmed the identity and purity of 1 (Fig. S1†).

Compound 1 crystallizes in the P1̄ space group, and displays three crystallographically independent Ni atoms. Two of the Ni ions exhibit square pyramidal (SP) geometry, and the third one has trigonal bipyramidal geometry (TBP) (Fig. 1). All Ni centers experience slight distortion from the respective ideal geometries, reflected by the non-zero continuous-shape measurement parameters (Tables S5–S7† and related discussion).²⁰ The bulky κ³-chelating Tp^Ph capping ligands magnetically isolate individual Ni₃HITP units from neighboring molecules. The average Ni–N_Tp bond length, 2.063(6) Å, is in line with the values reported for high-spin Ni²⁺ complexes capped by Tp derivatives.²¹ The average length of the C–C bonds forming Ni–N–C–C–N metallocycles with each phenylenediamine arm within HITP is 1.462(7) Å, much longer than the adjacent C–C bond within the same aromatic ring, 1.398(8) Å (Fig. 1). This reflects a significant distortion of each phenylenediamine ring and evidences the “bisallyl”-type configuration resulting from the oxidation of a fully deprotonated HITP⁶⁻ moiety to HITP³⁻˙ (Scheme S2†).²² For metal–diamine complexes, the degree of oxidation on the diamine fragment is also reflected in the C–N bond lengths.²² In 1, the average C–N_HITP bond length, 1.322(6) Å, lies between that of trimetallic complexes with the fully-reduced HITP⁶⁻ (1.39–1.40 Å) and the more oxidized HITP²⁻ (1.305(6) Å), as may be expected for an intermediate oxidation in HITP³⁻˙.^23,24 Finally, although the Ni–N–C–C–N metallocycles are nearly planar, the triphenylene core of HITP³⁻˙ experiences significant distortion from planarity, with dihedral angles of 20.9°, 26.7°, and 40.1° between pairs of planes defined by the three Ni–N–C–C–N metallocycles (Fig. S2†). Such distortions are not uncommon in large aromatic systems and have been assigned to Jahn–Teller and crystal packing effects.²⁵

Fig. 1 (a) X-ray crystal structure of [(Tp^PhNi)₃(HITP)]. (b) Highlight of the coordination environments of the Ni centers. Turquois dashed lines mark the trigonal and tetragonal planes for Ni_TBP and Ni_SP. Ni–N bonds along the high-symmetry axes are colored pink. Thermal ellipsoids are plotted at 50% probability. Hydrogen atoms, phenyl groups, and solvent molecules are omitted for clarity.

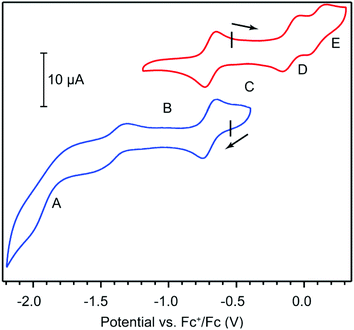
Cyclic voltammetry (CV) provided further evidence in assigning the formal oxidation state of HITP and offered clues on the electronic delocalization in 1. CV measurements in 0.15 M solution of tetrabutylammonium hexafluorophosphate (TBAPF₆) in tetrahydrofuran (THF) under a N₂ atmosphere reveal quasi-reversible electron transfer events centered at −1.41, −0.69, −0.10, and 0.10 V with respect to the ferrocenium/ferrocene couple (Fc⁺/Fc, Fig. 2 and Table S1†). These values are comparable to ligand-centered redox events for other trimetallic HXTP compounds (X = I, O), and are therefore assigned to the HITP^4−/5−, HITP^3−/4−, HITP^2−/3−, and HITP^−/2− redox couples.^18,24,26 In the context of classical mixed-valence theory, which relates electrochemical redox potentials to the degree of electronic delocalization, the potential difference between HITP^4−/5− and HITP^3−/4− corresponds to a comproportionation constant (K_c) of 10^12.2.²⁷ This large value indicates full delocalization among the three phenylenediamine/BQDI arms of the HITP ligand. Additionally, K_c values of 10^10.1 and 10^3.2 between the HITP^3−/4−/HITP^2−/3− and HITP^2−/3−/HITP^−/2− redox couples evidence less delocalization for the more oxidized HITP forms, suggesting that the middle oxidation state, HITP³⁻˙, is the more intriguing candidate for exploring magnetic interactions mediated by HITP.

Fig. 2 Cyclic voltammograms of 1 in a 0.15 M solution of TBAPF₆ in THF under N₂. Black tick marks indicate open circuit potentials. A, B, C, D, and E mark, respectively, the dominant species within the [Ni₃(HITPⁿ⁻)] series (n = 5, 4, 3, 2, 1).

Electron paramagnetic resonance (EPR) spectroscopy provided critical evidence for assigning the spin states in 1. X-band measurement of a frozen glass of 1 in toluene in the range 5–160 K reveals an axial pattern typical for an S = 1/2 spin with g∼2.26, suggesting a thermally-isolated spin state with significant Ni²⁺ character (Fig. S3a†). The absence of signals with g ≥ 4 suggests the absence of S > 1/2 excited states. Because Ni²⁺ possess integer spins (either S = 1 or 0), the observation of a half-integer spin state in 1 suggests the presence of a HITP-centered monoradical.

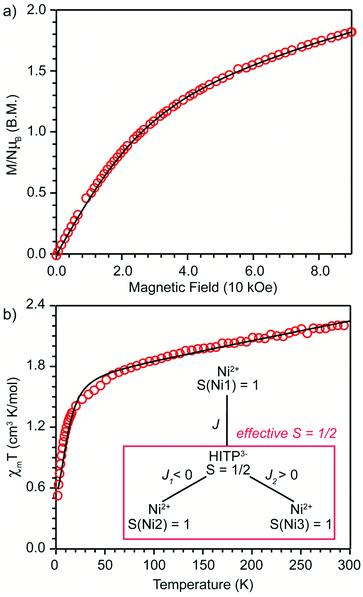
An estimation of the strength of magnetic coupling within 1 came from magnetometry. Variable-field magnetization measurements at 1.8 K reveal gradual increase of the magnetization to 1.83μ_B upon increasing the field to 90 kOe (Fig. 3a). This magnetization value is much higher than the value expected for an S = 1/2 spin (1.0μ_B with g = 2.0). The absence of a saturation plateau at high magnetic field or an inflection point are often associated with the presence of zero-field splitting. The temperature-dependent susceptibility data, χ_MT, at 1 and 10 kOe are superimposable (Fig. S4†), confirming the absence of ferromagnetic impurities. They reveal a gradual decrease from 300 K to 30 K, followed by a steeper drop down to 1.8 K, often also associated with zero-field splitting (Fig. 3b). The χ_MT value of 0.52 cm³ K mol⁻¹ at 1.8 K is close to the value expected for an S = 1/2 spin with g = 2.26 (0.48 cm³ K mol⁻¹), corroborating the ground state spin assignment based on EPR. Meanwhile, a χ_MT value of 2.21 cm³ K mol⁻¹ at 300 K is much smaller than the value expected for three uncoupled S = 1 Ni²⁺ centers and an S = 1/2 ligand (3.375 cm³ K mol⁻¹ with g = 2.0). Instead, it is closer to the value of 1.76 cm³ K mol⁻¹ expected for a two-spin system comprising an S = 1 spin center and an S = 1/2 center with g = 2.26. In 1, such a two-spin system could arise if we consider strong magnetic exchanges between two of the three Ni²⁺ centers and the HITP-centered radical (denoted as Ni–HITP–Ni), together forming a single S = 1/2 effective spin center, which itself then couples to the third Ni²⁺ center with S = 1. With this proposed effective two-spin model, the magnetic data for 1 can be fitted to the following Hamiltonian:

where S_eff and S_Ni represent the collective S = 1/2 spin system described above and the third S = 1 Ni²⁺ center. Good fits are obtained with g_eff = 2.16, g_Ni1 = 2.21, J = −0.79 ± 0.01 cm⁻¹, |D| = 30.2 ± 0.1 cm⁻¹, χ_TIP = 1.94 ± 0.05 × 10⁻³ cm³ mol⁻¹, and a modest intermolecular coupling zJ = +0.19 ± 0.01 cm⁻¹ (see Fig. S5† and related discussion on zJ). These g, J, and |D| values further allow satisfactory fit to the EPR data as well (Fig. S3b†). Meanwhile, two possibilities still remain for the effective S = 1/2 spin centered on Ni–HITP–Ni, with S(Ni2) = S(Ni3) equal to either 1 or 0. As will be discussed below, broken-symmetry density functional theory (BS-DFT) calculations suggest that S(Ni2) = S(Ni3) = 1 is the more appropriate representation for 1. 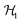Specifically, both strong antiferromagnetic (J₁) and ferromagnetic (J₂) exchange interactions persist at room temperature between independent Ni–HITP pairs, and can be described by incorporating the term −2J₁S_Ni2S_HITP − 2J₂S_Ni3S_HITP into (Fig. 3b inset). Although the weak temperature dependence of χ_MT above 30 K precludes accurate determination of J₁ and J₂, lower bounds can be estimated under the assumption |J₁| = |J₂|, suggesting −J₁ = J₂ ≥ 1300 cm⁻¹ (Fig. S6†). We note that these values should only serve as estimates, because the slope in the high-temperature region of χ_MT is sensitive to subtle changes in diamagnetic corrections.¹¹ Nevertheless, the large estimates for J_1,2 confirm that the tritopic radical bridge enables strong magnetic exchange interactions that persist at room temperature. Alternative spin models did not provide satisfactory fits (see discussion on page 12 in the ESI†).

Fig. 3 (a) Field-dependent magnetization (T = 1.8 K); (b) temperature-dependent χ_mT (H = 1.0 kOe) curves for 1. Solid black lines are fits described in text. Inset: magnetic coupling scheme proposed for 1. The red box highlights two Ni atoms and the HITP ligand forming a single spin system with effective S = 1/2.

BS-DFT analysis provided additional insight into the magnetic interactions in 1. Electronic and spin ground states of 1 were evaluated by comparing the single-point energy of the states with S = 1 (termed “BS state”) or S = 0 (termed “diamagnetic-Ni state”) for the two Ni atoms in the Ni–HITP–Ni moiety (Fig. 3b and S7a†). The calculation revealed the BS state lying 1524.8 cm⁻¹ below the diamagnetic-Ni state, supporting the assignment of all Ni²⁺ having S = 1 spin state in 1 (Fig. 4 and S7b†). Moreover, Löwdin spin density analysis for the BS state showed dominant positive spin density on two of the three Ni atoms, and negative density on HITP and the third Ni, contrasting the diamagnetic-Ni state (Tables S2 and S3†). Two antiferromagnetic and one ferromagnetic coupling pathways exist between HITP³⁻˙ and the three Ni²⁺ spins, in excellent agreement with our interpretation based on magnetometry and EPR. The HITP-centered delocalized spin is further strongly polarized by the Ni spins, an effect commonly observed for π-ligand bridges and radicals.^19,28 The larger asymmetry in the metal–ligand exchange coupling constants in 1 compared with 2 and 3 is likely related to stronger geometric distortion, which results from the more diffuse orbital of the bridgehead atoms and stronger ligand–metal covalent interaction for the nitrogen-based HITP.⁶ Additionally, the BS-DFT analysis together with crystallographic and magnetic characterizations allow tentative assignment of the Ni identity. Ni1 (Fig. 3 and 4) can be assigned as the crystallographic site Ni3A (Fig. S8†) due to its unique TBP geometry. The weaker exchange coupling with HITP³⁻˙ is likely due to poorer orbital overlap resulted from the larger geometric distortion from an ideal geometry (Table S7†). Because no alternative BS state (for instance J₁ > 0 and J₂ < 0) could be converged, the two Ni with TBP geometry, Ni2 and Ni3, can be assigned as the crystallographic sites of Ni2A and Ni1A, respectively. This reflects the influence of global symmetry, beside local symmetry, on the nature of exchange coupling between the metal and the radical bridge, as can be observed in the structurally related compounds 2 and 3.^18,19

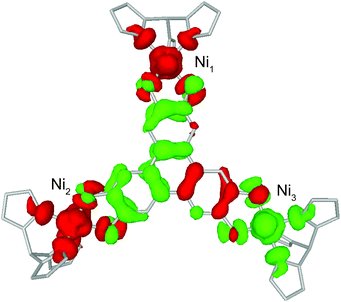Fig. 4 Calculated spin density isosurfaces (0.0015 a.u.) in the broken-symmetry state of 1. Red and green represent positive and negative spin densities. Labels for Ni are consistent with Fig. 3.

Conclusions

Altogether, crystallographic, electrochemical, magnetic, and computation analyses demonstrate that an HITP radical bridge enables strong magnetic coupling, exemplified here in a trinickel complex. The two Ni–HITP exchange interactions are rare examples of radical-mediated coupling persistent at room temperature in complexes with a tritopic radical bridge, and are comparable to the metal–radical coupling in well-known dinickel bis(BQDI) complexes.²⁹ These results also confirm that radical-mediated coupling with amine-based HITP in 1 is much stronger than with catechol-based HOTP in 2 and 3, and stronger too than with closed-shell HITP tritopic bridges.^18,19,24,26 The enhanced coupling for nitrogenous ligands is in line with previous observations in diradical-bridged complexes,³⁰ and is likely due to the more diffuse nitrogen orbitals of the radical bridge and better orbital energy match with the metal centers. These results provide motivation for using HITP³⁻˙ as a particularly attractive bridging ligand for other magnetic molecules and solids, where uniform strong coupling may be achieved through supramolecular design or crystal packing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Prof. T. D. Harris for valuable discussions. This research was funded by the National Science Foundation (Waterman Award to MD; DMR-1645232). We thank the Massachusetts Green High-Performance Computer C3DDB for providing computing resources.

Notes and references

1. P. Dechambenoit and J. R. Long, Chem. Soc. Rev., 2011, 40, 3249.
2. G. Mínguez Espallargas and E. Coronado, Chem. Soc. Rev., 2018, 47, 533–557.
3. A. E. Thorarinsdottir and T. D. Harris, Chem. Rev., 2020, 120, 8716–8789.
4. N. Motokawa, S. Matsunaga, S. Takaishi, H. Miyasaka, M. Yamashita and K. R. Dunbar, J. Am. Chem. Soc., 2010, 132, 11943–11951.
5. J. Zhang, W. Kosaka, K. Sugimoto and H. Miyasaka, J. Am. Chem. Soc., 2018, 140, 5644–5652.
6. S. Demir, I. R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176.
7. M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352.
8. A. Caneschi, D. Gatteschi, R. Sessoli and P. Rey, Acc. Chem. Res., 1989, 22, 392–398.
9. C. Benelli, A. Dei, D. Gatteschi and L. Pardi, Inorg. Chem., 1988, 27, 2831–2836.
10. V. I. Ovcharenko, E. V. Gorelik, S. V. Fokin, G. V. Romanenko, V. N. Ikorskii, A. V. Krashilina, V. K. Cherkasov and G. A. Abakumov, J. Am. Chem. Soc., 2007, 129, 10512–10521.
11. I.-R. Jeon, J. G. Park, D. J. Xiao and T. D. Harris, J. Am. Chem. Soc., 2013, 135, 16845–16848.
12. K. Chłopek, E. Bothe, F. Neese, T. Weyhermüller and K. Wieghardt, Inorg. Chem., 2006, 45, 6298–6307.
13. N. Mavragani, D. Errulat, D. A. Gálico, A. A. Kitos, A. Mansikkamäki and M. Murugesu, Angew. Chem., Int. Ed., 2021 DOI:10.1002/anie.202110813.
14. C. A. Gould, L. E. Darago, M. I. Gonzalez, S. Demir and J. R. Long, Angew. Chem., Int. Ed., 2017, 56, 10103–10107.
15. A. Datcu, N. Roques, V. Jubera, D. Maspoch, X. Fontrodona, K. Wurst, I. Imaz, G. Mouchaham, J.-P. Sutter, C. Rovira and J. Veciana, Chem. – Eur. J., 2012, 18, 152–162.
16. J. O. Moilanen, N. F. Chilton, B. M. Day, T. Pugh and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 5521–5525.
17. R. Breslow, B. Jaun, R. Q. Kluttz and C. Xia, Tetrahedron, 1982, 38, 863–867.
18. Y. Wang, F. Lambert, E. Rivière, R. Guillot, C. Herrero, A. Tissot, Z. Halime and T. Mallah, Chem. Commun., 2019, 55, 12336–12339.
19. L. Yang and M. Dincă, Angew. Chem., Int. Ed., 2021, 60, 23784–23789.
20. J. Cirera, E. Ruiz and S. Alvarez, Organometallics, 2005, 24, 1556–1562.
21. D. J. Harding, P. Harding, H. Adams and T. Tuntulani, Inorg. Chim. Acta, 2007, 360, 3335–3340.
22. S. Pascal and O. Siri, Coord. Chem. Rev., 2017, 350, 178–195.
23. F. Zhong, X. Yang, L. Shen, Y. Zhao, H. Ma, B. Wu and X. J. Yang, Inorg. Chem., 2016, 55, 9112–9120.
24. L. Yang, X. He and M. Dincǎ, J. Am. Chem. Soc., 2019, 141, 10475–10480.
25. T. Kato and T. Yamabe, Chem. Phys. Lett., 2005, 403, 113–118.
26. N. Hoshino and T. Akutagawa, Chem. – Eur. J., 2018, 24, 19323–19331.
27. D. E. Richardson and H. Taube, Coord. Chem. Rev., 1984, 60, 107–129.
28. T. Glaser, M. Heidemeier, J. B. H. Strautmann, H. Bögge, A. Stammler, E. Krickemeyer, R. Huenerbein, S. Grimme, E. Bothe and E. Bill, Chem. – Eur. J., 2007, 13, 9191–9206.
29. K. Chłopek, E. Bothe, F. Neese, T. Weyhermuller and K. Wieghardt, Inorg. Chem., 2006, 45, 6298–6307.
30. D. Schweinfurth, M. M. Khusniyarov, D. Bubrin, S. Hohloch, C.-Y. Su and B. Sarkar, Inorg. Chem., 2013, 52, 10332–10339.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2109142. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt01337a

---