Open Access Article
Open Access ArticleSurvival of newly formed particles in haze conditions†
Ruby
Marten
 a,
Mao
Xiao
a,
Birte
Rörup
a,
Mao
Xiao
a,
Birte
Rörup
 b,
Mingyi
Wang
c,
Weimeng
Kong
d,
Xu-Cheng
He
b,
Dominik
Stolzenburg
b,
Joschka
Pfeifer
ef,
Guillaume
Marie
b,
Mingyi
Wang
c,
Weimeng
Kong
d,
Xu-Cheng
He
b,
Dominik
Stolzenburg
b,
Joschka
Pfeifer
ef,
Guillaume
Marie
 f,
Dongyu S.
Wang
a,
Wiebke
Scholz
f,
Dongyu S.
Wang
a,
Wiebke
Scholz
 g,
Andrea
Baccarini
g,
Andrea
Baccarini
 ah,
Chuan Ping
Lee
ah,
Chuan Ping
Lee
 a,
Antonio
Amorim
i,
Rima
Baalbaki
b,
David M.
Bell
a,
Antonio
Amorim
i,
Rima
Baalbaki
b,
David M.
Bell
 a,
Barbara
Bertozzi
j,
Lucía
Caudillo
f,
Biwu
Chu
b,
Lubna
Dada
a,
Barbara
Bertozzi
j,
Lucía
Caudillo
f,
Biwu
Chu
b,
Lubna
Dada
 a,
Jonathan
Duplissy
a,
Jonathan
Duplissy
 dk,
Henning
Finkenzeller
dk,
Henning
Finkenzeller
 l,
Loïc Gonzalez
Carracedo
m,
Manuel
Granzin
f,
Armin
Hansel
l,
Loïc Gonzalez
Carracedo
m,
Manuel
Granzin
f,
Armin
Hansel
 g,
Martin
Heinritzi
f,
Victoria
Hofbauer
c,
Deniz
Kemppainen
b,
Andreas
Kürten
g,
Martin
Heinritzi
f,
Victoria
Hofbauer
c,
Deniz
Kemppainen
b,
Andreas
Kürten
 f,
Markus
Lampimäki
f,
Markus
Lampimäki
 b,
Katrianne
Lehtipalo
bn,
Vladimir
Makhmutov
b,
Katrianne
Lehtipalo
bn,
Vladimir
Makhmutov
 o,
Hanna E.
Manninen
o,
Hanna E.
Manninen
 e,
Bernhard
Mentler
e,
Bernhard
Mentler
 g,
Tuukka
Petäjä
g,
Tuukka
Petäjä
 b,
Maxim
Philippov
b,
Maxim
Philippov
 o,
Jiali
Shen
b,
Mario
Simon
o,
Jiali
Shen
b,
Mario
Simon
 f,
Yuri
Stozhkov
o,
António
Tomé
p,
Andrea C.
Wagner
f,
Yuri
Stozhkov
o,
António
Tomé
p,
Andrea C.
Wagner
 f,
Yonghong
Wang
b,
Stefan K.
Weber
f,
Yonghong
Wang
b,
Stefan K.
Weber
 e,
Yusheng
Wu
b,
Marcel
Zauner-Wieczorek
e,
Yusheng
Wu
b,
Marcel
Zauner-Wieczorek
 f,
Joachim
Curtius
f,
Joachim
Curtius
 f,
Markku
Kulmala
f,
Markku
Kulmala
 b,
Ottmar
Möhler
j,
Rainer
Volkamer
b,
Ottmar
Möhler
j,
Rainer
Volkamer
 l,
Paul M.
Winkler
m,
Douglas R.
Worsnop
q,
Josef
Dommen
l,
Paul M.
Winkler
m,
Douglas R.
Worsnop
q,
Josef
Dommen
 a,
Richard C.
Flagan
a,
Richard C.
Flagan
 d,
Jasper
Kirkby
ef,
Neil M.
Donahue
d,
Jasper
Kirkby
ef,
Neil M.
Donahue
 c,
Houssni
Lamkaddam
*a,
Urs
Baltensperger
a and
Imad
El Haddad
c,
Houssni
Lamkaddam
*a,
Urs
Baltensperger
a and
Imad
El Haddad
 *a
*a
aLaboratory of Atmospheric Chemistry, Paul Scherrer Institute, 5232 Villigen, Switzerland. E-mail: houssni.lamkaddam@psi.ch; imad.el-haddad@psi.ch
bInstitute for Atmospheric and Earth System Research (INAR)/Physics, Faculty of Science, University of Helsinki, 00014 Helsinki, Finland
cCenter for Atmospheric Particle Studies, Carnegie Mellon University, 15213 Pittsburgh, PA, USA
dCalifornia Institute of Technology, Division of Chemistry and Chemical Engineering 210-41, Pasadena, CA 91125, USA
eCERN, CH-1211 Geneva, Switzerland
fInstitute for Atmospheric and Environmental Sciences, Goethe University Frankfurt, 60438 Frankfurt am Main, Germany
gInstitute of Ion Physics and Applied Physics, University of Innsbruck, 6020 Innsbruck, Austria
hExtreme Environments Research Laboratory (EERL), École Polytechnique Fédérale de Lausanne, Sion, CH, Switzerland
iCENTRA, FCUL, University of Lisbon, 1749-016 Lisbon, Portugal
jInstitute of Meteorology and Climate Research, Karlsruhe Institute of Technology, 76021 Karlsruhe, Germany
kHelsinki Institute of Physics (HIP)/Physics, Faculty of Science, University of Helsinki, 00014 Helsinki, Finland
lDepartment of Chemistry, CIRES, University of Colorado Boulder, 215 UCB, Boulder, 80309, CO, USA
mFaculty of Physics, University of Vienna, Boltzmanngasse 5, A-1090 Vienna, Austria
nFinnish Meteorological Institute, Helsinki, Finland
oLebedev Physical Institute of the Russian Academy of Sciences, Leninsky Prospekt, 53, Moscow 119991, Russian Federation
pIDL-Universidade da Beira Interior, 6201-001 Covilhã, Portugal
qAerodyne Research, 01821 Billerica, MA, USA
First published on 8th April 2022
Abstract
Intense new particle formation events are regularly observed under highly polluted conditions, despite the high loss rates of nucleated clusters. Higher than expected cluster survival probability implies either ineffective scavenging by pre-existing particles or missing growth mechanisms. Here we present experiments performed in the CLOUD chamber at CERN showing particle formation from a mixture of anthropogenic vapours, under condensation sinks typical of haze conditions, up to 0.1 s−1. We find that new particle formation rates substantially decrease at higher concentrations of pre-existing particles, demonstrating experimentally for the first time that molecular clusters are efficiently scavenged by larger sized particles. Additionally, we demonstrate that in the presence of supersaturated gas-phase nitric acid (HNO3) and ammonia (NH3), freshly nucleated particles can grow extremely rapidly, maintaining a high particle number concentration, even in the presence of a high condensation sink. Such high growth rates may explain the high survival probability of freshly formed particles under haze conditions. We identify under what typical urban conditions HNO3 and NH3 can be expected to contribute to particle survival during haze.
Environmental significanceHaze and pollution affect visibility, local climate, and human health. Current understanding of new particle formation and growth mechanisms cannot explain how high number concentrations of nucleated particles are sustained during haze events, as the loss processes for new clusters seem to outcompete growth. It has been proposed that either scavenging of small particles is overestimated, or that there is a missing growth mechanism. We present measurements, and supporting model calculations, showing efficient scavenging of clusters involving unit sticking probability. Furthermore, we show that rapid growth from ammonium nitrate formation increases survival of clusters in the presence of haze. Ammonium nitrate formation may be a missing growth mechanism which contributes to sustaining high particle numbers during haze in urban environments. |
Introduction
Aerosols play a key role in cloud formation and climate,1–3 substantially offsetting the warming by greenhouse gases.4 It is therefore important to understand what mechanisms are driving the formation and growth of aerosols, so that climate models can include them. Of equal importance, nucleation and growth of aerosols leads to persistent pollution in megacities, which can also be responsible for changes in local weather systems and local climate forcing.5,6 In addition, particulate pollution causes millions of premature deaths annually, and is one of the leading causes of deaths globally.7–9Once new particles have been formed, they are able to grow via condensation of vapours. The growth must be fast enough to rival coagulation with larger particles, referred to as the coagulation sink. Particles smaller than 10 nm have high Brownian diffusivity and are therefore most vulnerable to coagulation loss.10 The likelihood of a particle's survival is dependent on a balance between growth rate and coagulation sink. Previous understanding was that growth rates in cities are only up to a few times greater than those in clean environments.11 Therefore, under highly polluted conditions seen in cities, newly formed particles are not expected to survive very long before sticking to larger particles. However, intense new particle formation events are regularly observed under these conditions, with particle formation rates up to hundreds of times higher than in clean environments,12–16 despite the high loss rates of nucleated clusters. Currently, there is a major gap in our understanding as to how the particle number concentration can be sustained under such highly polluted conditions. Higher than expected cluster survival through the most critical size range (the so-called “valley of death” between nucleated particles and ∼10 nm) implies either ineffective scavenging by pre-existing particles or a missing growth mechanism.17
Recently, Wang et al. (2020)18 presented a new mechanism of rapid particle growth, affecting particles as small as a few nanometers, via condensation of HNO3 and NH3. Ammonium nitrate is an important semi-volatile constituent of large particles, previously thought to be too volatile to contribute to early growth. However, Wang et al. (2020) demonstrated that in conditions of excess NH3 and HNO3 mixing ratios, with respect to ammonium nitrate saturation ratios, particles as small as a few nanometers can be activated to rapidly grow to much larger sizes, analogous to CCN activation. Ammonium nitrate growth affects particles once they reach a critical diameter, referred to as the activation diameter. This growth mechanism could play a key role in high survival of small particles and therefore explain the maintenance of high particle number concentration under highly polluted conditions. An alternative mechanism that has been also suggested would be that our current understanding of loss rates is incomplete, and clusters are not efficiently lost to large particles.17 However, neither theory has been experimentally tested or verified to date. In this work, we present the first combined experimental and model results of survival of small particles in the presence of a high coagulation sink, analogous to haze.
Methods
The CLOUD chamber at CERN
The experiments presented were undertaken at the CLOUD (Cosmics Leaving OUtdoor Droplets) chamber at CERN (European Organization for Nuclear Research). The conditions in the chamber were controlled to 5 °C and 60% relative humidity (RH). Further details on the CLOUD chamber experiments can be found in the ESI.†Modelling ammonium sulfate
The sulfuric acid and ammonia nucleation and growth model is based on the model described in detail in Xiao et al. (2021)11 which is developed from the general dynamic equation.19 Briefly, the model calculates particle and gas concentrations for each time step via a sum of production and losses for each gas, cluster or particle size bin. When organic oxidation products were present in the experiments, nucleation and growth were parameterised in the model to that of the experiment. This was achieved by increasing the H2SO4 concentration used in the model to account for enhanced growth rates since this model does not include organic oxidation products.Particle loss rates
For the particle loss rates in the chamber, we consider wall loss, dilution loss, and coagulation loss (or gain). We calculate the coagulation change in each size bin using the coagulation coefficient and the general dynamic equation from Seinfeld and Pandis (2006)19 and solving for the change in particle number for each size bin for each time step.11,20Modelling ammonium nitrate
We developed an ammonium nitrate growth model addition to the ammonium sulfate model. It is a polydisperse growth model, with 150 bins ranging from one ammonium sulfate cluster to 1000 nm, which also provides the time evolution of particle size and composition. We predict condensation of ammonium nitrate based on the equilibrium of NH3 and HNO3 in the gas phase. NH3 and HNO3 concentrations are also calculated by summing up production and losses at each time step (injection, photolysis, wall loss, dilution loss, condensation, etc.). For some experiments, gas phase concentration or formation rates were constrained from measurements. As shown in Wang et al. (2020)18 ammonium nitrate condensation behaves much like CCN activation, and the behaviour is consistent with the nano-Köhler theory. A mass flux is established, based on whether the ammonium nitrate is in supersaturation or not. The supersaturation was calculated based on the dissociation constant Kp,21 defined as the equilibrium product of gas phase NH3 and HNO3. Supersaturation of ammonium nitrate is equal to ([NH3]g × [HNO3]g)/Kp. The fluxes of HNO3 and NH3 are considered to be equal and dependent on the limiting gas, since formation of ammonium nitrate is equimolar. Therefore, we calculate the net flux of NH3 and HNO3 at every time step and include a Kelvin term and activity term in order to calculate the different fluxes for different particle sizes (see eqn (S.3) ESI† – Modelling ammonium nitrate).Results
Modelling rapid growth from ammonium nitrate condensation
Experiments were undertaken at the CLOUD chamber at CERN under various concentrations of H2SO4, NH3 and HNO3 at 5 °C and 60% relative humidity, and in some instances in the presence of dimethyl amine and/or organic oxidation products formed from α-pinene or toluene. Fig. 1(c) shows experimental CLOUD (2018) and kinetic model results and the dependence of the growth rate of particles after activation by ammonium nitrate on the excess ammonium nitrate concentration. The excess ammonium nitrate is calculated by subtracting the dissociation constant Kp from the product of the gas phase NH3 and HNO3 concentrations, this represents the amount of gas available for condensational growth, once the particles have grown as large as the activation diameter. In the majority of CLOUD experiments presented, the limiting gas for condensation was HNO3, as the experimental design was intended to be comparable to ambient conditions where NH3 is usually in excess. The modelled growth rates are in good agreement with measured growth rates from CLOUD, and the model replicates qualitatively and quantitatively the evolution of the entire size distribution with particles rapidly growing by ammonium nitrate condensation once they reach a critical diameter of ∼4 nm for the experiment shown.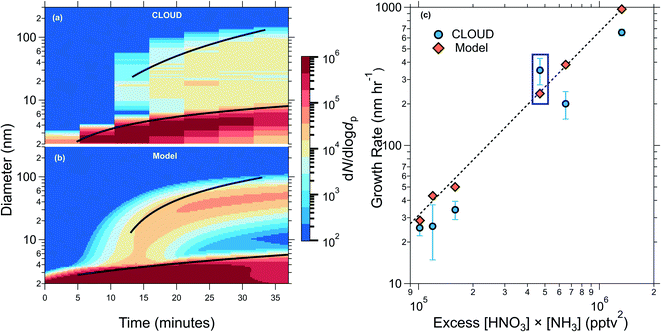 | ||
| Fig. 1 Comparison of measured and modelled growth rates. (a) Particle size distribution from an example CLOUD experiment showing rapid growth from NH4NO3 formation once the activation diameter (vapour supersaturation including the Kelvin effect) is reached. (b) Model prediction for the experiment in (a). The black traces in (a) and (b) show the 50% appearance time. The initial experimental conditions are 1891 pptv NH3, 352 pptv HNO3, and 3.9 × 107 molecules per cm3 H2SO4. The inputs to the model are the production rates of HNO3, NH3, and H2SO4, and the Kelvin diameter determined from other CLOUD experiments (see ESI† – Modelling ammonium nitrate). (c) Measured particle growth rates after activation versus excess [HNO3] × [NH3] vapour product (round points, previously shown in Wang et al. (2020)18). The excess vapour product is the supersaturation for the formation of ammonium nitrate, and is determined by subtracting the calculated equilibrium vapour product from the measured value. The round points were determined using the 50% appearance time method (see ESI† – growth rates). The diamond points show the growth rates obtained by fitting modelled data for each experiment. The growth rates corresponding to panels a and b are indicated by a blue box. The dashed black curve shows a power law fit through the model values of the form y = kxp, with p = 1.33 and k = 7 × 10−6. All experiments were performed at 5 °C and 60% relative humidity. | ||
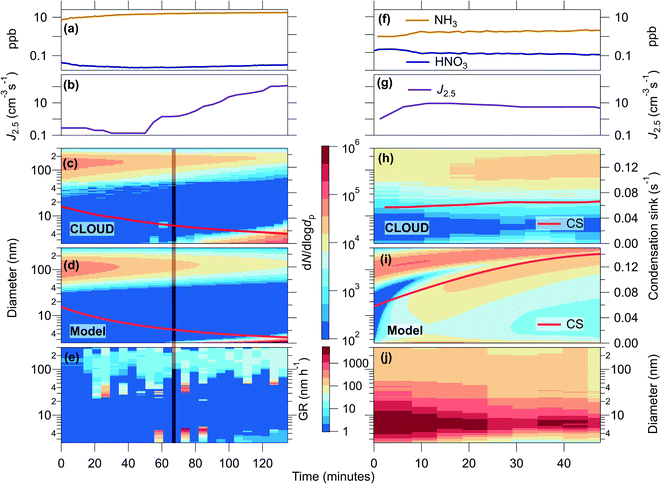
The effect of high growth rates in the presence of high coagulation sink
We generated a high condensation sink (CS), with loss rates comparable to those found during haze, in order to verify experimentally the loss rates of small clusters, and to test the effect of high growth rates on the survival of small particles. Condensation is a sink for condensable gases and depends on the surface area, and coagulation is a sink for particles that depends on the diameter of the colliding particles. In Fig. 2 we present two CLOUD experiments (one longer than the other) at 5 °C and 60% relative humidity, summarising the observations (panels a–c, e and f–h, j) and our kinetic model results (panels d and i).Run 1 of the CLOUD measurements shown in Fig. 2(a–c and e) presents results of an experiment in which we observed no nucleation under the initial high CS. The initial concentrations of this experiment were ∼2.5 × 106 molecules per cm3 H2SO4, ∼0.03 ppbv HNO3, ∼6 ppbv NH3 and an initial CS of ∼0.06 s−1. During the experiment the CS steadily decayed due to dilution in the CLOUD chamber, as well as evaporation of NH4NO3 due to sub-saturated conditions of gas phase NH3 and HNO3. The gas phase NH3 was constantly increasing, although the injection rate was constant, most likely due to increased production rate of NH3 by evaporation, combined with a decreasing loss rate to the CS resulting in a higher steady state concentration. HNO3 should experience the same changes in loss and production rates, but the increase in concentration in Fig. 2(a) is delayed. This is probably due to its higher wall loss rate (i.e. the walls are not an effective source and act as a sink), and the fact that HNO3 is not in steady state at the beginning of the experiment, as each run starts with the onset of lights and therefore HNO3 production. Nucleation of particles commenced once the CS dropped to approximately 0.03 s−1 (indicated with a vertical orange line). As the condensation sink decreased further, the nucleation rate continued to increase and the particles continued to grow, although at relatively slow rates. In this experiment, neither particle formation and growth nor condensation to the larger mode was sufficient to sustain the particle number and the CS.
Run 2 of the CLOUD measurements in Fig. 2(f–h and j) shows a second experiment, with similar initial conditions but higher HNO3 concentration (∼6 × 106 cm−3 H2SO4, ∼0.2 ppbv HNO3, ∼1.7 ppbv NH3, and an initial CS of ∼0.06 s−1). We observe that not only were the condensation sink and particle number sustained, but small particles were present from the beginning of the experiment, with measurable and continuous formation of 2.5 nm particles (J2.5) as well as high growth rates. Since loss rates of particles to dilution are the same between the two runs, comparing the progression of the large particle mode in Fig. 2(c and h) can elucidate much about the growth of particles. Although growth does not manifest as a typical new particle formation (NPF) and growth event in Fig. 2(h), it is clear from comparing to Fig. 2(c) that rapid and continuous growth is occurring. In Fig. 2(c), the lower end of the large pre-existing particle mode increases in diameter due to slow growth of the particles, while the CS and particle number decreases. However, in Fig. 2(h) there are continuous particle concentrations around 10 nm and a steady CS, which can only be explained by new particle formation and rapid growth. Furthermore, as time progresses in Fig. 2(h), the particle number concentration at large sizes (indicated by colour) increases, whereas for Fig. 2(c) it is decreasing. These results indicate that, with sufficient HNO3 and NH3, higher growth rates at small particle sizes can shepherd small particles to larger sizes through the so-called “valley of death”, and thus sustain particle number concentration and CS during haze events.
Panels e and j present size and time dependent growth rates calculated using the INSIDE method.22,23 Panel e shows that initially, before the onset of nucleation, the only measured growth is slow growth of large particles, most likely caused by condensable gases present other than NH3 and HNO3. While there are relatively low growth rates for the newly formed particles (<4 nm) in panel j, as soon as the activation diameter is reached the particles experience extremely rapid and continuous growth just above the activation diameter, leading to rapid condensational loss, resulting in the apparent gap in the particle-number size distribution. Similar observations of apparent gaps in the particle size distribution, due to ammonium nitrate growth, were also reported in Wang et al. (2020).18 The activation diameter is increasing during the first 20 minutes of run 2; this is visible as the leading edge of the nucleation mode is increasing in diameter (Fig. 2(h)), concurrent with lower growth rates (Fig. 2(j)). As the gas phase NH3 and HNO3 concentrations stabilise (Fig. 2(f)) the activation diameter also stabilises.
Panels d and i of Fig. 2 show the kinetic modelling results of these runs. Each model run had initial and boundary conditions consistent with the corresponding experimental run. We initialized both simulations with a condensation sink of ∼0.06 s−1, comprising particles with a 100 nm modal diameter. We constrained J2.5 and the concentrations of NH3 and HNO3 to the experimental values and the production rate of H2SO4. For run 1 (a–e), the model agrees qualitatively and quantitatively with the observations. For run 2 (f–j) the model agrees qualitatively but with evident differences that we shall discuss. In run 1, even with the rise in J2.5 after ∼65 min, the particles only grow a few nm before being lost, and the CS declines steadily due to ventilation without being counterbalanced by newly formed growing particles. A second simulation with J2.5 constrained to 10 cm−3 s−1 throughout the run shows very similar results, with essentially no growth before 65 min and only feeble growth afterwards (Fig. S1(a and b)†). Sensitivity tests show that the differences in H2SO4 and NH3 between the experiments also do not have a strong influence on the particle size distribution (Fig. S1(c and d)†). With these experiments, we demonstrate that our current understanding of coagulation loss rates of small particles, which we use in the model, is correct as the results match well with the experiments, i.e. clusters and small particles are efficiently lost to large particles, and inefficient coagulation is not the explanation for measured J rates in polluted conditions.
For run 2 (f–j) model simulation we found the lower limit where we could reproduce this experiment was at concentrations of ∼0.3 ppbv HNO3 and ∼3.8 ppbv NH3, around two times larger than the estimated concentrations in the chamber. This discrepancy is within the estimated errors of gas concentrations for these runs (see ESI†). The model reproduces the observed “smear” of particles across the size distribution, with an indistinct minimum near 5 nm. However, the “CS mode” at 100 nm also grows rapidly, in contrast to the observations. The rapidly increasing diameter of the gap in between the nucleation and Aitken modes in panel (i) is most likely an artefact of the initial conditions. We thus confirm the high particle survival as well as the persistent CS, which is sustained against losses as the result of ammonium nitrate-enabled particle activation. The model-measurement differences likely arise from multiple factors, predominantly because experimental conditions were changing dynamically, making it more difficult to constrain the model accurately. As seen in Fig. S2–S4 (ESI†) the activation diameter and especially the growth rate are very sensitive to the experimental, or ambient, conditions. Specifically, the growth rate depends on the diameter, and close to the activation diameter, dact, the growth rate rapidly increases with increasing diameter. The sensitivity is especially high when HNO3 and NH3 are near stoichiometric equivalence, such as in this case (Fig. S4†). The activation diameter is then also sensitive to the saturation concentration, S where a small change in S can result in a large change in activation diameter. Finally, certain data limitations (lack of particle composition measurements, lack of HNO3 measurements etc.) meant that the model could not be constrained to all experimental conditions. The result of these effects is that, in a dynamic situation such as in the CLOUD experiments or ambient environments, we expect to observe a size distribution as we have observed, due to changes in sinks and sources resulting in rapid changes in growth rate and activation. The differences in Fig. 2(h and i) indicate that ammonium nitrate growth would not necessarily be classified as a NPF event, and thus could be overlooked in ambient data. We also do not yet include the effect of van der Waals forces, which for sulfuric acid – NH3 growth can enhance sub-10 nm growth by up to a factor of 2.20 While van der Waals forces have a small effect on the overall results, they might contribute to high growth rates in the smallest particles without causing a higher growth at larger sizes (see ESI† – Modelling ammonium nitrate).
Effect of NH3 and HNO3 concentrations on particle survival
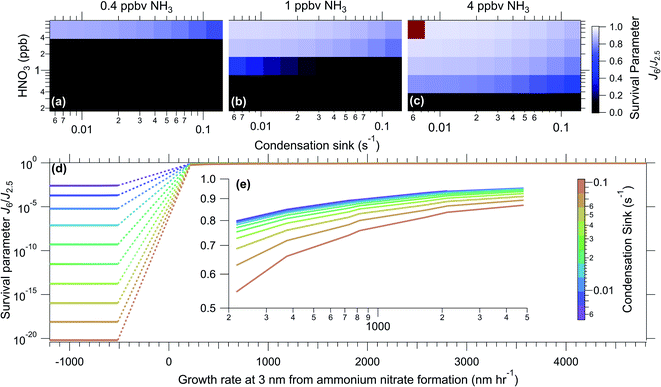
Results from Fig. 1 and 2 indicate that the model accurately captures the growth by ammonium nitrate, as well as particle loss rates; therefore, the model most likely accurately represents the underlying physics and chemistry of particle growth associated with ammonium nitrate activation. We now use the model to explore under which atmospherically relevant conditions ammonium nitrate condensation could enhance the survival of newly formed particles.The model was run at 5 °C with NH3 and HNO3 concentrations ranging from 400 pptv to 4 ppbv and the condensation sink ranging from 0.01 to 0.13 s−1 covering a range of low particle surface area to extremely high limits. We define the survival parameter as the ratio of the formation rate of 6 nm (J6) particles to that of 2.5 nm (J2.5) particles at steady state, i.e. the proportion of how many particles survived between 2.5 and 6 nm. We feed the model with 2.5 nm particles (J2.5 = 10 cm−3 s−1) and assume no evaporation of clusters of H2SO4 (kinetic nucleation). All model runs have the same production rate of H2SO4, which, in the absence of a condensation sink, leads to ∼10 nm h−1 early growth (1.8–3.2 nm) for non-activated particles.
Fig. 3 indicates the calculated ammonium-nitrate-driven growth rate at 3 nm of model and CLOUD experiments via symbol colour, with points plotted as survival parameter against condensation sink. The fuchsia diamond symbols represent a CLOUD run with low amounts of HNO3, as in Fig. 2, panels a–c. We can see that as the CS decayed and particles began to grow that the survival significantly increased compared to at higher CS. The purple diamond symbols represent the run with higher HNO3 (Fig. 2 panels f–h and j), and these points along with the model points show us that at high growth rates, the condensation sink has little effect on the survival, and these points even approach unity. Although there is relatively high survival at low condensation sinks (∼0.01 s−1), even with slower growth rates, at high condensation sinks the only experiments that saw high survival were those with activation and high growth rates. This confirms our theory that high growth rates are able to “shepherd” small particles through size ranges where they are most vulnerable to loss.
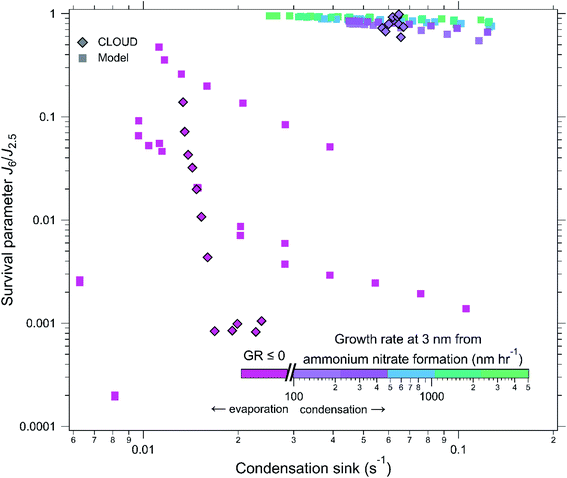 | ||
| Fig. 3 Survival parameter of newly formed particles versus condensation sink: the survival parameter is defined as the particle formation rate at 6 nm divided by the formation rate at 2.5 nm, i.e. J6/J2.5. CLOUD measurements are indicated by diamond symbols and model simulations by square symbols without outlines. The points are coloured according to the particle growth rate at 3 nm, calculated from the measured HNO3 and NH3 concentrations (Fig. 1), the fuchsia colour indicates conditions of either no growth (GR = 0) or evaporation of NH4NO3 (GR < 0). The CLOUD experiments are those shown in Fig. 2, the experimental conditions are listed in its caption. All the model simulations assume kinetic nucleation (zero evaporation), and ∼10 nm h−1 early growth (from H2SO4) for non-activated particles, in the absence of any particle condensation sink. The model assumes a constant J2.5 of 10 cm−3 s−1. The model conditions are 5 °C, HNO3 and NH3 between 400 pptv and 4 ppbv, and a condensation sink between 0.01 and 0.13 s−1. Experiments where the activation diameter is sufficiently low that the non-activated growth surpasses it result in activation of particles. Activated particles grow rapidly enough to survive loss in the presence of high condensation sinks whereas non-activated particles have very low survival probabilities. The experimental measurements show that the rapid particle growth rates from ammonium nitrate formation are sufficient to overcome losses of newly formed particles in high condensation sink environments. The good agreement of the model with the experimental data confirms that particle scavenging involves unit sticking probability, as expected from previous measurements in low condensation sink environments. | ||
Discussion and conclusions
Fig. 4 illustrates results from model runs over the selected concentration ranges. As can be seen, the results are almost binary, with a sharp transition from a region of no survival to a region of high survival, showing how crucial activation is for survival. In parts b and c, at high HNO3 concentrations, the effect of the condensation sink is very small. This can also be seen in part d of the Fig. 4, but with the calculated growth rate caused by ammonium nitrate formation (at 3 nm) on the x-axis. Growth rates from ammonium nitrate formation directly scale with the flux of HNO3 and NH3. The ammonium nitrate flux is dependent on the concentration of gas phase NH3 and HNO3, as well as on which gas is limiting, and the size of the particle, the full equations are found in the ESI.† The region between negative and positive growth rates (evaporation and condensation, respectively) is where we see a step in survival, and above this region the condensation sink has a smaller effect. In panel d, it is also more visible that at calculated negative growth rates the survival is highly dependent on the condensation sink (though it is always low). In this region, the survival is controlled by H2SO4 and NH3 growth, as without activation HNO3 does not contribute to nucleation and growth. Although the calculated flux, and therefore growth rate, of ammonium nitrate is negative, when there is no ammonium nitrate in the particles evaporation will not occur.Survival of particles will depend on not only the growth rate, but also the activation diameter, since if particles are not large enough for NH3 and HNO3 to condense on there will be no activation. Therefore the contribution of activation to survival of particles will also depend on the pre-existing particle distribution. Since we constrain J2.5 in our model, and the experiments with positive flux shown in Fig. 4(d and e) have activation diameters under 2.5 nm, all of the particles can be activated.
The observed differences in Fig. 2 parts (h) and (i) give a strong indication that although these processes may happen under ambient conditions, they are most probably masked to researchers as they do not appear as typical NPF events. This is especially the case because deviations from equilibrium are expected to be brief in the ambient atmosphere, and vapour concentrations of NH3 and HNO3 tend rapidly towards equilibrium. However, even short perturbations above saturation may drive the rapid growth of nucleating particles at rates up to one thousand times faster than growth by H2SO4 condensation, given the disparity between HNO3 and H2SO4 concentrations. Particles may not experience rapid growth for long, but they can grow sufficiently fast to escape the valley of death and continue to grow via other condensable gases. In ambient conditions, transient deviations from equilibrium are expected to occur, especially in inhomogeneous urban settings with strong local sources of ammonia (e.g. from traffic or urban geometry). Since HNO3 is usually the limiting gas, inhomogeneities in HNO3 could have a larger impact on particle size distributions, however since NH3 is directly emitted by a multitude of sources, it is more likely to be variable and therefore will likely have a larger impact in typical urban environments. Wang et al. (2020)18 show the strong temperature dependence of ammonium nitrate formation, therefore we also expect temperature changes characteristic of vertical convection to drive the vapour concentrations of NH3 and HNO3 out of equilibrium. Future analysis should investigate the effect of urban and vertical mixing on the rapid growth of nucleating particles by NH3 and HNO3 condensation.
While Wang et al. (2020)18 presented the first evidence of rapid growth by ammonium nitrate condensation, we have additionally provided the first experimental data and supporting modelling calculations demonstrating efficient scavenging of nucleating molecular clusters by larger sized particles under haze conditions. We also present experimental results of high survival of freshly nucleated particles even in the presence of a high condensation sink, confirming the hypothesis from Wang et al. (2020)18 that rapid growth caused by NH4NO3 formation can aid in particle survival through the valley of death. These results strongly support the hypothesis that the unexplained survival of particles is due to a missing growth mechanism, and that under typical ambient conditions of a megacity at 5 °C, rapid ammonium nitrate condensation could be that missing mechanism, increasing survival of nucleated particles, and thus sustaining particle number and poor visibility during haze.
Author contributions
Conceptualization: R. M., M. X., M. W., J. Dommen, J. K., N. M. D., H. L., U. B. and I. E. H. Resources, prepared the CLOUD facility or measuring instruments: R. M., B. R., M. W., W. K., X.-C. H., D. S., J. P., G. M., D. S. W., W. S., A. B., C. P. L., R. B., L. C., B. C., J. C., L. D., J. Duplissy, H. F., L. G. C., M. G., A. H., M. H., V. H., D. K., A. K., M. K., K. L., V. M., H. E. M., B. M., O. M., T. P., M. P., J. S., M. S., Y. S., A. T., R. V., A. W., Y. Wang, S. K. W., P. M. W., Y. Wu, M. Z.-W., R. C. F., J. K., H. L., and I. E. H. Investigation: R. M., M. X., B. R., M. W., W. K., X.-C. H., D. S., J. P., G. M., D. S. W., W. S., A. B., C. P. L., A. A., R. B., D. B., B. B., L. C., L. D., J. Duplissy, H. F., L. G. C., M. G., M. H., V. H., D. K., M. L., V. M., B. M., J. S., M. S., A. T., A. W., S. K. W., Y. Wu, M. Z.-W., J. K., H. L., and I. E. H. Formal analysis: R. M., B. R., M. W., W. K., X. H., D. S., J. P., G. M., D. S. W., W. S., C. P. L., L. C., L. D., M. S., S. K. W., P. M. W., R. C. F., N. M. D., H. L., and I. E. H. Scientific discussion: R. M., M. X., B. R., M. W., W. K., X.-C. H., D. S., W. S., C. P. L., D. B., J. C., L. D., H. F., K. L., J. Dommen, R. C. F., J. K., N. M. D., H. L., U. B., and I. E. H. Writing: R. M., B. R., M. W., W. K., X.-C. H., D. S., J. P., D. S. W., J. Dommen, J. K., N. M. D., H. L., U. B., and I. E. H.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the European Organization for Nuclear Research (CERN) for supporting CLOUD with technical and financial resources and for providing a particle beam from the CERN Proton Synchrotron. This research has received funding from the European Community (EC) Seventh Framework Programme and the European Union (EU) H2020 programme (Marie Skłodowska Curie ITN CLOUD-TRAIN grant number 316662 and CLOUD-MOTION grant number 764991); European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 895875 (“NPF-PANDA”); the Swiss National Science Foundation (no. 200021_169090, 200020_172602, 20FI20_172622); the US National Science Foundation (NSF; grant numbers AGS1602086, AGS1801329 and AGS-1801280); NASA graduate fellowship (NASA-NNX16AP36H); Project CLOUD-16 (project number 01LK1601C) funded by the German Bundesministerium für Bildung und Forschung (BMBF); ERC Advanced ‘ATM-GP’ grant no. 227463; The Portuguese Foundation for Science and Technology (project no. CERN/FIS-COM/0028/2019); ERC Consolidator grant NANODYNAMITE, 616075; the Austrian Science Fund (FWF; project no. P27295-N20); the Presidium of the Russian Academy of Sciences, the Program “Physics of Fundamental Interactions” 2017–2020; Ministry of Science and High education of the Russian Federation; VM acknowledges the Grant No. PCF IRN BR10965191.References
- E. M. Dunne, et al., Global atmospheric particle formation from CERN CLOUD measurements, Science, 2016, 354, 1119–1124 CrossRef CAS PubMed.
- J. Merikanto, D. V. Spracklen, G. W. Mann, S. J. Pickering and K. S. Carslaw, Impact of nucleation on global CCN, Atmos. Chem. Phys., 2009, 9, 8601–8616 CrossRef CAS.
- Intergovernmental Panel on Climate Change (IPCC), Climate Change 2013: the Physical Science Basis, 2013 Search PubMed.
- U. Lohmann and J. Feichter, Global indirect aerosol effects: a review, Atmos. Chem. Phys., 2005, 5, 715–737 CrossRef CAS.
- G. Chen, W.-C. Wang and J.-P. Chen, Circulation responses to regional aerosol climate forcing in summer over East Asia, Clim. Dyn., 2018, 51, 3973–3984 CrossRef.
- S. Guo, et al., Elucidating severe urban haze formation in China, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17373–17378 CrossRef CAS PubMed.
- J. S. Apte, M. Brauer, A. J. Cohen, M. Ezzati and C. A. Pope, Ambient PM2.5 Reduces Global and Regional Life Expectancy, Environ. Sci. Technol. Lett., 2018, 5, 546–551 CrossRef CAS.
- WHO, WHO Methods and Data Sources for Global Burden of Disease Estimates 2000–2019, 2014 Search PubMed.
- WHO, WHO Methods and Data Sources for Country-Level Causes of Death 2000–2019, 2014 Search PubMed.
- V.-M. Kerminen and M. Kulmala, Analytical formulae connecting the “real” and the “apparent” nucleation rate and the nuclei number concentration for atmospheric nucleation events, J. Aerosol Sci., 2002, 33, 609–622 CrossRef CAS.
- M. Xiao, et al., The driving factors of new particle formation and growth in the polluted boundary layer, Atmos. Chem. Phys., 2021, 21, 14275–14291 CrossRef CAS.
- D. Bousiotis, M. Dall'Osto, D. C. S. Beddows, F. D. Pope and R. M. Harrison, Analysis of new particle formation (NPF) events at nearby rural, urban background and urban roadside sites, Atmos. Chem. Phys., 2019, 19, 5679–5694 CrossRef CAS.
- Z. B. Wang, et al., Characteristics of regional new particle formation in urban and regional background environments in the North China Plain, Atmos. Chem. Phys., 2013, 13, 12495–12506 CrossRef.
- Z. Wang, et al., New particle formation in China: current knowledge and further directions, Sci. Total Environ., 2017, 577, 258–266 CrossRef CAS PubMed.
- L. Yao, Atmospheric new particle formation from sulfuric acid and amines in a Chinese megacity, Science, 2018, 361, 278–281 CrossRef CAS PubMed.
- S. Xiao, et al., Strong atmospheric new particle formation in winter in urban Shanghai, China, Atmos. Chem. Phys., 2015, 15, 1769–1781 CrossRef.
- M. Kulmala, V.-M. Kerminen, T. Petäjä, A. J. Ding and L. Wang, Atmospheric gas-to-particle conversion: why NPF events are observed in megacities?, Faraday Discuss., 2017, 200, 271–288 RSC.
- M. Wang, et al., Rapid growth of new atmospheric particles by nitric acid and ammonia condensation, Nature, 2020, 581, 184–189 CrossRef CAS PubMed.
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics, John Wiley & Sons, 2nd edn, 2006 Search PubMed.
- D. Stolzenburg, et al., Enhanced growth rate of atmospheric particles from sulfuric acid, Atmos. Chem. Phys., 2020, 20, 7359–7372 CrossRef CAS.
- M. Mozurkewich, The dissociation constant of ammonium nitrate and its dependence on temperature, relative humidity and particle size, Atmos. Environ., Part A, 1993, 27, 261–270 CrossRef.
- L. Pichelstorfer, et al., Resolving nanoparticle growth mechanisms from size- and time-dependent growth rate analysis, Atmos. Chem. Phys., 2018, 18, 1307–1323 CrossRef CAS.
- M. Ozon, D. Stolzenburg, L. Dada, A. Seppänen and K. E. J. Lehtinen, Aerosol formation and growth rates from chamber experiments using Kalman smoothing, Atmos. Chem. Phys., 2021, 21, 12595–12611 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2ea00007e |
| This journal is © The Royal Society of Chemistry 2022 |